立体几何高考题_模拟试题带答案解析

合集下载

2023届高考数学总复习《立体几何》附答案解析

（2）若点 N 为 BC 的中点，求四面体 A'MNB 的体积．
【解答】证明：（1）连接 BD，设 BD∩EC＝F，连接 MF，
由题意可得四边形 BCDE 为正方形，则 F 为 BD 的中点，
∴MF 为△A′BD 的中位线，可得 MF∥A′B，
又 A′B⊄平面 EMC，MF⊂平面 EMC，
∴A'B∥平面 EMC；
2023 年高考：立体几何复习题及答案
1．如图，已知直角梯形 ABCD，BC∥AD，BC＝CD＝2，AD＝4，∠BCD＝90°，点 E 为 AD 的中点，现将三角形 ABE 沿 BE 折叠，得到四棱锥 A'﹣BCDE，其中∠A'ED＝120°，点 M 为 A'D 的中点．
（1）求证：A'B∥平面 EMC；
第2页共3页
∵BE⊂平面 BEF，∴平面 BEF⊥平面 AMD，结合题意分析知，点 F 在线段 AD 上，连接 MF，过 A 作 AH⊥MF，交 MF 的延长线于点 H，
则结合已知条件得
，解得 AH ，
设 Dt ，
第3页共3页
【解答】解：（1）证明：由题意知 PC2+AC2＝PA2，∴PC⊥AC，同理，PC⊥BC，又 AC∩BC＝C，∴PC⊥平面 ABC， ∵D，E 分别是 AC，PA 的中点，∴DE∥PC， ∴DE⊥平面 ABC，又 DE⊂平面 BDE，∴平面 BDE⊥平面 ABC．（2）在△BDE 中，DE⊥BD，BD＝2 ，DE＝2，∴BE＝4，如图，过 A 作 AM⊥BE 于 M，连接 MD，在△ABE 中，AB＝BE＝4，AE＝2 ，解得 AM ，ME＝1， ∵DM⊂平面 BDE，∴AC⊥DM，在 Rt△ADM 中，AM ，AD＝2，∴DM ， ∴DM2+EM2＝DE2，∴MD⊥BE， ∵AM∩MD＝M，∴BE⊥平面 AMD，

专题04立体几何-2022年高考真题和模拟题数学分类汇编(解析版)

专题04 立体几何1．【2022年全国甲卷】如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为（）A．8B．12C．16D．20【答案】B【解析】【分析】由三视图还原几何体，再由棱柱的体积公式即可得解.【详解】由三视图还原几何体，如图，×2×2=12.则该直四棱柱的体积V=2+42故选：B.2．【2022年全国甲卷】在长方体ABCD―A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1 B所成的角均为30°，则（）A．AB=2AD B．AB与平面AB1C1D所成的角为30°C．AC=CB1D．B1D与平面BB1C1C所成的角为45°【解析】【分析】根据线面角的定义以及长方体的结构特征即可求出．【详解】如图所示：不妨设AB =a ,AD =b ,AA 1=c ，依题以及长方体的结构特征可知，B 1D 与平面ABCD 所成角为∠B 1DB ，B 1D 与平面AA 1B 1B 所成角为∠DB 1A ，所以sin30∘=c B 1D =bB 1D ，即b =c ，B 1D =2c =a 2+b 2+c 2，解得a =2c ．对于A ，AB =a ，AD =b ，AB =2AD ，A 错误；对于B ，过B 作BE ⊥AB 1于E ，易知BE ⊥平面AB 1C 1D ，所以AB 与平面AB 1C 1D 所成角为∠BAE ，因为tan ∠BAE =ca =22，所以∠BAE ≠30∘，B 错误；对于C ，AC =a 2+b 2=3c ，CB 1=b 2+c 2=2c ，AC ≠CB 1，C 错误；对于D ，B 1D 与平面BB 1C 1C 所成角为∠DB 1C ，sin ∠DB 1C =CD B1D=a2c =22，而0<∠DB 1C <90∘，所以∠DB 1C =45∘．D 正确．故选：D ．3．【2022年全国甲卷】甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S 甲和S 乙，体积分别为V 甲和V 乙．若S 甲S 乙=2，则V甲V 乙=（）A ．5B ．22C ．10D ．5104【答案】C 【解析】设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，根据圆锥的侧面积公式可得r 1=2r 2，再结合圆心角之和可将r 1,r 2分别用l 表示，再利用勾股定理分别求出两圆锥的高，再根据圆锥的体积公式即可得解.【详解】解：设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，则S 甲S 乙=πr 1l πr 2l =r 1r 2=2，所以r 1=2r 2，又2πr 1l+2πr 2l=2π，则r 1+r 2l=1，所以r 1=23l ,r 2=13l ，所以甲圆锥的高ℎ1=l 2―49l 2=53l ，乙圆锥的高ℎ2=l 2―19l 2=223l ，所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=49l 2×53l 19l 2×223l =10.故选：C.4．【2022年全国乙卷】在正方体ABCD ―A 1B 1C 1D 1中，E ，F 分别为AB ,BC 的中点，则（）A ．平面B 1EF ⊥平面BDD 1B ．平面B 1EF ⊥平面A 1BDC ．平面B 1EF //平面A 1ACD ．平面B 1EF //平面A 1C 1D【答案】A 【解析】【分析】证明EF ⊥平面BDD 1，即可判断A ；如图，以点D 为原点，建立空间直角坐标系，设AB =2，分别求出平面B 1EF ，A 1BD ，A 1C 1D 的法向量，根据法向量的位置关系，即可判断BCD .【详解】解：在正方体ABCD ―A 1B 1C 1D 1中，AC ⊥BD 且DD 1⊥平面ABCD ，又EF⊂平面ABCD，所以EF⊥DD1，因为E,F分别为AB,BC的中点，所以EF∥AC，所以EF⊥BD，又BD∩DD1=D，所以EF⊥平面BDD1，又EF⊂平面B1EF，所以平面B1EF⊥平面BDD1，故A正确；如图，以点D为原点，建立空间直角坐标系，设AB=2，则B1(2,2,2),E(2,1,0),F(1,2,0),B(2,2,0),A1(2,0,2),A(2,0,0),C(0,2,0)，C1(0,2,2)，=(0,1,2)，DB=(2,2,0),DA1=(2,0,2)，则EF=(―1,1,0),EB1AA1=(0,0,2),AC=(―2,2,0),A1C1=(―2,2,0),设平面B1EF的法向量为m=(x1,y1,z1)，⋅EF=―x1+y1=0，可取m=(2,2,―1)，⋅EB1=y1+2z1=0同理可得平面A1BD的法向量为n1=(1,―1,―1)，平面A1AC的法向量为n2=(1,1,0)，平面A1C1D的法向量为n3=(1,1,―1)，则m⋅n1=2―2+1=1≠0，所以平面B1EF与平面A1BD不垂直，故B错误；因为m与n2不平行，所以平面B1EF与平面A1AC不平行，故C错误；因为m与n3不平行，所以平面B1EF与平面A1C1D不平行，故D错误，故选：A.5．【2022年全国乙卷】已知球O 的半径为1，四棱锥的顶点为O ，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A ．13B ．12C ．33D ．22【答案】C 【解析】【分析】先证明当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时，底面ABCD 面积最大值为2r 2，进而得到四棱锥体积表达式，再利用均值定理去求四棱锥体积的最大值，从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD ，四边形ABCD 所在小圆半径为r ，设四边形ABCD 对角线夹角为α，则S ABCD =12⋅AC ⋅BD ⋅sin α≤12⋅AC ⋅BD ≤12⋅2r ⋅2r =2r 2（当且仅当四边形ABCD 为正方形时等号成立）即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时，底面ABCD 面积最大值为2r 2又r 2+ℎ2=1则V O―ABCD =13⋅2r 2⋅ℎ=23r 2⋅r 2⋅2ℎ2≤4327当且仅当r 2=2ℎ2即ℎ=33时等号成立，故选：C6．【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m 时，相应水面的面积为140．0km 2；水位为海拔157．5m 时，相应水面的面积为180．0km 2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m 上升到157．5m 时，增加的水量约为（7≈2.65）（）A ．1.0×109m 3B ．1.2×109m 3C ．1.4×109m 3D ．1.6×109m 3【答案】C 【解析】【分析】根据题意只要求出棱台的高，即可利用棱台的体积公式求出．【详解】依题意可知棱台的高为MN =157.5―148.5=9(m)，所以增加的水量即为棱台的体积V ．棱台上底面积S =140.0km 2=140×106m 2，下底面积S ′=180.0km 2=180×106m 2，∴V =13ℎS +S ′+=13×9×(140×106+180×106+140×180×1012)=3×(320+607)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m 3)．故选：C ．7．【2022年新高考1卷】已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且3≤l ≤33，则该正四棱锥体积的取值范围是（）A ．18,BCD ．[18,27]【答案】C 【解析】【分析】设正四棱锥的高为ℎ，由球的截面性质列方程求出正四棱锥的底面边长与高的关系，由此确定正四棱锥体积的取值范围.【详解】∵ 球的体积为36π，所以球的半径R =3,设正四棱锥的底面边长为2a ，高为ℎ，则l 2=2a 2+ℎ2，32=2a 2+(3―ℎ)2,所以6ℎ=l 2，2a 2=l 2―ℎ2所以正四棱锥的体积V =13Sℎ=13×4a 2×ℎ=23×(l 2―l436)×l 264―所以V ′=l 3=19l 当3≤l ≤26时，V ′>0，当26<l ≤33时，V ′<0，所以当l =26时，正四棱锥的体积V 取最大值，最大值为643，又l =3时，V =274，l =33时，V =814,所以正四棱锥的体积V 的最小值为274，故选：C.8．【2022年新高考2卷】已知正三棱台的高为1，上、下底面边长分别为33和43，其顶点都在同一球面上，则该球的表面积为（）A ．100πB ．128πC ．144πD ．192π【答案】A 【解析】【分析】根据题意可求出正三棱台上下底面所在圆面的半径r 1,r 2，再根据球心距，圆面半径，以及球的半径之间的关系，即可解出球的半径，从而得出球的表面积．【详解】设正三棱台上下底面所在圆面的半径r 1,r 2，所以2r 1=33sin60∘,2r 2=43sin60∘，即r 1=3,r 2=4，设球心到上下底面的距离分别为d 1,d 2，球的半径为R ，所以d 1=R 2―9，d 2=R 2―16，故|d 1―d 2|=1或d 1+d 2=1，即|R 2―9―R 2―16|=1或R 2―9+R 2―16=1，解得R 2=25符合题意，所以球的表面积为S =4πR 2=100π．故选：A．9．【2022年北京】已知正三棱锥P―ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={Q∈S|PQ≤5}，则T表示的区域的面积为（）A．3π4B．πC．2πD．3π【答案】B【解析】【分析】求出以P为球心，5为半径的球与底面ABC的截面圆的半径后可求区域的面积.【详解】设顶点P在底面上的投影为O，连接BO，则O为三角形ABC的中心，且BO=23×6×32=23，故PO=36―12=26.因为PQ=5，故OQ=1，故S的轨迹为以O为圆心，1为半径的圆，而三角形ABC内切圆的圆心为O，半径为2×34×363×6=3>1，故S的轨迹圆在三角形ABC内部，故其面积为π故选：B10．【2022年浙江】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A ．22πB ．8πC ．223πD ．163π【答案】C 【解析】【分析】根据三视图还原几何体可知，原几何体是一个半球，一个圆柱，一个圆台组合成的几何体，即可根据球，圆柱，圆台的体积公式求出．【详解】由三视图可知，该几何体是一个半球，一个圆柱，一个圆台组合成的几何体，球的半径，圆柱的底面半径，圆台的上底面半径都为1 cm ，圆台的下底面半径为2 cm ，所以该几何体的体积V =12×43π×13+π×12×2+13×2×(π×22+π×12+π×22×π×12)=22π3cm 3．故选：C ．11．【2022年浙江】如图，已知正三棱柱ABC ―A 1B 1C 1,AC =AA 1，E ，F 分别是棱BC ,A 1C 1上的点．记EF 与AA 1所成的角为α，EF 与平面ABC 所成的角为β，二面角F ―BC ―A 的平面角为γ，则（）A ．α≤β≤γB ．β≤α≤γC ．β≤γ≤αD ．α≤γ≤β【答案】A 【解析】【分析】先用几何法表示出α，β，γ，再根据边长关系即可比较大小．【详解】如图所示，过点F 作FP ⊥AC 于P ，过P 作PM ⊥BC 于M ，连接PE ，则α=∠EFP ，β=∠FEP ，γ=FMP ，tan α=PEFP =PEAB ≤1，tan β=FPPE =ABPE ≥1，tan γ=FPPM ≥FPPE =tan β，所以α≤β≤γ，故选：A ．12．【2022年新高考1卷】（多选）已知正方体ABCD ―A 1B 1C 1D 1，则（）A ．直线BC 1与DA 1所成的角为90°B ．直线BC 1与CA 1所成的角为90°C ．直线BC 1与平面BB 1D 1D 所成的角为45°D ．直线BC 1与平面ABCD 所成的角为45°【答案】ABD 【解析】【分析】数形结合，依次对所给选项进行判断即可.【详解】如图，连接B 1C 、BC 1，因为DA 1//B 1C ，所以直线BC 1与B 1C 所成的角即为直线BC 1与DA 1所成的角，因为四边形BB 1C 1C 为正方形，则B 1C ⊥ BC 1，故直线BC 1与DA 1所成的角为90°，A 正确；连接A 1C ，因为A 1B 1⊥平面BB 1C 1C ，BC 1⊂平面BB 1C 1C ，则A 1B 1⊥BC 1，因为B 1C ⊥ BC 1，A 1B 1∩B 1C =B 1，所以BC 1⊥平面A 1B 1C ，又A 1C ⊂平面A 1B 1C ，所以BC 1⊥CA 1，故B 正确；连接A 1C 1，设A 1C 1∩B 1D 1=O ，连接BO ，因为BB 1⊥平面A 1B 1C 1D 1，C 1O ⊂平面A 1B 1C 1D 1，则C 1O ⊥B 1B ，因为C 1O ⊥B 1D 1，B 1D 1∩B 1B =B 1，所以C 1O ⊥平面BB 1D 1D ，所以∠C 1BO 为直线BC 1与平面BB 1D 1D 所成的角，设正方体棱长为1，则C 1O =22，BC 1=2，sin ∠C 1BO =C 1O BC 1=12，所以，直线BC 1与平面BB 1D 1D 所成的角为30∘，故C 错误；因为C 1C ⊥平面ABCD ，所以∠C 1BC 为直线BC 1与平面ABCD 所成的角，易得∠C 1BC =45∘，故D 正确.故选：ABD13．【2022年新高考2卷】（多选）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，FB ∥ED ,AB =ED =2FB ，记三棱锥E ―ACD ，F ―ABC ，F ―ACE 的体积分别为V 1,V 2,V 3，则（）A．V3=2V2B．V3=V1C．V3=V1+V2D．2V3=3V1【答案】CD【解析】【分析】直接由体积公式计算V1,V2，连接BD交AC于点M，连接EM,FM，由V3=V A―EFM+V C―EFM计算出V3，依次判断选项即可.【详解】设AB=ED=2FB=2a，因为ED⊥平面ABCD，FB∥ED，则V1=13⋅ED⋅S△ACD=13⋅2a⋅12⋅(2a)2=43a3，V2=13⋅FB⋅S△ABC=13⋅a⋅12⋅(2a)2=23a3，连接BD交AC于点M，连接EM,FM，易得BD⊥AC，又ED⊥平面ABCD，AC⊂平面ABCD，则ED⊥AC，又ED∩BD=D，ED,BD⊂平面BDEF，则AC⊥平面BDEF，又BM=DM=12BD=2a，过F作FG⊥DE于G，易得四边形BDGF为矩形，则FG=BD=22 a,EG=a，则EM =(2a )2+(2a )2=6a ,FM =a 2+(2a )2=3a ，EF =a 2+(22a )2=3a ，EM 2+FM 2=EF 2，则EM ⊥FM ，S △EFM =12EM ⋅FM =322a 2，AC =22a ，则V 3=V A―EFM +V C―EFM =13AC ⋅S △EFM =2a 3，则2V 3=3V 1，V 3=3V 2，V 3=V 1+V 2，故A 、B 错误；C 、D 正确.故选：CD.14．【2022年全国甲卷】小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面ABCD 是边长为8（单位：cm ）的正方形，△EAB ,△FBC ,△GCD ,△HDA 均为正三角形，且它们所在的平面都与平面ABCD 垂直．(1)证明：EF //平面ABCD ；(2)求该包装盒的容积（不计包装盒材料的厚度）．【答案】(1)证明见解析；(2)64033．【解析】【分析】（1）分别取AB ,BC 的中点M ,N ，连接MN ，由平面知识可知EM ⊥AB ,FN ⊥BC ，EM =FN ，依题从而可证EM ⊥平面ABCD ，FN ⊥平面ABCD ，根据线面垂直的性质定理可知EM //FN ，即可知四边形EMNF 为平行四边形，于是EF //MN ，最后根据线面平行的判定定理即可证出；（2）再分别取AD ,DC 中点K ,L ，由（1）知，该几何体的体积等于长方体KMNL ―EFGH 的体积加上四棱锥B ―MNFE 体积的4倍，即可解出．(1)如图所示：，分别取AB,BC的中点M,N，连接MN，因为△EAB,△FBC为全等的正三角形，所以EM⊥AB, FN⊥BC，EM=FN，又平面EAB⊥平面ABCD，平面EAB∩平面ABCD=AB，EM⊂平面EAB，所以EM⊥平面ABCD，同理可得FN⊥平面ABCD，根据线面垂直的性质定理可知EM //FN，而EM=FN，所以四边形EMNF为平行四边形，所以EF//MN，又EF⊄平面ABCD，MN ⊂平面ABCD，所以EF//平面ABCD．(2)如图所示：，分别取AD,DC中点K,L，由（1）知，EF//MN且EF=MN，同理有，HE//KM,HE=KM，HG //KL,HG=KL，GF//LN,GF=LN，由平面知识可知，BD⊥MN，MN⊥MK，KM=MN= NL=LK，所以该几何体的体积等于长方体KMNL―EFGH的体积加上四棱锥B―MNFE体积的4倍．因为MN=NL=LK=KM=42，EM=8sin60∘=43，点B到平面MNFE的距离即为点B×42×43到直线MN的距离d，d=22，所以该几何体的体积V=(42)2×43+4×13×22=1283+25633=64033．15．【2022年全国甲卷】在四棱锥P―ABCD中，PD⊥底面ABCD,CD∥AB,AD=DC=CB=1,AB=2,DP=3．(1)证明：BD⊥PA；(2)求PD与平面PAB所成的角的正弦值．【答案】(1)证明见解析；(2)55.【解析】【分析】（1）作DE⊥AB于E，CF⊥AB于F，利用勾股定理证明AD⊥BD，根据线面垂直的性质可得PD⊥BD，从而可得BD⊥平面PAD，再根据线面垂直的性质即可得证；（2）以点D为原点建立空间直角坐标系，利用向量法即可得出答案.(1)证明：在四边形ABCD中，作DE⊥AB于E，CF⊥AB于F，因为CD//AB,AD=CD=CB=1,AB=2，所以四边形ABCD为等腰梯形，所以AE=BF=12，故DE=32，BD=DE2+BE2=3，所以AD2+BD2=AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD=D，所以BD⊥平面PAD，又因PA⊂平面PAD，所以BD⊥PA；(2)解：如图，以点D为原点建立空间直角坐标系，BD=3，则A(1,0,0),B(0,3,0),P(0,0,3)，则AP=(―1,0,3),BP=(0,―3,3),DP=(0,0,3)，设平面PAB的法向量n=(x,y,z)，则有{→n⋅→AP=―x+3z=0→n⋅→BP=―3y+3z=0，可取n=(3,1,1)，则cos〈n,DP〉n DP =55，所以PD与平面PAB所成角的正弦值为55.16．【2022年全国乙卷】如图，四面体ABCD中，AD⊥CD,AD=CD,∠ADB=∠BDC，E为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设AB =BD =2,∠ACB =60°，点F 在BD 上，当△AFC 的面积最小时，求三棱锥F ―ABC 的体积．【答案】(1)证明详见解析(2)34【解析】【分析】（1）通过证明AC ⊥平面BED 来证得平面BED ⊥平面ACD .（2）首先判断出三角形AFC 的面积最小时F 点的位置，然后求得F 到平面ABC 的距离，从而求得三棱锥F ―ABC 的体积.(1)由于AD =CD ，E 是AC 的中点，所以AC ⊥DE .由于AD =CD BD =BD ∠ADB =∠CDB，所以△ADB≅△CDB ，所以AB =CB ，故AC ⊥BD ，由于DE ∩BD =D ，DE ,BD ⊂平面BED ，所以AC ⊥平面BED ，由于AC ⊂平面ACD ，所以平面BED ⊥平面ACD .(2)依题意AB =BD =BC =2，∠ACB =60°，三角形ABC 是等边三角形，所以AC =2,AE =CE =1,BE =3，由于AD =CD ,AD ⊥CD ，所以三角形ACD 是等腰直角三角形，所以DE =1.DE 2+BE 2=BD 2，所以DE ⊥BE ，由于AC ∩BE =E ，AC ,BE ⊂平面ABC ，所以DE ⊥平面ABC .由于△ADB≅△CDB ，所以∠FBA =∠FBC ，由于BF =BF ∠FBA =∠FBC AB =CB，所以△FBA≅△FBC ，所以AF =CF ，所以EF ⊥AC ，由于S △AFC =12⋅AC ⋅EF ，所以当EF 最短时，三角形AFC 的面积最小值.过E 作EF ⊥BD ，垂足为F ，在Rt △BED 中，12⋅BE ⋅DE =12⋅BD ⋅EF ，解得EF =32，所以DF=12,BF =2―DF =32，所以BF BD =34.过F 作FH ⊥BE ，垂足为H ，则FH //DE ，所以FH ⊥平面ABC ，且FH DE =BF BD =34，所以FH =34,所以V F―ABC =13⋅S △ABC ⋅FH =13×12×2×3×34=34.17．【2022年全国乙卷】如图，四面体ABCD 中，AD ⊥CD ,AD =CD,∠ADB =∠BDC ，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设AB =BD =2,∠ACB =60°，点F在BD 上，当△AFC 的面积最小时，求CF 与平面ABD 所成的角的正弦值．【答案】(1)证明过程见解析(2)CF与平面ABD所成的角的正弦值为437【解析】【分析】（1）根据已知关系证明△ABD≌△CBD，得到AB=CB，结合等腰三角形三线合一得到垂直关系，结合面面垂直的判定定理即可证明；（2）根据勾股定理逆用得到BE⊥DE，从而建立空间直角坐标系，结合线面角的运算法则进行计算即可.(1)因为AD=CD，E为AC的中点，所以AC⊥DE；在△ABD和△CBD中，因为AD=CD,∠ADB=∠CDB,DB=DB，所以△ABD≌△CBD，所以AB=CB，又因为E为AC的中点，所以AC⊥BE；又因为DE,BE⊂平面BED，DE∩BE=E，所以AC⊥平面BED，因为AC⊂平面ACD，所以平面BED⊥平面ACD.(2)连接EF，由（1）知，AC⊥平面BED，因为EF⊂平面BED，AC⋅EF，所以AC⊥EF，所以S△AFC=12当EF⊥BD时，EF最小，即△AFC的面积最小.因为△ABD≌△CBD，所以CB=AB=2，又因为∠ACB=60°，所以△ABC是等边三角形，因为E为AC的中点，所以AE=EC=1，BE=3，AC=1,因为AD⊥CD，所以DE=12在△DEB中，DE2+BE2=BD2，所以BE⊥DE.以E为坐标原点建立如图所示的空间直角坐标系E―xyz，则A(1,0,0),B(0,3,0),D(0,0,1)，所以AD=(―1,0,1),AB=(―1,3,0)，设平面ABD的一个法向量为n=(x,y,z)，―x+z=0，取y=3，则n=(3,3,3)，―x+3y=0又因为C (―1,0,0),F 0,34，所以CF =1,34所以cos ⟨n ,CF⟩n ⋅CF |n ||CF |621×74=437，设CF 与平面ABD 所成的角的正弦值为θ0≤θ≤所以sin θ=|cos ⟨n ,CF⟩|=437，所以CF 与平面ABD 所成的角的正弦值为437.18．【2022年新高考1卷】如图，直三棱柱ABC ―A 1B 1C 1的体积为4，△A 1BC 的面积为22．(1)求A 到平面A 1BC 的距离；(2)设D 为A 1C 的中点，AA 1=AB ，平面A 1BC ⊥平面ABB 1A 1，求二面角A ―BD ―C 的正弦值．【答案】(1)2(2)32【解析】【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC⊥平面ABB1A1，建立空间直角坐标系，利用空间向量法即可得解.(1)在直三棱柱ABC―A1B1C1中，设点A到平面A1BC的距离为h，则V A―A1BC=13S△A1BC⋅ℎ=223ℎ=V A1―ABC=13S△ABC⋅A1A=13V ABC―A1B1C1=43，解得ℎ=2，所以点A到平面A1BC的距离为2；(2)取A1B的中点E,连接AE,如图，因为AA1=AB，所以AE⊥A1B,又平面A1BC⊥平面ABB1A1，平面A1BC∩平面ABB1A1=A1B，且AE⊂平面ABB1A1，所以AE⊥平面A1BC，在直三棱柱ABC―A1B1C1中，BB1⊥平面ABC，由BC⊂平面A1BC，BC⊂平面ABC可得AE⊥BC，BB1⊥BC，又AE,BB1⊂平面ABB1A1且相交，所以BC⊥平面ABB1A1，所以BC,BA,BB1两两垂直，以B为原点，建立空间直角坐标系，如图，由（1）得AE=2，所以AA1=AB=2，A1B=22，所以BC=2，则A(0,2,0),A1(0,2,2),B(0,0,0),C(2,0,0),所以A1C的中点D(1,1,1)，则BD=(1,1,1)，BA=(0,2,0),BC=(2,0,0),设平面ABD的一个法向量m=(x,y,z)，则{m⋅BD=x+y+z=0 m⋅BA=2y=0，可取m=(1,0,―1)，设平面BDC的一个法向量n=(a,b,c)，则{m⋅BD=a+b+c=0 m⋅BC=2a=0，可取n=(0,1,―1)，则cos〈m,n〉=m⋅n|m|⋅|n|12×2=12，所以二面角A―BD―C的正弦值为1―(12)2=32.19．【2022年新高考2卷】如图，PO是三棱锥P―ABC的高，PA=PB，AB⊥AC，E是PB 的中点．(1)证明：OE//平面PAC；(2)若∠ABO=∠CBO=30°，PO=3，PA=5，求二面角C―AE―B的正弦值．【答案】(1)证明见解析(2)1113【解析】【分析】（1）连接BO并延长交AC于点D，连接OA、PD，根据三角形全等得到OA=OB，再根据直角三角形的性质得到AO=DO，即可得到O为BD的中点从而得到OE//PD，即可得证；（2）过点A作Az//OP，如图建立平面直角坐标系，利用空间向量法求出二面角的余弦值，再根据同角三角函数的基本关系计算可得；(1)证明：连接BO并延长交AC于点D，连接OA、PD，因为PO是三棱锥P―ABC的高，所以PO⊥平面ABC，AO,BO⊂平面ABC，所以PO⊥AO、PO⊥BO，又PA=PB，所以△POA≅△POB，即OA=OB，所以∠OAB=∠OBA，又AB ⊥AC ，即∠BAC =90°，所以∠OAB +∠OAD =90°，∠OBA +∠ODA =90°，所以∠ODA =∠OAD所以AO =DO ，即AO =DO =OB ，所以O 为BD 的中点，又E 为PB 的中点，所以OE //PD ，又OE⊄平面PAC ，PD ⊂平面PAC ，所以OE //平面PAC(2)解：过点A 作Az //OP ，如图建立平面直角坐标系，因为PO =3，AP =5，所以OA =AP 2―PO 2=4，又∠OBA =∠OBC =30°，所以BD =2OA =8，则AD =4，AB =43，所以AC =12，所以O (23,2,0)，B (43,0,0)，P (23,2,3)，C (0,12,0)，所以E 33,1,则AE =33,1,，AB =(43,0,0)，AC =(0,12,0)，设平面AEB 的法向量为n =(x,y,z )⋅AE =33x +y +32z =0n ⋅AB =43x =0，令z =2，则y =―3，x =0，所以n=(0,―3,2)；设平面AEC 的法向量为m =(a,b,c )⋅AE =33a +b +32c =0m ⋅AC =12b =0，令a =3，则c =―6，b =0，所以m =(3,0,―6)；所以cos ⟨n ,m⟩=n m|n ||m |―1213×39=―4313设二面角C ―AE ―B 为θ，由图可知二面角C ―AE ―B 为钝二面角，所以cos θ=―4313，所以sin θ=1―cos 2θ=1113故二面角C ―AE ―B 的正弦值为1113；20．【2022年北京】如图，在三棱柱ABC ―A 1B 1C 1中，侧面BCC 1B 1为正方形，平面BCC 1B 1⊥平面ABB 1A 1，AB =BC =2，M ，N 分别为A 1B 1，AC 的中点．(1)求证：MN ∥平面BCC 1B 1；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB 与平面BMN 所成角的正弦值．条件①：AB ⊥MN ；条件②：BM =MN ．注：如果选择条件①和条件②分别解答，按第一个解答计分．【答案】(1)见解析(2)见解析【解析】【分析】（1）取AB 的中点为K ，连接MK ,NK ，可证平面MKN //平面CBB 1C 1，从而可证MN //平面CB B 1C 1.（2）选①②均可证明BB 1⊥平面ABC ，从而可建立如图所示的空间直角坐标系，利用空间向量可求线面角的正弦值.(1)取AB的中点为K，连接MK,NK，由三棱柱ABC―A1B1C1可得四边形ABB1A1为平行四边形，而B1M=MA1,BK=KA，则MK//BB1，而MK⊄平面CBB1C1，BB1⊂平面CBB1C1，故MK//平面CBB1C1，而CN=NA,BK=KA，则NK//BC，同理可得NK//平面CBB1C1，而NK∩MK=K,NK,MK⊂平面MKN，故平面MKN//平面CBB1C1，而MN⊂平面MKN，故MN//平面CBB1C1，(2)因为侧面CBB1C1为正方形，故CB⊥BB1，而CB⊂平面CBB1C1，平面CBB1C1⊥平面ABB1A1，平面CBB1C1∩平面ABB1A1=BB1，故CB⊥平面ABB1A1，因为NK//BC，故NK⊥平面ABB1A1，因为AB⊂平面ABB1A1，故NK⊥AB，若选①，则AB⊥MN，而NK⊥AB，NK∩MN=N，故AB⊥平面MNK，而MK⊂平面MNK，故AB⊥MK，所以AB⊥BB1，而CB⊥BB1，CB∩AB=B，故BB1⊥平面ABC，故可建立如所示的空间直角坐标系，则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2)，故BA=(0,2,0),BN=(1,1,0),BM=(0,1,2)，设平面BNM的法向量为n=(x,y,z)，则{n⋅BN=0n⋅BM=0，从而{x+y=0y+2z=0，取z=―1，则n=(―2,2,―1)，设直线AB与平面BNM所成的角为θ，则sinθ=|cos〈n,AB〉|=42×3=23.若选②，因为NK//BC，故NK⊥平面ABB1A1，而KM⊂平面MKN，故NK⊥KM，而B1M=BK=1,NK=1，故B1M=NK，而B1B=MK=2，MB=MN，故△BB1M≅△MKN，所以∠BB1M=∠MKN=90°，故A1B1⊥BB1，而CB⊥BB1，CB∩AB=B，故BB1⊥平面ABC，故可建立如所示的空间直角坐标系，则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2)，故BA=(0,2,0),BN=(1,1,0),BM=(0,1,2)，设平面BNM的法向量为n=(x,y,z)，则{n⋅BN=0n⋅BM=0，从而{x+y=0y+2z=0，取z=―1，则n=(―2,2,―1)，设直线AB与平面BNM所成的角为θ，则sinθ=|cos〈n,AB〉|=42×3=23.21．【2022年浙江】如图，已知ABCD和CDEF都是直角梯形，AB//DC，DC//EF，AB=5，DC=3，EF=1，∠BAD=∠CDE=60°，二面角F―DC―B的平面角为60°．设M，N分别为AE,BC的中点．(1)证明：FN⊥AD；(2)求直线BM与平面ADE所成角的正弦值．【答案】(1)证明见解析；(2)5714．【解析】【分析】（1）过点E、D分别做直线DC、AB的垂线EG、DH并分别交于点G、H，由平面知识易得FC=BC ，再根据二面角的定义可知，∠BCF =60∘，由此可知，FN ⊥BC ，FN ⊥CD ，从而可证得FN ⊥平面ABCD ，即得FN ⊥AD ；（2）由（1）可知FN ⊥平面ABCD ，过点N 做AB 平行线NK ，所以可以以点N 为原点，NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N ―xyz ，求出平面ADE 的一个法向量，以及BM ，即可利用线面角的向量公式解出．(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H ．∵四边形ABCD 和EFCD 都是直角梯形，AB //DC ,CD //EF ,AB =5,DC =3,EF =1，∠BAD =∠CDE =60°，由平面几何知识易知，DG =AH =2,∠EFC =∠DCF =∠DCB =∠ABC =90°，则四边形EFCG 和四边形DCBH 是矩形，∴在Rt △EGD 和Rt △DHA ，EG =DH =23，∵DC ⊥CF ,DC ⊥CB ，且CF ∩CB =C ，∴DC ⊥平面BCF,∠BCF 是二面角F ―DC ―B 的平面角，则∠BCF =60∘，∴△BCF 是正三角形，由DC ⊂平面ABCD ，得平面ABCD ⊥平面BCF ，∵N 是BC 的中点，∴ FN ⊥BC ，又DC ⊥平面BCF ，FN ⊂平面BCF ，可得FN ⊥CD ，而BC ∩CD =C ，∴FN ⊥平面ABCD ，而AD ⊂平面ABCD ∴FN ⊥AD ．(2)因为FN ⊥平面ABCD ，过点N 做AB 平行线NK ，所以以点N 为原点， NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N ―xyz ，设A (5,3,0),B (0,3,0),D (3,―3,0),E (1,0,3)，则M 3,32∴BM =3,―32,AD =(―2,―23,0),DE =(―2,3,3)设平面ADE 的法向量为n =(x ,y ,z )由n ⋅AD =0n ⋅DE =0 ，得―2x ―23y =0―2x +3y +3z =0，取n =(3,―1,3)，设直线BM 与平面ADE 所成角为θ，∴sin θ=|cos 〈n ,BM〉|=|n ⋅BM ||n |⋅BM ||33+32+332|3+1+3⋅9+34+94=537⋅23=5714．1．（2022·全国·模拟预测）已知正方体中1111ABCD A B C D -，E ，G 分别为11A D ，11C D 的中点，则直线1A G ，CE 所成角的余弦值为（）A B C D 【答案】C 【解析】【分析】根据异面直线所成角的定义，取AB 的中点F ，则∠ECF （或其补角）为直线1A G 与CE 所成角，再解三角形即可得解．【详解】如图所示：，取AB 的中点F ，连接EF ，CF ，易知1A G CF ∥，则∠ECF （或其补角）为直线1A G 与CE 所成角．不妨设2AB =，则CF =，EF =3EC =，由余弦定理得cos ECF ∠==1A G 与CE 故选：C ．2．（2022·全国·模拟预测（理））如图，在三棱台111ABC A B C -中，1AA ⊥平面ABC ，90ABC ∠=︒，111111AA A B B C ===，2AB =，则AC 与平面11BCC B 所成的角为（）A ．30°B ．45︒C ．60︒D ．90︒【答案】A 【解析】【分析】将棱台补全为棱锥，利用等体积法求A 到面11BCC B 的距离，结合线面角的定义求AC 与平面11BCC B 所成角的大小.【详解】将棱台补全为如下棱锥D ABC -，由90ABC ∠=︒，111111AA A B B C ===，2AB =，易知：2DA BC ==，AC =，由1AA ⊥平面ABC ，,AB AC ⊥平面ABC ，则1AA AB ⊥，1AA AC ⊥，所以BD =，CD =222BC BD CD +=，所以122BCD S =⨯⨯=△，若A 到面11BCC B 的距离为h ，又D ABC A BCD V V --=，则111222323h ⨯⨯⨯⨯=⨯，可得h =，综上，AC 与平面11BCC B 所成角[0,2πθ∈，则1sin 2h AC θ==，即6πθ=.故选：A3．（2022·浙江湖州·模拟预测）如图，已知四边形ABCD ，BCD △是以BD 为斜边的等腰直角三角形，ABD △为等边三角形，2BD =，将ABD △沿对角线BD 翻折到PBD △在翻折的过程中，下列结论中不正确的是（）A ．BD PC ⊥B ．DP 与BC 可能垂直C ．直线DP 与平面BCD 所成角的最大值是45︒D ．四面体PBCD 【答案】C 【解析】【分析】对于A ，取BD 的中点M ，即可得到BD ⊥面PMC ，A 选项可判断对于B ，采用反证法，假设DP BC ⊥，则BC ⊥面PCD ，再根据题目所给的长度即可判断；对于C ，当面PBD ⊥面BCD 时，此时直线DP 与平面BCD 所成角有最大值，判断即可；对于D ，当面PBD ⊥面BCD 时，此时四面体PBCD 的体积有最大值，计算最大体积判断即可【详解】如图所示，取BD 的中点M ，连接,PM CMBCD △是以BD 为斜边的等腰直角三角形,BD CM ∴⊥ABD △为等边三角形,BD PM ∴⊥BD ∴⊥面PMC ,BD PC ∴⊥ ,故A 正确对于B ，假设DP BC ⊥，又BC CD ⊥BC ∴⊥面PCD ，BC PC ∴⊥，又2,PB BC ==1PC ⎤⎦，故DP 与BC 可能垂直，故B 正确当面PBD ⊥面BCD 时，此时PM ⊥面BCD ，PDB ∠即为直线DP 与平面BCD 所成角此时60PDB ︒∠=，故C 错误当面PBD ⊥面BCD 时，此时四面体PBCD 的体积最大，此时的体积为：111(332BCD V S PM ==⨯=，故D 正确故选：C4．（2022·河南安阳·模拟预测（理））已知球O 的体积为125π6，高为1的圆锥内接于球O ，经过圆锥顶点的平面α截球O 和圆锥所得的截面面积分别为12,S S ，若125π8S =，则2S =（）A．2B C D ．【答案】C 【解析】【分析】根据给定条件，求出球O 半径，平面α截球O 所得截面小圆半径，圆锥底面圆半径，再求出平面α截圆锥所得的截面等腰三角形底边长及高即可计算作答.【详解】球O 半径为R ，由34π125π36R =得52R =，平面α截球O 所得截面小圆半径1r ，由21128π5πS r ==得1r因此，球心O 到平面α的距离1d r ==，而球心O 在圆锥的轴上，则圆锥的轴与平面α所成的角为45 ，因圆锥的高为1，则球心O 到圆锥底面圆的距离为132d =，于是得圆锥底面圆半径2r ===，令平面α截圆锥所得截面为等腰PAB △，线段AB 为圆锥底面圆1O 的弦，点C 为弦AB 中点，如图，依题意，145CPO ∠=，111CO PO ==，PC =AB ==，所以212AB S PC =⋅=.故选：C 【点睛】关键点睛：解决与球有关的内切或外接问题时，关键是确定球心的位置，再利用球的截面小圆性质求解.5．（2022·浙江·模拟预测）如图，矩形BDEF 所在平面与正方形ABCD 所在平面互相垂直，2,1BD DE ==，点P 在线段EF 上，给出下列命题：①存在点P ，使得直线//DP 平面ACF ②存在点P ，使得直线DP ⊥平面ACF③直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎦④三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π其中所有真命题的序号是（）A ．①③B ．①④C ．②④D ．①③④【答案】D 【解析】【分析】取EF 中点推理判断①；假定DP ⊥平面ACF ，分析判断②；确定直线DP 与平面ABCD 所成角，求出临界值判断③；求出ACF 外接圆面积判断④作答.【详解】令AC BD O = ，连接,FO DF ，令EF 中点为G ，连DG ，如图，依题意，O 是,BD AC 的中点，对于①，在矩形BDEF 中，//DO FG ，DO FG =，四边形DOFG 是平行四边形，直线//DG OF ，OF ⊂平面ACF ，DG ⊄平面ACF ，则//DG 平面ACF ，当P 是线段EF 中点G 时，直线//DP 平面ACF ，①正确；对于②，假定直线DP ⊥平面ACF ，由①知，DP OF ⊥，DP DG ⊥，当点P 在线段EF 上任意位置（除点G 外），PDG ∠均为锐角，即DP 不垂直于DG ，也不垂直于OF ，因此，不存在点P ，使得直线DP ⊥平面ACF ，②不正确；对于③，平面BDEF ⊥平面ABCD ，DP 在平面ABCD 内射影在直线BD 上，直线DP 与平面ABCD 所成角为PDB ∠，当点P 由点E 运动到点F 的过程中，PDB ∠逐渐减小，当P 与E 重合时，PDB ∠最大，为90EDB ∠= ，max (sin )1PDB ∠=，当P 与F 重合时，PDB ∠最小，为FDB ∠，min (sin )BF PDB DF∠==所以直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎦，③正确；对于④，在ACF 中，2AC =，|AF CF ==FO =，则sin OFFAC AF∠==由正弦定理得ACF 外接圆直径2sin FC r FAC ==∠半径r =圆面积为298S r ππ==，三棱锥A CDE -的外接球被平面ACF 所截取的截面是ACF 外接圆，因此三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π，④正确,所以所有真命题的序号是①③④.故选：D6．（2022·四川省泸县第二中学模拟预测（文））已知1O 是正方体1111ABCD A B C D -的中心O 关于平面1111D C B A 的对称点，则下列说法中正确的是（）A ．11O C 与1A C 是异面直线B ．11OC ∥平面11A BCD C ．11O C AD ⊥D ．11O C ⊥平面11BDD B 【答案】B 【解析】【分析】根据正方体的性质、空间直线与平面的位置关系，即可对选项做出判断.【详解】连接1A C 、1AC ，交于点O ，连接11AC 、11B D ，交于点P .连接AC 、BD 、1A B 、1D C 、1O O .由题可知，1O 在平面11A C CA 上，所以11O C 与1A C 共面，故A 错误；在四边形11OO C C 中，11//O O C C 且11O O C C =，所以四边形11OO C C 为平行四边形.11//O C OC ∴.OC ⊂Q 平面11A BCD ，11O C ⊄平面11A BCD ，11O C ∴∥平面11A BCD ，故B 正确；由正方体的性质可得1111AC B D ⊥，因为1111O B O D =，所以111O P B D ⊥，又111O P AC P = ，11B D ∴⊥平面111O A C ， 1111B D O C ∴⊥，又11//B D BD ，11BD O C ∴⊥，而AD 与BD 所成角为45︒，所以显然11O C 与AD 不垂直，故C 错误；显然11O C 与11O B 不垂直，而11O B ⊂平面11BDD B ，所以11O C 与平面11BDD B 不垂直，故D 错误.故选：B.7．（2022·北京·北大附中三模）已知平面,,αβγ，直线m 和n ，则下列命题中正确的是（）A ．若,m m αβ⊥⊥，则αβ∥B ．若,αγβγ⊥⊥，则αβ∥C ．若,m n m α⊥⊥，则n α∥D ．若,m n αα∥∥，则m n∥【答案】A 【解析】【分析】对于A 选项，垂直于同一条直线的两个平面互相平行；对于B 选项，垂直于同一个平面的两个平面有可能相交，也有可能互相平行；对于C 选项，由线面垂直的性质即可判断；对于D 选项，平行于同一个平面的两条直线有可能相交、平行或异面.【详解】选项A 正确，因为垂直于同一直线的两个平面互相平行；选项B 错误，平面α和β也可以相交；选项C 错误，直线n 可能在平面α内；选项D 错误，直线m 和n 还可能相交或者异面.故选：A.8．（2022·云南师大附中模拟预测（理））已知正方形ABCD 的边长为ABC 沿对角线AC 折起，使得二面角B AC D --的大小为90°.若三棱锥B ACD -的四个顶点都在球O 的球面上，G 为AC 边的中点，E ，F 分别为线段BG ，DC 上的动点（不包括端点），且BE =，当三棱锥E ACF -的体积最大时，过点F 作球O 的截面，则截面面积的最小值为（）A ．B ．2πC ．32πD ．89π【答案】D 【解析】【分析】根据面面垂直的判定定理得BG ⊥平面ACD ，继而表示出三棱锥E ACF -的体积，求出x =V 取得最大值，在△GCF 中，由余弦定理，得GF =当GF 垂直于截面时，截面圆的面积最小，继而得解.【详解】因为正方形ABCD 的边长为4AC =.如图，由于平面ABC ⊥平面ACD ，平面ABC 平面ACD AC =，又G 为AC 边的中点，则有BG AC ⊥，所以BG ⊥平面ACD ．设CF x =(0x <<，则BE ，所以三棱锥E ACF -的体积13ACF V S EG ==△211112sin 4))32323AC CF ACF EG x x ⨯∠=⨯⨯=- ，当x =时，V 取得最大值．由于GA GB GC GD ===，则球O 的球心即为G ，且球O 的半径2R =．又在△GCF 中，由余弦定理，得GF ==知，当GF 垂直于截面时，截面圆的面积最小，设其半径为r ，所以r ===3π2.故选：D ．9．（2022·浙江·乐清市知临中学模拟预测）如图，正方体1111ABCD A B C D -的棱长为a ，E 是棱1DD 的动点，则下列说法正确的（）个．①若E 为1DD 的中点，则直线1//B E 平面1A BD ②三棱锥11C B CE -的体积为定值313a③E 为1DD 的中点时，直线1B E 与平面11CDD C。

2023年高考数学总复习《立体几何》附答案解析

．
所以 z1＝0，
，故可取
，，，
于是＜，＞
，
设所成锐二面角为θ，所以 sinθ
，
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为．
第3页共3页
第1页共3页
∴CF CC1 AA1 ， ∵∠BAC＝90°，
∴CD
，
在 Rt△FCD 中，tan∠FDC 맨
，
故直线 DF 与平面 ABC 所成角的正切值为．
2．如图所示，四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形，∠BCD＝60°，E 是 CD 的中点，PA⊥底面 ABCD，PA＝2．（1）证明：平面 PBE⊥平面 PAB；（2）求平面 PAD 和平面 PBE 所成二面角（锐角）的正弦值．
【解答】（1）证明：如图所示，连接 BD，由 ABCD 是菱形且∠BCD＝60°，知△ABC 是等边三角形． ∵E 是 CD 的中点， ∴BE⊥CD，又 AB∥CD， ∴AB⊥BE，∴BE⊥平面 PAB，又 BE⊂平面 PBE， ∴平面 PBE⊥平面 PAB．（2）解：在平面 ABCD 内，过点 A 作 AB 的垂线，如图所示，以 A 为原点建立空间直角
【解答】（1）证明：连接 DG、FG，由直三棱柱的性质知，BB1∥CC1，且 BB1＝CC1， ∵B1E＝2EB，C1F＝2FC， ∴EB∥FC，且 EB＝FC， ∴四边形 BCFE 为平行四边形， ∴EF∥BC，EF＝BC， ∵BD＝2DA，CG＝2GA， ∴GD∥BC，且 GD BC， ∴EF∥GD，且 GD EF， ∴四边形 DEFG 为梯形，即 D、E、F、G 四点共面， ∴点 G 在平面 EFD 内．（2）解：由直三棱柱的性质知，CC1⊥平面 ABC， ∵F 为 CC1 上一点， ∴点 F 在平面 ABC 上的投影为点 C，连接 CD，则∠FDC 即为直线 DF 与平面 ABC 所成角． ∵点 D 在棱 AB 上，且 BD＝2DA， ∴AD AB ， ∵C1F＝2FC，

高考数学立体几何多选题测试试题附解析

高考数学立体几何多选题测试试题附解析一、立体几何多选题1．如图，在棱长为2的正方体ABCD A B C D ''''-中，M 为BC 边的中点，下列结论正确的有（）A ．AM 与DB ''10 B ．过三点A 、M 、D 的正方体ABCD A BCD ''''-的截面面积为92C ．四面体A C BD ''的内切球的表面积为3π D ．正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动并且使MAC PAC ''∠=∠，那么点P 的轨迹是椭圆【答案】AB 【分析】构建空间直角坐标系，由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误；同样设(,,0)P x y 结合向量夹角的坐标表示，2221543x y =++⨯P 的轨迹知D 的正误；由立方体的截面为梯形，分别求,,,MN AD AM D N ''，进而得到梯形的高即可求面积，判断B 的正误；由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ，进而求内切球表面积，判断C 的正误. 【详解】A ：构建如下图所示的空间直角坐标系：则有：(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D ''， ∴(1,2,0),(2,2,0)AM D B ''==-，10cos ,10||||58AM D B AM D B AM D B ''⋅''<>===''⨯，故正确.B ：若N 为CC '的中点，连接MN ，则有//MN AD '，如下图示，∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面，而2,2,5MN AD AM D N ''====322， ∴梯形的面积为132932222S =⨯=，故正确. C ：如下图知：四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积，∴118848323V =-⨯⨯⨯=，而四面体的棱长都为22，有表面积为142222sin 8323S π=⨯⨯⨯⨯=，∴若其内切圆半径为r ，则有188333r ⨯⋅=，即33r =，所以内切球的表面积为2443r ππ=.故错误. D ：正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动且MAC PAC ''∠=∠，即P 的轨迹为面A B C D ''''截以AM 、AP 为母线，AC’为轴的圆锥体侧面所得曲线，如下图曲线GPK ，构建如下空间直角坐标系，232(0,0,2),(2),(0,22,0)22A M C '-，若(,,0)P x y ，则232(,,0),(0,22,2),(,,2)22AM AC AP x y '=-=-=-，∴15cos ||||512AMAC MAC AM AC '⋅'∠==='⨯，2222cos ||||43AP AC y PAC AP AC x y '⋅+'∠=='++⨯，即222215543y x y +=++⨯，整理得22(102)9216(0)y x y +-=>，即轨迹为双曲线的一支，故错误.故选：AB 【点睛】关键点点睛：应用向量的坐标表示求异面直线的夹角，并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹，综合立方体的性质求截面面积，分割几何体应用等体积法求内切球半径，进而求内切球的表面积.2．已知正方体1111ABCD A B C D -的棱长为2，点E ，F 在平面1111D C B A 内，若||5AE =，AC DF ⊥，则（）A ．点E 的轨迹是一个圆B ．点F 的轨迹是一个圆C ．EF 的最小值为21-D ．AE 与平面1A BD 所成角的正弦值的最大值为21530+【答案】ACD 【分析】对于A 、B 、C 、D 四个选项，需要对各个选项一一验证. 选项A ：由2211||5AE AA A E =+=，得1||1A E =，分析得E 的轨迹为圆；选项B ：由AC DBF ⊥，而点F 在11B D 上，即F 的轨迹为线段11B D ，；选项C ：由E 的轨迹为圆，F 的轨迹为线段11B D ，可分析得min ||EF d r =-；选项D ：建立空间直角坐标系，用向量法求最值. 【详解】对于A:2211||5AE AA A E =+=，即221|25A E +=，所以1||1A E =，即点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上；故A 正确；对于B: 正方体1111ABCD A B C D -中，AC ⊥BD ，又AC DF ⊥，且BD ∩DF=D ，所以AC DBF ⊥，所以点F 在11B D 上，即F 的轨迹为线段11B D ，故B 错误；对于C:在平面1111D C B A 内，1A 到直线11B D 的距离为2,d =当点E ，F 落在11A C 上时，min ||21EF =；故C 正确；对于D:建立如图示的坐标系，则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上，可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =，则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1，则()1,1,1n =，设AE 与平面1A BD 所成角为α，则：22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时，sin α2215301515=，故D 正确故选：CD 【点睛】多项选择题是2020年高考新题型，需要要对选项一一验证．3．如图，在棱长为2的正方体1111ABCD A B C D -，中，E 为棱1CC 上的中点，F 为棱1AA 上的点，且满足1:1:2A F FA =，点F ，B ，E ，G ，H 为过三点B ，E ，F 的平面BMN 与正方体1111ABCD A B C D -的棱的交点，则下列说法正确的是（）A ．//HF BEB ．三棱锥的体积14B BMN V -=C ．直线MN 与平面11A B BA 所成的角为45︒D ．11:1:3D G GC = 【答案】ABD 【分析】面面平行性质定理可得出A 正确；等体积法求得B 正确；直线MN 与平面11A B BA 所成的角为1B MN ∠，求其正切值不等于1即可得出C 错误；利用面面平行性质定理和中位线求出11,D G GC 长度即可得出D 正确. 【详解】解：对于A.在正方体1111ABCD A B C D -中平面11//ADA D 平面11BCB C ，又平面11ADA D 平面BMN HF =，平面11BCB C ⋂平面BMN BE =，有平面与平面平行的性质定理可得//HF BE ，故正确；对于B.因为1:1:2A F FA =，所以111332B M A B ==，又E 为棱1CC 上的中点，所以14B N =, 所以1111234432B BMN N B BM V V --⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭，故正确；对于C.由题意及图形可判定直线MN 与平面11A B BA 所成的角为1B MN ∠，结合B 选项可得1114tan 13B N B MN B M ∠==≠，故错误；对于D.同A 选项证明方法一样可证的11//GC B M ，因为E 为棱1CC 上的中点，1C 为棱1B N 上的中点，所以1113=22GC B M = 所以11G=2D ，所以11:1:3D G GC =，故正确. 故选：ABD 【点睛】求体积的常用方法：（1）直接法：对于规则的几何体，利用相关公式直接计算；（2）等体积法：选择合适的底面来求几何体体积，常用于求三棱锥的体积，即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换；（3）割补法：首先把不规则的几何体分割成规则的几何体，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算.4．在直角梯形ABCD 中，2ABC BCD π∠=∠=，1AB BC ==，2DC =，E 为DC 中点，现将ADE 沿AE 折起，得到一个四棱锥D ABCE -，则下列命题正确的有（） A ．在ADE 沿AE 折起的过程中，四棱锥D ABCE -体积的最大值为13B ．在ADE 沿AE 折起的过程中，异面直线AD 与BC 所成的角恒为4π C ．在ADE 沿AE 折起的过程中，二面角A EC D --的大小为45︒D ．在四棱锥D ABCE -中，当D 在EC 上的射影恰好为EC 的中点F 时，DB 与平面ABCE【答案】ABD 【分析】对于A ，四棱锥D ABCE -的底面面积是固定值，要使得体积最大，需要平面DAE ⊥平面ABCE ，此时DE CE ⊥，可求得1133D ABCE ABCE V S DE -=⋅=可判断A ；对于B ，在ADE 沿AE 折起的过程中，//AE BC ，所以异面直线AD 与AE 所成的角即为AD 与BC所成角，由翻折前可知4DAE π∠=可判断B ；对于C ，利用线面垂直的判定定理，结合翻折前可知AE ⊥平面DEC ，又AE ⊂平面ABCE ，所以平面DEC ⊥平面ABCE ，即二面角A EC D --的在大小为2π判断C ；对于D ，利用线面垂直的判定定理可知DF ⊥平面ABCE ，所以DBF ∠为直线DB 与平面ABCE 所成的角，在直角DFB △中，tan DF DBF BF ∠==，可判断D 正确；【详解】对于A ，ADE 沿AE 折起得到四棱锥D ABCE -，由四棱锥底面面积是固定值，要使得体积最大，需要四棱锥的高最大，即平面DAE ⊥平面ABCE ，此时DE CE ⊥，由已知得1DE =，则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=，故A 正确；对于B ，在ADE 沿AE 折起的过程中，//AE BC ，所以异面直线AD 与AE 所成的角即为AD 与BC 所成角，又1AB BC ==，2DC =，E 为DC 中点，可知4DAE π∠=，即异面直线AD 与BC 所成的角恒为4π，故B 正确；对于C ，由翻折前知，,AE EC AE ED ⊥⊥，且ECED E =，则AE ⊥平面DEC ，又AE ⊂平面ABCE ，所以平面DEC ⊥平面ABCE ，即二面角A EC D --的大小为2π，故C 错误；对于D ，如图连接,DF BF ，由C 选项知，AE ⊥平面DEC ，又DF ⊂平面DEC ，则AE DF ⊥，又由已知得EC DF ⊥，且EC AE E ⋂=，则DF ⊥平面ABCE ，所以DBF ∠为直线DB 与平面ABCE 所成的角，在直角DFB △中，222222113122152tan 511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭，所以DB 与平面ABCE 所成的角的正切为155，故D 正确；故选：ABD 【点睛】关键点睛：本题考查立体几何综合问题，求体积，求线线角，线面角，面面角，解题的关键要熟悉几种角的定义，通过平移法找到线线角，通过证垂直找到线面角和面面角，再结合三角形求出角，考查了学生的逻辑推理能力，转化能力与运算求解能力，属于难题.5．已知棱长为1的正方体1111ABCD A B C D -，过对角线1BD 作平面α交棱1AA 于点E ，交棱1CC 于点F ，以下结论正确的是（）A ．四边形1BFD E 不一定是平行四边形B ．平面α分正方体所得两部分的体积相等C ．平面α与平面1DBB 不可能垂直D ．四边形1BFDE 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E ､F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E ､F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D , 又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.6．如图，已知矩形ABCD 中，2AB AD =，E 为边AB 的中点，将ADE ∆沿直线DE翻折成1A DE ∆，若M 为线段1A C 的中点，则ADE ∆在翻折过程中，下列说法正确的是（）A ．线段BM 的长是定值B ．存在某个位置，使1DE AC ⊥C ．点M 的运动轨迹是一个圆D ．存在某个位置，使MB ⊥平面1A DE【答案】AC【分析】取CD 中点F ，连接BF ，MF ，根据面面平行的判定定理可得平面//BMF 平面1A DE ，由面面平行的性质定理可知//BM 平面1A DE ，可判断D ；在BFM ∆中，利用余弦定理可求得BM a =为定值，可判断A 和C ；假设1DE A C ⊥，由线面垂直的判定定理可得DE ⊥平面1A CE ，由线面垂直的性质定理可知1DE A E ⊥，与11DA A E ⊥矛盾，可判断B ．【详解】解：取CD 的中点F ，连接BF ，MF ，∵M ，F 分别为1A C 、CD 中点，∴1MF A D ∥，∵1A D ⊂平面1A DE ，MF ⊄平面1A DE ，∴MF 平面1A DE ，∵DF BE ∥且DF BE =，∴四边形BEDF 为平行四边形，∴BF DE ，∵DE ⊂平面1A DE ，BF ⊄平面1A DE ，∴BF ∥平面1A DE ，又BF MF F =，BF 、MF ⊂平面BMF ，∴平面//BMF 平面1A DE ，∵BM ⊂平面BMF ，∴BM ∥平面1A DE ，即D 错误，设22AB AD a ==，则112MF A D a ==，BF DE ==，145A DE MFB ︒∠=∠=， ∴BM a ==，即BM 为定值，所以A 正确，∴点M 的轨迹是以B 为圆心，a 为半径的圆，即C 正确， ∵DE CE ==，2CD AB a ==， ∴222DE CE CD +=， ∴DE CE ⊥，设1DE A C ⊥，∵1A C 、CE ⊂平面1A CE ，1AC CE C =， ∴DE ⊥平面1A CE ，∵1A E ⊂平面1A CE ，∴1DE A E ⊥，与11DA A E ⊥矛盾，所以假设不成立，即B 错误.故选:AC .【点睛】本题考查立体几何中的翻折问题，涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点，考查学生的空间立体感和推理论证能力．7．已知正四棱柱1111ABCD A B C D -的底面边长为2，侧棱11AA =，P 为上底面1111D C B A 上的动点，给出下列四个结论中正确结论为（）A ．若3PD =，则满足条件的P 点有且只有一个B ．若PD =，则点P 的轨迹是一段圆弧C ．若PD ∥平面1ACB ，则DP 长的最小值为2D ．若PD ∥平面1ACB ，且PD =，则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD【分析】若3PD =，由于P 与1B 重合时3PD =，此时P 点唯一；()13PD =，，则1PD =P 的轨迹是一段圆弧；当P 为11A C 中点时，DP 有最小值为=断C ；平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆，其半径为32=，可得D . 【详解】如图：∵正四棱柱1111ABCD A B C D -的底面边长为2，∴1122B D =11AA =， ∴()2212213DB =+=，则P 与1B 重合时3PD =，此时P 点唯一，故A 正确； ∵()313PD =，，11DD =，则12PD P 的轨迹是一段圆弧，故B 正确；连接1DA ，1DC ，可得平面11//A DC 平面1ACB ，则当P 为11A C 中点时，DP 有最小值为()22213+=C 错误；由C 知，平面BDP 即为平面11BDD B ，平面BDP 截正四棱柱1111ABCD A B C D -的外接2221322122++=，面积为94π，故D 正确．故选：ABD ．【点睛】本题考查了立体几何综合，考查了学生空间想象，逻辑推理，转化划归，数学运算的能力，属于较难题.8．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点P 在线段B 1C 上运动，则（）A ．直线BD 1⊥平面A 1C 1DB ．三棱锥P ﹣A 1C 1D 的体积为定值C ．异面直线AP 与A 1D 所成角的取值范用是[45°，90°]D ．直线C 1P 与平面A 1C 1D 6 【答案】ABD【分析】在A 中，推导出A 1C 1⊥BD 1，DC 1⊥BD 1，从而直线BD 1⊥平面A 1C 1D ；在B 中，由B 1C ∥平面 A 1C 1D ，得到P 到平面A 1C 1D 的距离为定值，再由△A 1C 1D 的面积是定值，从而三棱锥P ﹣A 1C 1D 的体积为定值；在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，利用向量法能求出直线C 1P 与平面A 1C 1D 6．【详解】解：在A 中，∵A 1C 1⊥B 1D 1，A 1C 1⊥BB 1，B 1D 1∩BB 1＝B 1，∴A 1C 1⊥平面BB 1D 1，∴A 1C 1⊥BD 1，同理，DC 1⊥BD 1，∵A 1C 1∩DC 1＝C 1，∴直线BD 1⊥平面A 1C 1D ，故A 正确；在B 中，∵A 1D ∥B 1C ，A 1D ⊂平面A 1C 1D ，B 1C ⊄平面A 1C 1D ，∴B 1C ∥平面 A 1C 1D ，∵点P 在线段B 1C 上运动，∴P 到平面A 1C 1D 的距离为定值，又△A 1C 1D 的面积是定值，∴三棱锥P ﹣A 1C 1D 的体积为定值，故B 正确；在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]，故C 错误；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1，P （a ，1，a ），则D （0，0，0），A 1（1，0，1），C 1（0，1，1），1DA ＝（1，0，1），1DC ＝（0，1，1），1C P ＝（a ，0，a ﹣1），设平面A 1C 1D 的法向量(),,n x y z =，则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x ＝1，得1,1,1n ，∴直线C 1P 与平面A 1C 1D 所成角的正弦值为： 11||||||C P n C P n ⋅⋅＝22(1)3a a +-⋅＝21132()22a ⋅-+， ∴当a ＝12时，直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为63，故D 正确．故选：ABD ．【点睛】求直线与平面所成的角的一般步骤：（1）、①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解；（2）、用空间向量坐标公式求解.。

高三数学立体几何多选题测试附解析

高三数学立体几何多选题测试附解析一、立体几何多选题1．已知球O 为正方体1111ABCD A B C D -的内切球，平面11A C B 截球O 的面积为24π，下列命题中正确的有（）A ．异面直线AC 与1BC 所成的角为60°B ．1BD ⊥平面11AC B C ．球O 的表面积为36πD ．三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ，1A B ，通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ；通过反证法证明B ；由已知平面11A C B 截球O 的面积为24π求出正方体棱长，进而求出内切球的表面积可判断C ；利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ，连接11A C ，1A B ，由正方体1111ABCD A B C D -，可知11//A C AC ，11AC B ∴∠为异面直线AC 与1BC 所成的角，设正方体边长为a，则1111AC A B BC ==，由等边三角形知1160A C B ∠=，即异面直线AC 与1BC 所成的角为60，故A 正确；对于B ，假设1BD ⊥平面11A C B ，又1A B ⊂平面11A C B ，则11BD B A ⊥，设正方体边长为a ，则11A D a =，1A B =，1BD =，由勾股定理知111A D B A ⊥，与假设矛盾，假设不成立，故1BD 不垂直于平面11A C B ，故B 错误；对于C ，设正方体边长为a，则11AC =，内切球半径为2a，设内切球的球心O 在面11A C B 上的投影为O '，由等边三角形性质可知O '为等边11A C B △的重心，则11123233O A AC a ='=⨯=，又12OA a =，∴球心O 到面11A C B 的距离6a ==，又球心与截面圆心的连线垂直于截面，∴=，又截面圆的面积2246S a ππ⎛⎫= ⎪ ⎪⎝⎭=，解得12a =，则内切球半径为6，内切球表面积214644S ππ==⨯，故C 错误；对于D ，由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=，故D 正确；故选：AD【点睛】关键点点睛：本题考查了正方体和它的内切球的几何结构特征，关键是想象出截面图的形状，从而求出正方体的棱长，进而求出内切球的表面积及三棱锥的体积，考查了空间想象能力，数形结合的思想，属于较难题.2．如图，已知正方体1ABCD ABC D -的棱长为a ，E 是棱CD 上的动点.则下列结论中正确的有（）A ．11EB AD ⊥B ．二面角11E A B A --的大小为4π C ．三棱锥11A B D E -体积的最小值为313a D ．1//D E 平面11A B BA 【答案】ABD 【分析】连接1A D 、1B C ，则易证1AD ⊥平面11A DCB ，1EB ⊂平面11A DCB ，则由线面垂直的性质定理可以判断选项A 正确；二面角11E A B A --的平面角为1DA A ∠，易知14DA A π∠=，则可判断选项B 正确；用等体积法，将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积，当点E 与D 重合时，三棱锥11E AB D -的体积最小，此时的值为316a ，则选项C 错误；易知平面11//D DCC 平面11A B BA ，而1D E ⊂平面11D DCC ，则根据面面平行的性质定理可得1//D E 平面11A B BA ，可判断选项D 正确. 【详解】选项A ，连接1A D 、1B C ，则由正方体1ABCD ABC D -可知，11A D AD ⊥，111A B AD ⊥，1111A DA B A =，则1AD ⊥平面11A DCB ，又因为1EB ⊂平面11A DCB ，所以11EB AD ⊥，选项A 正确；选项B ，因为11//DE A B ，则二面角11E A B A --即为二面角11D A B A --，由正方体1ABCD ABC D -可知，11A B ⊥平面1DA A ，则1DA A ∠为二面角11D A B A --的平面角，且14DA A π∠=，所以选项B 正确；选项C ，设点E 到平面11AB D 的距离为d ，则11111113A B D E E AB D AB D V V S d --==⋅，连接1C D 、1C B ，易证平面1//BDC 平面11AB D ，则在棱CD 上，点D 到平面11AB D 的距离最短，即点E 与D 重合时，三棱锥11A B D E -的体积最小，由正方体1ABCD ABC D -知11A B ⊥平面1ADD ，所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=，则选项C 错误；选项D ，由正方体1ABCD ABC D -知，平面11//CC D D 平面11A B BA ，且1D E ⊂平面11CC D D ，则由面面平行的性质定理可知1//D E 平面11A B BA ，则选项D 正确. 故选：ABD. 【点睛】关键点点睛：本题对于选项C 的判断中，利用等体积法求三棱锥的体积是解题的关键.3．在三棱锥M ABC -中，下列命题正确的是（）A ．若1233AD AB AC =+，则3BC BD = B ．若G 为ABC 的重心，则111333MG MA MB MC =++C ．若0MA BC ⋅=，0MC AB ⋅=，则0MB AC ⋅=D ．若三棱锥M ABC -的棱长都为2，P ，Q 分别为MA ，BC 中点，则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图，在每个三角形中利用向量的线性运算可得. 【详解】对于A ，由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-，即2CD DB =，则32BD BD DC BC =+=，故A 错误；对于B ，由G 为ABC 的重心，得0GA GB GC ++=，又MG MA AG =+，MG MB BG =+，MG MC CG =+，3MA MB MC MG ∴++=，即111333MG MA MB MC =++，故B 正确；对于C ，若0MA BC ⋅=，0MC AB ⋅=，则0MC MA BC AB ⋅+⋅=，即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅，即0MB AC ⋅=，故C 正确；对于D ，111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-，又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=，1PQ ∴==，故D 错误. 故选：BC 【点睛】关键点睛：本题考查向量的运算，用已知向量表示某一向量的三个关键点： (1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量． (3)在立体几何中三角形法则、平行四边形法则仍然成立．4．在直角梯形ABCD 中，2ABC BCD π∠=∠=，1AB BC ==，2DC =，E 为DC 中点，现将ADE 沿AE 折起，得到一个四棱锥D ABCE -，则下列命题正确的有（） A ．在ADE 沿AE 折起的过程中，四棱锥D ABCE -体积的最大值为13B ．在ADE 沿AE 折起的过程中，异面直线AD 与BC 所成的角恒为4π C ．在ADE 沿AE 折起的过程中，二面角A EC D --的大小为45︒D ．在四棱锥D ABCE -中，当D 在EC 上的射影恰好为EC 的中点F 时，DB 与平面ABCE所成的角的正切为5【答案】ABD 【分析】对于A ，四棱锥D ABCE -的底面面积是固定值，要使得体积最大，需要平面DAE ⊥平面ABCE ，此时DE CE ⊥，可求得1133D ABCE ABCE V S DE -=⋅=可判断A ；对于B ，在ADE 沿AE 折起的过程中，//AE BC ，所以异面直线AD 与AE 所成的角即为AD 与BC所成角，由翻折前可知4DAE π∠=可判断B ；对于C ，利用线面垂直的判定定理，结合翻折前可知AE ⊥平面DEC ，又AE ⊂平面ABCE ，所以平面DEC ⊥平面ABCE ，即二面角A EC D --的在大小为2π判断C ；对于D ，利用线面垂直的判定定理可知DF ⊥平面ABCE ，所以DBF ∠为直线DB 与平面ABCE 所成的角，在直角DFB △中，15tan 5DF DBF BF ∠==，可判断D 正确；【详解】对于A ，ADE 沿AE 折起得到四棱锥D ABCE -，由四棱锥底面面积是固定值，要使得体积最大，需要四棱锥的高最大，即平面DAE ⊥平面ABCE ，此时DE CE ⊥，由已知得1DE =，则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=，故A 正确；对于B ，在ADE 沿AE 折起的过程中，//AE BC ，所以异面直线AD 与AE 所成的角即为AD 与BC 所成角，又1AB BC ==，2DC =，E 为DC 中点，可知4DAE π∠=，即异面直线AD 与BC 所成的角恒为4π，故B 正确；对于C ，由翻折前知，,AE EC AE ED ⊥⊥，且ECED E =，则AE ⊥平面DEC ，又AE ⊂平面ABCE ，所以平面DEC ⊥平面ABCE ，即二面角A EC D --的大小为2π，故C 错误；对于D ，如图连接,DF BF ，由C 选项知，AE ⊥平面DEC ，又DF ⊂平面DEC ，则AE DF ⊥，又由已知得EC DF ⊥，且EC AE E ⋂=，则DF ⊥平面ABCE ，所以DBF ∠为直线DB 与平面ABCE 所成的角，在直角DFB △中，222222113122152tan 5511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭，所以DB 与平面ABCE 所成的角的正切为15，故D 正确；故选：ABD 【点睛】关键点睛：本题考查立体几何综合问题，求体积，求线线角，线面角，面面角，解题的关键要熟悉几种角的定义，通过平移法找到线线角，通过证垂直找到线面角和面面角，再结合三角形求出角，考查了学生的逻辑推理能力，转化能力与运算求解能力，属于难题.5．如图，矩形ABCD 中， 22AB AD ==，E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △（点1A 不落在底面BCDE 内），若M 在线段1A C 上（点M 与1A ，C 不重合），则在ADE 翻转过程中，以下命题正确的是（）A ．存在某个位置，使1DE A C ⊥B ．存在点M ，使得BM ⊥平面1A DC 成立 C ．存在点M ，使得//MB 平面1A DE 成立D ．四棱锥1A BCDE -体积最大值为24【答案】CD 【分析】利用反证法可得A 、B 错误，取M 为1A C 的中点，取1A D 的中点为I ，连接,MI IE ，可证明//MB 平面1A DE ，当平面1A DE ⊥平面BCDE 时，四棱锥1A BCDE -体积最大值，利用公式可求得此时体积为24. 【详解】如图（1），取DE 的中点为F ，连接1,A F CF ，则45CDF ∠=︒，22DF =，故212254222222CF =+-⨯⨯=，故222DC DF CF ≠+即2CFD π∠≠．若1CA DE ⊥，因为11,A D A E DF FE ==，故1A F DE ⊥，而111A F A C A ⋂=，故DE ⊥平面1A FC ，因为CF ⊂平面1A FC ，故DE CF ⊥，矛盾，故A 错．若BM ⊥平面1A DC ，因为DC ⊂平面1A DC ，故BM DC ⊥，因为DC CB ⊥，BM CB B ⋂=，故CD ⊥平面1A CB ，因为1AC ⊂平面1A CB ，故1CD A C ⊥，但1A D CD <，矛盾，故B 错．当平面1A DE ⊥平面BCDE 时，四棱锥1A BCDE -体积最大值，由前述证明可知1A F DE ⊥，而平面1A DE平面BCDE DE =，1A F ⊂平面1A DE ，故1A F ⊥平面BCDE ，因为1A DE △为等腰直角三角形，111A D A E ==，故122A F =，又四边形BCDE 的面积为13211122⨯-⨯⨯=，故此时体积为13223224⨯⨯=D 正确．对于C ，如图（2），取M 为1A C 的中点，取1A D 的中点为I ，连接,MI IE ，则1//,2IM CD IM CD =，而1//,2BE CD BE CD =，故//,IM BE IM BE =即四边形IEBM 为平行四边形，故//IE BM ，因为IE ⊂平面1A DE ，BM ⊄平面1A DE ，故//MB 平面1A DE ，故C 正确．故选：CD.【点睛】本题考查立体几何中的折叠问题，注意对于折叠后点线面的位置的判断，若命题的不成立，往往需要利用反证法来处理，本题属于难题.6．（多选题）在四面体P ABC -中，以上说法正确的有（）A ．若1233AD AC AB =+，则可知3BC BD = B ．若Q 为△ABC 的重心，则111333PQ PA PB PC =++C ．若0PA BC =，0PC AB =，则0PB AC =D ．若四面体P ABC -各棱长都为2，M N ，分别为,PA BC 的中点，则1MN = 【答案】ABC 【分析】作出四面体P ABC -直观图，在每个三角形中利用向量的线性运算可得. 【详解】对于A ，1233AD AC AB =+，32AD AC AB ∴=+，22AD AB AC AD ∴-=- ， 2BD DC ∴=，3BD BD DC BC ∴=+=即3BD BC ∴=，故A 正确；对于B ，Q 为△ABC 的重心，则0QA QB QC ++=，33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=即111333PQ PA PB PC ∴=++，故B 正确；对于C ，若0PA BC =，0PC AB =，则0PA BC PC AB +=，()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+= 0CA BC PC AC ∴+=,0AC CB PC AC ∴+=()0AC PC CB ∴+=，0AC PB ∴=，故C 正确；对于D ，111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+22211122222222222222222=++-⨯⨯⨯-⨯⨯⨯+⨯⨯⨯=2MN ∴=，故D 错误.故选：ABC 【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键． (2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量． (3)在立体几何中三角形法则、平行四边形法则仍然成立．7．已知棱长为1的正方体1111ABCD A B C D -，过对角线1BD 作平面α交棱1AA 于点E ，交棱1CC 于点F ，以下结论正确的是（） A ．四边形1BFD E 不一定是平行四边形 B ．平面α分正方体所得两部分的体积相等 C ．平面α与平面1DBB 不可能垂直 D ．四边形1BFD E 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E ､F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E ､F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D ,又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.8．如图，正四棱锥S －BCDE 底面边长与侧棱长均为a ，正三棱锥A －SBE 底面边长与侧棱长均为a ，则下列说法正确的是（）A ．AS ⊥CDB ．正四棱锥S －BCDE 的外接球半径为22C ．正四棱锥S －BCDE 的内切球半径为212a ⎛- ⎝⎭ D ．由正四棱锥S －BCDE 与正三棱锥A －SBE 拼成的多面体是一个三棱柱【答案】ABD 【分析】取BE 中点H ，证明BE ⊥平面SAH 即可证AS CD ⊥；设底面中心为1O ，有112O B O S ==2；用等体积法求内切球半径即可判断；由////SA DE BC 且==SA DE BC 可知多面体是一个三棱柱.【详解】如图所示：A 选项：取BE 中点H 连接,AH SH ，正三棱锥A SBE -中，,AH BE SH BE ⊥⊥ 又AHSH H =，所以BE ⊥平面SAH ，则BE AS ⊥，又//BE CD 所以AS CD ⊥ ，故A 正确；B 选项：设底面中心为1O ，球心为O 半径为R ，因为正四棱锥S －BCDE 外接球球心在1O S 上，所以OS OB R ==，因为，正四棱锥S －BCDE 底面边长与侧棱长均为a所以112O B O S ==，由()22211OB O B O S OS =+- 得2222222R a R ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭解得2R =，故B 正确； C 选项：设内切球半径为r ，易求得侧面面积为2213sin 234S a a π=⋅=，由等体积法得222121134333a a r r =⋅+⋅⋅ 解得624a r = ，故C 错；D 选项：取SE 中点F ，连结AF ，DF ，BF ，则BFD ∠和BFA ∠分别是D SE B --和A SE B --的二面角的平面角，由)22222223321cos 2332aBF DF BDBFD BF DF ⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===-⋅⎫⎪⎝⎭2222222331cos 2332a AF BF BA AFD AF BF ⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===⋅⎫⎪⎝⎭，故BFD ∠与BFA ∠互补，所以ASDE 共面，又因为AS AE ED SD ===，则ASDE 为平行四边形，故AS ED BC故正四棱锥S－BCDE与正三棱锥A－SBE拼成的多面体是一个三棱柱，所以////D正确故选：ABD【点睛】求外接球半径的常用方法：（1）补形法：侧面为直角三角形或正四面体或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；（2）利用球的性质：几何体在不同面均对直角的棱必然是球的直径；（3）定义法：到各个顶点距离均相等的点为球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.。

高中数学立体几何多选题100含解析

高中数学立体几何多选题100含解析一、立体几何多选题1．如图，正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2，则下列说法正确的是（）A ．异面直线1AB 与1AD 所成的角是3πB ．1BD ⊥平面11AC DC ．平面1ACB 截正四面体11A BDC -所得截面面积为3D ．正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ，利用正方体的结构特征找到异面直线所成的角；选项B ，根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证；选项C ，由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一；选项D ，分别求出正方体的体对角线长和正四面体11A BDC -的高，然后判断数量关系即可得解. 【详解】A ：正方体1111ABCD ABCD -中，易知11//AD BC ，异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角，即11A BC ∠，11A BC 为等边三角形，113A BC π∠=，正确；B ：连接11B D ，1B B ⊥平面1111DC B A ，11A C ⊂平面1111D C B A ，即111AC B B ⊥，又1111AC B D ⊥，1111B B B D B ⋂=，有11A C ⊥平面11BDD B ，1BD ⊂平面11BDD B ，所以111BD AC ⊥，同理可证：11BD A D ⊥，1111AC A D A ⋂=，所以1BD ⊥平面11AC D ，正确；C ：易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=，错误；D ：易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -的高为22222262213⎛⎫--⨯= ⎪⎝⎭，故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23，正确. 故选：ABD. 【点睛】关键点点睛：利用正方体的性质，找异面直线所成角的平面角求其大小，根据线面垂直的判定证明1BD ⊥平面11AC D ，由正四面体的性质，结合几何图形确定截面的面积，并求高，即可判断C 、D 的正误.2．已知正方体1111ABCD A B C D -的棱长为2，点E ，F 在平面1111D C B A 内，若||5AE =，AC DF ⊥，则（）A ．点E 的轨迹是一个圆B ．点F 的轨迹是一个圆C ．EF 21-D ．AE 与平面1A BD 21530+【答案】ACD 【分析】对于A 、B 、C 、D 四个选项，需要对各个选项一一验证. 选项A ：由2211||5AE AA A E =+=1||1A E =，分析得E 的轨迹为圆；选项B ：由AC DBF ⊥，而点F 在11B D 上，即F 的轨迹为线段11B D ，；选项C ：由E 的轨迹为圆，F 的轨迹为线段11B D ，可分析得min ||EF d r =-；选项D ：建立空间直角坐标系，用向量法求最值. 【详解】对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =，即点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上；故A 正确；对于B: 正方体1111ABCD A B C D -中，AC ⊥BD ，又AC DF ⊥，且BD ∩DF=D ，所以AC DBF ⊥，所以点F 在11B D 上，即F 的轨迹为线段11B D ，故B 错误；对于C:在平面1111D C B A 内，1A 到直线11B D 的距离为2,d=当点E ，F 落在11A C 上时，min ||21EF =-；故C 正确；对于D:建立如图示的坐标系，则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上，可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =，则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩ 不妨令x =1，则()1,1,1n =，设AE 与平面1A BD 所成角为α，则：2|||sin|cos,|||||n AEn AEn AEπθα⎛⎫++⎪====⨯当且仅当4πθ=时，sinα15=，故D正确故选：CD【点睛】多项选择题是2020年高考新题型，需要要对选项一一验证．3．在正三棱柱111ABC A B C-中，AC=11CC=，点D为BC中点，则以下结论正确的是（）A ．111122A D AB AC AA=+-B．三棱锥11D AB C-的体积为6C．1AB BC⊥且1//AB平面11AC DD．ABC内到直线AC、1BB的距离相等的点的轨迹为抛物线的一部分【答案】ABD【分析】A ．根据空间向量的加减运算进行计算并判断；B．根据1111D AB C A DB CV V--=，然后计算出对应三棱锥的高AD和底面积11DB CS，由此求解出三棱锥的体积；C．先假设1AB BC⊥，然后推出矛盾；取AB中点E，根据四点共面判断1AB//平面11AC D是否成立；D．将问题转化为“ABC内到直线AC和点B的距离相等的点”的轨迹，然后利用抛物线的定义进行判断.【详解】A．()11111111222A D A A AD AD AA AB AC AA AB AC AA=+=-=+-=+-，故正确；B．1111D AB C ADB CV V--=，因为D为BC中点且AB AC=，所以AD BC⊥，又因为1BB⊥平面ABC，所以1BBAD⊥且1BB BC B=，所以AD⊥平面11DB C，又因为AD===11111122DB CS BB B C=⨯⨯=，所以1111111133226D AB C A DB C DB CV V AD S--==⨯⨯=⋅=，故正确；C ．假设1AB BC ⊥成立，又因为1BB ⊥平面ABC ，所以1BB BC ⊥且111BB AB B =，所以BC ⊥平面1ABB ，所以BC AB ⊥，显然与几何体为正三棱柱矛盾，所以1AB BC ⊥不成立；取AB 中点E ，连接11,,ED EA AB ，如下图所示：因为,D E 为,BC AB 中点，所以//DE AC ，且11//AC A C ，所以11//DE AC ，所以11,,,D E A C 四点共面，又因为1A E 与1AB 相交，所以1AB //平面11AC D 显然不成立，故错误；D ．“ABC 内到直线AC 、1BB 的距离相等的点”即为“ABC 内到直线AC 和点B 的距离相等的点”，根据抛物线的定义可知满足要求的点的轨迹为抛物线的一部分，故正确；故选：ABD. 【点睛】方法点睛：求解空间中三棱锥的体积的常用方法：（1）公式法：直接得到三棱锥的高和底面积，然后用公式进行计算；（2）等体积法：待求三棱锥的高和底面积不易求出，采用替换顶点位置的方法，使其求解高和底面积更容易，由此求解出三棱锥的体积.4．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===，O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH 平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ，在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ，在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=，所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===，所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由111100m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-，设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-，由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--， ()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG m CG m a CG m⋅<>===⨯⋅，设直线CG 与平面AEF 所成角为θ，则sin 63θ=，23cos 1sin θθ=-=，所以，sin tan 2cos θθθ==，C 选项正确；对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△，因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误. 故选：AC. 【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.5．在正方体1111ABCD A B C D -中，M 、N 分别是棱AB 、1CC 的中点，1MB P 的顶点P 在棱1CC 与棱11C D 上运动，有以下四个命题正确命题的序号是（）A ．平面1MB P 1ND ⊥ B ．平面1MB P ⊥平面11ND AC ．1MB P 在底面ABCD 上的射影图形的面积为定值 D ．1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC 【分析】取N 与P 重合，结合勾股定理可判断A 选项的正误；利用面面垂直的判定定理可判断B 选项的正误；分点P 在棱1CC 、11C D 上运动两种情况讨论，利用三角形的面积公式可判断C 选项的正误；取点P 与点1C 重合，判断1MB P 在侧面11D C CD 上射影图形形状，可判断D 选项的正误. 【详解】对于A 选项，设正方体1111ABCD A B C D -的棱长为2，如下图所示：当点P 与点N 重合时，若1ND ⊥平面1MB P ，1B N ⊂平面1MB P ，则11ND B N ⊥，由勾股定理可得2211115D N C N C D =+=，同理可得15B N =，1122B D =，2221111B N D N B D ∴+≠，则1ND 与1B N 不垂直，假设不成立，A 选项错误；对于B 选项，取1BB 的中点E ，连接1A E 、EN ，在正方体1111ABCD A B C D -中，11//BB CC ，且E 、N 分别为1BB 、1CC 的中点，则11//B E C N 且11B E C N =，所以，四边形11B ENC 为平行四边形，则11//EN B C 且11EN B C =，1111//A D B C 且1111A D B C =，所以，11//A D EN 且11A D EN =，所以，四边形11A END 为平行四边形，所以，11//A E D N ，111A B BB =，1B E BM =，11190A B E B BM ∠=∠=，所以，111Rt A B E Rt B BM ≅△△，所以，111B A E BB M ∠=∠，所以，111111190A EB BB M A EB B A E ∠+∠=∠+∠=，190B FE ∴∠=，所以，11B M A E ⊥，11A D ⊥平面11AA B B ，1B M ⊂平面11AA B B ，111B M A D ∴⊥， 1111A D A E A =，11A D 、1A E ⊂平面11ND A ，1MB ∴⊥平面11ND A ，1MB ⊂平面1MB P ，所以，平面1MB P ⊥平面11ND A ，B 选项正确；对于C 选项，设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时，1MB P 在底面ABCD 上的射影为MBC △，此时，射影图形的面积为21224MBCa a S a =⋅=△；若点P 在棱11C D 上运动时，设点P 在底面ABCD 上的射影点为G ，则G CD ∈，且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ，则1MB P 在底面ABCD 内的射影为MBG △，且21224MBGa a S a =⋅⋅=△.综上所述，1MB P 在底面ABCD 内的射影图形的面积为定值，C 选项正确；对于D 选项，当点P 与1C 重合时，P 、1B 两点在平面11D C CD 上的射影重合，此时，1MB P 在侧面11D C CD 上的射影不构成三角形，D 选项错误. 故选：BC. 【点睛】方法点睛：证明面面垂直常用的方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，一般假设面面垂直成立，然后利用面面垂直转化为线面垂直，即为所证的线面垂直，组织论据证明即可.6．如图，已知四棱锥P ABCD -所有棱长均为4，点M 是侧棱PC 上的一个动点（不与点,P C 重合），若过点M 且垂直于PC 的截面将该四棱锥分成两部分，则下列结论正确的是（）A ．截面的形状可能为三角形、四边形、五边形B ．截面和底面ABCD 所成的锐二面角为4π C ．当1PM =时，截面的面积为52D ．当2PM =时，记被截面分成的两个几何体的体积分别为()1212,>V V V V ，则123=V V 【答案】BCD 【分析】点M 是侧棱PC 上的一个动点，根据其不同位置，对选项逐一进行判断即可. 【详解】A 选项中，如图，连接BD ，当M 是PC 中点时，2MC =，由题意知三角形PDC 与三角形PBC 都是边长为4的正三角形，所以DM PC ⊥,BM BC ⊥，又DM ，BM 在面MBD 内，且相交，所以PC ⊥平面PBD ，三角形MBD 即为过点M 且垂直于PC 的截面，此时是三角形，点M 向下移动时，2MC <，如图，仍是三角形；若点M 由中点位置向上移动，2MC >，在平面PDC 内作EM PC ⊥，交PD 于E ，在平面PBC 内作FM PC ⊥交PB 于F ，平面MEF 交平面PAD 于EG ，交PAB 于FH ，即交平面ABCD 于GH ，则五边形MEGHF 即为过点M 且垂直于PC 的截面，此时是五边形；故截面的形状可能为三角形、五边形，A 错误；B 选项中，因为截面总与PC 垂直，所以不同位置的截面均平行，截面与平面ABCD 所成的锐角为定值，不妨取M 是中点，连接AC ，BD ，MB ，MD ，设AC ，BD 交点是N ，连接PN ，由题意知，四边形ABCD 是边长为4的菱形，BD AC ⊥，因为MB =MD ，所以MN BD ⊥，故MNC ∠是截面与平面ABCD 所成的锐角，过点M 作MQ AC ⊥，垂足Q.在三角形PAC中，MN =2，2，故在直角三角形MNQ 中，2cos 2NQ MNC MN ∠==，故4MNC π∠=，故B 正确；C 选项中，当PM =1时，M 是PC 中点，如图，五边形MEGHF 即为过点M 且垂直于PC 的截面，依题意，直角三角形PME 中，2cos PMPE EPM==∠，故E 为PD 的中点，同理，F是PB 的中点，则EF 是三角形PBD 的中位线，1222EF BD ==G ，H 分别在,AD AB 的中点上，证明如下，当G ，H ，也是中点时，1//,2GH BD GH BD =，有//,22GH EF GH EF ==EFHG 是平行四边形.依题意，三角形PAC 中4,42PA PC AC ===，故PA PC ⊥，故PC GE ⊥，易见，正四棱锥中BD ⊥平面PAC ，故BD PC ⊥，GH PC ∴⊥，因为 ,GE GH 均在平面EFHG 内，且相交，所以PC ⊥平面EFHG ，故此时平面EFHG 和平面MEF 即同一平面.又BD ⊥平面PAC ，有GH ⊥面平面PAC ，GH GM ⊥，根据对称性有GH GE ⊥，四边形EFHG 是矩形. 即五边形MEGHF 即为过点M 且垂直于PC 的截面，平面图如下:依题意，22GH EF ==，2EG FG ==，三角形高为()()22321h =-=，面积是122122⨯⨯=，四边形面积是22242⨯=，故截面面积是52. 故C 正确；D 选项中，若PM =2，看B 选项中的图可知，21124M BCD P BCD P ABCD V V V V ---===，故剩余部分134P ABCD V V -=，所以123=V V ，故D 正确. 故选：BCD. 【点睛】本题考查了棱锥的截面问题，考查了二面角、体积等计算问题，属于难题.7．如图，点E 为正方形ABCD 边CD 上异于点C ，D 的动点，将ADE 沿AE 翻折成SAE △，在翻折过程中，下列说法正确的是（）A ．存在点E 和某一翻折位置，使得SB SE ⊥ B ．存在点E 和某一翻折位置，使得//AE 平面SBCC ．存在点E 和某一翻折位置，使得直线SB 与平面ABC 所成的角为45°D ．存在点E 和某一翻折位置，使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项：当SE CE ⊥时，⊥SE SB ，A 正确，//AE 平面SBC ，则//AE CB ，这与已知矛盾，故B 错误，取二面角D AE B --的平面角为α，取4=AD ，计算得到2cos 3α=，C 正确，取二面角D AE B --的平面角为60︒，计算得到tan θ=，故D 正确，得到答案. 【详解】当SE CE ⊥时，SE AB ⊥，SE SA ⊥，故SE ⊥平面SAB ，故⊥SE SB ，A 正确；若//AE 平面SBC ，因AE ⊂平面ABC ，平面ABC 平面SBC BC =，则//AE CB ，这与已知矛盾，故B 错误；如图所示：DF AE ⊥交BC 于F ，交AE 于G ，S 在平面ABCE 的投影O 在GF 上，连接BO ，故SBO ∠为直线SB 与平面ABC 所成的角，取二面角D AE B --的平面角为α，取4=AD ，3DE =，故5AE DF ==，1CE BF ==，125DG =，12cos 5OG α=，故只需满足12sin 5SO OB α==，在OFB △中，根据余弦定理：2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得2cos 3α=，故C 正确；过O 作OMAB ⊥交AB 于M ，则SMO ∠为二面角S AB C --的平面角，取二面角D AE B --的平面角为60︒，故只需满足22DG GO OM ==，设OAG OAM θ∠=∠=，84ππθ<<，则22DAG πθ∠=-，tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭，化简得到2tan tan 21θθ=，解得tan 5θ=，验证满足，故D 正确；故选：ACD .【点睛】本题考查了线线垂直，线面平行，线面夹角，二面角，意在考查学生的计算能力，推断能力和空间想象能力.8．在长方体1111ABCD A B C D -中，23AB =12AD AA ==，,,P Q R 分别是11,,AB BB AC 上的动点，下列结论正确的是（） A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥ B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥ C ．当1AR A C ⊥时，1AR D R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABD 【分析】如图所示建立空间直角坐标系，计算142D P CQ b ⋅=-，()12222D R CQ b λλ⋅=--，134AR D R ⋅=-，10D R n ⋅=，得到答案.【详解】如图所示，建立空间直角坐标系，设()2,,0P a ，0,23a ⎡∈⎣，()2,23,Q b ，[]0,2b ∈，设11A R AC λ=，得到()22,23,22R λλλ--，[]0,1λ∈. ()12,,2P a D -=，()2,0,CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；()122,23,2D R λλλ=--，()12222D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确； 1AR A C ⊥，则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=， 14λ=，此时11333313,,,,022224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，C 错误； 113AC A R =，则4234,,333R ⎛⎫ ⎪ ⎪⎝⎭，14232,,333D R ⎛⎫=- ⎪ ⎪⎝⎭，设平面1BDC 的法向量为(),,n x y z =，则10n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得()3,1,3n =-，故10D R n ⋅=，故1//D R 平面1BDC ，D 正确. 故选：ABD .【点睛】本题考查了空间中的线线垂直，线面平行，意在考查学生的计算能力和空间想象能力，推断能力.9．在边长为2的等边三角形ABC 中，点,D E 分别是边,AC AB 上的点，满足//DE BC 且AD ACλ=，（()01λ∈，），将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中，下列结论不成立的是（）A ．在边A E '上存在点F ，使得在翻折过程中，满足//BF 平面A CD 'B ．存在102λ∈⎛⎫⎪⎝⎭,，使得在翻折过程中的某个位置，满足平面A BC '⊥平面BCDEC ．若12λ=，当二面角A DE B '--为直二面角时，||104A B '=D ．在翻折过程中，四棱锥A BCDE '-体积的最大值记为()f λ，()f λ的最大值为23【答案】ABC 【分析】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，即可判断出结论.对于B ，102λ∈⎛⎫⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，即可判断出结论. 对于C ，12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，可得AM ⊥平面BCDE .可得22A B AM BM '=+，结合余弦定理即可得出.对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-，()01λ∈，，利用导数研究函数的单调性即可得出.【详解】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，如图所示，则可得FN 平行且等于BG ，即四边形BGNF 为平行四边形， ∴//NG BE ，而GN 始终与平面ACD 相交，因此在边A E '上不存在点F ，使得在翻折过程中，满足//BF 平面A CD '，A 不正确.对于B ，102λ∈⎛⎫⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，因此不满足平面A BC '⊥平面BCDE ，因此B 不正确. 对于C.12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，如图所示：可得AM ⊥平面BCDE ，则22223111010()1()21cos12022224A B AM BM '=+=++-⨯⨯⨯︒=≠，因此C 不正确；对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-，()01λ∈，，()213f λλ'=-，可得3λ=时，函数()f λ取得最大值()312313f λ⎛⎫=-=⎪⎝⎭，因此D 正确. 综上所述，不成立的为ABC. 故选：ABC. 【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值，考查了推理能力空间想象能力与计算能力，属于难题.10．如图所示，正方体ABCD A B C D ''''-的棱长为1，E ，F 分别是棱AA '，CC '的中点，过直线EF 的平面分别与棱BB '，DD '交于点M ，N ，以下四个命题中正确的是（）A ．0MN EF ⋅=B ．ME NE =C ．四边形MENF 的面积最小值与最大值之比为2:3D ．四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3 【答案】ABD 【分析】证明EF ⊥平面BDD B ''，进而得EF MN ⊥，即可得A 选项正确；证明四边形MENF 为菱形即可得B 选项正确；由菱形性质得四边形MENF 的面积12S MN EF =⋅，再分别讨论MN 的最大值与最小值即可；根据割补法求解体积即可. 【详解】对于A 选项，如图，连接BD ，B D ''，MN ．由题易得EF BD ⊥，EFBB '⊥，BD BB B '⋂=，所以EF ⊥平面BDD B ''，又MN ⊂平面BDD B ''，所以EF MN ⊥，因此0MN EF ⋅=，故A 正确．对于B 选项，由正方体性质得：平面''//BCC B 平面''ADD A ，平面''BCC B 平面EMFN MF =，平面''ADD A 平面EMFN EN =，所以//MF EN ，同理得//ME NF ，又EF MN ⊥，所以四边形MENF 为菱形，因此ME NE =，故B 正确．对于C 选项，由B 易得四边形MENF 的面积12S MN EF =⋅，所以当点M ，N 分别为BB '，DD '的中点时，四边形MENF 的面积S 最小，此时MN EF ==，即面积S 的最小值为1；当点M ，N 分别与点B （或点B '），D （或D ）重合时，四边形MENF 的面积S 最大，此时MN =，即面积S 的最大值为2所以四边形MENF 的面积最小值与最大值之比为2C 不正确．对于D 选项，四棱锥A MENF -的体积11113346M AEF N AEF AEF V V V DB S --=+=⋅==△；因为E ，F 分别是AA '，CC '的中点，所以BM D N '=，DN B M '=，于是被截面MENF 平分的两个多面体是完全相同的，则它们的体积也是相同的，因此多面体ABCD EMFN -的体积21122ABCD A B C D V V ''''-==正方体，所以四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3，故D 正确．故选：ABD ．【点睛】本题考查立体几何与向量的综合、截面面积的最值、几何体的体积，考查空间思维能力与运算求解能力，是中档题.本题解题的关键在于证明四边形MENF 为菱形，利用割补法将四棱锥A MENF -的体积转化为三棱锥M AEF - 和N AEF -的体积之和，将多面体ABCD EMFN -的体积转化为正方体的体积的一半求解.。

高三数学立体几何试题答案及解析

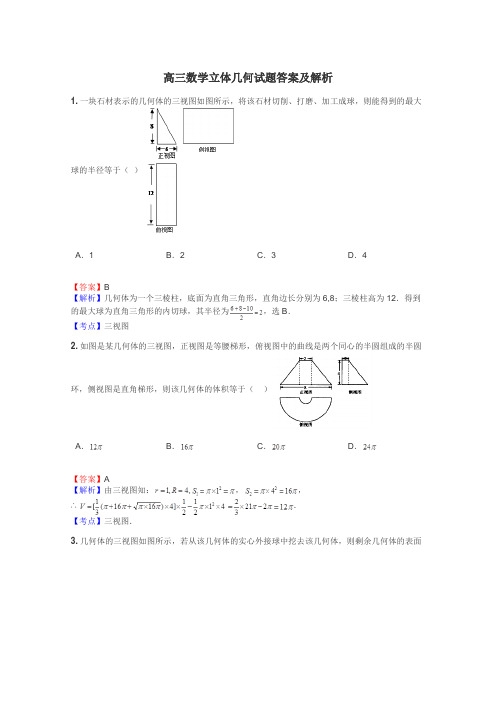
高三数学立体几何试题答案及解析1.一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A．1B．2C．3D．4【答案】B【解析】几何体为一个三棱柱，底面为直角三角形，直角边长分别为6,8；三棱柱高为12．得到的最大球为直角三角形的内切球，其半径为，选B．【考点】三视图2.如图是某几何体的三视图，正视图是等腰梯形，俯视图中的曲线是两个同心的半圆组成的半圆环，侧视图是直角梯形，则该几何体的体积等于（）A．B．C．D．【答案】A【解析】由三视图知：，，∴．【考点】三视图．3.几何体的三视图如图所示，若从该几何体的实心外接球中挖去该几何体，则剩余几何体的表面积是（注：包括外表面积和内表面积）（）A．133B．100C．66D．166【答案】D【解析】由三视图知，该几何体为底面半径为3，搞为8的圆柱．其外接球时半径为5的球．则剩余几何体的表面积是球的表面积与该圆柱表面积的和，即．故选D．【考点】多面体及与其外接球的关系及几何体表面积计算问题．4.（本小题满分12分）如图，已知五面体，其中内接于圆，是圆的直径，四边形为平行四边形，且平面．（1）证明：；（2）若，，且二面角所成角的正切值是，试求该几何体的体积．【答案】（1）见解析；（2）8．【解析】（1）将问题转化为证明平面，再转化为证明（由直径可证）与（由平面可证）；（2）考虑建立空间直角坐标系，通过求两个法向量的夹角来确定二面角所成角的正切值，并确定的长，进而可求得几何体的体积．试题解析：（1）证明：是圆的直径，，又平面，又平面，且，平面又平面，（2）设，以所在直线分别为轴，轴，轴，如图所示则，，，由（Ⅰ）可得，平面，平面的一个法向量是设为平面的一个法向量由条件得，，即不妨令，则，，．又二面角所成角的正切值是，，得该几何体的体积是【考点】1、空间直线与直线、直线与平面的垂直的判定与性质；2、二面角；3、空间几何体的体积．【方法点睛】用空间向量处理某些立体几何问题时，除要有应用空间向量的意识外，关键是根据空间图形的特点建立恰当的空间直角坐标系．若坐标系选取不当，计算量就会增大．总之树立用数解形的观念，即用数形结合的思想解决问题，而建立空间直角坐标系通常考虑以特殊点为坐标原点（如中点、正方体的顶点），特殊直线（如有两两垂直的直线）为坐标轴来建立．5.如图，在多面体中，为菱形，，平面，平面，为的中点，若平面．（1）求证：平面；（2）若，求二面角的余弦值．【答案】（1）见解析；（2）．【解析】（1）证明线面垂直，只要证明这条直线与平面内两条相交直线垂直即可，取中点，连接，可证，先证，即可证明，即可证明结论成立；（2）建立空间直角坐标系，求出平面与平面的法向量，由空间向量公式直接计算即可．试题解析：（1）取AB的中点M，连结GM，MC，G为BF的中点，所以GM //FA，又EC面ABCD， FA面ABCD，∵CE//AF，∴CE//GM，∵面CEGM面ABCD=CM，EG// 面ABCD，∴EG//CM，∵在正三角形ABC中，CM AB，又AF CM∴EG AB， EG AF，∴EG面ABF．（2）建立如图所示的坐标系，设AB=2，则B（）E（0，1，1） F（0，-1，2）=（0，-2，1），=（，-1，-1），=（，1， 1），设平面BEF的法向量=（）则令，则，∴=（）同理，可求平面DEF的法向量 =（-）设所求二面角的平面角为，则=．【考点】1．线面垂直的判定与性质；2．空间向量的应用．【方法点睛】本题主要考查线面垂直的判定与性质、空间向量的应用，属中档题．解答空间几何体中的平行、垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间的平行、垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；求二面角，则通过求两个半平面的法向量的夹角间接求解．此时建立恰当的空间直角坐标系以及正确求出各点的坐标是解题的关键所在．6.三棱锥及其三视图中的正视图和侧视图如下图所示,，则棱的长为．【答案】．【解析】由已知三视图可知，平面，且底面为等腰三角形．在中，，边上的高为，所以．在中，由可得，故应填．【考点】1、三视图．【易错点晴】本题主要考查了空间几何体的三视图及其空间几何体的面积、体积的计算，考查学生空间想象能力和计算能力，属中档题．其解题过程中容易出现以下错误：其一是不能准确利用已知条件的三视图得出原几何体的空间形状，即不能准确找出该几何体中线线关系、线面关系，导致出现错误；其二是计算不仔细，导致结果出现错误．解决这类问题的关键是正确地处理三视图与原几何体之间的关系．7.在三棱锥中，平面为侧棱上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（）A．平面且三棱锥的体积为B．平面且三棱锥的体积为C．平面且三棱锥的体积为D．平面且三棱锥的体积为【答案】C【解析】∵平面，∴，又，∴平面，∴，又由三视图可得在中，为的中点，∴平面．又平面．故．故选：C．【考点】1．直线与平面垂直的判定；2．命题的真假判断与应用；3．简单空间图形的三视图．8.已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的体积等于（）A．B．C．D．【答案】C【解析】题设三视图是下图中几何体的三视图，由三视图中的尺寸，知其体积为，故选C．【考点】三视图与几何体的体积．9.如图，在三棱柱ABC A1B1C1中，D，E分别为A1C1，BB1的中点，B1C⊥AB，侧面BCC1B1为菱形．求证：（Ⅰ）DE∥平面ABC1；（Ⅱ）B1C⊥DE．【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析．【解析】（Ⅰ）取AA1的中点F，连DF，FE，根据中点易证线线平行，从而平面DEF∥平面ABC1，又因为DE平面DEF，所以B1C⊥DE；（Ⅱ）在菱形中B1C⊥BC1，又B1C⊥AB，易证B1C⊥平面ABC1，再根据面面平行的性质，得：B1C⊥平面DEF，从而证明B1C⊥DE．试题解析：（Ⅰ）如图，取AA1的中点F，连DF，FE．又因为D，E分别为A1C1，BB1的中点，所以DF∥AC1，EF∥AB．因为DF平面ABC1，AC1平面ABC1，故DF∥平面ABC1．同理，EF∥平面ABC1．因为DF，EF为平面DEF内的两条相交直线，所以平面DEF∥平面ABC1．因为DE平面DEF，所以DE∥平面ABC1．（Ⅱ）因为三棱柱ABC A1B1C1的侧面BCC1B1为菱形，故B1C⊥BC1．……9分又B1C⊥AB，且AB，BC1为平面ABC1内的两条相交直线，所以B1C⊥平面ABC1．而平面DEF∥平面ABC1，所以B1C⊥平面DEF，因为DE平面DEF，所以B1C⊥DE．【考点】1、线面平行；2、面面平行；3、线面垂直；4、三角形中位线．【方法点晴】本题主要考查的是线面平行、线线平行、线线垂直和线面垂直，属于中档题．解题时一定要注意得线线平行的常用证明方法，构造中位线和平行四边形是最常用方法．证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线．10.已知，是两个不同的平面，，是两条不同的直线，则下列正确的是（）A．若，，则B．若，，，则C．若，，，则D．若，，，则【答案】C．【解析】A：或者，异面，故A错误；B：根据面面垂直的判定可知B错误；C：正确；D：或，故D错误，故选C．【考点】空间中直线平面的位置关系．11.已知三条不重合的直线和两个不重合的平面，下列命题正确的是（）A．若，，则B．若，，且，则C．若，，则D．若，，且，则【答案】D【解析】A．若，，则,错，有可能；B．若，，且，则，错，有可能；C．若，，则，错，有可能，或异面；D．若，，且，则，正确【考点】空间直线与平面，平面与平面的位置关系12.如图，三角形是边长为4的正三角形，底面，，点是的中点，点在上，且．（1）证明：平面平面；（2）求直线和平面所成角的正弦值．【答案】（1）证明见解析；（2）．【解析】（1）由底面，可得，又，可证的平面，问题得证；（2）在第一问证明的基础上，应用面面垂直的性质定理容易作出平面的垂线，即得斜线的射影，找出角，解直角三角形可得线面角的正弦．试题解析：（1）证明∵底面，底面，∴，又，，∴平面．又平面，∴平面平面．（2）解：过点作，连结．平面平面，平面平面，平面，∴平面，∴为直线和平面所成角．∵是边长为的正三角形，∴，．又∵，∴，，∴．即直线和平面所成角的正弦值为．【考点】空间垂直关系的应用和证明，直线与平面所成的角．【方法点晴】证明面面垂直只能证明线面垂直，而要证明线面垂直就得证明线线垂直，结合题中已知的垂直条件，分析容易找到哪个平面的垂线，逐步完成证明，组织步骤时一定要思路条理；对于直线与平面所成的角遵循作—证（指）—求—答的解题步骤，应当结合条件和前面证明的结论找到平面的垂线是解题的关键，本题中在第一问证明的基础上有了平面的垂面，利用面面垂直的性质定理过直线上一点作交线的垂线即为平面的垂线，连接垂足和斜足即得射影，找到线面角后解直角三角形得解．13.一个几何体的三视图如图所示，则这个几何体的外接球表面积为（）A．B．C．D．【答案】A【解析】几何体为一个三棱锥S-ABC，其中D为AC中点，且SD垂直平面ABC，BD垂直AC，则球心在SD上，设球半径为R，则外接球表面积为，选A.【考点】三视图【方法点睛】1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．14.已知正三角形的三个顶点都在半径为的球面上，球心到平面的距离为，点是线段的中点，过点作球的截面，则截面面积的最小值是_________．【答案】【解析】因为过作球的截面，当截面与垂直时，截面圆的半径最小，所以当截面与垂直时，截面圆的面积有最小值．设正三角形的外接圆圆心为，在中，，所以．在中，，所以，所以截面面积为【考点】1、多面体的外接球；2、球的截面圆性质．【方法点睛】“切”“接”问题的处理规律：①“切”的处理：解决与球的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决；②“接”的处理：把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．15.（2015•金家庄区校级模拟）如图正方形BCDE的边长为a，已知AB=BC，将△ABE沿BE边折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：①AB与DE所成角的正切值是；②AB∥CE；③VB﹣ACE的体积是a2；④平面ABC⊥平面ADC；⑤直线EA与平面ADB所成角为30°．其中正确的有．（填写你认为正确的序号）【答案】①③④⑤【解析】①由于BC∥DE，则∠ABC（或其补角）为AB与DE所成角；②AB和CE是异面直线；③根据三棱锥的体积公式即可求VB ﹣ACE的体积；④根据面面垂直的判定定理即可证明；⑤根据直线和平面所成角的定义进行求解即可．解：由题意，AB=BC，AE=a，AD⊥平面BCDE，AD=a，AC= a①由于BC∥DE，∴∠ABC（或其补角）为AB与DE所成角∵AB=a，BC=a，AC=a，∴BC⊥AC，∴tan∠ABC=，故①正确；②由图象可知AB与CE是异面直线，故②错误．③VB﹣ACE的体积是S△BCE×AD=×a3=，故③正确；（4）∵AD⊥平面BCDE，BC⊂平面BCDE，∴AD⊥BC，∵BC⊥CD，AD∩CD=D，∴BC⊥平面ADC，∵BC⊂平面ABC，∴平面ABC⊥平面ADC，故④正确；⑤连接CE交BD于F，则EF⊥BD，∵平面ABD⊥平面BDE，∴EF⊥平面ABD，连接F，则∠EAF为直线AE与平面ABD所成角，在△AFE中，EF=，AE=a，∴sin∠EAF==，则∠EAF=30°，故⑤正确，故正确的是①③④⑤故答案为：①③④⑤【考点】命题的真假判断与应用；空间中直线与直线之间的位置关系；平面与平面之间的位置关系．16.已知某几何体的三视图，则该几何体的体积是_______．【答案】．【解析】该几何体是一个四棱锥，底面是边长为2的正方形，高为，所以．【考点】1．空间几何体的表面积与体积；2．空间几何体的三视图与直观图．17.设三棱柱的侧棱垂直于底面，，且三棱柱的所有顶点都在同一球面上，则该球的表面积是．【答案】【解析】由题意可得：把三棱柱补成底面以2为边长的正方形，以为高的长方体，长方体的体对角线就是球的直径，所以，所以该球的表面积是；故填．【考点】空间几何体的表面积．18.某几何体的正视图与侧视图都是等腰梯形，则该几何体可以是下列几何体中的（）①三棱台，②四棱台，③五棱台，④圆台．A．①②B．③④C．①③D．②④【答案】D【解析】由题意得，几何体的正视图和侧视图都是等腰梯形，则根据几何体的三视图的规则可知，该几何体可能为四棱台或圆台，故选D．【考点】空间几何体的三视图．【方法点晴】本题主要考查了空间几何体的三视图的应用，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答中，只是给出了几何体的正视图和侧视图都是等腰梯形，从而可得这个几何体可能是四棱台或圆台．19.在直三棱柱中，，，且异面直线与所成的角等于，设.(1) 求的值；(2) 求三棱锥的体积．【答案】(1)； (2)【解析】(1)由BC ∥B 1C 1可得∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角，从而∠A 1BC =60°，再由AA 1⊥平面ABC ，AB=AC ，则A 1B=A 1C ，△A 1BC 为等边三角形，由已知可得，即可求得 (2)连接B 1C ，则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积，△的面积，又可得平面，利用三棱锥的体积公式可求得．试题解析：(1)∵BC ∥B 1C 1，∴∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角，即∠A 1BC =60°，又AA 1⊥平面ABC ，AB=AC ，则A 1B=A 1C ，∴△A 1BC 为等边三角形，由，， ∴； (2)连接B 1C ，则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积，即：， △的面积，又平面，所以，所以．【考点】异面直线所成的角及三棱锥的体积的求法.20. 如图，在四棱锥中，已知棱，，两两垂直，长度分别为1，2，2.若（），且向量与夹角的余弦值为.（1）求的值；（2）求直线与平面所成角的正弦值.【答案】（1）；（2）.【解析】（1）以为坐标原点，、、分别为、、轴建立空间直角坐标系，写出，的坐标，根据空间向量夹角余弦公式列出关于的方程可求；（2）设岀平面的法向量为，根据，进而得到，从而求出，向量的坐标可以求出，从而可根据向量夹角余弦的公式求出，从而得和平面所成角的正弦值.试题解析：（1）依题意，以为坐标原点，、、分别为、、轴建立空间直角坐标系，因为，所以，从而，则由，解得（舍去）或. （2）易得，，设平面的法向量，则，，即，且，所以，不妨取，则平面的一个法向量，又易得，故，所以直线与平面所成角的正弦值为.考点: 1、空间两向量夹角余弦公式；2、利用向量求直线和平面说成角的正弦.21.如图，在四棱锥中，平面，分别是棱的中点.（1）求证：平面；（2）求证：平面平面.【答案】（1）详见解析（2）详见解析【解析】（1）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与证明，往往需结合平面几何条件，如本题利用三角形中位线性质定理得（2）证明面面垂直，一般利用面面垂直判定定理，即从线面垂直出发给予证明，而线面垂直的证明，需多次利用线面垂直的判定与性质定理：先由平行四边形为菱形得，再由平面得，即，从而得平面试题解析：（1）设，连结，因为，为的中点，所以，所以四边形为平行四边形，所以为的中点，所以又因为平面，平面，所以平面.（2）（方法一）因为平面，平面所以，由（1）同理可得，四边形为平行四边形，所以，所以因为，所以平行四边形为菱形，所以，因为平面，平面，所以平面因为平面，所以平面平面.（方法二）连结，因为平面，平面，所以因为，所以，因为平面，平面，所以因为为的中点，所以，由（1），所以又因为为的中点，所以因为，平面，平面所以平面，因为平面，所以平面平面.【考点】线面平行判定定理，面面垂直判定定理22.如图，网格纸上小正方形的边长为1，粗线画出的是某个几何体的三视图，则该几何体的体积为（）A．B．C．D．【答案】A【解析】因为网格纸上小正方形的边长为,有三视图可知，该几何体是下面为底面半径为高为的圆柱体的一半、上面是底面半径为高为的圆锥体的一半，所以体积为，故选A.【考点】1、几何体的三视图；2、圆柱及圆锥的体积公式.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.23.已知如图所示的三棱锥的四个顶点均在球的球面上，和所在的平面互相垂直，，，，则球的体积为（）A．B．C．D．【答案】C【解析】因为，，，所以的中点为的外心，连接，则，又和所在的平面互相垂直，所以平面，上的每一点到距离相等，因此正三角形的中心即是外接球球心，其半径也是外接球半径，所以球半径，求体积为，故选C.【考点】1、外接球的性质及勾股定理；2、面面垂直及球的体积公式.【方法点睛】本题主要考查外接球的性质及勾股定理、面面垂直及三棱锥外接球体积的求法，属于难题.要求外接球的表面积和体积，关键是求出求的半径，求外接球半径的常见方法有：①若三条棱两垂直则用（为三棱的长）；②若面（），则（为外接圆半径）；③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.本题是根据方法④直接找出球心并求出半径进而得到求体积的.24.四棱锥的底面是正方形，，分别是的中点（1）求证：；（2）设与交于点，求点到平面的距离【答案】（1）证明见解析；（2）．【解析】（1）要证明线面垂直，一般先证明线线垂直，本题中，由于是中点，因此有，而与垂直，从而与平面垂直，结论得证；（2）要求点到平面的距离，考虑三棱锥，的面积易求（为面积的一半），另外由（1）的结论，此三棱锥以为底时，是高，体积易求，从而所求距离易得．试题解析：（1）证明：连接，由于分别是的中点，所以，又，平面，故，又为正方形，故故，故（2）连接交于点，连接，则交线为，又，故，由于分别是的中点，故为的中点，又，故为三棱锥的高又故，又设点到平面的距离为，，所以【考点】线面垂直的判断，点到平面的距离．25.某几何体的三视图如图，则该几何体的体积为（）A．B．C．D．【答案】C【解析】由题意得，由几何体的三视图，知该几何体是上下底面为梯形的直棱柱，所以该几何体的体积为，故选C.【考点】几何体的三视图及几何体的体积.【方法点晴】本题主要考查了空间几何体的三视图的应用，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答中，该几何体是上下底面为梯形的直棱柱是解答本题的关键，属于基础题.26.一个几何体的三视图如图，则这个几何体的表面积是（）A．B．C．D．【答案】C【解析】由题意得，根据给定的几何体的三视图，可知，原几何体为正方体的一部分，如图所示的红线部分，是一个棱长为的正四面体，所以此几何体的表面积为，故选C．【考点】几何体的三视图与表面积．27.某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2，体积是______cm3.【答案】80，40【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体，，．【考点】三视图.【方法点睛】解决由三视图求空间几何体的表面积与体积问题，一般是先根据三视图确定该几何体的结构特征，再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积．28.如图，在四棱锥中，平面平面，，，，，，.（Ⅰ）求证：平面；（Ⅱ）求直线PB与平面PCD所成角的正弦值；（Ⅲ）在棱PA上是否存在点M，使得BM∥平面PCD?若存在，求的值；若不存在，说明理由.【答案】（Ⅰ）见解析；（Ⅱ）；（Ⅲ）存在，.【解析】（Ⅰ）由面面垂直的性质定理知AB⊥平面，根据线面垂直的性质定理可知，再由线面垂直的判定定理可知平面；（Ⅱ）取的中点，连结，以O为坐标原点建立空间直角坐标系O-xyz，利用向量法可求出直线PB与平面PCD所成角的正弦值；（Ⅲ）假设存在，根据A，P，M三点共线，设，根据BM∥平面PCD，即（为平面PCD的法向量），求出的值，从而求出的值.试题解析：（Ⅰ）因为平面平面，，所以平面.所以.又因为，所以平面.（Ⅱ）取的中点，连结.因为，所以.又因为平面，平面平面，所以平面.因为平面，所以.因为，所以.如图建立空间直角坐标系.由题意得，.设平面的法向量为，则即令，则.所以.又，所以.所以直线与平面所成角的正弦值为.（Ⅲ）设是棱上一点，则存在使得.因此点.因为平面，所以平面当且仅当，即，解得.所以在棱上存在点使得平面，此时.【考点】空间线面垂直的判定定理与性质定理；线面角的计算；空间想象能力，推理论证能力【名师】平面与平面垂直的性质定理的应用：当两个平面垂直时，常作的辅助线是在其中一个平面内作交线的垂线，把面面垂直转化为线面垂直，进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系)，构造(寻找)二面角的平面角或得到点到面的距离等.29.如图，在四棱锥中，底面是菱形，，平面，，点分别为和中点.（1）求证：直线平面；（2）求三棱锥的表面积.【答案】（1）证明见解析；（2）．【解析】（1）要证线面平行，一般先证线线平行，考虑到，是中点，因此取的中点，可证得且，从而得平行四边形，因此有，最终得线面平行；（2）要求三棱锥的表面积，必须求得它的各个面的面积，由平面，得，三角形和的面积可求，由题设又可证，这样就有，另两个面的面积又可求得．试题解析：（1）证明：作FM∥CD交PC于M.∵点F为PD中点，∴. ∴，∴AEMF为平行四边形，∴AF∥EM，∵，∴直线AF平面PEC.（2）连结可知，，由此；；；；因此三棱锥的表面积.【考点】线面平行的判断，多面体的表面积．30.在棱长为3的正方体中，在线段上，且，为线段上的动点，则三棱锥的体积为（）A．1B．C．D．与点的位置有关【答案】B【解析】由于是定值,点到平面的距离是,因此点平面的距离是.所以三棱锥的体积,应选B.【考点】三棱锥体积的运算．31.如图，在多面体中，底面是边长为2的正方形，四边形是矩形，且平面平面，，和分别是和的中点.（1）求证：平面；（2）求.【答案】（1）证明见解析；（2）.【解析】（1）运用线面平行的判定定理求证；（2）借助题设条件及转化化归的思想求解即可. 试题解析:（1）证明：设，连接，在中，因为，，所以，又因为平面，平面，所以平面.（2）因为四边形是正方形，所以，又因为平面平面，平面平面，且平面，所以平面，则到平面的距离为的一半，又因为，所以，所以.【考点】直线与平面的位置关系及棱锥公式的运用．32.如图，在三棱柱中，，，，在底面的射影为的中点，是的中点.（1）证明：平面；（2）求二面角的平面角的余弦值.【答案】（1）证明见解析；（2）.【解析】（1）设为的中点，连接，依题意有，，故平面.根据分析有，故平面；（2）以的中点为原点，分别以射线为轴的正半轴，建立空间直角坐标系，利用向量法求得余弦值为.试题解析：（1）设为的中点，连接.由题意得：平面，所以.因为，所以，，故平面.由分别为的中点，得且，从而且，所以为平行四边形，故，又因为平面，所以平面.（2）方法一：作，且，连结.由，，得，由，，得与全等.由，得，因此为二面角的平面角.由，，，得，，由余弦定理得.方法二：以的中点为原点，分别以射线为轴的正半轴，建立空间直角坐标系，如图所示，由题意知各点坐标如下：，因此，，，设平面的法向量为，平面的法向量为，由，即，可取.由，即，可取，于是.由题意可知，所求二面角的平面角是钝角，故二面角的平面角的余弦值为.【考点】空间向量与立体几何.33.某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，从左往右为半个圆锥，一个圆柱，一个半圆，故体积为.【考点】三视图.34.如图，在四棱柱中，底面，为线段上的任意一点（不包括两点），平面与平面交于.（1）证明：；（2）证明：平面.【答案】（1）证明见解析；（2）证明见解析．【解析】（1）要证线线垂直，一般可证线面垂直，观察题中垂直条件，平面，则有，题中又有，从而有平面，因此结论得证；（2）要证线面平行，就是要证线线平行，直线是平面与平面的交线，因此要得平行，就要有线面平行，而这由可得平面，从而，结论得证．试题解析：（1）证明：因为平面，平面，所以.又，所以平面，而平面，所以.（2）在四棱柱中，，平面，平面，所以平面，又平面，平面与平面交于，所以，因为，所以，而平面，平面，所以平面.【考点】线面垂直的判定与性质，线面平行的判定与性质．【名师】证明线面（面面）平行（垂直）时要注意以下几点：（1）由已知想性质，由求证想判定，即分析法与综合法相结合寻找证题思路。

高三精选立体几何大题30题(含详细解答)

A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。

（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。

（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

. .. .2014 高考及模拟立体几何带答案一．解答题（共17小题）1．（2014•）如图，四棱锥P﹣ABCD中，AP⊥平面PCD，AD∥BC，AB=BC=AD，E，F分别为线段AD，PC的中点．（Ⅰ）求证：AP∥平面BEF；（Ⅱ）求证：BE⊥平面PAC．2．（2014•）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明：直线BC⊥平面ACC1A1；（Ⅱ）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．3．（2014•）在四棱锥P﹣ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）求证：BC⊥平面PBD；（Ⅲ）设Q为侧棱PC上一点，，试确定λ的值，使得二面角Q﹣BD﹣P为45°．4．（2014•）如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：（1）直线PA∥平面DEF；（2）平面BDE⊥平面ABC．5．（2014•一模）如图，PA垂直于矩形ABCD所在的平面，AD=PA=2，CD=2，E、F分别是AB、PD的中点．（1）求证：AF∥平面PCE；（2）求证：平面PCE⊥平面PCD；（3）求四面体PEFC的体积．6．（2014•南海区模拟）如图，四棱锥P﹣ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求证：OE∥平面PDC；（Ⅲ）求直线CB与平面PDC所成角的正弦值．7．（2014•天津模拟）如图，在四棱台ABCD﹣A1B1C1D1中，下底ABCD是边长为2的正方形，上底A1B1C1D1是边长为1的正方形，侧棱DD1⊥平面ABCD，DD1=2．（1）求证：B1B∥平面D1AC；（2）求证：平面D1AC⊥平面B1BDD1．8．（2013•）如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E 和F分别是CD和PC的中点，求证：（Ⅰ）PA⊥底面ABCD；（Ⅱ）BE∥平面PAD；（Ⅲ）平面BEF⊥平面PCD．9．（2013•天津）如图，三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．（Ⅰ）证明：EF∥平面A1CD；（Ⅱ）证明：平面A1CD⊥平面A1ABB1；（Ⅲ）求直线BC与平面A1CD所成角的正弦值．10．（2013•）如图，在四棱锥P﹣ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=，PA=，∠ABC=120°，G为线段PC上的点．（Ⅰ）证明：BD⊥平面PAC；（Ⅱ）若G是PC的中点，求DG与PAC所成的角的正切值；（Ⅲ）若G满足PC⊥面BGD，求的值．11．（2013•）如图．在直棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=，AA1=3，D是BC的中点，点E在棱BB1上运动．（1）证明：AD⊥C1E；（2）当异面直线AC，C1E 所成的角为60°时，求三棱锥C1﹣A1B1E的体积．12．（2012•）如图，几何体E﹣ABCD是四棱锥，△ABD为正三角形，CB=CD，EC⊥BD．（Ⅰ）求证：BE=DE；（Ⅱ）若∠BCD=120°，M为线段AE的中点，求证：DM∥平面BEC．13．（2012•）如图，在直三棱柱ABC﹣A1B1C1中，A1B1=A1C1，D，E分别是棱BC，CC1上的点（点D 不同于点C），且AD⊥DE，F为B1C1的中点．求证：（1）平面ADE⊥平面BCC1B1；（2）直线A1F∥平面ADE．14．（2011•天津）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC 中点，PO⊥平面ABCD，PO=2，M为PD中点．（Ⅰ）证明：PB∥平面ACM；（Ⅱ）证明：AD⊥平面PAC；（Ⅲ）求直线AM与平面ABCD所成角的正切值．15．（2011•）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．16．（2010•模拟）如图，在四棱锥S﹣ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，E、F分别是AB、SC的中点（1）求证：EF∥平面SAD（2）设SD=2CD，求二面角A﹣EF﹣D的大小．17．（2010•）如图，三棱锥P﹣ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB．（1）求证：AB⊥平面PCB；（2）求二面角C﹣PA﹣B的大小的余弦值．2014年12月05日的高中数学组卷参考答案与试题解析一．解答题（共17小题）1．（2014•）如图，四棱锥P﹣ABCD中，AP⊥平面PCD，AD∥BC，AB=BC=AD，E，F分别为线段AD，PC的中点．（Ⅰ）求证：AP∥平面BEF；（Ⅱ）求证：BE⊥平面PAC．考点：直线与平面垂直的判定；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（Ⅰ）证明四边形ABCE是平行四边形，可得O是AC的中点，利用F为线段PC的中点，可得PA∥OF，从而可证AP∥平面BEF；（Ⅱ）证明BE⊥AP、BE⊥AC，即可证明BE⊥平面PAC．解答：证明：（Ⅰ）连接CE，则∵AD∥BC，BC=AD，E为线段AD的中点，∴四边形ABCE是平行四边形，BCDE是平行四边形，设AC∩BE=O，连接OF，则O是AC的中点，∵F为线段PC的中点，∴PA∥OF，∵PA⊄平面BEF，OF⊂平面BEF，∴AP∥平面BEF；（Ⅱ）∵BCDE是平行四边形，∴BE∥CD，∵AP⊥平面PCD，CD⊂平面PCD，∴AP⊥CD，∴BE⊥AP，∵AB=BC，四边形ABCE是平行四边形，∴四边形ABCE是菱形，∴BE⊥AC，∵AP∩AC=A，∴BE⊥平面PAC．点评：本题考查直线与平面平行、垂直的判定，考查学生分析解决问题的能力，正确运用直线与平面平行、垂直的判定是关键2．（2014•）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明：直线BC⊥平面ACC1A1；（Ⅱ）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．考点：直线与平面垂直的判定；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（Ⅰ）先证明AA1⊥平面ABC，可得AA1⊥BC，利用AC⊥BC，可以证明直线BC⊥平面ACC1A1；（Ⅱ）取AB的中点M，连接A1M，MC，A1C，AC1，证明四边形MDEO为平行四边形即可．解答：（Ⅰ）证明：∵四边形ABB1A1和ACC1A1都为矩形，∴AA1⊥AB，AA1⊥AC，∵AB∩AC=A，∴AA1⊥平面ABC，∵BC⊂平面ABC，∴AA1⊥BC，∵AC⊥BC，AA1∩AC=A，∴直线BC⊥平面ACC1A1；（Ⅱ）解：取AB的中点M，连接A1M，MC，A1C，AC1，设O为A1C，AC1的交点，则O为AC1的中点．连接MD，OE，则MD∥AC，MD=AC，OE∥AC，OE=AC，∴MD∥OE，MD=OE，连接OM，则四边形MDEO为平行四边形，∴DE∥MO，∵DE⊄平面A1MC，MO⊂平面A1MC，∴DE∥平面A1MC，∴线段AB上存在一点M（线段AB的中点），使直线DE∥平面A1MC．点评：本题考查线面垂直的判定与性质的运用，考查存在性问题，考查学生分析解决问题的能力，属于中档题．3．（2014•）在四棱锥P﹣ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）求证：BC⊥平面PBD；（Ⅲ）设Q为侧棱PC上一点，，试确定λ的值，使得二面角Q﹣BD﹣P为45°．考点：直线与平面平行的判定；直线与平面垂直的判定；与二面角有关的立体几何综合题．专题：证明题．分析：（Ⅰ）取PD的中点F，连接EF、AF，由中位线得性质和AB∥CD及AB=1证出四边形ABEF为平行四边形，则BE∥AF，根据线面平行的判定得BE∥平面PAD；（Ⅱ）由平面PCD⊥底面ABCD，PD⊥CD证出PD⊥AD，利用三条线相互垂直关系，建立直角坐标系，求出，即BC⊥DB，再由PD⊥平面ABCD，可得PD⊥BC，即证BC⊥平面PBD；（Ⅲ）利用（Ⅱ）建立的坐标系和结论，求出平面PBD的法向量，利用求出Q的坐标，再利用垂直关系求平面QBD的法向量的坐标，由两个法向量的数量积运算表示二面角的余弦值，化简后求出λ∈（0，1）的值．解答：解：（Ⅰ）取PD的中点F，连接EF，AF，∵E为PC中点，∴EF∥CD，且，在梯形ABCD中，AB∥CD，AB=1，∴EF∥AB，EF=AB，∴四边形ABEF为平行四边形，∴BE∥AF，∵BE⊄平面PAD，AF⊂平面PAD，∴BE∥平面PAD．（4分）（Ⅱ）∵平面PCD⊥底面ABCD，PD⊥CD，∴PD⊥平面ABCD，∴PD⊥AD．（5分）如图，以D为原点建立空间直角坐标系D﹣xyz．则A（1，0，0），B（1，1，0），C（0，2，0），P（0，0，1）．（6分），，∴，BC⊥DB，（8分）又由PD⊥平面ABCD，可得PD⊥BC，∴BC⊥平面PBD．（9分）（Ⅲ）由（Ⅱ）知，平面PBD的法向量为，（10分）∵，，且λ∈（0，1）∴Q（0，2λ，1﹣λ），（11分）设平面QBD的法向量为=（a，b，c），，，由，，得，∴，（12分）∴，（13分）因λ∈（0，1），解得．（14分）点评：本题用了几何法和向量法进行证明平行及垂直关系、求值，有中点时通常构造中位线证明线线平行，根据线面平行的判定定理转化到线面平行；向量法主要利用数量积为零证明垂直，对待二面角、线面角问题用向量法要简单些，建立坐标系要利用几何体中的垂直条件．4．（2014•）如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：（1）直线PA∥平面DEF；（2）平面BDE⊥平面ABC．考点：平面与平面垂直的判定；直线与平面垂直的判定．专题：证明题；空间位置关系与距离．分析：（1）由D、E为PC、AC的中点，得出DE∥PA，从而得出PA∥平面DEF；（2）要证平面BDE⊥平面ABC，只需证DE⊥平面ABC，即证DE⊥EF，且DE⊥AC即可．解答：证明：（1）∵D、E为PC、AC的中点，∴DE∥PA，又∵PA⊄平面DEF，DE⊂平面DEF，∴PA∥平面DEF；（2）∵D、E为PC、AC的中点，∴DE=PA=3；又∵E、F为AC、AB的中点，∴EF=BC=4；∴DE2+EF2=DF2，∴∠DEF=90°，∴DE⊥EF；∵DE∥PA，PA⊥AC，∴DE⊥AC；∵AC∩EF=E，∴DE⊥平面ABC；∵DE⊂平面BDE，∴平面BDE⊥平面ABC．点评：本题考查了空间中的平行与垂直问题，解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系，是基础题目．5．（2014•一模）如图，PA垂直于矩形ABCD所在的平面，AD=PA=2，CD=2，E、F分别是AB、PD的中点．（1）求证：AF∥平面PCE；（2）求证：平面PCE⊥平面PCD；（3）求四面体PEFC的体积．考点：直线与平面平行的判定；棱锥的结构特征；平面与平面垂直的判定．专题：计算题；证明题．分析：（1）设G为PC的中点，连接FG，EG，根据中位线定理得到FG CD，AE CD，进而可得到AF∥GE，再由线面平行的判定定理可证明AF∥平面PCE，得证．（2）根据PA=AD=2可得到AF⊥PD，再由线面垂直的性质定理可得到PA⊥CD，然后由AD⊥CD结合线面垂直的判定定理得到CD⊥平面PAD，同样得到GE⊥平面PCD，再由面面垂直的判定定理可得证．（3）先由（2）可得知EG为四面体PEFC的高，进而求出S△PCF，根据棱锥的体积公式可得到答案．解答：解：（1）证明：设G为PC的中点，连接FG，EG，∵F为PD的中点，E为AB的中点，∴FG CD，AE CD∴FG AE，∴AF∥GE∵GE⊂平面PEC，∴AF∥平面PCE；（2）证明：∵PA=AD=2，∴AF⊥PD又∵PA⊥平面ABCD，CD⊂平面ABCD，∴PA⊥CD，∵AD⊥CD，PA∩AD=A，∴CD⊥平面PAD，∵AF⊂平面PAD，∴AF⊥CD．∵PD∩CD=D，∴AF⊥平面PCD，∴GE⊥平面PCD，∵GE⊂平面PEC，∴平面PCE⊥平面PCD；（3）由（2）知，GE⊥平面PCD，所以EG为四面体PEFC的高，又GF∥CD，所以GF⊥PD，EG=AF=，GF=CD=，S△PCF=PD•GF=2．得四面体PEFC的体积V=S△PCF•EG=．点评：本题主要考查线面垂直的判定定理和性质定理、面面垂直的判定定理．考查对立体几何中基本定理的掌握程度和灵活运用能力．6．（2014•南海区模拟）如图，四棱锥P﹣ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求证：OE∥平面PDC；（Ⅲ）求直线CB与平面PDC所成角的正弦值．考点：直线与平面平行的判定；直线与平面垂直的判定；直线与平面所成的角．专题：证明题．分析：（Ⅰ）由条件先证明四边形ABFD为正方形，由等腰三角形的性质证明PO⊥BD，由勾股定理求得PO⊥AO，从而证得PO⊥平面ABCD．（Ⅱ）过O分别做AD，AB的平行线，以它们做x，y轴，以OP为z轴建立如图所示的空间直角坐标系，求出和的坐标，由可得OE∥PF，从而证得OE∥平面PDC．（Ⅲ）设平面PDC的法向量为，直线CB与平面PDC所成角θ，求出一个法向量为，又，可得和夹角的余弦值，即为直线CB与平面PDC所成角的正弦值．解答：解：（Ⅰ）证明：设F为DC的中点，连接BF，则DF=AB．∵AB⊥AD，AB=AD，AB∥DC，∴四边形ABFD 为正方形．∵O为BD的中点，∴O为AF，BD的交点，∵PD=PB=2，∴PO⊥BD，…..（2分）∵=，∴=，，在三角形PAO中，PO2+AO2=PA2=4，∴PO⊥AO，…（4分）∵AO∩BD=O，∴PO⊥平面ABCD．…（5分）（Ⅱ）由（Ⅰ）知PO⊥平面ABCD，又AB⊥AD，所以过O分别做AD，AB的平行线，以它们做x，y轴，以OP为z轴建立如图所示的空间直角坐标系，如图所示：由已知得：A（﹣1，﹣1，0），B（﹣1，1，0），D（1，﹣1，0）F（1，1，0），C（1，3，0），，．则，，，．∴，∴OE∥PF，∵OE⊄平面PDC，PF⊂平面PDC，∴OE∥平面PDC．…（9分）（Ⅲ）设平面PDC的法向量为，直线CB与平面PDC所成角θ，则，即，解得，令z1=1，则平面PDC的一个法向量为，又，则，∴直线CB与平面PDC所成角的正弦值为．…（14分）点评：本题考查证明线面平行、线面垂直的方法，求直线和平面所成的角，体现了数形结合的数学思想，把CB和平面PDC所称的角的正弦值转化为CB和平面PDC的法向量夹角的余弦值，是解题的难点和关键．7．（2014•天津模拟）如图，在四棱台ABCD﹣A1B1C1D1中，下底ABCD是边长为2的正方形，上底A1B1C1D1是边长为1的正方形，侧棱DD1⊥平面ABCD，DD1=2．（1）求证：B1B∥平面D1AC；（2）求证：平面D1AC⊥平面B1BDD1．考点：直线与平面平行的判定；平面与平面垂直的判定．专题：证明题．分析：（1）设AC∩BD=E，连接D1E，根据平面ABCD∥平面A1B1C1D1的性质得B1D1∥BE，而B1D1=BE=，则四边形B1D1EB是平行四边形，从而B1B∥D1E，又因B1B⊄平面D1AC，D1E⊂平面D1AC，根据线面平行的判定定理可知B1B∥平面D1AC；（2）根据侧棱DD1⊥平面ABCD，AC⊂平面ABCD，得AC⊥DD1．而下底ABCD是正方形则AC⊥BD，根据DD1与DB是平面B1BDD1的两条相交直线，则AC⊥平面B1BDD1，AC⊂平面D1AC，根据面面垂直的判定定理可知平面D1AC⊥平面B1BDD1．解答：证明：（1）设AC∩BD=E，连接D1E，∵平面ABCD∥平面A1B1C1D1．∴B1D1∥BE，∵B1D1=BE=，∴四边形B1D1EB是平行四边形，所以B1B∥D1E．又因为B1B⊄平面D1AC，D1E⊂平面D1AC，所以B1B∥平面D1AC（2）证明：侧棱DD1⊥平面ABCD，AC⊂平面ABCD，∴AC⊥DD1．∵下底ABCD是正方形，AC⊥BD．∵DD1与DB是平面B1BDD1的两条相交直线，∴AC⊥平面B1BDD1∵AC⊂平面D1AC，∴平面D1AC⊥平面B1BDD1．点评：本题主要考查了直线与平面平行、直线与平面垂直的判定定理，同时考查了空间想象能力以及推理能力，涉及到的知识点比较多，知识性技巧性都很强．8．（2013•）如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E 和F分别是CD和PC的中点，求证：（Ⅰ）PA⊥底面ABCD；（Ⅱ）BE∥平面PAD；（Ⅲ）平面BEF⊥平面PCD．考点：直线与平面平行的判定；直线与平面垂直的判定；平面与平面垂直的判定．专题：空间位置关系与距离．分析：（Ⅰ）根据条件，利用平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅱ）根据已知条件判断ABED为平行四边形，故有BE∥AD，再利用直线和平面平行的判定定理证得BE∥平面PAD．（Ⅲ）先证明ABED为矩形，可得BE⊥CD ①．现证CD⊥平面PAD，可得CD⊥PD，再由三角形中位线的性质可得EF∥PD，从而证得CD⊥EF ②．结合①②利用直线和平面垂直的判定定理证得CD⊥平面BEF，再由平面和平面垂直的判定定理证得平面BEF⊥平面PCD．解答：解：（Ⅰ）∵PA⊥AD，平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，由平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅱ）∵AB∥CD，AB⊥AD，CD=2AB，E和F分别是CD和PC的中点，故四边形ABED为平行四边形，故有BE∥AD．又AD⊂平面PAD，BE不在平面PAD，故有BE∥平面PAD．（Ⅲ）平行四边形ABED中，由AB⊥AD可得，ABED为矩形，故有BE⊥CD ①．由PA⊥平面ABCD，可得PA⊥AB，再由AB⊥AD可得AB⊥平面PAD，∴CD⊥平面PAD，故有CD⊥PD．再由E、F分别为CD和PC的中点，可得EF∥PD，∴CD⊥EF ②．而EF和BE是平面BEF的两条相交直线，故有CD⊥平面BEF．由于CD⊂平面PCD，∴平面BEF⊥平面PCD．点评：本题主要考查直线和平面垂直的判定定理，直线和平面平行的判定定理，平面和平面垂直的判定定理、性质定理的应用，属于中档题．9．（2013•天津）如图，三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．（Ⅰ）证明：EF∥平面A1CD；（Ⅱ）证明：平面A1CD⊥平面A1ABB1；（Ⅲ）求直线BC与平面A1CD所成角的正弦值．考点：直线与平面平行的判定；平面与平面垂直的判定；直线与平面所成的角．专题：空间位置关系与距离；空间角．分析：（I）连接ED，要证明EF∥平面平面A1CD，只需证明EF∥DA1即可；（II）欲证平面平面A1CD⊥平面A1ABB1，即证平面一直线与另一平面垂直，根据直线与平面垂直的判定定理证得CD⊥面A1ABB1，再根据面面垂直的判定定理得证；（III）先过B作BG⊥AD交A1D于G，利用（II）中结论得出BG⊥面A1CD，从而∠BCG为所求的角，最后在直角△BGC中，求出sin∠BCG即可得出直线BC与平面A1CD所成角的正弦值．解答：证明：（I）三棱柱ABC﹣A1B1C1中，AC∥A1C1，AC=A1C1，连接ED，可得DE∥AC，DE=AC，又F为棱A1C1的中点．∴A1F=DE，A1F∥DE，所以A1DEF是平行四边形，所以EF∥DA1，DA1⊂平面A1CD，EF⊄平面A1CD，∴EF∥平面A1CD（II）∵D是AB的中点，∴CD⊥AB，又AA1⊥平面ABC，CD⊂平面ABC，∴AA1⊥CD，又AA1∩AB=A，∴CD⊥面A1ABB1，又CD⊂面A1CD，∴平面A1CD⊥平面A1ABB1；（III）过B作BG⊥A1D交A1D于G，∵平面A1CD⊥平面A1ABB1，且平面A1CD∩平面A1ABB1=A1D，BG⊥A1D，∴BG⊥面A1CD，则∠BCG为所求的角，设棱长为a，可得A1D=，由△A1AD∽△BGD，得BG=，在直角△BGC中，sin∠BCG==，∴直线BC与平面A1CD所成角的正弦值．点评：本题主要考查了平面与平面垂直的判定，直线与平面所成的角，以及直线与平面平行的判定，考查空间想象能力、运算能力和推理论证能力，属于基础题．10．（2013•）如图，在四棱锥P﹣ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=，PA=，∠ABC=120°，G为线段PC上的点．（Ⅰ）证明：BD⊥平面PAC；（Ⅱ）若G是PC的中点，求DG与PAC所成的角的正切值；（Ⅲ）若G满足PC⊥面BGD，求的值．考点：直线与平面垂直的判定；直线与平面所成的角；点、线、面间的距离计算．专题：空间位置关系与距离；空间角．分析：（Ⅰ）由PA⊥面ABCD，可得PA⊥BD；设AC与BD的交点为O，则由条件可得BD是AC的中垂线，故O为AC的中点，且BD⊥AC．再利用直线和平面垂直的判定定理证得BD⊥面PAC．（Ⅱ）由三角形的中位线性质以及条件证明∠DGO为DG与平面PAC所成的角，求出GO和AC的值，可得OC、OD的值，再利用直角三角形中的边角关系求得tan∠DGO的值．（Ⅲ）先证PC⊥OG，且PC==．由△COG∽△CAP，可得，解得GC的值，可得PG=PC﹣GC 的值，从而求得的值．解答：解：（Ⅰ）证明：∵在四棱锥P﹣ABCD中，PA⊥面ABCD，∴PA⊥BD．∵AB=BC=2，AD=CD=，设AC与BD的交点为O，则BD是AC的中垂线，故O为AC的中点，且BD⊥AC．而PA∩AC=A，∴BD⊥面PAC．（Ⅱ）若G是PC的中点，O为AC的中点，则GO平行且等于PA，故由PA⊥面ABCD，可得GO⊥面ABCD，∴GO⊥OD，故OD⊥平面PAC，故∠DGO为DG与平面PAC所成的角．由题意可得，GO=PA=．△ABC中，由余弦定理可得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+4﹣2×2×2×cos120°=12，∴AC=2，OC=．∵直角三角形COD中，OD==2，∴直角三角形GOD中，tan∠DGO==．（Ⅲ）若G满足PC⊥面BGD，∵OG⊂平面BGD，∴PC⊥OG，且PC==．由△COG∽△CAP，可得，即，解得GC=，∴PG=PC﹣GC=﹣=，∴==．点评：本题主要考查直线和平面垂直的判定定理的应用，求直线和平面所成的角，空间距离的求法，属于中档题．11．（2013•）如图．在直棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=，AA1=3，D是BC的中点，点E在棱BB1上运动．（1）证明：AD⊥C1E；（2）当异面直线AC，C1E 所成的角为60°时，求三棱锥C1﹣A1B1E的体积．考点：直线与平面垂直的性质；棱柱、棱锥、棱台的体积．专题：计算题；证明题；空间位置关系与距离．分析：（1）根据直三棱柱的性质，得AD⊥BB1，等腰△ABC中利用“三线合一”证出AD⊥BC，结合线面垂直判定定理，得AD⊥平面BB1C1C，从而可得AD⊥C1E；（2）根据AC∥A1C1，得到∠EC1A1（或其补角）即为异面直线AC、C1E 所成的角．由A1C1⊥A1B1且A1C1⊥AA1，证出A1C1⊥平面AA1B1B，从而在Rt△A1C1E中得到∠EC1A1=60°，利用余弦的定义算出C1E=2A1C1=2，进而得到△A1B1E面积为，由此结合锥体体积公式即可算出三棱锥C1﹣A1B1E的体积．解答：解：（1）∵直棱柱ABC﹣A1B1C1中，BB1⊥平面ABC，AD⊂平面ABC，∴AD⊥BB1∵△ABC中，AB=AC，D为BC中点，∴AD⊥BC又∵BC、BB1⊂平面BB1C1C，BC∩BB1=B∴AD⊥平面BB1C1C，结合C1E⊂平面BB1C1C，可得AD⊥C1E；（2）∵直棱柱ABC﹣A1B1C1中，AC∥A1C1，∴∠EC1A1（或其补角）即为异面直线AC、C1E 所成的角∵∠BAC=∠B1A1C1=90°，∴A1C1⊥A1B1，又∵AA1⊥平面A1B1C1，可得A1C1⊥AA1，∴结合A1B1∩AA1=A1，可得A1C1⊥平面AA1B1B，∵A1E⊂平面AA1B1B，∴A1C1⊥A1E因此，Rt△A1C1E中，∠EC1A1=60°，可得cos∠EC1A1==，得C1E=2A1C1=2又∵B1C1==2，∴B1E==2由此可得V=S△×A1C1=×=点评：本题给出直三棱柱的底面是等腰直角三角形，在已知侧棱长和底面边长的情况下证明线线垂直并求锥体的体积，着重考查了直棱柱的性质、空间线面垂直的判定与性质等知识，属于中档题．12．（2012•）如图，几何体E﹣ABCD是四棱锥，△ABD为正三角形，CB=CD，EC⊥BD．（Ⅰ）求证：BE=DE；（Ⅱ）若∠BCD=120°，M为线段AE的中点，求证：DM∥平面BEC．考点：直线与平面平行的判定．专题：证明题．分析：（1）设BD中点为O，连接OC，OE，则CO⊥BD，CE⊥BD，于是BD⊥平面OCE，从而BD⊥OE，即OE是BD的垂直平分线，问题解决；（2）证法一：取AB中点N，连接MN，DN，MN，易证MN∥平面BEC，DN∥平面BEC，由面面平行的判定定理即可证得平面DMN∥平面BEC，又DM⊂平面DMN，于是DM∥平面BEC；证法二：延长AD，BC交于点F，连接EF，易证AB=AF，D为线段AF的中点，连接DM，则DM∥EF，由线面平行的判定定理即可证得结论．解答：证明：（I）设BD中点为O，连接OC，OE，则由BC=CD知，CO⊥BD，又已知CE⊥BD，EC∩CO=C，所以BD⊥平面OCE．所以BD⊥OE，即OE是BD的垂直平分线，所以BE=DE．（II）证法一：取AB中点N，连接MN，DN，∵M是AE的中点，∴MN∥BE，又MN⊄平面BEC，BE⊂平面BEC，∴MN∥平面BEC，∵△ABD是等边三角形，∴∠BDN=30°，又CB=CD，∠BCD=120°，∴∠CBD=30°，∴ND∥BC，又DN⊄平面BEC，BC⊂平面BEC，∴DN∥平面BEC，又MN∩DN=N，故平面DMN∥平面BEC，又DM⊂平面DMN，∴DM∥平面BEC证法二：延长AD，BC交于点F，连接EF，∵CB=CD，∠BCD=120°，∴∠CBD=30°，∵△ABD是等边三角形，∴∠BAD=60°，∠ABC=90°，因此∠AFB=30°，∴AB=AF，又AB=AD，∴D为线段AF的中点，连接DM，DM∥EF，又DM⊄平面BEC，EF⊂平面BEC，∴DM∥平面BEC点评：本题考查直线与平面平行的判定，考查线面垂直的判定定理与面面平行的判定定理的应用，着重考查分析推理能力与表达、运算能力，属于中档题．13．（2012•）如图，在直三棱柱ABC﹣A1B1C1中，A1B1=A1C1，D，E分别是棱BC，CC1上的点（点D 不同于点C），且AD⊥DE，F为B1C1的中点．求证：（1）平面ADE⊥平面BCC1B1；（2）直线A1F∥平面ADE．考点：平面与平面垂直的判定；直线与平面平行的判定．专题：计算题．分析：（1）根据三棱柱ABC﹣A1B1C1是直三棱柱，得到CC1⊥平面ABC，从而AD⊥CC1，结合已知条件AD⊥DE，DE、CC1是平面BCC1B1的相交直线，得到AD⊥平面BCC1B1，从而平面ADE⊥平面BCC1B1；（2）先证出等腰三角形△A1B1C1中，A1F⊥B1C1，再用类似（1）的方法，证出A1F⊥平面BCC1B1，结合AD⊥平面BCC1B1，得到A1F∥AD，最后根据线面平行的判定定理，得到直线A1F∥平面ADE．解答：解：（1）∵三棱柱ABC﹣A1B1C1是直三棱柱，∴CC1⊥平面ABC，∵AD⊂平面ABC，∴AD⊥CC1又∵AD⊥DE，DE、CC1是平面BCC1B1的相交直线∴AD⊥平面BCC1B1，∵AD⊂平面ADE∴平面ADE⊥平面BCC1B1；（2）∵△A1B1C1中，A1B1=A1C1，F为B1C1的中点∴A1F⊥B1C1，∵CC1⊥平面A1B1C1，A1F⊂平面A1B1C1，∴A1F⊥CC1又∵B1C1、CC1是平面BCC1B1的相交直线∴A1F⊥平面BCC1B1又∵AD⊥平面BCC1B1，∴A1F∥AD∵A1F⊄平面ADE，AD⊂平面ADE，∴直线A1F∥平面ADE．点评：本题以一个特殊的直三棱柱为载体，考查了直线与平面平行的判定和平面与平面垂直的判定等知识点，属于中档题．14．（2011•天津）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC 中点，PO⊥平面ABCD，PO=2，M为PD中点．（Ⅰ）证明：PB∥平面ACM；（Ⅱ）证明：AD⊥平面PAC；（Ⅲ）求直线AM与平面ABCD所成角的正切值．考点：直线与平面垂直的判定；直线与平面平行的判定；直线与平面所成的角．专题：综合题；转化思想．分析：（I）由O为AC中点，M为PD中点．结合平行四边形的对角线性质，考虑连接BD，MO，则有PB∥MO，从而可证（II）由∠ADC=45°，且AD=AC=1，易得AD⊥AC，PO⊥AD，根据线面垂直的判定定理可证（III）取DO中点N，由PO⊥平面ABCD，可得MN⊥平面ABCD，从而可得∠MAN是直线AM与平面ABCD所成的角．在Rt△ANM中求解即可解答：解：（I）证明：连接BD，MO在平行四边形ABCD中，因为O为AC的中点，所以O为BD的中点，又M为PD的中点，所以PB∥MO因为PB⊄平面ACM，MO⊂平面ACM所以PB∥平面ACM（II）证明：因为∠ADC=45°，且AD=AC=1，所以∠DAC=90°，即AD⊥AC又PO⊥平面ABCD，AD⊂平面ABCD，所以PO⊥AD，AC∩PO=O，AD⊥平面PAC（III）解：取DO中点N，连接MN，AN因为M为PD的中点，所以MN∥PO，且MN=PO=1，由PO⊥平面ABCD，得MN⊥平面ABCD所以∠MAN是直线AM与平面ABCD所成的角．在Rt△DAO中，，所以，∴，在Rt△ANM中，==即直线AM与平面ABCD所成的正切值为点评：本题主要考查直线与平面平行、直线与平面垂直、直线与平面所成的角等基础知识，考查空间想象能力、运算能力、推理论证能力．15．（2011•）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．考点：直线与平面垂直的判定；点、线、面间的距离计算；用空间向量求直线间的夹角、距离．专题：综合题；转化思想．分析：（I）由已知条件可得ACBD，PABD，根据直线与平面垂直的判定定理可证（II）结合已知条件，设AC与BD的交点为O，则OB⊥OC，故考虑分别以OB，OC为x轴、y轴，以过O且垂直于平面ABCD的直线为z轴，建立空间直角坐标系，设PB与AC所成的角为θ，则，代入公式可求（III）分别求平面PBC的法向量，平面PDC的法向量由平面PBC⊥平面PDC可得从而可求t即PA解答：解：（I）证明：因为四边形ABCD是菱形，所以AC⊥BD，又因为PA⊥平面ABCD，所以PA⊥BD，PA∩AC=A所以BD⊥平面PAC（II）设AC∩BD=O，因为∠BAD=60°，PA=AB=2，所以BO=1，AO=OC=，以O为坐标原点，分别以OB，OC为x轴、y轴，以过O且垂直于平面ABCD的直线为z轴，建立空间直角坐标系O﹣xyz，则P（0，﹣，2），A（0，﹣，0），B（1，0，0），C（0，，0）所以，设PB与AC所成的角为θ，则cosθ=|（III）由（II）知，设，则设平面PBC的法向量=（x，y，z）则=0，所以令，平面PBC的法向量所以，同理平面PDC的法向量，因为平面PBC⊥平面PDC，所以=0，即﹣6+=0，解得t=，所以PA=．点评：本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的夹角、距离等问题，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力16．（2010•模拟）如图，在四棱锥S﹣ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，E、F分别是AB、SC的中点（1）求证：EF∥平面SAD（2）设SD=2CD，求二面角A﹣EF﹣D的大小．考点：直线与平面平行的判定；与二面角有关的立体几何综合题．专题：计算题；证明题；综合题；转化思想．分析：法一：（1）作FG∥DC交SD于点G，则G为SD的中点．要证EF∥平面SAD，只需证明EF平行平面SAD的直线AG即可．（2）取AG中点H，连接DH，说明∠DMH为二面角A﹣EF﹣D的平面角，解三角形求二面角A﹣EF﹣D 的大小．法二：建立空间直角坐标系，平面SAD即可证明（1）；（2）求出向量和，利用，即可解答本题．解答：解：法一：（1）作FG∥DC交SD于点G，则G为SD的中点．连接，又，故为平行四边形．EF∥AG，又AG⊂平面SAD，EF⊄平面SAD．所以EF∥平面SAD．（2）不妨设DC=2，则SD=4，DG=2，△ADG为等腰直角三角形．取AG中点H，连接DH，则DH⊥AG．又AB⊥平面SAD，所以AB⊥DH，而AB∩AG=A，所以DH⊥面AEF．取EF中点M，连接MH，则HM⊥EF．连接DM，则DM⊥EF．故∠DMH为二面角A﹣EF﹣D的平面角．所以二面角A﹣EF﹣D的大小为．法二：（1）如图，建立空间直角坐标系D﹣xyz．设A（a，0，0），S（0，0，b），则B（a，a，0），C（0，a，0），，．取SD的中点，则．平面SAD，EF⊄平面SAD，所以EF∥平面SAD．（2）不妨设A（1，0，0），则B（1，1，0），C（0，1，0），S（0，0，2），，．EF 中点，，，又，，所以向量和的夹角等于二面角A﹣EF﹣D的平面角．．所以二面角A﹣EF﹣D的大小为．点评：本题考查直线与平面平行的判定，二面角的求法，考查计算能力，逻辑思维能力，是中档题．17．（2010•）如图，三棱锥P﹣ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB．（1）求证：AB⊥平面PCB；（2）求二面角C﹣PA﹣B的大小的余弦值．考点：直线与平面垂直的判定；与二面角有关的立体几何综合题．专题：计算题；证明题；综合题；压轴题．分析：（1）要证AB⊥平面PCB，只需证明直线AB垂直平面PCB的两条相交直线PC、CD即可；（2）取AP的中点O，连接CO、DO；说明∠COD为二面角C﹣PA﹣B的平面角，然后解三角形求二面角C﹣PA﹣B的大小的余弦值．解答：（1）证明：∵PC⊥平面ABC，AB⊂平面ABC，∴PC⊥AB．∵CD⊥平面PAB，AB⊂平面PAB，∴CD⊥AB．又PC∩CD=C，∴AB⊥平面PCB．（2）解：取AP的中点O，连接CO、DO．∵PC=AC=2，∴C0⊥PA，CO=，∵CD⊥平面PAB，由三垂线定理的逆定理，得DO⊥PA．∴∠COD为二面角C﹣PA﹣B的平面角．由（1）AB⊥平面PCB，∴AB⊥BC，又∵AB=BC，AC=2，求得BC=PB=，CD=∴cos∠COD=．点评：本题考查直线与平面垂直的判定，二面角的求法，考查空间想象能力，逻辑思维能力，是中档题．。