g3.1046三角函数的图象
三角函数公式及图像大全

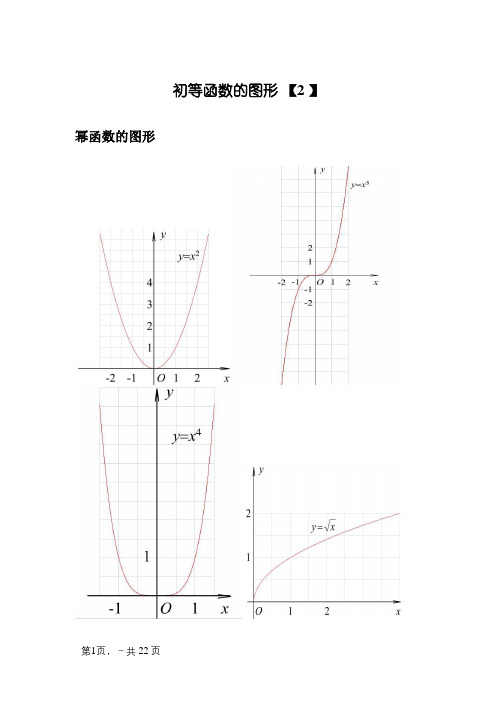
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscαcosα·secαtanα·cotα三角函数的性质函数y=sinx y=cosx y=tanx y=cotx定义域R R {x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max=1x=2kπ-2π时y min=-1[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π)(0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[-2π,2π])cos(arccosx)=x(x∈[-1,1])arccos(cosx)=x(x∈[0,π])tan(arctanx)=x(x∈R)arctan(tanx)=x(x∈(-2π,2π))cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=2π(x∈[-1,1])arctanx+arccotx=2π(X∈R)三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-cosAsinB cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=tanAtanB -1tanBtanA +tan(A-B)=tanAtanB 1tanBtanA +-cot(A+B)=cotA cotB 1-cotAcotB +cot(A-B)=cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA 2-Sin2A=2SinA•CosACos2A =Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A =3sinA-4(sinA)3cos3A =4(cosA)3-3cosA tan3a =tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=AA cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba -sina-sinb=2cos 2b a +sin2ba -cosa+cosb =2cos 2b a +cos2ba -cosa-cosb =-2sin 2b a +sin2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb =-21[cos(a+b)-cos(a-b)]cosacosb =21[cos(a+b)+cos(a-b)]sinacosb =21[sin(a+b)+sin(a-b)]cosasinb =21[sin(a+b)-sin(a-b)]sin(-a)=-sina cos(-a)=cosa sin(2π-a)=cosa cos(2π-a)=sina sin(2π+a)=cosa cos(2π+a)=-sinasin(π-a)=sina cos(π-a)=-cosa sin(π+a)=-sina cos(π+a)=-cosatgA=tanA =aacos sin 万能公式sina=2)2(tan 12tan2aa +cosa=22)2(tan 1)2(tan 1aa+-tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c)[其中tanc=a b ]a•sin(a)-b•cos(a)=)b (a 22+×cos(a-c)[其中tan(c)=b a ]1+sin(a)=(sin 2a +cos 2a )21-sin(a)=(sin 2a -cos 2a )2其他非重点三角函数csc(a)=asin 1sec(a)=a cos 1双曲函数sinh(a)=2e -e -aa cosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)=sinαcos (2kπ+α)=cosαtan (2kπ+α)=tanαcot (2kπ+α)=cotα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)=cosαcos (2π+α)=-sinαtan (2π+α)=-cotαcot (2π+α)=-tanαsin (2π-α)=cosαcos (2π-α)=sinαtan (2π-α)=cotαcot (2π-α)=tanαsin (23π+α)=-cosαcos (23π+α)=sinαtan (23π+α)=-cotαcot (23π+α)=-tanαsin (23π-α)=-cosαcos (23π-α)=-sinαtan (23π-α)=cotαcot (23π-α)=tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+B•sin(ωt+φ)=)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0注:方程有相等的两实根b2-4ac>0注:方程有一个实根b2-4ac<0注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A)ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB-ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r>0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β),|m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
常用三角函数值表图片素材大全

常用三角函数值表图片素材大全三角函数是数学中的重要概念,广泛应用于几何学、物理学、工程学等领域。
常用的三角函数包括正弦函数、余弦函数、正切函数等,它们在不同角度下的取值构成了三角函数值表。
本文将介绍常用三角函数值表的图片素材,帮助读者更直观地理解三角函数的性质。
正弦函数值表正弦函数(Sine,缩写为sin)是三角函数中的一种,定义如下:$$\\sin \\theta = \\frac{对边}{斜边}$$正弦函数的取值范围在-1到1之间。
下表展示了常见角度下的正弦函数值:角度0°30°45°60°90°正弦值00.5√2/2√3/21余弦函数值表余弦函数(Cosine,缩写为cos)是三角函数中的另一种,定义如下:$$\\cos \\theta = \\frac{邻边}{斜边}$$余弦函数的取值范围也在-1到1之间。
下表列出了常见角度下的余弦函数值:角度0°30°45°60°90°余弦值1√3/2√2/20.50正切函数值表正切函数(Tangent,缩写为tan)是三角函数中的又一种,定义如下:$$\\tan \\theta = \\frac{对边}{邻边}$$正切函数的取值范围为实数集。
下表给出了一些常见角度下的正切函数值:角度0°30°45°60°正切值01/√31√3通过以上表格,我们可以看出不同角度下三角函数的取值特点。
对于学习三角函数的人来说,这些图片素材将是十分有用的参考资料。
深入理解三角函数的性质对于解决各种实际问题将会起到重要的作用。
愿这些图片素材能够帮助您更好地掌握三角函数的知识。
声明:本文所使用的数值及公式仅供参考,如有错误请以权威资料为准。
以上是关于三角函数值表图片素材的内容,希望对您有所帮助。
感谢阅读!。
三角函数的图象和性质-课件

y 2
y=1+sinx x[0, 2]
1
o
3
2
-1
2
2
x
y=sinx x[0, 2]
y
y=cosx x[0, 2 ]
1
o
3
2
x
2
2
-1
y=-cosx x[0, 2 ]
小结:
正弦函数、余弦函数图象的五点法
练习:(1)画出函数y=-sinx x∈ [0,2π]
(2)画出函数y=1+cosx x∈ [0,2π] (3)画出函数y=2sinx x∈ [0,2π]
1
●
0
2
-1
●
3
2
●
●
2
x
练习:用“五点画图法”画出正弦函数
y=sinx x∈ [0, 2 ]的图象
一、余弦函数y=cosx(xR)的图象
sin(
x+
2
)= cosx
y
y=sinx的图象
1
2 0 3 2 3
2 -1 2
2
4 5
y=cosx的图象
6 x
余弦函数的“五点画图法”
(0,1)、(
•
13、知人者智,自知者明。胜人者有 力,自 胜者强 。2021/2/272021/2/272021/2/272021/2/272/27/2021
•
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021年2月27日星期 六2021/2/272021/2/272021/2/27
•
15、最具挑战性的挑战莫过于提升自 我。。2021年2月2021/2/272021/2/272021/2/272/27/2021
三角函数的图象PPT课件-42页精选文档

(1)求f(x)的解析式;
1
(2)将y=f(x)图象上所有点的横坐标缩短到原来的
3
(纵坐标不变),然后再将所得图象向 x 轴正方向
平移 3 个单位,得到函数y=g(x)的图象。
写出函数y=g(x)的解析式。
答(1)案f:(x)2sinx() (2)g(x)2sinx()
36
6
知识迁移四:利用图象解决一些三角不等式 及体现数形结合思想的习题
上的图像。
22
解:(1) f(x)2si2n x2sixncoxs
1 co 2 x ssi2 x n
12(s2 ixc no sco 2xssin )
4
4
1 2sin2x( )
4
所以函数f(x)的最小正周期为, 最大值为1 2
(2)由
y1 2sin2x()
4
x
3
8
y1 2sin2x( ) 4
特点: 在对称点处 y = 0
y 1
33 55 22
22 33 22
22
o 33
22
22
-1
22 55 33 x
22
2.余弦函数y=cosx的图象特征:
①对称轴方程:xk ,kZ
特点:在对称轴处,y取最大(小)值
②对称点坐标:(k,0) ,(kZ)
2
特点: 在对称点处 y = 0
y 1
1
8
1 2
3 88
1 1 2
5 8
1
故函数y=f(x)在区间 [ , ]上的图象是
22
y
5
2
2
3 2
1
1
2
2
3 84
o
三角函数公式和图像大全
初等函数的图形【2 】幂函数的图形指数函数的图形对数函数的图形三角函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA + tan(A-B) =tanAtanB 1tanBtanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+倍角公式tan2A =A tan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A)=2cos 1A - cos(2A)=2cos 1A + tan(2A)=A A cos 1cos 1+- cot(2A)=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin 2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba - cosa+cosb = 2cos 2b a +cos 2ba - cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=b a b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)]引诱公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =a acos sin全能公式 sina=2)2(tan 12tan2a a+ cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan2a a- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [个中tanc=a b] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [个中tan(c)=b a] 1+sin(a) =(sin 2a +cos 2a)2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数 csc(a) =a sin 1sec(a) =a cos 1双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa tg h(a)=)cosh()sinh(a a公式一设α为随意率性角,终边雷同的角的统一三角函数的值相等: sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二设α为随意率性角,π+α的三角函数值与α的三角函数值之间的关系:cos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三随意率性角α与 -α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四应用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五应用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:cos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosαcos (2π+α)= -sinαtan (2π+α)= -cotαcot (2π+α)= -tanαsin (2π-α)= cosαcos (2π-α)= sinαtan (2π-α)= cotαcot (2π-α)= tanαsin (23π+α)= -cosαcos (23π+α)= sinαtan (23π+α)= -cotαcot (23π+α)= -tanαsin (23π-α)= -cosαcos (23π-α)= -sinαtan (23π-α)= cotαcot (23π-α)= tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,愿望对大家有效 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证实(全体)公式表达式乘法与因式分化a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注:个中 R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]} 圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0 抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:个中,S'是直截面面积, L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h第21页,-共22页。
三角函数的图像与性质

三角函数的图像与性质三角函数是数学中的一类重要的函数,包括正弦函数(sin)、余弦函数(cos)、正切函数(tan),以及它们的倒数函数(csc,sec,cot)。
下面是关于三角函数的一些图像与性质:1. 正弦函数(sin)的图像:正弦函数是一个周期函数,它的图像在一个周期内呈现出振荡的形式,取值范围在-1到1之间。
当自变量取0、π/2、π、3π/2等特殊值时,正弦函数的值为0、1、0、-1,分别对应于函数的最小值、最大值、0点和最大负值。
2. 余弦函数(cos)的图像:余弦函数也是一个周期函数,它的图像与正弦函数的图像非常相似,只是相位差了π/2。
余弦函数的取值范围也在-1到1之间,当自变量取0、π/2、π、3π/2等特殊值时,余弦函数的值依次为1、0、-1、0。
3. 正切函数(tan)的图像:正切函数的图像在每个周期上有无穷多个交点,它的值可以为任何实数。
正切函数与正弦函数和余弦函数之间存在着一定的关系,即tan(x) =sin(x) / cos(x)。
当自变量取π/2、3π/2、5π/2等特殊值时,正切函数的值为正无穷大;取-π/2、-3π/2、-5π/2等特殊值时,正切函数的值为负无穷大。
4. 三角函数的周期性:正弦函数、余弦函数和正切函数都是周期函数,它们的周期分别为2π、2π和π。
这意味着,当自变量增加一个周期时,函数的值将重复出现。
例如,sin(x + 2π) = sin(x)。
5. 三角函数的奇偶性:正弦函数是奇函数,余弦函数是偶函数,正切函数是奇函数。
奇函数的图像关于原点对称,即f(-x) = -f(x);偶函数的图像关于y轴对称,即f(-x) =f(x)。
这些是关于三角函数图像与性质的一些基本信息,三角函数在数学、物理、工程等领域都有广泛的应用。
三角函数图像公式大全

幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)]cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin 万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ]a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a)2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -a a cosh(a)=2e e -a a + tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot(2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= c otα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosαcos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0 抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h-------------------------------------------------------------------------------------------- 三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1。
高中数学·三角函数 图像2021年04月09日

高中数学·三角函数图像2021年04月09日一、单选题(共1题;共2分)1.(2017高一下·菏泽期中)下列区间中,使函数y=cosx为增函数的是()A. [0,π]B. [ π2,3π2] C. [ −π2,π2] D. [π,2π]【答案】D【考点】余弦函数的单调性【解析】【解答】解:∵cosx的递增区间是[﹣π+2kπ,2kπ]k∈Z 当k=1时,递增区间为:[π,2π]故答案选:D【分析】根据余弦函数的单调性质可以一一分析判断符合要求的选项二、填空题(共48题;共55分)2.(2020·新课标Ⅲ·理)关于函数f(x)= sinx+1sinx有如下四个命题:①f(x)的图像关于y轴对称.②f(x)的图像关于原点对称.③f(x)的图像关于直线x= π2对称.④f(x)的最小值为2.其中所有真命题的序号是________.【答案】②③【考点】正弦函数的图象,正弦函数的奇偶性与对称性,正弦函数的定义域和值域【解析】【解答】对于命题①,f(π6)=12+2=52,f(−π6)=−12−2=−52,则f(−π6)≠f(π6),所以,函数f(x)的图象不关于y轴对称,命题①错误;对于命题②,函数f(x)的定义域为{x|x≠kπ,k∈Z},定义域关于原点对称,f(−x)=sin(−x)+1sin(−x)=−sinx−1sinx=−(sinx+1sinx)=−f(x),所以,函数f(x)的图象关于原点对称,命题②正确;对于命题③,∵f(π2−x)=sin(π2−x)+1sin(π2−x)=cosx+1cosx,f(π2+x)=sin(π2+x)+1sin(π2+x)=cosx+1cosx,则f(π2−x)=f(π2+x),所以,函数f(x)的图象关于直线x=π2对称,命题③正确;对于命题④,当−π<x<0时,sinx<0,则f(x)=sinx+1sinx<0<2,命题④错误.故答案为:②③.【分析】利用特殊值法可判断命题①的正误;利用函数奇偶性的定义可判断命题②的正误;利用对称性的定义可判断命题③的正误;取−π<x<0可判断命题④的正误.综合可得出结论.3.(2016高一上·徐州期末)函数y=3tan(2x+ 5π6)的最小正周期为________.【答案】π2【考点】三角函数的周期性及其求法【解析】【解答】解:由正切函数的周期公式得T= π2,故答案为:π2【分析】根据正切函数的周期公式进行求解即可.4.已知函数f(x)=2sinxcosx+2 √3sin2x,x∈R,则函数f(x)的单调递增区间为________.【答案】[kπ﹣π12,kπ+ 5π12](k∈Z)【考点】三角函数中的恒等变换应用,正弦函数的图象【解析】【解答】解:∵函数f(x)=2sinxcosx+2 √3sin2x=sin2x+2 √3• 1−cos2x2=sin2x﹣√3cos2x+ √3=2sin(2x﹣π3)+ √3,x∈R,令2kπ﹣π2≤2x﹣π3≤2kπ+ π2,求得kπ﹣π12≤x≤kπ+ 5π12,故函数f(x)的单调递增区间为为[kπ﹣π12,kπ+ 5π12],k∈Z,故答案为:[kπ﹣π12,kπ+ 5π12](k∈Z).【分析】利用三角恒等变换化简函数的解析式,再利用正弦函数的增区间求得函数f(x)的单调递增区间.5.(2019高一下·上海期中)函数f(x)=sinx⋅cosx的最小正周期是________.【答案】π【考点】三角函数的周期性及其求法【解析】【解答】f(x)=sinx⋅cosx=12sin2x,故最小正周期是2π2=π.故答案为:π【分析】利用降幂公式化简再求最小正周期即可.6.函数y=cos(2x﹣π4)的单调递减区间为________【答案】[kπ+π8,kπ+5π8],k∈Z【考点】余弦函数的单调性【解析】【解答】解:对于函数y=cos(2x﹣π4),令2kπ≤2x﹣π4≤2kπ+π,求得kπ+π8≤x≤kπ+5π8,故函数的减区间为[kπ+π8,kπ+5π8],k∈Z,故答案为:[kπ+π8, kπ+5π8],k ∈Z .【分析】由条件利用余弦函数的单调性求得函数y=cos (2x ﹣π4)的单调递减区间.7.函数y =2sin (πx 6−π3)(0≤x ≤9)的最大值与最小值之和为________【答案】2-√3【考点】正弦函数的单调性【解析】【解答】解:因为0≤x≤9,所以πx 6∈[0,2π3],故πx 6-π3∈[-π3, 7π6]所以2sin (πx 6-π3)∈[﹣√3 , 2],所以函数y=2sin (πx 6-π3)(0≤x≤9)的最大值与最小值之和为2﹣√3故答案为:2﹣√3 .【分析】通过x 的范围,求出 πx 6-π3的范围,然后求出函数的最值即可.8.函数 y =sin(π3−2x) 的最小正周期是________,在[0,π)上的单调递增区间是________. 【答案】 π;[ 5π12,11π12]【考点】三角函数的周期性及其求法【解析】【解答】解: y =sin(π3−2x) =﹣sin (2x ﹣ π3 ). 最小正周期T=2π2=π ;由 π2+2kπ≤2x −π3≤3π2+2kπ ,得5π12+kπ≤x ≤11π12+kπ,k ∈Z .取k=0,得 5π12≤x ≤11π12.∴在[0,π)上的单调递增区间是[ 5π12,11π12].故答案为:π,[ 5π12,11π12].【分析】利用诱导公式变形,然后利用周期公式求得周期,再由复合函数的单调性求得在[0,π)上的单调递增区间.9.(2016高三上·朝阳期中)函数f (x )=cos 2x ﹣sin 2x 的单调递减区间为________. 【答案】 [kπ,kπ+π2](k ∈z)【考点】二倍角的余弦,余弦函数的图象 【解析】【解答】解:对于函数y=cos 2x ﹣sin 2x=cos2x ,令2kπ≤2x≤2kπ+π,k∈Z,求得:kπ≤x≤kπ+ π2,k∈Z,可得函数的单调递减区间是:[kπ,kπ+π2](k∈z).故答案为:[kπ,kπ+π2](k∈z).【分析】由条件利用二倍角的余弦函数公式化简函数的解析式,再根据余弦函数的单调性求得函数的单调递减区间.10.(2016高一下·九江期中)已知函数f(x)= cos(πx−π)2x+22−x(x∈R),给出下面四个命题:①函数f(x)的图象一定关于某条直线对称;②函数f(x)在R上是周期函数;③函数f(x)的最大值为14;④对任意两个不相等的实数x1,x2∈(0,32),都有f(x1)−f(x2)x1−x2>110成立.其中所有真命题的序号是________.【答案】①③【考点】三角函数中的恒等变换应用,正弦函数的图象【解析】【解答】解:f(x)= cos(πx−π)2x+22−x = −cosπx2x+22−x.∵f(2﹣x)= −cos(2−x)2x+22−x =−cosπx2x+22−x=f(x),∴函数f(x)的图象一定关于直线x=1对称,故①正确;当x→+∞时,2x+22﹣x→+∞,则f(x)→0,∴函数f(x)在R上不是周期函数,故②错误;由①知,函数f(x)关于直线x=1对称,且当x>1时,随着x的增大,其图象大致形状如图:函数f(x)的最大值为14,故③正确;由图可知,在x=1右侧附近,连接曲线上两点的斜率小于0,故④错误.∴所有真命题的序号是①③.故答案为:①③.【分析】利用诱导公式化简函数解析式,由f(2﹣x)=f(x)说明①正确;函数f(x)的定义域是R,且其图象有对称轴,由函数解析式可以得出,其图象周期性穿过X轴,由于分母不断增大,图象往两边延伸都无限靠近于X轴,说明函数不是周期函数,②错误;由函数解析式抽象出函数图象的大致形状,说明③正确,④错误.11.(2015高一下·仁怀开学考)函数y=tan(2x−π3)的最小正周期为________.【答案】π2【考点】正切函数的周期性【解析】【解答】解:因为函数y=tan(2x−π3),所以T= π|ω|= π2.所以函数y=tan(2x−π3)的最小正周期为π2.故答案为:π2.【分析】直接利用正切函数的周期公式T=π|ω|,求出函数的最小正周期.12.(2017·南充模拟)如果函数f(x)=sin(2x+θ),函数f(x)+f'(x)为奇函数,f'(x)是f(x)的导函数,则tanθ=________.【答案】-2【考点】导数的运算,正弦函数的奇偶性【解析】【解答】解:∵f(x)=sin(2x+θ),∴f′(x)=2cos(2x+θ),则f(x)+f'(x)=sin(2x+θ)+2cos(2x+θ),∵f(x)+f'(x)为奇函数,∴sin(﹣2x+θ)+2cos(﹣2x+θ)=﹣sin(2x+θ)﹣2cos(2x+θ),即﹣sin(2x﹣θ)+2cos(2x﹣θ)=﹣sin(2x+θ)+2cos(2x+θ),则﹣sin2xcosθ+cos2xsinθ+2cos2xcosθ+2sin2xsinθ=﹣(sin2xcosθ+cos2xsinθ+2cos2xcosθ﹣sin2xsinθ)=﹣sin2xcosθ﹣cos2xsinθ﹣2cos2xcosθ+2sin2xsinθ,即2cos2xsinθ=﹣4cos2xcosθ,即sinθ=﹣2cosθ,即tanθ=﹣2,故答案为:﹣2【分析】求函数的导数,根据函数奇偶性的性质进行求解即可.13.(2017·海淀模拟)已知当x∈[0,π4]时,函数f(x)=2sin(ωx+π6)−1(ω>0)有且仅有5个零点,则ω的取值范围是________.【答案】[16,563)【考点】正弦函数的图象,根的存在性及根的个数判断【解析】【解答】解:可以将问题转化为研究函数函数g(x)=sin(ωx+π6)(ω>0)与直线y=12有且仅有5个交点.如图,是满足条件的两个临界状态,由此得到ωπ4+π6=4π+π6,ωπ4+π6=4π+5π6,计算可得临界态的ω=16,ω=563,依据题意可得ω∈[16,563).故答案为:[16,563)【分析】根据函数与方程之间的关系转化为两个图象的交点问题,利用数形结合进行求解即可.14.(2020高二下·杭州月考)函数y=log3(x2−2x)的单调减区间是________;已知函数f(x)=3+2cosx的图象经过点(π3,b),则b=________.【答案】(−∞,0);4【考点】函数的单调性及单调区间,复合函数的单调性,余弦函数的图象【解析】【解答】函数y=log3(x2−2x)的定义域为(−∞,0)∪(2,+∞)因为二次函数y=x2−2x的开口向上,对称轴轴为x=1所以函数y=log3(x2−2x)的单调减区间是(−∞,0);因为函数f(x)=3+2cosx的图象经过点(π3,b),所以3+2cosπ3=b,所以b=4故答案为:(−∞,0);4【分析】首先求出函数y=log3(x2−2x)的定义域,然后利用对数函数和二次函数的知识可求出y=log3(x2−2x)的单调递减区间,由函数f(x)=3+2cosx的图象经过点(π3,b)可直接求出b.15.(2019·十堰模拟)将函数f(x)=sin(4x−π6)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,则g(x)的最小正周期是________【答案】π【考点】三角函数的周期性及其求法【解析】【解答】依题意可得g(x)=sin(2x−π6),所以g(x)的最小正周期是T=2π2=π.故答案为π【分析】由已知利用正弦函数的周期性,即可求出g(x)的最小正周期.16.sinx>0,x∈[0,2π]的解集是________.【答案】(0,π)【考点】正弦函数的单调性【解析】【解答】解:如图所示是y=sin x,x∈[0,2π]的图象,由图可知满足sin x>0,x∈[0,2π]的解集是(0,π).故答案为:(0,π)【分析】,作出y=sin x,x∈[0,2π]的图象即可求得答案.17.函数y=3tan(π+x),(−π4<x<π6)的值域是________【答案】(-3,√3)【考点】正切函数的定义域和值域【解析】【解答】解:函数y=3tan(π+x)=3tanx,因为−π4<x<π6,正切函数是增函数,所以−3<y≤√3,所以函数的值域为:(-3,√3).故答案为:(-3,√3)18.(2019高二上·青岛月考)若“ ∃x∈[0,π4],tanx<m”是真命题,则实数m的取值范围是________. 【答案】m>0【考点】正切函数的单调性【解析】【解答】∃x∈[0,π4],tanx<m,即(tanx)min<m,y=tanx在x∈[0,π4]单调递增,(tanx)min=0即m>0.故答案为:m>0【分析】根据∃x∈[0,π4],tanx<m,实数m的取值范围,即(tanx)min<m.19.函数y=cosx的对称轴方程为________【答案】x=kπ,k∈Z【考点】余弦函数的奇偶性与对称性【解析】【解答】解:∵y=cosx的对称轴方程为x=kπ,k∈Z,故答案为:x=kπ,k∈Z.【分析】利用余弦函数的对称性即可求得答案.20.(2018高三上·吉林期中)关于函数f(x)=√3cos2x−2sin x cos x,有如下命题:(1)x=π3是f(x)图象的一条对称轴;(2)(π6,0)是f(x)图象的一个对称中心;(3)将f(x)的图象向左平移π6,可得到一个奇函数的图象。
三角函数的图像与性质

三角函数的图像与性质三角函数是高中数学中非常重要的一部分内容,它们在物理、工程、计算机科学等领域都有广泛的应用。
在学习三角函数时,我们需要了解它们的图像与性质,以便更好地理解它们的含义和用法。
本文将介绍三角函数的图像与性质,帮助读者更好地掌握这一知识点。
正弦函数(sin)正弦函数是最常见的三角函数之一,它描述了一个周期性变化的曲线。
正弦函数的图像是一个连续的波浪线,它在区间[-1,1]之间取值,且呈现周期性。
具体来说,当自变量的取值为0时,正弦函数的值为0;当自变量的取值为90°(或π/2)时,正弦函数的值为1;当自变量的取值为180°(或π)时,正弦函数的值再次为0;以此类推。
正弦函数的图像可以帮助我们观察周期性变化的现象,并用于解决相关问题,如天体运动、声音传播等。
余弦函数(cos)余弦函数也是一种常见的三角函数,它与正弦函数非常相似,但在图像上有一定的差异。
余弦函数的图像也是一个周期性变化的曲线,它在区间[-1,1]之间取值。
与正弦函数不同的是,当自变量的取值为0时,余弦函数的值为1;当自变量的取值为90°(或π/2)时,余弦函数的值为0;当自变量的取值为180°(或π)时,余弦函数的值再次为-1。
余弦函数的图像可以帮助我们观察周期性的振动现象,如弹簧的伸缩、机械摆动等。
正切函数(tan)正切函数是三角函数中的另一个重要概念,它描述了一个不断增大或减小的曲线。
正切函数的图像在某些点和正弦函数、余弦函数的图像相交,但在其他点上却有明显的区别。
正切函数的图像可以帮助我们观察角度的变化和斜率的变化,如坡度、天文观测等。
正切函数的自变量是角度的度数,因此它的取值范围没有限制。
需要注意的是,在某些角度上,正切函数的值会趋近于无穷大。
性质与应用除了图像之外,三角函数还有许多重要的性质和应用。
其中,周期性是最基本的特征之一。
正弦函数、余弦函数的周期均为360°(或2π),而正切函数的周期为180°(或π)。
三角函数的图象PPT

交流电的电压和电流是时间的三角函数,用于产生和 传输电力。
波动
在声学、电磁学等领域,波的传播和变化可以用三角 函数来描述。
在工程中的应用
机械振动
在机械工程中,三角函数用于模 拟和分析各种振动现象,如桥梁 振动、汽车悬挂系统等。
控制系统
在航空、航天、化工等领域,控 制系统中的信号处理和反馈控制 算法常常用到三角函数。
信号处理
在通信、雷达、声呐等领域,信 号的调制和解调常常涉及到三角 函数的应用。
在数学其他分支中的应用
微积分
01
在微积分中,三角函数用于求解微分方程、积分方程等数学问
题。
线性代数
02
在矩阵运算和特征值求解中,三角函数也经常被用到。
复数分析
03
在复数分析中,三角函数用于表示复数的三角形式,以及处理
与之相关的数学问题。
三角函数的周期性
周期性定义
三角函数的周期性是指函数值按照一 定的规律重复出现的现象。对于正弦 和余弦函数,其周期为360度或2π弧 度。
周期计算
对于正弦和余弦函数,其周期T=2π; 对于正切函数,其周期T=π。
三角函数的奇偶性
奇偶性定义
三角函数的奇偶性是指函数值在原点两侧是否对称的现象。奇函数在对称轴两侧的值互为相反数,偶函数在对称 轴两侧的值相等。
横向伸缩变换
总结词
在x轴方向上伸缩函数的图像。
详细描述
对于函数y=sin(x),若图像在x轴方向上压缩为原来的k倍,则新的函数为y=sin(kx); 若图像在x轴方向上拉伸为原来的k倍,则新的函数为y=sin(kx)。
纵向伸缩变换
总结词
在y轴方向上伸缩函数的图像。
详细描述
三角函数的图象PPT课件

6
)
2. (04全国高考)
为了得到函数 y sin( 2 x
6
) 的图象,可以将
函数y cos 2 x 的图象( B )
A.向右平移
B.向右平移
6
个单位长度 个单位长度
3
C.向左平移
D.向左平移
6 3
个单位长度
个单位长度
3.将函数 y=f(x)sinx 的图象向右平移
则f(x) 可以是( B ) A. cosx B. 2cosx C. sinx
3
)
y=sin(x+
3
)
6
1
o
12
3
3
7 12
5 6
-1 -2
y=sin(2x+
3
)
3 5 2 2 3 y=sinx
x
评注: 作出正弦型函数的图象以五点法最为方便, 但必须清楚它的图象与正弦函数图象间的关系,
即弄清正弦型函数的图象是怎样由正弦函数的图
象经过几种变换得到的。要注意虽然各种变换的
例2.已知下图是 y
Asin( x )( A 0, 0, )
y
2
的图象,试确定该函数的解析式。 解:由图知A=2, 即函数 y
7 ,0)与点(0,1) 又函数图象过点 P( -2 12 7 7 sin( ) 0 2 12 12 解得 : 1 sin 6 6 2
A.关于直线 x 对称
6
B.关于直线 x 对称 12
g3.1046三角函数的图象

g3.1046三角函数的图象一、知识回顾(一)熟悉.三角函数图象的特征:y =tanx y =cotx(二)三角函数图象的作法: 1.几何法(利用三角函数线)2. 描点法:五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).3.利用图象变换作三角函数图象.三角函数的图象变换有振幅变换、周期变换和相位变换等,重点掌握函数y =Asin (ωx +φ)+B 的作法.函数y =Asin (ωx +φ)的物理意义:振幅|A|,周期2||T πω=,频率1||2f Tωπ==,相位;x ωϕ+初相ϕ(即当x =0时的相位).(当A >0,ω>0 时以上公式可去绝对值符号),(1)振幅变换或叫沿y 轴的伸缩变换.(用y/A 替换y )由y =sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象.(2)周期变换或叫做沿x 轴的伸缩变换.(用ωx 替换x)由y =sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x 的图象.(3)相位变换或叫做左右平移.(用x +φ替换x)由y =sinx 的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动|φ|个单位,得到y =sin (x +φ)的图象.(4)上下平移(用y+(-b)替换y )由y =sinx 的图象上所有的点向上(当b >0)或向下(当b <0)平行移动|b |个单位,得到y =sinx +b 的图象.注意:由y =sinx 的图象利用图象变换作函数y =Asin (ωx +φ)+B (A >0,ω>0)(x ∈R )的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象延x 轴量伸缩量的区别。
二、基本训练1、为了得到函数)63sin(π+=x y 的图象,只需把函数x y 3sin =的图象 ( )A 、向左平移6π B 、向左平移18π C 、向右平移6π D 、向右平移18π2、函数|2|sin 2)(π-=x x f 的部分图象是 ( )3、函数)cos (sin cos 2x x x y +=的图象一个对称中心的坐标是 ( )OO2 2ABA 、)0,83(π B 、)1,83(π C 、)1,8(π D 、)1,8(--π4、(00)函数y=-xcosx 的部分图象是5、已知函数a x x x f -++-=1cos 4sin 4)(2,当]32,4[ππ-∈x 时)(x f =0恒有解,则a 的范围是______。
三角函数图像公式大全

幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质函数y=sinx y=cosx y=tanx y=cotx定义域R R {x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max=1x=2kπ-2π时y min=-1[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[-2π,2π])cos(arccosx)=x(x∈[-1,1])arccos(cosx)=x(x∈[0,π])tan(arctanx)=x(x∈R)arctan(tanx)=x(x∈(-2π,2π))cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=2π(x∈[-1,1]) arctanx+arccotx=2π(X∈R)三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)]cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin 万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ]1+sin(a) =(sin 2a +cos 2a )21-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanαcot(2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosαcos (2π+α)= -sinαtan (2π+α)= -cotαcot (2π+α)= -tanαsin (2π-α)= cosαcos (2π-α)= sinαtan (2π-α)= c otαcot (2π-α)= tanαsin (23π+α)= -cosαcos (23π+α)= sinαtan (23π+α)= -cotαcot (23π+α)= -tanαsin (23π-α)= -cosαcos (23π-α)= -sinα tan (23π-α)= cotαcot (23π-α)= tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0 抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h-------------------------------------------------------------------------------------------- 三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)tanA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1。
三角函数公式和图像大全

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质 函数y=sinxy=cosxy=tanxy=cotx 定义域 R R{x |x ∈R 且x≠kπ+2π,k ∈Z }{x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π 时y max =1 x=2kπ-2π 时y min =-1[-1,1] x=2kπ时y max =1x=2kπ+π时y min =-1 R无最大值 无最小值R无最大值 无最小值周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数 单调性在[2kπ-2π,2kπ+2π ]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k ∈Z) 在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k ∈Z) 在(kπ-2π,kπ+2π)内都是增函数(k ∈Z)在(kπ,kπ+π)内都是减函数(k ∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx 表示属于[-2π,2π]且正弦值等于x 的角arccosx 表示属于[0,π],且余弦值等于x 的角 arctanx 表示属于(-2π,2π),且正切值等于x 的角arccotx 表示属于(0,π)且余切值等于x 的角 性质 定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域[-2π,2π] [0,π](-2π,2π) (0,π) 单调性 在〔-1,1〕上是增函数在[-1,1]上是减函数 在(-∞,+∞)上是增数在(-∞,+∞)上是减函数 奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosx arctan(-x)=-arcta nx arccot(-x)=π-a rccotx 周期性 都不是同期函数恒等式sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2π])cos(arccosx)=x(x ∈[-1,1]) arccos(cosx)=x(x ∈[0,π])tan(arctanx)=x(x ∈R)arctan(tanx)=x(x ∈(-2π,2π))cot(arccotx)=x (x ∈R)arccot(cotx)=x (x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinαcos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= cosαtan (-α)= -tanαcot (-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -tanαcot (π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosαcos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2asin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]} 圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
三角函数与反三角函数的图像与性质

三角函数与反三角函数的图像与性质本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March三角函数与反三角函数的图像与性质一、三角函数的图像和性质1. 正弦与余函数的图像与性质 函数 x y sin =x y cos =图像定域义 RR值域 []1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时,时,2, 1 2,1x k y k Z x k y k Z πππ==∈=+=-∈最大最小时,时, 单调性[2,2]223[2,2]22Z k k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2] Zk k k k k ππππππ-++∈在每个上递增在每个上递减 奇偶性 奇函数偶函数周期性 是周期函数,2π为最小正周期 是周期函数,2π为最小正周期 对称性对称中心(,0)k π,:,()2x k k Z ππ=+∈对称轴对称中心(,0)2k ππ+,:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质 函数 x y tan = x y cot =图像定域义 {|,}2x x R x k k Z ππ∈≠+∈且{|,}x x R x k k Z ππ∈≠+∈且值域 RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性 奇函数奇函数周期性 是周期函数,π为最小正周期 是周期函数,π为最小正周期 对称性对称中心(,0)2k π 对称中心(,0)2k π二、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质 函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦,的反函数 反余弦函数arccos y x =是[]cos 0,y x x π=∈,的反函数 图像定域义 []1,1-[]1,1- 值域 ,22ππ⎡⎤-⎢⎥⎣⎦[]0,π单调性 [1,1]-+在上递增[1,1]-+在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性 对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质 函数反正切函数arctan y x = 是tan (,)22y x x ππ=∈-,的反函数 反余切函数arccot y x = 是()cot 0,y x x π=∈,的反函数图像定域义 (,,)-∞+∞(,,)-∞+∞值域 ,22ππ⎛⎫- ⎪⎝⎭()0,π单调性(,,)-∞+∞在上递增(,,)-∞+∞在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性 对称中心(0,0)对称中心(0,)2π。
三角函数公式、图像大全

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosA Cos2A =Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c)[其中tanc=ab]a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin 2a +cos 2a)21-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosαtan(2kπ+α)= tanα cot(2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系:sin(2π+α)= cosαcos(2π+α)= -sinαtan(2π+α)= -cotαcot(2π+α)= -tanαsin(2π-α)= cosαcos(2π-α)= sinαtan(2π-α)= cotαcot(2π-α)= tanαsin(23π+α)= -cosαcos(23π+α)= sinαtan(23π+α)= -cotαcot(23π+α)= -tanαsin(23π-α)= -cosαcos(23π-α)= -sinαtan(23π-α)= cotαcot(23π-α)= tanα(以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b |a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos (A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2) tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB-ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n2 2+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n (n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/ 41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1 )=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2 ]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0 抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2) cos(C/2) (3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBco sC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)co sβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1) t an(α+β)=(1+m)/(1-m)tanβ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
g3.1046三角函数的图象一、知识回顾(一)熟悉.三角函数图象的特征:y =tanxy =cotx(二)三角函数图象的作法: 1.几何法(利用三角函数线)2. 描点法:五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).3.利用图象变换作三角函数图象.三角函数的图象变换有振幅变换、周期变换和相位变换等,重点掌握函数y =Asin (ωx +φ)+B 的作法.函数y =Asin (ωx +φ)的物理意义:振幅|A|,周期2||T πω=,频率1||2f Tωπ==,相位;x ωϕ+初相ϕ(即当x =0时的相位).(当A>0,ω>0 时以上公式可去绝对值符号), (1)振幅变换或叫沿y 轴的伸缩变换.(用y/A 替换y )由y =sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象.(2)周期变换或叫做沿x 轴的伸缩变换.(用ωx 替换x )由y =sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x的图象.(3)相位变换或叫做左右平移.(用x +φ替换x )由y =sinx 的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动|φ|个单位,得到y =sin (x +φ)的图象.(4)上下平移(用y+(-b)替换y )由y =sinx 的图象上所有的点向上(当b >0)或向下(当b <0)平行移动|b |个单位,得到y =sinx +b 的图象.注意:由y =sinx 的图象利用图象变换作函数y =Asin (ωx +φ)+B (A >0,ω>0)(x ∈R )的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象延x 轴量伸缩量的区别。
二、基本训练1、为了得到函数)63sin(π+=x y 的图象,只需把函数x y 3sin =的图象 ( )A 、向左平移6π B 、向左平移18π C 、向右平移6π D 、向右平移18π2、函数|2|sin 2)(π-=x x f 的部分图象是 ( )3、函数)cos (sin cos 2x x x y +=的图象一个对称中心的坐标是 ( )A 、)0,83(πB 、)1,83(πC 、)1,8(π D 、)1,8(--π4、(00)函数y=-xcosx 的部分图象是5、已知函数a x x x f -++-=1cos 4sin 4)(2,当]32,4[ππ-∈x 时)(x f =0恒有解,则a 的范围是______。
6、方程)3sin(||lg π+=x x 有___个实数根。
三、例题分析例1、已知函数)32sin(2π+=x y 。
(1)求它的振幅、周期和初相; (2)用五点法作出它的图象;(3)说明)32sin(2π+=x y 的图象可由x y sin =的图象经过怎样的变换而得到?例2、把函数x x y sin cos 3-=的图象向左平移)0(>m m 个单位,所得的图象关于y 轴对称,求m 的最小值。
例3、如图为)sin(ϕω+=x A y (0,0,||)2A πωϕ<><的图象的一段,求其解析式。
OO2 2AB例4、受日月的引力,海水会发生涨落,这种现象叫做潮汐,在通常情况下,船在涨潮时驶进航道,靠近船坞;缺货后落潮时返回海洋。
某港口水的深度y (米)是时间t (240≤≤t ,单位:时)的函数,记作)(t f y =,下面是该港口在某季节每天水深的数据:经长期观察,(1) 根据以上数据,求出函数)(t f y =的近似表达式;(2) 一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米。
如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需的时间)?例5.(00) 已知函数(I )当函数y 取得最大值时,求自变量x 的集合;(II )该函数的图象可由y=sinx (x ∈R )的图象经过怎样的平移和伸缩变换得到?四、作业 同步练习g3.1046三角函数的图象1、若函数)sin(3)(ϕω+=x x f 对任意实数x ,都有)4()4(x f x f -=+ππ,则)4(πf 等于A 、0B 、3C 、-3D 、3或-32、把函数)32cos(3π+-=x y 的图象向右平移)0(>m m 个单位,设所得图象的解析式为)(x f y =,则当)(x f y =是偶函数时,m 的值可以是A 、3πB 、6πC 、4πD 、12π3、(05福建卷)函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则 A .4,2πϕπω==B .6,3πϕπω==C .4,4πϕπω==D .45,4πϕπω==4、(05天津卷)函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达式为)(A ))48sin(4π+π-=x y (B ))48sin(4π-π=x y(C ))48sin(4π-π-=x y (D ))48sin(4π+π=x y5、函数)62sin(3π+=x y 与y 轴距离最近的对称轴是______.6、将函数)(sin )(R x x x f y ∈⋅=的图象向右平移4π个单位后,再作关于x 轴的对称变换,得到函数x y 2sin 21-=的图象,则)(x f 可以是_______。
7、给出下列命题:①存在实数α,使1cos sin =αα;②存在实数α,使23cos sin =+αα;③)225sin(x y -=π是偶函数;④8π=x 是函数)452sin(π+=x y 的一条对称轴方程;⑤若α、β是第一象限角,且αβ>,则βαtan tan >。
其中正确命题的序号是_______。
(注:把你认为正确命题的序号都填上)8、(05上海卷)函数[]π2,0|,sin |2sin )(∈+=x x x x f 的图象与直线k y =有且仅有两个不同的交点,则k 的取值范围是__________。
9、(05湖南卷)设函数f (x )的图象与直线x =a ,x =b 及x 轴所围成图形的面积称为函数f (x )在[a ,b]上的面积,已知函数y =sinn x 在[0,nπ]上的面积为n 2(n ∈N * ),(i )y =sin3x 在[0,32π]上的面积为 34 ;(ii )y =sin (3x -π)+1在[3π,34π]上的面积为 .10、已知函数)cos (sin sin 2)(x x x x f +=。
(1)求它的振幅、周期和初相; (2)用五点法作出它的图象;(3)说明)cos (sin sin 2)(x x x x f +=的图象可由x y sin =的图象经过怎样的变换而得到?11、若函数)(x f y =的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,然后将所得图象先向左平移2π 个单位,再向下平移1个单位,得到的曲线与x y cos 21=的图象相同,求)(x f y =的表达式。
12、函数)2||,0,0)(sin(πϕωϕω<>>+=A x A y 在)32,0(π∈x 内只取到一个最大值和一个最小值,且当12π=x 时,函数的最大值为3,当127π=x 时,函数的最小值为-3,试求此函数的解析式。
13、设函数()sin()(0,||)2f x x πωϕωϕ=+><,给出以下四个论断:①它的图象关于直线12π=x 对称;②它的图象关于点)0,3(π对称; ③它的周期是π; ④它在区间]0,6[π-上是增函数。
以其中的两个论断作为条件,余下的两个论断作为结论,写出你认为正确的两个命题,并对其中一个命题加以证明。
参考答案:基本练习:1、B 2、C 3、B 4、D 5、[-4, 5] 6、6例题分析:例1(1)振幅2,周期π,初相3π;(2)略;(3)把x y sin =的图象上所有的点左移3π个单位,得到)3sin(π+=x y 的图象,再把)3sin(π+=x y 的图象上的点的横坐标缩短到原来的21(纵坐标不变),得到)32sin(π+=x y 的图象,最后把)32sin(π+=x y 图象上点的纵坐标伸长到原来的2倍(横坐标不变),即可得到)32sin(2π+=x y 的图象 例2、65π例3、)3y x π=+ 例4(1) 3sin 10(024)6y t t π=+≤≤;(2) 该船最早能在凌晨1时进港,下午17时出港,在港口至多停留16小时 作业:1—4、DBCA5、直线6x π= 6、()2cos f x x = 7、③④ 8、13k << 9、32+π10、振幅2,周期π,初相3π;(2)略;(3)把x y sin =的图象上所有的点右移4π个单位,得到sin()4y x π=-的图象,再把sin()4y x π=-的图象上的点的横坐标缩短到原来的21(纵坐标不变),得到sin(2)4y x π=-的图象,然后最把sin(2)4y x π=-图象上点的纵坐标伸长到原来的,得到)4y x π=-的图象,最后把)4y x π=-的图象向上平移1个单位,即可得到)14y x π=-+的图象,即)cos (sin sin 2)(x x x x f +=的图象11、1sin 212y x =+ 12、)32sin(3π+=x y13、①③⇒②④;②③⇒①④。
