必修二第一章知识点检测

合集下载

必修2第一章单元测试题

高一化学必修2第一章过关单元测试题1．下列元素中，最高正化合价数值最大的是A ．CB ．FC ．SD ．Ne2．已知某粒子 n A Z R，则元素R 的原子序数是 A ．Z B ．A-Z C ．Z-n D ．Z+n3．元素的性质随着元素原子序数的递增而呈周期性变化的原因是A ．元素原子的核外电子排布呈周期性变化B ．元素的原子半径呈周期性变化C ．元素的化合价呈周期性变化D ．元素的金属性、非金属性呈周期性变化4. 19世纪门捷列夫的突出贡献是A .提出了原子学说B .提出了分子学说C .发现了稀有气体D .发现了元素周期律5．下列四种元素中，非金属性最强的是A ．ClB ．PC ．SD ．Si6．下列各物质中酸性最弱的是A ．H 2CO 3B ．H 3PO 4C ．H 2SO 4D ．H 3SiO 37．下列关于O 168的叙述正确的是A ．质量数为8B ．质子数为8C ．中子数为16D ．电子数为168．下列化合物中，既有离子键又有共价键的是A ．NH 4ClB ．MgOC ．C 2H 6D ．CO 29．下列排序错误的是A . 原子半径：Na>Mg>C>N B. 热稳定性：HI<HBr<HCl<HFC . 最高正化合价：Si<P<S<Cl D. 碱性：Al(OH)3>Mg(OH)2>Ca(OH)2>KOH10. 某元素R 的气态氢化物为H 2R ，则它的最高价氧化物对应的水化物的化学式为A. HRO 3B. HRO 4C. H 2RO 4D. H 3RO 411. 下列各组元素中，原子半径依次增大的是A . Li 、Na 、K B. I 、Br 、F C. O 、Al 、S D. Li 、F 、Cl12．根据元素在周期表中的位置判断，下列元素中原子半径最小的是A ．氧B ．氟C ．碳D ．氮13．X 元素最高氧化物对应的水化物为H 3XO 4，则它对应的气态氢化物为A ．HXB ．H 2XC ．XH 4D ． XH 314．下列事实不能．．说明非金属性Cl ＞I 的是A ．Cl 2+2I -==2Cl -+I 2B ．稳定性：HCl ＞HIC ．酸性：HClO 4＞HIO 4D ．酸性：HClO 3＞HIO 315．下列说法错误．．的是 A ．原子半径：F ＜Mg ＜K B ．稳定性：PH 3＞H 2S ＞NH 3C ．酸性：H 3PO 4＜H 2SO 4＜HClO 4D ．碱性：Al(OH)3＜Mg(OH)2＜KOH16．运用元素周期律分析下面的推断，其中不正确．．．的是 A ．锂（Li ）与水反应比钠与水反应剧烈B ．砹（At ）为有色固体，AgAt 难溶于水也不溶于稀硝酸C ．在氧气中，铷（Rb ）的燃烧产物比钠的燃烧产物更复杂D ．HBrO 4的酸性比HIO 4的酸性强18．X 元素的阳离子和Y 元素的阴离子都具有与Ar 原子相同的电子层结构，下列叙述正确的是。

必修二第一单元随堂知识检测

一、基础知识1.下列加点字注音有误的一项是()A．倩．影(qiān)媛．女(yuán)鹢．首(yì) 婆娑．(shuō)B．羞涩．(sè) 蟋蟀．(shuài)啼唱(tí) 袅娜．(nuó)C．陪衬．(chèn) 瞥．见(piē)肋．骨(lèi) 澄．清(dènɡ)D．宛．然(wǎn) 斑．驳(bān)氛．围(fēn) 峭楞．楞(lénɡ)2.下列各组词语中有错别字的一项是()A．峥嵘委婉斑驳坚韧不拔B．寥廓渡越湮没礼尚往来C．风致弥望宛然含情默默D．黯然袅娜俨然沸反盈天3.下列各句空格处应填入的词语正确的一项是()①沿着荷塘，是一条曲折的小煤屑路。

这是一条________的路；白天也少人走，夜晚更加寂寞。

②秋的味，秋的色，秋的意境与姿态，总看不饱，尝不透，________不到十足。

③我为了这永远向着阳光生长的植物不快，因为它损害了我的自尊心。

可是我囚系住它，仍旧让________的枝叶垂在我的案前。

A．幽静品尝软弱B．幽僻品尝柔弱C．幽僻赏玩柔弱D．幽静赏玩软弱4.下列句子中，加点的成语使用不．正确的一项是()A．该会计师事务所的一份研究报告指出，中国机床制造业一些有实力的集团为向国外市场渗透，采取了更加咄咄逼人．．．．的收购策略。

B．随着贝克特等人的先后逝世，荒诞戏剧作为一个流派也渐渐偃旗息鼓．．．．了，但其创作成就和产生的影响依然存在。

C．从被科尼法官讲述的一起案件深深触动，到把科尼的故事写成《复活》，托尔斯泰惨淡经营．．．．了整整12年之久。

D．“千年杜鹃王”是森林公园工作人员在马岗子海拔2160米处发现的，树围达175厘米，鲜为人知．．．．。

经专家鉴定，其树龄已在900年以上。

5.下列四个句子都用了“像”字，其中没有运用比喻的一句是()A．树色一例是阴阴的，乍看像一团烟雾。

B．只在小路一旁，漏着几段空隙，像是特为月光留下的。

人教B版必修2练习第一章基本知能检测 Word版含解析

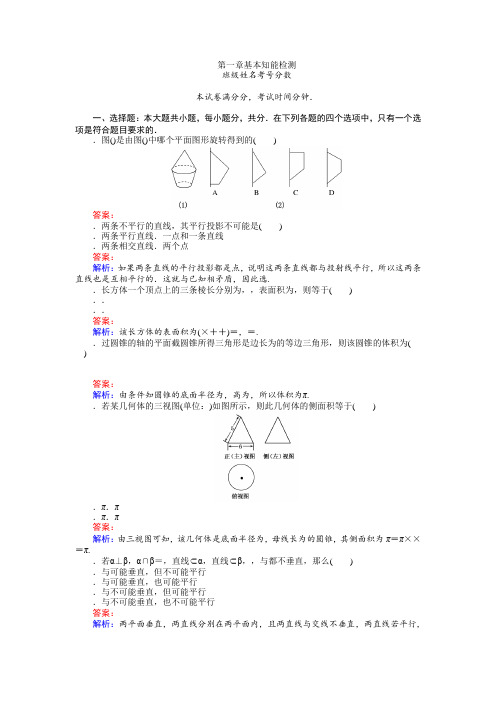
第一章基本知能检测班级姓名考号分数本试卷满分分，考试时间分钟．一、选择题：本大题共小题，每小题分，共分．在下列各题的四个选项中，只有一个选项是符合题目要求的．．图()是由图()中哪个平面图形旋转得到的( )答案：．两条不平行的直线，其平行投影不可能是( )．两条平行直线．一点和一条直线．两条相交直线．两个点答案：解析：如果两条直线的平行投影都是点，说明这两条直线都与投射线平行，所以这两条直线也是互相平行的．这就与已知相矛盾，因此选.．长方体一个顶点上的三条棱长分别为，，表面积为，则等于( )．．．．答案：解析：该长方体的表面积为(×＋＋)＝，＝.．过圆锥的轴的平面截圆锥所得三角形是边长为的等边三角形，则该圆锥的体积为()答案：解析：由条件知圆锥的底面半径为，高为，所以体积为π.．若某几何体的三视图(单位：)如图所示，则此几何体的侧面积等于( )．π．π．π．π答案：解析：由三视图可知，该几何体是底面半径为，母线长为的圆锥，其侧面积为π＝π××＝π.．若α⊥β，α∩β＝，直线⊂α，直线⊂β，，与都不垂直，那么( )．与可能垂直，但不可能平行．与可能垂直，也可能平行．与不可能垂直，但可能平行．与不可能垂直，也不可能平行答案：解析：两平面垂直，两直线分别在两平面内，且两直线与交线不垂直，两直线若平行，则均与交线平行，因此可能平行；若与垂直，根据面面垂直的性质，则与垂直或与垂直，与已知矛盾，选.．如图，长方体－的底面是边长为的正方形，高为，为线段的中点，则三棱锥－的体积为( )答案：解析：△＝××＝，∴－＝－＝△·＝××＝.．如图所示，水平放置的圆柱形物体的三视图是( )答案：解析：此题主要研究实物体到三种视图的转化过程，主视图是从正面观察物体的形状，左视图是从左侧面去观察，俯视图是从上往下看物体的形状如何．从正面看是个矩形，从左面看是个圆，从上往下看是一个矩形，对照图中、、、，可知是正确的．．设，是两条不同的直线，α，β是两个不同的平面，则下列命题错误的是( )．若⊥α，∥α，则⊥．若⊥α，∥，⊂β，则α⊥β．若⊥α，⊥β，α∥β，则∥．若∥α，∥β，则α∥β答案：解析：由题意可得、、项显然正确，对于选项：当α、β相交，且与α、β的交线平行时，有∥α，∥β，但此时α与β不平行．故选.．给出下列命题：①和直线都相交的两条直线在同一个平面内；②三条两两相交的直线在同一平面内；③有三个不同公共点的两平面重合；④两两平行的三条直线确定三个平面，其中正确命题的个数是( )．个．个．个．个答案：解析：两两相交且过同一点的直线，可以不在同一平面内，所以①②都错；两平面相交，也可以有三个不同的公共点，所以③错；两两平行的三条直线可以在同一平面内，所以④错．。

完整高中化学必修二第一章知识点和习题含答案

..元素周期律物质结构第一章一、原子结构质子（Z个）原子核注意：中子（N个）质量数(A)＝质子数(Z)＋中子数(N)原子1.个）核外电子（Z 元素、核素、同位素2. 的同一类原子的总称。

元素：具有相同的一种原子。

和一定数目的核素：具有一定数目的) (对于原子来说同位素：质子数相同而数不同的同一元素的不同原子互称为同位素。

②各电子层最多原子核外电子的排布规律：①电子总是尽先排布在能量最低的电子层里；3.2，次外层不超2个）个（K层为最外层不超过容纳的电子数是2n；③最外层电子数不超过8 32个。

过18个，倒数第三层电子数不超过七六三四五电子层：一（能量最低）二K L M N O P Q 对应表示符号：号元素原子核外电子的排布：～20★熟背前20号元素，熟悉1 K Ca Al Si P S Cl ArF ONe Na MgH He Li Be B C N二、元素周期表1.编排原则：) = = 核电荷数( 原子序数=①按原子序数递增的顺序从左到右排列）。

（周期序数＝原子的电子层数②将电子层数相同的各元素从左到右排成一横行．．．．．．．．。

③把最外层电子数相同的元素按电子层数递增的顺序从上到下排成一纵行．．．．．．．．．．) (主族序数＝原子最外层电子数完美格式eord..结构特点：2. 元素种类核外电子层数种元素第一周期 1 2 第二周期 2 8短周期种元素周期第三周期 3 8种元素元（7个横行）第四周期 4 18种元素素（7个周期）第五周期 5 18种元素周长周期第六周期 6 32种元素期第七周期7 未填满（已有26种元素）表主族：ⅠA～ⅦA共7个主族族副族：ⅢB～ⅦB、ⅠB～ⅡB，共7个副族（18个纵行）第Ⅷ族：三个纵行，位于ⅦB和ⅠB之间（16个族）零族：稀有气体n?A，则元素R的原子序数是（1．已知某粒子）。

R Z A．Z B．A-Z C．Z-n D．Z+n三、元素周期律1.元素周期律：元素的性质（核外电子排布、原子半径、主要化合价、金属性、非金属性）随着核电荷数的递增而呈周期性变化的规律。

(典型题)高中数学必修二第一章《立体几何初步》检测题(答案解析)

一、选择题1．如下图所示，在正方体1111ABCD A B C D -中，E 是平面11ADD A 的中心，M 、N 、F 分别是11B C 、1CC 、AB 的中点，则下列说法正确的是（）A ．12MN EF =，且MN 与EF 平行B ．12MN EF ≠，且MN 与EF 平行 C ．12MN EF =，且MN 与EF 异面 D ．12MN EF ≠，且MN 与EF 异面 2．在正方体1111ABCD A B C D -中，点,E F 分别是梭BC ，CD 的中点，则1A F 与1C E 所成角的余弦值为（）A ．5B ．25C ．5D ．25 3．如图，在正四棱锥P ABCD -中，设直线PB 与直线DC 、平面ABCD 所成的角分别为α、β，二面角P CD B --的大小为γ，则（）A ．,αβγβ>>B ．,αβγβ><C ．,αβγβ<>D ．,αβγβ<< 4．已知三棱锥A BCD -的各棱长都相等，E 为BC 中点，则异面直线AB 与DE 所成角的余弦值为（）A 13B 3C 33D 115．已知正三棱柱111ABC A B C -中，1AB AA =，M 是1CC 的中点，则异面直线AM 与1A B 所成角的大小为（）A ．π6B ．π4C ．π3D ．π2 6．如图，正三棱柱111ABC A B C -的高为4，底面边长为43，D 是11B C 的中点，P 是线段1A D 上的动点，过BC 作截面AP α⊥于E ，则三棱锥P BCE -体积的最小值为（）A ．3B ．23C ．43D ．127．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A ．24B ．30C ．47D ．7 8．一个底面为正三角形的棱柱的三视图如图所示，若在该棱柱内部放置一个球，则该球的最大体积为（）A ．6πB ．12πC ．43πD ．83π 9．一个正方体的平面展开图及该正方体的直观图如图所示，在正方体中，设BC 的中点为M ，GH 的中点为N ，下列结论正确的是（）A ．//MN 平面ABEB ．//MN 平面ADEC ．//MN 平面BDHD ．//MN 平面CDE10．如图是某个四面体的三视图，则下列结论正确的是（）A．该四面体外接球的体积为48πB．该四面体内切球的体积为2 3πC．该四面体外接球的表面积为323πD．该四面体内切球的表面积为2π11．某几何体的三视图如图所示，该几何体的体积为V，该几何体所有棱的棱长之和为L，则（）A．8,14253V L==+B．8,1425V L==+C．8,16253V L==+D．8,1625V L==+12．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A ．16B ．13C ．23D ．2二、填空题13．在边长为3的菱形ABCD 中，对角线3AC =，将三角形ABC 沿AC 折起，使得二面角B AC D --的大小为2π，则三棱锥B ACD -外接球的体积是_________________．14．已知三棱锥P ABC -的外接球O 的表面积为12π，PA ⊥平面ABC ，BA AC ⊥，2PA =，则ABC 面积的最大值为__________．15．已知四棱锥P ABCD -的底面ABCD 为矩形，且所有顶点都在球O 的表面上，侧面PAB ⊥底面ABCD ，23PA PB ==，120APB ∠=︒，4=AD ，则球O 的表面积为_______.16．在如图棱长为2的正方体中，点M 、N 在棱AB 、BC 上，且1AM BN ==，P 在棱1AA 上，α为过M 、N 、P 三点的平面，则下列说法正确的是__________．①存在无数个点P ，使面α与正方体的截面为五边形；②当11A P =时，面α与正方体的截面面积为33③只有一个点P ，使面α与正方体的截面为四边形；④当面α交棱1CC 于点H ，则PM 、HN 、1BB 三条直线交于一点．17．已知长方体1234ABCD A B C D -，底面是边长为4的正方形，高为2，点O 是底面ABCD 的中心，点P 在以O 为球心，半径为1的球面上，设二面角111P A B C --的平面角为θ，则tan θ的取值范围是________.18．如图，矩形ABCD 中，2AB AD =，E 为边AB 的中点，将ADE 沿直线DE 翻折成1A DE △．若M 为线段1A C 的中点，则在ADE 翻折过程中，下面四个选项中正确的是______（填写所有的正确选项）（1）BM 是定值（2）点M 在某个球面上运动（3）存在某个位置，使1DE A C ⊥（4）存在某个位置，使//MB 平面1A DE19．如图，在长方体1111ABCDA B C D ﹣中，O 是11B D 的中点，P 是线段AC 上一点，且直线1PA 交平面11AB D 于点M ．给出下列结论：①A ，M ，O 三点共线；②A ，M ，O ，1A 不共面；③A ，M ，C ，O 共面；④B ，1B ，O ，M 共面．其中正确结论的序号为______．20．如图，已知正四面体P ABC -的棱长为2，动点M 在四面体侧面PAC 上运动，并且总保持MB PA ⊥，则动点M 的轨迹的长度为__________.三、解答题21．如图，三棱柱111ABC A B C -中，122AB BC AC BB ===，1B 在底面ABC 上的射影恰好是点A ，E 是11A C 的中点.（1）证明：1//A B 平面1B CE ；（2）求1A B 与平面11BCC B 所成角的正弦值.22．如图，在直三棱柱111ABC A B C -中，底面ABC 为正三角形，1AB 与1A B 交于点O ，E ，F 是棱1CC 上的两点，且满足112EF CC =.（1）证明：//OF 平面ABE ；（2）当1CE C F =，且12AA AB =，求直线OF 与平面ABC 所成角的余弦值. 23．如图所示，在长方体1111ABCD A B C D -中，11,2AD AA AB ===，点E 是AB 的中点.（1）证明：1//BD 平面1A DE ；（2）证明：11D E A D ⊥；（3）求二面角1D EC D --的正切值.24．如图，已知三棱锥P ABC -﹐PC AB ⊥，ABC 是边长为23的正三角形，43PB =﹐60PBC ∠=，点F 为线段AP 的中点．（1）证明：PC ⊥平面ABC ；（2）求直线BF 与平面PAC 所成角的大小．25．在四棱锥P ABCD -中，90ABC ACD ∠=∠=，60BAC CAD ∠=∠=，PA ⊥平面ABCD ，E 为PD 的中点，M 为AD 的中点，24PA AB ==．（1）取PC 中点F ，证明：PC ⊥平面AEF ；（2）求点D 到平面ACE 的距离.26．如图，ABC 中，2AC BC AB ==，ABED 是边长为1的正方形，平面ABED ⊥平面ABC ，若G 、F 分别是EC 、BD 的中点．（1）求证：//GF 平面ABC ；（2）求证：AC ⊥平面EBC ．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】设正方体1111ABCD A B C D -的棱长为2，利用正方体性质可求得2MN =，3EF =知12MN EF ≠，再利用三角形中位线性质知1//MN B C ，从而//MN ED ，又EF 与ED 相交，可知MN 与EF 异面，即可选出答案.【详解】设正方体1111ABCD A B C D -的棱长为2，则22112MN MC C N =+=作E 点在平面ABCD 的投影点G ，即EG ⊥平面ABCD ，连接,EG GF ，在直角EGF △中，1EG =，222GF AG AF =+=2222123EF EG GF =+=+=以12MN EF ≠，故排除A 、C 连接DE ，由E 是平面11ADD A 的中心，得112DE A D = 又M N 、分别是11B C 、1CC 的中点，所以1//MN B C又11//A D B C ，所以//MN ED ，又EF ED E ⋂=，所以MN 与EF 异面故选：D.【点睛】关键点睛：本题考查正方体中的线面关系，线线平行的关系，及判断异面直线，解题的关键是熟记正方体的性质，考查学生的逻辑推理能力，属于基础题.2．D解析：D【分析】延长DA 至G ，使AG CE =，可证11//A G C E ，得1GA F ∠是异面直线1A F 与1C E 所成的角（或其补角）．在1AGF △中，由余弦定理可得结论．【详解】延长DA 至G ，使AG CE =，连接1,GE GA ,GF ，11,AC A C ，又//AG CE 所以AGEC 是平行四边形，//,GE AC GE AC =，又正方体中1111//,AC AC AC AC =，所以1111//,AC DE AC DE =，所以11AC EG 是平行四边形，则11//A G C E ，所以1GA F ∠是异面直线1A F 与1C E 所成的角（或其补角）．设正方体棱长为2，在正方体中易得15AG =10GF =22222112(21)3A F AA AF =+=++=，1AGF △中，2221111125cos 2253AG A F GF GA F AG A F +-∠===⋅⨯⨯．故选：D ．【点睛】方法点睛：本题考查空间向量法求异面直线所成的角，求异面直线所成角的方法：（1）定义法：根据定义作出异面直线所成的角并证明，然后解三角形得结论；（2）建立空间直角坐标系，由两异面直线的方向向量的夹角得异面直线所成的角．3．A解析：A 【分析】连接AC 、BD 交于O ，连PO ，取CD 的中点E ，连,OE PE ，根据正棱锥的性质可知，PCE α∠=，PCO β∠=，PEO γ∠=，再比较三个角的正弦值可得结果. 【详解】连接AC 、BD 交于O ，连PO ，取CD 的中点E ，连,OE PE ，如图：因为//AB CD ，所以PBA α∠=，又因为四棱锥P ABCD -为正四棱锥，所以PCE α∠=，由正四棱锥的性质可知，PO ⊥平面ABCD ，所以PCO β∠=，易得OE CD ⊥，PE CD ⊥，所以PEO γ∠=，因为sin PE PC α=，sin POPC β=，且PE PO >，所以sin sin αβ>，又,αβ都是锐角，所以αβ>，因为sin PO PE γ=，sin POPCβ=，且PC PE >，所以sin sin γβ>，因为,βγ都是锐角，所以γβ>. 故选：A 【点睛】关键点点睛：根据正棱锥的性质，利用异面直线所成角、直线与平面所成角、二面角的平面角的定义得到这三个角是解题关键，属于中档题.4．B解析：B 【分析】取AC 中点F ，连接,EF DF ，证明FED ∠是异面直线AB 与DE 所成角（或其补角），然后在三角形中求得其余弦值即可得．【详解】取AC 中点F ，连接,EF DF ，∵E 是BC 中点，∴//EF AB ，12EF AB =，则FED ∠是异面直线AB 与DE 所成角（或其补角），设1AB =，则12EF =，32DE DF ==， ∴在等腰三角形DEF 中，11324cos 63EFFED DE ∠===．所以异面直线AB 与DE 所成角的余弦值为36．故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．5．D解析：D 【分析】取AC 中点E ，连接1,A E BE ，先通过BE ⊥平面11ACC A 可得BE AM ⊥，再由1ACM A AE ≅可得1AM A E ⊥，即可得出AM ⊥平面1A BE ，即1AM A B ⊥.【详解】取AC 中点E ，连接1,A E BE ，ABC 为正三角形，BE AC ∴⊥，正三棱柱111ABC A B C -中，1CC ⊥平面ABC ，BE ⊂平面ABC ，1CC BE ∴⊥，1ACCC C =，BE ∴⊥平面11ACC A ，AM ⊂平面11ACC A ，BE AM ∴⊥，在直角三角形ACM 和直角三角形1A AE 中，1,AC A A CM AE ==,1ACM A AE ∴≅， 1CAM AA E ∴∠=∠，12CAM A EA π∴∴∠+∠=，则1AM A E ⊥，1BE A E E ⋂=，AM ∴⊥平面1A BE ，1A B ⊂平面1A BE ，1AM A B ∴⊥，故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解，解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.6．C解析：C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时，三棱锥P BCE -体积有最小值，建立坐标系求得当点E 的高为3时，问题得解.【详解】以点O 为原点，,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系，如图所示：设点(),0,E x z ，依题意得()6,0,0A ，则()6,0,AE x z =- ，(),0,OE x z = 因为过BC 作截面AP α⊥于E ，所以AE OE ⊥则0AE OE ⋅=，故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅=故选：C 【点睛】关键点点晴：本题的解题关键是将问题转化为求E ABC V -的最大值，通过建系求得三棱锥E ABC -的高的最大值即可.7．D解析：D 【分析】先找到几何体的原图，再求出几何体的高，再求几何体的体积得解. 【详解】由三视图可知几何体为图中的四棱锥1P CDD E -，由题得22437AD =-7 所以几何体的体积为11(24)676732⋅+⋅=. 故选：D 【点睛】方法点睛：通过三视图找几何体原图常用的方法有：（1）直接法；（2）拼凑法；（3）模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解.8．C解析：C 【分析】先由三视图计算底面正三角形内切圆的半径，内切圆的直径和三棱柱的高比较大小，确定球的半径的最大值，计算球的最大体积. 【详解】由三视图知该直三棱柱的高为4，底面正三角形的高为33半径为高的三分之一，即3r =234<，所以该棱柱内部可放置球的半径的最大3343433V ππ==.故选：C 【点睛】关键点点睛：本题的第一个关键是由三视图确定底面三角形的高是33定球的最大半径.9．C解析：C 【分析】根据题意，得到正方体的直观图及其各点的标记字母，取FH 的中点O ,连接ON ,BO ，可以证明MN ‖BO ,利用BO 与平面ABE 的关系可以判定MN 与平面ABE 的关系，进而对选择支A作出判定；根据MN 与平面BCF 的关系，利用面面平行的性质可以判定MN 与平面ADE 的关系，进而对选择支B 作出判定；利用线面平行的判定定理可以证明MN 与平面BDE 的平行关系，进而判定C ；利用M ,N 在平面CDEF 的两侧，可以判定MN 与平面CDE 的关系，进而对D 作出判定. 【详解】根据题意，得到正方体的直观图及其各点的标记字母如图所示，取FH 的中点O ,连接ON ,BO ，易知ON 与BM 平行且相等，∴四边形ONMB 为平行四边形，∴MN ‖BO , ∵BO 与平面ABE （即平面ABFE )相交，故MN 与平面ABE 相交，故A 错误； ∵平面ADE ‖平面BCF ,MN ∩平面BCF =M ,∴MN 与平面ADE 相交，故B 错误； ∵BO ⊂平面BDHF ,即BO ‖平面BDH ,MN ‖BO ,MN ⊄平面BDHF ,∴MN ‖平面BDH ,故C 正确；显然M ,N 在平面CDEF 的两侧，所以MN 与平面CDEF 相交，故D 错误. 故选：C.【点睛】本题考查从面面平行的判定与性质，涉及正方体的性质，面面平行，线面平行的性质，属于小综合题，关键是正确将正方体的表面展开图还原，得到正方体的直观图及其各顶点的标记字母，并利用平行四边形的判定与性质找到MN 的平行线BO .10．D解析：D 【分析】先找到几何体原图，再求出几何体的外接球的半径和内切球的半径，再判断每一个选项得解. 【详解】由三视图得几何体为下图中的三棱锥A BCD -，AB ⊥平面BCD ,42AB =2CE DE ==,2BE =,由题得2CBD π∠=.设外接球的球心为,O 外接球的半径为R ，则OE ⊥平面BCD , 连接,OB OA ,取AB 中点F ,连接OF .由题得1222OE BF AB ===,所以222(22)2,23R R =+∴=, 所以外接球的体积为34(23)3233ππ⨯=，所以选项A 错误；所以外接球的表面积为24(23)48ππ⨯=，所以选项C 错误；由题得22(42)(22)210AC AD ==+=，所以△ACD △的高为24026-=，设内切球的半径为r ，则1111111(422242222446)24423222232r ⨯⨯+⨯⨯+⨯⨯+⨯⨯=⨯⨯⨯⨯ 所以22r，所以内切球的体积为3422)323ππ⨯=（，所以选项B 错误；所以内切球的表面积为224()22ππ⨯=，所以选项D 正确. 故选：D【点睛】方法点睛：求几何体外接球的半径一般有两种方法:模型法和解三角形法.模型法就是把几何体放在长方体中，使几何体的顶点和长方体的若干个顶点重合，则几何体的外接球和长方体的外接球是重合的，长方体的外接球的半径22212r a b c =++几何体的外接球半径.如果已知中有多个垂直关系，可以考虑用此种方法.解三角形法就是找到球心O 和截面圆的圆心O '，找到OO '、球的半径OA 、截面圆的半径O A '确定的Rt OO A '△,再解Rt OO A '△求出球的半径OA .11．A解析：A【分析】由三视图还原几何体，由棱锥的体积公式可得选项. 【详解】在如图所示的正方体1111ABCD A B C D -中，P ，E 分别为11,B C BC 的中点，该几何体为四棱锥P ABCD -，且PE ⊥平面ABCD ．由三视图可知2AB =，则5,3PCPB PD PA ====，则21825681425,2233L V =++=+=⨯⨯=．故选：A.【点睛】方法点睛：三视图问题的常见类型及解题策略：(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．12．C解析：C 【分析】根据题中所给的几何体的三视图还原几何体，得到相应的三棱锥，之后利用椎体体积公式求得结果. 【详解】根据题中所给的几何体的三视图还原几何体如图所示：该三棱锥满足底面BCD△是等腰三角形，且底边和底边上的高线都是2；且侧棱AD⊥底面BCD，1AD=，所以112 =221=323V⨯⨯⨯⨯，故选：C.【点睛】方法点睛：该题考查的是有关根据所给几何体三视图求几何体体积的问题，解题方法如下：（1）应注意把握三个视图的尺寸关系：主视图与俯视图长应对正（简称长对正），主视图与左视图高度保持平齐（简称高平齐），左视图与俯视图宽度应相等（简称宽相等），若不按顺序放置和不全时，则应注意三个视图名称；（2）根据三视图还原几何体；（3）利用椎体体积公式求解即可.二、填空题13．；【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析：56π；【分析】分析菱形的特点，结合其翻折的程度，判断其外接球球心的位置，放到相应三角形中，利用勾股定理求得半径，利用球的体积公式求得外接球的体积.【详解】根据题意，画出图形，3的菱形ABCD 中，对角线3AC = 所以ABC 和DBC △都是正三角形，又因为二面角B AC D --的大小为2π，所以分别从两个正三角形的中心做面的垂线，交于O ，则O 是棱锥B ACD -外接球的球心，且11,2GD OG GE ===，所以球的半径2252R GD OG =+=，所以其体积为3344555(33V R ππ==⋅=， 55π. 【点睛】思路点睛：该题考查的是有关几何体外接球的问题，解题思路如下：（1）根据题中所给的条件，判断菱形的特征，得到两个三角形的形状；（2）根据直二面角，得到两面垂直，近一倍可以确定其外接球的球心所在的位置；（3）利用勾股定理求得半径；（4）利用球的体积公式求得结果；（5）要熟知常见几何体的外接球的半径的求解方法.14．2【分析】由球的表面积可求出半径取的中点可得设由基本不等式可得即可求出面积的最大值【详解】因为球的表面积为所以球的半径取的中点则为的外接圆圆心平面设由得因为所以当且仅当时取等因为的面积为所以面积的最解析：2 【分析】由球的表面积可求出半径3R =，取BC 的中点D ，可得1OD =，设AB x =，AC y =，由基本不等式可得4xy ≤，即可求出ABC 面积的最大值.【详解】因为球O 的表面积为12π，所以球O 的半径3R =．取BC 的中点D ，则D 为ABC 的外接圆圆心，PA ⊥平面ABC ，112OD PA ∴==，设AB x =，AC y =，由2222134+==+=+=x y R OC CD OD ，得228x y +=．因为222x y xy +≥，所以4xy ≤，当且仅当2x y ==时取等．因为ABC 的面积为1122⋅=AB AC xy ，所以ABC 面积的最大值为2．故答案为：2.【点睛】本题考查几何体的外接球问题，解题的关键是是建立勾股关系，利用基本不等式求出4xy ≤.15．【分析】首先利用垂直关系和底面和侧面外接圆的圆心作出四棱锥外接球的球心再计算外接球的半径以及球的表面积【详解】连结交于点取中点连结并延长于点点是外接圆的圆心侧面底面侧面底面平面过点作平面侧面所以点是解析：64π【分析】首先利用垂直关系和底面ABCD 和侧面ABCD 外接圆的圆心，作出四棱锥P ABCD -外接球的球心，再计算外接球的半径，以及球O 的表面积. 【详解】连结,AC BD ，交于点M ，取AB 中点N 连结AN ，MN ，并延长于点E ，点E 是PAB △外接圆的圆心，侧面PAB ⊥底面ABCD ，侧面PAB 底面ABCD AB =，MN AB ⊥ MN ∴⊥平面PAB ，过点M 作MO ⊥平面ABCD ，//EO MN ，EO ∴⊥侧面PAB ，所以点O 是四棱锥P ABCD -外接球的球心，可知四边形MNEO 是矩形，右图，23PA PB ==，120APB ∠=，2cos306AB PB ∴==，点E 是PAB △外接圆的圆心，sin 303PN PB ∴==，PBE △是等边三角形，23PE =， 2333NE ∴=-=，3MO ∴=，2211641322MC AC ==+=， 223134R OC MO MC ∴==+=+=，∴球O 的表面积2464S R ππ==故答案为：64π 【点睛】本题考查了球与几何体的综合问题，考查空间想象能力以及化归和计算能力，（1）当三棱锥的三条侧棱两两垂直时，并且侧棱长为,,a b c ，那么外接球的直径2222R a b c =++2）当有一条侧棱垂直于底面时，先找底面外接圆的圆心，过圆心做底面的垂线，球心在垂线上，根据垂直关系建立R 的方程.（3）而本题类型，需要过两个平面外接圆的圆心作面的垂线，垂线的交点就是球心.16．①②④【分析】让从开始逐渐向运动变化观察所得的截面从而可得正确的选项【详解】由题设可得为所在棱的中点当时如图（1）直线分别交与连接并延长于连接交于则与正方体的截面为五边形故①正确当如图（2）此时与正解析：①②④ 【分析】让P 从A 开始逐渐向1A 运动变化，观察所得的截面，从而可得正确的选项．【详解】由题设可得,M N 为所在棱的中点. 当203AP <<时，如图（1），直线MN 分别交,AD DC 与,T S ，连接TP 并延长1DD 于G ，连接GS 交1CC 于H ，则α与正方体的截面为五边形，故①正确.当11A P =，如图（2），此时α2，其面积为2362=33B 正确.当,A P 重合或1,A P 重合时，如图（3），α与正方体的截面均为四边形，故③错误.如图（4），在平面α内，设PM HN S ⋂=，则S PM ∈，而PM ⊂平面11A B BA ，故S ∈平面11A B BA ，同理S ∈平面11C B BC ，故S ∈平面11A B BA ⋂平面111C B BC BB =即PM 、HN 、1BB 三条直线交于一点. 故答案为：①②④. 【点睛】思路点睛：平面的性质有3个公理及其推理，注意各个公理的作用，其中公理2可用来证明三点共线或三线共点，公理3及其推理可用来证明点共面或线共面，作截面图时用利用公理2来处理.17．【分析】根据题意画出相应的图形结合题意找出什么情况下取最大值什么情况下取最小值利用和差角正切公式求得最值得到结果【详解】根据题意如图所示：取的中点过点作球的切线切点分别为可以判断为的最小值为的最大值解析：4747,⎡⎤-+⎢⎥⎣⎦【分析】根据题意，画出相应的图形，结合题意，找出什么情况下取最大值，什么情况下取最小值，利用和差角正切公式求得最值，得到结果. 【详解】根据题意，如图所示：取11A B 的中点H ，过H 点作球O 的切线，切点分别为,M N ，可以判断1O HN ∠为θ的最小值，1O HM ∠为θ的最大值，且1112tan 12OO O HO HO ∠===， 22,1OH OM ON ===，所以7HM HN ==tan tan 7NHO OHM ∠=∠=， 11171827477tan tan()7117O HN O HO NHO ----∠=∠-∠====++ 11171827477tan tan()7117O HM O HO OHM ++++∠=∠+∠====- 所以tan θ的取值范围是4747,33⎡+⎢⎣⎦，故答案为：4747-+⎣⎦.【点睛】方法点睛：该题考查的是有关二面角的求解问题，解题方法如下：（1）先根据题意画图；（2）结合题意，找出在什么情况下取最大值和最小值；（3）结合图形求得相应角的正切值；（4）利用和差角正切公式求得结果.18．（1）（2）（4）【分析】首先取中点连结先判断（4）是否正确再根据平行关系以及等角定理和余弦定理判断（1）再判断（2）假设成立根据直线与平面垂直的性质及判定可得矛盾来判断（3）【详解】取中点连结则平解析：（1）（2）（4）【分析】首先取CD 中点Q ，连结MQ ，BQ ，先判断（4）是否正确，再根据平行关系，以及等角定理和余弦定理判断（1），再判断（2），假设1DE A C ⊥成立,根据直线与平面垂直的性质及判定,可得11DA A E ⊥矛盾来判断（3）. 【详解】取CD 中点Q ，连结MQ ，BQ ，则1//MQ DA ，//BQ DE ，∴平面//MBQ 平面1A DE ，又MB ⊂平面MBQ ，//MB ∴平面1A DE ，故（4）正确；由1A DE MQB ∠=∠，112MQ A D ==定值，QB DE ==定值，由余弦定理可得2222cos MB MQ QB MQ QB MQB =+-⋅⋅∠ 所以MB 是定值，故（1）正确；B 是定点，M ∴是在以B 为球心，MB 为半径的球面上，故（2）正确；145A DE ADE ∠=∠=，45CDE ∠=，且设1AD =，2AB =，则2DE CE ==若存在某个位置,使1DE A C ⊥,则因为222DE CE CD +=,即CE DE ⊥,因为1AC CE C =,则DE ⊥平面1A CE ,所以1DE A E ⊥,与11DA A E ⊥矛盾，故（3）不正确.故答案为：（1）（2）（4）【点睛】关键点点睛：本题考查线线，线面位置关系时，首先判断（4）是否正确，其他选项就迎刃而解，而判断线面平行时，可根据面面平行证明线面平行.19．①③【分析】由公理1判断①正确；由公理2判断②错误③正确用反证法可得④错误【详解】∵连接∵是的中点∴平面与平面有公共点与则平面平面对于①平面则平面又平面则即三点共线故①正确；对于②在平面内由①知∴平解析：①③ 【分析】由公理1判断①正确；由公理2判断②错误③正确，用反证法可得④错误. 【详解】∵连接11A C ，∵O 是11B D 的中点，∴11O A C ∈．平面11AB D 与平面11AAC C 有公共点A 与O ，则平面11AAC C平面11AB D AO =．对于①，1M PA ∈，1PA ⊂平面11AAC C ，则M ∈平面11AAC C ，又M ∈平面11AB D ，则M AO ∈，即A ，M ，O 三点共线，故①正确；对于②，A ，O ，1A 在平面11AAC C 内，由①知M AO ∈，∴O ∈平面11AAC C ，即A ，M ，O ，1A 共面，故②错误；对于③，A ，O ，C 在平面11AAC C 内，由①知M AO ∈，∴O ∈平面11AA C CA ，则A ，M ，C ，O 共面11AAC C ，故③正确；对于④，连接BD ，则B ，1B ，O 都在平面11BB D D 上，若M ∈平面11BB D D ，则直线OM ⊂平面11BB D D ，∴A ∈面11BB D D ，显然A ∉面11BB D D 的，故④错误． ∴正确命题的序号是①③．故答案为：①③．【点睛】本题考查命题的真假判断与应用，考查空间中的直线与平面、平面与平面的位置关系，考查空间想象能力与思维能力，是中档题.20．【分析】取PA 的中点E 连接EBEC 推出PA ⊥平面BCE 故点M 的轨迹为线段CE 解出即可【详解】取PA 的中点E 连接EBEC 因为几何体是正四面体P ﹣ABC 所以BE ⊥PAEC ⊥PAEB∩EC ＝E ∴PA ⊥平面解析：3【分析】取PA 的中点E ，连接EB ，EC ，推出PA ⊥平面BCE ，故点M 的轨迹为线段CE ，解出即可．【详解】取PA 的中点E ，连接EB ，EC ，因为几何体是正四面体P ﹣ABC ，所以BE ⊥PA ，EC ⊥PA ，EB ∩EC ＝E ，∴PA ⊥平面BCE ，且动点M 在正四面体侧面PAC 上运动，总保持MB PA ⊥，∴点M 的轨迹为线段CE ，正四面体P ﹣ABC 的棱长为2，在等边三角形PAC 中求得CE ＝3232⨯=. 故答案为：3【点睛】本题考查了正四面体的性质和线面垂直与线线垂直的判定，判断轨迹是解题的关键，属于中档题．三、解答题21．（1）证明见解析；（2105. 【分析】（1）连接1BC 与1B C 相交于M ，连接EM ，证明1//EM A B ，再由线面平行的判定定理证明即可；（2）证明平面1AB F ⊥平面11BCC B ，得出NO ⊥平面11BCC B ，结合线面角的定义得出OBN ∠即为1A B 与平面11BCC B 所成角，再由相似三角形、勾股定理、直角三角形边角关系得出1A B 与平面11BCC B 所成角的正弦值. 【详解】（1）连接1BC 与1B C 相交于M ，连接EM由于E ，M 分别是11A C ，1BC 的中点，则1//EM A B因为EM ⊂平面1B CE ，1A B ⊄平面1B CE ，所以1//A B 平面1B CE .（2）取BC 中点F ，连接AF ，1B F ，则AF BC ⊥ 因为1B A ⊥平面ABC ，所以1B A BC ⊥又1,AF B A ⊂平面1AB F ，1AF B A A ⋂=，所以BC ⊥平面1AB F又BC ⊂平面11BCC B ，所以平面1AB F ⊥平面11BCC B ，过N 作1NO B F ⊥于O 因为NO ⊂平面1AB F ，平面1AB F ⋂平面111BCC B B F =所以NO ⊥平面11BCC B ，连接OB ，则OBN ∠即为1A B 与平面11BCC B 所成角设12BB =，易知2211022BN AN AB =+=+=，6AF =，1142B F = 由11ONB AFB △△，114214B N ON AF B F =⋅= 所以105sin 35ON OBN BN ∠==. 【点睛】关键点睛：解决第一问的关键在于由中位线定理证明线线平行，再由线面平行的判定定理证明线面平行；解决第二问的关键在于由线面垂直找出线面角，再由直角三角形边角关系求出正弦值.22．（1）证明见解析；（23【分析】（1）取AB 中点G ，连结OG ､EG ，可证明四边形OGEF 为平行四边形，则 OF EG ∥，由线面平行的判定定理即可求证；（2）由（1）可知，OF EG ∥，则直线OF 与平面ABC 所成角即为直线EG 与平面ABC 所成角，EC ⊥平面ABC ，则EGC ∠即为直线EG 与平面ABC 所成的角，在EGC 中即可求EGC ∠的余弦值. 【详解】（1）取AB 中点G ，连结OG ､EG ，在直三棱柱111ABC A B C -中，1OG BB ∥，则OG EF ∥，又112EF CC =，则OG EF =，所以四边形OGEF 为平行四边形，则 OF EG ∥，又EG ⊂平面ABE ，OF ⊄平面ABE ，故//OF 平面ABE .（2）由（1）可知，OF EG ∥，则直线OF 与平面ABC 所成角即为直线EG 与平面ABC 所成角，连接CG ，由直三棱柱111ABC A B C -可得EC ⊥平面ABC ，则EGC ∠即为直线EG 与平面ABC 所成的角，设2AB =，则114AA CC ==，又1CE C F =，则1CE =，3CG =2EG =，所以，直线EG 与平面ABC 所成角的余弦值为32，故直线OF 与平面ABC 3 【点睛】方法点睛：证明直线与平面平行的常用方法（1）定义法：证明直线与平面没有公共点，通常要借助于反证法来证明；（2）判定定理：在利用判断定理时，关键找到平面内与已知直线平行的直线，常考虑利用三角形中位线、平行四边形的对边平行或过已知直线作一平面，找其交线进行证明；（3）利用面面平行的性质定理：直线在一平面内，由两平面平行，推得线面平行；直线在两平行平面外，且与其中一平面平行，这这条直线与另一个平行.。

(完整word版)高中数学必修2第一章知识点习题

第一章空间几何体1.1 柱、锥、台、球的构造特点1.棱柱：有两个面相互平行，其他各面都是四边形，且每相邻两个四边形的公共边都相互平行，由这些面所围成的几何体。

几何特点：两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形。

2.棱锥：有一个面是多边形，其他各面都是有一个公共极点的三角形，由这些面所围成的几何体。

几何特点：侧面、对角面都是三角形；平行于底面的截面与底面相像。

3.棱台：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分几何特点：①上下底面是相像的平行多边形②侧面是梯形③侧棱交于原棱锥的极点1.2 空间几何体的三视图和直观图1.三视图：正视图：光芒从几何体的前面向后边正投影获得的投影图；侧视图：光芒从几何体的左面向右边正投影获得的投影图；俯视图：光芒从几何体的上边向下边正投影获得的投影图。

2.画三视图的原则：长对齐、高对齐、宽相等3.直观图：斜二测画法4. 斜二测画法的基本步骤：①成立适合直角坐标系②成立斜坐标系''y'' ''0（或 135x O，使xO y=45），注意它们确立的平面表示水平平面；③画对应图形，在已知图形平行于X 轴的线段，在直观图中画成平行于X‘轴，且长度保持不变；在已知图形平行于Y 轴的线段，在直观图中画成平行于Y‘轴，且长度变成本来的一半5.用斜二测画法画出长方体的步骤：（ 1）画轴（ 2）画底面（ 3）画侧棱（ 4）成图1.3 空间几何体的表面积与体积（一）空间几何体的表面积1 棱柱、棱锥的表面积：各个面面积之和2圆柱的表面积S2rl2r 23圆锥的表面积Srl r 24圆台的表面积Srl r 2Rl R25球的表面积S4 R 2（二）空间几何体的体积1 柱体的体积V S底 h3 台体的体积V 1S上 S下S下 ) h（ S上32 锥体的体积V1S底 h34 球体的体积V4R33xOy （尽可能使更多的点在座标轴上）第一章空间几何体一、选择题1．以下图是由哪个平面图形旋转获得的（）A B C D2.如图是一个物体的三视图，则此物体的直观图是()．3．有一个几何体的三视图以以下图所示，这个几何体可能是一个() ．主视图左视图俯视图A．棱台 B ．棱锥C．棱柱 D ．正八面体4. 图（ 1）为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成图（ 1）5．假如一个水平搁置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是() ．A． 2＋ 2 B ．1＋ 22＋ 2D ． 1＋ 22C．26．棱长都是1的三棱锥的表面积为() ．A． 3 B ． 2 3C．3 3 D ． 4 37．长方体的一个极点上三条棱长分别是3， 4，5，且它的8 个极点都在同一球面上，则这个球的表面积是 () ．A． 25π B ． 50πC．125π D ．都不对8．正方体的棱长和外接球的半径之比为() ．A． 3 ∶ 1 B ． 3 ∶ 2C．2∶ 3 D ． 3 ∶ 39．在△ ABC 中， AB＝ 2，BC＝，∠ ABC＝ 120°，若使△ ABC 绕直线BC旋转一周，则所形成的几何体的体积是() ．9753 A．π B ．πC．π D ．π2222 10．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9 和 15，则这个棱柱的侧面积是() ．A． 130 B ． 140C．150 D ． 16011．如图，在多面体ABCDEF 中，已知平面ABCD 是边长为 3 的正方形， EF ∥AB ，EF ＝3，且 EF 与平面 ABCD 的距离为 2，则该多面体的体积为() ．29( 第11题)15 A．C． 6B ． 5 D ．22 12.以下对于用斜二测画法画直观图的说法中，错误．．的是 () ．A．用斜二测画法画出的直观图是在平行投影下画出的空间图形B．几何体的直观图的长、宽、高与其几何体的长、宽、高的比率同样C．水平搁置的矩形的直观图是平行四边形D．水平搁置的圆的直观图是椭圆二、填空题1．一个棱柱起码有 ______个面，面数最少的一个棱锥有________个极点，极点最少的一个棱台有 ________条侧棱．2．若三个球的表面积之比是1∶2∶ 3，则它们的体积之比是 _____________．3．正方体 ABCD －A B C D1中， O 是上底面 ABCD 的中心，若正方体的棱长为a，111则三棱锥 O－ AB1D 1的体积为 _____________ ．4．如图， E，F 分别为正方体的面 ADD A 、面 BCC B的中心，则四边形 BFD E 在11111该正方体的面上的射影可能是___________ ．(第4题 )5．已知一个长方体共一极点的三个面的面积分别是 2 、 3 、 6 ，则这个长方体的对角线长是___________ ，它的体积为 ___________ ．6．一个直径为32 厘米的圆柱形水桶中放入一个铁球，球所有没入水中后，水面高升9 厘米则此球的半径为_________ 厘米．三、解答题1．如图，在四边形 ABCD 中，∠ DAB ＝ 90°，∠ ADC ＝ 135°， AB＝ 5，CD ＝ 2 2 ，AD ＝2，求四边形ABCD 绕 AD 旋转一周所成几何体的表面积及体积．( 第 2题 )2．以下图是一个四棱柱铁块，画出它的三视图．3.依所给实物图的形状，画出所给组合体的三视图．。

高一物理必修二第一章测试

必修二第一章测试一、选择题1．关于运动的性质，以下说法中正确的是（）A ．曲线运动一定是变速运动B ．变速运动一定是曲线运动C ．曲线运动一定是变加速运动D ．物体加速度大小、速度大小都不变的运动一定是直线运动2．关于运动的合成和分解，下列说法正确的是（）A ．合运动的时间等于两个分运动的时间之和B ．匀变速运动的轨迹可以是直线，也可以是曲线C ．曲线运动的加速度方向可能与速度在同一直线上D ．分运动是直线运动，则合运动必是直线运动3．关于从同一高度以不同初速度水平抛出的物体，比较它们落到水平地面上的时间（不计空气阻力）以下说法正确的是（）A ．速度大的时间长B ．速度小的时间长C ．一样长D ．质量大的时间长4．做平抛运动的物体，每秒的速度增量总是（）A ．大小相等，方向相同B ．大小不等，方向不同C ．大小相等，方向不同D ．大小不等，方向相同5．甲、乙两物体都做匀速圆周运动，其质量之比为1∶2 ，转动半径之比为1∶2 ，在相等时间里甲转过60°，乙转过45°，则它们所受外力的合力之比为（）A ．1∶4 B．2∶3 C．4∶9 D．9∶166．如图所示，在不计滑轮摩擦和绳子质量的条件下，当小车匀速向右运动时，物体A 的受力情况是（）A ．绳的拉力大于A 的重力B ．绳的拉力等于A 的重力C ．绳的拉力小于A 的重力D ．绳的拉力先大于A 的重力，后变为小于重力 7. 若已知物体的速度方向和它所受合力的方向如图所示，可能的运动轨迹是（）A v8. 小球做匀速圆周运动，半径R ＝0．1m ，向心加速度的大小为a ＝0．4m ／s2，下列说法不正确是 ( )A ．小球所受的合力为恒力B ．小球运动的角速度为2rad ／sC ．小球做匀速圆周运动的周期为π sD ．小球在t ＝π／4 s 内通过位移的大小为小π /20 m9．在宽度为d 的河中，水流速度为v2 ，船在静水中速度为v1（且v1＞v2），方向可以选择，现让该船开始渡河，则该船（）A ．可能的最短渡河时间为2d vB ．可能的最短渡河位移为dC ．只有当船头垂直河岸渡河时，渡河时间才和水速无关D ．不管船头与河岸夹角是多少，渡河时间和水速均无关10．关于匀速圆周运动的向心力，下列说法正确的是（）A ．向心力是指向圆心方向的合力，是根据力的作用效果命名的B ．向心力可以是多个力的合力，也可以是其中一个力或一个力的分力C ．对稳定的圆周运动，向心力是一个恒力D ．向心力的效果是改变质点的线速度大小二、填空题11．一物体在水平面内沿半径 R = 20cm 的圆形轨道做匀速圆周运动，线速度v = 0.2m/s ，那么，它的向心加速度为______m/s2 ，它的周期为______s 。

高一物理必修2第一章圆周运动知识点、测试题(附答案)

1.曲线运动1．曲线运动的特征（1）曲线运动的轨迹是曲线。

（2）由于运动的速度方向总沿轨迹的切线方向，又由于曲线运动的轨迹是曲线，所以曲线运动的速度方向时刻变化。

即使其速度大小保持恒定，由于其方向不断变化，所以说：曲线运动一定是变速运动。

（3）由于曲线运动的速度一定是变化的，至少其方向总是不断变化的，所以，做曲线运动的物体的中速度必不为零，所受到的合外力必不为零，必定有加速度。

（注意：合外力为零只有两种状态：静止和匀速直线运动。

）曲线运动速度方向一定变化，曲线运动一定是变速运动，反之，变速运动不一定是曲线运动。

2．物体做曲线运动的条件(1)从动力学角度看：物体所受合外力方向跟它的速度方向不在同一条直线上。

(2)从运动学角度看：物体的加速度方向跟它的速度方向不在同一条直线上。

3．匀变速运动：加速度（大小和方向）不变的运动。

也可以说是：合外力不变的运动。

4曲线运动的合力、轨迹、速度之间的关系（1）轨迹特点：轨迹在速度方向和合力方向之间，且向合力方向一侧弯曲。

（2）合力的效果：合力沿切线方向的分力F2改变速度的大小，沿径向的分力F1改变速度的方向。

①当合力方向与速度方向的夹角为锐角时，物体的速率将增大。

②当合力方向与速度方向的夹角为钝角时，物体的速率将减小。

③当合力方向与速度方向垂直时，物体的速率不变。

（举例：匀速圆周运动）2.绳拉物体合运动：实际的运动。

对应的是合速度。

方法：把合速度分解为沿绳方向和垂直于绳方向。

3.小船渡河例1:一艘小船在200m 宽的河中横渡到对岸，已知水流速度是3m/s ，小船在静水中的速度是5m/s ，求：（1）欲使船渡河时间最短，船应该怎样渡河？最短时间是多少？船经过的位移多大？（2）欲使航行位移最短，船应该怎样渡河？最短位移是多少？渡河时间多长？船渡河时间：主要看小船垂直于河岸的分速度，如果小船垂直于河岸没有分速度，则不能渡河。

min cos d dt t v v θ=⇒=船船（此时θ=0°，即船头的方向应该垂直于河岸）解：（1）结论：欲使船渡河时间最短，船头的方向应该垂直于河岸。

高中生物必修二第一章基础知识过关检测(含答案)

必修二基础知识过关检测第一章遗传因子的发现1、一种生物同一性状的不同表现类型，叫______性状2、杂种后代中同时出现显性性状和隐性性状的现象，叫_______ 。

3、F1（杂合子）与_________进行的杂交，叫测交。

4、在____对_____染色体的______位置上的，控制 ______性状的基因，叫等位基因。

一对等位基因通常用同一字母的大小写表示，如D与____可看作一对等位基因。

5、纯合子体细胞内每对遗传因子组成相同，杂合子体细胞内遗传因子组成不同。

纯合子自交后代纯合子，杂合子自交后代。

6、生物个体的基因型相同，表现型相同；表现型相同，基因型相同。

水毛茛水上的叶片面积大，而水下的叶片面积小，说明生物的性状是_______和_______ 共同作用的结果。

7、一对相对性状的遗传遵循_________定律；两对或两对以上相对性状的遗传遵循_______________定律。

8、一对相对性状的遗传实验P： DD高茎× dd矮茎↓F1： Dd 高茎（性性状） F1配子: _______↓F2：高茎∶矮茎（现象） F2的基因型:3 ∶ 1 （比）∶∶ = _______测交Dd高茎× _________↓__________ (基因型）__________（表现型）___________（分离比)9、孟德尔选择豌豆作杂交试验材料，是因为豌豆是____________植物，而且_________。

10、孟德尔获得成功的主要原因有①________________________②_____________________ ___③________________________④________________________。

11、生物体间的交配方式有测交、自交等。

测交的意义_______________________________；自交可运用于________________________________。

必修2第一章综合检测题

必修2第一章综合检测题一、选择题（本大题共12个小题，每小题5分，共60分）1.如下图所示，观察四个几何体，其中判断正确的是（）A .①是棱台B.②是圆台C.③是棱锥 D .④不是棱柱2.若一个三角形，采用斜二测画法作出其直观图，则其直观图的面积是原三角形面积的A•扣 B . 2倍 C.乎倍D.考咅3.（2012湖南卷）某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是（）4.已知某几何体的三视图如图所示，那么这个几何体是A .长方体B .圆柱C.四棱锥D.四棱台5.正方体的体积是64,则其表面积是（）A . 64 B. 16 C. 96 D .无法确定16.圆锥的高扩大到原来的2倍，底面半径缩短到原来的2,则圆锥的体积（A .缩小到原来的一半B .扩大到原来的2倍C .不变D .缩小到原来的7.三个球的半径之比为1:2:3，那么最大球的表面积是其余两个球的表面积之和的C."9倍D.7倍5 4&有一个几何体的三视图及其尺寸如下图（单位：cm）,则该几何体的表面积为A . 12 n cmB . 15 n cmC . 24 n cmD .9.圆台的一个底面周长是另一个底面周长的的半径为（）A . 7 B. 6 C . 5 36 n cm3倍，母线长为3，圆台的侧面积为84 n则圆台较小底面10 .如图所示是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等，相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为（）3.c2,c33 2 3A.2,1 B3，1 C.2, 2 D.3, 211. （2011 -2012广东惠州一模）某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为5的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为5的等腰三角形•则该几何体的体积为（）B .C. 64D. 2408012 ．如果用表示 1 个立方体，用表示两个立方体叠加表示3 个立方体叠加，那么图中由7 个立方体摆成的几何体，从正前方观察，可画出平面图形是( )二、填空题（本大题共4个小题，每小题5分，共20 分） 13．圆台的底半径为1 和2，母线长为3，则此圆台的体积为14 一个几何体的三视图如图所示，则这个几何体的体积为_15.圆柱的侧面展开图是边长为___________________ 6 n和4 n的矩形，则圆柱的表面积为.16.（2011 - 2012安徽皖南八校联考）一个几何体的三视图及其尺寸如下图所示，其中主视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是 _______ .三、解答题（本大题共6 个大题,共70分,解答应写出文字说明,证明过程或演算步骤）17.（本小题满分10 分）画出如图所示几何体的三视图.18.（本题满分12分）圆柱的高是8cm,表面积是130 n cm求它的底面圆半径和体积.19.（本题满分12分）如下图所示是一个空间几何体的三视图, 试用斜二测画法画出它的直观图（尺寸不限）.20.（本题满分12分）如图所示，设计一个四棱锥形冷水塔塔顶，四棱锥的底面是正方形，侧面是全等的等腰三角形，已知底面边长为2m,高为^m,制造这个塔顶需要多少铁板？21.（本题满分12分）如下图，在底面半径为2、母线长为4的圆锥中内接一个高为衍的圆柱，求圆柱的表面积.22.（本题满分12分）如图所示（单位：cm）,四边形ABCD是直角梯形，求图中阴影部分绕所成AB 旋转一周几何体的表面积和体积．。

必修二第一章测试题

必修二第一章测试题一、选择题（每题2分，共20分）1. 下列哪个选项是必修二第一章的重点内容？A. 历史事件的日期B. 科学原理的应用C. 政治制度的演变D. 文学作品的分析2. 必修二第一章中，哪个历史人物对政治制度的演变产生了重大影响？A. 孔子B. 牛顿C. 马克思D. 达尔文3. 在必修二第一章的学习中，我们主要关注哪个时间段的政治制度？A. 古代B. 中世纪C. 近现代D. 当代4. 必修二第一章提到的政治制度中，哪一个是封建制度的典型代表？A. 君主立宪制B. 共和制C. 封建制D. 社会主义制度5. 下列哪项不是必修二第一章中提到的政治制度的特点？A. 权力高度集中B. 法律至上C. 民主选举D. 世袭制度二、填空题（每空2分，共20分）6. 必修二第一章中，_________ 是政治制度演变的重要标志。

7. 在必修二第一章提到的政治制度中，_________ 是保障公民权利和自由的基石。

8. 必修二第一章强调了政治制度对于_________ 的重要性。

9. 必修二第一章中，_________ 是政治制度演变过程中的一个重要阶段。

10. 必修二第一章指出，政治制度的演变与_________ 的发展密切相关。

三、简答题（每题10分，共20分）11. 简述必修二第一章中提到的政治制度演变的几个主要阶段。

12. 必修二第一章中提到了哪些影响政治制度演变的因素？四、论述题（每题15分，共30分）13. 论述必修二第一章中提到的政治制度演变对现代社会的影响。

14. 根据必修二第一章的内容，分析政治制度演变与社会经济发展之间的关系。

五、案例分析题（15分）15. 请结合必修二第一章的内容，分析一个具体国家的政治制度演变过程，并讨论其对该国现代化进程的影响。

六、附加题（5分）16. 根据你对必修二第一章的理解，你认为未来政治制度的发展趋势可能是怎样的？请简要阐述你的观点。

高中高一必修二第一章单元总结复习检测

第一章章末检测卷(时间： 100 分钟满分： 100 分)一、选择题 (此题包含16 个小题，每题 3 分，共 48 分 )1．以下说法正确的选项是()A．宏观上的物质对外不显电性，是因为构成它们的微观粒子都是电中性的原子和分子B．某物质经科学测定只含有一种元素，则能够判定该物质是一种纯净物C．利用化学方法，我们能够制造出新的分子，但不可以制造出新原子D．由两种元素构成的电解质分子中，显正价的是阳离子，显负价的是阴离子2．天然铊有两种稳固同位素，81203Tl和81205Tl。

以下有关铊的同位素说法中，不正确的选项是( )203 205 203 205A. 81 Tl 和81 Tl 质子数同样B.81 Tl 和81 Tl 互为同素异形体C.81203Tl 和81205Tl 中子数之差为2D. 20581Tl 原子核内中子数与核外电子数之差为433．以下说法正确的选项是()A．形成离子键的阴、阳离子间只存在静电吸引力B．HF 、 HCl 、HBr 、 HI 的热稳固性和复原性从左到右挨次减弱C．第三周期非金属元素含氧酸的酸性从左到右挨次加强D．元素周期律是元素原子核外电子排布周期性变化的结果4．以下说法中错误的选项是()A．原子及其离子的核外电子层数等于该元素所在的周期数B．元素周期表中从Ⅲ B 族到Ⅱ B 族 10 个纵列的元素都是金属元素C．除氦外的罕有气体原子的最外层电子数都是8D．同一元素的各样同位素化学性质几乎完整同样5．已知：①钾比水轻；②钾的熔点低；③钾与水反响时要放出热量；④钾与水反响后溶液呈碱性。

某学生将一块金属钾投入滴有酚酞试液的水中，该实验能证明四点性质中的()A ．①④ B．①②④ C．①③④ D．①②③④6．以下摆列次序正确的选项是( )①热稳固性： HF＞HCl ＞ HBr ②原子半径： Na＞S＞ O③酸性： H 3PO4＞ H2 SO4＞ HClO 4④复原性： S2－＞O2－＞ F－A ．①②③ B．②③④ C．①②④ D ．①③④7．某分子的球棍模型以以下图所示。