2009考研数学一真题及答案

合集下载

2009—数一真题、标准答案及解析

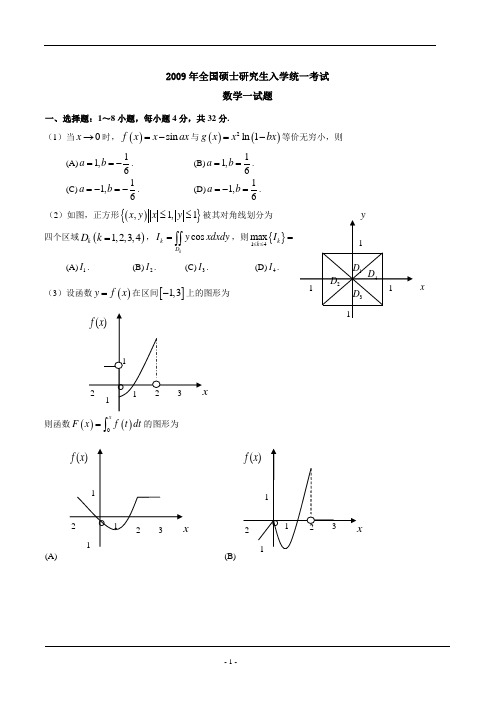
2009年全国硕士研究生入学统一考试数学一试题一、选择题：1～8小题，每小题4分，共32分.（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则(A)11,6a b ==-. (B)11,6a b ==. (C)11,6a b =-=-. (D)11,6a b =-=.（2）如图，正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max kk I ≤≤=(A)1I .(B)2I . (C)3I .(D)4I .（3）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)x(C)(D)（4）设有两个数列{}{},n n a b ，若lim 0n n a →∞=，则（A ）当1nn b∞=∑收敛时，1n nn a b∞=∑收敛. （B ）当1nn b∞=∑发散时，1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时，221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时，221n nn a b∞=∑发散.（5）设123,,ααα是3维向量空间3R 的一组基，则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为(A)101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B)120023103⎛⎫⎪⎪ ⎪⎝⎭.(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. （6）设,A B 均为2阶矩阵，**,A B 分别为,A B 的伴随矩阵，若2,3A B ==，则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为()A **32O B A O ⎛⎫⎪⎝⎭.()B **23O B A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.（7）设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭，其中()x Φ为标准正态分布函数，则EX =(A)0.(B)0.3. (C)0.7.(D)1.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布()0,1N ，Y 的概率分布为{}{}1012P Y P Y ====，记()Z F z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为 (A)0.(B)1.(C)2.(D)3.二、填空题：9~14小题，每小题4分，共24分.（9）设函数(),f u v 具有二阶连续偏导数，(),z f x xy =，则2zx y∂=∂∂ .（10）若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+，则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .（11）已知曲线(2:0L y x x =≤≤，则Lxds =⎰ .（12）设(){}222,,1x y z xy z Ω=++≤，则2z dxdydz Ω=⎰⎰⎰ .（13）若3维列向量,αβ满足2Tαβ=，其中T α为α的转置，则矩阵Tβα的非零特征值为 . (14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量，则k = .三、解答题：15~23小题，共94分. （15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值.（16）（本题满分9分）设n a 为曲线n y x =与()11,2,.....n y xn +==所围成区域的面积，记122111,n n n n S a S a ∞∞-====∑∑，求1S 与2S 的值.（17）（本题满分11分）椭球面1S 是椭圆22143x y +=绕x 轴旋转而成，圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. （Ⅰ）求1S 及2S 的方程（Ⅱ）求1S 与2S 之间的立体体积. （18）（本题满分11分）（Ⅰ）证明拉格朗日中值定理：若函数()f x 在[],a b 上连续，在(,)a b 可导，则存在(),a b ξ∈，使得()()()()f b f a f b a ξ'-=-（Ⅱ）证明：若函数()f x 在0x =处连续，在()()0,0δδ>内可导，且()0lim x f x A +→'=，则()0f +'存在，且()0f A +'=.（19）（本题满分10分）计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰，其中∑是曲面222224x y z ++=的外侧.（20）（本题满分11分）设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭，1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭. （Ⅰ）求满足21A ξξ=的2ξ. 231A ξξ=的所有向量2ξ,3ξ. （Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ证明1ξ,2ξ,3ξ无关.（21）（本题满分11分）设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型f 的矩阵的所有特征值；（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值. （22）（本题满分11分）袋中有1个红色球，2个黑色球与3个白球，现有回放地从袋中取两次，每次取一球，以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.（Ⅰ）求{}10p X Z ==；（Ⅱ）求二维随机变量(),X Y 概率分布.（23）（本题满分11 分）设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他，其中参数(0)λλ>未知，1X ，2X ,…n X 是来自总体X 的简单随机样本.(Ⅰ)求参数λ的矩估计量；（Ⅱ）求参数λ的最大似然估计量.2009年全国硕士研究生入学统一考试数学一试题解析一、选择题：1～8小题，每小题4分，共32分.（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则(A)11,6a b ==-. (B)11,6a b ==. (C)11,6a b =-=-. (D)11,6a b =-=.【答案】 A.【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除(B)、(C). 另外201cos lim3x a axbx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排(D). 所以本题选（A ）. （2）如图，正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max kk I ≤≤=(A)1I .(B)2I . (C)3I .(D)4I .【答案】 A.【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰；x{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为(A).（3）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征： ①[]0,1x ∈时，()0F x ≤，且单调递减. ②[]1,2x ∈时，()F x 单调递增.③[]2,3x ∈时，()F x 为常函数.④[]1,0x ∈-时，()0F x ≤为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为（D ）.（4）设有两个数列{}{},n n a b ，若lim 0n n a →∞=，则（A ）当1nn b∞=∑收敛时，1n nn a b∞=∑收敛. （B ）当1nn b∞=∑发散时，1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时，221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时，221n nn a b∞=∑发散.【答案】C. 【解析】方法一：举反例：（A）取(1)nn n a b ==- （B ）取1n n a b n ==（D ）取1n n a b n==故答案为（C ）.方法二：因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时，有1n a <又因为1nn b∞=∑收敛，可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时，有1n b <从而，当12n N N >+时，有22n nn a b b <，则由正项级数的比较判别法可知221n nn a b∞=∑收敛.（5）设123,,ααα是3维向量空间3R 的一组基，则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为(A)101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B)120023103⎛⎫⎪⎪ ⎪⎝⎭.(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. 【答案】A.【解析】因为()()1212,,,,,,n n A ηηηααα= ，则A 称为基12,,,n ααα 到12,,,n ηηη 的过渡矩阵. 则由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足()12233112311,,,,23M ααααααααα⎛⎫+++= ⎪⎝⎭12310111,,22023033ααα⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A).（6）设,A B 均为2阶矩阵，**,A B 分别为,A B 的伴随矩阵，若2,3A B ==，则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为()A **32O B A O ⎛⎫⎪⎝⎭.()B **23O B A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭. 【答案】B.【解析】根据CC C E *=，若111,C C C CC C*--*==分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O ⨯=-=⨯=（），即分块矩阵可逆 11116601O B BO A O A O A O B B O B B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B AO A O ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为（B ）.（7）设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭，其中()x Φ为标准正态分布函数，则EX =(A)0.(B)0.3. (C)0.7.(D)1.【答案】C.【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭，所以()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭，所以()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰而()0x x dx +∞-∞'Φ=⎰，()()11221222x x x dx u u u du +∞+∞-∞-∞--⎛⎫''Φ=+Φ= ⎪⎝⎭⎰⎰ 所以00.3520.7EX =+⨯=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布()0,1N ，Y 的概率分布为{}{}1012P Y P Y ====，记()Z F z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为 (A)0.(B)1.(C)2.(D)3.【答案】 B. 【解析】()()(0)(0)(1)(1)1[(0)(1)]21[(00)(1)]2Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=,X Y 独立1()[(0)()]2Z F z P X z P X z ∴=⋅≤+≤（1）若0z <，则1()()2Z F z z =Φ（2）当0z ≥，则1()(1())2Z F z z =+Φ0z ∴=为间断点，故选（B ）.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）设函数(),f u v 具有二阶连续偏导数，(),z f x xy =，则2zx y∂=∂∂ .【答案】"'"12222xf f xyf ++. 【解析】''12z f f y x ∂=+⋅∂，2"'""'"1222212222z xf f yx f xf f xyf x y∂=++⋅=++∂∂. （10）若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+，则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .【答案】2xy xe x =-++.【解析】由12()x y c c x e =+，得121λλ==，故2,1a b =-= 微分方程为''2'y y y x -+=设特解*y Ax B =+代入，',1y A A ==220,2A AxB x B B -++=-+==∴ 特解 *2y x =+∴ 12()2xy c c x e x =+++把 (0)2y = ， '(0)0y =代入，得120,1c c ==- ∴ 所求2x y xe x =-++ （11）已知曲线(2:0L y x x =≤≤，则Lxds =⎰ .【答案】136【解析】由题意可知，2,,0x x y x x ==≤ds ==，所以()201148Lxds x ==+⎰11386==（12）设(){}222,,1x y z xy z Ω=++≤，则2z dxdydz Ω=⎰⎰⎰ .【答案】415π. 【解析】方法一：2122220sin cos z dxdydz d d d ππθϕρϕρϕρ=⎰⎰⎰⎰⎰⎰()21240cos cos d d d ππθϕϕρρ=-⎰⎰⎰30cos 1423515d πϕπϕπ=⋅-⋅=⎰方法二：由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰所以，()212222400011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰ 14002214sin sin 33515d r dr d πππππϕϕϕϕ=⋅⋅=⎰⎰⎰（13）若3维列向量,αβ满足2Tαβ=，其中T α为α的转置，则矩阵Tβα的非零特征值为 . 【答案】2. 【解析】2Tαβ=()2T T βαββαββ∴==⋅, T βα∴的非零特征值为2.(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量，则k = .【答案】1-.【解析】2X kS -+ 为2np 的无偏估计 22()E X kX np -∴+=2(1)1(1)(1)11np knp p np k p p k p p k ∴+-=∴+-=∴-=-∴=-三、解答题：15~23小题，共94分. （15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值.【解析】2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=故10,x y e= =2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ = 则12(0,)12(2)xxef e ''=+，1(0,)0xyef ''=，1(0,)yy ef e ''=.0xxf ''> 而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e=-.（16）（本题满分9分）设n a 为曲线ny x =与()11,2,.....n y xn +==所围成区域的面积，记122111,n n n n S a S a ∞∞-====∑∑，求1S 与2S 的值.【解析】由题意，n y x =与n+1y=x 在点0x =和1x =处相交，所以112111111a ()()001212n n n n n x x dx x x n n n n +++=-=-=-++++⎰，从而1111111111S lim lim(-lim()23122+22Nn nN N N n n a a N N N ∞→∞→∞→∞=====-++=-=++∑∑ 2211111111111111=)22+1232N 2N+123456n n n S a n n ∞∞-====--++-=-+-+∑∑ （）（由2(1)1(1)2n n x x n-++-+ ln(1+x)=x- 取1x =得 22111ln(2)1()11ln 2234S S =--+=-⇒=-.（17）（本题满分11分）椭球面1S 是椭圆22143x y +=绕x 轴旋转而成，圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. （Ⅰ）求1S 及2S 的方程（Ⅱ）求1S 与2S 之间的立体体积.【解析】（I ）1S 的方程为222143x y z ++=，过点()4,0与22143x y +=的切线为122y x ⎛⎫=±- ⎪⎝⎭，所以2S 的方程为222122y z x ⎛⎫+=- ⎪⎝⎭.（II ）1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差，其中22135(4)44V x dx ππ=-=⎰.故所求体积为9544πππ-=. （18）（本题满分11分）（Ⅰ）证明拉格朗日中值定理：若函数()f x 在[],a b 上连续，在(,)a b 可导，则存在(),a b ξ∈，使得()()()()f b f a f b a ξ'-=-（Ⅱ）证明：若函数()f x 在0x =处连续，在()()0,0δδ>内可导，且()0lim x f x A +→'=，则()0f +'存在，且()0f A +'=.【解析】（Ⅰ）作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----，易验证()x ϕ满足：()()a b ϕϕ=；()x ϕ在闭区间[],a b 上连续，在开区间(),a b 内可导，且''()()()()f b f a x f x b aϕ-=--.根据罗尔定理，可得在(),a b 内至少有一点ξ，使'()0ϕξ=，即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取0(0,)x δ∈，则函数()f x 满足：在闭区间[]00,x 上连续，开区间()00,x 内可导，从而有拉格朗日中值定理可得：存在()()000,0,x x ξδ∈⊂，使得()0'00()(0)x f x f f x ξ-=-……()*又由于()'lim x f x A +→=，对上式（*式）两边取00x +→时的极限可得：()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故'(0)f +存在，且'(0)f A +=.（19）（本题满分10分）计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰，其中∑是曲面222224x y z ++=的外侧.【解析】2223/2()xdydz ydxdz zdxdy I x y z ∑++=++⎰⎰，其中222224x y z ++= 2222223/22225/22(,()()x y z x x x y z x y z ∂+-=∂++++ ① 2222223/22225/22(),()()y x z y y x y z x y z ∂+-=∂++++②2222223/22225/22(),()()z x y z z x y z x y z ∂+-=∂++++③ ∴①+②+③=2223/22223/22223/2(()()0()()()x y zx x y z y x y z z x y z ∂∂∂++=∂++∂++∂++ 由于被积函数及其偏导数在点（0，0，0）处不连续，作封闭曲面（外侧）222211:.016x y z R R ∑++=<<有 1132223/233313434()3xdydz ydxdz zdxdy xdydz ydxdz zdxdy R dV x y z R R R ππ∑∑∑Ω++++====⋅=++⎰⎰⎰⎰⎰⎰⎰⎰⎰ （20）（本题满分11分）设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭ 1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭（Ⅰ）求满足21A ξξ=的2ξ. 231A ξξ=的所有向量2ξ,3ξ. （Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ证明1ξ,2ξ,3ξ无关. 【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量，令32x =，由0Ax =解得，211,1x x =-= 求特解，令120x x ==，得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，其中1k 为任意常数.解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭故有两个自由变量，令21x =-，由20A x =得131,0x x ==求特解21200η⎛⎫ ⎪ ⎪= ⎪ ⎪⎪⎝⎭故 321121000k ξ⎛⎫⎪⎛⎫ ⎪⎪=-+ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭ ，其中2k 为任意常数.（Ⅱ）证明：由于12121212122111121112(21)()2()(21)222210k k k k k k k k k k k k k -+--=+++-+-+-+102=≠ 故123,,ξξξ 线性无关. （21）（本题满分11分）设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+- （Ⅰ）求二次型f 的矩阵的所有特征值；（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值. 【解析】（Ⅰ） 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+（Ⅱ）若规范形为2212y y +，说明有两个特征值为正，一个为0.则 1) 若10a λ==，则 220λ=-< ，31λ= ，不符题意2) 若20λ= ，即2a =，则120λ=>，330λ=>，符合3) 若30λ= ，即1a =-，则110λ=-< ，230λ=-<，不符题意综上所述，故2a =.（22）（本题满分11分）袋中有1个红色球，2个黑色球与3个白球，现有回放地从袋中取两次，每次取一球，以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数. （Ⅰ）求{}10p X Z ==；（Ⅱ）求二维随机变量(),X Y 概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球12113324(10)9C P X Z C C ⨯∴====⋅.（Ⅱ）X ，Y 取值范围为0，1，2，故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======（23）（本题满分11 分）设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他，其中参数(0)λλ>未知，1X ,2X ,…,n X 是来自总体X 的简单随机样本.(Ⅰ)求参数λ的矩估计量；（Ⅱ）求参数λ的最大似然估计量【解析】（1）由EX X =而22022ˆx EX x e dx X Xλλλλ+∞-===⇒=⎰为总体的矩估计量（2）构造似然函数()()12111L ,.....,;;nii nnx nn i i i i x x f x x eλλλλ=-==∑==⋅⋅∏∏取对数11ln 2ln ln n ni i i i L n x x λλ===+-∑∑令111ln 222001n i n ni i i i i d L n n x d x x n λλλ====⇒-=⇒==∑∑∑ 故其最大似然估计量为2Xλ''=.。

2009年全国考研数学一真题及答案.doc

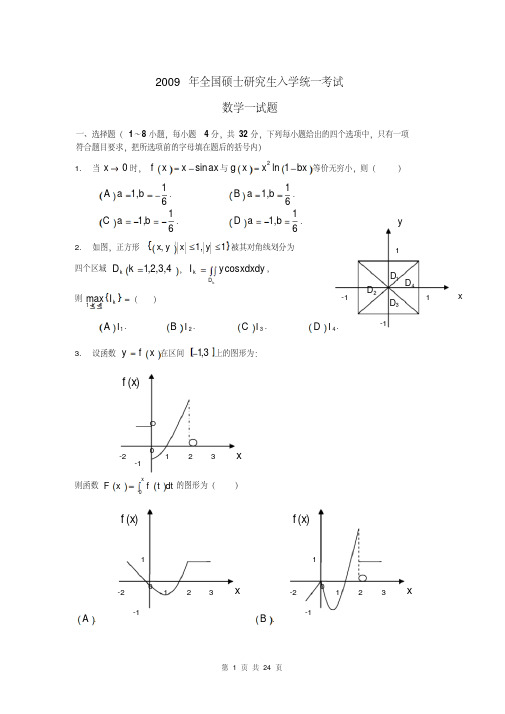
以 X ,Y , Z 分别表示两次取球所取得的红球、黑球与白球的个数。
（Ⅰ）求 p X 1 Z 0 ；
（Ⅱ）求二维随机变量 X , Y 概率分布。
第 4 页共 24 页
9. （本题满分 11 分）
设总体 X 的概率密度为 f ( x)
2xe x , x 0 ，其中参数 (
0,其他
0) 未知， X 1 ，
S1
an , S2
a2 n 1 ，求 S1 与 S2 的值。
n1
n1
3.
x2 （本题满分 11 分）椭球面 S1 是椭圆
y2 1 绕 x 轴旋转而成，圆锥面 S2 是过点
43
第 3 页共 24 页
x2 4,0 且与椭圆
4
y2 1
3
相切的直线绕 x 轴旋转而成。
（Ⅰ）求 S1及 S2 的方程
（Ⅱ）求 S1与 S2 之间的立体体积。
2z
9. 设函数 f u, v 具有二阶连续偏导数， z f x, xy ，则
。
xy
10. 若二阶常系数线性齐次微分方程
y ay by 0 的通解为 y C1 C2 x ex ，则非齐
次方程 y ay by x 满足条件 y 0 2, y 0 0的解为 y
。
11. 已知曲线 L : y x2 0 x
均值和样本方差。若 X kS2 为 np 2 的无偏估计量，则 k
。
三、解答题（ 15－ 23 小题，共 94 分 .请将解答写在答题纸指定的位置上明、证明过程或演算步骤 .）
.解答应写出文字说
1. （本题满分 9 分）求二元函数 f ( x, y) x2 2 y2 y ln y 的极值。
2. （本题满分 9 分）设 an 为曲线 y xn 与 y xn 1 n 1,2,..... 所围成区域的面积，记

2009年考研数学一试题与答案解析

2009年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则(A)11,6a b ==- (B)11,6a b ==(C)11,6a b =-=-(D)11,6a b =-=(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=(A)1I(B)2I (C)3I(D)4I(3)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则(A)当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B)当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基12233,,+++αααααα的过渡矩阵为 (A)101220033⎛⎫⎪ ⎪ ⎪⎝⎭(B)120023103⎛⎫⎪⎪ ⎪⎝⎭(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭(6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3==A B ,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭(B)**23OB A O ⎛⎫⎪⎝⎭(C)**32O A BO ⎛⎫ ⎪⎝⎭(D)**23O A BO ⎛⎫⎪⎝⎭(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =(A)0 (B)0.3(C)0.7(D)1(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A)0(B)1(C)2 (D)3二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ . (10)若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12e xy C C x =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11)已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12)设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13)若3维列向量,αβ满足2T=αβ,其中T α为α的转置,则矩阵Tβα的非零特征值为 .(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题(15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分9分)设n a 为曲线n y x =与()11,2,.....n y x n +==所围成区域的面积,记122111,n n n n S a S a ∞∞-====∑∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (1)求1S 及2S 的方程. (2)求1S 与2S 之间的立体体积.(18)(本题满分11分)(1)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(2)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分) 计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042--⎛⎫⎪=- ⎪ ⎪--⎝⎭A ,1112-⎛⎫ ⎪= ⎪ ⎪-⎝⎭ξ (1)求满足21=A ξξ的2ξ.231=A ξξ的所有向量2ξ,3ξ. (2)对(1)中的任意向量2ξ,3ξ证明123,,ξξξ无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-.(1)求二次型f 的矩阵的所有特征值;(2)若二次型f 的规范形为2212y y +,求a 的值.(22)(本题满分11分)袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(1)求{}10p X Z ==.(2)求二维随机变量(),X Y 概率分布. (23)(本题满分11 分)设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,1X ,2X ,…n X 是来自总体X 的简单随机样本.(1)求参数λ的矩估计量.(2)求参数λ的最大似然估计量.2009年考研数学试题答案与解析（数学一）一、选择题：1～8小题，每小题4分，共32分.（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则(A)11,6a b ==-. (B)11,6a b ==. (C)11,6a b =-=-. (D)11,6a b =-=.【答案】 A.【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除(B)、(C). 另外201cos lim3x a axbx →--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除(D).所以本题选（A ）. （2）如图，正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max kk I ≤≤=(A)1I .(B)2I . (C)3I .(D)4I .【答案】 A.【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰； {}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为(A).x（3）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：①[]0,1x ∈时，()0F x ≤，且单调递减. ②[]1,2x ∈时，()F x 单调递增. ③[]2,3x ∈时，()F x 为常函数.④[]1,0x ∈-时，()0F x ≤为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为（D ）.（4）设有两个数列{}{},n n a b ，若lim 0n n a →∞=，则（A ）当1nn b∞=∑收敛时，1n nn a b∞=∑收敛. （B ）当1nn b∞=∑发散时，1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时，221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时，221n nn a b∞=∑发散.【答案】C. 【解析】方法一：举反例：（A）取(1)nn n a b ==- （B ）取1n n a b n ==（D ）取1n n a b n==故答案为（C ）.方法二：因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时，有1n a <又因为1nn b∞=∑收敛，可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时，有1n b <从而，当12n N N >+时，有22n nn a b b <，则由正项级数的比较判别法可知221n nn a b∞=∑收敛.（5）设123,,ααα是3维向量空间3R 的一组基，则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为(A)101220033⎛⎫⎪ ⎪ ⎪⎝⎭.(B)120023103⎛⎫⎪⎪ ⎪⎝⎭.(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. 【答案】A.【解析】因为()()1212,,,,,,n n A ηηηααα=，则A 称为基12,,,n ααα到12,,,nηηη的过渡矩阵. 则由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足 ()12233112311,,,,23M ααααααααα⎛⎫+++= ⎪⎝⎭12310111,,22023033ααα⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A).（6）设,A B 均为2阶矩阵，**,A B 分别为,A B 的伴随矩阵，若2,3A B ==，则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23O B A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭. 【答案】B.【解析】根据CC C E *=，若111,C C C CC C*--*==分块矩阵O A B O ⎛⎫ ⎪⎝⎭的行列式221236O A A B B O ⨯=-=⨯=（），即分块矩阵可逆11116601O B BO A O A O A OB B O B B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O BOB AO A O ****⎛⎫⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为（B ）.（7）设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭，其中()x Φ为标准正态分布函数，则EX = (A)0.(B)0.3. (C)0.7.(D)1.【答案】C.【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭，所以()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭，所以()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰而()0x x dx +∞-∞'Φ=⎰，()()11221222x x x dx u u u du +∞+∞-∞-∞--⎛⎫''Φ=+Φ= ⎪⎝⎭⎰⎰ 所以00.3520.7EX =+⨯=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布()0,1N ，Y 的概率分布为{}{}1012P Y P Y ====，记()Z F z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为 (A)0.(B)1.(C)2.(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)1[(0)(1)]21[(00)(1)]2Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=,X Y 独立1()[(0)()]2Z F z P X z P X z ∴=⋅≤+≤（1）若0z <，则1()()2Z F z z =Φ（2）当0z ≥，则1()(1())2Z F z z =+Φ0z ∴=为间断点，故选（B ）.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）设函数(),f u v 具有二阶连续偏导数，(),z f x xy =，则2zx y∂=∂∂ . 【答案】"'"12222xf f xyf ++.【解析】''12z f f y x∂=+⋅∂，2"'""'"1222212222z xf f yx f xf f xyf x y ∂=++⋅=++∂∂. （10）若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+，则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = . 【答案】2xy xe x =-++.【解析】由12()xy c c x e =+，得121λλ==，故2,1a b =-=微分方程为''2'y y y x -+=设特解*y Ax B =+代入，',1y A A ==220,2A AxB x B B -++=-+==∴ 特解 *2y x =+∴ 12()2xy c c x e x =+++把 (0)2y = ， '(0)0y =代入，得120,1c c ==- ∴ 所求2xy xe x =-++ （11）已知曲线(2:0L y x x =≤≤，则Lxds =⎰ .【答案】136【解析】由题意可知，2,,0x x y x x ==≤≤，则ds ==，所以()21148Lxds x ==+⎰11386==（12）设(){}222,,1x y z xy z Ω=++≤，则2z dxdydz Ω=⎰⎰⎰ .【答案】415π. 【解析】方法一：2122220sin cos z dxdydz d d d ππθϕρϕρϕρ=⎰⎰⎰⎰⎰⎰()21240cos cos d d d ππθϕϕρρ=-⎰⎰⎰30cos 1423515d πϕπϕπ=⋅-⋅=⎰方法二：由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰ 所以，()21222240011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰14002214sin sin 33515d r dr d πππππϕϕϕϕ=⋅⋅=⎰⎰⎰（13）若3维列向量,αβ满足2Tαβ=，其中Tα为α的转置，则矩阵Tβα的非零特征值为 .【答案】2.【解析】2Tαβ=()2T T βαββαββ∴==⋅, T βα∴的非零特征值为2.(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量，则k = . 【答案】1-. 【解析】2X kS -+为2np 的无偏估计22()E X kX np -∴+=2(1)1(1)(1)11np knp p np k p pk p p k ∴+-=∴+-=∴-=-∴=-三、解答题：15~23小题，共94分. （15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值.【解析】2(,)2(2)0x f x y x y '=+= 2(,)2ln 10y f x y x y y '=++=故10,x y e= =2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ = 则12(0,)12(2)xxef e ''=+，1(0,)0xyef ''=，1(0,)yy ef e ''=.0xxf ''>而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e=-.（16）（本题满分9分）设n a 为曲线ny x =与()11,2,.....n y x n +==所围成区域的面积，记122111,n n n n S a S a ∞∞-====∑∑，求1S 与2S 的值.【解析】由题意，n y x =与n+1y=x 在点0x =和1x =处相交，所以112111111a ()()001212n n n n n x x dx x x n n n n +++=-=-=-++++⎰，从而1111111111S lim lim(-)lim()23122+22Nn nN N N n n a a N N N ∞→∞→∞→∞=====-++=-=++∑∑2211111111111111=)22+1232N 2N+123456n n n S a n n ∞∞-====--++-=-+-+∑∑（）（由2(1)1(1)2nn x x n-++-+ln(1+x)=x- 取1x =得22111ln(2)1()11ln 2234S S =--+=-⇒=-.（17）（本题满分11分）椭球面1S 是椭圆22143x y +=绕x 轴旋转而成，圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成.（Ⅰ）求1S 及2S 的方程（Ⅱ）求1S 与2S 之间的立体体积.【解析】（I ）1S 的方程为222143x y z ++=，过点()4,0与22143x y +=的切线为122y x ⎛⎫=±- ⎪⎝⎭，所以2S 的方程为222122y z x ⎛⎫+=- ⎪⎝⎭.（II ）1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差，其中22135(4)44V x dx ππ=-=⎰.故所求体积为9544πππ-=.（18）（本题满分11分）（Ⅰ）证明拉格朗日中值定理：若函数()f x 在[],a b 上连续，在(,)a b 可导，则存在(),a b ξ∈，使得()()()()f b f a f b a ξ'-=-（Ⅱ）证明：若函数()f x 在0x =处连续，在()()0,0δδ>内可导，且()0lim x f x A +→'=，则()0f +'存在，且()0f A +'=.【解析】（Ⅰ）作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----，易验证()x ϕ满足：()()a b ϕϕ=；()x ϕ在闭区间[],a b 上连续，在开区间(),a b 内可导，且''()()()()f b f a x f x b aϕ-=--.根据罗尔定理，可得在(),a b 内至少有一点ξ，使'()0ϕξ=，即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取0(0,)x δ∈，则函数()f x 满足：在闭区间[]00,x 上连续，开区间()00,x 内可导，从而有拉格朗日中值定理可得：存在()()000,0,x x ξδ∈⊂，使得()0'00()(0)x f x f f x ξ-=-……()*又由于()'lim x f x A +→=，对上式（*式）两边取00x +→时的极限可得：()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====- 故'(0)f +存在，且'(0)f A +=.（19）（本题满分10分）计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰，其中∑是曲面222224x y z ++=的外侧.【解析】2223/2()xdydz ydxdz zdxdy I x y z ∑++=++⎰⎰，其中222224x y z ++= 2222223/22225/22(),()()x y z x x x y z x y z ∂+-=∂++++①2222223/22225/22(),()()y x z y y x y z x y z ∂+-=∂++++② 2222223/22225/22(),()()z x y z z x y z x y z ∂+-=∂++++③ ∴①+②+③=2223/22223/22223/2()()()0()()()x y zx x y z y x y z z x y z ∂∂∂++=∂++∂++∂++ 由于被积函数及其偏导数在点（0，0，0）处不连续，作封闭曲面（外侧）222211:.016x y z R R ∑++=<<有 1132223/233313434()3xdydz ydxdz zdxdyxdydz ydxdz zdxdy R dV x y z R R R ππ∑∑∑Ω++++====⋅=++⎰⎰⎰⎰⎰⎰⎰⎰⎰（20）（本题满分11分）设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭ 1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭（Ⅰ）求满足21A ξξ=的2ξ. 231A ξξ=的所有向量2ξ,3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ证明1ξ,2ξ,3ξ无关. 【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量，令32x =，由0Ax =解得，211,1x x =-= 求特解，令120x x ==，得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，其中1k 为任意常数.解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭故有两个自由变量，令21x =-，由20A x =得131,0x x ==求特解21200η⎛⎫⎪ ⎪= ⎪ ⎪⎪⎝⎭故 321121000k ξ⎛⎫ ⎪⎛⎫ ⎪ ⎪=-+ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭ ，其中2k 为任意常数.（Ⅱ）证明：由于12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠ 故123,,ξξξ 线性无关. （21）（本题满分11分）设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+- （Ⅰ）求二次型f 的矩阵的所有特征值；（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值.【解析】（Ⅰ） 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+（Ⅱ）若规范形为2212y y +，说明有两个特征值为正，一个为0.则1) 若10a λ==，则 220λ=-< ，31λ= ，不符题意 2) 若20λ= ，即2a =，则120λ=>，330λ=>，符合3) 若30λ= ，即1a =-，则110λ=-< ，230λ=-<，不符题意综上所述，故2a =.（22）（本题满分11分）袋中有1个红色球，2个黑色球与3个白球，现有回放地从袋中取两次，每次取一球，以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数. （Ⅰ）求{}10p X Z ==；（Ⅱ）求二维随机变量(),X Y 概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球12113324(10)9C P X Z C C ⨯∴====⋅.（Ⅱ）X ，Y 取值范围为0，1，2，故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======（23）（本题满分11 分）设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他，其中参数(0)λλ>未知，1X ,2X ,…,n X 是来自总体X 的简单随机样本.(Ⅰ)求参数λ的矩估计量；（Ⅱ）求参数λ的最大似然估计量【解析】（1）由EX X =而22022ˆx EX x e dx X Xλλλλ+∞-===⇒=⎰为总体的矩估计量（2）构造似然函数()()12111L ,.....,;;nii nnx nn i i i i x x f x x eλλλλ=-==∑==⋅⋅∏∏取对数11ln 2ln ln n ni i i i L n x x λλ===+-∑∑令111ln 222001n i n n i i i i i d L n n x d x x n λλλ====⇒-=⇒==∑∑∑故其最大似然估计量为2Xλ''=。

2009年考研数学一真题及答案解析

2009年全国硕士研究生入学统一考试数学一试题一、选择题（1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.）（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则（）()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.（2）如图，正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max k k I ≤≤=（）()A 1I .()B 2I . ()C 3I .()DI （3）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为（）()A .()B .x()C .()D .（4）设有两个数列{}{},n n a b ，若lim 0n n a →∞=，则（）()A 当1n n b ∞=∑收敛时，1n n n a b ∞=∑收敛.()B 当1n n b ∞=∑发散时，1n n n a b ∞=∑发散.()C 当1nn b∞=∑收敛时，221n nn a b∞=∑收敛.()D 当1nn b ∞=∑发散时，221n nn a b∞=∑发散.（5）设123,,ααα是3维向量空间3R 的一组基，则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为（）()A 101220033⎛⎫⎪⎪ ⎪⎝⎭. ()B 120023103⎛⎫⎪⎪ ⎪⎝⎭.()C 111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.()D 111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. （6）设,A B 均为2阶矩阵，**,A B 分别为,A B 的伴随矩阵，若2,3A B ==，则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为（）()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23OB A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫ ⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.（7）设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭，其中()x Φ为标准正态分布函数，则EX =（）()A 0.()B 0.3. ()C 0.7.()D 1.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布()0,1N ，Y 的概率分布为{}{}1012P Y P Y ====，记()Z F z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为（）()A 0.()B 1. ()C 2.()D 3.二、填空题（9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.）（9）设函数(),f u v 具有二阶连续偏导数，(),z f x xy =，则2zx y∂=∂∂ 。

2009考研数一真题及解析

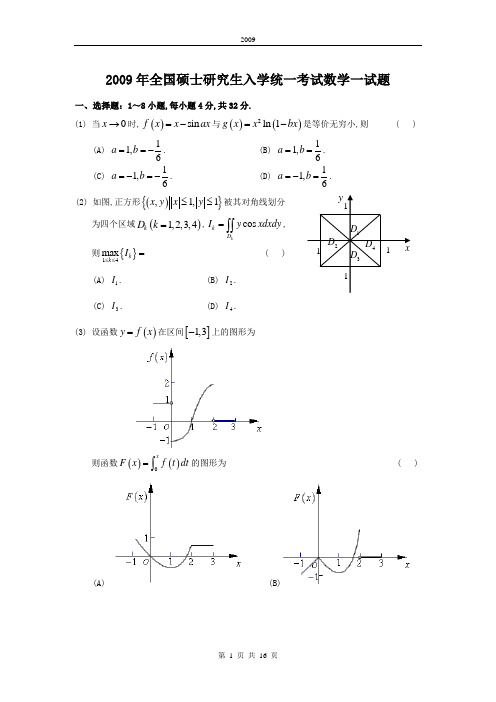
2009年全国硕士研究生入学统一考试数学一试题一、选择题：1～8小题,每小题4分,共32分.(1) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(2) 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤= ( )(A) 1I .(B) 2I .(C) 3I .(D) 4I .(3) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)(C)(D)(4) 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则 ( )(A) 当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B) 当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C) 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D) 当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5) 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为 ( )(A) 101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B) 120023103⎛⎫⎪⎪ ⎪⎝⎭.(C) 111246111246111246⎛⎫- ⎪ ⎪ ⎪-⎪ ⎪ ⎪- ⎪⎝⎭.(D) 111222111444111666⎛⎫-⎪ ⎪⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. (6) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B A O ⎛⎫⎪⎝⎭.(C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭.(7) 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布的分布函数,则EX = ( ) (A) 0. (B) 0.3. (C) 0.7. (D) 1.(8) 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 ( ) (A) 0. (B) 1. (C) 2. (D) 3.二、填空题：9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ .(10) 若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11) 已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12) 设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13) 若3维列向量,αβ满足2Tαβ=,其中T α为α的转置,则矩阵T βα的非零特征值为.(14) 设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题：15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分9分)设n a 为曲线n y x =与()11,2,n y xn +== 所围成区域的面积,记11,n n S a ∞==∑2211n n S a ∞-==∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是由过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (Ⅰ)求1S 及2S 的方程； (Ⅱ)求1S 与2S 之间的立体体积. (18)(本题满分11分)(Ⅰ)证明拉格朗日中值定理：若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明：若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分)计算曲面积分()32222xdydz ydzdx zdxdyI xy z∑++=++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ； (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明：123,,ξξξ线性无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值；(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==；(Ⅱ)求二维随机变量(),X Y 的概率分布. (23)(本题满分11 分)设总体X 的概率密度为2,0,()0,x xe x f x λλ-⎧>=⎨⎩其他, 其中参数(0)λλ>未知,12,,,n X X X 是来自总体X 的简单随机样本.(Ⅰ) 求参数λ的矩估计量；(Ⅱ )求参数λ的最大似然估计量.2009年全国硕士研究生入学统一考试数学一试题一、选择题：1～8小题,每小题4分,共32分. (1) 【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bxa ax ab axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛即36a b =-,故排除B,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选A.(2) 【答案】(A)【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令(,)cos f x y y x =,24,D D 两区域关于x 轴对称,(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==；13,D D 两区域关于y 轴对称,(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}{}1(,),013(,),012cos 0,2cos 0.x y y x x x y y x x I y xdxdy I y xdxdy ≥≤≤≤-≤≤=>=<⎰⎰⎰⎰所以正确答案为(A). (3) 【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征：① []1,0x ∈-时,()0F x ≤为线性函数,单调递增； ② []0,1x ∈时,()0F x ≤,且单调递减；③ []1,2x ∈时,()F x 单调递增； ④ []2,3x ∈时,()F x 为常函数； ⑤ ()F x 为连续函数. 结合这些特点,可见正确选项为(D). (4) 【答案】C【解析】解法1 举反例：取(1)nn n a b ==-,则lim 0n n a →∞=,1n n b ∞=∑是收敛的,但111n n n n a b n ∞∞===∑∑发散,排除(A)；取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但2111n n n n a b n ∞∞===∑∑收敛,排除(B)；取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但224111n n n n a b n∞∞===∑∑收敛,排除(D),故答案为(C).解法2 因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时,有1n a <；又因为1nn b∞=∑收敛,可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时,有1n b <,从而,当12n N N >+时,有22n nn a b b <,则由正项级数的比较判别法可知221n nn a b∞=∑收敛.(5) 【答案】(A)【解析】根据过渡矩阵的定义,知由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足：()12233112312311,,,,2310111,,220,23033M αααααααααααα⎛⎫+++= ⎪⎝⎭⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A). (6) 【答案】(B)【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O⨯=-=⨯=（）,即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B).(7) 【答案】(C)【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,所以 ()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭, 因此, ()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰.由于()x Φ为标准正态分布的分布函数,所以()0x x dx +∞-∞'Φ=⎰,()()()()11221222222,x x x dx u u u du u u du u du +∞+∞-∞-∞+∞+∞-∞-∞--⎛⎫''Φ=+Φ ⎪⎝⎭''=Φ+Φ=⎰⎰⎰⎰()10.30.3500.3520.72x EX x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ=+⨯= ⎪⎝⎭⎰⎰.(8) 【答案】(B)【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤. (1) 当0z <时,1()()2Z F z z =Φ；(2) 当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题：9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 【答案】12222xf f xyf '''''++ 【解析】12zf f y x∂''=+⋅∂, 21222212222zxf f yx f xf f xyf x y∂''''''''''=++⋅=++∂∂. (10) 【答案】(1)2x x e -+【解析】由常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+可知1x y e =,2x y xe =为其两个线性无关的解,代入齐次方程,有111222(1)010,[2(1)]020,x xy ay by a b e a b y ay by a a b x e a '''++=++=⇒++='''++=++++=⇒+=从而可见2,1a b =-=,非齐次微分方程为2y y y x '''-+=.设特解*y Ax B =+,代入非齐次微分方程,得2A Ax B x -++=,即11(2)202A A Ax A B x A B B ==⎧⎧+-+=⇒⇒⎨⎨-+==⎩⎩所以特解*2y x =+,通解()122xy C C x e x =+++.把()()02,00y y '==代入通解,得120,1C C ==-.所以所求解为2(1)2x x y xe x x e =-++=-+.(11)【答案】136【解析】由题意可知,2,0y x x =≤≤,则ds ==,所以()21148Lxds x ==+⎰11386==. (12) 【答案】415π 【解析】解法1：()212222002124013500sin cos cos cos cos 42.3515z dxdydz d d d d d d πππππθϕρϕρϕρθϕϕρρϕρππΩ==-⎛⎫=⋅-⋅= ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰解法2：由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰所以,()212222400011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰ 14002214sin sin 33515d r dr d ππππϕϕϕϕπ==⋅⋅=⎰⎰⎰. (13) 【答案】2 【解析】2Tαβ=,()2T T βαββαββ∴==⋅,又由于0β≠,T βα∴的非零特征值为2.(14) 【答案】1-【解析】由于2X kS +为2np 的无偏估计量,所以22()E X kS np +=,即2222()()()E X kS np E X E kS np +=⇒+=2(1)1(1)(1)1 1.np knp p np k p pk p p k ⇒+-=⇒+-=⇒-=-⇒=-三、解答题：15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)【解析】 2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,)21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+= 所以 2212(2)0,B AC e e -=-+<且0A >. 从而1(0,)f e 是(,)f x y 的极小值,极小值为11(0,)f e e=-.(16)(本题满分9分)【解析】曲线n y x =与1n y x +=的交点为(0,0)和(1,1),所围区域的面积112111111()()001212n n n n n a x x dx x x n n n n +++=-=-=-++++⎰, 111lim 1111111lim()lim(),2312222Nn nN n n N N S a a N N N ∞→∞==→∞→∞===-++-=-=+++∑∑22111211111111(1)22123456n n n n n S a n n n ∞∞∞-=====-=-+-++=-+∑∑∑ （）.考查幂级数1(1)n nn x n ∞=-∑,知其收敛域为(1,1]-,和函数为ln(1)x -+.因为2(1)()ln(1)n nn S x x x x n ∞=-==-+∑,令1x =,得2211(1)1ln 2n n S a S ∞-====-∑.(17)(本题满分11分)【解析】(I)椭球面1S 的方程为222143x y z ++=. 设切点为00(,)x y ,则22143x y +=在00(,)x y 处的切线方程为00143x x y y +=. 将4,0x y ==代入切线方程得01x =,从而032y ==±. 所以切线方程为142x y ±=,从而圆锥面2S 的方程为222(1)44x y z +-=,即222(4)440x y z ---=.(II)1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差,其中22135(4)44V x dx ππ=-=⎰. 故所求体积为9544πππ-=.(18)(本题满分11分) 【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且()()()()()(),()()()()()().f b f a F a f a a a f a b af b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()000()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈. 由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10分)【解析】取2221:1x y z ∑++=的外侧,Ω为∑与1∑之间的部分.()()()11322223322222222.xdydz ydzdx zdxdyI xy zxdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zxy z∑∑-∑∑++=++++++=+++++⎰⎰⎰⎰⎰⎰根据高斯公式()13222200xdydz ydzdx zdxdydxdydz x y z∑-∑Ω++==++⎰⎰⎰⎰⎰ .()1122232222134.x y z xdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zdxdydz π∑∑++≤++=++++==⎰⎰⎰⎰⎰⎰⎰所以4I π=.(20)(本题满分11分)【解析】(Ⅰ)对矩阵1()A ξ 施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ⎪---⎛⎫ ⎪⎪ ⎪=-→ ⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪⎝⎭可求得 2122122k kk ξ⎛⎫-+ ⎪ ⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ 施以初等行变换()211110220122201000044020000A ξ⎛⎫-⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭,可求得 312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1 由(Ⅰ)知12311122211,,102222ka ka kbξξξ--+--=-=-≠-, 所以123,,ξξξ线性无关.解法2 由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=, ①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=, ②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠，于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11分) 【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111aE A aa a a a λλλλλλλ---=-=--+----+, 所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1 由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫ ⎪ ⎪ ⎪⎝⎭,其秩为2,故 1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意. 当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意. 当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +. 综上可知,2a =.解法2 由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零. 又21a a a -<<+,所以2a =.(22)(本题满分11分)【解析】(Ⅰ) 12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========. (Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,0,0,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为(23)(本题满分11 分) 【解析】(Ⅰ)2202().x EX xf x dx x e dx λλλ+∞+∞--∞===⎰⎰令X EX =,即2X λ=,得λ的矩估计量为 12Xλ=. (Ⅱ)设12,,,(0,1,2,,)n i x x x x i n >= 为样本观测值,则似然函数为()12121,,,;,nii nx nn i i L x x x ex λλλ=-=∑=⋅∏11ln 2ln ln n ni i i i L n x x λλ===-+∑∑,由1ln 20n i i d L n x d λλ==-=∑,得λ的最大似然估计量为 22Xλ=.。

2009年全国硕士研究生入学统一考试数学一真题及答案

在本题中，
当时，
当时，
因此函数仅在处间断，故选（B）.
二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.
（9）设函数具有二阶连续偏导数，，则 .
【答案】
【考点】多元函数的偏导数
【难易度】★★
【详解】本题涉及到的主要知识点：
利用复合函数的链式求导法则求多元函数的偏导数的方法。
在本题中，
，
（10）若二阶常系数线性齐次微分方程的通解为，则非齐次方程满足条件的解为 .
【答案】
【考点】简单的二阶常系数非齐次线性微分方程
【难易度】★★
【详解】本题涉及到的主要知识点：
线性微分方程的解的性质即叠加原理，线性微分方程通解的结构为齐次方程的通解加上特解。
在本题中，
由通解表达式该二阶线性常系数齐次方程的特征值为，于是特征方程为
，
而在上，有连续的一阶偏导数且，于是
（在：上用高斯公式）
（20）（本题满分11分）
设， .
（Ⅰ）求满足的 . 的所有向量 , .
（Ⅱ）对（Ⅰ）中的任意向量 , 证明 , , 线性无关.
【考点】向量组的线性无关，非齐次线性方程组的通解
【难易度】★★★
【详解】本题涉及到的主要知识点：
非齐次线性微分方程的解的性质即叠加原理，非齐次线性微分方程通解的结构为齐次方程的通解加上特解。
收敛级数的和的概念，称为无穷级数的前n项的部分和。若部分和数列的极限存在，即，则称级数收敛。当级数收敛时，其和。
在本题中，
（Ⅰ）先求 .易求得与的交点为，，于是曲线与所围成区域的面积为
（Ⅱ）按定义求
（Ⅲ）求 .

2009年数学试题及解答

2009年全国硕士研究生入学统一考试数学一试题一、选择题：1~8小题，每小题8分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内。

（1）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-等价无穷小，则（）（A ）11,6a b ==-（B ）11,6a b ==（C ）11,6a b =-=- （D ）11,6a b =-=【解析与点评】考点：无穷小量比阶的概念与极限运算法则。

【答案】A2222sin sin 1cos sin limlimlimlimln(1)()36x x x x x ax x ax a x a ax x bx x bx bxbx→→→→---===----23sin lim166.x a ax ab baxa →==-=-36a b =-意味选项B ，C 错误。

再由21cos lim 3x a ax bx→-=-存在，故有1cos 0(0)a ax x -→→，故a=1，D 错误，所以选A 。

（2）如图，正方形{(,)|||1,||1}x y x y ≤≤被其对角线划分为四个区域，(1,2,3,4),cos KK K D D k I y xdxdy ==⎰⎰，则14max{}KK I≤≤=（）【解析与点评】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 关于x 轴对称，而cos y x -即被积函数是关于y 的奇函数，所以2413;,I I D D =两区域关于y 轴对称，cos()cos y x y x -=即被积函数是关于x 的偶函数，由积分的保号性，13{(,)|,01}{(,)|,01}2cos 0,2cos 0x y y x x x y y x x I y xdxdy I y xdxdy ≥≤≤≤-≤≤=>=<⎰⎰⎰⎰，所以正确答案为A 。

（3）设函数()y f x =在区间[-1,3]上的图形为则函数0()()x F x f t dt =⎰为（）【解析与点评】考点：函数与其变限积分函数的关系、函数与其导函数之间的关系，变限积分函数的性质（两个基本定理），定积分的几何意义。

2009考研数一真题答案及详细解析

f(t)dt
I: > �f'.J<t)dt+ 八 t)dt�f (x) dx.'
又由定积分的几何意义知，『 g (x)dx>O,故 2<x<3 时 F(x)>O.故应选 D.
(4) C
解
I; 若令
an= bn=
(-l)n
嘉,则nl-im= a
n
=
O, n=
l
从收敛，却有
co
nI=;l a
n从
=
nI=;l — n1
1,1],
和函数为—
ln(l+x).
因为5 (x)=
= I;
(—l)n
X
n=
X
— ln(l+x),令
x= l,得
n= 2 n
S 2= n�= la 加一1 = S(1)= 1- ln 2.
(17) 解
(I)
椭球面 S1
的方程为X— 42
+
沪
+z 3
2 =
1.
。设切点为
(x
口 Yo),
则
X—+
4
— y
y2dxdyd乏＝』之2dxdyd之，
{l
所以
w 上�+ ill f I I z'dxd:
。。。上 2
六
(x' 二三） dxdydz� 3
亢 d0
sin钊'P'r'dr�±. 穴． 15
{l
03) 2
n 解设入是P矿的非零特征值，是属于入的特征向量，从而p矿T/=入1
由于入=/=-0, TJ =/=-0,故a可=l=-0.

2009年全国考研数学一真题及答案.doc

故答案为（ C）方法二：
因为 lim an 0, 则由定义可知 N1, 使得 n N1 时，有 an 1 n
又因为
bn
收敛，可得
lim
n
bn
0, 则由定义可知
N 2, 使得 n N 2 时，有 bn
1
n1
从而，当 n N1 N 2 时，有 an2bn2 bn ，则由正项级数的比较判别法可知
an2bn2 收敛。
11 1, 2 2 , 3 3 到基
1 2 , 2 3 , 3 1 的过渡矩阵为（
）
101 A 2 2 0.
033
120 B 0 2 3.
103
11 1
24 6
C
11
1
.
24 6
1 11
2 46
1 11
2 22
D1 1
1
.
44 4
11 1
66 6
6. 设 A, B 均为 2 阶矩阵， A* , B* 分别为 A, B 的伴随矩阵，若 A 2, B 3 ，则分块矩
（Ⅱ）对①中的任意向量 2 , 3 证明 1 , 2 , 3 无关。 7. （本题满分 11 分）
设二次型 f x1, x2, x3 ax12 ax22 a 1 x32 2x1x3 2x2 x3
（Ⅰ）求二次型 f 的矩阵的所有特征值；
（Ⅱ）若二次型
f 的规范形为
2
y1
2
y2 ，求
a 的值。
8. （本题满分 11 分）袋中有 1 个红色球， 2 个黑色球与 3 个白球，现有回放地从袋中取两次，每次取一球，
n1
（5）设 1 , 2, 3 是 3 维向量空间 R3 的一组基，则由基

2009考研数学真题及答案详解

2009年全国硕士研究生入学统一考试数学一试题答案解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）当0x ®时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则()A 11,6a b ==-.()B 11,6a b ==.()C 11,6a b =-=-.()D 11,6a b =-=.【答案】 A【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则222200000()sin sin 1cos sinlim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx ®®®®®---==-×---洛洛230sin lim 166x aax a b b ax a®==-=-× 36a b \=- 故排除,B C 。

另外201cos lim 3x a axbx ®--存在，蕴含了1cos 0a ax -®()0x ®故 1.a =排D 。

所以本题选A 。

（2）如图，正方形(){},1,1x y x y ££被其对角线划分为四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =òò，则{}14max k k I ££=()A 1I .()B 2I . ()C 3I .()D 4I .【答案】A【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是-1 -1 1 1 xy 1D 2D3D4D关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ³££=>òò；{}3(,),012cos 0x y y x x I y xdxdy £-££=<òò.所以正确答案为A. （3）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0x F x f t dt =ò的图形为()A ()B()C ()D【答案】D【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：①[]0,1x Î时，()0F x £，且单调递减。

2009年全国硕士研究生入学考试数学一真题(2009考研数一真题答案解析)

2009年全国硕士研究生入学统一考试部分数学一试题答案解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=. 【答案】 A【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

另外201cos lim3x a axbx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除D 。

所以本题选A 。

（2）如图，正方形(){},1,1x y x y ≤≤四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max k k I ≤≤=()A 1I .()B 2I . ()C 3I .()D 4I .【答案】A【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是x关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰；{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为A.（3）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为()A ()B()C ()D【答案】D【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：①[]0,1x ∈时，()0F x ≤，且单调递减。

2009-数一标准答案及解析

= P( XY ≤ z ) = P( XY ≤ z Y= 0) P(Y= 0) + P( XY ≤ z Y= 1) P(Y= 1) FZ ( z ) 1 = [ P( XY ≤ z Y = 0) + P( XY ≤ z Y = 1)] 2 1 = [ P( X ⋅ 0 ≤ z Y = 0) + P( X ≤ z Y = 1)] 2
+∞
−∞
x −1 xΦ′ dx 2
∫
+∞
−∞
+∞ +∞ x −1 x −1 ′ ( u ) du 2 xΦ′ ( x ) dx = 0 ， ∫ xΦ′ dx = u 2 ∫ ( 2u + 1) Φ= −∞ −∞ 2 2
所以 EX = 0 + 0.35 × 2 = 0.7 . （ 8 ）设随机变量 X 与 Y 相互独立，且 X 服从标准正态分布 N ( 0,1) ， Y 的概率分布为
x −1 ， 2
0.7 x − 1 Φ′ ， 2 2
所以 EX =
∫
+∞
−∞
xF ′ ( x= )dx
∫
+∞
−∞
x − 1 x 0.3Φ′ ( x ) + 0.35Φ′ dx 2
= 0.3∫
而
+∞
−∞
xΦ′ ( x ) dx + 0.35∫
所以 I1
2
{( x , y ) y ≥ x ,0≤ x≤1}
∫∫
y cos xdxdy > 0 ；
梅花香自苦寒来，岁月共理想，人生齐高飞！第 - 6 - 页共 19 页

2009年考研数学一真题及答案解析

2009年全国硕士研究生入学统一考试数学一试题一、选择题(1〜8小题，每小题4分，共32分, 符合题目要求，把所选项前的字母填在题后的括号内(1 )当x 0 时，f x sin ax与g2x ln 1 bx等价无穷小，则( )1,b 1,b 1 6 . 1 6(2)如图，正方形x,y i,y四个区域D k k 123,4 ，IkDk1,b1,b 11被其对角线划分为ycosxdxdy，则m k a x I k (A I i.B丨2・C丨3・(3)设函数y在区间1,3 上的图形为: 则函数F-1f(x)-2 2 3 x-1F列每小题给出的四个选项中，只有一项.)B当b n发散时，a n b n发散•n 1 n 1D当b n发散时，a j b：发散.n 1 n 11 1则由基1,2 3到基2 3)2 02 3 .0 31116 6 6,B的伴随矩阵，若A 2, B 3，则分块A 当兰b n收敛时，n 1a nb n收敛.n 1C当b n 收敛时，a：b：收敛.n 1 n 1(5 )设 1,2,3 是3维向量空间R3的一组基1 2 , 23, 3 1的过渡矩阵为(1 0 1 1A 2 2 0 .B 00 3 3 11 1 12 4 6C1 1 1D 2 4 61 1 12 4 6设有两个数列0,a nb n，若(4)lim a nn则(矩阵的伴随矩阵为()B OAO*3B B O*2B * *3A2A o . OCO *3A O*2A * D *3B2B o . O)(6)设A, B均为2阶矩阵，A*,B*分别为2(7)设随机变量X的分布函数为F x 0.3 x 0.7 ，其中x为标准正态分布函数，则EX ()A 0.B 0.3.C 0.7.D 1.(8)设随机变量X与Y相互独立，且X服从标准正态分布N 0,1 , Y的概率分布为1P Y 0 P Y 1 —,记F Z z为随机变量Z XY的分布函数，贝U函数F z z2的间断点个数为( )A O.B 1.C 2.D 3.二、填空题(9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.)2(9)设函数f u,v具有二阶连续偏导数，z f x, xy，则z。

2009年考研数学一、二、三真题(含详解)

O
A
O
A O
A
1
O B1
B
O
B
O
B
O
6
A1
O
O
6
1 A
A
1 B
B
6
O
O
1 2
A
1 B 3 O
O 3A
6
6
(D) a 1,b 1 6
【解析】 f x x sin ax 与 g x x2 ln 1 bx 是 x 0 时的等价无穷小,则
lim
x0
f (x) g(x)
lim
x0
x sin ax x2 ln(1 bx)
lim
x0
x sin ax x2 (bx)
lim
x0
x
sin ax bx3
,且单调递减；
0
（定积分对应的图像位于 x 轴下方）
③ x 1, 2 时, F(x) x f (t)dt 0 单调递增； 0
④ x 2,3 时, F '(x) f (x) 0 为常函数；
⑤ F (x) 为连续函数. 结合这些特点,可见正确选项为(D)
(4)
设有两个数列
an
,
bn
,若
lim
n
则 max 1k 4
Ik
(
)
D1
D2
D4
-1
D3
1
x
(A) I1
(B) I2 (C) I3 (D) I4
-1
【答案】(A)
【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令 f (x, y) y cos x ,
D2, D4 两区域关于 x 轴对称, f (x, y) y cos x f (x, y) ,即被积函数是关于 y 的奇函数, 所以 I2 I4 0 ；