七年级同步上4

合集下载

人教版七年级数学上册同步备课《第四章》 4.1.3 点、线、面、体(教学设计)

4.1.3 点、线、面、体教学设计一、内容和内容解析1.内容本节课是人教版《义务教育教科书•数学》七年级上册（以下统称“教材”）第四章“几何图形初步”4.1.3 点、线、面、体，内容包括：认识点、线、面、体的几何特征；知道点、线、面、体之间的关系.2.内容解析本节课主要是在学生了解了我们身边的平面图形与立体图形的基础上，从流星雨、打开的扇面、商店和宾馆的旋转门等实例出发，引出了“点动成线，线动成面、面动成体”这一事实，从运动的观点揭示点线、面、体之间的内在联系，借助直观的图片与实例让学生从中感受点线、面、体的含义，体验它们之间的联系与区别.几何图形是由点、线、面、体组成的，点线面体的学习不仅是学生认识与理解图形，培养学生的抽象思维能力的基础，还是以后学好三角形、四边形、圆等内容的必要基础知识.基于以上分析，确定本节课的教学重点为：对点、线、面、体及它们之间的关系的认识.二、目标和目标解析1.目标(1)知道点、线、面、体是构成几何图形的元素，进一步认识点、线、面、体的几何特征.(2)知道点、线、面、体之间的关系.2.目标解析认识几何图形的基本元素：点、线、面：点、线、面也都是几何图形；认识到点动成线，线动成面，面动成体.经历从几何体中寻找点、线、面的过程，借助实例，通过触摸、观察、实验、举例等数学活动，变抽象为具体，发展抽象思维能力.提高热爱几何的热情，激发学习兴趣.三、教学问题诊断分析七年级学生仅对简单的几何图形有初步的直观认识，而对点线、面、体的抽象概念很难理解，需要让学生从直观中去感受抽象.由于七年级学生的理解能力和思维特征和生理特征，学生好动性,注意力易分散，爱发表见解，希望得到老师的表扬等特点，所以在教学中应抓住学生这一生理心理特点，一方面要运用直观生动的形象，引发学生的兴趣，使他们的注意力始终集中在课堂上；另一方面要创造条件和机会，让学生发表见解，发挥学生学习的主动性.心理上，学生对数学课的兴趣，老师应抓住这有利因素，引导学生认识到数学课的科学性，学好数学有利于其他学科的学习以及学科知识的渗透性.基于以上学情分析，确定本节课的教学难点为：对“点动成线”、“线动成面” 以及“面动成体”的理解.四、教学过程设计（一）情境引入猜谜语谜语：千条线万条线，落到水中看不见. (打一自然物)—雨点你能用数学语言来描述这一现象吗？(点动成线)（二）自学导航几何体我们先来认识“体”. 观察一本书、圆罐、篮球，从它们外形中分别可以抽象出什么立体图形？长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体. 几何体简称体.平面与曲面如图：四棱锥有___个面；圆柱有___个面；圆锥有___个面. 再联想上一课“展开图”的知识，可以得出结论：包围着体的是_____.观察这些面，它们有区别吗？四棱锥的5个面是平的；圆柱的侧面是曲的，上、下两个底面是平的；圆锥的侧面是曲的，底面是平的.面有平的面(平面)和曲的面(曲面)两种.观察我们的教室和周围环境，举出一些实际生活中“面”的例子，并指出哪些面是平的，哪些面是曲的？点与线思考：观察几何体模型，回答下列问题：(1)面与面相交的地方形成了什么图形？它们有什么不同？(2)线与线相交的地方形成了什么图形？它们有什么不同？面与面相交的地方形成线，线分为直线和曲线；线与线相交的地方是点，点只代表位置，没有大小，所以点都是相同的.线的形象点的形象思考：下图是一个长方体，它有____个面，面和面相交的地方形成了____条棱，棱和棱相交成____个顶点.几何图形都是由________________组成的.在点、线、面、体中最基本的元素是____.物体的运动会留下运动轨迹，这些运动轨迹往往也能抽象成几何图形. 如果把笔尖看成一个点，这个点在纸上运动时，形成的图形是什么？动手试一试.点动成线线动成面观察下列动画，你发现了什么？面动成体观察下列动画，你发现了什么？（三）考点解析例1.(1)正方体由____个面围成，它们都是____面；正方体有____个顶点，每个顶点处有____条棱.(2)圆柱的侧面和底面相交成一条线，是____线；圆柱由____个面围成，其中有____个平的面，____个曲的面.(3)用圆规在纸上画圆，这种现象说明_________；风扇的叶片在转动时看上去像一个平面，这种现象说明__________；硬币在桌面上快速地转动时，看上去像球，这种现象说___________.【迁移应用】1.(1)在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密地斜织着”的语句，这里把雨看成了线，这种现象可以反映的数学原理是________.(2)国扇文化有深厚的文化底蕴，历来中国有“制扇王国”之称如图，打开折扇时，随着扇骨的移动形成一个扇面，这种现象可以用数学原理解释为__________.2.如图是一个五棱柱，下列关于五棱柱的叙述正确的是( )A.有4条侧棱B.有5个面C.有10条棱D.有10个顶点3.图中的立体图形是由几个面围成的？是平面还是曲面？面与面相交成几条线？它们是直线还是曲线？解：图中的立体图形是由4个面围成的；3个平面，1个曲面；面与面相交成6条线；直线有4条，曲线有2条。

2022-2023学年浙江七年级数学上学期同步精讲精练专题4

专题4.1 单项式与多项式【十大题型】【浙教版】【题型1 列代数式】 (6)【题型2 单项式与多项式的概念】 (7)【题型3 直接确定单项式的系数与次数】 (8)【题型4 根据单项式的次数求参】 (8)【题型5 直接确定多项式的项与次数】 (9)【题型6 根据多项式的项与次数求参】 (9)【题型7 单项式与多项式综合运用】 (9)【题型8 单项式与多项式中的结论开放性问题】 (10)【题型9 单项式中的规律探究】 (10)【题型10 多项式中的规律探究】11【知识点1 代数式的概念】那个字母前加上“-”号.【题型1 列代数式】【例1】（2022秋•洛阳期末）如图，A，B两地之间有一条东西走向的道路．在A地的东边5km处设置第一个广告牌，之后每往东12km就设置一个广告牌．一辆汽车从A地出发，沿此道路向东行驶．当经过第n个广告牌时，此车所行驶的路程为（）A．（12n+7）km B．（12n+5）km C．（12n﹣7）km D．（12n﹣5）km【变式1-1】（2022秋•朝阳区期末）用代数式表示“m的3倍与n的差的平方”，正确的是（） A ．3m ﹣n 2B ．（m ﹣3n ）2C ．（3m ﹣n ）2D ．3（m ﹣n ）2【变式1-2】（2022秋•侯马市期末）一个两位数，个位数字和十位数字之和为10，个位数字为x ，用代数式表示这个两位数是．【变式1-3】（2022秋•正定县期末）如图，阴影部分是一个长方形截去两个四分之一的圆后剩余的部分，则它的面积是（其中a ＞2b ）（）A ．ab −πa 24B ．ab−πb 22C ．ab −πa 22D ．ab −πb 24【题型2 单项式与多项式的概念】【例2】（2022秋•莱阳市期中）下列整式中：m 4n 27、−12x 2y 、x 2+y 2﹣1、x 、3x 2y +3xy 2+x 4﹣1、32t 3、2x ﹣y ，单项式的个数为a ，多项式的个数为b ，则ab ＝．【变式2-1】（2022秋•东莞市校级期中）整式﹣0.3x 2y ，0，x+12，﹣22abc 2，13x 2，−14y ，−13ab 2−12a 2b 中单项式的个数有（） A ．6个B ．5个C ．4个D ．3个【变式2-2】（2022秋•太湖县期末）下列式子：2a 2b ，3xy ，﹣2y 2，a+b 2，4，﹣m ，x+yz 2，ab−c n其中是多项式的有（） A ．2个B ．3个C ．4个D ．5个【变式2-3】（2022秋•新洲区期末）（2022秋•端州区月考）把下列各式分别填在相应的大括号内．﹣2，x2y，−a3，2x2+3x﹣1，πx2y32，﹣y，1x，2x−y5单项式：{ …}多项式：{ …}．【题型3 直接确定单项式的系数与次数】【例3】（2022秋•滨江区期末）单项式πx 2y3的系数为，次数为．【变式3-1】（2022秋•长垣市月考）指出下列各单项式的系数和次数．（1）﹣12πxy2（2）﹣22a2bc（3）−32x2y3z．【变式3-2】（2022秋•商水县期末）已知|a+1|+（b﹣2）2＝0，则单项式﹣x a+2by b﹣a的次数是．【变式3-3】（2022秋•惠城区期末）已知单项式−34x2y2的系数为m，次数为n，则mn的值为．【题型4 根据单项式的次数求参】【例4】（2022秋•高密市期末）若（a﹣2）x2y|a|+1是x，y的五次单项式，则a＝．【变式4-1】（2022秋•孟津县期末）已知单项式6x2y4与﹣3a2b m+2的次数相同，则m2﹣2m的值为．【变式4-2】（2022秋•德惠市期中）已知x2y|a|+（b+2）是关于x、y的五次单项式，求a2﹣3ab的值．多项式的项：每个单项式叫做多项式的项，不含字母的项叫做常数项．（1）多项式的每一项包括它前面的符号．（2）一个多项式含有几项，就叫几项式，如：是一个三项式．多项式的次数：多项式里次数最高项的次数，叫做这个多项式的次数．（1）多项式的次数不是所有项的次数之和，而是多项式中次数最高的单项式的次数．（2）一个多项式中的最高次项有时不止一个，在确定最高次项时，都应写出．【题型5 直接确定多项式的项与次数】【例5】（2022秋•端州区校级期中）多项式xy 2﹣9xy +5x 2y ﹣36是次项式．【变式5-1】（2022秋•平原县校级期中）多项式2x 2y ﹣x 2+12x 2y 2﹣3的最高次项是，三次项的系数是，常数项是．【变式5-2】（2022春•杨浦区校级期末）多项式﹣3x 2y +4xy +x ﹣2的次数与项数之和为．【变式5-3】（2022秋•苍溪县期中）已知多项式﹣2m 3n 2﹣5中，含字母的项的系数为a ，多项式的次数为b ，常数为c ，则a +b +c ＝．【题型6 根据多项式的项与次数求参】【例6】（2022秋•呈贡区月考）若多项式12x |m |﹣（m ﹣4）x +7是关于x 的四次二项式，则m 的值是．【变式6-1】（2022秋•泰兴市校级期中）已知多项式x ﹣3xy m +1+x 3y ﹣3x 4﹣1是五次多项式，则m ＝．【变式6-2】（2022秋•陇县期末）多项式12x |m|−(m +2)x +7是关于x 的二次三项式，则m ＝．【变式6-3】（2022秋•莒县期末）如果（|k |﹣3）x 3﹣（k ﹣3）x 2﹣2是关于x 的二次多项式，则k 的值是．【题型7 单项式与多项式综合运用】【例7】（2022秋•麻城市期末）已知多项式−13x 2y m+1+xy 2−3x 3−6是五次四项式，单项式0.4x 2n y 5﹣m的次数与这个多项式的次数相同，则m ＝，n ＝．【变式7-1】（2022秋•赤壁市期中）已知单项式3x 2y n 的次数为5，多项式6+x 2y −12x 2−16x 2y m +3的次数为6，求单项式（m +n ）x m y n 的次数与系数的和．【变式7-2】（2022秋•建华区校级期中）已知多项式（m +4）x |m |y 2+xy ﹣4x +1六次四项式，单项式5x 2n y 6﹣m与多项式的次数相同，（m ，n 是常数），则m n ＝．【变式7-3】有三个单项式：a 2，b ，1，请问由这三个单项式与加、减、乘、除等运算符号能组成哪些多项式？2627x x --【题型8 单项式与多项式中的结论开放性问题】【例8】（2022秋•鄞州区期末）某单项式的系数为2，只含字母x，y，且次数是3次，写出一个符合条件的单项式可以是．【变式8-1】（2022秋•南川区期末）一个单项式满足下列两个条件：①系数是﹣3；②次数是四次．请写出一个同时满足上述两个条件的单项式．【变式8-2】（2022秋•朝阳区校级期中）试写出只含有字母x、y，同时满足下列条件的两个多项式：①六次三项式．②各项系数绝对值为1．③不含常数项．【变式8-3】（2022秋•朝阳区校级期中）写出同时满足下列4个条件的一个多项式：①该多项式含有字母x和y；②该多项式第一项是常数项；③该多项式是三次四项式；④该多项式各项系数和为零．【题型9 单项式中的规律探究】【例9】（2022秋•硚口区期中）观察下面有规律的三行单项式：x，2x2，4x3，8x4，16x5，32x6，…①﹣2x，4x2，﹣8x3，16x4，﹣32x5，64x6，…②2x2，﹣3x3，5x4，﹣9x5，17x6，﹣33x7，…③（1）根据你发现的规律，第一行第8个单项式为；（2）第二行第n个单项式为；（3）第三行第8个单项式为；第n个单项式为．【变式9-1】（2022•雁塔区校级开学）观察下列关于x的表达式，探究其规律：﹣x，﹣4x3，+7x5，﹣10x7，﹣13x9，16x11…，按照上述规律，第2017个表达式是．【变式9-2】（2012秋•和平区期中）观察下列排列的单项式的规律：1 2a2b，−14a2b2，18a2b3，−116a2b4，…．（1）请按照此规律写出第10个单项式；（2）试猜想写出第n个单项式，并写出其系数和次数．【变式9-3】（2022秋•海珠区期末）一组按规律排列的式子：a2，a 43，a65，a87，⋯则第1008个式子是．【题型10 多项式中的规律探究】【例10】（2022秋•北流市期中）观察下列依次排列的多项式：a+b，a2﹣b3，a3+b5，a4﹣b7，…，请写出第9个式子是．【变式10-1】（2022秋•黔东南州期末）观察下列多项式：2a﹣b，4a+b2，8a﹣b3，16a+b4，…按此规律，则可以得到第7个多项式是．【变式10-2】（2022•淮安一模）如图是有关x的代数式的方阵，若第10行第2项的值为1034，则此时x 的值为2．【变式10-3】（2022秋•永安市期末）观察右表，我们把某格中字母和所得到的多项式称为特征多项式，如第1格的“特征多项式”为4x+y，第3格的“特征多项式”为16x+9y，则第n格的“特征多项式”为．专题4.1 单项式与多项式【十大题型】【浙教版】【题型1 列代数式】 (6)【题型2 单项式与多项式的概念】 (7)【题型3 直接确定单项式的系数与次数】 (8)【题型4 根据单项式的次数求参】 (8)【题型5 直接确定多项式的项与次数】 (9)【题型6 根据多项式的项与次数求参】 (9)【题型7 单项式与多项式综合运用】 (9)【题型8 单项式与多项式中的结论开放性问题】 (10)【题型9 单项式中的规律探究】 (10)【题型10 多项式中的规律探究】11【知识点1 代数式的概念】那个字母前加上“-”号.【题型1 列代数式】【例1】（2022秋•洛阳期末）如图，A，B两地之间有一条东西走向的道路．在A地的东边5km处设置第一个广告牌，之后每往东12km就设置一个广告牌．一辆汽车从A地出发，沿此道路向东行驶．当经过第n个广告牌时，此车所行驶的路程为（）A．（12n+7）km B．（12n+5）km C．（12n﹣7）km D．（12n﹣5）km【分析】根据题意和图形，可以用代数式表示出这辆汽车行驶的路程，本题得以解决．【解答】解：由题意可得，一汽车在A 地出发，沿此道路向东行驶．当经过第n 个广告牌时，此车所行驶的路程为：5+12（n ﹣1）＝（12n ﹣7）km ，故选：C ．【变式1-1】（2022秋•朝阳区期末）用代数式表示“m 的3倍与n 的差的平方”，正确的是（） A ．3m ﹣n 2B ．（m ﹣3n ）2C ．（3m ﹣n ）2D ．3（m ﹣n ）2【分析】要明确给出文字语言中的运算关系，先表示出m 的3倍，再表示出与n 的差，最后表示出平方即可．【解答】解：m 的3倍与n 的差的平方表示为：（3m ﹣n ）2，故选：C ．【变式1-2】（2022秋•侯马市期末）一个两位数，个位数字和十位数字之和为10，个位数字为x ，用代数式表示这个两位数是．【分析】根据题意，先求出十位数字，然后写出这个两位数，注意化简．【解答】解：个位数字是x ，则十位数字是10﹣x ，所以这个两位数是（10﹣x ）×10+x ＝100﹣9x ．故答案为：100﹣9x【变式1-3】（2022秋•正定县期末）如图，阴影部分是一个长方形截去两个四分之一的圆后剩余的部分，则它的面积是（其中a ＞2b ）（）A ．ab −πa 24B ．ab −πb 22C ．ab −πa 22D ．ab −πb 24【分析】根据图形可得阴影部分的面积＝矩形的面积﹣两个扇形面积．【解答】解：S 矩形＝长×宽＝ab ， S 扇形=14•πb 2•2=12πb 2，S 阴影＝S 矩形﹣S 扇形＝ab −πb 22．故选：B ．一个字母也是单项式．注意：（1）单项式包括三种类型：①数字与字母相乘或字母与字母相乘组成的式子；②单独的一个数；③单独的一个字母．（2）单项式中不能含有加减运算，但可以含有除法运算．多项式的概念：几个单项式的和叫做多项式．【题型2 单项式与多项式的概念】【例2】（2022秋•莱阳市期中）下列整式中：m 4n 27、−12x 2y 、x 2+y 2﹣1、x 、3x 2y +3xy 2+x 4﹣1、32t 3、2x ﹣y ，单项式的个数为a ，多项式的个数为b ，则ab ＝ 12 ．【分析】先选出多项式和单项式，即可得出答案．【解答】解：单项式有m 4n 27、−12x 2y 、x 、32t 3，即a ＝4，多项式有x 2+y 2﹣1、3x 2y +3xy 2+x 4﹣1、2x ﹣y ，即b ＝3， ab ＝12，故答案为：12．【变式2-1】（2022秋•东莞市校级期中）整式﹣0.3x 2y ，0，x+12，﹣22abc 2，13x 2，−14y ，−13ab 2−12a 2b 中单项式的个数有（） A ．6个B ．5个C ．4个D ．3个【分析】根据单项式的定义判断即可．【解答】解：整式﹣0.3x 2y ，0，x+12，﹣22abc 2，13x 2，−14y ，−13ab 2−12a 2b 中单项式有﹣0.3x 2y ，0，﹣22abc 2，13x 2，−14y 共5个，故选：B ．【变式2-2】（2022秋•太湖县期末）下列式子：2a 2b ，3xy ，﹣2y 2，a+b 2，4，﹣m ，x+yz 2，ab−c n其中是多项式的有（） A ．2个B ．3个C ．4个D ．5个【分析】几个单项式的和叫做多项式，结合所给式子进行判断即可．【解答】解：式子：2a 2b ，3xy ，﹣2y 2，a+b 2，4，﹣m ，x+yz 2，ab−c n中，是多项式的有a+b 2，x+yz 2，共2个．故选：A ．【变式2-3】（2022秋•新洲区期末）（2022秋•端州区月考）把下列各式分别填在相应的大括号内．﹣2，x2y，−a3，2x2+3x﹣1，πx2y32，﹣y，1x，2x−y5单项式：{ …}多项式：{ …}．【分析】根据单项式是数与字母的积，单独一个数或一个字母也是单项式；几个单项式的和是多项式，可得答案．【解答】解：单项式：{﹣2，x2y，−a3，πx2y32，﹣y}；多项式：{2x2+3x﹣1，2x−y5}．故答案为：﹣2，x2y，−a3，πx2y32，﹣y；2x2+3x﹣1，2x−y5．【题型3 直接确定单项式的系数与次数】【例3】（2022秋•滨江区期末）单项式πx 2y3的系数为π3，次数为3．【分析】根据单项式的次数和系数进行解答．【解答】解：单项式πx 2y3的系数为π3；次数为3；故答案为π3，3．【变式3-1】（2022秋•长垣市月考）指出下列各单项式的系数和次数．（1）﹣12πxy2（2）﹣22a2bc（3）−32x2y3z．【分析】根据单项式系数、次数的定义来求解．单项式中数字因数叫做单项式的系数，所有字母的指数和叫做这个单项式的次数．【解答】解：（1））﹣12πxy 2 的系数是﹣12π，次数是3；（2）﹣22a 2bc 的系数是﹣4，次数是4；（3）−32x 2y 3z 的系数是−32，次数是6．【变式3-2】（2022秋•商水县期末）已知|a +1|+（b ﹣2）2＝0，则单项式﹣x a +2by b﹣a的次数是 4 ．【分析】先求出a 与b 的值，然后代入单项式中即可求出答案．【解答】解：由题意可知：a +1＝0，b ﹣2＝0， ∴a ＝﹣1，b ＝2，∴将a 与b 代入单项式中可得：﹣2xy 3 单项式的次数为：4 故答案为：4【变式3-3】（2022秋•惠城区期末）已知单项式−34x 2y 2的系数为m ，次数为n ，则mn 的值为 ﹣3 ．【分析】直接利用单项式的次数与系数的定义分别得出m ，n 的值，即可得出答案．【解答】解：∵单项式−34x 2y 2的系数为m =−34，次数为n ＝4，∴mn 的值为：−34×4＝﹣3．故答案为：﹣3．【题型4 根据单项式的次数求参】【例4】（2022秋•高密市期末）若（a ﹣2）x 2y |a |+1是x ，y 的五次单项式，则a ＝ ﹣2 ．【分析】根据单项式系数和次数的概念求解．【解答】解：∵（a ﹣2）x 2y |a |+1是x ，y 的五次单项式， ∴a ﹣2≠0，2+|a |+1＝5，解得：a ≠2，a ＝±2，则a ＝﹣2．故答案为：﹣2．【变式4-1】（2022秋•孟津县期末）已知单项式6x 2y 4与﹣3a 2b m +2的次数相同，则m 2﹣2m 的值为 0 ．【分析】根据两个单项式的次数相同可得2+4＝2+m +2，再解即可得到m 的值，进而可得答案．【解答】解：由题意得：2+4＝2+m +2，解得：m ＝2，则m 2﹣2m ＝0．故答案为：0．【变式4-2】（2022秋•德惠市期中）已知x 2y |a |+（b +2）是关于x 、y 的五次单项式，求a 2﹣3ab 的值．【分析】根据单项式及单项式次数的定义，可得出a 、b 的值，代入代数式即可得出答案．【解答】解：∵x 2y |a |+（b +2）是关于x ，y 的五次单项式， ∴{2+|a|=5b +2=0，解得：{a =±3b =−2，则当a ＝﹣3，b ＝﹣2时，a 2﹣3ab ＝9﹣18＝﹣9；当a ＝3，b ＝﹣2时，a 2﹣3ab ＝9+18＝27．【变式4-3】（2022秋•驻马店校级期中）若﹣mx 2y |n ﹣3|是关于x 、y 的10次单项式，且系数是8，求m +n 的值．【分析】利用单项式的定义得出m 的值，进而利用单项式次数的定义得出n 的值，进而得出答案．【解答】解：∵﹣mx 2y |n ﹣3|是关于x 、y 的10次单项式，且系数是8， ∴m ＝﹣8，且2+|n ﹣3|＝10，解得：n ＝11或﹣5，则m +n ＝3或m +n ＝﹣13．【题型5 直接确定多项式的项与次数】【例5】（2022秋•端州区校级期中）多项式xy 2﹣9xy +5x 2y ﹣36是三次四项式．【分析】要确定多项式是几次几项式，就要确定多项式的次数和项数，根据多项式次数和项数的概念可知，该多项式是三次四项式．【解答】解：多项式xy 2﹣9xy +5x 2y ﹣36是三次四项式．故答案为：三，四．【变式5-1】（2022秋•平原县校级期中）多项式2x 2y ﹣x 2+12x 2y 2﹣3的最高次项是 12x 2y 2 ，三次项的系数是 2 ，常数项是 ﹣3 ．【分析】直接利用多项式的各项确定方法分别求出答案．【解答】解：多项式2x 2y ﹣x 2+12x 2y 2﹣3的最高次项是：12x 2y 2，三次项的系数是：2，常数项是﹣3．故答案为：12x 2y 2，2，﹣3．【变式5-2】（2022春•杨浦区校级期末）多项式﹣3x 2y +4xy +x ﹣2的次数与项数之和为 7 ．【分析】根据多项式中次数最高的项的次数叫做多项式的次数．多项式的组成元素的单项式，即多项式的每一项都是一个单项式，单项式的个数就是多项式的项数可得答案．【解答】解：多项式x 2y ﹣xy 2+3xy ﹣1的次数与项数分别是3和4， 3+4＝7，故答案为：7．【变式5-3】（2022秋•苍溪县期中）已知多项式﹣2m 3n 2﹣5中，含字母的项的系数为a ，多项式的次数为b ，常数为c ，则a +b +c ＝ ﹣2 ．【分析】首先利用多项式的系数、次数及常数项确定a 、b 、c 的值，然后求和即可．【解答】解：∵多项式﹣2m 3n 2﹣5中，含字母的项的系数为a ，多项式的次数为b ，常数项为c ，∴a ＝﹣2，b ＝5，c ＝﹣5， ∴a +b +c ＝﹣2+5﹣5＝﹣2，故答案为：﹣2．【题型6 根据多项式的项与次数求参】【例6】（2022秋•呈贡区月考）若多项式12x |m |﹣（m ﹣4）x +7是关于x 的四次二项式，则m 的值是 4 ．【分析】根据四次二项式的定义可知，该多项式的最高次数为4，项数是2，所以可确定m 、n 的值，即可求解．【解答】解：由多项式是关于x 的四次二项式知： |m |＝4且m ﹣4＝0，解得m ＝4．故答案为：4．【变式6-1】（2022秋•泰兴市校级期中）已知多项式x ﹣3xy m +1+x 3y ﹣3x 4﹣1是五次多项式，则m ＝ 3 ．【分析】先观察多项式的各项，再确定每项的次数，最高次项的次数就是多项式的次数．【解答】解：∵多项式x﹣3xy m+1+x3y﹣3x4﹣1是五次多项式，∴1+m+1＝5，解得：m＝3．故答案为：3．x|m|−(m+2)x+7是关于x的二次三项式，则m＝2．【变式6-2】（2022秋•陇县期末）多项式12【分析】由于多项式是关于x的二次三项式，所以|m|＝2，但﹣（m+2）≠0，根据以上两点可以确定m 的值．【解答】解：∵多项式是关于x的二次三项式，∴|m|＝2，∴m＝±2，但﹣（m+2）≠0，即m≠﹣2，综上所述，m＝2，故填空答案：2．【变式6-3】（2022秋•莒县期末）如果（|k|﹣3）x3﹣（k﹣3）x2﹣2是关于x的二次多项式，则k的值是﹣3．【分析】直接利用多项式的定义得出|k|﹣3＝0，k﹣3≠0，进而得出答案．【解答】解：∵（|k|﹣3）x3﹣（k﹣3）x2﹣2是关于x的二次多项式，∴|k|﹣3＝0，k﹣3≠0，解得：k＝﹣3．故答案为：﹣3．【题型7 单项式与多项式综合运用】x2y m+1+xy2−3x3−6是五次四项式，单项式0.4x2n y5﹣m 【例7】（2022秋•麻城市期末）已知多项式−13的次数与这个多项式的次数相同，则m＝2，n＝1．x2y m+1+xy2−3x3−6是五次四项式，得到m+1＝3，根据单项式0.4x2n y5﹣m的【分析】根据多项式−13次数与这个多项式的次数相同，得到2n+5﹣m＝5，即可解答．x2y m+1+xy2−3x3−6是五次四项式，【解答】解：∵多项式−13∴m+1＝3，∴m＝2，∵单项式0.4x 2n y 5﹣m的次数与这个多项式的次数相同，∴2n +5﹣m ＝5， ∴n ＝1，故答案为：2，1．【变式7-1】（2022秋•赤壁市期中）已知单项式3x 2y n 的次数为5，多项式6+x 2y −12x 2−16x 2y m +3的次数为6，求单项式（m +n ）x m y n 的次数与系数的和．【分析】根据已知求出m 、n 的值，把m 、n 的值代入单项式，求出单项式的系数和次数，即可得出答案．【解答】解：∵单项式3x 2y n 的次数为5，多项式6+x 2y −12x 2−16x 2y m +3的次数为6，∴2+n ＝5，2+m +3＝6，解得：m ＝1，n ＝3，∴（m +n ）x m y n ＝4xy 3，系数是4，次数是1+3＝4， 4+4＝8，即单项式（m +n ）x m y n 的次数与系数的和是8．【变式7-2】（2022秋•建华区校级期中）已知多项式（m +4）x |m |y 2+xy ﹣4x +1六次四项式，单项式5x 2n y 6﹣m与多项式的次数相同，（m ，n 是常数），则m n ＝ 16 ．【分析】利用多项式的次数定义得出m 的值，进而利用单项式的次数得出n 的值，即可得出答案．【解答】解：∵多项式（m +4）x |m |y 2+xy ﹣4x +1六次四项式，单项式5x 2n y 6﹣m与多项式的次数相同，∴|m |+2＝6且m +4≠0，2n +6﹣m ＝6，解得m ＝4，n ＝2，则m n ＝42＝16．故答案为：16．【变式7-3】有三个单项式：a 2，b ，1，请问由这三个单项式与加、减、乘、除等运算符号能组成哪些多项式？【分析】根据单项式和多项式的定义即可得出答案．【解答】解：根据题意得，组成的多项式有：a 2+b +1；a 2+b ﹣1；a 2﹣b +1；a 2﹣b ﹣1；a 2b +1；a 2b ﹣1；﹣a 2+b +1；﹣a 2+b ﹣1；﹣a 2﹣b +1；﹣a 2﹣b ﹣1；﹣a 2b +1；﹣a 2b ﹣1．【题型8 单项式与多项式中的结论开放性问题】【例8】（2022秋•鄞州区期末）某单项式的系数为2，只含字母x，y，且次数是3次，写出一个符合条件的单项式可以是2xy2或2x2y（答案不唯一）．【分析】根据单项式系数、次数的定义来求解．单项式中数字因数叫做单项式的系数，所有字母的指数和叫做这个单项式的次数．【解答】解：2xy2或2x2y是只含字母x、y，系数为2，次数为3的单项式，故答案为：2xy2或2x2y（答案不唯一）．【变式8-1】（2022秋•南川区期末）一个单项式满足下列两个条件：①系数是﹣3；②次数是四次．请写出一个同时满足上述两个条件的单项式﹣3x4（答案不唯一）．【分析】根据单项式的数字因数为单项式的系数，单项式的所有字母的指数的和为单项式的次数可解决此题．【解答】解：根据单项式的系数与次数的定义，满足条件的单项式可为﹣3x4（答案不唯一）．故答案为：﹣3x4（答案不唯一）．【变式8-2】（2022秋•朝阳区校级期中）试写出只含有字母x、y，同时满足下列条件的两个多项式：①六次三项式．②各项系数绝对值为1．③不含常数项．【分析】根据多项式的相关概念回答即可．【解答】解：根据题意得：xy5﹣xy+xy2（答案为不唯一）．【变式8-3】（2022秋•朝阳区校级期中）写出同时满足下列4个条件的一个多项式：①该多项式含有字母x和y；②该多项式第一项是常数项；③该多项式是三次四项式；④该多项式各项系数和为零．【分析】根据题目的要求可直接写出符合条件的多项式，本题为开放题，答案不唯一．【解答】解：3﹣x+2y﹣4xy2（答案不唯一）．【题型9 单项式中的规律探究】【例9】（2022秋•硚口区期中）观察下面有规律的三行单项式：x，2x2，4x3，8x4，16x5，32x6，…①﹣2x，4x2，﹣8x3，16x4，﹣32x5，64x6，…②2x2，﹣3x3，5x4，﹣9x5，17x6，﹣33x7，…③（1）根据你发现的规律，第一行第8个单项式为128x8；（2）第二行第n个单项式为（﹣2）n x n；（3）第三行第8个单项式为﹣129x9；第n个单项式为（﹣1）n+1（1+2n﹣1）x n+1．【分析】通过观察很容易得到三组数据数字因数、字母次数之间的关系，根据规律写出相应的式子即可．【解答】解：（1）因为第一行的每个单项式，数字因数后面都是前面的2倍，字母次数与这个单项式是第几个有关，根据这个规律可得第一行第8个单项式为128x8；（2）因为第二行的每个单项式，数字因数后面都是前面的（﹣2）倍，字母次数与这个单项式是第几个有关，根据这个规律可得第n个单项式为（﹣2）n x n；（3）通过观察第三行的这组单项式，这组单项式符合（﹣1）n+1（1+2n﹣1）x n+1，第8个单项式是﹣129x9；第n个单项式为（﹣1）n+1（1+2n﹣1）x n+1．故答案为：（1）128x8，（2）（﹣2x）n，（3）﹣129x9 ，（﹣1）n+1（1+2n﹣1）x n+1【变式9-1】（2022•雁塔区校级开学）观察下列关于x的表达式，探究其规律：﹣x，﹣4x3，+7x5，﹣10x7，﹣13x9，16x11…，按照上述规律，第2017个表达式是﹣6049x4033．【分析】系数的规律：第n个对应的系数的绝对值是3n﹣2，指数的规律：第n个对应的指数是2n﹣1，依此即可求解．【解答】解：根据分析的规律，2017÷3＝672…1，第2017个表达式是：﹣6049x4033．故答案为：﹣6049x4033．【变式9-2】（2012秋•和平区期中）观察下列排列的单项式的规律：1 2a2b，−14a2b2，18a2b3，−116a2b4，…．（1）请按照此规律写出第10个单项式；（2）试猜想写出第n个单项式，并写出其系数和次数．【分析】（1）要看各单项式的系数和次数与该项的序号之间的变化规律．本题中，奇数项符号为负，偶数项符号为正，数字变化规律是（﹣1）n+112n，字母变化规律是a2b n；（2）利用（1）中规律得出答案．【解答】解：（1）∵12a2b，−14a2b2，18a2b3，−116a2b4，…∴第10个单项式为：−1210a2b10；（2）第n个单项式为：（﹣1）n+1×12n a2b n（n≥2），系数为：（﹣1）n+1×12n，次数为：2+n．【变式9-3】（2022秋•海珠区期末）一组按规律排列的式子：a2，a 43，a65，a87，⋯则第1008个式子是a20162015．【分析】观察分子、分母的变化规律，总结出一般规律即可求解．【解答】解：a2，a4，a6，a8…，分子可表示为：a2n，1，3，5，7，…分母可表示为2n﹣1，则第n个式子为：a 2n2n−1．故第1008个式子是a 20162015．故答案为：a 20162015．【题型10 多项式中的规律探究】【例10】（2022秋•北流市期中）观察下列依次排列的多项式：a+b，a2﹣b3，a3+b5，a4﹣b7，…，请写出第9个式子是a9+b17．【分析】把已知的多项式看成由两个单项式组成，分别找出两个单项式的规律，也就知道了多项式的规律．【解答】解：多项式的第一项依次是a，a2，a3，a4，…，a n，第二项依次是b，﹣b3，b5，﹣b7，…，（﹣1）n+1b2n﹣1，所以第9个式子即当n＝9时，代入到得到a n+（﹣1）n+1b2n﹣1＝a9﹣b17．故答案为：a9+b17．【变式10-1】（2022秋•黔东南州期末）观察下列多项式：2a﹣b，4a+b2，8a﹣b3，16a+b4，…按此规律，则可以得到第7个多项式是128a﹣b7．【分析】把已知的多项式看成由两个单项式组成，分别找出两个单项式的规律，也就知道了多项式的规律．【解答】解：多项式的第一项依次是2a，4a，8a，16a，…2n a，第二项依次是﹣b，b2，﹣b3…（﹣1）n b n，则可以得到第7个多项式是128a﹣b7．故答案为：128a﹣b7．【变式10-2】（2022•淮安一模）如图是有关x的代数式的方阵，若第10行第2项的值为1034，则此时x 的值为2．【分析】由方阵可以看出每一行的每一个式子的第一项为2n﹣1x，第二项是n，由此得出等式求得x的数值即可．【解答】解：∵每一个式子的第二项是2n﹣1x+n，∴第10行第2项的值为29x+10＝1034，解得x＝2，故答案为2．【变式10-3】（2022秋•永安市期末）观察右表，我们把某格中字母和所得到的多项式称为特征多项式，如第1格的“特征多项式”为4x+y，第3格的“特征多项式”为16x+9y，则第n格的“特征多项式”为（n+1）2x+n2y．【分析】先根据已知数据找出规律，根据所得的规律得出即可．【解答】解：∵第1格的“特征多项式”为4x+y＝（1+1）2x+12•y，第2格的“特征多项式”为9x+4y＝（2+1）2x+22•y，第3格的“特征多项式”为16x+9y＝（3+1）2x+32•y，∴第n格的“特征多项式为：（n+1）2x+n2y，故答案为：（n+1）2x+n2y．。

牛津译林版(2024年)七年级英语上册 Unit 4 同步练习(含答案)

2024-2025学年七年级英语上册牛津译林版（2024年）Unit 4Assessment&Future study一、完成句子12345She usually gets up at a quarter to eight and starts her 6 day. Then she has a shower and gets dressed. After that, she goes downstairs and has7 with her parents. She usually has milk, bread and an egg. Then she8 her teeth because she wants to keep them white and healthy!After that, she gets her schoolbag and goes to the bus stop to 9the school bus. Classes start at half past eight and finish at half past four. She usually has lunch at the school canteen with her 10 at about 12 o’clock. Her best friend is Amy, and Sophia always 11 next to her at lunch. They usually have rice, soup, salad and meat. They have a 12 for one and a half hours and then they go on with their afternoon classes.After school she returns home and does her homework. She is a very 13 pupil, so she never forgets any school tasks! After homework, she usually listens to music and watches TV a bit.At half past seven, it is time for dinner. She likes eating a sandwich with strawberry juice. Then she usually reads a book or 14 the school day with her parents for a while.15 , she goes to bed at about ten o’clock.6．A．bad B．boring C．tired D．busy 7．A．breakfast B．lunch C．dinner D．tea8．A．washes B．watches C．brushes D．worries9．A．find B．catch C．keep D．stop 10．A．brothers B．parents C．sisters D．classmates 11．A．sits B．waits C．plays D．works12．A．party B．meeting C．break D．lesson 13．A．famous B．hard-working C．quiet D．poor14．A．thinks about B．puts on C．listens to D．talks about 15．A．Finally B．Carefully C．Early D．Quickly三、选词填空请根据句子意思，用方框中所给单词或短语的适当形式填空并完成句子（不可重复使用）。

2023-2024学年七年级数学上册同步学与练(人教版)第04讲绝对值(含答案与解析)

i.-2的绝对值是（）5-4c-f D.且2【即学即练2】2.数轴上有力、B、C、。

四个点，其中绝对值等于2的点是（),4B C-J_I A二18・•]]L A-4-3-2-1012•345A.点力B.点BC.点。

D.点D【即学即练3】3.已矢口u—-2,b=l,则同+|-句的值为（)A.3B.1C.0D.-1知识点02绝对值的性质1.绝对值的非负性：由定义可知，绝对值表示到原点的距离，所以不能为O所以绝对值是一个,所以绝对值具有。

即若|。

|0o几个非负数的和等于o,这几个非负数一定分别等于0o即：若\a\+\b\+...+I m|=0,则一定有o题型考点：根据绝对值的非负性求值。

【即学即练1】4.已知|x-2|+加T|=0,则x-y的相反数为（）A.-1B.1C.3D.-3【即学即练2】5.若向+例=0,则口与力的大小关系是（)A.a=b=0B.口与力互为倒数C.Q与b异号D.口与力不相等知识点03绝对值与数轴1.绝对值与数轴：在数轴上，一个数离原点越近，绝对值就,一个数离原点越远，绝对值,题型考点：根据绝对值与数轴进行求解判断。

6.一个数的绝对值越小，则该数在数轴上所对应的点，离原点越・【即学即练2】7.如图，四个有理数m n,p,q在数轴上对应的点分别为N,P,0若乃+0=0,则秫，n,p,q四个有理数中，绝对值最小的一个是（）M OA.p知识点04绝对值与相反数1.绝对值与相反数：①数轴上互为相反数的两个数在原点的两侧，且到原点的距离相等，所以互为相反数的两个数他们的绝对值_________o即若。

与5互为相反数，贝」|q|\b\o②绝对值等于某个正数的数一定有,它们o即若|x|=q（q>0）,则③绝对值相等的两个数要么,要么o即若|。

|=|们，则有或o题型考点：根据相反数的绝对值进行求解。

【即学即练1】8.若|x|=5,贝0x—.【即学即练2】9.已知□=-5,同=|句，则人的值为（）A.±5B.-5C.+5D.0【即学即练3】10.绝对值等于5的数是,它们互为.知识点05求式子的绝对值1.求式子的绝对值：先判断式子与的大小关系，再对式子进行求绝对值。

人教版七年级数学上册第四章同步练习题

《图形认识初步》一、选择题（每小题3分，共30分）1．下列空间图形中是圆柱的为（）A. B. C. D.2．桌上放着一个茶壶，4个同学从各自的方向观察，请指出下图右边的四幅图，从左至右分别是由哪个同学看到的（）第2题图A．①②③④ B．①③②④ C．②④①③ D．④③①②3．将如图2所示的直角三角形ABC绕直角边AC旋转一周，所得的几何体从正面看是图3中（）4．小丽制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（）A图2A B C D图 35．如图所示，从A 地到达B 地，最短的路线是（）A.A →C →E →BB.A →F →E →BC.A →D →E →BD.A →C →G →E →B6.（2013•云南昭通中考）如图是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的面上标的字是（）A ．美B ．丽C ．云D ．南7.如图所示的立体图形从上面看到的图形是（）8.如果∠1与∠2互为补角,且∠1∠2,那么∠2的余角是( ) A.21∠ 1 B.21∠2 C.21(∠1-∠2) D.21(∠1+∠2)第7题图第5题图二、填空题（每小题2分，共20分）1．长方体由个面，条棱，个顶点.2．下列图形是一些立体图形的平面展开图，请将这些立体图形的名称填在对应的横线上.3．（2012•山东菏泽中考）已知线段AB=8 cm，在直线AB上画线段BC，使它等于3 cm，则线段AC=_______cm．4．（1）32度分秒。

48.（2）//042/72= 度。

235．如图甲，用一块边长为10 cm的正方形的厚纸板，做了一套七巧板.将七巧板拼成一座桥（如图乙），这座桥的阴影部分的面积是 .第5题图6．把一张长方形纸条按图的方式折叠后，量得∠AOB＇=110°，则∠B＇OC=______.7．下图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形，这些相同的小正方体的个数是_______.8．如图所示的几何体是由棱长为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），则第n个几何体中只有两个面．．．涂色的小立方体共有个．三、解答题1.计算：（1）22°18′×5；（2）90°-57°23′27″.1∠β的值2.已知∠α与∠β互余，且∠α比∠β小25°，求2∠α-33. 一个角的补角加上010后等于这个角的余角的3倍，求这个角.4．⑴已知如图，点C在线段AB上，线段AC＝10，BC＝6，点M、N分别是AC、BC的中点，求MN的长度。

人教版七年级上册Unit4 同步讲义和巩固练习(教师版)

七年级上册Unit4 Where’s my schoolbag?【重点短语】1.快点come on2.整洁的be tidy3.磁带播放机tape player4.飞机模型model plane5.有一个时钟have a clock6.在沙发上on the sofa7.在某人的书包里in one's schoolbag8.在某人的床下under one's bed9.在桌子上on the table【重点句型】1. Come on, Jack.(1)come on 此处表示催促，意为“赶快，快点儿”，还可用“Hurry (up)!”表示催促。

(2)Come on 的其他含义：1）用来表示请求、鼓励、劝说等，意为“来吧；行啦”。

2）用于体育竞赛等场合鼓励队员，意为“加油”。

3）用于挑战或激怒对方，意为“来吧；好吧；试试吧”。

4）用于招呼别人，意为“过来”。

2. I think it’s in your grandparents’ room.(1)I think...意为“我认为...”，用于表述自己的主观想法或看法，think后常接that引导的宾语从句，that可省略。

例句：I think (that) the keys are Alice’s.(2)grandparents’是复数名词grandparents的所有格，意为“（外）祖父母的”。

名词所有格用于表示“某个（些）人的”，可以在某个（些）人后加’s来表示所有关系，其构成：1)一般情况下，在单数名词的词尾加’s Jim’s book Jim的书2)以-s或-es结尾的复数名词在词尾加“ ’” the students’ basketball 学生们的篮球3)不以-s结尾的复数名词在词尾加’s。

Children’s Day 儿童节4)表示两者及以上的人共同拥有某人或某物时，为名词＋and＋名词’s Tomand Jim’s teacher5)表示两人各自拥有不同的人或者物时，为名词’s＋名词’s Tom’s and Jim’steachers3. Where are my books?(1)Where + be动词+ 主语？用来询问“某人/某物在哪里”，其中where用作疑问副词，表示“在哪里”用来引导特殊疑问句。

【人教版新目标】七年级英语上册Unit4同步练习(含答案)(精修版)

人教版英语精品资料（精修版）Unit 4 Where's my schoolbag一、单项选择（共20小题；共20分）1. My quilt is the bed and my shoes are the bed.A. in; onB. on; underC. under; inD. on; in2. --- Where are your shoes?--- They're the floor(地板) the room.A. in; onB. on; inC. on; underD. in; between3. The pencil box is the bed but the schoolbag is the bed.A. in; onB. on; onC. of; underD. on; under4. --- Is your baseball your room, Mike?--- Yes, it's my bed.A. on; inB. in; underC. on; underD. in; in5. --- my ruler?--- It's under the chair.A. WhereB. Where'sC. Where'reD. Where are6. Where the twins?A. isB. areC. amD. be7. You make lunch, I'll take care of the baby.A. butB. orC. forD. and8. I work harder at my lessons this year I have made good progress.A. butB. orC. andD. for9. The students are from England and maths teacher is from China.A. theyB. themC. theirD. theirs10. --- Hi, Xiao Ming! I haven't seen you for a long time.--- Yeah! It's you, Lin Tao. To surprise, we can see each other here.A. myB. herC. hisD. our11. The English book is the desk the room.A. on; underB. under; onC. over; inD. on; in12. most museums you can't make any noise.A. InB. OnC. AtD. Under13. Mrs. Green's flat is the eighth floor. She likes listening to music bed.A. at; underB. in; onC. by; onD. on; in14. The box is empty. There is nothing it.A. onB. inC. under15. --- Where my socks, Mom?--- Sorry, I don't know. Maybe you put them under the bed.A. isB. amC. areD. have16. --- that?--- I think it's Sam.A. What'sB. Who'sC. WhoseD. Where's17. In China, red represents power it is also the color of strong feelings.A. soB. orC. butD. and18. This is my pen, that is your pencil.A. inB. ofC. andD. but19. What places do they go on way to the cinema?A. past; theyB. pass; themC. by; theirD. across; theirs20. An old friend of my sister's always helps my brother and with English.A. I; ourB. me; ourselvesC. I; myD. me; our二、单词拼写(单句首字母填空)（共20小题；共20分）21. You should t up the room before your friends arrive.22. I asked them what they t about the movie.23. The orange is tasty. B it is a little sour.24. A speak English.25. Xiang Qiuchi was listening to the r at nine last night.26. Gina's books are everywhere, but I'm t .27. I t she is a good teacher. We all like her.28. I have a tennis racket, b I don't have a tennis ball.29. My mother a remembers my birthday.30. Where is Mary? Oh, she's listening to music on the r (收音机).31. We clean our classroom every day, so it's very clean and t .32. I t it's in your schoolbag.33. I have a pencil, b I don't have a pen.34. She a wears a red skirt and white shoes.35. Do you often listen to the r in English?36. --- What do you think of his room?--- It's really t !37. --- Where is my English book?--- I t it's in your bag.38. I like comedies b I don't like thrillers.39. She a reads English every morning.40. Kangkang often listens to the r to learn English.三、单词拼写(根据中文提示拼写单词)（共20小题；共20分）41. We always keep our classroom clean and (整洁).42. I hope you can miss me when you (回想起) back the time.43. In spring, you can see beautiful flowers (到处) in our schoolyard.44. "Where's my schoolbag?" Gina (总是) asks.45. Mr. White likes to listen to the (收音机).46. Mr. Wang's house has been (整洁的) since the robot came.47. Mike t (认为) English is interesting.48. We shouldn't throw rubbish e (到处) to protect environment.49. When I have trouble, my teacher can (总是) give me some help.50. I learned a lot from TV programmes, (收音机) and newspapers.51. Eric's room is (整洁的).52. At the moment Mr. Fox (想) "I'm right."53. We shouldn't throw rubbish (扔垃圾) (到处) to protect the environment (保护环境).54. She (总是) wears a T-shirt.55. The man is talking over the (无线电广播).56. My bedroom is (整洁的).57. Mike (认为) English is interesting.58. Jim's books are (到处都是), on his bed, on the sofa and under the chair.59. He is (总是) in the library.60. The (广播) says that it is going to rain tomorrow.四、完形填空（共10小题；共15分）I'm Jenny. I 61 in a big community with my parents. My home is on the fifth 62 of a tall building. It's 63 apartment building. It has fifteen floors. There are many families 64 young children living here.There are 65 places(地点) to have fun (玩的开心) near my home. There 66 a big park, a library, a museum, a supermarket and many restaurants in this area. We can 67 games in the park. And we can buy all kinds of things in the 68 . Sometimes I go to the library to read books. It's really69 I like reading there.70 do you think of our community? Welcome to my home.61. A. live B. take C. come D. get62. A. street B. room C. building D. floor63. A. a B. an C. the D. /64. A. from B. with C. and D. of65. A. a lot B. lot of C. a lot of D. the lot of66. A. is B. are C. has D. have67. A. make B. play C. take D. get68. A. library B. restaurant C. bank D. supermarket69. A. tall B. bad C. quiet D. noisy70. A. What B. When C. Who D. Where五、阅读理解（共17小题；共34分）AIt is fine today. An old woman takes some potatoes to the market.The road is narrow(狭窄的) and the old woman walks carefully. She doesn't want to fall down (摔倒) and lose her potatoes.A young man comes and he rides a bike. He rides very fast. He hits(撞) the old woman. The old woman falls down and the potatoes are everywhere.But the young man doesn't say anything and rides away. The old woman is very angry and she says, "Come back, young man! You lost something."When the young man hears this, he stops and asks, "What did I lose?""You lost your manners," the old woman says.71. 下列哪项陈述是正确的?A. The road is not wide.B. The woman takes some milk.C. The young man walks very fast.D. The young man says "sorry" to the woman.72. 划线单词 "manners" 的中文意思是 " ".A. 零件B. 思想C. 好处D. 礼貌BTom is seven years old. He doesn't like school. He talks a lot, in class, and the teacher is angry with him. He is often kept in(被留下) after school.He doesn't like to do his homework, but he likes sports. He swims very well. He is the best swimmer in his class. He likes swimming so much that sometimes he forgets to go to school. Tom's father has an alarm clock. It's a nice clock. It sings in the morning to wake Tom up. “What sings in the clock?” Tom wonders. So Tom opens the clock and takes it to parts(拆了). But he can't put the parts back.73. The teacher is angry with Tom because .A. he is seven years oldB. he likes schoolC. he talks too much in classD. he swims well74. Tom is good at .A. his homeworkB. his school workC. swimmingD. waking up75. What does Tom do with(处理) the alarm clock?A. He wakes it upB. He sings wellC. He forgets itD. He takes it to parts76. Who has the alarm clock?A. TomB. Tom's fatherC. Tom's motherD. The story doesn't tell us77. What's the best title(标题) this story?A. A naughty(淘气) childB. An alarm clockC. Tom and his schoolD. Tom's DayCWelcome to Class 4, Grade 7. This is our classroom. There are forty-five small desks and chairs in the classroom. Twenty-three of them are for boys and twenty-one of them are for girls. There is a desk and a chair in the front of the classroom. They are for teachers. There is a big blackboard on the front wall and a blackboard on the back wall. There are two maps on the wall. One is a map of China and the other is a map of the world. There are some photos about our school life on the wall, too. There are some flowers by the windows. What a beautiful classroom it is! We all like it.78. The passage tells us something about .A. a schoolB. a classroomC. a libraryD. a house79. There are students in Class 4, Grade 7.A. forty-fiveB. forty-fourC. twenty-threeD. twenty-one80. Where is the desk for teachers?A. It is in the front of the classroom.B. It is at the back of the classroom.C. It is in the middle of the classroom.D. It is behind the classroom.81. There is (are) blackboard(s) and map(s) in the classroom.A. one; twoB. two; oneC. two; twoD. one; one82. The classroom of Class 4, Grade 7 is very .A. cleanB. smallC. newD. beautifulDThis is a beautiful park near my home. People like to go to the park after work. Some of them go to the park every day. Look! This is Mr. Smith. He is sitting on a chair and watching the children. Some children are playing the game of hide-and-seek(捉迷藏). Some boys are playing yo-yo. Lucy and Lily are standing under a tree. They are talking. There is a small river in the park. We can see some boats in the river. Some children are sitting in the boats with their fathers and mothers. Listen! A lot of birds(鸟) are singing in the trees. This is really a nice park. I come here to read English after school every day.83. like to go to the park.A. ChildrenB. Fathers and mothersC. Lucy and LilyD. People84. Mr. Smith is .A. playing hide-and-seekB. playing yo-yoC. is sitting and watching the childrenD. is singing85. Which one (哪一项) is right(正确的)?A. Lucy and Lily are playing hide-and-seek with other childrenB. Lucy and Lily go to the park only on SundayC. Lucy and Lily are talking under the treeD. Lucy and Lily live far from the park86. The writer(作者) can't see in the park.A. fishB. childrenC. womenD. men87. What's the writer doing?A. He is singingB. He is sitting in a boatC. He's playing a gameD. He's watching the people in the park六、阅读与表达(判断式)（共5小题；共10分）Look! This is my bedroom. There is a bed in the middle of the bedroom. There is a football under the bed. What's on the bed? Oh, it's my cat. There is a desk near the bed. There is a pencil box and four keys(钥匙) on the desk. Where is my bag? Oh, it's on the floor. And there are some books and an alarm clock (闹钟) on the bookcase.根据短文内容，判断正误，正确的为T，错误的为F。

2024-2025学年初中语文七年级上册同步课件第四单元14回忆我的母亲(样例1)

对“我”产生巨大影响的母亲逝 • 得到母亲去世的消息，我很悲痛。我爱
世了，文章字里
我母亲，特别是她勤劳一生……
行间流露出“我” • 我应该感谢母亲……
对母亲怎样的感情？找出文章中直接表现作者情
• 母亲现在离我而去了，我将永不能再见她一面了，这个哀痛是无法补救的……
感的关键词句。 • 愿母亲在地下安息！
里行间的对母亲的深情。
作者
朱德（1886－1976），字玉阶，四川仪陇
简介
人。伟大的马克思主义者，伟大的无产阶级革
命家、政治家、军事家，中国人民解放军的主
要缔造者之一，中华人民共和国的开国元勋。
其主要著作收入《朱德选集》。
写
朱德同志的母亲锺太夫人是一位普通的劳动
作
背妇女，她一生勤劳俭朴，宽厚仁慈，坚忍顽强，
感谢您的观看
列事件要典型，有一定的代表性。
读准字音
韶关（ sháo ）佃农（ diàn ）溺水（ nì ）祖籍（ jí ）和蔼（ ǎi ）不辍（chuò ）
仪陇（ lǒng ）妯娌（zhóuli ）私塾（ shú ）横蛮（hèng mán ）勉强（qiǎng ）管束（ shù ）
理解词义
景
并始终如一地支持儿子投身革命事业，是一位令
人尊敬的伟大母亲。1944年锺太夫人逝世。朱德
得知母亲逝世的消息后，怀着悲痛的心情，写了
这篇回忆性文章。
文体
回忆录
知
回忆录是一种用叙述、描写、资料编排等
识方法，追忆本人或本人所熟悉的人物过去的生
活经历和社会生活的叙事性文体。它可以记叙
人物一生的事迹，也可以讲述人物故事中的一

人教版七年级数学上册第四章同步测试题(含答案)

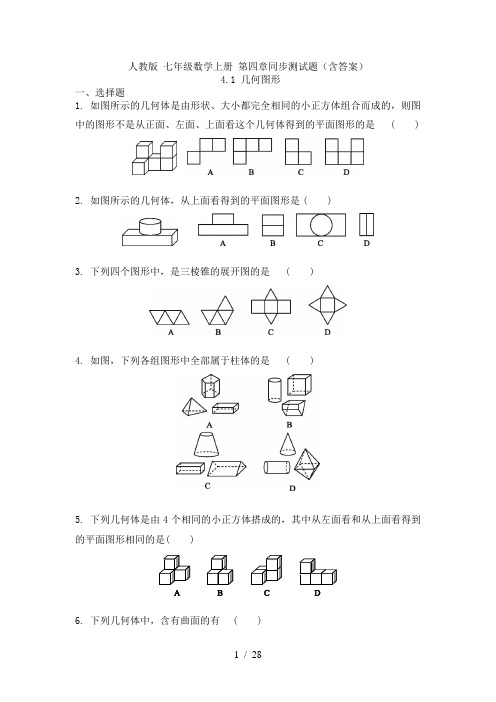
人教版七年级数学上册第四章同步测试题（含答案）4.1 几何图形一、选择题1. 如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的，则图中的图形不是从正面、左面、上面看这个几何体得到的平面图形的是()2. 如图所示的几何体，从上面看得到的平面图形是()3. 下列四个图形中，是三棱锥的展开图的是()4. 如图，下列各组图形中全部属于柱体的是()5. 下列几何体是由4个相同的小正方体搭成的，其中从左面看和从上面看得到的平面图形相同的是( )6. 下列几何体中，含有曲面的有()A.1个B.2个C.3个D.4个7. 圆柱是由长方形绕着它的一边所在的直线旋转一周得到的，那么如图所示的几何体是图中的哪一个图形绕着直线旋转一周得到的()8. 将如图所示的长方体的表面展开，则得到的平面图形不可能是图中的 ()9. 如图，给定的是一个纸盒的外表面，图中的几何体能由它折叠而成的是()10. 如果一个棱柱有18条棱，那么它的底面一定是()A.十八边形B.八边形C.六边形D.四边形二、填空题11. 如图，观察生活中的物体，根据它们所呈现的形状，填出与它们类似的立体图形的名称：(1)______；(2)______；(3)__________；(4)________．12. 苏轼的诗句“横看成岭侧成峰，远近高低各不同”说明的现象是.13. 如图所示的图形中，是棱柱的有______．(填序号)14. 如图所示的8个立体图形中，是柱体的有，是锥体的有，是球的有.(填序号)15. 如图所示是某几何体的展开图，那么这个几何体是.16. 如图，把下列实物图和与其对应的立体图形连接起来.三、解答题17. 如图，有一个外观为圆柱形的物体，它的内部构造看不到，当分别用一组平面沿水平方向(自上而下)和竖直方向(自左而右)截这个物体时，得到了如图所示的(1)(2)两组形状不同的截面，请你试着说出这个物体的内部构造.18. 如图，是长方体的展开图，将其折叠成一个长方体，那么:(1)与点N重合的点是哪几个?(2)若AG=CK=14 cm，FG=2 cm，LK=5 cm，则该长方体的表面积和体积分别是多少?图19. 如图①是三个直立于水平面上的形状完全相同的几何体(下底面为圆，单位:cm)，将它们拼成如图②所示的新几何体，求新几何体的体积(结果保留π).人教版七年级数学上册 4.1 几何图形同步课时训练-答案一、选择题1. 【答案】A2. 【答案】C3. 【答案】A4. 【答案】B5. 【答案】B6. 【答案】B7. 【答案】A8. 【答案】C9. 【答案】B10. 【答案】C[解析] 一个棱柱有18条棱，则这个棱柱是六棱柱，六棱柱的底面是六边形.二、填空题11. 【答案】(1)圆柱(2)圆锥(3)圆柱、圆锥的组合体(4)球[解析] 立体图形实际上是由物体抽象得来的．12. 【答案】观察同一个物体，由于方向和角度不同，看到的图形往往不同13. 【答案】②⑥14. 【答案】①②⑤⑦⑧④⑥③15. 【答案】圆柱16. 【答案】①-C，②-B，③-D，④-E，⑤-A 连线略三、解答题17. 【答案】解:这个物体的内部构造为:圆柱中间有一球形空洞.18. 【答案】解:(1)与点N重合的点是点H，J.(2)由AG=CK=14 cm，LK=5 cm，可得CL=CK-LK=14-5=9(cm)，所以长方体的表面积为2×(9×5+2×5+2×9)=146(cm2)，体积为5×9×2=90(cm3).19. 【答案】解:π×22×(4+6)+[π×22×(4+6)]=40π+20π=60π(cm3).答:新几何体的体积为60π cm3.4.2直线、射线、线段同步练习试题（一）一．选择题1．平面上有三点A、B、C，如果AB＝10，AC＝7，BC＝3，那么（）A．点C在线段AB上B．点C在线段AB的延长线上C．点C在直线AB外D．点C可能在直线AB上，也可能在直线AB外2．下列四个生产生活现象，可以用公理“两点之间，线段最短”来解释的是（）A．用两个钉子可以把木条钉在墙上B．植树时，只要定出两棵树的位置，就能使同一行树坑在一条直线上C．打靶的时候，眼睛要与枪上的准星、靶心在同一直线上D．为了缩短航程把弯曲的河道改直3．有下列生活、生产现象：①从A地到B地架设电线，总是尽可能沿着线段AB架设．②用两个钉子就可以把木条固定在墙上．③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线．④把弯曲的公路改直，就能缩短路程．其中能用“两点之间，线段最短”来解释的现象有（）A．①④B．②④C．①②D．③④4．已知点A，B，C在同一直线上，若AB＝20cm，AC＝30cm，点M、N分别是线段AB、AC中点，求线段MN的长是（）A．5cm B．5cm或15cm C．25cm D．5cm或25cm 5．已知点A，B，C为平面内三点，给出下列条件：①AC＝BC；②AB＝2BC；③AC ＝BC＝AB．选择其中一个条件就能得到“点C是线段AB中点”的是（）A．①B．③C．①或③D．①或②或③6．如图，点C是AB的中点，点D是BC的中点，下列结论：①CD＝AC﹣DB，②CD＝AB，③CD＝AD﹣BC，④BD＝2AD﹣AB，正确的有（）A．1个B．2个C．3个D．4个7．现实生活中“为何有人乱穿马路，却不愿从天桥或斑马线通过？”，请用数学知识解释图中这一现象，其原因（）A．两点之间，线段最短B．过一点有无数条直线C．两点确定一条直线D．两点之间线段的长度，叫做这两点之间的距离8．如图，某工厂有三个住宅区，A、B、C各区分别住有职工15人、20人、45人，且这三个区在一条大道上（A、B、C三点共线），已知AB＝1500m，BC＝1000m，为了方便职工上下班，该工厂打算从以下四处中选一处设置接送车停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（）A．A住宅区B．B住宅区C．C住宅区D．B、C住宅区中间D处9．老爷爷从家到超市有甲、乙、丙三条路可以选择，在不考虑其它因素的情况下，他选择了乙路前往，则其中蕴含着的数学道理是（）A．两点确定一条直线B．两点之间线段最短C．连结直线外一点与直线上各点的所有线段中，垂线段最短D．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线10．如图所示，某公司员工住在A，B，C三个住宅区，已知A区有2人，B区有7人，C区有12人，三个住宅区在同一条直线上，且AB＝150m，BC＝300m，D 是AC的中点．为方便员工，公司计划开设通勤车免费接送员工上下班，但因为停车位紧张，在A，B，C，D四处只能设一个通勤车停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠站应设在（）A．A处B．B处C．C处D．D处二．填空题11．如图所示是一段火车路线图，A、B、C、D、E是五个火车站，在这条线路上往返行车需要印制种火车票．12．点A到原点的距离为4，且位于原点的左侧，若一个点从A处向右移动2个单位长度，再向左移动7个单位长度，此时终点所表示的数为．13．如图，AE⊥AB于A点，DB⊥AB于B点，点P为线段AB上任意一点，若AE ＝2，DB＝4，AB＝8，则PE+PD的最小值是．14．曲桥是我国古代经典建筑之一，它的修建增加了游人在桥上行走的路程，有利于游人更好的观赏风光，如图，A、B两地间修建曲桥与修建直的桥相比，增加了桥的长度，其中蕴含的数学道理是．15．如图，建筑工人在砌墙时，经常用细线绳在墙的两端之间拉一条直的参照线，这样做的依据是．三．解答题16．如图所示，已知C、D是线段AB上的两个点，点M、N分别为AC、BD的中点．（1）若AB＝16cm，CD＝6cm，求AC+BD的长和M，N的距离；（2）如果AB＝m，CD＝n，用含m，n的式子表示MN的长．17．如图所示，把一根细线绳对折成两条重合的线段AB，点P在线段AB上，且AP：BP＝2：3．（1）若细线绳的长度是100cm，求图中线段AP的长；（2）从点P处把细线绳剪断后展开，细线绳变成三段，若三段中最长的一段为60cm，求原来细线绳的长．18．已知平面上点A，B，C，D（每三点都不在一条直线上）．（1）经过这四点最多能确定条直线．（2）如图这四点表示公园四个地方，如果点B，C在公园里湖对岸两处，A，D在湖面上，要从B到C筑桥，从节省材料的角度考虑，应选择图中两条路中的哪一条？如果有人想在桥上较长时间观赏湖面风光，应选择哪一条？为什么？19．已知如图，A，B，C三点在同一直线上，AB＝6，BC＝2．（1）已知点C在直线AB上，根据条件，请补充完整图形，并求AC的长；（2）已知点C在直线AB上，M，N分别是AB，BC的中点，根据条件，请补充完整图形，并求MN的长，直接写出MN与AC的长存在的数量关系；（3）已知点C在直线AB上，M，N分别是AC，BC的中点，根据条件，请补充完整图形，并求MN的长，直接写出MN与AB的长存在的数量关系．参考答案与试题解析一．选择题1．【解答】解：如图，在平面内，AB＝10，∵AC＝7，BC＝3，∴点C为以A为圆心，7为半径，与以B为圆心，3为半径的两个圆的交点，由于AB＝10＝7+3＝AC+BC，所以，点C在线段AB上，故选：A．2．【解答】解：A、根据两点确定一条直线，故本选项不符合题意；B、确定树之间的距离，即得到相互的坐标关系，故本选项不符合题意；C、根据两点确定一条直线，故本选项不符合题意；D、根据两点之间，线段最短，故本选项符合题意．故选：D．3．【解答】解：根据两点之间，线段最短，得到的是：①④；②③的依据是两点确定一条直线．故选：A．4．【解答】解：（1）当点C位于点B的右边时，MN＝（AC﹣AB）＝5cm，（2）当点C位于点A的左边时，MN＝（AC+AB）＝25cm故线段MN的长为5cm或25cm．故选：D．5．【解答】解：①点C在线段AB上，且AC＝BC，则C是线段AB中点故①不符合题意；②AB＝2BC，C不一定是线段AB中点故②不符合题意；③AC＝BC＝AB，则C是线段AB中点，故③符合题意．故选：B．6．【解答】解：∵点C是AB的中点，点D是BC的中点，∴AC＝BC＝AB，CD＝BD＝BC＝AC，∴①CD＝BC﹣DB＝AC﹣DB，正确；②CD＝BC＝AB，正确；③CD＝AD﹣AC＝AD﹣BC，正确；④BD＝AB﹣AD≠2AD﹣AB，错误．所以正确的有①②③3个．故选：C．7．【解答】解：现实生活中“为何有人乱穿马路，却不愿从天桥或斑马线通过？”，请用数学知识解释图中这一现象，其原因是两点之间，线段最短，故选：A．8．【解答】解：当停靠点在A区时，所有员工步行到停靠点路程和是：20×1500+45×2500＝142500m；当停靠点在B区时，所有员工步行到停靠点路程和是：15×1500+45×1000＝67500m；当停靠点在C区时，所有员工步行到停靠点路程和是：15×2500+20×1000＝57500m；当停靠点在D区时，设距离B区x米，所有员工步行到停靠点路程和是：15×（1500+x）+20x+45（1000﹣x）＝﹣10x+67500，由于k＝﹣10，所以，x越大，路程之和越小，∴当停靠点在C区时，所有员工步行到停靠点路程和最小．故选：C．9．【解答】解：图中三条路线，甲和丙是曲线，乙是线段，由两点间线段最短，∴乙最短，故选：B．10．【解答】解：BD＝（150+300）÷2﹣150＝75（m），以点A为停靠点，则所有人的路程的和＝7×150+12×（150+300）＝6450m，以点B为停靠点，则所有人的路程的和＝2×150+12×300＝3900m，以点C为停靠点，则所有人的路程的和＝2×（150+300）+7×300＝3000m，以点D为停靠点，则所有人的路程的和＝2×（150+300）÷2+7×75+12×（150+300）÷2＝3675m．故停靠点的位置应设在点C．故选：C．二．填空题11．【解答】解：图中线段有：AB、AC、AD、AE，BC、BD、BE，CD、CE、DE 共10条，∵每条线段应印2种车票，∴共需印10×2＝20种车票．故答案为：20．12．【解答】解：∵点A到原点的距离为4，且位于原点的左侧，∴点A表示的数为﹣4，∵一个点从A处向右移动2个单位长度，再向左移动7个单位长度，∴﹣4+2﹣7＝﹣9，故答案为：﹣9．13．【解答】解：过点D作DT⊥EA交EA的延长线于T，连接DE．∵AE⊥AB，DB⊥AB，DT⊥ET，∴∠B＝∠T＝∠BAT＝90°，∴四边形ABDT是矩形，∴BD＝AT＝4，AB＝DT＝8，∴ET＝AE+AT＝2+4＝6，∴DE＝＝＝10，∵PE+PD≥DE，∴PE+PD≥10，∴PE+PD的最小值为10．故答案为10．14．【解答】解：其中蕴含的数学道理是两点之间线段最短，故答案为：两点之间线段最短．15．【解答】解：建筑工人在砌墙时，经常用细线绳在墙的两端之间拉一条参照线，使垒的每一层砖在一条直线上，沿着这条线就可以砌出直的墙，则其中的道理是：两点确定一条直线．故答案为：两点确定一条直线．三．解答题16．【解答】解：（1）∵AB＝16cm，CD＝6cm，∴AC+BD＝AB﹣CD＝10cm，∴MN＝AB﹣（AM+BN）＝AB﹣（AC+BD）＝16﹣5＝11（cm）；（2）∵AB＝m，CD＝n，∴AC+BD＝AB﹣CD＝m﹣n，∴MN＝AB﹣（AM+BN）＝AB﹣（AC+BD）＝m﹣（m﹣n）＝．17．【解答】解：（1）∵AB＝100＝50，AP：BP＝2：3，∴AP＝20；（2）∵AP：BP＝2：3，∴设AP＝2x，BP＝3x，若一根绳子沿B点对折成线段AB，则剪断后的三段绳子中分别为2x，2x，6x，∴6x＝60，解得x＝10，∴绳子的原长＝2x+2x+6x＝10x＝100（cm）；若一根绳子沿A点对折成线段AB，则剪断后的三段绳子中分别为4x，3x，3x，∴4x＝60，解得x＝15，∴绳子的原长＝4x+3x+3x＝10x＝150（cm）；综上所述，绳子的原长为100cm或150cm．故答案为100cm或150cm．18．【解答】解：（1）经过这四点最多能确定6条直线：直线AB，直线AD，直线BC，直线CD，直线AC，直线BD，故答案为：6；（2）从节省材料的角度考虑，应选择图中路线2；如果有人想在桥上较长时间观赏湖面风光，应选择路线1，因为两点之间，线段最短，路线2比路线1短，可以节省材料；而路线1较长，可以在桥上较长时间观赏湖面风光．19．【解答】解：（1）如图，如图1，∵AB＝6，BC＝2．∴AC＝AB+BC＝8；如备用图1，AC＝AB﹣BC＝4．答：AC的长为8或4；（2）如图，∵M，N分别是AB，BC的中点，∴BM＝AB＝3，BN＝BC＝1，∴MN＝BM+BN＝3+1＝4，或MN＝BM﹣BN＝3﹣1＝2．答：MN的长为4或2；（3）如图，∵M，N分别是AC，BC的中点，∴MC＝AC＝4，NC＝BC＝1，∴MN＝MC﹣NC＝4﹣1＝34.3角同步练习试题（一）一．选择题1．如图，射线OA表示的方向是（）A．北偏东65°B．北偏西35°C．南偏东65°D．南偏西35°2．如图，∠AOC＝90°，OC平分∠DOB，且∠DOC＝22°36′，∠BOA度数是（）A．67°64′B．57°64′C．67°24′D．68°24′3．下列说法正确的是（）A．射线比直线短B．从同一点引出的两条射线所组成的图形叫做角C．若AP＝BP，则P是线段AB的中点D．两点之间的线段叫做这两点之间的距离4．下列语句错误的个数是（）①一个角的补角不是锐角就是钝角；②角是由两条射线组成的图形；③如果点C是线段AB的中点，那么AB＝2AC＝2BC；④连接两点之间的线段叫做两点的距离．A．4个B．3个C．2个D．1个5．按图1～图4的步骤作图，下列结论错误的是（）A．∠AOB＝∠AOP B．∠AOP＝∠BOPC．2∠BOP＝∠AOB D．∠BOP＝2∠AOP6．如图，用量角器度量∠AOB，可以读出∠AOB的度数为（）A．30°B．60°C．120°D．150°7．如图，小王从A处出发沿北偏东40°方向行走至B处，又从B处沿南偏东60°方向行走至C处，则∠ABC等于（）A．90°B．100°C．110°D．120°8．如图，将一副三角板按不同位置摆放，其中α和β互为余角的是（）A．B．C．D．9．如果∠1与∠2互补，∠2与∠3互余，那么∠1与∠3的关系是（）A．∠1＝90°+∠3 B．∠3＝90°+∠1 C．∠1＝∠3 D．∠1＝180°﹣∠310．为防止森林火灾的发生，会在森林中设置多个观测点，如图，若起火点M 在观测台B的南偏东46°的方向上，点A表示另一处观测台，若AM⊥BM，那么起火点M在观测台A的（）A．南偏东44°B．南偏西44°C．北偏东46°D．北偏西46°二．填空题11．若两个角互补，且度数之比为3：2，求较大角度数为．12．若∠A＝59.6°，则它的余角为°′．13．将一副三角板按如图方式摆放在一起，且∠1比∠2大20°，则∠1的度数等于．14．如图，点C在点B的北偏西60°的方向上，点C在点A的北偏西30°的方向上，则∠C等于度．15．如图，点A在点O的北偏西60°的方向上，点B在点O的南偏东20°的方向上，那么∠AOB的大小为°．三．解答题16．如图所示，O为直线上的一点，且∠COD为直角，OE平分∠BOD，OF平分∠AOE，∠BOC+∠FOD＝117°，求∠BOE的度数．17．如图，已知∠AOB＝128°，OC平分∠AOB，请你在∠COB内部画射线OD，使∠COD和∠AOC互余，并求∠COD的度数．18．已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．（1）如图①，当∠BOC＝40°时，求∠DOE的度数；（2）如图②，当射线OC在∠AOB内绕O点旋转时，OD，OE始终是∠AOC与∠BOC的平分线．则∠DOE的大小是否发生变化，说明理由；（3）当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，OD，OE仍始终是∠AOC与∠BOC的平分线，直接写出∠DOE的度数（不必写过程）．19．如图①，点O为直线AB上一点，过点O作射线OC，将一直角三角板如图摆放（∠MON＝90°）．（1）若∠BOC＝35°，求∠MOC的大小．（2）将图①中的三角板绕点O旋转一定的角度得图②，使边OM恰好平分∠BOC，问：ON是否平分∠AOC？请说明理由．（3）将图①中的三角板绕点O旋转一定的角度得图③，使边ON在∠BOC的内部，如果∠BOC＝50°，则∠BOM与∠NOC之间存在怎样的数量关系？请说明理由．参考答案与试题解析一．选择题1．【解答】解：射线OA表示的方向是南偏东65°，故选：C．2．【解答】解：∵OC平分∠DOB，∴∠DOC＝∠BOC＝22°36′．∵∠AOC＝∠AOB+∠BOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣22°36′＝67°24′．故选：C．3．【解答】解：A．射线和直线不可以比较长短，原说法错误，故本选项不符合题意；B．从同一点引出的两条射线所组成的图形叫做角，原说法正确，故本选项符合题意；C．若点P在线段AB上，AP＝BP，则P是线段AB的中点，原说法错误，故本选项不符合题意；D．两点之间的线段的长度叫做这两点之间的距离，原说法错误，故本选项不符合题意；故选：B．4．【解答】解：①直角的补角是直角，故原说法错误；②角是由有公共的端点的两条射线组成的图形，故原说法错误；③如果点C是线段AB的中点，那么AB＝2AC＝2BC，说法正确；④连接两点之间的线段的长度叫做两点的距离，故原说法错误．故错误的个数有①②④共3个．故选：B．5．【解答】解：∵OP是∠AOB的平分线，∴∠AOB＝2∠AOP＝2∠BOP，∠AOP＝∠BOP＝∠AOB，∴选项A、B、C均正确，选项D错误．故选：D．6．【解答】解：看内圈的数字可得：∠AOB＝120°，故选：C．7．【解答】解：如图：∵小王从A处沿北偏东40°方向行走至点B处，又从点B处沿南偏东60°方向行走至点C处，∴∠DAB＝40°，∠CBE＝60°，∵向北方向线是平行的，即AD∥BE，∴∠ABE＝∠DAB＝40°，∴∠ABC＝∠ABE+∠EBC＝40°+60°＝100°．故选：B．8．【解答】解：A、α和β互余，故本选项正确；B、α和β不互余，故本选项错误；C、α和β不互余，故本选项错误；D、α和β不互余，故本选项错误．故选：A．9．【解答】解：∵∠1+∠2＝180°∴∠1＝180°﹣∠2又∵∠2+∠3＝90°∴∠3＝90°﹣∠2∴∠1﹣∠3＝90°，即∠1＝90°+∠3．故选：A．10．【解答】解：如图：因为AM⊥BM，所以∠2+∠3＝90°，因为南北方向的直线平行，所以∠2＝46°，∠1＝∠3，所以∠3＝90°﹣∠2＝90°﹣46°＝44°，所以∠1＝44°，所以起火点M在观测台A的南偏西44°，故选：B．二．填空题11．【解答】解：因为两个角的度数之比为3：2，所以设这两个角的度数分别为（3x）°和（2x）°．根据题意，列方程，得3x+2x＝180，解这个方程，得x＝36，所以3x＝108．即较大角度数为108°．故答案为108°．12．【解答】解：∵∠A＝59.6°，∴∠A的余角为90°﹣59.6°＝30.4°＝30°24'，故答案为30；24．13．【解答】解：设∠2为x，则∠1＝x+20°；根据题意得：x+x+20°＝90°，解得：x＝35°，则∠1＝35°+20°＝55°；故答案为：55°．14．【解答】解：如图：根据题意可得：∠1＝60°，∠2＝30°，∵AE∥DB∥CF，∴∠BCF＝∠1＝60°，∠ACF＝∠2＝30°，∴∠ACB＝30°．故答案为：30．15．【解答】解：如图，∵点A在点O北偏西60°的方向上，∴OA与西方的夹角为90°﹣60°＝30°，又∵点B在点O的南偏东20°的方向上，∴∠AOB＝30°+90°+20°＝140°．故答案为：140．三．解答题16．【解答】解：设∠BOE＝α°，∵OE平分∠BOD，∴∠BOD＝2α°，∠EOD＝α°．∵∠COD＝∠BOD+∠BOC＝90°，∴∠BOC＝90°﹣2α°．∵OF平分∠AOE，∠AOE+∠BOE＝180°，∴∠FOE＝∠AOE＝（180°﹣α°）＝90°﹣α°，∴∠FOD＝∠FOE﹣∠EOD＝90°﹣α°﹣α°＝90°﹣α°，∵∠BOC+∠FOD＝117°，∴90°﹣2α°+90°﹣α°＝117°，∴α＝18，∴∠BOE＝18°．17．【解答】解：作OD⊥OA，则∠COD和∠AOC互余，如图所示．∵∠AOB＝128°，OC平分∠AOB，∴∠AOC＝∠AOB＝64°，∵∠COD和∠AOC互余，∴∠COD＝90°﹣∠AOC＝26°．18．【解答】解：（1）如图，∠AOC＝90°﹣∠BOC＝50°，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC＝25°，∠COE＝∠BOC＝20°，∴∠DOE＝∠COD+∠COE＝45°；（2）∠DOE的大小不变，理由是：∠DOE＝∠COD+∠COE＝∠AOC+∠BOC＝（∠AOC+∠BOC）∠AOB ＝45°；（3）∠DOE的大小分别为45°和135°，如图3，则∠DOE为45°；如图4，则∠DOE为135°．分两种情况：如图3所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC，∠COE＝∠BOC，∴∠DOE＝∠COD﹣∠COE＝（∠AOC﹣∠BOC）＝45°；如图4所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC，∠COE＝∠BOC，∴∠DOE＝∠COD+∠COE＝（∠AOC+∠BOC）＝×270°＝135°．19．【解答】解：（1）∵∠MON＝90°，∠BOC＝35°，∴∠MOC＝∠MON+∠BOC＝90°+35°＝125°．（2）ON平分∠AOC．理由如下：∵∠MON＝90°，∴∠BOM+∠AON＝90°，∠MOC+∠NOC＝90°．又∵OM平分∠BOC，∴∠BOM＝∠MOC．∴∠AON＝∠NOC．∴ON平分∠AOC．（3）∠BOM＝∠NOC+40°．理由如下：∵∠CON+∠NOB＝50°。

人教部编版七年级历史上册同步知识点归纳--第四课夏商周的更替

第四课夏商周的更替
年，禹建立夏朝，这是我国历史上的第一个王朝。

我国漫长的原始社会结束，奴隶社会开始了。

2.禹死后，启继承父位，成为夏朝的第二代国王。

从此，世袭制代替了禅让制，“公天下”变成了家天下。

3. 夏朝的建立，标志着我国早期国家的产生。

4.夏朝的暴君是桀
商朝为殷商。

7. 商朝最后一个暴君是：商纣王
9.武王伐纣中商朝灭亡的决定性战役是牧野之战，商纣自焚而死。

10.西周的众多诸侯是通过分封制产生的。

周天子把土地和平民，分给亲属、功臣等，封他们为诸侯。

诸侯必须服从周天子的命令，向天子交纳贡品，平时镇守疆土，战时带兵随从天子作战。

11.
15.
周平王东迁洛阳，史称东周。

东周分为春秋和战国两个时期。

17.夏、商、西周三朝灭亡的共同原因有哪些？都是由于国君暴虐无道，统治残暴、腐败，失去民心。

18.从夏朝和商朝灭亡中我们能得什么启示？得民心者得天下，失民心者失天下；得道者多助，失道者寡助。

概括：夏、商、周的更替：。

2019秋北师大版深圳专用数学七年级上册同步分层训练第四章专题训练(四)基本平面图形中的三种思想方法含答案

专题训练(四) 基本平面图形中的三种思想方法► 类型一分类讨论思想1．已知∠AOB ＝70°，以O 为端点作射线OC ，使∠AOC ＝42°，则∠BOC 的度数为( ) A ．28° B ．112° C ．28°或112° D ．68°2．已知A ，B ，C 是直线l 上的三点，线段AB ＝6 cm ，且AB ＝12AC ，则BC ＝______________．3．已知A ，B ，C 三点在同一条直线上，M ，N 分别为线段AB ，BC 的中点，且AB ＝60，BC ＝40，则MN 的长为__________．4．平面上有三个点，过其中任意两个点画直线，一共可以画几条直线？5．已知∠AOB ＝60°，∠BOC ＝20°，求∠AOC 的度数．6．已知线段AB ＝10 cm ，直线AB 上有一点C ，且BC ＝2 cm ，D 是线段AB 的中点，求线段DC 的长．7．已知∠BOC在∠AOB的外部，OE平分∠AOB，OF平分∠BOC，OD平分∠AOC，∠AOE＝30°，∠BOD＝20°，试求∠COF的度数．8．[2017·宜黄县月考]有两根木条，一根长8 cm，一根长10 cm，将它们的一端重合，放在同一条直线上，试求此时两根木条的中点之间的距离．► 类型二方程思想9．如图4－ZT －1，已知AC ＝56CB ，AD ＝14CB ，CD 的长为7，求AB 的长．图4－ZT －110．如图4－ZT －2，B ，C 两点把线段AD 分成2∶5∶3的三部分，M 为AD 的中点，BM ＝6 cm ，求CM 和AD 的长．图4－ZT －211．如图4－ZT－3，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠COD＝18°，求∠AOC的度数．图4－ZT－312．如图4－ZT－4，∠AOC，∠BOD都是直角，∠AOB∶∠AOD＝2∶11，求∠AOB与∠BOC的度数．图4－ZT－4►类型三整体思想13．已知：如图4－ZT－5，OM平分∠AOB(∠AOB<180°)，ON平分∠BOC.图4－ZT－5(1)当∠AOC＝90°，∠BOC＝60°时，∠MON＝________°；(2)当∠AOC＝80°，∠BOC＝60°时，∠MON＝________°；(3)当∠AOC＝80°，∠BOC＝50°时，∠MON＝________°；(4)猜想：不论∠BOC的度数是多少，∠MON的度数总等于________的度数的一半．14．如图4－ZT－6，点C在线段AB上，AC＝8 cm，BC＝6 cm，M，N分别是AC，BC的中点．(1)求线段MN的长；(2)若C为线段AB上任意一点，满足AC＋BC＝a cm，其他条件不变，你能猜想MN的长度吗？并说明理由；(3)若点C在线段AB的延长线上，且满足AC－BC＝b cm，M，N分别为AC，BC的中点，你能猜想MN 的长度吗？请画出图形，写出你的结论，并说明理由．图4－ZT－6详解详析1．C2．6 cm 或18 cm [解析] 分两种情况讨论：①当点B 在线段AC 上时，由AB ＝6 cm ，且线段AB ＝12AC ，得AC ＝2AB ＝12 cm.由线段的和差，得BC ＝AC －AB ＝12－6＝6(cm)；②当点B 在线段AC 的反向延长线上时，由AB ＝6 cm ，且线段AB ＝12AC ，得AC ＝2AB ＝12 cm.由线段的和差，得BC ＝AC ＋AB ＝12＋6＝18(cm)．故答案为6 cm 或18 cm.3．50或10 [解析] (1)当点C 在线段AB 的延长线上时，如图①. 因为M ，N 分别为AB ，BC 的中点，所以BM ＝12AB ＝30，BN ＝12BC ＝20.所以MN ＝50.(2)当点C 在线段AB 上时，如图②.同理可知BM ＝30，BN ＝20，所以MN ＝10. 故MN 的长为50或10.4．[解析] 本题没有指明三点的具体位置，因此要考虑两种不同的情况．解：分两种情形讨论：(1)当三点不在同一条直线上时，过每两点可画1条直线，一共可画3条直线(如图①)； (2)当三点在同一直线上时，只能画1条直线(如图②)．故一共可以画1条或3条直线． 5．解：分两种情形讨论：(1)当∠BOC 在∠AOB 内部时，∠AOC ＝∠AOB －∠BOC ＝60°－20°＝40°； (2)当∠BOC 在∠AOB 外部时，∠AOC ＝∠AOB ＋∠BOC ＝60°＋20°＝80°. 故∠AOC 的度数为40°或80°.6．[解析] 由于点C 相对于A ，B 两点的位置关系不确定，所以要进行分类讨论，然后再求解．解：分两种情形讨论：(1)当点C 在线段AB 的延长线上时，如图①所示．因为D 是线段AB 的中点，所以DB ＝12AB ＝12×10＝5(cm)．所以DC ＝DB ＋BC ＝5＋2＝7(cm)． (2)当点C 在线段AB 上时，如图②所示．因为D 是线段AB 的中点，所以DB ＝12AB ＝12×10＝5(cm)．所以DC ＝DB －BC ＝5－2＝3(cm)．故线段DC 的长为7 cm 或3 cm.7．[解析] 当题目中没有给出具体的图形，而根据题设又有可能出现多种情况时，就应不重不漏地分情况加以讨论．本例∠AOB 既可大于∠BOC ，也可小于∠BOC ，故应分这两种情况进行求解．解：分两种情形讨论：(1)当∠AOB 大于∠BOC 时，如图①所示．由题意易得∠BOE ＝∠AOE ＝30°. 因为∠BOD ＝20°，所以∠DOE ＝10°，∠AOD ＝40°.因为∠COD ＝∠AOD ＝40°，∠BOD ＝20°，所以∠BOC ＝20°. 因为OF 平分∠BOC ，所以∠COF ＝12∠BOC ＝12×20°＝10°.(2)当∠AOB 小于∠BOC 时，如图②所示．由题意易得∠BOE ＝∠AOE ＝30°. 因为∠BOD ＝20°，所以∠AOD ＝80°.因为∠COD ＝∠AOD ＝80°，∠BOD ＝20°，所以∠BOC ＝100°. 因为OF 平分∠BOC ，所以∠COF ＝12∠BOC ＝12×100°＝50°.故∠COF 的度数为10°或50°.8．解：设木条AB ＝8 cm ，木条CD ＝10 cm ，E 为AB 的中点，F 为CD 的中点．(1)如图①，当CD 的端点C 接在AB 的端点B 处(此时点B 与点C 重合)，且点D 在AB 的延长线上时，AD ＝AB ＋CD ＝18 cm.所以EF ＝12AB ＋12BD ＝12(AB ＋BD )＝12AD ＝12×18＝9(cm)；(2)如图②，当AB 的端点B 在CD 的端点D 处(此时点B 与点D 重合)，且点A 在CD 上时，EF ＝12CD －12AB ＝12(CD －AB )＝12×(10－8)＝1(cm)．综上可知，两根木条的中点之间的距离为1 cm 或9 cm. 9．解：设CB ＝x ，则AC ＝56x ，AD ＝14x .因为AC －AD ＝CD ，所以56x －14x ＝7，解得x ＝12.这时AC ＝56×12＝10，所以AB ＝AC ＋CB ＝22.10．解：设AB ＝2x cm ，BC ＝5x cm ，CD ＝3x cm ，所以AD ＝AB ＋BC ＋CD ＝10x cm.因为M 为AD 的中点，所以AM ＝MD ＝12AD ＝5x cm. 所以BM ＝AM －AB ＝5x －2x ＝3x (cm)．因为BM ＝6 cm ，所以3x ＝6，解得x ＝2.故CM ＝MD －CD ＝5x －3x ＝2x ＝2×2＝4(cm)，AD ＝10x ＝10×2＝20(cm)．11．[解析] 此题比较复杂，难以理清角之间的关系，而通过设未知数，寻找相等关系，运用方程知识，则问题可迅速获解．解：设∠AOC 的度数为x °，则∠BOC 的度数为(2x )°，∠AOB 的度数为(3x )°.因为OD 平分∠AOB ，所以∠AOD ＝(32x )°. 根据∠AOD －∠AOC ＝∠COD ，列方程32x －x ＝18，解得x ＝36.即∠AOC 的度数为36°. 12．解：设∠AOB ＝2x °，则∠AOD ＝11x °.根据题意，得2x ＋90＝11x ，解得x ＝10.所以∠AOB ＝20°.所以∠BOC ＝90°－20°＝70°.13．(1)45 (2)40 (3)40 (4)∠AOC14．解：(1)因为M ，N 分别是AC ，BC 的中点，所以MC ＝12AC ＝12×8＝4(cm)，NC ＝12BC ＝12×6＝3(cm)．所以MN ＝MC ＋NC ＝4＋3＝7(cm)．(2)能．猜想：MN ＝12a cm.理由如下：因为M ，N 分别是AC ，BC 的中点，所以MC ＝12AC ，NC ＝12BC . 所以MN ＝MC ＋NC ＝12AC ＋12BC ＝12(AC ＋BC )＝12a cm. (3)能．画图如下：结论：MN ＝12b cm. 理由如下：因为M ，N 分别是AC ，BC 的中点，所以MC ＝12AC ，NC ＝12BC . 所以MN ＝MC －NC ＝12AC －12BC ＝12(AC －BC )＝12b cm.。

数学课件华东师大版七年级上册同步教学第4章图形的初步认识第五节最基本的图形

【点拨】因为 E 为 DB 的中点，且 EB＝3，所以 BD＝2BE＝6. 因为线段 AB＝20，C 为 AB 的中点，所以 CB＝AC＝10，所以 CD＝BC－BD＝10－6＝4.
9．【中考·日照】如图，已知 AB＝8 cm，BD＝3 cm，C 为 AB 的中点，则线段 CD 的长为____1___题
16 见习题
17 见习题
答案显示
1．线段的长短比较方法： (1)度量法：分别度量出每条线段的__长__度____，再按长度的大小，
比较线段的长短，线段的长短关系和它们__长__度____的大小关系是一致的．
(2)叠合法：比较两条线段 AB，CD 的长短，可将线段 AB 放到线段 CD 上，点 A 和点 C 重合，观察另外两个端点 B，D 的位置，如果点 B 和点 D 重合，则_A__B_＝__C_D_____；如果点 D 在线段 AB 内部，则__A_B__>_C_D_______；如果点 D 在线段 AB 外部，则___A__B_<_C_D______．
3．经过两点有___一_____条直线，并且只有___一_____条直线．即两点确定___一_____条直线．
1．下列表示方法不正确的是( B )
2．下列图形中直线 AB，线段 CD，射线 EF 不可能相交的是( A )
3．如图所示，下列说法错误的是( D ) A．直线 AB 经过点 C B．点 D 不在直线 AC 上 C．点 C 在线段 AB 的延长线上 D．点 A 在线段 BC 的延长线上
【点拨】因为 C 为 AB 的中点，AB＝8 cm，所以 BC＝12AB＝12×8＝4(cm)．因为 BD＝3 cm，所以 CD＝BC－BD＝4－3＝1(cm)．
10．按要求完成下列任务．实践与操作：画线段 AB，并延长 AB 至 C，使 BC＝2AB，取 AC 的中点 D. 推理与计算：若线段 CD＝9，求线段 BD 的长．解：如图所示．因为点 D 是 AC 的中点，CD＝9，所以 AC＝2CD＝18，因为 BC＝2AB，所以 BC＝12，所以 BD＝BC－CD＝12－9＝3.

2021—2022学年人教新目标七年级英语上册Unit 4 同步练习及答案

Unit 4 Section A (1a-2d)Ⅰ.用方框中所给的介词填空under, of, in, about, at1.What’s this English?2.Mimi is the name my cat.3.Hi, I’m Cindy. What you?4.E-mail me 52486@.5.—Where is my ball, Dad?—Is it your bed?Ⅱ.根据句意及汉语提示完成句子6.I (认为) your schoolbag is on your bed.7.—Where is my pen, Mom?—It’s (在……下) the computer game.8.In the (房间), you can find your notebook and pencil box.9.— (在哪里) is your English book?—It’s in my schoolbag.10.A computer is (在……上) a table in the school library. Ⅲ.用括号内所给单词的适当形式填空11.They are my friends. (they) names are Jack and Mike.12.—Where are the (table)?—Oh, they are in the next room.13.These are our (bed).They are new.14.—Where (be) our English teacher?—Oh, she is in our classroom.15.I have two (dictionary) at school.Ⅳ.根据图片提示完成句子16.You can see a in the picture.17.This is not my .18.The is blue.19.It is Jim’s .20.I found a in the classroom.21.Is the yours?22.The is round(圆的).23.Where’s the ?Ⅴ.根据汉语提示完成句子24.—Where’s the schoolbag?Is it (在桌子下面)?—No, it isn’t. It is on the table.25.—Where are the books?Are they on the sofa?—No, they aren’t.They are (在床上).26.—Where are the keys?Are they (在你的书包里)? —No. They are on the sofa.27. (快点儿), Mike! We are late(迟的).28. (我认为) his book is (在书柜里). Ⅵ.按要求完成下列各题,每空一词29.The computer is on the desk.(改为一般疑问句) the computer the desk?30.His keys are in the bag.(对画线部分提问) his keys?31.His hat is on his head.(改为复数句)Their hats on .32.I think the ruler is hers.(改为否定句)I think the ruler hers.33.Is it in your bag?(作否定回答) , it .Ⅶ.阅读理解I’m Linda.Welcome to my room.My school ID card and my schoolbag are on the sofa.What are those in the bookcase? Oh, they are my tape player and some tapes.My name is Jack.This is my room.Look! My books are on the sofa.My blue jacket is on the bed.In the bookcase is my brother John’s dictionary.Where is my pencil box? Oh, it is on the chair.Hi, I’m Sally.What can you see in my room? My computer is on the desk.The CDs are in the bookcase.What are those under the bed? Oh, they are three baseballs.They are my sister Alice’s. ( )34.Where is Linda’s tape player?A.On the sofa.B.On the desk.C.In the bookcase.( )35.Jack’s jacket is .A.blackB.redC.blue( )36.The underlined word “it” refers to .A.the bedroomB.the jacketC.the pencil box( )37.What is NOT in Sally’s room?A.Her bookcase.B.Three baseballs.C.Her computer games.( )38.What’s the best title(标题) of this passage?A.Linda’s roomB.My roomC.My friendⅧ.完形填空I’m Linda. This 39 my room. 40 a nice, big room.Some things are 41 the room.The TV 42 computer game are on the table. 43 my schoolbag? It isn’t on the table.Oh!It’s on the bed.My pencils aren’t on the bed.My pencils are on the desk(书桌). Where’s 44　watch? It’s on the desk, 45　.Are my key and ID 46 on the desk? No, they 47　.Theyare on my dictionary.It’s 48 English-Chinese dictionary.( )39.A.is B.am C.are( )40.A.It’s B.They’re C.I’m( )41.A.on B.of C.in( )42.A.of B.and C.for( )43.A.What’s B.How C.Where’s( )44.A.my B.I C.me( )45.A.to B.too C.two( )46.A.book B.pen C.card( )47.A.isn’t B.aren’t C.am not( )48.A.an B.a C.theⅨ.语篇填空通读下面的短文,然后在空白处填入1个适当的单词或括号内单词的正确形式。

人教版七年级上册英语Unit4 同步复习(含答案)

知识图谱Unit 4 Where’s my schoolbag?知识精讲一、必背词汇where /weə/ adv. 在哪里；到哪里table /'teibl/ n. 桌子bed /bed/ n. 床bookcase /'bukkeis/ n. 书架；书柜sofa /'səufə/ n. 沙发chair /tʃeə/ n. 椅子on /ɔn/ prep. 在.......上under /'ʌndə/ prep. 在.......下come /kʌm/ v. 来；来到desk /desk/ n. 书桌think /θiŋk/ n. 认为；想；思考room /ru:m/ n. 房间their /ðeə/ pron. 他（她、它）们的hat /hæt/ n. 帽子head /hed/ n. 头know /nəu/ v. 知道；了解radio /'reidiəu/ n. 收音机；无线电广播clock /klɔk/ n. 时钟tape /teip/ n. 磁带；录音带；录像带player /pleiə/ n.播放机tape player 录音机model /'mɔdl/ n. 模型plane /plein/ n. 飞机tidy /'taidi/ adj.整洁的；井井有条的but /bʌt/ conj. 但是our /'auə/ pron. 我们的everywhere /'evriweə/ adv. 处处；到处；各地always /'ɔ:lweiz/ adv. 总是二、重点词汇1. think verb & noun /θɪŋk/1). verb. to believe something or have an opinion or idea 相信；觉得；思考例句：I don't think Emma will get the job.我认为埃玛不会获得这份工作。

七年级_上_Unit4同步测试

1. There are some birds ____ the sky.
2. Shall we meet ____ the bus stop?
3. My best friend sits ____ me. He often helps me.
4. 76 is ____ 75 and 77.
5． I don't want to fall ____ others.
She is looking at the picture. Her father and mother are in the school. They work hard.
1． Is there only one room in Kate's house? ____.
A． Yes, there is
A． have
B． has
C． there is
D． there are
10． There ____ an orange and two apples on the table.
A． are
B． has
C． is
D． have
11． I find there ____ no pencils in my pencil case.
B． on
C． at
14． There isn't a ____ in the classroom.
D． under
◎
A． child
B． children
C． people
D． teachers
45
15． Look at the picture ____ the right.
A． in
B． on

第04讲探索与表达规律(6类热点题型讲练)(原卷版)-七年级数学上册同步学与练(北师大版)

第04讲探索与表达规律(6类热点题型讲练)1.探索运用符号表示数字规律和图形规律的方法.2.提高观察图形、探索规律的能力，培养创新意识.知识点01规律探究常见的数字规律规律总结数列形式21n -1，3，5，7，9，···，21n -2n 2，4，6，8，10，···，2n 13+n 4，7，10，13，16，···，13+n 13-n 2，5，8，11，14，···，13-n n 22，4，8，16，32，···，n 212+n 3，5，9，17，33，···，12+n 21n +2，5，10，17，26，···，21n +21n -0，3，8，15，24，···，21n -(1)n x -x -，x +，x -，x +，x -，x +，···，(1)n x-1(1)n x+-x +，x -，x +，x -，x +，x -，···，1(1)n x+-(1)2n n +1，3，6，10，15，21，···，(1)2n n +斐波那契数列1，1，2，3，5，8，13，…，从第三个数开始每个数等于与它相邻的前两个数之和知识点02规律探究方法总结1.规律探究的核心是找出每个数与对应的位次（即n ）之间的关系；2.若数列为分数数列，则分子分母分开找规律；3.若数列是正负交替排列，则在答案前加上n )1(-；若数列是负正交替排列，则在答案前加上1)1(+-n ；4.若是选择题，则可以用代值法，再利用排除法选出正确答案即可.知识点03高斯求和定理2)1(2)(14321nn n n ⋅+=⨯+=+-+⋅⋅⋅++++项数末项首项.题型01数字类规律探索之排列问题【典例1】（2023·浙江衢州·校考一模）观察下列数据：0，3，8，15，24，…，它们是按一定规律排列的，依照此规律，第201个数据是（）A ．40400B ．40040C ．4040D ．404【变式1】（2022春·黑龙江哈尔滨·六年级校考期中）一组数据x ，23x -，35x ，47x -，59x …请按这种规律写出第十个数是．【变式2】（2022秋·浙江金华·七年级校考期中）从3开始的连续奇数按右图的规律排列，其余位置数字均为0．（1）第5行第10列的数字是．（2）数字2023在图中的第行，第列．题型02数字类规律探索之末尾数字问题【典例2】（2022秋·江苏连云港·七年级校考阶段练习）观察下列算式：031=，133=，239=，3327=，4381=，53243=，63729=，732187=…归纳各计算结果中个位数字的规律，可得20033的个位数字是（）A ．1B ．3C ．9D ．7【变式1】（2023春·江苏南京·七年级校考阶段练习）观察下列算式：①2(1)(1)1x x x -+=-；②23(1)(1)1x x x x -++=-；③324(1)(1)1x x x x x -+++=-寻找规律，并判断(2011)(2017)222221++⋯+++的值的末位数字为（）A ．1B ．3C ．5D ．7【变式2】（2023春·江苏泰州·七年级统考期中）发现规律解决问题是常见解题策略之一．已知数5555551234529a =++++++ ，则这个数a 的个位数为（）A ．3B ．4C ．5D ．6【变式3】（2023春·江苏连云港·七年级统考期末）生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n 来表示，即：122=，224=，328=，4216=，5232=，……，请你推算123452023222222+++++⋅⋅⋅⋅⋅⋅+的个位数字是（）A ．8B ．6C ．4D ．2题型03数字类规律探索之新运算问题【典例3】（2022·湖南株洲·统考二模）定义一种关于整数n 的“F ”运算：（1）当n 是奇数时，结果为35n +；（2）当n 是偶数时，结果是2k n （其中k 是使2kn是奇数的正整数），并且运算重复进行．例如：取58n =，第一次经F 运算是29，第二次经F 运算是92，第三次经F 运算是23，第四次经F 运算是74，……；若9n =，则第2020次运算结果是（）A ．1B ．2C ．7D ．8【变式1】（2022秋·江苏扬州·七年级校考阶段练习）a 是不为2的有理数，我们把22a-称为a 的“哈利数”．如：3的“哈利数”是2223=--，2-的“哈利数”是()21222=--，已知14a =，2a 是1a 的“哈利数”，3a 是2a 的“哈利数”，4a 是3a 的“哈利数”，．．．，依此类推，则2022a =（）A ．4B ．1-C ．23D ．32【变式2】（2023秋·全国·七年级专题练习）已知整数1a ，2a ，3a ，4a ，……满足下列条件：10a =，211a a =-+，321a a =-+，431a a =-+…，以此类推，则6a 的值为，2022a 的值为题型04数字类规律探索之等式问题【典例4】（2022秋·江西九江·七年级统考期中）观察下面的变形规律：111122=-⨯；1112323=-⨯；1113434=-⨯；解答下面的问题：(1)若n 为正整数，请你猜想()11n n =+______；(2)计算111112233420222023+++⋯⋯+⨯⨯⨯⨯．(3)计算；111124466820202022+++⋯⋯+⨯⨯⨯⨯．【变式1】（2022秋·湖南永州·七年级校考期中）观察算式：()()()132153174131351357.,222,+⨯+⨯+⨯+=++=+++=按规律填空：135799+++++=．【变式2】（2023春·安徽合肥·七年级校考期末）观察算式：①213142⨯+==；②224193⨯+==；③2351164⨯+==；④2461255⨯+==；⋯，根据你发现的规律解决下列问题：(1)写出第5个算式：______；(2)写出第n 个算式：______；(3)计算：111111111324351820⎛⎫⎛⎫⎛⎫⎛⎫+⨯++⨯⨯+ ⎪ ⎪⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭．题型05图形类规律探索之数字问题【典例5】（2022秋·湖北黄冈·七年级校考阶段练习）如图，根据图形中数的规律，可推断出a 的值为（）A ．128B ．216C ．226D ．240【变式1】（2023春·贵州毕节·七年级统考期末）根据图中数字的规律，若第n 个图中A B C D ++-的值为196，则n =（）A ．12B ．13C ．14D ．15【变式2】（2022秋·河南周口·七年级校考期中）如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，则第n （n 为正整数）个三角形中，用n 表示y 的式子为（）A ．21n +B ．2n n +C ．12n n ++D ．21n n ++题型06图形类规律探索之数量问题【典例6】（2023·江苏·七年级假期作业）用大小一样的黑白两种颜色的小正方形纸片，按如图的规律摆放：(1)第5个图案有张黑色小正方形纸片；(2)第n 个图案有张黑色小正方形纸片；(3)第几个图案中白色纸片和黑色纸片共有81张？【变式1】（2023秋·全国·七年级专题练习）如图，用棋子摆方阵，那么，图⑥要摆枚棋子，图n 要摆枚棋子．【变式2】（2023·安徽淮北·淮北市第二中学校考二模）如图，利用黑白两种颜色的五边形组成的图案，根据图案组成的规律回答下列问题：(1)图案④中黑色五边形有______个，白色五边形有______个；(2)图案n中黑色五边形有______个，白色五边形有______个；（用含n的式子表示）(3)图案n中的白色五边形可能为2023个吗？若可能，请求出n的值；若不可能，请说明理由．1．（2023秋·全国·七年级专题练习）观察下列各单项式：234562481632a a a a a a ---，，，，，，…，根据你发现的规律，第10个单项式是（）A ．9102a -B ．9102a C ．11002a D ．10102a -2．（2023秋·全国·七年级专题练习）一列数1a ，2a ，3a …n a ，其中11a =-，2111a a =-，3211a a =-，…，11n na a =-，则1232020a a a a ⨯⨯⨯⨯= （）A ．1-B ．1C ．2020D ．2020-3．（2023春·河南信阳·七年级校联考阶段练习）如图，用棋子摆出下列一组图形，如果按照这种规律摆下去，那么第10个图形里棋子的个数为（）A ．72B ．66C ．56D ．784．（2023春·云南临沧·七年级统考期末）如图，用字母“C ”、“H ”按一定规律拼成图案，其中第1个图案中有4个H ，第2个图案中有6个H ，第3个图案中有8个H ，……，按此规律排列下去，第2023个图案中字母H 的个数为()A ．4044B ．4046C ．6069D ．40485．（2023春·福建宁德·七年级校联考期中）我国宋代数学文杨辉所著《详解九章算法》中记载了用如图所示的一角形解释了二项和的乘方展开式中的系数规律，我们把这种数字三角形叫做“杨辉三角”．请你利用杨辉三角，计算()6a b -的展开式中，含3b 项的系数是（）()0a b +=1…………1()1a b +=a b +…………11()2a b +=222a ab b ++…………121()3a b +=322333a a b ab b +++ (1331)()4a b +=++++432234a 4a b 6a b 4ab b (14641)A ．15-B ．15C ．20-D ．20【答案】C【分析】根据图中规律，可得()2a b +的展开式中含3b 项的系数，再根据()6a b -的展开式中，系数的绝对值与()2a b +的展开式中的系数相同，符号从左往后为奇数项为正，偶数项为负．【详解】解：由题意可知，下排每个数等于上方两个数字的绝对值之和，∴5()a b +的展开式系数从左往右分别是1,5,10,10,5,1，6()a b ∴+的展开式系数从左往右分别是1,6,15,20,15,6,1，根据图中，可知()6a b -含有3b 项的项为从左往右第四项，且符号为负，故()6a b -的展开式中，含3b 项的系数是20-，故选：C ．【点睛】本题考查了数字变化规律，通过观察、分析、归纳发现其中规律，并应用发现的规律是解题的关键．6．（2022秋·四川南充·七年级校考期中）正整数按图中的规律排列．由图知，数字6在第二行，第三列，请写出数字2021在第行，第列．7．（2023春·山东泰安·六年级校考期中）观察下列各式，探索规律：21321⨯=-；23541⨯=-；25761⨯=-；27981⨯=-；2911101⨯=-；用含正整数n 的等式表示你所发现的规律为．8．（2023春·黑龙江绥化·七年级校考期末）观察下列算式：133=，239=，3327=，4381=，53243=，⋯，根据上述算式中的规律，你认为20233的末位数字是．9．（2023春·河北石家庄·七年级行唐一中校考开学考试）观察下列图形的构成规律，按此规律，第6个图形中棋子的个数为个，第n 个图形中棋子的个数为个．10．（2022秋·江苏宿迁·七年级校考阶段练习）已知整数1234a a a a ⋅⋅⋅、、、、满足下列条件：11a =-，212a a =-+，323a a =-+，434a a =-+，…，11n n a a n +=-++（n 为正整数）依此类推，则2025a 的值为．11．（2022春·黑龙江哈尔滨·六年级哈尔滨市第十七中学校校考阶段练习）观察下列三行数：2-，4，8-，16，32-，64，……0，6，6-，18，30-，66， (1)2-，1，2-，4，8-，16……(1)第①行数第七个数是128-，那么第二行数第七个数是_____，第三行第七个数是_____．(2)列式计算：取每行的第9个数，求这三个数的和．12．（2023春·云南昭通·七年级统考期中）小明计算：2399100122222++++++L 的过程如下：解：令2399100122222S =++++++①L 则23100101222222S =+++++ ②②-①得10121S =-∴239910010112222221++++++=-L 请参照小明的方法，计算：2320222023155555++++++L ．13．（2023春·安徽阜阳·七年级校考阶段练习）观察下列图形，完成下列问题．(1)数一数，完成下列表格．直线的条数2345交点的个数(2)若有n 条直线相交，则最多有交点__________个．（用含n 的代数式表示）14．（2022秋·江苏连云港·七年级校考阶段练习）观察下列各式：322111124==⨯⨯，33221129234+==⨯⨯，33322112336344++==⨯⨯，33332211234100454+++==⨯⨯L 回答下面的问题：(1)333331234100+++++=（写出算式即可）；(2)计算33333312341920++++++ 的值；(3)计算333311121920++++ 的值．15．（2022秋·江苏宿迁·七年级校考阶段练习）探索规律：观察下面※由组成的图案和算式，解答问题：21342+==213593++==21357164+++==213579255++++==(1)请猜想135719++++⋅⋅⋅+=_________；(2)请猜想()135721n ++++⋅⋅⋅+-=_________；(3)请用上述规律计算：616365199+++⋅⋅⋅+的值．16．（2023秋·浙江·七年级专题练习）找规律，完成下列各题：(1)如图①，把正方形看作1，1111244+=-=．(2)如图②，把正方形看作1，111112488++=-=．(3)如图③，把正方形看作1，1111124816+++=-=．(4)计算：11111 2481632++++=．(5)计算：111111111 248163264128256512++++++++=．17．（2023春·安徽·九年级专题练习）用若干个“○”与“▲”按如图方式进行拼图：(1)观察图形，寻找规律，并将下面的表格填写完整：图1图2图3图4○的个数3921______▲的个数1410______(2)根据你所观察到的规律，分别写出图n中“○”与“▲”的个数（用含n的代数式表示）．18．（2023·河北秦皇岛·统考一模）为迎接七一建党节，某社区党委在广场上设计了一座三角形展台，需在它的每条边上摆放上相等盆数的鲜花进行装饰．若每条边上摆放两盆鲜花，共需要3盆鲜花；若每条边上摆放3盆鲜花，共需要6盆鲜花；……，按此要求摆放下去（如图所示，每个小圆圈表示一盆鲜花）．(1)填写下表：每条边上摆放的盆数（n）23456…需要的鲜花总盆数（y）369__________…(2)写出需要的鲜花总盆数y与n之间的关系式：__________(3)能否用2023盆鲜花作出符合要求的摆放？如果能，请计算出每条边上应摆放的盆数；如果不能，请说明理由．。

人教版七年级上数学同步练习题,复习补习资料：第4章《几何图形初步》全章配套习题包(含答案)

第四章几何图形初步4.1几何图形4.1.1立体图形与平面图形第1课时几何图形能力提升1.下列所列举的物体,与圆锥的形状类似的是()A.足球B.字典C.易拉罐D.标枪的尖头2.下列图形属于柱体的是()3.在如图所示的几何体中,由四个面围成的几何体是()4.下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a☉b,那么由此可知,下面第二行的图中可以记作a☉d的是()5.下图各几何体中,是三棱柱的是.(只填序号)6.圆柱由个面围成;圆锥由个面围成.它们的底面是,侧面是.7.如图,用简单的平面图形画出三位携手同行的好朋友,请你仔细观察,图中共有三角形个,圆个.8.有一个几何体,形状如图所示,这个几何体的面数为.创新应用★9.请利用图中的几何体拼出汽车、凉亭、蘑菇等图案,并和同伴一起交流,尽量拼出最多的图案.参考答案能力提升1.D2.C3.C A有五个面;B有三个面;C有四个面;D有三个面,故选C.4.A根据题意,知a代表长方形,d代表直线,所以记作a☉d的图形是长方形和直线的组合,故选A.5.④6.32平面曲面7.448.6创新应用9.分析:本题是开放性试题,只要所给答案合理即可.解:答案不唯一,如图.第2课时几何图形的三种形状图与展开图能力提升1.下列四个图中,是三棱锥的表面展开图的是()2.下列图形经过折叠,能围成圆锥的是()3.将右面正方体的平面展开图重新折成正方体后,“共”字对面的字是()A.阖B.家C.幸D.福4.骰子是一种特殊的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是()5.下图是从不同方向看某一几何体得到的平面图形,则这个几何体是.6.根据下列多面体的平面展开图,填写多面体的名称:(1),(2),(3).7.将下图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去.(填序号)8.如图,画出所给几何体的从正面看、左面看和上面看得到的图形.创新应用★9.如图是火箭腾空的立体图形(火箭圆柱底面的周长不等于圆柱的高),请你画出火箭的平面展开图.★10.如图,水平放置的长方体的底面是边长为2和4的长方形,从左边看该长方体,得到的图形的面积是6,试求该长方体的体积.参考答案能力提升1.B三棱锥的四个面都是三角形,还要能围成一个立体图形,可排除C,D;而A不能围成立体图形,故选B.2.B3.C4.C根据题意,骰子的平面展开图共有六个面,其中面“1”与面“6”相对,面“4”与面“3”相对,面“2”与面“5”相对.所以只有C中的相对两个面上的点数与立体图形一致.5.圆柱6.(1)长方体(2)三棱柱(3)三棱锥7.1或2或68.解:创新应用9.解:10.解:由题意知长方体的高为3,则体积为4×2×3=24.4.1.2点、线、面、体能力提升1.如左下图,绕虚线旋转得到的实物图是()2.下列几何体中,有6个面的几何图形有()①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.A.1个B.2个C.3个D.4个3.如果一个直棱柱有12个顶点,那么它的面的个数是()A.10B.9C.8D.74.下列说法正确的有()①四面体的各个面都是三角形;②圆柱、圆锥的底面都是圆;③圆柱是由两个面围成的;④长方体的面不可能是正方形.A.1个B.2个C.3个D.4个5.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是()6.薄薄的硬币在桌面上转动时,看上去像球,这说明了.7.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:(1)一只小蚂蚁爬行留下的路线可解释为.(2)电动车车辐条运动形成的图形可解释为.8.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是cm2.9.观察如图所示的图形,写出下列问题的结果:(1)这个图形的名称是;(2)这个几何体有个面,有个底面,有个侧面,底面是形,侧面是形.(3)侧面的个数与底面多边形的边数有什么关系?10.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.11.观察下列多面体,并把下表补充完整.观察上表中的结果,你能发现a,b,c之间有什么关系吗?请写出关系式.★12.如图所示,长方形绕虚线旋转一周后,形成的图形是什么?旋转半周呢?创新应用★13.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是.(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.参考答案能力提升1.D要能想象到它转动后的形状,面动成体.一个梯形以底所在直线为轴旋转,上、下两部分形成圆锥,中间形成圆柱,是由两个圆锥和一个圆柱组合而成,故应选D.2.C3.C直棱柱有12个顶点,一定是六棱柱,所以它的面的个数是8.4.B①②正确;圆柱是由三个面围成的,所以③错误;长方体的面可能是正方形,所以④错误.5.D由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,旋转一周后可能形成的立体图形是一个管状的物体.6.面动成体从运动的观点可知,薄薄的硬币在桌面上转动时,看上去像球,这种现象说明面转动成体.7.(1)点动成线(2)线动成面8.18将正方形旋转一周所形成的图形是圆柱,从正面看圆柱是一个长方形,长方形的一边长为3cm,另一边长为6cm.所以面积为18cm2.9.解:(1)六棱柱(2)826六边长方(3)侧面的个数与底面多边形的边数相等.10.解:从第一行的平面图形绕某一边旋转或沿某一方向平移可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.(1)→(三)→(D);(2)→(二)→(C);(3)→(四)→(B);(4)→(一)→(A).11.解:填表为:根据表中结果,发现a,b,c之间的关系为a+c-b=2.12.解:长方形绕图示虚线旋转一周后形成的图形是圆柱,旋转半周所形成的图形也是圆柱.创新应用13.解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为V+F-E=2.(2)由题意得,F-8+F-30=2,解得F=20.(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,所以共有24×3÷2=36条棱.那么24+F-36=2,解得F=14,所以x+y=14.4.2直线、射线、线段第1课时直线、射线、线段能力提升1.下列说法中错误的是()A.过一点可以作无数条直线B.过已知三点可以画一条直线C.一条直线通过无数个点D.两点确定一条直线2.射线OA,射线OB表示同一条射线,下面正确的是()3.图中共有条线段.4.看图填空:(1)点C在直线AB;(2)点O在直线BD,点O是直线与直线的交点;(3)过点A的直线共有条,它们是.5.如图所示,在线段AB上任取D,E,C三个点,则这个图中共有条线段.6.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,你可以同伙伴试一试这种方法,并说一说其中的道理.7.按下列语句画出图形.(1)直线l经过A,B,C三点,点C在点A与点B之间;(2)经过点O的三条直线a,b,c;(3)两条直线AB与CD相交于点P;(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.★8.阅读下表:361015解答下列问题:(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系?(2)根据上述关系解决如下实际问题:有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有多少种不同的票价?②要准备多少种车票?创新应用★9.如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内再画第三条直线l3,那么这3条直线最多可有个交点;如果在这个平面内再画第4条直线l4,那么这4条直线最多可有个交点.由此,我们可以猜想:在同一平面内,n(n为大于1的整数)条直线最多可有个交点.(用含n的式子表示)参考答案能力提升1.B过三点画直线,要看这三点在不在一条直线上,若不在,则无法画出.2.B射线自端点向一方无限延伸,因为表示射线时字母有顺序性,即端点字母写在前面,所以点A、点B应在点O的同侧且三点在同一条直线上.3.104.(1)外(2)上AC BD(3)3直线AD、直线AB、直线AC这类题,必须认真观察图形,弄清各元素的位置关系,用精练、准确的语言表达.5.10只要有一个端点不相同,就是不同的线段.6.解:经过两点有且只有一条直线.7.解:(1)(2)(3)(4)8.解:(1)N=1+2+3+…+(n-1)=-.(2)①A,B两地之间有三个站点,说明在这条线段上有5个点,则共有-=10条线段,即有10种票价;②由于从A到B和从B到A的车票不同,则要准备10×2=20种车票.创新应用9.36-通过作图发现:3条直线最多有交点1+2=3(个);4条直线最多有交点1+2+3=6(个);5条直线最多有交点1+2+3+4=10(个)……n条直线最多有交点1+2+3+…+(n-1)=-(个).第2课时线段的性质能力提升1.如图所示,要在直线PQ上找一点C,使PC=3CQ,则点C应在()A.P,Q之间B.点P的左边C.点Q的右边D.P,Q之间或在点Q的右边2.如果线段AB=5 cm,BC=3 cm,那么A,C两点间的距离是()A.8 cmB.2 cmC.4 cmD.不能确定3.C为线段AB的一个三等分点,D为线段AB的中点,若AB的长为6.6 cm,则CD的长为()A.0.8 cmB.1.1 cmC.3.3 cmD.4.4 cm4.如图所示,C是线段AB的中点,D是CB上一点,下列说法中错误的是()A.CD=AC-BDB.CD=BCC.CD=AB-BDD.CD=AD-BC5.下面给出的4条线段中,最长的是()A.dB.cC.bD.a6.已知A,B是数轴上的两点,点A表示的数是-1,且线段AB的长度为6,则点B表示的数是.7.已知线段AB=7 cm,在线段AB所在的直线上画线段BC=1 cm,则线段AC=. 8.如图所示,设A,B,C,D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?请说明理由.9.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.(1)如果AB=20 cm,AM=6 cm,求NC的长;(2)如果MN=6 cm,求AB的长.10.在桌面上放了一个正方体的盒子,如图所示,一只蚂蚁在顶点A处,它要爬到顶点B处找食物,你能帮助蚂蚁设计一条最短的爬行路线吗?要是食物在顶点C处呢?★11.已知线段AB=12 cm,直线AB上有一点C,且BC=6 cm,M是线段AC的中点,求线段AM 的长.创新应用★12.在同一条公路旁,住着5人,他们在同一家公司上班,如图,不妨设这5人的家分别住在点A,B,D,E,F所示的位置,公司在点C处,若AB=4 km,BC=2 km,CD=3 km,DE=3 km,EF=1 km,他们全部乘出租车上班,车费单位报销.出租车收费标准是:起步价6元(3 km以内,包括3 km),超过3 km超出的部分每千米1.5元(不足1 km,以1 km计算),每辆车能容纳3人.(1)若他们分别乘出租车去上班,公司应支付车费多少元?(2)如果你是公司经理,你对他们有没有什么建议?参考答案能力提升1.D注意本题中的条件是在直线PQ上找一点C,所以C可以在P,Q之间,也可以在点Q的右侧.2.D A,B,C三点位置不确定,可能共线,也可能不共线.3.B如图,AD=AB=3.3cm,AC=AB=2.2cm,所以CD=AD-AC=3.3-2.2=1.1(cm).4.B5.A6.-7或5点B可能在点A的左侧,也有可能在点A的右侧.若点B在点A的左侧,则点B表示的数比点A表示的数小6,此时点B表示的数为-7;若点B在点A的右侧,则点B表示的数比点A表示的数大6,此时点B表示的数为5.7.8 cm或6 cm分两种情况:①点C在线段AB内,②点C在线段AB的延长线上.8.解:连接AC,BD,交点P即为购物中心的位置.理由:根据公理“两点之间,线段最短”,要使购物中心到A,B,C,D的距离和最小,购物中心既要在AC上,又要在BD上.9.解:(1)因为M为AC的中点,所以MC=AM.又因为AM=6cm,所以AC=2×6=12(cm).因为AB=20cm,所以BC=AB-AC=20-12=8(cm).又因为N为BC的中点,所以NC=BC=4(cm).(2)因为M为AC的中点,所以MC=AM.因为N为BC的中点,所以CN=BN.所以AB=AC+BC=2(MC+CN)=2MN=2×6=12(cm).10.解:如图所示,是该正方体的侧面展开图.食物在B处时的最短路线为线段AB,食物在C处时的最短路线为线段AC.11.解:(1)当点C在线段AB上时,如图①,图①因为M是AC的中点,所以AM=AC.又因为AC=AB-BC,AB=12cm,BC=6cm,所以AM=(AB-BC)=×(12-6)=3(cm).(2)当点C在线段AB的延长线上时,如图②,图②因为M是AC的中点,所以AM=AC.又因为AC=AB+BC,AB=12cm,BC=6cm,所以AM=AC=(AB+BC)=×(12+6)=9(cm).故AM的长度为3cm或9cm.创新应用12.解:(1)在A处乘车的车费为6+(4+2-3)×1.5=10.5(元);在B处乘车的车费为6元;在D处乘车的车费为6元;在E处乘车的车费为6+(3+3-3)×1.5=10.5(元);在F处乘车的车费为6+(1+3+3-3)×1.5=12(元),合计45元.(2)A,B同乘一辆车,从A开出,D,E,F同乘一辆车,从F开出,合计22.5元.4.3角4.3.1角能力提升1.下列说法中正确的是()A.两条射线组成的图形叫做角B.角是一条线段绕它的一个端点旋转而成的图形C.有公共端点的两条线段组成的图形叫做角D.角是一条射线绕着它的端点旋转而成的图形2.如图,O是直线AB上一点,图中小于180°的角的个数为()A.7B.9C.8D.103.下午2点30分时(如图),时钟的分针与时针所成角的度数为()A.90°B.105°C.120°D.135°(第2题图)(第3题图)4.若∠1=75°24',∠2=75.3°,∠3=75.12°,则()A.∠1=∠2B.∠2=∠3C.∠1=∠3D.以上都不对5.由2点15分到2点30分,钟表的分针转过的角度是()A.30°B.45°C.60°D.90°6.(1)32.6°=°';(2)10.145°=°'″;(3)50°25'12″=°.7.小明说:我每天下午3:00准时做“阳光体育”活动.则下午3:00这一时刻,时钟上分针与时针所夹的角等于.8.指出图中所示的小于平角的角,并把它们表示出来.★9.如图,从点O引出的5条射线OA,OB,OC,OD,OE组成的图形中共有几个角?创新应用★10.观察下图,回答下列问题.(1)在∠AOB内部任意画1条射线OC,则图①中有个不同的角;(2)在∠AOB内部任意画2条射线OC,OD,则图②中有个不同的角;(3)在∠AOB内部任意画3条射线OC,OD,OE,则图③中有个不同的角;(4)在∠AOB内部任意画10条射线OC,OD,…,则共形成个不同的角.参考答案能力提升1.D2.B3.B时钟上每一大格是30°,2点30分时时针与分针之间是3.5个格,所以夹角为3.5×30°=105°.4.D因为∠1=75°24'=75.4°,所以∠1,∠2和∠3都不相等.5.D6.(1)3236(2)10842(3)50.427.90°8.解:满足条件的角有6个,它们是∠A,∠D,∠ABE,∠ABF,∠DCE,∠DCF.9.解:图形中有∠AOB,∠AOC,∠AOD,∠AOE,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE,共10个角.创新应用10.(1)3(2)6(3)10(4)66(1)2+1=3;(2)3+2+1=6;(3)4+3+2+1=10;(4)11+10+9+…+3+2+1=66.4.3.2角的比较与运算能力提升1.如图,如果∠AOB=∠COD,那么()A.∠α>∠βB.∠α<∠βC.∠α=∠βD.∠α+∠β=∠COD2.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,则下列各式中正确的是()A.∠COD=∠AOCB.∠AOD=∠AOBC.∠BOD=∠AOBD.∠BOC=∠AOB3.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠BFE=()A.70°B.65°C.60°D.50°4.用一副三角板,不可能画出的角度是()A.15°B.75°C.165°D.145°5.已知∠AOB=30°,∠BOC=45°,则∠AOC=()A.15°B.75°C.15°或75°D.不能确定6.如图,将一副三角尺折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=.7.如图,已知直线AB,CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠BOD的度数是.8.如图,∠AOC=40°,∠BOD=50°,OM,ON分别是∠AOC,∠BOD的角平分线,则∠MON=.9.计算:(1)153°19'42″+26°40'28″;(2)90°3″-57°21'44″;(3)33°15'16″×5.★10.如图,OD是∠AOB的平分线,OE是∠BOC的平分线,且∠AOC=130°,求∠DOE的度数.★11.如图,∠1∶∠2∶∠3∶∠4=1∶1∶3∶4,求∠1,∠2,∠3,∠4的度数.创新应用★12.在飞机飞行时,飞行的方向是用飞行路线与实际的南北方向线之间的夹角大小来表示的.如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角,从A到达B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D的飞行方向角为145°,试求AB与AC之间夹角及AD与AC之间夹角的大小.参考答案能力提升1.C2.A由角平分线的定义可知,∠BOC=∠AOC=∠AOB,∠BOD=∠COD=∠BOC,所以选项A中,∠COD=∠BOC=∠AOC正确.3.B根据折叠后的两个角相等,可知∠BFE=(180°-∠1)÷2=65°.4.D用三角板只能画出度数是15的整数倍的角,因为145不是15的整数倍,所以用三角板不能画出145°的角.5.C本题没有给出图形,所以∠AOB和∠BOC的位置不确定,有两种情况.6.180°由图可知,∠AOC+∠DOB=∠AOB+∠COD=90°+90°=180°.7.70°由OE平分∠COB,得∠BOC=2∠EOB=2×55°=110°,所以∠BOD=180°-∠BOC=180°-110°=70°.8.135°由角平分线的定义,得∠COM=∠AOC=×40°=20°,∠DON=∠BOD=×50°=25°,所以∠MON=180°-∠COM-∠DON=180°-20°-25°=135°.9.解:(1)153°19'42″+26°40'28″=179°59'70″=179°60'10″=180°10″.(2)90°3″-57°21'44″=89°59'63″-57°21'44″=32°38'19″.(3)33°15'16″×5=165°75'80″=165°76'20″=166°16'20″.10.分析:OD,OE分别是∠AOB,∠BOC的平分线,而∠DOE刚好是∠AOB与∠BOC和的一半.解:因为OD是∠AOB的平分线,OE是∠BOC的平分线,所以∠DOB=∠AOB,∠EOB=∠BOC.因为∠DOE=∠DOB+∠EOB,所以∠DOE=∠AOB+∠BOC=(∠AOB+∠BOC)=∠AOC=×130°=65°.11.分析:∠1,∠2,∠3,∠4构成一个周角为360°,再根据题目中∠1∶∠2∶∠3∶∠4=1∶1∶3∶4,所以可以用代数方法解决本题.解:设∠1=x°,则∠2=x°,∠3=3x°,∠4=4x°.依题意,得x°+x°+3x°+4x°=360°,9x°=360°,则x°=40°.故∠1=40°,∠2=40°,∠3=120°,∠4=160°.创新应用12.解:由题意,知∠NAB=35°,∠NAC=60°,所以∠BAC=∠NAC-∠NAB=60°-35°=25°.因为∠NAC=60°,∠NAD=145°,所以∠DAC=∠NAD-∠NAC=145°-60°=85°.答:AB与AC之间的夹角为25°,AD与AC之间的夹角为85°.4.3.3余角和补角能力提升1.如图,A,O,B三点在一条直线上,已知∠AOD=25°,∠COD=90°,则∠BOC的度数为()A.25°B.85°C.115°D.155°2.如果∠AOB+∠BOC=90°,∠BOC+∠COD=90°,那么∠AOB与∠COD的关系是()A.互余B.互补C.相等D.不能确定3.如图,点O在直线AB上,∠COB=∠DOE=90°,则图中相等的角的对数是()A.3B.4C.5D.74.如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是()A.右转80°B.左转80°C.右转100°D.左转100°5.在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=30°时,∠BOD的大小是()A.60°B.120°C.60°或90°D.60°或120°6.如图,将两块三角板的直角顶点重合后叠放在一起,若∠1=40°,则∠2=.7.如图,射线OP表示的方向是.8.如图,桌面上平放着一块三角板和一把直尺,小明将三角板的直角顶点紧靠直尺的边缘,他发现无论是将三角板绕直角顶点旋转,还是将三角板沿直尺平移,∠1与∠2的和总是保持不变,则∠1与∠2的和是度.9.学校、电影院、公园在平面图上的标点分别为A,B,C,如果电影院在学校的正东方向上,公园在学校的南偏西25°的方向上,那么平面图上的∠CAB=度.10.互余的两个角的度数之比为3∶7,则这两个角的度数分别是多少?11.如图,一只蚂蚁从点O出发,沿北偏东45°的方向爬行2.5 cm,碰到障碍物(记作B)后折向北偏西60°的方向爬行3 cm(此时位置记作点C).(1)画出蚂蚁的爬行路线;(2)求出∠OBC的度数.注:如图,,∠1=∠2★12.如图所示,已知O是直线AB上一点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE 互余的角有哪些?与∠DOE互补的角有哪些?并说明理由.创新应用★13.按如图所示的方法折纸,然后回答问题:(1)∠2是多少度的角?为什么?(2)∠1与∠3有何关系?(3)∠1与∠AEC,∠3和∠BEF分别有何关系?★14.根据互余和互补的定义知,20°角的补角为160°,余角为70°,160°-70°=90°;25°角的补角为155°,余角为65°,155°-65°=90°;50°角的补角为130°,余角为40°,130°-40°=90°;75°角的补角为105°,余角为15°,105°-15°=90°……观察以上几组数据,你能得到什么结论?写出你的结论.参考答案能力提升1.C因为∠AOC=∠COD-∠AOD=90°-25°=65°,所以∠BOC=180°-∠AOC=180°-65°=115°.2.C3.C因为∠COB=90°,所以∠AOC=180°-∠BOC=180°-90°=90°,所以∠AOC=∠BOC=∠DOE;因为∠BOD+∠COD=∠EOC+∠COD=90°,所以∠EOC=∠BOD;因为∠AOE+∠EOC=∠COD+∠EOC=90°,所以∠AOE=∠COD,共5对.4.A如图,∠ECF=20°,∠FCD=60°,要从BC方向转向CD方向,需转过的角为∠ECD=∠ECF+∠FCD=20°+60°=80°,即右转80°.5.D根据题意画图为如图①和图②,在图①中∠BOD的度数是60°,在图②中∠BOD的度数是120°,所以∠BOD的度数是60°或120°.6.40°7.南偏西62°8.90由图形知∠1,∠2与直角三角板的直角形成一个平角,所以无论是将三角板绕直角顶点旋转,还是将三角板沿直尺平移,形成的始终是一个平角.所以∠1与∠2的和是90度.9.11510.解:设这两个角的度数分别为3x°,7x°,由题意,得3x°+7x°=90°,解得x°=9°,3x°=27°,7x°=63°.答:这两个角的度数分别是27°,63°.11.解:(1)如图.(2)∠OBC=90°-60°+90°-45°=75°.12.解:与∠DOE互余的角有∠EOF,∠BOD,∠BOC;与∠DOE互补的角有∠BOF,∠COE.理由:∠DOE+∠EOF=90°,∠DOE+∠BOD=∠BOE=180°-∠AOE=90°,∠DOE+∠BOC=∠DOE+∠BOD=90°,∠DOE+∠BOF=∠AOF+∠BOF=180°,∠DOE+∠COE=∠DOE+∠BOF=180°.创新应用13.解:(1)∠2=90°.因为折叠,则∠1与∠3的和与∠2相等,而这三个角加起来,正好是平角∠BEC,所以∠2=×180°=90°.(2)因为∠1与∠3组成的大角和∠2相等,且三个角加起来恰好是一个平角,所以∠1+∠3=90°.所以∠1与∠3互余.(3)因为∠1与∠AEC的和为180°,∠3与∠BEF的和为180°,所以∠1与∠AEC互补,∠3与∠BEF互补.14.解:设一个角的度数为x°,则补角为(180-x)°,它的余角为(90-x)°.因为180-x-(90-x)=90,所以一个角的补角比它的余角大90°.4.4课题学习设计制作长方体形状的包装纸盒能力提升1.如图所示,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是()2.一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是()A.和B.谐C.社D.会★3.用边长为1的正方形纸板制成一副七巧板(如图①所示),将它拼成“小天鹅”图案(如图②所示),则图②中∠ABC+∠GEB=()A.360°B.270°C.225°D.180°4.如图所示的是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得它们折叠后所成正方体相对的面上的两数相同,则填入正方形A,B,C内的三个数依次为.5.图中的甲、乙是否是几何体的平面展开图,先想一想,再折一折,如果是,请说出折叠后的几何体名称、底面形状、侧面形状、棱数、侧棱数与顶点数.★6.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)创新应用★7.如图所示,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐.请问壁虎从A处到B处的最短路线是什么?参考答案能力提升1.C2.D3.B4.1,2,0C与0是对面,B与2是对面,A与1是对面.5.解:甲是长方体,底面是正方形,侧面是长方形,有12条棱,4条侧棱,8个顶点.乙不是几何体的平面展开图.6.分析:本题考查的是正方体的平面展开图,只要添加的正方形与原来的正方形恰好是一个完整的正方体的展开图即可.解:本题答案不唯一,下图只是一种情况.创新应用7.分析:壁虎既要沿圆柱表面走,又要使路线最短,这样就要考虑圆柱的侧面展开图.解:展开圆柱的侧面,如图所示.展开图为长方形,B为中点,则AB即为所求的最短路线.第四章几何图形初步单元测试卷(时间:45分钟,满分:100分)一、选择题(每小题4分,共32分)1.下列立体图形中,侧面展开图是扇形的是()2.下列图形中,∠1和∠2互为余角的是()3.如图,点A位于点O的方向上.()A.南偏东35°B.北偏西65°C.南偏东65°D.南偏西65°4.如图,一个斜插吸管的盒装饮料从正面看到的图形是()5.下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是()A.用两个钉子就可以把木条固定在墙上B.把弯曲的公路改直,就能缩短路程C.利用圆规可以比较两条线段的大小关系D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线6.一块手表如图,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是()A.60°B.80°C.120°D.150°7.将一长方形纸片,按下图的方式折叠,BC,BD为折痕,则∠CBD的度数为()。

2019年秋人教版七年级上册数学同步练习(PDF,无答案)：4.4 课题学习设计制作长方体形状的包装纸盒

４.４㊀课题学习㊀设计制作长方体形状的包装纸盒一㊁旧知链接１.长方体的面数ꎬ有盖的长方体的展开图和无盖的长方体的展开图情况.２.立体图形与平面图形的联系.二㊁新知速递１.通过设计和制作长方体纸盒的实践活动ꎬ我们可以进一步体会㊀㊀㊀图形和㊀㊀㊀图形之间的相互转化.２.日常生活中ꎬ我们可以看到各种各样的长方体的包装盒.设计这类包装盒时ꎬ首先绘制㊀㊀㊀㊀㊀ꎬ再把它剪开并折叠成㊀㊀㊀㊀㊀.３.一个无盖的正方体纸盒ꎬ将它展开成平面图形ꎬ可能的情形共有(㊀㊀).Ａ１１种Ｂ９种Ｃ８种Ｄ７种图４－４－１０４.如图４－４－１０是一个长方体的表面展开图ꎬ每个面上都标注了字母ꎬ请根据要求回答问题:(１)如果Ａ面在长方体的底部ꎬ那么哪一个面会在上面?(２)如果Ｆ面地前面ꎬＢ面在左面ꎬ那么哪一个面会在上面?(字母朝外)(３)如果Ｃ面在右面ꎬＤ面在后面ꎬ那么哪一个面会在上面?(字母朝外)１.如图４－４－１１所示的正方体的展开图是(㊀㊀).图４－４－１１㊀㊀第四章㊀几何图形初步２.如图４－４－１２ꎬＱＱ软件里的礼盒图标示一个表面印有黑色实线ꎬ顶端有图示箭头的正方体.下列图形中ꎬ是该几何体的表面展开图的是(㊀㊀).讲评:根据题意可得出正方体向对面上的线段应该平行或在一条直线上ꎬ故符合题意得只有Ａ图４－４－１２㊀㊀㊀㊀㊀图４－４－１３３.明明用纸(如图４－４－１３)折成了一个正方体的盒子ꎬ里面装了一瓶墨水ꎬ与其他空盒子混放在一起ꎬ只凭观察ꎬ选出墨水在哪个盒子中.(㊀㊀)基础训练１.将如图４－４－１４的正方体盒子沿某些棱展开后ꎬ能得到的图形是(㊀㊀).㊀㊀图４－４－１４２.在正方体的表面上画有如图４－４－１５所示的粗线ꎬ则其展开后正确的是(㊀㊀).㊀㊀图４－４－１５３.下面图形中ꎬ不能折成无盖的正方体盒子的是(㊀㊀).４.如图４－４－１６ꎬ若要把一个正方体纸盒沿棱剪开ꎬ平铺在桌面上ꎬ则至少需要剪开的棱的条数是(㊀㊀).Ａ５条Ｂ６条Ｃ７条Ｄ８条图４－４－１６拓展提高５.如图４－４－１７ꎬ纸板上有１０个无阴影的正方形ꎬ从中选１个ꎬ使得它与图中５个有阴影的正方形一起能折叠成一个正方体的纸盒ꎬ选法应该有(㊀㊀).Ａ４种Ｂ５种Ｃ６种Ｄ７种图４－４－１７㊀㊀㊀㊀㊀图４－４－１８６.小林同学在一个正方体盒子的每个面上都写了一个字ꎬ分别是:我㊁喜㊁欢㊁数㊁学㊁课ꎬ其表面展开图如图４－４－１８所示ꎬ那么在该正方体盒子中ꎬ和课相对的面上所写的字是㊀㊀㊀㊀㊀.图４－４－１９７.把立方体的六个面分别涂上六种不同颜色ꎬ并画上朵数不等的花ꎬ各面上的颜色与花的朵数情况列表如下.现将上述大小相同ꎬ颜色㊁花朵分布完全一样的四个立方体拼成一个水平放置的长方体(如图４－４－１９所示)ꎬ那么长方体的下底面共有多少朵花?颜色红黄蓝白紫绿花的朵数１２３４５６发散思维８.某同学的茶杯是圆柱形ꎬ如图４－４－２０的图１是茶杯的立体图ꎬ左边下方有一只蚂蚁ꎬ从Ａ处爬行到对面的中点Ｂ处.如果蚂蚁爬行路线最短ꎬ请画出这条最短路线图.解:如图４－４－２０中图２ꎬ将圆柱的侧面展开成一个长方形ꎬ则Ａ㊁Ｂ分别位于如图４－４－１９中图２所示的位置ꎬ连接ＡＢꎬ即是这条最短路线图.问题:某正方体盒子ꎬ如图４－４－２０的图３左边下方Ａ处有一只蚂蚁ꎬ从Ａ处爬行到侧棱ＧＦ上的中点Ｍ点处.如果蚂蚁爬行路线最短ꎬ请画出这条最短路线图.图４－４－２０。