编译原理报告:NFA转DFA(详解,附源代码)
nfa转化为dfa例题详解

确定有限自动机(NFA )到确定有限自动机(DFA )的转化是正则表达式和有限自动机等形式化语言理论中的一个重要概念。
这个过程涉及将非确定性自动机转化为等价的确定性自动机。
下面是一个简单的例子,演示如何将一个NFA 转化为DFA 。
示例 NFA:考虑一个NFA ,它接受所有包含子串 "01" 的二进制字符串。
NFA 状态转移图:NFA 状态转移规则:1. q0→0q12. q1→1q23. q2→1,εq34. q3→1,εq35. q3→0,εq0NFA 状态图解释:•q0 是起始状态。
•q2 是接受状态。
•从 q0 开始,读入 "0" 到达 q1,再读入 "1" 到达 q2,形成 "01" 子串。
•从 q2 通过 "1" 和 ε 达到 q3,表示可以在 "01" 后面追加 "1"。
•q3 可以通过 "1" 和 ε 一直回到自身,表示可以在 "01" 后面追加任意数量的 "1"。
• q3 还可以通过 "0" 和 ε 返回到 q0,表示可以在任意位置重新开始 "01" 的匹配。
NFA到DFA转换:下面是将上述NFA转化为DFA的步骤:1.构建子集构造法的初始状态:初始状态是 NFA 的起始状态的ε-闭包。
在这个例子中,初始状态为 {q0, q3}。
2.状态扩展:对于每个状态集合,找出它的ε-闭包,并对每个可能的输入符号应用状态转移规则,形成新的状态集合。
–对于输入 "0":•从 {q0, q3} 中的 q0 通过 "0" 可以到达 q1,形成 {q1}。
–对于输入 "1":•从 {q0, q3} 中的 q0 通过 "1" 可以到达 q2,形成 {q2}。
编译原理-NFA转化成DFA

编译原理-NFA转化成DFA
1.假定NFA M=<S,∑,f,S0,F> 对M的状态转换图进⾏以下改造:
①引进新的初态结点X和终态结点Y, X,Y∈S, 从X到S0中的任意结点连⼀条ε箭弧,从F中任意结点到Y连⼀条ε箭弧。
(解决初态的唯⼀性)
②引⼊新状态对M的状态转换图进⾏进⼀步的替换(简化弧上的标记)
2.NFA确定化:⼦集法(解决弧和转换问题)
设I是S的⼀个⼦集
①J为I中的某个状态经过⼀条a弧⽽到达的集合
②ε-closure(I):I∪{s'|从s∈I出发经过任意条ε弧能到达s'}
③Ia=ε-closure(J)
例:
I=ε-closure({1})={1,2}
J={5,4,3}
Ia=ε-closure({5,4,3})={5,4,3,6,2,7,8}
3.状态集转换表:
设只含两个字符a,b
①置第⼀⾏第⼀列为ε-closure({X}),求出Ia,Ib
②检查Ia,Ib看其是否已出现在表中的第⼀列,把未曾出现的填⼊后⾯空⾏的第⼀列,再求出Ia,Ib
③重复上述过程,直到所有2,3列⼦集全部出现在第⼀列为⽌
例:
化简和确定化的状态转换图:。
编译原理实验NFA确定化为DFA

实用文档2016.11.02不确定有穷状态自动机的确定化目录一、实验名称 (2)二、实验目的 (2)三、实验原理 (2)1、NFA定义 (2)2、DFA的定义 (2)3、closure函数 (2)4、move函数 (3)四、实验思路 (3)1、输入 (3)2、closure算法 (3)3、move算法 (3)4、构造子集 (4)5、输出 (4)五、实验小结 (4)1、输入存储问题 (4)2、closure算法问题 (4)3、输出问题 (5)六、附件 (5)1、源代码 (5)2、运行结果截图 (7)一、实验名称不确定有穷状态自动机的确定化二、实验目的输入:非确定有穷状态自动机NFA输出:确定化的有穷状态自动机DFA三、实验原理1、NFA定义一个不确定的有穷自动机M是一个五元组,M=(K,E,f,S,Z)其中a.K是一个有穷集,它的每个元素称为一个状态;b.E是一个有穷字母表,它的每个元素称为一个输入符号;c.f是一个从K×E*到K的子集的映像,即:K*E*->2k,其中2k表示K的幂集;d.S包含于K,是一个非空初态集;e.Z包含于K,是一个终态集。
2、DFA的定义一个确定的有穷自动机M是一个五元组,M=(K,E,f,S,Z)其中a.K是一个有穷集,它的每个元素称为一个状态;b.E是一个有穷字母表,它的每个元素称为一个输入符号;c.f是转换函数,是K×E->K上的映像,即,如f(ki,a)=kj(ki∈K,kj∈K)就意味着,当前状态为ki,输入字符为a时,将转换到下一状态kj,我们把kj称作ki的一个后继状态;d.S∈K,是唯一的一个初态;e.Z包含于K,是一个终态集,终态也称可接受状态或结束状态。
3、closure函数状态集合I的ε—闭包,表示为ε—closure(I),定义为一状态集,是状态集I中的任何状态S经任意条ε弧而能到达的状态的集合。
4、move函数状态集合I的a弧转换,表示为move(I,a),定义为状态集合J,其中J是所有那些从I中的某一状态经过一条a弧而到达的状态的全体。
NFA转化为DFA

NFA转化为DFANFA(不确定的有穷⾃动机)转化为DFA(确定的有穷⾃动机)NFA转换DFA,通常是将带空串的NFA(即:ε-NFA)先转化为不带空串的NFA(即:NFA),然后再转化为DFA。
提⽰:ε是空串的意思!空串没有任何字符!这⾥直接讲将ε-NFA转化为DFA的过程,将NFA转化为DFA的情况类似。
转化的过程总的来说有两⼤步骤:ε-NFA转化为DFA,以及DFA简化ε-NFA转化为DFA前件知识1、对状态图进⾏改造增加状态X,Y,使之成为新的唯⼀的初态和终态,从X引ε弧到原初态节点,从原终态节点引ε弧到Y节点。
2、利⽤⼦集法对NFA进⾏确定化。
⼦集法⼦集法:将NFA转化为接受同样语⾔的DFA。
DFA的每⼀个状态对应NFA的⼀组状态;DFA使⽤它的状态去记录NFA读⼊⼀个符号后可能达到的所有状态如上图,A对应ε-NFA的0和1状态,A代表的是⼀组状态。
因此,DFA使⽤它的状态去记录NFA读⼊⼀个符号后可能达到的所有状态。
构造状态转化表ε-closure(ε-闭包)状态集合I的ε-闭包是⼀状态集。
①任何状态q∈I,则q∈ε-closure(I)②任何状态q∈I,则q经任意条ε弧⽽能到达的状态q'∈ε-closure(I)⽐如上图,假设I={0},那么0∈ε-closure(I);并且0经ε弧能到达1状态,因此,1∈ε-closure(I)。
即:ε-closure({0})={0,1}。
案例再现可能前⾯的理论有些乱,理不清,这⾥⽤⼀个例题演绎如何将ε-NFA转化为DFA。
已知下⾯的NFA图,求确定后的DFA:①改造状态图:在起始状态分别加上X、Y状态,连接输⼊符号为ε。
②状态转换表状态集合 \状态01A={X,0,2,1}B={2,3,1}C={2,1}B={2,3,1}D={2,4,3,1,Y}C={2,1}C={2,1}B={2,3,1}C={2,1}D={2,4,3,1,Y}D={2,4,3,1,Y}C={2,1}!提⽰:A,B,C,D表⽰状态集合;0,1分别表⽰状态0和1。
编译原理实验NFA确定化为DFA

编译原理实验NFA确定化为DFA编译原理中的NFA(Non-deterministic Finite Automaton,非确定性有限自动机)是一种能够识别正则语言的形式化模型。
它的设计简单,但效率较低。
为了提高识别效率,需要将NFA转化为DFA(Deterministic Finite Automaton,确定性有限自动机)。
本文将介绍NFA确定化为DFA的一般方法,并以一个具体例子来说明该过程。
首先,我们来了解一下NFA和DFA的差异。
NFA可以有多个转移路径,每个输入符号可以对应多个状态转移,而DFA每个输入符号只能对应唯一的状态转移。
这使得NFA在识别过程中具有非确定性,无法确定下一个状态。
而DFA则能够准确地根据当前状态和输入符号确定下一个状态。
NFA确定化为DFA的一般方法如下:1.创建DFA的初始状态。
该状态对应NFA的起始状态以及从起始状态经过ε(空)转移可以到达的所有状态。
2.对DFA的每个状态进行如下处理:a)对当前状态的每个输入符号进行处理。
b)根据当前状态和输入符号,确定下一个状态。
如果有多个状态,需要将它们合并为一个DFA状态。
c)重复上述步骤,直到处理完所有输入符号。
3.对于合并的DFA状态,需要重复执行第2步的处理过程,直到没有新的合并状态产生为止。
4.最终得到的DFA包含的状态即为NFA确定化的结果。
下面以一个具体的例子来说明NFA确定化为DFA的过程。
考虑以下NFA:(状态)(输入符号)(转移状态)1a,ε1,22a33b44a5首先,创建DFA的初始状态,根据NFA的起始状态和通过ε转移可以到达的状态。
在该例子中,起始状态为1,通过ε转移可以到达状态1和2、因此,初始状态为{1,2}。
接下来,对初始状态{1,2}进行处理。
对于输入符号a,根据NFA的状态转移表可以得到DFA的下一个状态为{1,2,3},因为NFA的状态1通过a和ε可以到达状态3、对于输入符号b,当前状态没有转移。
nfa转换为dfa编译原理 c++

nfa转换为dfa编译原理 c++有限自动机(NFA)和确定有限自动机(DFA)是计算机科学中有限状态自动机的两种形式。
NFA可以接受多个转移状态,而DFA则只能有一个转移状态。
NFA到DFA的转换是一个重要的编译原理问题。
以下是NFA转换为DFA的步骤:1. 确定NFA的开始状态和接受状态。
2. 对于每个输入符号,确定NFA的转换规则和转换后的状态。
3. 重复第二步,直到我们不能获得新的状态。
4. 标记DFA中的状态,即从NFA的多个状态中派生出的状态。
5. 为DFA添加开始状态和接受状态。
开始状态是NFA的开始状态的ε闭包。
6. 对于每个输入符号,使用NFA的转移规则来定义DFA中的转移。
7. 扫描DFA的状态表,并删除不可到达的状态。
下面是在C++中实现的NFA到DFA转换过程的伪代码://定义状态类class State{public:string name;unordered_map<char, set<string>> transitions;bool is_final_state;};//定义NFA类class NFA{public:State start_state;set<State> final_states;unordered_set<State> all_states;};//定义DFA类class DFA{public:State start_state;set<State> final_states;unordered_set<State> all_states;};//NFA转换为DFADFA ConvertToDFA(NFA nfa){//创建DFA对象DFA dfa;//确定开始状态dfa.start_state = nfa.start_state;//确定接受状态dfa.final_states = nfa.final_states;//添加开始状态到DFA的所有状态dfa.all_states.insert(dfa.start_state);while (有新的状态可以加入DFA){//从DFA中选择一个未标记的状态State current_state = 选择一个未标记的状态;for (每个输入符号a){//根据当前状态的a过渡创建新状态State new_state = 创建新状态;//从当前状态开始,获得状态a的ε闭包set<State> epsilon_closure = current_state.获取状态a的ε闭包;//通过NFA的规则从当前状态和ε闭包中跳转到新状态set<State> transition_states = 通过NFA规则从当前状态和ε闭包中跳转到新状态;//确定新状态是否应该成为DFA的接受状态bool is_final_state = 确定新状态应该成为DFA的接受状态;//设置新状态的属性new_ = 新状态的名称;new_state.transitions = 转移函数;new_state.is_final_state = is_final_state;//将状态添加到DFA中dfa.all_states.insert(new_state);}}return dfa;}这是将NFA转换为DFA的基本伪代码。
[编译原理代码][NFA转DFA并最小化DFA并使用DFA进行词法分析]
![[编译原理代码][NFA转DFA并最小化DFA并使用DFA进行词法分析]](https://img.taocdn.com/s3/m/4706449103d276a20029bd64783e0912a2167c14.png)
[编译原理代码][NFA转DFA并最⼩化DFA并使⽤DFA进⾏词法分析]#include <iostream>#include <vector>#include <cstring>#include "stack"#include "algorithm"using namespace std;int NFAStatusNum,AlphabetNum,StatusEdgeNum,AcceptStatusNum;char alphabet[1000];int accept[1000];int StartStatus;int isDFAok=1;int isDFA[1000][1000];/** NFA状态图的邻接表*/vector<vector<int>> Dstates;int Dstatesvisit[1000];int Dtran[1000][1000];vector<int> Dtranstart;vector<int> Dtranend;int isDtranstart[1000];int isDtranend[1000];class Edge{public:int to,w,next;} ;Edge edge[10000];int edgetot=0;int Graph[1000];void link(int u,int v,int w){edge[++edgetot].to=v;edge[edgetot].w=w;edge[edgetot].next=Graph[u];Graph[u]=edgetot;}void input(){int u,v,w;memset(Dtran,-1,sizeof(Dtran));scanf("%d %d %d %d\n",&NFAStatusNum,&AlphabetNum,&StatusEdgeNum,&AcceptStatusNum);for(int i=1;i<=AlphabetNum;i++){ //读⼊字母表scanf("%c",&alphabet[i]);}for(int i=1;i<=AcceptStatusNum;i++){scanf("%d",&accept[i]);}//开始状态序号scanf("%d",&StartStatus);for(int i=0;i<StatusEdgeNum;i++){scanf("%d%d%d\n",&u,&v,&w);link(u,v,w);if(isDFA[u][v]==0){isDFA[u][v]=1;}else{isDFAok=0;}if(w==0){isDFAok=0;}}//读⼊测试字符串}void e_clouser(vector<int> &T,vector<int> &ans){int visit[1000];memset(visit,0,sizeof(visit));stack<int> Stack;//T all push in Stack and copy to ansfor (int i=0;i < T.size();++i){Stack.push(T[i]);ans.push_back(T[i]);visit[T[i]]=1;while(Stack.empty()!=1){int t = Stack.top(); Stack.pop();for(int p=Graph[t];p!=0;p=edge[p].next){if(edge[p].w==0){if(visit[edge[p].to]==0){visit[edge[p].to]=1;Stack.push(edge[p].to);ans.push_back(edge[p].to);}}}}sort(ans.begin(),ans.end());}void move(vector<int> &T,int a,vector<int> &ans){ int visit[1000];memset(visit,0,sizeof(visit));for(int i=0;i<T.size();i++) {int t=T[i];for (int p = Graph[t]; p != 0; p = edge[p].next) { if (edge[p].w == a) {if (visit[edge[p].to] == 0) {visit[edge[p].to] = 1;ans.push_back(edge[p].to);}}}}}bool notin(vector<int> &a,int &U){for(int i=0;i<Dstates.size();i++){int ok=1;if(Dstates[i].size()==a.size()){for(int j=0;j<a.size();j++){if(Dstates[i][j]!=a[j]){ok=0;break;}}if(ok==1) {U=i;return false;}}}U=Dstates.size();return true;}void nfatodfa(){vector<int> s,t;s.push_back(StartStatus);e_clouser(s,t);Dstates.push_back(t);stack<int> Stack;Stack.push(Dstates.size()-1);while(Stack.empty()!=1){int T=Stack.top();Stack.pop();int U;for(int i=1;i<=AlphabetNum;i++){vector<int> ans,ans2;move(Dstates[T],i,ans2);e_clouser(ans2,ans);if(notin(ans,U)){Dstates.push_back(ans);Stack.push(Dstates.size()-1);}Dtran[T][i]=U;}}}void getDtranStartEnd(){for(int i=0;i<Dstates.size();i++){int ok=1;for(int j=0;j<Dstates[i].size();j++){if(Dstates[i][j]==StartStatus){Dtranstart.push_back(i);isDtranstart[i]=1;}for(int k=1;k<=AcceptStatusNum;k++){if(Dstates[i][j]==accept[k]){ok=0;Dtranend.push_back(i);isDtranend[i]=1;}}}}}}vector<vector<int>> newDstates;int newDstatesvisit[1000];int newDtran[1000][1000];int set[1000];vector<int> newDtranstart;vector<int> newDtranend;int isnewDtranstart[1000];int isnewDtranend[1000];void simple(){int visit[1000];memset(visit,0,sizeof(visit));vector<int> a,b;//接受结点加⼊afor(int i=0;i<Dtranend.size();i++){a.push_back(Dtranend[i]);visit[Dtranend[i]]=1;set[Dtranend[i]]=0;}//剩余结点加⼊bfor(int i=0;i<Dstates.size();i++){if(visit[i]==0){b.push_back(i);set[i]=1;}}newDstates.push_back(a);newDstates.push_back(b);while(1){int ok=0;for(int i=0;i<newDstates.size();i++){for (int k = 1; k <= AlphabetNum; k++) {for(int j=1;j<newDstates[i].size();j++) {int pp= Dtran[newDstates[i][0]][k];int u = newDstates[i][j], v = Dtran[u][k];if (set[v] != set[pp] ) {//将u剥离newDstates[i].erase(newDstates[i].begin() + j); vector<int> temp;temp.push_back(u);set[u] = newDstates.size();newDstates.push_back(temp);ok = 1;break;}if (ok == 1) break;}if(ok==1) break;}if(ok==1) break;}if(ok==0) break;}//isnewDtranstart,isnewDtranend,newDtranfor(int i=0;i<Dstates.size();i++) {for (int j = 1; j <= AlphabetNum; j++) {newDtran[set[i]][j]=set[Dtran[i][j]];}if(isDtranend[i]==1)isnewDtranend[set[i]]=1;if(isDtranstart[i]==1)isnewDtranstart[set[i]]=1;}//isnewDtranstart,isnewDtranend}bool dfa(char *S){int status=0;for(int i=0;i<newDstates.size();i++){if(isnewDtranstart[i]==1){status=i;}}for(int i=0;i<strlen(S);i++) {//这⾥我偷懒了,懒得弄个map存映射,直接对这个例⼦进⾏操作,就是 S[i]-'a'+1; int p=S[i]-'a'+1;status=newDtran[status][p];}if(isnewDtranend[status]==1) return true;else return false;}int main() {freopen("E:\\NFATODFA\\a.in","r",stdin);input();if(isDFAok==0){printf("This is NFA\n");nfatodfa();}else{printf("This is DNA\n");}//打印DFAprintf("\nPrint DFA's Dtran:\n");printf(" DFAstatu a b");getDtranStartEnd();for(int i=0;i<Dstates.size();i++){printf("\n");if(isDtranstart[i]==1)printf("start ");else if(isDtranend[i]==1)printf("end ");else printf(" ");printf("%5c ",i+'A');for(int j=1;j<=AlphabetNum;j++)printf("%5c ",Dtran[i][j]+'A');}printf("\nPrint simple DFA's Dtran:\n");simple();printf(" DFAstatu a b");for(int i=0;i<newDstates.size();i++){printf("\n");if(isnewDtranstart[i]==1)printf("start ");else if(isnewDtranend[i]==1)printf("end ");else printf(" ");printf("%5c ",i+'A');for(int j=1;j<=AlphabetNum;j++)printf("%5c ",newDtran[i][j]+'A');}printf("\n");char S[1000];while(scanf("%s\n",S)!=EOF){if(dfa(S)){printf("%s belongs to the DFA\n",S);}elseprintf("%s don't belong to the DFA\n",S);}return 0;}。
NFA转化为DFA编译原理实验报告

编译原理实验报告实验名称正则表达式与有限自动机院系信息工程学院班级计算机科学与技术1班学号 2013550336 姓名朱义一、实验目的通过本次实验,加深对正则表达式,NFA,DFA及其识别的语言的理解二、实验题目编程实现NFA确定化为NFA的过程三、算法思想1.一个自动机是一个五元组,分别是<状态集,符号集,f函数,起始状态,终止状态>2.使用子集法的步骤是:1)将起始状态求闭包,得到S0。
2)从0开始直到totss对每个子集求各个字符所能到达的新子集将其加入tot+1子集中。
3)检查tot+1子集是否与之前的子集重合或者为空,如果重合或为空则子集不增加.4)记录新的状态转换函数。
3. 根据NFA转化为DFA的过程一步步模拟进行操作。
四、数据结构介绍程序里将NFA五元组分别储存在以下数据结构里初态集储存在 int数组 sta_statu[maxs]里 maxs为元素的最大数终态集储存在 int数组 end_statu[maxs]里字符集储存在 char数组 cha[maxs]里状态储存为0~n-1(n个状态情况)状态转换函数储存于结构 stuct statu里struct Edge{ //转化边char cost; //消耗int dest; //指向的终点};struct statu{Edge node[50]; // 终点int cnt;//边的数量statu(){cnt=0;for(int i=0;i<50;i++){node[i].cost=’#';node[i].dest=0;}}}sta[50];//起点五、具体实现使用子集法实现:函数接口解释:void creat_subset(void); 构造子集函数Ins(int a,int ss) 用深搜(dfs)求状态ss的闭包,并将闭包里的所有元素加入到子集closure[a]里。
void ins_subset(int a,int ss,char target)求状态ss通过字符target所能到达的所有状态,并将这些状态加入到子集closure[a]里。
编译原理 NFA转DFA

实验一:利用子集法构造DFA一.实验目的掌握将非确定有限自动机确定化的方法和过程。
二.实验要求、内容及步骤实验要求:1.输入一个NFA,输出一个接受同一正规集的DFA;2.采用C++语言,实现该算法;3.编制测试程序;4.调试程序。
实验步骤:1.输入一个NFA关系图;2.通过一个转换算法将NFA转换为DFA;3.显示DFA关系图。
三.实验设备计算机、Windows 操作系统、Visual C++ 程序集成环境。
四.实验原理1.NFA-DFA转换原理:从NFA的矩阵表示中可以看出,表项通常是一状态的集合,而在DFA的矩阵表示中,表项是一个状态,NFA到相应的DFA的构造的基本思路是:DFA的每一个状态对应NFA的一组状态。
DFA使用它的状态去记录在NFA读入一个输入符号后可能到达的所有状态。
输入:一个NFA N输出:一个接受同样语言的DFA D方法:为D构造转换表Dtran,DFA的每个状态是NFA的状态集。
D的状态集合用Dstates表示。
D的开始状态为ε-closure(s0),s0是N的开始状态。
使用下列算法构造D的状态集合Dstates和转换表Dtran。
如果D的某个状态是至少包含一个N的接受状态的NFA状态集,那么它是D的一个接受状态。
2.子集构造法:初始时, ε-closure(S0) 是Dstates中唯一的状态且未被标记;while Dstates中存在一个未标记的状态T do begin标记T;for 每个输入符号a do beginU := ε-closure ( move (T, a) );if U 没在Dstates中then将U作为一个未被标记的状态添加到 Dstates.Dtran [ T, a ] := Uendend3.ε-closure的计算:将T中所有状态压入栈stack;将ε-closure (T) 初始化为T;while stack不空 do begin将栈顶元素t弹出栈;for 每个这样的状态u:从t到u有一条标记为ε的边do if u不在ε-closure ( T )中 do begin将u 添加到ε-closure ( T );将u压入栈stack中 endend五.程序设计1.总体设计2.子程序设计识别模块读入字符识别模块识别标识符识别分界符、运算符识别常数输出六.程序中的结构说明1.结构体Symbolrecord 结构体结构体成员名 成员属性Symbol[10] 用于存储关键字编码名 id用于存储关键字对应的编码读取字符字母识别标识符数字识别数字/识别注释打印并结束FTFTFTentrytype结构体结构体成员名成员属性idname[10] 用于存储识别后标识符名address 用于存储标识符的地址type 用于存储标识符的类型digittype结构体结构体成员名成员属性num 用于存储识别后的数字address 用于存储标识符数字的地址tokentype结构体结构体成员名成员属性id 用于存储被识别的类型名entry 用于存储标识符的地址idname[10] 用于存储被识别的标识符名2.符号编码表符号编码表符号名代码符号名代码Begin 0 } 14End 1 ( 15If 2 ) 16 Then 3 < 17 Else 4 <= 18for 5 = 19do 6 != 20while 7 > 21+ 8 >= 22- 9 := 23* 10 ‘’24/ 11 Id 25; 12 Const 26{ 133.重要函数介绍tokentype recogid(char ch)//识别标识符算法tokentype recogdig(char ch) ///识别数字函数tokentype recogdel(char ch) //识别算符和界符函数tokentype handlecom(char ch) //handlecom函数,识别注释函数void sort(char ch) //sort函数,读取文件内容,并根据读入内容调用不同的识别函数void scanner()//scanner函数,打开文件七.函数代码#include <stdio.h>#include <string.h>#include <ctype.h>#include <stdlib.h>;-----------------------定义单词编码表的数据结构-------------------- struct symbolrecord{ char symbol[10];int id;} ;;-------------------------定义符号表的数据结构---------------------- struct entrytype{ char idname[10];int address;int type;};;-------------------------定义常数表的数据结构---------------------- struct digittype{ int num;int address;};;---------------------------Token字的数据结构----------------------- struct tokentype{ int id;int entry;char idname[10];};FILE *fp; //源文件指针struct digittype d[10]; //定义常数表,个数指针struct entrytype a[40];int k=0,t=0;;---------------------------单词编码表初始化------------------------ struct symbolrecord s[26]={ "Begin",0,"End",1,"If",2,"Then",3, "Else",4, "for",5, "do",6,"while",7, "+",8,"-",9,"*",10,"/",11,";",12,"{",13,"}",14,"(",15,")",16,"<",17,"<=",18, "=",19,"!=",20, ">",21,">=",22, ":=",23, " ",24,"const",26 };;---------------------------识别标识符算法-------------------------- tokentype recogid(char ch){ tokentype tokenid;FILE *fs;int flag,fflag;char word[10]={0};int i,j;i=0;while(isalpha(ch)||isdigit(ch)){ word[i]=ch;ch=fgetc(fp);i=i+1;}ungetc(ch,fp);word[i]='\0';for(j=0;j<=8;j++){ flag=strcmp(word, s[j].symbol);if(flag==0) //是关键字{ tokenid.id=j;tokenid.entry=-1;break;} }if(flag!=0){ for(j=0;j<=k;j++){ fflag=strcmp(a[j].idname,word);if(fflag==0) //在符号表中可以找到{ tokenid.id=25;tokenid.entry=a[j].address;break;} }if(fflag!=0){ fs=fopen("symbol.txt","a"); //符号表中不存在的标识符 strcpy(a[k].idname, word);a[k].address=k;a[k].type=25;tokenid.id=25;tokenid.entry=k;for(j=0;j<9;j++)fprintf(fs,"%c",word[j]);fprintf(fs,"%c",'\t');fprintf(fs,"%d",a[k].address);fprintf(fs,"%c",'\t');fprintf(fs,"%d",a[k].type);fprintf(fs,"%c",'\n');fclose(fs);k=k+1;} }strcpy(tokenid.idname, word);//自行添加的return tokenid;};-----------------------------识别数字函数-------------------------- tokentype recogdig(char ch){ int flag;int i=0,j;int num=0;tokentype tokenid;while(isdigit(ch)){ num=(ch-48)+num*10;ch=fgetc(fp);i=i+1;}for(j=0;j<=t;j++)if(d[j].num==num){ flag=1;tokenid.id=26;tokenid.entry=d[j].address;break;}if(flag!=1){ d[t].num=num;d[t].address=t;tokenid.id=26;tokenid.entry=t;t=t+1;}sprintf(tokenid.idname, "%d", num);//int>>charreturn tokenid;};------------------------识别算符和界符函数------------------------- tokentype recogdel(char ch){ tokentype tokenid;switch(ch){ case'{':{ tokenid.id=13;strcpy(tokenid.idname, "{");//自行添加的}break;case'}':{ tokenid.id=14;strcpy(tokenid.idname, "}");}break;case';':{ tokenid.id=12;strcpy(tokenid.idname, ";");}break;case'=':{ tokenid.id=19;strcpy(tokenid.idname, "=");}break;case':':ch=fgetc(fp);if(ch=='=') tokenid.id=23; break;case'!':{ ch=fgetc(fp);if(ch=='=') tokenid.id=20;strcpy(tokenid.idname, "!="); } break;case'<':{ch=fgetc(fp);if(ch=='='){ tokenid.id=18;strcpy(tokenid.idname, "<=");}else{ tokenid.id=17;strcpy(tokenid.idname, "<");ungetc(ch,fp);}}; break;case'>':ch=fgetc(fp);if(ch=='='){tokenid.id=22;strcpy(tokenid.idname, ">=");}else { tokenid.id=21;strcpy(tokenid.idname, ">");ungetc(ch,fp);}; break;case'+':{ tokenid.id=8;strcpy(tokenid.idname, "+");}break;case'*':{ tokenid.id=10;strcpy(tokenid.idname, "*");}break;case'(':{ tokenid.id=15;strcpy(tokenid.idname, "(");}break;case')':{ tokenid.id=16;strcpy(tokenid.idname, ")");}break;}tokenid.entry=-1;return tokenid;};---------------------------handlecom函数--------------------------- tokentype handlecom(char ch){ tokentype tokenid;char ch1;int flag=0;if(ch!='*' ){ tokenid.id=25;tokenid.entry=-1;}else{ while(flag==0){ ch1=ch;ch=fgetc(fp);if((ch1='*')&&(ch='/'))flag=1;}}return tokenid;};---------------------------sort函数---------------------------- void sort(char ch){struct tokentype tokenword;FILE * fq = fopen("tokenfile.txt","a");if(isalpha(ch))tokenword=recogid(ch); //字母else if(isdigit(ch))tokenword=recogdig(ch); //数字else if(ch=='/')tokenword=handlecom(ch);elsetokenword=recogdel(ch);printf("%s\t%d\t%d\n",tokenword.idname,tokenword.id,tokenword.entry) ;fprintf(fq,"%d",tokenword.id);fprintf(fq,"%c",'\t');fprintf(fq,"%d",tokenword.entry);fprintf(fq,"%c",'\n');fclose(fq);};--------------------------scanner函数---------------------------- void scanner(){ char ch;fp=fopen("source.txt","r");ch=getc(fp);while(ch!=EOF){ if(!isspace(ch)){ sort(ch);}ch=fgetc(fp);}fclose(fp);};------------------------------主函数------------------------------ int main(){ int i;printf("输出token字如下:\n");printf("idname\ttype\taddress\n");scanner();printf("************************************\n");printf("输出符号表如下:\n");printf("%s\t%s\t%s\n","idname","address","type");for(i=0;i<=k-1;i++)printf("%s\t%d\t%d\n",a[i].idname,a[i].address,a[i].type);printf("************************************\n"); printf("输出常数表如下:\n");printf("%s\t%s\n","num","address");for(i=0;i<=t-1;i++)printf("%d\t%d\n",d[i].num,d[i].address);printf("\n\n");system("pause");}八.程序测试Source源文件程序截图main(){If a!=35end;do whileend;36}九.实验小结子集构造法的基本思想是构造得到的DFA的每个状态对应于NFA的一个状态集合。
NFA转化为DFA的转换算法及实现

NFA转化为DFA的转换算法及实现确定有限状态自动机(NFA)与确定有限状态自动机(DFA)是两种不同类型的有限状态机。
NFA允许多个状态和转换到一个状态的ε转换。
而DFA每个状态只能有一个确定的转移。
因此,将NFA转换为DFA可以简化状态机的操作和分析。
NFA转换为DFA的转换算法通常有以下几个步骤:1.确定NFA的起始状态集合。
-如果NFA的起始状态包含ε转换,则找到所有可以通过ε转换到达的状态,将它们作为DFA的起始状态集合。
-否则,将NFA的起始状态直接作为DFA的起始状态。
2.对于每个DFA状态集合,找到从该状态集合出发,通过各个输入符号可以到达的NFA状态集合。
-对于DFA状态集合中的每个状态,找到通过该状态的转换(不包括ε转换)可以到达的NFA状态集合。
-将得到的NFA状态集合作为新的DFA状态集合。
3.重复步骤2,直到不再产生新的DFA状态集合。
-持续重复步骤2,直到没有新的DFA状态集合被创建。
4.为DFA中的每个状态集合标记是否包含NFA的终止状态。
-如果一个DFA状态集合包含一个或多个NFA终止状态,将该DFA状态集合标记为终止状态。
5.根据DFA状态集合之间的转换生成DFA的转换表。
-对于每个DFA状态集合中的状态,找到通过各个输入符号可以到达的NFA状态集合。
-将这些NFA状态集合对应的DFA状态集合作为DFA转换表中的输入符号的转换目标。
6.完成DFA的构建。
以下是一个Python示例代码,用于将NFA转换为DFA:```pythonfrom collections import defaultdictdef nfa_to_dfa(nfa):dfa_start_states = epsilon_closure([nfa.start_state])dfa_states = [dfa_start_states]dfa_transitions = {}dfa_final_states = []while dfa_states:current_dfa_state = dfa_states.pop(0)if nfa.final_state in current_dfa_state:dfa_final_states.append(current_dfa_state)for symbol in nfa.alphabet:symbol_closure = epsilon_closure(move(current_dfa_state, symbol))if len(symbol_closure) == 0:continueif symbol_closure not in dfa_states:dfa_states.append(symbol_closure)dfa_transitions[(current_dfa_state, symbol)] =symbol_closurereturn DFA(dfa_start_states, dfa_final_states,dfa_transitions)def epsilon_closure(states):closure = set(states)stack = list(states)while stack:state = stack.popfor transition in state.transitions:if transition.symbol == EPSILON and transition.target_state not in closure:closure.add(transition.target_state)stack.append(transition.target_state)return frozenset(closure)def move(states, symbol):result = setfor state in states:for transition in state.transitions:if transition.symbol == symbol:result.add(transition.target_state)return resultclass NFAState:def __init__(self, transitions):self.transitions = transitionsclass NFA:def __init__(self, start_state, final_state, alphabet): self.start_state = start_stateself.final_state = final_stateself.alphabet = alphabetclass DFAState:def __init__(self, states):self.states = statesclass DFA:def __init__(self, start_state, final_states, transitions): self.start_state = start_stateself.final_states = final_statesself.transitions = transitions。
编译原理NFA转DFA

编译原理实验报告实验名称不确定有限状态自动机的确定化实验时间院系计算机科学与技术学院班级学号姓名1.试验目的输入:非确定有限(穷)状态自动机。
输出:确定化的有限(穷)状态自动机2.实验原理一个确定的有限自动机(DFA)M可以定义为一个五元组,M=(K,∑,F,S,Z),其中:(1)K是一个有穷非空集,集合中的每个元素称为一个状态;(2)∑是一个有穷字母表,∑中的每个元素称为一个输入符号;(3)F是一个从K×∑→K的单值转换函数,即F(R,a)=Q,(R,Q∈K)表示当前状态为R,如果输入字符a,则转到状态Q,状态Q称为状态R的后继状态;(4)S∈K,是惟一的初态;(5)Z⊆K,是一个终态集。
由定义可见,确定有限自动机只有惟一的一个初态,但可以有多个终态,每个状态对字母表中的任一输入符号,最多只有一个后继状态。
对于DFA M,若存在一条从某个初态结点到某一个终态结点的通路,则称这条通路上的所有弧的标记符连接形成的字符串可为DFA M所接受。
若M的初态结点同时又是终态结点,则称ε可为M所接受(或识别),DFA M所能接受的全部字符串(字)组成的集合记作L(M)。
一个不确定有限自动机(NFA)M可以定义为一个五元组,M=(K,∑,F,S,Z),其中:(1)k是一个有穷非空集,集合中的每个元素称为一个状态;(2)∑是一个有穷字母表,∑中的每个元素称为一个输入符号;(3)F是一个从K×∑→K的子集的转换函数;(4)S⊆K,是一个非空的初态集;(5)Z⊆K,是一个终态集。
由定义可见,不确定有限自动机NFA与确定有限自动机DFA的主要区别是:(1)NFA的初始状态S为一个状态集,即允许有多个初始状态;(2)NFA中允许状态在某输出边上有相同的符号,即对同一个输入符号可以有多个后继状态。
即DFA中的F是单值函数,而NFA中的F是多值函数。
因此,可以将确定有限自动机DFA看作是不确定有限自动机NFA的特例。
编译原理NFA转化为DFA的转换算法及实现

编译原理NFA转化为DFA的转换算法及实现编译原理是研究计算机程序语言的一门学科,其中一项重要的内容就是自动机理论,包括NFA(非确定性有限自动机)和DFA(确定性有限自动机)的转换。
NFA到DFA转换算法的实现分为几个关键步骤,下面将逐一进行介绍。
首先,我们需要了解NFA和DFA的基本概念。
NFA是一种具有状态、输入字母表和状态转移函数的自动机模型,允许多个状态同时转移到其他状态。
而DFA则是一种状态转移函数确定的自动机模型,每个输入字符只能引发一条状态转移。
接下来,我们将介绍NFA到DFA的转换算法。
1. 子集构造法(Subset Construction)子集构造法是将NFA转化为DFA的一种常用算法。
该算法的基本思想是,将NFA的每个状态集表示为DFA的状态。
转换过程如下:-创建DFA的初始状态集,初始状态集即为NFA的初始状态的ε闭包。
-逐个处理DFA的状态集,对于每个状态集,针对输入字符进行转移,计算新的状态集的ε闭包。
-若新的状态集已存在于DFA中,则不需要再次处理,若不存在,则将其加入到DFA中。
-迭代上述步骤,直至没有新的状态集加入。
2. ε闭包(ε-closure)ε闭包是指在NFA中的一些状态集S中,能够通过连续零个或多个ε转移到达的状态集合。
在转换过程中,需要计算新的状态集的ε闭包,来确定DFA的状态集。
具体步骤如下:-初始化ε闭包为输入的状态集S。
-对于S中的每个状态,获取其所有的ε转移目标状态,并将其添加到ε闭包中。
-重复上述步骤,直到ε闭包不再发生变化为止。
3. 状态转移(Transition)在NFA中,状态可以同时转移到多个状态。
而在DFA中,每个状态只能转移到一个状态。
因此,在转换过程中,需要确定每个状态在一些输入字符下的转移目标。
-对于每个状态集S、输入字符a,计算S在输入字符a下的转移目标状态集,即计算S中每个状态通过输入字符a能够到达的状态集。
-根据计算的转移目标状态集,将其作为DFA中S状态在输入字符a下的转移目标。
NFA转化为DFA编译原理实验报告

NFA转化为DFA编译原理实验报告一、引言正则表达式是一种用于描述字符串模式的符号语言,可以通过正则表达式来进行字符串匹配、替换和等操作。
而有限状态自动机(NFA)是一种可以识别正则表达式的数学模型,是实现正则表达式的基础。
二、实验内容本实验使用Python语言编写,主要实现了以下功能:1.输入正则表达式,构建对应的NFA。
2.将NFA转化为DFA。
3.输出DFA的状态转移表。
三、实验过程1.构建NFA首先,通过用户输入正则表达式,使用Thompson算法构建对应的NFA。
Thompson算法使用了三种基本构建块:连接、选择和闭包。
通过多个基本构建块的组合,可以构建出更加复杂的正则表达式的NFA。
其中,连接操作通过在两个状态之间添加一个空转移实现,选择操作通过添加两个新的开始和接受状态,并将其与原始状态进行连接。
闭包操作通过添加两个新的开始和接受状态,并分别连接到原始状态和自身。
2.NFA转DFANFA转DFA的主要思路是从NFA的初始状态开始,通过遍历所有可能的输入字符,计算对应的闭包和移动集合。
闭包集合表示从当前状态出发通过空转移可以到达的所有状态,移动集合表示从当前状态出发经过一次输入字符转移的所有可能状态。
通过计算闭包和移动集合,可以得到DFA的所有状态和状态转移关系。
在转换过程中,需要考虑ε-closure运算和move运算的效率和正确性。
3.输出DFA状态转移表最后,将计算得到的DFA的状态转移关系输出为状态转移表的形式,方便后续的分析和使用。
四、实验结果本实验通过输入不同的正则表达式,得到了对应的NFA,并成功将NFA转化为DFA,并输出了DFA的状态转移表。
通过实验结果可以发现,无论正则表达式的复杂度如何,DFA都可以给出准确的匹配结果,实现了对正则表达式的准确识别。
五、实验总结通过本实验,我进一步理解了正则表达式、NFA和DFA之间的关系。
正则表达式作为一种表示字符串模式的符号语言,可以通过NFA来进行匹配和等操作。
编译原理nfa-dfa
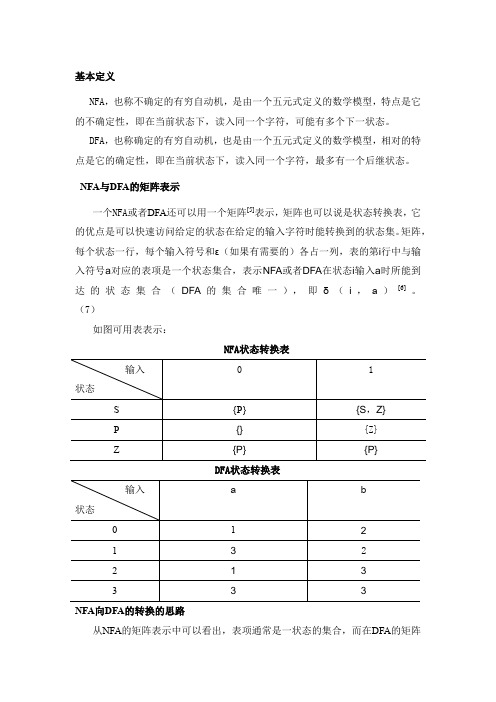
基本定义NFA,也称不确定的有穷自动机,是由一个五元式定义的数学模型,特点是它的不确定性,即在当前状态下,读入同一个字符,可能有多个下一状态。
DFA,也称确定的有穷自动机,也是由一个五元式定义的数学模型,相对的特点是它的确定性,即在当前状态下,读入同一个字符,最多有一个后继状态。
NFA与DFA的矩阵表示一个NFA或者DFA还可以用一个矩阵[5]表示,矩阵也可以说是状态转换表,它的优点是可以快速访问给定的状态在给定的输入字符时能转换到的状态集。
矩阵,每个状态一行,每个输入符号和ε(如果有需要的)各占一列,表的第i行中与输入符号a对应的表项是一个状态集合,表示NFA或者DFA在状态i输入a时所能到达的状态集合(DFA的集合唯一),即δ(i,a)[6]。
(7)如图可用表表示:NFA状态转换表DFA状态转换表NFA向DFA的转换的思路从NFA的矩阵表示中可以看出,表项通常是一状态的集合,而在DFA的矩阵表示中,表项是一个状态,NFA到相应的DFA的构造的基本思路是:DFA的每一个状态对应NFA的一组状态DFA使用它的状态记录在NFA读入一个输入符号后可能达到的所有状态[4]。
NFA和DFA之间的联系在非确定的有限自动机NFA中,由于某些状态的转移需从若干个可能的后续状态中进行选择,故一个NFA对符号串的识别就必然是一个试探的过程。
这种不确定性给识别过程带来的反复,无疑会影响到FA的工作效率。
而DFA则是确定的,将NFA转化为DFA将大大提高工作效率,因此将NFA转化为DFA是有其一定必要的。
子集构造法已证明:非确定的有限自动机与确定的有限自动机从功能上来说是等价的,也就是说,我们能够从:NFA M使得L(M)=L(M’)为了使得NFA确定化,我们首先给出两个定义:定义1:集合I的ε-闭包:令I是一个状态集的子集,定义ε-closure(I)为:1)若s∈I,则s∈ε-closure(I);2)若s∈I,则从s出发经过任意条ε弧能够到达的任何状态都属于ε-closure(I)。
NFA转换为DFA

NFA转换为DFA摘抄:⼤家好,欢迎⼤家来到coding迪斯尼,上⼀节我们研究了如何使⽤NFA识别输⼊字符串,同时提出了来个概念,⼀个是ε闭包操作,⼀个是move得到转移集合。
这两个操作在我们今天的主题,将NFA转换为DFA的算法中将占据主导地位。
我们任然以上⼀节⽤到的NFA状态机为例⼦,看看它是怎么转换为DFA的NFA转DFA算法:我们先获取NFA的起始节点,然后计算它的ε闭包:ε-closure({17}) = { 17, 3 , 1, 4, 5, 9}我们知道,处于ε闭包中的任何⼀个状态节点时,我们可以不⽤输⼊任何字符就可以直达其他节点,因此,闭包中的所有节点其实可以等价于⼀个节点,这个节点就可以作为NFA对应的DFA中的⼀个节点。
因此我们把集合{ 17, 3 , 1, 4, 5, 9}对应于⼀个节点,记为S0:(S0, { 17, 3 , 1, 4, 5, 9})于此同时把上⾯的节点标记加⼊⼀个队列中,最为队列的开头:[(S0, { 17, 3 , 1, 4, 5, 9})]NFA状态机可接受的字符是数字字符和字符 ’.’ ,接下来我们计算S0对数字字符和字符’.’ 的转移集合:Move(S0, .) = Move({ 17, 3 , 1, 4, 5, 9}, . ) = {6}接着计算{6}的ε闭包:ε-closure({6}) = {6,7}, 然后看看{6,7}在上⾯的队列中是否存在,由于当前队列只有⼀个元素:[(S0, { 17, 3 , 1, 4, 5, 9})],所以{6,7}在队列中不存在,于是我们把{6,7}当做DFA的第⼆个状态节点记做(S1, {6,7}), 把它加⼊到队列中:[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]这样我们就有了两个节点的对应关系 S0-(.)->S1.我们再计算S0对应数字字符时所得的转移集合:Move(S0, D) = Move({ 17, 3 , 1, 4, 5, 9}, D) = {2, 10}然后对{2,10}做闭包操作:ε-closure({2,10}) = {2,10,4,5,1,11}看看队列中是否有{2,10,4,5,1,11}对应的节点,由于没有对应节点,所以该集合可作为DFA的⼀个节点,记做(S2, {2,10,4,5,1,11}). 然后把它加⼊队列:[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]->[(S2, {2,10,4,5,1,11})]于是我们⼜有了⼀个节点对应关系:S0-(D)->S2最后我们得到DFA的三节点关系图:⼤家要注意,从图上看S0 到 S2 只有⼀条边,但是D代表的是数字字符的集合[0-9],所以实际上S0到S2有10条边,也就是S0有10条出去的边,边对应的字符分别是0,1,2…9, 这⼗条边都指向S2,上图为了简明,所以把这⼗条边抽象为1条边,在后续我们代码中,构造的DFA将会有10条边指向S2,这个差别⼤家要留⼼。
编译实验三NFA转换成DFA和DFA化简要点

编译实验三NFA转换成DFA和DFA化简要点NFA转换成DFA是正则表达式、有限自动机以及编译原理等课程的重要内容之一、本文将从NFA的定义、转换方法和DFA化简方法这三个方面进行详细讲解。
一、NFA的定义有限自动机(NFA)是一种图形化工具,用于描述正则表达式的结构和过程。
它由状态集合、输入字母表、状态转换函数和初始状态、接受状态组成。
1. 状态集合:NFA的状态集合是有限的,用Q表示,可以表示为{q1, q2, ..., qn}。
2. 输入字母表:NFA的输入字母表是有限的,用Σ表示,可以表示为{a1, a2, ..., am}。
3.状态转换函数:NFA的状态转换函数是从状态集合到状态集合的映射,用δ表示,可以表示为δ:Q×Σ→2^Q,即对于状态q和输入a,转换函数δ(q,a)表示从状态q经过输入a可能到达的一组状态。
4.初始状态:NFA的初始状态是一个状态,用q0表示,它属于状态集合Q。
5.接受状态:NFA的接受状态是一组状态,用F表示,属于状态集合Q。
二、NFA转换成DFA的方法将NFA转换成DFA是为了更方便地处理和理解正则表达式。
下面介绍两种常用的NFA转DFA的方法:子集法和马勒机法。
1.子集法:子集法是NFA转DFA的一种常用方法。
具体步骤如下:(1)根据NFA的接受状态构造DFA的接受状态。
(2)以NFA的初始状态为起点,利用状态转换函数生成新的状态。
(3)重复第二步,直到没有新状态为止。
2.马勒机法:马勒机法是NFA转DFA的另一种常用方法。
具体步骤如下:(1)将NFA的状态集合拆分成两组,一组是NFA接受状态的集合,另一组是其余状态的集合。
(2)建立一个新的DFA状态对应于每一组。
(3)将NFA状态转换函数进行转换,使得DFA状态和输入字母的组合对应一个新的DFA状态。
三、DFA化简方法对于转换完成的DFA,为了提高运行效率和降低资源消耗,一般需要进行化简,即将等价的状态合并为一个。
编译原理报告:NFA转DFA(详解-附源代码).doc

编译原理实习报告学号:******班级:******姓名:******日期:2015目录1.题目及需求分析 (3)2.设计分析 (3)3.调试分析 (7)4.用户手册 (7)5.测试结果 (7)6.总结 (7)7.源代码 (8)题目:NFA 转换为等价的DFA 实习时间:2015.10.12【问题描述】以定理“设L 为一个由不确定的有穷自动机接受的集合,则存在一个接受L 的确定的有穷自动机”为理论基础,设计算法实现将不确定的有穷自动机(NFA)转换为与之等价的确定的有穷自动机(DFA)。
【基本要求】① 确定能够表示FA 的合适的结构,以便FA 的输入和输出② 设计的算法既要成功实现题目要求的功能,又要高效、鲁棒③ 程序中的函数、变量等命名要规则,可读性要强(易懂) 1.需求分析(1) 要将以状态转换图表示的NFA 转换为DFA ,首先应设计一个结构来表示FA ,以便图形式的FA 便于输入和输出。
(2) 设计合适的算法来实现NFA 的确定化,这里用子集法来构造等价的DFA 。
(3) 测试数据:课本P59例4.8转换前的NFA 转换后的DFA2.设计(1)数据结构设计由于FA 是一个图,可想到用图的存储结构来存储FA ,但是,FA 中两个结点之间的路径可以不只一条,这让想考虑用邻接矩阵来存储的FA 处理起来有点复杂,我采用的是“结点-边-结点”式的三元组来表示FA 。
FA 有多少条边就应该有多少个这样的三元组,以一个数组来存放这些三元组,那么一个FA 就可以表示出来了。
此外,由子集法的步骤可见,集合(set)这一结构应该使用,,set 结构符合我们数学的集合要求,不含相同元素,并且两个集合间还可以进行比较是否相等,十分有利于我们的程序实现。
表示FA 的结构:集合与栈使用库里面的标准集合、栈。
即包含头文件set 、stack//Triad(三元组):S → aB 即(S,a,B ) struct Triad{ char start; char edge; char end; };(2)文件结构程序不是很复杂,加之使用到的数据结构是标准库里的,文件只有一个N2D.cpp,其中有#include<set>和#include<starck>。
编译原理:NFA转DFA(含数据可视化)

编译原理:NFA转DFA(含数据可视化)def printlist(l):for i in range(len(l)):print(l[i], end=" ")print("----------------------------输⼊NFA样例-----------------------------")ab = eval(input("请输⼊变量的个数"))print("请输⼊变量名称(⽤_(下划线)表⽰空)")aabb = []for i in range(1, ab + 1):aabb_eval = input("第" + str(i) + "个变量的名称是: ")aabb.append(aabb_eval)printlist(aabb)# [a,b,c]# 输⼊变量的个数之后将为这个创造字典l = [{} for i in range(ab)] # 创建和变量相同个数的字典n = 0while n < ab:print("开始构造变量" + aabb[n] + "的两节点状态")while True:status = input("请输⼊起始状态")end_status = input("请输⼊终⽌状态")if status != '#' or end_status != '#':l[n].setdefault(status, end_status)else:print(aabb[n] + "变量的构造输⼊已经结束")breakn = n + 1for i in range(len(l)):if aabb[i] == '_':print("空变量的节点起始关系为:" + str(l[i]))else:print("变量" + aabb[i] + "的节点起始关系为:" + str(l[i]))print(l)# 空变量的节点起始关系为:{'2': '3', '1': '4', '5': '6'}# 变量a的节点起始关系为:{'1': '4', '3': '5'}# 变量b的节点起始关系为:{'5': '2', '3': '5'}key_list = []for i in range(len(l)):for k in l[i].keys():if k not in key_list:key_list.append(k)print("状态节点有:", end=" ")# {1,2,3,4,5}printlist(key_list)print()start = input('请输⼊起始节点')end_list = []a = ""while a != "#":a = input("请输⼊终⽌节点(集),以#表⽰结束")end_list.append(a)end_list.pop()print("起始节点是:" + start)print("终⽌节点(集)是:", end="")printlist(end_list)# 变量a的节点起始关系为:{'1': '2', '3': '4'}# 变量b的节点起始关系为:{'1': '3', '5': '2'}# 空变量的节点起始关系为:{'2': '3', '4': '5'}# 状态节点有: 1 3 5 2 4# 请输⼊起始节点1# 请输⼊终⽌节点(集),以#表⽰结束3# 请输⼊终⽌节点(集),以#表⽰结束## 起始节点是:1# 终⽌节点(集)是:3print()print("\n-------------------将状态节点保存到⽂件中-----------------")with open('nfa.txt', 'w') as f:f.write(start + "\n")for i in range(len(end_list)):f.write(end_list[i] + " ")f.write("\n")for j in range(len(l)): # j表⽰第⼏个字典for k in range(len(l[j])): # k表⽰第⼏个键值对for m in l[j].keys(): # m表⽰第⼏个键f.write(m + " " + aabb[j] + " " + l[j][m] + "\n")print("\n------------------读取⽂件中的信息----------------------")with open('nfa.txt', 'r') as r:nfa = []for line in r.readlines(): # 将⽂件数据内容保存到nfa列表当中line_rstrip = line.rstrip('\n')nfa.append(line_rstrip)# print(nfa)begin_start = nfa[0].split() # 起始节点#print(begin_start)end_end_list = nfa[1].split() # 终⽌节点#print(end_end_list)# 如果是按照前⾯的⽅法创建的,那么以上代码没有必要,直接⽤start和end_list即可trans_nfa = nfa[2:]#print(trans_nfa)for i in range(len(trans_nfa)):trans_nfa[i] = trans_nfa[i].split()#print(trans_nfa)# #[['1', 'a', '2'], ['3', 'a', '4'], ['1', 'a', '2'], ['3', 'a', '4'], ['1', 'b', '2'], ['3', 'b',# '4'], ['1', 'b', '2'], ['3', 'b', '4'], ['1', '_', '2']] 所有的状态已经标识好了state_to_draw = [] # 状态节点para_to_draw = [] # 转换变量for i in range(len(trans_nfa)):state_to_draw.append(trans_nfa[i][0])state_to_draw.append(trans_nfa[i][2])para_to_draw.append(trans_nfa[i][1])# print(state_to_draw)# print(para_to_draw)state0 = list(set(state_to_draw)) # 去除节点重复state0.sort(key=state_to_draw.index) # 对节点进⾏排序para0 = list(set(para_to_draw))para0.sort(key=para_to_draw.index)# print(state0) # ['0', '1', '2', '4', '3', '6', '5', '7', '8', '9', '10']# print(para0) # ['_', 'a', 'b']if '_' in para0:para0.remove('_')# 去掉空_closure = dict() # 表⽰空串可以到达的集合print("\n--------------开始作图-------------------")from graphviz import Digraphdef draw_nfa():g = Digraph('G', filename='nfa.gv', format='png')for i in range(len(trans_nfa)):g.edge(trans_nfa[i][0], trans_nfa[i][2], label=trans_nfa[i][1])for i in range(len(begin_start)):g.node(begin_start[i], color='red')for i in range(len(end_end_list)):g.node(end_end_list[i], shape='doublecircle')g.view()draw_nfa()print("\n------------nfa作图完毕------------------")print("\n-----------开始进⾏NFA转DFA---------------")## 寻找所有空闭包for i in range(len(state0)):res = [state0[i]] # 第i个节点# print(res)for j in range(len(trans_nfa)):if trans_nfa[j][0] == state0[i] and trans_nfa[j][1] == '_':# 如果⽬前研究的节点⾥⾯存在着空res.extend(trans_nfa[j][2])# 这⾥⽤_closure[state0[i]] = list(set(res))# 到此,⼀个状态所有的空闭包都会显现出来,接下来只要⼀查到底即可# print(_closure)# {'0': ['1', '0', '7'], '1': ['1', '2', '4'], '2': ['2'], '4': ['4'], '3': ['6', '3'], '6': ['7', '6', '1'], '5': ['5', '6'], '7': ['7'], '8': ['8'], '9': ['9'], '10': ['10']} # 空闭包的递归查询------def find_closure(state_input):state_now = _closure[state_input] # 查询输⼊⼀个状态下是否有空闭包 ['1', '0', '7']state_now_list = []for state_now_para in state_now:state_now_list = state_now_list + _closure[state_now_para] # 递归查询state_now_list = list(set(state_now_list))## 尝试输出#print(state_now_list) # ['0', '7', '1', '2', '4']while set(state_now) != set(state_now_list): # 多次查询state_now = state_now_liststate_now_list = []for state_now_para in state_now:state_now_list = state_now_list + _closure[state_now_para]state_now_list = list(set(state_now_list))return state_now_listA = find_closure(state0[0]) # 初始状态的空闭包#print(A) # ['1', '7', '4', '2', '0']def find_state(l_state):res = dict() # 创建⼀个字典,⾥⾯的值是状态集合for c in para0: # ['_', 'a', 'b']res_two = []for i in range(len(l_state)):for j in range(len(trans_nfa)): # [['0', '_', '1'], ['1', '_', '2'], ['1', '_', '4'], ['2', 'a', '3'], ['3', '_', '6'], ['4', 'b', '5'], ['5', '_', '6'], ['6', '_', '7'], ['7', 'a', '8'], ['8', 'b', '9'], ['9', 'b', '10'], ['6', '_', '1'], ['0', '_', '7']] if trans_nfa[j][0] == l_state[i] and trans_nfa[j][1] == c:res_two.append(trans_nfa[j][2])result = []for k in res_two:result = result + find_closure(k)res[c] = list(set(result))return resnumber = 0length = 1state_list = []state_list.append(A) # [['0', '7', '1', '2', '4']]while number < length:A2 = find_state(state_list[number])number = number + 1for c in para0:temp = 1for p in range(length):if set(A2[c]) == set(state_list[p]):temp = 0if temp == 1:state_list.append(A2[c])length = length + 1#print(state_list)# [['0', '2', '4', '1', '7'],# ['2', '3', '6', '4', '8', '1', '7'],# ['2', '6', '4', '5', '1', '7'],# ['9', '2', '6', '4', '5', '1', '7'],# ['2', '6', '4', '10', '5', '1', '7']]#获取开始节点和结束节点dfa_begin = []dfa_end = []for i in range(len(begin_start)):# 查看是否存在空……变量dfa_begin.append(find_closure(begin_start[i]))for j in range(len(end_end_list)):for k in range(len(state_list)):if end_end_list[j] in state_list[k]:#如果nfa的结束节点是在我的某⼀个状态列表⾥⾯if state_list[k] not in dfa_end:dfa_end.append(state_list[k])print(dfa_begin)print(dfa_end)while [] in state_list:state_list.remove([])print('DFA状态表: ', state_list)print("DFA起始状态: ", dfa_begin)print("DFA终⽌状态:", dfa_end)# DFA状态表为: [['4', '2', '0', '1', '7'], ['4', '2', '1', '7', '8', '3', '6'], ['4', '2', '1', '7', '6', '5'], ['4', '2', '1', '7', '9', '6', '5'], ['4', '2', '1', '7', '10', '6', '5']]# DFA开始状态: [['4', '2', '0', '1', '7']]# DFA终⽌状态: [['4', '2', '1', '7', '10', '6', '5']]def draw_dfa(state_list, begin, end):g = Digraph('G', filename='dfa.gv', format='png')begin_aaa = []end_aaa = []for i in range(len(begin)):begin_aaa.append(" ".join(sorted(begin[i])))for j in range(len(end)):end_aaa.append(" ".join(sorted(end[j])))for i in range(len(state_list)):dicttttt = find_state(state_list[i])for j in para0:if state_list[i] != [] and dicttttt[j] != []:g.edge(" ".join(sorted(state_list[i])), " ".join(sorted(dicttttt[j])), label=j) for k in range(len(begin_aaa)):g.node(begin_aaa[k], color='red', shape='circle')for i in range(len(state_list)):g.node(" ".join(sorted(state_list[i])), color='blue', shape='circle')for j in range(len(end_aaa)):if end_aaa[j]!=begin_aaa[0]:g.node(end_aaa[j], shape='doublecircle')else:g.node(end_aaa[j], shape='doublecircle',color='red')g.view()draw_dfa(state_list, dfa_begin, dfa_end)state_dfa_other_name=[ chr(65+i) for i in range(len(state_list))]#['A', 'B', 'C', 'D', 'E']start_char=state_dfa_other_name[ state_list.index(dfa_begin[0])]start_char=list(start_char)print(start_char)end_char=[]for i in range(len(dfa_end)):s=state_dfa_other_name[state_list.index(dfa_end[i])]end_char.append(s)print(end_char)效果图:。
编译原理实验(NFA转DFA,LL1文法)

编译原理实验(NFA转DFA,LL1⽂法)编译原理实验实验⼀:实现对 C/C++ 变量定义串的分析实验⼆:实现 NFA 转 DFA 并可视化实验三:实现对⽂法的 First,Follow集,预测分析表的求解,判别是否是LL1⽂法,以及对符号串的分析过程实验⼀:实现对 C/C++ 变量定义串的分析1. 分析的串如下:string text1 = "int a = 1, b = 2; const double x = 1.5; string s = \"hello world\"; char c = 'f';";string text2 = "int a = 1; intt b = 2;";string text3 = "const int t = 5, g;";string text4 = "int a = 1, b = 2";string text5 = "double a = 9; int a = 0.9";string text6 = "int 9s = 9;";2. 分析结果如下:image-20210512001844605实验⼆:实现 NFA 转 DFA 并可视化1. NFA 的存储:nfa_k = ['0', '1', '2', '3', '4'] #状态集nfa_t = ['a', 'b'] # 边nfa_f = [('0', 'a', '0'), ('0', 'a', '3'), # 图的信息('0', 'b', '0'), ('0', 'b', '1'),('1', 'b', '2'), ('2', 'a', '2'),('2', 'b', '2'), ('3', 'a', '4'),('4', 'a', '4'), ('4', 'b', '4')]nfa_s = ['0'] # 初态nfa_z = ['2', '4'] # 终态集2. ε_closure 和 move 操作:def ε_closure(S, f):res = []vis = {}q = Queue(maxsize = 0)for i in S:q.put(i)vis[i] = 1while q.empty() is False:node = q.get()if node not in res: res.append(node)for i in f:if i[0] == node and i[1] == 'ε' and i[2] not in vis:q.put(i[2])vis[i[2]] = 1res.sort()return resdef move(S, f, a):res = []for i in S:for j in f:if j[0] == i and j[1] == a:res.append(j[2])return res3. 可视化:⼯具:graphviz画图:def draw(K, f, S, Z, pic_name):dot = Digraph(name = pic_name, format = "png")for i in S:dot.node(name = i, label = i, color = 'green')for i in Z:dot.node(name = i, label = i, color = 'red')for i in K:if i not in S and i not in Z:dot.node(name = i, label = i)for i in f:dot.edge(i[0], i[2], label = i[1])dot.view(filename = pic_name, directory = "./picture")4. 效果:1. NFA 图:image-202105120029425662. DFA 图:image-20210512003020795实验三:LL1⽂法的分析1. 数据的存储:non_term = set() # ⾮终结符集合term = set() # 终结符集合First = {} # First 集Follow = {} # Follow 集Gram = [] # 读⼊的⽂法production = {} #预处理过后的产⽣式格式为:'S':{'a', 'EF'}AnalysisList = {} # 预测分析表start_sym = '' # ⽂法开始符号end_sym = '#' # 结束符号epsilon = 'ε' # 空符isLL1 = True2. 求解 First集:def getFirst() -> None:global non_term, term, First# 初始化⾮终结符的First集为空for it in non_term: First[it] = set()# 初始化终结符的First集合为⾃⼰for it in term: First[it] = set(it)flag = Truewhile flag: # 当First集没有更新就结束flag = Falsefor X in non_term:for Y in production[X]:i = 0mark = Truewhile mark and i < len(Y):if not First[Y[i]] - set(epsilon) <= First[X]: # 还存在没有添加的# print('First[' , X, '] = ', " ", First[X], 'First[', Y[i] , '] = ' , First[Y[i]]) # First[Yi] 中没有εif epsilon not in First[Y[i]] and Y[i] in non_term and i > 0:First[X] |= First[Y[i]]mark = Falseelse:First[X] |= First[Y[i]] - set(epsilon)flag = True# Yi 不能推出ε就标记为 Falseif epsilon not in First[Y[i]]: mark = Falsei += 1if mark: First[X] |= set(epsilon)return None3. 求解 Follow集:def getFollow() -> None:global non_term, term, First, Follow, start_symfor A in non_term: Follow[A] = set() # 初始化Follow[start_sym].add(end_sym) # 1. 将 # 号加⼊到Follow[s] 中flag = Truewhile flag: # 当Follow集不再更新,算法结束flag = Falsefor A in non_term:for B in production[A]:for i in range(len(B)):# bi 是终结符则跳过if B[i] in term: continuemark = Truefor j in range(i + 1, len(B)):if not First[B[j]] - set(epsilon) <= Follow[B[i]]: # 可以更新Follow[B[i]] |= First[B[j]] - set(epsilon) # 对应书上的步骤 2 flag = True # 发⽣了改变if epsilon not in First[B[j]]: mark = Falsebreakif mark: # A->αBβ and β->εif not Follow[A] <= Follow[B[i]]: # 可以更新Follow[B[i]] |= Follow[A]flag = Truereturn None4. 构造预测分析表:# 计算预测分析表|Select集,并判断是否是LL1⽂法def getAnalysisList() -> bool:# 初始化res = Truefor i in non_term:AnalysisList[i] = dict()for j in term:if j != epsilon: AnalysisList[i][j] = NoneAnalysisList[i][end_sym] = Nonefor i in production:r = production[i]for s in r:mark = Falsefor si in s:if epsilon not in First[si]: # 不能推出空for j in First[si]:if AnalysisList[i][j] != None:AnalysisList[i][j] += ', ->' + sres = Falseelse: AnalysisList[i][j] = smark = Falsebreakelse:mark = Truefor j in First[si] - set(epsilon):if AnalysisList[i][j] != None:res = FalseAnalysisList[i][j] += ', ->' + selse: AnalysisList[i][j] = sif mark: #First[s] 可以推出空for j in Follow[i]:if AnalysisList[i][j] != None:res = FalseAnalysisList[i][j] += ', ->' + selse: AnalysisList[i][j] = sreturn res5. 分析符号串:def analysis(s: str) -> PrettyTable():res = PrettyTable()res.field_names = ['步骤', '分析栈', '剩余输⼊串', '推导所⽤产⽣式或匹配'] stk = ''stk += end_symstk += start_symstep = 0while len(stk) and len(s):step += 1top = stk[len(stk) - 1]row = []row.append(step)row.append(stk)row.append(s)if top in term or top == end_sym: # 栈顶是终结符或 # 号if top == end_sym: # 结束:row.append('接受')res.add_row(row)return resif top == s[0]: # 匹配成功row.append('"' + s[0] + '"匹配')res.add_row(row)stk = stk.replace(stk[len(stk) - 1], '', 1)s = s.replace(s[0], '', 1)continueelse: # 匹配失败row.append('匹配失败')res.add_row(row)return restmp_production = AnalysisList[top][s[0]] # 推导所⽤的产⽣式if tmp_production == None: #产⽣式为空row.append('推导失败')res.add_row(row)return resrow.append(top + '->' + tmp_production)res.add_row(row)stk = stk.replace(stk[len(stk) - 1], '', 1)if tmp_production== epsilon: #推出了空字符则不push进栈中 continuetmp_production = tmp_production[::-1]stk += tmp_production# print(row)step += 1row = []row.append(step)row.append(stk)row.append(s)row.append('失败')res.add_row(row)return res6. 分析LL1⽂法结果:image-20210512003747986image-202105120038260027. 分析⾮LL1⽂法结果:image-20210512003928356。
编译原理课程设计--NFA转化为DFA的转换算法及实现

编译原理课程设计--NFA转化为DFA的转换算法及实现编译原理课程实践报告设计名称:NFA转化为DFA的转换算法及实现⼆级学院:数学与计算机科学学院专业:计算机科学与技术班级:计科本091班姓名:林⽟兰学号: 0904402102 指导⽼师:梁德塞⽇期: 2012年6⽉摘要确定有限⾃动机确定的含义是在某种状态,⾯临⼀个特定的符号只有⼀个转换,进⼊唯⼀的⼀个状态。
不确定的有限⾃动机则相反,在某种状态下,⾯临⼀个特定的符号是存在不⽌⼀个转换,即是可以允许进⼊⼀个状态集合。
在⾮确定的有限⾃动机NFA中,由于某些状态的转移需从若⼲个可能的后续状态中进⾏选择,故⼀个NFA对符号串的识别就必然是⼀个试探的过程。
这种不确定性给识别过程带来的反复,⽆疑会影响到FA的⼯作效率。
⽽DFA则是确定的,将NFA转化为DFA将⼤⼤提⾼⼯作效率,因此将NFA转化为DFA是有其⼀定必要的。
对于任意的⼀个不确定有限⾃动机(NFA)都会存在⼀个等价的确定的有限⾃动机(DFA),即L(N)=L(M)。
本⽂主要是介绍如何将NFA转换为与之等价的简化的DFA,通过具体实例,结合图形,详细说明转换的算法原理。
关键词:有限⾃动机;确定有限⾃动机(DFA),不确定有限⾃动机(NFA)AbstractFinite automata is determinate and indeterminate two class. Determine the meaning is in a certain state, faces a particular symbol only one conversion, enter only one state. Not deterministic finite automata is the opposite, in a certain state, faces a particular symbol is the presence of more than one conversion, that is to be allowed to enter a state set.Non deterministic finite state automata NFA, because of some state are transferred from a number of possible follow-up state are chosen, so a NFA symbol string recognition must be a trial process. This uncertainty to the recognition process brought about by repeated, will undoubtedly affect the efficiency of the FA. While the DFA is determined, converting NFA to DFA will greatly improve the working efficiency, thus converting NFA to DFA is its necessary.For any a nondeterministic finite automaton ( NFA ) can be an equivalent deterministic finite automaton ( DFA ), L ( N ) =L ( M ). This paper mainly introduces how to convert NFA to equivalent simplified DFA, through concrete examples, combined with graphics, a detailed description of the algorithm principle of conversion.Keywords::finite automata; deterministic finite automaton ( DFA ), nondeterministic finite automaton ( NFA⽬录1.前⾔: (1)1.1背景 (1)1.2实践⽬的 (1)1.2课程实践的意义 (1)2.NFA和DFA的概念 (2)2.1 不确定有限⾃动机NFA (2)2.2确定有限⾃动机DFA (3)3.从NDF到DFA的等价变化步骤 (5)3.1转换思路 (5)3.3⼦集构造法 (7)4程序实现 (9)4.1程序框架图 (9)4.2 数据流程图 (9)4.3实现代码 (10)4.4运⾏环境 (10)4.5程序实现结果 (10)5.⽤户⼿册 (12)6.课程总结: (12)7.参考⽂献 (12)8. 附录 (13)1.前⾔:1.1背景有限⾃动机作为⼀种识别装置,它能准确地识别正规集,即识别正规⽂法所定义的语⾔和正规式所表⽰的集合,引⼊有穷⾃动机这个理论,正是为词法分析程序的⾃动构造寻找特殊的⽅法和⼯具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
void determined(Triad [], int, char*, int);
const int MAX_NODES=20;
int main()
{
int N;
cout<<"请输入边数:"<<endl;
for(int j=0; j<N; j++){
Edge.insert(G[j].edge);
}
int n=Edge.size();
char* input=new char[n];
set<char>::iterator it;
j=0;
for (it = Edge.begin(); it != Edge.end(); iend);
S.push(G[i].end);
}
}
}
return U;
}
set<char> move(set<char> I, char a, Triad G[], int N){
set<char> U;
set<char>::iterator it;
7.源代码
#include<set>
#include<stack>
#include<iostream>
using namespace std;
//Triad(三元组):S→aB即(S,a,B)
struct Triad{
char start;
char edge;
char end;
};
set<char> e_closure(set<char>, Triad[], int) ;
cin>>N;
Triad* G=new Triad[N];
cout<<"请输入正规文法(*代表ε,#代表终态,约定输入时先输入以始态开始的三元组):"<<endl;
for(int i=0; i<N; i++){
cin>>G[i].start>>G[i].edge>>G[i].end;
}
set<char> Edge;
(3)测试数据:课本P59例4.8
转换前的NFA 转换后的DFA
2.设计
(1)数据结构设计
由于FA是一个图,可想到用图的存储结构来存储FA,但是,FA中两个结点之间的路径可以不只一条,这让想考虑用邻接矩阵来存储的FA处理起来有点复杂,我采用的是“结点-边-结点”式的三元组来表示FA。FA有多少条边就应该有多少个这样的三元组,以一个数组来存放这些三元组,那么一个FA就可以表示出来了。
(3)程序基本框架概览
(4)主要函数的实现
伪代码具有简明扼要的特点,利用伪代码子来表示程序流程有利于理解和后续实现。
子集法伪代码:
此外,求ε的传递闭包要利用栈这一数据结构做辅助,其伪代码如下:
再在伪代码的基础上来编写这些核心函数就方便多了,具体代码如下:
3.调试分析
优点分析:NFA的输入只要求输入边的条数即可开始输入组成FA的基本结构(即三元组),而有多少引起状态转换的输入都交给程序自己去完成,这一点就显得很简洁,对于用户来说也便捷!
5.测试结果……………………………………………………7
6.总结…………………………………………………………7
7.源代码………………………………………………………8
题目:NFA转换为等价的DFA
实习时间:2015.10.12
【问题描述】以定理“设L为一个由不确定的有穷自动机接受的集合,则存在一个接受L的确定的有穷自动机”为理论基础,设计算法实现将不确定的有穷自动机(NFA)转换为与之等价的确定的有穷自动机(DFA)。
input[j]=*it;
j++;
}
determined(G, N, input, n);
return 0;
}
set<char> e_closure(set<char> T, Triad G[], int N)
{
set<char> U = T;
stack<char> S;
set<char>::iterator it;
【基本要求】
1确定能够表示FA的合适的结构,以便FA的输入和输出
2设计的算法既要成功实现题目要求的功能,又要高效、鲁棒
3程序中的函数、变量等命名要规则,可读性要强(易懂)
1.需求分析
(1) 要将以状态转换图表示的NFA转换为DFA,首先应设计一个结构来表示FA,以便图形式的FA便于输入和输出。
(2) 设计合适的算法来实现NFA的确定化,这里用子集法来构造等价的DFA。
for (it = U.begin(); it != U.end(); it++)
S.push(*it);
char t;
while (!S.empty())
{
t = S.top();
S.pop();
for (int i=0;i<N;i++)
{
if (G[i].start== t && G[i].edge=='*')
编译原理实习报告
学号:******
班级:******
姓名:******
日期:2015
1.题目及需求分析……………………………………………3
2.设计分析……………………………………………………3
3.调试分析……………………………………………………7
4.用户手册……………………………………………………7
缺点分析:没有可视化,整个程序的输入输出是通过控制台完成的。
解决办法:可合适的使用MFC可视化编程完成(这个有余力可以考虑一下)。
4.用户手册
该程序的使用十分简单,直接按要求输入相应数据就是。
5.测试数据及测试结果
课本P59例4.8:
6.总结
优点通过这次的实习,对编译原理NFA、DFA及之间的等价转换有了更加深刻的理解,也学会了利用伪代码来设计程序,由框架到细节的实现,这种设计相当便利高效。团队成员之间交流思想取长补短也让我学到了好多思想和方法。
此外,由子集法的步骤可见,集合(set)这一结构应该使用,,set结构符合我们数学的集合要求,不含相同元素,并且两个集合间还可以进行比较是否相等,十分有利于我们的程序实现。
表示FA的结构:
集合与栈使用库里面的标准集合、栈。即包含头文件set、stack
(2)文件结构
程序不是很复杂,加之使用到的数据结构是标准库里的,文件只有一个N2D.cpp,其中有#include<set>和#include<starck>。
