yxzh_jy0801
国台湾大学九十三学博士班招生正,备取生名单

以上合計一般生正取生 6 名
所組名稱:心理學系博士班臨床心理學組 准考證號碼 2071014 2071020 2071006 2071023 2071010 姓 名 游勝翔 蘇逸人 鍾素英 張艾如 連盈如 錄取別 正取生 正取生 正取生 正取生 正取生 身 分 別 一般生 一般生 一般生 一般生 一般生
以上合計一般生正取生 1 名
所組名稱:人類學系博士班 准考證號碼 姓 名 錄取別 身 分 別
1091010 1091002 1091006
王美青 李宗正 顏廷
正取生 正取生 正取生
一般生 一般生 一般生
以上合計一般生正取生 3 名
所組名稱:圖書資訊學系博士班 准考證號碼 1101007 1101012 1101019 1101004 姓 名 吳紹群 蔡萬助 洪一梅 洪淑芬 錄取別 正取生 正取生 正取生 正取生 身 分 別 一般生 一般生 一般生 一般生
一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生
以上合計一般生正取生 21 名
所組名稱:化學系博士班 准考證號碼 2041045 2041007 2041001 2041031 2041012 2041014 2041030 2041039 2041006 2041027 2041022 2041018 姓 名 陳浩銘 劉朕與 何美霖 張進傳 周子琪 曾建銘 陳志昌 林喻偵 許旭辰 張秋玲 趙庭榕 沈錦昌 錄取別 正取生 正取生 正取生 正取生 正取生 正取生 正取生 正取生 正取生 正取生 正取生 正取生 身 分 別 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生 一般生
2013年定向招聘工作人员备案表榆林市汇总修改

地市: 县 (区)
横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县 横山县
(盖章) 聘用单位 姓名 性 别
男 女 男 女 女 女 女 女 女 女 女 女 女 女 女 女 女 女 女 女
2013年定向招聘工作人员备案表
定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 定边县 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 县人民医院 鲍娅红 丁元胤 王国安 闫芃颖 陈艳芬 陈丽君 刘小霞 刘红香 张世林 张瑞娟 李 李 龙 宇 女 女 男 女 女 女 女 女 男 女 男 男 女 女 男 女 女 女 女 女 男 女 女 612726198904203323 61272619880405122X 612726198708234819 612731199005162025 612726198801015127 612726198710043325 612726198903263025 612726198910036920 612726198802133918 陕西定边 陕西定边 陕西定边 陕西清涧 陕西定边 陕西定边 陕西定边 陕西定边 陕西定边 西安医学院 西安医学院 西安医学院 西安医学院 西安医学院 延安医学院 重庆医科大学 西安医学院 西安医学院 陕西中医学院 长治医学院 吉林医学院 西安医学院 西安医学院 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 本科 临床医学 临床医学 临床医学 临床医学 临床医学 护理学 护理学 护理学 护理学 护理学 医学影像 医学影像 医学影像 医学影像
网络教研员账号(10.21更新)03
王静丽
桂金龙
xy5804628 123456 xy5804630 123456 xy5804631 123456
xy5804632 xy5804633 xy5804634 xy5804635 xy5804637 xy5804638 123456 123456 123456 123456 123456 123456
xy5804661
123456 123456 123456 123456 123456 123456 123456 123456
123456
江全佐 付灿军
张文心 陈忠 黄军 张新柱 王佩军 林萍 方泽科 郭磊 王兵 蒋其松 闫艳 方振祥 周永新 徐红伟 宋宪利 崔新月 赵猛 杨启明 程丽华 孔祥娟 蒋崇海 任光庆 李天宇 张春磊 蒋坤 申君亭 王丰玉 贾淑敏 孙金仙 李新伟 娄巍 占建林 顾宝娟 刘晓华 王裕汉 张徽园 郭建军 廖水香 茹红忠 陈勇
123456 123456 123456 123456 123456 123456 123456 123456 123456 123456 123456 123456 123456 123456
汪军 陈阳 汪军 徐立权 付利 贾存布 张长征 梅永轩
金云
xy5804653 xy5804654 xy5804655 xy5804656 xy5804657 xy5804658 xy5804659 xy5804660
徐卫京
梁文深
袁祖德 李伟 张月芳 魏振军
魏秀梅 张延娇 宁朝新 张金发 李楠 孙启玲 张文娇 侯旭 刘伯哲
严鑫烨
王永强 吴立军 朱大朋 刘群海 范洪波 刘娟娟 梁春莉 邱敏 何彩梅 张桂红 代玉清 高虎 刘刚
cnki有效入口及密码

3、29阿健的台州学院期刊网https://61.153.205.122用户名:yingjj 密码:8381502(选择图书馆)https://61.153.205.122/A9230433434201835366066374/rap/index.jsp蜡笔小新/ty 16:15:54https://61.153.205.122/A9230420346323003892466511HE/htmlPlay/2011.Htm(此网址可下载MTV,把数字改一下就行)康同杰的网络相册:/photos/kangtj0123/在中国电子琴网上有个活雷锋在163免费油箱中放了一些书,你可以去看看下载一些。
是超星的PDG格式,需要超星阅览器。
到这下载/download/index.html因网站的附件有限制,书都放在163信箱中01-world@密码:gaobodzq请千万不要删除文件和更改密码书目: (不断增加中....) 希望大师们推荐一些好的书,我到超星是去找,如果有就传上来,当然如果你想找哪本书也可以告诉我,我帮你去找找(最好提供书名或作者,我好搜索)@@@@@@@@@@拜厄钢琴基础教程哈农钢琴练指法五线谱入门基础教程新概念乐理教程——五线谱、简谱—起学电子琴和弦图典:汉、英对照爵士鼓伴奏处理法及电子琴鼓机弹奏法全国电子琴演奏(业余)考级重奏作品集:第一级~第四级新编电子琴系列教程(上、下册)电子琴独奏曲20首电子琴典谱:中外名典精选100首车尔尼的599和849谱https://61.153.205.122/A9230434310168989152148454/TPI50/Brief.aspx?(直接登录)[3.23原创]期刊网的密码肯定能用!!!/index.htmsh0036/shsd[原创]绝对原创的cnki下载按照期刊分类的,目前维普类和万方类不能用,但是cnki绝对可用的,必须按照期刊名---****年*期----文章题目的顺序---全文下载,绝对free!这样就绕过了IP的限制啦!!!http://202.114.65.40/journal/3.23清华同方外文期刊整合系统访问网址:http://211.151.93.232/journal/index.htm用户名:idwem密码:wflk1、重庆工商大学入口地址:http://211.83.192.212/tpi50/2、浙江财经学院入口地址:http://210.32.20.250/tpi50/index128.aspx3、浙江杭州另一大学入口地址http://61.153.5.210/tpi50/cnki有效入口及密码http://210.32.20.250/tpi50/index128.aspxhttp://211.83.192.212/tpi50/http://61.153.5.210/tpi50/index128.aspxdx0452/scshkx推荐土木工程在线词典/word.asp12.20转贴-cnki报纸验证报纸可用。
成县事业单位编号表

240101 教育局 240102 教育局 240103 教育局 240104 教育局 240105 教育局 240106 教育局 240107 教育局 240108 教育局 240109 教育局 240110 教育局 240111 教育局 240112 教育局 240113 教育局 240114 教育局 240115 教育局 240116 教育局 240117 教育局 240118 教育局 240119 教育局 240120 教育局 240121 教育局
中央成县委党校 成县西城经济开发区 成县Байду номын сангаас兵武器装备仓库
241302 统计局 成县统计局乡镇基层统计站 241401 人口局 成县计划生育服务站
241402 人口局 成县乡镇计划生育办公室 241403 人口局 成县流动人口服务中心 241501 民政局 成县救助管理站
241502 民政局 成县双拥工作领导小组办公室 241601 发改局
主管 部门
住建局 住建局 文体局 文体局 文体局 文体局 文体局 文体局 文体局 文体局 卫生局
单位名称
成县城市园林绿化局 成县住房保障办公室 成县体委事业 成县同谷书画院 成县图书馆 成县文化馆 成县西峡文物管理所 成县乡镇文化站 成县业余体校 成县博物馆 成县妇幼保健站
240207 农牧局 成县农业技术推广中心 240208 农牧局 成县蚕桑技术推广中心 240209 农牧局 成县桑蚕中心乡站
成县纸坊学区 成县朱家桥学校
教育局 成县陕西师范大学成州中学 教育局 成县学生资助管理中心 农牧局 农牧局
240122 教育局 成县人民政府教育督导室 240123 教育局 240124 教育局 240125 教育局 240126 教育局 240127 教育局 240128 教育局 成县教育局教研室 成县南康学校 成县抛沙学区 成县青少年活动中心 成县三中 成县沙坝初中
华北电力大学保定2014研究生录取名单和成绩
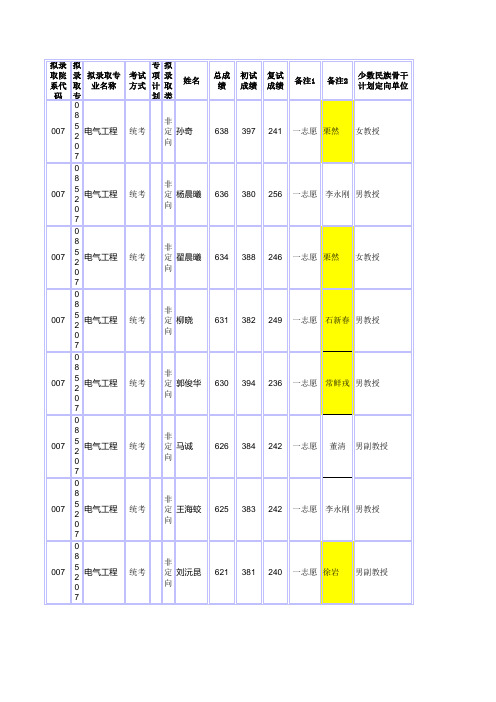
电气工程
0
7
0
8
007
5 2
电气工程
0
Hale Waihona Puke 708007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
统考 统考 统考 统考 统考 统考 统考
非 定 杨津鸣 551 341 210 一志愿 刘云鹏 男副教授 向
非 定 李红萍 551 336 215 一志愿 任惠 无 向
非 定 燕磊 向
567 345 222 一志愿 梁海峰 男讲师
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
电气工程
0
7
0
8
007
5 2
性别
职称
方向
女
教授
系统
男
教授
电机与电器
体检机构用户名整理
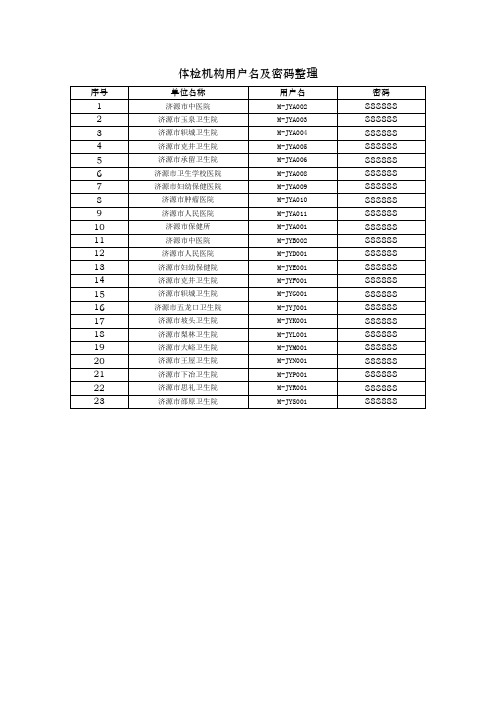
序号
单位名称
用户名
密码
1
济源市中医院
M-JYA002
888888
2
济源市玉泉卫生院
M-JYA003
888888
3
济源市轵城卫生院
M-JYA004
888888
4
济源市克井卫生院
M-JYA005
888888
5
济源市承留卫生院
M-JYA006
888888
6
济源市卫生学校医院
M-JYA008
888888
7
济源市妇幼保健医院
M-JYA009
888888
8
济源市肿瘤医院
M-JYA010
888888
9
济源市人民医院
M-JYA011
888888
10
济源市保健所
M-JYA001
888888
11
济源市中医院
M-JYB002
888888
12
济源市人民医院
M-JYD001
888888
13
济源市妇幼保健院
M-JYE001
888888
14
济源市克井卫生院
M-JYF001
888888
15
济源市轵城卫生院
M-JYG001
888888
16
济源市五龙口卫生院
M-JYJ001
888888
17
济源市坡头卫生院
M-JYK001
888888
18
济源市梨林卫生院
M-JYL001
888888
19
济源市大峪卫生院
M-JYM001
888888
2014湛江市粤东西北地区乡镇事业单位专项公开招聘免笔试人员名单

姓名 陈小宏 陈姝竹 张娟香 李金华 符海翠 黄艳 陈敏玲 林静 黄金霞 林文雁 黄月珠 蔡巨郊 邹梅 胡晓冰 蔡美花 杨成丽 梁雅微 陈玉弟 王栋 吴居穗 梁志明 梁老德 赵勃海 李华森 考试类别 考区代码 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 准考证号 111150180201 111150180301 111150180601 111150180701 111150180702 111150180703 111150180704 111150180801 111150180901 111150180902 111150180903 111150181001 111150181101 111150181102 111150181301 111150181501 111150181502 111150181503 111150181601 111150181901 111150181902 111150181903 111150282201 111150282202 岗位名称 护士 护士 医师 护士 护士 护士 护士 药剂员 护士 护士 护士 医师 护士 护士 护士 护士 护士 护士 医师 中医 中医 中医科 临床 临床 岗位代码 111151802 111151803 111151806 111151807 111151807 111151807 111151807 111151808 111151809 111151809 111151809 111151810 111151811 111151811 111151813 111151815 111151815 111151815 111151816 111151819 111151819 111151819 111152822 111152822
检察录取
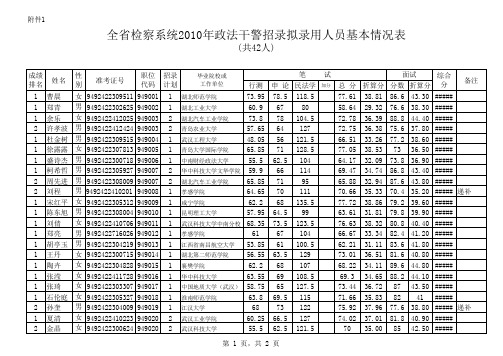
试
加分
综合 总 分 折算分 分数 折算分 分 77.61 58.64 72.78 72.75 66.51 77.05 64.17 69.47 65.88 70.66 77.72 63.61 76.63 66.67 62.21 73.01 68.22 69.3 73.44 71.66 75.92 74.02 70 38.81 29.32 36.39 36.38 33.26 38.53 32.09 34.74 32.94 35.33 38.86 31.81 38.32 33.34 31.11 36.51 34.11 34.65 36.72 35.83 37.96 37.01 35.00 86.6 76.6 88.8 75.6 77.2 73 73.8 86.8 87.6 70.4 79.2 79.8 80.8 82.4 83.6 81.6 89.6 88.2 87 82 77.6 81.8 85 43.30 38.30 44.40 37.80 38.60 36.50 36.90 43.40 43.80 35.20 39.60 39.90 40.40 41.20 41.80 40.80 44.80 44.10 43.50 41 38.80 40.90 42.50
毕业院校或 工作单位 武汉大学东湖分校
笔 行测 申 论 民法学 75.5 69.5 70 62.5 68.5 60 73.5 71.5 62.5 73 62 65 65 53 60 67.5 68.5 66.5 58 121.5 108 114.5 129.5 79 114.5 95.5 121.5 127.5 109 117 122.5 122 115 98 122 114.5 79 105
毕业院校或 工作单位 湖北师范学院
姓名 曹晨 郑青 余乐 许孝波 杜金树 徐露露 盛诗杰 柯希哲 周先进 刘程 宋红平 陈东旭 刘倩 郑亮 胡亭玉 王丹 陶卉 张滢 张琦 石伦庭 孙奎 夏清 金晶
笔试成绩公示
姓名 林大超 孙鹏飞 周志超 刘玥 韩春雪 刘爽 于美玲 相晓红 何美玲 于海峰 董宝珠 郁佳楠 陈卓 乔旭 李赫程 张瑜 齐昕 王秋月 韩立超 王雨濛 岳佳莉 李爽 李海红 信夫 付玲玲 关宏睿 田文武 徐明明 崔颖 李欣 何静 刘晶
准考证号 201430100421 201430100209 201430100424 201430100227 201430100129 201430100213 201430100224 201430100301 201430100109 201430100527 201430100222 201430100427 201430100113 201430100324 201430100310 201430100505 201430100110 201430100307 201430100308 201430100201 201430100221 201430100506 201430100108 201430100407 201430100204 201430100522 201430100121 201430100601 201430100223 201430100523 201430100304 201430100606
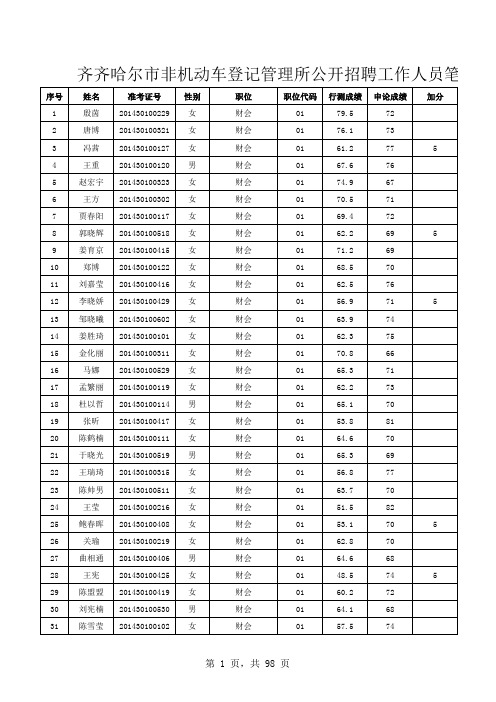
齐齐哈尔市非机动车登记管理所公开招聘工作人员笔试成绩
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 姓名 殷茵 唐博 冯茜 王重 赵宏宇 王方 贾春阳 郭晓辉 姜育京 郑博 刘嘉莹 李晓娇 邹晓曦 姜胜琦 金化丽 马娜 孟繁丽 杜以哲 张昕 陈鹤楠 于晓光 王瑞琦 陈帅男 王莹 鲍春晖 关瑜 曲相通 王宪 陈盟盟 刘宪楠 陈雪莹 准考证号 201430100229 201430100321 201430100127 201430100120 201430100323 201430100302 201430100117 201430100518 201430100415 201430100122 201430100416 201430100429 201430100602 201430100101 201430100311 201430100529 201430100119 201430100114 201430100417 201430100111 201430100519 201430100315 201430100511 201430100216 201430100408 201430100219 201430100406 201430100425 201430100419 201430100530 201430100102 性别 女 女 女 男 女 女 女 女 女 女 女 女 女 女 女 女 女 男 女 女 男 女 女 女 女 女 男 女 女 男 女 职位 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 财会 职位代码 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 行测成绩 79.5 76.1 61.2 67.6 74.9 70.5 69.4 62.2 71.2 68.5 62.5 56.9 63.9 62.3 70.8 65.3 62.2 65.1 53.8 64.6 65.3 56.8 63.7 51.5 53.1 62.8 64.6 48.5 60.2 64.1 57.5 申论成绩 72 73 77 76 67 71 72 69 69 70 76 71 74 75 66 71 73 70 81 70 69 77 70 82 70 70 68 74 72 68 74 5 5 5 5 5 加分
技师工种名称及代码

附件三技师工种名称及代码交通行业0101汽车驾驶技师 0102汽车维修技师建设行业1401木工技师 1402瓦工技师1405油漆工技师 1413管道工技师1423花卉工技师 1422绿化工技师1481育苗技师林业行业0301林木种苗技师 0305营林试验技师0302造林(更新)技师 0303抚育间伐技师0304森林管护技师 0382林机修理技师农业行业0201农艺工技师 0216农机修理技师0224蚕桑工技师 0202果树工技师0210农机驾驶技师 0204农业实验工技师0218农机试验技师民政行业1202尸体火化技师 1203尸体防腐技师1281特岗护理技师水利行业0401闸门运行技师 0402渠道维护技师0405水文勘测技师教育行业2481保育员技师 2482实验技师卫生行业2103卫生检验技师 2107卫生防疫技师2108护理技师2181药剂技师 2182妇幼保健技师体育行业1601体育场地技师畜牧行业0233兽医化验技师 0234兽医防治技师0235动物检疫检验技师 0246家畜饲养技师0251家禽饲养技师 0283饲料生产技师广播电视行业0548天线技师0581广播电视机电技师 0582摄影(像)录音机械技师0583无线广播电视机务技师 0584有线广播电视机线技师新闻出版行业0666图书发行技师贸易行业0801中式烹调技师 0802中式面点技师0806餐厅服务技师 0807客房服务技师机械行业1312钳工技师 1315车工技师1326电工技师 1329电焊技师测绘行业1014工程测量技师 1016地形测量技师1081地图制图技师技术监督行业0701长度量具计量检定技师 0726材料力学性能检验技师0708衡器计量检定技师电子行业1707电子仪表检定修理技师 1722计算机系统操作技师1781电梯维修技师 1782制冷维修技师环境保护行业2581大气环境监测技师 2582水环境监测技师2583土壤环境监测技师 2585环境噪声监测技师地矿行业0903工程地质钻探技师 0902水文水井钻探技师物资行业2381综合库保管技师。
各县考号
邯郸市护理技能竞赛笔试考号
单位: 武安市 姓名:李维英
考号:044
考号:065
邯郸市技能竞赛笔试考号
单位: 磁县 姓名:张爱东
邯郸市护理技能竞赛笔试考号
单位: 磁县 姓名:杨茗媛
考号:004
考号:066
邯郸市技能竞赛笔试考号
单位: 磁县 姓名:张超 单位:
邯郸市技能竞赛笔试考号
磁县 姓名:赵景云
考号:005
单位: 丛台区 姓名:高占红 单位:
邯郸市技能竞赛笔试考号
丛台区 姓名:贾姗姗
考号:072
考号:013
邯郸市技能竞赛笔试考号
单位: 丛台区 姓名:廉睿
邯郸市护理技能竞赛笔试考号
单位: 丛台区 姓名:李玲玲
考号:048
考号:073
邯郸市技能竞赛笔试考号
单位:大名县 姓名:王海峰
邯郸市护理技能竞赛笔试考号
邯郸市技能竞赛笔试考号
单位: 复兴区 姓名:王辉
考号:008
考号:046
邯郸市护理技能竞赛笔试考号
单位: 复兴区 姓名:蔡能霞
邯郸市技能竞赛笔试考号
单位:邯山区 姓名:李现稳
考号:069
考号:009
邯郸市技能竞赛笔试考号
单位: 邯山区 姓名:王彩虹
邯郸市护理技能竞赛笔试考号
单位: 邯山区 姓名:陈 辉
邯郸市技能竞赛笔试考号
单位: 鸡泽县 姓名:齐静丰
邯郸市技能竞赛笔试考号
单位: 鸡泽县 姓名:田亚峰
考号:037
考号:060
邯郸市护理技能竞赛笔试考号
单位:鸡泽县 姓名:郑现波
邯郸市技能竞赛笔试考号
单位:永年县 姓名:伊志刚
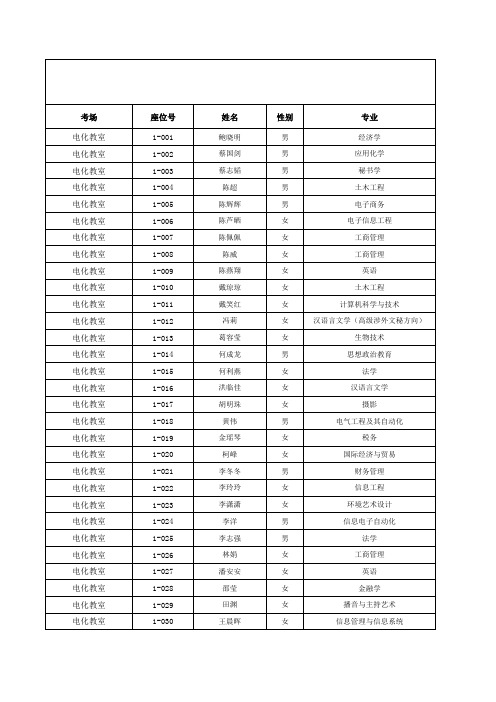
招聘表格
专业
工业设计 应用英语 商务英语 会计学 会计学 英语 现代物流管理 信用管理 国际贸易 行政管理 护理学 工程造价 旅游管理 市场营销 市场营销 机械设计制造与自动化 初等教育(数学方向) 酒店管理 会计 旅游管理 人力资源管理 会计学 中国乐器表演 会计 园林技术 工商管理 计算机信息管理 学前教育 工商企业管理
考场 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室 电化教室
姓名
王锋 王国林 王儒啸 王晓微 王形瑛 王以钢 王总 吴慧君 吴锦霞 吴婷婷 吴蔚蔚 吴小宝 吴瑶倩 奚海滨 夏林超 夏敏 项澄澄 项晶晶 项哲 谢蓓蕾 徐姹 徐建挺 徐玲丹 徐宁 徐若瑜 徐天洋 闫丽晶 严珍珍 杨静静 姚晓敏
性别
女 男 男 女 女 男 男 女 女 女 女 女 女 女 男 女 女 女 男 女 女 男 女 男 女 男 女 女 女 女
座位号 1-171 1-172 1-173 1-174 1-175 1-176 1-177 1-178 1-179 1-180 1-181 1-182 1-183 1-184 1-185 1-186 1-187 1-188 1-189 1-190 2-001 2-002 2-003 2-004 2-005 2-006 2-007 2-008 2-009 2-010
专业
动漫设计与制作 影视多媒体技术 商务英语 计算机应用与技术 表演艺术 涉外文秘 酒店管理 生物制药 楼宇智能化 药事管理 计算机信息管理 应用日语(项目管理) 会计 财务管理 药学 国际金融 国际金融 电气自动化 旅游管理 信息管理与信息系统 环境艺术设计 日语(翻译) 机械电子工程 环境专业与设备 石油工程 历史学 动画设计 广告学 英语 工商管理
The Split Common Fixed Point Problem for Nonexpans

The Split Common Fixed Point Problem for Nonexpansive Mapping and Quasi--Strict Pseudo-contraction Mapping in Banach SpaceXuejiao Zi, Lili Yang, Shaorong YangDepar tment of General Education, The College of Ar ts and Sciences•KunmingAbstract: In this article, we obtain a solution of split common fixed point problem for nonexpansive mapping and quasi--strict pseudo-contraction mapping by proposing an iterative scheme in Banach space. The strong convergence theorem of the sequence produced by our iterative scheme is proved.Keywords:Split common fixed point problem; Nonexpansive mapping; Quasi--strict pseudo-contraction mapping; Banach spaceDOI: 10.47297/taposatWSP2633-456910.20210202Funded project: This work was supported by the Scientific Reserch Foundation of College of Arts and Sciences Yunnan Normal University (No. 18KJYYB011).1. IntroductionThe split feasibility problem (SFP) was proposed for modeling inverse problems [1]. It is considered the problem as follows:find a pointand. (1.1)Where is a bounded linear operator. and be nonempty closed and convexsubsets of finite-dimensional Hilbert spacesand , respectively.Ifandare replaced by the fixed point sets of nonlinear operators and , respectively. (The fixed point sets of S and Yare represented byand)Then (1.1) is called the split common fixed problem (SCFPP):find a pointwithand. (1.2)Many conclusions of weak and strong convergence theorems on SFP in Hilbert space have been obtained by continuous research of authors, see for instance [5-9]. Last several years, some studies of SFP have attempted to generalize from Hilbert space to Banach space, for example, in [10-12], authors introduced different iterative schemes to find solution of SFP and gained the strong convergence theorems with the condition of semi-compactness on the operators. In 2018, Ma et al.[13] introduced iterative scheme converges strongly to a solution of following split feasibility and fixed point problem absence the assumption of semi-compactness on the operator:find a pointsuch thatand. (1.3)Vol.2 No.2 2021Where andbe two real Banach space and Q be a nonempty closed and convex subsetofbe a quasi-- nonexpansive mapping.In this article, enlightened by the research of [13], our main purpose is to use shrinking projective method to construct an iterative scheme and find a solution of the split common fixed point problem (1.2) in Banach space. The strong convergence theorem of the sequence produced by the constructed scheme is proved without the assumption of semi-compactness on the operators.2. PreliminariesThroughout this article, we suppose U be a real Banach space. is the dual space ofis called strictly convex iffor allwith. Themodulus of convexity of U is a function asfor any . We say U is uniformly convex if, and forany.The modulus of smoothness of U is a functionasIf as , we say U is uniformly smooth. Suppose that be a invariantreal number andis known as -uniformly smooth if there is a constant andfor any. Every -uniformly smooth Banach space is uniformly smooth iswell-know.Letdenotes the generalized duality pairing between U and.The normalized mappingis defined byL is uniformly norm-to-norm continuous on each bounded subset of U when U is uniformly smooth Banach spaces.Let U is a strictly convex, smooth and reflexive Banach space. Consider the following function defined in [14,15]:It is evident from (2.4) thatandTheory and Practice of Science and TechnologyandLet C be a closed and convex subset of U, In [14], the mapping , which is described the generalized projection, is defined byThat is , where is the unique solution to the minimization problem.Lemma 2.1([15]) Suppose be a nonempty closed convex subset of strictly convex, smooth and reflective Banach space U . Then we have:Definition 2.2 Let C be a nonempty closed convex subset of smooth Banach spac U a mapping is called:(i) Nonexpansive, if(ii) quasi--strict pseudo-contraction mapping, if and there is a constantwith .Definition 2.3 A mapping is known as closed if for any sequence withand as , then .Lemma 2.4([16]) Let and be two sequences of a uniformly convex and smoothBanach space U. If and either or is bounded, then .Lemma 2.5([17]) Let C be a nonempty, closed and convex subset of strictly convex, smooth, and reflective Banach space U let and . ThenLemma 2.6([18]) Suppose U be a 2-uniformly smooth Banach space and the best smoothness constants . Then we have that:3. Main ResultsTheorem 3.1 Suppose be a 2-uniformly convex and 2-uniformly smooth real Banachspace, its the best smoothness constant Let be a strictly convex, smooth and reflectiveBanach space. and be the normalized mapping of and , respectly. Let be aclosed quasi--strict pseudo-contraction mapping and be a nonexpansivemapping and Let be a bounded linear operator with its adjointLet and be a sequence generated by:Vol.2 No.2 2021with the following conditions hold:Proof. The proof is shown in following five steps.Step 1:We prove that and are closed and convex for anyFor is closed and convex based on Let is closed and convex forfor any ,due toWe get is closed and convex ofSince is closed and convex. Let is closed and convex for. For ,we obtainOwing to and are continuous and linear in , we haveis closed and convex.Step 2:We prove that .Let , it follows assumption that is a 2-uniformly smooth and 2-uniformly convexreal Banach space. We know is 2-uniformly smooth real Banach space andWhere is the normalized duality mapping of . By Lemma 2.6 and (3.1), we obtainTheory and Practice of Science and TechnologyFurthermore, it follows from Lemma 2.5 thatSubstituting (3.5) into (3.4), and by the assumption of , we haveSo, which implies next, we showNote that Let for , then for any ,according to the definition of S, we haveFurthermore, from (2.7), we obtainThese imply thatIt follows from (2.6) and (3.7), we getVol.2 No.2 2021From (2.7), we getBy (3.8) and (3.9), we havethen, which implies for all Thus, Thereforis well defined.Step 3:We verify that is a cauchy sequence.Let by Lemma 2.1, we knownThis implies that is bounded. In addition, by the construction , we get and for any . From Lemma 2.1, we obtainSince and for all we haveTherefore, is nondecreasing. So, the limit exists. From (3.11) wehaveaccording to Lemma 2.4, we obtain thathence is a cauchy sequence in .Step 4:We show that andFrom (3.14), we haveby (3.13) , the definition of and we getTheory and Practice of Science and Technologyfrom Lemma 2.4, we haveby (3.15) and (3.17), we knowsince we getby (3.15) (3.17)and (3.19), we obtainfrom Lemma 2.4, we haveFrom (3.6), we known thatSince is a 2-uniformly smooth and 2-uniformly convex real Banach space, isuniformly continuous from norm-to-norm. By (3.18), we haveAlso from (3.22) and the condition(2), we haveFrom (3.1) , we know thatfrom (3.18), (3.21) and condition (1), we haveowing to is norm-to-norm uniformly continuous, we know thatVol.2 No.2 2021Step 5:now we prove thatSince is a cauchy sequence, there is a such that By the closedness ofS and (3.18) (3.26) thatIn addition, from Lemma 2.5, we obtainand by N is a bounded linear operator. So, according to (3.23),thus, So we haveSuppose from and we havewhich implies thatWe have by the definition of Therefor,Here we complete the proof of Theorem 3.1.Remark 3.2 Theorem 3.1 extends the rusult of [13] from SFP to SCFPP and the nonlinear operator from quasi nonexpansive mapping extends to quasi strict pseudo-contraction mapping.References[1] Y. Censor, T. Elfving, A multiprojection algorithm using Bregman projection in a product splace, Numer. Al-gorithms, 8(1994), 221-39.[2] Y. Censor, T. Elfving, N. Kopf, T. Bortfeld, The multiple-sets split feasibility problem and its applications,Inverse Probl., 21(2005), 2071-84.[3] Y. Censor, A. Motova, A. Segal, Pertured projections and subgradient projections for the multiple-sets splitfeasibility problems, J. Math. Anal. Appl., 327(2007), 1244-56.[4] C. Byrne, Iterative oblique projection onto convex subsets and the split feasibility problems, Inverse Probl.,18(2002), 441-53.[5] A. Moudafi, A note on the split common fixed-point problem for quasi-nonexpansive operators, NonlinearTheory and Practice of Science and TechnologyAnal., 74(2011), 4083-87.[6] Y. Yao, M. Postolache, Y.C. Liou, Strong convergence of a self-adaptive method for the split feasibility prob-lem, Fixed Point Theory Appl. 2013, Art. No. 201 (2013).[7] K.R. Kazmi, S.H. Rizvi, An iterative method for split variational inclusion problem and fixed point problemfor a nonexpansive mapping, Optim Lett., 8(2014), 1113-24.[8] W. Takahashi, H.K. Xu and J.C. Yao., Iterative methods for generalized split feasibility problems in Hilbertspace, Set-Valued Var. Anal.,23(2015),205-21.[9] X.F. Zhang, L. Wang, Z.L. Ma and L.J. Qin, The strong convergence theorems for split common fixed pointproblem of asymptotically nonexpansive mappings in Hilbert spaces, J. Inequal. Appl. 2015, 2015:1. [10] J.F. Tang, S.S. Chang, L. Wang, X.R. Wang, On the split common fixed point problem for strict pseudocon-tractive and asymptotically nonexpansive mappings in Banach spaces, J. Inequal. Appl., (2015), 2015: 305.[11] Z.L. Ma, L. Wang, On the split equality common fixed point problem for asymptotically nonexpansivesemigroups in Banach spaces, J. Nonlinear Sci. Appl., 9(2016), 4003-15.[12] X.J. Tian, L. Wang, Z.L. Ma, On the split equality common fixed point problem for quasi-nonexpansivemulti-valued mappings in Banach spaces. J. Nonlinear Sci. Appl., 9(2016), 5536–43.[13] Z.L. Ma, L. Wang, S.S.Chang,On the split feasibility problem and fixed point problem of quasi-$\var-phi$-nonexpansive mapping in Banach spaces. Numer. Algorithm., 80(2019), 1203-18.[14] Ya. I. Alber, Metric and generalized projection operators in Banach spaces: properties and applications, in:A. G. Kartsatos(Ed.), Theory and Applications of Nonlinear Operators of Accretive and Monotonic Type,Marcel Dekker, New York, 1996, pp. 15-50.[15] Ya.I. Alber, S. Reich, An iterative method for solving a class of nonlinear operator equations in Banachspaces, Panamer. Math. J., 4(2)(1994), 39-54.[16] S. Kamimura, W. Takahashi, Strong convergence of a proximal-type algorithm in a Banach space, SIAM J.Optim.13(2002)938-45.[17] W. Takahashi, Nonlinear functional analysis:Fixed point theory and its applications, Yokohama publ., You-kohama(2000).[18] H.Y. Zhou, X.H. Gao, An iterative method of fixed points for closed and quasi-strict pseudo-contractions inBanach spaces, J Appl Math Comput., 33(2010), 227-37.[19] H.K. Xu, Inequalities in Banach spaces with applications, Nonlinear Anal. Theory Methods Appl.,16(1991)1127-38.。
河北工业大学2012年硕士研究生待录取名单
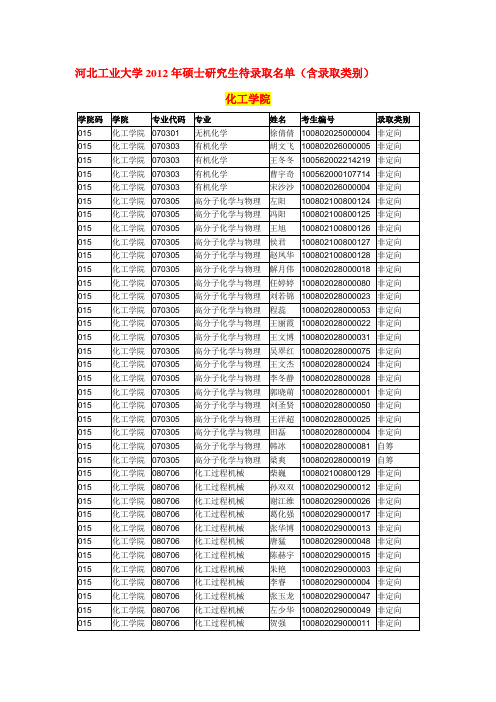
应用化学
牛彬波
100802033000127
非定向
015
化工学院
081704
应用化学
李杨
100802033000105
非定向
015
化工学院
081704
应用化学
崔丽华
100802033000079
非定向
015
化工学院
081704
应用化学
崔静
100802033000049
080706
化工过程机械
张华博
100802029000013
非定向
015
化工学院
080706
化工过程机械
唐猛
100802029000048
非定向
015
化工学院
080706
化工过程机械
陈赫宇
100802029000015
非定向
015
化工学院
080706
化工过程机械
朱艳
100802029000003
非定向
081704
应用化学
邹雪锋
100802033000165
非定向
015
化工学院
081704
应用化学
石兆瑞
100802033000068
非定向
015
化工学院
081704
应用化学
杨婷茹
100802033000155
非定向
015
化工学院
081704
应用化学
张国伟
100802033000096
非定向
015
化工学院
化工过程机械
柴巍
100802100800129
2011年河南省政法干警招录培养体制改革试点拟录取职位计划表

2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表安系统2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表2011年河南省政法干警招录培养体制改革试点拟录取职位计划表系统2011年河南省政法干警招录培养体制改革试点拟录取职位计划表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章治疗药物监测及个体化给药一、治疗药物监测(TDM,记住此简写)1.影响血药浓度的因素生理因素/病理因素/药物本身的因素(1)生理因素:年龄/性别/肥胖/遗传A.年龄(理解即可,常识可判断)新生儿:(血药浓度高)胃肠道处于发育阶段——口服药物吸收较成人慢;皮肤黏膜较薄——局部外用药物的吸收较成人快;血脑屏障尚未完全形成——药物在脑脊液中分布较多;代谢、排泄功能不健全——药的代谢、排泄减慢。
老年人:(即使常规剂量也能出现毒性反应)主要器官功能下降——药的代谢、排泄减慢;血浆蛋白与药物的结合率降低——游离型药物浓度增高。
B.性别(了解即可)女性较男性对药物更为敏感;女性对药物的清除比男性慢。
C.肥胖(了解即可,注意细节)药物在脂肪组织分布,脂肪组织血管分布少,血流缓慢——药物的分布、代谢、排泄均减慢——药物的表观分布容积(V d)增大,血浆半衰期延长。
肥胖者长期使用脂溶性药物——药物在脂肪组织蓄积——中毒。
D.遗传(了解即可)不同人种、不同民族、不同家族对于药物的吸收、分布、代谢、排泄均可存在差异。
(2)病理因素①肝、肾功能损害(理解的基础上记忆)消除速率常数(K值)——降低血浆半衰期(t1/2)——延长②心脏疾患患者(了解即可)影响血液分布、流速等血液动力学参数——影响药物消除。
如:心梗和慢性心衰患者,某些部位或脏器血流减少,药物消除缓慢。
③胃肠疾患(理解的基础上记忆)胃肠道PH值、胃排空速率、胃吸收面积、胃壁通透性、胃肠道内的酶等诸多因素——直接影响吸收速率常数(K a值)和吸收分数(F值)。
④其他(了解即可)某些疾病可改变药物与血浆蛋白的结合,包括肾病、高胆红素血症、高脂血症。
(3)药物因素①制剂因素(了解即可,常识可判断,常为ABCDE全选题)同一药物的不同剂型,甚至不同厂家、不同批号的相同剂型,虽然测得的药物含量相同,但所产生的临床疗效却不一定相同。
这主要是制剂方面的因素,包括:药物的理化性质、剂型、处方中辅料、制剂的工艺过程等,都会使血药浓度发生变化,影响临床疗效。
②药物相互作用(了解即可)合用两种或多种药物引起的某种药物药动学和药效学发生变化。
2.需要进行治疗药物监测的药物★(1)治疗药物需要监测的原则(1-2分A型题或多选题重点记忆下文红体字)▲①治疗指数低、安全范围窄、毒副作用强的药物:地高辛、茶碱(有效浓度与中毒浓度接近)。
▲②具有非线性药物动力学特征的药物:苯妥英钠、茶碱:血药浓度随剂量增大而延长,当剂量增大到一定程度时,剂量再稍有增加即可引起血药浓度很大变化。
▲③药物体内过程个体差异大:某些药物相同剂量进入患者体内的个体差异较大,如三环类抗抑郁药(丙咪嗪、去甲丙咪嗪、阿米替林、多塞平)。
此时需要通过进行治疗药物监测,获得具体患者的药动学参数,制订个体化给药方案。
④需长期使用某种药物一些慢性患者需要长期使用某种药物,可以引起药物在体内的蓄积,应当定期监测血药浓度,以免发生蓄积中毒。
⑤需合并使用多种药物一些患者,尤其是老年人,自身患有多种疾病,需要合并使用多种药物治疗,此时极易引起药物的相互作用,因而需要对某些易发生毒副作用的药物进行TDM。
▲⑥采用非常规给药方案某些情况下医师根据患者的病情可采用非常规的特殊给药方案,如对于癌症化疗患者,有时可尝试使用大剂量的化疗药,此时需要密切注意患者的血药浓度,以防发生严重的毒性反应。
⑦怀疑剂量不足或药物中毒有些药物的中毒表现和所治疗疾病的症状相似,如地高辛血药浓度过高引起毒性反应时也可表现为房颤,此时需要通过监测血药浓度来判断此表现是由于用药剂量不足还是由于药物中毒引起,进而增减用药剂量。
⑧特殊人群用药肾功能不全患者使用氨基糖苷类抗生素(主经肾脏排泄)。
(2)常用血药浓度测定方法的比较(了解即可)①分光光度法优点:操作简单,价格低缺点:灵敏度、精密度、准确度差②气相色谱法(GC)缺点:样品必须具备低沸点、易气化、热稳定性好气质联用(GS-MS)——操作条件高,价格昂贵③高效液相色谱法(HPLC)适用范围广④免疫学方法:放射免疫法、酶联免疫法、荧光免疫法灵敏度高、特异性强,取样量少▲(3)临床常需TDM的药品种类(1-2分A型题或多选题)①抗癫痫药:苯妥英钠、卡马西平、丙戊酸钠②抗心力衰竭药:强心苷类(地高辛、洋地黄毒苷)③抗心律失常药:普奈洛尔、奎尼丁、胺碘酮、普鲁卡因胺、利多卡因、美西律④镇静催眠药:苯巴比妥、地西泮⑤抗抑郁药:阿米替林、去甲替林、丙咪嗪、去甲丙咪嗪⑥平喘药:氨茶碱⑦氨基苷类抗生素:庆大霉素、妥布霉素等。
⑧抗肿瘤药:甲氨喋呤⑨免疫抑制药:环孢素、他克莫司治疗药物监测歌心律失常又癫痫;镇静催眠强心苷;抗瘤平喘抑免疫;最为抑郁氨基苷。
二、个体化给药1.个体化给药方案制订的方法(大体了解)(1)比例法(2)一点法预测维持剂量(3)重复一点法(4)血清肌酐法2.个体化给药的原则A.肝功能受损者给药个体化▲(1)需监测指标——肝功能指标(结合第三章记忆,1分A型题或多选题)血清谷氨酰转移酶(γ-GT)血清丙氨酸氨基转移酶(ALT)血清天门冬氨酸氨基转移酶(AST)血清碱性磷酸酶(ALP)血清胆红素血清总蛋白、白蛋白、球蛋白(2)肝功能受损患者个体化给药的原则建议(了解,常识可判断)①尽量避免使用对肝脏有损害的药物;②若治疗必需使用对肝脏有害的药物时,应减小剂量,延长给药间隔,不要长期用;③随时注意临床观察和检查肝功能;④注意生活习惯,戒除烟酒嗜好。
B.肾功能受损者给药个体化▲(1)需监测指标——肾功能指标(结合第三章记忆,1分A型题或多选题)血尿素氮(BUN)血肌酐(S cr)肌酐清除率(Cl cr)(2)肾功能受损患者个体化给药的原则建议(了解即可)了解患者/了解药物/定期化验/综合考虑肝肾功能C.遗传药理学在个体化给药中的应用(1)表型分型方法(大体了解)通过检测个体的代谢能力(服药后取血样或尿样,检测药物原型及药物代谢物浓度的比值)来间接地分析其基因变异;慢代谢(PM)中代谢(IM)快代谢(EM)极快代谢(VM)(2)基因分型方法(大体了解)提取受试者的DNA,直接分析基因变异。
例题:一、最佳选择题1.关于生物利用度(F)叙述不正确的是()A.是药物进入体循环的量与所给剂量的比值B.血管内给药时F<1,其他给药途径时F=1C.用来衡量血管外给药时进入体循环药物的相对数量D.又称吸收分数E.药物进入体循环的速度和程度[答疑编号111080101]『正确答案』B2.关于表观分布容积(V d)下列叙述不正确的是()A.是体内药量按血浆中同样浓度分布时所需体液的总体积B.是假定药物在体内均匀分布情况下求得的药物分布容积C.可以用来表示药物在体内分布的广泛性D.V d小,表明药物主要分布在血浆中,V d大,表明药物大多与某些器官有特异性结合E.实际上是存在的[答疑编号111080102]『正确答案』E3.关于生物半衰期(t1/2)下列叙述不正确的是()A.每经过一个t1/2,体内消除同样的药量B.是药物在体内消除一半所需的时间C.与消除速度常数k之间的关系为t1/2=0.693/kD.可用来衡量药物消除速度的快慢E.t1/2越大,表明药物代谢、排泄越慢[答疑编号111080103]『正确答案』A4.下列哪一个是不需要监测血药浓度的药物()A.地高辛B.茶碱C.卡马西平D.甲氨蝶呤E.雷尼替丁[答疑编号111080104]『正确答案』E『答案解析』治疗药物监测歌心律失常又癫痫;镇静催眠强心苷;抗瘤平喘抑免疫;最为抑郁氨基苷。
A.地高辛:强心苷B.茶碱:平喘药C.卡马西平:抗癫痫药D.甲氨蝶呤:抗肿瘤药E.雷尼替丁:抗消化性溃疡药5.下列哪项不是常用的血药浓度监测方法()A.分光光度法B.气相色谱法C.高效液相色谱法D.免疫学方法E.容量分析法[答疑编号111080105]『正确答案』E6.关于给药个体化确切的叙述是()A.不同的民族给予不同的剂量B.不同的种族给予不同的剂量C.不同年龄给药剂量不同D.不同性别给药剂量不同E.根据每个病人的具体情况制定给药方案[答疑编号111080106]『正确答案』E二、配伍选择题[7~10]A.丙米嗪B.苯妥英钠C.甲氨蝶呤D.地高辛E.妥布霉素7.具有非线性药代动力学特征的是()[答疑编号111080107]『正确答案』B——苯妥英钠和茶碱8.采用非常规给药方案的是()[答疑编号111080108]『正确答案』C——抗肿瘤化疗药,甲氨蝶呤9.由于肾功能损害患者使用的经肾脏排泄的药物,需进行TDM的是()[答疑编号111080109]『正确答案』E——妥布霉素10.治疗浓度范围是0.9~2.0ng/ml的是()[答疑编号111080110]『正确答案』D——地高辛三、多选题11.血药浓度的影响因素有()A.生理因素B.病理因素C.药物因素D.制剂因素E.心理因素[答疑编号111080111]『正确答案』ABCD12.影响血药浓度的生理因素包括()A.年龄B.性别C.肥胖D.遗传E.高脂血症[答疑编号111080112]『正确答案』ABCD13.下列哪些属于引起血药浓度改变的病理因素()A.肝功能受损B.肾功能受损C.充血性心衰D.胃肠道pHE.高脂血症[答疑编号111080113]『正确答案』ABCDE14.下列哪些属于引起血药浓度改变的病理因素()A.心肌梗死B.胃肠道酶的改变C.胃排空速率的改变D.高胆红素血症E.肾病[答疑编号111080114]『正确答案』ABCDE15.下列哪些属于引起血药浓度改变的剂型因素()A.同一制剂不同批号B.辅料的改变C.制备工艺的改变D.同一制剂厂家不同E.同一药物不同剂型[答疑编号111080115]『正确答案』ABCDE16.需要进行血药浓度监测的药物为()A.治疗指数高的药物B.安全范围窄的药物C.毒副作用强的药物D.具有线性药代动力学特征的药物E.具有非线性药代动力学特征的药物[答疑编号111080116]『正确答案』BCE。
