[学习]分解质因数与求最大公因数
求最大公因数和最小公倍数的四种方法汇总

求最大公因数和最小公倍数的四种方法汇总今天说说求最大公因数和最小公倍数的四种方法。
求最大公因数和最小公倍数四种方法分别是:列举法、筛选法、分解质因数法和短除法(具体过程见图片,对比去学),后两种方法在解题中使用广泛,尤其是短除法,简单、方便、快捷,建议掌握。
为什么要求两个数或多个数的最大公因数和最小公倍数呢?计算是应用之一,求最大公因数可以用来约分,将计算结果约成最简分数。
求最小公倍数可以用来通分,将异分母分数加减法转化为同分母分数加减法,所以分数的加减法计算和最大公因数、最小公倍数有千丝万缕的关系,那么要学好这一块的计算,首先就要学会求两个数的最大公因数和最小公倍数。
解决问题是应用之二,很多解决问题从题目文字表面表达中丝毫看不出是求最大公因数或最小公倍数,当你深入分析,归根结底就是求最大公因数或最小公倍数。
这一块,当然分析问题是重点,但你最终分析出来,还是必须依靠上面的四种方法来求,所以求最大公因数和最小公倍数是基础,四种方法至少会一种(建议重点弄清短除法)。
最大公因数[整理版]
![最大公因数[整理版]](https://img.taocdn.com/s3/m/dd4544c685254b35eefdc8d376eeaeaad1f31633.png)
最大公因数几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。
我们可以把自然数a、b的最公因数记作(a、b),如果(a、b)=1,则a和b互质。
求几个数的最大公因数可以用分解质因数和短除法等方法。
例题1 一张长方形的纸,长7分米5厘米,宽6分米。
现在要把它裁成一块块正方形,而且正方形边长为整厘米数,有几种裁法?如果要使裁得的正方形面积最大,可以裁多少块?分析7分米5厘米=75厘米,6分米=60厘米。
因为裁成的正方形的边长必须能同时整除75和60,所以边长是75和60的公因数。
75和60的公因数有1、3、5、15,所以有4种裁法。
如果要使正方形面积最大,那么边长也应该最大,应该取75和60的最大公因数15作为正方形的边长,所以可以裁(75÷15)×(60÷15)=20块。
练习一1,把1米3分米5厘米长、1米5厘米宽的长方形纸,裁成同样大小的正方形,至少能裁多少块?2,一块长45厘米、宽30厘米的长方形木板,把它锯成若干块正方形而无剩余,所锯成的正方形的边长最长是多少厘米?3,将一块长80米、宽60米的长方形土地划分成面积相等的小正方形,小正方形的面积最大是多少?例题2 一个长方体木块,长2.7米,宽1.8分米,高1.5分米。
要把它切成大小相等的正方体木块,不许有剩余,正方体的棱长最大是多少分米?分析 2.7米=270厘米,1.8分米=18厘米,1.5分米=15厘米。
要把长方体切成大小相等的正方体,不许有剩余,正方体的棱长应该是长、宽、高的公因数。
现要求正方体的棱长最大,所以棱长就是长、宽、高的最大公因数。
(270,18,15)=3,3厘米=0.3分米练习二1,一个长方体木块的长是4分米5厘米、宽3分米6厘米、高2分米4厘米。
要把它切成大小相等的正方体木块,不许有剩余,求所切正方体木块的棱长最长是多少厘米?2,有50个梨,75个橘子和100个苹果,要把这些水果平均分给几个小组,并且每个小组分得的三种水果的个数也相同,最多可以分给几个小组?3,五年级三个班分别有24人、36人、42人参加体育活动,要把他们分成人数相等的小组,但各班同学不能打乱,最多每组多少人?每班各可以分几组?例题3 有三根钢管,它们的长度分别是240厘米、200厘米和480厘米,如果把它们截成同样长的小段,每小段最长可以是多少厘米?分析要把三根钢管截成同样长的小段,每小段的长度数应该是240、200和480的公因数,而每小段要取最长,也就是求240、200和480的最大公因数。
最大公因数怎么求 公式

最大公因数怎么求公式最大公因数怎么求公式 1最大公因数或最大公约数是指能同时除两个或两个以上正整数的最大正整数。
最大公因数怎么求公式 2所有的质数(就是只有1和他本身2个因数的数字,例如2,3,5,7,11,13,17等)直接写1. 短除法是求最大公因数的一种方法,也可用来求最小公倍数。
求几个数最大公因数的方法,开始时用观察比较的方法,即:先把每个数的因数找出来,然后再找出公因数,最后在公因数中找出最大公因数。
例如:求12与18的最大公因数。
12的因数有:1、2、3、4、6、12。
18的因数有:1、2、3、6、9、18。
12与18的公因数有:1、2、3、6。
12与18的最大公因数是6。
这种方法对求两个以上数的最大公因数,特别是数目较大的数,显然是不方便的。
于是又采用了给每个数分别分解质因数的方法。
12=2×2×3 18=2×3×3 12与18都可以分成几种形式不同的乘积,但分成质因数连乘积就只有以上一种,而且不能再分解了。
所分出的质因数无疑都能整除原数,因此这些质因数也都是原数的约数。
从分解的结果看,12与18都有公因数2和3,而它们的乘积2×3=6,就是12与18的最大公因数。
采用分解质因数的方法,也是采用短除的形式,只不过是分别短除,然后再找公因数和最大公因数。
如果把这两个数合在一起短除,则更容易。
从短除中不难看出,12与18都有公因数2和3,它们的乘积2×3=6就是12与18的最大公因数。
与前边分别分解质因数相比较,可以发现:不仅结果相同,而且短除法竖式左边就是这两个数的公共质因数,而两个数的最大公因数,就是这两个数的公共质因数的连乘积。
实际应用中,是把需要计算的两个或多个数放置在一起,进行短除。
如果不懂可以离线留言,或者直接问老师。
学习中不懂就问,别害怕别人说你笨。
学到知识才是最重要的~~ 请采纳答案,支持我一下。
最大公因数怎么求公式 3短除法,左侧所有除数之积喂最大公约数,所有除数与所有商之积为最小公倍数最大公因数怎么求公式 4两个数的最大公因数可以用短除法,详见百度百科:baike.baidu/...93brxK 如在EXCEL中计算,则输入以下公式=GCD(number1,number2, ...)最大公因数怎么求公式 5求最大公因数和最小公倍数的方法:一、特殊情况: 1 、倍数关系的两个数,最大公因数是较小的数,最小公倍数是较大的数.(如; 6 和 12 的最大公因数是 6 ,最小公倍数是12 .) 2 、互质关系的两个数,最大公因数是1,最小公倍数是它们的乘积.(如, 5 和 7 的最大公因数时 1 ,最小公倍数是 5 × 7=35 )二、一般情况: 1 求最大公因数:列举法、单列举法、分解质因数法、短除法、除法算式法. ① 列举法:如,求 18和 27 的最大公因数先找出两个数的所有因数 18 的因数有:。
质因数的底数和指数

质因数的底数和指数质因数分解是初中数学中的一个重点,它是指将一个正整数分解成质数的积的过程,这个分解过程实际上是数的一个分解方法,因为每一个正整数都可以表示成一定数目的质因数的乘积,而且质因数的底数和指数是唯一的。
那么什么是质因数的底数和指数呢?本文将会对这一问题展开讲解。
一、什么是质因数?首先,我们需要了解质因数的概念。
我们把一个数分解成若干个质数的积,那么这些质数就叫做这个数的质因数。
质因数是指只能被1和它本身整除的数。
比如12可以分解为2和3的积,那么2和3就是12的质因数。
二、质因数的底数和指数质因数的底数指的是质数的基数,比如在分解12=2×2×3的式子中,2和3就是底数。
而指数指的是底数出现的次数,比如在12=2×2×3中,2出现了两次,因此指数是2。
因此,质因数可以表示成aᵢ的形式,其中a为底数,i 为指数。
通过计算,我们可以得知一个数的质因数分解式就可以表示为:N=a₁^i₁×a₂^i₂×…×aₘ^iₘ其中m是N的质因数个数,a₁,a₂,…,aₘ是N的m个质因数,i₁,i₂,…,iₘ是它们在分解中的指数。
以60为例,60可以分解为2×2×3×5,表示为60=2²×3×5。
三、质因数分解的应用质因数分解不仅是初中数学的重要内容,而且在数学中的很多应用中也占有重要地位。
比如:1、求最大公因数和最小公倍数求最大公因数和最小公倍数可以通过质因数分解得出。
例如,求12和18的最大公因数和最小公倍数。
首先分解12=2×2×3,18=2×3×3,然后取公共质因数和最大值,即2和3,可得12和18的最大公因数为6。
最小公倍数则取所有质因数和最大指数,即2²×3²=36,可得12和18的最小公倍数为36。
《最大公因数》教案

《最大公因数》教案一、教学目标1、知识与技能目标学生能够理解最大公因数的概念,掌握求两个数最大公因数的方法,包括列举法、分解质因数法和短除法。
2、过程与方法目标通过自主探究、合作交流等活动,培养学生观察、分析、比较、归纳和概括的能力,提高学生解决实际问题的能力。
3、情感态度与价值观目标让学生在探索最大公因数的过程中,体验数学与生活的密切联系,激发学生学习数学的兴趣,培养学生严谨的思维品质和合作精神。
二、教学重难点1、教学重点理解最大公因数的概念,掌握求两个数最大公因数的方法。
2、教学难点能灵活运用不同的方法求两个数的最大公因数,解决实际问题。
三、教学方法讲授法、讨论法、练习法四、教学过程1、导入新课通过展示一个实际生活中的问题引入新课,例如:“老师要把一张长方形的纸剪成大小相等的正方形,且没有剩余,正方形的边长要尽可能大,应该怎么剪呢?”引发学生的思考,从而引出最大公因数的概念。
2、讲授新课(1)定义讲解用直观的图形或具体的例子,向学生讲解最大公因数的定义。
例如:“12 和 18 的公因数有 1、2、3、6,其中 6 是最大的,所以 6 就是 12和 18 的最大公因数。
”(2)求最大公因数的方法①列举法分别列出两个数的因数,然后找出它们的公因数,其中最大的就是最大公因数。
以 12 和 18 为例,12 的因数有 1、2、3、4、6、12,18的因数有 1、2、3、6、9、18,它们的公因数有 1、2、3、6,所以最大公因数是 6。
②分解质因数法把两个数分别分解质因数,然后找出它们公有的质因数,将公有的质因数相乘,得到的积就是最大公因数。
例如:12 = 2×2×3,18 =2×3×3,公有的质因数是 2 和 3,所以最大公因数是 2×3 = 6。
③短除法用短除法求两个数的最大公因数,先用这两个数公有的质因数去除,一直除到商互质为止,然后把所有的除数相乘,所得的积就是最大公因数。
求最大公因数和最小公倍数的方法(简单实用)

求最⼤公因数和最⼩公倍数的⽅法(简单实⽤)⼀、特殊情况:1、倍数关系的两个数,最⼤公因数是较⼩的数,最⼩公倍数是较⼤的数。
(如;6和12的最⼤公因数是6,最⼩公倍数是12。
)2、互质关系的两个数,最⼤公因数是1,最⼩公倍数是它们的乘积。
(如,5和7的最⼤公因数时1,最⼩公倍数是5×7=35)⼆、⼀般情况:1求最⼤公因数:列举法、单列举法、分解质因数法、短除法、除法算式法。
①列举法:如,求18和27的最⼤公因数先找出两个数的所有因数 18的因数有:1、2、3、6、9、1827的因数有:1、3、9、27再找出两个数的公因数: 18的因数有:1、2、3、6、9、1827的因数有:1、3、9、27 1、3、9最后找出最⼤公因数: 9②单列举法:如,求18和27的最⼤公因数先找出其中⼀个数的因数:18的因数有:1、2、3、6、9、18再找这些因数中那些⼜是另⼀个数的因数:1、3、9⼜是27的因数最后找出最⼤公因数: 9③短除法:3 18 273 6 9 除到商是互质数为⽌,最后把所有的除数相乘2 3 3×3=9④除法算式法:⽤这两个数同时除以公因数,除到最⼤公因数为⽌。
18 ÷9就是18和27的最⼤公因数 272、求最⼩公倍数:列举法、单列举法、⼤数翻倍法、分解质因数法或短除法。
①列举法:如,求18和12的最⼩公倍数先按从⼩到⼤的顺序找出这两个数的倍数: 18的倍数:18、36、54、7212的倍数:12、24、36、48再找出两个数的最⼩公倍数: 18的倍数:18、36、54、7212的倍数:12、24、36、48②单列举法:如,求18和12的最⼩公倍数先找出⼀个数的倍数: 18的倍数有:18、36、54、72再按从⼩到⼤的顺序找这些倍数中那个⼜是另⼀个数的倍数,找出最⼩公倍数: 36 ③⼤数翻倍法:如,求18和12的最⼩公倍数把较⼤的数翻倍(2倍开始),每次翻倍后看结果是不是另⼀个数的倍数,直到找到最⼩公倍数为⽌。
分解质因数、最大公因数和最小公倍数知识点练习
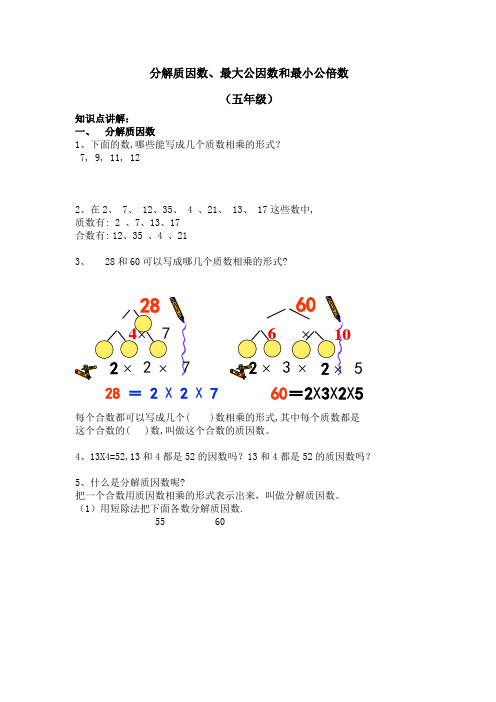
分解质因数、最大公因数和最小公倍数(五年级)知识点讲解:一、 分解质因数1、下面的数,哪些能写成几个质数相乘的形式?7, 9, 11, 122、在2、 7、 12、35、 4 、21、 13、 17这些数中,质数有: 2 、7、13、17合数有: 12、35 、4 、213、 28和60可以写成哪几个质数相乘的形式?每个合数都可以写成几个( )数相乘的形式,其中每个质数都是这个合数的( )数,叫做这个合数的质因数。
4、13X4=52,13和4都是52的因数吗?13和4都是52的质因数吗?5、什么是分解质因数呢?把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
(1)用短除法把下面各数分解质因数.55 6028 = 2 X 2 X 760=2X 3X 2X 55(2)能用短除法把下面各数分解质因数.80 12 16 72练习:一、选一选。
(1)把10分解质因数是( )A.10=2×5B.10=1×2×5C.10=1×10(2)把27分解质因数是( )A.3×9=27B.3×3×3=27C.27=3×3×3(2)看谁是小判官①把35分解质因数是 35=1×5×7( )②把49分解质因数是7×7=49 ( )③把30分解质因数是30=2×3×5 ( )④51不能分解质因数. ( )二、 用短除法找最大公因数1.用排列因数的方法求18和24的最大公因数。
2.用排列因数的方法求两个数的最大公约数方便吗?有没有比它简便的方法求最大公约数呢?今天我们就来研究求两个数的最大公因数简便方法。
.把18和24分解质因数。
如下:2 1 8 2 2 43 9 2 1 23×53 2 6318=2×3×324=2×2×2×3⑴18有哪几个质因数?24呢?⑵18和24相同的质因数有哪些?⑶它们相同的质因数叫做什么,给它们起一个名字:公有的质因数⑷18和24公有的质因数有哪几个?其它的2、2和3是公有的质因数吗?那这些质因数叫做什么质因数,给它们起一个名字:独有的质因数⑸你能根据18和24公有的质因数2和3计算出18和24所有的公因数吗?⑹怎么计算的?哪个最大?最大的是怎么计算出来的?⑺如果在2×3的后面再乘以一个质因数3,还是公约数吗?是最大公约数吗?多乘几个质因数呢?⑻如果在2×3的后面少乘以一个质因数3,还是公约数吗?是最大的公约数吗?⑼从这里可以看出:两个数的最大公因数是什么质因数的乘积?板书:所有的公有质因数的乘积=最大公约数⑽“所有的公有质因数”是什么意思?你是怎么理解的?⑾从这里可以看出:用分解质因数的方法求两个数的最大公约数先干什么?然后干什么?最后干什么?18和24的最大公约数是:2×3=6。
短除法求最大公因数与最小公倍数[详细讲解]
![短除法求最大公因数与最小公倍数[详细讲解]](https://img.taocdn.com/s3/m/bf506409fd4ffe4733687e21af45b307e871f903.png)
讲义编号学员编号:年级:小五 课时数:学员姓名:辅导科目:数学学科教师:学科组长签名及日期课 题分解质因数、最大公因数和最小公倍数 授课时间:教学目标 1.使学生进一步理解和掌握公约数和最大公约数的意义。
2、使学生掌握分解质因数的方法。
2.使学生理解和掌握用分解质因数的方法求两个数的最大公约数和最小公倍数的算理,并会用短除法求两个数的最大公约数和最小公倍数。
重点、难点 1、 用分解质因数的方法求两个数的最大公约数和最小公倍数的算理。
考点及考试要求 分解质因数,求最大公因数和最小公倍数教学内容知识点讲解:一、 分解质因数1、下面的数,哪些能写成几个质数相乘的形式?7, 9, 11, 122、在2、 7、 12、35、 4 、21、 13、 17这些数中,质数有: 2 、7、13、17合数有: 12、35 、4 、213、 28和60可以写成哪几个质数相乘的形式?287×22×7×428 = 2 X 2 X 760×23××6 60=2X 3X 2X 51025×每个合数都可以写成几个()数相乘的形式,其中每个质数都是这个合数的( )数,叫做这个合数的质因数。
4、13X4=52,13和4都是52的因数吗?13和4都是52的质因数吗?5、什么是分解质因数呢?把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
(1)用短除法把下面各数分解质因数.55605551155 = 5×11260233015560=2×2×3×5(2)能用短除法把下面各数分解质因数.80 121672练习:一、选一选。
(1)把10分解质因数是()A.10=2×5B.10=1×2×5C.10=1×10(2)把27分解质因数是()A.3×9=27B.3×3×3=27C.27=3×3×3(2)看谁是小判官①把35分解质因数是 35=1×5×7()②把49分解质因数是7×7=49 ( )③把30分解质因数是30=2×3×5( )④51不能分解质因数. ( )二、用短除法找最大公因数1.用排列因数的方法求18和24的最大公因数。
求最大公因数和最小公倍数

60和42
最后将所有的除数(公 因数)和商相乘,积就 是60和42的最小公倍数。
2 60 42 3 30 21 10 7
除到两个商只有 公因数1,为止。
2×3×10×7 = 420
60和42的最小公倍数是420。
4.接着用6和9的最 小公因数3去除。 6.最后将所有的除数 (公因数)相乘,积就 是18和27的最大公因数。
3 18 27 36 9 2 3
3×3=9
5.2和3只有公因数1,除 到两个数是互质数为止。
18和27的最大公因数是9。
2.求最小公倍数
用分解质因数的方法,求最大公因数。
60和42 60=2×2×3×5 42=2×3×7 将公有的质因数是2、3和各自还有的因数 2、5、7相乘:2×3×2×5×7=420 60和42的最小公倍数是420。
1.求最大公因数
用分解质因数的方法,求最大公因数。
18和27
18=2×3×3 27=3×3×3
将公有的质因数是3和3相乘: 3×3=9 18和27的最大公因数是9。
பைடு நூலகம்
2.用18和27的最小 公因数3去除。
18和27
1.先写短除号,将18 和27写在短除号内。 3.6和9还有公因数3, 写短除号继续除下去。
9.30求最大公因数和最小公倍数的方法

※求最大公因数的方法(.短除法、分解质因数法、除法算式法、小数缩小法、单列举法........................... ).①短除法 : 是18和48的公因数,用它分别除18、48,得到商分别是9,24; 是9与24的公因数,用它分别除9、24,得到的商分别是3,8。
一直除到所得的商是互质数为止,最后把所有的除数连乘起来,所得的积就是这两数的最大公因数:(18,48)=2×3=6②分解质因数法:将这两数分别写成质因数相乘的形式,然后将这两数公有的质因数连乘起来,所得到的积就是这两数的最大公因数。
18和48公有的一个因数3, 18和48公有的另一个公因数3(18,48)=2×3=6③除法算式法: 用这两个数18和48同时除以公因数,除到最大公因数为止。
④小数缩小法:把较小的数缩小(除以2开始)每次缩小后看得到的商是不是另一个数的因数,直到所得的商是另一个数的因数为止。
如:求18和48的最大公因数先用小数 18÷2=9,9不是48的因数,18÷3=6,6是48的因数,那么(18,48)=618 ÷ 48短除号2 18 483 9 243 8(18,48)=6 32⑤单列举法:一般是看哪个数的因数少,就先找出哪个数的因数,再看这个数的因数中哪些也是另一个数的因数,即这两个数的公因数,再从它们的公因数中找出最大的一个,就是这两个数的最大的公因数。
如,求18和27的最大公因数先看18和27这两个数哪个因数少,这两个数除1和本身两个因数外,18=2×9=3×6,27=3×9所以27的因数少,(前面这些只要学生观察一下便可以看出,不用写出来。
)因此先找出27的因数:1、3、9、27再看这些因数中哪些又是另一个数18的因数,即18和27的公因数;18与27的公因数是:1、3、9;最后从公因数中找出最大的一个,既(18,27)=9。
分解质因数及最大公因数和最小公倍数解答

分解质因数及最大公因数和最小公倍数练习解答这些内容是在小学5、6年级进行学习的,但在初中学习有理数的分数约简、分式约简、方程简化等运算中经常使用。
一、分解质因数1. 把下列各数写成几个质因数相乘的形式解:简单的数可以直接分解,但一般都用短除法(见第5题)84=2×2×3×7 105=3×5×7 120=2×2×2×3×5360=2×2×2×3×3×5 1001=7×11×132. 有三个自然数A、B、C,A×B=30,B×C=35、 A×C=42,①A+B+C是多少?②A×B×C是多少?解:各式相乘得(A×B×C) 2=30×35×42=(5×6×7) 2所以A×B×C=5×6×7由A×B=30=5×6,知C=7;同理可求得B=5,A=6,(当然根据C=7,也可由B×7=35、 A×7=42求A,B)①A+B+C=5+6+7=18,②A×B×C=5×6×73. 已知A=2×2×3×5,B=2×3×7,那么A、B的最大公因数是6;最小公倍数是420;解:A和B都含公因数2、3,而B的因数2,3都只有1个(A中因数3也只1个),所以,A、B的最大公因数:2×3=6;A和B全部不同的因数:2、3,5,7,其中A中因数2有两个,所以,A、B的最小公倍数:2×2×3×5×7=420,已知A=2×3×5×5,B=3×5×5×11,那么A、B的最大公因数是75;最小公倍数是1650。
人教版最大公因数说课稿

人教版最大公因数说课稿尊敬的各位评委、老师,大家好!今天我说课的题目是人教版小学数学教材中的“最大公因数”这一知识点。
我将从教材分析、教学目标、教学重难点、教学过程及板书设计五个方面进行详细的阐述。
教材分析“最大公因数”是人教版小学数学五年级下册“数与代数”单元中的一个重要内容。
在此之前,学生们已经学习了因数、倍数的概念,以及如何求一个数的因数。
本节课旨在帮助学生理解最大公因数的定义,掌握求两个数最大公因数的方法,并能够将所学知识应用于实际问题中。
教学目标1. 知识与技能目标:使学生理解最大公因数的概念,掌握求两个数最大公因数的一般方法。
2. 过程与方法目标:通过实际操作,培养学生的观察、比较和归纳能力,提高解题技巧。
3. 情感态度与价值观目标:激发学生学习数学的兴趣,培养学生合作交流的能力,强化学生的应用意识。
教学重难点1. 重点:理解最大公因数的概念,掌握求最大公因数的方法。
2. 难点:如何有效地引导学生从众多因数中找出最大公因数,并能够灵活运用于实际问题。
教学过程1. 导入新课- 通过提问学生关于因数的知识,复习旧知,为新课做铺垫。
- 利用具体的例子,如“12和16的公因数有哪些?”引导学生发现问题,激发求知欲。
2. 探究新知- 介绍最大公因数的定义,并通过比较不同数对的公因数,让学生理解最大公因数的特点。
- 引导学生通过列举法和分解质因数法求最大公因数,比较两种方法的优劣。
3. 巩固练习- 设计层次分明的练习题,包括基础题和拓展题,让学生在实践中巩固所学知识。
- 分组合作解题,培养学生的团队协作能力和交流技巧。
4. 应用拓展- 通过实际问题,如“将一块地均匀分成几个小区域,每个区域的面积尽可能大”,让学生体会最大公因数的应用价值。
- 鼓励学生思考和分享生活中的其他应用场景,拓宽知识的应用范围。
5. 总结反思- 总结最大公因数的概念和求法,强调其在实际问题中的重要性。
- 鼓励学生反思学习过程,提出疑问,教师及时解答,确保学生对知识的全面理解。
最大公倍数怎么求 公式

最大公倍数怎么求公式只有最大公因数和最小公倍数,没有最大公倍数。
最大公因数求法:第一种方法是枚举法。
所谓枚举法,就是将两个数的因数分别列举出来,再从中找到他们的公因数,最后从公因数中找到最大的公因数。
例如求6、15的最大公因数。
这种方法对于较小的数可以使用,对于较大的数来说不是很方便。
6的因数:1、2、3、6;15的因数:1、3、5、15;他们的公因数是1、3;所以他们的最大公因数是3。
第二种方法是短除法。
先用这两个数公有的质因数同时去除这两个数,直到所得的商互质(即没有公因数)为止,再将所有的除数相乘(即短除号左边的数),乘积即为这两个数的最大公因数。
这种方法最为简洁,最常用,对于较大数的最大公因数计算也很方便。
第三种时缩小倍数法,先把这两个数中较小数的因数列举出来,然后再从这些因数中找出较大数的因数,找出来的就是这两个数的公因数,再从这些公因数里面找最大,就是这两个数的最大公因数了。
这种方法跟第一种类似,同时不适用于计算较大的数的最大公因数。
最小公倍数求法:(1)分解质因数法先把这几个数的质因数写出来,最小公倍数等于它们所有的质因数的乘积(如果有几个质因数相同,则比较两数中哪个数有该质因数的个数较多,乘较多的次数)。
比如求45和30的最小公倍数。
45=3*3*530=2*3*5不同的质因数是2,3,5。
3是他们两者都有的质因数,由于45有两个3,30只有一个3,所以计算最小公倍数的时候乘两个3.最小公倍数等于2*3*3*5=90又如计算36和270的最小公倍数36=2*2*3*3270=2*3*3*3*5不同的质因数是5。
2这个质因数在36中比较多,为两个,所以乘两次;3这个质因数在270个比较多,为三个,所以乘三次。
最小公倍数等于2*2*3*3*3*5=54020和40的最小公倍数是40[3](2)公式法由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。
即(a,b)×[a,b]=a×b。
小学数学《求最大公因数》教后反思

小学数学《求最大公因数》教后反思
人教版小学数学《求最大公因数》教后反思
本课是在学生已经理解和掌握倍数、因数的含义,初步学会找一个数的倍数和因数,知道一个数的倍数和因数的特点的基础上进行
教学的。
这部分内容既是“数与代数”领域基础知识的重要组成部分,又是进一步学习约分和通分以及分数四则计算的基础。
第一节课,根据教材是以铺地砖的生活实际作为切入点,要铺整分米数的地砖而且要求要整数块,引入了求两个数的公因数的必要性。
教材主要的教学方法是先分别求出两个数的因数,并按照从大
到小的顺序排列出来,从而找出两个数的公有因数,称为这两个数
的公因数,其中最大的数就是这两个数的最大公因数。
通过例1的
教学后,我引导学生总结出求两数的公因数以及最大公因数的方法。
练习时发现部分学生还是容易在找一个数的因数的`有疏漏,导致求
出来的公因数和最大公因数出错。
第二节课,我引入了求最大公因数的另一种方法,分解质因数法,介绍用短除法求两个数的最大公因数。
这种方法学生掌握起来比较
容易,但也发现部分学生没有除尽,最后的商不是互质数,导致找
错最大公因数。
不过相对于第一钟方法,第二种方法在书写上更简便,学生解题时还是比较容易理解,写起来也比较简洁,大部分学生在求几个数
的最大公因数时还会选择第二种方法。
当然,我还是鼓励学生选择
自己喜欢的方法,关键是能理解,懂应用。
《求最大公因数》数学教学反思

《求最大公因数》数学教学反思
《求最大公因数》数学教学反思
本课是在学生已经理解和掌握倍数、因数的含义,初步学会找一个数的倍数和因数,知道一个数的倍数和因数的特点的基础上进行教学的。
这部分内容既是“数与代数”领域基础知识的重要组成部分,又是进一步学习约分和通分以及分数四则计算的基础。
第一节课,根据教材是以铺地砖的生活实际作为切入点,要铺整分米数的地砖而且要求要整数块,引入了求两个数的公因数的必要性。
教材主要的教学方法是先分别求出两个数的'因数,并按照从大到小的顺序排列出来,从而找出两个数的公有因数,称为这两个数的公因数,其中最大的数就是这两个数的最大公因数。
通过例1的教学后,我引导学生总结出求两数的公因数以及最大公因数的方法。
练习时发现部分学生还是容易在找一个数的因数的有疏漏,导致求出来的公因数和最大公因数出错。
第二节课,我引入了求最大公因数的另一种方法,分解质因数法,介绍用短除法求两个数的最大公因数。
这种方法学生掌握起来比较容易,但也发现部分学生没有除尽,最后的商不是互质数,导致找错最大公因数。
不过相对于第一钟方法,第二种方法在书写上更简便,学生解题时还是比较容易理解,写起来也比较简洁,大部分学生在求几个数的最大公因数时还会选择第二种方法。
当然,我还是鼓励学生选择自己
喜欢的方法,关键是能理解,懂应用。
72的最大公因数

72的最大公因数
在数学中,最大公因数是指两个或多个整数共有的约数中最大的一个。
对于数字72而言,它的约数有1、2、3、4、6、8、9、12、18、24、36和72,而它与自己的最大公因数为72。
但是,我们可以通过简单的数学运算,来求出72与另一个数字的最大公因数。
我们可以将72分解质因数,得到72=2^3 × 3^2。
然后,我们再将另一个数字进行分解质因数,得到它的质因数分解式。
接着,我们将两个数的质因数分解式中相同的质因数提取出来,这些质因数相乘的结果就是它们的最大公因数。
例如,假设我们要求72和90的最大公因数。
将72和90分别分解质因数,得到72=2^3 ×3^2,90=2 × 3^2 × 5。
然后,将它们的质因数分解式中相同的质因数提取出来,得到2 ×
3^2 = 18。
因此,72和90的最大公因数为18。
最大公因数在数学中有着广泛的应用,例如在分数的约分、多项式的因式分解等问题中都会用到。
因此,对于数学学习而言,掌握最大公因数的求法是非常重要的。
求质因数算法

求质因数算法
质因数计算方法:①短除法求最大公因数的一种方法,也可用来求最小公倍数.求几个数最大公因数的方法,开始时用观察比较的方法,即:先把每个数的因数找出来,然后再找出公因数,最后在公因数中找出最大公因数.例如:求12与18的最大公因数.12的因数有:1、2、3、4、6、12.18的因数有:1、2、3、6、9、18.12与18的公因数有:1、2、3、6.12与18的最大公因数是6.这种方法对求两个以上数的最大公因数,特别是数目较大的数,显然是不方便的.于是又采用了给每个数分别分解质因数的方法.12等于2乘2乘3,18等于2乘3乘3,12与18都可以分成几种形式不同的乘积,但分成质因数连乘积就只有以上一种,而且不能再分解了.所分出的质因数无疑都能整除原数,因此这些质因数也都是原数的约数.从分解的结果看,12与18都有公约数2和3,而它们的乘积2乘3等于6,就是12与18的最大公约数.②分解质因数法采用分解质因数的方法,也是采用短除的形式,只不过是分别短除,然后再找公约数和最大公约数.如果把这两个数合在一起短除,则更容易找出公约数和最大公约数.。
