AHP分析法的详细计算过程
AHP 分析法

0.105 0.032 0.637 0.039 0.258 0 C.R. 0.1051.12 0.637 0.9 0.258 0 0.041 0.1
通过一致性检验!
三、AHP计算练习
• AHP 层次分析法在建立多元化保障性住房体系中的应用。
• 为了合理供给居民不同保障性住房,用三个原则来衡量:全覆盖,即应 保尽保;财政承受能力,即提供的保障资金够用;切实解决居民基本住 房需要问题。 • 主要采取的方案为:棚户区改造;限价房+货币购房补贴;廉租房实物配 租;住房租赁补贴。该问题的递阶层次结构模型如图所示。
AHP方法计算过程分析
一、AHP计算理论 二、AHP例题计算 三、AHP计算练习
一、AHP计算理论
(一)层次分析法的步骤 • 1.分析决策系统中各因素之间的关系,建立 层次结构 • 2.构造判断矩阵 • 3.层次单排序及一致性检验 • 4.层次总排序及一致性检验
1.建立梯阶层次结构 目标层 准则层 最底层
根据公式
计算出C.R.。
当C.R.<0.1时,认为判断矩阵的一致性是可以接受的。否 则需要对判断矩阵进行修正。
4.层次总排序及一致性检验
• 计算某一层次所有因素对于最高层(总目标)相对重 要性的权值,称为层次总排序。 • 这一过程是从最高层次到最低层次依次进行的。 ⑴ B层m个因素B1, B2 ,, Bm ,
㈠建立层次结构模型
㈡构造判断矩阵
• 采用专家意见法,就层次结构中各因素两两进行 比较,构造判断矩阵。
1.判断重要性比较)。
表1 A B1 B2 B3 B1 1 5 3 B2 1/5 1 1/3 B3 1/3 3 1
2.判断矩阵B1-C(相对于改善劳动条件准则,各方案之间相对 重要性比较) 详见表2. 3.判断矩阵B1-C(相对于促进技术进步准则,各方案之间相对 重要性比较) 详见表3. 4.判断矩阵B3-C(相对于扩大生产能力准则,各方案之间相对 重要性比较) 详见表4. 表2: B1 C1 C2 C3 C4 C5
AHP(层次分析法)方法、步骤

归一化后的特征向量W= (w1, w2, …,wn) T
AW= λ W max
由此得到的特征向量W= (w1, w2, …,wn) T 就作 为对应评价单元的权重向量。 λmax和W的计算一般采用幂法、和法和方根法
2009.11
方根法
m
bn aibni i 1
2009.11
(4)评价层次总排序计 算结果的一致性
设:CI为层次总排序一致性指标: RI为层次总排序随机一致性指标。
其计算公式为:CI m aiCIi i 1
CIi为Ai相应的B层次中判断矩阵的一致性指标。 m RI ai RIi i 1
RIi为Ai相对应的B层次中判断矩阵随机一致性指标 并取 CR CI
在单层次判断矩阵A中,当
aij
aik a jk
时,称判断矩阵为一致性矩阵。
进行一致性检验的步骤如下:
(a)计算一致性指标C.I.:C.I. max n ,式中n为判断矩阵阶数。
n 1 (b)计算平均随机一致性指标R.I.
R.I.是多次重复进行随机判断矩阵特征值的计算后取算术平均数得到的 ,下表给出1~15维矩阵重复计算1000次的平均随机一致性指标:
max 4
d3 W23
d4 w24
d5 w25
C.R.=0
C1
C2
C3
d1 d2 d3 d4 d5
2009.11
(3)计算各元素的总权重
准则 权重 方案 d1 d2 d3 d4 d5
C1
0.105
0.491 0.232 0.092 0.136 0.046
C2
0.637
0 0.055 0.564 0.118 0.265
AHP分析法的详细计算过程

供应商的选择一、层次分析法基本原理供应商的选择多采用层次分析法。
层次分析法(Analytia1 Hierarchy Process,简称AHP)是美国匹兹堡大学教授A.L.Saaty于20世纪70年代提出的一种系统分析方法。
AHP是一种能将定性分析与定量分析相结合的系统分析方法。
AHP是分析多目标、多准则的复杂大系统的有力工具。
它具有思路清晰、方法简便、适用面广、系统性强等特点,最适宜于解决那些难以完全用定量方法进行分析的决策问题,便于普及推广,可成为人们工作和生活中思考问题、解决问题的一种方法。
将AHP引入决策,是决策科学化的一大进步。
应用AHP解决问题的思路是:首先, 把要解决的问题分层系列化, 即根据问题的性质和要达到的目标,将问题分解为不同的组成因素,按照因素之间的相互影响和隶属关系将其分层聚类组合,形成一个递阶的、有序的层次结构模型。
然后,对模型中每一层次因素的相对重要性,依据人们对客观现实的判断给予定量表示,再用数学方法确定每一层次全部因素相对重要性次序的权值。
最后,通过综合计算各层因素相对重要性的权值,得到最低层(方案层)相对于最高层(总目标)的相对重要性次序的组合权值,以此作为评价和选择决策方案的依据。
现举例来说明层次分析法的基本原理。
假定有n个物体, 它们的重量分别为 W1、W2、……,Wn,并且假定它们的重量和为1个单位,即。
两两比较它们之间的重量很容易得出判断矩阵:显然 aij=1/ aji , aii=1aij=aik/ ajk ; i,j,k=1,2,…,n用重量向量W=[W1,W2,……,Wn]右乘A矩阵,其结果为从上式不难看出,以n个物体重量为分量的向量W是判断矩阵的特征向量。
根据矩阵理论,n为上述矩阵A的唯一非零的,同时也是最大的特征值,而W是该特征值所对应的特征向量。
上面的例子显示,如果有一组物体需要估算它们的相对重量,而又没有称重仪器,那么可以通过两两比较这组物体相对重量的方法,得出每对物体的重量比值,从而形成判断矩阵,通过求解判断矩阵的最大特征值和所对应的特征向量,就可以计算出这组物体的相对重量。
ahp法具体计算步骤

ahp法具体计算步骤AHP(Analytic Hierarchy Process)法是一种常用的多准则决策方法,它基于判断者对不同准则的评价来确定最佳选择。
下面将介绍AHP法的具体计算步骤。
1. 确定决策层次结构:首先,需要确定决策问题的层次结构,包括目标层、准则层和方案层。
目标层是决策问题的直接目标,准则层是实现目标的评价指标,方案层是具体的可行方案。
2. 建立判断矩阵:在准则层中的各个准则之间需要建立判断矩阵,以表达判断者对它们之间相对重要性的判断。
判断矩阵是一个方阵,其中每个元素表示一个准则对另一个准则的相对重要程度,并通过用数字1到9的标度进行比较。
标度1表示两个准则具有相同的重要性,标度9表示一个准则比另一个准则极其重要。
3. 计算权重向量:通过对准则层中各准则的判断矩阵做归一化处理,可以得到每个准则的权重,从而反映其在决策中的相对重要性。
归一化处理可以计算每一行的平均值,再除以各行平均值的总和,得到权重向量。
4. 一致性检验:进行一致性检验是为了确定所建立的判断矩阵是否合理。
通过计算判断矩阵的最大特征值和随机一致性指标RI,可以得到一致性比例CR。
若CR小于0.1,则认为判断矩阵通过一致性检验,权重向量可信。
5. 计算方案的综合评价值:通过将各个准则的权重与其在方案层中的表现值相乘,可以得到各方案的综合评价值。
综合评价值越高,表示方案越好。
以上即是AHP法的具体计算步骤。
通过合理建立层次结构、构建判断矩阵、计算权重向量、进行一致性检验和计算方案的综合评价值,可以帮助决策者系统地进行多准则决策,提高决策的可靠性和准确性。
AHP法在工程管理、资源分配、投资决策等领域有广泛的应用。
ahp 法

ahp 法AHP法是一种重要的判断问题的方法,被广泛应用于决策、评价、排序、公司管理等方面。
该方法由美国学者Thomas L. Saaty在20世纪70年代初提出,是一种透过分析与归纳来解决具有复杂性的判断问题的方法。
AHP法的原理是将一些复杂的判断问题转化为层次结构,通过定量的分析和计算,得出最终的判断结果。
在进行AHP法判断时,需要先将问题转化为层次结构,根据问题的特点以及实际情况,将问题分解成若干个层次。
每个层次包括若干个因素,每个因素具有不同的重要性分值。
通过分析各因素之间的相对重要性,得出最终的判断结果。
AHP法的具体步骤如下:1. 确定判断问题的层次结构,将问题分解成若干个层次。
2. 构造层次结构模型,建立各层之间的关系,确定评价指标以及评价因素,并赋予权重。
3. 建立判断矩阵,对各因素之间的相对重要性进行量化。
4. 计算权重向量,通过计算各因素的权重和,得出各评价指标的权重向量。
5. 一致性检验,计算每个评价指标和判断因素的一致性比率,确保判断结果的可靠性。
6. 得出最终结果,根据各评价指标的权重向量和各因素的得分,得出最终的判断结果。
AHP法的应用范围广泛,包括项目管理、战略规划、投资决策、人才选拔、企业评估等领域。
在实际应用中,AHP法需要结合实际情况进行灵活运用,尤其是在确定权重系数时,需要兼顾客观性和主观性,避免过分依赖主观因素而导致判断失误。
同时,一致性检验是AHP法的核心步骤之一,必须认真发现和解决评价指标及因素之间存在的矛盾和不一致性问题,确保判断结果的准确性。
总的来说,AHP法是一种基于系统分析的判断方法,可帮助人们有效解决各种复杂的判断问题,并且已被广泛应用于实际生活中的各个领域。
AHP层次分析法基础教程-绝对打分方法

层次分析法(AHP)具体步骤:
✓建立两两比较的判断矩阵 判断矩阵表示针对上一层次
某单元(元素),本层次与它有关 单元之间相对重要性的比较。一般 取如下形式:
AHP层次分析法基础教程-绝对打分方法
判 阵断
矩
Cs p1 p2 … … pn
p1 b11 b12 … … b1n p2 b21 b22 … … b2n ……………… ……………… pn bn1 bn2 … … bnn
AHP层次分析法基础教程-绝对打分方法
当 n<3时,判断矩阵永远具有 完全一致性。判断矩阵一致性指标 C.I. 与同阶平均随机一致性指标 R.I. 之比称为随机一致性比率 C.R.(Consistency Ratio)。
C.I C.R. =
R.I.
AHP层次分析法基础教程-绝对打分方法
当 C.R.< 0.10 时,便认为 判断矩阵具有可以接受的一致性 。当C.R. ≥0.10 时,就需要调整 和修正判断矩阵,使其满足 C.R.< 0.10 ,从而具有满意的一 致性。
标度
定义与说明
1 两个元素对某个属性具有同样重要性
3 两个元素比较,一元素比另一元素稍微重要
5 两个元素比较,一元素比另一元素明显重要
7 两个元素比较,一元素比另一元素重要得多
9 两个元素比较,一元素比另一元素极端重要
2,4,6,8 表示需要在上述两个标准之间拆衷时的标度
1/bij
两个元素的反比较
层次分析法
AHP层次分析法基础教程-绝对打分方法
➢层次分析法(AHP) 美国运筹学家A.L.Saaty于本世
纪 70 年 代 提 出 的 层 次 分 析 法 ( Analytical Hierar-chy Process,简 称AHP方法),是一种定性与定量 相结合的决策分析方法。它是一种 将决策者对复杂系统的决策思维过 程模型化、数量化的过程。
AHP层次分析法步骤讲解

AHP层次分析法AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。
层次分析法基本原理AHP层次分析法是将定量分析与定性分析结合起来,用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以用定量方法解决的课题。
AHP层次分析法的操作步骤完整的AHP层次分析法通常包括五个步骤:第一步:建立层次结构模型在深入分析问题的基础上,将决策的目标、考虑的因素和决策对象按相关关系分为最高层、中间层和最低层。
●最高层:决策的目的、要解决的问题●中间层(若干层):考虑的因素、决策的准则●最底层:决策时的备选方案比如现在想选择一个最佳旅游景点,当前有三个选择标准(分别是景色,门票和交通),并且对应有三种选择方案。
现通过旅游专家打分,希望结合三个选择标准,选出最佳方案,层次模型大致如下图:第二步:标度确定和构造判断矩阵通过各因素之间的两两比较确定合适的标度。
在建立层次结构之后,需要比较因子及下属指标的各个比重,为实现定性向定量转化需要有定量的标度,此过程需要结合专家打分最终得到判断矩阵表格。
比如对旅游景点选择的4个影响因素(分别是景色,门票,交通和拥挤度)进行评价(即专家评价),最终得出四个影响因素的权重。
采用1-5分标度法(也或者1-9标度法),即比如门票相对景色更加重要,此时门票打3分,那么景色相对于门票就是取其倒数1/3即0.3333分。
交通相对于景色来更重要为2分,景色相对于交通就是0.5分等。
如果A因素相对B因素非常重要,此时打5分(最高5分),那么B因素相对于A因素就是1/5即0.2分如果使用SPSSAU进行分析,操作此步骤时,需要设置【判断矩阵阶数】,可以理解为需要评价权重的因素个数,并且在白色单元格处输入各项分别的名字以及专家打分,蓝色底纹处会自动变化,不需要输入。
AHP层次分析法算法流程

AHP层次分析法算法流程AHP(Analytic Hierarchy Process)层次分析法是一种用于决策问题的数学模型和方法,它通过对问题进行分析和层次化处理,准确地确定各影响因素的权重,从而帮助决策者做出最佳选择。
下面是AHP层次分析法的算法流程:1.确定决策的目标:明确待解决问题的最终目标。
例如,选择供应商、评估项目风险等。
2.建立层次结构:将问题分解成若干个层次,从最终目标开始逐级向下,形成一个层次结构。
最终目标位于最顶层,中间层次为各个子目标,最底层是各个可选方案或决策因素。
3.构建判断矩阵:对于每个相邻的层次,评价它们之间的相对重要性。
在层次结构矩阵中,将每一对子目标之间的相对重要性填入,构建一个判断矩阵。
判断矩阵的大小等于层次中的层数的平方。
4.设置标准化比较尺度:由于决策者往往无法准确比较不同层次之间的重要性,AHP引入了一套标准化比较尺度来帮助决策者进行判断。
常用的标准化比较尺度包括9级尺度和4级尺度。
5.一致性检验:在判断矩阵中填入各个单元格后,需要进行一致性检验,判断矩阵是否满足一致性。
一致性是指判断矩阵的矩阵元素之间的相互关系是否合理。
6.层次单排序:利用判断矩阵计算每个子目标的权重向量,通过对判断矩阵的特征向量进行归一化来获得权重向量。
7.一致性检验:再次进行一致性检验,验证计算得到的权重向量的一致性。
8.综合决策:将各个子目标的权重向量与它们对应的可选方案或决策因素进行综合,得出最终的决策。
9.灵敏度分析:根据实际情况进行灵敏度分析,检验得出的权重向量对最终决策的影响,以及各个决策因素的敏感程度。
10.结果分析与解释:对最终决策进行分析和解释,确保决策的科学性和合理性,为问题的解决和决策的执行提供支持。
AHP层次分析法通过逐层比较,将问题分解为易于理解和处理的小块,通过判断矩阵和权重向量计算,确定各个子目标的重要性和最终的决策。
它能够提供量化的决策依据,并具有一定的灵活性和可解释性。
AHP分析法的详细计算过程

供应商的选择一、层次分析法基本原理供应商的选择多采用层次分析法。
层次分析法(Analytial Hierarchy Process ,简称AHP 是美国匹兹堡大学教授 A . L . Saaty 于20世纪70年代提出的一种系统分析方法。
AHP 是一种能将定性分析与定量分析相结合的系统分析方法。
AHP 是分析多目标、多准则的复杂大系统的有力工具。
它具有思路清晰、方法简便、适用面广、系统性强等特点,0最适宜于解决那些难以完全用定量方法进行分析的决策问题,便于普及推广,可成为人们工作和生活中思考问题、 解决问题的一种方法。
将AHP 引入决策,是决策科学化的一大进步。
应用AHP 解决问题的思路是:首先,把要解决的问题分层系列化,即根据问题的性质和要达到的目标, 将问题分解为不同的组成因素,按照因素之间的相互影响和隶属关系将其分层聚类组合,形成一个递阶的、有序的层次结构模型。
然后,对模型中每一层次因素的相对重要性,依据人们对客观现实的判断给予定量 表示,再用数学方法确定每一层次全部因素相对重要性次序的权值。
最后,通过综合计算各层因素相对重要性的权值,得到最低层(方案层)相对于最高层(总目标)的相对重要性次序的组合权值,以此作为 评价和选择决策方案的依据。
I F附2l> I >1显然 aij = 1/ aji , aiiaij = aik/ ajk ; i,j,k=1,2, …,n用重量向量W =[W1,W2,……,Wn]右乘A 矩阵,其结果为从上式不难看岀,以n 个物体重量为分量的向量W 是判断矩阵的特征向量。
根据矩阵理论,n 为上现举例来说明层次分析法的基本原理。
假定有n 个物体,它们的重量分别为 W1、W2wr ,并且假定它们的重量和为 1个单位,即 ~两两比较它们之间的重量很容易得岀判断矩阵:AW =述矩阵A的唯一非零的,同时也是最大的特征值,而W是该特征值所对应的特征向量。
上面的例子显示,如果有一组物体需要估算它们的相对重量,0而又没有称重仪器,那么可以通过两两比较这组物体相对重量的方法,得岀每对物体的重量比值,从而形成判断矩阵,通过求解判断矩阵的最大特征值和所对应的特征向量,就可以计算岀这组物体的相对重量。
层次分析法(AHP)具体步骤
层次分析法(AHP)具体步骤:
明确问题
在分析社会、经济的以及科学管理等领域的问题时,首先要对问题有明确的认识,弄清问题的范围,了解问题所包含的因素,确定出因素之间的关联关系和隶属关系。
层次分析法(AHP)具体步骤:
递阶层次结构的建立
根据对问题分析和了解,将问题所包含的因素,按照是否共有某些特征进行归纳成组,并把它们之间的共同特性看成是系统中新的层次中的一些因素,而这些因素
本身也按照另外的特性组合起来,形成更高层次的因素,直到最终形成单一的最高层次因素。
最高层是目标层
中间层是准则层
……..
最低层是方案层或措施层
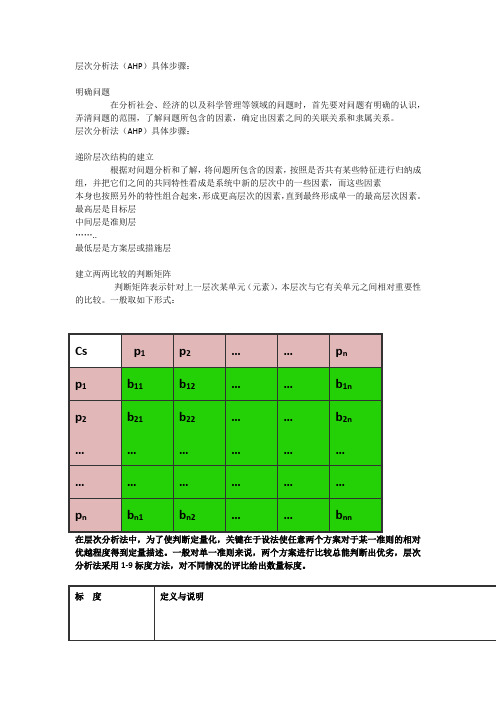
建立两两比较的判断矩阵
判断矩阵表示针对上一层次某单元(元素),本层次与它有关单元之间相对重要性的比较。
一般取如下形式:
Cs p1p2……p n
p1b11b12 (1)
p2b21b22 (2)
………………………………
p n b n1b n2……b nn
在层次分析法中,为了使判断定量化,关键在于设法使任意两个方案对于某一准则的相对优越程度得到定量描述。
一般对单一准则来说,两个方案进行比较总能判断出优劣,层次分析法采用1-9标度方法,对不同情况的评比给出数量标度。
判断矩阵B具有如下特征:
o b ii = 1
o b ji = 1/ b ij
o b ij = b ik/ b jk
(i,j,k=1,2,….n)
判断矩阵中的b ij是根据资料数据、专家的意见和系统分析人员的经验经过反复研究后确定。
应用层次分析法保持判断思维的一致性是非常重要的,只要矩阵中的b ij满足上述三条关系式时,就说明判断矩阵具有完全的一致性。
用人话讲明白AHP层次分析法(非常详细原理+简单工具实现)

用人话讲明白AHP层次分析法(非常详细原理+简单工具实现)文章目录1、前言与算法简述2、AHP层次分析法过程 2.1 构建层次评价模型 2.2 构造判断矩阵2.3 层次单排序与一致性检验 2.3.1 层次单排序 2.3.2 求解最大特征根与CI值 2.3.3 根据CI、RI值求解CR值,判断其一致性是否通过。
2.4 层次总排序与一致性检验3、案例以及工具实现 3.1 外出旅游最重视的因素3.1.1 使用工具 3.1.2 案例操作 3.1.3 分析结果解读 3.1.4 小结 3.2 选择最佳外出旅游地 3.2.1 使用工具 3.2.2 案例操作3.1.3 分析结果解读 3.2.4 小结4、代码实现1、前言与算法简述今天应粉丝要求,梳理一下层次分析法。
层次分析法,即Analytic HierarchyProcess(AHP) ,是美国运筹学家 Saaty 于20世纪70年代初期提出的一种主观赋值评价方法。
层次分析法将与决策有关的元素分解成目标、准则、方案等多个层次,并在此基础上进行定性和定量分析,是一种系统、简便、灵活有效的决策方法。
这个算法是一个多指标综合评价算法,由于这个算法简单、实用,因此在经管类或者实际生活中应用的非常多,其一般有两个用途:指标定权给指标制定权重,打个比方,例如选择旅游地这个决策,可能一般我们由以下5个因素组成,但是每个人(主观)对因素的重视程度不一,ahp可以实现在无需搜集数据的情况下,给这些指标制定权重。
量化方案选择同样是选择旅游地这个决策,可能我们有一些方案,例如苏杭、北戴河、桂林这三个方案,层次分析法可以综合以上5个因素,给这些方案计算得出一个量化得分,例如苏杭0.3分、北戴河0.35分、桂林0.45分,这样根据分值大小,我们就可以选择得到内心或者经验上最心怡的方案了。
通过上面讲解层次分析法的作用,在生活、工作中其实我们可以应用这个模型的渠道是非常广的,特别是那些需要主观决策的、或者需要用经验判断的决策方案,例如:买房子(主观决策)选择旅游地(主观决策)给员工进行绩效评估(经验判断)选择开店地址(经验判断)2、AHP层次分析法过程层次分析法的原理,是在分析一个现象或问题之前,首先将现象或问题根据它们的性质分解为有关因素,并根据它们之间的关系分类而形成一个多层次的结构模型。
AHP(层次分析法)具体步骤

AHP 法是将各要素配对比较,根据要素的相对重要程度进行判断,然后通过计算判断矩阵的特征值获得权重向量。
对于各级指标将同级指标配对比较构成判断矩阵为:
(1) 其中
的标度方法[9]如下
表1 九级标度
标度
含义 1
表示两个因素相比,具有同样重要性 }
3
表示两个因素相比,一个因素比另外一个因素稍微重要 5
表示两个因素相比,一个因素比另外一个因素明显重要 7
表示两个因素相比,一个因素比另外一个因素强烈重要 9 表示两个因素相比,一个因素比另外一个因素极端重要 2,4,6,8
上述两相邻判断的中值 \
倒数
因素i 和就j 比较的判断,则因素j 和i 比较判断
通过解矩阵A 的特征值,可求得相应的特征向量,经归一化后得到的权重向量为:
(2)
其中就是不同指标的相对权重。
为了度量判断的可靠程度,可以计算一致性指标[10]: max 1n CI n λ-=
- (3)
○
1CI =0,有完全的一致性 ○
2CI 接近于0,有满意的一致性 …
○
3CI 越大,不一致越严重 为了衡量CI 的大小,引入随机一致性指标RI :
表2随机一致性指标
r12345,
7891011
6
RI00
得到一致性比率[11]:
CR 时,认为的不一致程度在容许范围当一致性比率0.1
内,有满意的一致性,通过一致性检验,可用其归一化特征向量作为全向量,否则要重新构造成对比较矩阵,对加以调整。
运用以上方法求得每个指标的权重矩阵:
(5)。
层次分析法(AHP法)计算过程
是对难于完全定量的复杂系统作出决策的模型和方 法。
• 决策是指在面临多种方案时需要依据一定的标准选 择某一种方案。日常生活中有许多决策问题。举例
“选择旅游地”中 准则层对目标的权 向量及一致性检验
最大特征根λ=5.073
准则层对目标的成对比较阵
⎡ 1 1/ 2
⎢ ⎢
2
1
A = ⎢ 1/ 4 1/7
⎢ ⎢
1/3
1/5
⎢⎣ 1 / 3 1 / 5
4 3 3⎤
7
5
5
⎥ ⎥
1 1/ 2 1/ 3⎥
2
1
1
⎥ ⎥
3 1 1 ⎥⎦
权向量(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T
定义一致性指标: CI = λ − n n −1
CI=0,有完全的一致性 CI接近于0,有满意的一致性 CI 越大,不一致越严重
为衡量CI 的大小,引入随机一致性指标 RI。方法为
随机构造500个成对比较矩阵 A1, A2,L, A500
则可得一致性指标 CI1,CI2,L,CI500
RI
=
CI1
+ CI2
素相互比较的困难,以提高准确度。
判断矩阵是表示本层所有因素针对上一层某一个因素的 相对重要性的比较。判断矩阵的元素aij用Santy的1—9标 度方法给出。
心理学家认为成对比较的因素不宜超过9个,即每层 不要超过9个因素。
判断矩阵元素aij的标度方法
AHP层次分析法步骤讲解

AHP层次分析法AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。
层次分析法基本原理AHP层次分析法是将定量分析与定性分析结合起来,用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以用定量方法解决的课题。
AHP层次分析法的操作步骤完整的AHP层次分析法通常包括五个步骤:第一步:建立层次结构模型在深入分析问题的基础上,将决策的目标、考虑的因素和决策对象按相关关系分为最高层、中间层和最低层。
●最高层:决策的目的、要解决的问题●中间层(若干层):考虑的因素、决策的准则●最底层:决策时的备选方案比如现在想选择一个最佳旅游景点,当前有三个选择标准(分别是景色,门票和交通),并且对应有三种选择方案。
现通过旅游专家打分,希望结合三个选择标准,选出最佳方案,层次模型大致如下图:第二步:标度确定和构造判断矩阵通过各因素之间的两两比较确定合适的标度。
在建立层次结构之后,需要比较因子及下属指标的各个比重,为实现定性向定量转化需要有定量的标度,此过程需要结合专家打分最终得到判断矩阵表格。
比如对旅游景点选择的4个影响因素(分别是景色,门票,交通和拥挤度)进行评价(即专家评价),最终得出四个影响因素的权重。
采用1-5分标度法(也或者1-9标度法),即比如门票相对景色更加重要,此时门票打3分,那么景色相对于门票就是取其倒数1/3即0.3333分。
交通相对于景色来更重要为2分,景色相对于交通就是0.5分等。
如果A因素相对B因素非常重要,此时打5分(最高5分),那么B因素相对于A因素就是1/5即0.2分如果使用SPSSAU进行分析,操作此步骤时,需要设置【判断矩阵阶数】,可以理解为需要评价权重的因素个数,并且在白色单元格处输入各项分别的名字以及专家打分,蓝色底纹处会自动变化,不需要输入。
AHP(层次分析法)示例说明

AHP(层次分析法)示例说明AHP (层次分析法)示例说明(The Analgtic Hierarachy Process----AHP)一. AHP 预备知识为了更好地理解AHP ,需要准备一些矩阵方面的知识,以下知识都可以从《线性代数》中找到。
1.1 特征根与特征向量设()n m ij a A ⨯=为n 阶方阵,若存在常数λ和非零n 维向量),,,(21ng g g g =,使得g g Aλ= (1) 则称,λ是矩阵A 的特征根(或特征值),非零向量g 是矩阵A 关于特征根λ的特征向量。
1.2 特征根的求法由(1)得()00=-⇒=-g E A g g Aλλ,这是一个n 元一次线性齐次方程组,该方程组如果有非零解,则其充分必要条件为:系数行列式为零,即0=-E A λ (2)称(2)式为矩阵A 的特征方程,它是一个一元n 次方程,由线性代数基本定理知,该方程有且只有n 个根。
1.3 重量模型设nu u u ,,,21为n 个物体,重量分别是ng g g ,,,21。
但是,我们并不知道物体的重量,只知两两之间重量比的比值:ji ij g g a =设准则C 为比较重量,问题是:已知),1(n j i a ij≤≤,在准则C 下对元素nu u u ,,,21排序,也就是按其重量大小排序已知。
()⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==⨯nn n n n n mn ij g g g g g g g g g g g g g g g g g g a A212221212111 对于以下三个特性: (1)0>ija(2)jiija a1=(3)ikjk ija a a=⋅()ija 显然满足(1)与(2),但是,(3)式通常不被满足(因为统计或构造这么完整的数据很难),满足(1)、(2)的矩阵A 为正互反矩阵;满足(1)、(2)并且(3)也成立时的矩阵A 称为一致性判断矩阵。
问题是:已知判断矩阵A ,在准则C 下对n 个物体排序。
ahp权重计算过程

ahp权重计算过程AHP(Analytic Hierarchy Process)是一种用于多准则决策的方法,它通过对准则之间的比较和权重计算,帮助决策者做出最优选择。
本文将介绍AHP权重计算的过程。
AHP权重计算过程主要包括以下几个步骤:建立层次结构、构建判断矩阵、计算特征向量、一致性检验和权重归一化。
首先,建立层次结构。
层次结构是指将决策问题分解为不同层次的准则和子准则,形成一个层次结构图。
在AHP中,通常将问题分为目标层、准则层和方案层。
目标层是最高层,表示决策的目标;准则层是中间层,表示实现目标所需的准则;方案层是最底层,表示可供选择的方案。
其次,构建判断矩阵。
判断矩阵是用于比较准则之间相对重要性的工具。
在AHP中,决策者需要对每个准则进行两两比较,根据其相对重要性给出一个判断矩阵。
判断矩阵的元素表示准则之间的重要性比较,通常使用1-9的尺度进行评价,其中1表示两个准则具有相同重要性,9表示一个准则比另一个准则重要性高出很多。
然后,计算特征向量。
特征向量是判断矩阵的特征根对应的特征向量,它表示每个准则的权重。
通过对判断矩阵进行特征值分解,可以得到特征向量。
特征向量的元素表示每个准则的权重,可以通过归一化处理,使得所有权重之和为1。
接下来,进行一致性检验。
一致性检验是为了判断决策者在比较准则时是否存在一致性问题。
一致性指标CI(Consistency Index)和一致性比例CR(Consistency Ratio)用于评估判断矩阵的一致性。
如果CR小于0.1,则认为判断矩阵具有较好的一致性,否则需要重新进行比较。
最后,进行权重归一化。
在AHP中,准则的权重需要进行归一化处理,使得所有准则的权重之和为1。
通过将每个准则的权重除以所有准则权重之和,可以得到归一化后的权重。
综上所述,AHP权重计算过程包括建立层次结构、构建判断矩阵、计算特征向量、一致性检验和权重归一化。
通过这一过程,决策者可以得到每个准则的权重,从而进行多准则决策。
ahp法计算总得分

层次分析法(AHP)计算总得分一、确定评价因素在层次分析法中,首先需要确定评价因素。
这些因素通常与目标或决策问题相关,并且可以按照不同的层级进行组织。
在确定评价因素时,需要确保它们具有清晰明确的定义和范围,并且能够全面反映目标或问题的各个方面。
二、构造判断矩阵判断矩阵是层次分析法的核心,用于比较不同因素之间的相对重要性。
根据判断矩阵的定义,我们需要比较同一层级的不同因素,确定它们相对于上一层级的相对重要性。
比较可以采用1-9标度法或其他适合的方法,确保判断的一致性和准确性。
三、计算权重向量权重向量是根据判断矩阵计算出的各因素相对于上一层级的相对重要性权重。
计算权重向量的常用方法是特征向量法或和积法等。
计算出的权重向量需要满足一致性检验,以确保判断矩阵的一致性。
四、一致性检验一致性检验是检验判断矩阵是否满足一致性的标准。
如果判断矩阵不满足一致性要求,需要重新构造判断矩阵或调整判断值。
一致性检验常用的方法是计算一致性比率CR=CI/RI,其中CI为一致性指标,RI为随机一致性指标。
通常CR 小于0.1时,认为判断矩阵满足一致性要求。
五、计算总得分总得分是根据权重向量和各因素的评分计算出的综合得分。
首先需要对每个因素进行评分,然后根据权重向量进行加权平均,得出综合得分。
评分可以采用专家打分、调查问卷等方式获得。
六、结果分析结果分析是根据综合得分对评价因素进行排序和分析的过程。
通过结果分析,可以找出影响目标或决策问题的关键因素,以及各因素之间的相互关系和影响程度。
结果分析需要根据实际情况进行深入分析,得出科学合理的结论和建议。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
供应商的选择一、层次分析法基本原理供应商的选择多采用层次分析法。
层次分析法(Analytia1 Hierarchy Process,简称AHP)是美国匹兹堡大学教授A.L.Saaty于20世纪70年代提出的一种系统分析方法。
AHP是一种能将定性分析与定量分析相结合的系统分析方法。
AHP是分析多目标、多准则的复杂大系统的有力工具。
它具有思路清晰、方法简便、适用面广、系统性强等特点,0最适宜于解决那些难以完全用定量方法进行分析的决策问题,便于普及推广,可成为人们工作和生活中思考问题、解决问题的一种方法。
将AHP引入决策,是决策科学化的一大进步。
应用AHP解决问题的思路是:首先, 把要解决的问题分层系列化, 即根据问题的性质和要达到的目标,将问题分解为不同的组成因素,按照因素之间的相互影响和隶属关系将其分层聚类组合,形成一个递阶的、有序的层次结构模型。
然后,对模型中每一层次因素的相对重要性,依据人们对客观现实的判断给予定量表示,再用数学方法确定每一层次全部因素相对重要性次序的权值。
最后,通过综合计算各层因素相对重要性的权值,得到最低层(方案层)相对于最高层(总目标)的相对重要性次序的组合权值,以此作为评价和选择决策方案的依据。
现举例来说明层次分析法的基本原理。
假定有n个物体, 它们的重量分别为 W1、W2、……,Wn,并且假定它们的重量和为1个单位,即。
两两比较它们之间的重量很容易得出判断矩阵:显然 aij=1/ aji , aii=1aij=aik/ ajk ; i,j,k=1,2,…,n用重量向量W=[W1,W2,……,Wn]右乘A矩阵,其结果为从上式不难看出,以n个物体重量为分量的向量W是判断矩阵的特征向量。
根据矩阵理论,n为上述矩阵A的唯一非零的,同时也是最大的特征值,而W是该特征值所对应的特征向量。
上面的例子显示,如果有一组物体需要估算它们的相对重量,0而又没有称重仪器,那么可以通过两两比较这组物体相对重量的方法,得出每对物体的重量比值,从而形成判断矩阵,通过求解判断矩阵的最大特征值和所对应的特征向量,就可以计算出这组物体的相对重量。
同样,对于复杂的社会的、经济的以及管理科学等领域的问题,通过建立层次分析模型,构造两两因素判断矩阵,就可应用求解最大特征值和特征向量的方法,来确定出相应的各种方案、措施、政策等相对于总目标的重要性排序权值,以供决策使用。
应用层次分析法保持判断思维的一致性是非常重要的,所谓判断一致性,即判断矩阵A有如下关系:aij=aik/ ajk ; i,j,k=1,2,…,n判断矩阵在满足上述完全一致性的条件下,具有唯一非零的、同时也是最大的特征值λmax=n(n为判断矩阵的阶数)。
但是,在一般决策问题中,决策者不可能给出精确的Wi/Wj度量, 只能对它们进行判断估计。
这样, 实际给出的aijj判断与理想的iWi/Wj 有偏差,不能保证判断矩阵具有完全的一致性。
因此, 为了保证应用层次分析法得到的结论基本合理,还需要对构造的判断矩阵进行一致性检验。
根据矩阵理论,如果λ1,λ2,…λn,满足Ax=λx,即λ1,λ2,…λn是矩阵 A的特征值,并且对所有aii=1,有,当矩阵A具有完全一致性时,λmax=n,其余特征值都为零。
而当矩阵A不具有完全一致性时,有λ1=λmax>n,其余特征值l2,l3,…λn有如下关系:或当矩阵A具有满意一致性时,λmax稍大于n,也就是λmax越接近n,一致性越好,反之,一致性越差。
因此,引入判断矩阵最大特征值以外其余特征值和平均值作为判断矩阵一致性的指标,即用检测决策者判断思维的一致性。
为了度量不同判断矩阵是否具有满意一致性,根据经验,还需引入判断矩阵的平均随机一致性指标RI值。
对于1-9阶判断矩阵,RI值分别为表5-2 平均随机一致性指标1234567890.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45当阶数大于2时,判断矩阵的一致性指标CI与同阶平均随机数一致性指标RI之比称为随机一致性比率,记为CR。
当时,即认为判断矩阵具有满意一致性,否则就需要调整判断矩阵,使之具有满意一致性。
综上所述,使用层次分析法的基本步骤是:1. 建立评价结构模型深入分析所面临的问题,将问题中所包含的因素划分为不同的层次,用框图形式说明层次的递阶结构与因素的从属关系。
2. 构造判断矩阵判断矩阵的值反映了专家对各因素相对重要性(或优劣、强度等)的认识,一般采用1-9及其倒数的标度方法。
3. 层次单排序及其一致性检验通过等式Ax=λmaxx,求解判断矩阵的最大特征值λmax所对应的解W,经规一化处理后即为同一层次相应因素相对重要性的排序权值,这一过程称为层次单排序。
对每一个判断矩阵需进行一致性检验。
当随机一致性比率满足时,认为层次单排序的结果有满意的一致性,否则需要调整判断矩阵的元素取值。
4. 层次总排序及其一致性检验计算同一层次所有因素对于最高层(总目标)相对性的排序权值,称为层次总排序。
这一过程是最高层次到最低层次逐层进行的。
若上一层次A包含n个因素, A1,A2,…,其层次总排序权值分别为a1,a2,…an,下一层次B包含m个元素B1,B2,…Bm,它们对于因素Aj的层次单排序权值分别为b1j,b2j,…bmj (当Bk与Aj无联系时,b kj=0),此时B层次总排序权值由下表给出。
表5-3 层次总排序计算表A1A2…AnB 层次总排序权值a1a2…a nB1b11b12 (1)B2b21b22 (2)┇┇┇┇┇┇B m b m1b m2…b mn层次一致性检验也是从高到低逐层进行的。
如果B层次某些因素对于Aj单排序的一致性指标为CIj ,相应的平均随机一致性指标为CRj,则当B层次总排序随机一致性比率:时,认为层次总排序结果具有满意的一致性,否则需要重新调整判断矩阵的元素取值。
二、供应商选择步骤第一步设定评价指标体系供应商评价问题涉及因素众多,评价指标多种多样,既有定性的,又有定量的,而且指标权重各不相同,因此有必要建立一套通用的、可扩展的供应商评价指标体系,该指标体系应遵循一定的原则:1. 完备、简洁性原则供应商的指标体系应能全面、准确地反映供应商各个方面的情况,并且能将各个评价指标与系统的总体目标有机地联系起来,组成一个层次分明的整体。
在供应商信息尽量充分的前提下,所选指标数目应尽可能少,各指标之间不应有强相关性,不应出现过多的信息包容和涵盖现象。
2. 客观、可比性原则指标筛选过程应尽可能不受主观因素的影响,尽可能选用可量化的指标,确保评价结果的真实性和可比性。
3. 可重构、可扩充性原则评价指标不仅要有数量上的变化,而且还要有指标内容上的变化,应该可以根据不同的要求对指标体系进行修改、增加和删除。
例5-1 对某一物料,假设有甲、乙、丙、丁四家供应商,确立的指标体系为:价格水平、质量水平、交货周期、售后服务。
建立的供应商评价指标体系如下图所示:评价尺度如下表所示:表5-4 判断矩阵标度含义表评价尺度评价描述评分极端重要9很重要7明显重要 5稍微重要 3重要性相同 1中间值 2 、 4 、 6 、 8 、介于各评分值中间第二步构造判断矩阵在指标层由专家对四个指标进行两两比较打分,得到判断矩阵。
注意要保证aii=1,aij=1/ aji ,即评价指标评分与自身相比,重要性相同,与矩阵主对角线相对称的数值互为倒数。
表5-5 评价指标两两比较判断矩阵初始矩阵:评价指标——两两比较价格水平质量水平交货周期售后服务价格水平 1 1/2 3 5质量水平 2 1 3 2交货周期1/3 1/3 1 1/4售后服务1/5 1/2 4 1在价格、质量、交货周期和售后服务水平上,对甲乙丙丁四家企业两两比较得判断矩阵如表5-6~表5-9所示。
表5-6 价格水平供应商两两比较判断矩阵初始矩阵:评价指标——两两比较价格水平质量水平交货周期售后服务价格水平 1 1/2 3 5质量水平 2 1 3 2交货周期1/3 1/3 1 1/4售后服务1/5 1/2 4 1表5-7 质量水平供应商两两比较判断矩阵价格水平甲乙丙丁甲 1 1 1/2 6乙 1 1 1/2 6丙 2 2 1 7丁1/6 1/6 1/7 1表5-8交货周期供应商两两比较判断矩阵质量水平甲乙丙丁甲 1 3 5 5乙1/3 1 2 2丙1/5 1/2 1 1丁1/5 1/2 1 1表5-9 售后服务供应商两两比较判断矩阵售后服务甲乙丙丁甲 1 3 5 5乙1/3 1 3 3丙1/5 1/3 1 1丁1/5 1/3 1 1第三步计算最大特征值及其对应的特征向量首先计算第一个判断矩阵的最大特征值及其对应的特征向量。
根据矩阵理论,利用计算机得到理想精度的最大特征值及其对应的特征向量。
但是,由于判断矩阵本身有相当的误差范围,所以计算最大特征值及其对应的特征向量并不需要追求较高的精确度。
这里,介绍一种近似算法──方根法,计算最大特征值及其对应的特征向量,可以非常方便地完成计算。
方根法计算最大特征值及其对应的特征向量步骤(1)计算判断矩阵每一行元素的乘积Mi,(2)计算Mi的n次方根(3)对向量进行正规化处理,即。
则即为所求的特征向量。
(4)计算判断矩阵的最大特征值λmax式中(AW)i表示向量的第i个元素,A为判断矩阵。
运用上述步骤,本例具体计算如下:(1)计算判断矩阵每一行元素的乘积M1=1×1/2×3×5=7.5M2=2×1×3×2=12M3=1/3×1/3×1×1/4=0.0278M4=1/5×1/2×4×1=0.4(2)计算Mi的n次方根(3)对向量进行正规化则所求的特征向量(4)计算判断矩阵的最大特征值λmax则(5)一致性判断λmax - n 4.4984 - 4CI = ---------- = ------------ = 0.1661n - 1 4 - 1由表5-2可知,当n=4时,RI=0.9CI 0.1661CR = -------- = ---------- = 0.1864>0.1RI 0.9所以不能达到满意一致性,修正原判断矩阵,重复上述计算步骤,直到一致性检验通过。
表5-10评价指标判断矩阵计算价格水平质量水平交货周期售后服务权重价格水平 1 2 3 3 0.4275质量水平1/2 1 5 2 0.3104交货周期1/3 1/5 1 1/4 0.0746售后服务1/3 1/2 4 1 0.1876 CI=0.0783 RI=0.9 CR=0.0870表5-11价格水平供应商单排序计算供应商层次单排序价格水平指标排序甲乙丙丁权重甲 1 1 1/2 6 0.2539乙 1 1 1/2 6 0.2539丙 2 2 1 7 0.4438丁1/6 1/6 1/7 1 0.0484 λmax =4.0365 CI=0.0122 RI=0.9 CR=0.0135其余四个判断矩阵的计算与上述步骤相同,计算结果如下:表5-12质量水平供应商单排序计算供应商层次单排序质量水平指标排序甲乙丙丁权重甲 1 3 5 5 0.5723乙1/3 1 2 2 0.2090丙1/5 1/2 1 1 0.1094丁1/5 1/2 1 1 0.1094 λmax =4.0042 CI=0.0014 RI=0.9 CR=0.0015表5-13交货周期供应商单排序计算供应商层次单排序交货周期指标排序甲乙丙丁权重甲 1 1 1/2 1/2 0.1650乙 1 1 1/2 1/2 0.1650丙 2 2 1 2 0.3925丁 2 2 1/2 1 0.2775λmax =4.0604 CI=0.0201 RI=0.9 CR=0.0224表5-14后援服务供应商单排序计算供应商层次单排序售后服务指标排序甲乙丙丁权重甲 1 3 5 5 0.5579乙1/3 1 3 3 0.2494丙1/5 1/3 1 1 0.0963丁1/5 1/3 1 1 0.0963 λmax =4.0434 CI=0.0145 RI=0.9 CR=0.0161第四步层次总排序计算及一致性检验甲乙丙丁四个供应商相对域价格水平、质量水平、交货周期和售后服务四项指标的层次总排序计算结果如下表所示表5-15供应商总排序计算价格水平质量水平交货周期售后服务层次0.4275 0.3104 0.0746 0.1875总排序甲0.2539 0.5723 0.1650 0.5579 0.4031乙0.2539 0.2090 0.1650 0.2494 0.2325丙0.4438 0.1094 0.3925 0.0963 0.2710丁0.0484 0.1094 0.2775 0.0963 0.0934最后,还要对层次总排序进行一致性检验,如果达不到满意指标,则仍需调整前面的判断矩阵,层次总排序一致性检验如下:CI == 0.4275×0.0122+0.3104×0.0014+0.0746×0.0201+0.1875×0.0145= 0.0099RI == 0.4275×0.9+0.3104×0.9+0.0746×0.9+0.1875×0.9= 0.9CI 0.0099CR = ----- = ---------- = 0.0110<0.1 符合一致性检验。
