武汉二中2017年分配生数学试题(word版含答案)

合集下载

2017武汉中考数学试卷及答案(Word精校版)

第1页 / 共10页2017年武汉市初中毕业生考试数学试卷一、选择题(共10小题，每小题3分，共30分)1.计算36的结果为( ) A ．6 B ．-6 C ．18 D ．-182.若代数式14a -在实数范围内有意义，则实数a 的取值范围为( )A ．a ＝4B ．a ＞4C ．a ＜4D ．a ≠4 3.下列计算的结果是x 5的为( )A ．x 10÷x 2B ．x 6-xC ．x 2·x 3D ．(x 2)3 4.在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：成绩/m1.50 1.60 1.65 1.70 1.75 1.80 人数2 3 2 3 4 1 则这些运动员成绩的中位数、众数分别为( ) A ．1.65、1.70 B ．1.65、1.75 C ．1.70、1.75 D ．1.70、1.70 5.计算(x +1)(x +2)的结果为( ) A ．x 2+2 B ．x 2+3x +2 C ．x 2+3x +3 D ．x 2+2x +2 6.点A (-3，2)关于y 轴对称的点的坐标为( ) A ．(3，-2) B ．(3，2) C ．(-3，-2) D ．(2，-3) 7.某物体的主视图如图所示，则该物体可能为( )A. B. C. D.8.按照一定规律排列的n 个数：-2、4、-8、16、-32、64、……，若最后三个数的和为768，则n 为( ) A ．9 B ．10 C ．11 D ．12 9.已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为( )A ．32B ．32C ．3D ．2310.如图，在Rt △ABC 中，∠C ＝90°，以△ABC 的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多为( ) A ．4 B ．5 C ．6 D ．7二、填空题(本大题共6个小题，每小题3分，共18分) 11.计算2×3+(-4)的结果为___________12.计算2111-++x x x 的结果为___________ 13.如图，在 ABCD 中，∠D ＝100°，∠DAB 的平分线AE 交DC 于点E ，连接BE .若AE ＝AB ，则∠EBC 的度数为___________14.一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同.随机摸出两个小球，摸出两个颜色相同的小球的概率为___________15.如图，在△ABC 中，AB ＝AC ＝23，∠BAC ＝120°，点D 、E 都在边BC 上，∠DAE ＝60°.若BD ＝2CE ，则DE 的长为___________16.已知关于x的二次函数y＝ax2+(a2-1)x-a的图象与x轴的一个交点的坐标为(m，0).若2＜m＜3，则a的取值范围是___________三、解答题(共8题，共72分)17.(本题8分)解方程：4x-3＝2(x-1)18.(本题8分)如图，点C、F、E、B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB 之间的关系，并证明你的结论19.(本题8分)某公司共有A、B、C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表各部门人数分布扇形图部门员工人数每人所创的年利润/万元A510B b8C c5(1)①在扇形图中，C部门所对应的圆心角的度数为___________②在统计表中，b＝___________，c＝___________(2)求这个公司平均每人所创年利润20.(本题8分)某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件.其中甲种第2页 / 共10页第3页 / 共10页奖品每件40元，乙种奖品每件30元(1) 如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件？(2) 如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案？21.(本题8分)如图，△ABC 内接于⊙O ，AB ＝AC ，CO 的延长线交AB 于点D (1) 求证：AO 平分∠BAC(2) 若BC ＝6，sin ∠BAC ＝35，求AC 和CD 的长22.(本题10分)如图，直线y ＝2x +4与反比例函数ky x的图象相交于A (-3，a )和B 两点(1)求k的值(2)直线y＝m(m＞0)与直线AB相交于点M，与反比例函数的图象相交于点N.若MN＝4，求m的值(3)直接写出不等式65xx>-的解集第4页 / 共10页23.(本题10分)已知四边形ABCD的一组对边AD、BC的延长线交于点E (1)如图1，若∠ABC＝∠ADC＝90°，求证：ED·EA＝EC·EB(2)如图2，若∠ABC＝120°，cos∠ADC＝35，CD＝5，AB＝12，△CDE的面积为6，求四边形ABCD的面积(3)如图3，另一组对边AB、DC的延长线相交于点F.若cos∠ABC＝cos∠ADC＝35，CD＝5，CF＝ED＝n，直接写出AD的长(用含n的式子表示)第5页 / 共10页24.(本题12分)已知点A(-1，1)、B(4，6)在抛物线y＝ax2+bx上(1)求抛物线的解析式(2)如图1，点F的坐标为(0，m)(m＞2)，直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H.设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE(3)如图2，直线AB分别交x轴、y轴于C、D两点.点P从点C出发，沿射线CD方向匀速运动，速度为每秒2个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝2PM，直接写出t的值第6页 / 共10页2017年武汉中考数学参考答案与解析一、选择题1 2 3 4 5 6 7 8 9 10A D C CB B A BC D提示：9.利用面积法做题，先作高求出一般三角形的面积，再求内切圆半径.过B作BD⊥AC于D，设AD=x，2222 57(8)x x-=--，解得52x=，532BD=，583223578Sra b c⨯===++++10. 共7种情况，如图所示二、填空题11.212.1x-13.30︒14.2515.333-16. 32a-<<-或1132a<<提示：15.方法一，向左边旋转，令EC =x，BD=2x ，22233)()(63)2x x x+=-（33(630,),63333x x DE x=±->=-=-舍正方法二，向右边旋转∠HCE=60°，令EC=x，HC=2x，所以∠CEH=90°，EH=3x=DE，所以3x+3x=6，x=3-3，DE=6-3x=33-3HHD E CD E CBA AB16.方法一：由题意可知，x=m时y=022(1)0am a m a+--=(1)()0am m a-+=121,m m aa==-①123m<<得1132a<<②223m<<得32a-<<-DBAC第7页 / 共10页第8页 / 共10页方法二：由题意可知，x =2对应的函数值与x =3对应的函数值异号(此时必有0∆≥)当x =2时，2242(1)232y a a a a a =+--=+-当x =3时，2293(1)383y a a a a a =+--=+- 22(232)(383)0a a a a +-+-< (21)(2)(31)(3)0a a a a -+-+<由图示可知蓝色区域为所求，故32a -<<-或1132a <<三、解答题17. 12x =18. CD =AB 且CD ∥AB (提示：线段的关系包括数量关系和位置关系)19. (1)①108°；②b =9，c =6(2)510+98+65=7.620⨯⨯⨯万元20. 解：(1)设甲产品购买x 件，乙产品购买y 件，由题意可得：204030650x y x y +=⎧⎨+=⎩ 515x y =⎧⎨=⎩解得所以，甲产品购买5件，乙产品购买15件(2)设甲奖品购买a 件，乙奖品购买()20a -件，由题意可得()202403020650a a a a -≤⎧⎨+-≤⎩ 解得2083a ≤≤a 为正整数 ∴78a =或，共有2种方案方案一：甲奖品购买7件，乙奖品购买13件；方案二：甲奖品购买8件，乙奖品购买12件.21.解：(1)如图1，连接AO . 在△ABO 和△ACO 中，AB AC AO AO BO CO =⎧⎪=⎨⎪=⎩△ABO ≌△ACO (SSS )∴∠BAO =∠CAO ∴AO 平分∠BAC(2)如图2，延长AO 交BC 于点H . AB =AC ，∠BAO =∠CAO ∴AH ⊥BC ∴BH =CH =12BC =3∠BOH =2∠BAO =∠BAC ∴sin ∠BOH = sin ∠BAC =35∴BH =3，BO =5，OH =4+_++_-31/2-21/3图1DBCAOPDAO第9页 / 共10页在Rt △ABH 中， AB =222293310AH BH +=+=∴AC =AB =310延长CD 交O 于点P ，连接PB ，PC 为直径， ∴∠PBC =90° ∴PB ∥OH ∴PB =2OH =8∴△AOD ∽△BPD ， 58DO AO PD PB ==∴DO =5251313PO =， CD =CO +DO =901322. 解：(1)将点()3,A a -代入24y x =+中得64a =-+∴2a =-将点()3,2A --代入y =k x 中得6k =∴k 的值为6(2) 将y m =代入24y x =+中得42m x -=将y m =代入 y =k x 中得6x m = ∴M (42m -，m ) N (6m，m )①当点M 在点N 右侧时4642m m--= 解得1643m =+，1643m =-(舍)②当点M 在点N 左侧时6442m m --= 解得32m =，41m =-(舍)综上所述，m 的值为643+或2 (3)1x <-或56x <<23. 解：(1) ∠E =∠E ，∠EDC =∠B =90° ∴△EDC ∽△EBAED EC EB EAEA ED EB EC ∴=∴⋅=⋅ (2)过点C 作CH ⊥AE 于点H在Rt △CDH 中，cos ∠ADC =35，CD =5∴CH =4162CDE S ED CH ∆=⋅= ∴ED =3过点A 作AG ⊥EB 交EB 的延长线于点G ∠ABC =120°，∴∠ABG =60°，AB =12∴在Rt △ABG 中，BG =6，AG =63 ∠AGE =∠CHE =90°，∠E =∠E∴△EHC ∽△EGA469363936CH EH EG AG EG EGEB EG BG ∴=∴=∴=∴=-=- DBE ACGHCD AB E xy M 2M 1N 1N 2BAO第10页 / 共10页75183ABE ECD ABCD S S S =-=-△△四边形(3)2556+nAD n+=24. 解：(1)将点()1,1A -和点()4,6B 代入2y ax bx =+中得16164a b a b =-=+⎧⎨⎩ 解得：1212a b ⎧⎪⎪⎨==-⎪⎪⎩∴该抛物线的解析式为21122y x x =-(2) 过点A 作AN x ⊥轴于点N设AF 的解析式为y kx m =+()0k ≠ ∴1k m =-+ ∴1k m =-∴AF 的解析式为()1y m x m =-+联立()211221y x xy m x m =-=-+⎧⎪⎨⎪⎩解得11x =-，22x m = ∴2G H x x m ==∴在Rt FOH △中OF m =，2OH m = 在Rt ANE △中1AN =，2NE =∴12OF AN OH NE ==∴Rt FOH Rt ANE △∽△ ∴FHO AEN ∠=∠ ∴FH AE ∥(3)t 的值为13892+或13892-或151136+或151136-xyQ H KMPCB A D O xy QMP C BA DOxy MPQG FAEOxyM PQ GFA EOxyNHGF A EO。

50武汉二中分配生考试试题16-17(附答案)

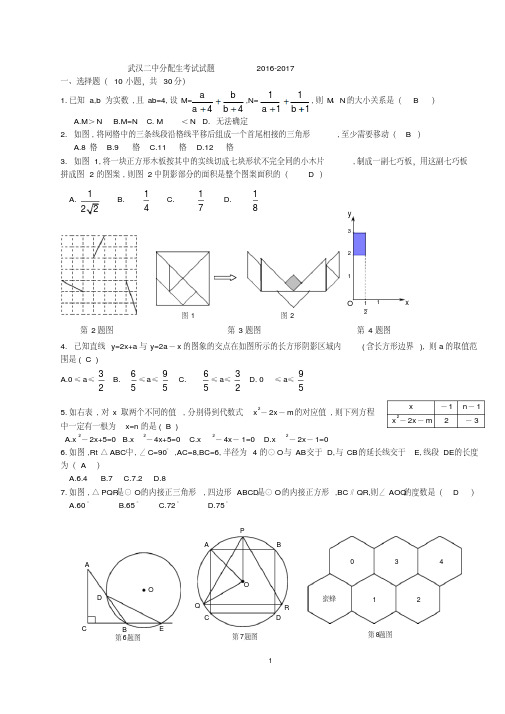
6. 如图 ,Rt △ ABC中 , ∠ C=90° ,AC=8,BC=6, 半径为 4 的⊙ O与 AB交于 D,与 CB的延长线交于 E, 线段 DE的长度
为（ A ）
A.6.4 B.7 C.7.2 D.8
7. 如图 , △ PQR是⊙ O的内接正三角形 , 四边形 ABCD是⊙ O的内接正方形 ,BC∥QR,则∠ AOQ的度数是（ D ）
武汉二中分配生考试试题
2016-2017
一、选择题（ 10 小题，共 30 分）
1. 已知 a,b 为实数 , 且 ab=4, 设 M= a
b
1
,N=
1 , 则 M、N 的大小关系是（ B ）
a 4 b 4 a1 b1
A.M＞ N B.M=N C. M ＜ N D. 无法确定
2. 如图 , 将网格中的三条线段沿格线平移后组成一个首尾相接的三角形
4
=1-
=1-
4
22
=1-
22
；
S 1 6 6 23
(2)
A2B2C2 ＝ 3 =1- 9 =1- 32 =1- 32 ；
(3)
S
79 A3 B3C3 ＝ 16 =1- 16 =1-
9 42
=1-
33 42 ；
………
S 7 3 43
∴
A7B7C7 ＝ 1-
82
=
64
13、函数 y＝ x2－ (k ＋1)x － 4(k ＋5) 的图象如图所示，它与 x 轴交于 A、 B 两点，且 OB＝4OA，则 k＝ ______.
2
2
③b － 5ac ＞ 0 时，则一元二次力程 ax ＋ bx ＋c＝ 0 一定有两个不相等的实数根；

2017年武汉市中学考试数学试卷含问题详解解析汇报版

实用标准文档文案大全2017年武汉市中考数学试卷一、选择题（共10小题，每小题3分，共30分）1．计算的结果为（）A．6 B．﹣6 C．18 D．﹣182．若代数式在实数范围内有意义，则实数a的取值范围为（）A．a=4 B．a＞4C．a＜4D．a≠43．下列计算的结果是x5的为（）A．x10÷x2 B．x6﹣xC．x2?x3 D．（x2）34．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：成绩/m1.51.61.61.71.71.8人数232341则这些运动员成绩的中位数、众数分别为（）A．1.65、1.70 B．1.65、1.75 C．1.70、1.75 D．1.70、1.705．计算（x+1）（x+2）的结果为（）A．x2+2 B．x2+3x+2 C．x2+3x+3 D．x2+2x+26．点A（﹣3，2）关于y轴对称的点的坐标为（）A．（3，﹣2）B．（3，2）C．（﹣3，﹣2）D．（2，﹣3）7．某物体的主视图如图所示，则该物体可能为（）A．B．C．D．8．按照一定规律排列的n个数：﹣2、4、﹣8、16、﹣32、64、…，若最后三个数的和为768，则n为（）实用标准文档文案大全A．9 B．10 C．11 D．129．已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（）A．B．C．D．10．如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）A．4 B．5 C．6 D．7二、填空题（本大题共6个小题，每小题3分，共18分）11．计算2×3+（﹣4）的结果为12．计算﹣的结果为13．如图，在?ABCD中，∠D=100°，∠DAB的平分线AE交DC于点E，连接BE．若AE=AB，则∠EBC的度数为14．一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为15．如图，在△ABC中，AB=AC=2，∠BAC=120°，点D、E都在边BC 上，∠DAE=60°．若BD=2CE，则DE的长为16．已知关于x的二次函数y=ax2+（a2﹣1）x﹣a的图象与x轴的一个交点的坐标为（m，0）．若2＜m＜3，则a的取值范围是三、解答题（共8题，共72分）实用标准文档文案大全17．（8分）解方程：4x﹣3=2（x﹣1）18．（8分）如图，点C、F、E、B在一条直线上，∠CFD=∠BEA，CE=BF，DF=AE，写出CD与AB之间的关系，并证明你的结论．19．（8分）某公司共有A、B、C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表员工每人所创的年利万元A510B b8C c5（1）①在扇形图中，C部门所对应的圆心角的度数为②在统计表中，b=，c=（2）求这个公司平均每人所创年利润．20．（8分）某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件．其中甲种奖品每件40元，乙种奖品每件30元（1）如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件？（2）如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案？实用标准文档文案大全21．（8分）如图，△ABC内接于⊙O，AB=AC，CO的延长线交AB 于点D（1）求证：AO平分∠BAC；（2）若BC=6，sin∠BAC=，求AC和CD的长．22．（10分）如图，直线y=2x+4与反比例函数y=的图象相交于A（﹣3，a）和B两点（1）求k的值；（2）直线y=m（m＞0）与直线AB相交于点M，与反比例函数的图象相交于点N．若MN=4，求m的值；（3）直接写出不等式＞x的解23．（10分）已知四边形ABCD的一组对边AD、BC的延长线交于点E．（1）如图1，若∠ABC=∠ADC=90°，求证：ED?EA=EC?EB；（2）如图2，若∠ABC=120°，cos∠ADC=，CD=5，AB=12，△CDE的面积为6，求四边形ABCD的面积；（3）如图3，另一组对边AB、DC的延长线相交于点F．若cos∠ABC=cos ∠ADC=，CD=5，CF=ED=n，直接写出AD的长（用含n的式子表示）实用标准文档文案大全24．（12分）已知点A（﹣1，1）、B（4，6）在抛物线y=ax2+bx上（1）求抛物线的解析式；（2）如图1，点F的坐标为（0，m）（m＞2），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE；（3）如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM=2PM，直接写出t的值．实用标准文档文案大全2017年湖北省武汉市中考数学试卷一、选择题（共10小题，每小题3分，共30分）1．（3分）（2017?武汉）计算的结果为（）A．6B．﹣6 C．18 D．﹣18解：=6．故选：A．2．（3分）（2017?武汉）若代数式在实数范围内有意义，则实数a的取值范围为（）A．a=4 B．a＞4C．a＜4D．a≠4解：依题意得：a﹣4≠0，解得a≠4．故选：D．3．（3分）（2017?武汉）下列计算的结果是x5的为（）A．x10÷x2 B．x6﹣x C．x2?x3 D．（x2）3解：A、x10÷x2=x8．B、x6﹣x=x6﹣x．C、x2?x3=x5．D、（x2）3=x64．（3分）（2017?武汉）在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：成绩/m1.501.601.651.701.751.80人数232341则这些运动员成绩的中位数、众数分别为（）A．1.65、1.70 B．1.65、1.75 C．1.70、1.75 D．1.70、1.70解：共15名学生，中位数落在第8名学生处，第8名学生的跳高成绩为1.70m，故中位数为1.70；跳高成绩为1.75m的人数最多，故跳高成绩的众数为1.75；故选C．实用标准文档文案大全5．（3分）（2017?武汉）计算（x+1）（x+2）的结果为（）A．x2+2 B．x2+3x+2 C．x2+3x+3 D．x2+2x+2解：原式=x2+2x+x+2=x2+3x+2，故选B6．（3分）（2017?武汉）点A（﹣3，2）关于y轴对称的点的坐标为（）A．（3，﹣2）B．（3，2）C．（﹣3，﹣2）D．（2，﹣3）解：A（﹣3，2）关于y轴对称的点的坐标为（3，2），故选：B．7．（3分）（2017?武汉）某物体的主视图如图所示，则该物体可能为（）A．B．C．D．解：A、球的主视图为圆，符合题意；B、圆锥的主视图为矩形，不符合题意；C、六棱柱与六棱锥的组合体的主视图为矩形和三角形的结合图，不符合题意；D、五棱柱的主视图为矩形，不符合题意，故选：A．8．（3分）（2017?武汉）按照一定规律排列的n个数：﹣2、4、﹣8、16、﹣32、64、…，若最后三个数的和为768，则n为（）A．9B．10 C．11 D．12解：由题意，得第n个数为（﹣2）n，那么（﹣2）n﹣2+（﹣2）n﹣1+（﹣2）n=768，当n为偶数：整理得出：3×2n﹣2=768，解得：n=10；当n为奇数：整理得出：﹣3×2n﹣2=768，则求不出整数，故选B．为（﹣2）n是解9．（3分）（2017?武汉）已知一个三角形的三边长分别为5、7、8，则其内切圆实用标准文档文案大全的半径为（）A．B．C．D．解：如图，AB=7，BC=5，AC=8，内切圆的半径为r，切点为D、E、F，作AD⊥BC于D，设BD=x，则CD=5﹣x．由勾股定理可知：AD2=AB2﹣BD2=AC2﹣CD2，即72﹣x2=82﹣（5﹣x）2，解得x=1，∴AD=4，∵?BC?AD=（AB+BC+AC）?r，×5×4=×20×r，∴r=，故选C10．（3分）（2017?武汉）如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）A．4 B．5 C．6 D．7解：如图：实用标准文档文案大全故选D．二、填空题（本大题共6个小题，每小题3分，共18分）11．（3分）（2017?武汉）计算2×3+（﹣4）的结果为2解：原式=6﹣4=2，故答案为：212．（3分）（2017?武汉）计算﹣的结果为解：原式=，故答案为：13．（3分）（2017?武汉）如图，在?ABCD中，∠D=100°，∠DAB的平分线AE交DC于点E，连接BE．若AE=AB，则∠EBC的度数为30°解：∵四边形ABCD是平行四边形，∴∠ABC=∠D=100°，AB∥CD，∴∠BAD=180°﹣∠D=80°，∵AE平分∠DAB，∴∠BAE=80°÷2=40°，实用标准文档文案大全∵AE=AB，∴∠ABE=（180°﹣40°）÷2=70°，∴∠EBC=∠ABC﹣∠ABE=30°；故答案为：30°14．（3分）（2017?武汉）一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为解：画树状图如下：由树状图可知，共有20种等可能结果，其中取出的小球颜色相同的有8种结果，∴两次取出的小球颜色相同的概率为=，故答案为：15．（3分）（2017?武汉）如图，在△ABC中，AB=AC=2，∠BAC=120°，点D、E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为3﹣3解：将△ABD绕点A逆时针旋转120°得到△ACF，连接EF，过点E作EM ⊥CF于点M，过点A作AN⊥BC于点N，如图所示．∵AB=AC=2，∠BAC=120°，∴BN=CN，∠B=∠ACB=30°在Rt△BAN中，∠B=30°，AB=2，∴AN=AB=，BN==3，∴BC=6．∵∠BAC=120°，∠DAE=60°，∴∠BAD+∠CAE=60°，实用标准文档文案大全∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°在△ADE和△AFE中，，∴△ADE≌△AFE（SAS），∴DE=FE．∵BD=2CE，BD=CF，∠ACF=∠B=30°，∴设CE=2x，则CM=x，EM=x，FM=4x﹣x=3x，EF=ED=6﹣6x．．在Rt△EFM中，FE=6﹣6x，FM=3x，EM=x，∴EF2=FM2+EM2，即（6﹣6x）2=（3x）2+（x）2，解得：x1=，x2=（不合题意，舍去），∴DE=6﹣6x=3﹣3．故答案为：3﹣3．16．（3分）（2017?武汉）已知关于x的二次函数y=ax2+（a2﹣1）x﹣a的图象与x轴的一个交点的坐标为（m，0）．若2＜m＜3，则a的取值范围是＜a＜或﹣3＜a＜﹣2解：∵y=ax2+（a2﹣1）x﹣a=（ax﹣1）（x+a），∴当y=0时，x1=，x2=﹣a，∴抛物线与x轴的交点为（，0）和（﹣a，0）．∵抛物线与x轴的一个交点的坐标为（m，0）且2＜m＜3，∴当a＞0时，2＜＜3，解得＜a＜；当a＜0时，2＜﹣a＜3，解得﹣3＜a＜﹣2．故答案为：＜a＜或﹣3＜a＜﹣2．三、解答题（共8题，共72分）17．（8分）（2017?武汉）解方程：4x﹣3=2（x﹣1）实用标准文档文案大全解：4x﹣3=2（x﹣1）4x﹣3=2x﹣24x﹣2x=﹣2+32x=1x=18．（8分）（2017?武汉）如图，点C、F、E、B在一条直线上，∠CFD=∠BEA，CE=BF，DF=AE，写出CD与AB之间的关系，并证明你的结论．解：CD∥AB，CD=AB，理由是：∵CE=BF，∴CE﹣EF=BF﹣EF，∴CF=BE，在△AEB和△CFD中，，∴△AEB≌△CFD（SAS），∴CD=AB，∠C=∠B，∴CD∥AB．19．（8分）（2017?武汉）某公司共有A、B、C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表部门员工人数每人所创的年利润/万元A510B b8C c5（1）①在扇形图中，C部门所对应的圆心角的度数为108°实用标准文档文案大全②在统计表中，b=9，c=6（2）求这个公司平均每人所创年利润．（1）①在扇形图中，C部门所对应的圆心角的度数为：360°×30%=108°；解：②A部门的员工人数所占的百分比为：1﹣30%﹣45%=25%，各部门的员工总人数为：5÷25%=20（人），∴b=20×45%=9，c=20×30%=6，故答案为：108°，9，6；（2）这个公司平均每人所创年利润为：=7.6（万元）．20．（8分）（2017?武汉）某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件．其中甲种奖品每件40元，乙种奖品每件30元（1）如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件？（2）如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案？解：（1）设甲种奖品购买了x件，乙种奖品购买了（20﹣x）件，根据题意得40x+30（20﹣x）=650，解得x=5，则20﹣x=15，答：甲种奖品购买了5件，乙种奖品购买了15件；（2）设甲种奖品购买了x件，乙种奖品购买了（20﹣x）件，根据题意得，解得≤x≤8，∵x为整数，∴x=7或x=8，实用标准文档文案大全当x=7时，20﹣x=13；当x=8时，20﹣x=12；答：该公司有2种不同的购买方案：甲种奖品购买了：7件，乙种奖品购买了13件或甲种奖品购买了8件，乙种奖品购买了12件．21．（8分）（2017?武汉）如图，△ABC内接于⊙O，AB=AC，CO的延长线交AB于点D（1）求证：AO平分∠BAC；（2）若BC=6，sin∠BAC=，求AC和CD的长．（1）证明：延长AO交BC于H，连接BO，如图1所示：∵AB=AC，OB=OC，∴A、O在线段BC的垂直平分线上，∴AO⊥BC，又∵AB=AC，∴AO平分∠BAC；（2）解：延长CD交⊙O于E，连接BE，如图2所示：则CE是⊙O的直径，∴∠EBC=90°，BC⊥BE，∵∠E=∠BAC，∴sinE=sin∠BAC，∴=，∴CE=BC=10，∴BE==8，OA=OE=CE=5，∵AH⊥BC，实用标准文档文案大全∴BE∥OA，∴=，解得：OD=，∴CD=5+=，∵BE∥OA，即BE∥OH，OC=OE，∴OH是△CEB的中位线，∴OH=BE=4，CH=BC=3，∴AH=5+4=9，在Rt△ACH中，AC===322．（10分）（2017?武汉）如图，直线y=2x+4与反比例函数y=的图象相交于A（﹣3，a）和B两点（1）求k的值；（2）直线y=m（m＞0）与直线AB相交于点M，与反比例函数的图象相交于点N．若MN=4，求m的值；（3）直接写出不等式＞x的解集．实用标准文档文案大全（1）∵点A（﹣3，a）在y=2x+4与y=的图象上，∴2×（﹣3）+4=a，∴a=﹣2，∴k=（﹣3）×（﹣2）=6；（2）∵M在直线AB上，∴M（，m），N在反比例函数y=上，∴N（，m），∴MN=x N﹣x m=﹣=4或x M﹣x N=﹣=4，解得：∵m＞0，∴m=2或m=6+4；（3）x＜﹣1或x5＜x＜6，由＞x得：﹣x＞0，∴＞0，∴＜0，∴＞＜或＞，结合抛物线y=x2﹣5x﹣6的图象可知，由＞＜得＜或＞＜，实用标准文档文案大全∴＜＜或＜，∴此时x＜﹣1，由＜＞得，＜＞，∴＜＜＞，解得：5＜x＜6，综上，原不等式的解集是：x＜﹣1或5＜x＜6．23．（10分）（2017?武汉）已知四边形ABCD的一组对边AD、BC的延长线交于点E．（1）如图1，若∠ABC=∠ADC=90°，求证：ED?EA=EC?EB；（2）如图2，若∠ABC=120°，cos∠ADC=，CD=5，AB=12，△CDE的面积为6，求四边形ABCD的面积；（3）如图3，另一组对边AB、DC的延长线相交于点F．若cos∠ABC=cos ∠ADC=，CD=5，CF=ED=n，直接写出AD的长（用含n的式子表示）实用标准文档文案大全解：（1）如图1中，∵∠ADC=90°，∠EDC+∠ADC=180°，∴∠EDC=90°，∵∠ABC=90°，∴∠EDC=∠ABC，∵∠E=∠E，∴△EDC∽△EBA，∴=，∴ED?EA=EC?EB．（2）如图2中，过C作CF⊥AD于F，AG⊥EB于G．在Rt△CDF中，cos∠ADC=，∴=，∵CD=5，∴DF=3，∴CF==4，实用标准文档文案大全∵S△CDE=6，∴?ED?CF=6，∴ED==3，EF=ED+DF=6，∵∠ABC=120°，∠G=90°，∠G+∠BAG=∠ABC，∴∠BAG=30°，∴在Rt△ABG中，BG=AB=6，AG==6，∵CF⊥AD，AG⊥EB，∴∠EFC=∠G=90°，∵∠E=∠E，∴△EFC∽△EGA，∴=，∴=，∴EG=9，∴BE=EG﹣BG=9﹣6，∴S四边形ABCD=S△ABE﹣S△CDE=（9﹣6）×6﹣6=75﹣18（3）如图3中，作CH⊥AD于H，则CH=4，DH=3，∴tan∠E=，作AG⊥DF于点G，设AD=5a，则DG=3a，AG=4a，∴FG=DF﹣DG=5+n﹣3a，∵CH⊥AD，AG⊥DF，∠E=∠F，易证△AFG∽△CEH，∴=，实用标准文档文案大全∴=，∴a=，∴AD=5a=24．（12分）（2017?武汉）已知点A（﹣1，1）、B（4，6）在抛物线y=ax2+bx 上（1）求抛物线的解析式；（2）如图1，点F的坐标为（0，m）（m＞2），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE；（3）如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM=2PM，直接写出t的值．解：（1）将点A（﹣1，1）、B（4，6）代入y=ax2+bx中，，解，∴抛物线的解析式为x2﹣x．（2）证明：设直线AF的解析式为y=kx+m，将点A（﹣1，1）代入y=kx+m中，即﹣k+m=1，∴k=m﹣1，实用标准文档文案大全∴直线AF的解析式为y=（m﹣1）x+m．联立直线AF和抛物线解析式成方程组，，解得：，，∴点G的坐标为（2m，2m2﹣m）．∵GH⊥x轴，∴点H的坐标为（2m，0）．∵抛物线的解析式为x x=x（x﹣1），∴点E的坐标为（1，0）．设直线AE的解析式为y=k1x+b1，将A（﹣1，1）、E（1，0）代入y=k1x+b1中，，解得：，∴直线AE的解析式为y x+设直线FH的解析式为y=k2x+b2，将F（0，m）、H（2m，0）代入y=k2x+b2中，，解得，∴直线FH的解析式为y=﹣x+m．∴FH∥AE．（3）设直线AB的解析式为y=k0x+b0，将A（﹣1，1）、B（4，6）代入y=k0x+b0中，，解得：，∴直线AB的解析式为y=x+2．当运动时间为t秒时，点P的坐标为（t﹣2，t），点Q的坐标为（t，0）．当点M在线段PQ上时，过点P作PP′⊥x轴于点P′，过点M作MM′⊥x轴于点M′，则△PQP′∽△MQM′，如图2所示．实用标准文档文案大全∵QM=2PM，∴=，∴QM′=，MM′=t，∴点M的坐标为（，t）．又∵点M在抛物线x2﹣x上，∴t=×（）（），解得：t=；当点M在线段QP的延长线上时，同理可得出点M的坐标为（t﹣4，2t），∵点M在抛物线x2﹣x上，∴2t=×（t﹣4）（t﹣4），解得：t=综上所述：当运动时间为秒、秒、秒或秒时，QM=2PM．。

湖北省武汉市2017年中考数学试题及答案(Word版)

湖北省武汉市2017年中考数学试题及答案（试卷满分120，考试时间120分钟）一、选择题（共10小题，每小题3分，共30分） 1．计算36的结果为（）A ．6B ．－6C ．18D ．－182．若代数式41a 在实数范围内有意义，则实数a 的取值范围为（） A ．a ＝4B ．a ＞4C ．a ＜4D ．a ≠43．下列计算的结果是x 5的为（）A ．x 10÷x2B ．x 6－xC ．x 2·x3D ．(x 2)34．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：则这些运动员成绩的中位数、众数分别为（）A ．1.65、1.70B ．1.65、1.75C ．1.70、1.75D ．1.70、1.70 5．计算(x ＋1)(x ＋2)的结果为（）A ．x 2＋2B ．x 2＋3x ＋2C ．x 2＋3x ＋3D ．x 2＋2x ＋26．点A (－3，2)关于y 轴对称的点的坐标为（）A ．(3，－2)B ．(3，2)C ．(－3，－2)D ．(2，－3)7．某物体的主视图如图所示，则该物体可能为（）8．按照一定规律排列的n 个数：－2、4、－8、16、－32、64、……，若最后三个数的和为768，则n 为（） A ．9B ．10C ．11D ．129．已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（）A ．23 B ．23C ．3D ．3210．如图，在Rt △ABC 中，∠C ＝90°，以△ABC 的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多为（） A ．4B ．5C ．6D ．7二、填空题（本大题共6个小题，每小题3分，共18分）11．计算2×3＋(－4)的结果为___________ 12．计算111+-+x x x 的结果为___________ 13．如图，在□ABCD 中，∠D ＝100°，∠DAB 的平分线AE 交DC 于点E ，连接BE ．若AE ＝AB ，则∠EBC 的度数为___________14．一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为__________15．如图，在△ABC 中，AB ＝AC ＝32，∠BAC ＝120°，点D 、E 都在边BC 上，∠DAE ＝60°．若BD ＝2CE ，则DE 的长为___________16．已知关于x 的二次函数y ＝ax 2＋(a 2－1)x －a 的图象与x 轴的一个交点的坐标为(m ，0)．若2＜m ＜3，则a 的取值范围是___________ 三、解答题（共8题，共72分）17．（本题8分）解方程：4x －3＝2(x －118．（本题8分）如图，点C 、F 、E 、B 在一条直线上，∠CFD ＝∠BEA ，CE ＝BF ，DF ＝AE ，写出CD 与AB 之间的关系，并证明你的结论19．（本题8分）某公司共有A 、B 、C 三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表各部门人数分布扇形图(1) ① 在扇形图中，C 部门所对应的圆心角的度数为___________ ② 在统计表中，b ＝___________，c ＝___________ (2) 求这个公司平均每人所创年利润20．（本题8分）某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件．其中甲种奖品每件40元，乙种奖品每件30元(1) 如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件？ (2) 如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案？21．（本题8分）如图，△ABC 内接于⊙O ，AB ＝AC ，CO 的延长线交AB 于点D (1) 求证：AO 平分∠BAC(2) 若BC ＝6，sin ∠BAC ＝53，求AC 和CD 的长22．（本题10分）如图，直线y ＝2x ＋4与反比例函数xky =的图象相交于A (－3，a )和B 两点 (1) 求k 的值(2) 直线y ＝m （m ＞0）与直线AB 相交于点M ，与反比例函数的图象相交于点N ．若MN ＝4，求m 的值(3) 直接写出不等式x x >-56的解集23．（本题10分）已知四边形ABCD 的一组对边AD 、BC 的延长线交于点E (1) 如图1，若∠ABC ＝∠ADC ＝90°，求证：ED ·EA ＝EC ·EB(2) 如图2，若∠ABC ＝120°，cos ∠ADC ＝53，CD ＝5，AB ＝12，△CDE 的面积为6，求四边形ABCD 的面积(3) 如图3，另一组对边AB 、DC 的延长线相交于点F ．若cos ∠ABC ＝cos ∠ADC ＝53，CD ＝5，CF ＝ED ＝n ，直接写出AD 的长（用含n 的式子表示）24．（本题12分）已知点A (－1，1)、B (4，6)在抛物线y ＝ax 2＋bx 上 (1) 求抛物线的解析式(2) 如图1，点F 的坐标为(0，m )（m ＞2），直线AF 交抛物线于另一点G ，过点G 作x 轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE (3) 如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒2个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝2PM，直接写出t的值11。

湖北省武汉市第二中学2016-2017学年高二上学期期末考试数学(理)试题含答案

武汉二中2016—2017学年度上学期期末考试高二数学试卷命题学校：武汉二中命题教师: 审题教师：试卷满分：150分一、选择题（每小题5分,共60分）1．在武汉二中选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为（）A 、6B 、8C 、10D 、12 2．已知,,a b c R ∈，命题“若3a b c ++=，则2223ab c ++≥”的否命题是(）A 、若3a b c ++≠，则2223a b c ++< B 、若3a b c ++=,则2223a b c ++<C 、若3a b c ++≠，则2223ab c ++≥D 、若2223ab c ++≥，则3a b c ++=3．设()f x 是区间[,]a b 上的函数，如果对任意满足a x y b ≤<≤的,x y 都有()()f x f y ≤，则称()f x 是[,]a b 上的升函数,则()f x 是[,]a b 上的非升函数应满足（）。

A 、存在满足x y <的,[,]x y a b ∈使得()()f x f y >B 、不存在,[,]x y a b ∈满足x y <且()()f x f y ≤C 、对任意满足x y <的,[,]x y a b ∈都有()()f x f y >D 、存在满足x y <的,[,]x y a b ∈都有()()f x f y ≤4．阅读右边的程序框图,运行相应的程序，则输出i 的值为（）A 、3B 、4C 、5D 、6 5．已知集合,,A B C 满足{,,}AB a b c =,则满足条件的组合(,)A B 共有（）组.A 、4B 、8C 、9D 、276．设n m l ,,表示三条不同的直线，γβα,,表示三个不同的平面，给出下列四个命题：①若βα⊥⊥⊥m l m l ,,，则βα⊥；②若β⊂m ，n 是l 在β内的射影，n m ⊥，则l m ⊥；③若γαβα⊥⊥,,则βα//其中真命题的个数为（） A 、0 B 、1 C 、2 D 、37．“2a =-”是“直线(2)310a x ay +++=与直线(2)(2)30a x a y -++-=相互垂直”的( ）条件。

2017年初中毕业升学考试(湖北武汉卷)数学(带解析)

绝密★启用前2017年初中毕业升学考试（湖北武汉卷）数学（带解析）学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、计算的结果为（）A ．6B ．-6C ．18D ．-182、若代数式在实数范围内有意义，则实数的取值范围为（）A ．B ．C ．D ．3、下列计算的结果是的为（）A ．B ．C ．D ．4、在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示．成绩/1.50 1.60 1.65 1.701.75 1.80 人数 2 3 2 3 4 1则这些运动员成绩的中位数，众数分别为（）A ．1．65，1．70B ．1．65，1．75C ． 1．70，1．75D ．1．70，1．705、计算的结果为（）A ．B ．C ．D ．6、点关于轴对称的坐标为（）A ．B ．C ．D ．7、某物体的主视图如图所示，则该物体可能为（）A ．B ．C ．D ．8、按照一定规律排列的个数：-2，4，-8，16，-32，64，…．若最后三个数的和为768，则为（）A ．9B ．10C ．11D ．129、已知一个三角形的三边长分别为5，7，8．则其内切圆的半径为（）A ．B ．C ．D ．10、如图，在中，，以的一边为边画等腰三角形，使得它的第三个顶点在的其他边上，则可以画出的不同的等腰三角形的个数最多为（）A ．4B ．5C ．6D ．7第II卷（非选择题）二、填空题（题型注释）11、计算的结果为．12、计算的结果为．13、如图，在ABCD中，∠D=100°，∠DAB的平分线AE交DC于点E，连接BE，若AE=AB，则∠EBC的度数为．14、一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为．15、如图△ABC中，AB=AC，∠BAC=120°，∠DAE=60°，BD=5，CE=8，则DE的长为．16、已知关于x的二次函数y=ax2+(a2-1)x-a的图象与轴的一个交点的坐标为(m,0)，若2<m<3，则a的取值范围是．三、解答题（题型注释）17、解方程：．18、如图，点在一条直线上，，．写出与之间的关系，并证明你的结论．19、某公司共有三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图．各部门人数及每人所创年利润统计表（1）①在扇形图中，C 部门所对应的圆心角的度数为___________； ②在统计表中，___________，___________；（2）求这个公司平均每人所创年利润．20、某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件，其中甲种奖品每件40元，乙种奖品每件30元．（1）如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件；（2）如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案．21、如图，内接于，的延长线交于点．（1）求证平分；（2）若，求和的长．22、如图，直线与反比例函数的图象相交于和两点．（1）求的值；（2）直线与直线相交于点，与反比例函数的图象相交于点．若，求的值；（3）直接写出不等式的解集．23、已知四边形的一组对边的延长线相交于点．（1）如图1，若，求证；（2）如图2，若，，，，的面积为6，求四边形的面积；（3）如图3，另一组对边的延长线相交于点，若，，，直接写出的长（用含的式子表示）．24、已知点在抛物线上．（1）求抛物线的解析式；（2）如图1，点的坐标为，直线交抛物线于另一点，过点作轴的垂线，垂足为，设抛物线与轴的正半轴交于点，连接，求证；（3）如图2，直线分别交轴，轴于两点，点从点出发，沿射线方向匀速运动，速度为每秒个单位长度，同时点从原点出发，沿轴正方向匀速运动，速度为每秒1个单位长度，点是直线与抛物线的一个交点，当运动到秒时，，直接写出的值．参考答案1、A.2、D.3、C.4、C.5、B.6、B.7、D8、A.9、C10、C11、2.12、x-1.13、30°.14、．15、7.16、-3<a<-2，<a<.17、x=.18、证明见解析：19、（1）①108°；②9，6；（2）7.6万元.20、（1）甲、乙两种奖品分别购买5件、15件.（2）该公司有两种不同的购买方案：方案一：购买甲种奖品7件，购买乙种奖品13件；方案二、购买甲种奖品8件，购买乙种奖品12件.21、（1）证明见解析；（2）；.22、(1)-6;(2) m=2或6+;(3) x<-1或5<x<623、(1)证明见解析；（2）75-18；（3）24、（1）抛物线的解析式为：y=x2-x；（2）证明见解析；（3）；.【解析】1、试题解析：∵=6故选A.考点：算术平方根.2、试题解析：根据“分式有意义，分母不为0”得：a-4≠0解得：a≠4.故选D.考点：分式有意义的条件.3、试题解析：A．=x8，该选项错误；B．与不能合并，该选项错误；C．=，该选项正确；D．=x6，该选项错误.故选C.考点：1.同底数幂的除法；2.同底数幂的乘法；3.积的乘方与幂的乘方.4、试题解析：将数据从小到大排列为：1.50，150，1.60，1.60，160，1.65，1.65，1.70，1.70，1.70，1.75，1.75，1.75，1.75，1.80.众数为：1.75；中位数为：1.70．故选C．考点：1.中位数；2.众数.5、试题解析：=x2+2x+x+2= x2+3x +2.故选B.考点：多项式乘以多项式6、试题解析：根据关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得：点A（-3，2）关于y轴对称的坐标为（3，2）.故选B.考点：关于x轴、y轴对称的点的坐标特征7、试题解析：只有选项A的图形的主视图是拨给图形，其余均不是.故选A.考点：三视图.8、试题解析：设后3个的数和为：（-1）n+1×2n-1+（-1）n+2×2n+（-1）n+3×2n+1=768，当n为偶数：整理得出：-5×（-2）n-1=768，则求不出整数，当n为奇数：整理得出：3×2n-1=768，解得：n=9．故选A.考点：数字变化规律.9、试题解析：如图，AB=7，BC=5，AC=8过A作AD⊥BC于D，设BD=x，则CD＝5-x由勾腰定理得：72-x2=82-（5-x）2解得：x=1∴AD=4设ΔABC的内切圆的半径为r，则有：（5r+7r+8r）= ×5×4解得：r=故选C.考点：三角形的内切圆.10、试题解析：①以B为圆心，BC长为半径画弧，交AB于点D，△BCD就是等腰三角形；②以A为圆心，AC长为半径画弧，交AB于点E，△ACE就是等腰三角形；③以C为圆心，BC长为半径画弧，交AC于点F，△BCF就是等腰三角形；④作AC的垂直平分线交AB于点H，△ACH就是等腰三角形；⑤作AB的垂直平分线交AC于G，则△AGB是等腰三角形；⑥作BC的垂直平分线交AB于I，则△BCI是等腰三角形．故选C.考点：画等腰三角形.11、试题解析：=6-4=2.考点：有理数的混合运算.12、试题解析：=考点：分式的加减法.13、试题解析：∵四边形ABCD是平行四边形∴AB∥DC，∠ABC=∠D∴∠DAB+∠D=180°，∵∠D=100°，∴∠DAB=80°, ∠ABC=100°又∵∠DAB的平分线交DC于点E∴∠EAD=∠EAB=40°∵AE=AB∴∠ABE=(180°-40°)=70°∴∠EBC=∠ABC-∠ABE=100°-70°=30°.考点：1.解平分线的性质；2.平行四边形的性质.共有20种所有等可能的结果，其中两个颜色相同的有8种情况，故摸出两个颜色相同的小球的概率为．考点：列表法和树状图法.15、试题解析：∵AB=AC，∴可把△AEC绕点A顺时针旋转120°得到△AE′B，如图，∴BE′=EC=8，AE′=AE，∠E′AB=∠EAC，∵∠BAC=120°，∠DAE=60°，∴∠BAD+∠EAC=60°，∴∠E′AD=∠E′AB+∠BAD=60°，在△E′AD和△EAD中∴△E′AD≌△EAD（SAS），∴E′D=ED，过E′作EF⊥BD于点F，∵AB=AC，∠BAC=120°，∴∠ABC=∠C=∠E′BA=30°，∴∠E′BF=60°，∴∠BE′F=30°，∴BF=BE′=4，E′F=4，∵BD=5，∴FD=BD-BF=1，在Rt△E′FD中，由勾股定理可得E′D=，∴DE=7．考点：1.含30度角的直角三角形；2.等腰三角形的性质．16、试题解析：把（m，0）代入y=ax2+(a2-1)x-a得，am2+(a2-1)m-a=0解得：m=∵2<m<3解得：-3<a<-2，<a<.考点：二次函数的图象.17、试题分析：去括号，移项，合并同类项，系数化为1后即可得解. 试题解析：去括号，得：4x-3=2x-2移项，得：4x-2x=3-2合并同类项得：2x=1系数化为1得：x=.考点：解一元一次方程.18、试题分析：通过证明ΔCDF≌ΔABE，即可得出结论试题解析：CD与AB之间的关系是：CD=AB，且CD∥AB证明：∵CE=BF，∴CF=BE在ΔCDF和ΔBAE中∴ΔCDF≌ΔBAE∴CD=BA，∠C=∠B∴CD∥BA考点：全等三角形的判定与性质.19、试题分析：（1）①在扇形图中，由C部门所占比例乘以360°即可得出C部门所对应的圆心角的度数.②先计算出A部门所占比例，再计算出总人数，根据B、C部门所占比例即可求出b、c的值.（2）利用加权平均数的计算公式计算即可．试题解析：（1）①360°×30%=108°；②∵a%=1-45%-30%=25%5÷25%=20∴20×45%=9（人）20×30%=6（人）（2）10×25%+8×45%+5×30%=7.6答：这个公司平均每人所创年利润是7.6万元.考点：1.扇形统计图；2.加权平均数.20、试题分析：（1）根据“两种奖品共20件”和“两种奖品共花费650元”列出方程组求解即可；（2）根据题意，列出不等式组求解即可.试题解析：（1）设甲、乙两种奖品分别购买x件、y件依题意，得：解得：答：甲、乙两种奖品分别购买5件、15件.（2）设甲种奖品购买m件，则乙种奖品购买（20-m）件依题意得：解得：∵m为整数，∴m=7或8当m=7时，20-m=13；当m=8时，20-m=12答：该公司有两种不同的购买方案：方案一：购买甲种奖品7件，购买乙种奖品13件；方案二、购买甲种奖品8件，购买乙种奖品12件.考点：1.二元一次方程组的应用；2.一元一次不等式组的应用.21、试题分析：（1）连接OB，证明ΔAOB≌ΔAOC即可得出结论；（2）过点C作CE⊥AB于E，由sin∠BAC=，设AC=5m，CE=3则可表示出AE=4m，BE=m，在RtΔCBE中，由勾股定理可求出m的值，即可得出AC的值；延长AO交BC于点H，则AH⊥BC，过点O作OF⊥AH，可求OF的值，由OF∥BC可得结论. 试题解析：（1）证明：连接OB∵AO=AO，BO=CO，AB=AC∴ΔAOB≌ΔAOC∴∠BAO=∠CAO即AO平分∠BAC（2）过点C作CE⊥AB于E∵sin∠BAC=,设AC=5m，则CE=3m∴AE=4m，BE=m在RtΔCBE中，m2+(3m)2=36∴m=，∴AC=延长AO交BC于点H，则AH⊥BC，且BH=CH=3，过点O作OF⊥AH交AB于点F，∵∠HOC=∠BAC∴OH=4，OC=5∴AH=9∴tan∠BAH=∴OF=AO=∵OF∥BC∴，即∴DC=.考点：1.全等三角形的判定与性质；2.解直角三角形；3.平行线分线段成比例.22、试题分析：（1）把A（-3，a）代入y=2x+4即可求出a=-2，把A（-3，-2）代入求得k=6；（2）联立方程组，求出M、N的坐标，根据MN=4，即可求出m的值；（3）令可求出函数y=x和y=的交点坐标，从而可求的解集.试题解析：（1）把A（-3，a）代入y=2x+4，得a=-2，∴A（-3，-2）把A（-3，-2）代入，得k=6；（2）∵M是直线y=m与直线AB的交点∴M（，m）同理，N（，m）∴MN=｜-｜=4∴-=±4解得m=2或-6或6±∵m>0∴m=2或6+（3）x<-1或5<x<6考点：1.求反比例函数解析式；2.反比例函数与一次函数交点问题.23、试题分析：（1）证明ΔEAB∽ΔECD，即可得解.（2）过点C作CG⊥AD于点G，过点A作AH⊥BC于点H，在RtΔCDG中利用已知条件可求出DG、CG的长，再根据ΔCDE的面积为6，可求出ED的长，在ΔABH中可求出BH 、AH长，利用（1）可知ΔECG∽ΔEAH，从而可求出EH的长，利用S四边形＝SΔAEH－SΔECG-SΔABH即可得解；ABCD（3）由（1）（2）提供的思路即可求解.试题解析：（1）∵∠ADC=90°∴∠EDC=90°∴∠ABE=∠CDE又∵∠AEB=∠CED∴ΔEAB∽ΔECD∴∴(2)过点C作CG⊥AD于点G，过点A作AH⊥BC于点H，∵CD=5，cos∠ADC=∴DG=3，CG=4∵SΔCED=6∴ED=3∴EG=6∵AB="12" ∠ABC=120°∴BH=6 AH=6由（1）有：ΔECG∽ΔEAH∴∴EH=9∴S四边形ABCD＝SΔAEH－SΔECG-SΔABH==75-18(3)考点：相似三角形的判定与性质.24、试题分析：（1）把A，B两点坐标代入，解方程组求出a，b的值，即可得到二次函数解析式；（2）过点A作AN⊥ｘ轴于点N，则N(-1，0)，再求出E点坐标，从而可求tan∠AEN=,再求出直线AF的解析式与抛物线方程联立,求出点G的坐标,则可得到tan∠FHO=，从而得证；（3）进行分类讨论即可得解.试题解析：（1）∵点A（-1，1），B（4，6）在抛物线y=ax2+bx上∴a-b=1，16a+4b=6解得：a=，b=-∴抛物线的解析式为：y=x2-x（2）过点A作AN⊥x轴于点N，则N(-1，0)∴AN=1当y=0时，x2-x=0解得：x=0或1∴E（1，0）∴EN=2∴tan∠AEN=设直线AF的解析式为y=kx+m∵A (-1,1)在直线AF上，∴-k+m=1即：k=m-1∴直线AF的解析式可化为：y=(m-1)x+m与y=x2-x联立，得（m-1）x+m=x2-x ∴(x+1)（x-2m）=0∴x=-1或2m∴点G的横坐标为2m∴OH=2m∵OF=m∴tan∠FHO=∴∠AEN=∠FHO∴FH∥AE（3）；.考点：二次函数综合题.。

武汉二中分配生考试数学试卷及答案

武汉⼆中分配⽣考试数学试卷及答案武汉⼆中分配⽣考试数学试卷及答案（考试时间：120分钟满分：120分）⼀、选择题（共10⼩题，共30分）1.规定“△”为有序实数对的运算，如下所⽰：（a ，b ）△(c ，d )=(ac +bd ，ad+bc ).若对任意实数a ，b 都有（a ，b ）△（x ，y ）=（a ，b ），则（x ，y ）为（）A.(0，1)B. (1，0)C. (-1，0)D. (0，-1) 解：依题意：，恒有=>，选B.2.⽤“△”、“O ”、“ □”分别表⽰三种物体的重量.若==+?O -O ?O ?□□，则△、O 、□这三种物体的重量⽐为（）A.2：3：4B. 2：4：3C. 3：4：5D. 2：5：4 解：令，，，令=> => =>令，，则，∴，选B3.如图，在△ABC 中，AB=AC ，D 、E 分别为边AB 、AC 上的点，DM 平分∠BDE ，EN 平分∠DEC .若∠DMN =110°，则∠DEA =（）A.40°B. 50°C. 60°D.70° 选A.4.对左下⽅的⼏何体变换位置或视⾓，则可以得到⼏何体是（）解：B5.某台球桌为如图所⽰矩形ABCD ，⼩球从A 沿45°⾓出击，恰好经过5次碰撞到B 处，则AB :BC =( )A.1：2B. 2：3C. 2：5D. 3：56.在平⾯直⾓坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经过两次变换后所得的新抛物线的解析式为（）A.22y x x =--+B.22y x x =-+-C. 22y x x =-++D. 22y x x =++ 解：第⼀次变换后，第⼆次变换后，选C.7.某养鸡场分3次⽤鸡蛋孵化出⼩鸡，每次孵化所⽤的鸡蛋数、每次的孵化率（孵化率=100%?孵化出的⼩鸡数孵化所⽤的鸡蛋数分别如图1，图2所⽰：如果要孵化出2000只⼩鸡，根据上⾯的计算结果，估计该养鸡场要⽤（）个鸡蛋. A.3000 B.2700 C.2500 D.2400解：即，∴，选C.8.如图在Rt △ABC 中，∠ACB =90°,∠BAC =30°，AB=2，D 是AB 边上的⼀个动点（不与点A 、B 重合），过点D 作CD 的垂线交射线CA 于点E ，设AD =x ，CE =y ，则下列图象中，能表⽰y 与x 的函数关系图象⼤致是（）分析：取的中点，考虑⊙的⼤⼩变化，⊙与相切时最⼩，时圆最⼤，选C.9.已知点A （11x y ，）、B （22x y ，）均在抛物线224(03)y ax ax a =++<<上，若12x x <，121x x a =-+，则（）A. 12y y >B. 12y y <C. 12y y =D. 12y y 与的⼤⼩不能确定解：∵抛物线开⼝向上，对称轴为，考虑与的⼤⼩，即可⽐较∴，∴选B.10.设I 是△ABC 的内⼼，r 是其内切圆半径，R 是其外接圆半径.若AI 的延长线交△ABC 的外接圆于点P ，则IA IP ?=( )A. 2RrB. 22R r C. 22Rr D. 222R r解：延长BO 交⊙O 于D ，作IH ⊥AC 于H ，证明Rt △DPB ∽Rt △AHI 即可选A.⼆、填空题（共6⼩题，共18分）11.罗马数字有7个基本符号，它们分别是Ⅰ，Ⅴ，Ⅹ，L ，C ，D ，M 分别代表1，5，10，50，100，500，1000.罗马数依靠着7个符号变换组合来表⽰的如Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅺ，Ⅻ，分别表⽰1，2，3，4，5，6，7；⽤Ⅸ，Ⅹ，Ⅺ，Ⅻ，分别表⽰9，10，11，12；根据以上规律，你认为L II 表⽰的数应该是 . 填52.12.如图，直线y=x 与直线14y x =分别与双曲线(0)ky x x=>交于A 、B 两点，3OAB S ?=，则k = .填2.13.有6张卡⽚，每张卡⽚上分别写有不同的从1到6的⾃然数，从中任意抽出两张卡⽚，则两张卡⽚中的数字之和为偶数的概率是 .14.在下表中，我们把第i ⾏第j 列的数记为i j a ，（其中i ，j 都是不⼤于5的正整数），对于表中的每个数i j a ，，规定如下：当i ≥j 时，i j a ，=1；当i15、现有⼀组数据共有100个数，其中有15个数在中位数和平均数之间.如果这组数据的中位数和平均数都不在这100个数中，这组数据中⼩于平均数的数据占这100个数据的半分⽐是 . 填写：35%或65% 16、如图，△ABC 内接于⊙O ，AB+AC=12，AD ⊥BC 于点D ，AD=3，则⊙O ⾯积的最⼤值为 . 解：易得∵，∴∴，，填三、解答题（共9题，共72分） 17、（本题6分）解⽅程：解：令，则，整理得解得或，∴（⽆解）或解得18、（本题6分）在平⾯直⾓坐标系中，将直线y=kx +3绕原点逆时针旋转90°刚好经过点（-2，1），求不等式kx +3≦x +2的解集解：原直线经点，该点绕原点逆时针旋转90°后为点，⼜旋转后的直线经过点∴易得新直线解析式为，∴旋转前的直线解析式为∴的解集为.19、（本题6分）我们把能平分四边形⾯积的直线称为“好线”.利⽤下⾯作图，可以得到四边形的“好线”：如图1，在四边形ABCD 中，取对⾓线BD 的中点O ，连接OA 、OC .显然，折线AOC 能平分四边形ABCD 的⾯积，再过O 作OE ∥AC 交CD 与点E ，则直线AE 即为⼀条“好线”. （1）试说明图1中的直线AE 是“好线”的理由；（2）如图2，AE 为⼀条“好线”，F 为AD 边上的⼀点，请作出经过F 点的“好线”，并对画图作适当的说明（不需要说明理由）.图1 图2BCB分析：（1）设AE 与OC 的交点是F ．要说明直线AE 是“好线”,根据已知条件中的折线AOC 能平分四边形ABCD 的⾯积,只需说明三⾓形AOF 的⾯积等于三⾓形CEF 的⾯积．则根据两条平⾏线间的距离相等,结合三⾓形的⾯积个数可以证明三⾓形AOE 的⾯积等于三⾓形COE 的⾯积,再根据等式的性质即可证明；（2）根据两条平⾏线间的距离相等,只需借助平⾏线即可作出过点F 的“好线”．（1）设AE 与OC 的交点是F ．因为OE ‖AC,所以S △AOE=S △COE, 所以S △AOF=S △CEF,⼜因为,折线AOC 能平分四边形ABCD 的⾯积,所以直线AE 平分四边形ABCD 的⾯积,即AE 是“好线”．（2）连接EF,过A 作EF 的平⾏线交CD 于点G,连接FG,则AE 为⼀条“好线”．∵AG ‖EF,∴S △AGE=S △AFG ．设AG 与EF 的交点是O ．则S △AOF=S △GOE,⼜AE 为⼀条“好线”,所以AE 为⼀条“好线”．20、（本题7分）如图，A 是直线l ：y=3x 上⼀点，AB ⊥l 于点A ，交y 轴正半轴于B (0，2). （1）求A 点的坐标；（2）将△OAB 沿着AB 翻着⾄△O 1AB ，则直线O 1B 的解析式为: ；将△OAB 沿着OA 翻着⾄△OAB 2，则直线OB 2的解析式为: ；将△OAB 绕O 点顺时针旋转90°⾄△OA 3B 3，则直线A 3B 3的解析式:_______________. (第(2)问直接写出答案，不写过程.)解：（1）作AH⊥y 轴于H ，设，由△∽△有即，解得：，∴（2）①；②；③21、（本题7分）如图，放在直⾓坐标系中的正⽅形ABCD 的边长为4.现作如下实验：转盘被划分成4个相同的⼩扇形，并分别标上数字1、2、3、4，分别转动两次转盘，转盘停⽌后，指针所指向的数字作为直⾓坐标系中M 点的坐标（第⼀次作横坐标，第⼆次作纵坐标），指针如果指向分界线上，则重新转动转盘.（1）请你⽤树状图或列表的⽅法，求M 点落在正⽅形ABCD ⾯上（含内部和边界）的概率；（2）将正⽅形ABCD 平移整数个单位，则是否存在某种平移，使点M 落在正⽅形ABCD ⾯上的概率为34若存在，指出⼀种具体的平移过程若不存在，请说明理由.解：（1）正⽅形四个顶点的坐标分别是A （-2，2）；B （-2，-2）；C （2，-2）；D （2，2），列表得：a 1 2 3 4 b2 （1，2）（2，2）（3，2）（4，2）3 （1，3）（2，3）（3，3）（4，3）4 （1，4）（2，4）（3，4）（4，4） M 点的坐标所有的情况有共16种，其中落在正⽅形ABCD ⾯上（含内部与边界）的有（1，1），（1，2），（2，1），（2，2），共4种，所以M 点落在正⽅形ABCD ⾯上（含内部与边界）的概率是（2）若使点M 落在正⽅形ABCD ⾯上的概率为，则只有4个点不在正⽅形内部，所以可把正⽅形ABCD 向右平移2个单位长度，再向上平移1个单位长度或者向右平移1个单位长度，向上平移2个单位长度即可．22、（本题8分）如图，⊙O 的弦，C 是优弧︵AB 的中点，点是劣弧︵AB 上任意⼀点，过作⊙的切线，与⊙在点、处的切线、分别交点、，、与弦分别交于点、.（1）求证：平分；（2）求的长度.（1）证明：易得，得证. （2）过作的平⾏线交、的延长线于、.则，由（1）知，∴∴，同理，∴设交于，由∥易得，同理∴.23.（本题10分）如图，在平⾯直⾓坐标系中，矩形的顶点、分别在轴、轴上，顶点在第⼀象限内，、分别是、上的点，将△沿翻折，使点恰好落在线段上的点处.经过抛物线：（）顶点的每⼀条直线总平分矩形的周长，若点在线段上，的长为整数，且抛物线与线段有两个不同的交点，求实数的取值范围.解：设抛物线的顶点.则，①，，②∵经过抛物线的顶点的每⼀条直线总平分矩形的周长∴即为矩形的中⼼，也是的中点，∴，.∵点在线段的上⽅，抛物线与线段有两个不同的交点，∴只能有抛物线开⼝向下（否则⽆交点），从⽽24.（本题10分）如图，在四边形中，，∥，，，点在边的延长线上，，点在边上，与边交于点，.设，.（1）求关于的函数关系式，并写出⾃变量的取值范围；（2）当时，求的长度；（3）若半径为的⊙与半径为的⊙相切，则此时⊙的半径为 .解：（1）∵，，∴∵∥，∴，即∵，∴△∽△∴，即，即：，其中.（2）由（1）知，，∴. ∵，，.∴，整理得：易得是⽅程的根，则是多项式的⼀个因式，从⽽易得：∴或，∴或（负数根舍去）（3）依题意，，△与△均为等腰直⾓三⾓形.∴.25.（本题12分）如图1，抛物线的顶点在轴的正半轴，与轴交于点，连接，若.（1）求抛物线的解析式；（2）如图2，将图1中的抛物线沿对称轴向下平移个单位长度，新抛物线的顶点为，它与直线相交于、两点，连接、.探究：当取何值时，；（3）如图3，为直线上⼀动点，经过点的直线交抛物线于、两点（点在线段上），若，求点的横坐标的取值范围.解：（1）抛物线顶点，∵，∴.把点代⼊抛物线解析式，得：，解得：∴抛物线解析式为：.（2）如图2，把平移后的抛物线图像及直线的图像向上平移个单位，再向左平移的单位，使得抛物线的顶点在原点，此时在轴上，作于，轴于，则△∽△，易得此时，（过程略），即，∴（3）易得,，从⽽或。

湖北省武汉二中2017-2018学年高二上学期期末数学试卷(理科)Word版含解析

2017-2018学年湖北省武汉二中高二（上）期末数学试卷（理科）一、选择题：（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有最新试卷十年寒窗苦，踏上高考路，心态放平和，信心要十足，面对考试卷，下笔如有神，短信送祝福，愿你能高中，马到功自成，金榜定题名。

一个选项是符合题目要求的，把正确选项的代号填在答题卡上.）1．两个事件对立是两个事件互斥的（）A．充分非必要条件B．必要非充分条件C．充要条件 D．既不充分又不必要条件2．设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（x i，y i）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x﹣85.71，则下列结论中不正确的是（）A．y与x具有正的线性相关关系B．回归直线过样本点的中心（，）C．若该大学某女生身高增加1cm，则其体重约增加0.85kgD．若该大学某女生身高为170cm，则可断定其体重必为58.79kg3．下列正确的是（）A．若p，q为两个，则“p且q为真”是“p或q为真”的必要不充分条件B．若p为：?x∈R，x2+2x≤0则￢p为：?x∈R，x2+2x＞0C．p为真，q为假．则p∧（￢q），（￢p）∨q都是真D．“若￢p，则q”的逆否是“若p，则￢q”．4．从2003件产品中选取50件，若采用下面的方法选取：先用简单随机抽样从2003件产品中剔除3件，剩下的2000件再按系统抽样的方法抽取，则每件产品被选中的概率（）A．不都相等 B．都不相等C．都相等，且为D．都相等，且为5．在下列中：①若向量、共线，则向量、所在的直线平行；②若向量、所在的直线为异面直线，则向量、不共面；③若三个向量、、两两共面，则向量、、共面；④已知空间不共面的三个向量、、，则对于空间的任意一个向量，总存在实数x、y、z，使得；其中正确的的个数是（）A．0 B．1 C．2 D．36．一个三位自然数百位、十位、个位上的数字依次为a，b，c，当且仅当其中有两个数字的和等于第三个数字时称为“有缘数”（如213，341等）．若a，b，c∈{1，2，3，4}，且a，b，c互不相同，任取一个三位自然数，则它是“有缘数”的概率是（）A．B．C．D．7．如果ξ～B，则使P（ξ=k）取最大值时的k值为（）A．5或6 B．6或7 C．7或8 D．以上均错8．已知实数x∈[1，9]，执行如图所示的流程图，则输出的x不小于55的概率为（）A．B．C．D．9．若（ax2+x+y）5的展开式的各项系数和为243，则x5y2的系数为（）A．10 B．20 C．30 D．6010．若某同学连续三次考试的名次（第一名为1，第二名为2，以此类推且没有并列名次情况）不超过3，则称该同学为班级的尖子生．根据甲、乙、丙、丁四位同学过去连续3次考试名次数据，推断一定不是尖子生的是（）A．甲同学：均值为2，中位数为 2 B．乙同学：均值为2，方差小于 1C．丙同学：中位数为2，众数为 2 D．丁同学：众数为2，方差大于 111．设甲、乙两人每次射击命中目标的概率分别为，且各次射击相互独立，若按甲、乙、甲、乙…的次序轮流射击，直到有一人击中目标就停止射击，则停止射击时，甲射击了两次的概率是（）A．B．C． D．12．已知双曲线的左、右焦点分别是F1、F2，过F2的直线交双曲线的右支于P、Q两点，若|PF1|=|F1F2|，且3|PF2|=2|QF2|，则该双曲线的离心率为（）A．B．C．2 D．二、填空题：（本大题共有4个小题，每小题5分，共20分.把正确答案填在答题卡的相应位置.）13．有5名数学实习老师，现将他们分配到高二年级的三个班实习，每班至少1名，最多2名，则不同的分配方案有______种（用数字作答）．14．甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示．现从这20名学生中随机抽取一人，将“抽出的学生为甲小组学生”记为事件A；“抽出的学生英语口语测试成绩不低于85分”记为事件B．则P（A|B）的值是______．15．在一个正方体ABCD﹣A1B1C1D1中，P为正方形A1B1C1D1四边上的动点，O为底面正方形ABCD的中心，M，N分别为AB，CD的中点，点Q为平面SKABCD内一点，线段D1Q与OP互相平分，则满足=λ的实数λ的值有______个．16．已知圆P：x2+y2=4y及抛物线S：x2=8y，过圆心P作直线l，此直线与上述两曲线的四个交点，自左向右顺次记为A，B，C，D，如果线段AB，BC，CD的长按此顺序构成一个等差数列，则直线l的斜率为______．三、解答题：（本大题共6个小题，共70分.解答应写出文字说明、证明过程或推演步骤.）17．已知p：方程﹣=1表示焦点在y轴上的椭圆；q：双曲线﹣=1的离心率e∈（1，2）．若p、q有且只有一个为真，求m的取值范围．18．设函数f（x）=x2+bx+c，其中b，c是某范围内的随机数，分别在下列条件下，求事件A“f（1）≤5且f（0）≤3”发生的概率．（1）若随机数b，c∈{1，2，3，4}；（2）已知随机函数Rand（）产生的随机数的范围为{x|0≤x≤1}，b，c是算法语句b=4*Rand（）和c=4*Rand（）的执行结果．（注：符号“*”表示“乘号”）19．如图，在三棱柱ABC﹣A1B1C1中，AB⊥AC，顶点A1在底面ABC上的射影恰为点B，且AB=AC=A1B=2．（1）证明：平面A1AC⊥平面AB1B；（2）求棱AA1与BC所成的角的大小；（3）若点P为B1C1的中点，并求出二面角P﹣AB﹣A1的平面角的余弦值．20．某市一高中经过层层上报，被国家教育部认定为2015年全国青少年足球特色学校．该校成立了特色足球队，队员来自高中三个年级，人数为50人．视力对踢足球有一定的影响，因而对这50人的视力作一调查．测量这50人的视力（非矫正视力）后发现他们的视力全部介于4.75和5.35之间，将测量结果按如下方式分成6组：第一组[4.75，4.85），第二组[4.85，4.95），…，第6组[5.25，5.35]，如图是按上述分组方法得到的频率分布直方图．又知：该校所在的省中，全省喜爱足球的高中生视力统计调查数据显示：全省100000名喜爱足球的高中生的视力服从正态分布N（5.01，0.0064）．（1）试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况；（2）求这50名队员视力在 5.15以上（含 5.15）的人数；（3）在这50名队员视力在 5.15以上（含 5.15）的人中任意抽取2人，该2人中视力排名（从高到低）在全省喜爱足球的高中生中前130名的人数记为ξ，求ξ的数学期望．参考数据：若ξ～N（μ，σ2），则P（μ﹣σ＜ξ≤μ+σ）=0.6826，P（μ﹣2σ＜ξ≤μ+2σ）=0.9544，P（μ﹣3σ＜ξ≤μ+3σ）=0.9974．21．已知椭圆C：=1（a＞b＞0）的离心率为，以原点O为圆心，椭圆C的长半轴为半径的圆与直线2x﹣y+6=0相切．（1）求椭圆C的标准方程；（2）已知点A，B为动直线y=k（x﹣2）（k≠0）与椭圆C的两个交点，问：在x轴上是否存在点E，使2+?为定值？若存在，试求出点E的坐标和定值，若不存在，说明理由．22．在平面直角坐标系xOy中，已知点Q（1，2），P是动点，且三角形POQ的三边所在直线的斜率满足+=．（1）求点P的轨迹C的方程；（2）过点D（1，0）任作两条互相垂直的直线l1，l2，分别交轨迹C于点A，B和M，N，设线段AB，MN的中点分别为E，F求证：直线EF恒过一定点．2015-2016学年湖北省武汉二中高二（上）期末数学试卷（理科）参考答案与试题解析一、选择题：（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的，把正确选项的代号填在答题卡上.）1．两个事件对立是两个事件互斥的（）A．充分非必要条件B．必要非充分条件C．充要条件 D．既不充分又不必要条件【考点】互斥事件与对立事件．【分析】根据对立事件和互斥事件的意义知，两个事件是互斥事件那么这两个事件不一定是对立事件，若两个事件是对立事件，则这两个事件一定是互斥事件，即前者能够推出后者，后者不一定能够推出前者．【解答】解：根据对立事件和互斥事件的意义知，两个事件是互斥事件那么这两个事件不一定是对立事件，若两个事件是对立事件，则这两个事件一定是互斥事件，所以两个时间对立是两个事件互斥的充分不必要条件，故选A．2．设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（x i，y i）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x﹣85.71，则下列结论中不正确的是（）A．y与x具有正的线性相关关系B．回归直线过样本点的中心（，）C．若该大学某女生身高增加1cm，则其体重约增加0.85kgD．若该大学某女生身高为170cm，则可断定其体重必为58.79kg【考点】回归分析的初步应用．【分析】根据回归方程为=0.85x﹣85.71，0.85＞0，可知A，B，C均正确，对于D回归方程只能进行预测，但不可断定．【解答】解：对于A，0.85＞0，所以y与x具有正的线性相关关系，故正确；对于B，回归直线过样本点的中心（，），故正确；对于C，∵回归方程为=0.85x﹣85.71，∴该大学某女生身高增加1cm，则其体重约增加0.85kg，故正确；对于D，x=170cm时，=0.85×170﹣85.71=58.79，但这是预测值，不可断定其体重为58.79kg，故不正确故选D．3．下列正确的是（）A．若p，q为两个，则“p且q为真”是“p或q为真”的必要不充分条件B．若p为：?x∈R，x2+2x≤0则￢p为：?x∈R，x2+2x＞0C．p为真，q为假．则p∧（￢q），（￢p）∨q都是真。

2017年武汉高中招生考试数学试卷

2017年武汉市初中毕业生学业考试数学试题（含答案全解全析）第Ⅰ卷(选择题,共30分)一、选择题(共10小题,每小题3分,共30分)1.计算的结果为()A.6B.-6C.18D.-182.若代数式在实数范围内有意义,则实数a的取值范围为()A.a=4B.a>4C.a<4D.a≠43.下列计算的结果是x5的为()A.x10÷x2B.x6-xC.x2·x3D.(x2)34.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:则这些运动员成绩的中位数、众数分别为()A.1.65,1.70B.1.65,1.75C.1.70,1.75D.1.70,1.705.计算(x+1)(x+2)的结果为()A.x2+2B.x2+3x+2C.x2+3x+3D.x2+2x+26.点A(-3,2)关于y轴对称的点的坐标为()A.(3,-2)B.(3,2)C.(-3,-2)D.(2,-3)7.某物体的主视图如图所示,则该物体可能为()8.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后三个数的和为768,则n为()A.9B.10C.11D.129.已知一个三角形的三边长分别为5,7,8,则其内切圆的半径为()A. B. C. D.210.如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为()A.4B.5C.6D.7第Ⅱ卷(非选择题,共90分)二、填空题(共6小题,每小题3分,共18分)11.计算2×3+(-4)的结果为.12.计算-的结果为.13.如图,在▱ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为.14.一个不透明的袋中共有5个小球,分别为2个红球和3个黄球,它们除颜色外完全相同.随机摸出两个小球,摸出两个颜色相同的小球的概率为.15.如图,在△ABC中,AB=AC=2,∠BAC=120°,点D,E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为.16.已知关于x的二次函数y=ax2+(a2-1)x-a的图象与x轴的一个交点的坐标为(m,0).若2<m<3,则a的取值范围是.三、解答题(共8小题,共72分)17.(本小题满分8分)解方程4x-3=2(x-1).18.(本小题满分8分)如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE.写出CD与AB之间的关系,并证明你的结论.某公司共有A,B,C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.各部门人数及每人所创年利润统计表各部门人数分布扇形图(1)①在扇形图中,C部门所对应的圆心角的度数为;②在统计表中,b=,c=;(2)求这个公司平均每人所创年利润.某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪．几种．．不同的购买方案.21.(本小题满分8分)如图,△ABC内接于☉O,AB=AC,CO的延长线交AB于点D.(1)求证:AO平分∠BAC;(2)若BC=6,sin∠BAC=,求AC和CD的长.如图,直线y=2x+4与反比例函数y=的图象相交于A(-3,a)和B两点.(1)求k的值;(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数y=的图象相交于点N,若MN=4,求m的值;(3)直接写出不等式>x的解集.23.(本小题满分10分)已知四边形ABCD的一组对边AD,BC的延长线相交于点E.(1)如图1,若∠ABC=∠ADC=90°,求证ED·EA=EC·EB;(2)如图2,若∠ABC=120°,cos∠ADC=,CD=5,AB=12,△CDE的面积为6,求四边形ABCD 的面积;(3)如图3,另一组对边AB,DC的延长线相交于点F,若cos∠ABC=cos∠ADC=,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).24.(本小题满分12分)已知点A(-1,1),B(4,6)在抛物线y=ax2+bx上.(1)求抛物线的解析式;(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH,AE,求证:FH∥AE;(3)如图2,直线AB分别交x轴,y轴于C,D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.答案全解全析：一、选择题1.A因为62=36,所以36的算术平方根是6,即=6.2.D根据分式有意义的条件,得a-4≠0,解得a≠4.故选D.3.C选项A,x10÷x2=x8,该选项不符合题意;选项B,x6与x不能合并,该选项不符合题意;选项C,x2·x3=x5,该选项符合题意;选项D,(x2)3=x6,该选项不符合题意.故选C.4.C将数据从小到大排列为1.50,1.50,1.60,1.60,1.60,1.65,1.65,1.70,1.70,1.70,1.75,1.75,1.75,1.75,1.80.1.75出现的次数最多,故众数为1.75,最中间的数是1.70,故中位数为1.70,故选C.5.B(x+1)(x+2)=x2+2x+x+2=x2+3x+2.故选B.6.B根据关于y轴对称的两点坐标的特点:横坐标互为相反数,纵坐标相等,可得点A(-3,2)关于y轴对称的点的坐标为(3,2).7.A只有选项A中物体的主视图是圆,故选A.8.B根据规律可知,第n个数为(-1)n2n,则最后三个数为(-1)n-22n-2,(-1)n-12n-1,(-1)n2n,当n为奇数时,(-1)n-22n-2+(-1)n-12n-1+(-1)n2n=768,即-2n-2+2n-1-2n=768,∴-2n-2(1-2+4)=768,∴-2n-2=256,此方程无解;当n为偶数时,(-1)n-22n-2+(-1)n-12n-1+(-1)n2n=768,即2n-2-2n-1+2n=768,∴2n-2(1-2+4)=768,∴2n-2=28,∴n-2=8,∴n=10.9.C如图,AB=7,BC=5,AC=8.过点A作AD⊥BC于点D,设BD=x,则CD=5-x.由勾股定理得AB2-BD2=AD2,AC2-CD2=AD2,则72-x2=82-(5-x)2,解得x=1,∴AD=4.设△ABC的内切圆的半径为r,则有×(5+7+8)r=×5×4,解得r=.故选C.10.D①如图1,以B为圆心,BC长为半径画弧,交AB于点D,则△BCD就是等腰三角形;②如图2,以A为圆心,AC长为半径画弧,交AB于点E,则△ACE就是等腰三角形;③如图3,以C为圆心,BC长为半径画弧,交AB于M,交AC于点F,则△BCM、△BCF是等腰三角形;④如图4,作AC的垂直平分线交AB于点H,则△ACH就是等腰三角形;⑤如图5,作AB的垂直平分线交AC于点G,则△AGB就是等腰三角形;⑥如图6,作BC的垂直平分线交AB于I,则△BCI就是等腰三角形.故选D.二、填空题11.答案2解析2×3+(-4)=6-4=2.12.答案x-1解析-===x-1.13.答案30°解析∵四边形ABCD是平行四边形,∴BC∥AD,AB∥DC,∠ABC=∠D,∴∠DAB+∠D=180°,∵∠D=100°,∴∠DAB=80°,∠ABC=100°.又∵∠DAB的平分线交DC于点E,∴∠EAD=∠EAB=40°.∵AE=AB,∴∠ABE=×(180°-40°)=70°,∴∠EBC=∠ABC-∠ABE=100°-70°=30°.14.答案解析记2个红球分别为红1,红2,3个黄球分别为黄1,黄2,黄3,根据题意,列表如下:共有20种等可能的结果,其中两个颜色相同的共有8种结果,故摸出两个颜色相同的小球的概率为=.15.答案3-3解析如图,将△ABD沿AD翻折得△AFD,连接EF,∴AB=AF=AC,BD=DF,∠AFD=∠B=30°,∵∠BAC=120°,∠DAE=60°,∴∠BAD+∠CAE=60°,又∠BAD=∠FAD,∴∠FAD+∠CAE=60°,∴∠CAE=∠FAE,∴△ACE≌△AFE(SAS),∴CE=EF,∠AFE=∠C=30°,∴∠DFE=60°.过点E作EH⊥DF,交DF于点H,过点A作AM⊥BC,交BC于点M.设CE=2x,则BD=2CE=4x,EF=2x,DF=4x,FH=x,EH=x,DH=3x,又BC=2BM=2AB·cos30°=6,∴DE=6-6x,在Rt△DEH中,DE2=DH2+EH2,即(6-6x)2=(3x)2+(x)2,解得x1=,x2=(舍去).∴DE=6-6x=3-3.16.答案-3<a<-2或<a<解析把(m,0)代入y=ax2+(a2-1)x-a得,am2+(a2-1)m-a=0.解得m==,∴m1=,m2=-a,∵2<m<3,∴2<<3或2<-a<3,解得<a<或-3<a<-2.三、解答题17.解析去括号,得4x-3=2x-2,移项,得4x-2x=3-2,合并同类项,得2x=1,系数化为1,得x=.18.解析CD与AB之间的关系为CD=AB,且CD∥AB.证明:∵CE=BF,∴CF=BE.在△CDF和△BAE中,∴△CDF≌△BAE,∴CD=BA,∠C=∠B,∴CD∥BA.19.解析(1)①108°.②9;6.(2)10×(1-45%-30%)+8×45%+5×30%=7.6(万元).答:这个公司平均每人所创年利润是7.6万元.20.解析(1)设购买甲种奖品x件,则购买乙种奖品(20-x)件,由题意得40x+30(20-x)=650,解得x=5,∴20-x=15.答:购买甲种奖品5件,乙种奖品15件.(2)设购买甲种奖品y件,则购买乙种奖品(20-y)件,则解得≤y≤8,∵y为整数,∴y=7或8.当y=7时,20-y=13;当y=8时,20-y=12.答:该公司有两种不同的购买方案:方案一:购买甲种奖品7件,购买乙种奖品13件;方案二:购买甲种奖品8件,购买乙种奖品12件.21.解析(1)证明:连接BO.∵AB=AC,OB=OC,∴A、O在线段BC的中垂线上,∴AO⊥BC.又∵AB=AC,∴AO平分∠BAC.(2)如图,延长AO交BC于点H,过点D作DK⊥AO,交AO于点K.由(1)知AO⊥BC,∵OB=OC,BC=6,∴BH=CH=BC=3,∠COH=∠BOC,∵∠BAC=∠BOC,∴∠COH=∠BAC.∴sin∠COH=sin∠BAC==.∵CH=3,∴sin∠COH==,∴CO=AO=5,∴OH===4,∴AH=AO+OH=5+4=9,tan∠COH=tan∠DOK=.在Rt△ACH中,∠AHC=90°,AH=9,CH=3,∴tan∠CAH===,AC===3,由(1)知∠CAH=∠BAH,∴tan∠BAH=tan∠CAH=.设DK=3a(a>0),在Rt△ADK中,tan∠DAK=,在Rt△DOK中,tan∠DOK=,∴OK=4a,DO=5a,AK=9a,∴AO=OK+AK=13a=5,∴a=,∴DO=5a=,∴CD=OC+DO=5+=.22.解析(1)∵点A(-3,a)在直线y=2x+4上,∴a=2×(-3)+4=-2.∵点A(-3,-2)在y=的图象上,∴k=6.(2)∵点M是直线y=m与直线AB的交点,∴M.∵点N是直线y=m与反比例函数y=的图象的交点,∴N.∴MN=x N-x M=-=4或MN=x M-x N=-=4.解得m=2或m=-6或m=6±4,∵m>0,∴m=2或m=6+4.(3)x<-1或5<x<6.23.解析(1)证明:∵∠ADC=90°,∠EDC+∠ADC=180°,∴∠EDC=90°,又∠ABC=90°,∴∠EDC=∠ABC,又∠E为公共角,∴△EDC∽△EBA,∴=,∴ED·EA=EC·EB.(2)过点C作CF⊥AD,交AE于点F,过点A作AG⊥EB,交EB的延长线于点G.在Rt△CDF中,cos∠FDC=,∴=,又CD=5,∴DF=3,∴CF==4,又S△CDE=6,∴ED·CF=6,∴ED==3,∴EF=ED+DF=6.∵∠ABC=120°,∠G=90°,∠G+∠BAG=∠ABC,∴∠BAG=30°,在Rt△ABG中,BG=AB=6,AG==6,∵CF⊥AD,AG⊥EB,∴∠EFC=∠G=90°,又∠E为公共角,∴△EFC∽△EGA,∴=,∴=,∴EG=9,∴BE=EG-BG=9-6,∴S四边形ABCD=S△ABE-S△CED=BE·AG-6=×(9-6)×6-6=75-18.(3)AD=.详解:过点C作CH⊥AD,交AE于点H,则CH=4,DH=3,∴EH=n+3,∴tan∠E=.过点A作AG⊥DF,交DF于点G,设AD=5a,则DG=3a,AG=4a,∴FG=FD-DG=5+n-3a,由CH⊥AD,AG⊥DF,∠E=∠F知△AFG∽△CEH,∴=,∴=,∴=,∴a=,∴AD=.24.解析(1)将点A(-1,1),B(4,6)代入y=ax2+bx有解得∴抛物线的解析式为y=x2-x.(2)证明:设直线AF的解析式为y=kx+m(k≠0).将点A(-1,1)代入解析式,得-k+m=1,∴m=k+1,∴直线AF的解析式为y=kx+k+1,∴F(0,k+1).由消去y得x2-x=kx+k+1,解得x1=-1,x2=2k+2,∴点G的横坐标为2k+2,又GH⊥x轴,∴点H的坐标为(2k+2,0).设直线FH的解析式为y=k0x+b0(k0≠0),则解得∴直线FH的解析式为y=-x+k+1.设直线AE的解析式为y=k1x+b1(k1≠0),易知点E的坐标为(1,0),则解得∴直线AE的解析式为y=-x+,∴FH∥AE.(3)t=或t=或t=或t=.详解:由已知易得,Q(t,0),P(t-2,t),由题意,知点M只可能在线段QP上或QP的延长线上.①若M在线段QP上,则利用QM=2PM,构造三角形相似,得M,代入抛物线y=x2-x,可得·=,解得t=;②若M在线段QP的延长线上,则由QM=2PM知点P为MQ的中点,构造三角形全等,得M(t-4,2t),代入抛物线y=x2-x,可得(t-4)(t-5)=2t,解得t=.综上所述,t的值为,,或.。

湖北省实验2017年分配生考试数学试题及答案

C.y= − 3x x −1
D.y= − 8x x−4
7.如图，矩形 AEHC 是由三个全等矩形拼成的，AH 与 BE、BF、DF、DG、CG 分别交于点 P、Q、K、M、N，设△BPQ，△DKM，△CNH 的面积依次是 S1 、 S2 、 S3 ，若 S1 + S3 =20，
则 S2 =（ A.6 B.8
四边形 ABFE’的面积是（）
A． 6 + 3 2 2
B． 6 + 3 2 4
C． 6 + 5 2 2
D． 6 + 5 2 4
二、填空题（本大题共 6 小题，每小题 4 分，共 24 分） 11．现定义运算“☆”．对于任意实数 a，b，都有 a☆b＝a2－3a＋b，如：3☆5＝32－3×3
＋5．若 x☆2＝6，则实数 x 的值是________．
三、解答题（本大题共 5 小题，共 46 分）
( )2018
17．（本小题满分 8 分）求值（1） ( 3 + 2)2016 3 − 2
（2）已知 x＝ 3 − 2 ，y＝ 3 + 2 ，求 3x2－5xy＋3y2 的值
3+ 2
3− 2
．
18．（本小题满分 8 分）已知 AB 是⊙O 的直径，点 C 在⊙O 上，点 D 在半径 OA 上（不与点 O、A 重合）武汉教育资源网联系 QQ1220012921
x 边分别与 x 轴的正半轴，直线 y＝x 交于点 E、F，问是否存在点 E，使得 PE＝PF？若存在，求点 E 的坐标；若不存在，请说明理由．
20．（本小题满分 10 分）如图，把△EFP 放置在菱形 ABCD 中，使得顶点 E、F、P 分别在线段 AB、AD、AC 上，已知 EP＝FP＝6，EF＝6 3 ，∠BAD＝60°，且 AB>6 3 ．

二中2017年分配生考试数学试题及答案

（ tan 7842 ≈5.00， tan 31 ≈0.60， tan1118 ≈0.20）
y
B 59° 19°42′
A 路面
D
x C
土丘 E
堂 V课
鱼
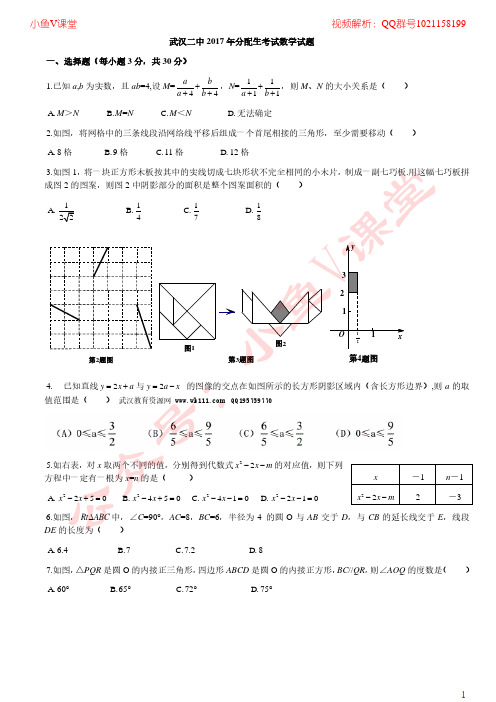
小 22.（本题 10 分）如图，点 A、B 分别在 x 轴、y 轴正半轴上，△OAB 的周长为 4，BC 平分∠OBA 的外角， C ：分别与 x 轴、AB 相切于 F、G.武汉教育资源网 QQ195759770
④若方程 ax2 + bx + c = 0 有两个不相等的实数根，则方程 cx2 + bx + a = 0 也一定有两个不相等的实数根.
鱼 A.1
B. 2
C. 3
D. 4
10.如图 1，有一副三角板，中间各有一个直径为 2cm 的圆洞.将三角板 a 的 30°角的那一头插入三角板 b 的圆洞
小内（如图 2），求三角板 a 通过三角板 b 的圆洞的那一部分的最大面积为（ b
号
众 5.如右表，对 x 取两个不同的值，分别得到代数式 x2 − 2x − m 的对应值，则下列
方程中一定有一根为 x=n 的是（）
x
－1 n－1
A. x2 − 2x + 5 = 0 B. x2 − 4x + 5 = 0 C. x2 − 4x −1 = 0 D. x2 − 2x −1 = 0
x2 − 2x − m
D. 无法确定
2.如图，将网格中的三条线段沿网络线平移后组成一个首尾相接的三角形，至少需要移动（）
A. 8 格
B.9 格
C. 11 格
D. 12 格
3.如图 1，将一块正方形木板按其中的实线切成七块形状不完全相同的小木片，制成一副七巧板.用这幅七巧板拼

武汉二中2017年分配生数学试题(word版含答案)

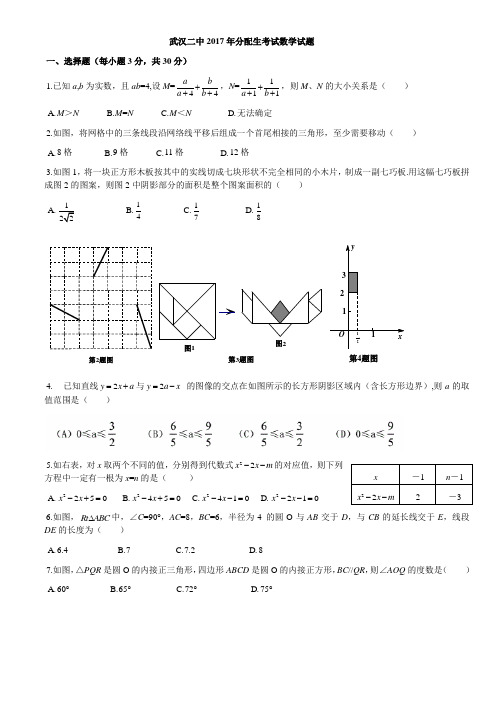
武汉二中2017年分配生考试数学试题一、选择题（每小题3分，共30分） 1.已知a ,b 为实数，且ab =4,设M =44a b a b +++，N=1111a b +++，则M 、N 的大小关系是（） A.M ＞N B.M =N C.M ＜N D.无法确定2.如图，将网格中的三条线段沿网络线平移后组成一个首尾相接的三角形，至少需要移动（） A.8格 B.9格 C.11格 D.12格3.如图1，将一块正方形木板按其中的实线切成七块形状不完全相同的小木片，制成一副七巧板.用这幅七巧板拼成图2的图案，则图2中阴影部分的面积是整个图案面积的（） A.22B.14 C.17 D.18第2题图图2图1第3题图121Oxy 321第4题图4. 已知直线2y x a =+与2y a x =- 的图像的交点在如图所示的长方形阴影区域内（含长方形边界）,则a 的取值范围是（）5.如右表，对x 取两个不同的值，分别得到代数式22x x m --的对应值，则下列方程中一定有一根为x =n 的是（）A.2250x x -+=B.2450x x -+=C.2410x x --=D.2210x x --=6.如图，Rt ABC ∆中，∠C =90°，AC =8，BC =6，半径为4 的圆O 与AB 交于D ，与CB 的延长线交于E ，线段DE 的长度为（）A.6.4B.7C.7.2D.87.如图，△PQR 是圆O 的内接正三角形，四边形ABCD 是圆O 的内接正方形，BC //QR ，则∠AOQ 的度数是（） A.60°B.65°C.72°D.75° x －1 n －1 22x x m --2－3第6题图第7题图2143蜜蜂第7题图8.假定有一排蜂房，形状如图所示，一只蜜蜂在左下角的蜂房中，由于受伤，只能爬，不能飞，而且只能永远向右方（包括右上、右下）爬行，从一间蜂房爬到与之相邻的右蜂房中去，则从最初位置爬到4号蜂房中，不同的爬法有（）A.4种B.6种C.8种D.10种9.下列四个说法，正确的有（）个①b=a+c时，则一元二次方程20ax bx c++=一定有实数根；②若b=2a+3c，则一元二次方程20ax bx c++=有两个不相等的实数根；③25b ac-＞0时，则一元二次方程20ax bx c++=一定有两个不相等的实数根；④若方程20ax bx c++=有两个不相等的实数根，则方程20cx bx a++=也一定有两个不相等的实数根.A.1B.2C.3D.410.如图1，有一副三角板，中间各有一个直径为2cm的圆洞.将三角板a的30°角的那一头插入三角板b的圆洞内（如图2），求三角板a通过三角板b的圆洞的那一部分的最大面积为（）（不计三角板的厚度）.图2图1A.B.2C.4D.二、填空题（6小题，共18分）11.关于x的不等式组212(1)3x ax a->⎧⎨-<⎩的整数解为3,4,5，则a的取值范围是________________.12.如图，已知△ABC的面积ABCS∆=1.在图（1）中，若11112AA BB CCAB BC CA===，则111A B CS∆=14；在图（2）中，若22213AA BB CCAB BC CA===，则222A B CS∆=13；在图（3）中，若33314AA BB CCAB BC CA===，则333A B CS∆=716；按此规律，若77718AA BB CCAB BC CA===，则777A B CS∆=___________.CBA(3)CBA(2)(1)C 33A 3A 2B 2C 2C 11A 1AB13.函数2(1)4(5)y x k x k =-+-+的图像如图所示，它与x 轴交于A 、B 两点，且OB =4OA ，则k=________.第13题1第14题14.如图，直线12l l ⊥于O 点，A ，B 是直线1l 上的两点，且OB =2，AB 1l 绕点O 逆时针方向旋转，旋转角度为α(0180)α︒<<︒.若在直线2l 上始终存在点P ，使得△BP A 是以∠B 为顶角的等腰三角形，则旋转角α的取值范围是____________________.15. △ABC 中，∠ACB =90°，BC =2AC =4,D 、E 两点分别在边AB 、BC 上，将三角形的一部分沿DE 翻折，使B 点落到射线BC 上的F 点，当△ADF 为直角三角形时，折痕DE 的长度为_______________. 16.若关于x 的方程242x x kx -=+有两个不等的实数根，则k 的取值范围是______________. 三、解答题（共8题，共72分）17.（本题8分）已知210x x --=，210y y --=，且1xy ≠，求1xy y+的值.18.（本题8分）四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点，如图1，点P 为四边形ABCD 对角线AC 所在直线上的一点，PD =PB ，P A ≠PC ，则点P 为四边形ABCD 的准等距点.（1）（2分）如图2，作出四边形ABCD 的一个准等距点（尺规作图，保留作图痕迹，不要求写作法）；（2）（6分）如图3，在四边形ABCD 中，P 是AC 上的点，P A ≠PC ，延长BP 交CD 于点E ，延长DP 交BC 于点F ，且∠CDF =∠CBE ，CE =CF .求证：点P 是四边形ABCD 的准等距点.图1ABCDP 图2AD CB图3FABCDEP19.（本题8分）某班进行一项比赛，要将班级40名同学分为两组，现设计下列分组方式：在一个不透明的布袋中，分别装入甲、乙两支签，摸到甲签的同学分在第一组，摸到乙签的同学分在第二组，若其中一组人数到达20，分组结束.（1）（2分）请用树状图求出前三名同学同时分在第一组的概率；（2）（3分）归纳：直接写出前n 名同学都分在第一组（20n …，且n 为整数）的概率是___________; （3）（3分）应用：直接写出前n 名同学摸签后（分组结束前），分在不同两组的概率为___________. 20.（本题8分）我们学过二次函数的图像的平移，如：将二次函数y =32x 的图像向左平移2个单位，再向下平移4个单位，所得图像的函数表达式是y =32(2)4x +-.类比二次函数的图像的平移，我们对反比例函数的图像作类似的变换：（1）（2分）将1y x=的图像向右平移1个单位，再向上平移1个单位，所得图像的函数表达式为_____________; （2）（2分）函数12x y x -=-的图像可看作由1y x=的图像向___________（左或右）平移_______个单位，再上__________（上或下）平移__________个单位得到的；（3）（4分）推广运用：已知不等式114x x >的解集是2x <-或0＜x ＜2，请直接写出不等式211344x x x ->+-的解集为_______________________________.21.（本题8分）如图，AB 、CD 是竖立在公路两侧，且架设了跨过公路的高压电线的电杆，AB =CD =16米.现在点A 处观测电杆CD 的视角为19°42′，视线AD 与AB 的夹角为59°.以点B 为坐标原点，向右的水平方向为x 轴的正方向，建立平面直角坐标系.（1）（4分）求电杆AB 、CD 之间的距离和点D 的坐标；（2）（4分）在今年年初的冰雪灾害中，高压电线由于结冰下垂近似成抛物线21100y x bx =+（b 为常数）.在通电情况，高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时，是否有危险？并说明理由.（tan7842'︒≈5.00，tan31︒≈0.60，tan1118'︒≈0.20）22.（本题10分）如图，点A 、B 分别在x 轴、y 轴正半轴上，△OAB 的周长为4，BC 平分∠OBA 的外角，Ce 分别与x 轴、AB 相切于F 、G . （1）（3分）求证：C e 与y 轴相切；（2）（3分）当AB +BC 取得最小值时，求直线AB 的解析式；（3）（4分）过点C 的直线分别与x 轴、y 轴正半轴交于D 、E 两点，求OD +OE 的最小值.23.（本题10分）如图，AD 为Rt △ABC 斜边BC 上的高，点E 为DA 延长线上一点，连接BE ，过C 作CF ⊥BE 于F ，分别交AB 、AD 于M 、N .（1）（4分）若线段AM 、AN 的长是关于x 的一元二次方程222x mx n -+254mn m -+=0的两个实数根，求证：AM =AN ；（2）（6分）在（1）的条件下，:ABE AMN S S ∆∆=64:9，且线段BF 与EF 的长度是关于y 的一元二次方程25y 16ky -+ 10k +5=0的两个实数根，求BC 的长度.NMABCDEF24.（本题12分）如图1，直线l 的解析式为384y x =+，与x 轴、y 轴分别交于A 、B 两点，C 是x 轴上一点，以C 为圆心的圆与直线l 相切于B 点. （1）（3分）求点C 的坐标及C e 的半径；（2）（4分）若C e 从上述位置出发，以每秒103个单位沿x 轴向左运动，同时C e 的半径以每秒32个单位变小，设C e 的运动时间为t 秒，在运动过程中，直线l 被C e 截得的弦长为a . ①求t 的取值范围；②求a 的最大值；（3）（5分）如图3，点D （4,n -）在直线AB 上，过D 点任作一条直线分别交抛物线214y x =于M 、N 两点，在该抛物线上是否存在一个定点P ，使∠MPN =90°始终成立？若存在，求出点P 的坐标；若不存在，请说明理由.图2参考答案1.A2.B3.D4.C5.B6.A 7D分两种情况：①蜜蜂先向右爬，则可能的爬法有：1⇒2⇒4、1⇒3⇒4、1⇒3⇒2⇒4，共有3种爬法．②蜜蜂先向右上爬，则可能的爬法有：0⇒3⇒4、0⇒3⇒2⇒4、0⇒1⇒2⇒4、0⇒1⇒3⇒4、0⇒1⇒3⇒2⇒4，共5种爬法．因此不同的爬法共有3＋5＝8种． 9.B (1,2对)10.B11.3103＜a ≤22321++a x a ＜＜不等式组的解集为 ∵整数解为3,4,5∴⎪⎪⎩⎪⎪⎨⎧≤++≤622353212a a＜＜ ∴ ⎪⎩⎪⎨⎧≤≤3103853a a ＜＜ ∴3103＜a ≤ 12.当64431813)81(3812=+⨯-==S x 时， 13.1114. 或你15.4543或 16.21224--＜或＞k k 17.01111,0122=--≠=--y y xy y y 得由 ∵012=--x x ∴的两根是方程、0112=--m m yx111=+=+yx y xy20.12)2(,11，上，右，）（-=x xy （3）421＜＜或＜x x 21.（1）连CF,CG,作CH ⊥OE 于H∵BC 平分∠EBA ∴CH=CG易证GA=AF ∴CH=CF ∴圆C 与y 轴相切（2）易证△OAB 的周长=OH+OF=4 ∴OH=OF=2 ∴C(2，2)作C 关于y 轴的对称点C ’(-2，2),过C ’作圆C 的切线AB,切点为G,此时AB+BC 最小∵CG=CH='21CC ∴︒=∠30'C ∴HB=332 OB=OH-HB=3322- ∴)33220(-，B ∴直线AB:332233-+-=x y （3）∵CH ∥OB ∴DE CD OE CF DE EC OD CH ==同理, ∴1=+OECF OD CH ∴OE OD OE OD •=+21 23.24.1）如图，由于直线l：y= 3/4 x+8与x轴、y轴分别交于A、B两点，所以A、B两点的坐标可以求出，线段OA、OB的长度也可以求出，又OB⊥AC，AB切⊙C于B点，可以得到△ABO∽△BCO，以求出OC，BC，求得C点坐标（6，0），半径CB=10．2)若⊙C以每秒10/3 个单位沿x轴向左运动，同时⊙C的半径以每秒3/ 2 个单位变小，设⊙C的运动时间为t秒，且⊙C始终与直线l有交点，试求t的取值范围；R≥点C到直线L的距离，则⊙C始终与直线l有交点．C[（6- 10/3 t），0]，R=10- 3/2 t，L：3x-4y+32=0点C到直线L的距离H=|10-2t|10- 3/2 t≥|10-2t|10- 3/2 t≥10-2t≥-（10- 3/2 t）解得：0≤t≤40/7 ；设⊙C被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值一定存在t的值，使a最大（a2 ）2=R2-H2=（10- 3/2 t）2-（10-2t）2=（- 32/9 ）•（t- 15/4 ）2+50则a2=-7t2+40t，t= 40/14 = 20/7 时，a2最大= 400/7 ，a最大=7720。

【真题】2017年武汉市中考数学试卷及答案解析(word版)

湖北省武汉市2017年中考数学试题第Ⅰ卷（选择题共30分）一、选择题（共10小题，每小题3分，共30分）1 ）A ．6B ．-6C ．18D ．-18 【答案】A. 【解析】故选A.考点：算术平方根. 2．若代数式14a -在实数范围内有意义，则实数a 的取值范围为（） A ．4a = B ．4a > C ．4a < D ．4a ≠ 【答案】D.考点：分式有意义的条件.3．下列计算的结果是5x 的为（）A ．102x x ÷B ．6x x -C ．23x xD ．23()x 【答案】C. 【解析】试题解析：A ．102x x ÷=x 8，该选项错误；B ．6x 与x 不能合并，该选项错误；C ．23x x =5x ，该选项正确；D ．23()x =x 6，该选项错误. 故选C.考点：1.同底数幂的除法；2.同底数幂的乘法；3.积的乘方与幂的乘方.4．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示．则这些运动员成绩的中位数，众数分别为（）A ．1．65，1．70B ．1．65，1．75C ． 1．70，1．75D ．1．70，1．70 【答案】C. 【解析】考点：1.中位数；2.众数.5．计算(1)(2)x x ++的结果为（）A ．22x +B ．232x x ++C ． 233x x ++D ．222x x ++ 【答案】B. 【解析】试题解析：(1)(2)x x ++=x 2+2x+x+2= x 2+3x +2. 故选B.考点：多项式乘以多项式6．点(3,2)A -关于y 轴对称的坐标为（）A ．(3,2)-B ．(3,2)C ． (3,2)--D ．(2,3,)- 【答案】B.【解析】试题解析：根据关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得：点A（-3，2）关于y轴对称的坐标为（3，2）.故选B.考点：关于x轴、y轴对称的点的坐标特征7．某物体的主视图如图所示，则该物体可能为（）A． B． C． D．【答案】D【解析】试题解析：只有选项A的图形的主视图是拨给图形，其余均不是.故选A.考点：三视图.8．按照一定规律排列的n个数：-2，4，-8，16，-32，64，…．若最后三个数的和为768，则n为（）A．9 B．10 C．11 D．12【答案】A.考点：数字变化规律.9．已知一个三角形的三边长分别为5，7，8．则其内切圆的半径为（）A B ．32C ．D ．【答案】C考点：三角形的内切圆.10．如图，在Rt ABC ∆中，90C ∠=，以ABC ∆的一边为边画等腰三角形，使得它的第三个顶点在ABC ∆的其他边上，则可以画出的不同的等腰三角形的个数最多为（）A．4 B．5 C． 6 D．7【答案】C考点：画等腰三角形.第Ⅱ卷（非选择题共90分）二、填空题（共6小题，每小题3分，共18分）⨯+-的结果为．11．计算23(4)【答案】2.【解析】⨯+-=6-4=2.试题解析：23(4)考点：有理数的混合运算.12．计算2111xx x-++的结果为．【答案】x-1. 【解析】试题解析：2111xx x-++=211)(1)=111（-+-=-++x x xxx x考点：分式的加减法.13．如图，在ABCD中，∠D=100°，∠DAB的平分线AE交DC于点E，连接BE，若AE=AB，则∠EBC的度数为．【答案】30°.【解析】考点：1.解平分线的性质；2.平行四边形的性质.14．一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为．【答案】25．【解析】试题解析：根据题意可得：列表如下共有20种所有等可能的结果，其中两个颜色相同的有8种情况，故摸出两个颜色相同的小球的概率为82= 205．考点：列表法和树状图法.15．如图△ABC中，AB=AC，∠BAC=120°，∠DAE=60°，BD=5，CE=8，则DE的长为．【答案】7.【解析】考点：1.含30度角的直角三角形；2.等腰三角形的性质．16．已知关于x的二次函数y=ax2+(a2-1)x-a的图象与x轴的一个交点的坐标为(m,0)，若2<m<3，则a 的取值范围是．【答案】-3<a<-2，13<a<12. 【解析】试题解析：把（m ，0）代入y=ax 2+(a 2-1)x-a 得，am 2+(a 2-1)m-a=0解得：22（--1）(+1）2a a a±=∵2<m<3 解得：-3<a<-2，13<a<12. 考点：二次函数的图象.三、解答题（共8小题，共72分）在答题卡指定位置写出必要的演算过程或证明过程．17．解方程：432(1)x x -=-．【答案】x=12.考点：解一元一次方程.18．如图，点,,,C F E B 在一条直线上，CFD BEA ∠=∠，,CE BF DF AE ==．写出CD 与AB 之间的关系，并证明你的结论．【答案】证明见解析：【解析】试题分析：通过证明ΔCDF ≌ΔABE ，即可得出结论试题解析：CD 与AB 之间的关系是：CD=AB ，且CD ∥AB 证明：∵CE=BF ，∴CF=BE 在ΔCDF 和ΔBAE 中CF=BE CFD=BEA DF=AE ⎧⎪∠∠⎨⎪⎩∴ΔCDF ≌ΔBAE ∴CD=BA ，∠C=∠B ∴CD ∥BA考点：全等三角形的判定与性质.19．某公司共有,,A B C 三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图．各部门人数及每人所创年利润统计表（1）①在扇形图中，C 部门所对应的圆心角的度数为___________；②在统计表中，b =___________，c =___________；（2）求这个公司平均每人所创年利润．【答案】（1）①108°；②9，6；（2）7.6万元.5÷25%=20∴20×45%=9（人）20×30%=6（人）（2）10×25%+8×45%+5×30%=7.6答：这个公司平均每人所创年利润是7.6万元.考点：1.扇形统计图；2.加权平均数.20．某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件，其中甲种奖品每件40元，乙种奖品每件30元．（1）如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件；（2）如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种．．．不同的购买方案．【答案】（1）甲、乙两种奖品分别购买5件、15件.（2）该公司有两种不同的购买方案：方案一：购买甲种奖品7件，购买乙种奖品13件；方案二、购买甲种奖品8件，购买乙种奖品12件.（2）设甲种奖品购买m 件，则乙种奖品购买（20-m ）件依题意得：20-240+30（20-m ）650m mm ⎧≤⎨≤⎩解得：2083m ≤≤ ∵m 为整数，∴m=7或8当m=7时，20-m=13；当m=8时，20-m=12答：该公司有两种不同的购买方案：方案一：购买甲种奖品7件，购买乙种奖品13件；方案二、购买甲种奖品8件，购买乙种奖品12件.考点：1.二元一次方程组的应用；2.一元一次不等式组的应用. 21．如图，ABC ∆内接于O ，,AB AC CO =的延长线交AB 于点D ．（1）求证AO 平分BAC ∠；（2）若36,sin 5BC BAC =∠=，求AC 和CD 的长．【答案】（1）证明见解析；（2）；9013.（2）过点C作CE⊥AB于E∵sin∠BAC=35,设AC=5m，则CE=3m∴AE=4m，BE=m在RtΔCBE中，m2+(3m)2=36∴，∴AC=延长AO交BC于点H，则AH⊥BC，且BH=CH=3，考点：1.全等三角形的判定与性质；2.解直角三角形；3.平行线分线段成比例. 22．如图，直线24y x =+与反比例函数ky x=的图象相交于(3,)A a -和B 两点．（1）求k 的值；（2）直线(0)y m m =>与直线AB 相交于点M ，与反比例函数ky x=的图象相交于点N ．若4MN =，求m 的值；（3）直接写出不等式65xx>-的解集．【答案】(1)-6;(2) m=2或6+或5<x<6（2）∵M是直线y=m与直线AB的交点∴M（42m-，m）同理，N（6m，m）∴MN=｜42m--6m｜=4∴42m--6m=±4解得m=2或-6或6±∵m>0∴m=2或6+（3）x<-1或5<x<6考点：1.求反比例函数解析式；2.反比例函数与一次函数交点问题. 23．已知四边形ABCD的一组对边,AD BC的延长线相交于点E．（1）如图1，若90ABC ADC ∠=∠=，求证ED EA EC EB =；（2）如图2，若120ABC ∠=，3cos 5ADC ∠=，5CD =，12AB =，CDE ∆的面积为6，求四边形ABCD 的面积；（3）如图3，另一组对边,AB DC 的延长线相交于点F ，若3cos cos 5ABC ADC ∠=∠=，5CD =，CF ED n ==，直接写出AD 的长（用含n 的式子表示）．【答案】(1)证明见解析；（2）；（3）5256n n ++（3）由（1）（2）提供的思路即可求解. 试题解析：（1）∵∠ADC=90° ∴∠EDC=90° ∴∠ABE=∠CDE 又∵∠AEB=∠CED ∴ΔEAB ∽ΔECD ∴EB EAED EC= ∴ED EA EC EB =由（1）有：ΔECG ∽ΔEAH ∴EG CGEH AH=∴∴S 四边形ABCD ＝S ΔAEH －S ΔECG -S ΔABH=116622⨯⨯--⨯⨯(3)5256n n ++考点：相似三角形的判定与性质.24．已知点(1,1),(4,6)A B -在抛物线2y ax bx =+上．（1）求抛物线的解析式；（2）如图1，点F 的坐标为(0,)(2)m m >，直线AF 交抛物线于另一点G ，过点G 作x 轴的垂线，垂足为H ，设抛物线与x 轴的正半轴交于点E ，连接,FH AE ，求证//FH AE ；（3）如图2，直线AB 分别交x 轴，y 轴于,C D 两点，点P 从点C 出发，沿射线CD 方向个单位长度，同时点Q 从原点O 出发，沿x 轴正方向匀速运动，速度为每秒1个单位长度，点M 是直线PQ 与抛物线的一个交点，当运动到秒时，2QM PM =，直接写出的值．【答案】（1）抛物线的解析式为：y=12x 2-12x ；（2）证明见解析；（3.（3）进行分类讨论即可得解.试题解析：（1）∵点A （-1，1），B （4，6）在抛物线y=ax 2+bx 上 ∴a-b=1，16a+4b=6 解得：a=12，b=-12∴抛物线的解析式为：y=12x 2-12x设直线AF的解析式为y=kx+m∵A (-1,1)在直线AF上，∴-k+m=1即：k=m-1∴直线AF的解析式可化为：y=(m-1)x+m与y=12x2-12x联立，得（m-1）x+m=12x2-12x∴(x+1)（x-2m）=0 ∴x=-1或2m∴点G的横坐标为2m考点：二次函数综合题.。

湖北省武汉二中2017-2018学年高一下学期期末数学试卷(理科)Word版含解析.pdf

C．（，1）
D．（，）
10．如图，正方体 ABCD ﹣ A 1B 1C1D1 的棱长为 1，E， F 分别为线段 AA 1，B1C 上的点，则三棱锥 D1﹣ EDF 的体积为（）
A．
B．
C．
D．
11．在 Rt△ ABC 中，∠ C=90 °， AC=4 ， BC=2 ，D 是 BC 的中点，若 E 是 AB 的中点， P 是
D ．相交且可能过圆心
8．已知 a，b 是正数，且满足
2＜ a+2b＜ 4．那么
22
a +b
的取值范围是（）
A ．（，）
B．（， 16）
C．（ 1， 16）
D ．（
， 4）
9．已知数列 {a n} 满足 an=
a 的取值范围是（） A ．（，1）
B．（，）
（ n∈N * ），若 {a n} 是递减数列，则实数
解答：解： sin15°+cos15°= （ sin15°+ cos15°）
然后利用
= （ sin15°cos45°+cos15°sin45°） = sin（ 15°+45°） = sin60 °
= ×= ．
故选 C．点评：考查学生灵活运用两角和的正弦函数公式的逆运算化简求值，数值．
牢记特殊角的三角函
21．四棱锥 P﹣ ABCD 底面是平行四边形，面 PAB⊥面 ABCD ，PA=PB=AB= AD ，
∠BAD=60 °，E， F 分别为 AD ， PC 的中点．（1）求证： EF∥平面 PAB；（2）求二面角 D﹣ PA﹣ B 的余弦值．
22．设 Sn 是非负等差数列 {a n} 的前 n 项和， m， n， p∈N+，若 m+n=2p ，求证：（1） Sn， S2n﹣ Sn， S3n﹣ S2n 成等差数列；