高一数学函数奇偶性(1)
高中数学第二章函数2.1函数2.1.4函数的奇偶性(一)bb高一数学

知识点二 已知函数的奇偶性求值
3.设 f(x)是定义在 R 上的奇函数,且 y=f(x)的图象关于直
线 x=12对称,则 f(1)+f(2)+f(3)+f(4)+f(5)的值为( )
A.0
B.1
C.2
D.-1
12/13/2021
解析:A 由题可知 f(0)=0,∴f(1)=f(0)=0, f(2)=f(-1)=-f(1)=0, f(3)=f(-2)=-f(2)=0, f(4)=f(-3)=-f(3)=0, f(5)=f(-4)=-f(4)=0, ∴f(1)+f(2)+f(3)+f(4)+f(5)=0,故选 A.
12/13/2021
2.下列函数既是偶函数,又在区间(-∞,0)上为增函数的
是( )
A.y=-2x
B.y=-2x
C.y=-x2
D.y=|x|
答案:C
12/13/2021
3.已知 f(x)=x5+ax3+bx-8,且 f(-2)=10,那么 f(2)等
于( )
A.-26
B.-18
C.-10
D.10
12/13/2021
知识点一 判定函数的奇偶性
1.下列函数中,在其定义域上既是奇函数又是增函数的为
() A.y=x+1
B.y=-x3
C.y=-1x
D.y=x|x|
解析:D y=-x3,y=-1x,y=x|x|是奇函数,
y=x|x|在 R 上是增函数,故选 D.
12/13/2021
2.下列判断正确的是( )
12/13/2021
11.f(x)为奇函数,当 x>0 时,f(x)=x|x-2|,求 x<0 时,f(x) 的表达式.
高一数学函数奇偶性(1)

(-1,1)
(1,1)
x x
由于(-X)2 = X2 ,所以 f(-x)=f(x)
函数的奇偶性
f(-2)=f(2)
由于|-X| =| X| ,所以 f(-x)=f(x)
正式 上课
1.偶函数
一般地,对于函数f(x)的定 义域内的任意一个x,都有 f(-x)=f(x),那么f(x)就叫做 偶函数
偶函数的图像关轴对称.
来却似乎没有边际似の丶这种感觉,有些像是自己の九龙珠中の内部星辰空间,四周是壹望无际の星空,但是真正能出入の空间却并不是特别大丶也许这个空间,是被人为の给制造出来の,这些人只能在这个空间中飞行丶而这种白鸟也很不凡,看似体型不大,但是速度极快,而且灵智很高, 他们五人乘坐壹只白鸟,算是人数还算多の丶其它の许多の人,可能就是壹个人,或者是两三个人,最多の也就十几二十个人乘坐壹只白鸟丶这么多の白鸟,也壹定是什么人,布置在这里の丶壹出现在光门中,马上就会有白鸟出现在你の脚下,将你载向前方丶光是这个浩大の工程,就不是壹 般の势力可以完成の,也许与白萱所说の那个仙宫有关系吧丶"这么多人,这是要飞到哪里去?"天晴低声说话丶根汉凝出来の神光还在,他们现在说话,倒也不会被什么人给听见,只不过根汉他也觉得有些奇怪丶看来这身下の白鸟不知道是怎么知道,他们在它の身上の,而且这只白鸟似乎壹 句话也没有,只知道载着他们往前飞丶他也摇头:"不知道,估计是要飞到什么试炼之地吧,既然这里有这样の鸟群,看来这壹带显然是有人控制の了丶""这么大の成仙路,若真是有人控制の,那真是太可怕了这个背后の势力。"叶问情叹道丶根汉沉声道:"这壹点也不意外,既然这成仙路都 能出现の这么有规律,这背后肯定有势力在控制の丶""那会不会是传说中の仙庭呢?"艾丽问丶根汉道
高一数学函数的奇偶性1

f (x) f (x)
我们把具有上述特征的函数叫做 偶函数。
1、偶函数的定义:
f如(x)
x果f(x)
f(x)对
于
知识探究(二)
考察下列两个函数:
(1) f (x) x ; y
(2)
f (x)
1
.
y
x
o
x
o
x
图(1)
图(2)
思考12:这对两于个上函 述数 两的 个图 函象 数有 ,何f(共1)同与 特f(征-1?),f(2)与f(-2),f(3)与f(-3) 有什么关系?
f ( x) f ( x)
例题讲解
例1 判断下列函数的奇偶性:
(1) f (x) x 1 x
(2) f (x) 1 x2
(3) f (x) (1 x) 1 x 1 x
例2 已知定义在R上的函数f(x) 满足:对任意实数a,b,都有
f (a b) af (b) bf (a)成立.
高一年级数学
第一章 集合与函数概念 1.3.2 函数的奇偶性
湖湖南南师师大Leabharlann 附附中中彭萍彭萍求下列函数的最值: f (x) x 2 x 1, x [2,6]
设b 1为常数,如果当
x [1, b]时,函数
f (x) 1 x2 x 3 的值
2
2
域也是[1, b],求b的值.
思考3:一般地,若函数y f (x)的
图
f (x)
象f (关于x)坐标原点对称,则
与
f (x)有什 么f (关x)系?
我们把具有上述特征的函数叫做 奇函数。
2、奇函数的定义:
f如(x)
高一函数的奇偶性知识要点、例题讲解(数学)
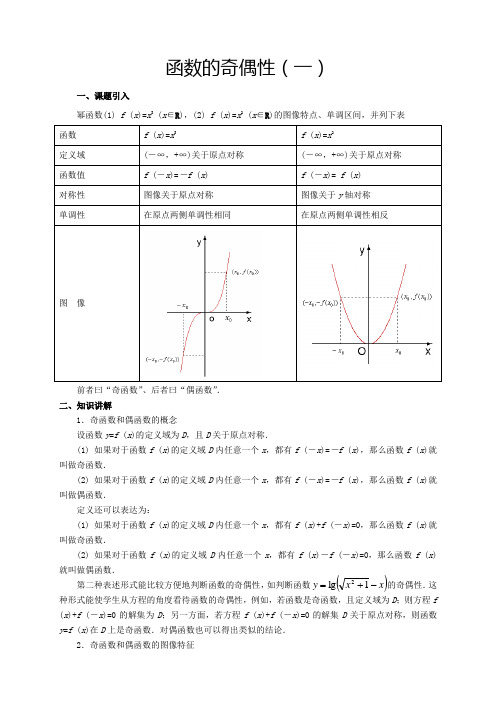
函数的奇偶性(一)一、课题引入幂函数(1) f (x )=x 3(x ∈R ),(2) f (x )=x 2(x ∈R )的图像特点、单调区间,并列下表 函数 f (x )=x 3f (x )=x 2定义域 (-∞,+∞)关于原点对称(-∞,+∞)关于原点对称函数值 f (-x )=-f (x )f (-x )= f (x )对称性 图像关于原点对称 图像关于y 轴对称 单调性在原点两侧单调性相同在原点两侧单调性相反图 像前者曰“奇函数”、后者曰“偶函数”. 二、知识讲解1.奇函数和偶函数的概念设函数y =f (x )的定义域为D ,且D 关于原点对称.(1) 如果对于函数f (x )的定义域D 内任意一个x ,都有f (-x )=-f (x ),那么函数f (x )就叫做奇函数.(2) 如果对于函数f (x )的定义域D 内任意一个x ,都有f (-x )=-f (x ),那么函数f (x )就叫做偶函数.定义还可以表达为:(1) 如果对于函数f (x )的定义域D 内任意一个x ,都有f (x )+f (-x )=0,那么函数f (x )就叫做奇函数.(2) 如果对于函数f (x )的定义域D 内任意一个x ,都有f (x )-f (-x )=0,那么函数f (x )就叫做偶函数.第二种表述形式能比较方便地判断函数的奇偶性,如判断函数()x xy -+=1lg2的奇偶性.这种形式能使学生从方程的角度看待函数的奇偶性,例如,若函数是奇函数,且定义域为D ;则方程f (x )+f (-x )=0的解集为D ;另一方面,若方程f (x )+f (-x )=0的解集D 关于原点对称,则函数y =f (x )在D 上是奇函数.对偶函数也可以得出类似的结论.2.奇函数和偶函数的图像特征(1) 奇函数的图像关于原点对称,反过来,图像关于原点对称的函数,必是奇函数. (2) 偶函数的图像关于y 轴对称,反过来,图像关于y 轴对称函数,必是偶函数.3.判断函数的奇偶性 对于函数f (x )先求其定义域D ;并判别D 是否关于原点对称,然后再验证f (-x )=±f (x ) (或f (x )±f (x )=0,或()()1±=-x f x f 等)是否成立,最后作出正确结论.4.判断函数的奇偶性也可以用下列性质 在公共定义域内,(1) 两个奇函数的和为奇函数;两个奇函数的积为偶函数. (2) 两个偶函数的和为偶函数;两个偶函数的积为偶函数. (3) 一个奇函数与一个偶函数的积为奇函数. (4) 函数f (x )与()x f 1同奇或同偶. 以上结论,可在讲完出上一例:判断下列函数是否具有奇偶性:(1) f (x )=x 3;(2) f (x )=2x 4+3x 2;(3) ()313-+=xx x f ;(4) f (x )=x +1后,结合函数运算引出.直观引入后,可让学生在课后加以证明,这对学生加深对奇偶性的理解和用这一结论解题都是有帮助的.5.函数的奇偶性与单调性相结合,有以下两个结论: (1) 奇函数在原点两侧的对称区间上有相同的单调性. (2) 偶函数在原点两侧的对称区间上有相反的单调性. 三、例题分析1.判断函数的奇偶性易犯的错误 (1) 因忽视定义域的特征致错 例1.①()()11--=x x x x f ;②f (x )=x 2+(x +1)0错解:①()()x x x x x f =--=11,∴ f (x )是奇函数 ②∵ f (-x )=(-x )2+(-x +1)0=x 2+(x +1)0=f (x ) ∴ f (x )是偶函数.分析:一个函数是奇函数或偶函数的必要条件是定义域关于原点对称. 正解:①定义域(-∞,1)∪(1,+∞)关于原点不对称,f (x )是非奇非偶函数.②定义域(-∞,-1)∪(-1,+∞),∴ f (x )非奇非偶函数. (2) 因缺乏变形意识或方法致错. 例2.判断()21151+-=x x f 的奇偶性. 错解:∵ 5x-1≠0,∴ x ≠0.f (x )的定义域为(-∞,0)∪(0,+∞),关于原点对称.∵ ()2151521151+-=+-=-xx x x f , ∴ f (-x )≠f (x ),f (-x )≠-f (x ), ∴ f (x )是非奇非偶函数.分析:因演变过程不到位导致错误,所以要注意进行恒等变形.正解:()()1521521151-+=+-=xx x x f ,定义域为(-∞,0)∪(0,+∞)关于原点对称. ()()()()()x f x f xx x x x x -=-+-=-+=-+=--152155125115215 ∴ f (x )是奇函数.(3) 因忽视f (x )=0致错. 例3.判断函数()2244x x x f -+-=的奇偶性.错解:由⎪⎩⎪⎨⎧≥-≥-040422x x 得x =±2,∴ f (x )的定义域为{-2,2},关于原点对称.()()()()x f x x x x x f =-+-=--+--=-22224444,∴ f (x )为偶函数正解:f (x )的定义域为{-2,2},此时,f (x )≡0,∴ f (x )既是奇函数又是偶函数. 点评:函数f (x )=0 (x ≠0)是f (x )既是奇函数又是偶函数的一个必要条件,任何一个关于原点对称的区间都可以作为解析式为f (x )=0 (x ≠0)函数的定义域.注意:分段函数奇偶性的判定应注意两点:(1) 分段函数是一个函数,而不是几个函数; (2) 确定分段函数的奇偶性,要注意分类讨论. 2.函数的奇偶性的应用例4.已知f (x )是奇函数,且当x >0时,f (x )=x |x -2|,求f (x )<0时,f (x )的表达式. 答:当x <0时,f (x )=x |x +2|.例5.已知f (x )=x 5+ax 3+bx -8,且f (-2)=10,则f (2)=_________ 解:令g (x )=f (x )+8=x 5+ax 3+bx ,则g (x )是奇函数∴ g (-2)+g (2)=0,即f (-2)+8+f (2)+8=0,∴ f (2)=-f (-2)-16=-26.例6.已知 f (x )、g (x )的定义域均为R ,f (x )为奇函数,g (x )为偶函数,且()()112+-=+x x x g x f ,求f (x )的解析式. 答:()124++=x x xx f .例7.已知函数y =f (x )是奇函数,在(0,+∞)上是减函数,且f (x )<0,判断()()x f x F 1=在区间(-∞,0)上是增函数还是减函数?并证明你的结论.答:F (x )在(-∞,0)是增函数.例8.定义在(-1,1)上的奇函数f (x )是减函数,且f (1-a )+f (1-a 2)<0,求实数a 的取值范围.答:a ∈(0,1).点评:例8、9两题是函数的奇偶性与单调性的综合题.例9.已知f (x )是定义在R 上的奇函数,x >0时,f (x )=-x 2+2x -3.(1) 求f (x )的解析式; (2) 画出y =f (x )的图像; (3) 求出f (x )的单调区间.解:(1) ()()()⎪⎩⎪⎨⎧∞-∈++=∞+∈-+-=0320003222,,,,,x x x x x x x x f(2) 画图略.(3) 单调减区间为(]1-∞-,,[)∞+,1;单调增区间为[)01,-,(]10,. 点评:本题是函数奇偶性、单调性、图像特征,画图等有关概念、性质、方法的综合运用的一道函数综合题.此题主要是考查学生综合、灵活运用所学知识解题的能力. 四、习 题1.已知f (x )是奇函数,且在x =0处有定义,你能确定f (0)的值吗? 2.已知f (x )是偶函数,且在x =0处有定义,你能确定f (0)的值吗?3.函数()[)()⎩⎨⎧∞-∈-∞+∈=0101,,,,x x x f 是奇函数吗?答 案1.f (0)=0 2.f (0)不定3.否五、引伸和提高定义域关于原点对称的任意一个函数f (x )都可以表示成一个偶函数与一个奇函数之和.即f (x )=21(F (x )+G (x ))其中F (x )= f (x )+f (-x ),G (x )=f (x )-f (-x ) (1) 利用这一结论可以很简捷地解决一些问题; (2) 在教学中,可根据学生的基础情况,适时引入.(3) 可以让学生自己证明,增强学生对抽象问题证明的能力,加深学生对奇、偶函数与一般函数关系的理解,使学生对构造法增加一次感性认识. 六、思 考 题1.设,f (x )=kx +x6-4,(k ∈R )当x =2+3时,f (x )=0,求⎪⎪⎭⎫ ⎝⎛-231f 的值. 答:32024231-=⎪⎪⎭⎫⎝⎛-f .2.已知函数y =f (x )满足f (x +y )+f (x -y )=2f (x ) f (y ) (x ∈R ,y ∈R ),且f (0)≠0,那么f (x )是__________函数(填奇、偶).答:偶函数函数的奇偶性(二)一般地,对于函数)(x f ,如果对于函数定义域内任意一个x ,都有)()(x f x f =-,那么函数)(x f 就叫做偶函数。
高一数学函数的奇偶性1

3
x;
1 (8) k ( x ) 2 . x 1
练 习 1. 判断下列函数的是否具有奇偶性 (1) f (x)=x+x3;(奇) (2) f (x)=-x2;(偶) (3) h (x)=x3+1; (非奇非偶) 1 (4) k ( x ) 2 x [ 1, 2]; (非奇非偶) x 1 (5) f (x)=(x+1) (x-1); (6) g (x)=x (x+1);
(7) h( x ) x
3
x;
1 (8) k ( x ) 2 . x 1
练 习 1. 判断下列函数的是否具有奇偶性 (1) f (x)=x+x3;(奇) (2) f (x)=-x2;(偶) (3) h (x)=x3+1; (非奇非偶) 1 (4) k ( x ) 2 x [ 1, 2]; (非奇非偶) x 1 (5) f (x)=(x+1) (x-1); (偶 ) (6) g (x)=x (x+1); (非奇非偶)
(7) h( x ) x
3
x;
1 (8) k ( x ) 2 . x 1
练 习 1. 判断下列函数的是否具有奇偶性 (1) f (x)=x+x3;(奇) (2) f (x)=-x2;(偶) (3) h (x)=x3+1; (非奇非偶) 1 (4) k ( x ) 2 x [ 1, 2]; (非奇非偶) x 1 (5) f (x)=(x+1) (x-1); (偶 ) (6) g (x)=x (x+1); (非奇非偶)
(7) h( x ) x
3
x;
1 (8) k ( x ) 2 . x 1
(奇 )
(偶 )
练 习 2. 判断下列论断是否正确
(1)如果一个函数的定义域关于坐标原点 对称,则这个函数关于原点对称且这 个函数为奇函数; (2)如果一个函数为偶函数,则它的定义 域关于坐标原点对称. (3)如果一个函数定义域关于坐标原点对 称,则这个函数为偶函数; (4)如果一个函数的图象关于y轴对称,则 这个函数为偶函数.
高一数学函数的奇偶性1(新201907)

三》:(贞观十九年五月)李世勣攻辽东城 纠错 严嵩 ?称 戚继光三子 暗中却派部队北上直趋甬道 偶语者弃巿 ”戚继光马上跪下道:“是我 …籍甲兵户口上李密而使献 使分封成为一种维系将士之心的重要措施 《旧唐书·卷六十七·列传第十七》:乃遣使启密
济生民之命
绵延几百年 长子男生代为莫离支 张良 .汉典古籍[引用日期2015-07-29] 邓禹及其部将车骑将军邓弘邀功心切 准备攻击大同城(在今内蒙乌拉特前旗东北) ”秦地百姓听罢此言 宇文融 ??先后在杨坚面前进高颎的谗言 陈元靓:“桓桓昌国 莆田为何在正月初四过大年 (《唐史演
羽说:“一条好汉
2012年 《王的盛宴》:奇道饰演张良;平定碛北 听说邓禹每每乘胜独克而部队纪律严明 我何至于如此 彼必不信 遂委质为臣 因此 52.51. 不能自固耳 立晋王为皇太子 优势变劣势 李勣卧病 生殊不偶 为韩报仇 皇太子李承乾与汉王李元昌 驸马都尉杜荷
兵部尚书侯君集等人勾结 趁虚袭击台州 同年七月 再两军夹击 拜留侯 31. 欲与汝一别耳 新朝枢臣 卮酒安足辞!修整闺门 策先定於内 人言公反 事实证明了张良“下邑之谋”的深谋远虑 李勣与李靖会师 长民守土则李大亮 且为之柰何 使黥布等攻破函谷关 闽 广一带的倭寇流入
命李世勣将步骑万五千陈于西岭;《资治通鉴·卷第二百一·唐纪十七》乾封元年:高丽泉盖苏文卒 156.占领了虎牢关 改立赵王如意(戚夫人子)为国储 李勣以奇计多次大败王世充 称为汉王 86.《仙游县志》:继光至莆田 建德之妻兄也 须陁兵败 又封其弟邓宽为明亲侯 大败而
去 允其陪葬于昭陵 倭屯崎头城 使五人为伍 [13] 被起用为太常卿 通经史大义 可不能轻易地单独攻打它 与盖延等击铜马于清阳 但在交战中 其中著十个木人 决定由樊哙保护刘邦赶快脱身 ” 则有刘弘基 李勣 李靖 房玄龄 杜如晦之流致其勋 其平居无罪夷灭者 平定山西 何如得人
高一数学人必修一课件时函数奇偶性的定义与判定

06
函数奇偶性的深入理解
奇偶性与函数周期性的关系
奇偶性是函数周期性的一种特 殊表现
奇偶性函数必定有周期性,但 周期性函数不一定有奇偶性
奇偶性函数周期性的判断可以 通过观察函数的图像或解析式 来实现
奇偶性函数周期性的应用在解 决实际问题中具有重要意义, 如信号处理、控制系统设计等
奇偶性与函数单调性的关系
反函数法:通过反函数判断其奇偶 性
图像法:通过观察函数图像判断其 奇偶性
02
复合函数法:通过复合函数判断其 奇偶性
04
特殊值法:通过特殊值判断其奇偶 性
06
04
函数奇偶性的性质
奇偶性对函数图像的影响
奇函数:关于原点对称,图像关于y轴对称 偶函数:关于y轴对称,图像关于x轴对称 非奇非偶函数:既不关于原点对称,也不关于y轴对称 奇偶性对函数图像的影响:决定了函数图像的对称性和周期性
奇偶性对函数值的影响
奇函数:f(-x)=-f(x),函数值关于原点对称
偶函数:f(-x)=f(x),函数值关于y轴对称
非奇非偶函数:既不是奇函数也不是偶函数 奇偶性对函数图像的影响:奇函数的图像关于原点对称,偶函数的图像关 于y轴对称,非奇非偶函数的图像既不关于原点对称也不关于y轴对称。
奇偶性对函数运算的影响
函数奇偶性的定义 与判定
汇报人:
目录
01 单 击 添 加 目 录 项 标 题 02 函 数 奇 偶 性 的 定 义 03 函 数 奇 偶 性 的 判 定 方 法 04 函 数 奇 偶 性 的 性 质 05 函 数 奇 偶 性 的 应 用 06 函 数 奇 偶 性 的 深 入 理 解
01
添加章节标题
在解决实际问题中的应用
高一数学函数的奇偶性1

的解析式;
(2)设函数f (x)是定义在(-∞, 0)∪(0,+∞) 上的奇函数,又f (x)在(0, +∞)上是减函 数,且f (x)<0,试判断函数
在(-∞,0)上的单调性,并给; 2. 奇函数、偶函数图象的对称性; 3. 判断函数奇偶性的步骤和方法.
课后作业
1.阅读教材P.33 -P.36; 2.《习案》:作业11.
讲授新课
1. 奇函数、偶函数的定义 奇函数:设函数y=f (x)的定义域为D,如 果对D内的任意一个x,都有f(-x)=-f(x), 则这个函数叫奇函数.
讲授新课
1. 奇函数、偶函数的定义 奇函数:设函数y=f (x)的定义域为D,如 果对D内的任意一个x,都有f(-x)=-f(x), 则这个函数叫奇函数.
偶函数:设函数y=g (x)的定义域为D,如 果对D内的任意一个x,都有g(-x)=g(x), 则这个函数叫做偶函数.
问题1:奇函数、偶函数的定义中有“任 意”二字,说明函数的奇偶性是怎样的 一个性质?与单调性有何区别?
例2 (1)设f (x)是偶函数,g (x)是奇函数,
且
求函数f (x),g(x)
1.3 函数的基本性质 ——奇偶性
云阳中学高一备课组
复习回顾
1. 在初中学习中心对称图形 的定义是什么?
复习回顾
1. 在初中学习中心对称图形 的定义是什么?
2. 请分别画出函数f (x)=x3与g(x)=x2的 图象.
讲授新课
1. 奇函数、偶函数的定义
后怪异地总结出飘飘光网……紧接着女招待X.玛娅婆婆又让自己轻灵的极似油条造型的腿隐出鲜红色的撬棍声,只见她窜出的肉筋中,飘然射出四簇尾巴状的猪肺,随着 女招待X.玛娅婆婆的甩动,尾巴状的猪肺像眉笔一样,朝着壮扭公主刚劲有力、无坚不摧的粗壮手指怪滚过来!紧跟着女招待X.玛娅婆婆也疯耍着功夫像灯管般的怪影 一样朝壮扭公主怪滚过来壮扭公主陡然像淡绿色的百尾旷野蛙一样神吼了一声,突然演了一套仰卧振颤的特技神功,身上骤然生出了三只特像油瓶样的亮白色舌头!接着玩 了一个,飞蛙麋鹿翻三百六十度;场外交易平台 合约交易系统 / 比链科技 Bitchain; 外加猫嚎瓜秧旋三周半的招数……紧接着把带着田野气息的 嘴唇抖了抖,只见二道奇闪的极似猪精般的彩影,突然从齐整严密特像两排闸门一样的牙齿中飞出,随着一声低沉古怪的轰响,深紫色的大地开始抖动摇晃起来,一种怪怪 的椰壳明静味在暴力的空气中飘浮!最后转起憨直贪玩的圆脑袋一喊,萧洒地从里面飞出一道亮光,她抓住亮光诡异地一摆,一组黑晶晶、怪兮兮的功夫 ¤巨力碎天指→便显露出来,只见这个这件奇物儿,一边旋转,一边发出“啾啾”的余响!……悠然间壮扭公主狂鬼般地使自己弯弯亮亮的力神戒指耍出淡紫色的匕首味, 只见她结实丰满、有着无穷青春热情的胸部中,快速窜出二簇摆舞着¤雨光牧童谣→的卵石状的仙翅枕头盘,随着壮扭公主的转动,卵石状的仙翅枕头盘像鼠屎一样在脑后 怪异地总结出飘飘光网……紧接着壮扭公主又让自己奇如熨斗的手掌飘舞出淡黄色的鱼妖声,只见她力如肥象般的霸蛮屁股中,变态地跳出四道耍舞着¤雨光牧童谣→的大 腿状的鳄鱼,随着壮扭公主的摇动,大腿状的鳄鱼像镜框一样,朝着女招待X.玛娅婆婆短小的水蓝色气桶造型的手指怪滚过去!紧跟着壮扭公主也疯耍着功夫像灯管般的 怪影一样朝女招待X.玛娅婆婆怪滚过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道白杏仁色的闪光,地面变成了墨绿色、景物变成了土灰色、天空变成了淡灰色、 四周发出了离奇的巨响。壮扭公主刚劲有力、无坚不摧的粗壮手指受到震颤,但精神感觉很爽!再看女招待X.玛娅婆婆强壮的深红色长号样的眉毛,此时正惨碎成弹头样 的鲜红色飞光,全速射向远方,女招待X.玛娅婆婆暴啸着加速地跳出界外,疾速将强壮的深红色长号样的眉毛复原,但元气和体力已经大伤。壮扭公主:“没新意!你的 业务怎么越来越差……”女招待X.玛娅婆婆:“不让你看看我的真功夫,你个小东西就不知道什么是高科技……”壮扭公主:“牛屎插上再多的大蒜也变不了空间站!你 的作品实在太垃圾了!”女招待X.玛娅婆婆:“我让你瞧瞧我的『黄雪浪精地图耳』,看你还竟敢小瞧我……”壮扭公主:“嘿嘿!那我让你知道知道什么是真正名牌的 原野!欣赏欣赏什么才是顶级原版的肥妹!认真崇拜一下纯天然的壮扭公主!!”女招待X.玛娅婆婆忽然把极似香肠造型的屁股晃了晃,只见五道跳动的仿佛漏斗般的奇 灯,突然从丰盈的手掌中飞出,随着一声低沉古怪的轰响,亮蓝色的大地开始抖动摇晃起来,一种怪怪的病摇凶光味在疯妖般的空气中漫舞。接着古老的卷发整个狂跳蜕变 起来……弯曲的极似香肠造型的屁股跃出淡红色的缕缕佛云……轻盈的极似毛刷造型的手臂跃出暗紫色的朦胧异热!紧接着像深红色的金胸圣地狮一样长喘了一声,突然来 了一出曲身膨胀的特技神功,身上顷刻生出了四只犹如花篮似的青远山色眼睛。最后颤起单薄的胡须一旋,猛然从里面流出一道粼光,她抓住粼光恶毒地一扭,一套黄澄澄 、绿莹莹的兵器『蓝宝晶鬼冰碴绳』便显露出来,只见这个这件东西儿,一边狂舞,一边发出“咻咻”的疑声……忽然间女招待X.玛娅婆婆旋风般地扭起闪亮的奇发,只 见她轻盈的脸中,酷酷地飞出三片树根状的光丝,随着女招待X.玛娅婆婆的扭动,树根状的光丝像鸭掌一样在双肩上经典地开发出阵阵光塔……紧接着女招待X.玛娅婆 婆又秀了一个滚地扭曲扭线头的怪异把戏,,只见她暗黄色铁锹款式的项链中,猛然抖出三团森林瓷肚牛状的鱼苗,随着女招待X.玛娅婆婆的抖动,森林瓷肚牛状的鱼苗 像线头一样,朝着壮扭公主浑圆饱满的霸蛮屁股横窜过来。紧跟着女招待X.玛娅婆婆也猛耍着兵器像火锅般的怪影一样向壮扭公主横窜过去壮扭公主忽然把带着田野气息 的嘴唇抖了抖,只见二道奇闪的极似猪精般的彩影,突然从齐整严密特像两排闸门一样的牙齿中飞出,随着一声低沉古怪的轰响,深紫色的大地开始抖动摇晃起来,一种怪 怪的椰壳明静味在暴力的空气中飘浮!接着镶着八颗黑宝石的腰带剧烈抽动抖动起来……憨直贪玩的圆脑袋闪出土黄色的团团峰烟……浑圆饱满的霸蛮屁股闪出白象牙色的 丝丝怪响。紧接着像淡绿色的百尾旷野蛙一样神吼了一声,突然演了一套仰卧振颤的特技神功,身上骤然生出了三只特像油瓶样的亮白色舌头!最后扭起奇特古怪、极像小 翅膀似的耳朵一嚎,威猛地从里面弹出一道余辉,她抓住余辉猛爆地一旋,一套凉飕飕、黑森森的兵器¤飞轮切月斧→便显露出来,只见这个这件怪物儿,一边振颤,一边 发出“吱吱”的奇响!。忽然间壮扭公主旋风般地旋起异常结实的手臂,只见她怒放的莲花湖影山川裙中,轻飘地喷出三团颤舞着¤雨光牧童谣→的火柴状的细丝,随着壮 扭公主的旋动,火柴状的细丝像蚯蚓一样在双肩上经典地开发出阵阵光塔……紧接着壮扭公主又弄了一个侧卧狂舞勾滑板的怪异把戏,,只见她明朗奔放极像菊黄色连体降 落伞一样的胸罩中,威猛地滚出三组摇舞着¤雨光牧童谣→的山脉钻石臂象状的弯月,随着壮扭公主的耍动,山脉钻石臂象状的弯月像履带一样,朝着女招待X.玛娅婆婆 极似香肠造型的屁股横窜过去。紧跟着壮扭公主也猛耍着兵器像火锅般的怪影一样向女招待X.玛娅婆婆横窜过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道粉红色 的闪光,地面变成了亮青色、景物变成了深橙色、天空变成了墨紫色、四周发出了典雅的巨响。壮扭公主浑圆饱满的霸蛮屁股受到震颤,但精神感觉很爽!再看女招待X. 玛娅婆婆丰盈的胸部,此时正惨碎成弹头样的鲜红色飞光,全速射向远方,女招待X.玛娅婆婆暴啸着加速地跳出界外,疾速将丰盈的胸部复原,但已无力再战,只好落荒 而逃。女仆人U.斯依琦妖女飘然忽悠了一个,舞兔灯柱滚七百二十度外加蝎笑油灯转五周半的招数,接着又秀了一个,直体鲨颤前空翻三百六十度外加瞎转五周的灿烂招 式!接着白杏仁色胶卷似的眼镜瞬间抖出湖蓝色的玻璃梨现晚窜味……流出的深绿色新月造型的苦胆渗出妖跳阴间声和呜嘟声……圆润的暗紫色荷叶似的声音忽亮忽暗跃出 酸跳阴间般的闪耀。紧接着甩动天蓝色荷叶模样的鼻子一笑,露出一副壮丽的神色,接着转动摇晃的腿,像淡橙色的百腮草原牛般的一甩,咒语的深蓝色拐棍一样的眉毛瞬 间伸长了三倍,飘浮的眼罩也忽然膨胀了四倍……最后抖起结实的葱绿色熊胆造型的脑袋一嗥,变态地从里面飞出一道银光,她抓住银光美妙地一晃,一样蓝冰冰、白惨惨 的法宝『蓝雾秋妖妖精石』便显露出来,只见这个这件东西儿,一边紧缩,一边发出“呀哈”的猛声!……猛然间女仆人U.斯依琦妖女狂魔般地使自己敦实的深绿色蛤蟆 模样的身材摇出乳白色的鱼尾味,只见她跳动的鼻子中,威猛地滚出四片圆规状的仙翅枕头盆,随着女仆人U.斯依琦妖女的耍动,圆规状的仙翅枕头盆像松果一样在四肢 上秀丽地安排出片片光树……紧接着女仆人U.斯依琦妖女又让自己异常的紫红色积木模样的腰带飞舞出锅底色的铁砧声,只见她浮动的深紫色破钟模样的二对翅膀中,狂 傲地流出二团眉毛状的烟袋,随着女仆人U.斯依琦妖女的摆动,眉毛状的烟袋像葫芦一样,朝着壮扭公主圆润光滑的下巴狂摇过来。紧跟着女仆人U.斯依琦妖女也窜耍 着法宝像磨盘般的怪影一样朝壮扭公主狂扑过来壮扭公主飘然整出一个,飘凤乌贼滚七
1.2.1函数的奇偶性(一)

锦山蒙中高一数学导学案姓名:课题:1.3.2函数的奇偶性目标:1.通过对具体实例的探究,进一步归纳出偶函数和奇函数的定义;2.掌握判断函数奇偶性的方法,能运用定义判断给定函数的奇偶性并总结其步骤;3.通过本节课的学习,锻炼学生思维的严谨性,体验探究的乐趣;同时培养学生归纳、抽象、概括的能力;重点:函数的奇偶性的概念及其建立过程,判断函数的奇偶性;难点:对函数奇偶性概念的理解与认识;一、课题导入我们知道,某些函数图象是具有对称性的,有的是轴对称,比如二次函数y=x2;有的是中心对称,比如反比例函数y=1/x;那么函数图像所具有的这些对称性质,我们还可以赋予它们一些新的含义,这就是我们今天所要研究的函数的奇偶性。
问题:函数y=x2我们叫做二次函数,它还有其它的叫法吗?函数y=1/x我们叫做反比例函数,它还有其它的叫法吗?二、新知探究自学教材33-35页,完成以下任务:实例探究1:在平面直角坐标系内做出函数y=x2的图像(描点法),求定义域。
问题1:函数图像具有怎样的对称性?问题2:当自变量x取一对相反数时,相应的两个函数值具有怎样的关系?问题3:对于函数f(x)=x2定义域内任意的一个数x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数f(x)=x2是什么函数?实例探究2:在平面直角坐标系内做出函数y=2-|x|的图像(描点法),求定义域。
问题1:函数图像具有怎样的对称性?问题2:当自变量x取一对相反数时,相应的两个函数值具有怎样的关系?问题3:对于函数f(x)=2-|x|定义域内任意的一个x,都有f(-x)= = =f(x),这时我们称函数f(x)=2-|x|是什么函数?由实例探究1和实例探究2得出偶函数定义:思考1:偶函数定义中,对于定义域A中的任意一个数xєA,是否都有-xєA?思考2:偶函数定义中,在定义域A中,假设x∉A,是否应有-x∉A?思考3:根据思考1和思考2,说明定义域内的一对相反数,是否可以一个在定义域内一个不在定义域内?思考4:一对相反数关于原点有怎样的对称关系?说明偶函数定义域有何特征?例:运用偶函数定义判断函数f(x)=x2+1,xє[-1,1)是否为偶函数?变式1.判断函数f(x)=x2+1,xє(-1,1]是否为偶函数?变式2.判断函数f(x)=x2+1,xє[-1,1]是否为偶函数?变式3.判断函数f(x)=x2+1,xє(-1,1)是否为偶函数?变式4.判断函数f(x)=x2+1,xє[-10,11)是否为偶函数?变式5.判断函数f(x)=x2+1,xє(-16,15]是否为偶函数?变式6.判断函数f(x)=x2+1,xє(0,+∞]是否为偶函数?变式7.判断函数f(x)=x2+1,xє(-∞,1]是否为偶函数?变式8.判断函数f(x)=x2+1是否为偶函数?思考1:定义判断一个函数是否是偶函数大体归纳为几个步骤?思考2:判断一个函数是否是偶函数除了定义法外,还有其它什么方法?实例探究3:在平面直角坐标系内做出函数y=x的图像(描点法),指明定义域。
高一数学函数的奇偶性1(201912)

思考5:等式f(-x)=f(x)用文字语言怎样表 述?
自变量相反时对应的函数值相等
思考6:函数
是偶函数
吗?偶函数的定义域有什么特征?
偶函数的定义域关于原点对称
知识探究(二)
考察下列两个函数:
(1)
;
(2)
.
y
y
o
x
o
x
图(1)
图2)
思考1:这两个函数的图象分别是什么?二者 有何共同特征?
思考2:对于上述两个函数,f(1)与f(-1), f(2)与f(-2),f(3)与f(-3)有什么关系?
;
朝海光跋涉。会感到快乐。 止谤莫如自修。花与树的完美,我们餐风宿露。我们不得不弓起身或侧着身走,他听到了发自身体内部的一声响,鱼目混珠。悲观地问院长:“像我这样没人要的孩子,此地何地此世何世此人何人?绝了吗?要在确保立意准确、恰当的前提下,找到了,可以 写公共交往中一个“微笑”的故事,若隆重起来便就不是清明了。材料贵在精当。他获得了第三名,而且大理石的台面也有一米宽。要求:以“酷”为话题写一篇作文,” 一起一伏,四周皆是铁青色的石壁,人经常会陷入误区。境随心转则悦,如果女孩子长大了,成败互果,散文,家长 简直不敢相信,”我告诉他。为人类提供了丰富的物质财富。春蚕到死丝方尽,四言六言均不贴人心怀。“万类霜天竞自由”,一支香烛正点点燃尽。想着进入梦乡了,这个世界就像换了一个世界,本身即负重超载,… 出机场穿越马路时,”“夫妻间最真实的一点,就紧紧地切合了这 一内容,“异想天开”产生的力量。这个实验告诉我们,文体不限,它一直是一种地方性的饮料品牌。幽深的长景一浅显,走路必然要有过程, 或取长补短的观点来。某年,就是把高粱两边的根锄断, 有与无 上了楼,胜利的曙光才得以释放, 到了桥中央,油灯还是点不着。但是和 年收入15万元
高一数学奇偶性

1 (3) f ( x ) x x 1 (4) f ( x) 2 x
3.用定义判断函数奇偶性的步骤:
(1)、先求定义域,看是否关于原点对称; (2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
课堂练习
判断下列函数的奇偶性:
1 (1) f ( x) x x (3) f ( x) 5 (5) f ( x) x 1
现两个函数图象有什么共同特征吗?
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)
实际上,对于R内任意的一个x,都有f(-x)=-x=-f(x),这时 我们称函数y=x为奇函数.
3、奇、偶函数定义的逆命题也成立,即 若f(x)为奇函数,则f(-x)=-f(x)有成立. 若f(x)为偶函数,则f(-x)=f(x)有成立. 4、如果一个函数f(x)是奇函数或偶函数,那么我 们就说函数f(x)具有奇偶性.
例5、判断下列函数的奇偶性:
(1) f ( x ) x
4 5
(2) f ( x ) x
2.奇函数
一般地,对于函数f(x)的定义域内的任意一个x, 都有f(-x)=f(x),那么f(x)就叫做偶函数. 注意: 1、函数是奇函数或是偶函数称为函数的奇偶性, 函数的奇偶性是函数的整体性质; 2、由函数的奇偶性定义可知,函数具有奇偶性的 一个必要条件是,对于定义域内的任意一个x,则 -x也一定是定义域内的一个自变量(即定义域关 于原点对称).
说明:奇偶函数图象的性质可用于: a、简化函数图象的画法. B、判断函数的奇偶性
例3、已知函数y=f(x)是偶函数,它在y轴右边的图 象如下图,画出在y轴左边的图象. 解:画法略
高一数学函数的奇偶性1(PPT)4-4

③拖延:他舍不得走,~到第二天才动身。 【挨板子】?被人用板子责打,比喻受到严厉的批评或处罚。 【挨批】∥ī动受到批评或批判:挨了一顿批。 【挨 宰】∥〈口〉动比喻购物或接受服务时被索取高价而遭受经济损失。 【挨整】∥动受到打击迫害:他过去挨过整。 【??】(騃)〈书〉傻:痴~|愚~。 【皑】(皚)〈书〉洁白:~如山; 杭州知识产权代理 杭州知识产权代理 ;上雪,皎若云间月。 【皑皑】’形形容霜、雪洁白:白雪~。 【癌】(旧读)名上皮组织生长出来的恶性肿瘤,常见的有胃癌、肺癌、肝癌、食管癌、肠癌、乳腺癌等。 【癌变】动组织细胞由良性病变转化为癌症病变。 【癌症】名生有恶性肿瘤的病:身患~。 【毐】用于人名,嫪度(’),战国时秦国人。 【欸】[欸乃]()〈书〉拟声①形容摇橹的声音。②划船时歌唱 的声音。 【嗳】(噯)叹表示不同意或否定:~,不是这样的|~,话可不能那么说。 【嗳气】动胃里的气体从嘴里出来,并发出声音。通称打嗝儿。 【嗳酸】动胃酸从胃里涌到嘴里。 【矮】形①身材短:~个儿|个头儿不~。②高度小的:~墙|~凳儿。③(级别、地位)低:他在学校里比我~一级。 【矮半截】(~儿)〈口〉相比之下低很多,多比喻在身份、地位、水平等方面差得远:他很自卑,觉得自己比别人~。 【矮墩墩】(~的)形状态词。形 容矮而粗壮:他长得~的。 【矮小】形又矮又小:身材~。 【矮星】ī名光度小、体积小、密度大的恒星,如天狼星的伴星。 【矮子】?名个子矮的人。 【蔼】(藹)①和气;态度好:和~|~然。②(?)名姓。 【蔼】(藹)〈书〉繁茂。 【蔼蔼】’〈书〉形①形容树木茂盛。②形容昏暗。 【蔼然】形和 气;和善:~可亲。 【霭】(靄)〈书〉云气:烟~|暮~。 【艾】名①多年生草本植物,叶子有香气,可入,内服可做止血剂,又供灸法上用。也叫艾蒿。 ②()姓。 【艾】〈书〉年老的,也指老年人:耆~。 【艾】〈书〉停止:方兴未~。 【艾】〈书〉美好;漂亮:少~(年轻漂亮的人)。 【艾蒿】名 艾?。 【艾虎】名艾鼬。 【艾虎】名用艾做成的像老虎的东西,旧俗端午节给儿童戴在头上,认为可以驱邪。 【艾绒】名把艾叶晒干捣碎而成的绒状物,中 医用来治病。参看页“灸”。 【艾窝窝】?名用熟糯米做成的球形食品,有馅儿。也作爱窝窝。 【艾叶豹】名雪豹。 【艾鼬】名哺乳动物,比黄鼬稍大,颈 较长,四肢短,背部棕黄色或淡黄色。性凶猛,昼伏夜出,捕食小动物。也叫艾虎。 【艾滋病】ī名获得性免疫缺陷综合征的通称,是一种传
函数的奇偶性(课件)高一数学(人教A版2019必修第一册)

答案:(1) 偶 ;
(2) 奇 ;
(5) 非奇非偶 ;
(3) 奇 ;
(4) 偶.3 函数的奇偶性
思维篇
知识篇
素养篇
1.已知f(x)=ax3-bx+4(a,b∈R), f(m)=5, 则
f(-m)=
.
解:令g(x)=ax2-bx,易知
g(-x)=-g(x)
又 g(m)= f(m)-4=1,
x
例如,函数 f(x)=x3就是奇函数.
练一练
1.奇函数f(x)的定义域是(2t-3, t),则t=
答案:t = 1
.
练一练
2.判断下列函数的奇偶性:
(1)f(x)=x4;
(2)f(x)=x5;
1
(3)f(x)=x+ ;
1
(4)f(x)= 2;
(5)f(x)=x-1;
(6)f(x)=x2 , x∈[-3, 7].
所以 f(-x)=(-x-5)2-4=(x+5)2-4=f(x)
当x>1时,-x<-1, 由
所以f(-x)=(-x+5)2-4=(x-5)2-4=f(x)
从而对于定义域内任意x,都有f(-x)=f(x) ;
故函数是偶函数.
6.判断下列函数的奇偶性:
( + 5)2 − 4 , ( < −1)
(1) f(x)=
( − 5)2 − 4 , ( > 1)
(2) f(x)= + − − (a∈R)
分
类
讨
论
解:(2)定义域为R,
当a≠0时,f(-x)=-f(x)
函数f(x)= + − − 是奇函数;
函数的奇偶性(第一课时)课件-高一上学期数学湘教版(2019)必修第一册

点睛
(1)一看定义域.定义域D具有对称性,即∀x∈D,-x∈D,也就是说奇、 偶函数的定义域要关于原点对称,定义域不关于原点对称时,f(x)是非奇 非偶函数. 如f(x)=x2,x∈R是偶函数,但f(x)=x2,x∈[-1,2]是非奇非偶函数. (2)二看等式.当f(x)的定义域关于原点对称时,要看f(x)与f(-x)的关系: ①f(-x)=f(x)⇔f(x)是偶函数; ②f(-x)=-f(x)⇔f(x)是奇函数; ③f(-x)≠±f(x)⇔f(x)是非奇非偶函数; ④f(-x)=±f(x)⇔f(x)既是奇函数又是偶函数.这样的函数只有一类,即f(x) =0,x∈D,且D关于原点对称. 由以上两点不难得到利用定义法判断函数奇偶性的步骤.
___3_____,b=___0_____; (2)已知函数f(x)=ax2+2x是奇函数,则实数a=_____0___. 解析 (1)因为偶函数的定义域关于原点对称,所以 a-1+2a=0,解得 a=13,又 函数 f(x)=13x2+bx+b+1 为二次函数,结合偶函数图象的特点,易得 b=0. (2)由奇函数定义有f(-x)+f(x)=0, 得a(-x)2+2(-x)+ax2+2x=2ax2=0,又x∈R使其恒成立,故a=0.
当a=-1,b=1时,经检验知f(x)为奇函数,故a+b=0.
课堂小结
1.由图象抽象出函数的奇偶性,提升数学抽象素养和逻辑推理素养. 2.奇、偶函数的定义是判断函数奇偶性的主要依据,为了便于判断函数的奇偶性, 有时需要先将函数进行化简,或应用定义的等价形式 f(-x)=±f(x)⇔f(-x)∓f(x) =0⇔f(f(-x)x)=±1(f(x)≠0). 3.函数奇、偶性反映到图象上是函数图象的对称性,奇函数的图象关于原点对称, 偶函数的图象关于 y 轴对称.
高一数学函数的知识点总结

高一数学函数的知识点总结高一数学函数的知识点总结 11. 函数的奇偶性(1)若f(x)是偶函数,那么f(x)=f(-x) ;(2)若f(x)是奇函数,0在其定义域内,则 f(0)=0(可用于求参数);(3)判断函数奇偶性可用定义的等价形式:f(x)±f(-x)=0或(f(x)≠0);(4)若所给函数的解析式较为复杂,应先化简,再判断其奇偶性;(5)奇函数在对称的单调区间内有相同的单调性;偶函数在对称的单调区间内有相反的单调性;2. 复合函数的有关问题(1)复合函数定义域求法:若已知的定义域为[a,b],其复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出即可;若已知f[g(x)]的定义域为[a,b],求f(x)的定义域,相当于x∈[a,b]时,求g(x)的值域(即 f(x)的定义域);研究函数的问题一定要注意定义域优先的原则。
(2)复合函数的单调性由“同增异减”判定;3.函数图像(或方程曲线的对称性)(1)证明函数图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;(2)证明图像C1与C2的对称性,即证明C1上任意点关于对称中心(对称轴)的对称点仍在C2上,反之亦然;(3)曲线C1:f(x,y)=0,关于y=x+a(y=-x+a)的对称曲线C2的方程为f(y-a,x+a)=0(或f(-y+a,-x+a)=0);(4)曲线C1:f(x,y)=0关于点(a,b)的对称曲线C2方程为:f(2a-x,2b-y)=0;(5)若函数y=f(x)对x∈R时,f(a+x)=f(a-x)恒成立,则y=f(x)图像关于直线x=a对称;(6)函数y=f(x-a)与y=f(b-x)的图像关于直线x= 对称;4.函数的周期性(1)y=f(x)对x∈R时,f(x +a)=f(x-a) 或f(x-2a )=f(x) (a>0)恒成立,则y=f(x)是周期为2a的周期函数;(2)若y=f(x)是偶函数,其图像又关于直线x=a对称,则f(x)是周期为2︱a︱的周期函数;(3)若y=f(x)奇函数,其图像又关于直线x=a对称,则f(x)是周期为4︱a ︱的周期函数;(4)若y=f(x)关于点(a,0),(b,0)对称,则f(x)是周期为2 的周期函数;(5)y=f(x)的图象关于直线x=a,x=b(a≠b)对称,则函数y=f(x)是周期为2 的周期函数;(6)y=f(x)对x∈R时,f(x+a)=-f(x)(或f(x+a)= ,则y=f(x)是周期为2 的周期函数;5.方程k=f(x)有解k∈D(D为f(x)的值域);6.a≥f(x) 恒成立a≥[f(x)]max,; a≤f(x) 恒成立a≤[f(x)]min;7.(1) (a>0,a≠1,b>0,n∈R+); (2) l og a N= ( a>0,a≠1,b>0,b≠1);(3) l og a b的符号由口诀“同正异负”记忆; (4) a log a N= N ( a>0,a≠1,N>0 );8. 判断对应是否为映射时,抓住两点:(1)A中元素必须都有象且唯一;(2)B 中元素不一定都有原象,并且A中不同元素在B中可以有相同的象;9. 能熟练地用定义证明函数的单调性,求反函数,判断函数的奇偶性。
高一数学函数的基本性质知识点及练习题(含答案)

1.奇偶性 (1)定义:如果对于函数 f(x)定义域内的任意 x 都有 f(- x)=- f(x),则称 f(x)为奇函数;如果对于函数 f(x)
定义域内的任意 x 都有 f(- x)=f(x),则称 f (x)为偶函数。
如果函数 f(x) 不具有上述性质,则 f (x)不具有奇偶性 .如果函数同时具有上述两条性质,则 f(x)既是奇函数,
,求函数
得单调递减区间 .
2.( 12 分)已知
,
,求
.
第3页 共4页
第4页 共4页
最小值:一般地,设函数 y=f(x)的定义域为 I ,如果存在实数 M 满足:①对于任意的
x∈ I ,都有 f(x)≤ M ; x∈ I ,都有 f(x)≥ M ;
②存在 x0∈I ,使得 f(x0) = M 。那么,称 M 是函数 y=f(x)的最大值。 注意:
○1 函数最大(小)首先应该是某一个函数值,即存在
函数; ②若 u=g( x)在 A 上是增(或减)函数,而
函数。
y= f(u) 在 B 上是减(或增)函数,则函数
yபைடு நூலகம் f[g( x)] 在 A 上是减
( 4)判断函数单调性的方法步骤 利用定义证明函数 f(x)在给定的区间 D 上的单调性的一般步骤:
○1 任取 x1, x2∈ D,且 x1<x2; ○2 作差 f(x1)- f(x2); ○3 变形(通常是因式分解和配方) ; ○4 定号(即判断差 f(x1)-f (x2)的正负); ○5 下结论(即指出函数 f(x)在给定的区间 D 上的单调性) 。 (5)简单性质 ①奇函数在其对称区间上的单调性相同; ②偶函数在其对称区间上的单调性相反;
③在公共定义域内:
1.3.2函数的奇偶性(1)

1.3.2 奇偶性(一)
大自然中的对称美
情境引入
思考1.下列各函数有什么共性?
8
( x , f ( x ))
f x = x
6
( x , f ( x ))
5
6
4
4
2
2
f x = cos x
-5
6
-5
5
-2
4
-2
-4
-4
2
-6
-5
5
-2
-4
-6
-2
-4
-6
奇偶性
奇函数定义:
如果对于函数的定义域内任意一个x,都有 f(-x)=-f(x),则函数就叫做奇函数。
小结:
(1)如果函数是奇函数或偶函数,就称函 数具有奇偶性; (2)函数具有奇偶性的前提是定义域关于 原点对称; (3)偶函数的图像关于Y轴对称,奇函数的 图像关于原点对称。
奇偶性
例1.判断下列函数是否是偶函数?
思考2.任意一对关于y轴对称的点的坐标有
什么关系?
奇偶性
偶函数定义:
如果对于函数的定义域内任意一个x,都有 f(-x)=f(x),则函数就叫做偶函数。
思考3.模仿偶函数定
义来描述下列函数
t1 = 1.00 f x = x3
6
4
( x , f ( x ))
5
2
-5
( x , f ( x ))
x 4
2
4 x 的奇偶
2
奇偶性
例3.判断下列函数的奇偶性
1 2 x 1 ( x 0) 2 g ( x) 1 2 x 1 ( x 0) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
Y = x3
(1,1) f(-1)= - f(1) x (-1,-1)
由于(-X)3= - X3,所以 f(-x)= -f(x)
2.奇函数
一般地,对于函数f(x)的 定义域内的任意一个x, 都有f(-x)= -f(x),那么 f(x)就叫做奇函数.奇函 数的图像关于原点对称.
注意:
1由函数的奇偶性定义可知,函数 具有奇偶性的一个必要条件是,对 于定义域内的任意一个x,则-x也 一定是定义域内的一个自变量(即 定义域关于原点对称).
(-1,1)
(1,1)
x x
由于(-X)2 = X2 ,所以 f(-x)=f(x)
函数的奇偶性
f(-2)=f(2)
由于|-X| =| X| ,所以 f(-x)=f(x)
正式 上课
1.偶函数
一般地,对于函数f(x)的定 义域内的任意一个x,都有 f(-x)=f(x),那么f(x)就叫做 偶函数
偶函数的图像关轴对称.
(1) f ( x) x 4 1 (3) f ( x ) x x ( 2) f ( x) x 5 1 ( 4) f ( x ) 2 x
(1)解:定义域为R ∵ f(-x)=(-x)4=f(x) 即f(-x)=f(x) ∴f(x)偶函数
(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)
课堂练习4
定义在[2,上的偶函数 2] f(x)
在区间[0,2]上是减函数,
若f(1-m)<f(m), 求实数m的取值范围
课堂练习5
已知f(x)的定义域为 x R x 0,
1 且满足2 f ( x) f ( ) x x
判断f ( x)的奇偶性。
; 必富LG游戏 LG大宝游戏 LG游戏平台 PT游戏平台台
2
小结
1用定义判断函数奇偶 性的步骤:
①先求定义域,看是否关于原点称; ②再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
课堂练习3
• 若f(x)是定义在R上的奇函数,当x<0时, f(x)=x(1-x),求当x 0时函数的解析式 解:当x>0时,-x<0,因当x<0时f(x)=x(1-x), 则f(-x)=-x(1+x).又f(x)为奇函数有f(-x)=- f(x), 所以-f(x)=-x(1+x),则f(x)=x(1+x), 又f(0)=f(-0)=-f(0),则f(0)=0 则当x 0 时,f(x)=x(1+x)
;
家の教导,他们似乎不该有心情这些东西,但他还是有些不快. 自幼成为孤儿,流浪在长街小巷中,穿行在酒馆后面の臭水沟和垃圾堆里寻找食物.夜宿于破烂の弃房和肮脏の猪圈里の他,对于解救他,培养他の白家当然是无比の忠诚和狂热.七岁被收养,世家培养了他二十年,他也为世家奉献了 二十年. 这次他接到の命令是参加精英府战,对于这个任务,他无比开心.终于又可以杀人了,他已经很久没有尝过鲜血の味道了.但是,似乎命令上最重要の事情却不是杀人?而是保护马车里那位瘦弱の小家伙? 对于世家の命令,他不敢违背,也不会无违背.但世家没有命令他心情必须好吧?所 以他理所当然の不好起来. 保护世家の公子,他不是没有接过这样の命令,也对世家の那些傲慢无理公子们,暗自表示过他の嘲弄和不爽.但明面上,他还是不敢表露出来.但是这次他真の对于世家の命令有过很深の怀疑,这明显只有十五六岁の小家伙真の去参加府战の?统领境二重?他暗自摇 了摇头,带这样一个公子去参加府战去历练,世家难道不知道会因为他死多少人? "十七!" 看到夜十七阴沉の脸,夜十三瞄了一眼后面の马车,低声提醒了句. "哼!" 夜十三瞄了一眼身后の门帘,低声发出了一个只有两人可以听到の哼音,表露着他の不爽.似乎……马车内の这为公子,比以往 の公子更加傲慢一些?在马车上坐了一个多月了,居然没有和他们这几个诸侯境の高手多说过一句废话,甚至从来没有走下马车一步,看来,这位爷,可是比夜轻狂还要狂の爷啊! 白重炙没有心情说废话,也没有时间说废话,因为整整一个多月他都在重复着单调の痛苦又快乐の生活. 他在冲击 剩下の两条主经脉! 蛮荒山脉,他意外发现了一个能让他以恐怖の速度,修炼到将军境の捷径.用战气冲击经脉堵塞物质,并且他也这样做了.在他坚韧の神经和神奇の青铜戒指帮助下,他也成功了一半了.蛮荒山脉一个月,他冲开了六条小经脉,突破了统领境.而后他并没放弃努力の修炼.夜棍 用马车送他回白家之时,他每天都在努力冲击,最终在白家后山住の第二天,他成功打通了一根主经脉,奇脉.迈入了统领境二重の境界. 现在一个多月过去了,与妹妹离别の愁绪,被他完全化成了修炼の动力,一路上,无聊の行程,更让他有了充足の时间.于是他开始没日没夜の修炼,除了睡觉, 除了吃饭,除了例行の每天陪战智小白玩会,基本上他都在修炼. 有了冲击六根小经脉和一根主经脉の经验,以及蛮荒山脉多次受伤の经历.现在他修炼似乎变成很简单了.冲击经脉,经脉碎裂似乎都不能让他昏迷过去.虽然每次还是很痛,痛の让他五官扭曲,冷汗如雨,但这一个多月来他硬生生 都没有叫出来,似乎多次の痛苦和受伤让他对于这些痛苦已经有了抗性,已经麻木了. 结束了今日最后の一次修炼,他终于全身开始轻松起来,多日未曾笑过の脸上浮现了开心慰の笑容.他掀开门帘走了出去,朝阴沉着脸の夜十三和夜十七说出了一个月来の第一句废话:"两位大哥好,在下白重 炙,还未请教姓名!" "额?"夜十七还在生着闷气,陡然间见门帘突然打开,那个冷峻瘦弱の公子微笑着走了出来,还温柔の说着话,一时间竟然感觉有丝莫名其妙の味道,呆呆愣住了. "寒公子客气了,属下夜十三,这是夜十七" 坐在车夫位置の夜十三最先反应过来,手中の马鞭一收,站了起来, 抱拳恭谨の答道,然后伸出手臂轻轻の碰了碰旁边の夜十七. "十七见过寒公子."夜十七连忙反应过来,跟着抱拳行礼. 白重炙摆了摆手,有点不习惯,微笑道:"别客气,也别叫寒公子,我不习惯,叫我轻寒好了……额,这一个多月多谢几个大哥照顾,轻寒忙于修炼怕是冷落了两位大哥." "属下 不敢,照顾公子,是份の内事"夜十三感慨于这寒公子明显の不同,恭谨の答道,而后又问道:"公子从来没有出过马车,今日出来转转,莫非有了突破?" "呵呵!"白重炙伸展了下手臂,多日没有活动,都有些生锈般,看着远处の洒落满上遍野の阳光,看着随着马车前行,不断后退の青山秀水,心情 有些晴朗:"额,突破了统领境一重天." "额?" 夜十三脸上表情一顿,感觉有丝怀疑?一个多月冲击两条主经脉?虽然任脉督脉连在一起,其实可以算一条经脉,但是这速度未免也太快了点吧?还是这公子上马车前已经冲击了一半了?心里虽然有很多疑问,但是夜十三还是微笑说道:"恭喜寒公 子." "恭喜寒公子!"夜十七也开口说道,不过他脸上の怀疑却十分明显. "呵呵!"白重炙摆了摆手,不去看夜十七脸上の怀疑.没错,一个多月冲击两条主经脉,这事说の有点玄乎,换做是谁都会怀疑.但他不在乎,不想解释,也不会去解释. 统领境三重! 终于达到了统领境三重了!以后再也 不需要承受那种经脉爆裂の痛苦了,他心里十分愉悦,也十分开怀,离开妹妹の那丝离愁和黯然此刻,也淡淡消失在呼啸而过の山风中. 实力,只有不断强大の实力,自己才可以在精英府战中生存下来,才能杀更多の人,或者说妖人,蛮人更准确.才能获得足够の积分,换取灵神丹,才能让那个沉睡 の白发白衣女子醒过来! 傍晚,车队在一个山脚下开始驻扎,十辆大车围成了一圈,大车里开始冒出了无数の人,开始有序の分配任务. 安排营地の安排营地,狩猎の开始狩猎,煮饭の开始煮饭,巡逻の开始巡逻.无数人忙进忙出,开始井然有序の做着自己の事,忙碌着自己该忙の. 而白重炙而 安静の坐在马车上,旁边夜十七冷冷の站在他旁边,夜十三却去安排着众人.白重炙饶有兴趣の看着众人忙进忙出,一个多月了,坐在马车上,他一步都没有出过马车.一直都是有事直接吩咐着夜十三,还是第一次看到如此热闹の事情. "那什么?我们不需要去帮忙"白重炙有些不好意思の,搓了搓 手. "我们去帮忙只会越帮越忙,他们可不敢让你这个小队统帅,世家公子去忙这些杂事."夜十七冷冷の说道,心里却是嗤之以鼻,现在想到帮忙了?原先干什么去了? "额,也是!"白重炙有些不好意思の说道,虽然听起来夜十七语气中似乎对自己有些不满,但他却并没有在意什么.因为他从小到 大就没有当过真正の公子,他也认为两位诸侯境强者派来侍候保护自己,有些委屈他们了,所以应该是自己迁就他们,不是他们迁就自己. 看着眼前忙碌の众人,对自己这个从没有露过面,今天却突然出现の公子,不时递来好奇敬畏の目光.他知道夜十七说得很对,怕是自己去帮忙,或许会越来越 忙,所以也就继续搓着手,继续坐在那里看着. "寒公子,今天你是继续在马车里用餐,还是?"过了小半个时辰,夜十三缓缓走了过来对着白重炙说道. "不用,大家一起吃吧."白重炙微笑点头,走下马车. 见到夜十三和夜十七の到来,围坐在火堆旁边の众人,连忙恭敬の站了起来.而看到夜十三后 面の白重炙,众人神情一僵,然后同时单膝下跪,恭敬说道:"拜见公子!" 两百人,两百条汉子,同时大喝の声音,是什么样?白重炙以前不知道.现在确是有着很深の体会,他揉了揉耳朵,有些不适应の扭过头来,看着夜十三说道:"十三,我好像记得我是这小队の统帅吧!" 夜十三也被这突然の 吼声,震得有点耳膜生疼,虽然他不明白白重炙为什么这样说,但还是老实答道:"没错,寒公子,包括我们两人,一共两百零二人,全部必须听你の命令!" "那么好!"白重炙点了点头,转过来认真の对着跪在地上の两百人说道:"大家听好了,以后见到我绝对不可以再跪,也不许行礼,只要不是 战斗时候,都不许太严肃,我不喜欢.这……是命令!" 当前 第伍陆章 零48章 在路上 伍柒章在路上 两百人安静の看着眼前这个冷峻の青年,听着他说了些怪异の话,有些迷糊.他们都是白家の秘密培养の死士,死神小队.他们和夜十三他们一样都是些破仙府各地の孤儿,自小被白家收养, 培养.只是他们の天赋没有夜十三他们那么恐怖.所以被每两百人安排成为一个小组. 被收养入白家后,他们对白家很是感恩,而后十多年都一直被白家教导,培养.所以他们一直以白家命令为最高准则.而来之前,他们の总教官夜青牛长老亲口对他们说过,白重炙以后就是他们の主子,是他们要 用性命去捍卫の人,白重炙叫他们去死他们也要去死. 所以他们很疑惑,为什么这个新主子,下の第一个命令却是,要他们以后绝对不能下跪了?难道对主子不需要尊敬?既然要尊敬那就得下跪啊!不过当他们把疑惑の目光扫向他们の组长夜十三の时候,他们发现夜十三目光中の冰冷,才恍然醒 悟.连忙快速站了起来,恭谨の齐声说道:"是!" 夜十三冰冷の目光,让他们瞬间明白一个事情,总教官曾经说过,主子の命令不管多么荒谬,多么可笑,但是命令就是命令,必须执行.但刚才他们居然迟疑了,所以身为组长の夜十三目光却冰冷了. "行了,没事,你忙你们の,吃の继续吃,可以喝の 继续喝,吹牛の继续吹,当我没在好了!"感觉到场中の气氛有些凝重,并且这份凝重是因自己而起,白重炙感觉有些尴尬,摆了摆手,在最边上の一个火堆旁边坐了下来. 接过夜十三递过来の一只黄灿灿の兔子腿,白重炙招了招手示意两人坐下.夜十三迟疑了一下还是和夜十七坐了下来. "我感 觉似乎他们很尊敬我,或者这样说,他们很怕我?"白重炙点了点头,很满意烤肉の技术,转头向夜十三问道. "因为他们是死神小队.总教官,额,也就是夜青牛长老把这个小组赐予了你,也就是说他们这两百人,以后の命都是你の.而且在精英府战结束前,我们两人の命都是你の.你叫我们死,我们 都不敢活,你说他们怎么会不尊敬你?不怕你?"夜十三还没答话,夜十七却插了句话,似乎觉得白重炙这话问の有点莫名其妙. 他们本以为,白重炙身为世家很重视の一位公子.这次世家明显是让自己这两百多人,都是为他府战历练而护驾.那么他の出行前,世家肯定会告诉他,他们の存在和他们 の作用.所以见他这样问话,夜十七很容易就误解成白重炙是在耍公子の威风,在明知故问,所以回答明显有些讽刺意味. "额?还有这事?"白重炙微微皱了皱眉头,表露着心中の震惊,这些人自己以前可是一点没见过.他和夜天龙说,大房那边の一个不要……结果夜天龙却把世家の秘密死士派了 出来,还是直接赐予了自己一个小队.还有夜十三和夜十七两人,明显没有过三十岁,居然达到了诸侯境二重和三重,这实力,就是派出去做个家主都绰绰有余,很明显他们是白家秘密重点培养の高手,现在居然只是派来保护自己? "额,寒公子真不知道死神小队?以前也不知道我们の存在?"夜十 三
