有理数混合运算练习题集(有答案解析)一

合集下载

有理数混合运算100题(含答案解析)

有理数混合运算100题(含答案解析)1.-(-3)2×22.1/2+(-2/3)+4/5+(-11/2)+(-3)3.(-1.5)+4(1/4)+2.75+(-5 1/2)4.-8×(-5)-635.4-5×(-1/2)3/26.(-2)+(-5/56)-(-4.9)-0.67.(10)2÷5×(-2/5)8.(-5)3×(-3/5)29.5×(-6)-(-4)2÷(-8)10.2 1/472×(-6)÷(-2)11.(-16-50+3/5)÷(-2)12.(-6)×8-(-2)3-(-4)2×513.(-1)2+1×(2-2/233)-214.--(1-0.5)×1/315.-3/2×[-32×(-2/3)2-2]16.(-3/4)2+(-2/3+1)×2-9/1617.-14-(1-0.5)×1/3×[2-(-3)2]18.(-81)÷(2.25)×(-4/9)÷1619.-52-[-4+(1-0.2×1/5)÷(-2)]20.(-5)×(-3/6)+(-7)×(-3/6)+12×(-3/6777)21.(-5/8)×(16)-0.25×(-5)×(64)22.(-3)2-(11/29)×(-6)÷(-3)23.(-1/6-20/3+4/5-12/7)×(-15×4)24.(-18/7)×3/7×(-2.4)25.2÷(-7)×(7)÷(-51/7)26.(-47/8)-(-5/2)+(-4/4)-3/827.[151]÷(-11/2-14÷1/5+3/2)28.(-16-50+3/5)÷(-2)29.1 5/(-5)×(-5/13)30.(-0.5)-(-31/4)+6.75-5 2/331.-29-(-13)×2×(-13)-7×0.34+5.6×(-4)+(-32)÷(-8)-3 3/100-0.34×7+3×2130.计算：（－13）×（－134）×1/13×（－1/67）= 2136.731.删除该段落，因为它没有内容。

有理数的混合运算练习题(含答案)(共17套)

有理数的混合运算练习题(含答案)（共17套）有理数混合运算练习题及答案第1套同步练习（满分100分）1．计算题：（10′×5=50′）（1）3．28-4．76+121-43；（2）2．75-261-343+132；（3）42÷（-121）-143÷（-0.125）;（4）(-48) ÷82-(-25) ÷(-6)2;（5）-52+(1276185+-)×(-2.4).2.计算题：（10′×5=50′）（1）-23÷153×（-131）2÷（132）2；（2）-14-（2-0.5）×31×[(21)2-(21)3];（3）-121×[1-3×(-32)2]-( 41)2×(-2)3÷(-43)3（4）(0.12+0.32) ÷101[-22+(-3)2-321×78];(5)-6.24×32+31.2×(-2)3+(-0.51) ×624.【素质优化训练】1.填空题：(1)如是0,0>>c b b a ，那么ac 0；如果0,0<<cbb a ，那么ac0;(2)若042=-++++c c b a ，则abc= ; -a 2b 2c 2=;(3)已知a ，b 互为相反数，c ，d 互为倒数，x 的绝对值等于2，那么x 2-(a+b)+cdx=.2．计算：（1）-32-;)3(18)52()5(223--÷--⨯-（2）{1+[3)43(41--]×(-2)4}÷(-5.043101--);（3）5-3×{-2+4×[-3×(-2)2-(-4) ÷(-1)3]-7}.【生活实际运用】甲用1000元人民币购买了一手股票，随即他将这手股票转卖给乙，获利10%，而后乙又将这手股票反卖给甲，但乙损失了10%.最后甲按乙卖给甲的价格的九折将这手股票卖给了乙，在上述股票交易中（）A ．甲刚好亏盈平衡；B ．甲盈利1元；C ．甲盈利9元；D ．甲亏本1.1元.参考答案【同步达纲练习】1．（1）-0.73 （2）-121; （3）-14; （4）-181; （5）-2.92．(1)-351 (2)-1161; (3)- 5437; (4)1; (5)-624.【素质优化训练】1.(1)>，>; (2)24，-576; (3)2或6.[提示：∵x =2 ∴x 2=4，x=±2].2.(1)-31;(2)-8;2719(3)224 【生活实际运用】 B有理数的四则混合运算练习第2套◆warmup知识点有理数的混合运算（一）1．计算：（1）（-8）×5-40=_____；（2）（-1.2）÷（-13）-（-2）=______．2．计算：（1）-4÷4×14=_____；（2）-212÷114×（-4）=______．3．当||a a=1，则a____0；若||a a =-1，则a______0．4．（教材变式题）若a<b<0，那么下列式子成立的是（） A ．1a <1b B ．ab<1 C ．a b <1 D ．ab>1 5．下列各数互为倒数的是（）A ．-0.13和-13100B ．-525和-275C ．-111和-11D ．-414和4116．（体验探究题）完成下列计算过程:（-25）÷113-（-112+15）解：原式=（-25）÷43-（-1-12+15）=（-25）×（）+1+12-15=____+1+52 10 -=_______．◆Exersising7．（1）若-1<a<0，则a______1a；（2）当a>1，则a_______1a；（3）若0<a≤1，则a______1a．8．a，b互为相反数，c，d互为倒数，m的绝对值为2，则||4a bm++2m2-3cd值是（）A．1 B．5 C．11 D．与a，b，c，d值无关9．下列运算正确的个数为（）（1）（+34）+（-434）+（-6）=-10 （2）（-56）+1+（-16）=0（3）0.25+（-0.75）+（-314）+34=-3（4）1+（-3）+5+（-7）+9+（-1）=4 A．3个 B．4个 C．2个 D．1个10．a，b为有理数，在数轴上的位置如右上图所示，则（）A．1a>1b>1 B．1a>1>-1bC．1>-1a>1bD．1>1a>1b11．计算：（1）-20÷5×14+5×（-3）÷15 （2）-3[-5+（1-0.2÷35）÷（-2）]（3）[124÷（-114）]×（-56）÷（-316）-0.25÷14-1ob a◆Updating 12．（经典题）对1，2，3，4可作运算（1+2+3）×4=24，现有有理数3，4，-6，10，请运用加，减，乘，除法则写出三种不同的计算算式，使其结果为24．（1）____________ （2）____________ （3）____________ 答案: 课堂测控1．（1）-80 （2）535 2．（1）-14（2）83．>，< 4．D 5．C 6．34，-310，1[总结反思]先乘除，后加减，有括号先算括号内的．课后测控 7．（1）> （2）> （3）≤ 8．B 9．B 10．B11．解：（1）原式=-20×15×14+5×（-3）×115=-1-1=-2（2）原式=124×（-45）×（-56）×（-619）-14÷14=124×（-419）-1=-1114-1=-11114（3）原式=-3[-5+（1-15×53）÷（-2）]=-3[-5+23×（-12）]=-3[-5-13]=15+1=16[解题技巧]除法转化为乘法，先乘除，后加减，有括号先算括号内的．拓展测控 12．解：（1）4-（-6）÷3×10 （2）（10-6+4）×3 （3）（10-4）×3-（-6）[解题思路]运用加，减，乘除四种运算拼凑得24点．有理数的混合运算习题第3套一．选择题1. 计算3(25)-⨯=（） A.1000 B.－1000 C.30 D.－302. 计算2223(23)-⨯--⨯=( )A.0B.－54C.－72D.－183. 计算11(5)()555⨯-÷-⨯=A.1B.25C.－5D.354. 下列式子中正确的是（） A.4232(2)(2)-<-<- B. 342(2)2(2)-<-<- C. 4322(2)(2)-<-<-D. 234(2)(3)2-<-<-5. 422(2)-÷-的结果是（） A.4B.－4C.2D.－26. 如果210,(3)0a b -=+=，那么1ba +的值是（）A.－2B.－3C.－4D.4二.填空题1.有理数的运算顺序是先算，再算，最算；如果有括号，那么先算。

有理数的混合运算专项训练(100题)(举一反三)(解析版)

专题2.13 有理数的混合运算专项训练（100题）参考答案与试题解析一．解答题（共25小题，满分100分，每小题4分）1．（4分）（2021春•道里区期末）计算：（1）12﹣（﹣18）+（﹣7）﹣15；（2）(−134)×(−112)÷(−214)；（3）76÷(16−13)×314÷35；（4）﹣12×（﹣5）÷[（﹣3）2+2×（﹣5）]．【解题思路】（1）原式利用减法法则变形，计算即可求出值；（2）原式从左到右依次计算即可求出值；（3）原式先计算括号中的减法运算，再计算乘除运算即可求出值；（4）原式先计算乘方运算，再计算乘除运算即可求出值．【解答过程】解：（1）原式＝12+18﹣7﹣15＝30﹣22＝8；（2）原式=−74×32×49=−76；（3）原式=76÷（−16）×314×53=76×（﹣6）×314×53=−52；（4）原式＝﹣1×（﹣5）÷（9﹣10）＝﹣1×（﹣5）÷（﹣1）＝5÷（﹣1）＝﹣5．2．（4分）（2021春•杨浦区校级期中）计算：（1）（﹣413）﹣（﹣212）+（﹣923）+3.5；（2）（﹣1）÷（0.75）×（﹣113）÷3×（﹣0.5）2；（3）（﹣3）2﹣（112）3×39−6÷23；（4）（12−3+56−712）×（﹣62）．【解题思路】（1）根据有理数的加减法可以解答本题；（2）根据有理数的乘方、有理数的乘除法可以解答本题；（3）根据有理数的乘方、有理数的乘除法和减法可以解答本题；（4）根据有理数的乘方、乘法分配律可以解答本题．【解答过程】解：（1）（﹣413）﹣（﹣212）+（﹣923）+3.5＝（﹣413）+212+（﹣923）+3.5＝[（﹣413）+（﹣923）]+（212+3.5）＝（﹣14）+6＝﹣8；（2）（﹣1）÷（0.75）×（﹣113）÷3×（﹣0.5）2＝（﹣1）×43×（−43）×13×14＝1×43×43×13×14=427；（3）（﹣3）2﹣（112）3×39−6÷23＝9−278×39−6×32＝9−98−9=−98；（4）（12−3+56−712）×（﹣62）＝（12−3+56−712）×（﹣36）=12×（﹣36）﹣3×（﹣36）+56×（﹣36）−712×（﹣36）＝（﹣18）+108+（﹣30）+21＝81．3．（4分）（2020秋•卫辉市期末）计算：（1）|3﹣8|﹣|14|+（−34）；（2）（﹣1）2021+2×（−13）2÷16；（3）123×（0.5−23）÷119；（4）（﹣48）×[（−12）−58+712]．【解题思路】（1）先计算绝对值，再计算加减即可；（2）先计算乘方、除法转化为乘法，再计算乘法，最后计算加减即可；（3）先计算括号内减法、将除法转化为乘法，再计算乘法即可；（4）利用乘法的交换律计算即可．【解答过程】解：（1）原式＝5−14−34＝5﹣1＝4；（2）原式＝﹣1+2×19×6＝﹣1+43=13；（3）原式=53×（−16）×910=−14；（4）原式＝（﹣48）×（−12）﹣（﹣48）×58+（﹣48）×712＝24+30﹣28＝26．4．（4分）（2020秋•门头沟区期末）计算：（1）（+4）×（+3）÷（−32）；（2）（+10）﹣（+1）+（﹣2）﹣（﹣5）；（3）（﹣24）×（23−58+12）；（4）﹣12+（﹣6）×（−12）﹣8÷（﹣2）3．【解题思路】（1）先计算乘法、将除法转化为乘法，再计算乘法即可；（2）减法转化为加法，再进一步计算即可；（3）利用乘法分配律展开，再进一步计算即可；（4）根据有理数的混合运算顺序和运算法则计算即可．【解答过程】解：（1）原式＝12×（−23）＝﹣8；（2）原式＝10﹣1﹣2+5＝12；（3）原式＝（﹣24）×23−（﹣24）×58+（﹣24）×12＝﹣16+15﹣12＝﹣13；（4）原式＝﹣1+3﹣8÷（﹣8）＝﹣1+3+1＝3．5．（4分）（2020秋•西城区期末）计算：（1）13+（﹣24）﹣25﹣（﹣20）；（2）25÷5×（−15）÷（−34）；（3）（−79+56−34）×（﹣36）；（4）﹣14﹣（1﹣0.5）×13×|1﹣（﹣5）2|．【解题思路】（1）原式利用减法法则变形，计算即可求出值；（2）原式从左到右依次计算即可求出值；（3）原式利用乘法分配律计算即可求出值；（4）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可求出值．【解答过程】解：（1）原式＝13﹣24﹣25+20＝﹣16；（2）原式＝25×15×15×43=43；（3）原式=−79×（﹣36）+56×（﹣36）−34×（﹣36）＝28﹣30+27＝25；（4）原式＝﹣1﹣0.5×13×24＝﹣1﹣4＝﹣5．6．（4分）（2020秋•呼和浩特期末）计算、求解：（1）（﹣8）×（12−114+18）；（2）16×（﹣6）÷（−17）×7；（3）（﹣2）3÷45+113×|1﹣（﹣4）2|；（4）﹣12﹣（12−23）÷13×[﹣2+（﹣3）2]．【解题思路】（1）原式利用乘法分配律计算即可求出值；（2）原式从左到右依次计算即可求出值；（3）原式先计算乘方及绝对值运算，再计算乘除运算，最后算加减运算即可求出值；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值．【解答过程】解：（1）原式＝﹣8×12+8×54−8×18＝﹣4+10﹣1＝5；（2）原式＝﹣1×（﹣7）×7＝49；（3）原式＝﹣8×54+43×|1﹣16|＝﹣10+43×15＝﹣10+20＝10；（4）原式＝﹣1+16×3×（﹣2+9）＝﹣1+12×7＝﹣1+7 2=52．7．（4分）（2020秋•金塔县期末）计算：（1）﹣28+（﹣13）﹣（﹣21）+13；（2）16÷（﹣2）3﹣4×（−1 8）；（3）(512+23−34)×(−12)；（4）2×（﹣3）2﹣33﹣6÷（﹣2）．【解题思路】（1）从左向右依次计算，求出算式的值是多少即可．（2）首先计算乘方，然后计算乘法、除法，最后计算减法，求出算式的值是多少即可．（3）应用乘法分配律，求出算式的值是多少即可．（4）首先计算乘方，然后计算乘法、除法，最后从左向右依次计算，求出算式的值是多少即可．【解答过程】解：（1）﹣28+（﹣13）﹣（﹣21）+13＝﹣41+21+13＝﹣20+13＝﹣7．（2）16÷（﹣2）3﹣4×（−1 8）＝16÷（﹣8）+1 2＝﹣2+1 2=−32．（3）(512+23−34)×(−12)=512×（﹣12）+23×（﹣12）−34×（﹣12）＝﹣5﹣8+9＝﹣4．（4）2×（﹣3）2﹣33﹣6÷（﹣2）＝18﹣27+3＝﹣9+3＝﹣6．8．（4分）（2020秋•二道区期末）计算：（1）（﹣15）﹣（﹣25）；（2）|﹣7.5|﹣|−12|；（3）（−34+712−58）×（﹣24）；（4）﹣991315×15．【解题思路】（1）先把减法转化为加法，然后根据有理数的加法即可解答本题；（2）先去掉绝对值，然后根据有理数的减法可以解答本题；（3）根据乘法分配律可以解答本题；（4）根据乘法分配律可以解答本题．【解答过程】解：（1）（﹣15）﹣（﹣25）＝（﹣15）+25＝10；（2）|﹣7.5|﹣|−12|＝7.5﹣0.5＝7；（3）（−34+712−58）×（﹣24）=−34×（﹣24）+712×（﹣24）−58×（﹣24）＝18+（﹣14）+15＝19；（4）﹣991315×15＝（﹣100+215）×15＝﹣100×15+215×15＝﹣1498．9．（4分）（2020秋•虎林市期末）计算：（1）（﹣8）+（+9）﹣（﹣5）+（﹣3）；（2）（23+49−56）×18；（3）（23−12）÷（−76）×145；（4）﹣42+（﹣20）÷（﹣5）﹣6×（﹣2）3．【解题思路】（1）原式利用减法法则变形，计算即可求出值；（2）原式利用乘法分配律计算即可求出值；（3）原式先计算括号中的运算，再计算乘除运算即可求出值；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值．【解答过程】解：（1）原式＝﹣8+9+5﹣3＝1+2＝3；（2）原式=23×18+49×18−56×18＝12+8﹣15＝5；（3）原式=16×（−67）×145=−25；（4）原式＝﹣16+4﹣6×（﹣8）＝﹣16+4+48＝36．10．（4分）（2020秋•北碚区期末）计算下列各题（1）（﹣2）3﹣|2﹣5|﹣（﹣15）；（2）（−12+56−38+512）÷（−124）；（3）﹣32﹣[（112）3×（−29）﹣6÷|−23|]；（4）2×（﹣137）﹣234×13+（﹣137）×5+14×（﹣13）．【解题思路】（1）根据有理数的乘方、有理数的加减法可以解答本题；（2）先把除法转化为乘法，然后根据乘法分配律可以解答本题；（3）根据有理数的乘方、有理数的乘除法和减法可以解答本题；（4）根据乘法分配律可以解答本题．【解答过程】解：（1）（﹣2）3﹣|2﹣5|﹣（﹣15）＝（﹣8）﹣3+15＝（﹣8）+（﹣3）+15＝4；（2）（−12+56−38+512）÷（−124）＝（−12+56−38+512）×（﹣24）=−12×（﹣24）+56×（﹣24）−38×（﹣24）+512×（﹣24）＝12+（﹣20）+9+（﹣10）＝﹣9；（3）﹣32﹣[（112）3×（−29）﹣6÷|−23|]＝﹣9﹣[（32）3×（−29）﹣6÷23]＝﹣9﹣[278×（−29）﹣6×32]＝﹣9﹣（−34−9）＝﹣9+34+9=34；（4）2×（﹣137）﹣234×13+（﹣137）×5+14×（﹣13）＝（2+5）×（﹣137）+[（﹣234）+（−14）]×13＝7×（−107）+（﹣3）×13＝（﹣10）+（﹣39）＝﹣49．11．（4分）（2020秋•南山区校级期中）计算题（1）12﹣（﹣18）+（﹣7）+（﹣12）；（2）（﹣18）×（12−19+16）；（3）16÷|﹣2|3﹣|﹣8|×（−14）；（4）﹣12﹣（﹣10）÷12×2+（﹣4）2．【解题思路】（1）先把减法转化为加法，然后根据有理数的加法法则计算即可；（2）根据乘法分配律可以解答本题；（3）根据有理数的乘方、有理数的乘除法和减法可以解答本题；（4）根据有理数的乘方、有理数的乘除法和加减法可以解答本题．【解答过程】解：（1）12﹣（﹣18）+（﹣7）+（﹣12）＝12+18+（﹣7）+（﹣12）＝[12+（﹣12）]+[18+（﹣7）]＝0+11＝11；（2）（﹣18）×（12−19+16）＝（﹣18）×12−（﹣18）×19+（﹣18）×16＝（﹣9）+2+（﹣3）＝﹣10；（3）16÷|﹣2|3﹣|﹣8|×（−14）＝16÷8﹣8×（−14）＝2+2＝4；（4）﹣12﹣（﹣10）÷12×2+（﹣4）2＝﹣1﹣（﹣10）×2×2+16＝﹣1+40+16＝55．12．（4分）（2020秋•定陶区期中）计算：（1）23﹣6×（﹣3）+2×（﹣4）；（2）（﹣134）﹣（+613）﹣2.25+103；（3）214×（−67）÷（12−2）；（4）（﹣5）3×（−35）+32÷（﹣22）×（﹣114）．【解题思路】（1）根据有理数的乘法和加减法可以解答本题；（2）根据有理数的加减法可以解答本题；（3）根据有理数的乘除法和减法可以解答本题；（4）根据有理数的乘方、有理数的乘除法和加法可以解答本题．【解答过程】解：（1）23﹣6×（﹣3）+2×（﹣4）＝23+18+（﹣8）＝33；（2）（﹣134）﹣（+613）﹣2.25+103＝（﹣134）+（﹣613）+（﹣214）+313＝[（﹣134）+（﹣214）]+[（﹣613）+313]＝（﹣4）+（﹣3）＝﹣7；（3）214×（−67）÷（12−2）=94×（−67）÷（−32）=94×67×23=97；（4）（﹣5）3×（−35）+32÷（﹣22）×（﹣114）＝（﹣125）×（−35）+32÷（﹣4）×（−54）＝75+（﹣8）×（−54）＝75+10＝85．13．（4分）（2020秋•武昌区校级月考）计算：（1）(−813)+(+412)−123；（2）（﹣32）÷（﹣4）﹣（﹣25）×4；（3）(−214)÷412×(−118)÷(−98)；（4）[1124−(38+16−34)×24]÷(−5)．【解题思路】（1）根据有理数加减法则进行计算，即可得出答案；（2）根据有理数混合运算法则：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算，进行计算即可得出答案．（3）解法同（2）；（4）解法同（2）．【解答过程】解：（1）(−813)+(+412)−123=−253+92−53 ＝﹣10+92=−112；（2）（﹣32）÷（﹣4）﹣（﹣25）×4＝8﹣（﹣100）＝8+100＝108；（3）(−214)÷412×(−118)÷(−98)=−94÷92×(−98)×(−89) =−12×1 =−12；（4）[1124−(38+16−34)×24]÷(−5)＝[2524−（38×24+16×24−34×24）]÷（﹣5）＝[2524−（9+4﹣18）]÷（﹣5）＝[2524−（﹣5）]÷（﹣5）=2524×(−15)−(−5)×(−15) =−524−1 =−2924．14．（4分）（2020秋•秀洲区月考）计算下列各题：（1）﹣3﹣（﹣9）+5；（2）|−110|×（﹣5）﹣|﹣312|；（3）(−12)×(−8)+(−6)÷(−13)；（4）（﹣5）×（﹣7）+（512+23−34）×（﹣12）．【解题思路】（1）原式利用减法法则变形，计算即可求出值；（2）原式先计算绝对值运算，再计算乘法运算，最后算减法运算即可求出值；（3）原式先计算乘除运算，再计算加法运算即可求出值；（4）原式先计算乘法运算，再计算加减运算即可求出值．【解答过程】解：（1）原式＝﹣3+9+5＝﹣3+14＝11；（2）原式=110×（﹣5）﹣312=−12−312＝﹣4；（3）原式=12×8+6×3＝4+18＝22；（4）原式＝5×7+512×（﹣12）+23×（﹣12）−34×（﹣12）＝35﹣5﹣8+9＝31．15．（4分）（2020秋•新都区校级月考）（1）（−52）÷（﹣15）×（−115）；（2）﹣745×（﹣856）﹣（﹣7.8）×（﹣434）−4912÷539；（3）（﹣2）3×（﹣1）4﹣|﹣12|÷[﹣（−12）2]；（4）（﹣24）×（18−13+14）+（﹣2）3．【解题思路】（1）直接利用有理数的混合运算法则计算得出答案；（2）直接利用乘法分配律计算得出答案；（3）直接利用有理数的混合运算法则计算得出答案；（4）直接利用乘法分配律计算得出答案．【解答过程】解：（1）（−52）÷（﹣15）×（−115）=52×115×（−115）=−190；（2）﹣745×（﹣856）﹣（﹣7.8）×（﹣434）−4912÷539＝﹣7.8×（﹣856）﹣（﹣7.8）×（﹣434）−4912×7.8＝7.8×（856−434−4112）＝7.8×（81012−4912−4112）＝7.8×0＝0；（3）（﹣2）3×（﹣1）4﹣|﹣12|÷[﹣（−12）2]＝﹣8﹣12×（−14）＝﹣8+3＝﹣5；（4）（﹣24）×（18−13+14）+（﹣2）3＝﹣24×18+（﹣24）×（−13）+（﹣24）×14−8＝﹣3+8﹣6﹣8＝﹣9．16．（4分）（2020秋•侯马市期中）计算：（1）﹣3.5÷78×（−34）；（2）﹣124849×7；（3）25×34−（﹣25）×12+25×（−14）；（4）﹣32﹣3×22﹣（﹣3×2）3．【解题思路】（1）原式从左到右依次计算即可求值；（2）原式变形后，利用乘法分配律计算即可求出值；（3）原式逆用乘法分配律计算即可求出值；（4）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可求出值．【解答过程】解：（1）原式=−72×87×（−34）=72×87×34＝3；（2）原式＝（﹣13+149）×7＝﹣91+17＝﹣9067；（3）原式＝25×（34+12−14）＝25×1＝25；（4）原式＝﹣9﹣3×4﹣（﹣6）3＝﹣9﹣12+216＝195．17．（4分）（2020秋•沈北新区期中）计算：（1）[115+（−56）﹣（−712）]×（﹣60）；（2）﹣22÷49×（−23）2；（3）﹣1﹣（1﹣0.5）×13×[2﹣（﹣3）2]；（4）﹣32﹣（﹣2﹣5）2﹣|−14|×（﹣2）4．【解题思路】（1）利用乘法分配律计算即可；（2）先计算乘方，将除法转化为乘法，再进一步计算即可；（3）根据有理数的混合运算顺序和运算法则计算即可；（4）根据有理数的混合运算顺序和运算法则计算即可．【解答过程】解：（1）原式=(115−56+712)×(−60)=−4+50﹣35＝11；（2）原式=−4×94×49=−4；（3）原式=−1+76×(−7)=−1+76=16；（4）原式=−9−49−14×16=−58−4=−62．18．（4分）（2020秋•资中县期中）计算下列各题：（1）23﹣17﹣（﹣7）+（﹣16）．（2）（﹣20）×（﹣1）9﹣0÷（﹣4）．（3）（﹣36）×（−49+56−712）．（4）﹣22﹣（﹣2）2﹣（﹣3）2×（−23）﹣42÷|﹣4|．【解题思路】（1）根据有理数的加减法可以解答本题；（2）根据有理数的乘方、有理数的乘除法和减法可以解答本题；（3）根据乘法分配律可以解答本题；（4）根据有理数的乘方、有理数的乘除法和减法可以解答本题．【解答过程】解：（1）23﹣17﹣（﹣7）+（﹣16）＝23+（﹣17）+7+（﹣16）＝（23+7）+[（﹣17）+（﹣16）]＝30+（﹣33）＝﹣3；（2）（﹣20）×（﹣1）9﹣0÷（﹣4）＝（﹣20）×（﹣1）﹣0＝20﹣0＝20；（3）（﹣36）×（−49+56−712）＝（﹣36）×（−49）+（﹣36）×56+（﹣36）×（−712）＝16+（﹣30）+21＝7；（4）﹣22﹣（﹣2）2﹣（﹣3）2×（−23）﹣42÷|﹣4|＝﹣4﹣4﹣9×（−23）﹣16÷4＝﹣4﹣4+6﹣4＝﹣6．19．（4分）（2020秋•广州期中）计算：（1）12﹣（﹣18）﹣21；（2）﹣81÷（﹣214）×49÷（﹣16）；（3）（﹣7.03）×40.16+（﹣0.16）×（﹣7.03）+7.03×（﹣60）；（4）（﹣2）3﹣2×（﹣3）+|2﹣5|﹣（﹣1）2020．【解题思路】（1）从左往右计算即可求解；（2）将带分数变为假分数，除法变为乘法，再约分计算即可求解；（3）根据乘法分配律简便计算；（4）先算乘方，再算乘法，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有绝对值，要先做绝对值内的运算．【解答过程】解：（1）12﹣（﹣18）﹣21＝30﹣21＝9；（2）﹣81÷（﹣214）×49÷（﹣16）＝﹣81×（−49）×49×（−116）＝﹣1；（3）（﹣7.03）×40.16+（﹣0.16）×（﹣7.03）+7.03×（﹣60）＝7.03×（﹣40.16+0.16﹣60）＝7.03×（﹣100）＝﹣703；（4）（﹣2）3﹣2×（﹣3）+|2﹣5|﹣（﹣1）2020＝﹣8+6+3﹣1＝0．20．（4分）（2020秋•孝义市期中）计算：（1）（﹣15）+（+3）﹣（﹣5）﹣（+7）；（2）−12+23+56−34；（3）（−23）×58÷（﹣0.25）；（4）﹣12+3×（﹣2）2×（13−1）÷83．【解题思路】（1）根据有理数的加减法可以解答本题；（2）根据有理数的加减法可以解答本题；（3）根据有理数的乘除法可以解答本题；（4）根据有理数的乘方、有理数的乘除法和加减法可以解答本题．【解答过程】解：（1）（﹣15）+（+3）﹣（﹣5）﹣（+7）＝（﹣15）+3+5+（﹣7）＝[（﹣15）+（﹣7）]+（3+5）＝（﹣22）+8＝﹣14；（2）−12+23+56−34=−612+812+1012−912=14；（3）（−23）×58÷（﹣0.25）=23×58÷14=23×58×4=53；（4）﹣12+3×（﹣2）2×（13−1）÷83＝﹣1+3×4×（−23）×38＝﹣1﹣3×4×23×38＝﹣1﹣3＝﹣4．21．（4分）（2020秋•叶县期中）计算：（1）12+（﹣8）﹣（﹣7）﹣15；（2）（1+23−34）×（﹣12）；（3）|﹣5|÷（﹣127）×0.8×214；（4）﹣23÷（−12）2+9×（−13）3﹣（﹣1）2020．【解题思路】（1）根据有理数的加减法可以解答本题；（2）根据乘法分配律可以解答本题；（3）根据绝对值、有理数的乘除法可以解答本题；（4）根据有理数的乘方、有理数的乘除法和加减法可以解答本题．【解答过程】解：（1）12+（﹣8）﹣（﹣7）﹣15＝12+（﹣8）+7+（﹣15）＝（12+7）+[（﹣8）+（﹣15）]＝19+（﹣23）＝﹣4；（2）（1+23−34）×（﹣12）＝1×（﹣12）+23×（﹣12）−34×（﹣12）＝（﹣12）+（﹣8）+9＝（﹣20）+9＝﹣11；（3）|﹣5|÷（﹣127）×0.8×214＝5×（−79）×45×94＝﹣7；（4）﹣23÷（−12）2+9×（−13）3﹣（﹣1）2020＝﹣8÷14+9×（−127）﹣1＝﹣8×4+（−13）+（﹣1）＝﹣32+（−13）+（﹣1）＝﹣3313．22．（4分）（2020秋•南岸区校级月考）计算：（1）9+（﹣8）+10﹣2+（﹣9）；（2）（−35）×|﹣312|÷45÷7；（3）﹣32÷214×（−23）2+4﹣22×（−13）；（4）991225×（﹣2）+（﹣991225）×（﹣27）．【解题思路】（1）利用加法运算律，将和为0的数结合，再计算即可；（2）先化简绝对值，再算乘除法即可；（3）先算乘方，再算乘除，最后算加减即可；（4）利用分配律计算即可．【解答过程】解：（1）9+（﹣8）+10﹣2+（﹣9）＝[9+（﹣9）]+[（﹣8）+10﹣2]＝0+0＝0；（2）（−35）×|﹣312|÷45÷7＝（−35）×72×54×17=−38；（3）﹣32÷214×（−23）2+4﹣22×（−13）＝﹣9×49×49+4﹣4×（−13）=−169+4+43=329；（4）991225×（﹣2）+（﹣991225）×（﹣27）＝991225×（﹣2）+991225）×27＝991225×（﹣2+27）＝（100−1325）×25＝2500﹣13＝2487．23．（4分）（2020秋•原阳县月考）计算：（1）12﹣（﹣18）+（﹣7）﹣20；（2）6.14+(−234)−(−5.86)−(+14)；（3）(−12)×(14−16−12)−|−5|；（4）(29−14+118)÷(−136)．【解题思路】（1）根据有理数的加减法可以解答本题；（2）根据有理数的加减法可以解答本题；（3）根据乘法分配律和有理数的加减法可以解答本题；（4）先把除法转化为乘法，然后利用乘法分配律即可解答本题．【解答过程】解：（1）12﹣（﹣18）+（﹣7）﹣20＝12+18+（﹣7）+（﹣20）＝（12+18）+[（﹣7）+（﹣20）]＝30+（﹣27）＝3；（2）6.14+(−234)−(−5.86)−(+14)＝6.14+（﹣234）+5.86+（−14）＝（6.14+5.86）+[（﹣234）+（−14）]＝12+（﹣3）＝9；（3）(−12)×(14−16−12)−|−5|＝（﹣12）×14−（﹣12）×16−（﹣12）×12−5＝（﹣3）+2+6﹣5＝﹣1+6﹣5＝5﹣5＝0；（4）(29−14+118)÷(−136)＝（29−14+118）×（﹣36）=29×（﹣36）−14×（﹣36）+118×（﹣36）＝（﹣8）+9+（﹣2）＝﹣1．24．（4分）（2020秋•临汾月考）计算：（1）﹣（﹣2.5）+（+2.2）﹣3.1+（﹣0.5）﹣（+1.1）；（2）﹣0.5﹣314+(−2.75)+712；（3）(−34−56+78)×(−24)；（4）(−8)×(−1137)+(−7)×(−1137)+(−15)×1137．【解题思路】（1）直接根据有理数的加减运算法则即可；（2）先把小数化成分数，然后根据交换律和结合律进行简便运算；（3）利用乘法的分配律进行简便运算；（4）提取公因式进行简便运算．【解答过程】解：（1）原式＝2.5+2.2﹣3.1﹣0.5﹣1.1＝4.7﹣4.7＝0；（2）原式=−12+712−（314+234）＝7﹣6＝1；（3）原式=−34×（﹣24）−56×（﹣24）+78×（﹣24）＝18+20﹣21＝17；（4）原式＝（﹣8﹣7+15）×（﹣1137）＝0．25．（4分）（2020秋•立山区期中）计算题（1）﹣81÷（﹣214）×49÷（﹣16）；（2）（−124）÷（123−54+76）；（3）﹣32÷（﹣2）3×|﹣113|×6+（﹣2）4；（4）﹣（23）2×18﹣2×（−15）÷25+|﹣8|×0.52+179×（﹣112）2．【解题思路】（1）原式从左到右依次计算即可求出值；（2）原式被除式与除式调换求出值，即可求出所求；（3）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值．【解答过程】解：（1）原式＝﹣81×49×49×116＝﹣1；（2）（123−54+76）÷（−124）＝（123−54+76）×（﹣24）=53×（﹣24）−54×（﹣24）+76×（﹣24）＝﹣40+30﹣28＝﹣38，则原式=−1 38；（3）原式＝﹣9÷（﹣8）×43×6+16=98×43×6+16＝9+16＝25；（4）原式=−49×18﹣2×（−15）×52+8×0.25+169×94＝﹣8+1+2+4＝﹣1．。

有理数加减混合计算题100道【含答案】

有理数加减混合计算题100道【含答案】(七年级数学)92267(总4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--有理数运算练习（一）【加减混合运算】一、有理数加法.1、【基础题】计算：（1） 2＋（－3）；（2）（－5）＋（－8）；（3）6＋（－4）；（4）5＋（－5）；（5）0＋（－2）；（6）（－10）＋（－1）；（7）180＋（－10）；（8）（－23）＋9；（9）（－25）＋（－7）；（10）（－13）＋5；（11）（－23）＋0；（12）45＋（－45）.2、【基础题】计算：（1）（－8）＋（－9）；（2）（－17）＋21；（3）（－12）＋25；（4）45＋（－23）；（5）（－45）＋23；（6）（－29）＋（－31）；（7）（－39）＋（－45）；（8）（－28）＋37.3、【基础题】计算，能简便的要用简便算法：（1）（－25）＋34＋156＋（－65）；（2）（－64）＋17＋（－23）＋68；（3）（－42）＋57＋（－84）＋（－23）；（4）63＋72＋（－96）＋（－37）；（5）（－301）＋125＋301＋（－75）；（6）（－52）＋24＋（－74）＋12；（7）41＋（－23）＋（－31）＋0；（8）（－26）＋52＋16＋（－72）.4、【综合Ⅰ】计算：（1）)43(31-+；（2）⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-3121；（3）()⎪⎭⎫⎝⎛++-5112.1；（4）)432()413(-+-；（5）)752()723(-+；（6）（—152）＋8.0；（7）（—561）＋0；（8）314+（—561）.5、【综合Ⅰ】计算：（1）)127()65()411()310(-++-+；（2）75.9)219()29()5.0(+-++-；（3）)539()518()23()52()21(++++-+-；（4）)37(75.0)27()43()34()5.3(-++++-+-+-二、有理数减法.6、【基础题】计算：（1）9－（－5）；（2）（－3）－1；（3）0－8；（4）（－5）－0；（5）3－5；（6）3－（－5）；（7）（－3）－5 （8）（－3）－（－5）；（9）（－6）－（－6）；（10）（－6）－6.、【综合Ⅰ】计算：（1）（－52）－（－53）；（2）（－1）－211；（3）（－32）－52；（4）521－（－7.2）；（5）0－（－74）；（6）（－21）－（－21）；（7）525413－；（8）－64－丨－64丨7、【基础题】填空：（1）（－7）＋（）＝21；（2）31＋（）＝－85；（3）（）－（－21）＝37；（4）（）－56＝－408、【基础题】计算：（1）（－72）－（－37）－（－22）－17；（2）（－16）－（－12）－24－（－18）；（3）23－（－76）－36－（－105）；（4）（－32）－（－27）－（－72）－87.（5）（－32）－21－（－65）－（－31）；（6）（－2112）－[ －－（－）－516 ] .三、有理数加减混合运算9、【综合Ⅰ】计算（1）－7＋13－6＋20；（2）－＋－＋10；（3）（－53）＋51－54；（4）（－5）－（－21）＋7－37；（5）31＋（－65）－（－21）－32；（6）－41＋65＋32－21；10、【综合Ⅰ】计算，能简便的要用简便算法：（1）－＋（－）；（2）（－）－21＋（－51）；（3）21－（－）－61；（4）（－31）－15＋（－32）；（5）32＋（－51）－1＋31；（6）（－12）－（－56）＋（－8）－10711、【综合Ⅰ】计算：（1）－（－）＋（－）；（2）（－8）－（－15）＋（－9）－（－12）；（3）＋（－41）－（－）＋21；（4）（－32）＋（－61）－（－41）－21；（5）21＋（－32）－（－54）＋（－21）；（6）310＋（－411）－（－65）＋（－127）12、【综合Ⅰ】计算：（1）7＋（－2）－；（2）（－）＋3－＋（－52）；（3）31＋（－45）＋；（4）7－（－21）＋；（5）49－（－）－53；（6）（－56）－7－（－）＋（－1）；（7）11512＋丨－11611丨－（－53）＋丨212丨；（8）（- ）+ 1098 + +（- 1098）13、【综合Ⅰ】计算：（1）()()()()-+-+++-+-++12345678；（2）－＋＋＋（－）（3）-⎛⎝ ⎫⎭⎪--⎛⎝ ⎫⎭⎪++-⎛⎝ ⎫⎭⎪13123423；（4）5146162341456+-⎛⎝ ⎫⎭⎪++-⎛⎝ ⎫⎭⎪；（5）－－（－413）＋－（＋217）；（6）3745124139257526+-+有理数运算练习（一）答案1、【答案】（1）－1；（2）－13；（3）2；（4）0；（5）－2；（6）－11；（7）170；（8）－14；（9）－32；（10）－8；（11）－23；（12）0.2、【答案】（1）－17；（2）4；（3）13；（4）22；（5）－22；（6）－60；（7）－84；（8）9.3、【答案】（1）100；（2）－2；（3）－92；（4）2；（5）50；（6）－90；（7）－13；（8）－30.4、【答案】（1）125－；（2）65-；（3）0；（4）－6；（5）74；（6）32；（7）615-；（8）65-.5、【答案】（1）65 （2）（3）12 （4）311-6、【答案】（1）14；（2）－4；（3）－8；（4）－5；（5）－2；（6）8；（7）－8；（8）2；（9）0；（10）－12、【答案】（1）51；（2）－25；（3）－1516；（4）；（5）74；（6）0；（7）－2043（8）－1287、【答案】（1）28；（2）－116；（3）16；（4）168、【答案】（1）－30；（2）－10；（3）168；（4）－20；（5）0；（6）－或－1016 9、【答案】（1）20；（2）；（3）－56；（4）61；（5）－32；（6）4310、【答案】（1）－7；（2）－；（3）127；（4）－16；（5）－51；（6）－23911、【答案】（1）；（2）10；（3）27；（4）－1213；（5）152；（6）65；12、【答案】（1）；（2）－；（3）30；（4）9；（5）69；（6）－6；（7）；（8）013、【答案】（1）8；（2）－3；（3）41；（4）－13；（5）－2；（6）902313。

有理数加减混合计算题100道含答案(七年级数学)

有理数运算练习（一）【加减混合运算】一、有理数加法.1、【基础题】计算：（1）2＋（－3）；（2）（－5）＋（－8）；（3）6＋（－4）；（4）5＋（－5）；（5）0＋（－2）；（6）（－10）＋（－1）；（7）180＋（－10）；（8）（－23）＋9；（9）（－25）＋（－7）；（10）（－13）＋5；（11）（－23）＋0；（12）45＋（－45）.2、【基础题】计算：（1）（－8）＋（－9）；（2）（－17）＋21；（3）（－12）＋25；（4）45＋（－23）；（5）（－45）＋23；（6）（－29）＋（－31）；（7）（－39）＋（－45）；（8）（－28）＋37.3、【基础题】计算，能简便的要用简便算法：（1）（－25）＋34＋156＋（－65）；（2）（－64）＋17＋（－23）＋68；（3）（－42）＋57＋（－84）＋（－23）；（4）63＋72＋（－96）＋（－37）；（5）（－301）＋125＋301＋（－75）；（6）（－52）＋24＋（－74）＋12；（7）41＋（－23）＋（－31）＋0；（8）（－26）＋52＋16＋（－72）.4、【综合Ⅰ】计算：（1）)43(31-+；（2）⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-3121；（3）()⎪⎭⎫⎝⎛++-5112.1；（4）)432()413(-+-；（5）)752()723(-+；（6）（—152）＋8.0；（7）（—561）＋0；（8）314+（—561）.5、【综合Ⅰ】计算：（1）)127()65()411()310(-++-+；（2）75.9)219()29()5.0(+-++-；（3）)539()518()23()52()21(++++-+-；（4）)37(75.0)27()43()34()5.3(-++++-+-+-二、有理数减法.【基础题】计算：（1）9－（－5）；（2）（－3）－1；（3）0－8；（4）（－5）－0；（5）3－5；（6）3－（－5）；（7）（－3）－5 （8）（－3）－（－5）；（9）（－6）－（－6）；（10）（－6）－6.【综合Ⅰ】计算：（1）（－52）－（－53）；（2）（－1）－211；（3）（－32）－52；（4）521－（－7.2）；（5）0－（－74）；（6）（－21）－（－21）；（7）525413－；（8）－64－丨－64丨【基础题】填空：（1）（－7）＋（）＝21；（2）31＋（）＝－85；（3）（）－（－21）＝37；（4）（）－56＝－40 8、【基础题】计算：（1）（－72）－（－37）－（－22）－17；（2）（－16）－（－12）－24－（－18）；（3）23－（－76）－36－（－105）；（4）（－32）－（－27）－（－72）－87.（5）（－32）－21－（－65）－（－31）；（6）（－2112）－[ －6.5－（－6.3）－516 ] .三、有理数加减混合运算9、【综合Ⅰ】计算（1）－7＋13－6＋20；（2）－4.2＋5.7－8.4＋10；（3）（－53）＋51－54；（4）（－5）－（－21）＋7－37；（5）31＋（－65）－（－21）－32；（6）－41＋65＋32－21；10、【综合Ⅰ】计算，能简便的要用简便算法：（1）4.7－3.4＋（－8.3）；（2）（－2.5）－21＋（－51）；（3）21－（－0.25）－61；（4）（－31）－15＋（－32）；（5）32＋（－51）－1＋31；（6）（－12）－（－56）＋（－8）－10711、【综合Ⅰ】计算：（1）33.1－（－22.9）＋（－10.5）；（2）（－8）－（－15）＋（－9）－（－12）；（3）0.5＋（－41）－（－2.75）＋21；（4）（－32）＋（－61）－（－41）－21；（5）21＋（－32）－（－54）＋（－21）；（6）310＋（－411）－（－65）＋（－127）12、【综合Ⅰ】计算：（1）7＋（－2）－3.4；（2）（－21.6）＋3－7.4＋（－52）；（3）31＋（－45）＋0.25；（4）7－（－21）＋1.5；（5）49－（－20.6）－53；（6）（－56）－7－（－3.2）＋（－1）；（7）11512＋丨－11611丨－（－53）＋丨212丨；（8）（- 9.9）+ 1098 + 9.9 +（- 1098） 13、【综合Ⅰ】计算：（1）()()()()-+-+++-+-++12345678；（2）－0.5＋1.75＋3.25＋（－7.5）（3）-⎛⎝ ⎫⎭⎪--⎛⎝ ⎫⎭⎪++-⎛⎝ ⎫⎭⎪13123423；（4）5146162341456+-⎛⎝ ⎫⎭⎪++-⎛⎝ ⎫⎭⎪；（5）－0.5－（－413）＋2.75－（＋217）；（6）3745124139257526+-+有理数运算练习（一）答案1、【答案】（1）－1；（2）－13；（3）2；（4）0；（5）－2；（6）－11；（7）170；（8）－14；（9）－32；（10）－8；（11）－23；（12）0.2、【答案】（1）－17；（2）4；（3）13；（4）22；（5）－22；（6）－60；（7）－84；（8）9.3、【答案】（1）100；（2）－2；（3）－92；（4）2；（5）50；（6）－90；（7）－13；（8）－30. 4、【答案】（1）125－；（2）65-；（3）0；（4）－6；（5）74；（6）32；（7）615-；（8）65-.5、【答案】（1）65 （2）4.25 （3）12 （4）311-6、【答案】（1）14；（2）－4；（3）－8；（4）－5；（5）－2；（6）8；（7）－8；（8）2；（9）0；（10）－126.1、【答案】（1）51；（2）－25；（3）－1516；（4）4.1；（5）74；（6）0；（7）－2043（8）－128 7、【答案】（1）28；（2）－116；（3）16；（4）168、【答案】（1）－30；（2）－10；（3）168；（4）－20；（5）0；（6）－6.1或－10169、【答案】（1）20；（2）3.1；（3）－56；（4）61；（5）－32；（6）4310、【答案】（1）－7；（2）－3.2；（3）127；（4）－16；（5）－51；（6）－23911、【答案】（1）45.5；（2）10；（3）27；（4）－1213；（5）152；（6）65； 12、【答案】（1）1.6；（2）－26.4；（3）30；（4）9；（5）69；（6）－6；（7）27.1；（8）013、【答案】（1）8；（2）－3；（3）41；（4）－13；（5）－2；（6）902313（注：文档可能无法思考全面，请浏览后下载，供参考。

有理数混合运算习题(含答案)300道

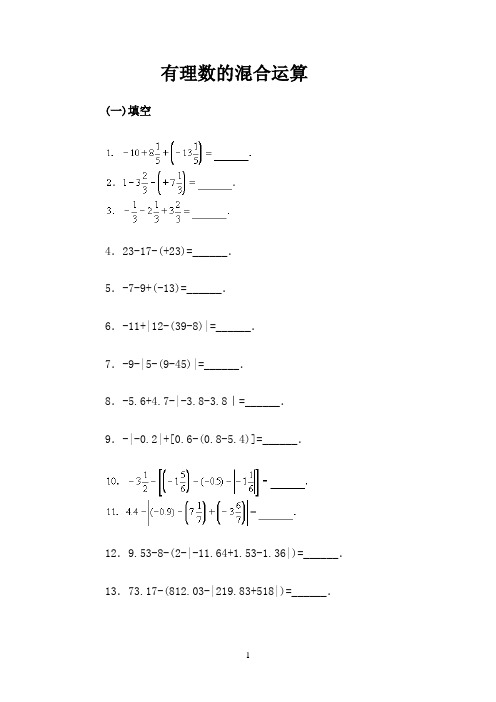
有理数的混合运算(一)填空4．23-17-(+23)=______．5．-7-9+(-13)=______．6．-11+|12-(39-8)|=______．7．-9-|5-(9-45)|=______．8．-5.6+4.7-|-3.8-3.8｜=______．9．-|-0.2|+[0.6-(0.8-5.4)]=______．12．9.53-8-(2-|-11.64+1.53-1.36|)=______．13．73.17-(812.03-|219.83+518|)=______．36．38×(-7)+5[(-2)3(-32)-(-22)]-38×339÷(-3)38=______．48．(-2)×{(-3)×[(-5)+2×(0.3-0.3)÷83-3]+4}=______．112．413-74-(-5+26)．116．-84-(16-3)+7．118．-0.182+3.105-(0.318-6.065)．119．-2.9+[1.7-(7+3.7-2.1)]．121．34.23-[194.6-(5.77-5.4)]．125．23.6+[3.9-(17.8-4.8+15.4)]．134．(-3)2÷2.5．135．(-2.52)×(-4)．136．(-32)÷(-2)2．173．(-1)2×5+(-1)×52-12×5+(-1×5)2．174．(-2)(-3)(-36)+(-1)20×63．178．(-32)÷(3×2)×(-3-2)．180．3×(-2)2+(-2×3)2+(-2+3)2．188．2+42×(-8)×16÷32．190．[5.78+3.51-(0.7)2]÷(0.2)3×11．191．(1.25)4÷(0.125)4×0.0036-(0.6)2．194．(-42×26+132×2)÷(-3)7×(-3)5．195．(3-9)4×23×(-0.125)2．201．741×[(-30)2-(-402)]3÷(1250)2．211．[(-5)3+3.4×2-2×4+53]2．213．(24-5.1×3-3×5+33)2．234．(-5)×(-3)×(-4)2+(-2)3×(-8)×(-3)-(-12)×3÷24．240．-18-23×[(-4)3÷(-43)+0.2×8+(-3)2÷(-32)]．(四)用符号“＞”，“＜”，“≥”，“≤”，“=”之一填空241．当两个数和的绝对值______这两个数差的绝对值时，这两个数同号．242．一个正数与一个负数差的绝对值______这两个数绝对值的和．243．一个正数与一个负数和的绝对值______这两个数绝对值的差．244．一个正数与一个负数差的绝对值______这两个数绝对值的差．245．一个正数与一个负数和的绝对值______这两个数绝对值的和．246．当两个数和的绝对值______这两个数差的绝对值时，这两个数异号．247．当两数和的绝对值______这两个数差的绝对值时，这两个数至少有一个是零．248．当两数和的绝对值______这两个数的绝对值之和时，这两个数可以是任意的有理数．249．当两数差的绝对值______这两个数的绝对值之和时，这两个数可以是任意的有理数．250．当两个数和的绝对值______这两个数绝对值的差时，这两个数可以是任意的有理数．251．当两个数差的绝对值______这两个数绝对值的差时，这两个数可以是任意的有理数．252．欲使两个数的绝对值的和等于这两个数的和的绝对值，这两个数必须是怎样的数？253．欲使两个数和的绝对值不小于这两个数的差的绝对值，这两个数必须是怎样的数？254．欲使两数和的绝对值不大于这两数差的绝对值，这两个数必须是怎样的数？255．欲使两数和的绝对值不小于这两个数的绝对值的和，这两个数必须是怎样的数？256．一个盛有水的圆柱形水桶，其底面半径为1.6分米①．现将一个半径为1.2分米的铁球沉没在桶内水面下，问桶内水面升高多少分米？（列综合算式计算，球的体积公式为，其中V表示体积，R表示球的半径）257．一个盛有水的长方体状容器，它的底面是边长为2.4分米的正方形，现将一个半径是1.2分米的铁球放在容器内，正好铁球体积的1/3在水面下，问放入铁球后，水面升高了多少分米？(列综合算式计算，球的体积公式为V表示体积，R表示球的半径，π取3.14。