§10-6 电容和电容器
电容的能量电容器的能量存储与能量密度的计算

电容的能量电容器的能量存储与能量密度的计算电容的能量:电容器的能量存储与能量密度的计算电容器是一种能够存储电荷和能量的电子元件。
它由两个金属导体板(称为电极)和介质层(称为电介质)组成。
当电容器接入电路后,电荷会在电容器的两个电极板之间存储。
本文将介绍电容器能量存储的原理以及如何计算能量密度。
一、电容器能量存储的原理电容器的能量存储是基于两个关键因素:电容和电压。
1. 电容电容是电容器存储电荷的能力。
它的单位是法拉(F)。
电容的大小取决于电极板之间的距离以及电介质的介电常数。
具体而言,电容可以用以下公式表示:C = ε₀ * εᵣ * A / d其中,C表示电容,ε₀为真空中的介电常数(约为8.854 × 10⁻¹²F/m),εᵣ为电介质的相对介电常数,A为电极板的面积,d为电极板之间的距离。
2. 电压电压是电容器两个电极板之间的电势差。
它的单位是伏特(V)。
电压可以通过电源施加到电容器的两个端点,使电荷在电容器中进行移动。
二、电容器的能量存储电容器存储的能量与电荷量和电压有关。
当电容器装上电荷后,其存储的能量可以通过以下公式计算:E = 1/2 * C * V²其中,E表示电容器储存的能量,C为电容,V为电压。
三、电容器的能量密度电容器的能量密度是指单位体积内存储的能量量。
能量密度可以用以下公式计算:D =E / V其中,D表示能量密度,E为电容器储存的能量,V为电容器的体积。
通过上述公式,我们可以得出结论:能量密度随着电容器的电容和电压的增加而增加。
这意味着,选择高容量和高电压的电容器可以实现更高的能量密度,从而更有效地储存能量。
电容器的能量存储和能量密度的计算对于许多应用至关重要。
例如,电动汽车的电池就是一种电容器,能够存储大量的能量,提供电动机的动力。
此外,电容器还在电子设备、通信系统和能源储存等领域中得到广泛应用。
在实际应用中,我们需要计算电容器的能量和能量密度,以便选择合适的电容器来满足需求。
大学物理第10章 电荷和静电场-2
例如 孤立的导体球的电容
Q
Q C V
地球
Q Q 4π 0 R
4π 0 R
6
R
4
RE 6.4 10 m, CE 7 10 F
二 电容器
导体组合,使之不受周 围导体的影响 ——电容器
电容器的电容:
当电容器的两极板分
别带有等值异号电荷Q时 ,电量Q与两极板间相应 的电势差VA-VB的比值。
详细说明如下
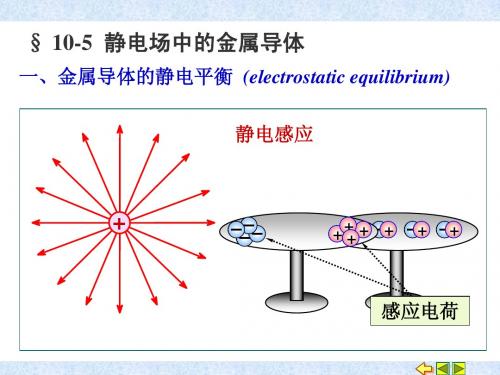
二、导体表面的电荷和电场 导体表面电荷的分布与导体本身的形状以及附近 带电体的状况等多种因素有关。
孤立导体的电荷面密度与其表面的曲率有关,曲率越大 电荷面密度越大。 表面突出尖锐部分曲率大, 电荷面密度大;
表面比较平坦部分曲率小, 电荷面密度小; 表面凹进部分曲率为负, 电荷面密度最小。
S
–q'
说明空腔内表面所带总电量与空腔内带电体的电量 相等、符号相反。导体空腔是等势体,腔内场强不 为零,不是等电势区间。
四、导体静电平衡性质的应用
1. 静电屏蔽 (electrostatic shielding)
+q +q +q
-q
-q
利用导体静电平衡的性质,使导体空腔内部空 间不受腔外电荷和电场的影响,或者将导体空腔 接地,使腔外空间免受腔内电荷和电场影响,这 类操作都称为静电屏蔽。无线电技术中有广泛应 用,例如,常把测量仪器或整个实验室用金属壳 或金属网罩起来,使测量免受外部电场的影响。
Cn
VB
等效
VA
C
VB
令 U VA VB
q1 C1U
q2 C2U
•导导体表面外附近的场强 E 0
★ 注意:
E 仅由 S 处电荷产生而与其它电荷无关吗?为什么?
电容计算方法

电容计算方法电容是电路中常见的元件,用于存储电荷和能量。
在电路设计和分析中,计算电容值是非常重要的。
本文将介绍几种常见的电容计算方法,希望能对大家有所帮助。
首先,我们来看一下最基本的电容计算方法——平行板电容的计算公式。
平行板电容的电容值可以通过以下公式来计算:C = ε0 εr A / d。
其中,C代表电容值,ε0代表真空介电常数(8.85 x 10^-12 F/m),εr代表介质的相对介电常数,A代表平行板的面积,d代表平行板的间距。
通过这个公式,我们可以很方便地计算出平行板电容的数值。
除了平行板电容,我们还有其他形式的电容,比如球形电容和圆柱形电容。
对于球形电容,其电容值可以通过以下公式计算:C = 4πε0εrR。
其中,C代表电容值,ε0代表真空介电常数,εr代表介质的相对介电常数,R代表球形电容的半径。
而对于圆柱形电容,其电容值可以通过以下公式计算:C = 2πε0εrL/ln(b/a)。
其中,C代表电容值,ε0代表真空介电常数,εr代表介质的相对介电常数,L代表圆柱形电容的长度,a和b分别代表内外半径。
除了以上介绍的几种电容计算方法,还有一种常见的方法是通过电容器的标称值来计算。
电容器的标称值是指制造商在生产电容器时标注在外壳上的电容值。
但由于电容器的实际电容值会受到环境温度、频率等因素的影响,因此在实际电路设计中,我们需要根据实际情况进行修正计算。
在实际电路设计中,我们还需要考虑电容的串联和并联问题。
对于串联电容,其总电容值可以通过以下公式计算:1/C = 1/C1 + 1/C2 + 1/C3 + ...而对于并联电容,其总电容值可以通过以下公式计算:C = C1 + C2 + C3 + ...通过以上介绍,我们可以看到,电容的计算方法有多种,我们需要根据具体的情况选择合适的计算方法。
在实际应用中,我们还需要考虑到电容器的稳定性、精度、温度特性等因素,这些都需要在电路设计中进行综合考虑。
电容器种类分类
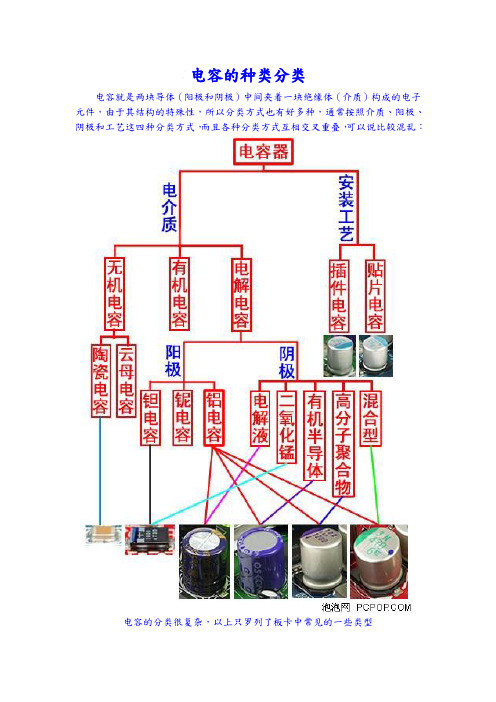
电容的种类分类电容就是两块导体(阳极和阴极)中间夹着一块绝缘体(介质)构成的电子元件,由于其结构的特殊性,所以分类方式也有好多种,通常按照介质、阳极、阴极和工艺这四种分类方式,而且各种分类方式互相交叉重叠,可以说比较混乱:电容的分类很复杂,以上只罗列了板卡中常见的一些类型开始详细介绍各类电容的特性和优缺点。
首先按照介质的不同分为无机电容、有机电容和电解电容三大类:● 无机介质电容器:无机电容主要有陶瓷电容和云母电容,其基本结构就是在陶瓷片或者云母片的两面电镀金属材料比如银,电脑配件中陶瓷电容很常见。
陶瓷电容性质非常稳定、高频性能很好、无极性、耐压、耐热、低阻抗、体积小,综合性能好因此使用非常广泛,它可以应用在GHz级别的超高频器件上,比如军用雷达、电磁干扰发射器等精密仪器,当然CPU、GPU、Chipset表面也只能使用陶瓷电容。
CPU背面、GPU表面和GPU四周PCB上的小颗粒都是陶瓷电容陶瓷电容之所以如此普及,这是因为能够在超高频率下正常工作的也只有陶瓷电容。
所以我们可以看到,在主板CPU插槽四周/背面,显卡GPU四周/背面,还有内存、显存、芯片组、PCI-E插槽等,凡是高频器件周围都会有密密麻麻的陶瓷电容!数字供电主要依靠高性能的多层陶瓷电容但是,陶瓷电容的价格比较昂贵,而且容量有限,因此不适合作为供电模块的滤波电容。
不过近年来随着技术的发展,高档数字供电主控芯片也可以使用大量多层陶瓷电容,这可以让抗干扰能力、稳定性和转换效率都得到大幅提高!薄膜电容的基本构造就是2层聚丙乙烯塑料和2层金属箔膜交替夹杂然后捆绑而成。
这种电容的介质为高分子有机物,所以统称为有机电容,其特点与陶瓷电容类似,无极性、无感、高频特性好、体积小、耐压,但也同样存在容量不大、成本较高的缺点,另外它的介质是有机物,因此耐高温能力一般。
● 电解电容器:电介质的材料除了无机物就是有机物,为什么还会单独分出一个电解电容来呢?这是因为无机电容和有机电容的绝缘材料在生产时就已确定,比如陶瓷、云母、塑料等。
物体的电容和电容器

物体的电容和电容器电容是电学中的重要概念,用来描述电路中储存电荷的能力。
在物理学和电工学中,电容常用C表示,单位是法拉(F)。
物体的电容是指物体在给定电势差下储存电荷的能力。
而电容器则是一种专门用来储存电荷的装置,我们通常使用电容器来调节电路中的电荷量和电压。
一、物体的电容物体的电容受到物体的形状、材料和尺寸等因素的影响。
根据电容的定义,物体的电容可以表示为C = Q/V,其中C为物体的电容,Q为物体上储存的电荷量,V为物体上的电势差。
1. 形状和尺寸的影响物体的形状和尺寸会对其电容产生影响。
通常情况下,平行板电容器是最常见的电容器,由两个平行的金属板组成,之间有介质或真空隔开。
平行板电容器的电容正比于平行板的面积A,反比于平行板之间的距离d,可以用公式C = ε0*A/d表示,其中ε0为真空介电常数,约为8.85×10-12 F/m。
除了平行板电容器,还有其他形状的电容器,如圆柱形电容器、球形电容器等。
这些电容器的电容计算方法略有不同,但基本原理相似,都是通过改变形状和尺寸来调节电容。
2. 材料的影响物体的材料也会对电容产生影响。
在电容器中,介质的选择对电容器的性能有很大影响。
不同介质的相对介电常数εr不同,它表示介质相对于真空的电容变化倍数。
通常,介电常数越大,电容器的电容就越大。
另外,物体的电容还与物体的导电性能有关。
导电性能好的物体,如金属,对电荷的储存能力较强,因此具有较大的电容。
相反,绝缘体(非导电体)的电容较小。
二、电容器电容器是一种专门用来储存电荷的设备,它由两个导体之间的绝缘介质隔开。
常见的电容器包括平行板电容器、电解电容器、固态电容器等。
下面主要介绍平行板电容器和电解电容器。
1. 平行板电容器平行板电容器是由两个平行的金属板和一层绝缘介质组成的。
金属板通常由导电性能好的金属材料制成,如铜或铝。
绝缘介质可以是空气、纸、陶瓷等,或者是高介电常数的材料,如聚乙烯、聚四氟乙烯等。
四、电场中的导体、电容和电容器

εS εS U 1 ∝ 而C = ,E = ∝ 4π kd d d d
U Q 4π KQ E= = = , d dC ε ⋅s
(2)充电后断开 ,保持电容器电量 恒定,这种情 充电后断开S,保持电容器电量Q恒定 恒定, 充电后断开 况下
E与d无关.
【例4】平行板电容器充电后与电源断开,负极板接 】平行板电容器充电后与电源断开, 在两极板间有一正电荷(电量很小)固定在P点 地,在两极板间有一正电荷(电量很小)固定在 点, 如图所示, 表示两极板间的电场强度, 表示电 如图所示,以E表示两极板间的电场强度,U表示电 表示两极板间的电场强度 容器两极间的电压; 表示正电荷在 点的电势. 表示正电荷在P点的电势 容器两极间的电压;W表示正电荷在 点的电势.若 保持负极板不动, 保持负极板不动,将正极板移到图中虚线所示的位 置,则( ) A.U变小,E不变; B.E变大,W变大; 变小, 不变 不变; 变大, 变大 变大; 变小 变大 C.U变小,W不变; D.U不变,W不变 变小, 不变 不变; 不变, 不变 变小 不变 由于极板间距离减小,知电容 解:由于极板间距离减小 知电容 增大; 由于极板间距离减小 知电容C 增大; 由充电后与电源断开,知带电量 不变; 知带电量Q不变 由充电后与电源断开 知带电量 不变 Q 由 U= 知: 可得极板间电压 减小. 可得极板间电压U减小 减小. CεS Q 根据 C= 和U= 知 E = U = Q = 4π KQ , 4 kπ d C d dC ε ⋅s 所以E不变 不变. 所以 不变. 因为E不变 不变, 点与负极板间的距离不变 点与负极板间的距离不变, 因为 不变,P点与负极板间的距离不变,所以 与负极板间的电压不变, 点的电势φ 可知 P与负极板间的电压不变,即 P点的电势 p不 与负极板间的电压不变 点的电势 就不变. 变,那么正电荷的电势能 W=qφp就不变. =
大学物理下PPT课件一等奖新名师优质课获奖比赛公开课

a = 0,b = , p点旳电场强度只有ya
25
§10-2 电场和电场强度
例9: 均匀带电圆环轴线上一点旳场强。设圆环带电
量为q,半径为R。
dE
x
dE//
dE⊥
r
思考
dq R
L
二分之一径为R旳半圆细环上 均匀分布电荷Q,求环心处旳场强。
26
(1)一种电荷在另一种电荷处产生旳电场强度;(2)作用 在每个电荷上旳力。
例6:有一均匀带电旳细棒,长度为L, 所带总电量为q。求: (1)细棒延长线上到棒中心旳距离为a处 旳电场强度,而且a>>L; (2)细棒中垂线上到棒中心旳距离为a处 旳电场强度,而且a>>L。
21
§10-2 电场和电场强度
3、两个带有等量同号电荷,形状相同旳金属小球A和B 相互之间旳作用力为f ,它们之间旳距离远不小于小球 本身旳直径。目前用一种带绝缘柄旳原来不带电旳相同 旳金属小球C去和小球A接触,再和B接触,然后移去, 则球A球B之间旳作用力变为
(a) f / 2 (b) f / 4 (c) 3f / 8 (d) f /10
例7:求两个相距为l,等量异号点电荷中垂线上 距离点电荷连线中心任一点Q处旳电场强度。
等量异号电荷 +q、-q ,相距为l (l<<r) ,称
该带电体系为电偶极子
E
解:建立如右图旳坐标系
E
E
1
4π 0
r2
q (l / 2)2
Q点旳场强 E 旳y分量为零, x 分量是
Q
E
E
r
E+ 和 E- 在x方向分量旳代数和:
C、q1=-Q/4;q2=5Q/4 D、q1=-Q/2;q2=3Q/2
电容器损耗角

电力电容器的损耗、损耗角正切和等值电路电力电容器是一种实际电容器、不是理想电容器,在外施交流电压的作用下,除了会输出一定容量的无功功率Q之外,在电容器的内部介质中、在电容器的极板(铝箔)中、引线等导体中,以及在瓷瓶间的漏泄电流等都会产生一定的有功损耗功率Po 通常把电容器的有功功率P与无功功率Q的比值称做为该电容器的损耗角正切,并用下式表示:tan^=P/Q (1)式中:tan §—电容器的损耗角正切(%);P—电容器的有功功率(W);Q—电容器的无功功率(var)正因为电力电容器不是理想电容器,所以通常要用一个等值电路來表示。
(1)串联等值电路在此等值电路中,理想电容器C产生的无功功率为:Qc=l^Xc(2)式中:Qc—电容器的无功功率(var):Xc—电容器C的容抗(Q);Ic-流过电容器的电流(A)而在此电路中由电阻r产生电容器的损耗功率为:F.=E・ r (3)式中:P「一由r产生的等值损耗功率匚一流经等值电阻r的电流由式(1)、(2)、(3)可得:tan^=而由图1可知=H(5>所以由式(4>、(5)可得;•tan$=r7Xc (6>由式(6)可知,当tan§值很小(例如全膜电容器),Xc也很小时(例如大容量集合式电容器),其等值串联电阻也十分微小(通常只有10一'〜10-Q) o所以在测量大容量全膜介质电容器时,一定要尽一切可能降低测量回路中的接触电阻和导线电阻,以减小测量误差。
(2)并联等值电路电力电容器除了可用图1所示的串联等值电路来表示外,也可用图2所示的并联等值电路来表示。
由图2可得:(6)QH%、(7)由式(1〉、(6)、(7)可得:tan0 = Q" = T x(7i ⑻式中:山一等值电路两端的电压(V);Uc-理想电容器两端的电压(V);Xc-电容器的容抗(Q )从图2中可知:U R=U C,所以由式(9)可以看出,对于低损耗的全膜电容器其并联等值电阻是相当大的,当在电容器内部并联放电电阻会降低其等值电阻R,从而使电容器的实际损耗和损耗角正切增大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1F(法 ) 10 µF(微 ) =10 pF(皮 ) 拉 = 法 法
6 12
1
二、电容器(capacitor) 电容器 在周围没有其它带电导体影响时, 在周围没有其它带电导体影响时,由两个导体 组成的导体体系,称为电容器 电容器。 组成的导体体系,称为电容器。 如图所示,用导体空腔B把导体 把导体A 如图所示 , 用导体空腔 把导体 包围起来, B以外的导体和电场都 包围起来 , 以外的导体和电场都 不会影响导体A以及 以及A、 之间的电 不会影响导体 以及 、 B之间的电 可以证明,导体A、 之间的电 场。可以证明,导体 、B之间的电 势差V 与导体A所带电量成正 势差 A−VB 与导体 所带电量成正 而与外界因素无关。 比,而与外界因素无关。 电容器的 电容定义为
§10-6 电容和电容器
一、孤立导体的电容 孤立导体的电容(capacity) 电容 q 定义: 定义:孤立导体的电容 C = U 孤立导体的电容只决定于导体自身的性状, 孤立导体的电容只决定于导体自身的性状,而 与所带电荷和电势无关, 与所带电荷和电势无关,它反映了孤立导体储存 电荷和电能的能力。 电荷和电能的能力。 Q 例如,半径为R 带电量为Q的孤立 例如,半径为R,带电量为Q的孤立 V= 4 πε 0 R 导体球, 导体球,其电势表示为 Q 孤立导体球的电容为 C = = 4 πε 0 R V 电容的单位: 电容的单位: 法拉) 库仑/伏特 。 称作F 法拉 库仑 称作 (法拉 或记为 C / V (库仑 伏特 )。
B
(R A > r > RB )
-Q
两球壳间的电势差为 RB E⋅ dl = ∫
Q Q 1 1 dr = ( − ) 2 RA 4π r ε0 4πε0 RA RB
Q QC = UAB
4πε0RARB ∴C = RA − RB
4
3. 圆柱形电容器(同轴电缆) 圆柱形电容器(同轴电缆) 的圆柱体, 两个长为 l 的圆柱体,圆柱面上带有等量异号的 电荷, 线电荷密度为λ=Q/l 。 电荷,其间距离 RB−RA<< l ,线电荷密度为
RB RA
+Q
-Q
QA q C= = VA −VB UAB
2
三、电容的计算 1. 平行板电容器 平行板电容器面积为S 板间距为d 平行板电容器面积为 ,板间距为 且 S >> d
2
σ0 Q QE = = ε 0 ε 0S
B
σ
v E
−σ
v v Q d Q AB = ∫ E⋅ dl = Ed = U A ε0S Q ε0S ∴C = = UAB d
如图建立坐标系, 解 如图建立坐标系, 1 λ λ 坐标轴上x处的场强可 E = ( + ) 2πε0 x d − x 由高斯定理求出 两导线间的电势差为
d−a v v d−a UAB = ∫a E ⋅ dx = ∫a
O
x
a
方向沿x轴正方向,式中λ是正电导线单位长度所带电量。 是正电导线单位长度所带电量。 方向沿 轴正方向, 轴正方向
λ Q QE = = 2πε 0r 2πε 0lr
v v RB λ ∴ AB = ∫ E⋅ dl = ∫ U dr AB RA 2π ε0 λ RB = ln 2πε0 RA
RA
RB
l
Q 2πε0l ∴C = = UAB ln( RB / RA)
5
四、电容器的联接 1. 并联电容器的电容
C = ∑ Ci
由此可算得单 位长度的电容为
( + )dx = ln ≈ ln 2πε0 x d − x πε0 a πε0 a πε0 λ C= = UAB ln(d / a)
8
1
1
1
λ
d −a
λ
d
U = U1 +U2 +L+Un
q q C1 = , C2 = , ⋅ ⋅ ⋅ , Cn = q U1 U2 Un
q q QC = = U U1 +U2 +L+Un
1 1 1 1 ∴ = + +L+ C C1 C2 Cn 1 1 ∴ =∑ 7 C i Ci
两根距离为d 例1 两根距离为 的平行无限长直导线带等量异号 电荷, 构成电容器,设导线半径a<<d,求单位长度 电荷 构成电容器,设导线半径 , d 的电容。 的电容。 x
i
C 1
VA
C2
Cn
VB
等效
VA
C
VB
令 U = VA −VB
q1 = C1U
q2 = C2U
qn = CnU
q1 + q2 + L+ qn QC = U
∴C = C1 +C2 +L+Cn
6
2. 串联电容器的电容
1 VA C
1 1 =∑ C i Ci
C2
C 3
Cn
VB
等效
VA C VB
令 U = VA −VB
与两极板之间的距离d成反比。 与两极板之间的距离 成反比。 成反比
Q =σ ⋅ S 平行板电容器的电容与极板的面积S成正比 成正比, 平行板电容器的电容与极板的面积 成正比,
3
2. 同心球形电容器 两个同心金属球壳带有等量异号电荷 电量为Q, 电量为 ,两球壳之间的场强为
RB RA
+Q
E=
Q 4 πε 0 r 2
