【免费下载】数字逻辑课后习题答案科学出版社 第五版
数字逻辑课本习题答案
习 题 五1. 简述时序逻辑电路与组合逻辑电路的主要区别。
解答组合逻辑电路:若逻辑电路在任何时刻产生的稳定输出值仅仅取决于该时刻各输入值的组合,而与过去的输入值无关,则称为组合逻辑电路。
组合电路具有如下特征:②信号是单向传输的,不存在任何反馈回路。
时序逻辑电路:若逻辑电路在任何时刻产生的稳定输出信号不仅与电路该时刻的输入信号有关,还与电路过去的输入信号有关,则称为时序逻辑电路。
时序逻辑○1○2 电路中包含反馈回路,通过反馈使电路功能与“时序”○3 电路的输出由电路当时的输入和状态(过去的输入)共同决定。
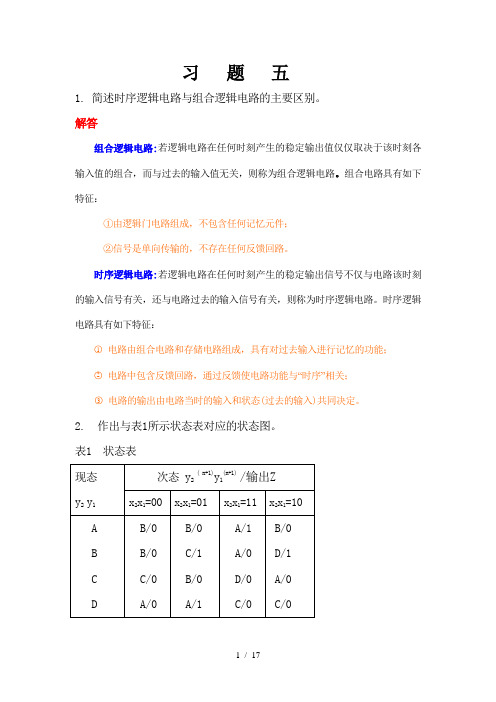
2. 作出与表1所示状态表对应的状态图。
表 1解答根据表1所示状态表可作出对应的状态图如图1所示。
图13.已知状态图如图2所示,输入序列为x=11010010,设初始状态为A,求状态和输出响应序列。
图 2解答状态响应序列:A A B C B B C B输出响应序列:0 0 0 0 1 0 0 14. 分析图3所示逻辑电路。
假定电路初始状态为“00”,说明该电路逻辑功能。
图 3 解答○1根据电路图可写出输出函数和激励函数表达式为 xK x,J ,x K ,xy J y xy Z 1111212=====○2 根据输出函数、激励函数表达式和JK 触发器功能表可作出状态表如表2所示,状态图如图4所示。
表2图4○3由状态图可知,该电路为“111…”序列检测器。
5. 分析图5所示同步时序逻辑电路,说明该电路功能。
图5解答○1根据电路图可写出输出函数和激励函数表达式为 )(D ,x y x D y y x Z 21112121212y x y y y y y x ⊕=+=+=○2 根据输出函数、激励函数表达式和D 触发器功能表可作出状态表如表3所示,状态图如图6所示。
表3图6○3由状态图可知,该电路是一个三进制可逆计数器(又称模3可逆计数器),当x=0时实现加1计数,当x=1时实现减1计数。
6.分析图7所示逻辑电路,说明该电路功能。
数字逻辑 课后习题答案

4. 最简电路是否一定最佳?为什么?
解答
一个最简的方案并不等于一个最佳的方案。最佳方案应满足全面的性能指标 和实际应用要求。所以,在求出一个实现预定功能的最简电路之后,往往要根据 实际情况进行相应调整。
2. 数字逻辑电路具有哪些主要特点?
解答
数字逻辑电路具有如下主要特点:
● 电路的基本工作信号是二值信号。 ● 电路中的半导体器件一般都工作在开、关状态。 ● 电路结构简单、功耗低、便于集成制造和系列化生产。产品价格低
廉、使用方便、通用性好。 ● 由数字逻辑电路构成的数字系统工作速度快、精度高、功能强、可
第二章
1 假定一个电路中,指示灯 F 和开关 A、B、C 的关系为 F=(A+B)C
试画出相应电路图。 解答
电路图如图 1 所示。
图1
2 用逻辑代数的公理、定理和规则证明下列表达式:
(1) AB + AC = AB + AC (2) AB + AB + AB + AB = 1 (3) AABC = ABC + ABC + ABC
= (A + B) ⋅ (A + B) =B
( ) F = BC + D + D ⋅ B + C ⋅ (AC + B)
= BC + D + (B + C)(AC + B) = BC + D + BC(AC + B) = BC + D + AC + B = B + D + AC
数字逻辑+课后答案数字逻辑+课后答案

习题解答1-3:(1)(1110101)2=(117)10=(165)8=(75)16 (2)(0.110101.2=(0.828125)10=(0.65)8=(0.D4)16 (3)(10111.01)2=(23.25)10=(27.2)8=(17.4)16 1-7:[N ]原=1.1010;[N ]反=1.0101;N =-0.1010 1-10:(1)(011010000011)8421BCD =(683)10=(1010101011)2 (2)(01000101.1001)8421BCD =(45.9)10=(101101.1110)2 2-4:(1)()();'()()F A C B C F A C B C =++=++(2)()()();'()()()F A B B C A CD F A B B C A CD =+++=+++ (3)[()()];'[()()]F A B C D E F G F A B C D E F G =++++=++++ 2-6:(1)F =A +B (2)F =1 (3)F =A BD +2-7:(1)F (A ,B ,C )=ABC ABC ABC ABC ABC ++++=∑m(0,4,5,6,7);F (A ,B ,C )=()()()A B C A B C A B C ++++++=∏M(1,2,3)(2)F (A ,B ,C ,D )=∑m(4,5,6,7,12,13,14,15);F (A ,B ,C ,D )=∏M(0,1,2,3,8,9,10,11) (3)F (A ,B ,C ,D )=∑m(0,1,2,3,4);F (A ,B ,C ,D )=∏M(5,6,7,8,9,10,11,12,13,14,15) 2-8:(1) F (A ,B ,C )=()A C BC A B C +=+(2)F (A ,B ,C ,D )=()()AB AC BC A B C A B C ++=++++ (3)F (A ,B ,C ,D )=B D B D +=+2-11:(1)F (A ,B ,C ,D )=A BD +, ∑d(1,3,4,5,6,8,10)=0;(2) 123(,,,)(,,,)(,,,)F A B C D BD ABCD ABCD ABDF A B C D BD ABCD ACD A CD F A B C D ABCD ABCD ABC=+++=+++=++,3-1:(1)F (A ,B ,C )=AC BC AC BC +=⋅F (A ,B ,C )=()()A C B C A C B C ++=+++(2)F (A ,B ,C )=∏M(3,6)=B AC AC B AC AC ++=⋅⋅F (A ,B ,C )=∏M(3,6)=()()A B C A B C A B C A B C ++++=+++++(4)F (A ,B ,C ,D )=AB A C BCD AB ++=F (A ,B ,C ,D )=0AB A C BCD A B A B ++=+=++3-3:F (A ,B ,C )=[()()][()()]A B C B C A C B C B C ABC ABC ABC +++⋅+++=++ 3-7:(2)根据真值表,列出逻辑函数表达式,并化简为“与非”式。
数字电路第五版课后答案

第一章数字逻辑习题1.1 数字电路与数字信号图形代表的二进制数1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)解:(2)(127)D= 27 -1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB解:真值表如下由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。
用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E++ +( ) = + +解:A+ABC ACD C D E++ +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式 (3)ABC B( +C)解:ABCB( +C)= + +(A B C B C)( + )=AB AC BB BC CB C+ + + + +=AB C A B B+ ( + + +1)=AB C+(6)(A + + + +B A B AB AB ) ( ) ( )() 解:(A + + + +B A B AB AB ) () ( )( )= A B ⋅+ A B ⋅+(A + B A )(+ B )=AB(9)ABCD ABD BCD ABCBD BC + + + +解:ABCD ABD BCD ABCBD BC +++ +=ABC D D ABD BC D C ( + +) + ( + ) =B AC AD C D ( + + + ) =B A C AD ( + + + ) =B A C D ( + + ) =AB BC BD + +画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门B AB AB = + + AB B = + A B = +(1)L AB AC =(2) ( ) L DAC = +已知函数L (A ,B ,C ,D )的卡诺图如图所示,试写出函数L 的最简与或表达式用卡诺图化简下列个式(3) ( )() L ABCD=+ +解: ( , , , ) L ABCDBCDBCDBCDABD = + + +(1)ABCD ABCD AB AD ABC+ + + +解:ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D++ ( + )( + +)( + )( + +)( + )=ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + + + + +(6)L A B C D( , , , )=∑m(0,2,4,6,9,13)+∑d(1,3,5,7,11,15)解:L= +A D(7)L A B C D( , , , )=∑m(0,13,14,15)+∑d(1,2,3,9,10,11)解:L AD AC AB= + +已知逻辑函数L AB BC CA=+ + ,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC ⋅ ⋅4>由已知函数的与非-与非表达式画出逻辑图2> 由真值表画出卡诺图3> 由卡诺图,得逻辑表达式 LABBCAC = + +第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数,试选择一种最合适工作在高噪声环境下的门电路。
《逻辑与计算机设计基础》(原书第五版)课后习题答案-chapter01_solutions-5th

1CHAPTER 1© 2016 Pearson Education, Inc.1-1.(a)(1) Calm:(2) 10 mph(3) 100 mphor(b) The microcomputer requires a table or equation for converting from rotations/second to miles/hour. The pulses produced by the rotating disk must be counted over a known period of time, and the table or equation used to convert the binary count to miles per hour.1-2.–34° quantizes to –30° => 1 V => 0001+31° quantizes to +30° => 7 V => 0111 +77° quantizes to +80° => 12 V => 1100 +108° quantizes to +110° => 15 V => 11111-3.*Decimal, Binary, Octal and Hexadecimal Numbers from (16)to (31)1-4.1020301281282131,0723232233,554,4328828,589,934,592=⨯==⨯==⨯=K Bits M Bits G Bits21-5.220 = (1,000,00010 + d ) where d = 48,576 1Tb = 240 = (220)2 = (1,000,000 + d )2= (1,000,000)2 + 2(1,000,000) d + d 2 = 1,000,000,000,000 + 97,152,000,000 + 2,359,627,776 = 1,099,511,627,7761-6.112511212047252133,554,4311 Bits 1 Bits ⇒-=⇒-=1-7.*63202641013275321142(1001101)222277(1010011.101)22222283.625(10101110.1001)2222222174.5625----=+++==+++++==++++++=1-8.1 1 0 0 0 0 0 0 0 0 0 1 0 11-9.*1-10.*a)0.45 × 8 = 3.6 =>0.60 × 8 = 4.8 =>0.80 × 8 = 6.4 =>0.20 × 8 = 3.2 =>10= (16612.3463)8b) (1938.257)10 = (792.41CB)16c) (175.175)10 = (10101111.001011)21-11.*a) (673.6)8= (110 111 011.110)2= (1BB.C)16b) (E7C.B)16= (1110 0111 1100.1011)2= (7174.54)8c) (310.2)4= (11 01 00.10)2= (64.4)81-12.a) 1010 b) 0110 c) 1111001×1100 ×1001 ×0111010000 0110 11110010000 0000 0000001010 0000 11110011010 0110 11110011111000 0110110 11110010000000110110110101341-13.+1000110110101101010000000010000110001101011-----Quotient = 10001R emainder = 1 1-14.(a) 6 × 123 + 8 × 122 + 7 × 121 + 4 = 11608 (b)12 1-15.a)0 1 2 3 4 5 6 7 8 9 A BCDEFGHIJb) 20c) 21012010(.)1120122018201620(4658.8)BCI G -=⨯+⨯+⨯+⨯=1-16.*a) (BEE)r = (2699)1021021114142699111426850r r r r r ⨯+⨯+⨯=⨯+⨯-=By the quadratic equation: r = 15 or ≈ –16.27 ANSWER: r = 15 b) (365)r = (194)102102365194361890r r r r r ⨯+⨯+⨯=⨯+⨯-=By the quadratic equation: r = – 9 or 7 ANSWER: r = 751-17.Errata: The text has an error: 1480 should be 1460. This will be corrected in future printings.Noting the order of operations, first add (34)r and (24)r101010(34)34(24)24(34)(24)58r r r r r r r r r r =⨯+⨯=⨯+⨯+=⨯+⨯Now, multiply the result by (21)r101021(21)(58)10218⨯+⨯⨯⨯+⨯=⨯+⨯+r r r r r r Next, set the result equal to (1480)r and reorganize.21321321010218146161580⨯+⨯+=⨯+⨯+⨯⨯-⨯-⨯-⨯=r r r r r r r r r Finally, find the roots of this cubic polynomial. Solutions are: r = 8, – 1, – 1ANSWER: The chicken has 4 toes on each foot (half of 8).1-18.*a) (0100 1000 0110 0111)BCD = (4867)10= (1001100000011)2 b) (0011 0111 1000.0111 0101)BCD= (378.75)10=(101111010.11)21-19.*(694)10 = (0110 1001 0100)BCD (835)10=(1000 0011 0101)BCD1001 0100 +0011 +0101 1100 1001 +0110 +00001 001010011-20.*(a)101 1000111 1000Move R 011 1100 0 100 column > 0111Subtract 3 −0011011 1001 0Subtract 3 −001101 1001Move R 0 1100 110 100 column > 0111Subtract 3 −00110 1001 110Move R 0100 1110Move R 010 01110Move R 01 001110Move R 0 1001110 Leftmost 1 in BCD numbershifted out: Finished(b) 102101 1000011 1001 0111Move R 001 1100 1011 1 101 and 100 columns > 0111Subtract 3 −0011 -0011001 1001 1000 1Move R 00 1100 1100 01 101 and 100 columns > 0111Subtract 3 −0011 −001100 1001 1001 01Move R 0 0100 1100 101 100 column > 0111Subtract 3 −00110 0100 1001Move R 0010 0100 1101Move R 001 0010 01101Move R 00 1001 001101 100 column > 0111Subtract 3 −001100 0110 001101Move R 0 0011 0001101Move R 0001 10001101Move R 000 110001101 Leftmost 1 in BCDnumber shifted out: Finished 1-21.(a) 10210110011110001st Move L 1 1110002nd Move L 11 110003rd Move L 111 1000 100 column > 100Add 3 00111010 10004th Move L 1 0101 000 100 column > 100Add 3 00111 1000 0005th Move L 11 0000 006th Move L 110 00000 101 column > 100Add 3 00111001 0000 07th Move L 1 0001 00000 Least significant bit in binary number moved in:Finished(b) 103102101100011100101111st Move L 0 11100101112nd Move L 01 1100101113rd Move L 011 100101114th Move L 0111 0010111 100 column > 100Add 3 001161010 00101115th Move L 1 0100 0101116th Move L 10 1000 10111 100 column > 100Add 3 001110 1011 101117th Move L 101 0111 0111 101 & 100 columns > 100Add 3 0011 00111000 1010 01118th Move L 1 0001 0100 1119th Move L 10 0010 1001 11 100 column > 100Add 3 001110 0010 1100 1110th Move L 100 0101 1001 1 101 &100 columns > 100Add 3 0011 0011100 1000 1100 111th Move L 1001 0001 1001 Least significant bit in binary number moved in: Finished1-22.From Table 1-5, complementing the bit B6 will switch an uppercase letter to a lower case letter and vice versa.1-23.a) The name used is Brent M. Ledvina. An alternative answer: use both upper and lower case letters.0100 0010 B 0101 0010 R 0100 0101 E0100 1110 N 0101 0100 T 0010 0000 (SP)0100 1101 M 0010 1110 . 0010 0000 (SP)0100 1100 L 0100 0101 E 0100 0100 D0101 0110 V 0100 1001 I 0100 1110 N0100 0001 Ab) 0100 0010 1101 0010 1100 01010100 1110 1101 0100 1010 00000100 1101 0010 1110 1010 00001100 1100 1100 0101 0100 01000101 0110 1100 1001 0100 11100100 00011-24.1000111 G1101111 o01000001000011 C1100001 a1110010 r1100100 d1101001 i1101110 n1100001 a (Errata: This number appears as 110001, which would be “1”)1101100 l1110011 s0100001 !781-25.*a) (11111111)2b) (0010 0101 0101)BCD c) 011 0010 011 0101 011 0101ASCIId)0011 00101011 01011011 0101ASCII with Odd Parity1-26.a) U+0040 = 01000000b) U+00A2 = 11000010 10100010c) U+20AC = 11100010 10000010 10101100d)U+1F6B2 = 11110000 10011111 10011010 101100101-27.Binary Numbers from (32)to (47) with Odd and Even Parity1-28.Gray Code for Hexadecimal Digits1-29.(a) Wind Direction Gray CodeDirectionCode WordN 000 S 110 E 011 W 101 NW 100 NE 001 SW 111 SE0109(b) Wind Direction Gray Code (directions in adjacent order)DirectionCode WordN 000 NE 001 E 011 SE 010 S 110 SW 111 W 101 NW100As the wind direction changes, the codes change in the order of the rows of this table, as suming that the bottom row is “next to” the top row. From the table, the codes that result due to a wind direction change always change in a single bit.1-30.+The percentage of power consumed by the Gray code counter compared to a binary code counter equals:Number of bit changes using Gray code Number of bit changes using binary codeAs shown in Table 1-6, and by definition, the number of bit changes per cycle of an n-bit Gray code counter is 1 per count = 2n .Number of bit changes using Gray code = 2nFor a binary counter, notice that the least significant bit changes on every increment. The second least significant bit changes on every other increment. The third digit changes on every fourth increment of the counter, and so on. As shown in Table 1-6, the most significant digit changes twice per cycle of the binary counter.Number of bit changes using binary code 11222n n -+++(1)110221(21)122nni i n n i i ++==⎡⎤==-=--=-⎢⎥⎣⎦∑∑ % Power (1)210022n n +=⨯-。
数字逻辑(科学出版社第五版)课后习题答案综述

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 0 0 1 0 0 0 0 1 1 1 1 1 0 0 0 0 1 0 1 1 1 1 1 0 1 1 1 1 1 0 07.证明下列等式(1) A+A B=A+B证明:左边= A+A B =A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2) ABC+A B C+AB C =AB+AC证明:左边= ABC+A B C+AB C = ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
《电子技术基础》第五版(数字部分)高教版课后答案

第一章数字逻辑习题1.1 数字电路与数字信号1.1.2 图形代表的二进制数MSB LSB0121112(ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2(2)127 (4)解:(2)(127)D=27-1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码1.4.1 将下列十进制数转换为8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)yo u (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43 的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,33逻辑函数及其表示方法解: (a)为与非,(b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3) A⊕B AB AB(A⊕B)=AB+AB解:真值表如下A(1BC ) ACD C DEA ACD C DEA CDCD EA C D E2.1.4 用代数法化简下列各式(3) ABC B C)A B A B(A B)(A B)B AB ABAB BA BAB(9) ABC D ABD BC D ABCBD BC 解:ABC D ABD BC D ABCBD BCB( A C D) L D( A C)(3) (L A B)(C D)2.2.2 已知函数L(A,B,C,D)的卡诺图如图所示,试写出函数L 的最简与或表达式解:L( A, B, C, D) BC D BCD B C D ABD2.2.3 用卡诺图化简下列个式(1)ABCD ABCD AB AD ABC3解:ABCD ABCD AB AD ABCABCD ABCD AB C C D D AD B B C C ABC D D)()()()()( ABCD ABCD ABC D ABCD ABC D ABC D ABC D(6)L( A, B, C, D) ∑m解:(0, 2, 4, 6, 9,13)∑d(1, 3, 5, 7,11,15)L A D(7)L( A, B, C, D) ∑m解:(0,13,14,15)∑d(1, 2, 3, 9,10,11)2.2.4 已知逻辑函数L AB BC C A,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表3>由卡诺图,得逻辑表达式L AB BC AC用摩根定理将与或化为与非表达式L AB BC AC AB B C A C4>由已知函数的与非-与非表达式画出逻辑图第三章习题MOS 逻辑门电路3.1.1 根据表题 所列的三种逻辑门电路的技术参数,试选择一 种最合适工作在高噪声 环境下的门电路。
电子技术基础(数字部分)第五版答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:〔1〕周期;〔2〕频率;〔3〕占空比例MSBLSB0 1 2 11 12 〔ms〕解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制1.2.2将以下十进制数转换为二进制数,八进制数和十六进制数〔要求转换误差不大于 42. 〔2〕127 〔4〕2.718解:〔2〕〔127〕D=-1=〔10000000〕B-1=〔1111111〕B=〔177〕O=〔7F〕H 72〔4〕〔2.718〕D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将以下十进制数转换为8421BCD码:〔1〕43 〔3〕254.25解:〔43〕D=〔01000011〕BCD1.4.3试用十六进制写书以下字符繁荣ASCⅡ码的表示:P28〔1〕+ 〔2〕@ 〔3〕you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
〔1〕“+〞的ASCⅡ码为0101011,那么〔00101011〕B=〔2B〕H〔2〕@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明以下恒等式(3)ABABAB⊕=+〔A⊕B〕=AB+AB 解:真值表如下ABAB⊕ABABAB⊕AB+AB111111111111由最右边2栏可知,与AB+AB的真值表完全相同。
《数字逻辑-应用与设计》部分习题参考答案

6.4d 激励表达式: T1=F1+F3’F2’ T2=F2+F3’F1’x1’+F3’x1x2’x3+F3’F2’F1’x3’ T3=F3F2’+F2F1+F1x1’+F1x3’
十进制 +12 -12 +9.5 -22.5
+19.75 -17.25
以 1 为基的补码 01100 10011 01001.1
1 01001.0 10011.11 101110.10
以 2 为基的补码 01100 10100 01001.1
1 01001.1 10011.11 101110.11
Made by HeYuchu&QinPiqi
5.b 略(见课本附录 B-奇数号习题参考答案)
6.1c 激励表达式:
S3=F2F1’x S2=F3’F1x+F3F1’x S1=F1’x+F2F1’+F3x R3=F3 R2=x’+F3’F1’ R1=F3’F2’F1+F1x’
6.1d 激励表达式:
R1=F1 R2=F2 R3=F1’ S1=F3’F2’F1’ S2=F3’F2’F1’x1’+F3’F2’F1’x3’+F3’F2’x1x2’x3 S3=F2F1+F1x1’+F1x2+F1x3’
or=A’B+A’C=(A+B’)’+(A+C’)’=[(A+B’)(A+C’)]’ f. (A’B’)’(CD’)’=(A’B’+CD’)’=(A+B)’+(C’+D)’ g. W+Q=(W’Q’)’ h. (A+B+C)D=(AD+BD+CD)=(A’+D’)’+(B’+D’)’+(C’+D’)’ i. (AB’+C’D+EF)’=[(A’+B)’+(C+D’)’+(E’+F’)’]’=(A’+B)(C+D’)(E’+F’) j. [(A+B)’+C’]’=(A’B’+C’)’=(A’B’)’C=(A+B)C
数字逻辑(科学出版社 第五版)课后习题答案

(1)
化简得F=
(2)
化简得F=
(3)F(A,B,C,D)=∑m(0,1,2,5,6,7,8,9,13,14)
化简得F=
(4) F(A,B,C,D)=∑m(0,13,14,15)+∑ (1,2,3,9,10,11)
化简得F=
11.利用与非门实现下列函数,并画出逻辑图。
(1)F= =
12.用适当门电路,设计16位串行加法器,要求进位琏速度最快,计算一次加法时间。
解:全加器真值表如下
Ai
Bi
Ci-1
Si
Ci+1
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
可以写出以下表达式
要使进位琏速度最快,应使用“与或非”门。具体连接图如下。
若“与或非”门延迟时间为t1,“非门”延迟时间为t2,则完成一次16位加法运算所需时间为:
G的卡诺图
化简得:
第三章时序逻辑
1.写出触发器的次态方程,并根据已给波形画出输出Q的波形。
解:
2.说明由RS触发器组成的防抖动电路的工作原理,画出对应输入输出波形
解:
3.已知JK信号如图,请画出负边沿JK触发器的输出波形(设触发器的初态为0)
4.写出下图所示个触发器次态方程,指出CP脉冲到来时,触发器置“1”的条件。
数字逻辑课后习题答案(科学出版社_第五版)

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边(3)EDCCDACBAA)(++++=A+CD+E证明:左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=CB AC AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1) F=A+ABC+A C B +CB+C B = A+BC+C B(2) F =(A+B+C )(A+B+C) = (A+B)+C C = A+B(3) F =ABC D +ABD+BC D +ABCD+B C = AB+BC+BD(4) F=C AB C B BC A AC +++= BC(5) F=)()()()(B A B A B A B A ++++=BA 9.将下列函数展开为最小项表达式(1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111ABCD 00 01 11 1000011110化简得F=DA B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111AB CD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑第6章习题参考解答.docx

第6章习题参考解答6-3画出74x27三输入或非门的德摩根等效符号。
解:图形如下浒"3 .............. ::BAWD5 ........ :OH6-10在图X6.9电路中采用74AHCT00替换74LS00,利用表6-2的信息,确定从输入端到输出端的最大吋间延迟。
解:该图中从输入到输出需要经过6个NAND2;每个NAND2 (74AHCT00)的最大时间延迟为9 ns;所以从输入端到输出端的最大时间延迟为:54 nso6-31 BUT门的可能定义是:“如果Al和Bl为1,但A2或B2为0,则Y1为1; Y2 的定义是对称的。
”写出真值表并找出BUT门输出的最小“积之和”表达式。
画出用反相门电路实现该表达式的逻辑图,假设只冇未取反的输入可用。
你可以从74x00、04、10、20、30组件中选用门电路。
解:真值表如下利用卡诺图进行化简,可以得到最小积Z 和表达式为Y1=A1B1A2,+A1B1B2, Y2=A 1' • A2 B2+B 1' A2 B2Y2采用74x04得到各反相器 采用74x10得到3输入与非 采用74x00得到2输入与非 实现的逻辑图如下:6-32做出练习题6-31定义的BUT 门的CMOS 门级设计,可以采用各种反相门逻辑的 组合(不一定是二级“积Z 和”),要求使用的品体管数目最少,写出输出表达式并画出 逻辑图。
解:CMOS 反相门的晶体管用量为基本单元输入端数量的2倍;对6・31的函数式进行变换:yi = A1B1-A2'+41 ・ Bl • B2'=(41 • Bl ) •(A2'+B2‘) =(A1 ・ Bl )(A2 • B2) Y2 = A2-B2-AY+A2- B2 • BV=⑷.B2)•⑷+B1) =(A2 • B2)-(A1 • Bl )利用圈■圈逻辑设计,可以得到下列结构:Y\ = ((41 • B1)+(A2 • B2『) Y2 = ((A2 • B2),+(A1 • Bl ))HANDS74X0011H AN Di-Y13(A2 B2 A1 丁 (A2 B2 时“翔此 .....dz >Y2 674X10HANDS 5HANDS5^133 2./1U3㈣D36(A1 EM A2)1此结构晶体管用量为20只(原设计屮晶体管用量为40只)6-20采用一片74x138或74x 139二进制译码器和NAND 门,实现下列单输出或多数 出逻辑函数。
【免费下载】数字逻辑课后习题答案科学出版社 第五版

所以由真值表得证。
(2) A B C =A B C
X= A BC+A B C+AB C +ABC
A B+BC=1 (A+B+C)( A + B + C )=1 ( A B+A C )B=1 A B+BC=0 (A+B+C)( A + B + C )=1 ( A B+A C )B=1 A B+BC=0 (A+B+C)( A + B + C )=1 ( A B+A C )B=0
4.列出真值表,写出 X 的真值表达式
A BC X 0000 0010 0100 0111 1000
二进制 110001 110101 1111111 1001111011 111.1111 10011001.0110111
十进制 10 61 92 0.59375 47 13
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
数字逻辑课后答案

F = ABC + ABC
= (A + B + C)(A + B + C )
10
1
0
1
1
F的卡诺图 的卡诺图 ABC
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题 章习题 2.8用卡诺图化简法求出最简与-或表达式和最简或-与表达式。 ⑵ F(A, B, C, D ) = BC + D + D(B + C )⋅ (AD + B) 解: 画出逻辑函数的卡诺图。 先转换成与或表达式
Y2 = B Y2 = A
EN = 1 门2、4打开 Y1 = B
A B EN Y1 Y2
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题 章习题 3.13 在图3.65(a)所示的D触发器电 路中,若输入端D的波形如图 3.66(b) 所示,试画出输出端Q的波 形(设触发器初态为0)。 解: 触发器初态为0 在CP=1期间, Qn+1=D Q CP D
F = (A + B)(A + C)(C + D )(B + D )
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题 章习题 2.9用卡诺图判断函数F(A,B,C,D)和G(A,B,C,D) 之间的关系。
F(A, B, C, D ) = BD + A D + CD + ACD G (A, B, C, D ) = BD + CD + ACD + ABD
⊕ ⊕⊕⊕ ⊕
⊕ ⊕⊕⊕ ⊕⊕
⑵ (1100110)2 = 64+32+4+2 = (102)10 = (0001 0000 0010)8421码 (1100110)2 =( 1010101 )格雷码 ?
2023年大学_数字逻辑课后答案免费下载

2023年数字逻辑课后答案免费下载2023年数字逻辑课后答案免费下载数字逻辑是数字电路逻辑设计的简称,其内容是应用数字电路进行数字系统逻辑设计。
电子数字计算机是由具有各种逻辑功能的逻辑部件组成的,这些逻辑部件按其结构可分为组合逻辑电路和时序逻辑电路。
组合逻辑电路是由与门、或门和非门等门电路组合形成的逻辑电路;时序逻辑电路是由触发器和门电路组成的具有记忆能力的逻辑电路。
有了组合逻辑电路和时序逻辑电路,再进行合理的设计和安排,就可以表示和实现布尔代数的基本运算。
数字逻辑:概念主要用以研究有两个离散状态的开关器件所构成的数字电路。
能对电路的输入与输出之间的关系提供理想描述,研究这种描述的特性和电路的实现,并探讨将数字电路或数字模块互连起来完成特定逻辑功能的理论和方法。
具有两个或多个离散状态的开关器件或单元是:可断开和闭合的开关或继电器的触点;能正偏和反偏的整流二极管;能饱和和截止的开关电子管或开关晶体管;能在两个饱和方向中任意一个方向上磁化的磁心。
具有二个离散状态的开关器件是最常见的。
数字逻辑不考虑特殊条件下动作或稳定的物理现象和从一个状态过渡到另一个状态的细节。
数字逻辑数字逻辑的部分理论建立在数理逻辑,特别是布尔代数和时序机的理论基础上。
数字逻辑可分为组合逻辑和时序逻辑。
在一个逻辑系统中,输出结果仅取决于当前各输入值的称组合逻辑;输出结果既由当前各输入值,又由过去的输入值来决定的称时序逻辑。
组合逻辑不包含存储元件,时序逻辑至少包含一个存储元件。
数字逻辑的应用范围极广,日常生活的决策过程是组合逻辑的`典型例子。
电话号码的拨号和号码锁的开启过程,则是时序逻辑的典型例子。
数字逻辑在数字电路设计中有广泛的用途。
组合逻辑组合逻辑的输出由其输入确定的法则,通常称为开关函数。
因为变量是离散的,一个开关函数可以用表格形式的真值表来表示,也可以用各种图来表示。
如果函数和变量是二进制的,符号“1”和“0”通常用来表示这两个值。
《电子技术基础》数字部分第五版课后答案

第一章数字逻辑习题1.1数字电路与数字信号1.1.2图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0121112(ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2−1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127(4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43(3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+(2)@(3)you(4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1.6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解:(a)为与非,(b)为同或非,即异或第二章逻辑代数习题解答2.1.1用真值表证明下列恒等式(3)A B AB AB ⊕=+(A⊕B)=AB+AB 解:真值表如下A B A B⊕ABAB A B⊕AB +AB00010110110000101000011111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
数字逻辑与数字系统设计习题参考答案

4.10解:根据题意,列出功能表如下:
十进制数
余3码ABCD
输出F
0
d
1
d
2
d
3
0011
1
4
0100
1
5
0101
1
6
0110
0
7
0111
0
8
1000
0
9
1001
0
10
1010
1
11
1011
1
12
1100
1
13
d
14
d
15
d
根据功能表绘制卡诺图如下:
考虑无关项可得化简后的表达式:
F=
4'b1011: f<=1'b1;
4'b1100: f<=1'b1;
default: f<=1'b0;
endcase
endmodule
//4.11的Verilog HDL描述
module ex11(a,b,c,f);
input a,b,c;
output[1:0] f;
reg[1:0] f;
always @(a or b or c)
(4)BC+AD=(B+A)(B+D)(A+C)(C+D)
证明:右边=(B+AB+BD+AD)(AC+C+AD+CD)
=(B+AD)(C+AD)
=BC+ACD+ABD+AD=BC+AD=左边
2.7解:
(1) =(A+ +C)( +B+C)( + + )
数字逻辑概论第五版

2、数字集成电路旳特点
(1)稳定性高,成果旳再现性好 (2)易于设计 (3)大批量生产,成本低廉 (4)可编程性 (5)高速度,低功耗
3、数字电路旳分析、设计与测试
(1)数字电路旳分析措施: 分析工具:逻辑代数、计算机仿真
(2)数字电路旳设计措施: 设计过程:方案旳提出、验证、修改 设计方式:老式旳设计方式;EDA软件设计方式
八进制数
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17
十六进制数
0 1 2 3 4 5 6 7 8 9 A B C D E F
1.2.2 数制转换
将N进制数按权展开,即能够转换为十进制数。 1、二进制数与八进制数旳相互转换
(1)二进制数转换为八进制数: 将二进制数由小数点开始, 整数部分向左,小数部分向右,每3位提成一组,不够3位补 零,则每组二进制数便是一位八进制数。
(2)基 数:进位制旳基数,就是在该进位制中可能用到 旳数码个数。
(3) 位 权(位旳权数):在某一进位制旳数中,每一位 旳大小都相应着该位上旳数码乘上一种固定旳数,这个固 定旳数就是这一位旳权数。权数是一种幂。
1、十进制 数码为:0~9;基数是10。 运算规律:逢十进一,即:9+1=10。 十进制数旳权展开式:
例1.3.3 求1001与1011旳积。
解:
1001
×) 1 0 1 1
1001
1001
0000
1001
1100011
11 1
即:1001×1011=1100011
可见,乘法运算法运算和除法运算
除法法则:
0 1 0 111
例1.3.4 求1010与111之商。
逻辑电平与电压值旳关系(正逻辑) :
逻辑与计算机设计基础第五版课后答案chapter06

逻辑与计算机设计基础第五版课后答案Chapter066.1 填空题1.逻辑电路中,5个逻辑门包括与门、或门、非门、与非门和或非门。
2.组合逻辑电路是由逻辑门组成的。
3.子电路是由节点和逻辑门组成的。
4.逻辑门的输入端数称为其阶数。
5.卡诺图的横纵坐标是逻辑变量。
6.卡诺图上的每个矩形对应一个最小项。
7.复杂逻辑函数可以用几个较小的逻辑单元构成。
8.门电路可不断扩展到更复杂的逻辑电路。
9.简化布尔函数是优化逻辑电路的一种方法。
10.简化布尔函数可以减少电路中的逻辑门数量。
6.2 选择题1.LogicWorks软件包含设计逻辑电路所需的全部功能,以下哪个是LogicWorks的主要特点?A. 用户界面简洁易用,适合初学者使用。
B. 提供了强大的绘图工具和仿真工具。
C. 方便学生理解和掌握基本逻辑电路的设计方法。
D. 以上三项都是。
答案:D2.LogicWorks 是一个集成功能强大的绘图工具和仿真工具于一身的逻辑设计软件,它具有如下特点,除了__B__之外全部是()。
A. 用户界面简介易用,适合初学者使用。
B. 它可以为学生编写和作业设计电路图。
C. 提供由身强大的仿真工具。
D. 方便学生理解和掌握基本逻辑电路的设计方法。
答案:B3.在 LogicWorks 软件中,可以通过输入“ EN ” 来实现一个与逻辑电路的启停。
假设“ EN ” 通入值为高电位则电路启动,“ EN ” 通入值为低电位则电路停止。
A. 对B. 错答案:A4.LogicWorks 中连接点上的箭头表示其状态,仅当断头朝上是高电平表示 1,断头朝下是低电平表示 0。
A. 对B. 错答案:B5.以下哪一项是LogicWorks软件中可以直接编辑数字逻辑电路的操作?A. 点击元件图形中每个连接点上方那一根看不见的电线就可以显示与进一步编辑节点的名称。
B. 在每个连接点上方那根看不见的线上点击鼠标右键可以弹出含有描述节点名称的对话框。
C. 鼠标左键只点击连接点上方的连线,可以改变该位的电平状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八进制 61 65 177 1173 7.74 231.334
八进制 12 75 134 0.46 57 15
1011 1101 1111
5.求下列函数的值
当 A,B,C 为0,1,0时: 当 A,B,C 为1,1,0时: 当 A,B,C 为1,0,1时:
6.用真值表证明下列恒等式
(1) (A B) C=A (B C)
=AC(B+ B )+AB(C+ C )
=AB+AC =右边
(3) A ABC ACD (C D )E =A+CD+E
证明:左边= A ABC ACD (C D )E
=A+CD+A B C + CD E
=A+CD+ CD E
=A+CD+E
A B C AB C
00 0
1
0
0
1
0
1
1
0
A B C
1 0 0 1 0 1 1 0
(4)
=右边
AB ABC ABC = AB AC BC
证明:左边= AB ABC ABC
= ( AB ABC ) ABC ABC
= AB AC BC =右边
8.用布尔代数化简下列各逻辑函数表达式
AB C 00 01 11 10
01 1 1 1
10 0 0 0 化简得 F= C
(2) F ABCD ABC D AB AD ABC
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
0
1
1
0
1
0
0
1
0
1
1
0
1
0
0
1
7.证明下列等式
(1) A+ A B=A+B
(2)
证明:左边= A+ A B
=A(B+ B )+ A B
=AB+A B + A B
=AB+A B +AB+A B
=A+B =右边
ABC+A B C+AB C =AB+AC
证明:左边= ABC+A B C+AB C
= ABC+A B C+AB C +ABC
(1) F=A+ABC+A BC +CB+ C B = A+BC+ C B (2) F=(A+B+ C )(A+B+C) = (A+B)+C C = A+B (3) F=ABC D +ABD+BC D +ABCD+B C = AB+BC+BD (4) F= AC ABC BC ABC = BC
所以由真值表得证。
(2) A B C =A B C
X= A BC+A B C+AB C +ABC
A B+BC=1 (A+B+C)( A + B + C )=1 ( A B+A C )B=1 A B+BC=0 (A+B+C)( A + B + C )=1 ( A B+A C )B=1 A B+BC=0 (A+B+C)( A + B + C )=1 ( A B+A C )B=0
4.列出真值表,写出 X 的真值表达式
A BC X 0000 0010 0100 0111 1000
二进制 110001 110101 1111111 1001111011 111.1111 10011001.0110111
十进制 10 61 92 0.59375 47 13
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
1.将下列十进制数化为二进制数和八进制数
十进制 49 53 127 635 7.493 79.43
第一章 开关理论基础
2.将下列二进制数转换成十进制数和八进制数
二进制 1010 111101 1011100 0.10011 101111 01101
3.将下列十进制数转换成8421BCD 码
1997=0001 1001 1001 0111 65.312=0110 0101.0011 0001 0010 3.1416=0011.0001 0100 0001 0110 0.9475=0.1001 0100 0111 0101
00 1
01 0
011
100
101
110
111
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
