公交转车问题(数学建模)

合集下载

南京市公交转车优化问题

理学院专业实践报告题目：南京市公交转车优化问题专业信息与计算科学学生姓名班级学号指导教师实习单位理学院日期2014年2月28日一、问题描述问题 3 在转车次数最小的情况下，设计南京市地铁转乘的算法。

南京市任意两个公交站点的最小转车次数的最大值是多少？即最多只要转乘几次公交，即可从南京市的任一站点乘到其它任一站点。

解决此问题时，假设相邻公汽站平均行驶时间(包括停站时间)，相邻地铁站平均行驶时间(包括停站时间)，公汽换乘公汽平均耗时，地铁换乘公汽平均耗时，公汽换乘地铁平均耗时都是一个定值。

对以下站点给出乘车方案：南京邮电大学仙林校区——新街口南京邮电大学仙林校区――中山陵南京邮电大学仙林校区――夫子庙南京邮电大学仙林校区——湖南路南京邮电大学仙林校区——玄武湖公园二、问题分析针对问题，我们要解决的是合理给出两站点间的最佳路线选择问题。

根据调查和分析，对影响线路选择的因素进行筛选，最终确定了以下三个影响较大的因素：第一是换乘次数；第二是乘车站数；第三是乘车费用。

从实际情况分析，人们通常宁愿多乘坐几站地也不愿换车，为了解决换乘次数最少，乘车站数相对较少、乘车费用相对较少的问题，选择Dijkstra方法对问题进行解决，由于问题中出现的站数较少Dijkstra的运算量也不会很大。

通过Matlab编制程序，给出了任意两站点间的最佳乘车路线以及换车的地点，最后还提出了进一步的意见和建议。

三、问题假设解决此问题时，假设相邻公汽站平均行驶时间(包括停站时间)，相邻地铁站平均行驶时间(包括停站时间)，公汽换乘公汽平均耗时，地铁换乘公汽平均耗时，公汽换乘地铁平均耗时都是一个定值。

公汽票价： 2元。

地铁票价：3元（无论地铁线路间是否换乘）。

四、建模分析（1）最小转车次数模型。

设n表示问题中的两目的地之间的站点数,其中矩阵B=表示直达0-1矩阵，即设m为从的最小转车次数最小转车次数模型为：（，）。

（2）最小乘车站数模型对于本模型建立只需对最小转车次数模型进行简单修改即可。

公交换乘

数学建模公交换乘问题的matlab程序共享乘公交看奥运，下面的程序是找出最佳乘公交的路径，直达的线路，一次转乘或两次转乘的线路题目：乘公交，看亚运（中找最佳路线问题）2010年11月12日第16届亚运会在广州举行，为了让全体市民更好看亚运会，广州市政府决定在亚运期间放假3天、以及全体市民可在亚运及亚残运会期间免费坐公交、地铁30个工作日等惠民政策，这一政策的施行在很大程度上加剧了广州市交通出行的困难。

附件一，附件二是广州市公交（包括地铁）的一些信息，为了方便游客看亚运会，请你用数学建模的方法，为广州市设计一个公交线路查询系统，满足查询者的各种不同需求。

请你们解决如下问题：1、在亚运会开幕前，仅考虑公汽线路，给出任意两公汽站点之间线路选择问题的一般数学模型与算法。

并根据附录数据，利用你们的模型与算法，求出以下3对起始站→终到站之间的最佳路线（要有清晰的评价说明）。

(1)、华穗路→交通大厦(2)、越秀桥→山村(3)、江南大道北→策边村程序中用到的lx0.xls数据下载/view/bc9efa4de45c3b3567ec8bfd.html原始数据（原始线路信息、站点编号表、公交说明）附录二：线路.xls 下载地址/view/ff5a660b844769eae009ed94.html有问题QQ869896537尽量解决如果你的题目的数据不是这样的，即数据的量不同，你需要在程序中修改相应数据，例如循环次数的修改等数据Matlab 源程序代码：clear all;clc[a b c]=xlsread('lx0.xls');biao=unique(b);for i=1:length(biao)b(strcmp(b,biao(i)))={i-1};endbiao=biao(2:end);%公交站点编号对照表zhan=cell2mat(b);%公交数字站点信息for i=1:1108fl=zhan(i,:);fl(find(fl==0))=[];if length(fl)>47;zhan(i,:)=0;%去掉地铁线路endif length(fl)<6;qian(i)=2.5;elseif length(fl)<10&&length(fl)>=6;qian(i)=2.0;elseif length(fl)>=10;qian(i)=1.5;endendcx1=inputdlg('起站点：');cx2=inputdlg('到站点：'); for i=1:length(biao)if ismember(cx1,biao(i));shuzizhandian1=i; %将站名换成数字站点endif ismember(cx2,biao(i));shuzizhandian2=i;endendnum1=0;num2=0;for i=1:1:1108for j=1:55y=zhan(i,j);if shuzizhandian1==y;num1=num1+1;gj(num1)=i;%经过起站点的公交号zd(num1)=j;endif shuzizhandian2==y;num2=num2+1;gjend(num2)=i;%经过到起站的公交号zdend(num2)=j;endendendstart=[gj;zd]'; %起始站点可以选择的公交及在公交路线中的位置des=[gjend;zdend]'; %目的地可供选择的公交信息zhi=intersect(gj,gjend)' ; %可选的直达车信息cy=length(zhi); %cy为直达车的个数%******************……下面按照转乘车次数安排线路……***********************%%%clc;if cy~=0;for i=1:cyz1=[];z2=[];z1=find(gj==zhi(i));z2=find(gjend==zhi(i));% if zdend(z2(1,1))-zd(z1(1,1))<0;% zhi(i)=[];% endzs(i)=zdend(z2(1,1))-zd(z1(1,1));endfprintf(' 《《《《公交直达选择信息》》》》\n')xuanzhe=[zhi,zs'];you=sortrows(xuanzhe,2);%优先选择排序for i=1:cyww=zhan(you(i,1),:); %直达线路fprintf('%4d==\t<%3d站>\t',you(i,1),you(i,2));if find(ww==shuzizhandian1)-find(ww==shuzizhandian2)>0;forj=find(ww==shuzizhandian2):find(ww==shuzizhandian1)fprintf('<-- %s',biao{ww(j)});endfprintf('\n');elseforj=find(ww==shuzizhandian1):find(ww==shuzizhandian2)fprintf('--> %s',biao{ww(j)});endfprintf('\n');endendelse%*********************……下面求转乘一次的线路……*************************%fprintf('\n============================================= ==================================\n');fprintf(' 可惜！没有直达车！！\n 亲！可以选择换乘哦\n');ji=0 ;%第ji个可以换乘的公交length(gj);length(gjend);zc=[0];for i=1:length(gj)m=gj(i);for j=1:length(gjend)n=gjend(j);p1=zhan(m,:);p1(find(p1==0))=[];p2=zhan(n,:);p2(find(p2==0))=[];if intersect(p1,p2);ji=ji+1;hc(ji,:)=[m,n]; %转乘的两公交t=intersect(p1,p2); %转乘交点站zc(ji,1:length(t))=t;%转乘信息收集zc(ji,(length(t)+1):5)=0; %扩充来使数据集中放置endendendif max(max(zc))~=0;fprintf('\n============================================= ==================================\n');fprintf(' 可以选择换乘一次\n');patch=[hc ,zc];s=0;for i=1:jizc1=zc(i,:);zc1(find(zc1==0))=[];for j=1:length(zc1)s=s+1;patch1(s,:)=[hc(i,:),zc1(j)];endendfprintf(' \n\t 首坐车\t 转乘车\t 中途下车站点\n');disp(patch1) %for i=1:see1=zhan(patch1(i,1),:); ee2=zhan(patch1(i,2),:);iffind(ee1==shuzizhandian1)-find(ee1==patch1(i,3))<0;long=abs(find(ee1==shuzizhandian1)-find(ee1==patch1(i,3)));fprintf('%4d==\t<%3d站>\t',patch1(i,1),long);t1=long*3;forj=find(ee1==shuzizhandian1):find(ee1==patch1(i,3))fprintf('--> %s',biao{ee1(j)});endfprintf('\n');elselong=abs(find(ee1==shuzizhandian1)-find(ee1==patch1(i,3)));fprintf('%4d==\t<%3d站>\t',patch1(i,1),long);t1=long*3;forj=find(ee1==shuzizhandian1):-1:find(ee1==patch1(i,3))fprintf('<-- %s',biao{ee1(j)});endfprintf('\n');endiffind(ee2==shuzizhandian2)-find(ee2==patch1(i,3))>0;long=abs(find(ee2==shuzizhandian2)-find(ee2==patch1(i,3)));t2=long*3;fprintf('%4d==\t<%3d站>\t',patch1(i,2),long);forj=find(ee2==patch1(i,3)):find(ee2==shuzizhandian2)fprintf('--> %s',biao{ee2(j)});endfprintf('\n');elselong=abs(find(ee2==shuzizhandian2)-find(ee2==patch1(i,3)));t2=long*3;fprintf('%4d==\t<%3d站>\t',patch1(i,2),long);forj=find(ee2==patch1(i,3)):-1:find(ee2==shuzizhandian2)fprintf('<-- %s',biao{ee2(j)});endfprintf('\n');endlufei=qian(patch1(i,1))+qian(patch1(i,2));t(i)=t1+t2+5;T=t1+t2+5;fprintf('!选择（%2d）===========',i);fprintf('!路费=%3d元',lufei);fprintf('!\t\ttime=%3d分钟\n\n',T);disp('-------------------------------------------------------------------------------------------------------------------------------');endzuikuai=find(t==min(t));fprintf('!最快的选择是————》选择（%3d）\n',zuikuai);disp('-------------------------------------------------------------------------------------------------------------------------');else%*********************……下面求转乘两次的线路……*************************%fprintf('\n============================================= ==================================\n');fprintf(' 换乘一次无法找到\n');buyao=union(gj,gjend);%经过起点或终点的公交quan=[1:1108];disan=setdiff(quan,buyao);%可供选择的转乘车ds2=[];ds3=[];for j=1:length(gj)ds2=union(zhan(gj(j),:),ds2);%经过起点的车可以覆盖的地点ds2(find(ds2==0))=[];endfor k=1:length(gjend)ds3=union(zhan(gjend(k),:),ds3);%经过终点的车可以覆盖的地点ds3(find(ds3==0))=[];endl=0;%中间车计数量zj1=0;zuihou=0;for i=1:length(disan)%转乘车数量ds1=[];ds1=zhan(disan(i),:);ds1(find(ds1==0))=[];if intersect(ds1,ds3);%寻找中间车if intersect(ds1,ds2);l=l+1;zjc(l)=disan(i);%可考虑的中间转乘车车号for j=1:length(gj)jj=zhan(gj(j),:);jj(find(jj==0))=[];if intersect(ds1,jj);j1=intersect(ds1,jj);%第1次下车站点% zj1=zj1+1;%xx(zj1,:)=[gj(j),disan(i),j1(1)] ;%第一二辆车及转点for k=1:length(gjend)kk=zhan(gjend(k),:);kk(find(kk==0))=[];if intersect(ds1,kk);j2=intersect(ds1,kk);%第2次下车站点zj1=zj1+1;xx(zj1,:)=[gj(j),j1(1),disan(i),j2(1),gjend(k)];zuihou=1;endendendendendendendif zuihou==0;fprintf('\n============================================= ==================================\n');fprintf(' sorry没有两次以内的转乘安排\n');elsefprintf('\n============================================= ==================================\n');fprintf(' 为你安排的两次转乘路线：\n');disp(' 起点车一下车站点中间车二下车站点到终点车');for i=1:zj1ss1=zhan(xx(i,1),:); ss2=zhan(xx(i,3),:); ss3=zhan(xx(i,5),:);iffind(ss1==xx(i,2))-find(ss1==shuzizhandian1)<0||find(ss2==xx(i,4))-find (ss2==xx(i,2))<0||find(ss3==shuzizhandian2)-find(ss3==xx(i,4))<0;xx(i,:)=0;%去除逆行线路endendxx(all(xx==0,2),:)=[];disp(xx);if length(xx(:,1))==0;fprintf('没有找到正向线');elsefor i=1:length(xx(:,1))ss1=zhan(xx(i,1),:); ss2=zhan(xx(i,3),:); ss3=zhan(xx(i,5),:);long1=find(ss1==xx(i,2))-find(ss1==shuzizhandian1);fprintf('%4d==\t<%3d站>\t',xx(i,1),long1);forj=find(ss1==shuzizhandian1):find(ss1==xx(i,2))fprintf('--> %s',biao{ss1(j)});endfprintf('\n');long2=find(ss2==xx(i,4))-find(ss2==xx(i,2));fprintf('%4d==\t<%3d站>\t',xx(i,1),long2);for j=find(ss2==xx(i,2)):find(ss2==xx(i,4))fprintf('--> %s',biao{ss2(j)});endfprintf('\n');long3=find(ss3==shuzizhandian2)-find(ss3==xx(i,4));fprintf('%4d==\t<%3d站>\t',xx(i,1),long3);forj=find(ss3==xx(i,4)):find(ss3==shuzizhandian2)fprintf('--> %s',biao{ss3(j)});endlufei2=qian(xx(i,1))+qian(xx(i,3))+qian(xx(i,5));% timetwo(i)=3*(long1+long2+long3)+10;T2=3*(long1+long2+long3)+10;fprintf('\n线路《%3d》========!路费=%d元',i,lufei2);fprintf('!\t\ttime=%3d分钟\n\n',T2);fprintf('\n\n');endzuikuai2=find(timetwo==min(timetwo));fprintf('!最快的选择是————》选择线路《%3d》\n',zuikuai2);fprintf('!最短时间：《%3d分钟》\n',min(timetwo(zuikuai2)));disp('-------------------------------------------------------------------------------------------------------------------------');endendendend。

公交线路的车辆调度问题_2001年全国大学生数学建模竞赛B题

发车间隔 / min
13 13 13 11 11 11 11 11
9
第1期
何永强, 黄剑, 陆新根: 公交线路的车辆调度问题
17
为了顾及双方的利益, 取为 0. 5, 所以可得 5 00- 6 00 的发车间隔为 11min 以后各个时间段都是用
这种方法进行求解见表 3, 并根据发车间隔可以制定出发车时间表, 见表 4.
表 3 各时间段的发车间隔
表 4 各时间段的调度方案
时间段
6 00 9 00 9 00 16 00 16 00 19 00 19 00 20 00 22 00 23 00
发车间隔 / min 2 11 4 11 15
时间段
5 00 6 00 6 00 9 00 9 00 16 00 16 00 19 00 19 00 22 00 22 00 23 00
( 5) 汽车的运行时间只包括乘客上下车时间和必要的运行时间, 不考虑其它时间.
( 6) 在同一时间段内按等间隔发车, 以方便工人操作.
( 7) 假设车上载客人数小于 50 为空车. 以( 50- 此刻车上人数) 为缺载人数
总空车时间= i 号车缺载人数运行时间
( 8) 假设未搭上车的乘客为留乘乘客,
11
12
和车公里数减少了, 总留乘时间必然增加. 它们
13
分别代表了公交公司的利益和乘客的利益. 此
14
时间主要考虑两个方面, 总留乘时间和车公里
15
数, 为了计算方便, 现使它们的量纲一致. 即车
1 02 82 9277. 4 8642. 2 8140. 8 7166. 7 6651. 7 6327. 1 6067. 5
总留乘时间= ( 第 i 个车站留乘人数) ( 留乘时间)

全国建模竞赛一等奖公交线路中寻求最优路线的模型与算法

公交线路中寻求最优路线的模型与算法摘要本文对公交线路查询问题进行了研究。

根据查询者的各种不同需求，以换乘车次最少为约束条件，分别以出行耗时和出行费用为目标函数，建立多目标规划模型，运用公交换乘搜索算法可得到合理的出行路线。

针对问题一，在仅考虑公汽线路时，用520条公汽线路构建公共交通矩阵。

以此矩阵作为搜索对象，运用基于广度优先的公交换乘搜索算法，找出符合“换乘次数最少”的可行解。

分别以出行耗时和出行费用为目标建立规划模型。

然后，对有限个可行解采用枚举法，将其出行耗时和出行费用一一求出，通过比较得到规划模型的最优解，结果见正文第6页表3。

同时，在换乘次数和是否穿过地铁站等方面对结果作了清晰评价。

公汽线路。

重新构建共公交通矩阵。

在考虑地铁站与公汽站点相互连通的情况下，运用问题一的解法求得规划模型的最优解，结果见正文第7页表4。

针对问题三，当已知所有站点之间的步行时间时，在模型二的基础上对公交换乘搜索算法改进，相邻近的两站点间乘客可以通过步行到达，并对整个乘车过程中步行次数和步行时间进行约束得出了问题三的模型。

关键词：公共交通矩阵公交换乘搜索算法目标规划相邻站点第29届奥林匹克运动会将于2008年8月在首都北京举行，这是我国第一次成功的申办奥运会，极大的鼓舞了全国人民。

经过近六年筹备，各大奥运会场馆相继竣工。

作为奥运会的重要交通工具，举办城市的公共交通系统也有了很大发展。

现在北京市的公汽线路已达800以上，较好的满足了到现场观看奥运比赛的国内外观众的交通需求，使公众的出行更加通畅、便利，与此同时人们也面临着多条线路的选择问题。

因此，根据市场需求，某公司准备研制开发一个解决公汽线路选择问题的自主查询计算机系统，系统核心是线路选择的模型与算法。

设计该系统要从实际情况出发考虑，满足查询者的各种不同需求，现有三个问题需要解决：1、仅考虑公汽线路，给出任意两公汽站点之间线路选择问题的一般数学模型和算法。

利用此模型与算法，求出以下6对起始站到终到站之间的最佳路线，并给出清晰的评价说明。

公交转车的最短时间模型及求解

第38卷第14期2008年7月数学的实践与认识M A TH EM A TI CS I N PRA CT I CE AND TH EO R YV o l 138　N o 114　July,2008　公交转车的最短时间模型及求解叶　军,　杨振华(南京邮电大学数理学院,江苏南京　210003)摘要:　针对2007年全国大学生数学建模竞赛B 题——“乘公交,看奥运”中的关于公交线路的选择问题,建立了最短时间的数学模型,并给出了该数学模型的精确求解.关键词:　数学模型;公交线路选择;最短时间1　问题分析收稿日期:2008204201 2007年全国大学生数学建模竞赛的B 题是一道公交线路选择问题,它是一个多目标规划问题,要分别在换乘次数最少、费用最省、时间最短等目标下分别求解问题[1].在换乘次数和费用两个目标下较容易求出最优解.在时间最少这一目标下,较难求出最优解.在给定起点与终点的情形下,一般的方法是分别在给出转车次数为0,1,2等情形下分别给出其最短乘车时间,然后进行比较,从而求得最短时间.这种思路可以帮助我们求得最短时间,但是还有两个难点:一是由于计算复杂性,当转车次数增加时,程序运行时间较长;二是要说明最优必须遍历任意乘车次数,这显然无法实现.我们必须在理论上解决这一困难.2　仅考虑公共汽车线路时的最短时间模型及求解2.1　数学模型设N =3957表示问题中的公汽站点数,A 0=(a (i ,j ,0))N ×N 是直达最小站数矩阵,当存在公共汽车从站点S i 直达站点S j 时,a (i ,j ,0)表示从S i 直达S j 的最小站数.否则该元素取为+∞.令A m =(a (i ,j ,m ))N ×N 是m 次转乘最小站数矩阵,其元素a (i ,j ,m )表示m 次转车情形下,从S i 到S j 的最小站数.显然a (i ,j ,m )=m in{a (i ,k ,0)+a (k ,j ,m -1) 1Φk ΦN ,k ≠i ,k ≠j }(1) 转车次数为m 时,从S i 到S j 的总时间为t S (i ,j ,m )=5m +3a (i ,j ,m ),我们得到仅考虑公共汽车线路时的最短时间模型.模型1m in 0Φm Φ∞t S (i ,j ,m )=5m +3a (i ,j ,m )2.2　模型求解要对转车次数m 进行全遍历是不可能的,我们给出函数t S (i ,j ,m )的一个下界.设n S (i ,j )=m in 0Φm Φ∞a (i ,j ,m )表示公共汽车从S i 到S j 的最小乘车站数(可以转车任意次).将公汽站点设为有向图中的结点.若S i 乘公汽1站可以到达S j ,我们就设一条有向边从结点i 指向结点j .对于每一条有向边,指定其权为1,显然求n S (i ,j )就转化为有向图中结点i 到结点j 的最短路径问题.对任意给定的i ,j ,我们可以采用D ijk stra 算法求得n S (i ,j ).下面定理显然成立.定理1　t S (i ,j ,m )Ε5m +3n S (i ,j )对于给定的站点S i ,S j ,根据定理1,我们可以给出求解最短时间模型的方法:Step 1　利用D ijk stra 算法求出n S (i ,j ),令m =0;Step 2　根据(1)式求出a (i ,j ,m );令t S (i ,j ,m )=5m +3a (i ,j ,m )Step 3　若T S (i ,j ,m )=m in 0Φk Φmt S (i ,j ,k )Φ5(m +1)+3n S (i ,j ),则T S (i ,j ,m )即为最短乘车时间;否则令m ∶=m +1,转Step 2.注　1)若T S (i ,j ,m )Φ5(m +1)+3n S (i ,j ),表明转车次数大于m 时,总时间已经不小于转车次数不大于m 时的总时间,显然T S (i ,j ,m )即为最短乘车时间;2)在编程计算时,可定义一矩阵B ,它共有N 行,第i 行记录的是站点S i 能够直达的站点,即使得a (i ,j ,0)<∞的j 的集合.从而在计算a (i ,j ,m )时不必从1到N 进行循环.对于原问题中的第一对站点,我们给出求解过程.i =3359,j =1828,n S (i ,j )=13.表1　站点S 3359至站点S 1828的最小乘车时间求解过程m 01234ts (i ,j ,m )∞101646971T s (i ,j ,m )∞1016464645(m +1)+3ns (i ,j )4449545964根据表1得出,对于第一对站点,最短乘车时间为64分,需转2次车.对于原问题的6对站点,我们给出结果见表2.表2　6对站点最小乘车时间求解过程点对ts (i ,j ,m )123456m 3ns (i ,j )5(m 3+1)+3ns (i ,j )T 333592182810164369714136464155720481∞106993101103425100990971204851281033105104106427106103000820073836763593644136459014820485∞1061023104106955251051020087236766546351563105046注　1)m 3=m in{m T S (i ,j ,m )Φ5(m +1)+3n S (i ,j )},即为最小转乘次数;T3表示最短乘车时间;2)m =0时,对6个点对均有t S (i ,j ,0)=∞.72214期叶　军,等:公交转车的最短时间模型及求解3　综合考虑公共汽车和地铁线路时的最短时间模型及求解3.1　数学模型综合考虑公汽和地铁时,我们首先研究这样一个问题:在考虑时间最少时,线路中是否存在先乘地铁,再转公汽,再乘地铁这样的乘车方案?定理2　考察下面两种方案(A )从地铁站D k 乘地铁到地铁站D k 1然后由公汽站S s 1乘到公汽站S s 2,再转地铁站D l 1,乘地铁到地铁站D l ;(B )直接乘地铁由地铁站D k 到D l .则方案(B )的总时间T 2不大于方案(A )的总时间T 1.证明　我们结合计算机编程的结果给出证明.我们只要证明方案(B )的时间T 2小于方案(A )的时间T 1即可.设t DB (i ,j )表示乘地铁由地铁站D i 到地铁站D j 的最短时间,n SA (i ,j )表示可以由地铁站D i 转乘的公汽站乘公汽到可以由地铁站D j 转乘的公汽站的最小公汽站数.显然T 1Εt DB (k ,k 1)+3n SA (k 1,l 1)+t DB (l 1,l )+13,其中13表示地铁转公汽的时间与公汽转地铁的时间之和.若3n SA (k 1,l 1)+13-t DB (k 1,l 1)Ε0,则T 1-T 2Εt DB (k ,k 1)+3n SA (k 1,l 1)+t DB (l 1,l )+13-t DB (k ,l )Εt DB (k ,k 1)+t DB (k 1,l 1)+t DB (l 1,l )-t DB (k ,l )Ε0. 我们通过计算机程序(对k 1,l 1从1到39进行遍历搜索)求得只有4组(k 1,l 1)使得3n SA (k 1,l 1)+13-t DB (k 1,l 1)<0,分别为(13,30),(16,30),(30,15),(30,16).对这4组(k 1,l 1)均有n SA (k 1,l 1)=1.对这4组(k 1,l 1),分别编程求出t DB (k ,k 1)+t DB (l 1,l )+16-t DB (k ,l )的最小值(对k ,l 从1到39进行遍历搜索,且k ,k 1,l 1,l 两两不相等).可以得到这4个最小值都为2.于是T 1-T 2Εt DB (k ,k 1)+3n SA (k 1,l 1)+t DB (l 1,l )+13-t DB (k ,l )Εt DB (k ,k 1)+t DB (l 1,l )+16-t DB (k ,l )Ε2.证毕.根据定理2,对于起点和终点都不能由地铁站直接转乘的两个公汽站,只需考察下面的乘车方案:乘p 次(转p -1次)公汽,再乘地铁,最后乘q 次(转q -1次)公汽到达终点的方案,下面将这样的方案记为pD q .求任意公汽站点S i 到公汽站点S j 在pD q 方案下的最短时间,即对任意的p ,q ,以及任意的地铁站D k ,D l ,求出起点乘p 次公汽到可以直接转乘地铁站D k 的公汽站的最短时间,加上D k 到D l 的最短时间,再加上可以由地铁站D l 直接转乘的公汽站乘公汽q 次到达终点公汽站的最短时间.故S i →D k →D l →S j 在pD q 方案下所需的总时间为:t SD S (i ,j ,p ,q ,k ,l )=3N 1(i ,k ,p -1)+3N 2(l ,j ,q -1)+5(p +q -2)+13+2.5n D (k ,l )=3N 1(i ,k ,p -1)+3N 2(l ,j ,q -1)+2.5n D (k ,l )+5(p +q )+3(2)其中N 1(i ,k ,p -1)表示起点公汽站S i 乘p 次公汽到可以直接转乘地铁站D k 的公汽站的最小站数,N 2(l ,j ,q -1)表示由地铁站D l 直接转乘的公汽站乘公汽q 次到达终点公汽站S j822数　学　的　实　践　与　认　识38卷的最小站数.n D (k ,l )表示地铁站D k 到地铁D l 时所经过的最小站数,13表示公汽转地铁、地铁转公汽转乘所花费的时间之和.对于站点S i ,S j ,若已知p ,q ,那么N 1(i ,k ,p -1),N 2(l ,j ,q -1)仍然是两个公汽站点间的计算问题,可以借助于仅乘公汽方案的工作来进行计算.比如计算N 1(i ,k ,p -1)时首先找与地铁站D k 可以直接转乘的公汽站,然后利用(1)式计算公交站S i 乘p 次公汽分别到这些站点的最小站数,进一步比较得出最终的最小站数.类似可以计算N 2(l ,j ,q -1).若已知k ,l ,由于只有两条地铁线路,n D (k ,l )是容易计算的.下面是公汽转地铁再转公汽的最短时间模型.模型2m in{t SD S (i ,j ,p ,q ,k ,l ) 1Φp ,q <+∞,1Φk ,l Φ39,k ≠l } 注:要求得综合考虑公共汽车和地铁线路时的最短时间,只需比较单纯乘公汽的最短时间和上述最短时间就可以得到.3.2　模型求解在求解模型2时,对于k ,l 的遍历计算量并不是很大,主要困难在于p ,q 的遍历问题.我们也给出函数t SD S (i ,j ,p ,q ,k ,l )的一个下界.设n SD S (i ,j )表示从S i 乘车(公汽或地铁,可以转车任意次)到S j 的最小乘车站数.我们可以用D ijk stra 算法求出n SD S (i ,j ).定理3　t SD S (i ,j ,p ,q ,k ,l )ΕA (p +q ,i ,j ),其中A (x ,i ,j )=5.5x +2.5n SD S (i ,j )+3.(3) 证明　记M =N 1(i ,k ,p -1)+N 2(l ,j ,q -1)为乘车方案中乘公汽的站数,显然M Εp +q .由于总的最小站数为n SD S (i ,j ),显然有M +n D (k ,l )Εn SD S (i ,j ).于是t SD S (i ,j ,p ,q ,k ,l )=3M +2.5n D (k ,l )+5(p +q )+3Ε3M +2.5(n SD S (i ,j )-M )+5(p +q )+3=0.5M +2.5n SD S (i ,j )+5(p +q )+3Ε5.5(p +q )+2.5n SD S (i ,j )+3证毕.对于给定的站点S i ,S j ,根据定理3,我们可以给出求解综合考虑公共汽车和地铁线路时的最短时间模型的方法:Step 1　利用D ijk stra 算法求出nSD S (i ,j );令h =2;Step 2　令p 从1开始到h -1结束;q =h -p ;利用(2)、(3)式计算tSD S (i ,j ,p ,q ,k ,l )和A (p +q ,i ,j );对k ,l 遍历得:f (p ,h )=m in{tSD S (i ,j ,p ,q ,k ,l ) 1Φk ,l Φ39,k ≠l ;T SD S (i ,j ,h )=m in{f (p ,r ) 2Φr Φh }; Step 3　若T SD S (i ,j ,h )ΦA (p +q ,i ,j ),停,此时T SD S (i ,j ,h )即为最短乘车时间;否则令h =h +1,转Step 2;下面针对原题中的6对站点来求解.首先用D ijk stra 计算n SD S (i ,j ),结果见表3.92214期叶　军,等:公交转车的最短时间模型及求解表3　各对站点最短路径n SDS(i,j)点对335921828155720481097120485000820073014820485008723676 n SD S(i,j)12252411228对于第六对站点,由表3知S0087→S3676在公交转地铁再转公交情况下所需的时间根据定理3知最少需要5.5(1+1)+2.5×8+3=34m in,如果设r为乘公交的公交站数,在公交转地铁和地铁转公交两种情况下,即rΕ1,故所需的时间为3×r+2.5×(8-r)+5+4+4=33+0.5rΕ33.5m in由于站点S0087和S3676在地铁站附近,故而直接从S0087进地铁站D27做T2线经过8站到D36到S3676所需的时间是8×2.5+4+4+2=30m in,可见直接乘地铁的时间最短.但对于前5对站点,由于它们都不在地铁站附近,我们首先考虑公汽-地铁-公汽这种方案下的最短乘车时间.表4给出了在p+qΦ5时的求解.从表4中我们可以看到第1,3,4,5对站点,均有T SD S(i,j,5)<A(6,i,j).于是T SD S(i, j,5)已经是公汽转地铁再转公汽方案下的最短时间.表4　前5对站点最小乘车时间求解过程点对335921828155720481097120485000820073014820485t SD S(p+q)1+184.5116.59653.5387.5 1+27111095358.586.53 2+175.5118.51015492.5 1+376107310063.591.5 2+26231121005991.5 3+180.5117.5105.55697.5 1+47711210568.596.5 2+3671091056496.5 3+267114104.56196.5 4+185.5122.5110.559.5102.5T SD S(i,j,5)621079553.586.5A(6,i,j)6698.59663.591注　3)1+1,…,4+1表示p+q的取值情况.对于第二个点对S1557→S0481,我们可以继续扩大p+q的取值来求得最短乘车时间.这里我们采用另一简单的方法求出总的最短时间(仅考虑公汽以及综合考虑公汽和地铁).S1557到地铁线的最小站数为12(将S1557到地铁线附近的各个公汽站点作遍历搜索得到),而地铁到S0481最少站数显然不小于1.在p+q=6时,根据定理3的证明过程有t SD S(i,j,p,q,k,l)Ε0.5M+2.5n SD S(i,j)+5(p+q)+3Ε0.5×13+2.5×25+5×6=102但在表2中对于第二个点对不乘地铁时经过4次公交转乘只需要99m in,所以我们可以看出032数　学　的　实　践　与　认　识38卷第二个点对仅仅乘公汽进行转换就已经是最优的了.4　时间最优乘车方案综合以上内容,我们可以得出在公交转乘次数不超过5次的情况下,仅乘公汽及综合考虑公汽和地铁的最优方案及最优时间,见表5.仅乘公汽的时间最优解方案:S3359L324下行3站S1746L458唤行14站S1784L167下行1站S1828S1557L84下行12站S1919L189下行3站S3186L91上行10站S0902L254上行3站S0481S0971L13下行16站S2517L290环行13站S2159L469上行2站S0485S0008L198上行2站S1691L476下行5站S2085L017环行2站S0483L328上行2站S0525L103上行2站S0073S0148L308上行15站S3604L81下行2站S2361L156上行9站S2210L417下行3站S0485S0087L21下行1站S0088L231环行10站S0427L97下行1站S3676综合考虑公汽和地铁的时间最优解方案:S3359L324下行2站S2027L201上行3站S0609(D12)T26站S1961(D37)L428上行2站S1671L041下行1站S1828S1557L84下行12站S1919L189下行3站S3186L91上行10站S0902L254上行3站S0481S0971L049上行6站S0567(D01)T114站S2534(D15)L 156上行5站S2210L417下行3站S0485S0008L200上行6站S2534(D15)T13站D12T22站S0525(D25)L103上行2站S0073S0148L024上行4站S1487(D02)T113站S2534(D15)L156上行5站S2210L417下行3站S0485S0087(D27)T28站S3676(D36)表5　各对站点的最短乘车时间(注:时间不包括起始的3分钟)点对最短时间仅考虑公汽同时考虑公汽与地铁S3359→S1*******S1557→S0*******S0971→S048510395S0008→S0*******.5S0148→S048510286.5S0087→S3*******参考文献:[1]　2007年高教社杯全国大学生数学建模竞赛的B题评阅要点13214期叶　军,等:公交转车的最短时间模型及求解232数　学　的　实　践　与　认　识38卷M athematical M odel and Solution of theSystem of the Buses Cho icesYE Jun,　YAN G Zhen2hua(Co llege of M athem atics and Physics,N anjing U niversity of Po sts&T elecomm unicati ons,N anjing210003,Ch ina)Abstract:　W e establish the m athem atical model of p roblem one of p roblem B of2007Ch ineseU ndergraduate M athem atical Contest in M odeling the system of the buses cho ices.T hen w egive the exact so luti on of th is model.Keywords:　m athem atical model;the cho ice of the bus;the sho rtest ti m e期刊简介本刊主要刊登数学的最新的理论成果,及其在工业、农业、环境保护、军事、教育、科研、经济、金融、管理、决策等工程技术、自然科学和社会科学中的应用成果、方法和经验.主要任务是沟通数学工作者与其他科技工作者之间的联系,推动应用数学在我国的发展,为四化建设作贡献.主要栏目:数学建模、管理科学、工程、应用、问题研究、知识与进展、学科介绍、方法介绍、高等数学园地、数学史、研究简报、书刊评介、简讯.注:①投稿一式二份,原稿自己保存,编辑部不退还投稿的稿件.②编辑部不接收网上投稿.。

公交车数学建模[整理版]

摘要本文是为了开发一个解决长沙市公交线路选择问题的自主查询计算机系统。

在充分理解题意的基础上，我们从总体上把握，一致认为这是运筹学中的最短路问题。

我们所提供的这个系统，对于当乘客输入起始站和终点站，点击查询结果后，查询机就能很快地给出乘车路线及乘车所需要的最短时间，并且还可以给出相应的乘车费用。

也可以在有多个乘车站点的情况下，自主选择出最优乘车顺序以及相应的乘车最短时间和乘车费用。

公众的出行更加通畅、便利，但同时也面临多条线路的选择问题。

针对市场需求，我们设计了一个解决公交线路选择问题的自主查询计算机系统。

其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的各种不同需求。

对于问题一，在仅仅考虑公共汽车的换乘的时候，我们以最短的乘车时间和最优的乘车费用作为两个目标函数，建立相应的双目标规划模型：()Tmin和()Mmin。

对于问题二，在问题一的基础上，我们添加了排列组合模型，全列出所有的乘车顺序情况，由问题一所建模型求出各种情况下的最优时间和最优路费，然后综合比较选出所有情况中的最优乘车顺序。

利用Dijkstra算法解出我们所需要的结果。

我们同样利用了双目标函数的统筹规划原理，在Dijkstra的算法下，解决了在公共汽车换乘的问题，求得最短时间问题，找到了最合适的公交路线，均为最短的乘车时间和最优的乘车费用，从而更加完善了我们的公交系统。

本文的特点是在建立模型和算法的基础上，进行编程，使其具备系统查询功能，克服了人工查询数据的繁杂过程，使得到的结果更为准确，同时，此程序可以进行推广使用，为解决日常生活中最优路径的选择问题提供了方法，给人们的出行带来方便。

关键词：最短行程双目标网络模型 Dijkstra算法排列组合一、问题重述公共交通作为长沙市交通网络中的重要组成部分，由于公共交通对资源的高效利用，使得通过大力发展公共交通，实行公交优先成为缓解日趋严重的道路交通紧张状况的必然选择。

然而，面对迅速发展和不断更新的长沙市公共交通网，如何快速的寻找一条合理的乘车路线或换乘方案，成为长沙市居民和外地游客一个比较困惑的问题。

公交转车问题(数学建模)全解

问题分析
如何处理上面的多个目标？多目标的处理最常用的方法是单目标化，即采用加权平均等方法将多个目标结合形成一个单一的目标。本问题中，单目标化并不合适，比较适当的方法是对每个目标寻求最佳线路，然后让乘客按照自己的需求进行选择。
南京邮电大学数理学院杨振华制作 yangzhenhua@
问题分析
从实际情况考虑，不同的查询者有不同的要求。在数学上体现出目标的不同。一般可以考虑转车次数、乘车费用、乘车时间这3个目标。问题可以归结为多目标优化问题。
南京邮电大学数理学院杨振华制作 yangzhenhua@
公交转车问题
南京邮电大学理学院杨振华制作 yangzhenhua@
公交转车问题
针对市场需求，某公司准备研制开发一个解决北京市公交线路选择问题的自主查询计算机系统。为了设计这样一个系统，其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的各种不同需求。公交：指公共交通工具，包括公共汽车与地铁。
南京邮电大学数理学院杨振华制作 yangzhenhua@
基本参数设定
相邻公汽站平均行驶时间(包括停站时间)： 3分钟相邻地铁站平均行驶时间(包括停站时间)： 2.5分钟公汽换乘公汽平均耗时： 5分钟(其中步行时间2分钟) 地铁换乘地铁平均耗时： 4分钟(其中步行时间2分钟) 地铁换乘公汽平均耗时： 7分钟(其中步行时间4分钟) 公汽换乘地铁平均耗时： 6分钟(其中步行时间4分钟) 公汽票价：分为单一票价与分段计价两种，标记于线路后；其中分段计价的票价为：0～20站：1元；21～40站：2元； 40站以上：3元地铁票价：3元（无论地铁线路间是否换乘）注：以上参数均为简化问题而作的假设，未必与实际数据完全吻合。

一类公交车调度问题的数学模型及其解法

一类公交车调度问题的数学模型及其解法1. 背景介绍公交车作为城市交通的重要组成部分，其运营效率和服务质量直接影响市民出行体验。

而公交车调度问题则是保障公交线路运营效率和准时性的重要环节之一。

在日常运营中，由于路况、乘客量、车辆故障等影响因素，公交车的调度往往面临诸多挑战。

如何利用数学模型解决公交车调度问题成为了一个备受关注的课题。

2. 公交车调度问题的数学建模公交车调度问题的数学建模主要涉及到车辆的合理分配以及路线的优化规划。

在数学建模时，需要考虑的主要因素包括但不限于乘客量、车辆容量、交通状况、站点分布等。

而个体车辆的运行轨迹则需要综合考虑上述因素以及最优化算法对其进行分析。

3. 数学模型的构建针对上述因素，可以将公交车调度问题构建成一个复杂的优化模型。

该模型主要包括以下几个方面的内容：（1）乘客需求预测：通过历史数据和大数据分析，预测不同时段和不同线路的乘客需求，为车辆调度提供依据。

（2）车辆分配优化：根据乘客需求预测和实际路况，采用最优化算法确定每辆车的运行路线和发车间隔。

（3）站点排队优化：结合乘客上下车规律和站点的停靠条件，优化车辆在不同站点的排队顺序，以减少候车时间和提升服务效率。

（4）交通状况仿真：通过交通仿真模型，考虑城市交通状况对公交车运行的影响，提前对可能出现的拥堵情况进行预判，以调整车辆的发车时间和路线。

4. 数学模型的求解在构建好数学模型后，需要采用合适的方法对其进行求解。

常见的求解方法主要包括但不限于线性规划、遗传算法、模拟退火算法等。

在实际求解过程中，需要充分考虑不同方法的适用场景和对模型的拟合程度，以选择最合适的求解方法。

5. 案例分析以某市的公交系统为例，采用上述数学模型对其进行调度优化。

通过收集该市的实际路况数据、站点分布情况以及历史乘客需求数据，建立完整的数学模型。

然后运用遗传算法对其进行求解，得到了最优的车辆运行路线和发车间隔。

在模型求解后，将其应用于实际公交车调度中，并进行了一段时间的实际运行试验。

数学建模论文公交车调问题

2011年数学建模论文——对公交车调度问题的研究摘要：本文根据所给的客流量及运营情况排出公交车调度时刻表，以及反映客运公司和乘客的利益有多个指标，建立了乘客的利益及公司利益两个目标函数的多目标规划数学模型。

基于多目标规划分析法，进行数值计算，从而得到原问题的一个明确、完整的数学模型，并在模型扩展中运用已建的计算机模拟系统对所得的结果和我们对于调度方案的想法进行分析和评价。

首先通过数据的分析，并考虑到方案的可操作性，将一天划为；引入乘客的利益、公司利益作为两个目标函数，建立了两目标优化模型。

通过运客能力与运输需求(实际客运量) 达到最优匹配、满载率高低体现乘客利益；通过总车辆数较少、发车次数最少表示公司利益建立两个目标函数。

应用matlab中的fgoalattain进行多目标规划求出发车数，以及时间步长法估计发车间隔和车辆数。

关键字：公交车调度；多目标规划；数据分析；数学模型；时间步长法，matlab一问题的重述：1、路公交线路上下行方向各24站，总共有L 辆汽车在运行，开始时段线路两端的停车场中各停放汽车m辆，每两车可乘坐S人。

这些汽车将按照发车时刻表及到达次序次发车，循环往返地运行来完成运送乘客的任务。

建立数学模型，根据乘客人数大小，配多少辆车、多长时间发一班车使得公交公司的盈利最高，乘客的抱怨程度最小。

假设公交车在运行过程中是匀速的速度为v。

1路公交车站点客流量见下表从新汽车站出发到市检察院站点名称新汽车站汉庭花园天九湾电信公司天九湾车场西环小区步行街上车人数11 3 1 1 1 2 下车人数1 0 0 0 4 等待时间3.8 5 2 1.5 2站点名称实验小学莆一中后门十字街旧汽车站新街口市农行上车人数5 1 3 4 8 3下车人数1 0 0 1 0 1 等待时间3.8 3 5.3 14.1 3.8站点名称市公交公司中国银行凤凰山八十亩小区石室路口市公交稽证处上车人数3 1 3 3 2 2 下车人数2 3 3 9 2 3 等待时间1.7 1 0.52.5 2.2 5.5 站点名称北磨交通花园三信家园市政府龙桥市场市检察院上车人数2 0 0 0 0 0 下车人数4 2 25 7 10 等待时间4从市检察院出发到新汽车站站点名称市检察院龙桥市场市政府三信家园交通花园北磨上车人数17 3 0 1 2 7 下车人数0 1 1 1 1 4 等待时间3.5 1.2 2.84.8 2.6 4站点名称市公交稽证处石室路口八十亩小区凤凰山中国银行市公交公司上车人数2 3 1 5 8 3 下车人数1 0 12 2 1 等待时间3.3 1.6 5 4 0 9 站点名称市农行新街口旧汽车站十字街莆一中后门实验小学上车人 2 0 2 4 1 0数下车人数2 7 2 5 2 2 等待时间3.4 6 5 1站点名称步行街西环小区天九湾车场天九湾电信公司汉庭花园新汽车站上车人数0 0 1 0 0 0 下车人数3 1 24 3 14 等待时间11 已知数据及问题的提出我们要考虑的是莆田市的一路公交线路上的车辆调度问题。

公交车数学建模

B题：重庆市主城区公交线网的优化与评价姓名学院年级专业学号联系电话相关学科成绩高等数学线性代数概率统计数学模型数学实验英语四级英语六级徐清鹏09电气学院07班0989 87573 475张雅洁09电气学院01班0991 75566 480刘维09电气学院0109 92 83 525重庆市主城区公交线网的优化与评价摘要: “畅通重庆”是建设五个重庆的战略目标之一，通过有效融合公交网和轻轨网的,是实现这一目标的有效途径。

因此对重庆市主城区现有的地面公交线路进行优化和调整具有十分重要的意义。

针对问题一：采用定性与定量相结合的递阶层次分析法(AHP)对重庆市市现有的公交线路网现状进行进行分析，筛选了与公交线路网评价有关的四个方面（线路网络能力、客运能力、经济效益、环境影响）下的12个主要指标建立模型。

建立各个层次的判断矩阵，通过MATLAB 软件计算各个方面的总权重值并进行排序，并采用一致性判断指标决定判断的合理程度。

最后采用线性加权的的方法建立综合评价模型：N =∑E 1i ω1i +∑E 2i ω2i +∑E 3i ω3i +∑E 4i ω4i 3i=13i=13i=13i=1依据查询在重庆市主城通行的公交车数据及与选取指标相关数据，计算出各指标的有关系数，并参照公交线网络指标评价标准的建议值对各个指标评分，得出其得分为，等级为中。

针对问题二：鉴于公交系统网络的复杂性，我们没有采用常规的Dijkstra 算法,而是采用了基于公交停靠站换乘功能进行OD 预测。

算出铁路（或轻轨）停靠站的公交客运量。

同时建立了分别以剩余客流量,接运站点数量为目标的优化模型。

然后对OD 客流量剩余值进行确定，得到的由三部分（需要保留的路线，改变的路线布设，合并和消除的路线）构成的“轨道-接运公交网”。

针对问题三:我们主要以轻轨地铁路线为主干线对重庆市主城的公交线路进行规划设计。

由于规划年限较短，我们对乘坐公交的人口，公交车数量，客流量等因素采用马尔萨斯（Malthus ）模型。

全国大学生数学建模竞赛题目B题

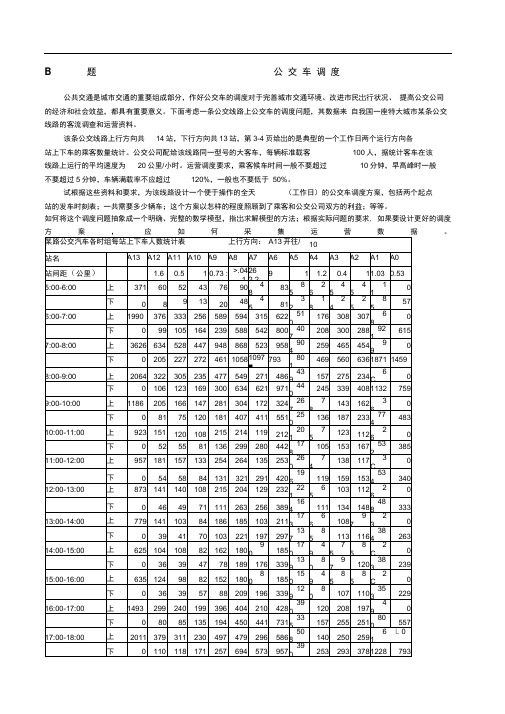
B 题公交车调度
公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民岀行状况、提高公交公司的经济和社会效益，都具有重要意义。

下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。

该条公交线路上行方向共14站，下行方向共13站，第3-4页给岀的是典型的一个工作日两个运行方向各
站上下车的乘客数量统计。

公交公司配给该线路同一型号的大客车，每辆标准载客100人，据统计客车在该
线路上运行的平均速度为20公里/小时。

运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般
不要超过5分钟，车辆满载率不应超过120%，一般也不要低于50%。

试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点
站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。

如何将这个调度问题抽象成一个明确、完整的数学模型，指岀求解模型的方法；根据实际问题的要求, 如果要设计更好的调度方案，应如何采集运营数据。

全国大学生数学建模竞赛题目B题

B题公交车调度公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。

下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。

该条公交线路上行方向共14站，下行方向共13站，第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。

公交公司配给该线路同一型号的大客车，每辆标准载客100 人，据统计客车在该线路上运行的平均速度为20公里/小时。

运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般不要超过5分钟，车辆满载率不应超过 120%，一般也不要低于50%。

试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。

如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。

公交线路转乘选择的优化-模型_毕业论文

公交线路转乘选择的优化模型摘要：本文以奥运会的公交线路换乘为大背景，建立了在公汽线路、地铁以及步行三种方式中综合进行路线转乘的模型。

此问题可以归结为两个站点之间的最短路问题，由于直接以站点构建最短路问题计算量较大，本文在处理三个问题时分别提出了相应的模型与求解算法，以乘坐时间最短为标准回答了问题一与问题二，对问题三提出了最短路模型。

在问题一建模过程中，我们以任意两条线路是否可以直接换乘为突破口，建立了以每条线路为顶点，两条线路之间的换乘信息为弧的图，将问题一归结为弧长可变的最短路问题，提出了结合动态规划方法与分枝定界思想的算法。

首先将题目所给出的路线与站点信息翻译为两条线路是否可以直接相交以及在何处相交的信息矩阵；其次以换乘时间最短或者费用最小为决策函数，建立动态规划问题；再次设计相应的算法进行求解。

通过求解，以最短时间为目标，问题一的结果如下所示（以(1),(2)组为例，其它见正文表1）：组（1）：S3359→S1828，1828458290333594120115S S S S L L L −→−−−→−−→−，最短时间73分钟，费用3元；组（2）：S1557→S0481，48131861919155746018984S S S S L L L −−→−−−→−−−→−，最短时间106分钟，费用3元。

同时文章对运算结果进行了相关分析。

在问题二建模过程中，沿用问题一的求解思想，将新增加的地铁视为新的线路，将所有线路信息转化为新的转乘矩阵，同时按照新的背景得到新的乘车时间与费用计算方法，同样以最短时间为目标，相同的算法可以得到问题二的结果（以(5),(6)组为例，具体见正文表2）：组（5）：S0148→S0485，48546621021487014851124S S D D S S L T L −→−-−→−-−−→−最短时间87.5分钟，费用5元；组（6）：S0087→S3676，3676362700872S D D S T -−→−-，最短时间28分钟（已经加上地铁站到地面站点的步行时间，其中地铁运行时间20分钟），费用3元。

数学建模论文_公交线路优化选择模型及算法

公交线路优化选择模型及算法摘要本文主要是针对两公汽站点之间的最佳公交路线选择问题而建立模型，对于给定的三种不同的具体情况，我们建立了以总换乘次数最少，乘车所消耗总时间最短以及乘车费用最少的多目标规划模型。

为建模方便，我们首先设定由起始站到终到站所经过的站点序列，并构建了各个站点换乘情况的0-1决策变量，将所有站点的换乘情况进行叠加得到总换乘次数。

乘车所消耗的总时间和总乘车费用，在不同情况下计算方式不同。

问题一只考虑公汽。

由从起点到终点经过的站点数目和换乘次数可得到总消耗时间，同时引入计价因子表示公汽计价方式计算乘车费用。

我们在5.1.5中设计了适当的算法并用Visual C++编程计算，得到各个目标值如下：按照起始站→终到站, 换乘次数, 总时间, 总票价的顺序为S3359→S1828, 1, 101, 3；S1557→S0481, 2, 106, 3；S0971→S0485, 1, 128, 3；S0008→S0073, 1, 83, 2；S0148→S0485, 2, 106, 3；S0087→S 3676, 1, 65, 2；详细结果及分析见5.1.6和附录1；同时我们还在5.1.7和5.1.8中讨论了适当增加换乘次数对乘车时间和费用的影响。

问题二同时考虑加入地铁的情况。

我们假定只有公汽换乘地铁和地铁换乘公汽两种情况。

乘地铁消耗的时间类似乘公汽消耗时间可计算得出；因换乘消耗的时间与初始的交通方式相关，我们引入了起点乘车方式因子λ。

总乘车费用类似问题一的情况可得。

利用Visual C++编程计算，我们得到此时各目标值如下：起始站→终到站, 换乘次数, 总时间, 总票价, S3359→S1828, 2, 101, 5；S1557→S0481, 2, 117, 5；S0971→S0485, 2, 96, 5, 13, 20；S0008→S0073, 2, 65.5, 5；S0148→S0485, 2, 87.5, 5；S0087→S 3676, 0, 33, 3；详细结果及分析见5.2.6。