有理数的加减混合运算(第3课时)课件
合集下载
有理数的加减混合运算(第3课时)课件

有何感受 感受 ?
我们感受到数学是一门十分有用的科学, 它能帮助我们分析、解决许多生活中实 际问题。
让我们在学习数学 中共同进步吧!
1.光明中学初一(1)班学生的平均身高是160厘米. (1)下表给出了该班6名同学的身高情况(单位:厘米). 试完成下表:
姓名 身高 身高与平均身高的差 小明 159 -1 +2 0 小彬 小丽 小亮 小颖 小山 154 +3 165
0 7 2 5.
(利用运算律进行结合)
如果取下关段的警戒水位作为0点,那么图 中的其他数据可以分别记作什么?并说明你 的思路. 最高水位记作:+1.9米
最高水位 35.3米
平均水位记作:-10.8 米 最低水位记作:-21.9 米
下关段
警戒水位 33.4 米 平均水位22.6 米 水位
解:该出租车离出发点的距离为: 15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4+( -5) =13千米 答:他距离出车的出发点13千米
有何收获?
生活中处处有数学, 只要我们去观察研究
会用数学去解决生活中的变化现象,对于几次 连续的变化情况可以用有理数的加减法去解决
很多实际问题可以转化为有理数的加减混合运 算来解决,根据需要可以“人为”地规定零点. 我们可以借助表格和折线统计图形象直观的反 映事物的变化情况
星期
练一练
某一中学初一(2)班学生的平均身高是160厘米 (1)下表给出了该班6名同学的身高情况(单位:厘
米),试完成下表.
姓名 小明 小彬 小丽 小亮 小颖 小山 154 163 -6 165 +5 159 162 160 身高 身高与平均身高的差值 -1 +2 0
有理数的加减混合运算(第3课时)精选教学PPT课件

2 3 2 3 8 1 1 1 2 1 1 (利用运算律进行结合) 4 4 2 2 44
0 7 2 5.
如果取下关段的警戒水位作为0点,那么图 中的其他数据可以分别记作什么?并说明你 的思路.
最高水位记作:+2米 平均水位记作:-3.1米 最低水位记作:-6.2米
日 一 二 三 四 五 六日
星期
如果让大家去研究水位的变化情 况,你该怎么做呢?说说你的计划?
实地考察
记录数据
分析数据
写出考察报告
练一练
某一中学初一(2)班学生的平均身高是160厘米
(1)下表给出了该班6名同学的身高情况(单位:厘
米),试完成下表.
姓名
小明 小彬 小丽 小亮 小颖 小山
身高
159 162 160 154 163 165
方法一: 通过计算每天的实际水位进行比较
星期
一二三四五六日
水位变化(米) +0.2 +0.81 -0.35 +0.03 +0.28 -0.36 -0.01
实际水位(米) 8.7 9.51 9.16 9.19 9.47 9.11 9.10
方法二: 对水位变化的数据求和
+0.2 + (+0.81) + (-0.35) + (+0.03) + (+0.28) + (-0.36) + (-0.01) = 0.60(米)
0.5+(-0.1)+0.42+(-0.15)+0.7+(-0.15)+0.75+(-0.1)+0.55+0.48 = 2.9 < 3
有理数的加减法混合运算PPT

有理数的加减法混合运 算PPT
演讲人
板块一、有理数基 本加、减混合运算
有理数的加减法混合运算PPT
有理数加法法则:
同号两数相加,取相同的符号,并 把绝对值相加.
同号两数相加,取相同的符号,并把绝对值相加.
②绝对值不相等的异号两数相加,取绝对值较大的加数符号,并用较大的绝对值减 去较小的绝对值.
两个加数相加,交换加数的位置,和不变.
示例:a+b=b+a(加法 交换律)
在右侧编辑区输入内容
②三个数相加,先把前两个数相加, 或者先把后两个数相加,和不变.
示例: (a+b)+c=a+(b+c)(
加法结合律) 有理数加法的运算技巧:
①分数与小数均有时,应 先化为统一形式.
在右侧编辑区输入内容
②带分数可分为整数与分 数两部分参与运算.
在右侧编辑区输入内容
③多个加数相加时,若有互为相反数 的两个数,可先结合相加得零.
在右侧编辑区输入内容
④若有可以凑整的数,即相 加得整数时,可先结合相加.
在右侧编辑区输入内容
⑤若有同分母的分数或易通 分的分数,应先结合在一起.
在右侧编辑区输入内容
两个加数相加,交换加数的位置,和不变.
1
⑥符号相同的数可以先结合 在一起.
一个数同0相加,仍得这个数.
一个数同0相加,仍得这个数.
有理数加法的运算步骤:
法则是运算的依据,根 据有理数加法的运算法 则,可以得到加法的运 算步骤:
①确定和的符号;
求和的绝对值,即确定是两个加数 的绝对值的和或差.
求和的绝对值,即确定是两个加数的绝对值的和或差.
有理数加法的运算律:
两个加数相加,交换加数的位置, 和不变.
演讲人
板块一、有理数基 本加、减混合运算
有理数的加减法混合运算PPT
有理数加法法则:
同号两数相加,取相同的符号,并 把绝对值相加.
同号两数相加,取相同的符号,并把绝对值相加.
②绝对值不相等的异号两数相加,取绝对值较大的加数符号,并用较大的绝对值减 去较小的绝对值.
两个加数相加,交换加数的位置,和不变.
示例:a+b=b+a(加法 交换律)
在右侧编辑区输入内容
②三个数相加,先把前两个数相加, 或者先把后两个数相加,和不变.
示例: (a+b)+c=a+(b+c)(
加法结合律) 有理数加法的运算技巧:
①分数与小数均有时,应 先化为统一形式.
在右侧编辑区输入内容
②带分数可分为整数与分 数两部分参与运算.
在右侧编辑区输入内容
③多个加数相加时,若有互为相反数 的两个数,可先结合相加得零.
在右侧编辑区输入内容
④若有可以凑整的数,即相 加得整数时,可先结合相加.
在右侧编辑区输入内容
⑤若有同分母的分数或易通 分的分数,应先结合在一起.
在右侧编辑区输入内容
两个加数相加,交换加数的位置,和不变.
1
⑥符号相同的数可以先结合 在一起.
一个数同0相加,仍得这个数.
一个数同0相加,仍得这个数.
有理数加法的运算步骤:
法则是运算的依据,根 据有理数加法的运算法 则,可以得到加法的运 算步骤:
①确定和的符号;
求和的绝对值,即确定是两个加数 的绝对值的和或差.
求和的绝对值,即确定是两个加数的绝对值的和或差.
有理数加法的运算律:
两个加数相加,交换加数的位置, 和不变.
有理数的除法第3课时有理数的加减乘除混合运算课件人教版七年级数学上册

解:原式=35 - (-6) =35+6 =41
先算乘除法 再将减法统一成加法计算
(3)4-(-6)÷3×10
解:原式= 4 -(-2)×10 = 4 -(-20) =4+20
先算乘除法 再将减法统一成加法计算
=24
(4)3×(-4)+ (-28)÷7
解:原式= - 12+(- 4) 先算乘除法 = -(12+4) 再按照加法法则进项计算 =-16
B.(-3)-(-3)
C.(-3)×(-3) D.(-3)÷(-3)
2.计算3-2×(-1)=( A )
A C
540
归纳总结
有理数加减乘除混合运算顺序:
1.先算乘除,再算加减; 2.同级运算从左往右依次计算; 3.如有括号,先算括号内的; 4.能用运算律的,应利用运算律.
作业设计
教材P38 习题1.4 第 8 题。
1.4.2 有理数的除法 第3课时 加减乘除运算
汇报人:郭项敏
学习目标 01 进一步掌握有理数的运算法则和运算律. 02 熟练地按有理数运算顺序进行混合运算. (重点、
难点).
复习旧知
你还记得怎么计算么? 计算:18-35+17-12 解:原式=18+(-35)+17+(-12)
=[18+17+(-35)]+(-12) =+(-12) =-12
课堂练习
例题精讲
例2、计算:
(1)[12 – 4(3-10)]÷4
解:原式= [12-4×(-7)]÷4
= [12 – (-28)]÷4
=40÷4 =10
归纳:有理数加减乘除混合运算,先
有理数的加减混合运算(第3课时)

三
-0.35
四五
+0.03 +0.28
六
-0.36
日
-0.01
(1)本周哪一天河流的水位最高?哪一天河 流的水位最低?它们位于警戒水位之上还 是之下?与警戒水位的距离分别是多少米?
解: 本周每天的水位记录为: 周一:33.4+0.20=33.60(m), 周二:33.4+0.20+0.81=34.41(m), ……
解: 本周每天的水位记录为: 周一:33.4+0.20=33.60(m), 周二:33.4+0.20+0.81=34.41(m), 周三:33.4+0.20+0.81-0.35=34.06(m), 周四:33.4+0.20+0.81-0.35+0.03=34.09(m), 周五:33.4+0.20+0.81-0.35+0.03+0.28=34.37(m),
如果规定向东为正,向西为负,司机小李 行车里程(单位:千米)为:
15、-2、5、-1、-10、-3、-2、12、4、-5.
解: 该出租车离出发点的距离为:
15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4
+( -5)=13(千米).
1.用正、负数表示相反意义的量.
2.利用有理数的加减混合运算解决实 际问题.
身高 159
154
165
身高与平均 身高的差
-1
+2
0
+3
(2)这6名学生中谁最高?
(3)最高与最矮的学生身高相差多少?
有理数的加减混合运算ppt课件(优秀)PPT资料

解: 1430.5 解: 2 .4 3 .5 4 .6 3 .5
= 4 0 .5 13 = 2 .4 4 .6 3 .5 3 .5
=4.54 =0.5.
=77 = 0.
( 3 ) ( 7 ) ( 5 ) ( 4 ) ( 1 0 ) ; 解: ( 7 ) ( 5 ) ( 4 ) ( 1 0 );
(- 2 0 ) + ( + 3 ) + ( + 5 ) + (- 7 ).
使问题转化为几个 有理数的加法.
例 计算: (- 2 0 ) + (+ 3 ) - (- 5 ) - (+ 7 ).
解: (- 2 0 )+ (+ 3 )- (- 5 )- (+ 7 ) = ( 2 0 ) ( 3 ) ( 5 ) ( 7 )
= [ ( - 2 0 ) + ( - 7 ) ] + [ ( + 5 ) + ( + 3 ) ]
= (-27)+(+8)
=-19.
这里使用了哪 些运算律?
引入相反数后,加减混合运算可以统一为加法运算.
a b c a b ( c).
算式
( 2 0 ) ( 3 ) ( 5 ) ( 7 )
是-20,3,5,-7 这四个数的和,为书写简单, 可以省略算式中的括号和加号,把它写为
答:这6只企鹅的总体重是24.15kg.
想一想:还可以怎样求?哪个方 法比较简便?
1. 有理数的加减混合运算可以统一为什么运算? 2. 你能说说使用加法结合律时遵循什么原那么么?
1.互为相反数的数相结合; 2.能凑整的数相结合; 3.同分母的数相结合.
-0.08, +0.09, +0.05,
-0.05, +0.08, +0.06
解:(-0.08)+(+0.09)+(+0.05)+(-0.05)+(+0.08)+(+0.06) =[(-0.08)+0.08]+[0.05+(-0.05)]+(0.09+0.06) =0+0+0.15 =0.15 4X6+0.15=24.15(kg)
北师大版七年级上册数学《有理数的加减混合运算》有理数及其运算培优说课教学复习课件(第3课时)

探究新知
下表是今年雨季流花河一周内的水位变化情况(上周末
的水位达到警戒水位).
星期 一 二 三 四 五 六 日
水位 变化 /m
+0.20 +0.81 -0.35 +0.03 +0.28 -0.36 -0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们 位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
课堂检测
拓广探索题
一家饭店,地面上18层,地下1层,地面上1楼为接待处, 顶楼为公共设施处,其余16层为客房;地下1层为停车场.
(1)客房7楼与停车场相差几层楼? (2)某会议接待员把汽车停在停车场,进入该层电梯,往 上14层,又下5层,再下3层,最后上6层,你知道他最后在哪 里? (3)某日,电梯检修,一服务生在停车场停好汽车后,只 能走楼梯,他先去客房,依次到了8楼、接待处、4楼,又回接 待处,最后回到停车场,他共走了几层楼梯?
周五:33.4+0.20+0.81-0.35+0.03+0.28=34.37(m).
周六:33.4+0.20+0.81-0.35+0.03+0.28-0.36=34.01(m). 周日:33.4+0.20+0.81-0.35+0.03+0.28-0.36-0.01=34.00(m). 所以周二的水位最高,周一的水位最低,它们都在警戒水位 之上。
课堂检测
能力提升题
则:(1)周三收盘时,每股是34.5元. (2)本周收盘最高价是每股35.5元,最低收盘价是每股26元. (3)买入时交易额为27×1000=27000(元), 手续费为27000×1.5‰=40.5(元), 卖出时交易额为28×1000=28000(元), 手续费和交易税共28000×(1.5‰+1‰)=70(元), 所以总收益为28000-27000-40.5-70=889.5(元).
有理数的加减混合运算(第3课时)课件

课堂小结
省略括号和加号的和的情势的化简与读法: 原理:在含有加减混合运算的式子中,利用有理数减法法 则将减法转化成加法,这样混合运算就被统一成加法运算, 本来的算式就转化为求几个正数、负数的和. 写法:在和式里,通常把各个加数的括号和它前面的加号 省略不写,写成省略括号和加号的和的情势.
新课讲授
典例分析
例2.下表为某个雨季某水库管理员记录的水库一周内的水位变化情 况,警戒水位为15 m(上周末的水位到达警戒水位).
星期 一 二 三 四 五 六 日 水位变 + + + + - + - 化/m 0.38 0.25 0.54 0.13 0.45 0.36 0.19 注:正数表示比前一天水位上升,负数表示比前一天水位降落. (1)本周哪一天水位最高?有多少米? (2)根据给出的数据,请利用折线统计图分析本周内 该水库的水位变化情况(在不放水的情况下).
以警戒水位为0点,用折线统计图表示在 不放水的情况下该水库一周内的水位变化
情况如图所示.
当堂小练
1.某地一天早晨的气温是-5 ℃,中午上升了9 ℃,午夜又降 落了7 ℃,则午夜的气温是( ) A.-3 ℃ B.-5 ℃ C.5 ℃ D.-9 ℃
当堂小练
2.小明近期几次数学测试成绩如下:第一次85分,第二次比第一
星期
一二 三 四 五 六 日
水位变化/m +0.20+0.81 -0.35 +0.03 +0.28 -0.36 -0.01
注:正号表示水位比前一天上升,负号表示水位比前一天降落. (1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位 于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
新课讲授
新课讲授
解:(1)星期四水位最高为(+0.38+0.25+0.54+0.13)+15=16.3(m); (2)由已知条件,可求出一周内各天相对于警戒水位的变化情况,列表
有理数的加减混合运算3 公开课一等奖课件

观察与思考
法一: 4.5+(-3.2)+(+1.1)+(-1.4) =5.6+(-4.6) =1(千米)
4.5+(-3.2)+(+1.1)+(-1.4)
法二: 4.5-3.2+1.1-1.4 =1.3+1.1-1.4 =2.4-1.4 =1(千米)
= 4.5-3.2+1.1-1.4 算式4.5-3.2+1.1-1.4的意义
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校:北京二中 报考高校: 北京大学光华管理学 院 北京市文科状元 阳光女孩--何旋
来自北京二中,高考成绩672分,还有20 分加分。“何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。” 班主任吴京梅说,何旋是个阳光女孩。 “她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。”吴老师说,何旋考出好成绩的秘 诀是心态好。“她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区 的学校捐书”。
结论
一、4.5减去3.2加上1.1减去1.4 二、4.5、-3.2、+1.1、-1.4的和
在代数里,一切加法与减法运算,都可以统 一成加法运算。 在一个和式里,把加号和每个数的括号省略, 所得到的算式并不会改变运算的结果;我们把这 个算式称作代数和。 如把和式4.5+(-3.2)+1.1+合运算可以统一成加法;
二、加法运算可以写成省略括号的形式。
语文
小魔方站作品 盗版必究
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取
有理数的加减混合运算(PPT)3-1
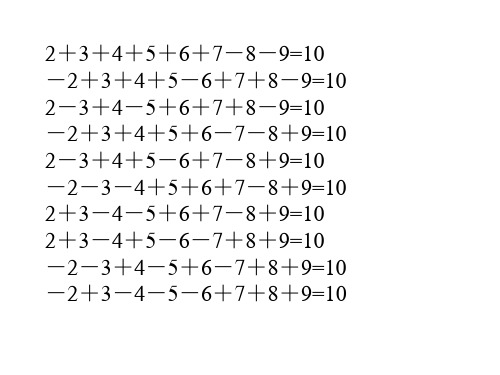
台拍摄的灶神星照片。黎明号在抵达灶神星之前会减速,预计每周发布更多照片。黎明号预计年7月日进入环灶神星轨道。美国宇航局证实黎明 号在年7月日进入环灶神星轨道,成为首个环绕小行星带小行星的探测器。黎明号确切入轨时间尚不清楚,这是由于当时天文学家只能估计灶神 星质量与重力场,无法准确得知其数据。而黎明号已进入轨道,便能反过来计算灶神星的质量与重力场。黎明号在7月7日:UTC重新检测搭载的设 备仪器。黎明号在9月7日进入距离灶神星8公里的公转轨道,环绕一周的时间为.小时。黎明号后来在月8日进入另一个公转轨道,距离灶神星只 有公里,环绕一周的时间为.小时 。美国宇航局在年月首度公开黎明号获得的灶神星初步数据,估计灶神星的金属核心直径为公里。美国宇航局 科学家进一步将灶神星视为特别的一种小行星,认为它是; 老域名::老域名购买 ;与岩石行星同时形成的大型小行星残存。 年9月7日,“黎明”号已在美国东部时间日凌晨时分离开灶神星轨道,向谷神星飞去。若一切顺利,“黎明”号有望成为第一个环绕两颗不同天 体运行的无人探测器。木星是一个巨大的液态氢星体。随着深度的增加,在距离表面至少千米深处,液态氢在高压和高温环境下形成。据推测,
例1填空:
(-8)+ =-5;(-8)+ 8+ =-7;(-8)+ =48)- =4
=-3; =-3;
解:(-8)+ 3 =-5;(-8)+ 5 =-3; 8+ (-15 ) =-7;(-8)+ 12 =4 (-8)- (-3) =-5;(-8)- (-5) =-3; 8- 15 =-7;(-8)- (-12) =4
木星的中心是一个含硅酸盐和铁等物质组成的核区,物质组成与密度呈连续过渡。木星是四个气体行星(又称类木行星)中的一个:即不以固体 物质为主要组成的行星,它是太阳系中体积最大的行星,赤道直径为98千米。木星的密度为.g/cm,在气体行星中排行第二,但远低于太阳系中 四个类地行星。组成成分木星的高层大气是由体积或气体分子百分率约88-9%的氢和约8-%的氦所组成。由于氦原子的质量是氢原子的四倍,探 讨木星的质量组成时比例会有所改变:大气层中氢和氦分别占了总质量的7%及%,余的%为其他气体物质,包括微量的甲烷、水蒸气、氨以及 硅的化合物。另外木星也含有微量的碳、乙烷、硫化氢、氖、氧、磷化氢、硫等物质。大气最外层有冷冻的氨的晶体。木星上也透过红外线及紫
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
星期
一
+0.20
二
+0.81
三
-0.35
四
+0.03
五 六
+0.28 -0.36
日
-0.01
水位变化 (米)
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(4): 以警戒水位为0点,用折线统计图表示本 周的水位情况。 水位/米
1.0
0.8 0.6 0.4 0.2
日
一 二 三 四 五 六 日
二
+0.81
三
-0.35
四
+0.03
五 六
+0.28 -0.36
日
-0.01
水位变化 (米)
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
从表格的数据中你能获得哪些信息
(1)本周哪一天河流的水位最高?哪一天 最低?它们位于警戒水位之上还是之下? 与警戒水位的距离分别为多少米?
(1)方法一: 通过计算每天的实际水位进行比较 星期 一 二 三 四 五 六 日
解:该出租车离出发点的距离为: 15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4+( -5) =13千米 答:他距离出车的出发点13千米
有何收获?
生活中处处有数学, 只要我们去观察研究
会用数学去解决生活中的变化现象,对于几次 连续的变化情况可以用有理数的加减法去解决
很多实际问题可以转化为有理数的加减混合运 算来解决,根据需要可以“人为”地规定零点. 我们可以借助表格和折线统计图形象直观的反 映事物的变化情况
(2)谁最高? 谁最低? (3)最高与最矮的学生身高相差多少?
2.小明的父亲上星期六买进某公司股票1000股, 每股27元,下表为本周内每日该股票的涨跌情 况(单位:元)
星期 一 二 三 四 五 六
每股 张跌
+4
+4.5
—1
-2.5
-6
+2
⑴星期三收盘时,每股是多少元? ⑵本周内最高价是每股多少元?最低每 股多少元? ⑶已知小明父亲买进股票时付了1.5‰的手 续费,卖出时需付成交额1.5‰的手续费 和1‰的交易税,如果他在周六收盘前将 全部股票卖出,他的收益情况如何?
第二章 有理数及其运算
6. 有理数的加减混合运算(三)
梳理知识 1.有理数加减混合运算的步骤
(1)把算式中的减法都转化为加法; (2)进行运算(尽可能利用运算律简化计算).
3 1 1 计算: 2 (8 ) (2 ) 0.25 1.5 2.75 4 2 4 3 1 1 1 1 3 解:原式 2 8 2 1 2 (把加减运算统一为加法) 4 2 4 4 2 4 3 3 1 1 1 1 2 2 8 1 2 4 4 2 2 4 4
0 7 2 5.
(利用运算律进行结合)
如果取下关段的警戒水位作为0点,那么图 中的其他数据可以分别记作什么?并说明你 的思路. 最高水位记作:+1.9米
最高水位 35.3米
平均水位记作:-10.8 米 最低水位记作:-21.9 米
下关段
警戒水位 33.4 米 平均水位22.6 米 水位
星期
练一练
某一中学初一(2)班学生的平均身高是160厘米 (1)下表给出了该班6名同学的身高情况(单位:厘
米),试完成下表.
姓名 小明 小彬 小丽 小亮 小颖 小山 154 163 -6 165 +5 159 162 160 身高 身高与平均身高的差值 -1 +2 0
+3
(2)谁最高?谁最矮?
小山最高,小亮最矮
最低水位 11.5米
住在江边的小明同学记录了今年梅雨季 节下关段一周的水位变化情况:(上周日 的水位达到了警戒水位)
星期 水位变化 (米)
一
+0.20
二
+0.81
三
-0.35
四
+0.03
五 六
+0.28 -0.36
日
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
星期
一
+0.20
水位变化(米) +0.2 +0.81 -0.35 +0.03 +0.28 -0.36 -0.01 实际水位(米) 33.60 34.41 34.06 34.09 34.37 34.01 34.00
方法二: 通过计算每天的水位变化进行比较。
星期
一
+0.20
二
+0.81
三
-0.35
四
+0.03
五 六
+0.28 -0.36
日
-0.01
水位变化 (米)
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(2)与上周日相比,本周日河流的水位是 上升了还是下降了?为什么?你是怎么知 道的?有哪些方法?
(2): 通过对水位变化的数据求和来判断。
(+0.2 0)+ (+0.81) + (-0.35) + (+0.03) +(+0.28) +(-0.36) + (-0.01) = 0.60(米)
11厘米
(3)最高与最矮的学生身高相差多少?
帮帮我
做个有心人
南京出租车司机小李某一时段 全是在中山东路上来回行驶,你能否知道 在他将最后一位乘客送到目的地时,他距 离出车的出发点有多远?
的看 数我 据记 ຫໍສະໝຸດ 录如果规定向东为正,向西为负,我行车里 程(单位:千米)为: 15, -2, 5, -1, -10, -3, -2, 12, 4, -5,
有何感受 感受 ?
我们感受到数学是一门十分有用的科学, 它能帮助我们分析、解决许多生活中实 际问题。
让我们在学习数学 中共同进步吧!
1.光明中学初一(1)班学生的平均身高是160厘米. (1)下表给出了该班6名同学的身高情况(单位:厘米). 试完成下表:
姓名 身高 身高与平均身高的差 小明 159 -1 +2 0 小彬 小丽 小亮 小颖 小山 154 +3 165
