一般约束非线性规划问题的光滑牛顿法

合集下载

高斯牛顿法求解非线性问题

高斯牛顿法求解非线性问题在科学研究、工程设计等领域中，有许多问题都可以归纳为非线性问题，例如曲线拟合、最小二乘法拟合、非线性规划等。

如何高效地求解这些问题是一个重要的课题。

高斯牛顿法(Gauss-Newton method)是一种常用的优化算法，被广泛应用于求解非线性问题。

高斯牛顿法的基本思想是：将非线性问题转化为最小二乘问题，然后使用线性最小二乘法求解。

具体而言，假设有一个由m个参数和n个数据点组成的非线性模型：f(x) = (f1(x),f2(x),...,fn(x))^T其中，x = (x1,x2,...,xm)^T 为参数向量，fi(x)为第i个观测值。

若将f(x)看作一个向量函数，则该函数在x处的导数可以用雅可比矩阵来表示：J(x) = [∂f1(x)/∂x1,∂f1(x)/∂x2,...,∂f1(x)/∂xm；∂f2(x)/∂x1,∂f2(x)/∂x2,...,∂f2(x)/∂xm；.............................∂fn(x)/∂x1,∂fn(x)/∂x2,...,∂fn(x)/∂xm]雅可比矩阵是一个n×m的矩阵，表示参数向量对向量函数的导数。

对于非线性模型，其导数难以直接求解，因此需要采用近似方法。

高斯牛顿法采用的是一阶泰勒展开式，将非线性模型在x 处展开：f(x+Δx) ≈ f(x) + J(x)Δx其中，Δx为参数向量x的增量，即x+Δx为新的参数向量。

将上式两边平方，再加上一个权重矩阵W，得到最小二乘问题：min Δx ||sqrt(W)(f(x+Δx)-f(x))||^2上式中，||·||表示向量的欧几里得长度，W为一个n×n的对角矩阵，其作用是赋予不同观测值不同的权重。

将上式展开，得到：min Δx (f(x)+J(x)Δx-y)^TW(f(x)+J(x)Δx-y)其中，y为n×1的向量，表示原始数据点。

求解非线性互补问题的光滑牛顿法的开题报告

求解非线性互补问题的光滑牛顿法的开题报告一、研究背景和意义非线性互补问题（nonlinear complementarity problem，NCP）在社会、经济、工程、物理等领域中有着广泛的应用。

例如，在经济学领域中，NCP可以用来研究市场竞争中的均衡状态；在工程学领域中，NCP可以用来描述交通、能源等系统的优化问题。

然而，NCP问题的求解并不容易，因为其非线性程度较高，求解难度较大。

为了提高求解NCP问题的效率和精度，需要发展有效的算法和方法来解决此类问题。

牛顿法是一种非常有效的数值方法，被广泛应用于求解最优化问题。

在解决NCP 问题时，牛顿法也是常用的算法之一。

与线性最优化问题类似，牛顿法通过迭代的方式逐步逼近最优解。

但是，由于NCP问题非线性程度较高，导致求解牛顿迭代中的线性方程组非常困难。

因此，如何利用牛顿法来高效地求解NCP问题，成为了理论和应用研究的热点之一。

二、研究内容本文将研究非线性互补问题的光滑牛顿法。

首先，对NCP问题进行深入的分析和研究，介绍了NCP问题的定义和性质以及牛顿法求解NCP的基本思想。

随后，进一步介绍了光滑化技术及其应用。

由于NCP问题非线性程度较高，求解难度较大，因此，本文选择使用光滑化技术来对问题进行处理。

在此基础上，结合牛顿法的基本思想，提出了光滑牛顿法求解NCP问题的具体算法流程，并对该算法的存在性和收敛性进行理论分析和证明。

三、研究方法本文将采用理论分析和数值实验相结合的方法，对光滑牛顿法进行研究和验证。

在理论分析部分，通过对光滑牛顿法的存在性、收敛性和收敛速度进行分析和讨论，并对算法进行改进和优化，以提高算法的收敛速度和精度。

在数值实验部分，选取不同的NCP实例，在MATLAB等数值计算软件上进行算法实现和验证，并通过比较不同算法的计算时间、迭代次数、收敛速度等指标，评价不同算法的优劣性。

四、研究进展目前，本文已对非线性互补问题进行了深入的研究和分析，理论分析部分已取得了一定的进展。

最优化理论方法——牛顿法

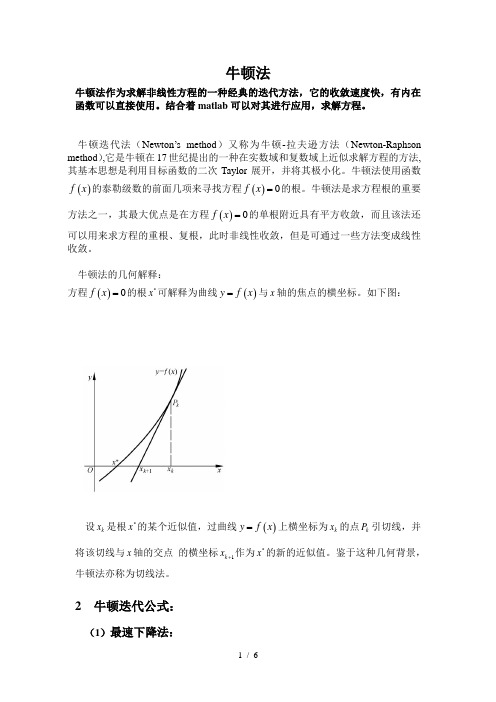
牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法，它的收敛速度快，有内在函数可以直接使用。

结合着matlab 可以对其进行应用，求解方程。

牛顿迭代法（Newton ’s method ）又称为牛顿-拉夫逊方法（Newton-Raphson method ）,它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开，并将其极小化。

牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。

牛顿法是求方程根的重要方法之一，其最大优点是在方程()0f x =的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时非线性收敛，但是可通过一些方法变成线性收敛。

牛顿法的几何解释：方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。

如下图：设k x 是根*x 的某个近似值，过曲线()y f x =上横坐标为k x 的点k P 引切线，并将该切线与x 轴的交点的横坐标1k x +作为*x 的新的近似值。

鉴于这种几何背景，牛顿法亦称为切线法。

2 牛顿迭代公式：（1）最速下降法：以负梯度方向作为极小化算法的下降方向，也称为梯度法。

设函数()f x 在k x 附近连续可微，且()0k k g f x =∇≠。

由泰勒展开式： ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- （*）可知，若记为k k x x d α-=，则满足0Tk k d g <的方向k d 是下降方向。

当α取定后，Tk k d g 的值越小，即T kk d g -的值越大，函数下降的越快。

由Cauchy-Schwartz 不等式：T k k kk d g d g ≤，故当且仅当k k d g =-时，Tk k d g 最小，从而称k g -是最速下降方向。

最速下降法的迭代格式为： 1k k k k x x g α+=-。

数学优化中的牛顿法和拟牛顿法

数学优化中的牛顿法和拟牛顿法在数学中，优化是一个非常重要的研究领域，其目的是找到使某个函数达到最大或最小值的变量集合。

在实际应用中，很多问题都可以转化为优化问题，如机器学习、经济学、物理学等。

在优化领域中，牛顿法和拟牛顿法是两种常见的方法。

本文将介绍这两种优化方法的基本原理、优缺点以及应用场景。

一、牛顿法牛顿法（Newton's method）是由数学家牛顿发明的非线性优化方法，其思想是利用函数的泰勒级数展开进行逼近。

具体来说，牛顿法先求出目标函数的一阶和二阶导数，然后使用二阶导数来逼近目标函数本身，进而得到近似最优解。

牛顿法的数学公式如下：$$\boldsymbol{x}_{k+1}= \boldsymbol{x}_{k} -{\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)^{-1}}\boldsymbol{\nabla} f(\boldsymbol{x}_k)$$其中，$\boldsymbol{x}_k$ 表示第 $k$ 次迭代的解，$\boldsymbol{\nabla} f(\boldsymbol{x}_k)$ 和$\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)$ 分别表示目标函数在$\boldsymbol{x}_k$ 处的一阶和二阶导数。

牛顿法的优点是收敛速度非常快，通常只需要很少的迭代次数即可达到最优解。

另外，牛顿法适用于连续可微、二阶可导的函数，因此适用范围广。

然而，牛顿法也存在一些缺点，例如无法处理不可导或一阶可导但二阶不可导的函数。

此外，牛顿法需要计算目标函数的二阶导数，因此在大规模问题上计算成本很高。

二、拟牛顿法拟牛顿法（quasi-Newton method）是一类基于牛顿法的优化算法，它通过逼近目标函数的海森矩阵来求解。

拟牛顿法没有计算海森矩阵的显式表达式，而是通过估计海森矩阵的变化来逼近。

最简单和最流行的拟牛顿法是BFGS算法和L-BFGS算法。

五种最优化方法

五种最优化方法1. 最优化方法概述最优化问题的分类1）无约束和有约束条件；2）确定性和随机性最优问题（变量是否确定）；3）线性优化与非线性优化（目标函数和约束条件是否线性）；4）静态规划和动态规划（解是否随时间变化）。

最优化问题的一般形式（有约束条件）：cnin f（X）h （X} = OJ = U^.Ls, （X）2OJ = \…2m式中f（X）称为目标函数（或求它的极小，或求它的极大）,si（X）称为不等式约束，hj（X）称为等式约束。

化过程就是优选X,使目标函数达到最优值。

2. 牛顿法简介1）解决的是无约束非线性规划问题；2）是求解函数极值的一种方法:3）是一种函数逼近法。

原理和步骤牛顿法的基本思想是.在槌小点咐近用二阶Taylor 名法式近似口标函敷理而求出相小点的估计值考志问题min /（.r ） . r G B 1, i 9. 3. I ）—U) \ / NX M J7 在贝「附近・r a s ，x 因此可用函数忒」，的极小点作为目标函数js 的槌小点的估计.如果L 是J'）的极小点的•个估iR 苏么利用（9.拌式可以待到极小的的个迎•步的彷计，这样，利用迭代公式【4 3.2）^以得到一个序列｝*可以旺明,在 ■定条件下「这个序列收敛于问题3.以）的最优解，而且是2级收敛...■h - …n -i .m. v . ■» rt l f » JL i ■』-A-l- rv J- E -1 4dT_ n. u. ♦・3. 最速下降法（梯度法）最速下降法简介1）解决的是无约束非线性规划问题；2）是求解函数极值的一种方法;3）沿函数在该点处目标函数下降最快的方向作为搜索方向:最速下降法算法原理和步骤4. 模式搜索法（步长加速法）简介1）解决的是无约束非线性规划问题；型\ uf 符到.*『）的洗点,记作I ' J ' JL ■M]2）不需要求目标函数的导数，所以在解决不可导的函数或者求导异常麻烦的函数的优化问题时非常有效。

牛顿法原理

牛顿法原理
牛顿法是一种可以将非线性收敛到最小值的迭代法，是以传统意义上的函数最小值求解和极值求解具有重要意义的数值解法之一。

牛顿法（Newton's Method）或称牛顿迭代法，由英国数学家牛顿提出。

它是一种以逐步逼近的方式来求解极值，也就是最优求解法。

它可以帮助求解数学中连续函数极值及根的值，是近代数值分析的重要组成部分，也是当今最重要的最优方法之一。

牛顿法的基本思想是，如果一个连续函数的图像在某一点处有极值，那么该点处函数的导数为零，它即为函数的极值点。

根据这一思想，牛顿法寻找极值点，即就是不断从起点开始，计算梯度并根据梯度计算新的点，然后继续重复上面的步骤，直到收敛为止。

牛顿法的具体步骤有：
（1）确定变量的初始值，使用方程组求解；
（2）计算变量的一阶偏导数；
（3）根据一阶偏导数的函数值更新变量的值；
（4）用新值计算梯度，若精度满足要求，则可结束；若未满足要求，则重复步骤2和3。

在求解函数极值时，牛顿法优于迭代法。

牛顿法不仅使函数值逐渐收敛到极值，而且保持精度高。

其收敛速度快，收敛精度高，且稳定性好，而迭代法则收敛缓慢，而且收敛精度也不高。

总之，牛顿法是通过不断迭代计算求取函数极值的一种简便有效的求解方法，利用它求解特定类型函数的极值及其根可以弥补非线性方程其他求解方法的盲点，大大的提高了求解的效率。

非线性方程的牛顿法

求函数 f x x 10 x 精度要求： 106
3

例题2
2
19.68x 10.944 的正实根
用Matlab画图，查看根的分布情形
从图形中我们可以看出：在x=7和x=8 之间有一单根；在x=1和x=2 之间有一重根。
初值x0＝8.0 时,计算的是单根, The iterative number is 28,The numerical solution is 7.600001481 初值x0＝1.0 ,计算的是重根, The iterative number is 1356,The numerical solution is 1.198631981
重复上述过程
xk 1
f ( xk ) xk f ( xk )
牛顿法的几何意义
Tangent line : y f ( x0 ) f ( x0 )( x x0 )
y
f ( x0 ) x1 x0 f ( x0 )
x*
x2
x
x1 x0
牛顿法也称为切线法
f ( x1 ) x2 x1 f ( x1 )
例3:设C为正实数,导出用牛顿法求 C 的公式,并证明 2 en 迭代序列的误差 en xn C 满足 en 1 2 xn 2 x C 解：设 x C ，则于是有
f ( x) x 2 C, f ' ( x) 2x, f ' ' ( x) 2
由于 f (0) C, f ( C 1) 2 C 1 0 ], 所以在 [0,1 C ] 内有一正根.又在 [0,1 C 内 f ' ( x) 0, f ' ' ( x) 0根据定理得牛顿迭代格式为:

求解非线性互补问题的一个新的光滑牛顿法

１光滑牛顿算法
首先定义函数：＋Ｘ尺＋Ｒ＋如下：
卢＝ＨｚＩｉ｛，Ｉ（）ｌ｝（）ｙＩ（）Ｉｎ１ｌ彳Ｉ，１ｍ
其中 ∈ ０１是某个常数．（，）
（０１）
第２期
陈
争，昌凤：马求解非线性互补问题的一个新的光滑牛顿法
陈争马昌凤２，
（．１福建江夏学院信息系，福建福州３００；．建师范大学数学与计算机科学学院，５１８２福福建福州３００）５０７
摘要：通过利用带惩罚项的ＦＢ函数将非线性互补问题转化为等价的光滑方程组．并在此基础上提出
了一个求解Ｐ一函数非线性互补问题的光滑牛顿法，０同时给出了算法的全局收敛性以及局部二次收敛性结果．
Ｄ３：ｉ｛。） … ，（），（）＝ｄａ｛】） … ，ｚ｝（）＝ｄａｃ（，Ｃ｝Ｄ４ｚ：ｉｄ（，ｄ（），ｇｎｇ
其中
ａ＝ｉ－：（一ｚ）、ｃ＝（）ｉ詈＋（Ｆｚ（）
’‘ ・舌，ｂ＝ｉ一耋（兰ｚ）、））（斋，１＋
数值实验表明所提出的算法是有效的．
关键词：非线性互补问题；光滑牛顿法；全局收敛性；部二次收敛性局文献标识码：Ａ文章编号：６３—１７（０２００００１７６０２１）２— ０１— ５中圈分类号：２２２０４．３
０引言
通常利用ＮＰ函数把非线性互补问题（）Ｃ１转化成一个非线性方程组（）０＝来求解．但一般来说这里的：是非光滑的，这就给求解方程组带来了数值上的困难．为了解决这一困难，一般是通过构

非线性优化与约束优化问题的求解方法

非线性优化与约束优化问题的求解方法非线性优化问题是在目标函数和约束条件中包含非线性项的优化问题。

约束优化问题是在目标函数中加入了一些约束条件的优化问题。

解决这些问题在实际应用中具有重要意义，因此研究非线性优化和约束优化问题的求解方法具有重要的理论和实际意义。

一、非线性优化问题的求解方法非线性优化问题的求解方法有很多，下面介绍几种常见的方法：1. 黄金分割法：黄金分割法是一种简单但有效的搜索方法，它通过不断缩小搜索范围来逼近最优解。

该方法适用于目标函数单峰且连续的情况。

2. 牛顿法：牛顿法利用目标函数的一阶和二阶导数信息来逼近最优解。

该方法收敛速度较快，但在计算高阶导数或者初始点选取不当时可能产生不稳定的结果。

3. 拟牛顿法：拟牛顿法是对牛顿法的改进，它通过逼近目标函数的Hessian矩阵来加快收敛速度。

拟牛顿法可以通过不同的更新策略来选择Broyden-Fletcher-Goldfarb-Shanno（BFGS）方法或者DFP方法。

4. 全局优化方法：全局优化方法适用于非凸优化问题，它通过遍历搜索空间来寻找全局最优解。

全局优化方法包括遗传算法、粒子群优化等。

二、约束优化问题的求解方法约束优化问题的求解方法也有很多，下面介绍几种常见的方法：1. 等式约束问题的拉格朗日乘子法：等式约束问题可以通过引入拉格朗日乘子来转化为无约束优化问题。

通过求解无约束优化问题的驻点，求得原始约束优化问题的解。

2. 不等式约束问题的罚函数法：不等式约束问题可以通过引入罚函数来转化为无约束优化问题。

罚函数法通过将违反约束条件的点处添加罚项，将约束优化问题转化为无约束问题。

3. 逐次二次规划法：逐次二次规划法是一种常用的求解约束优化问题的方法。

该方法通过依次处理逐个约束来逼近最优解，每次处理都会得到一个更小的问题，直至满足所有约束条件。

4. 内点法：内点法是一种有效的求解约束优化问题的方法。

该方法通过向可行域内部逼近，在整个迭代过程中都保持在可行域内部，从而避免了外点法需要不断向可行域逼近的过程。

非线性规划的解法

非线性规划的解法非线性规划是一类重要的数学规划问题，它包含了很多实际应用场景，如金融市场中的资产配置问题，工程界中的最优设计问题等等。

由于非线性目标函数及约束条件的存在，非线性规划问题难以找到全局最优解，面对这样的问题，研究人员提出了众多的解法。

本文将从梯度法、牛顿法、共轭梯度法、拟牛顿法等方法进行介绍，着重讨论它们的优劣性和适用范围。

一、梯度法首先介绍的是梯度法，在非线性规划中，它是最简单的方法之一。

梯度法的核心思想是通过寻找函数的下降方向来不断地优化目标函数。

特别是在解决单峰函数或弱凸函数方面优势明显。

然而，梯度算法也存在一些不足之处，例如：当函数的梯度下降速度过慢时，算法可能会陷入局部最小值中无法跳出，还需要关注梯度方向更新的频率。

当目标函数的梯度非常大，梯度法在求解时可能会遇到局部性和发散性问题。

因此，它并不适合解决多峰、强凸函数。

二、牛顿法在牛顿法中，通过多项式函数的二阶导数信息对目标函数进行近似，寻找下降方向，以求取第一个局部极小值，有时还可以找到全局最小值。

牛顿法在计算方向时充分利用二阶导数的信息，使梯度下降速度更快，收敛更快。

因此，牛顿法适用于单峰性函数问题，同时由于牛顿法已经充分利用二阶信息，因此在解决问题时更加精确，准确性更高。

但牛顿法的计算量比梯度法大，所以不适合大规模的非线性规划问题。

此外，当一些细节信息不准确时，牛顿法可能会导致计算数值不稳定和影响收敛性。

三、共轭梯度法共轭梯度法是非线性规划的另一种解法方法。

共轭梯度法沿预定义的方向向梯度下降，使梯度下降的方向具有共轭性，从而避免了梯度下降法中的副作用。

基于共轭梯度的方法需要存储早期的梯度，随着迭代的进行，每个轴线性搜索方向的计算都会存储预定的轴单位向量。

共轭梯度方法的收敛速度比梯度方法快，是求解非线性规划的有效方法。

四、拟牛顿法拟牛顿法与牛顿法的思路不同，它在目标函数中利用Broyden、Fletcher、Goldfarb、Shanno（BFGS）算法或拟牛顿法更新的方法来寻找下降方向。

非线性规划的相关概念

非线性规划的相关概念引言非线性规划是数学规划领域中的一个重要研究方向，它是线性规划的推广和扩展。

在许多实际问题中，约束条件和目标函数往往是非线性的，因此需要非线性规划方法来解决这些问题。

本文将介绍非线性规划的基本概念和相关理论。

基本概念1. 可行解在非线性规划中，可行解指的是满足约束条件的解。

具体地，给定约束条件和目标函数，如果存在一组解使得所有约束条件都得到满足，那么这组解就是可行解。

非线性规划的目标是找到一个可行解，使得目标函数值最小或最大。

2. 局部极小解和全局极小解在非线性规划中，局部极小解指的是在某个局部范围内，目标函数值最小的可行解。

全局极小解指的是在整个可行域内，目标函数值最小的可行解。

在非线性规划中，寻找全局极小解往往非常困难，因为非线性规划问题一般没有全局最优解的性质。

因此，通常采用近似算法来寻找接近全局极小解的解。

3. 无约束问题和约束问题非线性规划可以分为无约束问题和约束问题。

无约束问题是指在没有约束条件的情况下，找到目标函数的最小值或最大值。

约束问题是指在满足一组约束条件的情况下，找到目标函数的最小值或最大值。

约束问题通常比无约束问题更加复杂，因为需要考虑约束条件的影响。

相关理论1. 梯度下降法梯度下降法是非线性规划中常用的优化方法之一。

基本思想是通过迭代更新解，使得目标函数值逐渐降低。

具体地，梯度下降法使用目标函数的梯度信息来指导搜索方向，并选择适当的步长来更新解。

该方法通常在局部范围内找到局部极小解，并且易于实现。

2. 牛顿法牛顿法是一种经典的非线性优化方法，广泛应用于非线性规划问题的求解。

它利用目标函数和约束条件的一阶和二阶导数信息来更新解。

具体地，牛顿法通过计算目标函数的海森矩阵来确定搜索方向，并选择适当的步长来更新解。

该方法在局部范围内通常能够快速收敛到极小解。

3. 二次规划二次规划是非线性规划中的一种特殊形式，目标函数是二次函数，约束条件是线性条件。

它可以通过求解一组二次方程组来得到最优解。

拉格朗日牛顿法

拉格朗日牛顿法
拉格朗日牛顿法是一种优化算法，也被称为条件最优化算法。

它的主要特点是在考虑
约束的基础上寻找函数的极值点。

通过约束条件的加入，一些问题可以被转化为新的形式，从而更容易解决。

这种方法常常被用于经济学、物理学、工程学等领域中。

拉格朗日牛顿法的产生是为了解决一类非线性规划问题，它将约束条件与目标函数结
合起来，形成一个新的函数，通过求这个函数的偏导数找到最优解。

拉格朗日牛顿法的基
本思想是第一步通过拉格朗日乘子法将约束转化为新的函数形式，第二步通过牛顿迭代法
求解函数的极值点。

牛顿迭代法是一种常见的数值求解算法，它的基本思路是使用泰勒展开式逼近目标函数，然后通过求解近似函数的根来逐步逼近真实解。

该方法需要计算目标函数的一阶导数
和二阶导数。

在应用拉格朗日牛顿法时，需要注意以下几个问题。

首先，在确定拉格朗日乘子时，
需要考虑乘子为正数或者负数的情况。

其次，对于一些特殊问题，如非线性规划问题，可
能需要使用二次规划或其他方法进行求解。

最后，拉格朗日牛顿法需要计算目标函数的一
阶导数和二阶导数，如果目标函数存在高次导数，计算的复杂度将会很大。

总之，拉格朗日牛顿法是一种非常有效的优化算法，可以成功解决许多实际问题。

它
的主要思路是通过将约束条件转化为新的函数形式，然后使用牛顿迭代法求解函数的极值点。

但在应用时需要注意一些问题，如选择拉格朗日乘子和计算目标函数的高次导数。

非线性规划算法介绍

非线性规划算法介绍在优化问题中，线性规划被广泛应用，但是有时候我们需要解决一些非线性问题。

非线性规划问题是指目标函数或约束条件至少有一个是非线性的优化问题，求解非线性规划问题是在一些工程和科学领域中很重要的任务。

这篇文章将会介绍非线性规划算法的一些概念和原理。

1. 概述非线性规划（Non-linear programming，简称NLP）是指存在非线性的目标函数和约束的最优化问题。

相对于线性规划问题，非线性规划问题的求解要困难得多，因此需要更复杂的算法来解决。

然而，在实际应用中非线性规划问题比比皆是，如金融风险管理、科学研究、交通规划等，因此非线性规划算法的研究意义非常重大。

2. 常见算法(a) 梯度下降法梯度下降法（Gradient descent algorithm）是求解最小化目标函数的一种方式。

在非线性规划问题中，该方法利用目标函数的梯度方向来确定下降的方向，迭代调整参数，直到梯度为零或达到可接受的误差范围。

梯度下降法有多种变形，包括共轭梯度法、牛顿法等。

(b) 拟牛顿法拟牛顿法（Quasi-Newton methods）是用来求解非线性约束优化问题的经典算法之一。

拟牛顿法利用牛顿法的思想，但不需要求解目标函数的二阶导数，转而用近似的Hessian矩阵来取代二阶导数，并用更新步长向量的方式近似求解目标函数的最小值。

虽然有缺点，但启发式算法具有较强的鲁棒性和适应性，可用于非线性规划问题的求解。

常见的启发式算法包括模拟退火、遗传算法、蚁群算法、粒子群算法等。

3. 应用案例非线性规划算法在实际应用中发挥着不可或缺的作用。

这里介绍两个基于非线性规划算法的应用案例。

(a) 水利工程在水利工程中，常常需要寻找最优的方案来解决水库调度、灌溉、排洪等问题。

非线性规划算法能够通过寻找水资源的最优利用方法，保证水利工程的经济和社会效益。

最优化理论方法——牛顿法

牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法，它的收敛速度快，有内在函数可以直接使用。

结合着matlab 可以对其进行使用，求解方程。

牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。

牛顿法的几何解释：方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。

如下图：设k x 是根*x 的某个近似值，过曲线()y f x =上横坐标为k x 的点k P 引切线，并将该切线与x 轴的交点的横坐标1k x +作为*x 的新的近似值。

鉴于这种几何背景，牛顿法亦称为切线法。

2 牛顿迭代公式：（1）最速下降法：以负梯度方向作为极小化算法的下降方向，也称为梯度法。

设函数()f x 在k x 附近连续可微，且()0k k g f x =∇≠。

由泰勒展开式： ()()()()()T k k k k fx f x x x f xx x ο=+-∇+- （*）可知，若记为k k x x d α-=，则满足0T k k d g <的方向k d 是下降方向。

当α取定后，T k k d g 的值越小，即T k k d g -的值越大，函数下降的越快。

由Cauchy-Schwartz 不等式：Tk k kk d g d g ≤，故当且仅当k k d g =-时，T k k d g 最小，从而称k g -是最速下降方向。

最速下降法的迭代格式为： 1k k k k x x g α+=-。

基于MATLAB的非线性规划问题光滑算法研究

一般来说, 解非线性规划问题要比求解线性规划问题困难得多, 而且也不像线性规划那样有统一的数学模型及如单纯形法这一通用解法。非线性规划的各种算法大都有自己特定的适用范围,都有一定的局限性,到目前为止还没有适合于各种非线性规划问题的一般算法,这正是需要人们进一步研究的课题。针对这种情况, 本文提供了一种有效的求解非线性规划问题的方
软件天地
《微计算机信息》(测控自动化 )2010 年第 26 卷第 7-1 期
double vo, double t, int iNode,int jNode, int mNode,int nNode ); QuaConcreteEle(); virtual-QuaconcreteEle(); }; typedef CArray <QuaConcreteEle,QuaConcreteEle& >QQua－ ConcreteEles;
法—— —光滑化牛顿算法。该算法引入了光滑函数,利用光滑函数的性质,在算法中不必保证迭代点的非负性,也不要求初始点在可行域内,并且克服了互补函数的不可微性。
2 光滑化牛顿算法
算法的流程图
王立明: 本科
- 228 - 360元 / 年邮局订阅号：82-946
图1 《现场总线技术应用 200 例》
技 we give a smoothing Newton method for solving the reformulated system by constructing the smoothing function of the NCP function. Then we use the MATLAB Language to compile a program, and get the numerical results for this method. By choosing the different

非线性方程(组)的数值解法——牛顿法、弦切法

—— Newton 法 —— 弦截法、抛物线法
1
本讲内容
Newton 法及其收敛性牛顿下山法弦截法与抛物线法
2
Newton 法
基本思想将非线性方程线性化
设 xk 是 f (x)=0 的近似根，将 f(x) 在 xk 处 Taylor 展开
f ( ) f ( x ) f ( xk ) f ( xk )( x xk ) ( x xk ) 2 2! f ( xk ) f ( xk )( x xk ) P ( x )
弦截法迭代格式：
xk xk 1 xk 1 xk f ( xk ) f ( xk ) f ( xk 1 )
k = 1, 2, 3, . . . 注：弦截敛性
定理：设 x* 是 f(x) 的零点， f(x) 在 x* 的某邻域 U(x,) 内有二阶连续导数，且 f’(x)0，若初值 x0， x1 U(x,)，则当 U(x,) 充分小时，弦截法具有 p 阶收敛性，其中
1 5 p 2
( p2 p 1 0)
17
弦截法几何含义
y
x* xk xk+1 xk-1
x
18
抛物线法
抛物线法
基本思想：用二次曲线与 x 轴的交点作为 x* 的近似值
19
抛物线法
y xk+1 xk
xk-1 xk-2
20
抛物线法
计算过程二次曲线方程 (三点 Newton 插值多项式)
f [ xk , xk 1 , xk 2 ]( x xk )( x xk1 )
xk 1 xk
2 f ( xk )
2 4 f ( xk ) f [ xk , xk 1 , xk 2 ]

非线性不等式组的Jacobian光滑牛顿法

ｇｏｌｏｖｒｅｃｌｂａｎｅｇｎｅｃ
Ｏ引言
考虑非线性不等式组问题 ¨，即求Ｘ，使得ＥＲ
，（）０（）１
Ｖ＝ｘｘ …，Ｙ（，，）∈ 记ｘ（，，）＝ＹＹ …，Ｒ，ｉ２，ｌ２
第２卷第１４期
２１年１００月
湖
南
工
业大
学
学
报
Ｖｏ．４Ｎｏ１１．２
ＪｕａｆｎｎＵｎｖｒｉｆｅｈｏｏｙｏｒｌｎｏＨｕａｉｅｓｔｏｃｎｌｇｙＴ
Ｊｎ．２１ａＯ０
非线性不等式组的Ｊｃｂａ光滑牛顿法ａｏｉｎ
文中，Ｃ（）其中：假设 ∈ ｎ，Ｒ
Ｃ表示具有二阶连续导数的函数集；Ｑ表示不等式（）的解空间集。１引入记号，对
（＝【（】【（］０ｘ去Ｆ＋，＋。））。）＝
构造辅助函数
（）５
’收稿日期：２０－９００９０－８基金项目：湖南省教育厅基金资助项目（８６８０Ｃ６）通信作者：何郁波（９９），湖南岳阳人，怀化学院教师，１７－，男硕士，主要研究方向为变分不等式与互补问题的数值算法，
Ａｂｓｒｃ：Ｒｅｏｍｕａｅｏｌｅｒｉｅｕｌｉｓａｏｌｎａｕｔｎｏｏｖｎｒｂｅ．ｅｈｎｆｒｙｓｏ — ｔａｔｆｒｌｔｓｎｎｉａｑａｉｅｓｎｎｉｅｅａｉｓｆｒｓｌｉｇｐｏｌｍｓＵｓｓｔｅｕｉｏｍｌｍｏｔｎｎｔｒｑｏｈｉｐｒａｈｎｇｏｕｉａｙｆｎｔｏｎａｏｉｎｃｎｉｔｎｙ，ｓｗｅｌａｕｃｓｉｐｒｉｔｏｍｏｔｉｇＮｅｏｎｇａｐｏｃｉｆａｘｌｒｕｃｎａｄＪｃｂａｏｓｓｅｃａｌｓａｓｃｅｓｖｅａｐｏｘｍａｉｎｓｏｈｎｗｔｎｉｉｍｅｈｄｔｏｖｅｎｎｓｏｉｇｅｕａｏ．ｄｕｄｒｓｍｅａｓｍｐｏ，ｇｒｔｍｌｂｏｖｒｅｃｕｒｎｅｄｔｏｏｓｌｅｔｏ —ｍｏｔｎｑｔｎｓＡｎｎｅｏｓｕｔｎａｏｈｇｏａｃｎｅｇｎｅｉｇａａｔｅ．ｈｈｉｉｌｉｌｓＫｅｗｏｄｙｒｓ：ｎｎｉｅｅｕａｉｅ；ｓｏｔｉｇＮｅｏｔｏｏｌｎａｉｑｌｉｓｍｏｈｎｗｔｎｍｅｄ；ｓｃｅｓｖｐｒｘｍａｉｎ；Ｊｃｂａｏｓｓｅｃｒｎｔｈｕｃｓｉｅａｐｏｉｔｏａｏｉｃｎｉｔｎｙ；ｎ

非线性规划理论和算法

非线性规划理论和算法非线性规划是一种数学规划问题，其目标函数和约束条件是非线性的。

与线性规划相比，非线性规划更具挑战性，因为非线性函数的特性使得求解过程更加困难。

然而，非线性规划在实际应用中具有广泛的应用领域，例如优化问题、工程规划、经济决策等。

为了解决非线性规划问题，需要发展相应的理论和算法。

1.非线性规划理论凸规划理论：凸规划是非线性规划的一个特殊情况，其目标函数和约束条件都是凸函数。

凸规划具有许多重要的性质，如唯一最优解、稀疏性、全局最优解等。

凸规划理论为非线性规划提供了重要的指导。

拉格朗日乘子法：拉格朗日乘子法是一种常用的求解非线性规划的方法，其基本思想是通过构建拉格朗日函数将原问题转化为无约束优化问题。

拉格朗日乘子法为非线性规划提供了一种有效的解法。

拟牛顿法：拟牛顿法是一类迭代方法，用于求解无约束和约束非线性优化问题。

其基本思想是通过构建近似的黑塞矩阵来更新方向。

拟牛顿法具有收敛速度快和全局收敛性好的优点，被广泛应用于实际问题求解中。

2.非线性规划算法直接方法：直接方法包括穷举法、划分法、割平面法等。

这些方法适用于问题维度和约束条件较少的情况，可以通过枚举或分割解空间来找到最优解。

然而，直接方法的计算复杂度较高，在高维问题中效率较低。

迭代方法：迭代方法通过迭代更新方向来逐步逼近最优解。

常用的迭代方法包括牛顿法、拟牛顿法、共轭梯度法等。

这些方法在求解非线性规划问题时表现出较好的收敛性和效率。

近年来，随着计算机性能的提高和优化算法的进一步发展，一些先进的非线性规划算法也得到了广泛应用，例如粒子群优化算法、遗传算法、模拟退火算法等。

这些算法基于不同的策略和模拟自然现象的原理，可以有效克服非线性规划问题中的局部最优和高维度等挑战。

总结起来，非线性规划理论和算法是解决实际问题中非线性优化问题的重要工具。

非线性规划理论提供了问题求解的基本原理和数学模型，而非线性规划算法则根据不同问题的特点和性质选择合适的求解方法。

非线性方程求解方法和优化算法的使用技巧

非线性方程求解方法和优化算法的使用技巧随着科学技术的不断发展，非线性问题在各个领域中的应用越来越广泛。

而非线性方程的求解是解决这些问题的关键。

本文将介绍一些常用的非线性方程求解方法和优化算法的使用技巧，帮助读者更好地应对实际问题。

一、牛顿迭代法牛顿迭代法是一种常用的非线性方程求解方法。

它通过不断迭代逼近方程的根，直到满足预设的精度要求。

该方法的核心思想是利用方程的局部线性近似来逼近根的位置，并通过迭代逐步接近真实根。

在使用牛顿迭代法时，需要注意以下几点技巧：1. 初始值的选择：初始值的选择对迭代的效果有很大影响。

一般来说，初始值应该尽量靠近方程的根。

可以通过绘制方程的图像或者利用已知的近似解来选择初始值。

2. 收敛性判断：牛顿迭代法并不总能收敛到方程的根，因此需要对迭代过程进行收敛性判断。

常用的方法是判断迭代值的相对误差是否小于预设的精度要求。

3. 迭代次数的控制：为了避免无限迭代，需要设定最大迭代次数。

如果达到最大迭代次数仍未满足精度要求，则可以考虑调整初始值或者选择其他求解方法。

二、拟牛顿法拟牛顿法是一类利用迭代近似求解非线性方程的方法。

与牛顿迭代法不同的是，拟牛顿法不需要计算方程的导数，而是通过构造一系列近似矩阵来逼近方程的根。

在使用拟牛顿法时，需要注意以下几点技巧：1. 近似矩阵的选择：拟牛顿法的关键是构造合适的近似矩阵。

常用的近似矩阵有DFP算法和BFGS算法等。

选择合适的近似矩阵可以提高算法的收敛速度和稳定性。

2. 步长的确定：拟牛顿法需要确定每一步的迭代步长。

一般来说，步长应该保证在迭代过程中能够逐步逼近方程的根，但又不能过大导致迭代发散。

可以使用线性搜索或者信赖域方法来确定合适的步长。

三、遗传算法遗传算法是一种基于生物进化原理的优化算法。

它通过模拟自然界中的进化过程，不断迭代搜索最优解。

在求解非线性方程时，遗传算法可以用来寻找方程的最优解或者近似解。

在使用遗传算法时，需要注意以下几点技巧：1. 个体编码方式的选择：个体编码方式决定了问题的表示形式。