431角PPT课件

动态角的概念
角也可以看成是一条射线绕着它的端点旋转而成的图形。 起始位置的射线叫做这个角的始边。 终止位置的射线叫做这个角的终边。
终边
顶点
始边
角的表示 角用符号“∠”来表示。
（1）用三个大写字母表示，三个字母应 A
分别写在顶点及两边上的点，顶点的字 O
母必须写在中间。
B
∠AOB 或∠BOA 表示的是同一个角
A
A
A
A
A
B
C
∠ACB
（× ）
B
CB
C
∠CAB
∠ABC
（× ）
（√ ）
B
C
∠B
（√ ）
B
C
∠A
（× ）
2、下面表示∠DEF的图是（ （3） ）
D
E
D
D
E
E
F
（1）
D
F
（2）
E
F
（3）
F
E
（4）
静态角的概念
边
顶点

边
角是由两条有公共端点的射线所组成的图形。 这个公共端点叫做这个角的顶点 这两条射线叫做这个角的边
B
C
A
D
图中有几个角，它们 是 ∠BAC、 ∠BAD、 DAC ．
B
A
C 图中又有几个角，它们是
．
D E
∠BAC、 ∠BAD、 ∠BAE、 ∠CAD、
∠CAE、 ∠DAE
若以A为端点引n条射线，此时又 有几个角？
A
B O
C
1、若称浙江、北京、重庆所成的角为∠OAC，则
∠ACB表示
。
2、甘肃、北京、浙江所成的角为
分别写在顶点及两边上的点，顶点的字 O
母必须写在中间。
B
∠AOB 或∠BOA 表示的是同一个角
（2）角也可用一个大写字母表示，这个
字母写在顶点处，它只适用于顶点处只 O
∠O
用一个角。
（3）用一个数字加弧线表示
1
∠1
（4）用一个小写希腊字母加弧线表示 α
∠α
谁来做一做
1、判断下面各角的表示方法是否正确
其 中 正 确 语 句 的 个 数 是 （ A）
A.0 B.2C .3D.4
3、如图所示，一只昆虫要从正方体的一个顶点 A•爬到相距它最远的另一个顶点B，哪条路径 最短？说明理由．
4.3.1角
房顶的角
吊 扇 扇 叶 的 夹 角
剪刀的角
人 仰 视 时 的 视 角
楼梯的折角
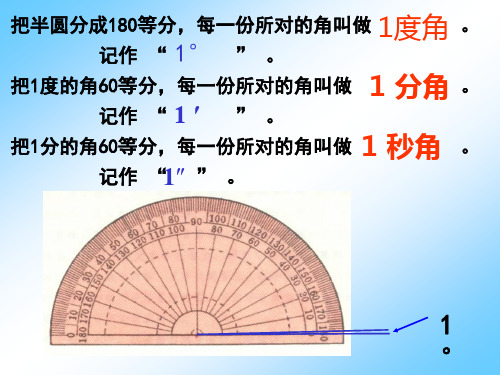
时针和分针的夹角
一个周角分成360份，一份就是1°，把 1°分成60份，一份就是1′，把1′分成 60份，一份就是1″，以度分秒为单位的 角的度量制就是角度制 .
角的度量单位及其换算
1°＝ 60′， 1′＝ 60″； 11′周角＝(＝610 2)°平，角＝41直″角＝＝( 631060) ′°．． 1平角＝2直角＝180°．
（2）角也可用一个大写字母表示，这个
字母写在顶点处，它只适用于顶点处只 O
∠O
用一个角。
（3）用一个数字加弧线表示
1
∠1
（4）用一个小写希腊字母加弧线表示 α
∠α
谁来做一做
3、你能把图中的角表示出来吗?
A B
∠AOB ∠BOC
O
C
∠AOC
4、写出图中（1）能用一个字母表示的角
A
( ∠A 和∠C
)
E
（A）∠AOB （B） ∠BOC
（C） ∠a
(D) ∠O
7、把图3中的角表示成下列形式：
（1） ∠APO，（2） ∠AOP ， （3） ∠OPC ，
（4） ∠O，（5） ∠COP ，（6）∠P （7） ∠a C
A
Pa
图3
O
其中正 （1），（3），（6），（7） 确
。
D C
A
B
8、如图，射线AC和射线AB构成的 角是∠BAC ，∠BDC的两边分别 是 射线DB和射线DC 。
34
⑷34.37°＝ ″
′＝960 ″
°14 ′24
22 12
4.3.1角
课前练习
1．图是一个自制骰子的展开图，请根据要求 回答问题： （1）如果1点在前面，从左面看是 2点，那么 哪一点会在上面？
（2）如果从右面看是4点，5点在后面，那么 哪一点会在上面？
2 .判 断 下 列 语 句 中 正 确 的 个 数 ： (1)线 段 AB就 是 AB两 点 间 的 距 离 ； (2)线 段 的 AB一 半 就 是 线 段 AB的 中 点 ； ( 3 )在 所 有 连 接 两 点 的 线 中 直 线 最 短 ； (4)如 果 AB=BC=CD,则 AD=3AB
终边
顶点
始边
B
O
A
如果一个角的终边继续旋转，旋转到与始 边成一条直线时，所成的角叫做平角。
O
A （B）
当旋转到终边与始边重合时，所成 的角叫做周角。
判断：有人说，平角是一条直线，周角是一条 射线对吗？
A
B
直线
A
O
射线
A
O
B
平角
A
B
O
周角
角的表示方法？
角的表示
角用符号“∠”来表示。
（1）用三个大写字母表示，三个字母应 A
例1
计算:
⑴1.45°等于多少分?
⑵1800″等于多少分?
2、 计算
(1)把18.18°化成度、分、秒为 18°10′48 ″ . (2)把59°31′30 ″化成度的形式为 59.525°.
练习
1.用度、分、秒表示：
⑴0.75°＝45
′2＝700 ″
⑵(1－45 )°＝16
⑶16.24°＝16 ″
（2）以B为顶点的角
B
C
（
∠ABE、∠EBC、
）
∠ABC
（3）图中共有几个角（小于平角的角）
（ 7个角
）
（∠A 、∠C 、∠ABE 、∠EBC、 ∠ABC、 ∠AEB 、∠CEB）
5、你能用不同的方法 表示图（1）的各个角吗？
A
B
O
a 2
E
C
图1
Oa
C
A
图2
6、图2中，下列表示角的方法错误的为（ D ）
鳄鱼张开的嘴
角
通过上面对角的认识，
谁能用自己的话来对角 作一下解释？
静态角的概念
边
顶点
边
角是由两条有公共端点的射线所组成的图形。 这个公共端点叫做这个角的顶点 这两条射线叫做这个角的边
你会画出角的图形吗？ 边
角有什么特征？
顶点
边
公共端点 两条射线
练一练：下列图形是角吗？
抢答题
1、在小学，大家学习过角的分类，试看⑴是 锐角
。
思考：从一个点引出几条射线，它们
共形成了几个角？和射线的条数有没有
关系？规律是什么？ n n 1
2
引申：往返于A、B两个城市的客车，中
途有两个停靠点.
（1）该客车有多少种不同的票价？
（2）该客车上要准备多少种车票？
角的度量
———角度制
经常用量角器度量一个角的度数，
度、分、秒是常用的角的度量单位，把
，
⑵是 直角 ， ⑶是 钝角 。
外部 内部
外部 内部
(1)
⑵
2、指出右面角的内部和外部
外部
内部
⑶
外部
内部
3、判断：下面的图形那些是角？
⑴
⑵
⑶
⑷
⑸
⑹
角
通过刚才的演示， 你能否再给角一个定义呢？
动态角的概念
角也可以看成是一条射线绕着它的端点旋转而成的图形。 起始位置的射线叫做这个角的始边。 终止位置的射线叫做这个角的终边。