2012年希望杯六年级初赛试题

小学六年级“希望杯”第1-10届试题及详解(第一试和第二试)

第四届小学“希望杯”全国数学邀请赛六年级第1试以下每题5分，共120分。

1．2006×2008×()＝________。

2．900000－9＝________×99999。

3．＝________。

4．如果a＝，b＝，c＝，那么a，b，c中最大的是________，最小的是________。

5．将某商品涨价25％，如果涨价后的销售金额与涨价前的销售金额相同，则销售量减少了________％。

6．小明和小刚各有玻璃弹球若干个。

小明对小刚说：“我若给你2个，我们的玻璃弹球将一样多。

”小刚说：“我若给你2个，我的弹球数量将是你的弹球数量的三分之一。

”小明和小刚共有玻璃弹球________个。

7．一次测验中，小明答错了10道题，小刚答错了8道题，小强答对的题的数量等于小明与小刚答对题的数量之和，且小强答错了3道题。

这次测验共有________道题。

8．一个两位数，加上它的个位数字的9倍，恰好等于100。

这个两位数的各位数字之和的五分之三是________。

9．将一个数A的小数点向右移动两位，得到数B。

那么B＋A是B－A的________倍。

(结果写成分数形式)10．用10根火柴棒首尾顺次连接接成一个三角形，能接成不同的三角形有________个。

11．希望小学举行运动会，全体运动员的编号是从1开始的连续整数，他们按图中实线所示，从第1珩第1列开始，按照编号从小到大的顺序排成一个方阵。

小明的编号是30，他排在第3行第6列，则运动员共有________人。

12．将长为5，宽为3，高为1的长方体木块的表面涂上漆，再切成15块棱长为l的小正方体。

则三个面涂漆的小正方体有________块。

13．如图，∠AOB的顶点0在直线l上，已知图中所有小于平角的角之和是400度，则∠AOB＝________度。

14．如图，桌面上有A、B、C三个正方形，边长分别为6，8，10。

B的一个顶点在A 的中心处，C的一个顶点在B的中心处，这三个正方形最多能盖住的面积是________。

2012希望杯第2试全部试题详解及分析

2012年第十届希望杯六年级二试试题详解 1、原式=33111113331814124533===441684235⨯⨯+++⨯⨯⨯⨯（）（） 2、原式=（2+3+5+13）+（2222355779911+++⨯⨯⨯⨯）+（3239355779++⨯⨯⨯） =23+（1112211311557577-++++⨯⨯）（） =23+8111313355757++-++（） =248333、因为1+2+3+.......+n=n ⨯(n+1) ÷2≈2012所以n ⨯(n+1) ≈=4024 则约为631+2+3+.......+63=63⨯64÷2=2016则漏加的数为：2016-2012=44、最大：0.2012041.5（5循环），最小：0.2.012041.5（0120415循环）5、依题意：412132m ⨯⨯=+⨯，⇒ m=2 3*12=431243122423312677⨯⨯⨯⨯==⨯+⨯⨯ 6、第一次变化后周长变为：9⨯3⨯43=36 第二次变化后周长变为：36⨯43=48 第三次变化后周长变为：48⨯43=64 第四次变化后周长变为：64⨯43=2563 7、这是常规题，多次遇到，分类统计，共35个。

8、依据约数个数判定定理：8=2⨯4=（1+1）⨯（3+1）， ⇒ N=312540⨯=8=2⨯2⨯2=（1+1）⨯（1+1）⨯（1+1）⇒ N=11123530⨯⨯=所以N 的最小值为309、因为（189，147）=3⨯7=21，所以购买的数量有三种情况情况一：3个，则单价为：147÷3=49，不合题意，情况二：7个，则单价为：147÷7=21，符合题意，情况三：21个，则单价为：147÷21=7，不合题意。

故实际单价为：21元，共买了7个10、阴影部分面积为大圆面积减去2个小圆面积：3.14⨯（40/2）2-2⨯3.14⨯102=3.14⨯（400-200）=628（平方厘米）11、 44==743v v -甲乙 ∴ 33438=336=÷⨯⨯⨯ 12、甲：13份，乙：12份，丙：122=83⨯份平均每人：（13+12+8）÷3=11（份）丙差：11-8=3（份），每份：9÷3=3（元）支付甲：3⨯(13-11)=6(元) 支付乙：3⨯（12-11）=3（元）13、答案不唯一，在此公提供两种：14、甲共行：3+4+4=11（份）乙共行：4+3+3=10（份） 603==804v v 甲乙若乙不休息，可行：11÷34=443（份）少行了：443-10=143（份）所以乙的速度为：143÷14=13（份），则第一次相遇时间为：4÷13=12（分）所以AB=（60+80）⨯12=1680（米）15、可能堆成的长方体有如下8种可能：100=1⨯1⨯100 =1⨯2⨯50 =1⨯4⨯25=1⨯5⨯20=1⨯10⨯10=2⨯2⨯25 =2⨯5⨯10=4⨯5⨯5欲使堆成的表面积尽可能小，长、宽、高的差要尽可能小，所以应选择100=1⨯4⨯25=1⨯5⨯20=1⨯10⨯10=2⨯2⨯25=2⨯5⨯10=4⨯5⨯5这6种组合方式，计算的表面积从小到大（从后向前）依次是130、160、208、240、250、258。

希望杯六年级近五年真题大全

希望杯目录真题希望杯简介 ......................................................................... .. (Ⅰ)近三年真题分析.......................................................................... (Ⅱ)2014第 12 届希望杯六年级第 1 试试题....................................................................... .. (1)2013第 11 届希望杯六年级第 1 试试题....................................................................... .. (3)2012第 10 届希望杯六年级第 1 试试题....................................................................... .. (5)2011 第 9 届希望杯六年级第 1 试试题........................................................................... (7)2010第 8 届希望杯六年级第 1 试试题....................................................................... . (9)2014第 12 届希望杯六年级第 2 试试题...................................................................... . (11)2013第 11 届希望杯六年级第 2 试试题...................................................................... . (13)2012第 10 届希望杯六年级第 2 试试题...................................................................... . (15)2011 第 9 届希望杯六年级第 2 试试题........................................................................... . (17)2010第 8 届希望杯六年级第 2 试试题...................................................................... (19)参考答案2014第 12 届希望杯六年级第 1 试试题分析....................................................................... . (21)2013第 11 届希望杯六年级第 1 试试题分析....................................................................... . (23)2012第 10 届希望杯六年级第 1 试试题分析....................................................................... . (25)2011第 9 届希望杯六年级第 1 试试题分析 (27).........2010第 8 届希望杯六年级第 1 试试题分析....................................................................... (29)2014第 12 届希望杯六年级第 2 试试题分析....................................................................... . (31)2013第 11 届希望杯六年级第 2 试试题分析....................................................................... . (33)2012第 10 届希望杯六年级第 2 试试题分析....................................................................... . (35)2011第 9 届希望杯六年级第 2 试试题分析....................................................................... (37)2010第 8 届希望杯六年级第 2 试试题分析....................................................................... (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛．“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容，适当地拓宽知识面；启发他们注意数学与其它课程的联系和数学在实际中的应用；激励他们去钻研和探究；培养他们科学的思维能力、创新能力和实践能力；树立他们为振兴中华而努力成才的自信．“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲，不超出教学进度，贴近现行的数学课本，源于课本，高于课本．题目活而不难，巧而不偏；既大众化又富于思考性和启发性．力求体现科学思维之美，寓科学于趣味之中，将知识、能力的考察和思维能力的培养结合起来．“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生．每年举行一次，为一届．每次举行两试，三月中旬第 1 试，考小时；四月中旬第 2 试，考 2 小时．“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单，做到以下两点，希望杯获奖轻松惬意：1．利用寒假做完希望杯 100 题和希望杯历年真题；2．春季再做一遍；3．结合一试的试题，有针对性的准备二试．希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖，整个深圳市也就 20 个左右的名额；而全国三等奖就有好几百个，具体规则如下：根据希望杯的评奖规则，全国一二等奖在赛区内统一标准，按照初赛人数的约千分之三评定．全国三等奖按报名单位初赛人数和规定比例评定，由报名单位按照下述要求评定：1．各单位获奖总指标（一二三等奖）：中学每满 30 人初赛给一个指标，不足 30 人不给；小学每满 20 人初赛给一个指标，不足 20 人不给．若评出人数多于计划指标，组委会将按照从后到前的顺序去掉多出指标．2．各单位评奖时应当按照复赛分数由高到低的原则，赛分数相同时按初赛成绩排序．3．各单位指标可在小学内部中学内部调剂使用，得在二者之间调剂．4．凡是列入全国一二等奖推荐名单的，提供该生的一试试卷和二试试卷，奖励等级由全国组委会统一确定．深圳地区奖项设置有特、一、二、三等奖，2014 年 2000 多名进入二试的学生中，有 120 个特等奖，400 个一等奖，所有进入二试的选手至少能获三等奖！！近三年真题分析“希望杯”题型涉及内容广泛，为了更好备战 2015 年“希望杯”，我们需要对历年考试情况有一个详细了解。

2012年第十届希望杯复赛试题及答案(六年级)

第十届小学“希望杯”全国数学邀请赛六年级第2试2012年4月8日上午9:00至11:00 得分一、填空题（每小题5分，共60分。

）1. 计算：=⨯⨯⨯⨯+⨯⨯⨯52322153432351413121 2. 计算： =+++++++1553525631199213532 3. 王涛将连续的自然数1,2,3,…逐个相加，一直加到某个自然数为止，由于计算时漏加了一个自然数而得到错误的结果2012。

那么，他漏加的自然数是。

4. 在数0.20120415中的小数后面的数字上方加上循环点，得到循环小数，这些循环小数中，最大的是，最小的是。

5. 对任意两个数x ，y 规定运算“*”的含义是：yx m y x y x ⨯+⨯⨯⨯=*34（其中m 是一个确定的数），如果1*2 = 1，那么m = ，3*12 = 。

6.对于一个多边形，定义一种“生长”操作：如图1，将其一边AB 变成向外凸的折线ACDEB ，其中C 和E 是AB 的三等分点，C ，D ，E 三点可构成等边三角形，那么，一个边长是9的等边三角形，经过两次“生长”操作（如图2），得到的图形的周长是；经过四次“生长”操作，得到的图形的周长是。

图 1（3）（2）（1）图 27. 如图3所示的“鱼”形图案中共有个三角形。

8. 已知自然数N 的个位数字是0，且有8个约数，则N 最小是。

9. 李华在买某一商品的时候，将单价中的某一数字“7”错看成了“1”，准备付款489元，实际应付147元，已知商品的单价及购买的数量都是整数，则这种商品的实际单价是元，李华共买了件。

10. 如图4，已知AB = 40cm ，图中的曲线是由半径不同的三种半圆弧平滑连接而成，那么阴影部分的面积是 cm 2。

（π取3.14）11. 快车和慢车同时从甲、乙两地相对开出，快车每小时行33千米，相遇行了全程的74，已知慢车行完全程需要8小时，则甲、乙两地相距千米。

12. 甲、乙、丙三人去郊游，甲买了9根火腿，乙买了6个面包，丙买了3瓶矿泉水，乙花的钱是甲的1312，丙花的钱是乙的32，丙根据每人所花钱的多少拿出9元钱分给甲和乙，其中，分给甲元，分给乙元。

希望杯六年级近五年真题汇编

欢迎来主页下载---精品文档希望杯目录真题希望杯简介 (Ⅰ)近三年真题分析 (Ⅱ)2014 第 12 届希望杯六年级第 1 试试题 (1)2013 第 11 届希望杯六年级第 1 试试题 (3)2012 第 10 届希望杯六年级第 1 试试题 (5)2011 第 9 届希望杯六年级第 1 试试题 (7)2010 第 8 届希望杯六年级第 1 试试题 (9)2014 第 12 届希望杯六年级第 2 试试题 (11)2013 第 11 届希望杯六年级第 2 试试题 (13)2012 第 10 届希望杯六年级第 2 试试题 (15)2011 第 9 届希望杯六年级第 2 试试题 (17)2010 第 8 届希望杯六年级第 2 试试题 (19)参考答案2014 第 12 届希望杯六年级第 1 试试题分析 (21)2013 第 11 届希望杯六年级第 1 试试题分析 (23)2012 第 10 届希望杯六年级第 1 试试题分析 (25)2011 第 9 届希望杯六年级第 1 试试题分析 (27)2010 第 8 届希望杯六年级第 1 试试题分析 (29)2014 第 12 届希望杯六年级第 2 试试题分析 (31)2013 第 11 届希望杯六年级第 2 试试题分析 (33)2012 第 10 届希望杯六年级第 2 试试题分析 (35)2011 第 9 届希望杯六年级第 2 试试题分析 (37)2010 第 8 届希望杯六年级第 2 试试题分析 (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛．“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容，适当地拓宽知识面；启发他们注意数学与其它课程的联系和数学在实际中的应用；激励他们去钻研和探究；培养他们科学的思维能力、创新能力和实践能力；树立他们为振兴中华而努力成才的自信．“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲，不超出教学进度，贴近现行的数学课本，源于课本，高于课本．题目活而不难，巧而不偏；既大众化又富于思考性和启发性．力求体现科学思维之美，寓科学于趣味之中，将知识、能力的考察和思维能力的培养结合起来．“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生．每年举行一次，为一届．每次举行两试，三月中旬第 1 试，考1.5小时；四月中旬第 2 试，考 2 小时．“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单，做到以下两点，希望杯获奖轻松惬意：1．利用寒假做完希望杯 100 题和希望杯历年真题；2．春季再做一遍；3．结合一试的试题，有针对性的准备二试．希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖，整个深圳市也就 20 个左右的名额；而全国三等奖就有好几百个，具体规则如下：根据希望杯的评奖规则，全国一二等奖在赛区内统一标准，按照初赛人数的约千分之三评定．全国三等奖按报名单位初赛人数和规定比例评定，由报名单位按照下述要求评定：1．各单位获奖总指标（一二三等奖）：中学每满 30 人初赛给一个指标，不足 30 人不给；小学每满 20 人初赛给一个指标，不足 20 人不给．若评出人数多于计划指标，组委会将按照从后到前的顺序去掉多出指标．2．各单位评奖时应当按照复赛分数由高到低的原则，赛分数相同时按初赛成绩排序．3．各单位指标可在小学内部中学内部调剂使用，得在二者之间调剂．4．凡是列入全国一二等奖推荐名单的，提供该生的一试试卷和二试试卷，奖励等级由全国组委会统一确定．深圳地区奖项设置有特、一、二、三等奖，2014 年 2000 多名进入二试的学生中，有 120 个特等奖，400 个一等奖，所有进入二试的选手至少能获三等奖！！近三年真题分析“希望杯”题型涉及内容广泛，为了更好备战2015年“希望杯”，我们需要对历年考试情况有一个详细了解。

希望杯六年级近五年真题大全

希望杯目录真题希望杯简介 (Ⅰ)近三年真题分析 (Ⅱ)2014 第 12 届希望杯六年级第 1 试试题 (1)2013 第 11 届希望杯六年级第 1 试试题 (3)2012 第 10 届希望杯六年级第 1 试试题 (5)2011 第 9 届希望杯六年级第 1 试试题 (7)2010 第 8 届希望杯六年级第 1 试试题 (9)2014 第 12 届希望杯六年级第 2 试试题 (11)2013 第 11 届希望杯六年级第 2 试试题 (13)2012 第 10 届希望杯六年级第 2 试试题 (15)2011 第 9 届希望杯六年级第 2 试试题 (17)2010 第 8 届希望杯六年级第 2 试试题 (19)参考答案2014 第 12 届希望杯六年级第 1 试试题分析 (21)2013 第 11 届希望杯六年级第 1 试试题分析 (23)2012 第 10 届希望杯六年级第 1 试试题分析 (25)2011 第 9 届希望杯六年级第 1 试试题分析 (27)2010 第 8 届希望杯六年级第 1 试试题分析 (29)2014 第 12 届希望杯六年级第 2 试试题分析 (31)2013 第 11 届希望杯六年级第 2 试试题分析 (33)2012 第 10 届希望杯六年级第 2 试试题分析 (35)2011 第 9 届希望杯六年级第 2 试试题分析 (37)2010 第 8 届希望杯六年级第 2 试试题分析 (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛．“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容，适当地拓宽知识面；启发他们注意数学与其它课程的联系和数学在实际中的应用；激励他们去钻研和探究；培养他们科学的思维能力、创新能力和实践能力；树立他们为振兴中华而努力成才的自信．“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲，不超出教学进度，贴近现行的数学课本，源于课本，高于课本．题目活而不难，巧而不偏；既大众化又富于思考性和启发性．力求体现科学思维之美，寓科学于趣味之中，将知识、能力的考察和思维能力的培养结合起来．“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生．每年举行一次，为一届．每次举行两试，三月中旬第 1 试，考1.5小时；四月中旬第 2 试，考 2 小时．“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单，做到以下两点，希望杯获奖轻松惬意：1．利用寒假做完希望杯 100 题和希望杯历年真题；2．春季再做一遍；3．结合一试的试题，有针对性的准备二试．希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖，整个深圳市也就 20 个左右的名额；而全国三等奖就有好几百个，具体规则如下：根据希望杯的评奖规则，全国一二等奖在赛区内统一标准，按照初赛人数的约千分之三评定．全国三等奖按报名单位初赛人数和规定比例评定，由报名单位按照下述要求评定：1．各单位获奖总指标（一二三等奖）：中学每满 30 人初赛给一个指标，不足 30 人不给；小学每满 20 人初赛给一个指标，不足 20 人不给．若评出人数多于计划指标，组委会将按照从后到前的顺序去掉多出指标．2．各单位评奖时应当按照复赛分数由高到低的原则，赛分数相同时按初赛成绩排序．3．各单位指标可在小学内部中学内部调剂使用，得在二者之间调剂．4．凡是列入全国一二等奖推荐名单的，提供该生的一试试卷和二试试卷，奖励等级由全国组委会统一确定．深圳地区奖项设置有特、一、二、三等奖，2014 年 2000 多名进入二试的学生中，有 120 个特等奖，400 个一等奖，所有进入二试的选手至少能获三等奖！！近三年真题分析“希望杯”题型涉及内容广泛，为了更好备战2015年“希望杯”，我们需要对历年考试情况有一个详细了解。

小学“希望杯”培训100题(六年级)及解析

小学“希望杯”培训100题（六年级）一、解答题（共100小题）1．计算：=．2．计算：2012×2014×（）．3．．4．计算：（0.+0.3）×0.×0.7×=．5．计算：=．6．计算：=7．兄弟俩都有点傻，一位只有自己过一年长一岁而别人不会长．某天，哥哥对弟弟说：”再过3年我的年龄就是你的2倍．”弟弟说：”不对，再过3年我和你一样大．”今年，他们俩分别是岁，岁．8．有一堆黑白棋子，黑棋的粒数是白棋的2倍，每次从中取出白棋3粒黑棋5粒，白棋恰好取完时黑棋还剩20粒．则原来这堆棋子共有粒．9．如图，边长12cm的正方形与直径为16cm的圆部分重叠，若没有重叠的两空白部分的面积分别是S1，S2，则S1﹣S2=．（π取3）10．有一列数：8，18，24，49，55，60，65，77，81，98，100．它们的最小公倍数是．（以乘方形式表示，不用写出计算结果）11．王老师将200块糖分给了甲乙丙三个小朋友，甲比乙的2倍还要多，乙比丙的3倍还要多，那么甲最少有块糖，丙最多有块糖．12．建军路小学有钢琴，小提琴这两个兴趣班，这两个班的学员都是来自A班或者B班的．钢琴班有来自A班，小提琴班有来自B班，并且钢琴班的总人数是小提琴班总人数的倍，那么这两个兴趣班中来自B班的人数与总人数的比值是．13．定义：”如果一个数有12个约数，那么称这样的数为’好数’”．则将所有的”好数”由小到大依次排列，第三个是．14．有一口枯井，用一根绳子测井口到井底的深度，将绳对折后垂到井底，绳子超过井口9米；将绳子三折后垂到井底，绳子超过井口2米，则绳长米，井深米．15．将100个梨分给10个同学，每个同学的梨个数互不相同．分得梨个数最多的同学，至少得到个梨．16．31500的约数中与6互质的共有个．17．如图2，S△ABC=24，D是AB的中点．E在AC上，AE：EC=2：1．DC交BE于点O．若s△DBO=a，S△CEO=b，则a﹣b=．18．已知有三个连续的自然数，它们中最小的一个是9的倍数，中间一个是7的倍数，最大的一个是5的倍数，那么这些自然数最小分别是．19．快速公交3号线行驶于安定门与宏福苑小区之间，已知它的发车间隔时间是相等的，苏老师开车从宏福苑小区到安定门，每过3分钟她的迎面就驶来一辆快速公交，每隔12分钟她就超过一辆快速公交．快速公交全程是45分钟，假设公交车和苏老师开车的速度都不变，那么苏老师开车从宏福苑小区到安定门需要分钟．20．将自然数1，2，3，…，依次写下去，组成一个数：12345678910111213…，当写到2054时，这个大数除以9的余数是．21．地震时，地震中心同时向各个方向传播出纵波和横波．纵波的传播速度是3.96km/s，横波的传播速度是2.58km/s，某次地震，地震监测点用地震仪接收到地震的纵波之后，隔了18.5s，接收到这个地震的横波，那么这次地震的地震中心距离地震监测点km．22．对于非零自然数n，如果能找到非零自然数a，b使得n=a+b+ab，则称n是一个”联谊数”，如：3=1+1+1×1，则3就是一个”联谊数”，那么从1到20这20个自然数当中，”联谊数”共有个．23．甲乙丙丁四个人去购物，付账时每人都拿出一些钱，已知，乙丙丁三人付钱的总和是甲的5倍，甲丙丁三人付钱的总和是乙的4倍，甲乙丁三人付钱的总和是丙的3倍，丁付了46元，那么四个人共花了元．24．一个自然数，在3进制中的数字和是24．它在9进制中的数字和最小是，最大是．25．设N=1×2×…×209×210，则：（1）N的末尾一共出现个连续的数字”0”；（2）用N不断除以12，知道结果不能被12整除为止，一共可以除以次．26．如果长方形，正方形，正三角形分别有a，b，c条对称轴，则（a+b+c）2=．27．在数4，11，19，73，93，118，125，238中相邻若干个数之和是3的倍数而不是9的倍数的数组共有组．28．A，B两校的男、女生人数的比分别为8：7和30：31，两校合并后男、女生人数的比是27：26，则A，B两校合并前人数比是．29．甲、乙、丙、丁四人参加数学竞赛，赛后猜测他们之间的考试乘绩情况是：甲说：“我可能考的最差．”乙说：“我不会是最差的．”丙说：“我肯定考的最好．”丁说：“我没有丙考的好，但也不是最差的．”成绩公布后，只有一人猜错了，则此四人的实际成绩从高到低的次序是．30．若在同一斜坡上往返，上坡速度为5m/s，下坡速度为7m/s，则往返一次的平均速度是________米/秒．31．若三个连续偶数的最小公倍数是1008，则这三个自然数的和是．32．某数除以7余4，除以9余6，除以11余2，那么这个数的最小可能是．33．某店原来将一批羽绒服按100%的利润定价出售，淡季，商家按38%的利润重新定价，这样售出了其中的40%．旺季价格有所回升，售出了余下的全部羽绒服．结果，实际获得的总利润是原定利润的45.2%，那么旺季的价格是原定价格的%．（注：”按100%的利润定价”指的是”利润=成本×100%”）34．统计局统计了664座城市，按空气污染情况可分为三类：良好，轻度污染和严重污染．其中，空气质量良好的城市数比严重污染城市数的3倍多52座，轻度污染城市数是严重污染城市数的2倍．则空气严重污染城市有座．35．如图中三个正方形的边长分别为10，20，30，那么图中阴影部分的面积是．36．在1到2013这2013个数中，共有个数与四位数5678相加时不发生进位．37．如图，在正方形ABCD中，E，F分别是边AB，BC的中点．那么，以这6个点中的任意三个为顶点可组成的不同的三角形的个数是．38．若整数x满足不等式，则x=．39．如图，三个同心圆的半径分别是1厘米，3厘米，5厘米，AB，CD，EF，GH八等分这个圆，且都过圆心O．图中阴影部分的面积与非阴影部分的面积之比是．40．如下表，自然数以一定的规律排列，横为行，竖为列，如9在第3行第2列，记为9=（3，2），则2013=（，）．41．如图是由边长为1的25个小正方形拼成的图形，则阴影部分的面积是．42．生活中，有人习惯用1/2表示1月2日，也有人习惯用1/2表示2月1日，这样一来，如果遇到1/2，就不能明确这究竟是1月2日还是2月1日了．一年中这种容易混淆的日期表示共有天．43．计算：．44．在下面的括号里填上不同的自然数，使等式成立．（答案不唯一，写出一个即可）．45．如图，在△ABC 中，，E ，G 分别是AD ，ED 的中点，若△EFG 的面积为1，则△ABC 的面积是．46．如图（1），（2），（3），边长相等的三个正方形内分别紧排着9个，16个，25个等圆．设三个正方形内的阴影部分面积分别为S 1，S 2，S 3，则S 1，S 2，S 3的大小关系是．47．有甲乙两只圆柱形玻璃杯，其内直径分别是20厘米，24厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了6厘米；然后将铁块沉没于乙杯，且乙杯中的水没外溢，则这时乙杯中的水位上升了厘米．48．建筑公司计划修一条隧道．当完成任务的时，公司引进新设备，修建速度提高了20%，每天的工作时间缩短为原来的80%，实际185天完成了任务．若按原计划，则天可完成任务．49．如果一个自然数能表示成两个非零自然数的平方差，则称这个数为”吉祥数”，如：9=52﹣42，9是”吉祥数”．那么从1开始的自然数中，第2013个”吉祥数”是．50．有3个整数，如果第2个数的5倍是第1个数与1的差的4倍，第3个整数的5倍是第2个数与1的差的4倍，那么第1个数的最小值是．51．春蕊班的每位同学都参加了课外体操班或围棋班，有的同学还同时参加了两个班．如果同时参加两个班的人数是参加围棋班的，是参加体操班人数的．那么这个班只参加体操与只参加围棋班的人数之比是．52．甲乙两个硬盘的成本共1600元，甲按30%的利润定价，乙按40%的利润定价，甲按定价的90%出售，乙按定价的85%出售，供货的利润290元．那么甲的成本是元．53．已知，其中a，b，c，d，e都是整数，则其中最大的数的值是．54．咖啡店新推出一款杯子，定价是88元/个，实际销售时降了价，结果销量比预计的增加了，收入增加了，则每个杯子被降价元．55．若三个连续自然数的平方的和等于245，则这三个连续自然数的和是．56．已知长方体表面积是148cm2，底面面积是30cm2，底面的周长是22cm，则这个长方体的体积是cm3．57．用棱长为2厘米的小正方体，如图所示层层重叠放置．则当重叠了5层时，这个立方体的表面积是平方厘米．58．由长度分别为2，3，4，5，6的五条线段为边，可以组成个不同的三角形．59．若字母a，b，c分别表示不同的非零数字，则由a，b，c组成的各个数位上数字不同的三位数共有个，若除三位数外，其余几个的和为2874，则=．60．如图，边长为2a的正方形ABCD内有一个最大的圆圆O，圆O内有一个最大的正方形EFGH．用S1，S2，S3依次表示△EOF的面积，弓形EmF的面积，带弧边EmF的△EBF的面积，则S1*S2*S3=．（圆周率π取3）61．从12点开始，经过分钟，时针与分针第一次成90°角；12点之后，时针与分针第二次成90°角的时刻是．62．已知一列数：1，1，2，3，5，8，13，21，34，55，89，144，233，…，若第n个数比第n+2个数小233，则n=．63．一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周．它在三条边上的速度分别是每秒3cm，4cm，5cm（如图）．且当它到达拐点（A，B，C）时会休息26秒，当它爬完一周回到点A时，行程结束．这期间，蚂蚁的平均速度是cm/s．64．至多含有一个奇数数字且能被25整除的四位数共有个．65．观察下面的数表：（横排为行，竖排为列）表中第1列都是单位分数，分母依次为1，2，3…，每行自第2个分数起，每个分数的分子等于左边分数的分子加1，分母等于左边分数的分母减1，直到分数的分母等于1．则位于第行，第列．66．从最小的质数算起，若连续n（n是大于1的自然数）个质数的和是完全平方数，则n 最小是．67．现有3个互不相等的数，甲说是2，a+1，b+2；乙说是2b﹣1，3，a．若两人都说对了，则这三个数的乘积是．68．若×=6657，其中x，y，z都代表非零数字，则=．69．两个直角三角板如图放置，则∠BFE的度数是∠CAF的倍．70．一个长方体相邻的两个面的面积之和是130，它的长，宽，高都是不超过13的整数，且均为互不相等的质数，则这个长方体的体积是．71．如图，一个物体由2个圆柱组成，它们的半径分别是3厘米和6厘米，而高分别是5厘米和10厘米，则这个物体的表面积是平方厘米．72．植树节，5名小朋友给5棵树浇水，每个小朋友至少浇一棵树，但一个小朋友不能重复给同一棵树浇水，一桶水也只能浇一棵树．活动结束后，5个小朋友分别浇了2，2，3，5，x桶水，5棵树分别被浇了1，1，2，4，y 桶水，那么x=，y=．73．小明出去散步前看了一下手表，回来时又看了一下手表，发现此时手表的时针，分针的位置正好与出去时的分针，时针位置相同．若他在外逗留的时间不足一小时，则他在外待了分钟．74．如图所示，共有个三角形．75．一个长为4，宽为3的长方形如图竖直放置，在其右上角有一个红点A，长方形绕右下角旋转90°，成为一个横放的长方形，再绕右下角旋转90°，成为一个竖放的长方形，…，当小红点A第一次回到右上角时所走过的路程是．76．书架第一层有依次排列的10本不同的故事书，现将2本不同的漫画书也放入第一层，则不同的放法共有种．77．分母是385的所有最简真分数的和等于．78．有价值总和为174万元的三批货物，这三批货物的质量比是3：4：5，单位质量的价格比是6：5：4．这三批货物各价值万元．79．将分数化成小数后，如果小数点后第一位起连续N个数位上数字之和等于2013，那么N=．80．如图所示是一个边长为120m的等边三角形，甲乙同时分别从A点，B点按顺时针方向出发，甲每分钟走120m，乙每分钟走180m，但经过每个顶点时，因转弯都要耽误5s，则乙出发s后第一次追上甲．81．原来，单独打开进水管3小时能将水池注满，单独打开出水管4小时可排完一池水．后来，这个水池漏水了，同时打开进水管与出水管14小时才能将水池注满，则只打开进水管需要小时可以注满这个漏的水池．82．图书馆，游泳馆，少年宫三个站在一条笔直的公路上，且游泳馆到图书馆，少年宫两站的距离相等．小明和小华分别从图书馆，少年宫两站同时出发相向而行．小明超过游泳馆站100米后与小华相遇．然后二人继续前进．小明到达少年宫站后立即沿原路返回，经过游泳馆站后300米追上小华．则图书馆，少年宫两站相距米．83．马和狗约好去牛哥家做客，牛哥说他忘了去超市买面包，狗说他去，一会儿，马到了牛哥家，听说狗去买东西了，他急了，他说，狗跑5步的时间我能跑6步，我跑4步的距离相当于狗跑7步．而且我比他力气大，买东西的活儿我去，于是马也奔超市去了，此时狗已跑出550米了．超市离牛哥家有2000米，则马要跑米才能追上狗，此时离超市还有米．84．12和60是很有趣的两个数，这两个数的积恰好是这两个数的和的10倍：12×60=720=10×（12+60）．满足这两个条件的非零自然数对还有：．85．明明，亮亮，军军三人都参加了数学竞赛，他们共解出了100道题，每人都解出了其中的60道题目，若三个人都解出来的题称为基础题；只有两个人解出来的题称为中等题；只有一个人解出来的题称为难题，则在他们解出的100道题中，难题的数量比基础题的数量（填：多或少）道．86．一块木片沿河漂流，从河边的A地到B地，用了24小时．一只快艇在静水中的速度是18千米/小时，它从A驶到B所用的时间是从B驶到A所用时间的．则AB间的距离是千米．87．如图，AB∥CE，AC∥DE，且CE=DE=2AB=2AC，则=．88．小明和小林是两个集邮爱好者，他们共有邮票400多张，如果小明给小林a张邮票，小明就比小林少；如果小林给小明a张邮票，则小林就比小明少．那么小明原有张邮票，小林原有张邮票．89．用底面内半径和高分别是12cm，20cm的空心圆锥和空心圆柱各一个组成如图所示竖放的容器，在这个容器内注入一些细沙，能填满圆锥，还能填部分圆柱，经测量，圆柱部分的沙子高5cm，若将这个容器倒立，则沙子的高度是cm．90．为确保信息安全，信息需加密传输，发送方将明文加密成密文，接收方收到密文后解密可得明文．已知有一种加密方式是将英文26个小写字母a，b，c，…，依次对应0，1，2，…，25这26个整数（见下表），当明文中的字母对应的序号为a时，将a+10除以26后所得的余数作为密文中的字母对应的序号，例如明文”a”对应密文”k”．””91．如图，在正方形场地ABCD的四周有32个洞（每边9个洞），一个工人扛着32面旗子，从A洞开始插旗，按顺时针方向，每隔5个洞就插一面旗，当他绕着正方形走完5圈时，发现有n个洞不能插旗，求n．92．某校有960套桌凳需要维修．现有甲乙两个木工，甲单独修理这批桌凳比乙多用20天；乙每天比甲多修8套；甲乙每天的修理费分别是80元，120元．在修理桌凳过程中，学校要委派一名维修工进行质量监督，并由学校负担他每天10元的生活补助．现有以下三种修理方案共选择：①由甲单独修理；②由乙单独修理；③由甲乙共同合作修理．你认为哪种方案即省时又省钱？试比较说明．93．甲乙丙三辆汽车分别从A地开往千里之外的B地．乙比甲晚出发40分钟，出发后160分钟后能追上甲；丙比乙晚出发20分钟，出发后5小时追上乙．那么如果甲比乙先出发10分钟，乙比丙先出发10分钟，那么乙追上甲之后过多久丙能追上甲？94．已知甲乙丙三位同学在北京，广州，上海的大学学习软件设计，服装设计，城市规划．有下列判断：①甲不在北京学习；②乙不在广州学习；③在北京学习的同学不学城市规划；④在广州学习的同学是学软件设计的；⑤乙不学服装设计．三位同学各在什么城市学习什么专业？95．如图，长方形ABCD，ABEF，AGHF的长与宽的比相同，且，长方形BEHG的周长是22，求长方形ECDF的面积．96．在小于30的所有质数中，是否存在差与平方和都是质数的两个质数？若存在，有几组？若不存在，请说明理由．97．甲容器内有物质A和物质B，其质量比是2：3，乙容器内有物质B和物质C，其质量比是1：2，丙容器内有物质A和物质C．现将甲乙丙三容器中的物质以1：2：3的比例取出，混合，则所得新的混合物中，A，B，C三种物质的质量比是183：152：385．求丙容器内物质A和物质C的质量比．98．程序员设计了一款新游戏，共20级．小刚一次晋级2级游戏，或一次晋级3级游戏，那么他从入门（0级）晋级到第20级共有多少种不同的方法？10月份，小强的家里用了23m的居民用水，他开的餐厅，用了102m的餐饮用水，则这个月他应该交多少元水费？100．0．买一盒牙膏，一瓶沐浴露和一瓶洗发露共付款100元．若1瓶沐浴露比2盒牙膏贵，2瓶洗发露比7瓶沐浴露贵，8盒牙膏比1瓶洗发露贵，且每个产品的单价都是整数元，分别求一盒牙膏，一瓶沐浴露，一瓶洗发露的价格．小学“希望杯”培训100题（六年级）参考答案与试题解析一、解答题（共100小题，满分0分）1．计算：=．2．计算：2012×2014×（）=2．3．（2010•成都校级自主招生）．解：++…+，=×（﹣+﹣+…+﹣），=×（﹣）=×（）=×=．4．计算：（0.+0.3）×0.×0.7×=．+0.3）×0.7×，（+×××，×××（×××，=××=×=5．=102．解：，=（1+3+5+..+19）+3×=102+3×（1﹣）=100+=102．6．=．解：设n=++，m=，则：（1+++）×（+++）﹣（1++++）×（++），=（1+n）×m﹣（1+m）×n=m+mn﹣n﹣mn=m﹣n，=（）﹣（++）=．7．兄弟俩都有点傻，以为只有自己过一年长一岁而别人不会长．某天，哥哥对弟弟说：”再过3年我的年龄就是你的2倍．”弟弟说：”不对，再过3年我和你一样大．”今年，他们俩分别是6岁，9岁．解：弟弟：（3+3）÷（2﹣1）=6（岁）；哥哥：6+3=9（岁）．8．有一堆黑白棋子，黑棋的粒数是白棋的2倍，每次从中取出白棋3粒黑棋5粒，白棋恰好取完时黑棋还剩20粒．则原来这堆棋子共有180粒．解：取了：20÷（6﹣5）=20（次），共有：20×3×（1+2）=180（粒）；9．如图，边长12cm的正方形与直径为16cm的圆部分重叠，若没有重叠的两空白部分的面积分别是S1，S2，则S1﹣S2=48cm2．（π取3）S1﹣S2=（S1+S阴）﹣（S2+S阴）=S圆﹣S正=3×（16÷2）2﹣122=192﹣144=48（平方厘米）；10．有一列数：8，18，24，49，55，60，65，77，81，98，100．它们的最小公倍数是23×34×52×72×11×13．（以乘方形式表示，不用写出计算结果）11．王老师将200块糖分给了甲乙丙三个小朋友，甲比乙的2倍还要多，乙比丙的3倍还要多，那么甲最少有121块糖，丙最多有19块糖．12．建军路小学有钢琴，小提琴这两个兴趣班，这两个班的学员都是来自A班或者B班的．钢琴班有来自A班，小提琴班有来自B班，并且钢琴班的总人数是小提琴班总人数的倍，那么这两个兴趣班中来自B班的人数与总人数的比值是．）×=3﹣×=3班的人数与总人数的比值是；故答案为：．13．定义：”如果一个数有12个约数，那么称这样的数为’好数’”．则将所有的”好数”由小到大依次排列，第三个是84．14．有一口枯井，用一根绳子测井口到井底的深度，将绳对折后垂到井底，绳子超过井口9米；将绳子三折后垂到井底，绳子超过井口2米，则绳长42米，井深12米．对应的分率的差额是：﹣）（）15．将100个梨分给10个同学，每个同学的梨个数互不相同．分得梨个数最多的同学，至少得到15个梨．16．31500的约数中与6互质的共有8个．17．如图2，S△ABC=24，D是AB的中点．E在AC上，AE：EC=2：1．DC交BE于点O．若s△DBO=a，S△CEO=b，则a﹣b=4．S=S18．已知有三个连续的自然数，它们中最小的一个是9的倍数，中间一个是7的倍数，最大的一个是5的倍数，那么这些自然数最小分别是153，154，155．19．快速公交3号线行驶于安定门与宏福苑小区之间，已知它的发车间隔时间是相等的，苏老师开车从宏福苑小区到安定门，每过3分钟她的迎面就驶来一辆快速公交，每隔12分钟她就超过一辆快速公交．快速公交全程是45分钟，假设公交车和苏老师开车的速度都不变，那么苏老师开车从宏福苑小区到安定门需要27分钟．则苏老师与公车速度和为问题；苏老师与公车速度差为，因为这时是相遇问题；那么苏老师速度（+），所以苏老师与公车速度比：，，+），公车速度（﹣），苏老师与公车速度比：=520．将自然数1，2，3，…，依次写下去，组成一个数：12345678910111213…，当写到2054时，这个大数除以9的余数是3．21．地震时，地震中心同时向各个方向传播出纵波和横波．纵波的传播速度是3.96km/s，横波的传播速度是2.58km/s，某次地震，地震监测点用地震仪接收到地震的纵波之后，隔了18.5s，接收到这个地震的横波，那么这次地震的地震中心距离地震监测点136.96km．t=﹣，22．对于非零自然数n，如果能找到非零自然数a，b使得n=a+b+ab，则称n是一个”联谊数”，如：3=1+1+1×1，则3就是一个”联谊数”，那么从1到20这20个自然数当中，”联谊数”共有12个．23．甲乙丙丁四个人去购物，付账时每人都拿出一些钱，已知，乙丙丁三人付钱的总和是甲的5倍，甲丙丁三人付钱的总和是乙的4倍，甲乙丁三人付钱的总和是丙的3倍，丁付了46元，那么四个人共花了120元．=，丙占总数的；；﹣﹣）÷，24．一个自然数，在3进制中的数字和是24．它在9进制中的数字和最小是24，最大是72．25．设N=1×2×…×209×210，则：（1）N的末尾一共出现51个连续的数字”0”；（2）用N不断除以12，知道结果不能被12整除为止，一共可以除以102次．26．如果长方形，正方形，正三角形分别有a，b，c条对称轴，则（a+b+c）2=81．27．在数4，11，19，73，93，118，125，238中相邻若干个数之和是3的倍数而不是9的倍数的数组共有6组．28．A，B两校的男、女生人数的比分别为8：7和30：31，两校合并后男、女生人数的比是27：26，则A，B两校合并前人数比是45：61．29．（2011•成都）甲、乙、丙、丁四人参加数学竞赛，赛后猜测他们之间的考试乘绩情况是：甲说：“我可能考的最差．”乙说：“我不会是最差的．”丙说：“我肯定考的最好．”丁说：“我没有丙考的好，但也不是最差的．”成绩公布后，只有一人猜错了，则此四人的实际成绩从高到低的次序是乙丙丁甲．30．若在同一斜坡上往返，上坡速度为5m/s，下坡速度为7m/s，则往返一次的平均速度是米/秒．，那么上坡的时间就是，下坡的时间就是；用总路程+）÷，（米故答案为：．31．若三个连续偶数的最小公倍数是1008，则这三个自然数的和是48．32．某数除以7余4，除以9余6，除以11余2，那么这个数的最小可能是123．33．某店原来将一批羽绒服按100%的利润定价出售，淡季，商家按38%的利润重新定价，这样售出了其中的40%．旺季价格有所回升，售出了余下的全部羽绒服．结果，实际获得的总利润是原定利润的45.2%，那么旺季的价格是原定价格的75%．（注：”按100%的利润定价”指的是”利润=成本×100%”）34．统计局统计了664座城市，按空气污染情况可分为三类：良好，轻度污染和严重污染．其中，空气质量良好的城市数比严重污染城市数的3倍多52座，轻度污染城市数是严重污染城市数的2倍．则空气严重污染城市有102座．35．如图中三个正方形的边长分别为10，20，30，那么图中阴影部分的面积是600．36．在1到2013这2013个数中，共有51个数与四位数5678相加时不发生进位．37．如图，在正方形ABCD中，E，F分别是边AB，BC的中点．那么，以这6个点中的任意三个为顶点可组成的不同的三角形的个数是18．38．若整数x满足不等式，则x=3．因为不等式，＜3，2，39．如图，三个同心圆的半径分别是1厘米，3厘米，5厘米，AB，CD，EF，GH八等分这个圆，且都过圆心O．图中阴影部分的面积与非阴影部分的面积之比是1：3．厘米的圆面积的厘米的圆面积的，圆中，据此40．如下表，自然数以一定的规律排列，横为行，竖为列，如9在第3行第2列，记为9=（3，2），则2013=（4，60）．41．如图是由边长为1的25个小正方形拼成的图形，则阴影部分的面积是18．42．生活中，有人习惯用1/2表示1月2日，也有人习惯用1/2表示2月1日，这样一来，如果遇到1/2，就不能明确这究竟是1月2日还是2月1日了．一年中这种容易混淆的日期表示共有132天．43．计算：．2+））﹣，）2+）2+），．，2012+．44．在下面的括号里填上不同的自然数，使等式成立．（答案不唯一，写出一个即可）．的分子、分母同时扩大倍，变成的分子、分母同时扩大倍，变成===﹣=﹣﹣，==++++，==﹣﹣=+，45．如图，在△ABC中，，E，G分别是AD，ED的中点，若△EFG的面积为1，则△ABC的面积是18．中，，且，据此利用分数除法的意义即可解答问题．中，的面积的，÷=1846．如图（1），（2），（3），边长相等的三个正方形内分别紧排着9个，16个，25个等圆．设三个正方形内的阴影部分面积分别为S1，S2，S3，则S1，S2，S3的大小关系是相等．47．有甲乙两只圆柱形玻璃杯，其内直径分别是20厘米，24厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了6厘米；然后将铁块沉没于乙杯，且乙杯中的水没外溢，则这时乙杯中的水位上升了厘米．。

第八-十二届希望杯全国数学邀请赛六年级试题及答案解析

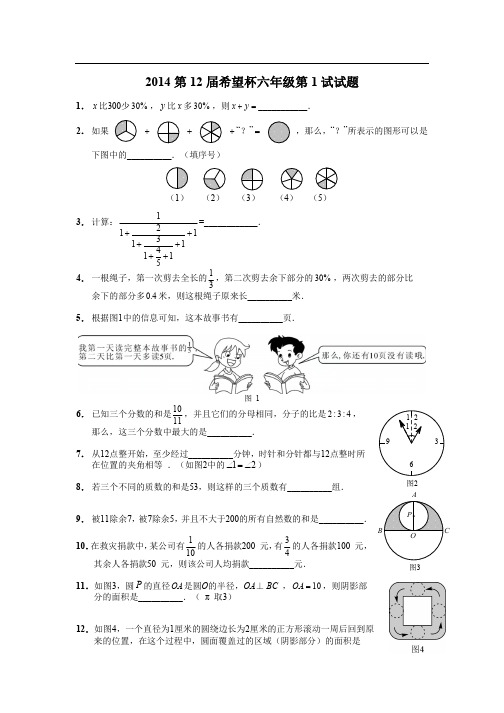
4. 一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是__________．
5. 22012 的个位数字是__________．（其中 2n 表示 n 个 2 相乘）
6. 下图（左）是一个正方体的展开图，图中（右）的四个正方体中只有一个是和这个展开图对应的，这个正方体是__________．（填序号）
10. 在一个两位数的中间加上小数点，得到一个小数，若这个小数与原来的两位数的和是 86.9 ，则原来的两位数是___________．
11. A、B 两校的男、女生的人数的比分别是 8:7 和 30:31，两校合并后，男、女生人数的比
是 27:26，则 A、B 两校合并前人数的比是___________． 12. 有 2013 名学生参加数学竞赛，共有 20 道竞赛题，每个学生有基础分 25 分，此外，答
b (若a b).
1.1 7 1 0.1
例如： 3.5 2 3.5,1 1.2 1.2, 7 7 1，则
33 4 0.8
___________．
5
7. 有一口无水的井，用一根绳子测井的深度，将绳子对折后垂到井底，绳子的一端高出井口 9m；将绳子三折后垂到井底，绳子的一端高出井口 2m，则绳子长___________m，井深___________m．
①
②
③
④
7. 一列快车从甲地开往乙地需要 5 小时，一列慢车从乙地开往甲地所需时间比快车多 1 ， 5
两车同时从甲乙两地相对开出 2 小时后，慢车停止前进，快车继续行驶 40 千米后恰与慢车相遇，则甲乙两地相距__________千米．
8. 对任意两个数 x，y，定义新的运算“*”为： x y x y
1 1

希望杯六年级近五年真题大全

希望杯目录真题希望杯简介 ......................................................................... .. (Ⅰ)近三年真题分析.......................................................................... (Ⅱ)2014第 12 届希望杯六年级第 1 试试题....................................................................... .. (1)2013第 11 届希望杯六年级第 1 试试题....................................................................... .. (3)2012第 10 届希望杯六年级第 1 试试题....................................................................... .. (5)2011 第 9 届希望杯六年级第 1 试试题........................................................................... (7)2010第 8 届希望杯六年级第 1 试试题....................................................................... . (9)2014第 12 届希望杯六年级第 2 试试题...................................................................... . (11)2013第 11 届希望杯六年级第 2 试试题...................................................................... . (13)2012第 10 届希望杯六年级第 2 试试题...................................................................... . (15)2011 第 9 届希望杯六年级第 2 试试题........................................................................... . (17)2010第 8 届希望杯六年级第 2 试试题...................................................................... (19)参考答案2014第 12 届希望杯六年级第 1 试试题分析....................................................................... . (21)2013第 11 届希望杯六年级第 1 试试题分析....................................................................... . (23)2012第 10 届希望杯六年级第 1 试试题分析....................................................................... . (25)2011第 9 届希望杯六年级第 1 试试题分析 (27).........2010第 8 届希望杯六年级第 1 试试题分析....................................................................... (29)2014第 12 届希望杯六年级第 2 试试题分析....................................................................... . (31)2013第 11 届希望杯六年级第 2 试试题分析....................................................................... . (33)2012第 10 届希望杯六年级第 2 试试题分析....................................................................... . (35)2011第 9 届希望杯六年级第 2 试试题分析....................................................................... (37)2010第 8 届希望杯六年级第 2 试试题分析....................................................................... (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛．“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容，适当地拓宽知识面；启发他们注意数学与其它课程的联系和数学在实际中的应用；激励他们去钻研和探究；培养他们科学的思维能力、创新能力和实践能力；树立他们为振兴中华而努力成才的自信．“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲，不超出教学进度，贴近现行的数学课本，源于课本，高于课本．题目活而不难，巧而不偏；既大众化又富于思考性和启发性．力求体现科学思维之美，寓科学于趣味之中，将知识、能力的考察和思维能力的培养结合起来．“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生．每年举行一次，为一届．每次举行两试，三月中旬第 1 试，考小时；四月中旬第 2 试，考 2 小时．“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单，做到以下两点，希望杯获奖轻松惬意：1．利用寒假做完希望杯 100 题和希望杯历年真题；2．春季再做一遍；3．结合一试的试题，有针对性的准备二试．希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖，整个深圳市也就 20 个左右的名额；而全国三等奖就有好几百个，具体规则如下：根据希望杯的评奖规则，全国一二等奖在赛区内统一标准，按照初赛人数的约千分之三评定．全国三等奖按报名单位初赛人数和规定比例评定，由报名单位按照下述要求评定：1．各单位获奖总指标（一二三等奖）：中学每满 30 人初赛给一个指标，不足 30 人不给；小学每满 20 人初赛给一个指标，不足 20 人不给．若评出人数多于计划指标，组委会将按照从后到前的顺序去掉多出指标．2．各单位评奖时应当按照复赛分数由高到低的原则，赛分数相同时按初赛成绩排序．3．各单位指标可在小学内部中学内部调剂使用，得在二者之间调剂．4．凡是列入全国一二等奖推荐名单的，提供该生的一试试卷和二试试卷，奖励等级由全国组委会统一确定．深圳地区奖项设置有特、一、二、三等奖，2014 年 2000 多名进入二试的学生中，有 120 个特等奖，400 个一等奖，所有进入二试的选手至少能获三等奖！！近三年真题分析“希望杯”题型涉及内容广泛，为了更好备战 2015 年“希望杯”，我们需要对历年考试情况有一个详细了解。

2012年第十届小学“希望杯”全国数学邀请赛(六年级第1试)

第十届小学“希望杯”全国数学邀请赛六年级第1试2012年3月11日上午8:30至10:00 得分______ 以下每题6分，共120分。

1. 计算：21111.2511125%=9943⨯+⨯-⨯______.2. 计算：251251= 2008200920092010+⨯⨯______.3. 在小数3.1415926的两个数字上方加2个循环点，得到循环小数，这样的循环小数中，最小的______.4. 一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是______.5. 20122的个位数字是______.（其中，2n表示n个2相乘）6. 图1是一个正方体的展开图，图2的四个正方体中只有一个是和这个展开图对应的，这个正方体是______.（填序号）7. 一列快车从甲地开往乙地需要5小时，一列慢车从乙地开往甲地所需时间比快车多15，两车同时从甲、乙两地相对开出2小时后，慢车停止前进，快车继续行驶40千米后恰与慢车相遇，则甲、乙两地相距______千米.8. 对任意两个数x ，y ，定义新的运算“*”为：2x yx y m x y⨯*=⨯+⨯（其中m 是一个确定的数）.如果1*2=25，那么m=______，2*6=______. 9. 甲、乙两家商店出售同一款兔宝宝玩具，每只原售价都是25元，为了促销，甲店先提价10%，再降价20%；乙店则直接降价10%.那么，调价后对于这款兔宝宝玩具，______店的售价更便宜，便宜______元。

10. 图3中的三角形的个数是______.11. 若算式（□+121×3.125）÷121的值约等于3.38，则□中应填入的自然数是______.12. 认真观察图4中的三幅图，则第三幅图中的阴影部分应填的数字是______.13. 图5中每一个圆的面积都是1平方厘米，则六瓣花形阴影部分的面积是______平方厘米.14. 如图6，正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形，小正方形的面积的值已标在图中，分别为20和10，18和12，则正方形ABCD和EFGH中，面积较大的是正方形______.15. 早晨7点10分，妈妈叫醒小明，让他起床，可小明从镜子中看到的时刻还没有到起床的时刻，他对妈妈说：“还早呢！”小明误以为当时是______点______分.16. 从五枚面值为1元的邮票和四枚面值为1.60元的邮票中任取一枚或若干枚，可组成不同的邮资______种.17. 从1，2，3，4，…，15，16这十六个自然数中，任取出n个数，其中必有这样的两个数：一个是另一个的3倍，则n最小是______.18. 某工程队修建一条铁路隧道，当完成任务的13时，工程队采用新设备，使修建速度提高了20%，同时为了保养新设备，每天工作时间缩短为原来的45，结果，前后共用185天完工.由以上条件可推知，如果不采用新设备，完工共需______天.19. 王老师在黑板上写了若干个从1开始的连续自然数：1，2，3，4，…，然后擦去三个数（其中有两个质数），如果剩下的数的平均数是8199，那么王老师在黑板上共写了______个数，擦去的两个质数的和最大是______.20. 小强和小林共有邮票400多张，如果小强给小林一些邮票，小强的邮票就比小林的少619；如果小林给小强同样多的邮票，则小林的邮票就比小强的少617.那么，小强原有______张邮票，小林原有______张邮票.。

2012年第10届希望杯六年级一试试题详解】

2012年希望杯六年级第1试试题1、计算：21111.2511125%9943⨯+⨯-⨯=______.【答案】1.25 【解析】2111.251 1.25993⎛⎫=⨯+-= ⎪⎝⎭原式2、计算：2512512008200920092010+=⨯⨯______. 【答案】18040 【解析】11111112512512008200920092010200820108040⎡⎤⎛⎫⎛⎫⎛⎫=⨯-+-=⨯-=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦原式 3、在小数3.1415926的两个数字上方加2个循环点，得到循环小数，这样的循环小数中，最小的是______.【答案】3.1415926∙∙【解析】略4、一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是______.【答案】90【解析】最小的两位数是10，所以被除数最大是10990⨯=5、20122的个位数字是______.（其中，2n 表示n 个2相乘）【答案】6【解析】2的次方的个位数字的规律是2、4、8、6、2、4、8、6、……，它是4个数为一个周期的，而20124503÷=，则20122的个位数字是66、图1是一个正方体的展开图，图2的四个正方体中只有一个是和这个展开图对应的，这个正方体是_______.（填序号）图1 图2【答案】【解析】略7、一列快车从甲地开往乙地需要5小时，一列慢车从乙地开往甲地所需时间比快车多1/5，两车同时从甲乙两地相对开出2小时候，慢车停止前进，快车继续行驶40千米后恰与慢车相遇，则甲乙两地相距______千米.【答案】150千米【解析】快车需要5小时，慢车需要6小时，设快车速度为6份，则慢车速度为5份，则全长为30份，两车相对开出2小时后，两车行驶的路程和为22份，则8份的距离对应40千米，则甲乙两相距40830150÷⨯=千米。

8、对任意两个数x ，y ，定义新的运算*为：*2x y x y m x y ⨯=⨯+⨯ （其中m 是一个确定的数）.如果21*25=，那么m =______,2*6=_______. 【答案】1m =，62*67= 【解析】1221*21225m ⨯==⨯+⨯，则1m =，2662*612267⨯==⨯+⨯9、甲、乙两家商店出售同一款兔宝宝玩具，每只原售价都是25元，为了促销，甲店先提价10%，再降价20%；乙店则直接降价10%.那么，调价后对于这款兔宝宝玩具，______店的售价更便宜，便宜_____元。

2012第十届六年级希望杯培训题100道及答案解析

2012第十届六年级“希望杯”培训题1．计算 129×10 ＋2210×11 ＋…＋51259×602．计算：1×2×3×4＋3×6×9×122×4×6×83．计算4．用简便方法计算3＋1949×（158 －12007 ）＋58×（11949 －12007 ）－2007×（11949 ＋158）5．图l 所示正方体的展开图是．(填序号)6．一串数字2134…，从第三个数字起，每个数字都是它前面两个数字之和的个位数字，则这串数字的第2012个数字是．7．一个三位数是3的倍数，去掉它的个位数字后，所得的两位数是17的倍数．这个三位数最大是．8．将被11除余1，被l5除余12的自然数按从小到大的顺序排成一列则；若，则= 。

9．某市人口总数与上年相比的情况是：2007年比2006年增加1％，2008年比2007年又增加1％，2009年比2008年减少1％，2010年比2009年又减少1％，那么2010、年与2006年相比，该市的人口总数 (填“增加”或“减少”)的百分数大约是．10．用运算符号及括号将1，3，7，8连接成一个算式(每个数只使用一次)，试给出一个使用了“÷”且结果等于24的算式．11．将3，4，5，6，7，，8填入下面的方框里，使两个三位数的乘积最大．□□□×□□□则7月8日中的“8”排在数串的第位．13．已知，，则= 。

14．若A，B，C分别代表l～9的某个自然数，已知等式成立，则A＝，B＝，C＝．15．请选择一个你喜欢的两位数，将它连续写5遍组成一个十位数(如：两位数12连续写5遍成为1212121212)，将这个十位数除以这个两位数，所得到的商再除以9，所得的余数是．16．图2是一个新月形图案，则用两条直线最多可以将该图案分成部分．17．将一个正三角形的三条边分别2、3、4等分，获得一些相同的小正三角形，如图3所示．如果将正三角形的三条边都10等分，那么．得到的相同的小正三角形有个．图318．六年级1班有30多人，个子最高的小明发现，放学站队时无论是2人、还是3人或者4人站成一排，他都只能自己单独站在最后，没有人与他站一排．则六年级1班共有人．19．设a、b、c分别是甲、乙、丙三人独自完成某项工程所需天数．令，则A、B的大小关系是．20．公交车的线路号是由数字显示器显示的三位数，其中每个数字由横竖放置的七支荧光管显示，如图4，分别显示689，547和234．图4某公交线路号的数字的应显示器的两支应显示的荧光管不能显示，结果线路号的显示成了“234”，则该公交线路号有种可能．21．甲、乙两人的钱数比是3：2，如果甲给乙8元，则甲、乙两人的钱数比变成2：3，则两人共有钱元。

2012希望杯复赛六年级真题解析1

1
一、填空题(每小题5分，共60分。

)
1．计算：11113332345245122235
⨯⨯⨯+⨯⨯⨯⨯＝__________。

2．计算：2112552351399633515
+++++++＝__________。

3．王涛将连续的自然数1，2，3 …逐个相加，一直加到某个自然数为止，由于计算时漏加了一个自然数而得到错误的结果2012，那么，他漏加的自然数是_______。

4．在数0.20120415中的小数点后面的数字上方加上循环点，得到循环小数，这些循环小数中，最大的是_______，最小的是_______。

5．对任意两个数x ，y ，规定运算“﹡”的含义是：x ﹡y ＝43x y m x y
⨯⨯⨯+⨯(其中m 是一个确定的数)。

如果1﹡2＝1，那么m ＝________，3﹡12＝________。

6．对于一个多边形，定义一种“生长”操作：如图1，将其一边AB 变成向外凸的折线ACDEB ，其中C 和E 是AB 的三等分点，C 、D 、E 三点可构成等边三角形。

那么，一个边长是9的等边三角形，经过两次“生长”操作(如图2)，得到的图形的周长是_______；经过四次“生长”操作，得到的图形的周长是______。

7．如图3所示的“鱼”形图案中共有_______个三角形。

8．已知自然数N 的个位数字是0，且有8个约数，则N 最小是_________。

2012第十届希望杯初赛六年级(含解析)

第十届小学"希望杯”全国数学邀请赛六年级第1试2012年3月11日上午8:30至10:00亲爱的小朋友，欢迎你参加第十届小学”希望杯”全国数学邀请赛！你将进入一个新颖、有趣、有挑战性的数学天地，将会留下一个难忘的经历以下每题6分，共120分.1 •计算：2 1 1 11.25 —1-1—125% —9 9 4 32•计算：251 2512008 2009 2009 20103•在小数3.1415926的两个数字上方加2个循环点，得到循环小数，这样的循环小数中，最小的 ______________________________ 4•一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是5. 22012的个位数字是_______________ •（其中，2n表示n个2相乘）6•左图是一个正方体的展开图，右图的四个正方体中只有一个是和这个展开图对应的，这个正方体是____________ •（填序号）7•—列快车从甲地开往乙地需要5小时，一列慢车从乙地开往甲地所需时间比快车多［，两车同时从甲乙5 两地相对开出2小时后，慢车停止前进，快车继续行驶40千米后恰与慢车相遇，则甲乙两地相距____________ 千米.那么m ___________ ，2*6 _________9•如图2,甲、乙两家商店出售同一款兔宝宝玩具，每只原售价都是25元，为了促销，甲店先提价10%再降价20%乙店则直接降价10%那么，调价后对于这款兔宝宝玩具， _____________________________ 店的售价更便宜，便宜_____________ 元.① ② ③&对任意两个数x , y，定义新的运算“ * ”为：x* y一（其中m是一个确定的数）m x 2 y•如果1*2=-5，10.图中的三角形的个数是11 •若算式([121 3.125) 121的值约等于3. 38,则□中应填入的自然数是 ______________________________ 12•认真观察图中的三幅图，则第三幅图中的阴影部分应填的数字是14•如图，正方形 ABCD 和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形，小正方形的面积已标在图中，分别为20和10, 18和12，则正方形ABCD 和EFGH 中，面积较大的正方形是 __________________15•早晨7点10分，妈妈叫醒小明，让他起床，可小明从镜子中看到的时刻还没有到起床的时刻，他对妈妈说：“还早呢！ ”小明误以为当时是 ____________________ 点 _____________ 分.16. 从五枚面值为1元的邮票和四枚面值为 1 . 60元的邮票中任取一枚或若干枚，可组成不同的邮资种. 17. 从1 , 2, 3, 4,…，15, 16这十六个自然数中，任取出 n 个数，其中必有这样的两个数：一个是另个的3倍，贝U n 最小是 _______________ .K4 %13•图中每一个圆的面积都是 1平方厘米，则六瓣花形阴影部分的面积是____________ 平方厘米.□ 20 |r s□了保养新设备，每天工作时间缩短为原来的-，结果，前后共用185天完工，由以上条件可推知，如5果不采用新设备，完工共需 __________________ 天.19.王老师在黑板上写了若干个从1开始的连续自然数：1, 2, 3, 4,…，然后擦去三个数（其中有两个质数），如果剩下的数的平均数是 198，那么王老师在黑板上共写了 _____________________ 个数，擦去的两个质9数的和最大是 _______________ .20•小强和小林共有邮票 400多张，如果小强给小林一些邮票，小强的邮票就比小林的少-1 ;如果小林给 19小强同样多的邮票，则小林的邮票就比小强的少6，那么小强原有 _________________ 张邮票，小林原有17____________ 张邮票.18.某工程队修建一条铁路隧道，当完成任务的1时，工程队采用新设备，使修建速度提高了320%同时为5. 22012的个位数字是 •（其中，2n 表示n 个2相乘）2012年第十届小学"希望杯”全国数学邀请赛1试小学六年级参考答案部分解析2 1 11 1 •计算：1.25 — 1- 1— 125% —9 9 43【考点】分小百互化、简便计算【难度】★ 【答案】54W后R 4-C1 2 1 1 1 5 2 10 5 5 1 5 2 10 1 5 5 【解析】1 25 - 1 1 125%(-) 19 9 4 3 4 9 9 4 4 3 4 9 93 4 4【考点】裂项3•在小数3. 1415926的两个数字上方加 2个循环点，得到循环小数，这样的循环小数中，最小的 ______________________________【考点】循环小数【难度】★★ 【答案】3,415926【解析】要使小点数最小，则循环节开始的几位尽量小，因此从1开始循环，下一位为 4，依次往下，最小的为 3,415926 •4•一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是____________ •【考点】有余数的除法【难度】★★ 【答案】98【解析】最小的两位数是10,因此商为10,除数为一位数，最大为9,余数最大为8，被除数为9 10 8 98 •2•计算:2512008 2009 2512009 2010【答案】1 8040【解析】251 251 2008 20092009 2010251 (二2008200920092010)251 (2008爲 8040【考点】周期问题【难度】★★★ 【答案】6【解析】依次列举个位数字，21个位为2; 22个位为4; 23个位为8; 24个位为6; 25个位为2, 4个数为一周期，2012 4 503，没有余数，22012个位数字为周期中最后一个，为6.6•左图是一个正方体的展开图，右图的四个正方体中只有一个是和这个展开图对应的，这个正方体是【考点】立体图形展开图【难度】★★ 【答案】①【解析】②中右面应为三角形；③上面的圆为颜色较深的一个；④正面应为三角形，用排除法，故①正确.7•—列快车从甲地开往乙地需要5小时，一列慢车从乙地开往甲地所需时间比快车多［，两车同时从甲乙5两地相对开出2小时后，慢车停止前进，快车继续行驶 40千米后恰与慢车相遇，则甲乙两地相距____________ 千米. 【考点】行程问题【难度】★★ 【答案】150【解析】慢车走完全程用时：5 (1 -)6 (时)，2小时走全程的--;56 3快车2小时走完全程的-;全程为40 (1 - -) 150 ( km ).55 3x _y(其中m 是一个确定的数)m x 2 y那么 m ___________ , 2*6 _________【考点】定义新运算【难度】★★ 【答案】1; 671 2 2【解析】1*2= ------------------------ 整理得2m 810,解得m 1 ; 2*6m 1 2 2 5，整理得9•甲、乙两家商店出售同一款兔宝宝玩具，每只原售价都是25元，为了促销，甲店先提价10%再降价20%乙店则直接降价10%那么，调价后对于这款兔宝宝玩具， _____________________________ 店的售价更便宜，便宜____________ 元. 【考点】经济问题【难度】★★&对任意两个数x , y ，定义新的运算“ * ”为：x* y .如果1*2=-5，12 2 6【答案】甲；【解析】甲：0.525 (1 10%) (1 20%) 22 (元)；乙：25 (1 10%) 22.5 (元)，22.5 22 0.5 (元).10.图中的三角形的个数是__________________【考点】图形计数【难度】★★★【答案】35【解析】五边形被分成11块，按组成三角形的块数分类：一块的三角形：10个；两块的三角形：10个；三块的三角形：10个；五块的三角形：5个，共35个.11•若算式£ 121 3.125) 121的值约等于3. 38,则□中应填入的自然数是 _____________________________ .【考点】方程【难度】★★【答案】31【解析】设x，有(x 121 3.125) 121 3.38，整理得—3.125 3.38 — 0.255121 12130 31 ■0.255 121 30.855，当x 30 时，型0.248 ；当x 31 时，出0.255，故31 .121 121 J12•认真观察图中的三幅图，则第三幅图中的阴影部分应填的数字是【考点】找规律【难度】★★★★【答案】5【解析】观察知区域中的数字代表的是这个区域中曲线的条数，因此阴影中填5.13•图中每一个圆的面积都是1平方厘米，则六瓣花形阴影部分的面积是 ___________ 平方厘米.【考点】图形面积【难度】★★★【答案】2【解析】3个花瓣，3个弯角，3个弓形构成一个圆•阴影部分正好是两个圆，面积为2•如图:14•如图，正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形，小正方形的面积已标在图中，分别为20和10, 18和12，则正方形【考点】最值问题【难度】★★★★【答案】EFGH【解析】小正方形的面积之和为30时，两个正方形面积差越小，大正方形面积越大，如图，因此EFGH较大.151D手内&0 15•早晨7点10分，妈妈叫醒小明，让他起床，可小明从镜子中看到的时刻还没有到起床的时刻，他对妈妈说：“还早呢！”小明误以为当时是____________________ 点 ____________ 分.【考点】时间问题【难度】★★★【答案】4点50分【解析】从镜中看到的时针与分针指针与实际正好相反，7点10分，时针在7和8中间，分针指向2,对称后时针批向4和5之间，分针指向10,为4点50分.16. 从五枚面值为1元的邮票和四枚面值为1.60元的邮票中任取一枚或若干枚，可组成不同的邮资种.【考点】计数一一加乘原理【难度】★★★【答案】29【解析】1元可取0枚，1枚，2枚，…，5枚，共6种取法；1.60元可取0枚，1枚，2枚，…，4枚，共5种取法；但两种不能同时都取0枚.共5 6 1 29 （种）.17. 从1 , 2, 3, 4,…，15, 16这十六个自然数中，任取出n个数，其中必有这样的两个数：一个是另一个的3倍，贝U n最小是______________ .【考点】抽屉原理【难度】★★★★【答案】13【解析】有3倍关系的数放入一组：（1 , 3, 9）、（2, 6 ）、（4, 12 ）、（5, 15）,其余7个数每个数放入一组，第一组最多取2个（1和9）,其余每组最多只能取1个，因此最多取12个保证没有3倍关系，再多取一个就可以保证有一个数是另一个数的3倍.18. 某工程队修建一条铁路隧道，当完成任务的1时，工程队采用新设备，使修建速度提高了20%同时为3了保养新设备，每天工作时间缩短为原来的-，结果，前后共用185天完工，由以上条件可推知，如5果不采用新设备，完工共需_________________ 天.【考点】列方程解应用题（工程）【难度】★★★★【答案】1802【解析】设不采用新设备需x天.- 3185，解得x 180 .3 1 43—（1 20%）-x 519. 王老师在黑板上写了若干个从1开始的连续自然数：1, 2, 3, 4,…，然后擦去三个数（其中有两个质数），如果剩下的数的平均数是198，那么王老师在黑板上共写了个数，擦去的两个质9数的和最大是______________ .【考点】数论【难度】★★★★★【答案】60【解析】1 2 3…n 。

2012希望杯六年级考前热身—历年真题精讲(三)

2012希望杯六年级考前热身—历年真题精讲（三）------计数（1）熟练解几何计数问题和显示屏问题1.历年希望杯几何计数如何考？2.显示屏问题如何考？3.熟练解相关问题。

例题1：（06年·六年级1试第10题）用10根火柴棒首尾顺次连接接成一个三角形，能接成不同的三角形有____个。

例题2：（07年·六年级1试第16题）一种电子表在10点28分6秒时，显示的时间如图所示。

那么10点至10点半这段时间内，电子表上六个数字都不相同有_____个。

例题3：（08年·六年级1试第8题）如图，由小正方形构成的长方形网格中共有线段______条。

例题4：（10年·六年级2试第13题）有一个电子计算器的数字显示屏坏了，有部分区域在该亮时不亮，使原本的一道一位数乘以一位数，积是两位数的乘法算式，出现如下图所示的怪样（不妨用火柴棍来表示）小明对此用火柴棍推出一种可能的算式：9×5=45。

请问：下图表示的算式的乘积还有几种？例题5：（11年·六年级1试第17题）某电子表在6时20分25秒时，显示6：20：25，那么从5时到6时这一个小时里，此表显示的五个数字都不相同的情况共有______种。

例题6：（11年·六年级1试第11题）图中一共有____个长方形（不含正方形）。

（即是该课程的课后测试）1、用11根火柴棒首尾顺次连接接成一个三角形，能接成不同的三角形有____个。

2、一种电子表在7点15分9秒时，显示的时间07:15:09。

那么7点至8点这段时间内，电子表上六个数字都不相同有_____个。

3、某电子表在2时11分5秒时，显示2：11：05，那么从2时到3时这一个小时里，此表显示的五个数字都不相同的情况共有______种。

4、如图，由小正方形构成的长方形网格中共有线段______条。

5、图中一共有____个长方形（包含正方形）。

1、解：11根火柴棒可以分成（1,5,5）、（2,4,5）、（3,3,5）、（3,4,4），所以能接成不同的三角形4个。

新希望杯历年真题精选(六年级)-答案版

【考点】变速问题【答案】9600 米根据题意，绘制行程图如下：
可根据时间相差量的条件来进行分析，因为 BC 段恰好为一条边长，故先分析乙比丙晚 10 分钟，通过行程图可知，乙比丙晚 10 分钟的原因是在 BC 段乙提前减速，使得乙晚 10 分钟到达。故结合速度比来分析： V原 : V现 1 :
武汉市新希望杯历年真题精选
计算精选题
主要知识：繁分数、高斯记号（2012 新希望决赛）已知 3
1 1 1 13 8 x

2012 ，则 x ______。 517
【考点】繁分数【答案】56 2012 461 1 1 1 1 3 3 3 3 3 ，即 x 56 ． 517 56 1 1 517 517 1 1 1 461 13 461 461 8 56 56
（2015 新希望杯决赛）已知 S [
201 1 201 1 201 1 ， 101 101 101 201 1 201 100 201 1 201 100 201 1 201 100 201 1 201 100 101 101 101 101 101 101 201 101 101 201 1 201 100 由于左边是整数，那么右边也是整数，只能是是整数，只能是 1，所 101 101 以前后配对的结果是 201 1 200 同理两两配对，一共 50 对，所以总和是 200 50 10000
5 （2013 新希望初赛）用 x 表示不超过 x 的最大整数，如 1.2 1 ， 3 3 ， 4 4 。已知 6 n n n n 且满足等式： n ，则 n 的取值共有______ n 为不超过 2013 的自然数， 2 4 6 12 个．【考点】高斯记号【答案】168 个 n n n n 由于 n ，故 n 一定位 2、 4、 6、 12 的公倍数，即 12 的倍数， 2013 12 167 9 2 4 6 12 故有 167 个另有 0 也是自然数，故（分）才能追上

第4-12届小学“希望杯”全国数学邀请赛六年级1试

第四届小学“希望杯”全国数学邀请赛六年级第1试1．1120062008()2006200720072008⨯⨯+=⨯⨯________。

2．900000－9＝________×99999。

3．＝________。

4．如果a＝20052006，b＝20062007，c＝20072008，那么a，b，c中最大的是________，最小的是________。

5．将某商品涨价25％，如果涨价后的销售金额与涨价前的销售金额相同，则销售量减少了________％。

6．小明和小刚各有玻璃弹球若干个。

小明对小刚说：“我若给你2个，我们的玻璃弹球将一样多。

”小刚说：“我若给你2个，我的弹球数量将是你的弹球数量的三分之一。

”小明和小刚共有玻璃弹球________个。

7．一次测验中，小明答错了10道题，小刚答错了8道题，小强答对的题的数量等于小明与小刚答对题的数量之和，且小强答错了3道题。

这次测验共有________道题。

8．一个两位数，加上它的个位数字的9倍，恰好等于100。

这个两位数的各位数字之和的五分之三是________。

9．将一个数A的小数点向右移动两位，得到数B。

那么B＋A是B－A的________倍。

(结果写成分数形式)10．用10根火柴棒首尾顺次连接接成一个三角形，能接成不同的三角形有________个。

11．希望小学举行运动会，全体运动员的编号是从1开始的连续整数，他们按图中实线所示，从第1珩第1列开始，按照编号从小到大的顺序排成一个方阵。

小明的编号是30，他排在第3行第6列，则运动员共有________人。

12．将长为5，宽为3，高为1的长方体木块的表面涂上漆，再切成15块棱长为l的小正方体。

则三个面涂漆的小正方体有________块。

13．如图，∠AOB的顶点0在直线l上，已知图中所有小于平角的角之和是400度，则∠AOB＝________度。

14．如图，桌面上有A、B、C三个正方形，边长分别为6，8，10。

希望杯六年级近五年真题汇编

希望杯目录真题希望杯简介 (Ⅰ)近三年真题分析 (Ⅱ)2014 第 12 届希望杯六年级第 1 试试题 (1)2013 第 11 届希望杯六年级第 1 试试题 (3)2012 第 10 届希望杯六年级第 1 试试题 (5)2011 第 9 届希望杯六年级第 1 试试题 (7)2010 第 8 届希望杯六年级第 1 试试题 (9)2014 第 12 届希望杯六年级第 2 试试题 (11)2013 第 11 届希望杯六年级第 2 试试题 (13)2012 第 10 届希望杯六年级第 2 试试题 (15)2011 第 9 届希望杯六年级第 2 试试题 (17)2010 第 8 届希望杯六年级第 2 试试题 (19)参考答案2014 第 12 届希望杯六年级第 1 试试题分析 (21)2013 第 11 届希望杯六年级第 1 试试题分析 (23)2012 第 10 届希望杯六年级第 1 试试题分析 (25)2011 第 9 届希望杯六年级第 1 试试题分析 (27)2010 第 8 届希望杯六年级第 1 试试题分析 (29)2014 第 12 届希望杯六年级第 2 试试题分析 (31)2013 第 11 届希望杯六年级第 2 试试题分析 (33)2012 第 10 届希望杯六年级第 2 试试题分析 (35)2011 第 9 届希望杯六年级第 2 试试题分析 (37)2010 第 8 届希望杯六年级第 2 试试题分析 (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛．“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容，适当地拓宽知识面；启发他们注意数学与其它课程的联系和数学在实际中的应用；激励他们去钻研和探究；培养他们科学的思维能力、创新能力和实践能力；树立他们为振兴中华而努力成才的自信．“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲，不超出教学进度，贴近现行的数学课本，源于课本，高于课本．题目活而不难，巧而不偏；既大众化又富于思考性和启发性．力求体现科学思维之美，寓科学于趣味之中，将知识、能力的考察和思维能力的培养结合起来．“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生．每年举行一次，为一届．每次举行两试，三月中旬第 1 试，考1.5小时；四月中旬第 2 试，考 2 小时．“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单，做到以下两点，希望杯获奖轻松惬意：1．利用寒假做完希望杯 100 题和希望杯历年真题；2．春季再做一遍；3．结合一试的试题，有针对性的准备二试．希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖，整个深圳市也就 20 个左右的名额；而全国三等奖就有好几百个，具体规则如下：根据希望杯的评奖规则，全国一二等奖在赛区内统一标准，按照初赛人数的约千分之三评定．全国三等奖按报名单位初赛人数和规定比例评定，由报名单位按照下述要求评定：1．各单位获奖总指标（一二三等奖）：中学每满 30 人初赛给一个指标，不足 30 人不给；小学每满 20 人初赛给一个指标，不足 20 人不给．若评出人数多于计划指标，组委会将按照从后到前的顺序去掉多出指标．2．各单位评奖时应当按照复赛分数由高到低的原则，赛分数相同时按初赛成绩排序．3．各单位指标可在小学内部中学内部调剂使用，得在二者之间调剂．4．凡是列入全国一二等奖推荐名单的，提供该生的一试试卷和二试试卷，奖励等级由全国组委会统一确定．深圳地区奖项设置有特、一、二、三等奖，2014 年 2000 多名进入二试的学生中，有 120 个特等奖，400 个一等奖，所有进入二试的选手至少能获三等奖！！近三年真题分析“希望杯”题型涉及内容广泛，为了更好备战2015年“希望杯”，我们需要对历年考试情况有一个详细了解。

希望杯六年级近五年真题大全

希望杯目录真题希望杯简介 ......................................................................... .. (Ⅰ)近三年真题分析.......................................................................... (Ⅱ)2014第 12 届希望杯六年级第 1 试试题....................................................................... .. (1)2013第 11 届希望杯六年级第 1 试试题....................................................................... .. (3)2012第 10 届希望杯六年级第 1 试试题....................................................................... .. (5)2011 第 9 届希望杯六年级第 1 试试题........................................................................... (7)2010第 8 届希望杯六年级第 1 试试题....................................................................... . (9)2014第 12 届希望杯六年级第 2 试试题...................................................................... . (11)2013第 11 届希望杯六年级第 2 试试题...................................................................... . (13)2012第 10 届希望杯六年级第 2 试试题...................................................................... . (15)2011 第 9 届希望杯六年级第 2 试试题........................................................................... . (17)2010第 8 届希望杯六年级第 2 试试题...................................................................... (19)参考答案2014第 12 届希望杯六年级第 1 试试题分析....................................................................... . (21)2013第 11 届希望杯六年级第 1 试试题分析....................................................................... . (23)2012第 10 届希望杯六年级第 1 试试题分析....................................................................... . (25)2011第 9 届希望杯六年级第 1 试试题分析 (27).........2010第 8 届希望杯六年级第 1 试试题分析....................................................................... (29)2014第 12 届希望杯六年级第 2 试试题分析....................................................................... . (31)2013第 11 届希望杯六年级第 2 试试题分析....................................................................... . (33)2012第 10 届希望杯六年级第 2 试试题分析....................................................................... . (35)2011第 9 届希望杯六年级第 2 试试题分析....................................................................... (37)2010第 8 届希望杯六年级第 2 试试题分析....................................................................... (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛．“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容，适当地拓宽知识面；启发他们注意数学与其它课程的联系和数学在实际中的应用；激励他们去钻研和探究；培养他们科学的思维能力、创新能力和实践能力；树立他们为振兴中华而努力成才的自信．“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲，不超出教学进度，贴近现行的数学课本，源于课本，高于课本．题目活而不难，巧而不偏；既大众化又富于思考性和启发性．力求体现科学思维之美，寓科学于趣味之中，将知识、能力的考察和思维能力的培养结合起来．“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生．每年举行一次，为一届．每次举行两试，三月中旬第 1 试，考小时；四月中旬第 2 试，考 2 小时．“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单，做到以下两点，希望杯获奖轻松惬意：1．利用寒假做完希望杯 100 题和希望杯历年真题；2．春季再做一遍；3．结合一试的试题，有针对性的准备二试．希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖，整个深圳市也就 20 个左右的名额；而全国三等奖就有好几百个，具体规则如下：根据希望杯的评奖规则，全国一二等奖在赛区内统一标准，按照初赛人数的约千分之三评定．全国三等奖按报名单位初赛人数和规定比例评定，由报名单位按照下述要求评定：1．各单位获奖总指标（一二三等奖）：中学每满 30 人初赛给一个指标，不足 30 人不给；小学每满 20 人初赛给一个指标，不足 20 人不给．若评出人数多于计划指标，组委会将按照从后到前的顺序去掉多出指标．2．各单位评奖时应当按照复赛分数由高到低的原则，赛分数相同时按初赛成绩排序．3．各单位指标可在小学内部中学内部调剂使用，得在二者之间调剂．4．凡是列入全国一二等奖推荐名单的，提供该生的一试试卷和二试试卷，奖励等级由全国组委会统一确定．深圳地区奖项设置有特、一、二、三等奖，2014 年 2000 多名进入二试的学生中，有 120 个特等奖，400 个一等奖，所有进入二试的选手至少能获三等奖！！近三年真题分析“希望杯”题型涉及内容广泛，为了更好备战 2015 年“希望杯”，我们需要对历年考试情况有一个详细了解。