线性代数自考A卷答案

合集下载

自考线性代数试题及答案

自考线性代数试题及答案一、选择题（每题2分，共20分）1. 下列矩阵中，哪一个是可逆矩阵？A. [1, 2; 3, 4]B. [2, 0; 0, 1]C. [1, 1; 1, 1]D. [0, 1; 1, 0]答案：B2. 设向量v = (1, 2, 3)，向量w = (4, 5, 6)，则向量v与向量w 的点积为：A. 32B. 34C. 36D. 38答案：A3. 对于线性变换T: R^3 → R^2，如果T(x, y, z) = (x + z, y - z)，那么T的秩是：A. 1B. 2C. 3D. 4答案：B4. 设A和B是两个n阶方阵，若AB = BA，则称矩阵A和B是可交换的。

若A和B是两个n阶实对称矩阵，且AB = BA，那么：A. A和B一定可交换B. A和B一定不可交换C. A和B可交换或不可交换D. 无法判断A和B是否可交换答案：A5. 对于任意的n阶方阵A，以下哪个选项是正确的？A. |A| = |A^T|B. det(A) = det(A^T)C. trace(A) = trace(A^T)D. A * A^T 一定是对称矩阵答案：C6. 设A是m×n矩阵，B是n×p矩阵，若AB = 0，则：A. 必有B = 0B. 必有A = 0C. 必有rank(A) + rank(B) ≤ max(m, p)D. rank(AB) ≤ rank(A)答案：D7. 对于n维向量空间V，以下哪个命题是线性代数的基本定理？A. 每个向量都可以由V的一组基唯一表示B. V中任意两个不同的向量都是线性无关的C. V中任意非零向量都是可逆的D. V中任意两个向量都线性相关答案：A8. 设λ是n阶方阵A的一个特征值，对应的特征向量为v，则：A. (A - λI)v = 0B. Av = vC. A^2v = λ^2vD. (A + I)v = λv答案：A9. 对于任意矩阵A，以下哪个选项是正确的？A. |A| = |A^2|B. det(A) = det(A^2)C. trace(A) = trace(A^2)D. A^2 一定是可逆的答案：B10. 设A是m×n矩阵，B是n×m矩阵，且AB = Im，则：A. B一定是A的逆矩阵B. A一定是B的逆矩阵C. A和B互为逆矩阵D. A和B不一定是方阵答案：C二、填空题（每题3分，共15分）11. 设矩阵A = [1, 2; 3, 4]，则A的特征多项式为f(λ) = _______。

线性代数试题A及答案

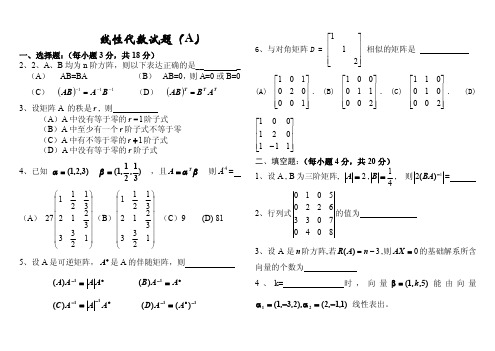
线性代数试题（A ）一、选择题：（每小题3分，共18分）2、2、A 、B 均为n 阶方阵，则以下表达正确的是__ _ （A ） AB=BA （B ） AB=0，则A=0或B=0 （C ） ()111---=B A AB （D ） ()T T TA B AB =3、设矩阵A 的秩是r , 则（A ）A 中没有等于零的1-r 阶子式（B ）A 中至少有一个r 阶子式不等于零（C ）A 中有不等于零的1+r 阶子式（D ）A 中没有等于零的r 阶子式4、已知 )3,2,1(=a )31,21,1(=b ，且b a T A = 则4A =（A ） 27÷÷÷÷÷÷øöççççççèæ1233321231211（B ）÷÷÷÷÷÷øöççççççèæ1233321231211 （C ）9 (D) 81 5、设A 是可逆矩阵，*A 是A 的伴随矩阵，则*-=A A A A 1)( *-=A A B 1)( *--=A AA C 11)( 11)()(-*-=A A D6、与对角矩阵D = úúúûùêêêëé211 相似的矩阵是 (A) úúúûùêêêëé100020101. (B) úúúûùêêêëé200110001. (C) úúúûùêêêëé200010011. (D) úúúûùêêêëé-111021001 二、填空题：（每小题4分，共20分）1、设A , B 为三阶矩阵, 2=A ,41=B , 则12-)(BA = 2、行列式8040703362205010的值为 3、设A 是n 阶方阵,若3-=n A R )(,则0=AX 的基础解系所含向量的个数为4、k= 时，向量)5,,1(k =b 能由向量)1,1,2(),2,3,1(21-=a -=a 线性表出。

自考线性代数试题及答案

自考线性代数试题及答案一、选择题（每题2分，共20分）1. 在线性代数中，向量空间的基具有什么性质？A. 唯一性B. 线性无关性C. 任意性D. 可数性答案：B2. 矩阵的秩是指什么？A. 矩阵的行数B. 矩阵的列数C. 矩阵中线性无关行的最大数目D. 矩阵中线性无关列的最大数目答案：D3. 线性变换的核是指什么？A. 变换后的向量集合B. 变换前的向量集合C. 变换后为零向量的向量集合D. 变换前为零向量的向量集合答案：C4. 线性方程组有唯一解的条件是什么？A. 方程的个数等于未知数的个数B. 方程组是齐次的C. 方程组的系数矩阵是可逆的D. 方程组的系数矩阵的秩等于增广矩阵的秩答案：D5. 特征值和特征向量在矩阵理论中具有什么意义？A. 矩阵的对角化B. 矩阵的转置C. 矩阵的行列式D. 矩阵的迹答案：A6. 以下哪个矩阵是正交矩阵？A. 对角矩阵B. 单位矩阵C. 任意矩阵D. 零矩阵答案：B7. 矩阵的迹是矩阵对角线上元素的什么？A. 和B. 差C. 积D. 比答案：A8. 线性代数中的线性组合是什么？A. 向量的加法B. 向量的数乘C. 向量的加法和数乘的组合D. 向量的点积答案：C9. 矩阵的行列式可以用于判断矩阵的什么性质？A. 可逆性B. 秩C. 正交性D. 特征值答案：A10. 线性变换的值域是指什么？A. 变换前的向量集合B. 变换后的向量集合C. 变换前的向量空间D. 变换后的向量空间答案：B二、填空题（每空1分，共10分）11. 矩阵的转置是将矩阵的______交换。

答案：行与列12. 方程组 \( Ax = 0 \) 是一个______方程组。

答案：齐次13. 矩阵 \( A \) 和矩阵 \( B \) 相乘，记作 \( AB \)，其中\( A \) 的列数必须等于______的行数。

答案：B14. 向量 \( \mathbf{v} \) 的长度（或范数）通常表示为\( \left\| \mathbf{v} \right\| \)，它是一个______。

(完整版)线性代数试卷及答案详解

《线性代数A 》试题（A 卷）试卷类别：闭卷考试时间：120分钟考试科目：线性代数考试时间：学号：姓名：3的一组标准正交基，=___________《线性代数A》参考答案（A卷）一、单项选择题（每小题3分，共30分）二、填空题（每小题3分，共18分）1、 256；2、 132465798⎛⎫ ⎪--- ⎪ ⎪⎝⎭； 3、112211221122000⎛⎫⎪- ⎪ ⎪-⎝⎭； 4、； 5、 4； 6、 2 。

三．解：因为矩阵A 的行列式不为零,则A 可逆,因此1X A B -=.为了求1A B -,可利用下列初等行变换的方法：231211201012010*******121011411033110331023211027210027810027801141010144010144001103001103001103---⎛⎫⎛⎫⎛⎫⎪⎪⎪-−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫⎛⎫⎪⎪⎪−−→--−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭―――――（6分）所以1278144103X A B -⎛⎫ ⎪==-- ⎪ ⎪⎝⎭.―――――（8分）四．解：对向量组12345,,,,ααααα作如下的初等行变换可得：1234511143111431132102262(,,,,)21355011313156702262ααααα--⎛⎫⎛⎫⎪ ⎪----- ⎪ ⎪=→ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭111431212011310113100000000000000000000--⎛⎫⎛⎫⎪⎪---- ⎪ ⎪→→⎪ ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭――――（5分）从而12345,,,,ααααα的一个极大线性无关组为12,αα，故秩12345{,,,,}ααααα＝2（8分）且3122ααα=-，4123ααα=+，5122ααα=--――――（10分）五．解：对方程组的增广矩阵进行如下初等行变换：221121121121110113011311101112002421120113400(2)(1)42p p p p p p p p p p p p p p p p p p p p p ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪−−→--−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--+--+⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪−−→------- ⎪ ⎪-+-+⎝⎭(分)(1) 当10,(2)(1)0,p p p -≠-+-≠且时即1,2,p p ≠≠-且时系数矩阵与增广矩阵的秩均为3,此时方程组有唯一解.――――（5分） (2) 当1,p =时系数矩阵的秩为1,增广矩阵的秩为2,此时方程组无解.――――（6分）(3) 当2,p =-时此时方程组有无穷多组解. 方程组的增广矩阵进行初等行变换可化为1122112211221211033301112111033300001011011180000------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-−−→-−−→-- ⎪ ⎪ ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭--⎛⎫⎪−−→------ ⎪ ⎪⎝⎭（分）故原方程组与下列方程组同解:132311x x x x -=-⎧⎨-=-⎩ 令30,x =可得上述非齐次线性方程组的一个特解0(1,1,0)Tξ=--;它对应的齐次线性方程组13230x x x x -=⎧⎨-=⎩的基础解系含有一个元素,令31,x =可得1(1,1,1)T ξ=为该齐次线性方程组的一个解,它构成该齐次线性方程组的基础解系.此时原方程组的通解为001101,,.k k k k ξξ+这里为任意常数――――（12分）六．解：（1）由于A的特征多项式2124||222(3)(6)421I A λλλλλλ----=-+-=+----故A 的特征值为13λ=-（二重特征值），36λ=。

线性代数考试(A)参考答案及评释学习资料

线性代数考试(A)参考答案及评释华南农业大学期末考试试卷（A 卷）2005学年第一学期考试科目：线性代数考试类型：闭卷考试时间：120分钟学号姓名年级专业这是题文这是参考答案填空题.（每小题3分，共30分）1.若行列式D 各行元素之和等于0，则该行列式等于0. 各行加到第一行上去, 则第一行全为零P98奇数阶实反对称阵的行列式为零P64定理2.7非齐次线性方程组有解的充要条件 41141222222n n n --**⎛⎫===⋅= ⎪⎝⎭A A A重要关系*=AA A E ( P34定理1.9); 1n -*=A A(p44题1.18)5.设()()1,1,5,3,9,2,3,5,TTαβ=--=---则α与β的距离为9.()8,3,2,29-===αβ由正交矩阵的定义T =A A E 立即得到1T -=A A 且1T ===A A A A E若λ是A 的特征值, 则1λ是1-A 的特征值, 因为()110x x x x λλ-=≠⇒=A A x . 参考P87定理4.4: ()ϕA 的特征值是()ϕλ.8．如果()222123123121323,,2246f x x x x x tx x x x x x x =+++++是正定的，则t 的取值范围是5t >.11212323t ⎛⎫⎪= ⎪ ⎪⎝⎭A 1231121110,10,123501223t t ∆=>∆==>∆==-> p100定理5.6由2=AA 推出()()22-+=-A E A E EEnglish!二、单选题（每题3分，共15分）1.n 元齐次线性方程组0,AX =秩()(),R A r r n =<则有基础解系且基础解系含（ D ）个解向量.（A ）n （B ）r （C ）r n - （D ）n r - P62 line 5: 基础解系含n r -个解向量2. 设四阶方阵A 的秩为2，则其伴随矩阵A *的秩为（ D ）（A ）1 （B ）2 （C ）3 （D ）0.A的余子式(3阶子式)全为零.*A是零矩阵.3. 设A是n阶方阵，满足2A E=，则（ B ）（A）A的行列式为1 （B）,-+不同时可逆.A E A E=（D）A的特征值全是1 （C）A的伴随矩阵*A A2000或.A E A E A E A E A E=⇒+-=⇒+=-=4. 设n阶方阵,,A B C满足ABC E=，其中E是n阶单位阵，则必有（ C ）（A）ACB E== (D) BAC E= (C) BCA E= (B) CBA E()()A E.p7性质1.2, p35定理1.10=⇒=A BC E BC或者141231234142332,3,4333411111111111111110000111111000101111101111100010000010001001000100010000101001000000i r r i c c c c r r r r r r r r x x x x x x x x x x x xxxxx x x x x-=+++-+-↔↔-------+---==----+-----====.2.给定向量组()()121,1,1,1,1,1,1,1,TTαα==--()32,1,2,1Tα=， ()41,1,1,1,Tα=--求1234,,,αααα的一个最大无关组和向量组的秩.()213141434212341121112111110212,,,112100021111021011211121021202120002000200020000r r r r r r r r r r A αααα---+-⎛⎫⎛⎫⎪ ⎪----- ⎪ ⎪==−−−→ ⎪⎪--⎪ ⎪---⎝⎭⎝⎭⎛⎫⎛⎫⎪ ⎪------⎪ ⎪−−−→−−−→ ⎪ ⎪--⎪ ⎪⎝⎭⎝⎭可见()1234,,,3R αααα=，124,,ααα是一个最大无关组。

全校各专业《线性代数》课程试卷及答案A卷

全校各专业《线性代数》课程试卷及答案A 卷试卷 A 考试方式闭卷考试时间（120分钟）一、选择题（本题共4小题，每小题4分，满分16分。

每小题给出的四个选项中，只有一项符合题目要求） 1、设A ，B 为n 阶方阵，满足等式0=AB，则必有（） (A)0=A 或0=B ; (B)0=+B A ；（C ）0=A 或0=B ; (D)0=+B A 。

2、A 和B 均为n 阶矩阵，且222()2A B A AB B +=++，则必有（） (A) A E =； (B)B E =；（C ） A B =. (D) AB BA =。

3、设A 为n m ⨯矩阵，齐次方程组0=Ax 仅有零解的充要条件是（）(A) A 的列向量线性无关； (B) A 的列向量线性相关；（C ） A 的行向量线性无关； (D) A 的行向量线性相关. 4、 n 阶矩阵A 为奇异矩阵的充要条件是（） (A) A 的秩小于n ； (B) 0A ≠；(C) A 的特征值都等于零； (D) A 的特征值都不等于零；二、填空题（本题共4小题，每题4分，满分16分）5、若4阶矩阵A 的行列式5A =-，A *是A 的伴随矩阵，则*A = 。

6、A 为n n ⨯阶矩阵，且220A A E --=，则1(2)A E -+= 。

7、已知方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-+43121232121321x x x a a 无解，则a = 。

8、二次型2221231231213(,,)2322f x x x x x tx x x x x =++++是正定的，则t 的取值范围是。

三、计算题（本题共2小题，每题8分，满分16分）9、计算行列式1111111111111111x x D y y+-=+-10、计算n 阶行列式121212333n n n n x x x x x x D x x x ++=+四、证明题（本题共2小题，每小题8分，满分16分。

完整版)线性代数试卷及答案

完整版)线性代数试卷及答案线性代数A试题（A卷）试卷类别：闭卷考试时间：120分钟考试科目：线性代数学号：______ 姓名：______题号得分阅卷人一．单项选择题（每小题3分，共30分）1.设A经过初等行变换变为B，则(B)。

(下面的r(A),r(B)分别表示矩阵A,B的秩)。

A) r(A)。

r(B)；(D)2.设A为n(n≥2)阶方阵且|A|=，则(C)。

A) A中有一行元素全为零；(B) A中必有一行为其余行的线性组合；(C) A有两行（列）元素对应成比例；(D) A的任一行为其余行的线性组合。

3.设A,B是n阶矩阵(n≥2),AB=O,则下列结论一定正确的是: (D)A) A=O或B=O。

(B) B的每个行向量都是齐次线性方程组AX=O的解。

(D) R(A)+R(B)≤n.4.下列不是n维向量组α1,α2.αs线性无关的充分必要条件是（A）A) 存在一组不全为零的数k1,k2.ks使得k1α1+k2α2+。

+ksαs≠O；(B) 不存在一组不全为零的数k1,k2.ks使得k1α1+k2α2+。

+ksαs=O(C) α1,α2.αs的秩等于s；(D) α1,α2.αs 中任意一个向量都不能用其余向量线性表示。

5.设n阶矩阵(n≥3)A=，若矩阵A的秩为n-1，则a必为（）。

11；(C) -1；(D)。

(A) 1；(B)6.四阶行列式a1a2a3a4b1b2b3b4的值等于（）。

A) a1a2a3a4+b1b2b3b4；(B) (a1a2-b1b2)(a3a4-b3b4)；(C)a1a2a3a4-b1b2b3b4；(D) (a2a3-b2b3)(a1a4-b1b4)。

1.设A为四阶矩阵且A=b，则A的伴随矩阵A的行列式为b^3.(C)2.设A为n阶矩阵满足A+3A+In=O，In为n阶单位矩阵，则A=−A−3In。

《线性代数》试卷A及答案

《线性代数》试卷A适用专业：试卷类型：闭卷考试时间：120分钟总分100分考试日期：一.选择题（2分×6=12分）1.排列4 1 3 2 5 的逆序数为（） A.4 B.1 C.3 D.22. 设0λ是可逆矩阵A 的一个特征值，则13-A 必有特征值（）A.021λ B. 023λ C.30λ D. 20λ 3. 设A 为n 阶可逆阵，则下列成立的是( ) A.112)2(--=A A B. 11)2()2(--=T T A AC. [][]1111)()(----=TTA A D.[][]TTT AA 111)()(---=4.如果333231332221131211a a a a a a a a a =d,则行列式131211232221333231222333a a a a a a a a a ---=( )A. –6dB. 6dC. 4dD. –4d5．设A 为3阶方阵，且2=A ，则A 2=（） A.4 B.8 C.16 D.216.已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=403212221A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=11a α，且αA 与α线性相关，则=a （）。

A.1-B.1C. 2D.3二．填空题（2分×11=22分）1．设A 、B 均为3阶方阵，且|A |=3，|B |=-2，则|AB |=2. 设A 为方程组⎩⎨⎧=+=+02121x x x x λλ有非零解,则λ=3．已知3阶方阵A 的特征值为1,1,2-，则方阵2A 的特征值是、、4.向量组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321,211的正交化向量为5. A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321,B=[1,2,3],则BA= 6．设32212221321424),,(x x x x x x x x x f -++-=，则二次型矩阵为7.设y x ,为实数，则当=x ，且=y 时，010100=---yx y x8.设⎥⎦⎤⎢⎣⎡--=x A 112与⎥⎦⎤⎢⎣⎡=Λ31相似，则=x 三. 计算题：（总共66分）1.计算 600300301395200199204100103=D （6分） 2.求13211A -⎥⎦⎤⎢⎣⎡--=（4分）院系________________ 姓名_____________ 班级________________ 序号_______________3．设3351110243152113-----=D ,(1)求行列式D的值，(2)求4443424123A A A A +-+ （12分）4.讨论λ为何值时，线性方程组⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x 有：1）唯一解； 2）无解； 3）无穷多解？此时求出其通解（12分）5．求矩阵E A 2-的逆矩阵，其中A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡300041003 （ 10分）7．设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=101121002A 。

2020-2021(1)《线性代数A》A卷参考答案

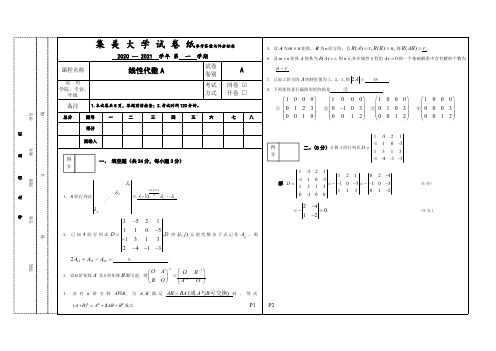
3 ,1)T . 2
(3) 当 k 1时 R( A) 1; 当 k 2 时 R( A) 2; 当 k 1且 k 2 时 R( A) 3.
(12 分) (15 分)
P5
x1 3x2 2x3 x4 3
得分
六、（12
分）求非齐次线性方程组
x1 x1
x2 x2
x4 x3
1 2
五
六
七
八
得分
阅卷人
得
一、填空题（共 24 分，每小题 3 分）
分
1． n 阶行列式
1
2
n ( n 1)
(1) 2 1n .
n
3 5 2 1
2. 已知 4 阶行列式 D 1 1 1 3
0 5 1 3 ,D 的 (i, j) 元的代数余子式记作 Aij ，则
2 4 1 3
学院
考专业装
生
信
息姓名
班级
栏学号线
订
集美大学试卷纸参考答案与评分标准
2020 — 2021 学年第一学期
课程名称
适用学院、专业、
年级
线性代数 A
试卷卷别
考试方式
A
闭卷 □√ 开卷 □
备注
1.本试卷共 8 页，答题前请检查；2.考试时间 120 分钟。
总分
题号
一
二
三
四
生
信
息姓名
班级
栏学号线
订
1 2 3k
得
五、（15
分）设矩阵
A
1 k
2k 2
3 3
，
分
（1）求行列式 A ；

自考试题线性代数题库及答案

自考试题线性代数题库及答案线性代数是数学的一个重要分支，广泛应用于工程、物理、计算机科学等领域。

以下是一套自考试题线性代数题库及答案，供学习者参考。

一、选择题1. 下列矩阵中，哪一个是可逆矩阵？A. \( A = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \)B. \( B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)C. \( C = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)D. \( D = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \)答案： C2. 设 \( A \) 是一个 \( n \times n \) 矩阵，\( I \) 是 \( n\times n \) 的单位矩阵，若 \( A^2 = I \)，则 \( A \) 称为：A. 正交矩阵B. 反对称矩阵C. 正交变换矩阵D. 反射变换矩阵答案： D二、填空题1. 设向量 \( \mathbf{v} = (1, 2, 3) \)，向量 \( \mathbf{w} =(4, 5, 6) \)，这两个向量的点积为 __________。

答案： 322. 若 \( A \) 是一个 \( m \times n \) 矩阵，\( B \) 是一个\( n \times p \) 矩阵，则 \( AB \) 的行列数为 __________。

答案： \( m \times p \)三、解答题1. 证明：若 \( A \) 是一个 \( n \times n \) 矩阵，且 \( A^n =I \)，则 \( A \) 必定可逆。

解答：由于 \( A^n = I \)，我们可以得出 \( A \) 的 \( n \) 次幂是单位矩阵。

线性代数试题A答案[大全5篇]

线性代数试题A答案[大全5篇]第一篇：线性代数试题A答案2006-2007学年第二学期线性代数试题A卷参考答案及评分标准一．填空题（本题满分12分，每小题3分）⎛1-20 0 -25 -111、1；2、-3；3、A=00 3 1 00-3⎝0⎫⎪0⎪2⎪；4、2 ⎪3⎪1⎪⎪3⎭二、选择题（本题满分12分，每小题3分，．在每小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后的括号内）1．C；2．C；3．A；4、B 三．计算行列式（本题满分6分）解 1 10Dn=001-110010Λ00-111000-11=100010100200Λ03ΛΛ1Λ00Λ0100Λ00n3-1ΛΛ011ΛΛΛΛΛΛΛΛΛΛΛΛ分Λn-1=n3分解2 10Dn=001-110010Λ00-111000=Dn-1+13分-1ΛΛ011ΛΛΛΛΛΛΛΛ-11=n3分四．（本题满分12分）解：⑴ 由等式A+B=AB，得A+B-AB+E=E，即(A-E)(B-E)=E3分因此矩阵A-E可逆，而且(A-E)=B-E．2分-1⑵ 由⑴知，A-E=(B-E)，即A=(B-E)+E-1-1A=(B-E)+E或A=B(B-E)-12分-1⎛0-10-30100⎛⎫⎛⎫⎪⎪1=200⎪+010⎪=-3 001⎪001⎪0⎝⎭⎝⎭⎝⎛1 1=-3 0 ⎝1210⎫0⎪⎪0⎪ 2分⎪2⎪⎪⎭1200⎫0⎪100⎫⎪⎛⎪0⎪+010⎪3分⎪⎪1⎪⎝001⎭⎪⎭五．（本题满分14分）解：110⎤⎡1⎡11⎢01⎥⎢0221⎥→⎢A=⎢⎢0-1a-3-2b⎥⎢0⎢⎥⎢321a-1⎣⎦⎣01110⎤1221⎥⎥4分0a-10b+1⎥⎥00a-10⎦所以，⑴ 当a≠1时，rA=r(A)=4，此时线性方程组有唯一解．2分⑵ 当a=1，b≠-1时，r(A)=2，rA=3，此时线性方程组无解．2分⑶ 当a=1，b=-1时，rA=r(A)=2，此时线性方程组有无穷多组解．2分此时，原线性方程组化为()()()⎧x1+x2+x3+x4=0 ⎨⎩x2+2x3+2x4=1因此，原线性方程组的通解为⎧x1=x3+x4-1⎪x=-2x-2x+1⎪234 ⎨x=x3⎪3⎪x4⎩x4=或者写为⎡x1⎤⎡1⎤⎡1⎤⎡-1⎤⎢x⎥⎢-2⎥⎢-2⎥⎢1⎥2⎢⎥=k⎢⎥+k⎢⎥+⎢⎥4分⎢x3⎥1⎢1⎥2⎢0⎥⎢0⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣0⎦⎣1⎦⎣0⎦⎣x3⎦六．（本题满分12分）3-λ解 A-λE=-101202-λ1=(2-λ)(3-λ)，2分03-λ所以得特征值λ1=2,λ2=λ3=32分⎛101⎫⎪对λ1=2，解方程组(A-2E)x=0，由A-2E=-101⎪，得特征向量001⎪⎝⎭⎛0⎫⎪ξ1=1⎪0⎪⎝⎭⎛0⎫⎪所以对应λ1=2的全部特征向量为c1 1⎪,c1≠03分0⎪⎝⎭⎛0 1对λ2=λ3=3，解方程组(A-3E)x=0，由A-3E=-0⎝01⎫1⎛10⎪r 1-1⎪−−→0 0100⎪0 ⎭⎝00⎫⎪⎪，⎪⎭⎛1⎫⎛1⎫⎪⎪得特征向量ξ2=-1⎪,全部特征向量为c2 -1⎪,c2≠03分0⎪0⎪⎝⎭⎝⎭A没有三个线性无关的特征向量，所以不能对角化.2分七．（本题满分12分）⎛1λ解：f的矩阵为A=λ4 -12⎝-1⎫⎪2⎪．…………2分 4⎪⎭因此，二次型f为正定二次型．⇔矩阵A为正定矩阵．⇔矩阵A的各阶顺序主子式全大于零．…………2分而矩阵A的各阶顺序主子式分别为D1=1>0，D2=1λ=4-λ2，…………2分λ41D3=A=λλ-12=-4(λ-1)(λ+2)．…………2分 44-12所以，二次型f 为正定二次型．⇔D2=4-λ2>0，且D3=-4(λ-1)(λ+2)>0由 D2=4-λ2>0，得-2<λ<2 ．由 D3=-4(λ-1)(λ+2)>0，得-2<λ<1 ．因此，得-2<λ<1 ．即，二次型f为正定二次型．⇔-2<λ<1…………4分八．（本题满分8分）已知三维向量空间的一组基为α1=(1，1，0)，α2=(1，0，1)，α3=(0，1，1)求向量β=(2，0，0)在上述基下的坐标．解：设向量β在基(α1，α2，α3)下的坐标为(x1，x2，x3)，则有x1α1+x2α2+x3α3=β，2分写成线性方程组的形式，有⎛1⎫⎛1⎫⎛0⎫⎛2⎫⎪⎪⎪⎪x1 1⎪+x2 0⎪+x3 1⎪=0⎪2分 0⎪1⎪1⎪0⎪⎝⎭⎝⎭⎝⎭⎝⎭即⎧x1+x2=2⎪⎨x1+x3=0，⎪x+x=03⎩2得唯一解x1=1，x2=1，x3=-1，3分，1，-1)．1分因此所求坐标为(1九．（本题满分12分）证法1：记A=(α1,α2,Λ,αm),B=(α1,α2,Λ,αm,β)，显然r(A)≤r(B).1°因为α1,α2,Λ,αm线性无关，知r(A)=m1分2°因为α1,α2,Λ,αm,β线性相关，知r(B)<m+1 1分因此r(B)=m，1分Ax=(α1,α2,Λ,αm)x=b有解且唯一。

线性代数自考试题及答案

线性代数自考试题及答案一、选择题（每题2分，共10分）1. 下列矩阵中，哪个不是方阵？A. [1, 2; 3, 4]B. [1, 2]C. [1, 2; 3, 4; 5, 6]D. [1, 2; 3, 4; 5, 6; 7, 8]答案：B2. 对于向量空间中的向量组，线性相关的定义是什么？A. 向量组中的任意向量都可以用其他向量表示B. 向量组中存在非零向量可以表示为零向量C. 向量组中的向量线性组合为零向量D. 向量组中所有向量都是零向量答案：A3. 矩阵的特征值是什么？A. 矩阵对角线上的元素B. 使得方程Ax = λx 成立的标量λC. 矩阵的行数D. 矩阵的列数答案：B4. 对于矩阵 A，下列哪个矩阵是 A 的伴随矩阵？A. A^TB. A^(-1)C. adj(A)D. det(A)答案：C5. 如果一个向量是另一个向量的标量倍，这两个向量是什么关系？A. 线性无关B. 线性相关C. 正交D. 单位向量答案：B二、填空题（每题3分，共15分）6. 矩阵的秩是指_________。

答案：矩阵中线性无关的行（或列）的最大数目7. 向量空间的基是指一组_________的向量，它们能生成整个向量空间。

答案：线性无关8. 对于任意矩阵 A，|A| 表示_________。

答案：矩阵 A 的行列式9. 如果矩阵 A 可逆，那么 A 的逆矩阵记作_________。

答案：A^(-1)10. 线性变换 T: R^n → R^m 的标准矩阵是指_________。

答案：线性变换 T 对标准基的坐标表示矩阵三、解答题（共75分）11. （15分）设 A 是一个3×3 的实对称矩阵，证明其特征值都是实数。

答案：略12. （20分）给定两个向量 v1 = [1, 2, 3]^T 和 v2 = [4, 5, 6]^T，求它们的叉积v3 = v1 × v2，并证明 v3 与 v1, v2 都正交。

线性代数自考试题及答案

线性代数自考试题及答案一、单项选择题（每题2分，共20分）1. 矩阵A的行列式为0，则矩阵A（）A. 可逆B. 不可逆C. 行等价于零矩阵D. 列等价于零矩阵答案：B2. 若矩阵A的秩为r，则矩阵A的齐次线性方程组的解空间的维数为（）A. rB. r-1C. n-rD. n+r答案：C3. 向量组α1，α2，…，αs线性无关，则（）A. 向量组α1+α2，α2+α3，…，αs-1+αs线性无关B. 向量组kα1，kα2，…，kαs线性无关，其中k为非零常数C. 向量组α1+α2，α2+α3，…，αs-1+αs，αs线性无关D. 向量组kα1，kα2，…，kαs线性相关，其中k为非零常数答案：B4. 设A为n阶方阵，且|A|≠0，则下列命题中正确的是（）A. A与A*的秩相等B. A*与A^(-1)的秩相等C. A与A^(-1)的秩相等D. A与A*的秩不相等答案：C5. 矩阵A=（）A. 行最简形矩阵B. 行阶梯形矩阵C. 行等价于单位矩阵的矩阵D. 行等价于零矩阵的矩阵答案：C6. 设A为3×3矩阵，且|A|=2，则|2A|=（）A. 4B. 8C. 16D. 32答案：C7. 设A为n阶方阵，且A^2=0，则（）A. A=0B. |A|=0C. A可逆D. A不可逆答案：D8. 设A为n阶方阵，且A^2=E，则（）A. A=0B. |A|=0C. A可逆D. A不可逆答案：C9. 设A为n阶方阵，且A^T=A，则（）A. A为对称矩阵B. A为反对称矩阵C. A为正交矩阵D. A为斜对称矩阵答案：A10. 设A为n阶方阵，且|A|=1，则|A^(-1)|=（）A. 0B. 1C. -1D. 2答案：B二、填空题（每题2分，共20分）11. 若A为n阶方阵，且|A|=-3，则|-2A|=______。

答案：1212. 设A为n阶方阵，且A^2=0，则矩阵A的秩r(A)满足______。

学历类《自考》自考公共课《工程数学-线性代数》考试试题及答案解析

学历类《自考》自考公共课《工程数学-线性代数》考试试题及答案解析姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分评卷人得分1、设v(x,y)在区域D内为u(x,y)的共轭调和函数，则下列函数中为内解析函数的是A、v(x,y)+iu(x,y)B、v(x,y)-iu(x,y)C、u(x,y)-iv(x,y)D、正确答案：B答案解析：暂无解析2、下列命题中，正确的是A、设v1,v2在区域D内均为u的共轭调和函数，则必有v1v2B、解析函数的实部是虚部的共轭调和函数C、若f(z)=u+iv在区域D内解析，则xu为D内的调和函数D、以调和函数为实部与虚部的函数是解析函数正确答案：C答案解析：暂无解析3、设c为任意实常数，那么由调和函数u=x²-y²确定的解析函数f(z)=u+iv是A、iz²+cB、iz²+icC、z²+cD、z²+ic正确答案：D答案解析：暂无解析4、设f(z)在单连通域B内处处解析且不为零，c为B内任何一条简单闭曲线，则积分A、等于2πiB、等于-2πiC、等于0D、不能确定正确答案：C答案解析：暂无解析5、设c为正向圆周|z|1/2，则A、2π（3cos1-sin1）B、0C、6πicos1D、-2πsin1正确答案：B答案解析：暂无解析6、设c为正向圆周|z|=1/2，则A、2π（3cos-sin1）B、0C、6paiicos1D、-2πsin1正确答案：B答案解析：暂无解析7、设c为正向圆周|z|=2，则A、-sin1B、sin1C、-2πisin1D、2πisin1正确答案：C答案解析：暂无解析8、设:c1：|z|为负向，c2:|z|3正向，则A、-2πiB、0C、2πiD、4πi正确答案：B答案解析：暂无解析9、设c为不经过点1与1的正向简单闭曲线，则A、B、C、0D、(A)(B)(C)都有可能正确答案：D答案解析：暂无解析10、设c为从原点沿y²=x至1+i的弧段，则A、B、C、D、正确答案：D答案解析：暂无解析11、设X为随机变量，其方差存在，c为任意非零常数，则下列等式中正确的是A、D(X+c)=D(X)B、D(X+c)=D(X)+cC、D(X-c)=D(X)-cD、D(cX)=cD(X)正确答案：A答案解析：暂无解析12、设随机变量X～N(u,4²),Y～N(u,5²),P1=P{X≤u-4},P2=P{Y≥u+5},则有A、对于任意的u,P1=P2B、对于任意的u,P1P2正确答案：A答案解析：暂无解析13、下列各函数中可以作为某个随机变量的概率密度函数的是A、B、C、D、正确答案：D答案解析：暂无解析14、对于任意两个随机变量X和Y，若E(XY)=E(X)E(Y)，则有A、X和Y独立B、X和Y不独立C、D(X+Y)=D(X)+D(Y)D、D(XY)=D(X)D(Y)正确答案：C答案解析：暂无解析15、某人打靶3发，事件Ai表示“击中i发”，i=0,1,2,3.那么事件A=A1∪A2∪A3表示A、全部击中B、至少有一发击中C、必然击中D、击中3发正确答案：B答案解析：暂无解析16、某人打靶3发，事件Ai表示“击中i发”，i=0,1,2,3.那么事件A=A1∪A2∪A3表示A、全部击中B、至少有一发击中C、必然击中D、击中3发正确答案：B答案解析：暂无解析17、对于任意两个随机变量X和Y，若E(XY)=E(X)E(Y)，则有A、X和Y独立B、X和Y不独立C、D(X+Y)=D(X)+D(Y)D、D(XY)=D(X)D(Y)正确答案：C答案解析：暂无解析18、下列各函数中可以作为某个随机变量的概率密度函数的是A、B、C、D、正确答案：D答案解析：暂无解析19、设随机变量X～N(u,4²),Y～N(u,5²),P1=P{X≤u-4},P2=P{Y≥u+5},则有A、对于任意的u,P1=P2B、对于任意的u,P1P2正确答案：A答案解析：暂无解析20、设X为随机变量，其方差存在，c为任意非零常数，则下列等式中正确的是A、D(X+c)=D(X)B、D(X+c)=D(X)+cC、D(X-c)=D(X)-cD、D(cX)=cD(X)正确答案：A答案解析：暂无解析21、设3阶矩阵A的特征值为-1，1，2，它的伴随矩阵记为A*，则|A*+3A–2E|=正确答案：9答案解析：暂无解析22、设有3个元件并联，已知每个元件正常工作的概率为P，则该系统正常工作的概率为正确答案：1–(1–P)³答案解析：暂无解析23、设随机变量X的概率密度函数为f(x)=2x0xA,f(x)=0, 则概率正确答案：3/4答案解析：暂无解析24、设二维连续型随机变量(X,Y)的联合概率密度函数为，则系数k=正确答案：12答案解析：暂无解析25、设c为正向圆周|z|=3，则正确答案：6πi答案解析：暂无解析26、解析函数在圆心处的值等于它在圆周上的正确答案：平均值答案解析：暂无解析27、设u(x,y)的共轭调和函数为v(x,y)，那么v(x,y)的共轭调和函数为正确答案：-u（x，y）答案解析：暂无解析28、发报台分别以概率0.6和0.4发出信号“1”和“0”。

线性代数试卷及答案卷A

河南工业大学成教学院课程线性代数试卷专业班级：卷A姓名：学号：注：（1）不得在密封线以下书写班级、姓名。

（2）必须在密封线以下答题，不得另外加纸。

………………………………………密封线 ………………………………………………………一 .单项选择题（每题3分）1.若 111221226a a a a =，则 121122212020021a a a a -- 的值为（ A ）（A ）12 (B) –12 (C) 18 (D) 02.设A 、B 都是n 阶矩阵，且AB=0,则下列一定成立的是（ C ）（A ）A=0或B=0 (B) A 、B 都不可逆（C ）A 、B 中至少有一个不可逆（D ）A+B=03. 若齐次线性方程组1231231230020kx x x x kx x x x x ++=⎧⎪+-=⎨⎪-+=⎩仅有零解，则（ B ）(A) 4k =或1K =- (B) K= 4－或K=1(C) 4K ≠且1K ≠- (D) 4K ≠-且1k ≠4. A 、B 均为n 阶可逆矩阵，则AB 的伴随矩阵()*AB =( D )(A) A B ** (B) 11||AB A B -- (C) 11B A -- (D) B A **5.设n 元齐次线性方程组0AX =的系数矩阵的秩为r ，则0AX =有非零解的充分必要条件是（D ）（A ）r n = （B ） r n ≥ （C ） r n > （D ）r n <二 .填空题（每题3分）1．行列式 12342345_______32005000= 1602．若n n ⨯阶矩阵A 的行列式|A|＝3，A *是A 的伴随矩阵，则A *__3^n-1____3. A 为n n ⨯阶矩阵，且2320A A E -+=,则1A -=______4. n1100⎡⎤=⎢⎥⎣⎦___1__(n 为正整数)5. 设1101A -⎡⎤=⎢⎥⎣⎦, 则1(2A)________=－三．计算题（共63分）1. 计算行列式12n12n 12nb a a a a b a a a a b a ＋＋＋(12分)解：r2-r1、r3=r1、...ri-r1、...rn-r1D=|b+a1 a2 a3 ....................... an|-b b 0 0-b 0 b 0.............................-b 0 0 .......................... bc1+c2+c3+...+cj+...+cn=|b+a1+a2+...+an a2 ............... an|0 b ................. 0 ......................................0 0 .................... b=(b+Σai)*[b^(n-1)]=b^n+[b^(n-1)]*(a1+a2+...+an)2．3411231100250013A⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦, 求1A-（12分）3 41 12 5解：令B= ，C= ，D= ，则原矩阵可以写为分块2 3 -1 1 1 3B C B ^-1 -B ^-1CD^-1 矩阵的形式A= ，它的逆矩阵易得为A^-1=0 D 0 D ^-1而利用伴随矩阵与逆矩阵的关系可以直接得到3 -4 3 -4B^-1=1/ B B *=1×=-2 3 -2 32 -53 -5D^-1=1/ D D *=1×=-1 3 -1 2-15 38计算可得-B^-1CD^-1=11 -283 -4 -22 37-2 3 16 -27所以A^-1= 0 0 3 -50 0 -1 23.求解齐次线性方程组1234123412342202220430x x x xx x x xx x x x+++=⎧⎪+--=⎨⎪---=⎩.（15分）解：基础解系为：1 2 2 1 2 2 1 0 -2 -5/32 1 -2 -2 -3 -6 -4 1 2 4/3 1 -1 -4 -3 0 0 0 0 0 0通解为：X12k1+5/3k2 2 5/3X=k1ξ1+ k2ξ2= X2 = -2k1-4/3k2 =k1 -2 +k2 -4/3X3 k1 1 0X4 k2 0 14.设211210111A-⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,311342B⎡⎤-=⎢⎥⎣⎦求解矩阵方程XA B=（12分）解:5. 计算矩阵3112322140511135524aA⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦的秩为3，求a (12分)解：r4-r2,r1-r3,r2-2r30 1 1 a-1 -20 2 1 -1 -61 0 1 1 50 1 2 4 0r1-r4,r2-2r40 0 -1 a-5 -20 0 -3 -9 -61 0 1 1 50 1 2 4 0r3*(-1/3), r1+r20 0 0 a-2 00 0 1 3 21 0 1 1 50 1 2 4 0交换行1 0 1 1 50 1 2 4 00 0 1 3 20 0 0 a-2 0因为 r(A)=3, 所以 a = 2.四.证明题（7分）设32=,证明5A E+可逆，并求1A E+（7分）A E-(5)解：（A+5E）【1/127（A^2-5A+25E）】=1/127（A+5E）（A^2-5A+25E）=1/127（A^3+5A^2-5A^2-25A+25A+125E）=1/127（A^3+125E）由于A^3=2E，所以1/127（A^3+125E）=1/127（127E）=E，所以（A+5E）可逆，且（A+5E）^-1=1/127（A^2-5A+25E）。

线性代数测试试卷及答案

线性代数（A卷）一﹑选择题（每小题3分，共15分）1. 设﹑是任意阶方阵，那么下列等式必成立的是（）(A）（B) （C） (D）2。

如果元齐次线性方程组有基础解系并且基础解系含有个解向量，那么矩阵的秩为（）（A） (B）（C) （D）以上答案都不正确3.如果三阶方阵的特征值为，那么及分别等于( ）（A）（B）（C) (D）4。

设实二次型的矩阵为,那么（）(A) （B) (C） (D)5.若方阵A的行列式,则（）（A） A的行向量组和列向量组均线性相关 (B）A的行向量组线性相关，列向量组线性无关（C） A的行向量组和列向量组均线性无关 (D）A的列向量组线性相关,行向量组线性无关二﹑填空题（每小题3分，共30分)1 如果行列式有两列的元对应成比例，那么该行列式等于；2. 设,是的伴随矩阵，则；3. 设,是非齐次线性方程组的解，若也是它的解，那么；4. 设向量与向量正交，则；5。

设为正交矩阵,则；6。

设是互不相同的三个数，则行列式；7. 要使向量组线性相关，则；8. 三阶可逆矩阵的特征值分别为,那么的特征值分别为；9. 若二次型是正定的，则的取值范围为；10。

设为阶方阵，且满足，这里为阶单位矩阵，那么.三﹑计算题（每小题9分，共27分）1. 已知,,求矩阵使之满足。

2. 求行列式的值。

3 求向量组的一个最大无关组和秩.四﹑(10分）设有齐次线性方程组问当取何值时, 上述方程组(1）有唯一的零解﹔（2）有无穷多个解，并求出这些解.五﹑（12分）求一个正交变换，把下列二次型化成标准形：.六﹑（6分)已知平面上三条不同直线的方程分别为试证：这三条直线交于一点的充分必要条件为。

线性代数(A卷）答案一﹑1。

D 2。

C 3。

B 4. A 5。

A二﹑1。

0 2. 3。

1 4。

3 5。

1或—16. 7。

0 8。

9。

10。

三﹑1。

解由得。

(2分）下面求。

由于(4分)而. (7分)所以。

（9分）2。

（完整版）全国自考历年线性代数试题及答案

（完整版）全国⾃考历年线性代数试题及答案浙02198# 线性代数试卷第1页（共54页）全国2010年1⽉⾼等教育⾃学考试《线性代数（经管类）》试题及答案课程代码：04184试题部分说明：本卷中，A T 表⽰矩阵A 的转置，αT 表⽰向量α的转置，E 表⽰单位矩阵，|A |表⽰⽅阵A 的⾏列式，A -1表⽰⽅阵A 的逆矩阵，r （A ）表⽰矩阵A 的秩.⼀、单项选择题（本⼤题共10⼩题，每⼩题2分，共30分）在每⼩题列出的四个备选项中只有⼀个是符合题⽬要求的，请将代码填写在题后的括号内。

错选、多选或未选均⽆分。

1.设⾏列式==1111034222,1111304z y x zy x则⾏列式（）A.32B.1C.2D.38 2.设A ，B ，C 为同阶可逆⽅阵，则（ABC ）-1=（） A. A -1B -1C -1 B. C -1B -1A -1 C. C -1A -1B -1D. A -1C -1B -13.设α1，α2，α3，α4是4维列向量，矩阵A =（α1，α2，α3，α4）.如果|A |=2，则|-2A |=（） A.-32 B.-4 C.4D.324.设α1，α2，α3，α4 是三维实向量，则（） A. α1，α2，α3，α4⼀定线性⽆关 B. α1⼀定可由α2，α3，α4线性表出 C.α1，α2，α3，α4⼀定线性相关D. α1，α2，α3⼀定线性⽆关5.向量组α1=（1，0，0），α2=（1，1，0），α3=（1，1，1）的秩为（） A.1 B.2 C.3D.46.设A 是4×6矩阵，r （A ）=2，则齐次线性⽅程组Ax =0的基础解系中所含向量的个数是（）A.1B.2C.3D.47.设A 是m ×n 矩阵，已知Ax =0只有零解，则以下结论正确的是（） A.m ≥nB.Ax =b （其中b 是m 维实向量）必有唯⼀解浙02198# 线性代数试卷第2页（共54页）C.r （A ）=mD.Ax =0存在基础解系8.设矩阵A =??---496375254，则以下向量中是A 的特征向量的是（） A.（1，1，1）T B.（1，1，3）T C.（1，1，0）TD.（1，0，-3）T9.设矩阵A =--111131111的三个特征值分别为λ1，λ2，λ3，则λ1+λ2+λ3 = （）A.4B.5C.6D.710.三元⼆次型f （x 1，x 2，x 3）=233222312121912464x x x x x x x x x +++++的矩阵为（）A.??963642321 B.??963640341 C.??960642621 D.??9123042321⼆、填空题（本⼤题共10⼩题，每⼩题2分，共20分）请在每⼩题的空格中填上正确答案。

线性代数自考试题及答案

线性代数自考试题及答案一、单项选择题（每题2分，共10分）1. 向量组α1，α2，α3线性无关的充分必要条件是（）。

A. 齐次方程组Ax=0只有零解B. 齐次方程组Ax=0有非零解C. 齐次方程组Ax=0只有零解，且α1，α2，α3线性相关D. 齐次方程组Ax=0只有零解，且α1，α2，α3线性无关答案：A2. 矩阵A与矩阵B相等的充分必要条件是（）。

A. A与B的行数相同B. A与B的列数相同C. A与B的行数相同，且A与B的列数相同D. A与B的行数相同，且A与B的列数相同，且对应元素相等答案：D3. 设A为n阶矩阵，若A的行列式|A|=0，则A是（）。

A. 可逆矩阵B. 非可逆矩阵C. 正交矩阵D. 反对称矩阵答案：B4. 设A为3阶矩阵，且A的特征多项式为f(λ)=λ(λ-1)(λ+2)，则A的迹为（）。

A. 0B. 1C. 2D. -3答案：C5. 设A为3阶矩阵，且A的秩为2，则A的零度为（）。

A. 0B. 1C. 2D. 3答案：B二、填空题（每题3分，共15分）1. 若矩阵A的行列式|A|=2，则矩阵A的伴随矩阵的行列式|adj(A)|=______。

答案：42. 设矩阵A=\(\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\)，则矩阵A的逆矩阵A^{-1}=______。

答案：\(\begin{bmatrix}-2 & 1 \\ 1.5 & -0.5\end{bmatrix}\)3. 若向量α=(1,2,3)，β=(4,5,6)，则向量α与向量β的夹角的余弦值为______。

答案：\(\frac{1}{3}\)4. 设矩阵A的特征值λ1=2，λ2=3，对应的特征向量分别为α1和α2，则矩阵A+E的特征值λ3=______，对应的特征向量为______。

答案：3，α1；4，α25. 设矩阵A=\(\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\)，则矩阵A的秩为______。

全国自学考试线性代数历年考试真题及答案

全国自学考试线性代数历年考试真题及答案20XX年4月全国自学考试线性代数答案第一部分选择题(共20分)一、单项选择题(本大题共10小题。

每小题2分，共20分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．对任意n阶方阵A、B总有( )A．AB=BA B．|AB|=|BA|2．在下列矩阵中，可逆的是 ( )3．设A是3阶方阵( )A．-2D．24．设A是m×n矩阵，则齐次线方程线Ax=0仅有零解的充分必要条件是 ( ) A．A的行向量组线性无关 B．A的行向量组线性相关C．A的列向量组线性无关 D．A的列向量组线性相关5．设有m维向量组，则 ( )A．当m<n时，(I)一定线性相关 B．当m>n时，(I)一定线性相关C．当m<n时，(I)一定线性无关 D．当m>n时，(I)一定线性无关6．已知是非齐次线性方程组Ax=b的两个不同的解，是其导出组Ax=0的一个基础解系，为任意常数，则方程组Ax=b的通解可表成 ( )7．设n阶可逆矩阵A有一个特征值为2，对应的特征向量为x，则下列等式中不正确的是( )A．Ax=2x8．设矩阵的秩为2，则λ= ( )A．2 8．1C．0 D．-l9．二次型的矩阵是( )10．二次型是 ( )A．正定的 B．半正定的C．负定的 D．不定的第二部分非选择题(共80分)二、填空题(本大题共10小题。

每小题2分，共20分)请在每小题的空格中填上正确答案。

错选、不填均无分。

1 1．行列式的值为___．12．设向量a=(2，1，2),则与它同方向的单位向量为__．13．设α=(2，1，-2)，β=(1，2，3)，则2α=3β=____．14．向量组a=(1，2，3，4，5)的秩为____．15．设m×n矩阵A的，m个行向量线性无关，则矩阵的秩为____．16．若线性方程组无解，则=______．17．设2阶方阵均为2维列向量，且|A|=|B|=1，则|A+B|=_______．18．设矩阵，则A的全部特征值为___．19．设P为n阶正交矩阵，α、β为n维列向量，已知内知(α，β)=-l，则(Pa，Pβ)________20．设二次型的正惯性指数为P，负惯性指数为q，则p-q=______.三、计算题(本大题共8小题，每小题6分，共48分)21．设向量22．设，矩阵X满足方程求矩阵X．23．当t取何值时，向量组线性相关?24．求下列矩阵的秩：25．设矩阵矩阵A由矩阵方程确定，试求的通解(要求用它的一个特解和导出组的基础解系表示)．27．设3阶方阵A的三个特征值为的特征向量依次为求方阵A．28．设为正定二次型，试确定实数a的最大取值范围．四、证明题(本大题共2小题，每小题6分，共12分)30．设向量β可由向量组线性表示．试证明：线性表示法唯一的充分必要条件是线性无关．参考答案一、单项选择题1．B 2．D 3．B 4．D 5．A 6．D 7．C 8．B 9.C 10.A二、填空题11．O13．(1,-4,-l3)14．115．ml6．017．418．1，1，-l19．-l20．O三、计算题知当且仅当t=3时该向量组线性相关．所求通解x=都是非零列向量，故题设条件说明A有特征值对应的特征向量分别为因为A为3阶方阵．故1，0．-l就是A的全部特征值，因A的特征值互不相同，于是由推论4．1知A可对角化，令矩阵由上式得28．解，的矩阵为，A的顺序主子式为四、证明题所以30．证由条件，存在常数若表示法唯一，设有一组数20XX年10月自考线性代数试题答案全国20XX 年10月高等教育自学考试线性代数试题课程代码：02198试卷说明：A T 表示矩阵A 的转置矩阵，A *表示矩阵A 的伴随矩阵，E 是单位矩阵，|A|表示方阵A 的行列式。

线性代数自考A卷答案

自考线性代数试题及答案

线性代数试题A及答案

自考线性代数试题及答案

(完整版)线性代数试卷及答案详解

线性代数考试(A)参考答案及评释学习资料

全校各专业《线性代数》课程试卷及答案A卷

完整版)线性代数试卷及答案

《线性代数》试卷A及答案

2020-2021(1)《线性代数A》A卷参考答案

自考试题线性代数题库及答案

线性代数试题A答案[大全5篇]

线性代数自考试题及答案

线性代数自考试题及答案

学历类《自考》自考公共课《工程数学-线性代数》考试试题及答案解析

线性代数试卷及答案 卷A

线性代数测试试卷及答案

（完整版）全国自考历年线性代数试题及答案

线性代数自考试题及答案

全国自学考试线性代数历年考试真题及答案

线性代数试卷及答案卷A