关于圆的内接四边形课件
合集下载
24.1.4 .2圆内接四边形课件 2024-2025学年人教版数学九年级上册

求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
随堂练习
8. 如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,
求∠ADE的度数.
随堂练习
5. 如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且
∠A=55°,∠E=30°,则∠F=
解析:∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
解析:∵四边形ABCD是圆内接四边形,
∴∠B+∠ADC=180°.
∵四边形OABC为平行四边形,
∴∠AOC=∠B.
知识讲解
知识点 圆内接四边形的性质
【例 1】如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形
OABC为平行四边形,则∠OAD+∠OCD=________度.
又由题意可知∠AOC=2∠ADC.
∵∠BAE=∠CBD,
∴∠1=∠2.
随堂练习
10. 如图,四边形ABCD的顶点都在⊙O上,BD平分∠ADC,且BC=CD.
求证:AB=CD.
证明:∵BD平分∠ADC,
∴∠ABD=∠CDB,
∴ AB = BC
∴AB=BC,
∵BC=CD,
∴AB=CD.
课后小结
圆内接多边形
定义
多边形外接圆
证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
随堂练习
8. 如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,
求∠ADE的度数.
随堂练习
5. 如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且
∠A=55°,∠E=30°,则∠F=
解析:∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
解析:∵四边形ABCD是圆内接四边形,
∴∠B+∠ADC=180°.
∵四边形OABC为平行四边形,
∴∠AOC=∠B.
知识讲解
知识点 圆内接四边形的性质
【例 1】如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形
OABC为平行四边形,则∠OAD+∠OCD=________度.
又由题意可知∠AOC=2∠ADC.
∵∠BAE=∠CBD,
∴∠1=∠2.
随堂练习
10. 如图,四边形ABCD的顶点都在⊙O上,BD平分∠ADC,且BC=CD.
求证:AB=CD.
证明:∵BD平分∠ADC,
∴∠ABD=∠CDB,
∴ AB = BC
∴AB=BC,
∵BC=CD,
∴AB=CD.
课后小结
圆内接多边形
定义
多边形外接圆
3.6圆内接四边形专题培训课件

D
B
C
E
C
O
A B
A
O
D
F
E
如图:圆内接四边形ABCD中, ∠A+∠C的和为多少
D
A
同理∠B+∠D的和呢? O
B
C
小组合作,一起比一比!
如图:圆内接四边形ABCD中,
∵ 弧BCD和弧BAD所对的
圆心角的和是周角
D
∴∠A+∠C=180 A
同理∠B+∠D=°180°
O
B
C
圆的内接四边形的对角互补。
如果延长BC到E,那么 ∠DCE+∠BCD = 180° D
的内接四边形,已知∠BOD=
100°,求∠BAD及∠BCD的度
数。
A
O
Байду номын сангаас
B
D
C
求证:圆内接平行四边形是矩形。
已知:如图,四边形ABCD是
圆的内接四边形并且ABCD是
平行四边形。
求证:四边形ABCD A
B
是矩形。
O
D
C
若一个四边形各顶点都在同一个圆上, 那么,这个四边形叫做圆内接四边形, 这个圆叫做这个四边形的外接圆。
如图,四边形ABCD为 ⊙O的内接四边形; ⊙O为四边形ABCD的外 接圆。
D
A
O
B
C
定理: 圆的内接四边形的 对角互补,并且任何一个 外角都等于它的内对角。
课堂小结!!!!!!
则∠BOD=
150º
O
B
D
C
E
当堂巩固
例 如图⊙O1与⊙O2都经过A、B两点, 经过点A的直线CD与⊙O1 交于点C,与 ⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。
圆内接四边形的性质与判定ppt课件

性质定理1
圆内接四边形的对角互补
如果一个四边形的对角互补,那么它的四个顶 点共圆.
性质定理2 圆内接边形的外角等于它的内角 的对角。
如果四边形的一个外角等于它的内角的 对角,那么它的四个顶点共圆.
性质定理的逆命题成立吗?
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
(2)如果点D在⊙O内部。 则∠B+∠E=180°
∵∠B+∠ADC=180°∴∠E=∠ADC
同样矛盾。∴点D不可能在⊙O内。
综上所述,点D只能在圆周上,四点共圆。 A D
E O
B
C
(2)
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).
A
E
D
证明:(1)如果点D在⊙O外部。 则∠AEC+∠B=180°因∠B+∠D=180° B
得∠ D=∠AEC与“三角形外角大于任意
O
C
(1)
不相邻的内角”矛盾。故点D不可能在圆外。
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
o 圆 1与
圆o2都经过A,B两点。经过点A
的直线CD与圆o1交于点C,与圆o2交与点经过点B
的直线EF与圆o1交于点E,与圆o2交与点F.
求证:CE//DF. 证明:连接AB
圆内接四边形的对角互补
如果一个四边形的对角互补,那么它的四个顶 点共圆.
性质定理2 圆内接边形的外角等于它的内角 的对角。
如果四边形的一个外角等于它的内角的 对角,那么它的四个顶点共圆.
性质定理的逆命题成立吗?
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
(2)如果点D在⊙O内部。 则∠B+∠E=180°
∵∠B+∠ADC=180°∴∠E=∠ADC
同样矛盾。∴点D不可能在⊙O内。
综上所述,点D只能在圆周上,四点共圆。 A D
E O
B
C
(2)
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).
A
E
D
证明:(1)如果点D在⊙O外部。 则∠AEC+∠B=180°因∠B+∠D=180° B
得∠ D=∠AEC与“三角形外角大于任意
O
C
(1)
不相邻的内角”矛盾。故点D不可能在圆外。
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
o 圆 1与
圆o2都经过A,B两点。经过点A
的直线CD与圆o1交于点C,与圆o2交与点经过点B
的直线EF与圆o1交于点E,与圆o2交与点F.
求证:CE//DF. 证明:连接AB
圆的内接四边形PPT教学课件
例
E
题
D
演
A
练
B
C
新知应用
已知:如图,⊙O1和⊙O2相交于A、B两点, 经过点A的直线CD与⊙O1交于点C,与⊙O2 交于点D,经过点B的直线EF与⊙O1交于点E, 与⊙O2交于点F。
求证:CE∥DF
A
D
C
E O1• B
•
O2 F
如果图形有如下变化,上题的结论 CE∥DF还成立吗?怎样证明?
变 式 练E 习
形容词) 4. 宫妇左右莫不私王(偏爱,动词)
复习导入
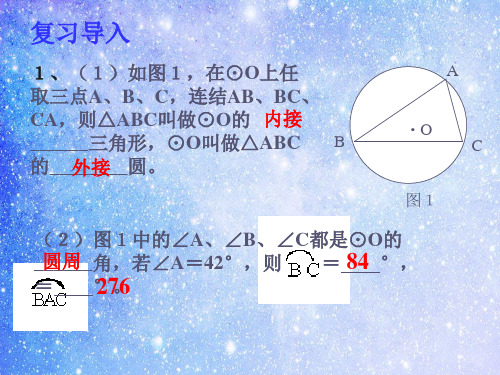
1、(1)如图1,在⊙O上任 取三点A、B、C,连结AB、BC、 CA,则△ABC叫做⊙O的 内接 ______三角形,⊙O叫做△ABC B 的___外__接___圆。
A
·O C 图1
(2)图1中的∠A、∠B、∠C都是⊙O的
_圆__周___角,若∠A=42°,则 = 84 °,
= °27。6
B
D
O C
(1)左图中,∠A+∠C=?; ∠B+∠D=?
观 (2)右图中,∠DCE和∠A有什
察 么关系?
与
A
思 考
A
D
D
B
C
B
E C
圆的内接四边形的对角互补,
并且任何一个外角等于它的内
定
对角
∠A+∠C=∠B+∠D=180;
∠DCE=∠A
D
理
A
D
A
B
C
B
CE
1、如图,A、B、C、D都在⊙O上,(1)指出 图中内接四边形的外角及其内对角。
邹忌讽齐王纳谏
1、 邹忌比美 臣之妻→私我 臣之妾→畏我 臣之客→求我
圆的内接四边形课件

04
圆的内接四边形的实际应用
在几何图形中的应用
性质研究
圆的内接四边形具有一系列独特的性 质,如对角和定理、外角定理等,这 些性质在几何证明和解题中有着广泛 的应用。
图形变换
通过圆的内接四边形的性质,可以实 现图形的对称、旋转、平移等变换, 有助于解决复杂的几何问题。
在建筑设计中的应用
Hale Waihona Puke 建筑设计构思圆的内接四边形PPT课件
目 录
• 圆的内接四边形的定义和性质 • 圆的内接四边形的判定定理 • 圆的内接四边形的面积和周长计算 • 圆的内接四边形的实际应用 • 圆的内接四边形的拓展知识
01
圆的内接四边形的定义和性质
定义
总结词
圆的内接四边形的定义
详细描述
圆的内接四边形是指四个顶点都在同一个圆上的四边形。
性质
总结词
圆的内接四边形的性质
详细描述
圆的内接四边形具有一些特殊的性质,如对角互补、外角等于内对角等。这些性 质在解题时可以发挥重要的作用。
分类
总结词
圆的内接四边形的分类
详细描述
根据四边形的不同性质,可以将圆的内接四边形分为不同的类型,如矩形、正方形等。不同类型的内接四边形具 有不同的性质和特点,在解题时需要根据具体情况进行分析。
参加数学竞赛有助于提高对圆的内接 四边形的理解和应用能力。
实践应用
通过解决实际问题,加深对圆的内接 四边形的理解。
THANKS
感谢观看
圆的内接四边形可以作为建筑设计的 基本构图元素,通过调整四边形的形 状和角度,可以创造出富有创意和美 感的建筑结构。
建筑结构稳定性分析
利用圆的内接四边形的性质,可以对 建筑结构的稳定性进行分析和优化, 提高建筑的安全性和耐久性。
圆内接四边形的性质与判定PPT教学课件

将图2 61中的线段AB延长到点E,
得到图2 62.由于ABC EBC
1800 ,所以EBC D.
E
于是又得性质定理2 :
O A
B
图2 62
定理2 圆内接四边形的外角等于它的内角的对角.
经过上面的讨论, 我们得到了圆内接四边形的两条 性 质.一 个 自 然 的 想 法 是, 它 们 的 逆 命 题 成 立 吗? 如 果 成立 ,就可以得到四边形存在外接圆的判定定理.
割 线与圆的交点的两条线段长的积相等.
下 面 继 续 用 运 动 变 化 思想 探 究.
探究 在图2 24 中, 使割线 P PB绕 P 点运动到切线位置
图2 25, 是否还有PA PB
PC PD?
连接AC、AD,同样可以证明 PAC ~ PDA (请同学们自
己证明),因而1 式仍然成立.
D
C
过A、B引两条弦AD和BE, 相交于
A
C.求证 : AC AD BC BE AB2.
FO
B
证明 连接AE、BD,过C作 CF AB,与AB交于F.
图2 31
因为AB是圆的直径,所以AEB ADB 900.
又因为AFC 900 ,故A、F、C、E四点共圆.
BC BE BF BA.同理 F、B、D、C四点共圆.
直线EF // CB,交AD的延长线于F, FG切圆于G.
求证 : 1DFE ~ EFA;2EF FG.
2由1知DFE ~ EFA,
C
所以 EF FD ,即 FA EF
EF 2 FA FD .
因为FG是圆的切线, 所以FG2 FA FD,
B O
E
A DF
G
图2 29
圆内接四边形PPT课件

C.32
D.2 3 3
【点拨】如图,作OE⊥AD于点E,连接BD,OD. ∵⊙O为四边形ABCD的外接圆,∠BCD=120°, ∴∠BAD=60°. 又∵AD=AB=2,∴△ABD是等边三角形. 易得DE=1AD=1,∠ODE=1∠ADB=30°,∴OE=1 OD. 在Rt△OE2D中,根据勾股定理2可得OE2+DE2=OD2,得2 OD=2 3.
(2)当m=5 时,方程的两根分别是矩形的长和宽,求该矩形 2
外接圆的直径; 解:当m=5 时,原方程可化为x2-5x+5=0.
2 设方程的两个根分别为x1,x2, 则x1+x2=5,x1·x2=5. ∵该矩形外接圆的直径是矩形的对角线,
∴d= x21+x22= (x1+x2)2-2x1x2= 52-2×5= 15. 即该矩形外接圆的直径是 15.
在△ABC和△MEC中,
∠ABC=∠MEC, ∠BAC=∠EMC, CB=CE, ∴△ABC≌△MEC(AAS).
∴AB=ME.
∵ME+EB=BM,
∴AB+BC=BM.
14.(中考·绥化)已知关于x的一元二次方程x2-5x+2m=0 有实数根.
(1)求m的取值范围; 解: (1)∵方程有实数根, ∴Δ=(-5)2-4×1×2m≥0. ∴m≤285.
习题链接
13 见习题 14 见习题 15 见习题 16 见习题
17 见习题 18 会;44 19 乙;909
答案呈现
课堂导练
1.家庭电路是最常见、最基本的实用电路,它由两根 _进__户__线___、_电__能__表___、_总__开__关___、_保__险__装__置_、用电器 和导线等组成。家庭电路中的各用电器之间是 ___并___联的;控制用电器的开关与用电器____串____联 ,接在____火____线和用电器之间。
九年级数学圆的内接四边形课件

∴∠1=∠F
D
∴∠E+∠F=180° A
∴CE∥DF
C
1
O1
O2
F
E
B
圆内接四边形的判定定理:
如果一个四边形的一组对角互补, 那么这个四边形内接于圆。
已 知 :BD1800 求 证 :四 边 形 ABCD内 接 于 圆
D 反证法:以D在圆外为例
A
D’
BCຫໍສະໝຸດ ABOD
C
3. 如图⊙O1与⊙O2都经过A、B两点,经
过点A的直线CD与⊙O1交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于 点E,与⊙O2 交于点F。
求证:CE∥DF
D A
C
O1
O2
F
E
B
证明:连结AB
∵ABEC是⊙O1的内接四边形, ∴∠E+∠1=180°
∵ADFB是⊙O2的内接四边形,
结论:
A
圆内接四边形的一个
O
外角等于它的内对角。
B
E C
6D
A5
7
4
3
O
B2
E 1C
定理:
圆的内接四边形的对角互补,并 且任何一个外角都等于它的内对 角。
练习:
1、如图,四边形ABCD为⊙O 的内
接四边形,∠BOD=100°,求
∠BAD及∠BCD的度数。
A
O
B
D
C
2.圆内接平行四边形是 矩?形
心角的和是周角
D
∴∠A+∠C=180° A
同理∠B+∠D=180°
O
圆内接四边形的对角互补。B
C
如果延长BC到E,那么
∠DCE+∠BCD =180°
《圆内接四边形》课件

圆的内接四边形
复习提问:
1、如图(1),△ABC叫⊙O的_内__接__三角形,⊙O叫△ABC 的 外___接_ 圆.
2、 如上图(1),若弧BC的度数为1000, 则
∠BOC=1_0_0_º__ ,∠A5=0_º____
3、如图(2)四边形ABCD中, ∠B与∠1互补,AD的延长线 与DC所夹∠2=600 ,
D 1E
O
B
C
几何表达式:(如图)
∵ 四边形ABCD内接于⊙O
∴ ∠A+∠C=180°,∠B=∠1
例1 :如图⊙O1与⊙O2都经过A、B两点,经过 点A的直线CD与⊙O1 交于点C,与⊙O2 交于点 D.经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F.
求证:CE∥DF
D A
C O1
O
2
F
则∠1=_1_2_0_º_,∠B=6_0_º___.
A
A
O
1
D
2
E
B
C B
C
图1
图2
什么是圆内接四边形?
A
D 如果一个四边形
O 的所有顶点都在
B
同一个圆上,那么
C
这个四边形叫做圆内接四边形 这个圆叫做这个四边形的外接圆.
猜想:圆内接四边形的对角有什么关系呢?
思路:在一般的圆内接四边形中,如果把圆心O与一
组,证对明顶猜点A想、C分别相连,能得到D什么结果呢?
∵
1
∠D= 2
x
1 ,∠B= 2
y
yO
x
C
A
∴∠D+∠B=
1(xy)13601B80
2
2
用几何画板来验证!
如果延长BC到E,那么∠A与
复习提问:
1、如图(1),△ABC叫⊙O的_内__接__三角形,⊙O叫△ABC 的 外___接_ 圆.
2、 如上图(1),若弧BC的度数为1000, 则
∠BOC=1_0_0_º__ ,∠A5=0_º____
3、如图(2)四边形ABCD中, ∠B与∠1互补,AD的延长线 与DC所夹∠2=600 ,
D 1E
O
B
C
几何表达式:(如图)
∵ 四边形ABCD内接于⊙O
∴ ∠A+∠C=180°,∠B=∠1
例1 :如图⊙O1与⊙O2都经过A、B两点,经过 点A的直线CD与⊙O1 交于点C,与⊙O2 交于点 D.经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F.
求证:CE∥DF
D A
C O1
O
2
F
则∠1=_1_2_0_º_,∠B=6_0_º___.
A
A
O
1
D
2
E
B
C B
C
图1
图2
什么是圆内接四边形?
A
D 如果一个四边形
O 的所有顶点都在
B
同一个圆上,那么
C
这个四边形叫做圆内接四边形 这个圆叫做这个四边形的外接圆.
猜想:圆内接四边形的对角有什么关系呢?
思路:在一般的圆内接四边形中,如果把圆心O与一
组,证对明顶猜点A想、C分别相连,能得到D什么结果呢?
∵
1
∠D= 2
x
1 ,∠B= 2
y
yO
x
C
A
∴∠D+∠B=
1(xy)13601B80
2
2
用几何画板来验证!
如果延长BC到E,那么∠A与
圆内接四边形的性质与判定定理 课件

圆内接四边形的性质与判定定理
● 1.圆内接四边形的性质
●( 1 ) 圆 的 内 接 四 边 形 _ _ _对_角_ _互_ _补_ _ .
●如图:四边形ABCD内接于⊙O,则有: ∠A+_∠__C__=180°,∠B+∠_D____= 180°. (2) 圆 内 接 四 边 形 的 外 角 等 于 它 的
圆内接多边形的综合应用
(辽宁高考)已知△ABC 中,如
︵
图,AB=AC,D 是△ABC 外接圆劣弧AC 上 的点(不与点 A、C 重合),延长 BD 至 E.
(1)求证:AD 的延长线平分∠CDE; (2)若∠BAC=30°,△ABC 中 BC 边上的高为 2+ 3,求△ ABC 外接圆的面积.
● 解析: (1)证明:如图,设F为AD延长线上一点. ● ∵A、B、C、D四点共圆, ● ∴∠CDF=∠ABC. ● 又AB=AC,∴∠ABC=∠ACB. ● 又∵∠ADB=∠ACB. ● ∴∠ADB=∠CDF. ● 又∠EDF=∠ADB,∴∠EDF=∠CDF, ● 即AD的延长线平分∠CDE.
证明点共圆问题
●
如图所示,在△ABC中,AD
=DB,DF⊥AB交AC于F,AE=EC,
EG⊥AC交AB于G.求证:
●(1)D、E、F、G四点共圆;
●(2)G、B、C、F四点共圆.
● [思路点拨] (1)要证D、E、F、G四点共圆,只需找到过这四点的外接圆的圆心,证明圆心到四 点的距离相等,可取GF的中点H,证点H即为圆心.
BD,且AC⊥BD,∠BAD=72°,求四边Hale Waihona Puke 其余的各角.● [思路点拨]
● [解题过程] ∵四边形ABCD是圆内接四边形, ● ∴∠BAD+∠BCD=180°. ● 又∵∠BAD=72°,∴∠BCD=108°. ● 又∵AC平分BD,并且AC⊥BD, ● ∴AC是四边形ABCD外接圆的直径. ● ∴∠ABC=∠ADC=90°. ● [规律方法] 如何利用圆内接四边形的性质定理求角? ● (1)观察图形,找出圆内接四边形的对角或内对角; ● (2)利用圆内接四边形的性质定理1或性质定理2求出所要求的角.
● 1.圆内接四边形的性质
●( 1 ) 圆 的 内 接 四 边 形 _ _ _对_角_ _互_ _补_ _ .
●如图:四边形ABCD内接于⊙O,则有: ∠A+_∠__C__=180°,∠B+∠_D____= 180°. (2) 圆 内 接 四 边 形 的 外 角 等 于 它 的
圆内接多边形的综合应用
(辽宁高考)已知△ABC 中,如
︵
图,AB=AC,D 是△ABC 外接圆劣弧AC 上 的点(不与点 A、C 重合),延长 BD 至 E.
(1)求证:AD 的延长线平分∠CDE; (2)若∠BAC=30°,△ABC 中 BC 边上的高为 2+ 3,求△ ABC 外接圆的面积.
● 解析: (1)证明:如图,设F为AD延长线上一点. ● ∵A、B、C、D四点共圆, ● ∴∠CDF=∠ABC. ● 又AB=AC,∴∠ABC=∠ACB. ● 又∵∠ADB=∠ACB. ● ∴∠ADB=∠CDF. ● 又∠EDF=∠ADB,∴∠EDF=∠CDF, ● 即AD的延长线平分∠CDE.
证明点共圆问题
●
如图所示,在△ABC中,AD
=DB,DF⊥AB交AC于F,AE=EC,
EG⊥AC交AB于G.求证:
●(1)D、E、F、G四点共圆;
●(2)G、B、C、F四点共圆.
● [思路点拨] (1)要证D、E、F、G四点共圆,只需找到过这四点的外接圆的圆心,证明圆心到四 点的距离相等,可取GF的中点H,证点H即为圆心.
BD,且AC⊥BD,∠BAD=72°,求四边Hale Waihona Puke 其余的各角.● [思路点拨]
● [解题过程] ∵四边形ABCD是圆内接四边形, ● ∴∠BAD+∠BCD=180°. ● 又∵∠BAD=72°,∴∠BCD=108°. ● 又∵AC平分BD,并且AC⊥BD, ● ∴AC是四边形ABCD外接圆的直径. ● ∴∠ABC=∠ADC=90°. ● [规律方法] 如何利用圆内接四边形的性质定理求角? ● (1)观察图形,找出圆内接四边形的对角或内对角; ● (2)利用圆内接四边形的性质定理1或性质定理2求出所要求的角.
圆内接四边形的性质与判定定理 课件

图 2-2-3
【思路探究】 先利用 PC 是圆的直径,得到 PF∥BC, 再利用圆内接四边形的性质,得到 DF∥PC,最后利用平行
线分线段成比例证明结论.
【自主解答】 连接 DF、PF. ∵PC 是直径, ∴PF⊥AC. ∵BC⊥AC,
∴PF∥BC,∴PPAB=FFAC.
∵四边形 PCFD 内接于⊙O, ∴∠ADF=∠ACP, ∵AP=AC, ∴∠APC=∠ACP.
△ABC 外接圆劣弧 上的点(不与点 A,C 重合),延长 BD
至 E. (1)求证:AD 的延长线 DF 平
分∠CDE; (2)若∠BAC=30°,△ABC 中
BC 边上的高为 2+ 3,求△ABC 外接圆的面积.
图 2-2-7
【思路探究】 (1)利用同弧所对的圆周角相等及圆内接 四边形的性质定理求解.
∴∠ADF=∠APC.∴DF∥PC,
∴DDAP=FFAC,∴PPAB=DDAP.
1.在本题的证明过程中,都是利用角相等证明了两直 线平行,然后利用直线平行,得到比例式相等.
2.圆内接四边形的性质即对角互补,一个外角等于其 内对角,可用来作为三角形相似或两直线平行的条件,从而 证明一些比例式成立或证明某些等量关系.
如图 2-2-5 所示,在△ABC 中,AD=DB, DF⊥AB 交 AC 于 F,AE=EC,EG⊥AC 交 AB 于 G,求证:
(1)D、E、F、G 四点共圆; (2)G、B、C、F 四点共圆.
图 2-2-5
【思路探究】 (1)要证 D、E、F、G 四点共圆,只需找 到过这四点的外接圆的圆心,证明圆心到四点的距离相等, 可取 GF 的中点 H,证点 H 即为圆心.
圆内接四边形的性质与判定定理
1.圆内接四边形的性质定理 (1)定理 1:圆的内接四边形的 对角互补 .如图 2-2-1: 四边形 ABCD 内接于⊙O,则有:∠A+ ∠C=180°,∠B+ ∠D =180°.
【思路探究】 先利用 PC 是圆的直径,得到 PF∥BC, 再利用圆内接四边形的性质,得到 DF∥PC,最后利用平行
线分线段成比例证明结论.
【自主解答】 连接 DF、PF. ∵PC 是直径, ∴PF⊥AC. ∵BC⊥AC,
∴PF∥BC,∴PPAB=FFAC.
∵四边形 PCFD 内接于⊙O, ∴∠ADF=∠ACP, ∵AP=AC, ∴∠APC=∠ACP.
△ABC 外接圆劣弧 上的点(不与点 A,C 重合),延长 BD
至 E. (1)求证:AD 的延长线 DF 平
分∠CDE; (2)若∠BAC=30°,△ABC 中
BC 边上的高为 2+ 3,求△ABC 外接圆的面积.
图 2-2-7
【思路探究】 (1)利用同弧所对的圆周角相等及圆内接 四边形的性质定理求解.
∴∠ADF=∠APC.∴DF∥PC,
∴DDAP=FFAC,∴PPAB=DDAP.
1.在本题的证明过程中,都是利用角相等证明了两直 线平行,然后利用直线平行,得到比例式相等.
2.圆内接四边形的性质即对角互补,一个外角等于其 内对角,可用来作为三角形相似或两直线平行的条件,从而 证明一些比例式成立或证明某些等量关系.
如图 2-2-5 所示,在△ABC 中,AD=DB, DF⊥AB 交 AC 于 F,AE=EC,EG⊥AC 交 AB 于 G,求证:
(1)D、E、F、G 四点共圆; (2)G、B、C、F 四点共圆.
图 2-2-5
【思路探究】 (1)要证 D、E、F、G 四点共圆,只需找 到过这四点的外接圆的圆心,证明圆心到四点的距离相等, 可取 GF 的中点 H,证点 H 即为圆心.
圆内接四边形的性质与判定定理
1.圆内接四边形的性质定理 (1)定理 1:圆的内接四边形的 对角互补 .如图 2-2-1: 四边形 ABCD 内接于⊙O,则有:∠A+ ∠C=180°,∠B+ ∠D =180°.
初中数学微课课件:圆内接四边形

∠A+∠C=180°,∠B+∠D=180°
证法二
D AO
B C
圆内接四边形的性质定理: 圆的内接四边形对角互补
几何语言 ∵四边形ABCD内接于⊙O
∴ ∠A+∠C=180° ∠B+∠D=180°
D
AO
B C
做一做
1、已知圆内接四边形有一个内角 是500,求它的对角的度数
2、 若⊙O内接四边形ABCD中满足∠A=∠C, ∠B=∠D,则四边形ABCD是怎样的特殊的四 边形?
接圆于D,求证:DB=DC.
解:∵ AD是∠EAC的平分线
E
A D
∴∠DAC=∠DAE
四边形ABCD内接于⊙O ∴∠BAD+∠BCD=180° (圆内接四边形的对角互补) 又∵ ∠BAD+∠DAE=180°
O
B
C
∴∠BCD=∠DAE( ? )
而∠DBC=∠DAC ( ? ) ∠DAC=∠DAE
∴∠DBC=∠DCB
O
C
连结DE,求证:DE∥BC。
3、圆内接四边形ABCD中,A⌒DC与A⌒BC 的比为
3:2,求∠B、∠D的度数。
4、已知四边形ABCD, ∠A、∠B、∠C、∠D 的度数之比为3:1:2:5 ,判断这个四边形 是不是圆内接四边形?并说明理由。 5、圆内接四边形ABCD中, A⌒B、⌒BC、⌒CD、D⌒A 的度数之比为1:2:3:4 ,求四边形ABCD各 内角的度数
答:沿正方形ABCD的四条边,就可以锯出符合要求的截面
为正方形的木材,若原木长为15m,其体积为0.675m3.
作业题
1、已知:四边形ABCD内接于⊙O,∠A=50°, ∠D-∠B =40°求∠B、∠C、∠D的度数
圆内接四边形的性质与判定定理 课件

点共圆提供两个方法.
类型 1 性质定理的应用(规范解答)
[典例 1] 如图所示,⊙O 是等腰 三角形 ABC 的外接圆,AB=AC, 延长 BC 到点 D,使 CD=AC,连接 AD 交⊙O 于点 E,连接 BE 与 AC 交于点 F.
(1)判断 BE 是否平分∠ABC,并说明理由. (2)若 AE=6,BE=8,求 EF 的长., 所以 EF=AED·EEC=92.(10 分)
归纳升华 圆内接四边形的性质即对角互补,一个外角等于其内 角的对角,这两个性质可用来作为三角形相似的条件,从 而证明一些比例式成立或证明某些等量关系.
类型 2 判定定理的应用(互动探究)
圆内接四边形的性质与判定定理
1.圆内接多边形的定义 如果多边形的所有顶点都在一个圆上,那么这个多边 形叫做圆内接多边形,这个圆叫做多边形的外接圆. 2.圆内接四边形的性质定理 定理 1:圆内接四边形的对角互补. 定理 2:圆内接四边形的外角等于它的内角的对角.
3.圆内接四边形的判定定理 如果一个四边形的对角互补,那么这个四边形的四 个顶点共圆. 4.判定定理的推论 如果四边形的一个外角等于它的内角的对角,那么 这个四边形四个顶点共圆. 温馨提示 圆内接四边形判定定理及推论为证明四
审题指导:(1)判断 BE 是否平分∠ABC,关键是判断 ∠ABC=2∠EBC 是否成立.
(2)EF 的长可利用三角形相似来求. [规范解答] (1)BE 平分∠ABC.(2 分) 因为 AC=CD, 所以∠CAD=∠ADC,
所以∠ACB=∠CAD+∠ADC=2∠CAD.(4 分) 又因为 AB=AC, 所以∠ABC=∠ACB=2∠CAD. 因为∠CAD=∠EBC, 所以∠ABC=2∠EBC, 所以 BE 平分∠ABC.(6 分)
类型 1 性质定理的应用(规范解答)
[典例 1] 如图所示,⊙O 是等腰 三角形 ABC 的外接圆,AB=AC, 延长 BC 到点 D,使 CD=AC,连接 AD 交⊙O 于点 E,连接 BE 与 AC 交于点 F.
(1)判断 BE 是否平分∠ABC,并说明理由. (2)若 AE=6,BE=8,求 EF 的长., 所以 EF=AED·EEC=92.(10 分)
归纳升华 圆内接四边形的性质即对角互补,一个外角等于其内 角的对角,这两个性质可用来作为三角形相似的条件,从 而证明一些比例式成立或证明某些等量关系.
类型 2 判定定理的应用(互动探究)
圆内接四边形的性质与判定定理
1.圆内接多边形的定义 如果多边形的所有顶点都在一个圆上,那么这个多边 形叫做圆内接多边形,这个圆叫做多边形的外接圆. 2.圆内接四边形的性质定理 定理 1:圆内接四边形的对角互补. 定理 2:圆内接四边形的外角等于它的内角的对角.
3.圆内接四边形的判定定理 如果一个四边形的对角互补,那么这个四边形的四 个顶点共圆. 4.判定定理的推论 如果四边形的一个外角等于它的内角的对角,那么 这个四边形四个顶点共圆. 温馨提示 圆内接四边形判定定理及推论为证明四
审题指导:(1)判断 BE 是否平分∠ABC,关键是判断 ∠ABC=2∠EBC 是否成立.
(2)EF 的长可利用三角形相似来求. [规范解答] (1)BE 平分∠ABC.(2 分) 因为 AC=CD, 所以∠CAD=∠ADC,
所以∠ACB=∠CAD+∠ADC=2∠CAD.(4 分) 又因为 AB=AC, 所以∠ABC=∠ACB=2∠CAD. 因为∠CAD=∠EBC, 所以∠ABC=2∠EBC, 所以 BE 平分∠ABC.(6 分)
圆内接四边形精选教学PPT课件

它让女人更温柔娇羞,让男人更成熟大度 它让孩子更天真美丽 淡淡一点的裙衫很俏 淡淡的 而现在 因为在淡淡的想你
所以才有了这些淡淡的文字…… 一切都是淡淡的
只是那么淡淡一点的 过去,现在与未来, 人生的画卷轻轻地描绘 落下的泪和展开的笑 都用那淡淡的笔画 走在人群中,总有那么些女孩让人不断回首 没有红装绿裹的耀眼,风中飘逸的蓝衫紫裙 只有一身的青春和一派的清纯 淡淡一点的微笑很醇 当孩子见到陌生人,总会藏到大人的背后,然后悄悄地露出半边脸 淡淡的笑意,很自然地从眼中从嘴角流露出来 少年将散着淡淡一束芳香的玫瑰送到少女手中时,他已经装满了少女的心 淡淡一点的天空很高 没有朵朵云彩,没有蓝得逼眼的鲜亮,只是淡淡的 灰中有蓝,蓝中含灰 那缭绕着的,淡淡的炊烟 喜欢低吟“红了樱桃,绿了芭蕉”的
A
A
A
B
E
O B
O
DO
B
C
C
C
D
请观察,以上三个图形有何共同之处?
判断下列图形中的四边形是否是圆的
内接四边形,并说明理由.
A
A
OD B
C A (1) D
D BO
C D(2)
O
AO
B
(3)
C
B
C
(4)
问题1:四边形ABCD四个内角有何共同之处?
∠A对应哪条弧?∠BCD对应哪条弧?
请观察这两条弧有何特点?
你要知道,这份友情是金钱买不来的,是时间换不回的,那份真挚的友情是心与心的交融,是属于你一生的财富。 当你付出之后,不必老是企盼朋友对你说声谢谢。一千遍,一万遍的感谢,也许比不上一个理解的眼神!我拥有至少5个不用说谢的朋友,所以我感激上苍,也会珍惜这来之不易的情分!我喜欢淡淡的感觉,也许是因为一种忧郁?我不知道 我也不知道,我是否快乐。 我只是喜欢淡淡的感觉 我喜欢看枝头那淡淡的嫩绿
所以才有了这些淡淡的文字…… 一切都是淡淡的
只是那么淡淡一点的 过去,现在与未来, 人生的画卷轻轻地描绘 落下的泪和展开的笑 都用那淡淡的笔画 走在人群中,总有那么些女孩让人不断回首 没有红装绿裹的耀眼,风中飘逸的蓝衫紫裙 只有一身的青春和一派的清纯 淡淡一点的微笑很醇 当孩子见到陌生人,总会藏到大人的背后,然后悄悄地露出半边脸 淡淡的笑意,很自然地从眼中从嘴角流露出来 少年将散着淡淡一束芳香的玫瑰送到少女手中时,他已经装满了少女的心 淡淡一点的天空很高 没有朵朵云彩,没有蓝得逼眼的鲜亮,只是淡淡的 灰中有蓝,蓝中含灰 那缭绕着的,淡淡的炊烟 喜欢低吟“红了樱桃,绿了芭蕉”的
A
A
A
B
E
O B
O
DO
B
C
C
C
D
请观察,以上三个图形有何共同之处?
判断下列图形中的四边形是否是圆的
内接四边形,并说明理由.
A
A
OD B
C A (1) D
D BO
C D(2)
O
AO
B
(3)
C
B
C
(4)
问题1:四边形ABCD四个内角有何共同之处?
∠A对应哪条弧?∠BCD对应哪条弧?
请观察这两条弧有何特点?
你要知道,这份友情是金钱买不来的,是时间换不回的,那份真挚的友情是心与心的交融,是属于你一生的财富。 当你付出之后,不必老是企盼朋友对你说声谢谢。一千遍,一万遍的感谢,也许比不上一个理解的眼神!我拥有至少5个不用说谢的朋友,所以我感激上苍,也会珍惜这来之不易的情分!我喜欢淡淡的感觉,也许是因为一种忧郁?我不知道 我也不知道,我是否快乐。 我只是喜欢淡淡的感觉 我喜欢看枝头那淡淡的嫩绿
【数学课件】圆内接四边形

上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱
心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
A
B
O
D
C
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
好好学习,天天向上。 2、教育人就是要形成人的性格。——欧文
3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种
最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身
心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
A
B
O
D
C
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
好好学习,天天向上。 2、教育人就是要形成人的性格。——欧文
3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种
最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身
圆的内接四边形精选教学PPT课件

我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
最后,我打他一巴掌。干脆痛快,出手的瞬间,像那位绝望的母亲,远远掷出她的高跟鞋。掷中没有?并不重要。 有多爱,就有多不舍;有多温柔,就有多暴烈,爱得唇边有血,眼中有泪,胸口有纠缠的爱与恨,爱到如连体婴般骨肉相连。割爱,就一定不可能如拈去一片花叶般轻松微笑。 明知留不住,收不下,却不能自控我颠倒狂乱的脚步。那一遭,我是夜深街上,追逐汽车的女子。而我无声的哭泣,他没有听见。快乐是人类社会众望所归的最高境界。所谓君子之交谈如水。一个把名缰利锁看得太重的人。注定是不快乐的。快乐就是看淡尘世的物欲、烦恼,不慕荣利。假如你喜欢武侠小说,你没有必要愧对红楼梦; 假如你喜欢的人突然销声匿迹,你没有必要寻死觅活地断言他一定洒脱地离去;假如你的朋友不幸,你没有必要怨天尤人;假如你认为张曼玉艳美绝俗,你没有必要眼馋肚饱虐待老婆;假如你已经身心交病,那就去教堂忏悔,没有必要仇视别人的平庸;坦然面对心融神会,快乐就在你心里。我怜悯一个有点荣誉的人,就旁若无人而因此失 去快乐的人。能把名利得失置之度外,而凡事都能以诚相待的人一生将是快乐的。我们应从平谈的生活中去提炼体会,如:赤城待人的那种快乐。低待遇下一如既往工作的快乐,助人为乐一介不取的快乐,一片至诚去感化恶人的快乐,热心被人误解依然如故的快乐,信实可靠的服务态度为目的的快乐,尽责任吃苦耐劳的快乐,因为这些 “快乐”能保持住人内心的快乐,使人的容貌永远那么牵挂,一句亲切的问候。甚至一个关切的眼神,快乐无处不有,唯有胸襟开阔的人,才能体会到。形单影只的人仍然可以享受着闲情逸致的快乐。乐山乐水各不相同。爱静的人可以看书、听音乐、上网、写作、画画、搜集各种收藏品。爱动的人则不妨练习舞蹈、慢跑、爬山、游泳。看 电影、上健身房。做编织、陶艺。练瑜枷、潜心发明、闭门创作,摄影、观鸟,我们仍然兴复不浅,乐不可支。人生苦短,岁月如流,乐天知命,为什么不乐乐陶陶的。为什么要疾首蹙额,为眼前一时的顿挫心胆俱碎?为什么要对那些你看不惯的人和事心烦率乱?岂不知我们都是尘世间相映成趣的战友。人世一切冤天屈地,无妄之灾,荣 华富贵,香娇玉嫩……都将随身亡命殒。而人生长着百年,短则数十寒暑,又有何值得耀武扬威的,不过是烟云过眼矣?人生如月,月满则亏,凡事岂能尽人意,但求于心无愧。无愧我心,则恩同再造,那些得失又算不了甚么。世界上没有完美无缺得事物。奉劝多愁善感的朋友。饮醇自醉,快乐起来吧!芸芸众生,绿水青山,名胜古迹,
最后,我打他一巴掌。干脆痛快,出手的瞬间,像那位绝望的母亲,远远掷出她的高跟鞋。掷中没有?并不重要。 有多爱,就有多不舍;有多温柔,就有多暴烈,爱得唇边有血,眼中有泪,胸口有纠缠的爱与恨,爱到如连体婴般骨肉相连。割爱,就一定不可能如拈去一片花叶般轻松微笑。 明知留不住,收不下,却不能自控我颠倒狂乱的脚步。那一遭,我是夜深街上,追逐汽车的女子。而我无声的哭泣,他没有听见。快乐是人类社会众望所归的最高境界。所谓君子之交谈如水。一个把名缰利锁看得太重的人。注定是不快乐的。快乐就是看淡尘世的物欲、烦恼,不慕荣利。假如你喜欢武侠小说,你没有必要愧对红楼梦; 假如你喜欢的人突然销声匿迹,你没有必要寻死觅活地断言他一定洒脱地离去;假如你的朋友不幸,你没有必要怨天尤人;假如你认为张曼玉艳美绝俗,你没有必要眼馋肚饱虐待老婆;假如你已经身心交病,那就去教堂忏悔,没有必要仇视别人的平庸;坦然面对心融神会,快乐就在你心里。我怜悯一个有点荣誉的人,就旁若无人而因此失 去快乐的人。能把名利得失置之度外,而凡事都能以诚相待的人一生将是快乐的。我们应从平谈的生活中去提炼体会,如:赤城待人的那种快乐。低待遇下一如既往工作的快乐,助人为乐一介不取的快乐,一片至诚去感化恶人的快乐,热心被人误解依然如故的快乐,信实可靠的服务态度为目的的快乐,尽责任吃苦耐劳的快乐,因为这些 “快乐”能保持住人内心的快乐,使人的容貌永远那么牵挂,一句亲切的问候。甚至一个关切的眼神,快乐无处不有,唯有胸襟开阔的人,才能体会到。形单影只的人仍然可以享受着闲情逸致的快乐。乐山乐水各不相同。爱静的人可以看书、听音乐、上网、写作、画画、搜集各种收藏品。爱动的人则不妨练习舞蹈、慢跑、爬山、游泳。看 电影、上健身房。做编织、陶艺。练瑜枷、潜心发明、闭门创作,摄影、观鸟,我们仍然兴复不浅,乐不可支。人生苦短,岁月如流,乐天知命,为什么不乐乐陶陶的。为什么要疾首蹙额,为眼前一时的顿挫心胆俱碎?为什么要对那些你看不惯的人和事心烦率乱?岂不知我们都是尘世间相映成趣的战友。人世一切冤天屈地,无妄之灾,荣 华富贵,香娇玉嫩……都将随身亡命殒。而人生长着百年,短则数十寒暑,又有何值得耀武扬威的,不过是烟云过眼矣?人生如月,月满则亏,凡事岂能尽人意,但求于心无愧。无愧我心,则恩同再造,那些得失又算不了甚么。世界上没有完美无缺得事物。奉劝多愁善感的朋友。饮醇自醉,快乐起来吧!芸芸众生,绿水青山,名胜古迹,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可能在⊙O的外部.
的内角”矛盾,故点D不可
D
E
能在⊙O的内部.
A
综上所述, 点D只能在圆 A
D
E
周上,即A、
O
B、C、D四
O
B
C 点共圆.
B
C
3 四边形存在外接圆的判定定理
说明:在此判定定理的证明中,用到了分类讨论的思想和 反证法.又当问题的结论存在多种情形时,通过对每一种 情形分别讨论,最后获得结论的方法,称为穷举法.于是
在一个圆上,那么这个多边形叫做圆内
O
接多边形,这个圆叫做多边形的外接圆.
B
C
D
A
O
B
C
A
F
B
O·
E
C
D
思考:
(1 ) 任意三角形都有外接圆吗? (2)一般地,任意四边形都有外接圆吗? (3)任意矩形是否有外接圆?
那么任意四边形有外接圆吗?
探究:观察下图,这组图中的四边形都内接于圆. 你能发现这些四边形的共同特征吗? 特殊到一般的方法!
A
3、如图,四边形ABCD内接于⊙O,
∠DCE=75º,则∠BOD= 例1:如图⊙O1与⊙O2都经过A、B两点.经过点 A的直线CD与⊙O1交于点C,与⊙O2交于点D.经 过点B的直线EF与⊙O1交于点E,与⊙O2交于点F. 求证:CE∥DF. 分析:只要证明同旁内角互补即可!
证明:连接AB. 并利用圆内接四边形的性质定理.
点,连接EC,则有
部.显然AD的延长线必定与
∠AEC+∠B=180°.由题设 圆相交,设交点为E,连接
∠B+∠D=180°,可得
EC,则有∠E+∠B=180°.由
∠D=∠AEC .这与“三角 题设∠B+∠ADC=180°,可
形的外角大于任一不相邻
得∠E=∠ADC .这与“三
的内角”矛盾,故点D不
角形的外角大于任一不相邻
A D 的度数与B C 的度数和的一半等于∠APD的度数.
分析:由于∠APD既不是圆心角,
D
也不是圆周角,为此我们需要构造
B
一个与∠APD相等的圆心角或圆周
角,以便利用定理. A
证明:如图,过点C作CE//AB交
P C
圆于E,则有∠APD =∠C.
E
一 定理的探究
A
1.定义:如果多边形的所有顶点都
D
A
O
B
C
O
B
D
C
E
二 定理的应用
练习 :
A
1、如图,四边形ABCD为⊙O的 内接四边形,已知∠BOD=100°,
O
B
D
则∠BAD= 50º,∠BCD= 130º.
C
2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,
则∠A=60º ∠B=90º ∠C= 120º∠D= 90º
设A=2x,则C=4x. ∵A+C=180º, ∴x=30º.
3 四边形存在外接圆的判定定理
圆内接四边形的性质定理1: 圆的内接四边形的对角互补.
DE
A
圆内接四边形的性质定理2:
圆内接四边形的外角等于 它的内角的对角.
O
B
C
3 四边形存在外接圆的判定定理
已知:四边形ABCD中,∠B+∠D=180°,
求证:A、B、C、D在同一圆周上(简称四点共圆).
分析:不在同一直线上的三点确定一个圆.经过A、B、C三点 作⊙O,如果能够由条件得到⊙O过点D,那么就证明了命题.
证明:连接PQ.在四边形QFPC中, ∵ FP⊥BC,FQ⊥AC ,∴∠FQA=∠FPC.
∴Q、F、P、C四点共圆.
∴∠QFC=∠QPC.
又∵CF⊥AB,
C
∴∠QFC+∠QFA=90°.
而∠A+∠QFA=90°.
∴∠QFC=∠A.
Q
∴∠QPC=∠A.
∴A、B、P、Q四点共圆.
AF
P B
练习2:
1、(1)圆内接平行四边形一定是 矩 形.
(2)圆内接梯形一定是等腰梯形.
(3)圆内接菱形一定是 正方 形.
2.如果四边形一边上的两个顶点的视角 D
C
相等,那么四边形的四个顶点共圆.
已知:如图,四边形ABCD中,
∠ADB=∠ACB.
A
B
求证: A、B、C、D四点共圆.
∵四边形ABEC是⊙O1的内接四边形,∴ ∠BAD=∠E.
又∵四边形ABFD是⊙O2的内接四边形,
D
∴ ∠BAD+∠F=180º.
A
∴ ∠E+∠F=180º. ∴ CE//DF.
C
O1
E
B
O2
F
变式1:如图,⊙O1和⊙O2都经过A、B两点.过A点的
直线CD与⊙O1交于点C,与⊙O2交于点D.过B点的直线 EF与⊙O1交于点E,与⊙O2交于点F.求证:CE//DF.
2 圆内接四边形的性质定理
1.如图:圆内接四边形ABCD中,
∵ 弧BCD和弧BAD所对的 圆心角的和是周角.
∴∠A+∠C= 180°
A
同理∠B+∠D=180°
圆内接四边形的性质定理1:
B
圆的内接四边形的对角互补.
D O
C
D
2.圆内接四边形的性质定理
A O.
B
CE
圆内接四边形的性质定理2: 圆内接四边形的外角等于它的内角的对角.
圆内接四边形判定定理:如果一个四边形的对角互补,那 么这个四边形的四个顶点共圆.
应用格式:在四边形ABCD中,∵A+C=180°,∴四点A,B,C,D共圆.
圆内接四边形判定定理的推论:如果四边形的一个外角等 于它的内角的对角,那么这个四边形的四个顶点共圆.
应用格式:在四边形ABCD中,∵∠A=∠DCE,∴四A 点A,B,C,D共圆.
关于圆的内接四边 形
圆周角定理:圆上一条弧所对的圆周角等于它所对 的圆心角的一半.
圆心角定理:圆心角的度数等于它所对弧的度数.
推论1:在同圆或等圆中,同弧或等弧所对的圆周 角相等;反之,相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角; 反之,90°的圆周角所对的弦是直径.
例2. 如图,AB与CD相交于圆内一点P.求证:
显然, ⊙O与点D有且只有三种位置关系:
(1)点D在圆外;(2)点D在圆内;(3)点D在圆上.分类讨论思想
只要证明在假设条件下只有(3)成立,也就证明了命题.反证法
D
D
D
A
A
A
O
B
C
O
O
B
C
B
C
(1) 如果点D在⊙O的外 证明:(分类讨论思想及反证法)
部.设E是AD与圆周的交
(2)如果点D在⊙O的内
D
A
D
EO
O
C1
2
B
A
C
O1
O2
F
F
B
E
变式2:如图,⊙O1和⊙O2有两个公共点A﹑B.由例1可知:CE//DF,
过A﹑B两点的直线分别交⊙O1于C 、E,
又∵CD//EF, ∴DCEF为平行四边
交⊙O2于D 、F,且CD∥EF.求证:CE=DF.形. ∴CE=DF.
例2. 如图,CF是△ABC的AB边上的高,FP⊥BC,FQ⊥AC. 求证: A、B、P、Q四点共圆.
