广东工业大学应用数学学院《数学建模》教学大纲
《数学建模》课程教学大纲

《数学建模》课程教学大纲课程编号:20811012总学时数:32(理论 32)总学分数:2课程性质:专业基础和专业课程适用专业:数学与应用数学、信息与计算科学一、课程的任务和基本要求:课程的性质和任务:数学建模是数学与应用数学专业、信息与计算数学专业的一门必修课程,是大学数学课程的重要组成部分,它是在数学分析、高等代数、概率论与数理统计等课程基础上开设的重要教学环节,它将数学知识、实际问题与计算机应用有机地结合起来,旨在培养学生运用所学知识解决实际问题的意识和创新思维,激发学生学习数学的兴趣,了解数学广泛的应用领域,提高学生的综合素质和分析问题、解决问题的能力。
课程的基本要求:1、在大学数学基础课的教学内容基础上进一步突出培养学生解决实际问题的能力;2、学会运用数学知识建立实际问题的数学模型并求解,对较复杂的问题能够使用数学软件或编程求解;二、基本内容和要求:(一)建立数学模型内容:(1)初等建模示例:椅子能在不平地面上放稳吗,预报人口增长等;(2)有关数学建模的基本知识。
目的和要求:理解数学模型的意义、内容和方法,掌握建立数学模型的一般步骤。
(二)初等模型内容:(1)建模示例:公平席位分配,双层玻璃窗的功效等;(2)讨论与交流:录音机计数器,商品的包装。
目的和要求:由建模实例进一步了解和熟悉建模的方法和步骤,了解对实际问题的分析、抽象过程,基本掌握用初等方法建立数学模型。
(三)简单的优化模型内容:(1)建模示例:存储模型,森林救火,最优价格等;(2)讨论与交流:冰山运输目的和要求:基本掌握建立静态优化模型的一般方法,会利用微分法解决优化问题。
(四)数学规划模型内容:(1)建模示例:奶制品的生产与销售,汽车生产与原油采购,钢管和易拉罐下料等;(2)讨论与交流:自来水的输送,接力队员的选拔目的和要求:理解规划优化模型的思想与意义,掌握建立规划模型的一般方法,能够利用优化软件求解规划模型的解。
(五)微分方程模型内容:(1)建模示例:传染病模型,战争模型,药物在体内的分布和排除,人口的预测和控制等;(2)讨论与交流:烟雾的扩散和消失目的和要求:基本掌握用微分方程建立动态模型,并能够利用稳定性理论对问题的解进行讨论。
《数学建模》课程教学大纲

《数学建模》课程教学大纲第一部分大纲说明一、课程的作用与任务《数学建模》课程是中央广播电视大学数学与应用数学专业的一门限选课,它是应用数学专业的一门基础课程。
通过教学,使学生了解数学建模的基本知识,且具有用数学方法解决实际问题的初步能力,为后继的数学课程学习和进一步培养数学应用能力提供基础。
数学建模课程的主要内容数学建模方法论、初等数学模型、微分方程模型、运筹学模型、概率统计模型等。
二、课程的目的与教学要求根据整个教学计划的内容安排,以及学生主要是成人、在职、业余学习的特点,本课程将主要介绍初等数学模型,运筹学模型,微分方程模型和概率统计模型这四类常见数学模型中的较基本、较简单的部分,使学生对数学建模的基本想法与做法有一个较全面的初步的了解,为应用所学数学知识解决实际问题奠定一个较好的基础。
1 对相关课程内容的基本要求由于本课程的特点,对学生的基本数学基础有下列要求:熟练掌握常微分方程的基本内容,概率论与统计分析基础,运筹学中的线性规划、目标规划的初步知识,图论基础知识、决策论、存贮论与排队论初步知识。
2通过本课程的学习,应达到下列基本目标:(1)深化学生对所学数学理论的理解和掌握;(2)使学生了解数学科学的重要性和应用的广泛性,进一步激发学生学习数学的兴趣;(3)熟悉并掌握建立数学模型的基本步骤、基本方法和技巧;(4)培养学生应用数学理论和数学思想方法,利用计算机技术等辅助手段,分析、解决实际问题的综合能力;(5)培养学生的数学应用意识,同时进一步拓宽学生的知识面,培养学生的科学研究能力。
三、课程的教学要求层次教学要求层次:有关定义、定理、性质等概念的内容按“知道、了解、理解”三个层次要求;有关计算、解法、公式和法则等方法的内容按“会、掌握、熟练掌握” 三个层次要求。
第二部分学时、教材与教学安排一、学时分配本课程共4学分,讲授54学时(包括习题课)学时分配如下:项目内容学时电视学时IP课学时第一章数学建模方法论13第二章初等数学模型9第三章微分方程模型9第四章运筹学模型13第五章概率统计模型10合计541012二、教学安排数学建模课程安排在第6学期,一个学期完成全部教学任务。
《数学建模》课程教学大纲

《数学建模》课程教学大纲一、课程基本信息二、课程教学目标随着科学技术和计算机的迅速发展,数学向各个领域的广泛渗透已日趋明显,数学不仅在传统的物理学、电子学和工程技术领域继续发挥着重要的作用,而且在经济、人文、体育等社会科学领域也成为必不可少解决问题的工具,数学建模就是沟通实际问题与数学工具之间联系的必不可少的桥梁。
本课程作为信息与计算科学专业本科生开设的专业核心课,将数学方法应用到实际问题中去,主要是通过机理分析,根据客观事物的性质分析因果关系,在适当的假设条件下,利用合适的数学工具得到描述其特征的数学模型。
通过本课程的学习,希望学生能够达到以下能力目标:1. 培养学生利用数学工具解决实际问题的能力;2. 将实际问题“翻译”为数学语言并予以求解,然后再解释实际现象并应用于实际的能力;3. 逐步提高学生的数学素质和应用数学知识解决实际问题的能力。
三、教学学时分配《数学建模》课程理论教学学时分配表*理论学时包括讨论、习题课等学时。
《数学建模》课程实验内容设置与教学要求一览表四、教学内容和教学要求第一章建立数学模型(5学时)(一)教学要求通过本章内容的学习,了解数学描写和数学建模的不同于数学理论的思维特征,理解数学模型的意义及分类,掌握建立数学模型的方法及步骤等。
(二)教学重点与难点教学重点:从现实对象到数学模型,数学建模的方法和步骤,数学模型的特点和分类及怎样学习数学建模教学难点:数学建模的方法和步骤,数学模型的特点和分类(三)教学内容第一节从现实对象到数学模型第二节数学建模的重要意义第三节数学建模示例1.椅子能在不平的地面上放稳吗2.商人们怎样安全过河3. 如何施救药物中毒第四节数学建模的基本方法和步骤1.数学建模的基本方法2.数学建模的基本步骤第五节数学模型的特点和分类1.数学模型的特点2.数学模型的分类第六节数学建模能力的培养本章习题要点:要求学生完成作业5-8题。
其中概念题35%,应用题25%,计算题40%第二章初等模型(5学时)(一)教学要求通过本章内容的学习,了解初等模型的概念,理解比例方法、类比方法、图解法、定性分析方法建模的基本特点,掌握运用所学知识建立数学模型,并对模型进行综合分析等。
《 数学建模 》教学大纲最新
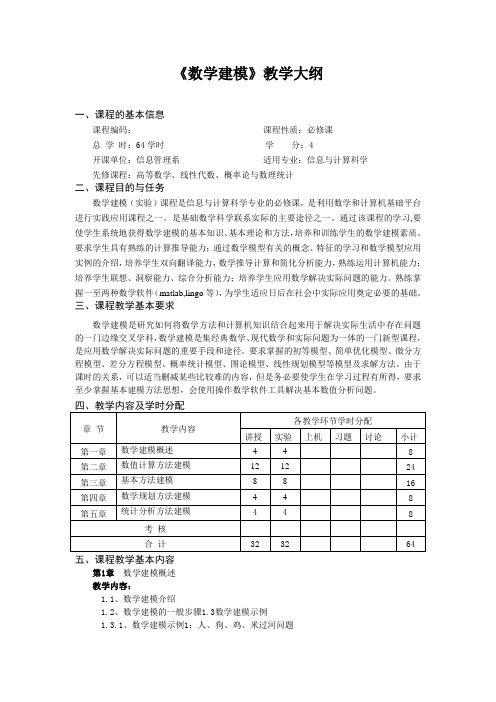
《数学建模》教学大纲一、课程的基本信息课程编码:课程性质:必修课总学时:64学时学分:4开课单位:信息管理系适用专业:信息与计算科学先修课程:高等数学、线性代数、概率论与数理统计二、课程目的与任务数学建模(实验)课程是信息与计算科学专业的必修课,是利用数学和计算机基础平台进行实践应用课程之一。
是基础数学科学联系实际的主要途径之一。
通过该课程的学习,要使学生系统地获得数学建模的基本知识、基本理论和方法,培养和训练学生的数学建模素质。
要求学生具有熟练的计算推导能力;通过数学模型有关的概念、特征的学习和数学模型应用实例的介绍,培养学生双向翻译能力,数学推导计算和简化分析能力,熟练运用计算机能力;培养学生联想、洞察能力、综合分析能力;培养学生应用数学解决实际问题的能力。
熟练掌握一至两种数学软件(matlab,lingo等),为学生适应日后在社会中实际应用奠定必要的基础。
三、课程教学基本要求数学建模是研究如何将数学方法和计算机知识结合起来用于解决实际生活中存在问题的一门边缘交叉学科,数学建模是集经典数学、现代数学和实际问题为一体的一门新型课程,是应用数学解决实际问题的重要手段和途径。
要求掌握的初等模型、简单优化模型、微分方程模型、差分方程模型、概率统计模型、图论模型、线性规划模型等模型及求解方法。
由于课时的关系,可以适当删减某些比较难的内容,但是务必要使学生在学习过程有所得,要求至少掌握基本建模方法思想,会使用操作数学软件工具解决基本数值分析问题。
五、课程教学基本内容第1章数学建模概述教学内容:1.1、数学建模介绍1.2、数学建模的一般步骤1.3数学建模示例1.3.1、数学建模示例1:人、狗、鸡、米过河问题1.3.2、数学建模示例2:人口预测问题1.4、数学建模能力的培养1.5、课后练习。
重点:1、数学建模基本方法;2、人口预测问题;3、数学建模能力的培养;难点:MATLAB软件应用;第2章数值计算方法建模教学内容:2.1非线性方程求解2.1.1非线性方程简介2.1.2非线性方程求解的MATLAB实现2.1.3建模示例:贷款问题2.2线性方程组的数值解法2.2.1线性方程组简介2.2.2线性方程组求解的MATLAB实现2.2.3建模示例:种群繁殖问题2.3插值2.3.1插值简介2.3.2一维插值的MATLAB实现2.3.3二维插值的MATLAB实现2.3.4建模示例:零件加工问题2.4数据拟合2.4.1数据拟合简介2.4.2数据拟合的MATLAB实现2.5数值差分与数值微分2.5.1数值差分与数值微分简介2.5.2数值微分的MATLAB实现2.5.3建模示例:湖水温度变化问题2.6数值积分2.6.1数值积分简介2.6.2数值积分的MATLAB实现2.6.3建模示例:煤炭储量计算问题2.7常微分方程(组)的数值解法2.7.1常微分方程简介2.7.2常微分方程(组)数值解法的MATLAB实现2.7.3建模示例:导弹追踪问题2.8课后练习重点:1、非线性方程求解;2、建模示例;3、插值,数据拟合;4、数值差分与数值微分5、常微分方程(组)的数值解法难点:插值,MATLAB软件编程求解建模示例;第3章基本方法建模教学内容:3.1平衡方法建模3.1.1平衡方法简介3.1.2建模示例:汽车的刹车距离问题3.2马尔可夫链方法建模3.2.1马尔可夫链方法简介3.2.2建模示例:遗传问题3.3比例方法建模3.5.1简单的优化方法简介3.5.2建模示例:血管分支问题3.6微分方程方法建模3.6.1微分方程方法介绍3.6.2建模示例:传染病问题3.7概率方法建模3.7.1概率方法介绍3.7.2建模示例:报童的售报问题重点:1、平衡方法建模;2、马尔可夫链方法建模;3、优化方法建模;4、概率方法建模难点:建模方法选择,应用MATLAB软件编程求解建模示例;第4章数学规划方法建模教学内容:4.1线性规划方法建模4.1.1线性规划方法简介Lingo软件初步4.1.2线性规划方法建模的基本技巧4.1.3线性规划的Lingo实现4.1.4线性规划方法建模示例4.2整数规划方法建模4.2.1整数规划方法简介4.2.2整数规划方法建模的基本技巧4.2.3整数规划方法的Lingo软件实现4.2.4整数规划方法建模示例4.3课后练习重点:1、线性规划方法建模;2、整数规划方法建模;难点:建模方法选择,灵活应用Lingo软件编程求解建模示例第5章统计分析方法建模教学内容:5.1.2概率论基本知识的MATLAB实现5.6回归分析5.6.1一元线性回归分析介绍5.6.2多元线性回归分析介绍5.6.3回归分析的MATLAB实现5.6.4建模示例:医院服务评价问题5.7聚类分析5.7.1聚类分析介绍5.7.2聚类分析的MATLAB实现重点:1、回归分析;2、聚类分析;难点:建模方法选择,灵活应用数学软件编程六、考核方式与成绩评定考核方式:考试用时:成绩评定:本课程成绩构成比例为:期末考试成绩占总成绩的 70 %,平时成绩占总成绩的30 %;平时成绩的构成及比例为:考勤占40%,课堂测验成绩占30%,实验成绩占0%,作业占30 %。
数学建模教学大纲

课程名称:数学建模课程编号:授课教师:任煜东职称:讲师授课对象:全校二、三年级在校大学生授课时数:32学时授课方式:多媒体授课,上机实验(开放实验)先修课程:高等数学、线性代数、概率论与数理统计一、课程的教学目的与要求《数学建模》课程是面向全校非数学类专业开设的数学素质、建模技能和数学实验、数学软件应用及计算机编程等高度融合的一门通选课程。
通过本课程的学习,使学生了解完整的建模过程,了解应用问题的各部分是怎样结合在一起的。
掌握各种常见的数学建模问题、解决问题的数学方法或途径、建立数学模型的过程、可用于模型求解的数学理论、算法、数学软件及计算机编程等。
同时,为了配合课程的学习,做到即时学习,同步实践,一般每周向所有参加课程学习的学生设2个学时的开放实验时间,以便熟练使用各类数学软件,结合数学软件及计算机编程,通过实验来观察、理解数学和实现各类数学模型的求解,从而为提高学生对实际科学、管理、工程等实际问题的建模能力和计算机综合实验技能。
二、基本学时内容和课时分配第一章对变化进行建模2~4学时1 用差分方程对变化进行建模2 用差分方程近似描述变化3 动力系统的解法4 差分方程组5 matlab入门第二章建模过程、比例性和几何相似性2~4学时1 数学模型2 利用比例性建模3 利用几何相似性建模4 体重和身高、力量和灵活性5 matlab画图第三章模型拟合2~4学时1 用图形为数据拟合模型2 模型拟合的解析方法3 应用最小二乘准则4 如何选择一个好模型5 matlab拟合第四章实验建模2~4学时1 chesapeake海湾的收成和其他单项模型2 高阶多项式模型3 光滑化:低阶多项式模型4 三阶样条模型5 matlab差值第五章模拟方法建模2~4学时1 确定行为的模拟:曲线下的面积2 随机数的生成3 随机行为的模拟4 存储模型:汽油与消费需求5 排队模型6 matlab实现模拟第六章离散概率模型2~4学时1 离散系统的概率模型2 部件和系统可靠性建模3 线性回归4 matlab多元回归第七章离散模型优化2~4学时1 优化建模概述2 线性规划一:几何解法3 线性规划二:代数解法4 线性规划三:单纯型法5 线性规划四:敏感性分析6 数值搜索解法7 lingo软件介绍第八章图论建模2~4学时1 图的描述2 图模型3 利用图模型解问题4 与数学规划的联系第九章量纲分析和相似性2~4学时1 表示为乘积形式的量纲2 量纲分析的步骤3 解释量纲分析的几个例子4 相似性第十章函数图表构成模型2~4学时1 军备竞赛2 对分阶段军备竞赛建立模型3 税收对能源危机的影响第十一章用微分方程建模2~4学时1 人口增长2 对药剂量开处方3 再论刹车距离4 对自治微分方程的图形解5 数值近似方法6 分离变量法7 线性方程第十二章用微分方程组建模2~4学时1 一阶自治微分方程组的图形解2 竞争捕猎模型3 捕食者——食饵模型4 两个军事方面的例子5 微分方程组的欧拉方法第十三章连续模型优化2~4学时1 库存问题:送货费用和储存费用最小化2 制造问题:竞争性产品生产中的利润最大化3 约束连续优化4 可再生资源的管理:渔业三、基本要求第一章对变化进行建模1 掌握用简单的有限差分方程对变化进行建模的而思想2 了解简单差分方程(组)的解法及差分方程解的长期趋势3 掌握matlab的基本应用第二章建模过程、比例性和几何相似性1 了解各种不同性质的数学模型2 理解、掌握数学建模的基本过程3 了解比例性和几何相似性概念,并应用比例性和几何相似性建模4 学会用matlab做二维和三维图形第三章模型拟合1 了解曲线拟合的三个准则,了解不同准则之间的联系2 应用最小二乘准则拟合模型,会把切比雪夫准则转化成规划问题5 会用matlab做最小二乘拟合第四章实验建模1 会用幂次阶梯表建立简单的单项模型2 了解高阶多项式的优缺点,了解拉格朗日多项式3 会用matlab做低阶多项式拟合和三阶样条插值第五章模拟方法建模1 了解蒙特卡洛方法,了解随机数的生成方法2 学会用模拟方法建模3 matlab实现模拟第六章离散概率模型1 学会用马尔科夫过程建立简单随机模型2 了解线性回归,学会建立线性回归模型3会用matlab做多元线性回归第七章离散模型优化1 了解优化模型2 建立简单的规划模型,了解规划模型的解法,理解敏感性分析3 了解简单的数值搜索解法4 lingo软件求解规划问题和用matlab解决简单的数值搜索解法第八章图论建模1 了解图的概念2学会利用图论建立模型和解决问题3 了解图论与数学规划之间联系第九章量纲分析和相似性了解量纲分析的概念和步骤第十章函数图表构成模型学会建立、分析图表模型第十一章用微分方程建模了解通过微元法建立常微分方程的基本方法和建模过程,掌握常微分方程(组)的数值求解方法,及Matlab求解方法。
《数学建模》教学大纲

《数学模型》课程教学大纲一、《数学模型》课程说明(一)课程编号:07251105(二)英文名称:Mathmatic Modeling(三)开课对象:数学与应用数学专业(四)课程的性质:数学建模是为数学与应用数学专业开设的一门学科基础课,其先修课程有数学分析、高等代数、概率论与数理统计、数学实验等。
它是研究如何将数学方法和计算机知识结合起来用于解决实际生活中存在问题的一门边缘交叉学科,是集经典数学、现代数学和实际问题为一体的一门新型课程,是应用数学解决实际问题的重要手段和途径。
(五)教学目的:数学建模是继本科生学习数学分析、高等代数、概率论与数理统计之后进一步提高运用数学知识解决实际问题,培育和训练综合能力所开设的一门新学科。
通过具体实例引入使学生掌握数学建模基本思想、基本方法、基本类型。
学会进行科学研究的一般过程,并能进入一个实际操作的状态.通过数学模型有关的概念、特征的学习和数学模型应用实例的介绍,培养学生数学推导计算和简化分析能力、熟练运用计算机能力;培养学生联想、洞察能力、综合分析能力;培养学生应用数学解决实际问题的能力。
(六)教学要求和方法1.教学要求本课程主要介绍在数学应用中已经比较完善的数学模型,包括初等模型、简单优化模型、线性规划模型、离散模型、离散模型、微分方程模型、差分方程、概率统计模型等内容。
要求学生了解数学建摸的基本概念及基本方法,学会将学过的数学方法和知识同周围的现实世界联系起来,甚至和真正的实际问题联系起来。
不仅应使学生知道数学有用、怎么用,更要使学生体会到在真正的应用中还需要继续学习。
2.教学方法本课程将课堂讲授与上机实习结合起来,以课堂讲授为主。
课堂讲授旨在教学生如何建立模型,讲授中穿插各类数模实例,与现实中的各类实际问题相结合,启发学生自主思考和研究问题,找寻解决问题的数学模型和实际方法。
除此外,还会讲解数学建模论文的书写方法,以论文的形式完成建模和研究工作。
上机旨在教学生如何求解模型,以学生自主学习为主,结合课堂学习内容完成课堂布置的作业,利用数学软件求解模型结果。
广东工业大学应用数学学院《数学建模》教学大纲

《数学建模》公共选修课程教学大纲Mathematics Modeling课程代码: 课程归属:科学类开课校区:大学城开课学期:下学期容纳学生数:160 不适用专业:数学、文科类总学时数:24 总学分数:1.5编写年月:2006年6月修订年月:2007年7月执笔:陈学松一、课程的目的数学建模课是培养学生在实际问题中的数学应用意识、训练学生把科技、社会等领域中的实际问题按照既定的目标归结为数学形式,以便于用数学方法求解得出更深刻的规律和属性,提高学生数学建模素质的一门数学应用类课程。
通过本课程的学习,使学生较为系统的获得利用数学工具建立数学模型的基本知识、基本技能与常用技巧,培养学生的抽象概括问题的能力,用数学方法和思想进行综合应用与分析问题的能力,并着力导引实践—理论—实践的认识过程,培养学生辩证唯物主义的世界观。
二、课程教学内容及学时分配第一章建立数学模型(2学时)1.1从现实对象到数学模型1.2数学建模示例:如何预报人口的增长1.3数学建模的基本方法和步骤1.4数学建模方法的特点和分类1.5数学建模能力的培养第二章初等数学模型(2学时)2.2录像机计数器;2.4汽车刹车距离2.6核军备竞赛;2.10量纲分析与无量纲化第三章简单优化模型(4学时)3.3森林救火;3.4最优价格3.6消费者的选择;3.7冰山运输第五章微分方程模型(4学时)5.1传染病模型;5.2经济增长模型5.6人口预测;5.7烟雾的扩散与消失第六章稳定性模型(2学时)6.1捕鱼业的持续收获;6.2军备竞赛6.3种群的相互竞争;6.6稳定性理论第七章差分方程模型(2学时)7.1市场经济中的蛛网模型;7.2减肥计划7.3差分形式的阻滞增长模型;7.5差分方程简介第八章离散模型(2学时)8.1层次分析模型;8.2循环比赛的名次8.3社会经济系统的冲量过程;8.4效益的合理配第九章概率模型(2学时)9.1传送系统的效率;9.2报童的诀窍9.3随机存储策略;9.6航空公司的预定票策略第十章统计回归模型(2学时)10.1牙膏的销售量;10.2软件开发人员的薪金10.3 酶促反应;10.5教学评估三、课程教学的基本要求本课程是一门理论与实践联系的很密切的专业基础课程,操作性较强。
《数学建模》课程教学大纲

《数学建模》课程教学大纲
数学建模课程是一门有趣且令人兴奋的学科,它将数学
和实际世界联系起来,可以用建模的方法来理解、表示和解决实际问题。
近几年,数学建模已经成为一门热门课程,得到了教育界和业界的广泛重视。
下面,我将介绍数学建模课程的教学大纲。
首先,数学建模课程主要涵盖以下内容:数学分析方法、统计分析方法、运筹学 methods,以及用于数学模型实验分析等基本数学技术。
其次,数学建模课程还教授相关的实例分析,让学生掌握实际问题的建模思路,并学习使用相关的软件工具,应用范围广泛,可以应用于金融、保险、社会科学等多个领域。
此外,还介绍相关建模课题,让学生熟悉数学建模应用各方面的知识,掌握方法,解决实际问题。
数学建模课程强调实践、鼓励创新,通过实践和创新,
让学生懂得如何利用数学原理和模型解决实际问题,培养学生思辨能力和批判性思维能力,启发学生善于分析、动态调整解决问题的思路。
总之,数学建模课程以数学分析方法、统计分析方法、
运筹学methods以及实践与创新为基础,让学生从不同方面了解数学建模,学习建模方法,掌握解决实际问题的技术,为拓宽学生的视野,扩大学生的应用能力奠定基础。
《数学建模》课程教学大纲

《数学建模》课程教学大纲
课程编号:122117 学分:2 总学时:34
大纲执笔人:项家梁大纲审核人:陈雄达
一、课程性质与目的
本课程是面对非数学系学生的选修课程,是理科学生在学习高等数学、线性代数后深入学习数学,利用数学工具解决问题的一门重要基础性课程。
二、课程基本要求
通过本课程的学习,要求学生能够掌握利用所学的数学工具、计算机工具来解决实际问题,学会对数据的科学处理以及用数据分析来揭示数据的内在规律,建立相应的数学模型并应用于实际问题。
三、课程基本内容
内容主要包括:初等数学模型、最优化模型、线性规划模型、概率模型、离散模型、微分方程模型。
四、实验或上机内容
Lingo Lindo与MatLab实验
五、能力培养与人格养成目标
该课程重点培养学生分析问题和解决问题的能力。
数学建模课程是一门应用型课程,涉及的知识面广,因此需要学生在解决问题的过程中,不断开拓自己的知识,真正做到学以致用,把自己成为一个复合型人才。
六、前修课程要求
高等数学,线性代数。
七、评价与考核
通过对学生的作业、论文进行考核。
目标,通过对本课程的学习,能解决一些中等程度的数学建模问题。
平时成绩由平时作业,上课考勤和讨论情况组成
总评成绩=期末考试成绩×70%+平时成绩×30%
八、学时分配
九、教材与主要参考书
《数学建模基础》,薛毅编,北京工业大学大学出版社
《数学建模》,姜启源编高等教育出版社
《数学建模讲义》,梁进、陈雄达、张华隆、项家梁编著,上海科学技术出版社,2014年。
《数学建模》教学大纲

数学建模教学大纲课程名称:数学建模课时数56(课堂教学部分)面向对象:理工农医、社会科学各专业本科生预修课程要求:微积分、线性代数、(常微分方程、概率论)一、课程介绍(100-150字)数学模型是应用数学知识和方法解决实际问题的重要工具。
本课程通过具体案例初步介绍数学建模的一般原则和常用方法,充实微分方程、概率统计、运筹优化等应用数学分支知识。
培养学生的科学素质和科学精神,加强文献查阅、计算机应用、论文写作等能力训练和综合素质培养,引导及鼓励学生开展科学研究,解决实际问题。
二、教学目标培养学生应用数学方法和工具解决实际问题的能力。
通过讲授数学在不同领域应用的典型案例、经典模型和常用方法,使学生体会到数学对科学技术和社会发展的巨大意义,初步掌握建立数学模型,解决实际问题的方法和步骤,加深对数学的理解。
通过研究性学习和课程实践,使学生初步具备发现问题,解决问题的能力,掌握文献查阅,计算机应用,论文撰写等科学研究的主要技能,逐步养成勇于尝试,善于创新的科研精神和不畏困难,大力协同的科研品格。
三、教学安排模块一、数学建模概论(6学时)阐述数学模型的意义和作用,建立数学模型的步骤和方法,数学建模需要具备的能力和应用数学研究的主要特点,并通过典型案例加以诠释。
结合本模块学习,学生可自主开展文献查阅,科技数据库使用,数学软件应用等方面的实践。
模块二、基本数学模型(16学时)本模块主要讲授应用微积分、线性代数、微分方程、概率论和初等数学等分支知识建立的经典数学模型。
通过本模块的学习,使学生熟悉建立模型和求解模型的思路和方法,激发学生学习基础课程的兴趣。
结合本模块的学习,学生可通过文献查阅,了解经典模型的新发展与新应用,并就若干具体问题建立简单数学模型。
1.微积分模型(3学时)建议案例:利息理论、蛛网模型等2.线性代数模型(4学时)建议案例:关灯游戏、量纲分析法、Leslie人口模型等3.微分方程模型(5学时)建议案例:万有引力定律、人口模型、传染病模型、Lanchester方程、种间关系等4.概率论模型(4学时)建议案例:招聘问题,赌徒破产问题、存储模型等(三)、运筹与统计模型(26学时)概要介绍运筹和统计的主要内容,为学生进一步学习和应用奠定基础。
《数学建模》教学大纲

《数学建模》教学大纲课程编码:1511101303课程名称:数学建模学时/学分:54/3先修课程:《数学分析》、《高等代数》、《数学软件与实验》、《概率论与数理统计》、《常微分方程》适用专业:数学与应用数学开课教研室:应用数学教研室一、课程性质与任务1.课程性质:本课程是数学与应用数学专业的专业基础课。
2.课程任务:本课程是研究如何将数学方法和计算机知识结合起来用于解决实际问题的一门交叉学科,是集经典数学、现代数学和实际问题为一体的一门新型课程,是应用数学解决实际问题的重要手段和途径。
通过数学建模有关的概念、特征的学习和数学建模实例的介绍,使学生较为系统地掌握利用数学工具建立数学模型的基本步骤、基本技能与常见方法,培养学生双向翻译能力,数学推导计算和简化分析能力和用数学方法和思想分析、解决实际问题的初步能力。
二、课程教学基本要求《数学建模》是一门应用性较强的新兴课程,主要培养学生应用数学理论和数学思想方法,利用计算机技术等辅助手段,分析、解决实际问题的综合能力。
由于该课程的性质、特点、内容不同于其它课程,教学形式应该是讲授与个人作业相结合,教学方法则是以启发式教学为主,学生动手实践为辅的双向教学模式。
本课程开设在第5学期,共54学时,其中课堂讲授36学时,课内实践18学时。
成绩考核形式:末考成绩(开卷考试)(70%)+平时成绩(平时测验、作业、课堂提问、课堂讨论等)(30%)。
成绩评定采用百分制,60分为及格。
三、课程教学内容第一章 数学建模概论1.教学基本要求让学生了解数学建模相关基本概念,了解课程特点,为后继学习奠定基础。
2.要求学生掌握的基本概念、理论、技能通过本章教学使学生了解数学模型、数学建模的概念,了解数学模型的特点和分类,初步掌握数学建模的基本方法和步骤,培养学生把实际问题翻译成数学问题的能力。
3.教学重点和难点教学重点是数学建模的基本步骤。
教学难点是如何把实际问题翻译成数学问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学建模》公共选修课程教学大纲
Mathematics Modeling
课程代码: 课程归属:科学类
开课校区:大学城开课学期:下学期
容纳学生数:160 不适用专业:数学、文科类
总学时数:24 总学分数:1.5
编写年月:2006年6月修订年月:2007年7月
执笔:陈学松
一、课程的目的
数学建模课是培养学生在实际问题中的数学应用意识、训练学生把科技、社会等领域中的实际问题按照既定的目标归结为数学形式,以便于用数学方法求解得出更深刻的规律和属性,提高学生数学建模素质的一门数学应用类课程。
通过本课程的学习,使学生较为系统的获得利用数学工具建立数学模型的基本知识、基本技能与常用技巧,培养学生的抽象概括问题的能力,用数学方法和思想进行综合应用与分析问题的能力,并着力导引实践—理论—实践的认识过程,培养学生辩证唯物主义的世界观。
二、课程教学内容及学时分配
第一章建立数学模型(2学时)
1.1从现实对象到数学模型
1.2数学建模示例:如何预报人口的增长
1.3数学建模的基本方法和步骤
1.4数学建模方法的特点和分类
1.5数学建模能力的培养
第二章初等数学模型(2学时)
2.2录像机计数器;2.4汽车刹车距离
2.6核军备竞赛;2.10量纲分析与无量纲化
第三章简单优化模型(4学时)
3.3森林救火;3.4最优价格
3.6消费者的选择;3.7冰山运输
第五章微分方程模型(4学时)
5.1传染病模型;5.2经济增长模型
5.6人口预测;5.7烟雾的扩散与消失
第六章稳定性模型(2学时)
6.1捕鱼业的持续收获;6.2军备竞赛
6.3种群的相互竞争;6.6稳定性理论
第七章差分方程模型(2学时)
7.1市场经济中的蛛网模型;7.2减肥计划
7.3差分形式的阻滞增长模型;7.5差分方程简介
第八章离散模型(2学时)
8.1层次分析模型;8.2循环比赛的名次
8.3社会经济系统的冲量过程;8.4效益的合理配
第九章概率模型(2学时)
9.1传送系统的效率;9.2报童的诀窍
9.3随机存储策略;9.6航空公司的预定票策略
第十章统计回归模型(2学时)
10.1牙膏的销售量;10.2软件开发人员的薪金
10.3 酶促反应;10.5教学评估
三、课程教学的基本要求
本课程是一门理论与实践联系的很密切的专业基础课程,操作性较强。
在教学方法上,主要采用课堂讲授和课后自学等教学形式。
(一)课堂讲授
对实际问题的分析。
模型的合理假设。
数学工具的恰当应用。
模型的建立及求解。
模型结果的合理解释。
模型的应用。
对具体模型的选择,任课教师可灵活掌握,但务必体现基本教学要求和重点。
(二)课后自学
为了培养学生实际动手操作能力,教师给出一些有代表性的课后上机和实践任务,以增强学生运用数学知识和数学软件的能力。
(三)平时测验
为及时了解教学情况,教师可适当挑选有代表性的学生进行建模练习。
(四)考核方式
提交数学建模论文
四、本课程与其它课程的联系与分工
先修课程:高等数学
五、建议教材及教学参考书
[1]《数学模型》(第三版). 姜启源等编. 北京:高等教育出版社. 2004。
