半环的粗糙子半环及粗糙理想
《木材学》考研核心考点归纳

【计算题】1、干缩率、干缩系数、差异干缩有一块标准的马尾松湿材,已知弦向尺寸为20cm,径向尺寸为15cm,现欲将其干燥到含水率为6%,弦向和径向尺寸分别变为10cm 和12cm,试分别计算弦向、径向干缩系数和差异干缩。
弦向干缩率:[(20-10)/20] ×100%=50%径向干缩率:[(15-12)/15] ×100%=20%弦向干缩系数:50%/(30%-6%)=2.08径向干缩系数:20%/(30%-6%)=0.83差异干缩:50%/20%=2.52、各种密度、孔隙度P=(1-ρ /1.5)、含水率3某种木材的绝干密度为0.51g/cm 3, 其孔隙度为(d)a.30%b.40%c.50%d.60%e.70% 纤维饱和点时的含水率, 在200C时为30%,在1200C时为(b) a. 增加b. 减小c. 不变【树种识别】【画图题】【问答题】◇什么是木材的pH 值和缓冲容量?有些树种木材的心材呈碱性,在采用脲醛胶进行胶合板生产时胶合质量不佳,其原因何在?答:木材的PH 值一般泛指木材中水溶性物质的酸性和碱性程度,是定量反应木材水溶液中氢离子溶度大小的指标,通常以木粉的抽提物的pH 值表征。
它不仅是木材的重要物化性质之一,也是木材加工利用的一个重要指标。
在化学上,在一些由弱酸及其弱酸盐,或弱碱及其弱碱盐组成的混合溶液中,加入一定量的酸或碱液时,溶液的pH 值变化很小,即能在一定程度上对外来的酸和碱具有缓冲能力,这种溶液叫座缓冲溶液。
木材的水抽提液是具有缓冲能力缓冲溶液,即木材具有缓冲容量。
因为脲醛胶的固化原理是,在加入氯化铵或硫酸铵作为固化剂的弱酸条件下,尿素与甲醛反应。
若树种的心材呈弱碱性,则会影响脲醛胶的固化,从而使得生产的胶合质量不佳。
◇木材具有各向异性的原因是什么?试从木材的干缩、渗透及力学强度三个方面说明木材的各向异性。
答:木材是天然生长的生物材料,由于组织构造的因素决定了木材的各向异性(anisotropy)木材干缩方面的各向异性主要表现在纵向和横向,弦向和径向之间的差异。
【国家自然科学基金】_同态映射_基金支持热词逐年推荐_【万方软件创新助手】_20140803

推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 同态 同态映射 逆系统 逆极限 赋范格h蕴涵代数同态 赋范格h蕴涵代数 纯正断面 特殊线性群 正则半群 模糊赋范格h蕴涵代数 极限映射 有限群 有界性 数列 广义自同构群 广义同态 布尔矩阵环 对合quantale范畴 对合quantale 子代数 反同态 一般线性群 ei代数 banach代数 afs结构 *n-同态
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2014年 科研热词 零积 脉冲神经网络 粒度函数 时标 广义模糊子半环 广义模糊双理想 广义模糊内理想 平衡解 同态映射 同态原像 同态像 反模糊理 反模糊半群 双线性映射 保值模糊映射 θ -模糊映射 θ -模糊同态 jordan零积 (λ ,μ )-模糊正规子群 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
细胞生物学题库答案 - 湖北大学

《细胞生物学》题库参考答案第八章 蛋白质的分选一、名词解释1.信号肽--是引导新合成肽链转移到内质网上的一段多肽,位于新合成肽链的N端,一般16~30个氨基酸残基,包括疏水核心区、信号肽的C端和N端等三部分,称信号肽(signal peptide)或信号序列(signal sequence)。
2.共转运--肽链边合成边转移至内质网腔中的方式。
3.后转运--蛋白质在细胞基质中合成以后再转移到某些细胞器中的转移方式。
4.开始转移序列--引导肽链穿过内质网腔的信号肽,称为开始转移序列(start transfer sequence)。
5.停止转移序列--肽链上的一段特殊序列,与内质网膜的亲合力很高,能阻止肽链继续进入内质网腔,使其成为跨膜蛋白质,称为停止转移序列(stop transfer sequence)。
6.分子伴侣--通称为结合蛋白,在细胞中这类蛋白能识别正在合成的多肽或部分折叠的多肽,并与多肽的一定部位相结合,帮助这些多肽的转运、正确折叠或组装,但其本身并不参与最终的形成。
7.导肽--又称转运肽(transit peptide)或导向序列(targeting sequence),它是游离核糖体上合成的蛋白质的N-端信号。
8.NLS序列--亲核蛋白上带有的一段特殊的氨基酸序列,这些特殊短肽保证了亲核蛋白质能通过核孔复合体被转运到细胞核内,这段具有"定向"、"定位"作同的序列被称为核定位信号(nuclear localization signal,NLS)。
9.内体--酸性的不含溶酶体的小囊泡。
10.信号假说--即分泌性蛋白N端序列作为信号肽,指导分泌性蛋白导内质网膜上合成,在蛋白合成结束之前信号肽被切除。
11.蛋白质跨膜运输--主要是指在细胞质基质中合成的蛋白质转运到内质网、线粒体、质体和过氧化物酶体等细胞器,但进入内质网与进入线粒体、叶绿体和过氧化物酶体等细胞器的机制又有不同。
半环的次极大理想与次极小理想

每 个真理 想都 可 以分 解成 一些 次极 大理 想的 交 ,且 每 个真理 想都 可 以分解成有 限个次极 大理 想的交. 同时 ,又 引入 半环 的 次极 小理 想的概 念 ,并证 明半 环 中的每 个真理 想也 可 以表 示成
0 引 言
通 过理 想研究 半环是 研究 半环 的一个基 本方 法 ,因此 理想 论在 半环 的研究 中具有 重要 价值 .半环 中任 意多个 理想 的交仍 为半环 的理想 ,因此 可 以设 想 能否 找到 一些基 本理 想 ,使 得每个 理 想都 可 以表 示 成这 些基 本理想 之交 文献 [ ] 2 1 ,[ ]分 别引入 了环 的次 极 大理 想 和 B K一代数 的 次 极大 理想 的 C 概 念 ,并将 环和 B K一代数 中每个 理想 都 分解 成 一 些 次极 大 理 想 的交 .本 文 首 先 引入 半 环 的次极 大 C 理想 的概 念 ,并证 明在半 环 中也 有类 似于文 献 [ ] [ ] 的结 论 .对 偶 地 ,又 引入 半 环 的次极 小 理 1, 2
S b x ma d a n ub n ma d a fs mii g u ma i li e la d s mi i li e lo e rn
CH EN i— yn Gu i g, ZHANG Ze— z n eg
( colfMahmac c ne Sh o o te tsSi c,Ua ̄eg U i rt,Laceg 22 5 , C ia i e o n nv sy iohn 5 0 9 hn ) ei
维普资讯
第 2 第 2期 7卷
2 08年 4月 0
《中国教育简史》复习题及参考标准答案

《中国教育简史》复习题及参考标准答案《中国教育简史》复习题及参考答案————————————————————————————————作者:————————————————————————————————日期:2《中国教育简史》复习题及参考答案一一、填空题(每小题1分,共10分)1、西周诸侯所设大学,规模比较简单,仅有一学,因半环以水,故称“”。
2、汉武帝采纳董仲舒的建议推行的文教政策是。
3、荀子把教学或学习的过程具体化为四个环节,并把行看作是教学的最终目标。
4、《中庸》把教学过程概括为5.韩愈《》的基本精神就在于“存师卫道”,从恢复与捍卫儒家道统的高度,对教师问题进行系统论述。
6.夏代“为政尚武”,故在国都设“”以培养武士。
7.稷下学宫采取“”的办学方针,保证了稷下先生学术自由。
8.中国近代教育史上最先制定的而又实际推行的系统的学校制度,是光绪二十九年(1903年)张之洞等人拟定的《》。
9.1927年5月,国民政府正式实施“”的教育方针。
10.洋务运动最早创办的外国语学堂是____________。
二、单项选择题(每小题1分,共10分)1.秦始皇采纳法家的建议推行的文教政策是……………………()A无为而治 B儒道释三教合一C以法为教,以吏为师 D罢黜百家,独尊儒术2.孔子把教学过程概括为………………………………………()A学、思、行 B闻、见、知、行C学、问、思、辨、行 D见闻为与开心意3.唐代科举考试设题指事,由被试者做文章的方法是………………()A帖经 B墨义 C诗赋 D策问4.朱熹认为大学教育的重点是…………………………………………()A学习四书五经B“明其理” C应科举D“学其事”5.王安石在太学的教学管理上实行了…………………………………()A苏湖教法 B三舍法 C监生历事制度D“升斋积分法”和“贡生制”。
6.西周时期教育主要特征为……………………………………………()A.政教一体,学在官府B.官学衰落,私学兴起C.以法为教,以吏为师D.罢黜百家,独尊儒术7.王守仁教育思想的理论基础是他的………………………………()A. “存天理,去人欲”说B. “致良知”说C. “教为圣人”说D. “知行合一”说8.明末清初进步思想家在教育目的上主张…………………………()A.培养经世致用的实用人才B.修己以安人C.提倡实学,重视自然科学D.学而优则仕9.陶行知生活教育理论的方法论是………………………………………()A. “生活即教育”B. “做中教、做中学、做中求进步”C. “主动”、“习行”D. “教学做合一”10. 王充把教学过程概括为………………………………………………()A.学、思、行B.闻、见、知、行C.学、问、思、辨、行D.见闻为与开心意三、名词解释(每小题5分,共25分)1、有教无类“有教无类“是孔子关于教育对象的思想,(1分)意思是说,实施教育,不分贵贱、贫富、地域、种族。
粗糙半环的性质

定义 2 设 是 u的非空粗糙子集 是 上 的一个 同余关 系. . 2 称 于 同余 的粗糙商半环 。 证 明 : ) k ∈ / , x ∈ , ( V X R 有 , X 因为 是粗糙半 环 , 以 x ∈ 1 y 所 y X为粗糙半环, ,z 置如果 x满足( Vx ,∈ y 1 R X , y RX () + e ( ) x
R(A ) R( ) X ) R() ) X XB XA R(B A R , A 故 B是 的上粗 左理 想. 类似可证其余结论 定理 3 设是 粗 糙半环 上 的同余关 系, . 3 在商集 X R中定义 [ / 叫 上的同余关系, 若 6(b∈ 刚( ' 回 , ) . R是加 显然, ) , R 6 , 6 E 还有 , ) c + d R 6 = 】[ [ 【 h则 XR是一个粗糙半环, ] R 】 6 = , n ] 叶b / 称为粗 糙半环 关 法半群( ,) + 上的同余关系, 又是乘法半群( ,) ・上的同余关系。
的一些性质, 补充和完善 了粗糙集理论。 【 关键词 】 粗糙半环 ; 粗糙理想 ; 粗糙 同态; 粗糙 同构
( R + ) 2 )尺 ) + )显 ( 旦 + ) ,一 + - ) 曰 。 B 粗糙集 ( og e 理论是 波兰数学家 P wa 于 18 年在文 献[ Ruh t s) al k 92 1 】 2粗 糙 半 环 的 性质 . 中提 出来的. 它不但是一种新型 的处理模糊和不确定知识 的数学工具, 定理 31 . 设 是半环 上的完备同余 关系, AB为 的两个子 若 , 而且是一个不完备 信息的新颖, 有效 的软计算 方法 , 前得 到广泛的 目 半环, AB B 则 A 且 = A, B也是 的上( 粗 子半环 。 下) 应用 . 文献∞ 将粗糙 集理论 和半群理论结合 进行研究 。 展彼此 的应用 扩 证明 』. 4 曰为 的两个子半环= B为 的两个上粗子半环( . 文献 范围 . 出了一些新的有价值 的概念, 提 如粗糙半群, 粗糙群, . 文将 粗 等本 的定理 1 似) ) ) R , R似) R , ) ㈣ CR( R㈣ R 似) 似) _ C ) R _ , 糙集引入半环的研究, 讨论其性质。
【国家自然科学基金】_模糊同余关系_基金支持热词逐年推荐_【万方软件创新助手】_20140802
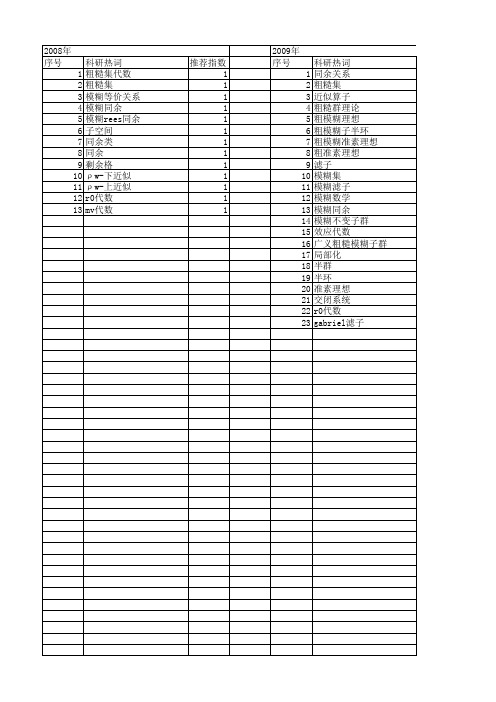
科研热词 同余关系 粗糙集 近似算子 粗糙群理论 粗模糊理想 粗模糊子半环 粗模糊准素理想 粗准素理想 滤子 模糊集 模糊滤子 模糊数学 模糊同余 模糊不变子群 效应代数 广义粗糙模糊子群 局部化 半群 半环 准素理想 交闭系统 r0代数 gabriel滤子
推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
科研热词 同态 蕴涵理想 模糊逻辑 商代数 同余 粗糙集 滤子 模糊闭包算子 模糊滤子 模糊完备格同余 模糊完备格 模糊同余关系 模糊偏序集 概率转移矩阵 概率有限状态自动机 同构 剩余格 伪准相等 交换 wbro-代数 wbr0-代数 swbro-代数 swbr0-代数 mtl-代数 leibniz代数
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
科研热词 模糊滤子 格 素理想 粗素理想 粗糙模糊子格 滤子 模糊子格 模糊同余关系 模糊关系同态 极大理想 效应代数 同余关系 同余 fi代数
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2010年 序号 1 2 3 4 5 6 7
科研热词 同余 模糊强φ -同余对 模糊强φ -同余 模糊强(p)-同余对 模糊强(p)-同余 φ -反演半群 (p)-反演半群
推荐指数 2 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
2011年 科研热词 模糊理想 模糊滤子 模糊子坡代数 模糊同余关系 蕴涵格 素滤子定理 等价刻画 直觉模糊有限自动机 直觉模糊变换半群 模糊逻辑 模糊等价关系 拓扑范畴 子完备格 同构 同态 同余关系 剩余格 t-模糊滤子 t-模糊同余 s-滤子 mp-滤子 mp*-滤子 推荐指数 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
第11章 环的定义及性质

i1j1
精选可编辑ppt
8
近世代数
实例
例2 在环中计算(a+b)3, (ab)2 . 解: (a+b)3 = (a+b)(a+b)(a+b)
= (a2+ba+ab+b2)(a+b) = a3+ba2+aba+b2a+a2b+bab+ab2+b3 (ab)2 = (ab)(ab) = a2baab+b2
对于任意的 [i], [j]∈Zp, [i] ≠ [0]有 [i] [j] = [0] p 整除 ij p| j [j] =[0]
所以 Zp 中无零因子.
注意:若 p不为素数,则Zp肯定不是域.
精选可编辑ppt
16
近世代数
域中除法及其性质
在域F中可以引入除法,如果a,b ∈F, a ≠ 0, 则b被a除记为b/a,且b/a=a-1b.
(3) 设nZ, n2, 则n阶实矩阵的集合Mn(R)关于矩阵 加法和乘法构成环,它是含幺环,但不是交换环和
无零因子环,也不是整环.
(4) (Z6,,)构成环,它是交换环, 含幺环, 但不是无 零因子环和整环. [2][3]=[3][2]=[0],[2]和[3]是零
因子.
精选可编辑ppt
14
近世代数
有以下性质:
精选可编辑ppt
17
近世代数
练习1
1. 在整数环中定义∗和◇两个运算, a,b∈Z 有 a∗b = a+b1, a◇b = a+bab.
证明(Z, ∗,◇)构成环.
证 a,b∈Z有a∗b, a◇b∈Z, 两个运算封闭. 任取a,b,c∈Z (a∗b)∗c = (a+b1)∗c = (a+b1)+c1 = a+b+c2 a∗(b∗c) = a∗(b+c1) = a+(b+c1)1 = a+b+c2 (a◇b)◇c = (a+bab)◇c = a+b+c (ab+ac+bc)+abc a◇(b◇c) = a◇(b+cbc) = a+b+c (ab+ac+bc)+abc
半环上的环同余刻画

21 第 1 ( 第 8 0 0年 期 总 6期 ) 2 1 0 0年 2月 出版
Ju m o aca g o ee or / r fN n hn l g Cl
N .Sms) Fb 00 o ( e. 1 1u 6 2
半环上的环同余刻画
俞文辉 付小勇 陆建秀
南 昌高 专 学报
及
21 0 O年
(+ ) ( x ( a bx a ) x = + = +
x [ + )( x+y b 1+E . + ( b c )(+ ) ]cT y ++ +
于 是 。 (+ + + )T我 们 有 2 b c xy h ,
由此 b x + e e .I +, aK r  ̄ 此 x P
定 理 29 P 映 射 (P( 一 , 中 c 是 群 (/ + 的 . . 0) 1 其 I P sP ) 零 元 。 一 个 从 半环 S上 的 se —ig同余 集 到 半环 S上 是 kw r n 的酉 的 半 正 规理 想 集 的 一一 保 序 映 射 .
定 的
, 证 明 是 SP 的单 位 元 . aS则存 在 xS满 下 /T 设 e, e (+ +旷ax +旷aa ( a x a ax l卜+ )l卜=+x + ++ )
满 足 a ) , 而存 在 hl ’ , 从 b ’T使得 h ab 1 由于 T是 稠 密 E + = +.
一
我 们 回顾 以下 定 义: 称半 环上 的一 个 同余 P为 一 个 C 同余 , SP是 一 个 C 一 环 . 环 S上 的 任 意 一 个 同余 若 / 半 半
P的核 定 义 为 :
[ + + +)h + += (++ +)blc 2 c xy+ ]a c2b cx y+ ++
半环的粗糙性质

・
) 子 集 , V y T 有 + ,y T 则 称 是 半 环 ( , , 的 子 半 环 , 为 .的 子 半 环 , ( e , T 的 若 ,e , Yxe , s+ ) 若 s 且 VsS t ) e 18 9 2年 波 兰 数 学 家 P wa al k在 文 献 [ ] 提 出 了 一 种 处 理 模 糊 和 不 确 定 知 识 的 数 学 工 具 — — 粗 糙 集 1中
设 ( ,・) 一 个 半 群 , . s 是 p是 .上 的 等 价 关 系 , 对 任 意 x S, 口, ) 可 得 ( ,x , 口,b , 称 s 若 e ( 6 b) ( x ) 则
p是 .上 的 同余 关 系 . [ ] 示 口所 在 Байду номын сангаас p 同余 类 .如 果 V口 6. [ ] [ s 用 口 表 ,E , a s
作者简介 : 民(92 )男 , 朱天 16 一 , 陕西合阳人 , 渭南师范学院数学 系副教授 , 理学硕士.
1 引言及预备
半环( , . +,・ 是 指 非 空 集 连 同定 义 在 它 上 面 的 2个 二 元 运 算 “+” “ ・ 所 形 成 的 代 数 系 统 , 里 s ) 和 ” 这
的 同余 关 系 . 半 群 ( ,・) 对 . s 的任 意 两 个 非 空 子 集 A, 记 A = { 6I B, B 口
=[ b 则 称 p是 S上 完 备 a ],
,e , A 为 A, b B} 称 B B在 . 的 积 . s上
关于一些半环性质的研究

3.研究了半环上的佗×礼矩阵半环.给出了半环上矩阵的分解方法.证明了 有限分配格的分解定理,得到了有限分配格上的矩阵分解方法.作为应用,讨论 了有限分配格上矩阵的周期与指标的更一般的计算方法.
The goal of this dissertation is to study this field.It mainly achieved in the
following aspects: 1.The semirings for which additive reducts are semilattices and multiplicar
4.研究了部分(弱)归纳+.半环.通过对这两类半环性质进行研究,证明了部 分(弱)归纳+一半环是部分Conway半环,得N--I部分(弱)归纳+-半环上I}qKleene定 理.
关键词
半环,偏序关系,分解定理,Green关系,部分(弱)归纳4一半环
Abstract
Algebraic theory of semiring is still one of the most active fields of algebra.
有助于我们来研究半环,如5礅[6-11].本文第二章研究了乘法半群为左正规纯
正群的半环. 本文从第三章开始研究一类特殊的半环(S+,·),s上还装有两个零元运
算0,1,满足条件: (1)(S+,o)和(S·,1)均是含幺半群; (2)(Va∈S)a·0=0·a=0.
从第三章开始,我们的半环通常指如上的半环.为了方便,在不做特殊说明的情 况下,我们将(S+,·,0,1)也叫做半环.这类半环在许多学科分支中也很有用, 例如:量子物理学、最优化理论、形式语言理论、自动机理论、及其理论计算 机科学等,如文献【12—36].
粗糙半环的性质

粗糙半环的性质【摘要】主要讨论粗糙集理论在半环中的应用,给出粗糙半环的概念并讨论其性质,进而由粗集中的粗糙同态和粗糙同构, 讨论粗糙半环的一些性质, 补充和完善了粗糙集理论。
【关键词】粗糙半环;粗糙理想;粗糙同态;粗糙同构0.引言粗糙集(Rough set)理论是波兰数学家Pawlak于1982年在文献[1]中提出来的,它不但是一种新型的处理模糊和不确定知识的数学工具,而且是一个不完备信息的新颖,有效的软计算方法, 目前得到广泛的应用.文献[2]将粗糙集理论和半群理论结合进行研究,扩展彼此的应用范围,提出了一些新的有价值的概念,如粗糙半群,粗糙群,等.本文将粗糙集引入半环的研究,讨论其性质。
1.粗糙半环的定义设A是半环(X,+,·)的子集,若?坌x,y∈A有x+y∈A,xy∈A,则称A是半环(X,+,·)的子半环,若A为X的子半环,且?坌x∈X,a∈A,xa∈A,则A称为X的左理想;ax∈A则称A为X的右理想;xa,ax∈A则称A为X的双边理想。
对半群(X,·)的任意两个非空子集A,B,记AB=ab│a∈A,b∈B,称AB为A,B 在X上的积;同理,在加半群(X,+)上有类似的记号A+B=a+b│a∈A,b∈B,称A+B 为A,B在X上的和.这样,若A是半环X的子集,则A是X的子半环,当且仅当A+A?哿A,AA?哿A.若A是半环X的子半环,则是A半环X的左理想,当且仅当XA?哿A;A是半环X的右理想,当且仅当AX?哿A;A是半环X的双边理想,当且仅当XA,AX?哿A。
定义2.1设(X,+,·)是半环,R是X上的等价关系,若对任意x∈X,(a,b)∈R,得(a+x,b+x)∈R,(x+a,x+b)∈R,(ax,bx)∈R,(xa,xb)∈R则称R是半环X上的同余关系,显然,若(a,b),(c,b)∈R,则(a+c,b+d),(ac,bd)∈R.还有R是加法半群(X,+)上的同余关系,又是乘法半群(X,·)上的同余关系。
半环的实理想与半实理想

要结果 推广 到交换半环上 。如下两个结果被建立 : 1 一个半环是半 实的 ,
一
关键词 : 半环 ; 严格素理想 ; 半实半环 ; 实半环 ; 半实理想 ; 实理想 ; 素理想 实
中 图分 类号 : 13 0 5
比如 , 在一个 半环 中 , 一个 真理想 q称作 一个 素理
She r cri 理论 是实域 论 的基 石 , 内容可 见诸 于文献 e 其 [ 3 。交换 环是一 种 比域 更 为一般 的代 数结 构 , 1— ] 人们 自然尝试 把实 域论 的概 念 , 理论 和方 法 推广 到
畴 中。
数 理论 的发展可 追溯 到著名 的德 国代 数学 家 E A— .r
t i n在 12 9 6年对 Hle 第 1 i r bt 7问题 的解 答 。为解 决 Hlet 1 i r第 7问题 , . rn和 0. c ri 把 实 数 域 b E At i S he r e 特有 的 “ 0不 能表为有 限个非 零实数 的平 方和 ” 一 这
想 , 由关 系式 a 若 b∈q 其 中 口 b∈S 可推 出 口∈q , , , 或 b∈q 同样 , 。 半环 s的一个对 于 S 中乘法 封 闭的非
空子集 将称 作 S的一 个乘 法 封 闭 子集 。 于半 环 的 对
其他基 本知识 , 可参 见于 文献 [ ] 9。 在下 文 中 , Ⅳ始终表 示 非 负整 数 集合 , Ⅳ 且 表
交换 环范 畴 中 。然 而 , 到上 世 纪 8 直 0年 代之 初 , 如 何 定 义 交 换 环 的 “ 性 ”尚 未 取 得 人 们 的 共 识 。 实 18 9 1年 ,. . o i —T e n 曾针 对 交 换 环 的 J E C lo l t hl e e “ 实性 ” 出如下 两种选 择 : 是“一1 能表为 环 中 提 一 不 元 素 的平 方和 ” 另一是 “ 元 0不 能 表为 环 中非 零 ; 零 元 的平方 和” 。其后 , . L m 把 满 足第 一种 “ T Y. a 实 性” 的交换 环称 为 “ 实环 ” 而满 足 第二 种 “ 半 , 实性 ” 的交 换环被 称 为 “ 环 ” 由于 “ 想 ” 交 换 环 的 实 。 理 是
半环的正锥与序

个 亚正 锥 , 得 ( +, 使 1+ )n ,=0, 则存 在 5的 个 正锥 ( q , P,) 使得 P且 , q 。 证 明 由文 献 [ ]中定 理 1 , 6 知 存在 .的一个 s
一
( )P\ 于 5中加法 是封 闭 的。 4 q对
一
凸的严格 素理想 q 使 得 , q 记 s为 5关 于理想 , 。
容 易证 明 , 是半环 S的一个理 想 , R对 于半 且 环 5的加法 和乘 法组 成 一 个 ( 必 有 单 位元 )没 有 未
给 出 了有关 交换半环 的序 的如下 。 定义 设 P是交换 半环 S的一 个子 半 环 。 P 称
关。 在此 基础上 , 实代数 学 中有关 “ 正锥 ”和“ ”的 序 主要结果 将在交换 半环 范畴 中得 到推广 。 本 文所 研究 的半 环 均指 含单 位 元 的交换 半环 ,
行 的。正锥 是域 ( 交 换 环 ) 或 的具有 特 定 性 质 的子 集, 这样 的子 集 和域 ( 或交 换 环 ) 的序 可 相 互转 化 ,
以致 “ 正锥 ” “ ” 称 谓 方 面往 往 被 混 为一 谈 。 和 序 在 因此 , 关域 ( 有 交换 环 ) 的正锥 和序 的研 究 结果 是实
作 为实代数理 论 中一 个 基本 事 实 , 和 交换 环 域 中元 素之 间是否存在某 种序关 系完全取 决于这些 代 数结 构是否 具 有 “ 性 ” 实 。因此 , 在实 代 数 理 论 中 ,
大 )亚序 , 它 满 足上 面定 义 中所 有 条 件 。 且 由此 可 知, 当半 环 不是环 时 , 文献 [ ]中上 述结果 显然成 5
n ∈Si , n由于∑ Ⅱ +7 P+ P 从 , =1…,。 『 '∈ P = 1 ,
半群中粗理想的性质

( f g fAp S dM ah mais UES o ia Ch n d 610 4 Co e eo p e te tc, l T f Chn eg u 05)
Abs r c Th s a tc e i s d o h o on nd t e pr p ri s o o gh s bs mi r u ta t i ri l s ba e n t e n t s a o e te f a r u u e g o p, i h r ug lf i e l o h igh i a ,o gh wo sd d d a a d o gh ii e i a e g o p.t o h e t d a , ug r t de lr u t -i e i e n r u b -d a n s mi r u I r l l c omb n s t e pp r n d l we p r xi ton i a e s tsy h e i e h u e a o r a p o mai s n s t a f t m o o o y,d s u sn s me i n tn ic s i g o pr pe te f t e p o c e e t ub e s i e g ou s a c r i o t e p op ri s o ome o ri s o r du toft s wo s s t n s mi r p c o d ng t r e e f s h h h t e pe i i l ub e ss h a u s mi r up a d i e l h e e rgo o oo s i e Th s t e s ca sng e s s t uc s b e g o d a ,t n t l s n h i r uspr fWa g v n u h
h-半环的模糊粗糙性研究的开题报告

h-半环的模糊粗糙性研究的开题报告
题目:半环的模糊粗糙性研究
一、选题的背景和意义
模糊粗糙性理论是模糊数学中重要的理论分支之一,有着广泛的应用背景。
在物联网、大数据等领域中,数据的模糊、不确定性和复杂性常常引起人们的关注。
而半环作为一个数学结构,在运用中也常常带有一定的模糊性和不确定性。
因此,对半环的模糊粗糙性研究将有助于更深入地认识半环的结构与性质,为实际应用提供更加全面和精确的数学工具。
二、研究内容和思路
1.半环、模糊半环的定义和性质;
2.半环的模糊粗糙性概念及其度量方法;
3.半环的模糊等价关系及其性质;
4.半环的模糊粗糙子集及其性质;
5.半环的模糊粗糙函数及其性质;
6.半环的模糊粗糙正则化问题。
三、研究方案和方法
本文将采用文献研究的方法,通过查阅相关文献、资料和论文,深入探讨半环的模糊粗糙性理论,构建其度量体系,研究半环的模糊等价关系、模糊粗糙子集和模糊粗糙函数等基本概念以及具体应用问题。
同时,通过具体例子展示半环的模糊粗糙性理论在实际问题中的应用价值,为实际应用提供数学支撑。
四、预期成果和意义
本文将构建半环的模糊粗糙度量体系,研究其模糊等价关系、模糊粗糙子集和模糊粗糙函数等基本概念及其应用问题,丰富和完善半环理论的研究内容和方法,为实际应用提供精确和实用的数学工具和方法。
同时,本文的研究成果也将为相关学科领域的理论研究和实际应用提供新的思路和参考。
半环的虚理想

半环的虚理想欧启通;陈玉成【摘要】利用泛代数的观点,借助环论的思想方法,提出了半环虚理想的概念,讨论了半环的虚理想经同态映射后仍然是虚理想,得到了半环的虚理想与伪理想的关系.【期刊名称】《厦门理工学院学报》【年(卷),期】2013(021)001【总页数】4页(P11-14)【关键词】半环;子半环;理想;虚理想【作者】欧启通;陈玉成【作者单位】厦门理工学院应用数学学院,福建厦门361024【正文语种】中文【中图分类】O153.3半环是一个代数(V,+,·),这里(V,+)是一个交换半群,(V,·)是一个半群,且满足下列的分配律:半环是最常见的代数结构.它不仅在拓扑学、分析学与最优化理论中有重要作用,而且在计算机科学中也有极其重要的应用.笔者在泛代数观点指导下,借助环论的思想方法,根据马合成先生提出的环的虚理想[1-2],引入了半环的虚理想概念,讨论了半环的虚理想经同态映射后仍然是虚理想等性质,得到了半环的虚理想与伪理想的关系.因为半环V的每一个元不一定都有负元,半环的性质要比环的性质更具一般性和复杂性,因此将环论的一些结果推广到半环进行研究有一定的理论意义.1 基本概念定义1[3]设R是半环V的一个非空子集.如果对于r1,r1+r2∈R,必有r2∈R,则称子集R是可减的.定义2[4]设V是一个半环.若其加法半群是幺半群,则称其是含零元半环.若其乘法半群是幺半群,则称其为幺半环.若其乘法半群是可换的,则称其是可换半环.若(V\{0},·)构成一个群,则称其为可除半环.本文所述的半环均指含零元的半环.子半环、理想、同态等的定义参看文献[4].定义3[5]设R是半环V的一个子半环.若对任意a∈V,r∈R,有a2r,ra2∈R,则称R是半环V的一个伪理想.定义4 设R是半环V的非零子半环.如果对任意r∈R,a∈V,有ra∈R蕴含a∈R及ar∈R蕴含a∈R,则称R是半环V的虚理想.显然,半环V是其本身的虚理想,不妨称为平凡虚理想.例1 设V是非负实数集,R是非负有理数集,S是非负整数集.V关于普通数的加法和乘法构成一个半环.显然,对任意非零元r∈R,则对于任意a∈V,只要有ra∈R就有a∈R及只要有ar∈R就有a∈R,因此R是半环V的一个虚理想.同理,S也是半环R或V的一个虚理想.但易知R不是半环V的理想.例2 设S是非负整数集,T是非负偶数集.关于普通数的加法和乘法T显然作成半环S的理想,但T不是半环S的虚理想.如2∈T,2×5∈T,但5T.2 主要结论从例1、例2可以看出,半环的虚理想不一定是半环的理想,而半环的理想也不一定是半环的虚理想.半环的理想对乘法具有吸收的性质,也就是说,半环V的理想R中的任意一个元素r与不属于R的元素a的乘积ar或ra都属于R.但半环的虚理想却完全相反,若半环V的虚理想S中的任意一个元素s与不属于S的元素b的乘积bs或sb一定都不属于S.因此半环的非平凡虚理想必定不是半环的理想.反之,半环的真理想也必定不是半环的虚理想.于是,半环的真理想与半环的非平凡虚理想是互不相容的.则有以下命题:命题1 半环V的真理想与半环V的非平凡虚理想是互不相容的.证明 (反证法)假设R是半环V的一个虚理想同时也是V的一个理想,且R≠V.由R是V的理想,则对于任意r∈R(r≠0),存在一个a∈V\R(由于R≠V,所以这样的a是存在的),有ar∈R.又由R是半环V的一个虚理想,得a∈R,这与a不属于R相矛盾.故R不可能既是半环V的理想又是V的虚理想.虽然半环的虚理想与半环的理想互不相容,但半环的虚理想在同态映射下也是保持的.命题2 设f是半环V到V'的满同态.若R是半环V的一个可减的虚理想,则f(R)是V'的一个可减的虚理想.证明易证f(R)是V'的子半环.由f是满同态,对任意a'∈V',r'∈f(R),存在a∈V,r∈R,使得a'=f(a),r'=f(r).于是有若有r'a'∈f(R),则有ra∈R.由R是半环V的一个虚理想,因此有a∈R,于是有a'=f(a)∈f(R).同理,若a'r'∈f(R),有a'∈f(R).所以f(R)是V'的一个虚理想.对任意r1',r2'∈V',存在r1,r2∈V,使得r1'=f(r1),r2'=f(r2).由r1'+r2'=f(r1)+f(r2)=f(r1+r2),若r1',r1'+r2'∈f(R),知r1,r1+r2∈R.由R 是可减的,得r2∈R,于是r2'∈f(R).故f(R)是V'的可减的虚理想.命题3 设f是半环V到V'的满同态.若R'是半环V'的一个可减的虚理想,则R'在f下的完全原像集f-1(R')是V的一个可减的虚理想.证明易证f-1(R')是V的子半环.又因为对任意r∈f-1(R')(r≠0),a∈V,有r'=f(r)∈R',a'=f(a)∈V',所以a'r'=f(a)f(r)=f(ar).若ar∈f-1(R'),则a'r'∈R'.由R'是半环V'的虚理想,知a'∈R',于是a∈f-1(R').若ra∈f-1(R'),同理可证a∈f-1(R').故f-1(R')是V的一个虚理想.对于任意r1,r2∈V,存在r1',r2'∈V',使得r1'=f(r1),r2'=f(r2).由r1'+r2'=f(r1)+f(r2)=f(r1+r2),若r1,r1+r2∈f-1(R'),知r1',r1'+r2'∈R'.由R'是可减的,得r2'∈R',于是r2∈f-1(R').故f-1(R')是半环V的可减的虚理想.命题4 设Rα(α∈Λ)是半环V的一族虚理想.若也是半环V的虚理想.证明假设Rα(α∈Λ)为半环V的一族虚理想,则显然为半环V的子半环.若{0},则对于任意非零元,若ra,有ra∈Rα(ar∈Rα),r∈Rα,因Rα为半环的虚理想,所以a∈Rα,从而Rα为 V 的虚理想.假设Ri(i=1,2,…,n)都是半环V的非空子集.定义并在R1×R2×… ×Rn上规定加法与乘法运算如下:其中,ri,ti∈ Ri,i=1,2,…,n.显然,若 Ri是半环,则R1× R2× … × Rn也是半环.命题5 设Ri(i=1,2,…,n)都是半环V的虚理想,则R1×R2×… ×Rn是半环V×V×… ×V的虚理想.证明因为Ri(i=1,2,…,n)都是半环V的虚理想,所以Ri(i=1,2,…,n)都是V的非零子半环.且对于任意ri∈Ri,ai∈V,若riai∈Ri(或airi∈Ri),就有ai∈Ri,i=1,2,…,n.所以对于任意及有ri∈Ri,ai∈V,且riai∈Ri(或airi∈Ri),于是有ai∈Ri,i=1,2,…,n.因此故R1×R2×… ×Rn是半环V×V×… ×V的虚理想.命题6 半环V的虚理想R1的虚理想R2也是V的虚理想.证明因为R2是R1的虚理想,所以R2是R1的非零子半环,显然也是V的非零子半环.对任意非零元r∈R2,任意a∈V,若ra∈R2,由R2R1,有ra∈R1.由R1是半环V的虚理想,得a∈R1,又由R2是R1的虚理想,得a∈R2.同理,若ar∈R2,也可证得a∈R2.于是R2也是V的虚理想.命题7 设V是一个满足乘法消去律的半环,R={r∈V|ar=ra,对任意a∈V}是半环V的中心.若R≠{0},则R是V的一个虚理想.证明显然半环V的中心R是V的一个非零子半环.对任意的a∈V及任意非零元r∈R,若ar∈R,则对任意b∈V,有b(ar)=(ar)b.由于r∈R,可得于是由V是一个满足乘法消去律,得ba=ab,所以a∈R.若ar∈R,同理可证得a∈R,于是R是V的一个虚理想.命题8 设半环V的子半环R是一个可除半环,则R是V的虚理想.证明对于任意的a∈V及任意非零元r∈R,因R是一个可除半环,则r-1∈R.若ar∈R,令b=ar,则a=br-1∈R.若ra∈R,同理可证得a∈R,于是R是V的虚理想.命题9 设V是一个可除半环,则V的虚理想R也是一个可除半环.证明因V是一个可除半环,所以V含有单位元1.又因为R是V的虚理想,所以对任意r∈R,有r=r·1∈R,于是1∈R.对任意r∈R,有r·r-1=1∈R,从而r-1∈R.于是(R\{0},·)构成一个群,因此R也是一个可除半环.命题10 设V是一个可除半环,R是V的一个非零伪理想,则R是V的虚理想.证明因R是V的一个非零伪理想,所以R是V的一个非零子半环.对任意非零元r∈R及a∈V,有ra2∈R.因为V是一个可除半环,故r-1∈V,于是可得r-1=r(r-1)2∈R.因此若有ra∈R且a≠0,由V是无零因子的,可知ra≠0,因此(ra)-1∈R.于是a=(ra)-1(ra2)∈R.若ra∈R且a=0,显然a∈R.对ar∈R,可类似证明a∈R.因此R是V的一个虚理想.命题11 设R是半环V的一个非空子集.若Mn(R)是矩阵半环Mn(V)的虚理想,则R是V的一个虚理想.证明若Mn(R)是矩阵半环Mn(V)的虚理想,可知Mn(R)是矩阵半环Mn(V)的非零子半环,从而R是V的一个非零子半环.对于任意r∈R,a∈V,若ra∈R,则且因为Mn(R)是Mn(V)的虚理想,因此有(aij)∈Mn(R),于是a∈R.对于任意r∈R,a∈V,若ar∈R,可类似证得a∈R,所以R是半环V的虚理想.[参考文献][1]马合成.环R的虚理想[J].许昌师专学报:自然科学版,1990,9(1):8-10.[2]马合成,海桦.关于环的虚理想的一些结果[J].天津教育学院学报,1996(3):4-5.[3]欧启通.半环上矩阵半环的几个性质[J].重庆大学学报:自然科学版,2007,30(11):108-110.[4]陈培慈.半环理论与语言和自动机[M].南昌:江西高校出版社,1993:1-5.[5]欧启通,苏良斌.半环的伪理想[J].成都大学学报:自然科学版,2008,27(4):297-299.。
数控车床高级工理论试题题库 5套含答案

1第八章数控车床高级工试题库第一节数控车床高级工理论(应知)试题库数控机床高级工理论(应知)试卷1单位:__________________姓名:______________准考证号:____________________一、填空:(每空1分,共20分)1.逐点比较法插补直线时,可以根据_______与刀具应走的总步数是否相等来判断直线是否加工完毕。
12.砂轮是由_______和______转接而成的多孔物体。
13.在同一台数控机床上,应用相同的加工程序、相同代码加工一批零件所获得的连续结果的一致程度,称为__________。
二、单项选择:(每题2分,共30分)1.8位计算机是指__________。
A.存储器的字由8个字节组成B.存储器有8KC.微处理器数据的宽度为8位D.数据存储器能存储的数字为8位2.工件材料相同,车削时温升基本相等,其热变形伸长量取决于______。
A.工件长度B.材料热膨胀系数C.刀具磨损程度3.直流伺服电机的PWM调速法具有调速范围宽的优点,是因为______。
9.磁尺位置检测装置的输出信号是_________。
A.滑尺绕组产生的感应电压B.磁头输出绕组产生的感应电压C.磁尺另一侧磁电转换元件的电压10.数控铣床在加工过程,NC系统所控制的总是______。
A.零件轮廓的轨迹B.刀具中心的轨迹C.工件运动的轨迹C系统一般可用几种方式得到工件加工程序,其中MDI是_______。
A.利用磁盘机读入程序B.从串行通信接口接收程序C.利用键盘以手动方式输入程序D.从网络通过Modem接收程序12.AutoCAD中要恢复最近一次被删除的实体,应选用_______命令。
A.OOPSB.UC.UNDOD.REDO7.AutoCAD绘图时,圆、圆弧、曲线在绘图过程中常会形成折线状,可以用重画REDRAW命令使其变得光滑。
8.使用千分尺时,用等温方法将千分尺和被测件保持同温,这样可以减少温度对测量结果的影响。
(整理)半环连接.

液压缸的结构•液压缸通常由后端盖、缸筒、活塞杆、活塞组件、前端盖等主要部分组成;为防止油液向液压缸外泄漏或由高压腔向低压腔泄漏,在缸筒与端盖、活塞与活塞杆、活塞与缸筒、活塞杆与前端盖之间均设置有密封装置,在前端盖外侧,还装有防尘装置;为防止活塞快速退回到行程终端时撞击缸盖,液压缸端部还设置缓冲装置;有时还需设置排气装置。
上图给出了双作用单活塞杆液压缸的结构图,该液压缸主要由缸底1、缸筒6、缸盖10、活塞4、活塞杆7和导向套8等组成;缸筒一端与缸底焊接,另一端与缸盖采用螺纹连接。
活塞与活塞杆采用卡键连接,为了保证液压缸的可靠密封,在相应位置设置了密封圈3、5、9、11和防尘圈12。
下面对液压缸的结构具体分析。
3.2.1 缸体组件•缸体组件与活塞组件形成的密封容腔承受油压作用,因此,缸体组件要有足够的强度,较高的表面精度可靠的密封性。
3.2.1.1 缸筒与端盖的连接形式常见的缸体组件连接形式如图3.10所示。
(1)法兰式连接(见图a),结构简单,加工方便,连接可靠,但是要求缸筒端部有足够的壁厚,用以安装螺栓或旋入螺钉,它是常用的一种连接形式。
(2)半环式连接(见图b),分为外半环连接和内半环连接两种连接形式,半环连接工艺性好,连接可靠,结构紧凑,但削弱了缸筒强度。
半环连接应用十分普遍,常用于无缝钢管缸筒与端盖的连接中。
(3)螺纹式连接(见图f、c),有外螺纹连接和内螺纹连接两种,其特点是体积小,重量轻,结构紧凑,但缸筒端部结构复杂,这种连接形式一般用于要求外形尺寸小、重量轻的场合。
•(4)拉杆式连接(见图d),结构简单,工艺性好,通用性强,但端盖的体积和重量较大,拉杆受力后会拉伸变长,影响效果。
只适用于长度不大的中、低压液压缸。
(5)焊接式连接(见图e),强度高,制造简单,但焊接时易引起缸筒变形。
•3.2.1.2 缸筒、端盖和导向套的基本要求•缸筒是液压缸的主体,其内孔一般采用镗削、绞孔、滚压或珩磨等精密加工工艺制造,要求表面粗糙度在 0.1~0.4μm,使活塞及其密封件、支承件能顺利滑动,从而保证密封效果,减少磨损;缸筒要承受很大的液压力,因此,应具有足够的强度和刚度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半 环 的 粗 糙 子 半 环 及 粗 糙 理 想
谢 莉 桃
( 曲靖 师范学院 摘 数 学与信 息科 学学院, 云 南 曲靖 6 5 5 0 1 1 )
要: 讨论 了半环 的粗 糙子半环的性质 , 进 一步引进 了半环 的伪理想 、 二型理 想、 双理想 的定义及
其粗糙性质 , 从 而补充和 丰富 了粗糙集理论. 关键 词 : 半环 ;粗糙子半环 ;粗糙理想 中图分类号 : 0 1 5 3 . 3 文献标识码 : A 文章编号 : 1 0 0 9—8 8 7 9 ( 2 0 1 5 ) 0 6— 0 0 1 9— 0 3
第3 4卷
第 6期
曲 靖 师 范 学 院 学 报
J O U R N A L O F Q U J I N G N O R MA L U N I V E R S I T Y
V 0 _ I . 3 4 No . 6
No v . 2 0l 5
2 0 1 5年 l 1月
粗糙 集理 论 在数 据 分 析 、 人工智能 、 知 识 发 现和模 式识 别 等领 域 中扮演 了非 常重 要 的角 色 . 粗糙 集概 念 由波 兰的 P a w l a k …首 次 提 出 , 解决 了
2 半 环 的粗 糙 子 半 环
定义 2 设 P是 半 环 S上 的 同余 关 系 ,
左( 右, 双侧) 理想.
1 预 备 知 识
定义 1 设 S是 半环 , 是 . s 的 子半环 , ( 1 )若 A S AC _A, 则称 A是 5的双理想 ; ( 2 )若 S A S CA, 则 称 A是 S的二 型理 想 ; ( 3 )若 A S AS AC _A, 则称 A是 | s的伪理 想.
A ≠咖 , A_ C S , 若 ( A ) ( ( A ) ) 是 5的子半环 , 则 称 A是 S上( 下) 粗子半环 ; 若 ( A ) 、 P ( A ) 都是 I s 的子半环, 则称 A是 s的粗糙子半环. 若 ( A ) ( p ( A) ) 是. s 的左 ( 右, 双侧 ) 理想 , 则 称 A是 s 的上 ( 下) 粗左 ( 右, 双侧 ) 理想 ; 若 A同时是 . s的 上、 下粗 左 ( 右, 双侧 ) 理想 , 则 称 A是 5的 粗 糙
信息系统中的一些不确定性问题. 随着时代 的发 展, 粗糙集理论被应用到代数系统 中, 得到一系 列成果( 见[ 2一l 1 ] ) . 本文在文献 [ 4 ] 的基础上 进一步探讨粗 糙子半环 , 引进 了半环 的伪理想 、 二型理想 、 双理想的定义并给出了它们的粗糙性 质, 得 到一 些结 果 .
A+ A+B+B A+ B +B是 S的子 半环 jA
证 明过程 类似 引理 1 , 略.
+ 是 S的上 粗 子半 环 . 类 似 可 以证 明 A+ 是
收 稿 日期 : 2 0 1 5—1 0— 2 8
作者简介 : 谢 莉桃 , 曲靖 师范学院数 学与信 息科 学学院讲师 , 主要从 事半群和粗糙集理论研究
半环 ; 若 p完备 , 则A B是 s的下 粗子 半环 .
证明 A, B是 S的子 半环 + A A, A A
A, 日+ B B, B 日 A B+ A B=A( B+ B) A B;
A+ A+ 曰+ B A+曰 = : 》 A+ B是 S的双 理想 = A+
A。 + B。 B B A +B +A +B =A +A +B +
引理 2 设 P是半环 S 上 的完备 同余关系 ,
A, 8 S且 A, B≠( b 贝 0
( A )+P ( ) p( A+ )
B A+B, ( A+B) ( A+B)=A A+丑 A+A +B B
引理 1 设 p是半环 s上的 同余关系 , A , B
| s , 且 A, B≠ 则 ( A) + ( ) ( A+ ) .
证明 c ∈ ( A)+ ( 曰) j 3口∈ ( A) , b ∈
半 环 , 则 A是 . s的 上 粗 子半 环 ; 若 p是 完 备 同余 , 则 是 s的下粗 子半 环.
定义 3 设 P是半环 S上的 同余关系 , s ≠
咖, A_ CS , 若 ( A) ( ( A ) 是 S的 双 ( 二型 , 伪) 理 想, 则称 A是 S的 上 ( 下) 粗双 ( 二型 , 伪) 理想 ; 若 A同 时 是 s的上 、 下粗双 ( 二型 , 伪) 理想, 则
称 A是 S的粗糙 双 ( 二型 , 伪) 理 想.
( ) , s t c =口+6 = 了 ∈[ a ] p nA, Y∈[ 6 ] p n = + y E[ 口 ] p +[ b ] p [ 口+6 ] p , + Y∈A+曰j [ a +6 ] 。 n( A+B ) ≠( b = n+b ∈ ( A+B) = ( A) +
( ) ( A+ ) .
定理 2 设 p是交换半环 I s 上的同余关 系, A, B是 S的 子 半 环 , 且 B A A, A B B, 则 A+B
是 S的上粗 子半 环 ; 若 P完 备 , 则 + 是 的下 粗 子半 环. 证 明 A, B是 . s的子 半环 jA+ A A, A A
・
l 9・
第 6期
曲 靖 师 范 学 院 学 报
第3 4卷
. s的下 粗子 半环 .
=
AS A +BS A +AS B +BS B AA +曰A +A日 +B
定理 3 设 p是半环 J s 上 的同余关系 , A , 曰 是 S的子 半 环 , 且 B A: A B, 则A B是 S的上 粗子
