形状相同的图形ppt课件三
合集下载
人教版数学《图形的相似》

人教版数学《图形的相似》(PPT优秀 课件)
检测反馈
1.下列四个命题:①所有的直角三角形都相
似;②所有的等腰三角形都相似;③所有的
正方形都相似;④所有的菱形都相似.其中
正确的有 ( D ) A.2个 B.3个 C.4个 D.1个
解析:所有的正方形的形状相同,所以③正确;直 角三角形、等腰三角形、菱形的形状和内角有关, 角度不同,图形的形状就不同,所以所有的直角 三角形、所有的等腰三角形、所有的菱形不一定
人教版数学《图形的相似》(PPT优秀 课件)
人教版数学《图形的相似》(PPT优秀 课件)
认识相似图形
问题思考
【思考1】 以上展示的图片之间有什么特点?它 们的形状和大小有怎样的关系?
它们形状相同、大小不等.
形状相同的图形叫做相似图形.
【思考2】全等形一定是相似图形吗?相似图形一 定全等吗?它们之间有什么关系?
全等图形是相似图形的一种特殊情况.全等图形一 定相似,相似图形不一定全等.
【思考3】 你能举出现实生活中一些相似图形的 例子吗?
人教版数学《图形的相似》(PPT优秀 课件)
人教版数学《图形的相似》(PPT优秀 课件)
相似图形的特征
观察下列每组图形,是不是相似图形?
【思考】
【结论】相似图形
(1)两个相似的平面图形之间有什么关系? 的特征是:形状相同.
得到的.
人教版数学《图形的相似》(PPT优秀 课件)
人教版数学《图形的相似》(PPT优秀 课件)
如图所示的是一个女孩从平面镜和哈哈 镜里看到的自己的形象,这些镜中的形象相似吗?
【思考】 (1)在平面镜中的像与
物体的形状 相同 , 大小 相等 ,则从平面 镜里看到的自己的形象与 女孩 是 相似图形(
图形的相似图形的位似ppt

。
工程制图
02
在工程制图中,可以利用位似图形来表示物体的形状和大小,
提高制图精度和效率。
艺术创作
03
艺术家可以利用位似图形创造出具有特殊效果的绘画作品,增
强艺术表现力。
03
图形的相似与图形的位似之间的关系
两者之间的联系
图形相似和图形位似都是图形变换的形式,它们都涉及到图 形形状和大小的变化。
图形的相似和位似都涉及到图形的形状和大小,它们都是图 形变换的基本概念。
性质
位似图形的对应线段、对应点所连线段平行(或在同一
图形的位似的判定方法
定义法
根据位似图形的定义进行判定 。
特征法
利用位似图形的性质进行判定 。
合同法
通过合同变换将两个图形转化 为位似图形。
图形的位似的应用
摄影
01
利用位似原理进行摄影,可以得到具有相同形状和大小的图片
在几何证明中的应用
证明定理
在几何证明中,图形的相似可以帮助证明几何定理。例如,通过使用相似图 形的性质,可以证明勾股定理或毕达哥拉斯定理。
推导公式
在几何中,图形的相似可以帮助推导重要的公式。例如,通过使用相似图形 的性质,可以推导出圆的面积公式或球的体积公式。
05
图形的相似与图形的位似在生活中的应 用
图形的相似的应用
艺术领域
在艺术领域中,人们经常利用相似图形的性质进行创作和设计,如相似三角 形在绘画中的应用。
实际生活
在日常生活中,我们也经常遇到相似图形的应用,如相似图形在广告、宣传 海报等方面的应用。
02
图形的位似
定义与性质
定义
如果两个图形形状相同,大小成比例,那么这两个图形称为位似图形。
形状相同的图形ppt课件一

O2( ) A2( ) B2(
3, 2) C(3 , 4
) C2( C(3 , 2)
4, 0 D(4 , 0)
) D2( D(4 , 0) )
表3
( x, y )
O(0 , 0) A(1 , 2)
B(2 , 4)
( 2 x , 2 y ) O3( 0, 0 ) A3( 2, 4) B3( 4, 8 ) C3( 6, 4 ) D3( 8, 0 )
它们形状相同 , 大小不一定相同
请从下图中找出形状相同的图形.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)与(3),(2)与(13),(4)与(11), (5)与(10),(6)(7)(8)(9)分别是形状 相同的图形。
做一做:利用下面的方法可以近似地将一个图形放大. 1.将2根长短相同的橡皮筋系在一起,联结处形成一 个结点. 2.选取一个图形,在图形外取一个定点. 3.将系在一起的橡皮筋的一端固定在定点,把一枝 铅笔固定在橡皮筋的另一端. 4.拉动铅笔,使2个橡皮筋的结 点沿所选图形的边缘运动,当 结点在已知图形上运动一圈时, 铅笔就画出了一个新的图形. 这个新图形与已知图形形状 相同.
y 4 B
⑶在上述得到的图形中, 2 A C C A O 哪些图形与原图形的形 -2 -1O 1 2 3 4D5 6 7 8D x -2 状相同?
1
B1
1
1
1
-4
( x ,y ) ( 2x ,y )
y 8 6 4 2
B2 A B
2
A C
y 8 6
B
3, 2) C(3 , 4
) C2( C(3 , 2)
4, 0 D(4 , 0)
) D2( D(4 , 0) )
表3
( x, y )
O(0 , 0) A(1 , 2)
B(2 , 4)
( 2 x , 2 y ) O3( 0, 0 ) A3( 2, 4) B3( 4, 8 ) C3( 6, 4 ) D3( 8, 0 )
它们形状相同 , 大小不一定相同
请从下图中找出形状相同的图形.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)与(3),(2)与(13),(4)与(11), (5)与(10),(6)(7)(8)(9)分别是形状 相同的图形。
做一做:利用下面的方法可以近似地将一个图形放大. 1.将2根长短相同的橡皮筋系在一起,联结处形成一 个结点. 2.选取一个图形,在图形外取一个定点. 3.将系在一起的橡皮筋的一端固定在定点,把一枝 铅笔固定在橡皮筋的另一端. 4.拉动铅笔,使2个橡皮筋的结 点沿所选图形的边缘运动,当 结点在已知图形上运动一圈时, 铅笔就画出了一个新的图形. 这个新图形与已知图形形状 相同.
y 4 B
⑶在上述得到的图形中, 2 A C C A O 哪些图形与原图形的形 -2 -1O 1 2 3 4D5 6 7 8D x -2 状相同?
1
B1
1
1
1
-4
( x ,y ) ( 2x ,y )
y 8 6 4 2
B2 A B
2
A C
y 8 6
B
相似图形的概念ppt课件
观察下面的图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(B)
(1)所有的圆都是形状相同的图形; (2)所有的正方形都是形状相同的图形; (3)所有的等腰三角形都是形状相同的图形; (4)所有的矩形都是形状相同的图形;
A、1个 B、2个 C、3个 D、4个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
4、下列说法中正确的是 (D ) A、所有平行四边形都是相似图形 B、所有菱形都是相似图形 C、所有等腰梯形都是相似图形 D、所有全等三角形都是相似图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
想一想:我们刚才所见到的图形有什么相同 和不同的地方?
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(B)
(1)所有的圆都是形状相同的图形; (2)所有的正方形都是形状相同的图形; (3)所有的等腰三角形都是形状相同的图形; (4)所有的矩形都是形状相同的图形;
A、1个 B、2个 C、3个 D、4个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
4、下列说法中正确的是 (D ) A、所有平行四边形都是相似图形 B、所有菱形都是相似图形 C、所有等腰梯形都是相似图形 D、所有全等三角形都是相似图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
想一想:我们刚才所见到的图形有什么相同 和不同的地方?
《形状相同的图形》相似图形PPT 图文

我们一路怀揣着爱,脚踏着万物,一声 绝唱, 飘然落 尘!也 许,你 我曾是 几百年 前的一 株草, 一朵花 ,一粒 尘,经 过几世 轮回的 转换变 成了今 生的亲 人,朋 友,爱 人…… 也许, 我们只 是来兑 现前世 的一场 盟约。 也许, 在百年 之后, 你我又 都化为 世间的 生灵, 守候在 天地之 间,彼 此相望 ,相顾 无言。 然而, 你我却 心灵相 犀,甘 为绿叶 ,守护 着这世 间一朵 花开的 时光!
时光就是这么不经用,很快自己做了母 亲,我 才深深 的知道 ,这样 的爱, 不带任 何附加 条件, 不因万 物毁灭 而更改 。只想 守护血 浓于水 的旧时 光,即 便峥嵘 岁月将 容颜划 伤,相 信一切 都是最 好的安 排。那 时的时 光无限 温柔, 当清水 载着陈 旧的往 事,站 在时光 这头, 看时光 那头, 一切变 得分明 。执笔 书写, 旧时光 的春去 秋来, 欢喜也 好,忧 伤也好 ,时间 窖藏, 流光曼 卷里所 有的宠 爱,疼 惜,活 色生香 的脑海 存在。
这世间,有一种相逢叫做缘份。如若有 缘,你 我会迎 着月, 奔着光 ,在人 生的某 个岔路 口相见 ,然后 又悄悄 离别。 像一朵 洁白似 雪的梨 花,轻 轻被风 吹落, 好像从 未被时 光染上 任何颜 色,永 远素雅 洁净。
有些人,在你生命里,走着走着就散了 ,走着 走着就 远了, 转身是 刹那, 离别早 已是天 涯。有 些人, 如同在 你的世 界打马 而过, 走时如 春风拂 面,未 曾留下 一丝一 痕。有 些人, 走时却 如惊涛 骇浪, 让你痛 彻心扉 ,就像 长在你 心里的 一根刺 ,怎么 拨也拨 不出来 ,只留 下浅浅 淡淡的 伤痕, 也许, 是思念 ;也许 ,是怨 念;也许 ,只是 记得… …
“十年生死两茫茫,不思量,自难忘。 千里孤 坟,无 处话凄 凉。纵 使相逢 应不识 ,尘满 面,鬓 如霜“ 。如若 今生, 你我遇 到一个 愿意为 自己陪 伴一生 的人, 那么, 请握紧 现在手 中的幸 福,珍 惜彼此 ,别等 失去, 再话凄 凉……
《形状相同的图形》相似图形PPT课件4

( x, y ) O(0 , 0) A (1 , 2) B (2 , 4) C (3 , 2) D(4 , 0) (2 x,2 y ) O3( 0, 0) A3( 2, 4) B3( 4 , 8 ) C3( 6 , 4 ) D3( 8 , 0 )
O(0,0 )
A(2,2 ) B(4,4 ) C(6,2 ) D(8,0 )
y
B7
4 2 A7
A
B
C7
C
-6 -5 D7-4 -3 -2 -1 O -2
1
2
3
4 D 5
6 x
( x, y ) ( x, y )
下列图形在原图形的基础上作了哪些变化,变化 后的图形和原图形形状相同吗?
补充练习(一):
(1)、油桶和杯子都是圆柱体,因此 这两个物体形状相同( )
(2)、课桌都是由桌面和四条腿构成 ,所有课桌形状相同( ) (3)、中国象棋和国际象棋棋盘都是 矩形,所以它们形状相同( ) (4)、所有正方体的形状相同( )
练 习:
指出下列图形中,形状 相同的图形是 (1)所有的三角形 (2)所有的等腰三角形
练 习:
(3)所有的等边三角形 (4)所有的直角三角形 (5)所有的边长之比是 3:4:5的三角形
练 习:
(6)所有等腰直角三角形 (7)所有的正方形 (8)所有的菱形
练 习:
(9)所有的矩形 (10)所有的梯形 (11)所有的正六边形 (12)所有的五边形
找一找:下列图形哪些形状相 同?用线连起来。 D
E F
A
B C
辨一辨
图中有哪些图 形的形状相同?
答:(1)与(3), (2)与(13) (4)与(11) (5)与(10) (6)、(7) (8)、(9) (14)与(16)
北师大版初中九年级上册数学课件 《图形的位似》图形的相似课件3

是位似图形。 位似中心是点A, 位似比是1:2。
二. 位似图形的性质
⑴一般性质:具有相似多边形的性质
周长比等于位似比 面积比等于位似比的平方
⑵特殊性质:位似图形上任意一对对应顶点到位似中心的距离之比等于位似比.
OA' (1),(2)图中,位似中心为 0,则: OA
=
OB' OB
=
…
=
A'B' AB
AF (3)图中,位似中心为 A,则:AD
=AAPC
=AAEB
=EBPC
=FDPC
三、位似图形的画法
A
以0为位似中心把△ABC
B
在同侧缩小为原来的一半A’
步骤:
1.画出ABC 2.选取中心点 O
B’ C
C’
3.连结OA、OB、OC
4.在OA、OB、OC上分别选取A’、B’、C’, 使OA’/OA=1/2、OB’/OB=1/2、OC’/OC=1/2 5.连结A’B’C’,所连成的图形就是所求作图形
A
B
D
A'
B'
D' C
C' O
探究
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在 OA、OB、OC、OD的反向延长线上取A',B'、C'、D',使得
OOAA'呢 OO?BB如' 果OOCC点' OOO取DD'在 12四边形ABCD内部呢?
分别画出这时得到的图形.
C'
O
D'
B'
2. 位似图形的性质:
✓位似图形上的任意一对对应点到位似中 心的距离之比等于位似比。 ✓以坐标原点为位似中心的位似变换有以 下性质:若原图形上点的坐标为(x,y), 与原图形的位似比为k,则像上的对应点 的坐标为(kx,ky)或(―kx,―ky)。
二. 位似图形的性质
⑴一般性质:具有相似多边形的性质
周长比等于位似比 面积比等于位似比的平方
⑵特殊性质:位似图形上任意一对对应顶点到位似中心的距离之比等于位似比.
OA' (1),(2)图中,位似中心为 0,则: OA
=
OB' OB
=
…
=
A'B' AB
AF (3)图中,位似中心为 A,则:AD
=AAPC
=AAEB
=EBPC
=FDPC
三、位似图形的画法
A
以0为位似中心把△ABC
B
在同侧缩小为原来的一半A’
步骤:
1.画出ABC 2.选取中心点 O
B’ C
C’
3.连结OA、OB、OC
4.在OA、OB、OC上分别选取A’、B’、C’, 使OA’/OA=1/2、OB’/OB=1/2、OC’/OC=1/2 5.连结A’B’C’,所连成的图形就是所求作图形
A
B
D
A'
B'
D' C
C' O
探究
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在 OA、OB、OC、OD的反向延长线上取A',B'、C'、D',使得
OOAA'呢 OO?BB如' 果OOCC点' OOO取DD'在 12四边形ABCD内部呢?
分别画出这时得到的图形.
C'
O
D'
B'
2. 位似图形的性质:
✓位似图形上的任意一对对应点到位似中 心的距离之比等于位似比。 ✓以坐标原点为位似中心的位似变换有以 下性质:若原图形上点的坐标为(x,y), 与原图形的位似比为k,则像上的对应点 的坐标为(kx,ky)或(―kx,―ky)。
图形的相似ppt课件
对应角相等,对应边成比例。
(对应边的比相等)
相似比
相似多边形对应边的比。(k > 0)
若相似比k =1 ,相 似图形有什么关系?
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
B1 对应边有什么关系?
C1
A A1
对 应 角 有 什 么 D关 系?
D1
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
知识要点
相似多边形
两个多边形相似的条件 ✓ 对应角相等。 ✓ 对应边成比例。
相似六边形
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
相似多边形的对应高
探究
你能来归归类吗?
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
四阶魔方和三阶魔方形状相同吗?大小呢?
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
《形状相同的图形》参考课件1

全等图形 不一定相同的图形._____________是特殊的形状相同的图形。
2、小明的文具袋里有一塑料的等腰直角三角板,教室的讲台上有一木制的大等 腰直角三角板,那么这两个三角板(A )
A、形状相同 B、形状不同 C、边长不成比例 D、无法比较 3、下列图形中,形状不一定相同的有( ) A、放大(或缩小)的图形与原图形 B、不同比例尺的中国地图 C、放大镜下的五角星与原来的五角星 D、同一底片冲印出来的不同尺寸的照片 E、放电影时胶片上的图像和它映射到屏幕上的图像 F、哈哈镜中人的形象与本人 G、平面镜中人的形象与本人 4、下列图形中形状一定相同的有( )。 A.所有的的圆 B.所有的等边三角形 C.所有的正方形 D.所有的矩形 E.所有的菱形 F.所有的正六边形 G.所有的等腰三角形 H. 所有的等腰梯形 I. 所有的圆柱 J. 横坐标相同,纵坐标成3倍关系的两个几何图形。
表3
( x, y ) O(0 , 0) A(1 , 2) B(2 , 4) C(3 , 2) D(4 , 0) (2 x,2 y ) O3( 0, 0 ) A3( 2, 4) B3( 4, 8 ) C3( 6, 4 ) D3( 8, 0 )
y 4 A B
B1
C D
O1(0,0)
2
A1
2
C1
D1
5 6 7 8 x 4
A1(2,2)
O1
-2 -1 O -2 1 3
B1(4,4)
C1(6,2)
D1(8,0)
-4
( x, y ) ( 2x , y)
y
8
B2 O2(0,0) A2
6 4 B
A2(1,4)
C2
C 2 D 3 4 5 D2 6 7 8 x
2、小明的文具袋里有一塑料的等腰直角三角板,教室的讲台上有一木制的大等 腰直角三角板,那么这两个三角板(A )
A、形状相同 B、形状不同 C、边长不成比例 D、无法比较 3、下列图形中,形状不一定相同的有( ) A、放大(或缩小)的图形与原图形 B、不同比例尺的中国地图 C、放大镜下的五角星与原来的五角星 D、同一底片冲印出来的不同尺寸的照片 E、放电影时胶片上的图像和它映射到屏幕上的图像 F、哈哈镜中人的形象与本人 G、平面镜中人的形象与本人 4、下列图形中形状一定相同的有( )。 A.所有的的圆 B.所有的等边三角形 C.所有的正方形 D.所有的矩形 E.所有的菱形 F.所有的正六边形 G.所有的等腰三角形 H. 所有的等腰梯形 I. 所有的圆柱 J. 横坐标相同,纵坐标成3倍关系的两个几何图形。
表3
( x, y ) O(0 , 0) A(1 , 2) B(2 , 4) C(3 , 2) D(4 , 0) (2 x,2 y ) O3( 0, 0 ) A3( 2, 4) B3( 4, 8 ) C3( 6, 4 ) D3( 8, 0 )
y 4 A B
B1
C D
O1(0,0)
2
A1
2
C1
D1
5 6 7 8 x 4
A1(2,2)
O1
-2 -1 O -2 1 3
B1(4,4)
C1(6,2)
D1(8,0)
-4
( x, y ) ( 2x , y)
y
8
B2 O2(0,0) A2
6 4 B
A2(1,4)
C2
C 2 D 3 4 5 D2 6 7 8 x
形状相同的图形课件

5. 其他形状:除了三角形、四边形、多边形和圆形之外, 还有一些其他形状也可以被归为形状相同图形。
形状相同图形的意义
形状相同图形在几何学中具有重 要的意义和应用。
它们可以被广泛应用于几何学的 教学和研究中,帮助人们更好地 理解和掌握几何学的基本概念和
性质。
同时,形状相同图形也具有一些 实际应用价值,例如在计算机图 形学、建筑设计、机械设计等领
美观度。
地理课件
地理课件中经常需要绘制各种地 标性建筑或者地理图形,利用形 状相同的图形课件可以帮助更好
地展示地理信息。
生物课件
在介绍细胞结构或者生物器官时, 形状相同的图形课件能够直观地 展示不同细胞或器官之间的相似 性和差异性。
04
形状相同图形的判定方法
判定方法
定义法
根据形状相同图形的定义,通过 比较两个图形的形状、大小、方 向等特征来确定它们是否形状相同。
方法3
利用面积法证明
习题练习
习题1
两个矩形相似,其中一个矩形的长为3cm, 宽为2cm,求另一个矩形的长和宽。
习题2
两个正方形相似,其中一个正方形的边长为 4cm,求另一个正方形的边长。
习题3
两个三角形相似,其中一个三角形的底边长 为3cm,高为2cm,求另一个三角形的底边 长和高。
03
形状相同图形的作图技巧
形状相同图形的可视化技术
可视化技术可以让形状相同图形更加直观易懂,提高了其在各领域 的应用效果。
对未来的期待与建议
加强跨学科合作
01
加强数学与其他学科的合作,推动形状相同图形在各领域的应
用和发展。
鼓励创新研究
02
鼓励科研人员和教师对形状相同图形的算法和应用进行深入研
形状相同图形的意义
形状相同图形在几何学中具有重 要的意义和应用。
它们可以被广泛应用于几何学的 教学和研究中,帮助人们更好地 理解和掌握几何学的基本概念和
性质。
同时,形状相同图形也具有一些 实际应用价值,例如在计算机图 形学、建筑设计、机械设计等领
美观度。
地理课件
地理课件中经常需要绘制各种地 标性建筑或者地理图形,利用形 状相同的图形课件可以帮助更好
地展示地理信息。
生物课件
在介绍细胞结构或者生物器官时, 形状相同的图形课件能够直观地 展示不同细胞或器官之间的相似 性和差异性。
04
形状相同图形的判定方法
判定方法
定义法
根据形状相同图形的定义,通过 比较两个图形的形状、大小、方 向等特征来确定它们是否形状相同。
方法3
利用面积法证明
习题练习
习题1
两个矩形相似,其中一个矩形的长为3cm, 宽为2cm,求另一个矩形的长和宽。
习题2
两个正方形相似,其中一个正方形的边长为 4cm,求另一个正方形的边长。
习题3
两个三角形相似,其中一个三角形的底边长 为3cm,高为2cm,求另一个三角形的底边 长和高。
03
形状相同图形的作图技巧
形状相同图形的可视化技术
可视化技术可以让形状相同图形更加直观易懂,提高了其在各领域 的应用效果。
对未来的期待与建议
加强跨学科合作
01
加强数学与其他学科的合作,推动形状相同图形在各领域的应
用和发展。
鼓励创新研究
02
鼓励科研人员和教师对形状相同图形的算法和应用进行深入研
《相似三角形的性质》PPT课件

《相似三角形的性质》PPT 课件
目录
• 相似三角形基本概念 • 相似三角形性质探究 • 相似三角形在几何证明中应用 • 相似三角形在解决实际问题中应用 • 拓展:全等三角形与相似三角形联系
与区别
01
相似三角形基本概念
定义及判定方法
定义
两个三角形如果它们的对应角相等,那 么这两个三角形相似。
AAA相似
01
利用相似三角形对应角相等 的性质,可以证明两个角相
等。
02
通过构造相似三角形,将待 证相等的两个角作为对应角 ,从而证明角度相等关系。
03
相似三角形中,若已知两角 对应相等,则第三角也必然 相等,这一性质可用于证明
复杂角度相等关系。
证明图形形状和大小关系
利用相似三角形形状相同的性质 ,可以证明两个图形形状相同。
01
04
对应角相等;
全等三角形的性质
02
05
面积相等;
对应边相等;
03
06
周长相等。
全等与相似关系探讨
联系 全等三角形是相似三角形的特例,即
相似比为1:1的情况;
全等和相似都涉及到两个三角形的形 状和大小关系。
区别
全等要求两个三角形完全重合,而相 似只要求形状相同,大小可以不同;
全等三角形的对应边和对应角都相等 ,而相似三角形只要求对应角相等, 对应边成比例。
02
相似三角形性质探究
对应角相等性质
01Biblioteka 0203性质描述
相似三角形的对应角相等 。
证明方法
通过三角形的相似定义和 角的对应关系进行证明。
应用举例
在几何问题中,利用相似 三角形的对应角相等性质 ,可以解决角度相关的问 题。
目录
• 相似三角形基本概念 • 相似三角形性质探究 • 相似三角形在几何证明中应用 • 相似三角形在解决实际问题中应用 • 拓展:全等三角形与相似三角形联系
与区别
01
相似三角形基本概念
定义及判定方法
定义
两个三角形如果它们的对应角相等,那 么这两个三角形相似。
AAA相似
01
利用相似三角形对应角相等 的性质,可以证明两个角相
等。
02
通过构造相似三角形,将待 证相等的两个角作为对应角 ,从而证明角度相等关系。
03
相似三角形中,若已知两角 对应相等,则第三角也必然 相等,这一性质可用于证明
复杂角度相等关系。
证明图形形状和大小关系
利用相似三角形形状相同的性质 ,可以证明两个图形形状相同。
01
04
对应角相等;
全等三角形的性质
02
05
面积相等;
对应边相等;
03
06
周长相等。
全等与相似关系探讨
联系 全等三角形是相似三角形的特例,即
相似比为1:1的情况;
全等和相似都涉及到两个三角形的形 状和大小关系。
区别
全等要求两个三角形完全重合,而相 似只要求形状相同,大小可以不同;
全等三角形的对应边和对应角都相等 ,而相似三角形只要求对应角相等, 对应边成比例。
02
相似三角形性质探究
对应角相等性质
01Biblioteka 0203性质描述
相似三角形的对应角相等 。
证明方法
通过三角形的相似定义和 角的对应关系进行证明。
应用举例
在几何问题中,利用相似 三角形的对应角相等性质 ,可以解决角度相关的问 题。
北师大版九年级数学上册第四章图形的相似PPT课件

第四章 图形的相似
第1节 成比例线段 第1课时
教学目标
1.结合实例了解线段的比及成比例线段的概念. 2.掌握比例的基本性质及其简单的运用.
教学重难点
重点:成比例线段及比例的基本性质. 难点:比例的基本性质的灵活运用.
情景导入
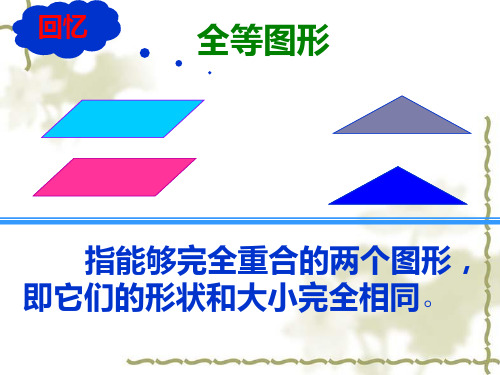
全等形
回忆
指能够完全重合的两个图形,即中,同学们还见过哪些 形状相同但大小不一定相等的图形?
(请讨论)
情景导入
黄山松
情景导入
情景导入
这几组图片有什么相同的地方?
1.如果选用 同一个 长度单位 量得 两条线段AB、CD
的 长度 分别是m、n,那么就说这两条线段的比AB∶
CD=m∶n,或写成
.其中,线段AB、CD分别叫
课堂小结
1.知道了可用相应线段长度的比来描述形状相同的 图形的大小关系. 2.成比例线段. 3.比例的基本性质.
布置作业
完成《课堂1+1》p36“课后练案”
谢谢!
第四章 图形的相似
第1节 成比例线段 第2课时
教学目标
1.掌握等比性质,并能灵活运用它解决有关问题. 2.了解合比、分比的性质.
(2)∵a=2cm,c=6cm,b=30m=3000cm,d=1000cm, ∴
则 ∴a、c、d、b是成比例线段.
6.直角三角形的斜边与斜边上的中线的比是 2 .
7.某图纸的比例尺是1∶20,图上零件长32mm,则实际长 为 64 cm.
8.已知线段a=3厘米,线段b=13毫米,则a与b的比是 (C)
解:2000m=200000cm, 这个地图的比例尺为:2∶200000=1∶100000.
点评:求线段的比时,要特别注意比的前项与后项的单位要 一致.
第1节 成比例线段 第1课时
教学目标
1.结合实例了解线段的比及成比例线段的概念. 2.掌握比例的基本性质及其简单的运用.
教学重难点
重点:成比例线段及比例的基本性质. 难点:比例的基本性质的灵活运用.
情景导入
全等形
回忆
指能够完全重合的两个图形,即中,同学们还见过哪些 形状相同但大小不一定相等的图形?
(请讨论)
情景导入
黄山松
情景导入
情景导入
这几组图片有什么相同的地方?
1.如果选用 同一个 长度单位 量得 两条线段AB、CD
的 长度 分别是m、n,那么就说这两条线段的比AB∶
CD=m∶n,或写成
.其中,线段AB、CD分别叫
课堂小结
1.知道了可用相应线段长度的比来描述形状相同的 图形的大小关系. 2.成比例线段. 3.比例的基本性质.
布置作业
完成《课堂1+1》p36“课后练案”
谢谢!
第四章 图形的相似
第1节 成比例线段 第2课时
教学目标
1.掌握等比性质,并能灵活运用它解决有关问题. 2.了解合比、分比的性质.
(2)∵a=2cm,c=6cm,b=30m=3000cm,d=1000cm, ∴
则 ∴a、c、d、b是成比例线段.
6.直角三角形的斜边与斜边上的中线的比是 2 .
7.某图纸的比例尺是1∶20,图上零件长32mm,则实际长 为 64 cm.
8.已知线段a=3厘米,线段b=13毫米,则a与b的比是 (C)
解:2000m=200000cm, 这个地图的比例尺为:2∶200000=1∶100000.
点评:求线段的比时,要特别注意比的前项与后项的单位要 一致.
九年级数学教学课件:23.2 相似图形(共23张PPT)

我们可以发现: ∠ ABC= ∠ A`B`C`, AB=___cm, BC=___cm; A′B′=___cm,B′C′=___cm. 显然两张地图中AB和 A′B′、BC和B′C′的长度都是 不相等的,那么它们之间 有什么关系呢?小地图是 由大地图缩小得来的,我 们能感到线段A′B′、B′C′与 AB、BC的长度相比都“同 样程度”地缩小了.
2、如图,矩形ABCD和矩形A1B1C1D1相似 D1 吗?为什么? C1
D C
1.5 1
A B
3
A1
2.5
B1
答案:不相似。 分析: 对应边长度的比不相等
思考
两个三角形一定是相似形 吗?两个等腰三角形呢?两 个等边三角形呢?
总结梳理
通过本节课的学习,同学们有了哪些收获?
相似多边形的性质: 对应边成比例,对应角相等。 相似多边形的定义(判定):
合作探究(二)
图23.2.2中两个四边形是相似形, 为了验证你的猜想是 否正确,可以用量角 仔细观察这两个图形,它们的对应 器量量看 边之间是否有以上的关系呢?对应 角之间又有什么关系?
概括:
由此可以得到两个相似多边形的性质:
相似多边形对应边成比例, 对应角相等.
( 你能用几何语言来表述这一性质吗?)
∴ 18:12=X:18; ∴ 12X=18 ×18; 即 X=27。 根据对应角相等,可得: α =360 °-(77 °+83 °+116 °) =84 °
巩固练习:
1、 如图,菱形ABCD和菱形A1B1C1D1相似 吗?为什么?
D D1
A
60
C
A1
45
C1 B1
B
答案:不相似。
分析: 对应角不相等
形状相同的图形

大小
形状相同的图形可以具有不同的 尺寸,但它们的比例和尺寸关系 是相同的。例如,两个正方形无 论它们的大小如何,都是相同的
图形。
方向
形状相同的图形可以具有不同的 方向,但它们的几何特性是相同 的。例如,两个平行四边形无论 它们的方向如何,都是相同的图
形。
03 形状相同图形的应用场景
建筑设计
建筑设计中的形状相同图形应用广泛,如圆形、方形、三角形等,可以用于规划 建筑物的整体布局和细节设计。
大小相同
两个图形的大小完全一样,即它 们是等比例缩放的。
分类:旋转、平移、镜像
旋转
镜像
一个图形绕着某一点旋转一定的角度 后与另一个图形重合。例如,正方形 绕着中心点旋转90度后与原来的正方 形重合。
一个图形关于某条直线对称后与另一 个图形重合。例如,一个等腰三角形 关于底边中垂线对称后与另一个等腰 三角形重合。
THANKS FOR WATCHING
感谢您的观看
随着科技的发展,形状相同图形可以与艺术更加紧密地结合,创 造出更具创意和表现力的作品。
数学理论的应用
数学是形状相同图形的基础,未来可以进一步探索数学理论在形状 相同图形中的应用,以推动其理论和实践的发展。
跨学科合作
可以与其他学科领域进行合作,如物理学、生物学等,以拓展形状 相同图形的应用领域和表现形式。
状相同图形。
结合计算机图形学
计算机图形学的发展为形状相同图 形的创造提供了更多可能性,可以 通过编程实现更复杂的形状相同图 形。
引入非线性变换
传统的形状相同图形主要基于线性 变换,未来可以尝试引入非线性变 换,以创造出更具有艺术性和视觉 冲击力的形状相同图形。
未来发展:结合科技、艺术和数学
人教版九年级数学下册相似三角形全章课件

∴△A′B′C′∽△ABC
B
E C
A A′
B
B′ C
C′
△ABC∽△A′B′C′
如果一个三角形的三条边和另一个三角形的三条边 对应成比例,那么这两个三角形相似. 简单地说:三边对应成比例,两三角形相似.
【例】在△ABC和△A′B′C′中,已知:AB=6cm,BC= 8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′ =30cm.试证明△ABC与△A′B′C′相似.
A C
B
D
P2 P3
P1 P4
E
P5 F
【解析】(1)△ABC和△DEF相似.根据勾股定理,
得
, ,BC=5;
,,
.
∵
,∴ △ABC∽△DEF.
(2) 答案不唯一,下面6个三角形中的任意2个均可.
A C
B
P3 E
D P1 P2
P4
P5 F
△P2P5D,△P4P5F,△P2P4D,
△P4P5D,△P2P4 P5,△P1FD.
4.(成都中考)如图,已知线段AB∥CD,AD与B
C相交于点K,E是线段AD上一动点。 (1)若BK= KC,
求 的值;
(2)连接BE,若BE平分∠ABC,则当AE= AD时,猜想线
段AB、BC、CD三者之间有怎样的等量关系?请写出你的
结论并予以证明.再探究:当AE= AD (n>2),而其余
MN∥AB交BC于N,量得MN=38cm,则AB的长为 152c . m
2.如图,在△ABC中,DG∥EH∥FI∥BC, (1)请找出图中所有的相似三角形;
△ADG∽△AEH∽△AFI∽△ABC
(2)如果AD=1,DB=3,那么DG:BC=_1_:_4__. A
图形的相似图形的位似ppt

艺术设计
在艺术设计中,位似变换也被广泛应用于图像处理和设计。例如,可 以通过位似变换来改变图像的大小和形状,以达到特定的艺术效果。
03
计算机图形学
在计算机图形学中,位似变换是实现图形缩放、旋转和平移等操作的
基础。同时,也涉及到图形的位似匹配问题,例如将两幅图像进行位
似变换后的匹配程度。
未来对图形位似的研究方向和挑战
常见的图形软件
如Adobe Photoshop、GIMP、Paintshop Pro和 CorelDraw等,都提供了位似变换的功能,用户可以通过这 些软件中的相关工具和菜单选项进行操作。
使用矩阵变换实现位似变换
矩阵变换的概念
矩阵变换是一种数学方法,可以用来描述图形的平移、缩放、旋转等变换。 在计算机图形学中,通过使用矩阵运算可以将一个图形从原始坐标系转换到 新的坐标系中。
对于两个位似图形,如果它们之间存在相似关系,那么它们一定也是位似图 形。
位似图形的性质
对应线段之比等于相似比
对于两个位似图形,任意一对对应线段之比等于它们的相似比。
对应角相等
对于两个位似图形,任意一对对应角相等。
对应点所连线段平行(或在同一直线上)
对于两个位似图形,将其中一个图形上的任意一点作为位似中心,另一个图形上对应点所连线段平行(或在同一直线上) 。
计算方法
可以使用矩阵乘法来计算位似变换,具体方法是将原图形上的点作为矩阵中的行向量,将 位似中心和位似比作为矩阵中的列向量,通过矩阵乘法得到变换后的点在原图形上的位置 。
06
图形位似的计算机实现
使用图形软件实现位似变换
位似变换的步骤
在图形编辑软件中,可以通过选择“变换”或“扭曲”菜单 中的“位似”选项来实现位似变换。然后,需要设置变换的 中心点、放大倍数和旋转角度等参数。
在艺术设计中,位似变换也被广泛应用于图像处理和设计。例如,可 以通过位似变换来改变图像的大小和形状,以达到特定的艺术效果。
03
计算机图形学
在计算机图形学中,位似变换是实现图形缩放、旋转和平移等操作的
基础。同时,也涉及到图形的位似匹配问题,例如将两幅图像进行位
似变换后的匹配程度。
未来对图形位似的研究方向和挑战
常见的图形软件
如Adobe Photoshop、GIMP、Paintshop Pro和 CorelDraw等,都提供了位似变换的功能,用户可以通过这 些软件中的相关工具和菜单选项进行操作。
使用矩阵变换实现位似变换
矩阵变换的概念
矩阵变换是一种数学方法,可以用来描述图形的平移、缩放、旋转等变换。 在计算机图形学中,通过使用矩阵运算可以将一个图形从原始坐标系转换到 新的坐标系中。
对于两个位似图形,如果它们之间存在相似关系,那么它们一定也是位似图 形。
位似图形的性质
对应线段之比等于相似比
对于两个位似图形,任意一对对应线段之比等于它们的相似比。
对应角相等
对于两个位似图形,任意一对对应角相等。
对应点所连线段平行(或在同一直线上)
对于两个位似图形,将其中一个图形上的任意一点作为位似中心,另一个图形上对应点所连线段平行(或在同一直线上) 。
计算方法
可以使用矩阵乘法来计算位似变换,具体方法是将原图形上的点作为矩阵中的行向量,将 位似中心和位似比作为矩阵中的列向量,通过矩阵乘法得到变换后的点在原图形上的位置 。
06
图形位似的计算机实现
使用图形软件实现位似变换
位似变换的步骤
在图形编辑软件中,可以通过选择“变换”或“扭曲”菜单 中的“位似”选项来实现位似变换。然后,需要设置变换的 中心点、放大倍数和旋转角度等参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y 8 6 4 A
O(0,0)
B
C
A(1,2) B(2,4) C(3,2)
D 4 5
2
-2 -1 O 1 -1 2 3 6 7 8 x
D(4,0)
在直角坐标系中描出点O1、A1、B1、C1、D1,并 按同样的方式连接各点,你得到了一个什么图形? 填写表2呢?填写表3呢? 表1
( x, y ) O(0 , 0) A(1 , 2) B(2 , 4) C(3 , 2) D(4 , 0) ( 2x , y ) O1( 0 ,0 ) A1(2 ,2 ) B1(4 ,4 ) C1(6 ,2 ) D1( 8 ,0 )
小游戏:移一移!
有一只用火柴摆成的头朝上的鱼,你能移 动图形中的三根火柴,使它头朝下吗?
小游戏:移一移!
有一只用火柴摆成的头朝上的鱼,你能移 动图形中的三根火柴,使它头朝下吗?
观察:游戏前后的两个小龙虾图形,形状改变了吗?
大小呢?
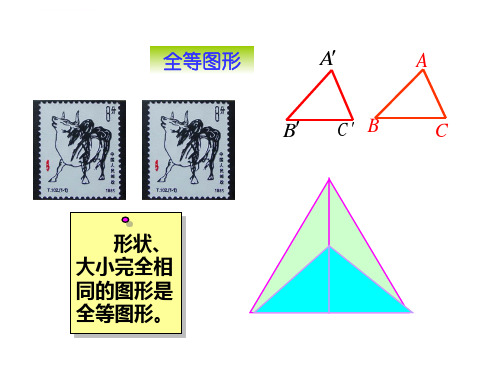
想 一 想 还记得什么是全等图形吗, 全等图形有何特征?
A
B
C
A
复印前后纸上对应图形 之间分别有什么关系?
综合以上各组图形我们体会到:
两个图形的形状完全相同 ________,但 图形的大小位置不一定相同 __________, 这样的两个图形叫做形状相同
的图形(相似图形)
随堂练习
请找出下图中, 形状相同的图形.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
请在下列图形中找出形状相同的图形
4
1
2 3 7
6
5
8 10 9
14
11
12
13
一起来探索一下吧!
随堂练习
在直角坐标系中描出点O(0,0)、 A(1,2)、B(2,4)、C(3,2)、 D(4,0)。先用线段顺次连接点O、 A、B、C、D,然后再用线段连接A、 C两点。 你得到了一个什么图形?
表2 ( x, y ) O(0 , 0) A (1 , 2) B (2 , 4) C (3 , 2) D(4 , 0) ( x,2 y ) O2( 0 , 0 ) A2(1 ,4 ) B2(2 ,8 ) C2( 3 ,4 ) D2( 4 , 0 ) 表3
( x, y ) O(0 , 0) A (1 , 2) B (2 , 4) C (3 , 2) D(4 , 0) (2 x,2 y ) O3(0 ,0 ) A3(2 ,4 ) B3(4 ,8 ) C3( 6 , 4 ) D3( 8 , 0 ) 得到的这些图形中哪两个是形状相同的图形?
横 向 为 原 来 的 2 倍
y
4
2 A
B
B1
C D
O1(0,0) C1 D1
5 6 7 8 x
O1
-2 -1 O -2 -4 1
A1
2
A1(2,2)
B1(4,4)
3
4
C1(6,2)
D1(8,0)
( x, y ) ( 2x , y)
纵 向 为 原 来 的 2 倍
y 8 6 4
B2
O2(0,0)
2
O3
-2 -1 O 1 -1 2 3
D 4 5
D3
6 7 8 x
( x, y ) (2x , 2y )
议一议 你能利用刚才所学到的方法, 将“A”字形缩小吗?
一个图形各点的坐标经过怎样的变化, 可以使所得到的图形与原图形的形状相 同? 答:一个图形各点的横坐标、纵坐标都乘以 或除以同一个不为零的数,可以使所得的新 图形与原图形的形状相同。
议一议:
学习了《形状相同的图形》之后,小 明和小张就一直在争论:小明说: “任意两个矩形都是形状相同的图 形。 ”而小张说:“不对,任意两 个圆形才是形状相同的图形。”
同学们请你来判断一下,他俩谁的说 法正确?
所有的矩形真的都是形状相同的图形吗?
A
D E F H G
B
C
1)所有的等边三角形都是形状相同的 图形 (真 ) 2)所有的等腰三角形都是形状相同的 (假 ) 图形 3)所有的等腰直角三角形都是形状相 (真 ) 同的图形 4)所有的圆柱体都是形状相同的图形
你还有其他的方法吗?
做一做:
1、将两根长短相同的橡皮筋系在一起,联结处形成 一个结点. 2、选取一个图形,在图形外取一个定点.
3、将系在一起的橡皮筋的一端固定在定点 ,把一枝 铅笔固定在橡皮筋的另一端.
4、拉动铅笔,使2个橡皮筋的结点沿所选图形的边 缘运动,当结点在已知图形上运动一圈时,铅笔就 画出了一个新的图形.
(假 )
5)所有的菱形都是形状相同的图形 (假)
所有的圆柱真的都是形状相同的吗?
所有的菱形真的都是形状相同的图形吗?
所有的等腰三角形真的都是形状相同的图 形吗?
1、什么是形状相同的图形?两个形状 相同的图形与这两个图形本身的大小 与位置有关吗? 2、形状相同的图形与全等的区别与 联系. 3、利用坐标系怎样使一个图形与 已知图形形状相同?
B
C
请观察以下图形
篮球巨星姚明同一张底片冲洗出来的2 寸照片和4寸照片中,人物的形状改变 了吗?大小呢?
符合国家标准的两面中国国 旗的形状相同吗?大小呢?
蕨类植物的整张叶片和它上面的 小叶片形状相同吗?大小呢?
四阶魔方和三阶魔方形状 相同吗?大小呢?
(三阶) (四阶)
这些足球和正方体的的形 状和大小怎么样?
利用这样的方法可以近似地将一个图 形放大,画出的图形与已知图形的形状相同.
A2
B
C2
C
A2(1,4) B2(2,8) C2(3,4) D2(4,0)
2
A 2
-2 -1 O
6
7
8 x
( x, y ) ( x , 2 y )
横 向 纵 向 都 是 原 来 的 2 倍
y 8 6 4
B3
O3(0,0) A3
A
B
C
C3
A3(2,4) B3(4,8) C3(6,4) D3(8,0)
