2018年春八年级数学下册19_2一次函数19_2_2一次函数特色训练题1新版新人教版

合集下载

2020-2021学年八年级数学人教版下册第十九章 19.2.2一次函数同步练习题

19.2一次函数【知识点】1.一次函数的定义：一般地，形如____________(k,b是常数，k________0)的函数，叫做一次函数．当b=0时，y=kx+b即______________,所以说正比例函数是一种特殊的一次函数．2.一次函数y=kx+b(k≠0).(1)图象是____________________；(2)其性质有：①k＞0，y随x增大而____________________；①k＜0，y随x增大而____________________；(3)图象的平移规律：一次函数y=kx+b(k≠0)的图象可以由直线y = kx 平移____________个单位长度得到(当b > 0 时，向上平移；当b < 0 时，向下平移).3.求一次函数的解析式:(1)确定正比例函数的解析式需要______________个条件，确定一次函数的解析式需要______________个条件.(2)用待定系数法求一次函数解析式的一般步骤：①设：先设一次函数的解析式为____________________；①代：将已知条件代入解析式中，建立____________________；(3)解：解方程或方程组，确定____________________；(4)写：写出解析式.【例题讲解】1.已知y＝(k－1)x∣k∣+(k2－4)是一次函数.(1)求k的值；(2)求x＝3时，y的值；(3)当y＝0时，x的值.2.已知一次函数y=(2m+4)x+(2n－4)．(1)m为何值时，y随x的增大而减小？(2)m,n为何值时，函数图象与y轴的交点在y轴的负半轴上？3.已知正比例函数y=kx的图象经过点P(2，3),如图19－27－1.(1)求这个正比例函数的解析式；(2)将该直线向上平移3个单位长度，求平移后所得直线的解析式.4.已知一个一次函数y=kx+b(k≠0),当自变量x=－2时，函数值y=－1;当x=3时，y=－3．求这个一次函数的解析式.5.如图，过点A(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B.(1)求该一次函数的解析式；(2)若该一次函数的图象与x轴交于点D，求△BOD的面积.【举一反三】1.已知y=(m－1)x2－|m|+n+3.(1)当m,n取何值时，y是x的一次函数？(2)当m,n取何值时，y是x的正比例函数？2.已知函数y＝(2m－1)x+m－4．(1)若函数图象经过原点，求m的值；(2)若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围．3.已知函数y＝x+2.(1)画出这个函数的图象；(2)判断点A(－3，1)是否在该函数的图象上，并说明理由；(3)将该直线向下平移2个单位长度，则所得新直线的解析式为___________.4.如图，一次函数y＝kx+b的图象经过A(2，4)，B(－2，－2)两点，与y轴交于点C.(1)求k，b的值，并写出一次函数的解析式；(2)求点C的坐标.5.已知一次函数的图象经过点(1，1)和(－1，－5).(1)求此函数的解析式；(2)求此函数的图象与x轴、y轴的交点坐标及它的图象与两坐标轴所围成的三角形面积.【知识操练】1.下列函数中，不是一次函数的是()7A. y＝x+4B. y＝3xC. y＝2－3xD. y＝x2.表示一次函数图象的是()3.一次函数y=－2x+4的图象与y轴的交点坐标是()A. (0，4)B. (4，0)C. (2，0)D. (0，2)4.若3y－4与2x－5成正比例，则y是x的()A.正比例函数B.一次函数C.没有函数关系D.以上均不正确5.若点P(1，2)在正比例函数的图象上，则这个正比例函数的解析式是()A. y ＝－2xB. y ＝2xC. y ＝－4xD. y ＝4x6. 已知一次函数y =kx +b (k ≠0)的图象经过(2，－1)，(－3，4)两点，则它的图象不经过( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 下列说法正确的是__________________(填序号).∣正比例函数一定是一次函数； ∣一次函数一定是正比例函数； ∣若y －1与x 成正比例，则y 是x 的一次函数； ∣若y =kx +b ，则y 是x 的一次函数.8. 已知函数y ＝－3x +b ，当x ＝－1时，y ＝－1，则b ＝______________.9. 已知一次函数y ＝－2x +b 的图象经过A(21，1)，则此一次函数的表达式为________________.10. 如图，在平面直角坐标系x O y 中，四边形OABC 是平行四边形，且A(4，0)，B(6，2)，则直线AC 的解析式为____________．11. 已知一次函数的图象经过点(0，2)与(1，0). 求这个一次函数的解析式.12. 在一次函数y =2x +3中，y 随x 的增大而______________(填“增大”或“减小”)，当0≤x ≤5时，y 的最小值为______________.13. 把直线y =2x －1向下平移4个单位长度，所得直线的解析式是__________________．14. 点A(－1，y 1)，B(3，y 2)是直线y =kx +b (k ＜0)上的两点，则y 1－y 2__________0. (填“＞”“＜”或“=”)15. 已知直线y =2x +3与x 轴相交于点A ，与y 轴相交于点B.(1)求A ，B 两点的坐标；(2)过点B 作直线BP 与x 轴相交于点P ，且使OP=2OA ，求∣ABP 的面积.16. 已知函数y ＝(2m +1)x +m －3.(1)若函数图象经过原点，求m 的值；(2)若函数图象在y 轴的截距为－2，求m 的值；(3)若函数的图象平行于直线y ＝3x －3，求m 的值；(4)若这个函数是一次函数，且y 随着x 的增大而减小，求m 的取值范围．17. 已知y －1与x 成正比例，且x ＝2时，y ＝7.(1)求y 与x 的函数关系式；(2)当x ＝－2时，求y 的值.18. 陈明同学乘车从学校出发回家，他离家的路程y (km )与所用时间x (h )之间的关系如图.(1)求y 与x 之间的关系式；(2)求学校和陈明同学家的距离.19. 如图，一次函数232+-=x y 的图象分别与x 轴、y 轴交于点A ，B ，以线段AB 为边在第一象限内作等腰直角三角形ABC ，∠BAC=90°，求过B ，C 两点的直线的解析式.20. 有这样一个问题：探究函数y ＝x +∣x －2∣的图象与性质.小明根据学习函数的经验，对函数y ＝x +∣x －2∣的图象与性质进行了探究.下面是小明的探究过程，请补充完成：(1)化简函数解析式，当x ≥2时，y ＝___________；当x ＜2时，y ＝____________.(2)根据(1)中的结果，请在图19－27－4中的坐标系中画出函数y ＝x +∣x －2∣的图象；(3)结合函数的图象，写出该函数的一条性质：_______________21. 如图，在平面直角坐标系中，过点B(6，0)的直线与直线OA 相交于点A(4，2)．(1)直线OA的解析式为________________；直线AB的解析式为_______________(直接写出答案，不必写过程);(2)求△OAC的面积;(3)一动点M沿路线O→A→C运动，当S△OCM＝3时，求点M的坐标．。

八年级数学下册第19章一次函数19.2一次函数19.2.2一次函数19.2.2.2一次函数的图象与性质课件新人教版

初中数学（人教版）
八年级下册
第十九章一次函数
知识点一正比例函数的定义
定义
举例
正比例一般地,形如y=kx(k是常数,k≠0)的函数,叫做函数正比例函数,其中k叫做比例系数
如y=-3x,y= 12 x均为正比例函数,比例系数分别为-3, 12
知识详解
(1)如果两个变量的比值是一个常数,那么这两个变量之间的关系就是正比例函数关系. (2)正比例函数y=kx(k是常数,k≠0)必须满足两个条件:①比例系数k≠0;②自变量x的次数是1
3
选项中符合条件的数只有2.故选B.
2.(2016浙江丽水中考)在平面直角坐标系中,点M,N在同一个正比例函数图象上的是 ( ) A.M(2,-3),N(-4,6) B.M(-2,3),N(4,6) C.M(-2,-3),N(4,-6) D.M(2,3),N(-4,6)
答案 A 设过点M的正比例函数图象对应的解析式为y=kx(k≠0).
x
⑤y=-1+x,即y=x-1,也不能化为y=kx(k≠0)的形式.只有②是正比例函数. 故选B. 答案 B 解题归纳 (1)判断一个函数是不是正比例函数,就是判断该函数能否化成y=kx(k≠0)的形式;(2)若一个函数是正比例函数,则必有k为常数,k ≠0且x的次数为1,关于自变量x的代数式必为单项式.
2
2
分析先确定函数自变量的取值范围,然后依次列表、描点、连线,即可得到函数图象,再进行比较.
解析列表:
x
…
-4
-2
0
2
4
…
y= 1 x 2
…
-2
-1
0
1
2
…
y=-1 x

八年级数学下册第十九章一次函数19-2一次函数19-2-2一次函数第1课时一次函数新人教版

(1)放入一个小球后水桶中水面升高________ cm； (2)求放入小球后水桶中水面的高度 y(cm)与小球的个数 x(个) 之间的一次函数关系式；(不要求写出自变量的取值范围) (3)水桶中至少放入几个小球时有水溢出？
解：(1)2； (2)因为每放入一个小球后，水面升高 2 cm，所以 y＝30＋2x； (3)由 2x＋30＞49，得 x＞9.5，即至少放入 10 个小球时有水溢出．
3．若一次函数 y＝kx＋b，当 x＝－2 时，y＝7；当 x＝1 时，y
＝－11.则 k，b 的值为( C )
A．k＝6，b＝5
B．k＝－1，b＝－5
C．k＝－6，b＝－5
D．k＝1，b＝5
4．据调查，某地铁自行车存放处某星期天的存车量为 4000 辆次，其中变速车存车费是每辆一次 0.30 元，普通自行车存车费是每辆一次 0.20 元，若普通自行车存车数为 x 辆，存车费总收入为 y 元，则 y 关于 x 的函数关系式为( D ) A．y＝0.10x＋800(0≤x≤4000) B．y＝0.10x＋1200(0≤x≤4000) C．y＝－0.10x＋800(0≤x≤4000) D．y＝－0.10x＋1200(0≤x≤4000)
(3)某车站规定旅客可以免费携带不超过 20 千克的行李，超过部分每千克收取 1.5 元的行李费，则旅客需交的行李费 y(元) 与携带行李质量 x(千克)(x＞20)的关系．
解：(1)y＝0.53x，是； (2)y＝10＋5x，是； (3)y＝1.5x－30，是．
10．某油箱容量为 60 L 的汽车，加满汽油后行驶了 100 km 时，油箱中的汽油大约消耗了15 ，如果加满汽油后汽车行驶的路程为 x(km)，油箱中剩油量为 y(L)，则 y 与 x 之间的函数解析式和自变量取值范围分别是( D ) A．y＝0.12x，x＞0 B．y＝60－0.12x，x＞0 C．y＝0.12x，0≤x≤500 D．y＝60－0.12x，0≤x≤500

新人教版八年级下《一次函数》测试题及答案

2018—2019学年度第二学期八年级（下）第十九章一次函数单元检测题班级＿＿＿＿姓名＿＿＿＿＿得分＿＿＿＿＿一、选择题（本大题共12个小题，每小题3分，共36分。

在每小题给出的四个选项中，只有一项是满足题目要求的，请把其代号填在答题栏中相应题号的下面）。

1. 若点A （2，4）在函数2y kx =-的图象上，则下列各点在此函数图象上的是（）．A ．（0，2-）B ．（32，0） C ．（8，20） D ．（12，12） 2.变量x,y 有如下关系：①x+y=10②y=x5-③y=|x-3④y 2=8x.其中y 是x 的函数的是 A. ①②②③④B. ①②③C. ①②D. ①3. 下列各曲线中不能表示y 是x 的函数是（）．A ．B ．C ．D ．4. 已知一次函数2y x a =+与y x b =-+的图象都经过A （2-，0），且与y 轴分别交于B 、C 两点，则△ABC 的面积为（）．A ． 4B ． 5C ． 6D ． 7 5.已知正比例函数y=(k+5)x,且y 随x 的增大而减小，则k 的取值范围是 A.k ＞5 B.k ＜5C.k ＞-5D.k ＜-56.在平面直角坐标系xoy 中，点M(a,1)在一次函数y=-x+3的图象上，则点N(2a-1,a)所在的象限是 A.一象限B. 二象限C. 四象限D.不能确定7.如果通过平移直线3x y =得到53x y +=的图象，那么直线3xy =必须（）． A ．向上平移5个单位 B ．向下平移5个单位 C ．向上平移53个单位 D ．向下平移53个单位8.经过一、二、四象限的函数是 A.y=7B.y=-2xC.y=7-2xD.y=-2x-79.已知正比例函数y=kx(k ≠0)的函数值y 随x 的增大而减小，则函数y=kx-k 的图象大致是10.若方程x-2=0的解也是直线y=(2k-1)x+10与x 轴的交点的横坐标，则k 的值为 A.2B.0C.-2D. ±211. 根据如图的程序，计算当输入3x =时，输出的结果y = ．12.已知直线y 1=2x 与直线y 2= -2x+4相交于点A.有以下结论：①点A 的坐标为A(1,2);②当x=1时，两个函数值相等；③当x ＜1时，y 1＜y 2④直线y 1=2x 与直线y 2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的是 A. ①③④ B. ②③ C. ①②③④ D. ①②③二、填空题（本大题共5个小题，每小题4分，共20分。

人教版八年级下《第19章一次函数》专项训练(2)含答案

第19章一次函数专项训练专训1.用一次函数巧解实际中方案设计的应用名师点金：做一件事情，有时有不同的方案，比较这些方案，从中选择最佳方案作为行动计划，是非常必要的．解决这些问题时，先要弄清题意，根据题意构建恰当的函数模型，求出自变量的取值范围，然后再结合实际问题确定最佳方案．合理决策问题1．某商场计划投入一笔资金采购一批紧俏商品，经市场调研发现，如果本月初出售，可获利10%，然后将本利再投资其他商品，到下月初又可获利10%；如果下月初出售可获利25%，但要支付仓储费8 000元．设商场投入资金x元，请你根据商场的资金情况，向商场提出合理化建议，说明何时出售获利较多．选择方案问题2．某教育行政部门计划今年暑假组织部分教师到外地进行学习，预订宾馆住宿时，有住宿条件一样的甲、乙两家宾馆供选择，其收费标准均为每人每天120元，并且各自推出不同的优惠方案．甲家是35人(含35人)以内的按标准收费，超过35人的，超出部分按九折收费；乙家是45人(含45人)以内的按标准收费，超过45人的，超出部分按八折收费．如果你是这个部门的负责人，你应选择哪家宾馆更实惠些？最佳效益问题3．甲、乙两个商场出售相同的某种商品，每件售价均为3 000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一件按原售价收费，其余每件优惠30%；乙商场的优惠条件是：每件优惠25%.设所买商品为x件时，甲商场收费为y元，乙商场收费为y2元．1(1)分别求出y1，y2与x之间的关系式．(2)当甲、乙两个商场的收费相同时，所买商品为多少件？(3)当所买商品为5件时，应选择哪个商场更优惠？请说明理由．专训2.全章热门考点整合应用名师点金：本章内容是中考的必考内容，主要考查一次函数的图象与性质，求函数解析式及建立一次函数模型解决利润大小、方案选择等实际问题，题型涉及选择题、填空题与解答题．其热门考点可概括为：三个概念，两个图象，一个性质，四个关系，一个方法，两个应用．三个概念概念1变量与常量1．(1)设圆柱的底面半径R不变，圆柱的体积V与圆柱的高h的关系式是V ＝πR2h，在这个变化过程中常量和变量分别是什么？(2)设圆柱的高h不变，在圆柱的体积V与圆柱的底面半径R的关系式V＝πR2h中，常量和变量分别又是什么？概念2函数2．两个变量之间存在的关系式是y2＝x＋1(其中x是非负整数)，y是不是x 的函数？如果变为用含y的代数式表示x的形式，x是不是y的函数？请说明原因．3．求下列函数中自变量的取值范围：(1)y＝－12x2－x＋6；(2)y＝－112x－3；(3)y＝16x－9 3x－2.概念3一次函数4．当m，n为何值时，y＝(5m－3)x2－n＋(m＋n)是关于x的一次函数？当m，n为何值时，y是关于x的正比例函数？两个图象图象1函数的图象5．小张的爷爷每天坚持体育锻炼，星期天爷爷从家里跑步到公园，打了一会儿太极拳，然后沿原路慢步走到家，下面能反映当天爷爷离家的距离y(米)与时间x(分钟)之间关系的大致图象是( )图象2一次函数的图象6．(中考·阜新)对于一次函数y＝kx＋k－1(k≠0)，下列叙述正确的是( )A．当0<k<1时，函数图象经过第一、二、三象限B．当k>0时，y随x的增大而减小C．当k<1时，函数图象一定交于y轴的负半轴D．函数图象一定经过点(－1，－2)7．若有理数a，b，c满足a＋b＋c＝0，且a＜b＜c，则函数y＝ax＋c的图象可能是( )一个性质8．已知点M(1，a)和点N(2，b)是一次函数y＝－2x＋1的图象上的两点，则a与b的大小关系是( )A．a＞b B．a＝bC．a＜b D．以上都不对9．已知一次函数的解析式是y＝(k－2)x＋12－3k.(1)当图象与y轴的交点位于原点下方时，判断函数值随着自变量的增大而变化的趋势；(2)如果函数值随着自变量的增大而增大，且函数图象与y轴的交点位于原点上方，确定满足条件的正整数k的值．四个关系关系1一次函数与正比例函数的关系10．下列函数中，哪些是一次函数？哪些是正比例函数？①y＝－2x－1；②y＝12x；③y＝2x；④y＝－x2－1；⑤2x－y＝0；⑥y＝－2(x－1)．11．如图，过A点的一次函数的图象与正比例函数y＝2x的图象相交于点B.(1)求一次函数的解析式；(2)判断点C(4，－2)是否在该一次函数的图象上，说明理由；(3)若该一次函数的图象与x轴交于D点，求△BOD的面积．(第11题)关系2 一次函数与一元一次方程的关系12．如图，在平面直角坐标系xOy 中，直线y ＝x ＋1与y ＝－34x ＋3交于点A ⎝ ⎛⎭⎪⎫87，157，两直线分别交x 轴于点B 和点C. (1)求点B ，C 的坐标； (2)求△ABC 的面积．(第12题)关系3 一次函数与二元一次方程(组)的关系13．下列各个选项中的网格都是边长为1的小正方形，利用函数的图象解方程5x －1＝2x ＋5，其中正确的是( )关系4 一次函数与不等式(组)的关系14．已知一次函数y ＝kx ＋3的图象经过点(1，4)．(1)求这个一次函数的解析式；(2)求关于x 的不等式kx ＋3≤6的解集．15．在同一平面直角坐标系中，画出一次函数y 1＝2x －4，y 2＝x ＋1的图象，根据图象求解下列问题：(1)二元一次方程组⎩⎨⎧y ＝2x －4，y ＝x ＋1的解；(2)一元一次不等式组⎩⎨⎧2x －4＞0，x ＋1＞0的解集．一个方法——待定系数法16．如图，一个正比例函数图象与一个一次函数图象交于点A(3，4)，且一次函数的图象与y 轴相交于点B(0，－5)．(1)求这两个函数的解析式； (2)求三角形AOB 的面积．(第17题)两个应用应用1给出解析式(或图象)解实际问题17．某游泳馆普通票价20元/张，暑期为了促销，新推出两种优惠卡：①金卡售价600元/张，每次凭卡不再收费；②银卡售价150元/张，每次凭卡另收10元．暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数．设游泳x次时，所需总费用为y元．(1)分别写出选择银卡、普通票消费时，y与x之间的函数关系式；(2)在同一个坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A，B，C的坐标；(3)请根据函数图象，直接写出选择哪种消费方式更合算．(第18题)应用2只给语言叙述或图表情境解实际问题18．为改善生态环境，防止水土流失，某村计划在河堤坡面种植白杨树，现有甲、乙两家林场可提供相同质量的白杨树苗，其具体销售方案如下：(1)该村需要购买1 500棵白杨树苗，若都在甲林场购买所需费用为________元，若都在乙林场购买所需费用为________元；(2)分别求出y 甲、y 乙与x 之间的函数关系式；(3)如果你是该村的负责人，应该选择到哪家林场购买树苗合算，为什么？答案1专训元，1y ．解：设如果商场本月初出售，下月初可获利1 ，x 0.21＝x 0.11＋x 0.1＝10%·x 0%)1＋(1＋x 10%＝1y 则 8 000.－x 0.25＝8 000－x 25%＝2y 元，则2y 设如果商场下月初出售，可获利；200 000＝x ，解得8 000－x 0.25＝x 0.21时，2y ＝1y 当；<200 000x ，解得8 000－x >0.25x 0.21时，2y >1y 当 >200 000.x ，解得8 000－x <0.25x 0.21时，2y <1y 当利相同；若商场投入资金少种出售方式获万元，两20所以若商场投入资金为售获利较万元，下月初出20万元，本月初出售获利较多；若投入资金多于20于多．＜35时，选择两家宾馆是一样的；当35≤x 当人，x 人数是．分析：设总2x时，两家宾馆的收费可以表示成人数x>45时，选择甲宾馆比较实惠；当45≤x 的函数，比较两个函数值的大小即可．元，乙y 元，乙宾馆的收费为甲y 人，甲宾馆的收费为x 解：设总人数是时，两家宾馆的费用是一样的；35≤x 当时，选择甲宾馆比较实惠；45≤35<x 当 108x＝甲y ，即35)－(x ×120×0.9＋120×35＝甲y 时，甲宾馆的收费x>45当，420＋ 1 080.＋x 96＝45)－120(x ×0.8＋120×45＝乙y 乙宾馆的收费；55＝x ，解得1 080＋96x ＝420＋108x 时，乙y ＝甲y 当；x>55，解得1 080＋420>96x ＋108x 时，乙>y 甲y 当 x<55.，解得1 080＋420<96x ＋108x 时，乙<y 甲y 当时，两家宾馆的费用是一样的；55＝x 或35≤x 综上可得，当时，选择甲宾馆比较实惠；35<x<55当时，选择乙宾馆比较实惠．x>55当 ×1)－3 000(x ＋3 000＝1y 时，1＞x ；当3 000＝1y 时，1＝x 当(1)．解：3900.＋x 2 100＝30%)－(1 ⎩⎨⎧3 000（x ＝1），2 100x ＋900（x ＞1，x 为整数）.＝1y 所以．)为正整数x (x 2 250＝25%)－(1x 3 000＝2y 故6.＝x ，解得x 2 250＝900＋x 2 100当甲、乙两个商场的收费相同时，(2)件．6甲、乙两个商场的收费相同时，所买商品为 2 100＝900＋x 2 100＝1y 时，5＝x ，理由如下：当乙商场更优惠应选择(3)，所25011 ＞11 400，因为11 250＝5×2 250＝x 2 250＝2y ，11 400＝900＋5×件时，应选择乙商场更优惠．5以当所买商品为 2专训 h.和V ，变量是R 和π常量是(1)．解：1 R.和V ，变量是h 和π常量是(2) 的值有两个，y ，此时1的值为±y 时，0的值是x 中，当1＋x ＝2y ．解：在2的函数．x 不是y 并不是唯一确定的，因此都有唯一确x 的每一个值，另一个变量y 后，对于1－2y ＝x 变形为1＋x ＝2y 的函数．y 是x 定的值与其对应，因此A7. C 6. B ．5 的图象上，1＋2x ＝－y 在一次函数b)，2N(和点a)，M(1点拨：∵点 A ．8的增大而减小，∴x 随y 中函数值1＋2x ＝－y 由一次函数图象性质可知一次函数a>b.位于原点3k)－12，(0原点下方，即点轴的交点位于y 因为图象与(1)．解：9，所以函数值随着自变量的增2>0－2>4－k 所以k>4.，解得3k<0－12下方，所以大而增大．k>2.，解得2>0－k 因为函数值随着自变量的增大而增大，所以(2) k<4.，解得3k>0－12轴的交点位于原点上方，所以y 因为函数图象与 2<k<4.的取值范围为k 所以 3.的值为k 所以满足条件的正整数．解：一次函数：①②⑤⑥10 正比例函数：②⑤，2)，(1的坐标是B ，则点2＝y ，得1＝x 中，令2x ＝y 在(1)．解：11，0)≠b(k ＋kx ＝y 设一次函数的解析式是 ⎩⎨⎧b ＝3，k ＝－1.解得⎩⎨⎧b ＝3，k ＋b ＝2，则 3.＋x ＝－y 故一次函数的解析式是＝x ，当3＋x ＝－y 不在该一次函数的图象上．理由：对于2)，－C(4点(2)不在该函数的图象上．2)，－C(4，所以点2≠－1＝－y 时，4 ，0)，(3的坐标是D ，则点3＝x ，得0＝y 中，令3＋x ＝－y 在(3)－＝1的交点的横坐标，因此画出与y5x的图象即可．y5＋＝2x4)，入(114y．解：(1)把点的坐标代4＝＋＝中，得k33.kx＋∴k＝1.y∴一次函数的解析式为＝＋x3.(1)(2)由知k1，＝＋∴原不等式为x3≤6.∴x3.≤4)的坐标代入，点拨：y(1)把点(1kx＝(2)k的值．中，用待定系数法求出＋3kx值代入不等式把求出的k＋中，求出不等式的解集．36≤15．解：图象略．3，所以横坐标为点因为A(2)点到A点纵坐标为－又因为B3.OB的距离为5，所以5.＝OB20x.＝y 普通票：，150＝y ，得150＋10x ＝y 代入0＝x 把(2) ．150)，A(0∴ ⎩⎨⎧y ＝20x ，y ＝10x ＋150，∵ ⎩⎨⎧x ＝15，y ＝300.∴ ．300)，B(15∴ 45.＝x ，得150＋10x ＝y 代入600＝y 把．600)，C(45∴ )，也正确15＜x ≤0注：若写成(时，选择购买普通票更合算；0<x<15当(3) 时，选择购买银卡、普通票的总费用相同，均比金卡合算；15＝x 当时，选择购买银卡更合算；15<x<45当时，选择购买金卡、银卡的总费用相同，均比普通票合算；45＝x 当时，选择购买金卡更合算．x>45当 6 000；(1)5 900．解：18 ，4x ＝甲y 时，1 000≤x ≤0当(2) 时，x>1 000当，002＋3.8x ＝1 000)－3.8(x ＋4 000＝甲y ＝甲y ∴ ⎩⎨⎧4x （0≤x ≤1 000且x 为整数）， 3.8x ＋200（x>1 000且x 为整数）. 时，2 000≤x ≤0当，4x ＝乙y 时，x>2 000当，800＋3.6x ＝2 000)－3.6(x ＋8 000＝乙y ＝乙y ∴ ⎩⎨⎧4x （0≤x ≤2 000且x 为整数）， 3.6x ＋800（x>2 000且x 为整数）. 由题意，得(3) 一样，时，两家林场白杨树苗单价1 000≤x ≤0当 ∴到两家林场购买所需费用一样．时，甲林场有优惠而乙林场无优惠，2 000≤1 000<x 当时，到甲林场购买合算；2 000≤1 000<x ∴当，200＋3.8x ＝甲y 时，x>2 000当，800＋3.6x ＝乙y 时乙y ＝甲y 当，800＋3.6x ＝200＋8x ．3 ，3 000＝x 解得时，到两家林场购买所需费用一样；3 000＝x ∴当时，乙<y 甲y 当，800＋3.6x ＜200＋8x ．3 x<3 000.解得时，到甲林场购买合算；2 000<x<3 000∴当时，乙>y 甲y 当，800＋200>3.6x ＋x 8．3 x>3 000.解得时，到乙林场购买合算．x>3 000∴当时，到两家林场购买所需费用一样，3 000＝x 或1 000≤x ≤0综上所述，当时，到甲林场购买合算；1 000<x<3 000当时，到乙林场购买合算．x>3 000当。

19-2-2 一次函数基础习题人教版八年级数学下册

19.2.2 一次函数基础习题一、选择题1.若一次函数y =x -3m +7的图象经过点（3，4），则m 的值为（） A ．2； B ．-2； C ．3； D ．-3。

2．一次函数y=kx+b ，当-3≤x ≤1时，对应的y 值为1≤y ≤9，则k 的值为（） A ．2 B ．-2 C ．-4或21 D ．2或-23．一次函数y=kx+b 满足x=0时，y=-1；x=1时，y=1，则这个一次函数是（ •） A ．y=2x+1 B ．y=-2x+1 C ．y=2x-1 D ．y=-2x-14.下列函数中，在同一坐标系内的图象与函数y=2x-1的图象相互平行的是（） A.21y x =-+B. 2(1)y x =+C. 132y x =+ D. 122y x =-- 5.将直线y=2x 向上平移两个单位，所得的直线是（）A.y=2x+2B.22y x =-C. 2(2)y x =-D. 2(2)y x =+ 6．已知一次函数y=kx+b ，当x=1时，y=2，且它的图象与y•轴交点的纵坐标是3，则此函数的解析式为（）A ．0≤x ≤3B ．-3≤x ≤0C ．-3≤x ≤D ．不能确定二、填空题7.函数y=2x －1经过 __________. 象限,y=-2x －1 经过 __________. 象限,y=2x+1经过 __________.象限 y=-2x+1经过 __________象限8．如果直线y=－2x+b 经过点（0，1），那么这条直线的解析式为 9.函数36-=x y 向上平移4个单位后得到新函数的解析式是。

10.若y +3与x 成正比例，且x =2时，y =5，则x =5时，y = ． 11.若2-y 与1+x 成正比例，比例系数是3，则y 与x 得关系式为__________，y 是x 的__________函数. 三、解答题12.已知一次函数图象过点（3，5）与（-4，-9），求这个一次函数的解析式．13.已知一次函数y=(1－2k)x+k 的函数值y 随x 的增大而增大，且与y 轴交于正半轴，求k的取值范围14．已知一次函数y=kx+b的图象与x轴交于点A（-6，0），与y轴交于点B•，•若△AOB的面积是12，且y随x的增大而减小，你能确定这个一次函数的关系式吗？15.玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子的价格打8折。

人教版数学八年级下册19.2.2 一次函数(1)同步练习(解析版)

19.2.2 一次函数(1)基础闯关全练1．下列函数关系式：①y=-x；②y=2x+11；③y=x²+x+1；④y=x1，其中一次函数的个数是（）A．1 B．2 C．3 D．42．函数y-（m-2）x+(m+1)是关于x的一次函数，那么m的取值范围是（）A．m≠2 B．m≠-1 C．m=-1 D．m≠2且m≠-13．一次函数y=-2x+3的图象不经过（）A．第一象限 B．第二象限 C．第三象限 D．第四象限4．在平面直角坐标系中，一次函数y=kx+b的图象如图19-2-2-1-1所示，观察图象可得（）A．k＞0，b＞0 B．k＞0，b＜0 C．k＜O，b＞0 D．k＜0，b＜0 5．一次函数y=kx+2(k为常数，且k≠0)的图象如图19-2-2-1-2所示，则k的可能值为_______．（写出一个即可）能力提升全练1．已知一次函数y=kx-m-2x的图象与y轴的负半轴相交，且函数值y随自变量x的增大而减小，则下列结论正确的是（）A．k＜2，m＞0 B．k＜2，m＜0 C．k＞2，m＞0 D．k＞2，m＜0 2．把函数y=x向上平移3个单位长度，下列点在该平移后的直线上的是（）A．(2,2) B．(2,3) C．(2,4) D．(2,5)3.如图19-2-2-1-3，一个函数的图象由射线BA、线段BC、射线CD组成，其中点A(-1，2)，B(1，3)，C(2，1)，D(6，5)，则此函数（）A．当x＜1时，y随x的增大而增大 B．当x＜1时，y随x的增大而减小C．当x＞1时，y随x的增大而增大 D．当x＞1时，y随x的增大而减小三年模拟全练一、选择题1．下列函数关系式：①y=-2x+1；②y=x；③y=2x²+1；④y=123x，其中一次函数有（）A．1个 B．2个 C．3个 D．4个2．关于函数y=-2x+1，下列结论正确的是（）A．图象必经过点（-2，1） B．图象经过第一、二、三象限C．当x＞21时，y＜0 D. y随x的增大而增大3．在如图19-2-2-1-4所示的计算程序中，y与x之间的函数关系所对应的图象应为（）A ．B ．C．D ．二、填空题4．若一次函数y=（1-2k）·x+k的图象经过第一、二、三象限，则k的取值范围是_______．三、解答题5．已知一次函数y=（3-m）x+m-5.(1)若一次函数的图象过原点，求实数m的值；(2)当一次函数的图象经过第二、三、四象限时，求实数m的取值范围．五年中考全练一、选择题1．若b＞0，则一次函数y=-x+b的图象大致是（）A ．B ．C ．D ．2．已知点（-1，y₁），(4，y₂)在一次函数y=3x-2的图象上，则y₁，y₂，0的大小关系是 ( )A．O＜y₁＜y₂B．y₁＜O＜y₂C．y₁＜y₂＜0 D．y₂＜O＜y₁二、填空题3．将直线y=x向上平移2个单位长度，平移后直线的解析式为_______．4．在平面直角坐标系中，已知一次函数y=-2x+1的图象经过P₁(x₁，y₁．)，P₂(x₂，y₂)两点，若x₁＜x₂，则y₁_______y₂（填“＞”“＜”或“=”）．5．已知点A是直线y=x+1上一点，其横坐标为-21，若点B与点A关于y轴对称，则点B的坐标为_________．核心素养全练1．已知关于x的一次函数y=(a+3)x+(b-2)．(1)当a为何值时，y随x的增大而减小？(2)当a，b为何值时，函数图象与y轴的交点在x轴上方？(3)当a，b为何值时，函数图象经过第一、三、四象限？(4)当a，b为何值时，函数图象经过原点？(5)当a，b为何值时，函数的图象与直线y=-3x平行？2．一次函数y=（m-2）x+m²-1的图象经过点A(0，3).(1)求m的值，并写出函数解析式；(2)若(1)中的函数图象与x轴交于点B，直线y=(n+2)x+n²-1也经过点A(0，3)，且与x轴交于点C，求线段BC的长．19.2.2一次函数(1)1.B①y=-x是一次函数；②y=2x+11是一次函数；③④不符合一次函数的定义，故不是一次函数，故选B．2．A根据一次函数的定义知，一次项系数不等于0．即m-2≠0．解得m≠2．3．C ∵k=-2＜0,∴一次函数y=-2x+3的图象必过第二、四象限，∴b=3，∴函数图象交y轴于正半轴，∴函数图象经过第一、二、四象限，不经过第三象限．故选C．4．A由图象可知，直线从左往右呈上升趋势，故k＞0，图象与y轴的交点在y轴正半轴上，故b＞0．5．答案 -2(答案不唯一)解析观察图象可知，OB＜OA，k＜0.当x=0时，y=kx+2=2，∴OA=2，令OB=1．则点B(1，0)，将(1，0)代入y=kx+2，得0=k+2，解得k=-2．1.A整理得y=（k-2）x-m，因为函数图象与y轴负半轴相交，所以-m＜0．即m＞0，又函数值y随x的增大而减小，所以k-2＜0．即k＜2.故选A．2.D 一次函数的平移规律是“左加右减，上加下减”，故把函数y=x向上平移3个单位长度后的函数关系式为y=x+3，当x=2时．y=2+3=5．故选D ．3.A 由函数图象可知，当x ＜1时，y 随x 的增大而增大，因此A 正确，B 错误；当1＜x ＜2时，y 随x 的增大而减小，当x ＞2时，y 随x 的增大而增大，因此C 、D 错误，故选A ．一、选择题1.B ①y=-2x+1和②y=x 是一次函数，③④不符合一次函数的定义．故选B ．2.C ∵k ＜0，所以y 随x 的增大而减小，故D 错误；∵k ＜0,b ＞0,∴图象经过一、二、四象限，故B 错误；当x=-2时，y=4+1=5，故A 错误．故选C ．3.A 由题意得y=-2x+3，所以当x=0时，y=3；当y=0时，x=1.5，即图象经过点(0，3)和点(1.5，0)，选项A 符合要求，故选A ．二、填空题4．答案0＜k ＜21解析 ∵一次函数y=(1-2k)x+k 的图象经过第一、二、三象限，∴⎩⎨⎧-,0,021＞＞k k ∴0＜k＜21. 三、解答题5．解析(1)∵一次函数图象过原点， ∴⎩⎨⎧，0=5-m ，0≠m -3解得m=5．(2)∵一次函数的图象经过第二、三、四象限，⎩⎨⎧，＜＜05-m ，0m -3∴3＜m ＜5．一、选择题1.C 对于一次函数y=kx+b(k ≠0)，当k ＞0时，图象从左到右上升；当k ＜0时，图象从左到右下降；当b ＞0时，图象与y 轴的交点在y 轴正半轴；当b=0时，图象与y轴的交点在原点；当b ＜0时，图象与y 轴的交点在y 轴负半轴∵-1＜0，∴图象从左到右下降，又b ＞0，∴图象与y 轴的交点在y 轴正半轴，故选C ．2．B 解法一：将x=-1代入y=3x-2，得y=-5，∴y ₁=-5；将x=4代入y=3x-2，得y=10，∴y ₂=10，所以y ₁＜O ＜y ₂．故选B ．解法二：∵k=3＞0，∴y 随x 的增大而增大，易知x=32时，y=0，又-1＜32＜4,∴y ₁＜0＜y ₁，故选B ．二、填空题 3．答案y=x+2解析由平移规律“左加右减，上加下减”，可知向上平移2个单位长度后，直线的解析式为y=x+2． 4．答案＞解析一次函数y=kx+b 中，当k ＞0时，y 随x 的增大而增大；当k ＜0时，y 随x 的增大而减小，因为y=-2x+1中的k=-2＜0，所以当x ₁＜x ₂时，y ₁＞y ₂. 5．答案(2121，)解析把x=-21代入y=x+1得y=21，∴点A 的坐标为（-2121，），∵点8和点A 关于y 轴对称，∴点B 的坐标为(2121，)．1．解析(1)由一次函数的性质可知，当a+3＜0，即a ＜-3时，y 随x 的增大而减小． (2)由题意知，当a+3≠0且b-2＞0时，即当a ≠-3且b ＞2时，函数图象与y 轴的交点在x 轴上方．(3)因为函数图象经过第一、三、四象限，所以a+3＞0且b-2＜0．所以a ＞-3且b ＜2，即当a ＞-3且b ＜2时，函数图象经过第一、三、四象限．(4)由题意，得a+3≠0且b-2=0，解得a ≠-3且b=2．即当a ≠-3且b=2时，函数图象经过原点．(5)由题意，得a+3=-3且b-2≠0，解得a=-6且b ≠2．所以当a=-6且b ≠2时，函数图象与直线y=-3x 平行． 2．解析(1)由题意得m ²-1=3，所以m=±2．又m-2≠0，即m ≠2，所以m=-2，所以y=-4x+3.(2)由题意可得B 点的坐标为(43,0)．因为直线y=(n+2)x+n ²-1经过点A(0，3)，所以n ²-1=3，所以n=±2．又n+2≠0．即n ≠-2．所以n=2．所以y=4x+3，所以C 点的坐标为(-43，0)．所以BC=2343--43=⎪⎭⎫ ⎝⎛．。

八年级数学下册第19章一次函数19.2一次函数19.2.2一次函数19.2.2.1一次函数的概念课件

5.(2017湖南邵阳一模)一次函数y=kx+2(k为常数,且k≠0)的图象如图19-
2-2-1-2所示,则k的可能值为
.(写出一个即可)
答案 -2(答案不唯一)
图19-2-2-1-2
解析观察图象可知,OB<OA,k<0.
当x=0时,y=kx+2=2,∴OA=2,
令OB=1,则点B(1,0),将(1,0)代入y=kx+2,得0=k+2,解得k=-2.
4
4
故当k=-1时,直线与x轴交于点
3 4
,
0
.
(4)当
1 2k
3k 1
0, 即
0,
1 3
<k<
1 2
时,直线经过第二、三、四象限.
(5)当1-3k=-3,2k-1≠-5,
即k= 4 时,已知直线与直线y=-3x-5平行.
3
方法归纳对于一次函数y=kx+b,(1)判断k值符号的方法:①增减性法, 当y随x增大而增大时,k>0;反之,k<0.②直线升降法,当直线从左到右上升时,k>0;反之,k<0.③经过象限法,直线过第一、三象限时,k>0;直线过第二、四象限时,k<0.(2)判断b值符号的方法:与y轴交点法,即直线y=kx+b 若与y轴交于正半轴,则b>0;若与y轴交于负半轴,则b<0;若与y轴交于原点,则b=0.
例3 下列函数图象中,不可能是关于x的一次函数y=mx-(m-3)的图象的是( )
解析一次函数y=mx-(m-3)中,x的系数m决定着直线从左至右呈上升或下降的趋势,-(m-3)即3-m决定着直线与y轴的交点是在正半轴、负半轴还是原点,这两个方面不得有矛盾之处,应该结合一次函数的图象进行分析.

(部编本人教版)最新八年级数学下册第十九章19.2.2 一次函数第2课时一次函数的图象与性质练习【经典练

第2课时一次函数的图象与性质知识点 1 一次函数的图象1．[2018·抚顺]一次函数y ＝－x －2的图象经过( )A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限2．[2018·湘西州]一次函数y ＝x ＋2的图象与y 轴的交点坐标为( )A ．(0，2)B ．(0，－2)C ．(2，0)D ．(－2，0)3．若点(3，1)在一次函数y ＝kx －2的图象上，则k 的值是( )A ．5B ．4C ．3D ．14．分别在同一平面直角坐标系中画出下列各函数的图象，并指出各函数图象的共同之处．(1)y ＝12x ＋2；(2)y ＝－x ＋2；(3)y ＝2x ＋2.知识点 2 一次函数图象的平移5．[2018·南充]直线y ＝2x 向下平移2个单位长度得到的直线的解析式是( )A ．y ＝2(x ＋2)B ．y ＝2(x －2)C ．y ＝2x －2D ．y ＝2x ＋26．[2018·娄底]将直线y ＝2x －3向右平移2个单位长度，再向上平移3个单位长度后，所得的直线的解析式为( )A ．y ＝2x －4B ．y ＝2x ＋4C ．y ＝2x ＋2D ．y ＝2x －27．若直线y ＝kx ＋2是由直线y ＝－2x －1平移得到的，则k ＝________，即直线y ＝－2x －1沿y 轴向________平移了________个单位长度．知识点 3 一次函数的性质8．对于函数y ＝2x －1，下列说法正确的是( )A ．它的图象过点(1，0)B ．y 随x 的增大而减小C ．它的图象经过第二象限D ．当x ＞1时，y ＞09．已知一次函数y ＝(m ＋2)x ＋1，若y 随x 的增大而增大，则m 的取值范围是________．10．[2018·济宁]在平面直角坐标系中，已知一次函数y ＝－2x ＋1的图象经过P 1(x 1，y1)，P2(x2，y2)两点，若x1＜x2，则y1________y2(填“＞”“＜”或“＝”)．11．[2018·眉山]已知点A(x1，y1)，B(x2，y2)在直线y＝kx＋b上，且该直线经过第一、二、四象限，当x1＜x2时，y1与y2的大小关系为________(用“>”连接)．12．在一次函数y＝kx＋2中，若y随x的增大而增大，则它的图象不经过第________象限．13．[2018·上海]如果一次函数y＝kx＋3(k是常数，k≠0)的图象经过点(1，0)，那么y的值随x值的增大而________(填“增大”或“减小”)．14．已知关于x的函数y＝(m－1)x＋1－3m为一次函数，试根据下列各条件确定m的值或取值范围．(1)该函数图象经过原点；(2)该函数图象与y轴相交于点(0，2)；(3)y随x的增大而减小．15．[2018·湘潭]若b＞0，则一次函数y＝－x＋b的图象大致是( )图19－2－816．[2018·贵阳]一次函数y＝kx－1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可能为( )A．(－5，3) B．(1，－3)C．(2，2) D．(5，－1)17．两条直线y＝ax＋b与y＝bx＋a在同一平面直角坐标系中的位置可能是( )图19－2－918．写出一个图象过点(0，3)，且函数值y随自变量x的增大而减小的一次函数解析式：________(填一个答案即可)．19．已知一次函数y＝kx＋2k＋3的图象与y轴的交点在y轴的正半轴上，且函数值y 随x的增大而减小，则k所有可能取得的整数值为________．20．若函数y＝2x＋3与y＝4x－b的图象交x轴于同一点，则b的值为________．21．如图19－2－10，一次函数y ＝kx ＋b 的图象与正比例函数y ＝2x 的图象平行且经过点A (1，－2)，则k ＝________，b ＝________．图19－2－1022．已知直线y ＝－12x －6与x 轴交于点A ，与y 轴交于点B ，求这条直线与坐标轴围成的三角形的面积．23．已知直线y ＝(1－3k )x ＋2k －1.(1)当k 为何值时，该直线经过第二、三、四象限？(2)当k 为何值时，该直线与直线y ＝－3x －5平行？拓广探究创新练冲刺满分24．如图19－2－11，已知直线y ＝2x ＋4与x 轴交于点A ，与y 轴交于点B ，点P 在坐标轴上，且PO ＝2AO .求△ABP 的面积．图19－2－11教师详解详析1．D [解析] 由一次函数图象的特点可知，当k ＞0时，图象必过第一、三象限；当k ＜0时，图象必过第二、四象限；当b ＞0时，图象必过第一、二象限；当b ＜0时，图象必过第三、四象限．∵－1＜0，－2＜0，∴一次函数y ＝－x －2的图象经过第二、三、四象限．故选D.2．A 3.D4．解：图象略．共同点：函数图象都是一条直线，且均与y 轴交于点(0，2)．5．C [解析] 直线y ＝2x 向下平移2个单位长度得到直线的解析式是y ＝2x －2，故选C.6．A [解析] 根据图象平移时“左加右减，上加下减”的规律，向右平移2个单位长度后为y ＝2(x －2)－3＝2x －7，再向上平移3个单位长度后为y ＝2x －7＋3＝2x －4.故选A.7．－2 上 38．D [解析] A ．把x ＝1代入解析式得到y ＝1，即函数图象经过点(1，1)，不经过点(1，0)，故本选项错误；B.函数y ＝2x －1中，k ＝2＞0，则y 随x 的增大而增大，故本选项错误；C.函数y ＝2x －1中，k ＝2＞0，b ＝－1＜0，则该函数图象经过第一、三、四象限，故本选项错误；D.当x ＞1时，2x －1＞1，则y ＞1，故y ＞0正确，故本选项正确．故选D.9．m ＞－210．＞ [解析] 因为y ＝－2x ＋1中的k ＝－2＜0，所以y 随x 的增大而减小，所以当x 1＜x 2时，y 1＞y 2.11．y 1>y 2 [解析] 由于一次函数的图象经过第一、二、四象限，∴k <0，∴y 随x 的增大而减小，∴当x 1＜x 2时，y 1>y 2.12．四 [解析] ∵在一次函数y ＝kx ＋2中，y 随x 的增大而增大，∴k ＞0.∵2＞0，∴此函数的图象经过第一、二、三象限，不经过第四象限．13．减小 [解析] 因为一次函数图象经过点(1，0)，故将其代入y ＝kx ＋3，得0＝k ＋3，解得k ＝－3<0，所以y 的值随x 值的增大而减小．14．解：(1)由1－3m ＝0且m －1≠0，得m ＝13. (2)把点(0，2)代入，得1－3m ＝2，解得m ＝－13. (3)由m －1<0，得m <1.15．C [解析] ∵k ＝－1＜0，∴图象从左到右是下降的．∵b ＞0，∴图象与y 轴的正半轴相交．故选C.16．C [解析] ∵一次函数y ＝kx －1中，y 的值随x 值的增大而增大，∴k ＞0.A ．把(－5，3)代入y ＝kx －1，得k ＝－45＜0，不符合题意； B ．把(1，－3)代入y ＝kx －1，得k ＝－2＜0，不符合题意；C ．把(2，2)代入y ＝kx －1，得k ＝32＞0，符合题意； D ．把(5，－1)代入y ＝kx －1，得k ＝0，不符合题意．故选C.17．A [解析] 分四种情况：①当a ＞0，b ＞0时，直线y ＝ax ＋b 和y ＝bx ＋a 均经过第一、二、三象限，选项中不存在此情况；②当a ＞0，b ＜0时，直线y ＝ax ＋b 经过第一、三、四象限，直线y ＝bx ＋a 经过第一、二、四象限，选项A 符合此条件；③当a ＜0，b ＞0时，直线y ＝ax ＋b 经过第一、二、四象限，直线y ＝bx ＋a 经过第一、三、四象限，选项A 符合此条件；④当a ＜0，b ＜0时，直线y ＝ax ＋b 经过第二、三、四象限，直线y ＝bx ＋a 经过第二、三、四象限，选项中不存在此情况．故选A.18．答案不唯一，如y ＝－x ＋319．－1 [解析] 由题意得⎩⎪⎨⎪⎧2k ＋3>0，k <0，解得－32＜k ＜0.∵k 为整数，∴k ＝－1. 20．－6 [解析] 函数y ＝2x ＋3的图象与x 轴的交点坐标是(－32，0)，函数y ＝4x －b 的图象与x 轴的交点坐标是(b 4，0)，所以－32＝b 4，解得b ＝－6. 21．2 －4 [解析] ∵一次函数y ＝kx ＋b 的图象与正比例函数y ＝2x 的图象平行， ∴k ＝2，∴y ＝2x ＋b ，把A (1，－2)代入y ＝2x ＋b ，得2＋b ＝－2，解得b ＝－4.22．解：当x ＝0时，y ＝－6.当y ＝0时，即－12x －6＝0，解得x ＝－12，所以点A ，B 的坐标分别为(－12，0)，(0，－6)，所以OA ＝||－12＝12，OB ＝||－6＝6，所以这条直线与坐标轴围成的三角形的面积为12OA ·OB ＝12×12×6＝36. 23．解：(1)当⎩⎪⎨⎪⎧1－3k ＜0，2k －1＜0，即13＜k ＜12时，该直线经过第二、三、四象限． (2)当⎩⎪⎨⎪⎧1－3k ＝－3，2k －1≠－5，即k ＝43时，该直线与直线y ＝－3x －5平行． 24．解：令y ＝0，则由0＝2x ＋4得x ＝－2，∴A (－2，0)，∴AO ＝2.令x ＝0，则y ＝2×0＋4＝4，∴B (0，4)，∴BO ＝4.∵PO ＝2AO ＝4，点P 在坐标轴上，∴点P 有以下四种情况：(1)当点P 在x 轴的负半轴上时，AP ＝2，∴S △ABP ＝12AP ·BO ＝12×2×4＝4； (2)当点P 在x 轴的正半轴上时，AP ＝6，∴S △ABP ＝12AP ·BO ＝12×6×4＝12； (3)当点P 在y 轴的负半轴上时，PB ＝PO ＋BO ＝4＋4＝8，∴S △ABP ＝12PB ·AO ＝12×8×2＝8； (4)当点P 在y 轴的正半轴上时，PO ＝4，点P ，B 重合，△ABP 不存在．。

人教版八年级下册八年级下第19章《一次函数》单元测试题及答案(1)

新人教版八年级数学第19章《一次函数》单元测试（1）时间：10分钟满分：120分一．选择题（每小题3分，共30分）1.函数y=21-x 中，自变量x 的取值范围是（）A.x ＞2B.x ＜2C.x ≠2D.x ≠-2 2.关于函数y=-2x+1,下列结论正确的是（）A.图形必经过点（-2,1）B.图形经过第一、二、三象限C.当x ＞21时,y ＜0 D.y 随x 的增大而增大 3.如图，一次函数y=kx+b(k ≠0) 的图象经过A,B 两点，则关于x 的不等式kx+b ＜0的解集是（）A.m ＞-1B.m ＜1C.-1＜m ＜1D.-1≤m ≤14.直线y=-2x+m 与直线y=2x-1的焦点在第四象限，则 m 的取值范围是（）A.m ＞-1B.m ＜1C.-1＜m ＜1D.-1≤m ≤1 5.若一次函数y=(1-2m)x+m 的图象经过点A(x 1， y 1)和点B(x 2，y2)，当x 1＜x 2时，y 1＜y2，且与y 轴相交于正半轴，则 m 的取值范围是（）A.m ＞0B.m ＜21C.0＜m ＜21D. .m ＞216.若函数y= 则当函数值y=8时，自变量x 的值是（） A. 6±B.4C. 6±或4 D.4或-67.一艘轮船在同一航线上往返于甲、乙两地，已知轮船在静水中的速度为15㎞/h,水流速度为5 ㎞/h,轮船先从甲地顺水航行到乙地在乙地停留一段时间后，又从乙地逆水航行返回甲地，设轮船从甲地出发所用时间为 t(h),航行的路程s(㎞),则s 与t 的函数图象大致是（）C8.一次函数y=kx+b 的图象如图所示，当x ＜1时，y 的取值范围是（） A.-2＜y ＜0 B. -4＜y ＜0 C. y ＜-2 D. y ＜-4 9.将直线y=-2x 向右平移2个单位所得直线的解析式为（）A.y=-2x+2B.y=-2(x+2)C.y=-2x-2D.y=-2(x-2)10.如图，小亮在操场上玩，一段时间内沿M →A →B →M 的路径匀速散步，能近似刻画小亮到出发点M 的距离y 与x 之间关系的函数图象是（）二. 填空题（每小题3分，共24分）11.将直线y=-2x+3向下平移2个单位得到的直线为。

人教版八年级数学下册《19.2 一次函数》同步练习包含答案

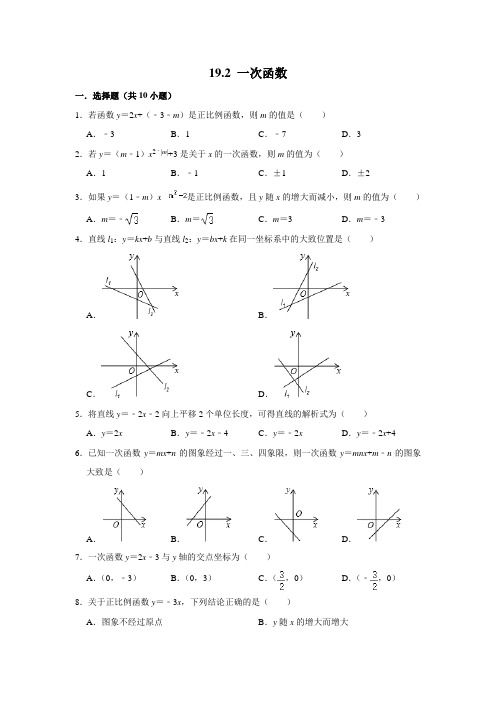
19.2 一次函数一．选择题（共10小题）1．若函数y＝2x+（﹣3﹣m）是正比例函数，则m的值是（）A．﹣3B．1C．﹣7D．32．若y＝（m﹣1）x2﹣|m|+3是关于x的一次函数，则m的值为（）A．1B．﹣1C．±1D．±23．如果y＝（1﹣m）x是正比例函数，且y随x的增大而减小，则m的值为（）A．m＝﹣B．m＝C．m＝3D．m＝﹣34．直线l1：y＝kx+b与直线l2：y＝bx+k在同一坐标系中的大致位置是（）A．B．C．D．5．将直线y＝﹣2x﹣2向上平移2个单位长度，可得直线的解析式为（）A．y＝2x B．y＝﹣2x﹣4C．y＝﹣2x D．y＝﹣2x+46．已知一次函数y＝mx+n的图象经过一、三、四象限，则一次函数y＝mnx+m﹣n的图象大致是（）A．B．C．D．7．一次函数y＝2x﹣3与y轴的交点坐标为（）A．（0，﹣3）B．（0，3）C．（，0）D．（﹣，0）8．关于正比例函数y＝﹣3x，下列结论正确的是（）A．图象不经过原点B．y随x的增大而增大C．图象经过第二、四象限D．当x＝时，y＝19．在平面直角坐标系中，一次函数y＝﹣2x+1的图象经过P1（﹣1，y1），P2（2，y2）两点，则（）A．y1＞y2B．y1＜y2C．y1＝y2D．y1≥y210．两个一次函数y1＝ax+b与y2＝bx+a（a，b为常数，且ab≠0），它们在同一个坐标系中的图象可能是（）A．B．C．D．二．填空题（共4小题）11．如果正比例函数y＝（k﹣3）x的图象经过第一、三象限，那么k的取值范围是．12．正比例函数的图象是，当k＞0时，直线y＝kx过第象限，y随x的增大而．13．一次函数y＝kx+b的图象如图所示，当y＞0时，x的取值范围是．14．如图，将含45°角的直角三角尺放置在平面直角坐标系中，其中A（﹣2，0），B（0，1），则直线BC的函数表达式为．三．解答题15．已知一次函数y＝kx+b（k≠0）的图象交x轴于点A（2，0），交y轴于点B，且△AOB 的面积为3，求此一次函数的解析式．16．正比例函数y＝kx中，当x增加2时，y增加3，求该正比例函数的解析式．17．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q 为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“距离“，记作d（M，N）．特别的，当图形M，N有公共点时，记作d（M，N）＝0．一次函数y＝kx+2的图象为L，L与y轴交点为D，△ABC中，A（0，1），B（﹣1，0），C（1，0）．（1）求d（点D，△ABC）＝；当k＝1时，求d（L，△ABC）＝；（2）若d（L，△ABC）＝0．直接写出k的取值范围；（3）函数y＝x+b的图象记为W，若d（W，△ABC）≤1，求出b的取值范围．18．如图，直线y＝x+4与x轴相交于点A，与y轴相交于点B．（1）求△AOB的面积；（2）过B点作直线BC与x轴相交于点C，若△ABC的面积是16，求点C的坐标．19．已知正比例函数y＝kx的图象经过点A（2，4），点B（6，0）为x轴正半轴上的一点．（1）求正比例函数的解析式；（2）点P为正比例函数图象上的一个动点，若△ABP为等腰三角形，求点P的坐标．20．在平面直角坐标系xOy中，函数y1＝x﹣2的图象与函数y2＝的图象在第一象限有一个交点A，且点A的横坐标是6．（1）求m的值；（2）补全表格并以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点，补充画出y2的函数图象；x﹣3﹣2﹣101 1.2 1.523456789 y2﹣1157 5.2 3.52112（3）写出函数y2的一条性质：．（4）已知函数y1与y2的图象在第一象限有且只有一个交点A，若函数y3＝x+n与y2的函数图象有三个交点，求n的取值范围．参考答案一．选择题（共10小题）1．A．2．B．3．B．4．C．5．C．6．A．7．A．8．C．9．A．10．B．二．填空题（共4小题）11．k＞3．12．一条直线；一、三；增大．13．x＜2．14．y＝﹣x+1．三．解答题15．解：∵A（2，0），S△AOB＝3，∴OB＝3，∴B（0，3）或（0，﹣3）．①当B（0，3）时，把A（2，0）、B（0，3）代入y＝kx+b中得∴，解得：．∴一次函数的解析式为．②当B（0，﹣3）时，把A（2，0）、B（0，﹣3）代入y＝kx+b中得，，解得：．∴．综上所述，该函数解析式为y＝﹣x+3或y＝x﹣3．16．解：∵当x增加2时，y增加3，∴y+3＝k（x+2），y+3＝kx+2k，∵y＝kx，∴3＝2k，解得：k＝，∴正比例函数解析式为y＝x．17．解：（1）一次函数y＝kx+2的图象与y轴交点D（0，2），d（点D，△ABC）表示点D到△ABC的最小距离，就是点D到点A的距离，即：AD＝2﹣1＝1，∴d（点D，△ABC）＝1当k＝1时，直线y＝x+2，此时直线L与AB所在的直线平行，且△ABC和△DOE均是等腰直角三角形，d（L，△ABC）表示直线L到△ABC的最小距离，就是图中的AF，在等腰直角三角形ADF中，AD＝1，AF＝1×＝d（L，△ABC）＝故答案为：1，；（2）若d（L，△ABC）＝0．说明直线L：y＝kx+2与△ABC有公共点，因此有两种情况，即：k＞0或k＜0，仅有一个公共点时如图所示，即直线L 过B点，或过C点，此时可求出k＝2或k＝﹣2，根据直线L与△ABC有公共点，∴k≥2或k≤﹣2，答：若d（L，△ABC）＝0时．k的取值范围为：k≥2或k≤﹣2．（3）函数y＝x+b的图象W与x轴、y轴交点所围成的三角形是等腰直角三角形，并且函数y＝x+b的图象与AB平行，当d（W，△ABC）＝1时，如图所示：在△AGM中，AG＝GM＝1，则AM＝，OM＝1+，M（0，1+）；即：b＝1+；同理：OQ＝OP＝1+，Q（0，﹣1﹣），即：b＝﹣1﹣，若d（W，△ABC）≤1，即b的值在M、N之间∴﹣1﹣≤b≤1+答：若d（W，△ABC）≤1，b的取值范围为﹣1﹣≤b≤1+．18．解：（1）把x＝0代入y＝x+4得：y＝4，即点B的坐标为：（0，4），把y＝0代入y＝x+4得：x+4＝0，解得：x＝﹣6，即点A的坐标为：（﹣6，0），S△AOB＝＝12，即△AOB的面积为12，（2）根据题意得：点B到AC的距离为4，S△ABC＝＝16，解得：AC＝8，即点C到点A的距离为8，﹣6﹣8＝﹣14，﹣6+8＝2，即点C的坐标为：（﹣14，0）或（2，0）．19．解：（1）把A（2，4）代入y＝kx得2k＝4，解得k＝2，所以正比例函数的解析式为y＝2x；（2）设P（t，2t），AP2＝（t﹣2）2+（2t﹣4）2，PB2＝（t﹣6）2+（2t）2，AB2＝（6﹣2）2+（0﹣4）2＝32，当AP＝PB时，（t﹣2）2+（2t﹣4）2＝（t﹣6）2+（2t）2，解得t＝﹣2，此时P点坐标为（﹣2，﹣4）；（t﹣2）2+（2t﹣4）2＝32，解得t＝，此时P点坐标为（，当AP＝AB时，）或（，）；当PB＝AB时，（t﹣6）2+（2t）2＝32，解得t1＝，t2＝2（舍去），此时P点坐标为（，）．综上所述，满足条件的P点坐标为（﹣2，﹣4）或（，）或（，）或（，）．20．解：（1）在y1＝x﹣2中，令x＝6，则y＝2，即A（6，2），代入y＝x+﹣6，可得2＝6+﹣6，解得m＝12；（2）∵y2＝，∴当x＝﹣1时，y2＝3；当x＝5时，y2＝；如图所示：（3）由图可得，函数y2的一条性质：当x≤1时，y2随着x的增大而增大；故答案为：当x≤1时，y2随着x的增大而增大；（4）函数y1与y2的图象在第一象限有且只有一个交点A，当n＝﹣2时，函数y3＝x+n与函数y1＝x﹣2的图象重合，此时函数y3＝x+n与y2的函数图象有两个交点，当函数y3＝x+n的图象经过（1，7）时，函数y3＝x+n与y2的函数图象有两个交点，此时，把（1，7）代入y3＝x+n，可得n＝；∵函数y3＝x+n与y2的函数图象有三个交点，∴n的取值范围为﹣2＜n＜．。

人教版八年级下数学《第19章一次函数》专项训练含答案

人教版八年级下数学《第19章一次函数》专项训练含答案专训1.一次函数的两种常见应用名师点金：一次函数的两种常见应用主要体现在解决实际问题和几何问题．能够从函数图象中得到需要的信息，并求出函数解析式从而解决实际问题和几何问题，是一次函数应用价值的体现，这种题型常与一些热点问题结合，考查学生综合分析问题、解决问题的能力．利用函数图象解决实际问题题型1 行程问题(第1题)1．甲、乙两车从A 城出发匀速行驶至B 城，在整个行驶过程中，甲、乙两车离开A 城的距离y(km )与甲车行驶的时间t(h )之间的函数关系如图所示，则下列结论①A ，B 两城相距300 km ；②乙车比甲车晚出发1 h ，却早到1 h ；③乙车出发后2.5 h 追上甲车；④当甲、乙两车相距50 km 时，t ＝54或154. 其中正确的结论有( )A．1个B．2个C．3个D．4个2．甲、乙两地相距300 km，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系，折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系，根据图象，解答下列问题：(1)线段CD表示轿车在途中停留了________h；(2)求线段DE对应的函数解析式；(3)求轿车从甲地出发后经过多长时间追上货车．(第2题)题型2工程问题3．甲、乙两组工人同时加工某种零件，乙组在工作中有一段时间停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y(件)与时间x(h)之间的函数图象如图所示．(1)求甲组加工零件的数量y与时间x之间的函数解析式．(2)求乙组加工零件总量a的值．(3)甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？(第3题)题型3实际问题中的分段函数4．某种铂金饰品在甲、乙两个商店销售．甲店标价为477元/g，按标价出售，不优惠；乙店标价为530元/g，但若买的铂金饰品质量超过3 g，则超出部分可打八折．(1)分别写出到甲、乙两个商店购买该种铂金饰品所需费用y(元)和质量x(g)之间的函数解析式；(2)李阿姨要买一条质量不少于4 g且不超过10 g的此种铂金饰品，到哪个商店购买合算？5．我国是世界上严重缺水的国家之一．为了增强居民的节水意识，某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一个月用水10 t以内(包括10 t)的用户，每吨收水费a元；一个月用水超过10 t的用户，10 t水仍按每吨a元收费，超过10 t的部分，按每吨b(b＞a)元收费．设一户居民月用水x t，应交水费y元，y与x之间的函数关系如图所示．(1)求a的值；某户居民上月用水8 t，应交水费多少元？(2)求b的值，并写出当x＞10时，y与x之间的函数解析式．(第5题)利用一次函数解几何问题题型4利用图象解几何问题6．如图①所示，正方形ABCD的边长为6 cm，动点P从点A出发，在正方形的边上沿A→B→C→D运动，设运动的时间为t(s)，三角形APD的面积为S(cm2)，S与t的函数图象如图②所示，请回答下列问题：(1)点P在AB上运动的时间为________s，在CD上运动的速度为________cm/s，三角形APD的面积S的最大值为________cm2；(2)求出点P在CD上运动时S与t之间的函数解析式；(3)当t为何值时，三角形APD的面积为10 cm2?(第6题)题型5利用分段函数解几何问题(分类讨论思想、数形结合思想)7．在长方形ABCD中，AB＝3，BC＝4，动点P从点A开始按A→B→C→D的方向运动到点D.如图，设动点P所经过的路程为x，△APD 的面积为y.(当点P与点A或D重合时，y＝0)(1)写出y与x之间的函数解析式；(2)画出此函数的图象．(第7题)专训2.二元一次方程(组)与一次函数的四种常见应用名师点金：二元一次方程(组)与一次函数的关系很好地体现了“数”与“形”的结合，其常见应用有：利用两条直线的交点坐标确定方程组的解；利用方程(组)的解求两直线的交点坐标；方程组的解与两个一次函数图象位置的关系；利用二元一次方程组求一次函数的解析式．利用两直线的交点坐标确定方程组的解1．已知直线y ＝－x ＋4与y ＝x ＋2如图所示，则方程组⎩⎪⎨⎪⎧y ＝－x ＋4，y ＝x ＋2 的解为( )(第1题)A .⎩⎪⎨⎪⎧x ＝3y ＝1 B .⎩⎪⎨⎪⎧x ＝1y ＝3 C .⎩⎪⎨⎪⎧x ＝0y ＝4 D .⎩⎪⎨⎪⎧x ＝4y ＝0 2．已知直线y ＝2x 与y ＝－x ＋b 的交点坐标为(1，a)，试确定方程组⎩⎪⎨⎪⎧2x －y ＝0，x ＋y －b ＝0的解和a ，b 的值．3．在平面直角坐标系中，一次函数y ＝－x ＋4的图象如图所示．(1)在同一坐标系中，作出一次函数y ＝2x －5的图象；(2)用作图象的方法解方程组⎩⎪⎨⎪⎧x ＋y ＝4，2x －y ＝5； (3)求一次函数y ＝－x ＋4与y ＝2x －5的图象与x 轴所围成的三角形的面积．(第3题)利用方程(组)的解求两直线的交点坐标4．已知方程组⎩⎪⎨⎪⎧－mx ＋y ＝n ，ex ＋y ＝f 的解为⎩⎪⎨⎪⎧x ＝4，y ＝6，则直线y ＝mx ＋n 与y ＝－ex ＋f 的交点坐标为( )A ．(4，6)B ．(－4，6)C ．(4，－6)D ．(－4，－6)5．已知⎩⎪⎨⎪⎧x ＝3，y ＝－2和⎩⎪⎨⎪⎧x ＝2，y ＝1是二元一次方程ax ＋by ＝－3的两个解，则一次函数y ＝ax ＋b 的图象与y 轴的交点坐标是( )A ．(0，－7)B ．(0，4)C .⎝ ⎛⎭⎪⎫0，－37D .⎝ ⎛⎭⎪⎫－37，0 方程组的解与两个一次函数图象位置的关系6．若方程组⎩⎪⎨⎪⎧x ＋y ＝2，2x ＋2y ＝3没有解，则一次函数y ＝2－x 与y ＝32－x 的图象必定( )A ．重合B ．平行C ．相交D ．无法确定7．直线y ＝－a 1x ＋b 1与直线y ＝a 2x ＋b 2有唯一交点，则二元一次方程组⎩⎪⎨⎪⎧a 1x ＋y ＝b 1，a 2x －y ＝－b 2的解的情况是( ) A ．无解 B ．有唯一解C ．有两个解D ．有无数解利用二元一次方程组求一次函数的解析式8．已知一次函数y ＝kx ＋b 的图象经过点A(1，－1)和B(－1，3)，求这个一次函数的解析式．9．已知一次函数y ＝kx ＋b 的图象经过点A(3，－3)，且与直线y ＝4x －3的交点B 在x 轴上．(1)求直线AB 对应的函数解析式；(2)求直线AB 与坐标轴所围成的三角形BOC(O 为坐标原点，C 为直线AB 与y 轴的交点)的面积．答案专训11．B2．解：(1)0.5(2)设线段DE对应的函数解析式为y＝kx＋b(2.5≤x≤4.5)．将D(2.5，80)，E(4.5，300)的坐标分别代入y＝kx＋b可得，80＝2.5k ＋b，300＝4.5k＋b.解得k＝110，b＝－195.所以y＝110x－195(2.5≤x≤4.5)．(3)设线段OA对应的函数解析式为y＝k1x(0≤x≤5)．将A(5，300)的坐标代入y＝k1x可得，300＝5k1，解得k1＝60.所以y＝60x(0≤x≤5)．令60x＝110x－195，解得x＝3.9.故轿车从甲地出发后经过3.9－1＝2.9(h)追上货车．3．解：(1)设甲组加工零件的数量y与时间x之间的函数解析式为y＝kx，因为当x＝6时，y＝360，所以k＝60.即甲组加工零件的数量y与时间x之间的函数解析式为y＝60x(0≤x≤6)．(2)a＝100＋100÷2×2×(4.8－2.8)＝300.(3)当工作2.8 h时共加工零件100＋60×2.8＝268(件)，所以装满第1箱的时刻在2.8 h 后．设经过x 1 h 装满第1箱．则60x 1＋100÷2×2(x 1－2.8)＋100＝300，解得x 1＝3.从x ＝3到x ＝4.8这一时间段内，甲、乙两组共加工零件(4.8－3)×(100＋60)＝288(件)，所以x>4.8时，才能装满第2箱，此时只有甲组继续加工．设装满第1箱后再经过x 2 h 装满第2箱．则60x 2＋(4.8－3)×100＝300，解得x 2＝2.故经过3 h 恰好装满第1箱，再经过2 h 恰好装满第2箱．4．解：(1)y 甲＝477x ，y 乙＝⎩⎪⎨⎪⎧530x （0≤x ≤3），424x ＋318（x ＞3）. (2)当477x ＝424x ＋318时，解得x ＝6.即当x ＝6时，到甲、乙两个商店购买所需费用相同；当477x<424x ＋318时，解得x<6，又x ≥4，于是，当4≤x ＜6时，到甲商店购买合算；当477x>424x ＋318时，解得x>6，又x ≤10，于是，当6＜x ≤10时，到乙商店购买合算．5．解：(1)当x ≤10时，由题意知y ＝ax.将x ＝10，y ＝15代入，得15＝10a ，所以a ＝1.5.故当x ≤10时，y ＝1.5x.当x ＝8时，y ＝1.5×8＝12. 故应交水费12元．(2)当x ＞10时，由题意知y ＝b(x －10)＋15.将x ＝20，y ＝35代入，得35＝10b ＋15，所以b ＝2.故当x ＞10时，y 与x 之间的函数解析式为y ＝2x －5.点拨：本题解题的关键是从图象中找出有用的信息，用待定系数法求出解析式，再解决问题．6．解：(1)6；2；18(2)PD ＝6－2(t －12)＝30－2t ，S ＝12AD·PD＝12×6×(30－2t)＝90－6t ，即点P 在CD 上运动时S 与t 之间的函数解析式为S ＝90－6t(12≤t ≤15)．(3)当0≤t ≤6时易求得S ＝3t ，将S ＝10代入，得3t ＝10，解得t ＝103；当12≤t ≤15时，S ＝90－6t ，将S ＝10代入，得90－6t ＝10，解得t ＝403.所以当t 为103或403时，三角形APD 的面积为10 cm 2. 7．解：(1)点P 在边AB ，BC ，CD 上运动时所对应的y 与x 之间的函数解析式不相同，故应分段求出相应的函数解析式．①当点P 在边AB 上运动，即0≤x ＜3时，y ＝12×4x ＝2x ； ②当点P 在边BC 上运动，即3≤x ＜7时，y ＝12×4×3＝6； ③当点P 在边CD 上运动，即7≤x ≤10时，y ＝12×4(10－x)＝－2x ＋20. 所以y 与x 之间的函数解析式为y ＝⎩⎪⎨⎪⎧2x （0≤x ＜3），6 （3≤x ＜7），－2x ＋20 （7≤x ≤10）.(2)函数图象如图所示．(第7题)点拨：本题考查了分段函数在动态几何中的运用，体现了数学中的分类讨论思想和数形结合思想．根据点P 在边AB ，BC ，CD 上运动时所对应的y 与x 之间的函数解析式不相同，分段求出相应的函数解析式，再画出相应的函数图象．专训21．B2．解：将(1，a)代入y ＝2x ，得a ＝2.所以直线y ＝2x 与y ＝－x ＋b 的交点坐标为(1，2)，所以方程组⎩⎪⎨⎪⎧2x －y ＝0，x ＋y －b ＝0的解是⎩⎪⎨⎪⎧x ＝1，y ＝2.将(1，2)代入y ＝－x ＋b ，得2＝－1＋b ，解得b ＝3.3．解：(1)画函数y ＝2x －5的图象如图所示．(2)由图象看出两直线的交点坐标为(3，1)，所以方程组的解为⎩⎪⎨⎪⎧x ＝3，y ＝1.(第3题)(3)直线y ＝－x ＋4与x 轴的交点坐标为(4，0)，直线y ＝2x －5与x 轴的交点坐标为⎝ ⎛⎭⎪⎫52，0，又由(2)知，两直线的交点坐标为(3，1)，所以三角形的面积为12×⎪⎪⎪⎪⎪⎪4－52×1＝34. 4．A 5.C 6.B 7.B8．解：依题意将A(1，－1)与B(－1，3)的坐标代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧k ＋b ＝－1，－k ＋b ＝3，解得k ＝－2，b ＝1，所以这个一次函数的解析式为y ＝－2x ＋1.9．解：(1)因为一次函数y ＝kx ＋b 的图象与直线y ＝4x －3的交点B 在x 轴上，所以将y ＝0代入y ＝4x －3中，得x ＝34，所以B ⎝ ⎛⎭⎪⎫34，0，把A(3，－3)，B ⎝ ⎛⎭⎪⎫34，0的坐标分别代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧3k ＋b ＝－3，34k ＋b ＝0，解得⎩⎪⎨⎪⎧k ＝－43，b ＝1.则直线AB 对应的函数解析式为y ＝－43x ＋1.(2)由(1)知直线AB 对应的函数解析式为y ＝－43x ＋1，所以直线AB 与y 轴的交点C 的坐标为(0，1)，所以OC ＝1，又B ⎝ ⎛⎭⎪⎫34，0，所以OB ＝34.所以S 三角形BOC ＝12OB·OC＝12×34×1＝38.即直线AB 与坐标轴所围成的三角形BOC 的面积为38.。

人教版初中数学八年级下册第19章习题课件 19.2.2 正比例函数的图象和性质

【点拨】由题意可知－3m＞0，∴m＜0，∴P(m，5)在第二象限．
9．已知函数 y＝(m－1)xm2－3 是正比例函数． (1)若 y 随 x 的增大而减小，求 m 的值；
解：由题意知m2－3＝1且m－1<0，故m＝－2.
(2)若函数的图象经过第一、三象限，求 m 的值；解：由题意知m2－3＝1且m－1>0，故m＝2.
第十九章一次函数
19.2 一次函数第2课时正比例函数的图象和性质
提示：点击进入习题
1 原点；第三；第二 2C 3D 4C 5 (1)增大 (2)减小
6A 7B示
1．正比例函数 y＝kx(k 是常数，k≠0)的图象是一条经过__原__点____ 的直线，也称它为直线 y＝kx；当 k＞0 时，直线经过第一、__第__三____象限；当 k＜0 时，直线经过__第__二____、第四象限．
5．(1)当 k>0 时，函数 y＝kx，y 随 x 的增大而__增__大____； (2)当 k<0 时，函数 y＝kx，y 随 x 的增大而__减__小____．
6．已知在正比例函数 y＝(a－1)x 中，y 随 x 的增大而减小，则 a 的取值范围是( A ) A．a＜1 B．a＞1 C．a≥1 D．a≤1
7．下列关于正比例函数 y＝－5x 的说法中，正确的是( B ) A．当 x＝1 时，y＝5 B．它的图象是一条经过原点的直线 C．y 随 x 的增大而增大 D．它的图象经过第一、三象限
*8.在正比例函数 y＝－3mx 中，函数 y 随 x 的增大而增大，则 P(m，5)在( B ) A．第一象限 B．第二象限 C．第三象限 D．第四象限
(2)在 x 轴上是否存在一点 P，使△AOP 的面积为 5？若存在，求点 P 的坐标；若不存在，请说明理由．