An ordinary differential equation model for the multistep transformation

合集下载

常微分方程的英文

常微分方程的英文Ordinary Differential EquationsIntroductionOrdinary Differential Equations (ODEs) are mathematical equations that involve derivatives of unknown functions with respect to a single independent variable. They find application in various scientific disciplines, including physics, engineering, economics, and biology. In this article, we will explore the basics of ODEs and their importance in understanding dynamic systems.ODEs and Their TypesAn ordinary differential equation is typically represented in the form:dy/dx = f(x, y)where y represents the unknown function, x is the independent variable, and f(x, y) is a given function. Depending on the nature of f(x, y), ODEs can be classified into different types.1. Linear ODEs:Linear ODEs have the form:a_n(x) * d^n(y)/dx^n + a_(n-1)(x) * d^(n-1)(y)/dx^(n-1) + ... + a_1(x) * dy/dx + a_0(x) * y = g(x)where a_i(x) and g(x) are known functions. These equations can be solved analytically using various techniques, such as integrating factors and characteristic equations.2. Nonlinear ODEs:Nonlinear ODEs do not satisfy the linearity condition. They are generally more challenging to solve analytically and often require the use of numerical methods. Examples of nonlinear ODEs include the famous Lotka-Volterra equations used to model predator-prey interactions in ecology.3. First-order ODEs:First-order ODEs involve only the first derivative of the unknown function. They can be either linear or nonlinear. Many physical phenomena, such as exponential decay or growth, can be described by first-order ODEs.4. Second-order ODEs:Second-order ODEs involve the second derivative of the unknown function. They often arise in mechanical systems, such as oscillators or pendulums. Solving second-order ODEs requires two initial conditions.Applications of ODEsODEs have wide-ranging applications in different scientific and engineering fields. Here are a few notable examples:1. Physics:ODEs are used to describe the motion of particles, fluid flow, and the behavior of physical systems. For instance, Newton's second law of motion can be formulated as a second-order ODE.2. Engineering:ODEs are crucial in engineering disciplines, such as electrical circuits, control systems, and mechanical vibrations. They allow engineers to model and analyze complex systems and predict their behavior.3. Biology:ODEs play a crucial role in the study of biological dynamics, such as population growth, biochemical reactions, and neural networks. They help understand the behavior and interaction of different components in biological systems.4. Economics:ODEs are utilized in economic models to study issues like market equilibrium, economic growth, and resource allocation. They provide valuable insights into the dynamics of economic systems.Numerical Methods for Solving ODEsAnalytical solutions to ODEs are not always possible or practical. In such cases, numerical methods come to the rescue. Some popular numerical techniques for solving ODEs include:1. Euler's method:Euler's method is a simple numerical algorithm that approximates the solution of an ODE by using forward differencing. Although it may not provide highly accurate results, it gives a reasonable approximation when the step size is sufficiently small.2. Runge-Kutta methods:Runge-Kutta methods are higher-order numerical schemes for solving ODEs. They give more accurate results by taking into account multiple intermediate steps. The most commonly used method is the fourth-order Runge-Kutta (RK4) algorithm.ConclusionOrdinary Differential Equations are a fundamental tool for modeling and analyzing dynamic systems in various scientific and engineering disciplines. They allow us to understand the behavior and predict the evolution of complex systems based on mathematical principles. With the help of analytical and numerical techniques, we can solve and interpret different types of ODEs, contributing to advancements in science and technology.。

ordinary的意思用法总结

ordinary的意思用法总结ordinary一般的,平常的,一般的,平凡的的意思。

那你们想知道ordinary的用法吗?今日我给大家带来了ordinary的用法 ,期望能够帮忙到大家，一起来学习吧。

ordinary的意思adj. 一般的,平常的,一般的,平凡的ordinary用法ordinary可以用作形容词ordinary的基本意思是“一般的”“平常的”“一般的”“平凡的”。

指与一般事物的性质标准相同,强调“平常”而无高超奇怪之处。

ordinary在句中可用作定语,也可用作表语,间或也可用作宾语补足语。

ordinary没有比较级和最高级。

ordinary用作形容词的用法例句I just want an ordinary car without the frills.我只要一辆没有多余装饰的一般汽车。

Now electrical appliances have entered into ordinary families.现在家用电器已经步入一般家庭。

It was an ordinary lunch of soup and a sandwich.那是一顿平淡的午餐:一份汤,一份三明治。

ordinary用法例句1、It was just an ordinary voice, but he sang in tune.他声音很一般，但唱得都在调子上。

2、Ordinary people are at the mercy of faceless bureaucrats.一般人的命运任凭那些平凡刻板的官僚们摆布。

3、This Human Rights Act is enforceable in the ordinary courts.这项《人权法案》适用于一般法庭。

ordinary词组 | 习惯用语in ordinary (职务等)常任的;(待修的船只等)闲搁着的ordinary people 一般人，一般人out of the ordinary 不平常的ordinary life 正常寿命;常规生命ordinary differential equation 常微分方程ordinary day 平常的一天;[地磁]平常日ordinary course 正常贸易;常规过程ordinary temperature 常温，室温ordinary portland cement 一般硅酸盐水泥ordinary workers 一般劳动者ordinary income 一般收入ordinary mail n. 平信ordinary share 一般股ordinary light 寻常光;一般光线ordinary level 一般程度的;(英)一般级考试(等于O leve)ordinary goods 一般品;一般货物ordinary quality 中等质量ordinary 英语例句库1.The royal family is insulated from many of the difficulties faced by ordinary people.王室成员都毋须应付平民所面临的很多困难。

Ordinary differential equations with only entire solutions

a rX iv:mat h /97621v1[mat h.CV]6J u n1997ORDINARY DIFFERENTIAL EQUATIONS WITH ONLY ENTIRE SOLUTIONS ERIK ANDERS ´EN Abstract.We prove necessary and suﬃcient conditions for a system ˙z i =z i p i (z )(p i a polynomial)to have only entire analytic functions as solutions. 1.preliminaries We will need the following elementary facts from Nevanlinna theory.For any entire function of one complex variable f (z )we set m (r,f )=1a and T (r,f )=m (r,f )+N (r,f ).In the deﬁnition of N ,the sum is taken over all poles a of f ,with regard to multiplicity.The function T (r,f )is called the Nevanlinna characteristic of f .The following properties are easily veriﬁed.T (r,f 1+f 2)≤T (r,f 1)+T (r,f 2)+O (1)T (r,f 1f 2)≤T (r,f 1)+T (r,f 2),T (r,f d )=dT (r,f ).(1)Here and in the sequel,the estimates O (g )and o (g )are as r →∞.The ﬁrst fundamental theorem of Nevanlinna theory says that T (r,1/f )=T (r,f )+O (1).We also have the Lemma of the logarithmic derivative (LLD),m (r,f ′/f )=o excl (T (r,f )).Here o excl means that the estimate holds outside a set of ﬁnite measure.We also use the corresponding notation O excl .From LLD and the preceding inequalities it follows thatm (r,f (k ))≤(1+o excl (1)))T (r,f )(2)m (r,f (k )/f )=o excl (T (r,f ))(3)2ERIK ANDERS´ENfor all positive integers k.2.Borel’s TheoremWe need a version of a theorem named after Borel,which is classical,but which is proved here since I have not found a good reference to it.We call an entire holomorphic function a unit if it has no zeros.Theorem1.Let f be an entire function and u1,u2,...,u n be units satis-fyingu i=f.(4) Then one of the following cases holds.1.T(r,u i)=O excl(T(r,f)+1)for all i.2.Some subsum i∈I u i=0.Proof.The proof is by induction.If n=1then Case1holds automatically so there is nothing to prove.We assume that the theorem holds for sums with less than n terms.If we diﬀerentiate(4)we getu(j)iORDINARY DIFFERENTIAL EQUATIONS WITH ONLY ENTIRE SOLUTIONS3(a)T(v i,r)=O excl(T(1,r)+1)=O excl(1)for all i.Then all v i areconstant and u i=a i u1for some a i.The sum(4)now becomes( a i+1)u1=f.If a i+1=0,then f=0and we haveCase2;otherwise,u1is proportional to f and then all u i are alsoproportional to f.We then have Case1.(b) i∈I v i=0for some set I.Then i∈I c i u i=0and this sum isshorter than(5).This is a contradiction.3.Differential equationsTheorem2.Let p i be Laurent-polynomials and˙z i=z i p i(z)z i(0)=c i1≤i≤n(7) be an ordinary diﬀerential equation such that for all c in some open set all components of the solutions are units.Thenp(Z)=n−1k=1u kθk(M(k))+u0.(8)Here u k∈C n,M(k)∈C[Z,Z−1]k is deﬁned by M(n)=Z andM(k−1)i= M(k)j a(k)ij for k=n,...,2,(9) where a(k)are(k−1,k)-matrices satisfying a(k)...a(n)u k=0andθk are Laurent-polynomials.Conversely,any system of the form(8)has only entire solutions,and all components are either units or identically zero.The proof needs a lemma.We write p(Z)=(p1(Z),...,p n(Z)),p(Z)= pαZαand pα=(pα,1,...,pα,n).We let Dg denote(˙g1/g1,...,˙g n/g n).Let S be the set of meromorphic functions satisfying T(r,f)=o excl(T(r,z1)+···+T(r,z n)+1).Lemma1.Let M be the multiplicative module generated by of N={Zα: pα,i=0for some i}.Then dim M<n.Proof.Choose c so that α∈A pα,i cα=0for all non-zero subpolynomials and all indices i,and so that all components of the solution are units.Let z(t) be the solution with z(0)=c.Apply Borel’s theorem to pα,i zα=˙z i/z i. Because of our choice of initial condition,Case2does not hold.Therefore, N⊂S.It follows from the rules(1)that M⊂S.Assume that the dimension of M is n.Then for each i there is d i such that z d i∈M⊂S.Again by(1),z i∈S for each i.This is impossible and therefore the dimension is less than n.Proof of Theorem2.The proof is by induction.The theorem holds if n=1, so we assume that it holds for systems with smaller number of variables.We ﬁrst prove the necessity of(8).Assume that(7)has only entire solutions. By Lemma1we can write p(Z)=f(M),where M=(M1,...,M l)and M i= Z a ij j,and l<n.We may assume that a=(a ij)has full rank since4ERIK ANDERS ´ENwe can otherwise drop some variables M i .If l <n −1we can complete a to an (n −1,n )-matrix of full rank,so we assume that l =n −1.Set m i = z a ij j .Then Dz =p (z )=f (m )and logarithmic diﬀerentiation gives Dm =af (m ).By induction,af (M )=n −2 k =1v k θk (M (k ))+v 0,where M (k )are given by (9)for k =n −1,...,2and a (k )...a (n −1)v k =0.Since a is surjective v k =au k for some u k sof (M )−n −2 k =1v k θk (M (k ))−v 0∈Ker a.Since this kernel is one-dimensional we havef (M )=u n −1θn −1(M )+n −2 k =1u k θk (M (k ))+u 0for some u n −1∈Ker a ⊂C n and some Laurent-polynomial θn −1.If we set M (n −1)=M and a (n −1)=a the ﬁrst half of the theorem is proved.If the system is of form (8)then we get as above thatDm =a(n )(n −1 k =1u k θk (m (k ))+u 0)=n −2 k =1a (n )u k θk (m (k ))+a (n )u 0since a (n )u n =0by assumption.By induction,this system has only entire solutions m (t ).An integration of ˙z i /z i =f i (m (t ))now proves the rest of the theorem.Remark .Although the form (8),(9)is complicated,the proof gives an extremely simple recursive algorithm to determine if all solutions to a system are entire.First compute the multiplicative span of all Z αsuch that p α,i =0for some i .If this is the whole space,the system does have non-entire solutions.Otherwise,let M i be a basis for this space,and express p (Z )=f (M )in terms of this basis.Diﬀerentiate logarithmically to get a new equation Dm =af (m )(with notations as in the theorem).The original system has only entire solutions if and only if this new system has.Remark .If the polynomials p i are genuine polynomials,it is immediately clear that all components of any solution are either zero-free or identically zero.Corollary 1.All complete polynomial vector ﬁelds on (C ∗)n are of the form(7)with p satisfying (8).ORDINARY DIFFERENTIAL EQUATIONS WITH ONLY ENTIRE SOLUTIONS5 Corollary2.All complete polynomial vectorﬁelds on(C∗)n preserve the volume form dz i/z i.Proof.The proof is again by induction.We computedz i =d˙z i z i−˙z i dz iz2i=d(p i(z)).This shows in particular that the result holds for n=1.Also,we compute dz i= i dz1dt dz i z n= i z i∂p i z i .We use the notation of the proof of the theorem and in particular the result that p(z)=f(m)and Dm=af(m).We have to prove that z i∂p i/∂z i(z)= 0,so we computei z i∂f i∂m j∂m j∂m j m j a ji∂m jm j a ji= j∂(af)j。

Differential equation

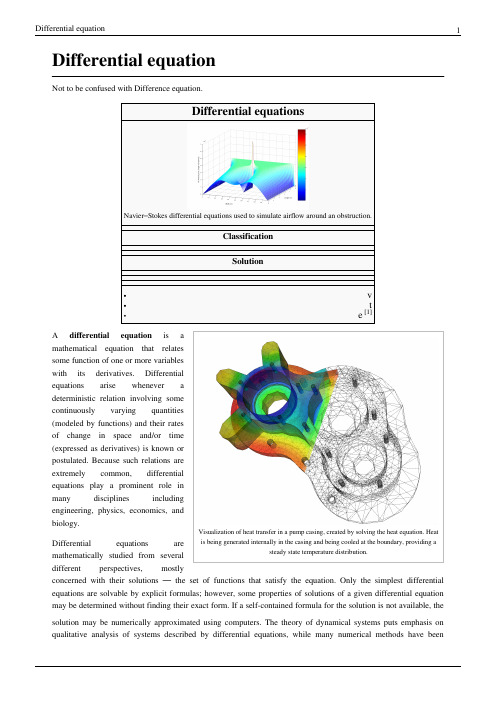
Differential equationNot to be confused with Difference equation.Stokes differential equations used to simulate airflow around an obstruction.ClassificationSolutionVisualization of heat transfer in a pump casing, created by solving the heat equation. Heat is being generated internally in the casing and being cooled at the boundary, providing a steady state temperature distribution.A differential equation is amathematical equation that relatessome function of one or more variableswith its derivatives. Differentialequations arise whenever adeterministic relation involving somecontinuously varying quantities(modeled by functions) and their ratesof change in space and/or time(expressed as derivatives) is known orpostulated. Because such relations areextremely common, differentialequations play a prominent role inmany disciplines includingengineering, physics, economics, andbiology.Differential equations aremathematically studied from severaldifferent perspectives, mostlyconcerned with their solutions — the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form. If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have beendeveloped to determine solutions with a given degree of accuracy.ExampleFor example, in classical mechanics, the motion of a body is described by its position and velocity as the time value varies. Newton's laws allow one (given the position, velocity, acceleration and various forces acting on the body) to express these variables dynamically as a differential equation for the unknown position of the body as a function of time.In some cases, this differential equation (called an equation of motion) may be solved explicitly.An example of modelling a real world problem using differential equations is the determination of the velocity of a ball falling through the air, considering only gravity and air resistance. The ball's acceleration towards the ground is the acceleration due to gravity minus the acceleration due to air resistance. Gravity is considered constant, and air resistance may be modeled as proportional to the ball's velocity. This means that the ball's acceleration, which is a derivative of its velocity, depends on the velocity (and the velocity depends on time). Finding the velocity as a function of time involves solving a differential equation and verifying its validity.Directions of studyThe study of differential equations is a wide field in pure and applied mathematics, physics, and engineering. All of these disciplines are concerned with the properties of differential equations of various types. Pure mathematics focuses on the existence and uniqueness of solutions, while applied mathematics emphasizes the rigorous justification of the methods for approximating solutions. Differential equations play an important role in modelling virtually every physical, technical, or biological process, from celestial motion, to bridge design, to interactions between neurons. Differential equations such as those used to solve real-life problems may not necessarily be directly solvable, i.e. do not have closed form solutions. Instead, solutions can be approximated using numerical methods.Mathematicians also study weak solutions (relying on weak derivatives), which are types of solutions that do not have to be differentiable everywhere. This extension is often necessary for solutions to exist.The study of the stability of solutions of differential equations is known as stability theory.NomenclatureThe theory of differential equations is well developed and the methods used to study them vary significantly with the type of the equation.Ordinary and partial•An ordinary differential equation (ODE) is a differential equation in which the unknown function (also known as the dependent variable) is a function of a single independent variable. In the simplest form, the unknown function is a real or complex valued function, but more generally, it may be vector-valued or matrix-valued: this corresponds to considering a system of ordinary differential equations for a single function.Ordinary differential equations are further classified according to the order of the highest derivative of the dependent variable with respect to the independent variable appearing in the equation. The most important cases for applications are first-order and second-order differential equations. For example, Bessel's differential equation(in which y is the dependent variable) is a second-order differential equation. In the classical literature a distinction is also made between differential equations explicitly solved with respect to the highest derivative and differential equations in an implicit form. Also important is the degree, or (highest) power, of the highest derivative(s) in the equation (cf. : degree of a polynomial). A differential equation is called a nonlinear differential equation if its degree is not one (a sufficient but unnecessary condition).• A partial differential equation (PDE) is a differential equation in which the unknown function is a function of multiple independent variables and the equation involves its partial derivatives. The order is defined similarly to the case of ordinary differential equations, but further classification into elliptic, hyperbolic, and parabolic equations, especially for second-order linear equations, is of utmost importance. Some partial differentialequations do not fall into any of these categories over the whole domain of the independent variables and they are said to be of mixed type.Linear and non-linearBoth ordinary and partial differential equations are broadly classified as linear and nonlinear.• A differential equation is linear if the unknown function and its derivatives appear to the power 1 (products of the unknown function and its derivatives are not allowed) and nonlinear otherwise. The characteristic property of linear equations is that their solutions form an affine subspace of an appropriate function space, which results in much more developed theory of linear differential equations. Homogeneous linear differential equations are a further subclass for which the space of solutions is a linear subspace i.e. the sum of any set of solutions or multiples of solutions is also a solution. The coefficients of the unknown function and its derivatives in a linear differential equation are allowed to be (known) functions of the independent variable or variables; if these coefficients are constants then one speaks of a constant coefficient linear differential equation.•There are very few methods of solving nonlinear differential equations exactly; those that are known typically depend on the equation having particular symmetries. Nonlinear differential equations can exhibit verycomplicated behavior over extended time intervals, characteristic of chaos. Even the fundamental questions of existence, uniqueness, and extendability of solutions for nonlinear differential equations, and well-posedness of initial and boundary value problems for nonlinear PDEs are hard problems and their resolution in special cases is considered to be a significant advance in the mathematical theory (cf. Navier–Stokes existence and smoothness).However, if the differential equation is a correctly formulated representation of a meaningful physical process, then one expects it to have a solution.Linear differential equations frequently appear as approximations to nonlinear equations. These approximations are only valid under restricted conditions. For example, the harmonic oscillator equation is an approximation to the nonlinear pendulum equation that is valid for small amplitude oscillations (see below).ExamplesIn the first group of examples, let u be an unknown function of x, and c and ω are known constants.•Inhomogeneous first-order linear constant coefficient ordinary differential equation:•Homogeneous second-order linear ordinary differential equation:•Homogeneous second-order linear constant coefficient ordinary differential equation describing the harmonic oscillator:•Inhomogeneous first-order nonlinear ordinary differential equation:•Second-order nonlinear (due to sine function) ordinary differential equation describing the motion of a pendulum of length L:In the next group of examples, the unknown function u depends on two variables x and t or x and y.•Homogeneous first-order linear partial differential equation:•Homogeneous second-order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:•Third-order nonlinear partial differential equation, the Korteweg–de Vries equation:Related concepts• A delay differential equation (DDE) is an equation for a function of a single variable, usually called time, in which the derivative of the function at a certain time is given in terms of the values of the function at earlier times.• A stochastic differential equation (SDE) is an equation in which the unknown quantity is a stochastic process and the equation involves some known stochastic processes, for example, the Wiener process in the case of diffusion equations.• A differential algebraic equation (DAE) is a differential equation comprising differential and algebraic terms, given in implicit form.Connection to difference equationsSee also: Time scale calculusThe theory of differential equations is closely related to the theory of difference equations, in which the coordinates assume only discrete values, and the relationship involves values of the unknown function or functions and values at nearby coordinates. Many methods to compute numerical solutions of differential equations or study the properties of differential equations involve approximation of the solution of a differential equation by the solution of a corresponding difference equation.Universality of mathematical descriptionMany fundamental laws of physics and chemistry can be formulated as differential equations. In biology and economics, differential equations are used to model the behavior of complex systems. The mathematical theory of differential equations first developed together with the sciences where the equations had originated and where the results found application. However, diverse problems, sometimes originating in quite distinct scientific fields, may give rise to identical differential equations. Whenever this happens, mathematical theory behind the equations can be viewed as a unifying principle behind diverse phenomena. As an example, consider propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of them may be described by the same second-order partial differential equation, the wave equation, which allows us to think of light and sound as forms of waves, much like familiar waves in the water. Conduction of heat, the theory of which was developed by Joseph Fourier, is governed by another second-order partial differential equation, the heat equation. It turns out that many diffusion processes, while seemingly different, are described by the same equation; the Black–Scholes equation in finance is, for instance, related to the heat equation.Notable differential equationsPhysics and engineering•Newton's Second Law in dynamics (mechanics)•Euler–Lagrange equation in classical mechanics•Hamilton's equations in classical mechanics•Radioactive decay in nuclear physics•Newton's law of cooling in thermodynamics•The wave equation•Maxwell's equations in electromagnetism•The heat equation in thermodynamics•Laplace's equation, which defines harmonic functions•Poisson's equation•Einstein's field equation in general relativity•The Schrödinger equation in quantum mechanics•The geodesic equation•The Navier–Stokes equations in fluid dynamics•The Diffusion equation in stochastic processes•The Convection–diffusion equation in fluid dynamics•The Cauchy–Riemann equations in complex analysis•The Poisson–Boltzmann equation in molecular dynamics•The shallow water equations•Universal differential equation•The Lorenz equations whose solutions exhibit chaotic flow.Biology•Verhulst equation – biological population growth•von Bertalanffy model – biological individual growth•Lotka–Volterra equations – biological population dynamics•Replicator dynamics – found in theoretical biology•Hodgkin–Huxley model – neural action potentialsEconomics•The Black–Scholes PDE•Exogenous growth model•Malthusian growth model•The Vidale–Wolfe advertising modelReferences•P. Abbott and H. Neill, Teach Yourself Calculus, 2003 pages 266-277•P. Blanchard, R. L. Devaney, G. R. Hall, Differential Equations, Thompson, 2006• E. A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, 1955• E. L. Ince, Ordinary Differential Equations, Dover Publications, 1956•W. Johnson, A Treatise on Ordinary and Partial Differential Equations[2], John Wiley and Sons, 1913, in University of Michigan Historical Math Collection [3]• A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2.•R. I. Porter, Further Elementary Analysis, 1978, chapter XIX Differential Equations•Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems[4]. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.• D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.[1]/w/index.php?title=Template:Differential_equations&action=edit[2]/cgi/b/bib/bibperm?q1=abv5010.0001.001[3]/u/umhistmath/[4]http://www.mat.univie.ac.at/~gerald/ftp/book-ode/External links•Lectures on Differential Equations (/courses/mathematics/18-03-differential-equations-spring-2010/video-lectures/) MIT Open CourseWare Videos•Online Notes / Differential Equations (/classes/de/de.aspx) Paul Dawkins, Lamar University•Differential Equations (/diffeq/diffeq.html), S.O.S. Mathematics•Differential Equation Solver (/tools/differential_equation_solver/) Java applet tool used to solve differential equations.•Introduction to modeling via differential equations (/mat/u-u/en/ differential_equations_intro.htm) Introduction to modeling by means of differential equations, with critical remarks.•Mathematical Assistant on Web (http://user.mendelu.cz/marik/maw/index.php?lang=en&form=ode) Symbolic ODE tool, using Maxima•Exact Solutions of Ordinary Differential Equations (http://eqworld.ipmnet.ru/en/solutions/ode.htm)•Collection of ODE and DAE models of physical systems (/research/models.htm) MATLAB models•Notes on Diffy Qs: Differential Equations for Engineers (/diffyqs/) An introductory textbook on differential equations by Jiri Lebl of UIUC•Khan Academy Video playlist on differential equations (/math/ differential-equations) Topics covered in a first year course in differential equations.•MathDiscuss Video playlist on differential equations (/category/courses/ solutions-differential-equations/homogeneous-linear-systems/)Article Sources and Contributors8Article Sources and ContributorsDifferential equation Source: /w/index.php?oldid=610771276 Contributors: 17Drew, After Midnight, Ahoerstemeier, Alarius, Alfred Centauri, Amahoney, AndreiPolyanin, Andres, AndrewHowse, Andycjp, Andytalk, AngryPhillip, Anonymous Dissident, Antoni Barau, Antonius Block, Anupam, Apmonitor, Arcfrk, Asdf39, Asyndeton, Attilios,Babayagagypsies, Baccala@, Baccyak4H, Bejohns6, Bento00, Berland, Bidabadi, Bigusbry, BillyPreset, Bob.v.R, Bolatbek, Brandon, Bryanmcdonald, Btyner, Bygeorge2512,Callumds, Charles Matthews, Christian75, Chtito, Cispyre, Cmprince, Coginsys, ConMan, Cxz111, Cybercobra, DAJF, Danski14, Dbroadwell, Ddxc, Delaszk, DerHexer, Dewritech, Difu Wu, Djordjes, DominiqueNC, Donludwig, Dpv, Dr sarah madden, Drmies, DroEsperanto, Duoduoduo, Dysprosia, EconoPhysicist, Elwikipedista, Epicgenius, EricBright, Erin.Annette.Brown,Estudiarme, F=q(E+v^B), Fintor, Fioravante Patrone, Fioravante Patrone en, Flameturtle, Friend of the Facts, FutureTrillionaire, Gabrielleitao, Gandalf61, Gauss, Genedronek, Geni, Giftlite,GoingBatty, Gombang, Grenavitar, Haham hanuka, Hamiltondaniel, Harry, Haruth, Haseeb Jamal, Heikki m, Holmes1900, Ilya Voyager, Iquseruniv, Iulianu, Izodman2012, J arino, J.delanoy, Ja 62, Jak86, JamesBWatson, Jao, Jarble, Jauhienij, Jayden54, Jeancey, Jersey Devil, Jim Sukwutput, Jim.belk, Jim.henderson, JinJian, Jitse Niesen, JohnOwens, Johndoeisnotmyname, JorisvS,Julesd, K-UNIT, Kayvan45622, KeithJonsn, Kensaii, Khalid Mahmood, Klaas van Aarsen, Kr5t, Krushia, LOL, Lambiam, Lavateraguy, Lethe, LibLord, Linas, Lumos3, Madmath789, Mandarax, Mankarse, MarSch, Martastic, Martynas Patasius, Maschen, Math.geek3.1415926, Matqkks, Mattmnelson, Maurice Carbonaro, Maxis ftw, Mazi, McVities, Mduench, Mets501, Mh, MichaelHardy, Mindspillage, MisterSheik, Mohan1986, Mossaiby, Mpatel, MrOllie, Mtness, Mysidia, Nik-renshaw, Nkayesmith, Norm mit, Okopecz, Oleg Alexandrov, Opelio, Pahio, Parusaro, Paul August, Paul Matthews, Paul Richter, PavelSolin, Pgk, Phoebe, Pine, Pinethicket, Pratyya Ghosh, PseudoSudo, Qwerty Binary, Qzd800, R'n'B, Rama's Arrow, Randomguess, Reallybored999, RexNL, Reyk, RichMorin, Robin S, Romansanders, Rosasco, Ruakh, SDC, SFC9394, SakeUPenn, Salix alba, Sam Staton, Sampathsris, Sardanaphalus, Senoreuchrestud, Silly rabbit, Siroxo,Skakkle, Skypher, SmartPatrol, Snowjeep, Spirits in the Material, Starwiz, Suffusion of Yellow, Sverdrup, Symane, TVBZ28, TYelliot, Tannkrem, Tbhotch, Tbsmith, TexasAndroid, Tgeairn, The Hybrid, The Thing That Should Not Be, Timelesseyes, Tranum1234567890, Tsirel, Tuseroni, User A1, Vanished User 0001, Vishwanathnm, Vthiru, Waffleguy4, Waldir, Waltpohl, Wavelength, Wclxlus, Wihenao, Willtron, Winterheart, Wsears, XJaM, Yafujifide, Zepterfd, ﺪﺟﺎﺳ ﺪﺠﻣﺍ ﺪﺟﺎﺳ, 363 anonymous editsImage Sources, Licenses and ContributorsFile:Airflow-Obstructed-Duct.png Source: /w/index.php?title=File:Airflow-Obstructed-Duct.png License: Public Domain Contributors: Original uploader was User A1 at en.wikipediaFile:Elmer-pump-heatequation.png Source: /w/index.php?title=File:Elmer-pump-heatequation.png License: Creative Commons Attribution-Sharealike 3.0Contributors: Christian1985, Crimerob, Kri, User A1, 2 anonymous editsLicenseCreative Commons Attribution-Share Alike 3.0///licenses/by-sa/3.0/。

仿射非线性系统状态方程的任意阶近似解

仿射非线性系统状态方程的任意阶近似解曹少中1,2)　刘贺平2)　涂序彦2)1)北京印刷学院信息与机电工程学院,北京102600　2)北京科技大学信息工程学院,北京100083摘　要　针对典型的仿射非线性系统,采用常微分方程理论对其进行求解.首先将系统在平衡点附近进行展开,求得其齐次方程的解,然后利用常数变易法将非线性微分方程变为等价的第二类非线性Volterra 积分方程.采用逐次逼近法,求得任意阶近似解,并证明解的收敛性.关键词　非线性系统;状态方程;常微分方程;Volterra 积分方程;逐次逼近法;近似解分类号　TP 273Any order approximate solution of the state equation for an aff ine nonlinear sys 2temCA O S haoz hong1,2),L IU Heping2),TU X uyan2)1)College of Information &Mechanical Engineering ,Beijing Institute of Graphic Communication ,Beijing 102600,China 2)School of Information Engineering ,University of Science and Technology Beijing ,Beijing 100083,ChinaABSTRACT The state equation of an typical affine nonlinear system was solved with the ordinary differential equation theory.By utilizing the expansion expression of equilibrium point of the system ,the homogeneous equation ’s solution was obtained ,and then the nonlinear differential equation was equivalent to its nonlinear Volterra ’s integral equation of the second kind by the constant variation method.Any order approximate solution of the equation was presented ,and its convergence was mathematically proved by the succes 2sive approximation method.KE Y WOR DS nonlinear system ;state equation ;ordinary differential equation ;Volterra ’s integral equation ;successive approxima 2tion method ;approximate solution收稿日期:2007204212　修回日期:2007207225基金项目:国家自然科学基金资助项目(No.60374032,No.60673101);北京市教育委员会科技发展计划面上项目(No.KM200810015003);北京市属市管高等学校人才强教计划资助项目(No.TXM2007-014223-044661);北京印刷学院引进人才科技研究项目(No.0917*******)作者简介:曹少中(1965—),男,副教授,博士,E 2mail :cszh6502@ 由于非线性控制理论的复杂性,人们在研究过程中,逐渐从以常微分方程理论作为主要数学工具,转到以拓扑学、微分几何等现代数学工具为主,从而在近几十年,使得非线性控制理论特别是对仿射非线性系统的研究取得了长足的发展[1-4].以微分几何为主要工具发展起来的精确线性化方法,为解决仿射非线性控制系统的分析与综合问题提供了强有力的手段.由于精确线性化方法必须满足苛刻的条件,且结构复杂,除了某些具有特殊结构(如三角形结构)的系统外,往往很难得到所需的非线性变换;因此研究非线性系统的近似处理方法具有相当的理论与应用意义,近年来也一直同样受到人们的高度重视.近似线性化方法[5-7]被证明在平衡点的某一邻域内是有效的,误差可以接受,所以广泛地应用于实际系统中.但是这些近似线性化方法误差较大,在精度要求较高的情况下不能满足要求.本文拟采用传统的常微分方程和积分方程理论,给出一种求解仿射非线性系统的近似线性化方法,本方法可使结果达到任意阶近似.本文采用传统的常微分方程和积分方程理论,对仿射非线性系统进行求解.首先将系统在平衡点x =0附近进行展开,求得其齐次方程的解;然后利用常数变易法将非线性微分方程变为等价的第二类非线性Volterra 积分方程.采用逐次逼近法,求得任意阶近似解,并证明解的收敛性.第30卷第6期2008年6月北京科技大学学报Journal of U niversity of Science and T echnology B eijingV ol.30N o.6Jun.20081　仿射非线性系统的任意阶近似解一个有限n 维的控制系统可以描述为:x ・=f (x ,u )y =h (x ,u)　x ∈M ,u ∈U(1)其中,M 是一个n 维流形,U 是容许控制集合.系统(1)的一个常用的特殊情况是仿射非线性系统,它是对状态x 非线性而对u 是线性的.实际上,仿射非线性系统可由如下方程描述[1-2]:x ・=f (x )+g (x )uy =h (x)　x ∈M ,u ∈U (2)其中,f (x )=(f 1(x ),f 2(x ),…,f n (x ))T,g (x )=g 11(x )g 12(x )…g 1m (x)g 21(x )g 22(x )…g 2m (x )…g n 1(x )g n 2(x )…g nm (x ),x =(x 1,x 2,…,x n )T为状态向量,u =(u 1,u 2,…,u m )T为控制向量,y =(y 1,y 2,…,y p )T为输出向量,h (x )=(h 1(x ),h 2(x ),…,h p (x ))T为输出函数向量.通常f 是光滑向量场,并且f (0)=0在h (x )=(h 1(x ),h 2(x ),…,h p (x ))T中的h i (x )满足h i (0)=0(i =1,2,…,p ),且它们是光滑的,另外在系统(2)中的g ij (x )(i =1,2,…,n ;j =1,2,…,m )也是M 上光滑的向量场.易知,x =0是该系统的平衡点(设u =0).将f (x )和g (x )在平衡点x =0(u =0)附近展开有:f i (x )=∑nj =1aij(t )x j +∑nj 1=1∑nj 2=1aij 1j 2(t )x j 1x j 2+∑nj 1=1∑nj 2=1∑nj 3=1aij 1j 2j 3(t )x j 1x j 2x j 3+…+∑nj 1=1∑nj 2=1…∑nj k=1aij 1j 2…j k(t )x j 1x j 2x j 3…x j k+ (3)令Ψi (x (t ),t )=∑nj 1=1∑nj 2=1aij 1j 2(t )x j 1x j 2+∑nj 1=1∑nj 2=1∑nj 3=1aij 1j 2j 3(t )x j 1x j 2x j 3+…+∑nj 1=1∑nj 2=1…∑nj k=1a ij 1j 2...j k (t )x j 1x j 2...x j k + (4)即为式(3)中的高次项部分,于是式(3)可写为:f i (x )=∑nj =1aij(t )x j +Ψi (x (t ),t )(5)同理,g ij (x )可写为线性和非线性两部分:g ij (x )=b ij (t )+G i (x (t ),t )(6)其中,b ij (t )与x 无关,G (x (t ),t )为高次项部分.将式(5)及(6)代入方程(2),则原方程变为下面的形式:x ・(t )=A (t )x (t )+B (t )u (t )+Ψ(x (t ),t )+G (x (t ),t )u (t )(7)其中,A (t )=a 11(t )a 12(t )…a 1n (t )a 21(t )a 22(t )…a 2n (t )…a n 1(t )a n 2(t )…a nn (t ),B (t )=b 11(t )b 12(t )…b 1m (t )b 21(t )b 22(t )…b 2m (t )…b n 1(t )b n 2(t )…b nm (t ),Ψ(x (t ),t )=(Ψ1(x (t ),t ),Ψ2(x (t ),t ),…Ψn (x (t ),t ))T,G (x (t ),t )=G 11(x (t ),t )G 12(x (t ),t )…G 1m (x (t ),t )G 21(x (t ),t )G 22(x (t ),t )…G 2m (x (t ),t )…G n 1(x (t ),t )G n 2(x (t ),t )…G nm (x (t ),t ).首先求解式(7)的齐次方程,x ^(t )=A (t )x (t )(8)初始条件为x (t =0)=x (0).该方程早已被人们采用Picad 递归积分法或时变距阵指数法分别给出如下形式的解:x (t )=R (t )x (0)(9)R (t )=I +∫tA (t 1)d t1+∫t 0∫t 1A (t 1)A (t 2)d t 2d t 1+…+∫t0∫t 10…∫t n-1A (t 1)A (t 2)…A (t n )d t n d t n -1…d t 2d t 1+…(10)或R (t )=exp∫tA (τ)d τ(11)・196・第6期曹少中等:仿射非线性系统状态方程的任意阶近似解在求得齐次方程解的基础上,采用常数变易法将非线状态方程(7)变为等价的积分方程.设式(7)的解的形式为:x (t )=R (t )C (t )(12)其中,C (t )为待求函数列向量,根据R (t )的初始条件R (0)=I (n ×n 单位矩阵),可知C (t )的初始条件为C (0)=x (0).把式(12)代入式(7),有d R (t )d t C (t )+R (t )d C (t )d t=A (t )R (t )C (t )+B (t )u (t )+Ψ(x (t ),t )+G (x (t ),t )u (t ),利用d R (t )d t=A (t )R (t ),则上式变为下面的形式:R (t )d C (t )d t=Ψ(x (t ),t )+(B (t )+G (x (t ),t ))u (t ).方程两边左乘以R (t )的逆R -1(t ),并从0到t 区间进行积分,可得C (t )的表达式如下:C (t )=x (0)+∫tR-1(τ)[Ψ(x (τ),τ)+(B (τ)+G (x (τ),τ))u (t )]d τ(13)把式(13)代入式(12),则得与微分方程(7)等价的积分方程如下:x (t )=R (t )x (0)+R (t )∫tR -1(τ){Ψ(x (τ),τ)+[B (τ)+G (x (τ),τ)]u (τ)}d τ(14)方程(14)是第二类非线性Volterra 积分方程,该积分方程可采用逐次逼近法进行求解:x (0)(t )=R (t )x (0)+R (t )∫tR-1(τ)B (τ)u (τ)d τx(1)(t )=R (t )x (0)+R (t )∫tR -1(τ){Ψ(x (0)(τ),τ)+ [B (τ)+G (x (0)(τ),τ)]u (τ)}d τx(2)(t )=R (t )x (0)+R (t )∫tR -1(τ){Ψ(x (1)(τ),τ)+ [B (τ)+G (x (1)(τ),τ)]u (τ)}d τ (x)(m )(t )=R (t )x (0)+R (t )∫tR -1(τ)・ {Ψ(x(m -1)(τ),τ)+[B (τ)+ G (x (m -1)(τ),τ)]u (τ)}dτ(15)显然式(15)是一个递推迭代公式,只要求得线性方程的解,就可以逐次求得非线性方程(14)的任意阶近似解.因此,综合以上结果,可以构造迭代函数形式如下:x (0)(t )=R (t )x (0)+R (t )∫tR-1(τ)B (τ)u (τ)d τx(m )(t )=R (t )x (0)+R (t )∫tR -1(τ)・ {Ψ(x(m -1)(τ),τ)+[B (τ)+ G (x (m -1)(τ),τ)]u (τ)}d τ,m ≥1(16)对于自由状态,即控制向量u =0,则式(16)就简化为文献[8-9]的结果,x (0)(t )=R (t )x (0)x(m )(t )=R (t )x (0)+R (t )∫tR-1(τ)・Ψ(x (m -1)(τ),τ)dτ(17)2　任意阶近似解的收敛性上面采用逐次逼近法获得仿射非线性系统的状态方程的任意阶近似解.下面从非线性积分方程(14)出发,根据积分方程理论讨论任意阶近似解的收敛性.令φ(t )=R (t )x (0)+R (t )∫tR -1(τ)B (τ)u (τ)d τ,F (x ,u ,t ,τ)=R (t )R-1(τ)[Ψ(x ,τ)+G (x ,τ)u (τ)],则式(14)可以写成以下形式:x (t )=φ(t )+∫tF (x ,u ,t ,τ)d τ(18)根据逐次逼近法,构造迭代函数序列如下:x (0)(t )=φ(t )x(m )(t )=φ(t )+∫tF (x ,u ,t ,τ)d τ,m ≥1(19)若上述迭代函数序列一致性收敛于某极限,亦即当m →∞时x (m )(t )的极限存在,则该极限就是积分方程(14)的解.现对φi (t )和F (x ,u ,t ,τ)作如下假定:(1)φi (t )在自变量t 的有限变化区间0≤t ≤d 上连续且有界,即|φi (t )|<C i ;(2)F i (x ,u ,t ,τ)关于全部变量在区间0≤t ≤d ,0≤τ≤t ,a i ≤x i ≤b i ,c i ≤u i ≤e i 上连续且有界,|F i (x ,u ,t ,τ)|<M i 且a i <φi (t )<b i ,以及F i (x ,u ,t ,τ)满足Lipschit 条件|F i (x ,u ,t ,τ)-F i (x ,u ,t ,τ)|≤・296・北　京　科　技　大　学　学　报第30卷K∑Nj =1|x j -x j |,j =1,2,…,N ,其中,K 是常数.如果上述假设成立,那么根据积分方程理论[10],可以证明由式(19)所构成的迭代函数序列{x(m )(t )}收敛,证明如下.由于x(m )i(t )=x(0)i(t )+∑ml =1[x(l )i (t )-x (l -1)i(t )],因此只要证明函数∑∞l =1[x(l )i(t )-x (l -1)i (t )]收敛即可.根据假设条件可知:|x(1)i(t )-x (0)i(t )|≤∫t|F i (x (τ),u (τ),t ,τ)|≤∫tM id τ=M it ,|x (2)i (t )-x (1)i (t )|≤∫t[F i(x (1)(τ),u (τ),t ,τ)-F i (x (0)(τ),u (τ),t ,τ)]d τ≤∫tK∑Nj =1|x(1)j(τ)-x(0)j(τ)|d τ≤12KM t 2,其中,M =∑N j =1M j.|x (3)i (t )-x (2)i (t )|≤∫t[F i (x (2)(τ),u (τ),t ,τ)-F i (x (1)(τ),u (τ),t ,τ)]d τ≤∫tK∑Nj =1|x (2)j (τ)-x (1)j (τ)d τ≤12×3M N K 2t 3,利用数学归纳法,可设|x (l )i (t )-x (l -1)i (t )|≤1l !M N l -2Kl -1t l,那么,|x (l +1)i (t )-x (l )i (t )|≤∫l[F i(x(l )(τ),u (τ),t ,τ)-F i (x(l -1)(τ),u (τ),t ,τ)]d τ≤∫tK∑Nj =1|x (l )j (τ)-x (l -1)j (τ)|d τ≤1(l +1)!M Nl -1K l tl +1.可见,从l =2开始,级数∑∞l =1[x (l )i (t )-x (l -1)i(t )]的每一项均小于等于幂级数M N 2K∑∞l =21l !(N Kt )l的相应项,而后者是收敛的,其极限为MN 2K[exp (N Kt )-1-N Kt ],因此函数级数∑∞l =1[x(l )i (t )-x (l -1)i (t )]都是绝对收敛和一致收敛的,从而证明迭代函数序列{x (m )(t )}在上述假设条件下收敛.对于实际问题,要判断其是否满足上述假设条件有时是很困难的,往往只能根据问题的物理性质做出判断.另外,上述假设条件仅是迭代函数序列收敛的充分条件,并非必要条件;也就是说,对于不满足上述假设条件的情况,迭代函数序列也有可能收敛.3　结论本文采用传统的微分方程及积分方程得到了仿射非线性系统状态方程的任意阶近似解.这一结果表明,用迭代函数序列逼近非线性Volterra 积分方程的解,只需迭代m -1次,即可得到m 阶近似解析解,十分简便.参　考　文　献[1]　Alberto I.Nonli near Cont rol Systems .3rd ed.London :Springer 2Verlag ,1995[2]　Hong Y G ,Cheng D Z.A nalysis and Cont rol on Nonli near Sys 2tems .Beijing :Science Press ,2005(洪奕光,程代展.非线性系统的分析与控制.北京:科学出版社,2005)[3]　Xie L L ,Guo L.Adaptive control of a class of discrete 2time affinenonlinear systems.S yst Cont rol Lett ,1998,35:202[4]　Popescu M.On minimum quadratic functional control of affinenonlinear systems.Nonli near A nal ,2004,56:1165[5]　Pei H L ,Zhou Q J.Approximate linearization of nonlinear sys 2tems a neural network approach.Cont rol Theory A ppl ,1998,15(1):34[6]　Verhulst F.Nonli near Dif f erential Equations and DynamicalS ystems .New Y ork :Spinger 2Verlag ,1992[7]　Xu Z G ,Hauser J.Higher order approximate feedback lineariza 2tion about a manifold for multi 2input systems.I EEE Trans A u 2tom Cont rol ,1995,40(9):833[8]　Liu C L ,Xie X.Any order approximate analytical solution of thenonlinear Volterra ’s integral equation for accelerator dynamic sys 2tems.Chi n J N ucl Sci Eng ,1992,12(2):161(刘纯亮,谢羲.加速器非线性动力系统Volterra 积分方程任意阶近似解析解.核科学与工程,1992,12(2):161)[9]　Liu C L ,Xie X ,Chen Y B.Any order approximate analytical so 2lution of the nonlinear Volterra ’s integral equation for accelerator dynamic systems.J N ucl Phys ,1991,13:261[10]　Shen Y D.Integral Equation .Beijing :Beijing Institute ofTechnology Press ,2002(沈以淡.积分方程.北京:北京理工大学出版社,2002)・396・第6期曹少中等:仿射非线性系统状态方程的任意阶近似解。

一阶常微分方程

Chapter 1 First-order ordinary differential equations (ODE)一階常微分方程1.1 基本概念()x f y =或()t f y =，y 是x 或t 的函數，y 是因變數(dependent variable )，x 或t 是自變數(independent variable )◎ 微分方程(differential equations)：一方程式包含有因變數y 關於自變數x 或t的導數(derivatives)y y ′ ,&或微分(differentials)dy 。

◎ 常微分方程(ordinary differential equations, ODE)：一微分方程包含有一個或數個因變數（通常為()x y ）關於僅有一個自變數x 的導數。

Ex. 222)2(2 ,09 ,cos y x y e y y x y y x y x +=′′+′′′′=+′′=′◎ 偏微分方程(partial differential equations, PDE)：一微分方程包含至少有一個因變數關於兩個以上自變數的部分導數。

Ex. 02222=∂∂+∂∂yux u◎ 微分方程的階數：在微分方程式中所出現最高階導數的階數。

◎ 線性微分方程：在微分方程式中所出現的因變數因變數因變數或其導數僅有一次式(first degree)而無二次以上的乘積（自變數可以有二次以上的乘積）。

Ex. x y y x y cos 24=+′+′′ 因變數：y ，自變數：x ，二階線性常微分方程 x y y y y cos 24=+′+′′ 因變數：y ，自變數：x ，二階非線性常微分方程 222)2(2 y x y e y y x x +=′′+′′′′ 因變數：y ，自變數：x ，三階非線性常微分方程□ 一階常微分方程(first-order ordinary differential equations)隱式形式(implicit form) 表示 0),,(=′y y x F (4)顯式形式(explicit form) 表示 ),(y x f y =′Ex. 隱式形式ODE 0423=−′−y y x ，當0≠x 時，可表示為顯式形式234y x y =′□ 解的概念(concept of solution)在某些開放間隔區間b x a <<，一函數)(x h y =是常微分方程常微分方程0),,(=′y y x F 的解，其函數)(x h 在此區間b x a <<是明確(defined)且可微分的(differentiable)，其)(x h 的曲線（或圖形）是被稱為解答曲線(solution curve)。

微积分英文词汇高数名词中英文对照高等数学术语英语翻

微积分英文词汇,高数名词中英文对照,高等数学术语英语翻译一览V、X、Z:Value of function ：函数值Variable ：变数Vector ：向量Velocity ：速度Vertical asymptote ：垂直渐近线Volume ：体积X-axis ：x轴x-coordinate ：x坐标x-intercept ：x截距Zero vector ：函数的零点Zeros of a polynomial ：多项式的零点T:Tangent function ：正切函数Tangent line ：切线Tangent plane ：切平面Tangent vector ：切向量Total differential ：全微分Trigonometric function ：三角函数Trigonometric integrals ：三角积分Trigonometric substitutions ：三角代换法Tripe integrals ：三重积分S:Saddle point ：鞍点Scalar ：纯量Secant line ：割线Second derivative ：二阶导数Second Derivative Test ：二阶导数试验法Second partial derivative ：二阶偏导数Sector ：扇形Sequence ：数列Series ：级数Set ：集合Shell method ：剥壳法Sine function ：正弦函数Singularity ：奇点Slant asymptote ：斜渐近线Slope ：斜率Slope-intercept equation of a line ：直线的斜截式Smooth curve ：平滑曲线Smooth surface ：平滑曲面Solid of revolution ：旋转体Space ：空间Speed ：速率Spherical coordinates ：球面坐标Squeeze Theorem ：夹挤定理Step function ：阶梯函数Strictly decreasing ：严格递减Strictly increasing ：严格递增Sum ：和Surface ：曲面Surface integral ：面积分Surface of revolution ：旋转曲面Symmetry ：对称R:Radius of convergence ：收敛半径Range of a function ：函数的值域Rate of change ：变化率Rational function ：有理函数Rationalizing substitution ：有理代换法Rational number ：有理数Real number ：实数Rectangular coordinates ：直角坐标Rectangular coordinate system ：直角坐标系Relative maximum and minimum ：相对极大值与极小值Revenue function ：收入函数Revolution , solid of ：旋转体Revolution , surface of ：旋转曲面Riemann Sum ：黎曼和Riemannian geometry ：黎曼几何Right-hand derivative ：右导数Right-hand limit ：右极限Root ：根P、Q:Parabola ：拋物线Parabolic cylinder ：抛物柱面Paraboloid ：抛物面Parallelepiped ：平行六面体Parallel lines ：并行线Parameter ：参数Partial derivative ：偏导数Partial differential equation ：偏微分方程Partial fractions ：部分分式Partial integration ：部分积分Partiton ：分割Period ：周期Periodic function ：周期函数Perpendicular lines ：垂直线Piecewise defined function ：分段定义函数Plane ：平面Point of inflection ：反曲点Polar axis ：极轴Polar coordinate ：极坐标Polar equation ：极方程式Pole ：极点Polynomial ：多项式Positive angle ：正角Point-slope form ：点斜式Power function ：幂函数Product ：积Quadrant ：象限Quotient Law of limit ：极限的商定律Quotient Rule ：商定律M、N、O:Maximum and minimum values ：极大与极小值Mean Value Theorem ：均值定理Multiple integrals ：重积分Multiplier ：乘子Natural exponential function ：自然指数函数Natural logarithm function ：自然对数函数Natural number ：自然数Normal line ：法线Normal vector ：法向量Number ：数Octant ：卦限Odd function ：奇函数One-sided limit ：单边极限Open interval ：开区间Optimization problems ：最佳化问题Order ：阶Ordinary differential equation ：常微分方程Origin ：原点Orthogonal ：正交的L:Laplace transform ：Leplace 变换Law of Cosines ：余弦定理Least upper bound ：最小上界Left-hand derivative ：左导数Left-hand limit ：左极限Lemniscate ：双钮线Length ：长度Level curve ：等高线L'Hospital's rule ：洛必达法则Limacon ：蚶线Limit ：极限Linear approximation：线性近似Linear equation ：线性方程式Linear function ：线性函数Linearity ：线性Linearization ：线性化Line in the plane ：平面上之直线Line in space ：空间之直线Lobachevski geometry ：罗巴切夫斯基几何Local extremum ：局部极值Local maximum and minimum ：局部极大值与极小值Logarithm ：对数Logarithmic function ：对数函数I:Implicit differentiation ：隐求导法Implicit function ：隐函数Improper integral ：瑕积分Increasing/Decreasing Test ：递增或递减试验法Increment ：增量Increasing Function ：增函数Indefinite integral ：不定积分Independent variable ：自变数Indeterminate from ：不定型Inequality ：不等式Infinite point ：无穷极限Infinite series ：无穷级数Inflection point ：反曲点Instantaneous velocity ：瞬时速度Integer ：整数Integral ：积分Integrand ：被积分式Integration ：积分Integration by part ：分部积分法Intercepts ：截距Intermediate value of Theorem ：中间值定理Interval ：区间Inverse function ：反函数Inverse trigonometric function ：反三角函数Iterated integral ：逐次积分H:Higher mathematics 高等数学/高数E、F、G、H:Ellipse ：椭圆Ellipsoid ：椭圆体Epicycloid ：外摆线Equation ：方程式Even function ：偶函数Expected Valued ：期望值Exponential Function ：指数函数Exponents , laws of ：指数率Extreme value ：极值Extreme Value Theorem ：极值定理Factorial ：阶乘First Derivative Test ：一阶导数试验法First octant ：第一卦限Focus ：焦点Fractions ：分式Function ：函数Fundamental Theorem of Calculus ：微积分基本定理Geometric series ：几何级数Gradient ：梯度Graph ：图形Green Formula ：格林公式Half-angle formulas ：半角公式Harmonic series ：调和级数Helix ：螺旋线Higher Derivative ：高阶导数Horizontal asymptote ：水平渐近线Horizontal line ：水平线Hyperbola ：双曲线Hyper boloid ：双曲面D:Decreasing function ：递减函数Decreasing sequence ：递减数列Definite integral ：定积分Degree of a polynomial ：多项式之次数Density ：密度Derivative ：导数of a composite function ：复合函数之导数of a constant function ：常数函数之导数directional ：方向导数domain of ：导数之定义域of exponential function ：指数函数之导数higher ：高阶导数partial ：偏导数of a power function ：幂函数之导数of a power series ：羃级数之导数of a product ：积之导数of a quotient ：商之导数as a rate of change ：导数当作变率right-hand ：右导数second ：二阶导数as the slope of a tangent ：导数看成切线之斜率Determinant ：行列式Differentiable function ：可导函数Differential ：微分Differential equation ：微分方程partial ：偏微分方程Differentiation ：求导法implicit ：隐求导法partial ：偏微分法term by term ：逐项求导法Directional derivatives ：方向导数Discontinuity ：不连续性Disk method ：圆盘法Distance ：距离Divergence ：发散Domain ：定义域Dot product ：点积Double integral ：二重积分change of variable in ：二重积分之变数变换in polar coordinates ：极坐标二重积分C:Calculus ：微积分differential ：微分学integral ：积分学Cartesian coordinates ：笛卡儿坐标一般指直角坐标Cartesian coordinates system ：笛卡儿坐标系Cauch’s Mean Value Theorem ：柯西均值定理Chain Rule ：连锁律Change of variables ：变数变换Circle ：圆Circular cylinder ：圆柱Closed interval ：封闭区间Coefficient ：系数Composition of function ：函数之合成Compound interest ：复利Concavity ：凹性Conchoid ：蚌线Cone ：圆锥Constant function ：常数函数Constant of integration ：积分常数Continuity ：连续性at a point ：在一点处之连续性of a function ：函数之连续性on an interval ：在区间之连续性from the left ：左连续from the right ：右连续Continuous function ：连续函数Convergence ：收敛interval of ：收敛区间radius of ：收敛半径Convergent sequence ：收敛数列series ：收敛级数Coordinate：s：坐标Cartesian ：笛卡儿坐标cylindrical ：柱面坐标polar ：极坐标rectangular ：直角坐标spherical ：球面坐标Coordinate axes ：坐标轴Coordinate planes ：坐标平面Cosine function ：余弦函数Critical point ：临界点Cubic function ：三次函数Curve ：曲线Cylinder：圆柱Cylindrical Coordinates ：圆柱坐标A、B:Absolute convergence ：绝对收敛Absolute extreme values ：绝对极值Absolute maximum and minimum ：绝对极大与极小Absolute value ：绝对值Absolute value function ：绝对值函数Acceleration ：加速度Antiderivative ：反导数Approximate integration ：近似积分Approximation ：逼近法by differentials ：用微分逼近linear ：线性逼近法by Simpson’s Rule ：Simpson法则逼近法by the Trapezoidal Rule ：梯形法则逼近法Arbitrary constant ：任意常数Arc length ：弧长Area ：面积under a curve ：曲线下方之面积between curves ：曲线间之面积in polar coordinates ：极坐标表示之面积of a sector of a circle ：扇形之面积of a surface of a revolution ：旋转曲面之面积Asymptote ：渐近线horizontal ：水平渐近线slant ：斜渐近线vertical ：垂直渐近线Average speed ：平均速率Average velocity ：平均速度Axes, coordinate ：坐标轴Axes of ellipse ：椭圆之轴Binomial series ：二项级数。

高阶常系数齐次线性微分方程的解法

高阶常系数齐次线性微分方程的解法凯歌【摘要】常微分方程是微积分学的重要组成部分，求解高阶微分方程是常微分方程的一难点问题，通常用适当的变量代换，达到降阶的目的来解决问题。

结合多年的教学经验，归纳总结给出高阶常系数齐次线性微分方程的一些求解方法，包括常系数齐次线性微分方程和欧拉方程以及可降阶的高阶微分方程等，并通过例题阐述各种方法。

%Ordinary Differential equation is an important part of differential and integration. Solving Ordinary Differential equation of difficult prob-lem is the differential equations of high order. Generally, in order to achieve the purpose to solve problems, it uses an appropriate variable substitution. With many years of teaching experience, summarizes to give some methods for solving the linear differential equation of higher-order, including homogeneous linear differential equation with constant coefficient, Euler equations and higher-order differential of reduce order and so on, gives an example to explain a variety of methods.【期刊名称】《现代计算机（专业版）》【年(卷),期】2016(000)002【总页数】4页(P26-28,51)【关键词】微分方程;特征方程;欧拉方程;齐次方程【作者】凯歌【作者单位】内蒙古财经大学统计与数学学院，呼和浩特 010070【正文语种】中文求解常微分方程的问题，常常通过变量分离、两边积分，如果是高阶微分方程则通过适当的变量代换，达到降阶的目的来解决问题。

Ordinarydifferentialequation

Ordinary differential equationIn mathematics, an ordinary differential equation (or ODE ) is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable.A simple example is Newton's second law of motion, which leads to the differential equationfor the motion of a particle of constant mass m . In general, the force F depends upon the position x(t) of the particle at time t , and thus the unknown function x(t) appears on both sides of the differential equation, as is indicated in the notation F (x (t )).Ordinary differential equations are distinguished from partial differential equations, which involve partial derivatives of functions of several variables.Ordinary differential equations arise in many different contexts including geometry, mechanics, astronomy and population modelling. Many famous mathematicians have studied differential equations and contributed to the field,including Newton, Leibniz, the Bernoulli family, Riccati, Clairaut, d'Alembert and Euler.Much study has been devoted to the solution of ordinary differential equations. In the case where the equation is linear, it can be solved by analytical methods. Unfortunately, most of the interesting differential equations are non-linear and, with a few exceptions, cannot be solved exactly. Approximate solutions are arrived at using computer approximations (see numerical ordinary differential equations).The trajectory of a projectile launched from a cannon follows a curve determined by an ordinary differential equation that is derived fromNewton's second law.Existence and uniqueness of solutionsThere are several theorems that establish existence anduniqueness of solutions to initial value problemsinvolving ODEs both locally and globally. SeePicard –Lindelöf theorem for a brief discussion of thisissue.DefinitionsOrdinary differential equationLet ybe an unknown function in x with the n th derivative of y , and let Fbe a given functionthen an equation of the formis called an ordinary differential equation (ODE) of order n . If y is an unknown vector valued function,it is called a system of ordinary differential equations of dimension m (in this case, F : ℝmn +1→ ℝm ).More generally, an implicit ordinary differential equation of order nhas the formwhere F : ℝn+2→ ℝ depends on y(n). To distinguish the above case from this one, an equation of the formis called an explicit differential equation.A differential equation not depending on x is called autonomous.A differential equation is said to be linear if F can be written as a linear combination of the derivatives of y together with a constant term, all possibly depending on x:(x) and r(x) continuous functions in x. The function r(x) is called the source term; if r(x)=0 then the linear with aidifferential equation is called homogeneous, otherwise it is called non-homogeneous or inhomogeneous. SolutionsGiven a differential equationa function u: I⊂ R→ R is called the solution or integral curve for F, if u is n-times differentiable on I, andGiven two solutions u: J⊂ R→ R and v: I⊂ R→ R, u is called an extension of v if I⊂ J andA solution which has no extension is called a global solution.A general solution of an n-th order equation is a solution containing n arbitrary variables, corresponding to n constants of integration. A particular solution is derived from the general solution by setting the constants to particular values, often chosen to fulfill set 'initial conditions or boundary conditions'. A singular solution is a solution that can't be derived from the general solution.Reduction to a first order systemAny differential equation of order n can be written as a system of n first-order differential equations. Given an explicit ordinary differential equation of order n (and dimension 1),define a new family of unknown functionsfor i from 1 to n.The original differential equation can be rewritten as the system of differential equations with order 1 and dimension n given bywhich can be written concisely in vector notation aswithandLinear ordinary differential equationsA well understood particular class of differential equations is linear differential equations. We can always reduce an explicit linear differential equation of any order to a system of differential equation of order 1which we can write concisely using matrix and vector notation aswithHomogeneous equationsThe set of solutions for a system of homogeneous linear differential equations of order 1 and dimension nforms an n-dimensional vector space. Given a basis for this vector space , which is called a fundamental system, every solution can be written asThe n × n matrixis called fundamental matrix. In general there is no method to explicitly construct a fundamental system, but if one solution is known d'Alembert reduction can be used to reduce the dimension of the differential equation by one.Nonhomogeneous equationsThe set of solutions for a system of inhomogeneous linear differential equations of order 1 and dimension ncan be constructed by finding the fundamental system to the corresponding homogeneous equation and one particular solution to the inhomogeneous equation. Every solution to nonhomogeneous equation can then be written asA particular solution to the nonhomogeneous equation can be found by the method of undetermined coefficients or the method of variation of parameters.Concerning second order linear ordinary differential equations, it is well known thatSo, if is a solution of: , then such that:So, if is a solution of: ; then a particular solution of , isgiven by:. [1]Fundamental systems for homogeneous equations with constant coefficientsIf a system of homogeneous linear differential equations has constant coefficientsthen we can explicitly construct a fundamental system. The fundamental system can be written as a matrix differential equationwith solution as a matrix exponentialwhich is a fundamental matrix for the original differential equation. To explicitly calculate this expression we first transform A into Jordan normal formand then evaluate the Jordan blocksof J separately asTheories of ODEsSingular solutionsThe theory of singular solutions of ordinary and partial differential equations was a subject of research from the time of Leibniz, but only since the middle of the nineteenth century did it receive special attention. A valuable but little-known work on the subject is that of Houtain (1854). Darboux (starting in 1873) was a leader in the theory, and in the geometric interpretation of these solutions he opened a field which was worked by various writers, notably Casorati and Cayley. To the latter is due (1872) the theory of singular solutions of differential equations of the first order as accepted circa 1900.Reduction to quadraturesThe primitive attempt in dealing with differential equations had in view a reduction to quadratures. As it had been the hope of eighteenth-century algebraists to find a method for solving the general equation of the th degree, so it was the hope of analysts to find a general method for integrating any differential equation. Gauss (1799) showed, however, that the differential equation meets its limitations very soon unless complex numbers are introduced. Hence analysts began to substitute the study of functions, thus opening a new and fertile field. Cauchy was the first to appreciate the importance of this view. Thereafter the real question was to be, not whether a solution is possible by means of known functions or their integrals, but whether a given differential equation suffices for the definition of a function of the independent variable or variables, and if so, what are the characteristic properties of this function.Fuchsian theoryTwo memoirs by Fuchs (Crelle, 1866, 1868), inspired a novel approach, subsequently elaborated by Thomé and Frobenius. Collet was a prominent contributor beginning in 1869, although his method for integrating a non-linear system was communicated to Bertrand in 1868. Clebsch (1873) attacked the theory along lines parallel to those followed in his theory of Abelian integrals. As the latter can be classified according to the properties of the fundamental curve which remains unchanged under a rational transformation, so Clebsch proposed to classify the transcendent functions defined by the differential equations according to the invariant properties of the corresponding surfaces f = 0 under rational one-to-one transformations.Lie's theoryFrom 1870 Sophus Lie's work put the theory of differential equations on a more satisfactory foundation. He showed that the integration theories of the older mathematicians can, by the introduction of what are now called Lie groups, be referred to a common source; and that ordinary differential equations which admit the same infinitesimal transformations present comparable difficulties of integration. He also emphasized the subject of transformations of contact.A general approach to solve DE's uses the symmetry property of differential equations, the continuous infinitesimal transformations of solutions to solutions (Lie theory). Continuous group theory, Lie algebras and differential geometry are used to understand the structure of linear and nonlinear (partial) differential equations for generating integrable equations, to find its Lax pairs, recursion operators, Bäcklund transform and finally finding exact analytic solutions to the DE.Symmetry methods have been recognized to study differential equations arising in mathematics, physics, engineering, and many other disciplines.Sturm–Liouville theorySturm–Liouville theory is a theory of eigenvalues and eigenfunctions of linear operators defined in terms of second-order homogeneous linear equations, and is useful in the analysis of certain partial differential equations.Software for ODE solving•FuncDesigner (free license: BSD, uses Automatic differentiation, also can be used online via Sage-server [2])•VisSim [3] - a visual language for differential equation solving•Mathematical Assistant on Web [4] online solving first order (linear and with separated variables) and second order linear differential equations (with constant coefficients), including intermediate steps in the solution.•DotNumerics: Ordinary Differential Equations for C# and [5] Initial-value problem for nonstiff and stiff ordinary differential equations (explicit Runge-Kutta, implicit Runge-Kutta, Gear’s BDF and Adams-Moulton).•Online experiments with JSXGraph [6]References[1]Polyanin, Andrei D.; Valentin F. Zaitsev (2003). Handbook of Exact Solutions for Ordinary Differential Equations, 2nd. Ed.. Chapman &Hall/CRC. ISBN 1-5848-8297-2.[2]/welcome[3][4]http://user.mendelu.cz/marik/maw/index.php?lang=en&form=ode[5]/NumericalLibraries/DifferentialEquations/[6]http://jsxgraph.uni-bayreuth.de/wiki/index.php/Differential_equationsBibliography• A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition)", Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2• A. D. Polyanin, V. F. Zaitsev, and A. Moussiaux, Handbook of First Order Partial Differential Equations, Taylor & Francis, London, 2002. ISBN 0-415-27267-X• D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.•Hartman, Philip, Ordinary Differential Equations, 2nd Ed., Society for Industrial & Applied Math, 2002. ISBN 0-89871-510-5.•W. Johnson, A Treatise on Ordinary and Partial Differential Equations (/cgi/b/bib/ bibperm?q1=abv5010.0001.001), John Wiley and Sons, 1913, in University of Michigan Historical Math Collection (/u/umhistmath/)• E.L. Ince, Ordinary Differential Equations, Dover Publications, 1958, ISBN 0486603490•Witold Hurewicz, Lectures on Ordinary Differential Equations, Dover Publications, ISBN 0-486-49510-8•Ibragimov, Nail H (1993), CRC Handbook of Lie Group Analysis of Differential Equations Vol. 1-3, Providence: CRC-Press, ISBN 0849344883.External links•Differential Equations (/Science/Math/Differential_Equations//) at the Open Directory Project (includes a list of software for solving differential equations).•EqWorld: The World of Mathematical Equations (http://eqworld.ipmnet.ru/index.htm), containing a list of ordinary differential equations with their solutions.•Online Notes / Differential Equations (/classes/de/de.aspx) by Paul Dawkins, Lamar University.•Differential Equations (/diffeq/diffeq.html), S.O.S. Mathematics.• A primer on analytical solution of differential equations (/mws/gen/ 08ode/mws_gen_ode_bck_primer.pdf) from the Holistic Numerical Methods Institute, University of South Florida.•Ordinary Differential Equations and Dynamical Systems (http://www.mat.univie.ac.at/~gerald/ftp/book-ode/ ) lecture notes by Gerald Teschl.•Notes on Diffy Qs: Differential Equations for Engineers (/diffyqs/) An introductory textbook on differential equations by Jiri Lebl of UIUC.Article Sources and Contributors7Article Sources and ContributorsOrdinary differential equation Source: /w/index.php?oldid=433160713 Contributors: 48v, A. di M., Absurdburger, AdamSmithee, After Midnight, Ahadley,Ahoerstemeier,AlfyAlf,Alll,AndreiPolyanin,Anetode,Ap,Arthena,ArthurRubin,BL,BMF81,********************,Bemoeial,BenFrantzDale,Benjamin.friedrich,BereanHunter,Bernhard Bauer, Beve, Bloodshedder, Bo Jacoby, Bogdangiusca, Bryan Derksen, Charles Matthews, Chilti, Chris in denmark, ChrisUK, Christian List, Cloudmichael, Cmdrjameson, Cmprince, Conversion script, Cpuwhiz11, Cutler, Delaszk, Dicklyon, DiegoPG, Dmitrey, Dmr2, DominiqueNC, Dominus, Donludwig, Doradus, Dysprosia, Ed Poor, Ekotkie, Emperorbma, Enochlau, Fintor, Fruge, Fzix info, Gauge, Gene s, Gerbrant, Giftlite, Gombang, HappyCamper, Heuwitt, Hongsichuan, Ht686rg90, Icairns, Isilanes, Iulianu, Jack in the box, Jak86, Jao, JeLuF, Jitse Niesen, Jni, JoanneB, John C PI, Jokes Free4Me, JonMcLoone, Josevellezcaldas, Juansempere, Kawautar, Kdmckale, Krakhan, Kwantus, L-H, LachlanA, Lethe, Linas, Lingwitt, Liquider, Lupo, MarkGallagher,MathMartin, Matusz, Melikamp, Michael Hardy, Mikez, Moskvax, MrOllie, Msh210, Mtness, Niteowlneils, Oleg Alexandrov, Patrick, Paul August, Paul Matthews, PaulTanenbaum, Pdenapo, PenguiN42, Phil Bastian, PizzaMargherita, Pm215, Poor Yorick, Pt, Rasterfahrer, Raven in Orbit, Recentchanges, RedWolf, Rich Farmbrough, Rl, RobHar, Rogper, Romanm, Rpm, Ruakh, Salix alba, Sbyrnes321, Sekky, Shandris, Shirt58, SilverSurfer314, Ssd, Starlight37, Stevertigo, Stw, Susvolans, Sverdrup, Tarquin, Tbsmith, Technopilgrim, Telso, Template namespace initialisation script, The Anome, Tobias Hoevekamp, TomyDuby, TotientDragooned, Tristanreid, Twin Bird, Tyagi, Ulner, Vadimvadim, Waltpohl, Wclxlus, Whommighter, Wideofthemark, WriterHound, Xrchz, Yhkhoo, 今古庸龍, 176 anonymous editsImage Sources, Licenses and ContributorsImage:Parabolic trajectory.svg Source: /w/index.php?title=File:Parabolic_trajectory.svg License: Public Domain Contributors: Oleg AlexandrovLicenseCreative Commons Attribution-Share Alike 3.0 Unported/licenses/by-sa/3.0/。

期权期货与其他衍生产品第九版课后习题与答案Chapter (15)

CHAPTER 15The Black-Scholes-Merton ModelPractice QuestionsProblem 15.1.What does the Black –Scholes –Merton stock option pricing model assume about the probability distribution of the stock price in one year? What does it assume about theprobability distribution of the continuously compounded rate of return on the stock during the year?The Black –Scholes –Merton option pricing model assumes that the probability distribution of the stock price in 1 year (or at any other future time) is lognormal. It assumes that thecontinuously compounded rate of return on the stock during the year is normally distributed.Problem 15.2.The volatility of a stock price is 30% per annum. What is the standard deviation of the percentage price change in one trading day?The standard deviation of the percentage price change in time t ∆is where σ is the volatility. In this problem 03=.and, assuming 252 trading days in one year, 12520004t ∆=/=. so that 00019=.=. or 1.9%.Problem 15.3.Explain the principle of risk-neutral valuation.The price of an option or other derivative when expressed in terms of the price of theunderlying stock is independent of risk preferences. Options therefore have the same value in a risk-neutral world as they do in the real world. We may therefore assume that the world is risk neutral for the purposes of valuing options. This simplifies the analysis. In a risk-neutral world all securities have an expected return equal to risk-free interest rate. Also, in arisk-neutral world, the appropriate discount rate to use for expected future cash flows is the risk-free interest rate.Problem 15.4.Calculate the price of a three-month European put option on a non-dividend-paying stock with a strike price of $50 when the current stock price is $50, the risk-free interest rate is 10% per annum, and the volatility is 30% per annum.In this case 050S =, 50K =, 01r=., 03σ=., 025T =., and12102417000917d d d ==.=-.=.The European put price is 0102550(00917)50(02417)N e N -.⨯.-.--.0102550046345004045237e -.⨯.=⨯.-⨯.=.or $2.37.Problem 15.5.What difference does it make to your calculations in Problem 15.4 if a dividend of $1.50 is expected in two months?In this case we must subtract the present value of the dividend from the stock price before using Black –Scholes-Merton. Hence the appropriate value of 0S is01667010501504852S e -.⨯.=-.=.As before 50K =, 01r =., 03σ=., and 025T =.. In this case12100414001086d d d ==.=-.=-.The European put price is 0102550(01086)4852(00414)N e N -.⨯..-.-. 010255005432485204835303e -.⨯.=⨯.-.⨯.=. or $3.03.Problem 15.6.What is implied volatility? How can it be calculated?The implied volatility is the volatility that makes the Black –Scholes-Merton price of an option equal to its market price. The implied volatility is calculated using an iterativeprocedure. A simple approach is the following. Suppose we have two volatilities one too high (i.e., giving an option price greater than the market price) and the other too low (i.e., giving an option price lower than the market price). By testing the volatility that is half way between the two, we get a new too-high volatility or a new too-low volatility. If we search initially for two volatilities, one too high and the other too low we can use this procedure repeatedly to bisect the range and converge on the correct implied volatility. Other more sophisticated approaches (e.g., involving the Newton-Raphson procedure) are used in practice.Problem 15.7.A stock price is currently $40. Assume that the expected return from the stock is 15% and its volatility is 25%. What is the probability distribution for the rate of return (with continuous compounding) earned over a two-year period?In this case 015=.μ and 025=.σ. From equation (15.7) the probability distribution for the rate of return over a two-year period with continuous compounding is:⎪⎪⎭⎫⎝⎛-ϕ225.0,225.015.022i.e.,)03125.0,11875.0(ϕThe expected value of the return is 11.875% per annum and the standard deviation is 17.7%per annum.Problem 15.8.A stock price follows geometric Brownian motion with an expected return of 16% and a volatility of 35%. The current price is $38.a) What is the probability that a European call option on the stock with an exercise price of $40 and a maturity date in six months will be exercised?b) What is the probability that a European put option on the stock with the same exercise price and maturity will be exercised?a) The required probability is the probability of the stock price being above $40 in six months time. Suppose that the stock price in six months is T S⎥⎦⎤⎢⎣⎡⨯⎪⎪⎭⎫ ⎝⎛-+5.035.0,5.0235.016.038ln ~ln 22ϕT Si.e.,()2247.0,687.3~ln ϕT SSince ln 403689=., we require the probability of ln(S T )>3.689. This is3689368711(0008)0247N N .-.⎛⎫-=-. ⎪.⎝⎭Since N(0.008) = 0.5032, the required probability is 0.4968.b) In this case the required probability is the probability of the stock price being less than $40 in six months time. It is10496805032-.=.Problem 15.9.Using the notation in the chapter, prove that a 95% confidence interval for T S is between22(2)196(2)19600andT T S e S e -/-.-/+.μσμσFrom equation (15.3):⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+T T S S T 220,2ln ~ln σσμϕ95% confidence intervals for ln T S are therefore20ln ()1962S T +--.σμand20ln ()1962S T +-+.σμσ95% confidence intervals for T S are therefore2200ln (2)196ln (2)196and S T S T e e +-/-.+-/+.μσμσi.e.22(2)196(2)19600andT T S e S e -/-.-/+.μσμσProblem 15.10.A portfolio manager announces that the average of the returns realized in each of the last 10 years is 20% per annum. In what respect is this statement misleading?This problem relates to the material in Section 15.3. The statement is misleading in that a certain sum of money, say $1000, when invested for 10 years in the fund would have realized a return (with annual compounding) of less than 20% per annum.The average of the returns realized in each year is always greater than the return per annum (with annual compounding) realized over 10 years. The first is an arithmetic average of the returns in each year; the second is a geometric average of these returns.Problem 15.11.Assume that a non-dividend-paying stock has an expected return of μ and a volatility of σ. An innovative financial institution has just announced that it will trade a derivative that pays off a dollar amount equal to ln S T at time T where T S denotes the values of the stock price at time T .a) Use risk-neutral valuation to calculate the price of the derivative at time t in term of the stock price, S, at time tb) Confirm that your price satisfies the differential equation (15.16)a) At time t , the expected value of ln S T is from equation (15.3) 2ln (/2)()S T t μσ+--In a risk-neutral world the expected value of ln S T is therefore2ln (/2)()S r T t σ+--Using risk-neutral valuation the value of the derivative at time t is()2[ln (/2)()]r T t e S r T t σ--+--b) If()2[ln (/2)()]r T t f e S r T t σ--=+--then()()2()2()2()22[ln (/2)()]/2r T t r T t r T t r T t fre S r T t e r tf e S S f e S S σσ--------∂=+----∂∂=∂∂=-∂The left-hand side of the Black-Scholes-Merton differential equation is()222()2ln (/2)()(/2)/2ln (/2)()r T t r T t e r S r r T t r r e r S r r T t rfσσσσ----⎡⎤+----+-⎣⎦⎡⎤=+--⎣⎦=Hence the differential equation is satisfied.Problem 15.12.Consider a derivative that pays off n T S at time T where T S is the stock price at that time. When the stock pays no dividends and its price follows geometric Brownian motion, it can be shown that its price at time t ()t T ≤ has the form()n h t T S ,where S is the stock price at time t and h is a function only of t and T .(a) By substituting into the Black –Scholes –Merton partial differential equation derive an ordinary differential equation satisfied by ()h t T ,.(b) What is the boundary condition for the differential equation for ()h t T ,? (c) Show that2[05(1)(1)]()()n n r n T t h t T eσ.-+--,= where r is the risk-free interest rate and σ is the stock price volatility.If ()()n G S t h t T S ,=, then n t G t h S ∂/∂=, 1n G S hnS -∂/∂=, and 222(1)n G S hn n S -∂/∂=- where t h h t =∂/∂. Substituting into the Black –Scholes –Merton differential equation we obtain21(1)2t h rhn hn n rh σ++-=The derivative is worth n S when t T =. The boundary condition for this differential equation is therefore ()1h T T ,= The equation2[05(1)(1)]()()n n r n T t h t T e σ.-+--,=satisfies the boundary condition since it collapses to 1h = when t T =. It can also be shown that it satisfies the differential equation in (a). Alternatively we can solve the differential equation in (a) directly. The differential equation can be written21(1)(1)2t h r n n n h σ=----The solution to this is21ln [(1)(1)]()2h r n n n T t σ=-+--or2[05(1)(1)]()()n n r n T t h t T e σ.-+--,=Problem 15.13.What is the price of a European call option on a non-dividend-paying stock when the stock price is $52, the strike price is $50, the risk-free interest rate is 12% per annum, the volatility is 30% per annum, and the time to maturity is three months?In this case 052S =, 50K =, 012r =., 030=.σ and 025T =..212105365003865d d d ==.=-.=. The price of the European call is 01202552(05365)50(03865)N e N -.⨯..-. 00352070425006504e -.=⨯.-⨯. 506=. or $5.06.Problem 15.14.What is the price of a European put option on a non-dividend-paying stock when the stock price is $69, the strike price is $70, the risk-free interest rate is 5% per annum, the volatility is 35% per annum, and the time to maturity is six months?In this case 069S =, 70K =, 005r =., 035=.σ and 05T =..212101666000809d d d ==.=-.=-. The price of the European put is 0050570(00809)69(01666)e N N -.⨯..--. 002570053236904338e -.=⨯.-⨯.640=. or $6.40.Problem 15.15.Consider an American call option on a stock. The stock price is $70, the time to maturity is eight months, the risk-free rate of interest is 10% per annum, the exercise price is $65, and the volatility is 32%. A dividend of $1 is expected after three months and again after sixmonths. Show that it can never be optimal to exercise the option on either of the two dividend dates. Use DerivaGem to calculate the price of the option.Using the notation of Section 15.12, 121D D ==, 2()0101667(1)65(1)107r T t K e e ---.⨯.-=-=., and 21()01025(1)65(1)160r t t K e e ---.⨯.-=-=.. Since 2()1(1)r T t D K e --<- and 21()2(1)r t t D K e --<-It is never optimal to exercise the call option early. DerivaGem shows that the value of the option is 1094..Problem 15.16.A call option on a non-dividend-paying stock has a market price of $2.50. The stock price is $15, the exercise price is $13, the time to maturity is three months, and the risk-free interest rate is 5% per annum. What is the implied volatility?In the case 25c =., 015S =, 13K =, 025T =., 005r =.. The implied volatility must becalculated using an iterative procedure.A volatility of 0.2 (or 20% per annum) gives 220c =.. A volatility of 0.3 gives 232c =.. A volatility of 0.4 gives 2507c =.. A volatility of 0.39 gives 2487c =.. By interpolation the implied volatility is about 0.396 or 39.6% per annum.The implied volatility can also be calculated using DerivaGem. Select equity as theUnderlying Type in the first worksheet. Select Black-Scholes European as the Option Type. Input stock price as 15, the risk-free rate as 5%, time to exercise as 0.25, and exercise price as 13. Leave the dividend table blank because we are assuming no dividends. Select the button corresponding to call. Select the implied volatility button. Input the Price as 2.5 in the second half of the option data table. Hit the Enter key and click on calculate. DerivaGem will show the volatility of the option as 39.64%.Problem 15.17.With the notation used in this chapter (a) What is ()N x '?(b) Show that ()12()()r T t SN d Ke N d --''=, where S is the stock price at time t21d =22d =(c) Calculate 1d S ∂/∂ and 2d S ∂/∂. (d) Show that when()12()()r T t c SN d Ke N d --=-()21()(r T t c rKe N d SN d t --∂'=--∂ where c is the price of a call option on a non-dividend-paying stock. (e) Show that 1()c S N d ∂/∂=.(f) Show that the c satisfies the Black –Scholes –Merton differential equation.(g) Show that c satisfies the boundary condition for a European call option, i.e., thatmax(0)c S K =-, as t tends to T.(a) Since ()N x is the cumulative probability that a variable with a standardized normal distribution will be less than x , ()N x ' is the probability density function for a standardized normal distribution, that is,22()x N x -'=(b)12()(N d N d ''=+2221()22d d T t σσ⎡⎤=---⎢⎥⎣⎦221()exp ()2N d d T t σσ⎡⎤'=--⎢⎥⎣⎦Because22d =it follows that()21exp ()2r T t Ked T t S σσ--⎡⎤--=⎢⎥⎣⎦As a result()12()()r T t SN d Ke N d --''=which is the required result.(c)22212S K d σσ==Hence1d S ∂=∂ Similarly222d σ=and2d S ∂=∂ Therefore:12d d S S∂∂=∂∂(d)()12()()12122()()()()()r T t r T t r T t c SN d Ke N d d d c SN d rKe N d Ke N d t t t------=-∂∂∂''=--∂∂∂ From (b):()12()()r T t SN d Ke N d --''=Hence()1221()()r T t d d c rKe N d SN d t tt --∂∂∂⎛⎫'=-+- ⎪∂∂∂⎝⎭ Since12d d -=12(d d t t t∂∂∂-=∂∂∂=Hence()21()(r T t c rKe N d SN d t --∂'=--∂(e) From differentiating the Black –Scholes –Merton formula for a call price weobtain()12112()()()r T t d d cN d SN d Ke N d S S dS--∂∂∂''=+-∂∂ From the results in (b) and (c) it follows that1()cN d S ∂=∂(f) Differentiating the result in (e) and using the result in (c), we obtain21121()(d cN d S SN d ∂∂'=∂∂'= From the results in d) and e)222()2122211()121()(21()(2[()()]r T t r T t c c c rS S rKe N d SN d t S S rSN d S N d r SN d Ke N d rcσσ----∂∂∂'++=--∂∂∂'++=-=This shows that the Black –Scholes –Merton formula for a call option does indeed satisfy the Black –Scholes –Merton differential equation(g) Consider what happens in the formula for c in part (d) as t approaches T . IfS K >, 1d and 2d tend to infinity and 1()N d and 2()N d tend to 1. If S K <, 1d and 2d tend to zero. It follows that the formula for c tends to max(0)S K -,.Problem 15.18.Show that the Black –Scholes –Merton formulas for call and put options satisfy put –call parity.The Black –Scholes –Merton formula for a European call option is 012()()rT c S N d Ke N d -=- so that 012()()rT rT rT c Ke S N d Ke N d Ke ---+=-+ or 012()[1()]rT rT c Ke S N d Ke N d --+=+- or 012()()rT rT c Ke S N d Ke N d --+=+-The Black –Scholes –Merton formula for a European put option is 201()()rT p Ke N d S N d -=--- so that 02010()()rT p S Ke N d S N d S -+=---+ or 0201()[1()]rT p S Ke N d S N d -+=-+-- or 0201()()rT p S Ke N d S N d -+=-+ This shows that the put –call parity result 0rT c Ke p S -+=+ holds.Problem 15.19.A stock price is currently $50 and the risk-free interest rate is 5%. Use the DerivaGemsoftware to translate the following table of European call options on the stock into a table of implied volatilities, assuming no dividends. Are the option prices consistent with the assumptions underlying Black –Scholes –Merton?Using DerivaGem we obtain the following table of implied volatilitiesBlack-Scholes European as the Option Type. Input stock price as 50, the risk-free rate as 5%, time to exercise as 0.25, and exercise price as 45. Leave the dividend table blank because we are assuming no dividends. Select the button corresponding to call. Select the implied volatility button. Input the Price as 7.0 in the second half of the option data table. Hit theEnter key and click on calculate. DerivaGem will show the volatility of the option as 37.78%. Change the strike price and time to exercise and recompute to calculate the rest of the numbers in the table.The option prices are not exactly consistent with Black –Scholes –Merton. If they were, the implied volatilities would be all the same. We usually find in practice that low strike price options on a stock have significantly higher implied volatilities than high strike price options on the same stock. This phenomenon is discussed in Chapter 20.Problem 15.20.Explain carefully why Black’s approach to evaluating an American call option on a dividend-paying stock may give an approximate answer even when only one dividend is anticipated. Does the answer given by Black’s approach understate or overstate the true option value? Explain your answer.Black’s approach in effect assumes that the holder of option must decide at time zero whether it is a European option maturing at time n t (the final ex-dividend date) or a European optionmaturing at time T . In fact the holder of the option has more flexibility than this. The holder can choose to exercise at time n t if the stock price at that time is above some level but nototherwise. Furthermore, if the option is not exercised at time n t , it can still be exercised attime T .It appears that Black ’s approach should understate the true option value. This is because the holder of the option has more alternative strategies for deciding when to exercise the option than the two strategies implicitly assumed by the approach. These alternative strategies add value to the option.However, this is not the whole story! The standard approach to valuing either an American or a European option on a stock paying a single dividend applies the volatility to the stock price less the present value of the dividend. (The procedure for valuing an American option is explained in Chapter 21.) Black’s approach when considering exercise just prior to the dividend date applies the volatility to the stock price itself. Black’s approach thereforeassumes more stock price variability than the standard approach in some of its calculations. In some circumstances it can give a higher price than the standard approach.Problem 15.21.Consider an American call option on a stock. The stock price is $50, the time to maturity is 15 months, the risk-free rate of interest is 8% per annum, the exercise price is $55, and the volatility is 25%. Dividends of $1.50 are expected in 4 months and 10 months. Show that it can never be optimal to exercise the option on either of the two dividend dates. Calculate the price of the option.With the notation in the text12121500333308333125008and 55D D t t T r K ==.,=.,=.,=.,=.=2()00804167155(1)180r T t K e e ---.⨯.⎡⎤⎢⎥⎣⎦-=-=. Hence2()21r T t D K e --⎡⎤⎢⎥⎣⎦<- Also:21()00805155(1)216r t t K e e ---.⨯.⎡⎤⎢⎥⎣⎦-=-=. Hence:21()11r t t D K e --⎡⎤⎢⎥⎣⎦<- It follows from the conditions established in Section 15.12 that the option should never be exercised early.The present value of the dividends is033330080833300815152864e e -.⨯.-.⨯..+.=.The option can be valued using the European pricing formula with:05028644713655025008125S K r T σ=-.=.,=,=.,=.,=.212100545003340d d d ==-.=-.=-.12()04783()03692N d N d =.,=.and the call price is00812547136047835503692417e -.⨯..⨯.-⨯.=. or $4.17.Problem 15.22.Show that the probability that a European call option will be exercised in a risk-neutral world is, with the notation introduced in this chapter, 2()N d . What is an expression for the value of a derivative that pays off $100 if the price of a stock at time T is greater than K ?The probability that the call option will be exercised is the probability that T S K > where T S is the stock price at time T . In a risk neutral world[]T T r S S T 220,)2/(ln ~ln σσϕ-+The probability that T S K > is the same as the probability that ln ln T S K >. This is21N ⎡⎤-2N =2()N d =The expected value at time T in a risk neutral world of a derivative security which pays off $100 when T S K > is therefore2100()N dFrom risk neutral valuation the value of the security at time zero is2100()rT e N d -Problem 15.23.Use the result in equation (15.17) to determine the value of a perpetual American put option on a non-dividend-paying stock with strike price K if it is exercised when the stock price equals H where H<K. Assume that the current stock price S is greater than H. What is the value of H that maximizes the option value? Deduce the value of a perpetual American put option with strike price K.If the perpetual American put is exercised when S=H , it provides a payoff of (K −H ). We obtain its value, by setting Q=K−H in equation (15.17), as 22/2/2)()(σσ-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=r r S H H K H S H K VNow1/222/222222/21/22/2222222)(212)(212-σσσ-σσ⎪⎭⎫ ⎝⎛σ⎪⎭⎫ ⎝⎛σ-+-+⎪⎭⎫ ⎝⎛σ-=⎪⎭⎫ ⎝⎛σ-+-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛σ-+⎪⎭⎫ ⎝⎛-=r r r r r S H S r H H K r S H H rK dH V d H H K r S H S H r S H K S H dH dVdV/dH is zero when222σ+=r rK H and, for this value of H , d 2V /dH 2 is negative indicating that it gives the maximum value of V .The value of the perpetual American put is maximized if it is exercised when S equals this value of H . Hence the value of the perpetual American put is 2/2)(σ-⎪⎭⎫ ⎝⎛-r H S H Kwhen H =2rK /(2r +σ2). The value is 2/22222)2(2σ-⎪⎪⎭⎫ ⎝⎛σ+σ+σr rK r S r K This is consistent with the more general result produced in Chapter 26 for the case where the stock provides a dividend yield.Problem 15.24.A company has an issue of executive stock options outstanding. Should dilution be taken into account when the options are valued? Explain you answer.The answer is no. If markets are efficient they have already taken potential dilution intoaccount in determining the stock price. This argument is explained in Business Snapshot 15.3.Problem 15.25.A company’s stock price is $50 and 10 million shares are outstanding. The company is considering giving its employees three million at-the-money five-year call options. Option exercises will be handled by issuing more shares. The stock price volatility is 25%, the five-year risk-free rate is 5% and the company does not pay dividends. Estimate the cost to the company of the employee stock option issue.The Black-Scholes-Merton price of the option is given by setting 050S =, 50K =, 005r =., 025σ=., and 5T =. It is 16.252. From an analysis similar to that in Section 15.10 the cost to the company of the options is 1016252125103⨯.=.+ or about $12.5 per option. The total cost is therefore 3 million times this or $37.5 million. Ifthe market perceives no benefits from the options the stock price will fall by $3.75.Further QuestionsProblem 15.26.If the volatility of a stock is 18% per annum, estimate the standard deviation of the percentage price change in (a) one day, (b) one week, and (c) one month.(a) %13.125218=(b) %50.25218=(c) %20.51218=Problem 15.27.A stock price is currently $50. Assume that the expected return from the stock is 18% per annum and its volatility is 30% per annum. What is the probability distribution for the stock price in two years? Calculate the mean and standard deviation of the distribution. Determine the 95% confidence interval.In this case 050S =, 018=.μ and 030=.σ. The probability distribution of the stock price in two years, T S , is lognormal and is, from equation (15.3), given by:⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+23.0,2209.018.050ln ~ln 2ϕT Si.e.,)42.0,18.4(~ln 2ϕT SThe mean stock price is from equation (15.4)018203650507167e e .⨯.==.and the standard deviation is from equation (15.5)018503183e .⨯=.95% confidence intervals for ln T S are418196042and 418196042.-.⨯..+.⨯.i.e.,335and 501..These correspond to 95% confidence limits for T S of 335501and e e ..i.e.,2852and 15044..Problem 15.28. (Excel file)Suppose that observations on a stock price (in dollars) at the end of each of 15 consecutive weeks are as follows:30.2, 32.0, 31.1, 30.1, 30.2, 30.3, 30.6, 33.0,32.9, 33.0, 33.5, 33.5, 33.7, 33.5, 33.2Estimate the stock price volatility. What is the standard error of your estimate?The calculations are shown in the table below2009471001145i i uu =.=.∑∑and an estimate of standard deviation of weekly returns is:002884=.The volatility per annum is therefore 002079.=. or 20.79%. The standard error of this estimate is 00393=. or 3.9% per annum.Problem 15.29.A financial institution plans to offer a security that pays off a dollar amount equal to 2T S at time T .(a) Use risk-neutral valuation to calculate the price of the security at time t in terms of the stock price, S , at time t . (Hint: The expected value of 2T S can be calculatedfrom the mean and variance of T S given in section 15.1.)(b) Confirm that your price satisfies the differential equation (15.16).(a) The expected value of the security is 2[()]T E S From equations (15.4) and (15.5), at time t :2()2()()2()var()[1]T t T T t T t T E S Se S S e e μμσ---==-Since 22var()[()][()]T T T S E S E S =-, it follows that 22[()]var()[()]T T T E S S E S =+ so that 22222()()22()(2)()2[()][1]T t T t T t T T t E S S e e S e S e μσμμσ---+-=-+=In a risk-neutral world r μ= so that222(2)()ˆ[()]r T t T E S S e σ+-= Using risk-neutral valuation, the value of the derivative security at time t is()2ˆ[()]r T t Te E S --22(2)()()r T t r T t S e e σ+---=22()()r T t S e σ+-=(b) If: 22222()()()()22()()2()()2()22r T t r T t r T t r T t f S e f S r e tf Se Sf e S σσσσσ+-+-+-+-=∂=-+∂∂=∂∂=∂ The left-hand side of the Black-Scholes –Merton differential equation is:222222()()2()()22()()()()2()2r T t r T t r T t r T t S r e rS e S e rS e rfσσσσσσ+-+-+-+--+++==Hence the Black-Scholes equation is satisfied.Problem 15.30.Consider an option on a non-dividend-paying stock when the stock price is $30, the exercise price is $29, the risk-free interest rate is 5% per annum, the volatility is 25% per annum, and the time to maturity is four months.a. What is the price of the option if it is a European call?b. What is the price of the option if it is an American call?c. What is the price of the option if it is a European put?d. Verify that put –call parity holds.In this case 030S =, 29K =, 005r =., 025=.σ and 412T =/2104225d ==.2202782d ==.(04225)06637(02782)06096N N .=.,.=.(04225)03363(02782)03904N N -.=.,-.=.a. The European call price is00541230066372906096252e -.⨯/⨯.-⨯.=.or $2.52.b. The American call price is the same as the European call price. It is $2.52.c. The European put price is00541229039043003363105e -.⨯/⨯.-⨯.=.or $1.05.d. Put-call parity states that:rT p S c Ke -+=+In this case 252c =., 030S =, 29K =, 105p =. and 09835rT e -=. and it is easy to verify that the relationship is satisfied,Problem 15.31.Assume that the stock in Problem 15.30 is due to go ex-dividend in 1.5 months. The expected dividend is 50 cents.a. What is the price of the option if it is a European call?b. What is the price of the option if it is a European put?c. If the option is an American call, are there any circumstances when it will beexercised early?a. The present value of the dividend must be subtracted from the stock price. This givesa new stock price of:01250053005295031e -.⨯.-.=.and 2103068d ==. 2201625d ==.12()06205()05645N d N d =.;=. The price of the option is therefore005412295031062052905645221e -.⨯/.⨯.-⨯.=.or $2.21.b. Because12()03795()04355N d N d -=.,-=. the value of the option when it is a European put is005412290435529503103795122e -.⨯/⨯.-.⨯.=.。

微分方程式（differentialequations）微分方程式微分方程式方程式或

微分方程式 (Differential Equations)微分方程式微分方程式: 方程式或等式中含有自變數之未知函數及其導函數或微分者稱之函數(因變數)y = f (x ); x :自變數 ⇒ 一般式或通式()0,=y x Fwhere ()()x f y y x F -=,函數的微分(differential) dy : 代表函數y 隨著自變數x 之變化―∆x ,而變化之∆y 的線性主部dx dxdy dy =()()dx x y x dy '=函數的導函數(derivative)()()xx y x x y x y dx dy y x x ∆-∆+=∆∆=='→∆→∆00lim lim※ 一個函數的自變量的增量∆x 趨近某一極限時，其因變量的增量∆y 與自變量的增量∆x 之商的極限※ 函數y 對自變數x 之瞬間變化率(instantaneous rate of change); 函數y 的無窮小的變化量dy (微分) 相對自變數x 的無窮小的變化量dx (微分)()()x y x x y y -∆+≡∆ ⇒()()εε+∆'=+=∆x x y x dy ydx x =∆⇒ ()ε+'=∆dx x y y()()⎩⎨⎧P.D.E. Equations, al Differenti Partial O.D.E. Equations, al Differenti Ordinary 偏微分方程式常微分方程式微分方程式常微分方程式（ordinary differential equation ，簡稱ODE ）是只含有一個自變數的函數及它們的一個或多個導函數的微分方程式偏微分方程式指含有兩個或兩個以上自變數的函數及及其偏導數的方程式定義一n 階常微分方程式通式如 ()()0,,,,='''n y y y y x F ()()0,,,='⇒='y y x F y x f ywhere ()()y x f y y y x F ,,,-'='()()()()()()()0,,,=-+'+''='''⇒=+'+''x f y x b y x a y y y y x F x f y x b y x a y()()()()()一階一次常微分方程式三階二次常微分方程式二階一次常微分方程式一階一次常微分方程式01413cos 62215252223322=-+=++⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+'+''=+dy y dx xe e t x dt x d dt x d x y y y y xy dxdy xt()0115522=-+⇒=-+y xe dx dy dy y dx xe xx 階(order): 微分方程式中出現之最高微分數稱為此微分方程式之階數次(degree): 微分方程式化成有理整式後，最高階微分相之最高幕次，稱為此微分方程式之次數線性常微分方程式 (linear ordinary differential equation): 微分方程式中自變數的函數(因變數) 及其導數的幕次均為一次方且無相互乘積項非線性常微分方程式 (nonlinear ordinary differential equation): 不屬於常線性微分方程式者均屬之()()()()()非線性常微分方程式非線性常微分方程式線性常微分方程式非線性常微分方程式01413cos 62215252223322=-+=++⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+'+''=+dy y dx xee t x dt x d dt x d x y y y y xy dxdy x t常微分方程式可表為下列通式者稱為線性常微分方程式()()()()()()()x R y x a y x a y x a y x a n n n n =+'+++--0111 1. ()n y y y y ,,,'''均為一次方且無乘積項 2. 無y 與其導數的非線性函數存在,()y e y y ,,sin3. ()()()()()x R x a x a x a x a n n ,,,,,011 -只為自變數的函數或常數齊次微分方程式 (homogeneous differential equation): R (x ) = 0 非齊次微分方程式 (inhomogeneous differential equation): R (x ) ≠ 0()()分方程式二階一次非線性齊次微式一次線性齊次微分方程三階0cos 0cos sin 32222332=++=+-y dxdydx y d y t dt y d t dt y d t微分方程式的解定義一n 階微分方程式在區間(a , b )的解為在區間(a , b )滿足該微分方程式之一n 次可微分函數定義一n 階微分方程式()()0,,,,,='''n y y y y x F 在某區間I 的解，為定義在區間I 並滿足該()()()()()()I x x x x x x F n ∈∀=''',0,,,,,φφφφ 之一n 次可微分函數()x φ證明函數()12-=x x φ為微分方程式22+=y dxdyx在區間∞<<∞-x 之解()()⎩⎨⎧'→='→-=y xx y x x 212φφ 02222=--⇒+=y dxdyxy dxdyx ()()02222212222222=-+-=---=--x x x x x y dxdyx∴()12-=x x φ為微分方程式22+=y dxdyx在區間∞<<∞-x 之解證明函數()x x x x y ln 22/12/1-=為微分方程式042=+''y y x 在區間()∞,0之解()x x x x x x x x x x x x y ln 21ln 21ln 212122/12/12/12/112/12/12/1--------=--=⎪⎭⎫⎝⎛+-='()2/32/312/12/321ln 41ln 2121------=⎪⎭⎫ ⎝⎛+--=''x x x x x x x x y()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧-=''-='-=---2/32/32/12/12/121ln 41ln 21ln 2x x x x y x xx y x x x x yln 22ln ln 221ln 41442/12/12/12/12/12/12/32/322=-+-=-+⎪⎭⎫⎝⎛-=+''--x x x x x x xx x x x x x y y x ∴ 函數()x x x x y ln 22/12/1-=為微分方程式042=+''y y x 在區間()∞,0之解證明函數()x x y ln =為微分方程式022=+dx dydxy d x 在區間()∞,0之解, 但在區間()∞∞-,則不為其解()x x y ln =的定義域為()∞,00111111222222=+-=+⎪⎭⎫ ⎝⎛-=+⇒⎪⎪⎩⎪⎪⎨⎧-==x x xx x dx dy dx y d x x dxyd x dx dy∴ 函數()x x y ln =為微分方程式022=+dx dydxy d x 在區間()∞,0之解 ∵對數函數在區間()0,∞-無定義⇒函數()x x y ln =不為微分方程式022=+dx dydxy d x 在區間()∞∞-,之解顯函數解: 一n 階微分方程式其解可表為下列形式者,稱之()0,,,,,210==n c c c c x f y隱函數解: 一n 階微分方程式其解需表為下列形式者,稱之()()0,0,,,,,,,210=⇔=y x c c c c y x F n φ一般而言, 線性常微分方程式所得到的解,大多可表為顯函數解. 非線性常微分方程式所得到的解,大多為隱函數解. 證明函數0ln 2=--x y xy 為微分方程式122--=xy y xy dx dy 之隱函數解將0ln 2=--x y xy 對x 隱微分⇒ ()()0210ln 2=--+⇒=--x dxdyy dx dy xy dxdx y xy dx d ∴y x dxdyy xy y x dx dy y x -=-⇒-=⎪⎪⎭⎫ ⎝⎛-2121⇒ ()12122--=--=xy y xy xy y x y dx dy ∴ 函數0ln 2=--x y xy 為微分方程式122--=xy y xy dx dy 之隱函數解通解(general solution): 包含n 個任意常數的n 階常微分方程式的解.一般而言, n 階常微分方程式的解所包含任意常數的數目等於該微分方程式的階數. 特解(particular solution): 解中之常數均為定值或將初始條件或邊界條件帶入通解,決定任意常數的值,所得的解稱之.奇異解(singular solution): 不能由通解初始條件或邊界條件得到,但仍能滿足原微分方程式的解稱之.一階微分方程式之通解()()0 ,==x,y,c F c x f y 或c 為任意常數+ (初始)條件(initial condition) : ()00y x y = ⇒ 特解,c 為定值x 0,y 0為已知值一階微分方程式之圖形特解為積分曲線(integral curve),通解則稱積分曲線族,因c 為任意常數,可得無限個積分曲線微分方程式y x dxdy-=在區間()∞∞-,具有一通解x e c x y -+-=01,試就 0.2,0.1,5.0,0,100000====-=c c c c c 決定其特解,並會出其積分曲線xx x x e x y c e x y c e x y c x y c e x y c ----+-=⇒=+-=⇒=+-=⇒=-=⇒=--=⇒-=210.210.15.015.0101100000證明ct t t y +=ln 為微分方程式t ty y t 12=-'在區間()∞,0之通解()c t c t y ct t t y ++=++='⇒+=1ln 1ln ln012=--'⇒=-'t y y t t t y y t()()0ln ln ln 1ln =---++=-+-++=--'t ct t t ct t t t t ct t t c t t t y y t∴ct t t y +=ln 為微分方程式t ty y t 12=-'在區間()∞,0之通解試證明微分方程式()12+-=x y dx dy 具有下列之解: ⎪⎩⎪⎨⎧=+-=x y c x x y :1:0奇異解通解()200011111c x c x dx d dx dy c x x y ++=⎪⎪⎭⎫ ⎝⎛+-=⇒+-= ()()01122=---⇒+-=x y dx dy x y dxdy∴01c x x y +-=為微分方程式()12+-=x y dx dy 的通解x y =無法由通解01c x x y +-=得到, ∴為微分方程式之奇異解若c 1與c 2為任意常數,試證x c x c y 2cos 2sin 21+=為微分方程式0422=+y dxyd的解⎪⎪⎩⎪⎪⎨⎧--=-=⇒+=x c x c dxyd x c x c dxdyxc x c y 2cos 42sin 42sin 22cos 22cos 2sin 21222121()()02cos 2sin 42cos 42sin 44212122=++--=+x c x c x c x c y dx yd∴函數x c x c y 2cos 2sin 21+=為微分方程式0422=+y dxyd 之解求函數4- 1,22x y x y c cx y =+=+=及與微分方程式02=-+⎪⎭⎫ ⎝⎛y dx dy x dx dy 之關係 (1) c dxdyc cx y =⇒+=2()0222=+-+=-+⎪⎭⎫ ⎝⎛cx c cx c y dx dy x dx dy⎩⎨⎧+=為任意常數滿足原微分方程式c c cx y 2 ⇒ 2c cx y +=為通解 (2) 11=⇒+=dxdyx y ()0112=+-+=-+⎪⎭⎫⎝⎛x x y dx dy x dx dy⎩⎨⎧=+=11c x y 滿足原微分方程式⇒ 1+=x y 為特解 (3) 242xdx dy x y -=⇒-=0424422222222=+-=⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=-+⎪⎭⎫ ⎝⎛x x x x x x x y dx dy x dx dy⎪⎩⎪⎨⎧-=無法由通解中得到不含任意常數滿足原微分方程式,42x y ⇒ 42x y -=為奇異解。

机械振动考题

第一章1.21.If energy is lost in any way during vibration, the system can be considered to be damped. (T)2.Superposition principle is valid for both linear and nonlinear systems(F)3.The frequency with which an initially disturbed system vibrates on its own is known as natural frequency(T)4.Any periodic function can be expanded into Fourier series(T)5.Harmonic motion is a periodic motion(T)6.The equivalent mass of several masses at different locations can be found using the equivalence of kinetic energy(T)7.The generalized coordinates are not necessarily Cartesian coordinates. (T)8.Discrete systems are same as lumped parameter systems(T)9.Consider the sum of harmonic motions,, withand The amplitude A is given by 30.8088(T)10.Consider the sum of harmonic motions, , withand The phase angle α is given by 1.57 rad. (F)第二章2.21.The amplitude of an undamped system will not change with time.(T)2.A system vibrating in air can be considered as a damped system(T)3.The equation of motion of a single degree of freedom system will be the same whether the mass moves in a horizontal plane or an inclined plane.(T)4.When a mass vibrates in a vertical direction, its weight can always be ignored in deriving the equation of motion(F)5.The principle of conservation of energy can be used to derive the equation of motion of both damped and undamped systems(F)6.The damped frequency can be larger that the undamped natural frequency of the system in some cases(F)7.The damped frequency can be zero in some cases. (T)8.The natural frequency of vibration of torsional system is given by where k and m denote the torsional spring constant and the polar mass moment of inertia, respectively(T)9.Rayleigh’s method is based on the principle of conservation of energy(T)10.The final position of the mass is always the equilibrium position in the case of Coulomb damping. (F)11.The undamped natural frequency of a system is given by , where is the static deflection of the mass(T)12.For an undamped system, the velocity leads the displacement by . (T)13.For an undamped system, the velocity leads the acceleration by (F)14.Coulomb damping can be called constant damping(T)15.The loss coefficient denotes the energy dissipated per radian per unit strain energy.(T)16.The motion diminishes to zero in both underdamped and overdamped cases. (T)17.The logarithmic decrement can be used to find the damping ratio(T)18.The hysteresis loop of the stress – strain curve of a material causes damping(T)19.The complex stiffness can be used to find the damping force in a system with hysteresis damping(T)20.The motion can be considered to be harmonic in the cases of hysteresis damping(T)第三章3.21.The magnification factor is the ratio of maximum amplitude and static deflection(T)2.The response will be harmonic if excitation is harmonic(T)3.The phase angle of the response depends on the system parameter m, c, k, and ω(T)4.The phase angle of the response depends on the amplitude of the forcing function.(F)5.During beating, the amplitude of the response builds up and then diminishes in a regular pattern (T)6.The Q-factor can be used to estimate the damping in a system (T)7.The half power points denote the values of frequency ratio where the amplification factor falls towhere Q is the Q-factor. (T)8.The amplitude ratio attains its maximum value at resonance in the case of hysteresis damping(F)9.The response is always in phase with the harmonic forcing function in the case of hysteresis damping(T)10.Damping reduces the amplitude ratio for all values of the forcing frequency. (T)11.The unbalance in a rotating machine causes vibration(T)12.The steady state solution can be assumed to be harmonic for small values of dry friction force(T)13.In a system with rotational unbalance, the effect of damping becomes negligibly small at higher speeds. A set is a collection of objects(T)第四章4.21.The change in momentum is called impulse (T)2.The response of a system under arbitrary force can be found by summing the responses due toseveral elementary impulses (T)3.The response spectrum corresponding to base excitation is useful in the design of machinery subject to earthquakes (T)4.Some periodic functions can not be replaced by a sum of harmonic functions (F)5.The amplitudes of higher harmonics will be smaller in the response of a system. (T)6.The Laplace transform method takes the initial conditions into account automatically (T)7.The equation of motion can be integrated numerically even when the exciting force is nonperiodic (T)8.The response spectrum gives the maximum response of all possible single degree of freedom systems (T_9.For a harmonic oscillator, the acceleration and displacement spectra can be obtained from the velocity spectrum. (T)第五章5.21.The normal modes can also be called principal modes (T)2.The generalized coordinates are linearly dependent (F)3.Principal coordinates can be considered as generalized coordinates (T)4.The vibration of a system depends on the coordinate system (F)5.The nature of coupling depends in the coordinate system (T)6.The principal coordinates avoid both static and dynamic coupling.(T)7.The use of principal coordinates helps in finding the response of the system (T)8.The mass, stiffness, and damping matrices of a two degree of freedom system are symmetric (T)9.The characteristics of a two degree of freedom system are used in the design of dynamic vibration absorber (T)10.Semi-definite systems are also known as degenerate systems (T)11.A semi-definite system can not have non-zero natural frequencies (F)12.The generalized coordinates are always measured form the equilibrium position of the body (F)13.During free vibration, different degrees of freedom oscillate with different phase angles (F)14.During free vibration, different degrees of freedom oscillate at different frequencies (F)15.During free vibration, different degrees of freedom oscillate with different amplitudes (T)16.The relative amplitude of different degrees of freedom in a two degree of freedom system depend on the natural frequency (T)17.The modal vectors of a system denote the normal modes of vibration (T)第六章6.21.For a multidegree of freedom system, one equation of motion can be written for each degree of freedom (T)grange’s equation cannot be used to derive the equations of motion of a multidegree of freedom system (F)3.The mass, stiffness, and damping matrices of a multidegree of freedom are always symmetric (T)4.The product of stiffness and flexibility matrices of a system is always an identity matrix (T)5.The modal analysis of a n-degree of freedom system can be conducted using r modes with r < n (T)6.For a damped multidegree of freedom system, all the eigenvalues can be complex (T)7.The modal damping ratio denotes damping in a particular normal mode (T)8.A multidegree of freedom system can have six of the natural frequencies equal to zero (T)9.The generalized coordinates will always have the unit of length (F)10.The generalized coordinates are independent of the conditions of constraint of the system (T)11.The generalized mass matrix of a multidegree of freedom system is always diagonal (F)12.The potential and kinetic energies of a multidegree of freedom system are always quadratic functions (T)13.The mass matrix of a system is always symmetric and positive definite (T)14.The stiffness matrix of a system is always symmetric and positive definite (F)15.The rigid body mode is also called the zero mode. (T)16.An unrestrained system is also known as a semi-definite system. (T)17.Newton’s second law of motion can always be used to derive the equations of motion of a vibrating system (T)第七章7.21.T he fundamental frequency given by Durkerley’s formula will always be larger than the exact value (F)2.The fundamental frequency given by Rayleigh’s method will always be larger than the exact value (T)3.is a standard eigenvalue problem (F)4.is a standard eigenvalue problem (T)5.Jacobi method can find the eigenvalues of only symmetric matrices. (T)6.Jacobi method uses rotation matrices. (T)7.The matrix iteration method requires the natural frequencies to be distinct and well separated (T)8.In matrix iteration method, any computational error will not yield incorrect results (T)9.The matrix iteration method will never fail to converge to higher frequencies. (F)10.When Rayleigh’s method is used for a shaft carrying several rotors, the static deflection curve can be used as the appropriate mode shape. (T)11.Rayleigh’s method can be considered to be same as the conservation of energy for a vibrating system (T)第八章8.21.Continuous systems are same as distributed systems. (T)2.Continuous systems can be considered to have infinite number of degrees of freedom. (T)3.The governing equation of a continuous system is an ordinary differential equation. (F)4.The free vibration equations corresponding to the transverse motion of a string, the longitudinal motion of a bar and the torsional motion of a shaft have the same form. (T)5.The normal modes of a continuous system are orthogonal. (T)6.A membrane has zero bending resistance. (T)7.Rayleigh’s method can be considered as a method of conservation of energy.(T)8.Rayleigh-Ritz method assumes the solution as a series of functions that satisfy the boundary conditions of the problem. (T)9.For a discrete system, the boundary conditions are to be applied explicitly. (T)10.The Euler-Bernoulli beam theory is more accurate than the Timoshenko theory. (F)第九章9.21.Vibration can cause structural and mechanical failures. (T)2.The response of a system can be reduced by the use of isolators and absorbers (T)3.Vibration control means the elimination or reduction of vibration (T)4.The vibration caused by a rotating unbalanced disc can be eliminated by adding a suitable mass to the disc (T)5.Any unbalanced mass can be replaced by two equivalent unbalanced masses in the end planes of the rotor (T)6.The oil whip in the bearings can cause instability in a rotor system (T)7.The natural frequency of a system can be changed by varying its damping (F)8.The stiffness of a rotating shaft can be altered by changing the location of its bearings (T)9.All practical systems have damping. (T)10.High loss factor of a material implies less damping (F)11.Passive isolation systems require external power to function (F)12.The transmissibility is also called the transmission ratio. (T)13.The force transmitted to the foundation of an isolator with rigid foundation can never be infinity (F)14.Internal and external friction can cause instability in a rotating shaft at speeds above the first critical speed (T)。

自动化专业英语课后单词及课后句子总结

P3U1architecture n. 体系结构instruction set 指令集binary-coded adj. 二进制编码的central processing unit (CPU) 中央处理器processor n. 处理器location n. （存储）单元word length 字长access v. 存取，接近fetch v., n. 取来field n. 域，字段opcode n. 操作码operand n. 操作数address n. 寻址single-precision adj. 单精度的floating-point adj. 浮点的terminal n. 终端complement v. 补充，求补decode v. 解码，译码request n. 请求inactive n. 不活动，停止I/O-mapped adj. 输入/输出映射的（单独编址）memory-mapped adj. 存储器映射的（统一编址）难句翻译[1] …how the instruction execution cycle is broken down into its various components.……指令执行周期怎样分解成不同的部分。

[2] One way to achieve meaningful patterns is to divide up the bits into fields…一种得到（指令）有效形式的方法是将（这些）位分成段……[3] The majority of computer tasks involve the ALU, but a great amount of data movement is required in order to make use of the ALU instructions.计算机的大多数工作涉及到ALU(逻辑运算单元)，但为了使用ALU指令，需要传送大量的数据。

differential equation例子

一、引言微分方程是描述自然现象中变化规律的数学工具，广泛应用于物理、工程、生物学等领域。

微分方程可以分为常微分方程和偏微分方程两大类，常微分方程是指未知函数的各阶导数只依赖于自变量的微分方程，偏微分方程则是指未知函数的各阶偏导数之间存在某种关系的微分方程。

二、常微分方程例子1. 一阶线性常微分方程：求解$\frac{dy}{dx}+py=q$考虑一阶线性常微分方程$\frac{dy}{dx}+py=q$，其中p和q为常数。

我们可以利用积分因子的方法来解这个微分方程。

将微分方程化为标准形式$\frac{dy}{dx}+p(x)y=q(x)$，然后求出积分因子$\mu(x)=e^{\int{p(x)}dx}$，最后用积分因子乘以微分方程两边并对等式两边积分，即可得到微分方程的解。

2. 二阶常微分方程：求解$y''+py'+qy=f(x)$考虑二阶常微分方程$y''+py'+qy=f(x)$，其中p、q和f(x)为已知函数。

我们可以利用常系数线性齐次微分方程的通解和特解的方法来求解这个微分方程。

求出对应齐次线性微分方程$y''+py'+qy=0$的通解$y_c(x)$，然后再求出非齐次线性微分方程$y''+py'+qy=f(x)$的一个特解$y_p(x)$，最终得出原方程的通解$y(x)=y_c(x)+y_p(x)$。

三、偏微分方程例子1. 热传导方程：求解$\frac{\partial u}{\partial t}=k\frac{\partial^2 u}{\partial x^2}$热传导方程描述了物体内部温度分布随时间变化的规律。

它是一个偏微分方程，可以利用分离变量法、变换变量法等方法来求解。

通过适当的变量分离和边界条件处理，可以得到热传导方程的解析解或数值解，进而研究物体内部的温度分布和传热规律。

2. 波动方程：求解$\frac{\partial^2 u}{\partialt^2}=c^2\frac{\partial^2 u}{\partial x^2}$波动方程描述了波在空间中传播的规律，也是一个重要的偏微分方程。

ode名词解释

ODE的名词解释ODE即Ordinary Differential Equation，中文名为常微分方程，是数学中的一个重要概念。

在许多科学领域，如物理学、工程学、生物学和经济学等，ODE都有广泛的应用。

本文将对ODE进行详细的解释和探讨，并介绍其基本概念、分类、解法和应用。

1. 基本概念ODE是描述关于一个或多个未知函数的导数与自变量之间关系的方程。

它常用于描述描述物质传输、电磁场分布、振动系统和生物系统等现象。

常微分方程的一般形式为：F(x,y,dydx,d2ydx2,…,d n ydx n)=0其中，x表示自变量，y表示未知函数，dydx表示y对x的导数，n表示最高阶导数的阶数。

解常微分方程的目标是确定一个或多个函数，使得方程成立。

不同的方程形式需要不同的方法进行求解。

2. 分类根据常微分方程的形式和性质，可以将其分为几类。

2.1 常系数线性微分方程形如d n ydx n +a n−1d n−1ydx n−1+⋯+a1dydx+a0y=f(x)的方程称为常系数线性微分方程。

常系数线性微分方程的解法通常涉及特征方程、齐次方程和非齐次方程，通过这些方法可以求得方程的通解或特解。

2.2 可分离变量的微分方程形如M(x)+N(y)dydx=0的方程称为可分离变量的微分方程。

可分离变量的微分方程可以通过分离变量、逐步积分的方法求解。

2.3 高阶线性微分方程高阶线性微分方程是包含高于一阶导数的方程。

比如d 2ydx2+p(x)dydx+q(x)y=0。

高阶线性微分方程需要利用特解和待定系数法等方法进行求解。

除了以上几种，还有常微分方程的其他分类，如二阶常系数齐次线性微分方程、二阶非齐次线性微分方程、一阶线性齐次微分方程等。

3. 解法解常微分方程的方法多种多样，根据方程的形式和性质选择不同的方法进行求解。

3.1 分离变量法对于可分离变量的微分方程，可以通过将方程中的变量分离，分别对自变量和未知函数进行积分来求解。

一阶常微分方程解法

一阶常微分方程解法常微分方程（Ordinary Differential Equation），简称ODE，是描述变量之间关系的数学方程。

一阶常微分方程是只含有一阶导数的方程。

解一阶常微分方程的方法有很多种，本文将介绍几种常用的解法。

一、分离变量法分离变量法是解一阶常微分方程常用的方法之一。

对于形如 dy/dx= f(x)g(y) 的方程，可以将 x 和 y 分离到方程两边，并对等式两边同时积分，得到解的形式。

例如，对于方程 dy/dx = x^2y，我们可以将 x 和 y 分离：dy/y = x^2 dx对两边同时积分：∫(1/y) dy = ∫x^2 dx得到：ln|y| = (1/3)x^3 + C解出 y 之后，我们可以得到原方程的解。

二、变量代换法变量代换法是解一阶常微分方程的另一种常用方法。

通过引入新的自变量，将原方程转化为一阶可分离变量的形式，从而求解方程。

例如，对于方程 dy/dx = 2xy，我们可以进行变量代换 y = v/x，其中v 是关于 x 的函数。

将这个代换带入原方程中：v/x + x dv/dx = 2x(v/x)整理得：v dv = 2xdx对两边同时积分：∫v dv = 2∫xdx得到：v^2/2 = x^2 + C将代换关系 y = v/x 带回，我们可以得到原方程的解。

三、齐次方程法对于形如 dy/dx = f(x, y)/g(x, y) 的一阶常微分方程，如果 f(x, y) 和g(x, y) 是齐次函数（即具有相同的次数），则可以使用齐次方程法解决。

例如，对于方程 dy/dx = (x^2+y^2)/(xy)，我们将 x 和 y 同时除以 x，得到：dy/(xdx) = (1+(y/x)^2) / (y/x)令 u = y/x，求导有 dy/(xdx) = du - u/x dx。

代入到方程中得到：du - u/x dx = (1+u^2)/u整理化简后可得：(1+u^2) du = dx/x对两边同时积分：∫(1+u^2) du = ∫dx/x得到：u + (1/3)u^3 = ln|x| + C将代换关系 u = y/x 带入，我们可以求得原方程的解。

常微分方程中的英文单词和短语

算子多项式
operator polynomial
rse transform
第七章
Chapter7Power Series Solutions of Differential Equations
柯西定理
Cauchy theorem
解析解
analytic solution
常数矩阵
constant matrix
非齐次线性微分方程组
non-homogeneous linear differential equations
常数列向量
constant arrange vector
常数变异公式
formula of variation of constant
计算公式
computing formula
若尔当标准型
Jordan normal form
矩阵函数
matrix function
实值解
real-valued function
复值解
complex-value function
代数余子式
algebraic cofactor
特征方程
characteristic equation
算子式
operator method
一阶线性方程
first-order linear equation
齐次
homogeneous
非齐次
non-homogeneous
积分因子法
method of integration factor
常数变易法
method of constants variation
初等变换法
elementary method of transformation