高一数学幂函数及函数奇偶性

合集下载

高一数学上册幂函数知识点

高一数学上册幂函数知识点幂函数是一种常见的函数形式，由于其在数学和实际问题中的广泛应用，掌握幂函数的知识点对高一学生来说至关重要。

本文将介绍高一数学上册幂函数的主要知识点，包括定义、性质以及解题方法等。

1. 幂函数的定义幂函数是指形如f(x) = x^a的函数，其中a为常数，x为自变量。

在幂函数中，底数x通常为正实数，指数a可以是正数、负数或零。

2. 幂函数的图像与性质（1）当指数a为正数时，幂函数的图像呈现递增的趋势。

若指数a大于1，则曲线斜率较大；若指数a介于0到1之间，则曲线斜率较小。

（2）当指数a为负数时，幂函数的图像呈现递减的趋势。

（3）当指数a为零时，幂函数的图像为一条水平直线。

3. 幂函数的基本性质（1）定义域：对于幂函数f(x) = x^a，其定义域为所有使得x^a有意义的实数x。

（2）值域：幂函数值域的范围可以是整个实数轴，或者是一个区间，具体取决于底数的正负和指数的奇偶性。

（3）对称性：当指数a为奇数时，幂函数关于原点对称；当指数a为偶数且底数x为正数时，幂函数关于y轴对称。

4. 幂函数的运算法则（1）幂函数的加法：若f(x) = x^a 和 g(x) = x^b 为幂函数，则它们的和函数是h(x) = x^a + x^b。

（2）幂函数的乘法：若f(x) = x^a 和 g(x) = x^b 为幂函数，则它们的乘积函数是h(x) = (x^a)(x^b) = x^(a+b)。

（3）幂函数的倒数：若f(x) = x^a 为幂函数，则其倒数函数是g(x) = 1/f(x) = 1/(x^a) = x^(-a)。

5. 幂函数的解题方法（1）求函数的定义域：根据幂函数的定义，求解所有使得x^a 有意义的实数x即可得到函数的定义域。

（2）求函数的值域：根据底数的正负和指数的奇偶性，可以确定函数的值域范围。

（3）求函数的性质与图像：通过计算函数的导数、二阶导数等信息，可以推断函数的增减性、凹凸性和图像的特征。

高中数学题：简单的幂函数与函数的奇偶性

高中数学题：简单的幂函数与函数的奇偶性一、幂函数的定义例1、已知函数是幂函数，求m的值。

分析：由幂函数的定义可知，只有形如的函数才是幂函数，故本题前的系数且，由此可解。

解：令及，可解得：m=2。

例2、当时，幂函数是减函数，则实数m的值为。

解答：依题意，。

又因为函数在时为减函数，故，故m=-1应舍去，从而m=2。

二、判断函数的奇偶性一般地，判断函数的奇偶性首先应确认函数的定义域关于原点对称，然后再根据f（x）和f（-x）的关系进行判断，若相等，则为偶函数；若相反，则为奇函数。

也可以根据图像的对称性来判断：若图像关于原点对称，则为奇函数；若图像关于y轴对称，则为偶函数。

例3、判断函数的奇偶性。

解答：因为函数的定义域是{x|x≠1}，关于原点不对称，所以该函数为非奇非偶函数。

若将此函数先化简得到f（x）= - x，则极易得到该函数是奇函数这样一个错误的结论；另外，本题最后的结论是该函数是非奇非偶函数，不可以说成“不具有奇偶性”。

例4、判断函数的奇偶性。

解答：分段函数的奇偶性的判断是一个难点，要注意分段进行判断，并要注意是将f（-x）和哪个区间上的f（x）进行比较。

三、复合函数的奇偶性复合函数y=f[g（x）]的奇偶性可以这样判断：当内外函数均为奇函数时，复合函数是奇函数；当内外函数中有一个是偶函数，而另一个函数无论是奇函数或偶函数，复合函数均为偶函数。

例5、判断函数的奇偶性。

解答：设，则g（x）是偶函数；又因为可视为的复合函数，故为偶函数。

四、利用函数的奇偶性解题例6、已知函数是奇函数，当x>0时，；求当x<0时的解析式。

解答：例7、试探究是否存在实数，使得函数是奇函数？若存在，求出实数，并证明函数是奇函数；若不存在，请说明理由。

解答：函数的定义域是（-1，1），若函数是奇函数，必有f（0）=0，解得，易证这是一个奇函数。

若奇函数在x=0时有意义，则必有f（0）=0。

五、幂函数的图像例8、函数的图像是（）解答：由是偶函数，排除B、C；又当0<x<1时，>x，故选D。

幂函数的性质

幂函数的性质幂函数是数学中常见的一种函数形式，由x的幂次和常数项构成。

幂函数的一般形式可以表示为f(x) = ax^n + b，其中a、n和b为常数，且n为正整数。

幂函数具有独特的性质，包括定义域、值域、奇偶性、单调性以及图像特点等，下面将详细探讨幂函数的各种性质。

一、定义域幂函数的定义域取决于幂指数n的奇偶性：当n为奇数时，幂函数的定义域为实数集；当n为偶数时，幂函数的定义域取决于系数a的正负性：- 若a>0，则幂函数的定义域为非负实数集，即x ≥ 0；- 若a<0，则幂函数的定义域为空集，即不存在实数使幂函数的结果为负数。

二、值域幂函数的值域也与幂指数n的奇偶性和系数a的正负性相关：当n为奇数时，幂函数的值域为全体实数；当n为偶数时，幂函数的值域取决于系数a的正负性：- 若a>0，则幂函数的值域为非负实数集，即f(x) ≥ 0；- 若a<0，则幂函数的值域在实数轴上存在最大值，即存在一个唯一的实数C使得f(x) ≤ C。

三、奇偶性幂函数的奇偶性由幂指数n来决定：当n为偶数时，幂函数为偶函数，即f(x) = f(-x)，图像关于y轴对称；当n为奇数时，幂函数为奇函数，即f(x) = -f(-x)，图像关于原点对称。

四、单调性幂函数的单调性与幂指数n的奇偶性和系数a的正负性相关：当n为正整数且n为奇数时，幂函数在整个定义域上单调递增或单调递减；当n为正整数且n为偶数时，幂函数在定义域上存在极值点，若系数a>0，则为单调递增，若系数a<0，则为单调递减。

五、图像特点幂函数的图像具有一些特点：当n为正整数时：- 当n为奇数时，幂函数的图像经过点(0, 0)且从第三象限经过第一象限，右上倾斜；- 当n为偶数时，幂函数的图像经过点(0, 0)，右侧在y轴上方且上升（a>0）或下降（a<0）。

综上所述，幂函数的性质主要包括定义域、值域、奇偶性、单调性以及图像特点。

高中幂函数知识点总结

引言：高中幂函数是高中数学中的重要部分，它在数学研究和实际问题中有着广泛的应用。

本文将对高中幂函数的知识点进行总结和整理，帮助学生完善对幂函数的理解和掌握。

概述：幂函数是指形如y=x^n的函数，其中n是常数。

幂函数的特点是具有单调性和奇偶性，其图象通常为一条曲线。

在研究幂函数时，需要掌握其定义、性质和应用。

正文：一、幂函数的定义1.1 幂函数的基本形式幂函数的基本形式是y=x^n，其中n是常数。

幂函数的定义域为所有实数，且n可以是正整数、负整数、零和有理数。

1.2 幂函数的图象当n为正奇数时，幂函数的图象在第一象限和第三象限上单调递增；当n为正偶数时，幂函数的图象在第一象限上单调递增，且具有对称轴y=0；当n为负数时，幂函数的图象在第一、三象限上单调递减。

1.3 幂函数的特殊情况当n=1时，幂函数变为一次函数；当n=0时，幂函数变为常数函数；当n为正无穷大时，幂函数趋向于正无穷大；当n为负无穷大时，幂函数趋向于零。

二、幂函数的性质2.1 幂函数的单调性幂函数在定义域上的单调性与n的值有关。

当n为正奇数时，幂函数是增函数；当n为正偶数时，在非负区间上是增函数，在负区间上是减函数；当n为负数时，在非负区间上是减函数，在负区间上是增函数。

2.2 幂函数的奇偶性幂函数的奇偶性与n的奇偶性有关。

当n为奇数时，幂函数是奇函数；当n为偶数时，幂函数是偶函数。

2.3 幂函数的零点当n为正奇数时，幂函数的零点为x=0；当n为正偶数时，幂函数的零点为x=0；当n为负奇数时，幂函数没有零点；当n为负偶数时，幂函数的零点为x=0。

三、幂函数的图象变换3.1 幂函数的平移幂函数的平移是指将幂函数的图象沿横轴或纵轴方向移动。

平移的方向和距离与平移的规律有关，具体可利用平移的公式进行计算。

3.2 幂函数的伸缩幂函数的伸缩是指将幂函数的图象进行纵向或横向的拉伸或压缩。

伸缩的方式和伸缩的规律有关，可利用伸缩的公式进行计算。

3.3 幂函数的翻折幂函数的翻折是指将幂函数的图象进行关于横轴或纵轴的翻折。

幂函数知识点高一必修一

幂函数知识点高一必修一幂函数是高中数学中的一个重要概念，它在解决实际问题和理论推导中都有广泛应用。

在高一必修一的数学课程中，学生将首次接触到幂函数的概念和相关知识。

本文将从定义、性质、图像和应用等方面进行介绍，帮助学生更好地理解和掌握幂函数。

一、幂函数的定义幂函数是形如$f(x)=x^a$的函数，其中$x$是自变量，$a$是常数且$a$可以为有理数、整数或实数。

当$a$为有理数时，幂函数的定义域是实数集；当$a$为整数时，幂函数的定义域可以是正实数集、负实数集或者零；当$a$为实数时，幂函数的定义域可以是正实数集和零集。

二、幂函数的性质1. 定义域：幂函数的定义域取决于指数的取值范围，通常为实数集或者特定的数集。

2. 奇偶性：当指数$a$为整数且为偶数时，幂函数是偶函数；当指数$a$为整数且为奇数时，幂函数是奇函数；当指数$a$为实数且为非整数时，幂函数既不是奇函数也不是偶函数。

3. 单调性：当指数$a>0$时，幂函数是增函数；当指数$a<0$时，幂函数是减函数。

4. 对称轴：当指数$a$为整数且为偶数时，幂函数的对称轴为$y$轴；当指数$a$为整数且为奇数时，幂函数没有对称轴。

三、幂函数的图像根据幂函数的性质可以推断出其图像的一些特点。

1. 当指数$a>1$时，幂函数的图像在原点左侧逐渐趋近于$x$轴且斜率逐渐增大；在原点右侧逐渐上升但斜率趋于0。

2. 当指数$a=1$时，幂函数的图像为直线$y=x$。

3. 当指数$0<a<1$时，幂函数的图像在整个定义域上单调递减，并且在$x$轴上趋于无穷。

4. 当指数$a=0$时，幂函数的图像为常数函数$y=1$。

5. 当指数$a<0$时，幂函数的图像在整个定义域上单调递减，但在$x$轴右侧逐渐趋近于0。

综上所述，幂函数的图像呈现出不同的形态和趋势，具体取决于指数的取值范围。

四、幂函数的应用幂函数在实际问题中有广泛的应用，尤其在自然科学和工程技术领域。

高一函数的奇偶性知识要点、例题讲解(数学)

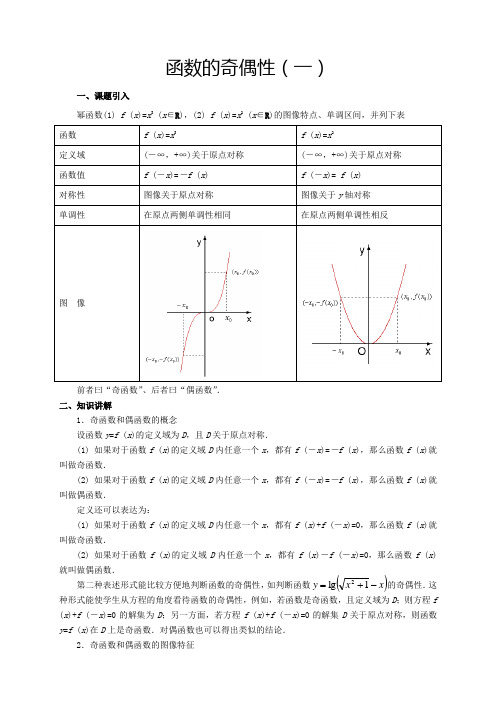
函数的奇偶性（一）一、课题引入幂函数(1) f (x )=x 3(x ∈R )，(2) f (x )=x 2(x ∈R )的图像特点、单调区间，并列下表函数 f (x )=x 3f (x )=x 2定义域 (－∞，+∞)关于原点对称(－∞，+∞)关于原点对称函数值 f (－x )=－f (x )f (－x )= f (x )对称性图像关于原点对称图像关于y 轴对称单调性在原点两侧单调性相同在原点两侧单调性相反图像前者曰“奇函数”、后者曰“偶函数”．二、知识讲解1．奇函数和偶函数的概念设函数y =f (x )的定义域为D ，且D 关于原点对称．(1) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (－x )=－f (x )，那么函数f (x )就叫做奇函数．(2) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (－x )=－f (x )，那么函数f (x )就叫做偶函数．定义还可以表达为：(1) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (x )+f (－x )=0，那么函数f (x )就叫做奇函数．(2) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (x )－f (－x )=0，那么函数f (x )就叫做偶函数．第二种表述形式能比较方便地判断函数的奇偶性，如判断函数()x xy -+=1lg2的奇偶性．这种形式能使学生从方程的角度看待函数的奇偶性，例如，若函数是奇函数，且定义域为D ；则方程f (x )+f (－x )=0的解集为D ；另一方面，若方程f (x )+f (－x )=0的解集D 关于原点对称，则函数y =f (x )在D 上是奇函数．对偶函数也可以得出类似的结论．2．奇函数和偶函数的图像特征(1) 奇函数的图像关于原点对称，反过来，图像关于原点对称的函数，必是奇函数． (2) 偶函数的图像关于y 轴对称，反过来，图像关于y 轴对称函数，必是偶函数．3．判断函数的奇偶性对于函数f (x )先求其定义域D ；并判别D 是否关于原点对称，然后再验证f (－x )=±f (x ) (或f (x )±f (x )=0，或()()1±=-x f x f 等)是否成立，最后作出正确结论．4．判断函数的奇偶性也可以用下列性质在公共定义域内，(1) 两个奇函数的和为奇函数；两个奇函数的积为偶函数． (2) 两个偶函数的和为偶函数；两个偶函数的积为偶函数． (3) 一个奇函数与一个偶函数的积为奇函数． (4) 函数f (x )与()x f 1同奇或同偶．以上结论，可在讲完出上一例：判断下列函数是否具有奇偶性：(1) f (x )=x 3；(2) f (x )=2x 4+3x 2；(3) ()313-+=xx x f ；(4) f (x )=x +1后，结合函数运算引出．直观引入后，可让学生在课后加以证明，这对学生加深对奇偶性的理解和用这一结论解题都是有帮助的．5．函数的奇偶性与单调性相结合，有以下两个结论： (1) 奇函数在原点两侧的对称区间上有相同的单调性． (2) 偶函数在原点两侧的对称区间上有相反的单调性．三、例题分析1．判断函数的奇偶性易犯的错误 (1) 因忽视定义域的特征致错例1．①()()11--=x x x x f ；②f (x )=x 2+(x +1)0错解：①()()x x x x x f =--=11，∴ f (x )是奇函数 ②∵ f (－x )=(－x )2+(－x +1)0=x 2+(x +1)0=f (x ) ∴ f (x )是偶函数．分析：一个函数是奇函数或偶函数的必要条件是定义域关于原点对称．正解：①定义域(－∞，1)∪(1，+∞)关于原点不对称，f (x )是非奇非偶函数．②定义域(－∞，－1)∪(－1，+∞)，∴ f (x )非奇非偶函数． (2) 因缺乏变形意识或方法致错．例2．判断()21151+-=x x f 的奇偶性．错解：∵ 5x－1≠0，∴ x ≠0．f (x )的定义域为(－∞，0)∪(0，+∞)，关于原点对称．∵ ()2151521151+-=+-=-xx x x f ， ∴ f (－x )≠f (x )，f (－x )≠－f (x )， ∴ f (x )是非奇非偶函数．分析：因演变过程不到位导致错误，所以要注意进行恒等变形．正解：()()1521521151-+=+-=xx x x f ，定义域为(－∞，0)∪(0，+∞)关于原点对称． ()()()()()x f x f xx x x x x -=-+-=-+=-+=--152155125115215 ∴ f (x )是奇函数．(3) 因忽视f (x )=0致错．例3．判断函数()2244x x x f -+-=的奇偶性．错解：由⎪⎩⎪⎨⎧≥-≥-040422x x 得x =±2，∴ f (x )的定义域为{－2，2}，关于原点对称．()()()()x f x x x x x f =-+-=--+--=-22224444，∴ f (x )为偶函数正解：f (x )的定义域为{－2，2}，此时，f (x )≡0，∴ f (x )既是奇函数又是偶函数．点评：函数f (x )=0 (x ≠0)是f (x )既是奇函数又是偶函数的一个必要条件，任何一个关于原点对称的区间都可以作为解析式为f (x )=0 (x ≠0)函数的定义域．注意：分段函数奇偶性的判定应注意两点：(1) 分段函数是一个函数，而不是几个函数； (2) 确定分段函数的奇偶性，要注意分类讨论． 2．函数的奇偶性的应用例4．已知f (x )是奇函数，且当x >0时，f (x )=x |x －2|，求f (x )<0时，f (x )的表达式．答：当x <0时，f (x )=x |x +2|．例5．已知f (x )=x 5+ax 3+bx －8，且f (－2)=10，则f (2)=_________ 解：令g (x )=f (x )+8=x 5+ax 3+bx ，则g (x )是奇函数∴ g (－2)+g (2)=0，即f (－2)+8+f (2)+8=0，∴ f (2)=－f (－2)－16=－26．例6．已知 f (x )、g (x )的定义域均为R ，f (x )为奇函数，g (x )为偶函数，且()()112+-=+x x x g x f ，求f (x )的解析式．答：()124++=x x xx f ．例7．已知函数y =f (x )是奇函数，在(0，+∞)上是减函数，且f (x )<0，判断()()x f x F 1=在区间(－∞，0)上是增函数还是减函数？并证明你的结论．答：F (x )在(－∞，0)是增函数．例8．定义在(－1，1)上的奇函数f (x )是减函数，且f (1－a )+f (1－a 2)<0，求实数a 的取值范围．答：a ∈(0，1)．点评：例8、9两题是函数的奇偶性与单调性的综合题．例9．已知f (x )是定义在R 上的奇函数，x >0时，f (x )=－x 2+2x －3．(1) 求f (x )的解析式； (2) 画出y =f (x )的图像； (3) 求出f (x )的单调区间．解：(1) ()()()⎪⎩⎪⎨⎧∞-∈++=∞+∈-+-=0320003222，，，，，x x x x x x x x f(2) 画图略．(3) 单调减区间为(]1-∞-，，[)∞+，1；单调增区间为[)01，-，(]10，．点评：本题是函数奇偶性、单调性、图像特征，画图等有关概念、性质、方法的综合运用的一道函数综合题．此题主要是考查学生综合、灵活运用所学知识解题的能力．四、习题1．已知f (x )是奇函数，且在x =0处有定义，你能确定f (0)的值吗？ 2．已知f (x )是偶函数，且在x =0处有定义，你能确定f (0)的值吗？3．函数()[)()⎩⎨⎧∞-∈-∞+∈=0101，，，，x x x f 是奇函数吗？答案1．f (0)=0 2．f (0)不定3．否五、引伸和提高定义域关于原点对称的任意一个函数f (x )都可以表示成一个偶函数与一个奇函数之和．即f (x )=21(F (x )+G (x ))其中F (x )= f (x )+f (－x )，G (x )=f (x )－f (－x ) (1) 利用这一结论可以很简捷地解决一些问题； (2) 在教学中，可根据学生的基础情况，适时引入．(3) 可以让学生自己证明，增强学生对抽象问题证明的能力，加深学生对奇、偶函数与一般函数关系的理解，使学生对构造法增加一次感性认识．六、思考题1．设，f (x )=kx +x6－4，(k ∈R )当x =2+3时，f (x )=0，求⎪⎪⎭⎫ ⎝⎛-231f 的值．答：32024231-=⎪⎪⎭⎫⎝⎛-f ．2．已知函数y =f (x )满足f (x +y )+f (x －y )=2f (x ) f (y ) (x ∈R ，y ∈R )，且f (0)≠0，那么f (x )是__________函数(填奇、偶)．答：偶函数函数的奇偶性（二）一般地，对于函数)(x f ，如果对于函数定义域内任意一个x ，都有)()(x f x f =-，那么函数)(x f 就叫做偶函数。

高一必修一幂函数的知识点

高一必修一幂函数的知识点高一必修一：幂函数的知识点高一数学课程中，幂函数是一个重要的学习内容。

幂函数是一种常见的函数形式，在生活和工作中有广泛的应用。

幂函数的研究是数学中的重要课题，掌握了幂函数的知识，对于理解数学的其他分支，如微积分等，具有重要的意义。

本文将重点介绍高一必修一中幂函数的知识点，帮助同学们更好地理解和应用幂函数。

一、幂函数的定义和性质幂函数是形如y = ax^n (a ≠ 0, n为整数)的函数，其中a称为底数，n称为指数。

幂函数的图象一般呈现出曲线的形式，其性质包括：1. 定义域和值域：当指数n为正整数时，定义域为全体实数集，值域为(0, +∞)；当指数n为负整数时，定义域为非零实数集，值域为(0, +∞)与(-∞, 0)的并集，并具有一至多个零点；当指数n为零时，定义域为整个实数集，值域为{1}。

2. 奇偶性：当指数n为奇数时，幂函数关于y轴对称；当指数n为偶数时，幂函数关于原点对称。

3. 单调性：当指数n为正数时，幂函数在整个定义域上是递增的；当指数n为负数时，幂函数在定义域的两侧是递减的。

4. 极限性质：当x无限趋近于正无穷时，幂函数的值也趋近于正无穷；当x无限趋近于负无穷时，幂函数的值的符号取决于指数的奇偶性。

二、幂函数与图像的关系幂函数的图像是通过对幂函数的底数进行相同倍数的拉伸或压缩得到的。

具体来说，我们可以通过以下几个方面了解幂函数与图像的关系。

1. 底数a的变化对图像的影响：当底数a大于1时，幂函数的图像被压缩，曲线变得更陡峭；当底数a小于1时，幂函数的图像被拉伸，曲线变得更平缓。

2. 指数n的变化对图像的影响：当指数n为正数时，幂函数的图像在y轴上方增长，形成上升的曲线；当指数n为负数时，幂函数的图像在y轴下方增长，形成下降的曲线。

3. 圆形与直线的比较：幂函数的图像与圆的曲线相似，但在其特定区间内，幂函数的图像会出现与直线相切的情况，这时幂函数的曲线呈现出直线的性质。

高一幂函数

高一幂函数一、幂函数的概念及基本性质幂函数是指形式为y=x^a（a是常数且不等于0）的函数。

其中，x 是自变量，a是指数，y是因变量。

1.幂函数的定义域：幂函数的定义域为实数集R。

2.幂函数的增减性：当a>0时，随着x的增大，幂函数也增大；当a<0时，随着x的增大，幂函数减小。

3.幂函数的奇偶性：当a为奇数时，幂函数是奇函数；当a为偶数时，幂函数是偶函数。

4.幂函数的图像：当a>1时，幂函数呈现指数增长的图像；当0<a<1时，幂函数图像逐渐下降；当a<0时，幂函数图像在x轴正半轴上下震荡。

二、幂函数的图像特点1.幂函数的图像关于y轴对称，除了x=0处，幂函数的图像只能在第一象限和第三象限中存在。

2.幂函数的图像在x轴上的唯一零点是x=0，当a>0时，y=0是幂函数的水平渐近线；当a<0时，幂函数没有水平渐近线。

3.幂函数的图像的特点还包括：在定义域内，随着a的增大，幂函数的曲线变得越来越陡峭，斜率越大，也越接近于坐标轴。

三、幂函数的应用实例幂函数在实际生活中有许多应用，如下所示：1.货币贬值：幂函数可以用来描述货币贬值的情况。

假设初始时某国家的货币价值为100，每年贬值5%，则可以用幂函数y=100(1-0.05)^x来表示货币价值随时间的变化，其中x表示年份，y表示货币价值。

2.物种数量变化：幂函数可以用来描述物种数量随时间的变化。

假设某种细菌在细菌培养皿中繁殖，每小时繁殖数量为原来的3倍，可以用幂函数y=2^x来表示细菌数量随时间的变化，其中x表示时间（小时），y表示细菌的数量。

3.电子产品价格变化：幂函数可以用来描述电子产品价格随时间的变化。

以手机为例，假设某款手机初始价格为3000元，每年价格下降20%，则可以用幂函数y=3000(1-0.2)^x来表示手机价格随时间的变化，其中x表示年份，y表示手机价格。

四、幂函数与其他函数的关系1.幂函数与线性函数的关系：幂函数和线性函数是两种不同的函数形式。

高考数学幂函数知识点总结

高考数学幂函数知识点总结一、幂函数的定义和性质幂函数是数学中一种常见的函数形式，它的定义形式为y = ax^n，其中a和n都为实数，x为自变量，y为因变量。

幂函数在数学中扮演着重要的角色，广泛应用于自然科学和工程技术领域。

下面我们来总结一些幂函数的重要性质和应用。

1. 幂函数的定义域和值域：幂函数y = ax^n的定义域为实数集R，值域则取决于a和n 的取值范围。

当a>0时，n为整数时，函数的值域为正实数集R+；当a<0时，n为奇数时，函数的值域为负实数集R-。

2. 幂函数的奇偶性：当n为偶数时，函数为偶函数；当n为奇数时，函数为奇函数。

具体而言，当n为偶数时，对于任意x，有f(-x)=f(x)；当n为奇数时，对于任意x，有f(-x)=-f(x)。

3. 幂函数的图像变换：幂函数y = ax^n在平面直角坐标系中的图像变换与参数a和n的取值相关。

当a>1时，函数图像沿y轴方向压缩，当0<a<1时，函数图像沿y轴方向拉伸；当n>1时，函数图像在原点左侧上升，当0<n<1时，函数图像在原点右侧上升。

4. 幂函数的极限：当a>1时，幂函数在正无穷大时趋于正无穷大；当0<a<1时，幂函数在正无穷大时趋于0。

若n>0，幂函数在负无穷大时趋于正无穷大；若n<0，幂函数在负无穷大时趋于0。

二、幂函数的常见应用幂函数因为其特殊的形式和性质，在科学和工程中有广泛的应用。

以下是幂函数在一些具体问题中的运用。

1. 物质的增长和衰减：在生物学和经济学中，常常需要研究物质的增长和衰减过程。

幂函数可用来描述这种过程。

例如，生物种群的增长可以用幂函数进行建模，其中a表示种群的初始数量，n表示增长率。

同样，经济学中的人口增长、环境污染以及经济发展等问题也可以利用幂函数进行分析。

2. 各种规律的描述：幂函数可以应用于描述一些规律和现象。

例如，光的强度随距离的关系、金融领域中财富分布的不平等系数、能量消耗与功率之间的关系等都可以用幂函数来表达。

数学高考知识点幂函数

数学高考知识点幂函数数学高考知识点：幂函数幂函数是高考数学中非常重要的一个知识点，它是指形如y=x^a的函数，其中a是一个实数。

在高考中，幂函数常常会与其他函数进行比较或者求解方程等相关问题，因此熟练掌握幂函数的性质和应用是非常重要的。

一、幂函数的性质1. 幂函数的定义域：幂函数y=x^a的定义域是所有使得x^a有意义的实数x。

2. 幂函数的奇偶性：当指数a为偶数时，幂函数具有关于y轴的对称性，即f(-x) = f(x)。

当指数a为奇数时，幂函数关于原点对称，即f(-x) = -f(x)。

3. 幂函数的单调性：当指数a大于0时，幂函数在定义域上是递增的；当指数a小于0时，幂函数在定义域上是递减的。

4. 幂函数的图像：幂函数的图像呈现出如下特点：当a>1时，幂函数在∞处增加，0处取到最小值；当0<a<1时，幂函数在∞处减小，0处取到最大值；当a<0时，幂函数在定义域上是奇函数，图像关于原点对称。

二、幂函数的应用1. 幂函数与对数函数的关系：幂函数和对数函数是互为反函数的，即y=x^a和y=loga(x)是一对反函数。

这一性质在解决指数方程和对数方程时非常有用。

2. 幂函数的极限：对于幂函数y=x^a，当x趋近于正无穷时，幂函数趋近于正无穷；当x趋近于负无穷时，幂函数趋近于零。

这一性质在求解极限时常常会被用到。

3. 幂函数的应用：幂函数在物理学、生物学、经济学等领域具有广泛的应用。

例如，在物理学中，速度和加速度的计算常常涉及到幂函数的运算。

三、幂函数在高考中的常见题型解析1. 求解方程：高考经常出现要求解幂函数方程的题目，在解这类问题时，我们可以利用幂函数和对数函数互为反函数的特性，将幂函数方程转化为对数方程进行求解。

2. 判断性质：高考中会出现判断幂函数性质的题目，例如给出一个函数的图像，要求判断该函数的奇偶性、单调性等。

在解这类问题时，我们需要运用幂函数的性质和图像特点进行分析。

幂函数与指数函数的性质

幂函数与指数函数的性质幂函数和指数函数是数学中常见的函数类型，它们在各个领域中都有广泛的应用。

本文将介绍幂函数和指数函数的性质，包括定义、图像、增减性、奇偶性等方面。

一、幂函数的性质幂函数的一般形式为y = x^a，其中x为自变量，a为常数。

1. 幂函数的定义域幂函数的定义域是所有使x^a有意义的实数x的集合。

根据x^a的定义，当x为负数时，a的值不能是分数或为奇数的负整数，否则会出现无意义的数学运算。

2. 幂函数的图像特点幂函数的图像特点取决于幂指数a的值。

当a为正数时，幂函数的图像在坐标系中从左下方无限趋近于x轴上方；当a为负数时，图像则从左上方无限趋近于x轴下方；当a为零时，图像为常函数y=1。

3. 幂函数的增减性对于幂函数y = x^a，当a为正数时，随着x的增大，y也随之增大，即幂函数是递增的；当a为负数时，随着x的增大，y反而减小，即幂函数是递减的。

当a为偶数时，幂函数的图像关于y轴对称，即为偶函数；当a为奇数时，幂函数的图像关于原点对称，即为奇函数。

二、指数函数的性质指数函数的一般形式为y = a^x，其中a为常数，x为自变量。

1. 指数函数的定义域指数函数的定义域是所有实数x。

2. 指数函数的图像特点指数函数的图像特点取决于底数a的值。

当a大于1时，指数函数的图像在坐标系中以点(0,1)为起点，随着x的增大而无限趋近于正无穷；当0<a<1时，图像则在坐标系中从点(0,1)向右无限延伸，逐渐接近x轴。

当a为1时，指数函数为常函数y=1。

3. 指数函数的增减性对于指数函数y = a^x，当底数a大于1时，随着x的增大，y也随之增大，即指数函数是递增的；当0<a<1时，随着x的增大，y反而减小，即指数函数是递减的。

指数函数没有奇偶性的特点。

综上所述，幂函数和指数函数在定义域、图像特点、增减性、奇偶性等方面都有一些共同点和区别。

它们的性质对于解决实际问题和理解数学概念都具有重要意义。

幂函数的增减性与奇偶性

幂函数的增减性与奇偶性幂数学函数是数学中的重要概念之一，而其中的一种常见函数类型为幂函数。

幂函数是指形如y = ax^n的函数，其中a为常数，n为幂数。

本文将探讨幂函数的增减性与奇偶性两个重要属性。

一、幂函数的增减性幂函数的增减性描述了幂函数在定义域内的函数值随自变量增加或减小而变化的趋势。

当幂函数的幂数为正时，函数呈现单调递增或单调递减的特点，具体取决于幂数的奇偶性。

1. 幂数为正偶数当幂数n为正偶数时，幂函数呈现出单调递增的趋势。

这是因为当x为正数时，不论a是正还是负，x的n次方都为正，所以当x增加时，函数值y也会随之增加；同理，当x为负数时，由于负数的偶次幂依然为正数，所以x减小时，函数值y也会减小。

2. 幂数为正奇数当幂数n为正奇数时，幂函数同样也呈现出单调递增的趋势。

但与幂数为正偶数的情况不同，当n为奇数时，若a为正数，则x取任意正负值时，y都为正数，所以函数整体呈现单调递增的特点；若a为负数，则x取正数时，y为负数；而当x取负数时，y则为正数。

所以，当幂数n为正奇数时，函数的增减性也取决于常数a的正负性。

3. 幂数为负数当幂数n为负数时，幂函数则呈现出单调递减的趋势。

这是因为当x是正数时，不论a是正还是负，x的n次方都为小于1的正数，所以当x增加时，函数值y则会减小；同理，当x是负数时，由于负数的负次幂依然是小于1的正数，所以x减小时，函数值y也会增加。

二、幂函数的奇偶性幂函数的奇偶性描述了幂函数图像关于y轴或者原点对称的特点，取决于幂数的奇偶性。

1. 幂数为偶数当幂数n为偶数时，函数的图像关于y轴对称。

这是因为当x取正值时，幂函数的函数值与x取相反数时的函数值相等，即满足关于y轴对称的特点。

2. 幂数为奇数当幂数n为奇数时，函数的图像关于原点对称。

这是因为当x取正值时，幂函数的函数值与x取相反数时的函数值互为相反数，即满足关于原点对称的特点。

结论：幂函数的增减性与奇偶性是幂函数在数轴上的两个重要特征。

高一上数学必修一第四章《4.4幂函数》知识点梳理

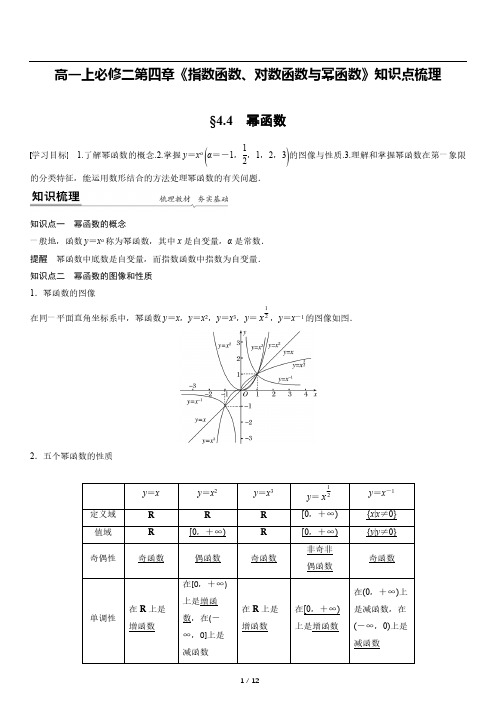
高一上必修二第四章《指数函数、对数函数与幂函数》知识点梳理§4.4　幂函数学习目标　1.了解幂函数的概念.2.掌握y ＝x α(α＝－1，12，1，2，3)的图像与性质.3.理解和掌握幂函数在第一象限的分类特征，能运用数形结合的方法处理幂函数的有关问题．知识点一　幂函数的概念一般地，函数y ＝x α称为幂函数，其中x 是自变量，α是常数．提醒　幂函数中底数是自变量，而指数函数中指数为自变量．知识点二　幂函数的图像和性质1．幂函数的图像在同一平面直角坐标系中，幂函数y ＝x ，y ＝x 2，y ＝x 3，y ＝，y ＝x －1的图像如图．2．五个幂函数的性质y ＝xy ＝x 2y ＝x 3y ＝y ＝x －1定义域R R R [0，＋∞){x |x ≠0}值域R [0，＋∞)R [0，＋∞){y |y ≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在R 上是增函数在[0，＋∞)上是增函数，在(－∞，0]上是减函数在R 上是增函数在[0，＋∞)上是增函数在(0，＋∞)上是减函数，在(－∞，0)上是减函数12x 12x公共点(1,1)1．y ＝－1x 是幂函数．(　×　)2．当x ∈(0,1)时，x 2>x 3.(　√　)3．y ＝与y ＝定义域相同．(　×　)4．若y ＝x α在(0，＋∞)上为增函数，则α>0.(　√　)一、幂函数的概念例1　(1)(多选)下列函数为幂函数的是( )A ．y ＝x 3 B ．y ＝(12)xC ．y ＝4x 2D ．y ＝x答案　AD解析　B 项为指数函数，C 中的函数的系数不为1，AD 为幂函数．(2)已知y ＝(m 2＋2m －2)＋2n －3是幂函数，求m ，n 的值．解　由题意得Error!解得Error!或Error!所以m ＝－3或1，n ＝32.反思感悟　判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y ＝x α(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1.跟踪训练1　已知f (x )＝ax 2a ＋1－b ＋1是幂函数，则a ＋b 等于( )A ．2 B ．1 C.12 D ．0答案　A解析　因为f (x )＝ax 2a ＋1－b ＋1是幂函数，所以a ＝1，－b ＋1＝0，即a ＝1，b ＝1，则a ＋b ＝2.32x 64x 22m x二、幂函数的图像例2　如图所示，图中的曲线是幂函数y ＝x n 在第一象限的图像，已知n 取±2，±12四个值，则对应于c 1，c 2，c 3，c 4的n 依次为( )A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－12答案　B解析　根据幂函数y ＝x n 的性质，故c 1的n ＝2，c 2的n ＝12，当n <0时，|n |越大，曲线越陡峭，所以曲线c 3的n ＝－12，曲线c 4的n ＝－2.反思感悟　解决幂函数图像问题应把握的两个原则(1)依据图像高低判断幂指数大小，相关结论为：在(0,1)上，指数越大，幂函数图像越靠近x 轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图像越远离x 轴(简记为指大图高)．(2)依据图像确定幂指数α与0,1的大小关系，即根据幂函数在第一象限内的图像(类似于y ＝x －1 或y ＝或y ＝x 3)来判断．跟踪训练2　函数f (x )＝的大致图像是( )答案　A解析　因为－12<0，所以f (x )在(0，＋∞)上单调递减，排除选项B ，C ；又f (x )的定义域为(0，＋∞)，故排除选项D.三、比较幂值的大小12x 12x例3　比较下列各组数中两个数的大小：(1)(25)0.5与(13)0.5；(2)(－23)－1与(－35)－1；(3)与.解　(1)∵幂函数y ＝x 0.5在(0，＋∞)上是单调递增的，又25>13，∴(25)0.5>(13)0.5.(2)∵幂函数y ＝x －1在(－∞，0)上是单调递减的，又－23<－35，∴(－23)－1>(－35)－1.(3)∵函数y 1＝(23)x为R 上的减函数，又34>23，∴>.又∵函数y 2＝在(0，＋∞)上是增函数，且34>23，∴>，∴>.反思感悟　比较幂值大小的方法跟踪训练3　比较下列各组值的大小：(1)，；(2)，，1.42.解　(1)∵y ＝为R 上的偶函数，∴＝.又函数y ＝为[0，＋∞)上的增函数，且0.31<0.35，3423⎛⎫⎪⎝⎭2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭3423⎛⎫ ⎪⎝⎭23x 2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭2334⎛⎫ ⎪⎝⎭3423⎛⎫⎪⎝⎭()650.31-650.35121.2121.465x ()650.31-650.3165x∴<，即<.(2)∵y ＝在[0，＋∞)上是增函数，且1.2<1.4，∴<.又∵y ＝1.4x 为增函数，且12<2，∴<1.42，∴<<1.42.幂函数性质的应用典例　已知幂函数y ＝x 3m －9 (m ∈N ＋)的图像关于y 轴对称且在(0，＋∞)上单调递减，求满足的a 的取值范围．解　因为函数y ＝x 3m －9在(0，＋∞)上单调递减，所以3m －9<0，解得m <3.又因为m ∈N ＋，所以m ＝1,2.因为函数的图像关于y 轴对称，所以3m －9为偶数，故m ＝1.则原不等式可化为.因为y ＝在(－∞，0)，(0，＋∞)上单调递减，所以a ＋1>3－2a >0或3－2a <a ＋1<0或a ＋1<0<3－2a ，解得23<a <32或a <－1.故a 的取值范围是Error!.[素养提升]　(1)幂函数y ＝x α中只有一个参数α，幂函数的所有性质都与α的取值有关，故可由α确定幂函数的定义域、值域、单调性、奇偶性，也可由这些性质去限制α的取值．(2)通过具体实例抽象出幂函数的概念和性质，并应用单调性求解，体现了数学中数学运算与直观想象的核心素养．650.31650.35()650.31-650.3512x 121.2121.4121.4121.2121.433(1)(32)m m a a --+<-1133(1)(32)a a --+<-13x-1．下列函数是幂函数的是( )A ．y ＝5x B ．y ＝x 5C ．y ＝5x D ．y ＝(x ＋1)3答案　B解析　函数y ＝5x 是指数函数，不是幂函数；函数y ＝5x 是正比例函数，不是幂函数；函数y ＝(x ＋1)3的底数不是自变量x ，不是幂函数；函数y ＝x 5是幂函数．2．幂函数y ＝x α(α∈R )的图像一定不经过( )A ．第四象限 B ．第三象限C ．第二象限 D ．第一象限答案　A解析　由幂函数的图像可知，其图像一定不经过第四象限．3．设α∈{－1，1，12，3}，则使函数y ＝x α的定义域为R 且为奇函数的所有α值为( )A ．1,3B ．－1,1C ．－1,3D ．－1,1,3答案　A解析　可知当α＝－1,1,3时，y ＝x α为奇函数，又因为y ＝x α的定义域为R ，则α＝1,3.4．已知幂函数f (x )＝kx α(k ∈R ，α∈R )的图像过点(12，2)，则k ＋α等于( )A.12 B ．1 C.32 D ．2答案　A解析　∵幂函数f (x )＝kx α(k ∈R ，α∈R )的图像过点(12，2)，∴k ＝1，f(12)＝(12)α＝2，即α＝－12，∴k ＋α＝12.5．已知f (x )＝，若0<a <b <1，则下列各式中正确的是( )A ．f (a )<f (b )<f(1a )<f(1b)B ．f (1a )<f(1b )<f (b )<f (a )C ．f (a )<f (b )<f (1b )<f(1a )D ．f (1a )<f (a )<f(1b )<f (b )12x答案　C解析　因为函数f (x )＝在(0，＋∞)上是增函数，又0<a <b <1<1b <1a ，故f (a )<f (b )<f(1b )<f(1a).1．知识清单：(1)幂函数的概念．(2)幂函数的图像．(3)幂函数的性质及其应用．2．方法归纳：数形结合．3．常见误区：幂函数与指数函数的区别；幂函数的奇偶性．1．幂函数f (x )＝x α的图像经过点(2,4)，则f (－12)等于( )A.12B.14 C ．－14 D ．2答案　B解析　幂函数f (x )＝x α的图像经过点(2,4)，则2α＝4，解得α＝2；∴f (x )＝x 2，∴f (－12)＝(－12)2＝14.2．下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的函数是( )A ．y ＝x －2 B ．y ＝x －1C ．y ＝x 2 D ．y ＝答案　A解析　所给选项都是幂函数，其中y ＝x －2和y ＝x 2是偶函数，y ＝x －1和y ＝不是偶函数，故排除选项B ，D ，又y ＝x 2在区间(0，＋∞)上单调递增，不合题意，y ＝x －2在区间(0，＋∞)上单调递减，符合题意．3．设a ＝，b ＝，c ＝，则a ，b ，c 的大小关系是( )12x 13x13x 2535⎛⎫ ⎪⎝⎭3525⎛⎫⎪⎝⎭2525⎛⎫⎪⎝⎭A ．a >c >bB ．a >b >cC ．c >a >bD ．b >c >a答案　A解析　∵y ＝(x >0)为增函数，又35>25，∴a >c .∵y ＝(25)x (x ∈R )为减函数，又25<35，∴c >b .∴a >c >b .4．在同一坐标系内，函数y ＝x a (a ≠0)和y ＝ax －1a的图像可能是( )答案　C解析　选项A 中，幂函数的指数a <0，则y ＝ax －1a 应为减函数，A 错误；选项B 中，幂函数的指数a >1，则y ＝ax －1a 应为增函数，B 错误；选项D 中，幂函数的指数a <0，则－1a >0，直线y ＝ax －1a在y 轴上的截距为正，D 错误．5．若幂函数f (x )的图像过点(2，2)，则函数g (x )＝f (x )－3的零点是( )A.3 B ．9 C ．(3，0) D ．(9,0)答案　B解析　∵幂函数f (x )＝x α的图像过点(2，2)，∴f (2)＝2α＝2，解得α＝12，∴f (x )＝，∴函数g (x )＝f (x )－3＝－3，由－3＝0，得x ＝9.∴函数g (x )＝f (x )－3的零点是9.6．已知幂函数f (x )＝x α的部分对应值如表：x11225x 12x 12x 12xf (x )122则f (x )的单调递增区间是________．答案　[0，＋∞)解析　因为f(12)＝22，所以(12)α＝22，即α＝12，所以f (x )＝的单调递增区间是[0，＋∞)．7．已知幂函数f (x )＝x α(α∈R )的图像经过点(8,4)，则不等式f (6x ＋3)≤9的解集为________．答案　[－5,4]解析　由题意知8α＝4，故α＝log 84＝23，由于f (x )＝＝x 2为R 上的偶函数且在(0，＋∞)上递增，故f (6x ＋3)≤9即为f (6x ＋3)≤f (27)，所以|6x ＋3|≤27，解得－5≤x ≤4.8．设a ＝，b ＝，c ＝，则a ，b ，c 从小到大的顺序是________．答案　b <a <c解析　由a ＝，b ＝，可利用幂函数的性质，得a >b ，可由指数函数的单调性得c >a ，∴b <a <c .9．已知幂函数f (x )＝x α的图像过点P (2，14)，试画出f (x )的图像并指出该函数的定义域与单调区间．解　因为f (x )＝x α的图像过点P (2，14)，所以f (2)＝14，即2α＝14，得α＝－2，即f (x )＝x －2，f (x )的图像如图所示，定义域为(－∞，0)∪(0，＋∞)，单调递减区间为(0，＋∞)，单调递增区间为(－∞，0)．10．已知幂函数f (x )＝x 9－3m (m ∈N ＋)的图像关于原点对称，且在R 上单调递增．(1)求f (x )的解析式；(2)求满足f (a ＋1)＋f (3a －4)<0的a 的取值范围．解　(1)由幂函数f (x )＝x 9－3m (m ∈N ＋)的图像关于原点对称，且在R上单调递增，可得9－3m >0，解得m <3，m ∈N ＋，可得m ＝1,2，12x 23x 2312⎛⎫⎪⎝⎭2315⎛⎫ ⎪⎝⎭1312⎛⎫⎪⎝⎭2312⎛⎫ ⎪⎝⎭2315⎛⎫⎪⎝⎭若m ＝1，则f (x )＝x 6的图像不关于原点对称，舍去；若m ＝2，则f (x )＝x 3的图像关于原点对称，且在R 上单调递增，成立．则f (x )＝x 3.(2)由(1)可得f (x )是奇函数，且在R 上单调递增，由f (a ＋1)＋f (3a －4)<0，可得f (a ＋1)<－f (3a －4)＝f (4－3a )，即为a ＋1<4－3a ，解得a <34.11．若函数f (x )＝(m ＋2)x a 是幂函数，且其图像过点(2,4)，则函数g (x )＝ log a (x ＋m )的单调递增区间为( )A ．(－2，＋∞) B ．(1，＋∞)C ．(－1，＋∞) D ．(2，＋∞)答案　B解析　由题意得m ＋2＝1，解得m ＝－1，则f (x )＝x a ，将(2,4)代入函数的解析式得，2a ＝4，解得a ＝2，故g (x )＝log a (x ＋m )＝log 2(x －1)，令x －1>0，解得x >1，故g (x )在(1，＋∞)上单调递增．12．函数y ＝－1的图像关于x 轴对称的图像大致是( )答案　B解析　y ＝的图像位于第一象限且为增函数，所以函数图像是上升的，函数y ＝－1的图像可看作由y ＝的图像向下平移一个单位长度得到的(如选项A 中的图所示)，将y ＝－1的图像关于x 轴对称后即为选项B.13．为了保证信息的安全传输，有一种密钥密码系统，其加密、解密原理为：发送方由明文到密文(加密)，接收方由密文到明文(解密)．现在加密密钥为y ＝x α(α为常数)，如“4”通过加密后得到密文“2”．若接收方接到密文“3”，则解密后得到的明文是________．答案　9解析　由题意可知加密密钥y ＝x α(α为常数)是一个幂函数，所以要想求得解密后得到的明文，就必须先求出α的值．由题意，得2＝4α，解得α＝12，则y ＝.由＝3，得x ＝9，即明文是9.14．已知幂函数f (x )＝，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．12x 12x 12x 12x 12x 12x 12x 12x答案　(3,5)解析　∵f (x )＝＝1x(x >0)，易知f (x )在(0，＋∞)上为减函数，又f (a ＋1)<f (10－2a )，∴Error!解得Error!∴3<a <5.15.幂函数y ＝x α，当α取不同的正数时，在区间[0,1]上它们的图像是一族美丽的曲线(如图)．设点A (1,0)，B (0,1)，连接AB ，线段AB 恰好被其中的两个幂函数y ＝x α，y ＝x β的图像三等分，即有BM ＝MN ＝NA ，那么，αβ等于________．答案　1解析　由条件，得M (13，23)，N (23，13)，可得13＝(23)α，23＝(13)β，即α＝13，β＝23.所以αβ＝13·23＝lg 13lg 23·lg 23lg 13＝1.16．已知幂函数g (x )过点(2，12)，且f (x )＝x 2＋ag (x )．(1)求g (x )的解析式；(2)讨论函数f (x )的奇偶性，并说明理由．解　(1)设幂函数的解析式g (x )＝x α(α为常数)．因为幂函数g (x )过点(2，12)，所以2α＝12，解得α＝－1，所以g (x )＝1x.(2)由(1)得f (x )＝x 2＋a x.①当a ＝0时，f (x )＝x 2.12x 23log 13log 23log 13log由于f(－x)＝(－x)2＝x2＝f(x)，可知f(x)为偶函数．②当a≠0时，由于f(－x)＝(－x)2＋a－x＝x2－ax≠x2＋ax＝f(x)，且f(－x)＝(－x)2＋a－x＝x2－ax≠－(x2＋a x)＝－f(x)，所以f(x)是非奇非偶函数．综上，①当a＝0时，f(x)为偶函数；②当a≠0时，f(x)为非奇非偶函数．。

高一幂函数知识点笔记

高一幂函数知识点笔记幂函数是数学中的一种特殊函数形式，常见的形式是f(x) = x^a，其中a是实数，x是自变量，a为常数。

幂函数主要有以下几个重要知识点需要注意：一、定义域和值域：幂函数的定义域取决于指数a的值。

当a为正整数时，定义域为全体实数集R；当a为负整数时，定义域为R\{0}，即除了0之外的所有实数；当a为零时，定义域为R\{0}。

幂函数的值域也取决于指数a的值，当a为奇数时，值域为R；当a为偶数时，当a>0时，值域为[0, +∞)，当a<0时，值域为(0, +∞)。

二、对称性：当指数a为奇数时，幂函数以原点为中心具有对称性，即f(-x) = -f(x)；当指数a为偶数时，幂函数以y轴为对称轴具有对称性，即f(-x) = f(x)。

三、奇偶性：当指数a为偶数时，幂函数为偶函数，即f(-x) = f(x)；当指数a为奇数时，幂函数为奇函数，即f(-x) = -f(x)。

四、增减性：当指数a大于0时，幂函数在定义域上是递增的；当指数a小于0时，幂函数在定义域上是递减的。

五、图像：幂函数的图像特点取决于指数a的正负和大小。

当指数a为正数时，图像从原点出发，向右上方逐渐增长；当指数a为负数时，图像从原点出发，先向右下方增长，再接近于x轴。

指数a的绝对值越大，图像越接近于x轴。

当指数a为零时，幂函数的图像为一条常值函数。

六、特殊函数图像：当指数a为1时，幂函数的图像为一条斜率为1的直线；当指数a为-1时，幂函数的图像为一条斜率为-1的直线；当指数a为1/2时，幂函数的图像为一条开口向上的抛物线；当指数a为-1/2时，幂函数的图像为一条开口向下的抛物线。

通过以上的知识点笔记，我们可以更好地理解和掌握幂函数的基本性质和特点。

在解题过程中，我们可以根据具体的指数值和题目要求灵活运用这些知识点，帮助我们更准确地解答相关问题。

幂函数是数学学习中常见的一种函数形式，掌握好这些基本知识点对于我们进一步学习和应用函数概念非常重要。

幂函数的增减性和奇偶性

幂函数的增减性和奇偶性幂函数是高中数学中常见的函数类型，它具有一定的性质和规律。

其中，增减性和奇偶性是幂函数的两个重要特征。

本文将详细介绍幂函数的增减性和奇偶性，并分析其应用和意义。

一、幂函数的增减性幂函数的一般形式为：f(x) = ax^k，其中a≠0，k是实数。

根据系数a和指数k的不同取值，幂函数可以具有不同的增减性。

1. 当a>0且k>0时，幂函数f(x) = ax^k在定义域上单调递增。

即随着自变量x的增大，函数值f(x)也随之增大。

例如，当a=2，k=2时，f(x) = 2x^2就是一个典型的上升的二次函数。

2. 当a<0且k>0时，幂函数f(x) = ax^k在定义域上单调递减。

即随着自变量x的增大，函数值f(x)反而减小。

例如，当a=-3，k=3时，f(x) = -3x^3就是一个典型的下降的三次函数。

3. 当k<0时，幂函数f(x) = ax^k在定义域上并不具有单调性。

而是随着自变量x的取值增大或减小而出现正负交替的变化。

例如，当a=4，k=-2时，f(x) = 4/x^2就是一个典型的具有正负交替的双曲线函数。

总结起来，幂函数的增减性取决于系数a和指数k的正负以及奇偶性。

当a>0且k为偶数时，函数单调递增；当a>0且k为奇数时，函数单调递减；当a<0且k为奇数时，函数单调递增；当a<0且k为偶数时，函数单调递减。

二、幂函数的奇偶性幂函数的奇偶性可以通过考察指数k的奇偶性来判断。

1. 当k为偶数时，幂函数f(x) = ax^k是一个偶函数。

即对于任意实数x，都有f(-x) = f(x)。

例如，f(x) = x^4是一个关于y轴对称的四次函数，无论x取正值还是负值，函数值都相同。

2. 当k为奇数时，幂函数f(x) = ax^k是一个奇函数。

即对于任意实数x，都有f(-x) = -f(x)。

例如，f(x) = x^3是一个关于原点对称的三次函数，当x取正值和负值时，函数值的相反数。

高一数学幂函数知识点总结

高一数学幂函数知识点总结在高一数学的学习中，幂函数是一个重要的知识点。

它不仅在函数的大家庭中具有独特的性质，而且在解决数学问题和实际应用中都有着广泛的用途。

接下来，咱们就一起来详细地梳理一下幂函数的相关知识。

一、幂函数的定义一般地，形如$y ＝x^α$（＄α$为常数）的函数，叫做幂函数。

其中$x$是自变量，＄α$是常数。

需要注意的是，这里的底数$x$是自变量，指数$α$是常数。

例如，＄y ＝ x^2$，＄y ＝ x^｛＼frac{1}｛2}｝＄，＄y ＝ x^｛－1}＄等都是幂函数。

但$y ＝2x^2$，＄y ＝x^2 ＋1$等就不是幂函数，因为它们不符合幂函数的定义。

二、幂函数的图像幂函数的图像因指数$α$的不同而呈现出不同的形状和特征。

当$α ＞ 0$时：若$α ＞ 1$，函数图像在区间$（0, ＋＼infty)＄上单调递增，且向上凸。

例如$y ＝ x^2$，其图像是一个开口向上的抛物线。

若$0 ＜α ＜ 1$，函数图像在区间$（0, ＋＼infty)＄上单调递增，且向上凹。

比如$y ＝ x^｛＼frac{1}｛2}｝＄，图像是半个抛物线。

当$α ＜ 0$时，函数图像在区间$（0, ＋＼infty)＄上单调递减，且曲线向下凸。

例如$y ＝ x^｛－1}＄，其图像是位于第一、三象限的双曲线。

三、幂函数的性质1、定义域对于幂函数$y ＝x^α$，其定义域与指数$α$的取值有关。

当$α$为正整数时，定义域为$R$。

当$α$为零或负整数时，定义域为$x ≠ 0$。

当$α$为正分数时，如果分母为奇数，定义域为$R$；如果分母为偶数，定义域为$x ≥ 0$。

当$α$为负分数时，如果分母为奇数，定义域为$x ≠ 0$；如果分母为偶数，定义域为$x ＞ 0$。

2、值域幂函数的值域也与指数$α$的取值有关。

当$α ＞ 0$时，值域为$0, ＋＼infty)＄。

当$α ＜ 0$时，值域为$（0, ＋＼infty)＄。

高中数学幂函数知识点

高中数学幂函数知识点高中数学幂函数学问11.函数的单调性(局部性质)(1)增函数设函数y=f(x)的定义域为I，假如对于定义域I内的某个区间D内的任意两个自变量x1，x2，当x1假如对于区间D上的任意两个自变量的值x1，x2，当x1f(x2)，那么就说f(x)在这个区间上是减函数.区间D称为y=f(x)的单调减区间.留意：函数的单调性是函数的局部性质;(2)图象的特点假如函数y=f(x)在某个区间是增函数或减函数，那么说函数y=f(x)在这一区间上具有(严格的)单调性，在单调区间上增函数的图象从左到右是上升的，减函数的图象从左到右是下降的.(3)函数单调区间与单调性的判定〔方法〕(A)定义法：a.任取x1，x2∈D，且x1b.作差f(x1)-f(x2);c.变形(通常是因式分解和配方);d.定号(即推断差f(x1)-f(x2)的正负);e.下结论(指出函数f(x)在给定的区间D上的单调性).(B)图象法(从图象上看升降)(C)复合函数的单调性复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性亲密相关，其规律：“同增异减”留意：函数的单调区间只能是其定义域的子区间,不能把单调性相同的区间和在一起写成其并集.8.函数的奇偶性(整体性质)(1)偶函数一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)就叫做偶函数.(2)奇函数一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=—f(x)，那么f(x)就叫做奇函数.(3)具有奇偶性的函数的图象的特征偶函数的图象关于y轴对称;奇函数的图象关于原点对称.利用定义推断函数奇偶性的步骤：a.首先确定函数的定义域，并推断其是否关于原点对称;b.确定f(-x)与f(x)的关系;c.作出相应结论：若f(-x)=f(x)或f(-x)-f(x)=0，则f(x)是偶函数;若f(-x)=-f(x)或f(-x)+f(x)=0，则f(x)是奇函数.留意：函数定义域关于原点对称是函数具有奇偶性的必要条件.首先看函数的定义域是否关于原点对称，若不对称则函数是非奇非偶函数.若对称，(1)再依据定义判定;(2)由f(-x)±f(x)=0或f(x)/f(-x)=±1来判定;(3)利用定理，或借助函数的图象判定.9、函数的解析表达式(1).函数的解析式是函数的一种表示方法，要求两个变量之间的函数关系时，一是要求出它们之间的对应法则，二是要求出函数的定义域.(2)求函数的解析式的主要方法有：1)凑配法2)待定系数法3)换元法4)消参法10.函数最大(小)值(定义见课本p36页)a.利用二次函数的性质(配方法)求函数的最大(小)值b.利用图象求函数的最大(小)值c.利用函数单调性的推断函数的最大(小)值：假如函数y=f(x)在区间[a，b]上单调递增，在区间[b，c]上单调递减则函数y=f(x)在x=b处有最大值f(b);假如函数y=f(x)在区间[a，b]上单调递减，在区间[b，c]上单调递增则函数y=f(x)在x=b处有最小值f(b);.高中数学幂函数学问2一、一次函数定义与定义式：自变量x和因变量y有如下关系：y=kx+b则此时称y是x的一次函数。

高一数学知识点幂函数知识点总结

高一数学知识点幂函数知识点总结幂函数是数学中的一种基本函数形式，它的形式为f(x) = x^a，其中a为常数。

在高一数学中，学习幂函数是非常重要的一部分，本文将对高一数学知识点中的幂函数进行总结和归纳。

一、幂函数的定义和性质幂函数可用 y = x^a 表示，其中a为常数。

以下是幂函数的一些基本性质：1. 自变量的取值范围：幂函数的自变量x可以是任意实数。

当a为正偶数时，幂函数定义域为正实数集；当a为负偶数时，幂函数定义域为负实数集；当a为奇数时，幂函数的定义域为全体实数集。

2. 定义域和值域：因为幂函数的定义域为全体实数集，所以其值域也是全体实数集。

3. 奇偶性：当a为正偶数时，幂函数是偶函数；当a为负偶数时，幂函数是奇函数；当a为奇数时，幂函数既不是偶函数也不是奇函数。

4. 单调性：若a>0，则幂函数在定义域上是递增函数；若a<0，则幂函数在定义域上是递减函数。

5. 图像特点：幂函数的图像一般存在一个不可见的特殊点(0,0)，当a>0时，图像在第一象限中单调递增，通过点(1,1)；当a<0时，图像在第四象限中单调递增，通过点(1,1)；当a为负偶数时，图像经过点(-1,1)。

二、幂函数的图像与变换1. 幂函数的基本图像：以y = x^2为例，当x取非负实数时，幂函数是递增曲线，在定义域上图像呈现开口向上的抛物线；当x取负实数时，幂函数的图像和x轴关于y轴对称。

2. 幂函数的图像平移：对于幂函数y = x^a，其中a为常数，在x轴向右平移c个单位长度的函数为y = (x-c)^a，表示为：f(x) --> f(x+c)。

3. 幂函数的图像伸缩：对于幂函数y = x^a，其中a为正常数，可以进行垂直方向的伸缩，即在y轴方向上缩放一定倍数。

若倍数k > 1，函数为y = kx^a；若0 < k < 1，函数为y = kx^a。

三、幂函数与指数函数的关系指数函数与幂函数是密切相关的，两者具有相似的性质。

6、幂函数与函数的奇偶性

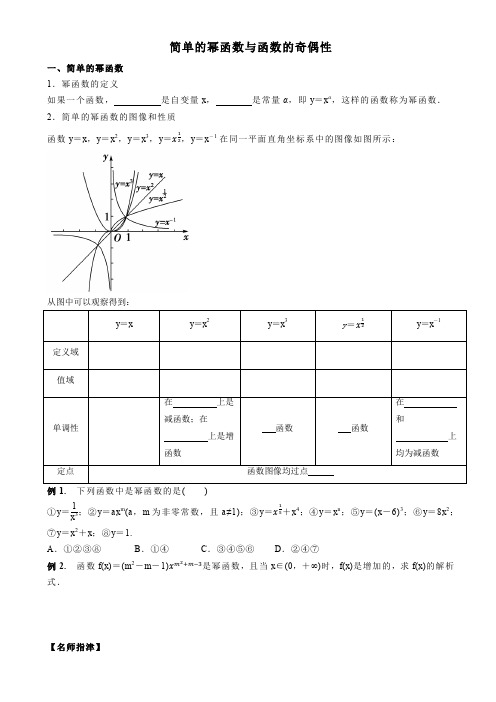
简单的幂函数与函数的奇偶性一、简单的幂函数1．幂函数的定义如果一个函数，是自变量x，是常量α，即y＝xα，这样的函数称为幂函数．2．简单的幂函数的图像和性质函数y＝x，y＝x2，y＝x3，y＝，y＝x－1在同一平面直角坐标系中的图像如图所示：从图中可以观察得到：例1.下列函数中是幂函数的是()①y＝1x3；②y＝axm(a，m为非零常数，且a≠1)；③y＝＋x4；④y＝x n；⑤y＝(x－6)3；⑥y＝8x2；⑦y＝x2＋x；⑧y＝1.A．①②③⑧B．①④C．③④⑤⑥D．②④⑦例2.函数f(x)＝(m2－m－1)是幂函数，且当x∈(0，＋∞)时，f(x)是增加的，求f(x)的解析式．【名师指津】1．形如y ＝x a 的函数叫幂函数，它有两个特点：(1)系数为1；(2)指数为常数，底数为自变量x .2．求幂函数的解析式常利用幂函数的图像特征或性质确定指数的特征值．例3.点(2，2)与点⎝⎛⎭⎫－2，－12分别在幂函数f (x )，g (x )的图像上，当x 为何值时，有①f (x )＞g (x )；②f (x )＝g (x )；③f (x )＜g (x )?变式练习1．已知幂函数f (x )＝x α的图像经过点A ⎝⎛⎭⎫12，2.(1)求实数α的值；(2)用定义证明f (x )在区间(0，＋∞)内的单调性．二、函数的奇偶性1、一般地，函数图像关于原点对称函数叫做，有；反之，若满足的函数y=f(x)一定是奇函数。

2、函数图像关于y 轴对称函数叫做，有；反之，若满足的函数y=f(x)一定是偶函数。

3、奇偶性当一个函数是奇函数或偶函数时，称该函数具有．例4.判断(正确的打“√”，错误的打“×”)(1)奇函数的图像一定过原点．( )(2)定义在R 上的函数f (x )，若存在x 0，使f (－x 0)＝f (x 0)，则函数f (x )为偶函数．( )(3)函数y ＝x 2，x ∈(－1,1]是偶函数．( )例5. 判断下列函数的奇偶性：(1)f (x )＝13x 5； (2)f (x )＝3x 2；(3)f (x )＝x 2－4＋4－x 2；(4)f (x )＝⎩⎪⎨⎪⎧ －x 2＋2x －3，x ＞0，x 2＋2x ＋3，x ＜0.例6．已知f （x ）是定义域为R 的奇函数，当x ＞0时，f （x ）=x （x ﹣2），求f （x ）的解析式．【名师指津】判断函数奇偶性的方法变式练习1．函数f (x )＝x 2(x ＜0)的奇偶性为( )A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．非奇非偶函数2.函数f (x )＝x 2＋x ( )A ．是奇函数B ．是偶函数C ．是非奇非偶函数D ．即是奇函数又是偶函数三、函数单调性与奇偶性的综合应用（一）比较大小例1、已知函数f （x ）是偶函数，且在区间[0，1]上是增函数，则)0(),1(),5.0(f f f --的大小关系是__________.（二）解不等式例2、定义在（－2，2）上的函数f （x ）是奇函数，并且在（－2，2）上是增函数，求满足条件0)21()2(>-++m f m f 的实数m 的取值范围。

幂函数特点

幂函数特点
幂函数是一种数学函数，形式为y = ax^n，其中a 和n 均为常数，x 为自变量。

其主要特点包括：
1. 奇偶性：当n 为偶数时，函数呈现出关于y 轴对称的偶函数特性；当n 为奇数时，函数呈现出关于原点对称的奇函数特性。

2. 极性：当n 为正整数时，函数呈现出正极性，在x>0 区间内递增；当n 为负整数时，函数呈现出负极性，在x>0 区间内递减。

3. 渐近线：幂函数与坐标轴之间会有渐进线，当n>0 时，函数有一条水平渐近线y=0；当n<0 时，函数有一条竖直渐近线x=0。

4. 变化趋势：随着n 的逐渐增大或减小，幂函数的变化趋势也不同，当n>1 时，函数呈现出快速增长的特性；当0<n<1 时，函数呈现出缓慢增长的特性；当
n<0 时，函数呈现出以一定速率趋近于零的特性。

5. 导函数：幂函数的导函数为y' = anx^(n-1)，可以用来计算函数在任意点上的斜率，也可用于研究函数的变化趋势和性质。

6. 常用形式：n=2 时，函数为二次函数，具有抛物线的特性；n=3 时，函数呈现出典型的三次函数特性。