初中八年级学生数学错题集

合集下载

八年级数学(初二数学)高频错题集

八年级数学高频错题集1.【题文】把根号外的因式移入根号内的结果是A. B. C. D.2.【题文】如图，的面积是，点、、、分别是、、、的中点，则的面积是A. B. C. D.3.【题文】若，，则的值用，可以表示为．A. B. C. D.4.【题文】下列由三条线段，，构成的三角形：①，，；②，，；③，，；④其中能构成直角三角形的有．A.个B.个C.个D.个5.【题文】若一次函数的图象不经过第三象限，则下列选项正确的是A.，B.，C.，D.，6.【题文】▱中，，是对角线上不同的两点．下列条件中，不能得出四边形一定为平行四边形的是A. B. C. D.7.【题文】在四边形中，，要判定此四边形是平行四边形，还需要满足的条件是A. B. C. D.8.【题文】已知正方形的边长为，如果边长增加，那么面积增加，则关于的函数关系式为A. B. C. D.9.【题文】若函数则当时，自变量的值是A. B. C.或 D.或10.【题文】快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系小欣同学结合图象得出如下结论：快车途中停留了快车速度比慢车速度多图中快车先到达目的地．其中正确的是A. B. C. D.11.【题文】如图所示，在平面直角坐标系中，菱形的顶点坐标是，则顶点、的坐标分别是______．12.【题文】若一个多边形的内角和与外角和之和是，则该多边形的边数是______．13.【题文】在矩形中，，，折叠矩形，使点与点重合，则的长为______．14.【题文】在▱中，平分交边于点，平分交边于点若，，则．15.【题文】一个长方形的长是，宽是，周长是，面积是．写出随变化而变化的关系式；写出随变化而变化的关系式；当时，等于多少？等于多少？16.【题文】小明在解决问题：已知，求的值．他是这样分析与解的：，，，，．请你根据小明的分析过程，解决如下问题：化简若，①求的值；②求代数式的值．17.【题文】“低碳环保，绿色出行”的概念得到广大群众的接受，越来越多的人喜欢选择骑自行车作为出行工具．小军和爸爸同时骑车去图书馆，爸爸先以米分的速度骑行一段时间，休息了分钟，再以米分的速度到达图书馆．小军始终以同一速度骑行，两人骑行的路程为米与时间分钟的关系如图．请结合图象，解答下列问题：填空：______；______；______．若小军的速度是米分，求小军第二次与爸爸相遇时距图书馆的距离．在的条件下，爸爸自第二次出发后，骑行一段时间后与小军相距米，此时小军骑行的时间为______分钟．18.【题文】如图，四边形中，，，，，于点。

初二数学高频错题集(含答案)

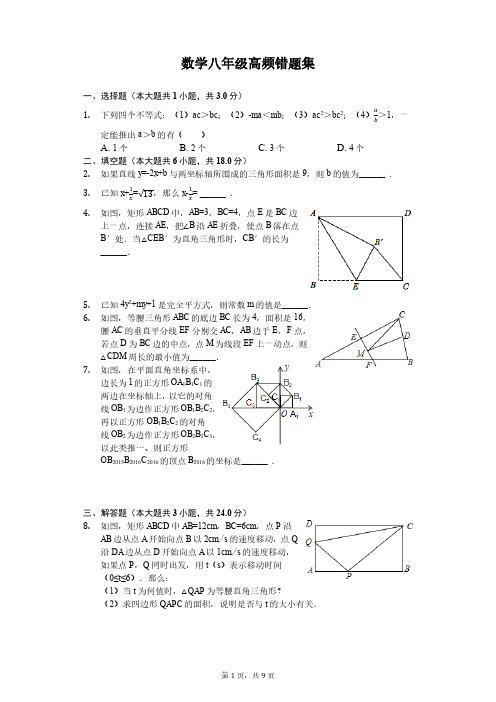
数学八年级高频错题集一、选择题（本大题共1小题，共3.0分）1.下列四个不等式：（1）ac＞bc；（2）-ma＜mb；（3）ac2＞bc2；（4）ab＞1，一定能推出a＞b的有（）A. 1个B. 2个C. 3个D. 4个二、填空题（本大题共6小题，共18.0分）2.如果直线y=-2x+b与两坐标轴所围成的三角形面积是9，则b的值为______ ．3.已知x+1x =√13，那么x-1x= ______ ．4.如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，CB′的长为______．5.已知4y2+my+1是完全平方式，则常数m的值是______．6.如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为______．7.如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是______ ．三、解答题（本大题共3小题，共24.0分）8.如图，矩形ABCD中AB=12cm，BC=6cm，点P沿AB边从点A开始向点B以2cm╱s的速度移动，点Q沿DA边从点D开始向点A以1cm╱s的速度移动，如果点P，Q同时出发，用t（s）表示移动时间（0≤t≤6）．那么：（1）当t为何值时，△QAP为等腰直角三角形？（2）求四边形QAPC的面积，说明是否与t的大小有关．9.如图1，点A是线段BC上一点，△ABD，△AEC都是等边三角形，BE交AD于点M，CD交AE于N．（1）求证：BE=DC；（2）求证：△AMN是等边三角形；（3）将△ACE绕点A按顺时针方向旋转90°，其它条件不变，在图2中补出符合要求的图形，并判断（1）、（2）两小题结论是否仍然成立，并加以证明．10.若多项式x2+ax+8和多项式x2-3x+b相乘的积中不含x3项且含x项的系数是-3，求a和b的值．答案和解析1.【答案】A【解析】解：在（1）中，当c＜0时，则有a＜b，故不能推出a＞b，在（2）中，当m＞0时，则有-a＜b，即a＞-b，故不能推出a＞b，在（3）中，由于c2＞0，则有a＞b，故能推出a＞b，在（4）中，当b＜0时，则有a＜b，故不能推出a＞b，综上可知一定能推出a＞b的只有（3），故选A．根据不等式的性质逐个判断即可求得答案．本题主要考查不等式的性质，掌握不等式的性质是解题的关键，特别是在不等式的两边同时乘或除以一个不为0的数或因式时，需要确定该数或因式的正负．2.【答案】±6【解析】解：当x=0时，y=b，当y=0时，x=，则根据三角形的面积公式：，解得b=±6．故答案为±6．先求出直线y=-2x+b与两坐标轴的交点，再根据三角形的面积公式列出关于b的方程，求出b的值即可．本题考查了一次函数图象上点的坐标特征，求出函数与x轴、y轴的交点是解题的关键．3.【答案】±3【解析】解：∵x+=，∴（x+）2=13，∴x2++2=13，∴x2+=11，∴x2+-2=（x-）2=9，∴x-=±3．故答案为：±3．直接利用完全平方公式得出x2+=11，进而得出x-的值．此题主要考查了二次根式的化简求值以及完全平方公式的应用，正确应用完全平方公式是解题关键．4.【答案】2或√10【解析】【分析】本题考查了折叠问题：折叠前后两图形全等，即对应线段相等；对应角相等．也考查了矩形的性质以及勾股定理．注意本题有两种情况，需要分类讨论，避免漏解．当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如答图1所示．连结AC，先利用勾股定理计算出AC=5，根据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=3，可计算出CB′=2，设BE=x，则EB′=x，CE=4-x，然后在Rt△CEB′中运用勾股定理可计算出x．②当点B′落在AD边上时，如答图2所示．此时ABEB′为正方形．【解答】解：当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如答图1所示．连结AC，在Rt△ABC中，AB=3，BC=4，∴AC=5，∵∠B沿AE折叠，使点B落在点B′处，∴∠AB′E=∠B=90°，当△CEB′为直角三角形时，只能得到∠EB′C=90°，∴点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，∴EB=EB′，AB=AB′=3，∴CB′=5-3=2；②当点B′落在AD边上时，如答图2所示．此时ABEB′为正方形，∴B'E=AB=3，∴CE=4-3=1，∴Rt△B'CE中，．综上所述，BE的长为2或．故答案为2或．5.【答案】±4【解析】【分析】利用完全平方公式的结构特征确定出m的值即可．此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．【解答】解：∵4y2+my+1是完全平方式，∴m=±4，故答案为±46.【答案】10【解析】解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC=BC•AD=×4×AD=16，解得AD=8，∵EF是线段AB的垂直平分线，∴点B关于直线EF的对称点为点A，∴AD的长为CM+MD的最小值，∴△CDM的周长最短=（CM+MD）+CD=AD+BC=8+×4=8+2=10．故答案为：10．连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．7.【答案】（21008，0）【解析】解：∵正方形OA1B1C1边长为1，∴OB1=，∵正方形OB1B2C2是正方形OA1B1C1的对角线OB1为边，∴OB2=2，∴B2点坐标为（0，2），同理可知OB3=2，∴B3点坐标为（-2，2），同理可知OB 4=4，B 4点坐标为（-4，0），B 5点坐标为（-4，-4），B 6点坐标为（0，-8），B 7（8，-8），B 8（16，0）B 9（16，16），B 10（0，32），由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍，∵2016÷8=252 ∴B 2016的纵横坐标符号与点B 8的相同，横坐标为正值，纵坐标是0， ∴B 2016的坐标为（21008，0）．故答案为：（21008，0）．首先求出B 1、B 2、B 3、B 4、B 5、B 6、B 7、B 8、B 9的坐标，找出这些坐标的之间的规律，然后根据规律计算出点B 2016的坐标．本题主要考查正方形的性质和坐标与图形的性质的知识点，解答本题的关键是由点坐标的规律发现每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍． 8.【答案】解：（1）∵点P 沿AB 边从点A 开始向点B 以2cm ╱s 的速度移动，点Q 沿DA 边从点D 开始向点A 以1cm ╱s 的速度移动，∴AP =2t ，AQ =AD -DQ =6-t ，∵△QAP 为等腰直角三角形，∴AP =AQ ，∴2t =6-t ，解得t =2，∴t =2s 时，△QAP 为等腰直角三角形；（2）四边形QAPC 的面积=12×6-12×12•t -12×6•（12-2t ）=36，所以，四边形QAPC 的面积与t 无关．【解析】（1）表示出AP 、AQ ，然后根据等腰直角三角形两直角边相等列方程求解即可；（2）根据四边形QAPC 的面积等于矩形的面积减去Rt △CDQ 和Rt △BCP 的面积列式整理即可得解．本题考查了矩形的性质，等腰直角三角形的判定，四边形的面积，熟记性质是解题的关键．9.【答案】证明：（1）∵△ABD ，△AEC 都是等边三角形，∴AB =AD ，AC =AE ，∠DAB =∠EAC =60°，∴∠DAC =∠BAE ，在△ABE 和△ADC 中，{AB =AD∠BAE =∠DAC AE =AC，∴△ABE ≌△ADC （SAS ），∴BE =DC ；（2）由（1）证得：△ABE ≌△ADC ，∴∠ABE =∠ADC ．在△ABM 和△ADN 中，{AB =AD∠ABM =∠ADN ∠BAM =∠DAN，∴△ABM ≌△ADN （ASA ），∴AM =AN ．∵∠DAE =60°，∴△AMN 是等边三角形；（3）∵△ABD ，△AEC 都是等边三角形，∴AB =AD ，AC =AE ，∠DAB =∠EAC =60°，∴∠DAC =∠BAE ，在△ABE 和△ADC 中，{AB =AD∠BAE =∠DAC AE =AC，∴△ABE ≌△ADC （SAS ），∴BE =DC ，∠ABE =∠ADC ，∵∠BAC =90°∴∠MAN ＞90°，∵∠MAN ≠60°，∴△AMN 不是等边三角形，∴（1）的结论成立，（2）的结论不成立．【解析】本题考查了全等三角形的判定与性质：有两组边对应相等，且它们所夹的角相等，那么这两个三角形全等；全等三角形的对应边相等．也考查了等腰直角三角形的判定与性质、矩形的性质、等边三角形的判定与性质．（1）根据等边三角形的性质得到AB=AD ，AC=AE ，∠DAB=∠EAC=60°，则∠DAC=∠BAE ，根据“SAS”可判断△ABE ≌△ADC ，则BE=DC ；（2）由△ABE ≌△ADC 得到∠ABE=∠ADC ，根据“AAS”可判断△ABM ≌△ADN （ASA ），则AM=AN ；∠DAE=60°，根据等边三角形的判定方法可得到△AMN 是等边三角形．（3）判定结论1是否正确，也是通过证明△ABE ≌△ADC 求得．这两个三角形中AB=AD ，AE=AC ，∠BAE 和∠CAD 都是60°+∠ACB ，因此两三角形就全等，BE=CD ，结论1正确．将△ACE 绕点A 按顺时针方向旋转90°，则∠DAC ＞90°，因此三角形AMN 绝对不可能是等边三角形．10.【答案】解：∵（x 2+ax +8）（x 2-3x +b ）=x 4+（-3+a ）x 3+（b -3a +8）x 2-（-ab +24）x +8b ，又∵不含x 3项且含x 项的系数是-3，∴{a −3=0−ab +24=3，解得{a =3b =7．【解析】多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．根据结果中不含x 3项且含x 项的系数是-3，建立关于a ，b 等式，即可求出．本题考查了多项式乘以多项式，根据不含x 3项且含x 项的系数是-3列式求解a 、b 的值是解题的关键．。

八年级上册数学错题集

⼋年级上册数学错题集1、如图①，分别以Rt△ABC三边为直径向外作三个半圆，其⾯积分别⽤S1，S2，S3表⽰，则不难证明S1=S2+S3．（1）如图②，分别以Rt△ABC三边为边向外作三个正⽅形，其⾯积分别⽤S1，S2，S3表⽰，写出它们的关系；（不必证明）（2）如图③，分别以Rt△ABC三边为边向外作正三⾓形，其⾯积分别⽤S1，S2，S3表⽰，确定它们的关系并证明；（3）若分别以Rt△ABC三边为边向外作三个⼀般三⾓形，其⾯积分别⽤S1，S2，S3表⽰，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三⾓形应满⾜什么条件？2、王伟准备⽤⼀段长30⽶的篱笆围成⼀个三⾓形形状的⼩圈，⽤于饲养家兔．已知第⼀条边长为a⽶，由于受地势限制，第⼆条边长只能是第⼀条边长的2倍多2⽶．（1）请⽤a表⽰第三条边长；（2）问第⼀条边长可以为7⽶吗？请说明理由，并求出a的取值范围3）能否使得围成的⼩圈是直⾓三⾓形形状，且各边长均为整数？若能，说明你的围法；若不能，说明理由．3、如图所⽰，将⼀根长为24cm的筷⼦，置于底⾯直径为5cm，⾼为12cm的圆柱形⽔杯中，设筷⼦露在外⾯的长为hcm，则h的取值范围是（）4、若5x+32的⽴⽅根等于-2，求x+17的平⽅根5、若a.b 均为正整数，且a ＞根号7，b＜2的⽴⽅根，则a+b 的最⼩值是（）6、如果正⽅形ABCD的两个相对顶点为B(3,0),D(0,3)，那么A、C两点的坐标分别为：7、已知点A（m+1，-2）和点B（3，m-1）,如果直线AB∥x轴，那么m的值为（）, 如果直线AB∥y轴，那么m的值为（）8、在平⾯直⾓坐标系中，点P在x轴的上⽅，点P到y轴的距离为1，且OP=2，画出图形并求P点坐标。

9、已知点M(x,y)与点A(-1/5,n)关于x轴对称，与点B(m,1/2)关于y轴对称，求代数式25x2+20xy+4y2+2013的值10、如图，平⾯直⾓坐标系中有四个点，它们的横纵坐标均为整数．若在此平⾯直⾓坐标系内移动点A，使得这四个点构成的四边形是轴对称图形，并且点A的横坐标仍是整数，则移动后点A的坐标为（）．11、如图，已知点C为直线y=x上在第⼀象限内⼀点，直线y=2x+1交y轴于点A，交x轴于B，将直线AB沿射线OC⽅向平移3倍根号2个单位,求平移后的直线解析式。

初中数学试卷错题集

一、选择题1. 错题：下列各数中，正数是（）A. -3B. 0C. 3D. -5错误原因：对正数、负数、零的概念理解不清晰。

正确答案：C2. 错题：若a、b是实数，且a < b，则下列不等式中错误的是（）A. a + 1 < b + 1B. a - 1 < b - 1C. a 2 < b 2D. a / 2 < b / 2错误原因：对不等式的性质理解不透彻。

正确答案：D二、填空题1. 错题：若x = 3，则2x + 1 = ______错误原因：对一元一次方程的解法掌握不牢固。

正确答案：72. 错题：若|a| = 5，则a的值为 ______错误原因：对绝对值的定义理解不全面。

正确答案：±5三、解答题1. 错题：解方程：3x - 5 = 2x + 4错误原因：对一元一次方程的解法掌握不牢固。

解答过程：3x - 2x = 4 + 5，x = 92. 错题：已知a、b是实数，且a + b = 5，ab = 4，求a^2 + b^2的值。

错误原因：对一元二次方程的应用不熟悉。

解答过程：根据(a + b)^2 = a^2 + 2ab + b^2，得到a^2 + b^2 = (a + b)^2 - 2ab = 5^2 - 2 4 = 25 - 8 = 17四、应用题1. 错题：某商品原价为x元，打八折后的价格为y元，求y与x的关系式。

错误原因：对打折问题中的应用不熟悉。

解答过程：y = x 80% = 0.8x2. 错题：某市甲、乙两地相距120千米，一辆汽车从甲地出发，以60千米/小时的速度行驶，求汽车到达乙地需要多少小时？错误原因：对行程问题的应用不熟悉。

解答过程：时间 = 距离 / 速度 = 120千米 / 60千米/小时 = 2小时总结：通过整理错题集，我们可以发现自己的不足之处，并加以改进。

在今后的学习中，我们要加强对基础知识的学习，提高解题能力，从而提高数学成绩。

八年级上数学错题集

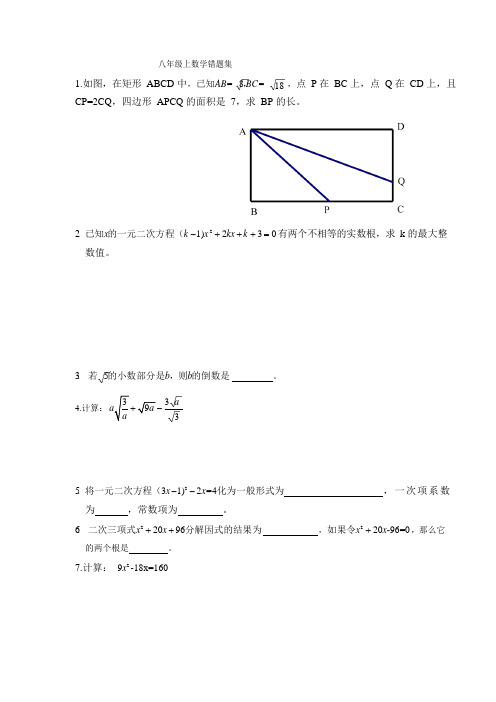
3 a 9a八年级上数学错题集1.如图，在矩形ABCD 中，已知AB=8，BC=，点P 在BC 上，点Q 在CD 上，且CP=2CQ，四边形APCQ 的面积是7，求BP 的长。

2.已知x的一元二次方程（k -1)x 2 + 2kx +k + 3 = 0 有两个不相等的实数根，求k 的最大整数值。

3.若5的小数部分是b，则b的倒数是。

4.计算：a +-5.将一元二次方程（3x -1)2 - 2x=4化为一般形式为，一次项系数为，常数项为。

6.二次三项式x2 + 20x + 96分解因式的结果为，如果令x2 + 20x-96=0 ，那么它的两个根是。

7.计算：9x2 -18x=160183 a38. 已知关于x的两个一元二次方程：方程：x2 + (2k -1)x +k 2 - 2k +13= 0 ①；2方程：x2 - (k + 2)x + 2k +9= 0 ②4（1）若方程①②都有实数根，求k 的最小整数值；（2）若方程①和②中只有一个方程有实数根，试判断方程①、②中，哪个没有实数根，并说明理由；（3）在（2）的条件下，若k 为正整数，解出有实数根的方程的解。

-310.11.已知方程ax2 + c = 0(其中a ≠ 0)没有实数根，则a和c的符号关系为。

12.当等号右边为非负数时，；当等号右边为负数时，方程。

13.已知x2 + 2x -a +1 = 0(a为已知数）没有实数根，试判断x2 + 2x+12a=1 是否一定有两个不相等的实数根，并说明理由。

x2 -2x + 33m 33 -2 32 5 + 152 + 39422314.m取什么值，关于x的方程mx 2 -(2m -1) x +m-2 =0（1）有两个相等的实数根？（2）有两个不相等的实数根？（3）没有实数根？15.如果=-x x +5,则x的取值范围是16.17.已知a +b =-4, ab = 3, 求：b +a a的值b18. 下列计算正确的是----------------------- （）（A）2 - 2 =(B) = 3(C)1=+ 2 (D) =19.下列各式计算错误的个数为------------------- ( )①3 2 2 = 6 2; ② 5 3 5 = 5 6;③27 -312=-= 1 ④= 3 -1(A) 1 (B) 2 (C) 3 (D) 420.2x -解不等式：- 6 x3x3 + 5x2ba33m5 226 - 22235-2 5+221. “如果 x - y 与 2x - y + 1是同类二次根式，则x, y .” 出题者所给的标准答案是“x=-1,y ≤ -1”,你认为出题者的标准答案是否正确？为什么？请说明理由。

八年级下册数学错题集

八年级下册数学错题集一、二次根式部分（5题）1. 化简：√(18)- 错解：√(18)=√(9 + 9)=3 + 3 = 6- 正解：√(18)=√(9×2)=3√(2)。

解析：二次根式化简时，要将被开方数分解成完全平方数与其他数相乘的形式，而不是简单的数字相加分解。

2. 计算：√(8)+√(18)- 错解：√(8)+√(18)=2√(2)+3√(2)=5√(2)√(2)=5×2 = 10- 正解：√(8)+√(18)=2√(2)+3√(2)=5√(2)。

解析：在计算二次根式加法时，最后结果应保留最简二次根式形式，不能再对√(2)进行错误的乘法运算。

3. 若√(x - 1)+√(1 - x)=y + 4，求x，y的值。

- 错解：由√(x - 1)+√(1 - x)=y + 4，得x-1≥0且1 - x≥0，解得x≥1且x≤1，所以x = 1或x = 0，当x = 0时，y=-4；当x = 1时，y=-4。

- 正解：由√(x - 1)+√(1 - x)=y + 4，因为二次根式有意义的条件是被开方数非负，所以x - 1≥0且1 - x≥0，解得x = 1。

把x = 1代入原式得y+4 = 0，解得y=-4。

解析：在确定x的值时，根据二次根式有意义的条件，x只能取1，不能取0。

4. 比较大小：2√(3)和3√(2)- 错解：因为2√(3)=√(12)，3√(2)=√(18)，所以2√(3)>3√(2)。

- 正解：因为2√(3)=√(12)，3√(2)=√(18)，所以2√(3)<3√(2)。

解析：比较二次根式大小时，先将它们化为最简二次根式对应的被开方数，再比较被开方数大小。

5. 已知a=√(5)+2，b=√(5)-2，求a^2+b^2的值。

- 错解：- 先求ab=(√(5)+2)(√(5)-2)=5 - 4 = 1。

- 然后a + b=√(5)+2+√(5)-2 = 2√(5)。

八年级上册数学错题

八年级上册数学错题八年级上册数学错题集一、三角形错题 1：一个三角形的两边长分别为 3 和 6，第三边长是方程x^2 10x + 21 = 0的根，则三角形的周长为（）A. 12B. 16C. 12 或 16D. 不能确定解析：解方程x^2 10x + 21 = 0，即(x 3)(x 7) = 0，解得x = 3或x = 7。

当第三边长为 3 时，因为 3 + 3 = 6，不满足三角形两边之和大于第三边，所以舍去。

当第三边长为 7 时，三角形的周长为 3 + 6 + 7 = 16。

故选 B。

错题 2：在\triangle ABC中，\angle A = 50^{\circ}，\angle B = \angle C，则\angle B的度数为（）A. 65°B. 50°C. 80°D. 40°解析：因为\angle A + \angle B + \angle C = 180^{\circ}，且\angle B = \angle C，所以\angle B = (180^{\circ}50^{\circ})÷ 2 = 65^{\circ}故选 A。

二、全等三角形错题 3：如图，已知AB = AD，那么添加下列一个条件后，仍无法判定\triangle ABC ≌ \triangle ADC的是（）A. CB = CDB. ∠BAC = ∠DACC. ∠B = ∠D = 90°D.∠BCA = ∠DCA解析：A 选项，因为AB = AD，CB = CD，AC = AC，根据 SSS 可判定\triangle ABC ≌ \triangle ADC。

B 选项，因为AB = AD，∠BAC = ∠DAC，AC = AC，根据 SAS 可判定\triangle ABC ≌ \triangle ADC。

C 选项，因为AB = AD，∠B = ∠D = 90°，AC = AC，根据 HL 可判定\triangle ABC ≌ \triangle ADC。

初二数学错题整理

初二数学错题整理1.题目：50 ÷ (2 + 3) × 2 - 3 = ?解析：根据数学运算的优先级，首先计算括号内的加法运算：2 + 3 = 5。

然后进行除法运算：50 ÷ 5 = 10。

接着进行乘法运算：10 × 2 = 20。

最后进行减法运算：20 - 3 = 17。

答案：172.题目：(2 + 3) × 4 + 5 = ?解析：同样根据数学运算的优先级，首先计算括号内的加法运算：2 + 3 = 5。

然后进行乘法运算：5 × 4 = 20。

最后进行加法运算：20 + 5 = 25。

答案：253.题目：3 + 2 × 4 - 6 = ?解析：根据数学运算的优先级，首先进行乘法运算：2 × 4 = 8。

然后进行加法和减法运算：3 + 8 = 11，11 - 6 = 5。

答案：5解析：根据数学运算的优先级，首先计算括号内的乘法运算：3 × 2 = 6。

然后进行加法运算：2 + 6 = 8。

最后进行除法运算：12 ÷ 8 = 1.5。

答案：1.55.题目：3 × (5 + 2) ÷ (4 - 1) = ?解析：根据数学运算的优先级，首先计算括号内的加法运算：5 + 2 = 7。

然后计算括号内的减法运算：4 - 1 = 3。

然后进行乘法运算：3 × 7 = 21。

最后进行除法运算：21 ÷ 3 = 7。

答案：76.题目：12 ÷ 6 × 3 + 4 = ?解析：根据数学运算的优先级，首先进行除法运算：12 ÷ 6 = 2。

然后进行乘法运算：2 × 3 = 6。

最后进行加法运算：6 + 4 = 10。

答案：10解析：根据数学运算的优先级，首先计算括号内的加法运算：2 + 2 = 4。

然后进行除法运算：8 ÷ 4 = 2。

八年级数学经典错题分析

八年级错题集1、如图11-1，,12,,ABE ACD B C ∆≅∆∠=∠∠=∠指出对应边和另外一组对应角。

错解：对应边是AB 与AD ，AC 与AE ，BD 与CE ，另一组对应角是∠BAD 与∠CAE 。

错误原因分析：对全等三角形的表示理解不清，在全等三角形的表示中对应顶点的位置需要对齐，不能根据对应顶点来确定对应角和对应边。

同时对全等三角形中对应角与对应边之间的对应关系也没有理解，对应角所对的边应该是对应边，如∠2所对的边是AB ，∠1所对的边是AC ，因为∠1=∠2，即∠1与∠2是对应角，所以AB 与AC 是对应边。

正解：对应边是AB 与AC ，AE 与AD ，BE 与CD ，另一组对应角是∠BAD 与∠CAE 。

2、如图11-2，在ABD ACE ∆∆和中，AB=AC ，AD=AE ，欲证ABD ACE ∆≅∆，须补充的条件是（）。

A 、∠B =∠C ； B 、∠D=∠E ； C 、∠BAC=∠DAE ；D 、∠CAD=∠DAE 。

错解：选A 或B 或D 。

错误原因分析：对全等三角形的判定定理（SAS ）理解不清，运用SAS 判定定理来证明两三角形全等时，一定要看清角必须是两条对应边的夹角，边必须是夹相等角的两对应边。

上题中AB 与AC ，AD 与AE 是对应边，并且AB 与AD 的夹角是∠BAD ，AC 与AE 的夹角是∠CAE,而∠B 与∠C ，∠D 与∠E 不是AB 与AC ，AD 与AE 的夹角，故不能选择A 或B 。

∠CAD 与∠DAE 不是ABD ∆和ACE ∆中的内角，故不能选择D 。

所以只有选择C ，因为∠BAC+∠CAD=∠DAE+∠CAD ，即：∠BAD=∠CAE 。

正解：选C 。

3、如图11-3所示，点0为码头，A ，B 两个灯塔与码头的距离相等，0A 、OB 为海岸线，一轮船离开码头，计划沿∠AOB 的平分线航行，在航行途中，测得轮船与灯塔A 和灯塔B 的距离相等，试问轮船航行是否偏离指定航线？错解：不能判断，因为应该是到角两边距离相等（即垂线段相等）的点才在角平分线上。

数学初二练习题错题集

数学初二练习题错题集题目一：整数的运算1. 求下列各式的值：（1）(-3) + 7（2）14 - (-5)（3）5 × (-2)（4）(-9) ÷ (-3)解析：（1）(-3) + 7 = 4（2）14 - (-5) = 14 + 5 = 19（3）5 × (-2) = -10（4）(-9) ÷ (-3) = 3题目二：一元一次方程2. 解方程：2x + 5 = 13解析：将2x + 5 = 13两边同时减去5，得到2x = 8。

再将2x除以2，得到x = 4。

题目三：平方根与立方根3. 求下列各式的值：（1）√25（2）∛27（3）√(16 - 9)解析：（1）√25 = 5（2）∛27 = 3（3）√(16 - 9) = √7题目四：平行线及其性质4. 若两条直线l1和l2平行，且l1上的一点A与l2上的一点B连接，求证∠CAB = 180°。

解析：根据平行线的性质，当两条平行线l1和l2被一条横截线AB相交时，其内错角相等，即∠CAB = 180°。

题目五：三角形的周长和面积5. 已知一个正三角形的周长为12cm，求其面积。

解析：正三角形的三条边长度相等，所以每条边的长度为12cm ÷3 = 4cm。

正三角形的面积可以通过公式S = (边长的平方×√3) ÷ 4进行计算。

代入边长4cm，得到S = (4×4×√3) ÷ 4 = 4√3 cm²。

题目六：概率6. 一个包里有4个红球，6个蓝球。

从中任取1个球，求：（1）取出的球是红色的概率。

（2）取出的球是蓝色的概率。

解析：（1）取出的球是红色的概率为红球的数目（4个）除以总球数（4个红球+6个蓝球），即4 ÷ (4+6) = 0.4。

（2）取出的球是蓝色的概率为蓝球的数目（6个）除以总球数，即6 ÷ (4+6) = 0.6。

八年级数学(下册)错题集

WORD格式整理第十六章《二次根式》易错题一、选择题1．当a＞0，b＞0时，n是正整数，计算的值是（）A．（b﹣a）B．（a n b3﹣a n+1b2）C．（b3﹣ab2） D．（a n b3+a n+1b2）错答：D考点：二次根式的性质与化简。

分析：把被开方数分为指数为偶次方的因式的积，再开平方，合并被开方数相同的二次根式．解答：解：原式=﹣=a n b3﹣a n+1b2=（a n b3﹣a n+1b2）．故选B．点评：本题考查的是二次根式的化简．最简二次根式的条件：被开方数中不含开得尽方的因式或因数．点评：解答此题，要弄清二次根式的性质：=|a|，分类讨论的思想．2．当x＜﹣1时，|x﹣﹣2|﹣2|x﹣1|的值为（）A．2 B．4x﹣6 C．4﹣4x D．4x+4错答：C考点：二次根式的性质与化简。

分析：根据x＜﹣1，可知2﹣x＞0，x﹣1＜0，利用开平方和绝对值的性质计算．解答：解：∵x＜﹣1∴2﹣x＞0，x﹣1＜0∴|x﹣﹣2|﹣2|x﹣1|=|x﹣（2﹣x）﹣2|﹣2（1﹣x）=|2（x﹣2）|﹣2（1﹣x）=﹣2（x﹣2）﹣2（1﹣x）=2．故选A．点评：本题主要考查二次根式的化简方法与运用：a＞0时，=a；a＜0时，=﹣a；a=0时，=0；解决此类题目的关键是熟练掌握二次根式、绝对值等考点的运算．3．化简|2a+3|+（a＜﹣4）的结果是（）A．﹣3a B．3a﹣C．a+D．﹣3a错答：B考点：二次根式的性质与化简；绝对值。

分析：本题应先讨论绝对值内的数的正负性再去绝对值，而根号内的数可先化简、配方，最后再开根号，将两式相加即可得出结论．解答：解：∵a＜﹣4，∴2a＜﹣8，a﹣4＜0，∴2a+3＜﹣8+3＜0原式=|2a+3|+=|2a+3|+=﹣2a﹣3+4﹣a=﹣3a．故选D．点评：本题考查的是二次根式的化简和绝对值的化简，解此类题目时要充分考虑数的取值范围，再去绝对值，否则容易计算错误．4．当x＜2y时，化简得（）A．x（x﹣2y）B．C．（x﹣2y）D．（2y﹣x）错答：C考点：二次根式的性质与化简。

初中八年级学生数学错题集

说明:1.题集所收录的是八年级（）班学生在日常学习中出现的具有代表性、典型性的题目;2.题集里面的题目无顺序、章节规律;3.对于题集里面出现的题目,拥有人应彻底掌握,再次遇到该题或此类题目不应再犯以前的错误.★1.若aa则,6.122________.错解:1.6 正解:6.1.★2.计算:mm m xx xx223122223.说明:本题并无多大难度,但部分学生在看到题目后会被题目吓倒,不敢下手!出现假不会的现象. 解:原式mm m x x x x 22312222322222222223m m m xxx ★3.若32433212nn ,试求n 的值.说明:本题是资料上所谓的开放探究创新题,说明白些就是资料(ˇ?ˇ)想告诉你本题是具有较大难度的!但真的是这样吗?解:32433212nn 48133322nn（这一步反向利用了同底数幂的乘法公式）4313342n（这一步主要是把公因式n23提出来）2,423343434242nnnn★4.计算3210的结果是【】（A ）510（B ）610（C ）510（D ）610说明:有学生选择（C ）答案,我想他（她）肯定是将同底数幂的乘法运算和幂的乘方运算弄混淆了,两种运算的公式是不一样的.本题考查的是幂的乘方运算公式.另外,还要用到结论:为奇数）为偶数）n A n A Annn(-(解:63232101010,选择（D ）.★5.42m a________.说明:这道题当时居然有人做错,而且不止一人,不过我宽恕了他们!出错的地方是没有利用乘法分配律.解:84424)2(442m m m m aaaa（够详细了）.★6.设d c b a dc b a,,,,5,4,3,211223344把按从小到大的顺序排列.说明:本题又是所谓的开放探究创新题,没有一个学生做出来.我们若仔细观察,就会发现d c b a ,,,的指数都是11的倍数,所以我们就往这个方向努力. 解:111141144416222a.516444273331111112112221111311333b ca d d cb 我们在任何时候都不要脱离了课本!★7.201020115775________.分析本题考查公式nm nmaaa 的反向利用,即nmnm a aa.解:2010201157757575175577575577557752010201020102010201012010★8.计算:23104.1.解:原式62321096.1104.1.评注:这道题你们真的没有做错,但你们过程写多了. ★9.若5127,n x xxxnmnm求的值.评注:这道题的正确率并不高,都出现了或多或少的问题.本题只能求出n 的值,m 的值是无法求出的. 解:nmnmxxx x.7127127055n nnm nm x xnm nm （题外话:把本章的公式、结论看看、背背）21第10题DABCE21EDAB C★10.如图所示,点B 、C 、E 在同一条直线上,△ABC 和△DCE 均为等边三角形,连结AE 、BD. （1）求证:AE=BD;（2）若把△DCE 绕点C 顺时针旋转一个角度,（1）中的结论还成立吗?请画出图形进行说明. 解:（1）∵△ABC 和△DCE 都是等边三角形∴∠1=∠2,BC=AC,CD=CE ∴∠1+∠ACD=∠2+∠ACD 即∠BCD=∠ACE 在△BCD 和△ACE 中∵CECDACEBCD ACBC∴△BCD ≌△ACE （SAS ）∴BD=AE;（2）如图所示,（1）中的结论还成立. 同理可证:△BCD ≌△ACE （SAS ）∴BD=AE.评注:这几个学生的胆子有点小,一看这个题目就不敢做了!如果认真思考、耐心看完题目是完全能够解决这个问题的.★11.已知2322,2y x yx y x 求的值.分析数学这一门学科,公式和定理、公理等都是给定的,我们必须在理解的基础上加以记忆,然后再进行一些适当的练习加以巩固,最终把知识变成我们自己的东西,才能灵活运用.当然,在运用这些定理、公式和公理等解决问题的时候,我们还会得出一些有用的、重要的结论,这些结论的总结其实是我们对知识深刻掌握的产物,是我们学会学习的一种表现.每一个学生都要学会总结结论,虽然每个人总结的结论不尽相同,但对每个人自己确是最适用的.另外,对同一个知识点的考查,有各种各样的题目,这些题目我们是做不完的,我们能做的是进行适当的练习,最终掌握相关的知识点! 解:∵2y x ∴2322yxyx1282444)(2552323yx yxyx y x y x 评注就是这么一个简单的题目,当时却没几个学生能做出来.我想他们还是没有深刻掌握相关的公式和结论等所导致的.他们应该对这个问题引起重视. ★12.已知10210510826的计算结果用科学记数法表示为n a an与求,10的值.分析科学记数法的一般形式为na 10,其中n a ,101为正整数.如8106.3、6108.2等都是合法的表示形式,而71036这样的表示却是不正确的!你们几个犯的就是这样的错误!两个用科学记数法表示的数相乘（除）的方法是:系数与系数相乘（除）,同底数幂相乘（除）.但要保证结果的系数的绝对值大于或等于1而小于10. 解:10210510826109261081080101010258★13.已知c b a xxx xb c x x a 、、求,34722222的值. 分析这是一个关于多项式相等的问题.我之前给你们总结了一个相关的结论:如果两个多项式相等,则它们对应．．的系数相等.如果F Ex DxC Bx Ax22,那么.ECD BC A注意:该结论里面各项之间是相加的.解:34722222xx xx b cx x a 324723472234722347222222222bacb ab a xxbacxb a x b axxb ac x b a x b a x x b bx bx ac ax ax 解之得:115cba.★14.若n mxxxx 284,则n m 、的值分别是【】（A ）4 , 32 （B ）4 , 32（C ）4, 32（D ）4,32分析这也是一个考查两个多项式相等的题目,出现的错误比较多!注意结论里面各项之间是相加的.解:nmxxxx 2843243243243243248222222nm n m nmxxx xn mxx x x n mx x x x x 正确答案是【 A 】.★15.若20112,01232xxxx 求的值.分析本题主要考查学生依据题目所给的条件,对要求值的式子进行变形处理的能力. 解:∵012x x ∴12x x ∴2011223x x2012201112011201112011222223x x xx x xxx★16.若n mx xx 21的计算结果中不含2x 项和x 项,则m________,n ________. 分析这是一个关于多项式中不含某项的问题,有这样的结论:若一个多项式中不含某一项,则该项的总系数等于0（总系数是指合并同类项之后的系数）. 解:nmx xx 210011223223nmm x x nxn mxmxn mx xnx mx x 项项和其计算结果中不含解之得:11nm .★17.。

八年级上册数学易错题

八年级上册数学易错题一、三角形相关1. 已知等腰三角形的两边长分别为3和5，则它的周长为（）错解：11或13。

正解：11或13。

解析：当腰长为3时，三边长为3，3，5，因为3 + 3>5，满足三角形三边关系，此时周长为3+3 + 5 = 11；当腰长为5时，三边长为5，5，3，因为5+3>5，也满足三角形三边关系，此时周长为5 + 5+3 = 13。

2. 在△ABC中，∠A=50°，高BE、CF所在直线相交于点O，则∠BOC的度数为（）错解：130°。

正解：130°或50°。

解析：当△ABC是锐角三角形时，因为∠A = 50°，∠AEB = 90°，∠AFC = 90°，在四边形AFOE中，根据四边形内角和为360°，可得∠EOF=360° 90°-90°50° = 130°，即∠BOC = 130°；当△ABC是钝角三角形时，∠A=50°，∠ABE = 40°，在Rt△BOE中，∠BOC = 50°。

二、全等三角形相关1. 如图，已知AB = AD，∠1 = ∠2，要使△ABC≌△ADE，还需添加的条件是（只需填一个）。

错解：AC = AE。

正解：AC = AE或∠B=∠D或∠C = ∠E。

解析：已知AB = AD，∠1 = ∠2，所以∠BAC = ∠DAE。

如果添加AC = AE，根据SAS（边角边）可证△ABC≌△ADE；如果添加∠B = ∠D，根据ASA（角边角）可证全等；如果添加∠C=∠E，根据AAS（角角边）可证全等。

2. 如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，连接EF 交AD于G。

求证：AD垂直平分EF。

错解：只证明了DE = DF，就得出AD垂直平分EF。

正解：因为AD是∠BAC的平分线，DE⊥AB，DF⊥AC，根据角平分线的性质可知DE = DF。

八年级上册数学错题集

读书破万卷下笔如有神1、女口图①，分别以Rt △ ABC 三边为直径向外作三个半圆，其面积分别用 S ,1S ，S 表示，则不难证明S=S+S . 32213 （ 1 ）如图②，分别以Rt △ ABC 三边为边向外作三个正方形，其面积分别用 S ，S ，S 表示，写出它们的关系；（不必证明）312 （2）如图③，分别以Rt △ ABC 三边为边向外作正三角形，其面积分别用S ，S ，S 表示，确定它们的关系并证明；312 （3）若分别以Rt △ ABC 三边为边向外作三个一般三角形，其面积分别用 S ，S ，S 表示，为使S ，S ，S 之间仍2、王伟准备用一段长30米的篱笆围成一个三角形形状的小圈，用于饲养家兔.已知第一条边长为a 米，由于受地势限制，第二条边长只能是第一条边长的 2倍多2米.（1）请用a 表示第三条边长；（2）问第一条边长可以为7米吗？请说明理由，并求出a 的取值范围3）能否使得围成的小圈是直角三角形形状，且各边长均为整数？若能，说明你的围法；若不能，说明理由.下笔如有神读书破万卷3、如图所示，将一根长为24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在外面的长为hcm，则h的取值范围是()4、若5X+32的立方根等于-2,求x+17的平方根5、若a.b均为正整数，且a ＞根号7,b v 2的立方根，则a+b的最小值是()6如果正方形ABCD的两个相对顶点为B(3,0),D(0,3)，那么A、C两点的坐标分别为：7、已知点A (m+1, -2)和点B (3，m-1),如果直线AB // x轴，那么m的值为),如果直线AB // y轴，那么m的值为( )8、在平面直角坐标系中，点P在x轴的上方，点P到y轴的距离为1,且0P=2, 画出图形并求P点坐标。

9、已知点M(x,y)与点A(-1/5,n)关于x轴对称，与点B(m,1/2)关于y轴对称，求代数式25x2+20xy+4y2+2013 的值10、如图，平面直角坐标系中有四个点，它们的横纵坐标均为整数.若在此平面直角坐标系内移动点A，使得这四个点构成的四边形是轴对称图形，并且点A的横坐标仍是整数，则移). 的坐标为(A动后点.读书破万卷下笔如有神_____________________________________11、如图，已知点C为直线y=x上在第一象限内一点，直线y=2x+1交y轴于点A，交x轴于B，将直线AB沿射线0C方向平移3倍根号2个单位，求平移后的直线解析式。

人教版八年级数学上册期末易错精选30题

人教版八年级数学上学期期末易错精选30题考试范围：全册的内容，共30小题.【答案】332+(1--【分析】以M为直角顶点，@（）V V，接着得到当NMB AMPSAS形的性质解答即可．【详解】解：如图，以M为直角顶点，【点睛】本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质、三角形的外角性质、利用了等量代换及转化的思想等知识点，熟练掌握相关判定与性质是解本题的关键．三、解答题（共14小题）17．（2022·山东德州·八年级期中）如图，在ABC V 中，AB AC =，AD (1)若42C Ð=°，求BAD Ð(2)若点E 在边AB 上，EF 【答案】(1)48BAD Ð=Ð°(2)AEF △为等腰三角形【分析】（1）根据直角三角形的两锐角互余即可求解；（2）根据三线合一得出BAD CAD Ð=Ð，根据平行线的性质得出F CAD Ð=Ð，等量代换可得BAD F Ð=Ð，根据等角对等边即可求解．【详解】（1）解：∵AB AC =，AD BC ^于点D ，∴BAD CAD Ð=Ð，90ADC Ð=°，又42C Ð=°，∴904248BAD CAD Ð=Ð=°-°=°．（2）证明：∵AB AC =，AD BC ^于点D ，∴BAD CAD Ð=Ð，∵EF AC ∥，∴F CAD Ð=Ð，∴BAD F Ð=Ð，∴AE FE =，∴AEF △为等腰三角形．【点睛】本题考查了直角三角形的两锐角互余，等腰三角形的性质与判定，掌握等腰三角形的性质与判定是解题的关键．18．（2022·江苏·仪征市第三中学八年级期中）如图，已知在四边形ABCD 中，点E 在AD 上，BCE ACD Ð=Ð，BAC D Ð=Ð，BC CE =．(1)求证：AC CD =；(2)若AC AE =，=90ACD Ð°，求DEC Ð的度数．【答案】(1)见解析(2)112.5Ð=°DEC 【分析】（1）证明()AAS ABC DHC @V V ，即可得到结论；（2）由=90ACD Ð°，AC CD =，得到45CAD D Ð=Ð=°，由AE AC =，得到67.5ACE AEC Ð=Ð=°，即可得到答案．【详解】（1）证明：∵BCE ACD Ð=Ð，∴BCE ACE ACD ACE Ð-Ð=Ð-Ð，∴ACB DCE Ð=Ð，在ABC V 和DEC V 中，BAC D ACB DCE BC CE Ð=ÐìïÐ=Ðíï=î，∴()AAS ABC DEC @V V ，∴AC CD =；（2）解：∵=90ACD Ð°，AC CD =，∴45CAD D Ð=Ð=°，∵AE AC =，∴67.5ACE AEC Ð=Ð=°，∴180112.5DEC ADC °Ð=-Ð=°．【点睛】此题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识，熟练掌握全等三角形的判定和性质是解题的关键．19．（2022·福建·莆田锦江中学八年级期中）如图，四边形ABCD ，分别延长AD 、AB(1)求证：FDC CBE A C Ð+Ð=Ð+Ð(2)如图2，FDC Ð与CBE Ð的角平分线相交于G 点，若6040A G Ð=°Ð=°，，求C Ð．【答案】(1)见解析；(2)140°【分析】（1）连接AC ，根据三角形的外角性质可得FDC FAC DCA Ð=Ð+Ð，CBE CAB BCA Ð=Ð+Ð，进而得出FDC CBE FAB DCB Ð+Ð=Ð+Ð，即FDC CBE A C Ð+Ð=Ð+Ð．（2）根据360ADC ABC A C Ð+Ð+Ð+Ð=°，得出300ADC ABC C Ð+Ð=°-Ð，进而得出2260CDG CBG C Ð+Ð=°+Ð，根据360ADG ABG A G Ð+Ð+Ð+Ð=°，得出40CDG CBG C Ð+Ð=Ð-°，联立方程即可得出答案．【详解】（1）连接AC ，∵FDC FAC DCA Ð=Ð+Ð∴FDC CBE FAC Ð+Ð=Ð∴FDC CBE FAB Ð+Ð=Ð（2）∵ADC ABC Ð+Ð∴300ADC ABC Ð+Ð=【答案】（1）115；140；（2）1()2P A B Ð=Ð+Ð；（3）1(2P A B Ð=Ð+Ð+Ð(1)若点D 是BC 的中点，则:ABD ACD S S =△△_____；(1)若=60B Ð°，求出发几秒后，(2)若=60B Ð°，求出发几秒后，(3)若AB AC =，点Q 与点动，当a 为何值时，BPD △【答案】(1)5秒(2)2.5秒或10秒∴=30BDP Ð°，∵20cm AB =，点D 为线段AB 的中点，∴10cm BD =，∴210cm BP BD ==，∴5cm BP =，∵动点P 以2cm /s 的速度运动，∴25x =，解得， 2.5x =；②当=90BDP Ð°时，∵=60B Ð°，∴=30BPD Ð°，∵20cm AB =，点D 为线段AB 的中点，∴10cm BD =，∴220cm BP BD ==，∵动点P 以2cm /s 的速度运动，∴220x =，解得，10x =；∴当P 出发2.5秒或10秒后，BPD △为直角三角形；（3）解：设运动时间为t 秒，∵AB AC =，∴B C Ð=Ð，∵20cm AB =，D 是AB 的中点，∴10cm BD =，①当BD QC =，BP CP =时，BDP CQP △≌△，则有，BP CP =，∵16cm BC =，∴8cm BP CP ==，∵动点P 以2cm /s 的速度运动，∴2BP t =，∴4t =，∵点Q 以cm/s a 的速度从C 点出发在线段CA 上运动，∴4CQ at a ==．∵CQ BD =，∵20cm AB =，D 是AB 的中点，(1)由已知和作图能得到ADC EDB V V ≌的理由是______．(2)求得AD 的取值范围是______．(3)如图2，在ABC V 中，点D 是BC 的中点，点M 在AB 边上，点BM CN MN +>．【答案】(1)SAS ；(2)17AD <<；(3)证明见解析．【分析】（1）根据全等三角形的判定定理解答即可；（2）根据三角形的三边关系计算；（3）延长MD 到E ，使MD DE =，连接NE ，CE ，证明()DMN DEN SAS △≌△，得到MN EN =，证明()≌DMB DEC SAS △△，得到MB EC =，再利用EC NC NE +>即可证明BM NC MN +>．【详解】（1）解：∵AD 是BC 边上的中线，∴BD DC =，在ADC △和EDB △中，BD DC BDE ADCDE AD =ìïÐ=Ðíï=î∴()ADC EDB SAS ≌△△，故答案为：SAS（2）解：∵()ADC EDB SAS ≌△△，∴6AC EB ==，∵8AB =，∴在ABE V 中，AB BE AE AB BE -<<+，即214AE <<，∵2AE AD =，∴17AD <<，故答案为：17AD <<（3）解：延长MD 到E ，使MD DE =，连接NE ，CE ，∵MD DN ^，∴MDN EDN Ð=Ð，在DMN V 和DEN V 中，MD DE MDN EDNDN DN =ìïÐ=Ðíï=î∴()DMN EDN SAS V V ≌，∴MN EN =，在DMB V 和DEC V 中，MD DE MDB EDCBD DC =ìïÐ=Ðíï=î∴()≌DMB DEC SAS △△，∴MB EC =，∵在NCE △中，EC NC NE +>，∴BM NC MN +>．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，三角形三边关系应用等知识；熟练掌握三角形的三边关系，作出辅助线，证明三角形全等是解题的关键．26．（2022·江苏盐城·七年级期中）（1）在下列横线上用含有a b ，的代数式表示相应图形的面积．_________________________________①②③④___________（2）请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达：___________．（3）利用（2）的结论计算2210.2320.469.779.77+´+的值．【答案】（1）①2a ，②2ab ，③2b ，④()2a b +；（2）2222()aab b a b ++=+；（3）400【分析】（1）根据正方形、长方形面积公式即可解答；（2）前三个图形的面积之和等于第四个正方形的面积；（3）借助于（2）中的结论解答即可．【详解】解：（1）①2a ，②2ab ，③2b ，④()2a b +；（2）画出的拼图为：观察图形可知，a （3）210.2320.46+2102321023..=+´()21023977..=+(1)求证：ADC △≌CEB V ；(2)若5AD =，13DE =，求BE 的长；(3)如图2，延长AD 至F ，连接CF ，过点C 作CG CF ^，且CG CF =，连接BG 交直线l 于点H ，若30CGH S =V ，10CD =，则AF =______．【答案】(1)见解析(2)8(3)12【分析】（1）先根据互余角性质得DAC ECB Ð=Ð，再根据AAS 得结论；（2）由（1）中全等三角形的性质求得AD CE =，再由线段和差求得结果；（3）过点G 作GM l ^于M ，先证明CDF V ≌GMC △，得10CD GM ==，再已知三角形的面积求得CH ，再证明BEH ≌GMH V 得EH MH =，最后由线段和差得结果．【详解】（1）证明：AD DE ^Q ，BE DE ^，∴90ADC CEB ACB Ð=Ð=Ð=°，∵90DAC DCA ECB DCA Ð+Ð=Ð+Ð=°，DAC ECB \Ð=Ð，在ADC △和CEB V 中，ADC CEB DAC ECB AC CB Ð=ÐìïÐ=Ðíï=î，ADC \V ≌()CEB AAS △；（2）解：ADC Q V ≌CEB V ，5AD =，∴5AD CE ==，CD BE =．∵13DE =，∴1358BE CD ==-=；（3）解：过点G 作GM l ^于M ，则另两个角分别为60°，90°，60230°=´°Q ，\有一个30°的直角三角形是“倍角三角形”，故答案为：②③；（2）①证明：AB AC =Q ，ABC ACB \Ð=Ð，Q 将ABC V 沿边AB 所在的直线翻折180°得到ABD △，ABC ABD \Ð=Ð，ACB ADB Ð=Ð，BC BD =，ADB ABD \Ð=Ð，2BAE ADB ABD ADB \Ð=Ð+Ð=Ð，BE BC =Q ，BD BE \=，E ADB \Ð=Ð，2BAE E \Ð=Ð，ABE \V 是“倍角三角形”；②解：由①可得2260BAE BDA C Ð=Ð=Ð=°，如图，若ABP V 是等腰三角形，则BPE V 是“倍角三角形”，ABP \V 是等边三角形，60APB \Ð=°，120BPE \Ð=°，60E EBP \Ð+Ð=°，BPE Q V 是“倍角三角形”，2EBP E \Ð=Ð或2E EBP Ð=Ð，于点P CE ，交BD 于点Q，连接BF ，请问BF 是否会平分CBD Ð？如果是，求出a ，如果不是，请说明理由；(3)在第（2）问的条件下，试猜想线段AF BF ，和CF 之间的数量关系，并说明理由．【答案】(1)见解析(2)不会BF 平分CBD Ð，理由见解析(3)AF CF BF +＝，理由见解析【分析】（1）由边角边即可证明三角形全等，根据全等三角形的性质即可得出结论．（2）由边角边即可证明三角形全等，再由面积法即可求出60AFB EFB Ð=Ð=°，再由三角形内角和定理可求得角相等，即可得AB DB =，与题干矛盾，即可求解．（3）由边角边即可证明三角形全等，可得AM CF =，即可得结论．【详解】（1）证明：∵ABC DBE ，V V 都是等边三角形，60AB BC BD BE ABC DBE \ÐÐ°＝，＝，＝＝，ABD CBE \ÐÐ＝，在ABD △和CBE △中，AB CB ABD CBEBD BE =ìïÐ=Ðíï=îABD CBE SAS \≌（）V V ，AD CE \＝；（2）解：不是，理由如下：如图3，过点B 作BN AD ^于N ，过点B 作BH CE ^于H ，ABC DBE ，Q V V 都是等边三角形，60AB BC BD BE ABC DBE \ÐÐ°＝，＝，＝＝，ABD CBE \ÐÐ＝，在ABD △和CBE △中，ABM CBFBM BF ïÐ=Ðíï=îABM CBF SAS \≌（）V V ，AM CF \＝，AF AM MF +＝Q ，AF CF BF \+＝．【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，角平分线的性质等知识，添加恰当辅助性构造全等三角形是解题关键．。

八年级上学期数学错题集

13.2--13.3错题集一、选择题1、下列说法正确的是（）A.面积相等周长相等的两个三角形全等B.全等三角形指形状完全相同的三角形C.全等三角形周长相等D.所有等边三角形全等2、下列不能唯一确定一个直角三角形的是（）A.已知两直角边B.已知一直角边和一斜边C.已知一斜边和一锐角D.已知两直角边3、下列说法正确的是（）A.有两条边分别相等的两个三角形全等B.一条直角边和一个锐角分别相等的两个直角三角形全等C.有一条边相等的两个等腰直角三角形全等D.两条直角边对应相等的两个直角三角形全等4、下列命题：①两个三角形中有两边及第三边上的中线对应相等的两个三角形全等；②两边及第三边的高对应相等的两个三角形全等；③两边及第三边的高对应相等的两个锐角三角形全等；④锐角为30 的两个直角三角形有一边相等，则这两个三角形全等；正确的是（）A.①②B.②③C.③④D.①③5、在△ABC中，AB=AC,AB的中垂线与AC所成的角为50 ，则∠B等于（）A.70B.20 或70C.40 或70D.40 或206、如图：在△ABC中，AD是∠BAC的平分线，DE⊥AC于E，DF⊥AB于F，且FB=CE，则下列结论：：①DE=DF，②AE=AF③BD=CD，④AD⊥BC。

其中正确的个数有（）A：1个 B：2个 C：3个 D：4个第7题第8题7、如图：在不等边△ABC中，PM⊥AB，垂足为M，PN⊥AC，垂足为N，且PM=PN，Q在AC上，PQ=QA，下列结论：①AN=AM，②QP∥AM，③△BMP≌△QNP，其中正确的是（）A：①②③ B：①② C：②③ D：①9、如图：直线a，b，c表示三条相互交叉环湖而建的公路，现在建立一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）A：1个 B：2个 C：3个 D：4个二、填空题1、如果两个三角形的两条边和其中一边上的高对应相等，那么这两个三角形的第三边所对的角的关系是_________1、等腰三角形的顶角为，则一腰上的高线与底边的夹角是______1、如图，AB=AC,D是AB上一点，且DE⊥BC于E,ED的延长线交CA的延长线于F,那么△ADF 是__________三角形如图：在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，③点P在∠AOB的平分线上。

八年级上册数学错题集

八年级上册数学错题集1、若关于x 的分式方程xx x m 2132=--+无解，则m 的值__________. 2、使代数式x x --312有意义的x 的取值范围________________ 3、若942+-mx x 是完全平方公式，则m=_____________4、关于x 的方程112=-+x a x 的解为正数，那么a 的取值范围是_______________ 5、已知xy ＜0，化简y x 2=________________6、若等腰三角形腰上的高是腰长的一半，则这个等腰三角形的底角是_____________7、已知三角形相邻两边长分别为20cm 和30cm ，第三边上的高为10cm ，则此三角形的面积为______________8、△ABC 的三边长分别为3，4，5，点P 是△ABC 内一点，且到三边的距离都为r ，则r=_____9、若101=+a a ，则aa 1-的值为__________ 10、已知多项式222++x x 与另一多项式相乘，得到b kx x x +--242，则3k+b=__________11、如果整数a 使得代数式2322-+-a a a 的值也为整数，那么a=______________ 12、某加油站储有a 天的常用油量m （t ），要使供油时间延长2天，每天就要比常用油量减少供油n （t ），则n=__________t13、计算：yx x y y x 235112342⨯÷- 11)1(---a a14、已知31=+x x ，求1242++x x x 的值15、已知x+y=-15，求)(2)(4)()()(2222222222y x xyy x x y xy y x y x y y x x +÷+--⋅-++-+的值16、已知312+=x ，312-=y ，（1）试求2x²+2y²-xy 的值（2）若x 的整数部分是a ，y 的小数部分是b ，求5a²+（x-b ）²-y 的值17、某超级市场销售一种计算机，每个售价48元后来计算机的进价降低了4%，但售价未变，所以让这种计算机的利润提升了5% 这种计算机的每个进价是多少？18、某商店经销一种泰山旅游纪念品，4月份的营业额为2000元，为扩大销售量，5月份该商店对这种纪念品打9折出售，结果销量增加20件，营业额增加700元。

八年级数学易错题20例(含解析)

八年级数学易错题20例1. 理解错误的题目：一些学生可能会误解题目的意思，从而得出错误的答案。

例如，题目要求求解一个方程，但是学生可能会误解为需要求解一个不同的方程。

2. 忘记变号：在进行等式运算时，有时会忘记在移项或者合并同类项时变号。

3. 计算错误：在进行复杂计算时，可能会出现计算错误，例如算错乘法、加法等。

4. 错误的应用公式：例如在使用勾股定理时，将直角三角形的边长错误地代入公式。

5. 忽视条件：在解决问题时，可能会忽视题目给出的某些条件，导致答案错误。

6. 图形理解错误：在几何问题中，可能会误解或错误地画出图形。

7. 错误的角度计算：在几何问题中，尤其是涉及角度的计算，容易出错。

8. 比例理解错误：在涉及比例的问题中，可能会对比例的概念理解错误。

9. 单位换算错误：在涉及单位换算的问题中，可能会换算错误。

10. 错误的概率计算：在概率问题中，可能会出现计算错误或者理解错误。

11. 忽视坐标系的方向：在平面直角坐标系中，有时会忽视坐标轴的方向，导致点的位置判断错误。

12. 函数理解不足：对于函数的理解不足，可能导致在解决与函数相关的问题时出错。

13. 三角形性质理解错误：例如，误将等边三角形的性质应用于等腰三角形等。

14. 分式运算错误：在进行分式的加减乘除运算时，可能会出现运算错误。

15. 错误的不等式解法：在解不等式时，可能会因为变号、计算等问题导致解答错误。

16. 数列求和公式使用不当：例如，等差数列和等比数列的求和公式混淆使用。

17. 根与系数的关系理解不清：对于二次方程的根与系数的关系理解不足，导致相关题目解答错误。

18. 圆的性质理解不足：例如，对圆心角、圆周角、弧长等性质理解不清，导致解题出错。

19. 忽视特殊情况：在一些数学问题中，可能存在特殊情况需要额外考虑，如果忽视这些特殊情况，可能会导致答案不完整或错误。

20. 不严谨的推理：在数学证明题中，推理过程不严谨，跳跃步骤或者逻辑不清晰，导致证明错误。

初二数学难题易错题集

初二数学错题档案1、平行四边形ABCD 的周长32, 5AB=3BC,则对角线AC 的取值范围为( ) A. 6<AC<10 B. 6<AC<16 C. 10<AC<16 D. 4<AC<162、如图所示，四边形ABCD 是平行四边形，按下列条件得到的四边形BFDE 是平行四边形的个数是（）①图甲，DE ⊥AC ，BF ⊥AC ②图乙，DE 平分∠ADC ，BF 平分∠ABC ③图丙，E 是AB 的中点，F 是CD 的中点 ④图丁，E 是AB 上一点，EF ⊥ABA 。

3个B 。

4个C ．1个D 。

2个3、如图，在□ABCD 中，DE 平分∠ADC ，BF 平分∠ABC 交AC 于E 、F ，求证：四边形BFDE 为平行四边形。

4、如图，在□ABCD 中，EF 是对角线AC 的垂直平分线交AB 于E ，交CD 于F ，求证：四边形AECF 是菱形。

5、将两块能完全重合的两张等腰直角三角形纸片拼成下列图形：①平行四边形（不包括菱形、矩形、正方形）②矩形③正方形④等边三角形⑤等腰直角三角形 ( ) A ．①③⑤ B．②③⑤ C．①②③ D ．①③④⑤6、下列说法错误的是（）A.一组对边平行且一组对角相等的四边形是平行四边形.B.每组邻边都相等的四边形是菱形.C.对角线互相垂直的平行四边形是正方形.第2题图 A B D E FE F A B D OD.四个角都相等的四边形是矩形.7、如图，以△ABC 的三边为边在BC 的同侧分别作三个等边三角形，即△ABD、 △BCE、△ACF ，请回答下列问题：（1）四边形ADEF 是什么四边形？并说明理由（2）当△ABC 满足什么条件时，四边形ADEF 是菱形？（3）当△ABC 满足什么条件时，以A 、D 、E 、F 为顶点的四边形不存在．8、如图，已知□ABCD 的对角线交点是O ，直线EF 过O 点，且平行于BC ，直线GH 过且平行于AB ，则图中能用字母表示的平行四边形共有( )个.A.10B.14C.16D.189、①若2m －4与3m －1是同一个数的平方根，则m 的值是（） A 、－3 B 、1 C 、－3 或1 D 、－1②若一个正数的平方根是2a －1和－a ＋2，则a ＝________③已知x 的平方根是2a ＋3和1－3a ，y 的立方根为a ，求x+y 的值. 10、已知2a b -=，ab+c +8=0(a ≥b ，c ≥0),那么a+b=11、①直角三角形有一条直角边长为11，另两条边长是连续的自然数，则三角形周长为 ( ) A ．130 B ．131 C ．132 D ．133 ②一个直角三角形的两边长分别为3cm 和4cm,则第三边的长为 12、如图,AB ∥CD,E,F 分别为AC,B D 的中点,若AB=5,CD=3,则EF 的长是( ) A.4 B.3 C.2D.113、如图，已知M 是Rt△ABC 斜边AB 的中点，CD=BM ，DM 与CB 的延长线交于点E 。