微分方程模型习题解答(人口的预测和控制模型)
微分方程模型(人口预测)

2、基本假设
根据《国家人口发展战略研究》报告,当前中国人口的 增长有如下特点:
1)中国正进入老龄化社会,老年人的比重在不断加大; 2)农村与城镇育龄妇女的生育率及出生人口性别比有 着较大的区别; 3)农村人口不断城镇化,根据《国家人口发展战略研究》 报告,估计转化率为百分之一。
人口的增长率取决于出生率、死亡率和不同人群之间的 迁移率。而出生率又取决于育龄妇女的生育率及育龄妇女在 总人口中所占得比例。因此,需要对这些相关数据进行分析。
上述矩阵是可以对角化的,即存在可逆矩阵P,使得
1 b 0 u 0 0
A
1
0
P
1
0
v
0
P
P
1BP
0 1 c 0 0 1 c
这样,就得到
(x1, x2 , x3 )Tn (P1Bn P)( x1, x2 , x3 )T0
然后再对xn进行规一化处理
yn ( y1n , y2n , y3n )T
需要考虑的一个问题:农村分别在1970年和1990年前后经 历了两个生于高峰,而指数拟合只能体现出未来分年龄段走势 的主趋势。
添加一个不断减弱的周期性震荡来描述这种周期性变化。
正弦函数
在某次生育高峰后还会周期性地出现新的生育高峰,而文 化素养的提高和晚婚晚育的政策会削弱这种峰值效应。
城镇男性
1 (t ) 2 (t)
试从中国的实际情况和人口增长的上述特点出发,参考附录2中的相关 数据(也可以搜索相关文献和补充新的数据),建立中国人口增长的数学模 型,并由此对中国人口增长的中短期和长期趋势做出预测;特别要指出你们 模型中的优点与不足之处。
附录1 《国家人口发展战略研究报告》 附录2 人口数据(《中国人口统计年鉴》中的部分数据)及其说明
微分方程模型--人口的预测

由统计数据用线性最小二乘法作参数估计
例:美国人口数据(百万)
t 1860 1870 1880 … 1960 1970 1980 1990 2000 x 31.4 38.6 50.2 … 179.3 204.0 226.5 251.4 281.4
r=0.2557/10年,xm =392.0886
年
1790 1800
Kkt
对x(t)求一阶、两阶导数:
x '(t)
cK 2keKkt (1 CeKkt )2
x(t )
CK 3k 2eKkt (CeKkt (1 CeKkt )3
1)
容易看出,x’(t)>0,即x(t)单调增加。
型的复合来研究便,研大究家若有兴趣可以根据生态系统的特征自
行建立相应的模型。
美丽的大自然
种群的数量本应取离散值,但由于种群数 量一般较大,为建立微分方程模型,可将种群 数量看作连续变量,甚至允许它为可微变量, 由此引起的误差将是十分微小的。
世界人口
§ 5.6 人口的预测
年
1625 1830 1930 1960 1974 1987 1999
人口(亿) 5
10
20 30 40 50 60
中国人口
年
1908 1933 1953 1964 1982 1990 2000
人口(亿) 3 4.7 6 7.2 10.3 11.3 12.95
数学建模人口预测模型正确答案

一、问题提出人口问题是当前世界上人们最关心的问题之一。
认识人口数量的变化规律,作出较准确的预报,是有效控制人口增长的前提。
要求:分别建立并求解两个最基本的人口模型,即:指数增长模型和Logistic 模型,并利用表1给出的近两百年的人口统计数据,画出图形拟合数据,对模型做出检验,最后用它预报2000年的人口。
表1 人口统计数据模型一:指数增长(Malthus )模型: 模型假设:人口(相对)增长率 r 是常数此模型由英国人口学家马尔萨斯(Malthus1766~1834)于1798年提出. [1] 假设:人口增长率r 是常数(或单位时间内人口的增长量与当时的人口成正比).[2] 建立模型: 记时刻t=0时人口数为x 0, 时刻t 的人口为()t x ,由于量大,()t x 可视为连续、可微函数.t 到t t ∆+时间内人口的增量为:()()()t rx tt x t t x =∆-∆+于是()t x 满足微分方程:()⎪⎩⎪⎨⎧==00x x rx d t d x(1)[3] 模型求解: 解微分方程(1)得()rt e x t x 0= (2)表明:∞→t 时,()∞→t x (r>0).[4] 模型的参数估计:要用模型的结果(2)来预报人口,必须对其中的参数r 进行估计,这可以用表1的数据通过拟合得到.通过表中1790-1980的数据拟合得:r=0.307. [5] 模型检验:将x 0=3.9,r=0.307 代入公式(2),求出用指数增长模型预测的1810-1920的人口数,见表2.画图:(根据拟合出的数据和原来数据填写表格)表2 美国实际人口与按指数增长模型计算的人口比较年以后的误差越来越大.(分析原因,该模型的结果说明人口将以指数规律无限增长。
而事实上,随着人口的增加,自然资源、环境条件等因素对人口增长的限制作用越来越显著。
下需要对该模型进行改进,即阻滞增长模型。
)分析原因,该模型的结果说明人口将以指数规律无限增长.而事实上,随着人口的增加,自然资源、环境条件等因素对人口增长的限制作用越来越显著.如果当人口较少时人口的自然增长率可以看作常数的话,那么当人口增加到一定数量以后,这个增长率就要随着人口增加而减少.于是应该对指数增长模型关于人口净增长率是常数的假设进行修改.下面的模型是在修改的模型中著名的一个模型二:Logistic 模型(阻滞增长模型) [1]假设:(a )人口增长率r 为人口()t x 的函数()x r (减函数),最简单假定()0, ,>-=s r sx r x r (线性函数),r 叫做固有增长率.(b )自然资源和环境条件年容纳的最大人口容量m x . [2]建立模型: 当mx x =时,增长率应为0,即()m x r =0,于是mx rs =,代入()sx r x r -=得:()⎪⎪⎭⎫⎝⎛-=m x x r x r 1 (3)将(3)式代入(1)得:模型为: ()⎪⎩⎪⎨⎧=⎪⎪⎭⎫⎝⎛-=001xx x x x r dt dx m (4)[3] 模型的求解: 解方程组(4)得()rt m me x x x t x -⎪⎪⎭⎫ ⎝⎛-+=110 (5)根据方程(4)作出x dtdx~ 曲线图,见图1-1,由该图可看出人口增长率随人口数的变化规律.根据结果(5)作出x~t 曲线,见图1-2,由该图可看出人口数随时间的变化规律.[4] 模型的参数估计:利用表1中1790-1980的数据对r 和x m 拟合得:r=0.2072, x m =464. [5] 模型检验:将r=0.2072, x m =464代入公式(5),求出用指数增长模型预测的1800-1990的人口数,见表3第3、4列.也可将方程(4)离散化,得图1-2 x~t 曲线)())(1()()()1(t x x t x r t x x t x t x m-+=∆+=+ t=0,1,2,… (6) 用公式(6)预测1800-1990的人口数,结果见表3第5、6列.画图:(根据拟合出的数据和原来数据填写表格)表3 美国实际人口与按阻滞增长模型计算的人口比较根据对比可知,第二个模型更好,所以我们用第二个模型来预测。
第二章微分方程模型-22人口问题模型

*** 模型修改
分析表明,以上这些现象的主要原因是 随着人口的增长,自然资源,环境条件等因 素对人口增长的限制作用越来越显著。人口 较少时,人口的自然增长率基本上是常数, 而当人口增加到一定数量以后,这个增长率 就要随着人口的增加而减少。因此,我们将 对指数模型关于净相对增长率是常数的基本 假设进行修改。
我国是世界第一人口大国,地球上每九 个人中就有二个中国人,在20世纪的一段 时间内我国人口的增长速度过快,如下表:
年
1908 1933 1953 1964 1982 1990 2000
人口(亿)3.0 4.7 6.0 7.2 10.3 11.3 12.95
2020年,13.4亿,2013年,13.5亿。有效地 控制人口的增长,不仅是使我国全面进入小 康社会、到21世纪中叶建成富强民主文明的 社会主义国家的需要,而且对于全人类社会 的美好理想来说,也是我们义不容辞的责任。
返回
*** 模型求解 分离变量得
dN
N
1
N Nm
=rdt 即
N
NmdN
Nm
N
=rdt
或
dN dN
N + Nm N =rdt 两边积分得
ln N -ln Nm-N =C1ert
代入边界条件,并整理得
N t=
Nm
1+
模型分析 容易看出
t 时,N t Nm.
陆地,每人只有9.3平方英尺的活动范围。
而到2670年,人口达到 361015亿,只有一个人
站到另一个的肩上了。 因此,Malthus人口模型是不完善的。从根本上 说是不完整的,必须修正。
问题在于:在上述模型中假设r是常数,从 而人口方程是线性常微分方程。这个模型 在群体总数不太大时才合理。而没有考虑 总数增大时,生物群体的各成员之间由于 有限的生存空间,有限的自然资源及食物 等原因,就要进行生存竞争。
数学建模—微分方程之预测模型

面积 B与 t2成正比, dB/dt与 t成正比.
模型建立
b b t1 , t 2 t1 x
b
假设1)
dB dt
假设2)
t 2 t1
B(t2 )
假设3)4)
t2
x
t1
0
x
t1
t2 t
0
2 2 2 bt t t1 2 1 B(t )dt 2 2 2(x )
f1 ( x) c1B(t2 ), f 2 ( x) c2 x(t2 t1 ) c3 x
C( x) f1 ( x) f 2 ( x)
目标函数——总费用
模型建立
2
目标函数——总费用
2 2
c1 t1 c1 t1 c2 t1 x C ( x) c3 x 2 2(x ) x
1 如何预报人口的增长
背景 世界人口增长概况
年 1625 1830 1930 1960 1974 1987 1999 人口(亿) 5 10 20 30 40 50 60 中国人口增长概况 年 1908 1933 1953 1964 1982 1990 1995 2000 人口(亿) 3.0 4.7 6.0 7.2 10.3 11.3 12.0 13.0 研究人口变化规律 控制人口过快增长
阻滞增长模型(Logistic模型)
人口增长到一定数量后,增长率下降的原因: 资源、环境等因素对人口增长的阻滞作用 且阻滞作用随人口数量增加而变大 假设 r是x的减函数
r ( x) r sx (r, s 0)
r s xm
r~固有增长率(x很小时)
xm~人口容量(资源、环境能容纳的最大数量)
应用微分方程求解世界各国人口发展问题

应用微分方程求解世界各国人口发展问题近年来,人口问题成为世界关注的热点之一。
不同国家的人口增长率不同,人口老龄化、人口减少等问题也开始受到世界各国的重视。
但是,应用微分方程求解人口问题的方法似乎比较少见。
本文将探讨如何应用微分方程解决世界各国人口发展问题。
一、人口增长率的微分方程模型首先,我们需要知道人口增长率的微分方程模型是什么。
假设一个国家的人口数量为P,其增长率为r(单位为人/人年),则有:dP/dt = rP其中,dP/dt表示P对t的导数,即人口数量随时间变化的速率。
由于r是为常数,我们可以将其写成:dP/P = rdt对上述式子两边同时求积分,得到:ln(P) = rt + C其中,C为积分常数。
解出P,得到:P = e^(rt+C)由于e^C是一个常数,我们可以将其表示为K,即:P = Ke^(rt)这个式子被称为人口数量的微分方程模型。
通过这个模型,我们可以预测一个国家在未来的某个时间点的人口数量。
二、应用微分方程预测人口数量根据上面的式子,我们可以计算未来某个时间点的人口数量。
例如,我们可以应用这个式子预测中国未来10年的人口数量。
首先,我们需要知道中国目前的人口数量和增长率。
根据联合国的统计数据,中国在2019年的人口数量为13.91亿人,增长率为0.44%。
因此,我们可以将r和P代入上面的式子,得到:P = Ke^(0.0044t)假设我们要预测中国10年后的人口数量,即t=10,则有:P = Ke^(0.044)我们可以通过以下方式计算K值:K = P/e^(rt)将t=0、P=13.91亿代入上面的式子,得到:K = 13.91亿/e^0 = 13.91亿因此,代入上面的式子,我们可以计算出中国未来10年的人口数量为:P = 13.91亿*e^(0.044*10) = 15.92亿通过微分方程模型,我们得出了中国未来10年的人口增长情况。
类似地,我们也可以预测其他国家的人口增长情况。
微分方程竞赛模型(传染病和人口发展模型)(精)

21
③参数的确定 1) 1——根据医学资料和有关数据推导而得。
2) q——由该城市的医疗水平和已知的统计数据分析,求其
统计平均值。
3) l——由经济发达程度和交通状况决定。
4) e1——根据医学研究和调查的有关结果和该城市的疫情发 展状况可得。 5) p——由流入该城市人群的地区分布情况和各其他地区的 疫情决定。
1
随
6
模型3(SIR模型)
假设: (1) 病人治愈后具有终生免疫力 , 成为移出者(Removed), 健康 者、病人和移出者所占人群比例分别为 s(t ), i (t ), r (t ) ; (2) , , 同 SIS 模型.
s( t ) i ( t ) r ( t ) 1 di dr N Ni , N Nsi Ni dt dt
17
2.2 总体假设 1.假设一个SARS康复者不会二度感染,他们已退出传染体系, 因此将其归为“退出者”。
2.不考虑这段时间内的自然出生率和死亡率, 由SARS引起的死 亡人数,归为“退出者”。 3.假设潜伏期为一常数t=5天。 4.根据国家卫生部资料可知处于潜伏期的SARS病人不具有传 染性。
⑥忽略迁移的影响。
11
这些比例系数可以是常数、时间的函数、时间和各类人口的函
数、或分几段取常数。当然,还可以根据需要做其它假设。建
立模型一般是将总人口分为易感者S(susceptible)、患者
I(infective)、恢复者R(removed),再仔细一些的还有潜伏者E,
隔离者Q(quarantinable)、疑似病人P(peradventure)和确诊病人 J等类型。叙述或作出各类人口之间流动的示意图,并根据传染 病建模的一般原理建立起如SIR, SEIR, SEQPIJR等类模型。这 些模型基本思路相同,差异在于人口分类的多少,关键在于参 数的确定。例如最简单的SIR模型为
人口控制与预测模型

模型分析:
在稳定的社会环境下,死亡率 、生育模式、女性比例、
婴儿存活率是可以假设为不变的,故 A(t) A, B(t) B
为常数矩阵.从而,
x(t 1) (A (t).B)x(t).............................................(3.14) 只要总生育率 (t) 确定下来,
i岁人口中死亡数与基数之比:
di (t)
xi (t)
xi1 (t xi (t)
1)
即:xi1 (t 1) (1 di (t)) xi (t), i i,2,..., m 1;t 0,1,2,...
4.设第t 年i岁女性的生育率:即每位女性平均生育婴儿 数为 bi (t) [i1,i2 ] 为生育区间. ki (t) 为第t年i岁人口的女性比
可见, (t) 表示每位妇女一生中平均生育的婴儿数,
称之为总和生育率.它反映了人口变化的基本因素.
模型建立: 根据上面的假设
x1
(t
1)
(1
d
0
(t
))
x0
(t
)
(1 d0 (t))(1 d00 (t)) f (t)
i2
(1 d0 (t))(1 d00 (t)) bi (t)ki (t)xi (t) i i1
为了全面系统地反映一个时期内人口数量的状况,
令
x(t) [x1 (t), x2 (t),..., xm (t)]/
0
1 d1 (t)
A(t) 0
.....
0
0 0 1 d2 (t) ..... 0
0... 0
微分方程数值解--案例(中国人口增长预测)

存在无穷多个解。所有满足上式的格式统称为 阶龙格 存在无穷多个解。所有满足上式的格式统称为2阶龙格 - 库 无穷多个解 塔格式。注意到, 塔格式。注意到,p = 1, λ 1 = λ 2 = 1 就是改进的欧拉法。 就是改进的欧拉法。
2
Q: 为获得更高的精度,应该如何进一步推广? 为获得更高的精度,应该如何进一步推广?
h2 y ( x i + 1 ) = y ( x i ) + h y ′( x i ) + y ′′( x i ) + O ( h 3 ) 2
3 则必须有: 要求 Ri = y( xi +1 ) − yi +1 = O( h ) ,则必须有:
1 λ1 + λ 2 = 1 , λ 2 p = 2
这里有 3 个未知 个方程。 数, 2 个方程。
truncation error */。 。
若某算法的局部截断误差为O(hp+1),则称该算法有 ,则称该算法有p 定义 若某算法的局部截断误差为 Ri 的主项 阶精度。 阶精度。 /* leading term */ 欧拉法的局部截断误差: 欧拉法的局部截断误差:
Ri = y( xi +1 ) − yi +1 = [ y( xi ) + hy′( xi ) + h2 y′′( xi ) + O(h3 )]− [ yi + hf ( xi , yi )]
微分方程及数学建模
一、常微分方程数值解法
考虑一阶常微分方程的初值问题 考虑一阶常微分方程的初值问题 /* Initial-Value Problem */: 一阶常微分方程的
dy = f ( x, y) dx y(a ) = y0 x ∈ [a , b ]
数学建模 人口增长详解
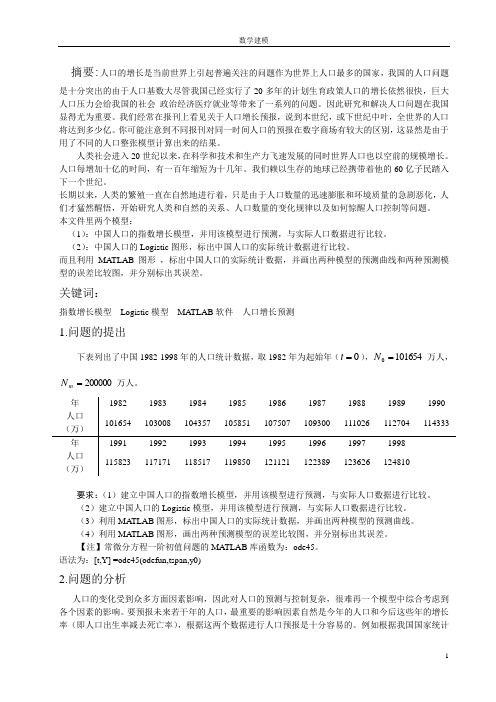
摘要:人口的增长是当前世界上引起普遍关注的问题作为世界上人口最多的国家,我国的人口问题是十分突出的由于人口基数大尽管我国已经实行了20多年的计划生育政策人口的增长依然很快,巨大人口压力会给我国的社会 政治经济医疗就业等带来了一系列的问题。
因此研究和解决人口问题在我国显得尤为重要。
我们经常在报刊上看见关于人口增长预报,说到本世纪,或下世纪中叶,全世界的人口将达到多少亿。
你可能注意到不同报刊对同一时间人口的预报在数字商场有较大的区别,这显然是由于用了不同的人口整张模型计算出来的结果。
人类社会进入20世纪以来,在科学和技术和生产力飞速发展的同时世界人口也以空前的规模增长。
人口每增加十亿的时间,有一百年缩短为十几年。
我们赖以生存的地球已经携带着他的60亿子民踏入下一个世纪。
长期以来,人类的繁殖一直在自然地进行着,只是由于人口数量的迅速膨胀和环境质量的急剧恶化,人们才猛然醒悟,开始研究人类和自然的关系、人口数量的变化规律以及如何惊醒人口控制等问题。
本文件里两个模型: (1):中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2):中国人口的Logistic 图形,标出中国人口的实际统计数据进行比较。
而且利用MATLAB 图形 ,标出中国人口的实际统计数据,并画出两种模型的预测曲线和两种预测模型的误差比较图,并分别标出其误差。
关键词:指数增长模型 Logistic 模型 MATLAB 软件 人口增长预测1.问题的提出下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(0=t ),1016540=N 万人,200000=m N 万人。
要求:(1)建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic 模型,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MA TLAB 图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
一阶常微分方程模型—人口模型与预测
辽宁工程技术大学数学建模课程成绩评定表一阶常微分方程模型—人口模型与预测一.摘要:二.模型的背景问题描述三.模型假设四.分析与建立模型下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(0=t ),1016540=N 万人,200000=m N 万人.要求:(1)建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic 模型,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MATLAB 图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
(4)利用MATLAB 图形,画出两种预测模型的误差比较图,并分别标出其误差。
模型一:指数增长模型(马尔萨斯(Malthus )模型)假设:人口净增长率r 是一常数符号:x(t )t --时刻时的人口,可微函数00x t --=时的人口 则()()()x t t x t r x t t+∆-=∆于是x(t)满足如下微分方程:00()dxrxdt x x ⎧=⎪⎨⎪=⎩解为:0()rt x t x e = 模型二:Logistic 模型人口净增长率应当与人口数量有关,即: r =r (x )从而有:00()()dxr x xdt x x ⎧=⎪⎨⎪=⎩对马尔萨斯模型引入一次项(竞争项),令 r (x )=r -ax 此时得到微分方程:()dxr ax x dt=-或(1)m dx x r x dt x =- 可改写成:()m mdx rx x x dt x =- 分离变量:11m dx rdt x x x ⎛⎫+=⎪-⎝⎭两边积分并整理得: 1mrtx x Ce-=+ 令x (0)=0x ,求得: 0001m mx x x C x x -==- 满足初始条件x (0)=0x 的解为: 011()()mrtm x x t xe x -=+-易见: lim ()m t x t x →+∞=五.模型的求解1、运行结果p = 0.0131 11。
数学建模 人口增长详解

摘要:人口的增长是当前世界上引起普遍关注的问题作为世界上人口最多的国家,我国的人口问题是十分突出的由于人口基数大尽管我国已经实行了20多年的计划生育政策人口的增长依然很快,巨大人口压力会给我国的社会 政治经济医疗就业等带来了一系列的问题。
因此研究和解决人口问题在我国显得尤为重要。
我们经常在报刊上看见关于人口增长预报,说到本世纪,或下世纪中叶,全世界的人口将达到多少亿。
你可能注意到不同报刊对同一时间人口的预报在数字商场有较大的区别,这显然是由于用了不同的人口整张模型计算出来的结果。
人类社会进入20世纪以来,在科学和技术和生产力飞速发展的同时世界人口也以空前的规模增长。
人口每增加十亿的时间,有一百年缩短为十几年。
我们赖以生存的地球已经携带着他的60亿子民踏入下一个世纪。
长期以来,人类的繁殖一直在自然地进行着,只是由于人口数量的迅速膨胀和环境质量的急剧恶化,人们才猛然醒悟,开始研究人类和自然的关系、人口数量的变化规律以及如何惊醒人口控制等问题。
本文件里两个模型: (1):中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2):中国人口的Logistic 图形,标出中国人口的实际统计数据进行比较。
而且利用MATLAB 图形 ,标出中国人口的实际统计数据,并画出两种模型的预测曲线和两种预测模型的误差比较图,并分别标出其误差。
关键词:指数增长模型 Logistic 模型 MATLAB 软件 人口增长预测1.问题的提出下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(0=t ),1016540=N 万人,200000=m N 万人。
要求:(1)建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic 模型,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MA TLAB 图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
《数学建模》习题及参考答案 第五章 微分方程模型

第五章部分习题1. 对于5.1节传染病的SIR 模型,证明:(1)若σ/10>s ,则()t i 先增加,在σ/1=s 处最大,然后减少并趋于零;()t s 单调减少至∞s 。
(2)若σ/10>s ,则()t i 单调减少并趋于零,()t s 单调减少至∞s 。
9. 在5.6节人口的预测和控制模型中,总和生育率()t β和生育模式()t r h ,是两种控制人口增长的手段,试说明我国目前的人口政策,如提倡一对夫妇只生一个孩子、晚婚晚育,及生育第2胎的一些规定,可以怎样通过这两种手段加以实施。
*16. 建立铅球掷远模型,不考虑阻力,设铅球初速度为v ,出手高度为h 出手角度为∂(与地面夹角),建立投掷距离与∂,,h v 的关系式,并在h v ,一定的条件下求最佳出手角度。
参考答案1. SIR 模型(14)式可写作().,1si dt di s i dt di λσμ-=-=由后一方程知()t s dtds ,0<单调减少。
1) 若σ10>s ,当01s s <<σ时,()t i dt di ,0>增加;当σ1=s 时,()t i dt di ,0=达到最大值m i ;当σ1<s 时,()t i dt di ,0<减少且()()式180=∞i 2) 若σ10<s ,()t i dt di ,0<单调减少至零 9. 一对夫妻只生一个孩子,即总和生育率()1=t β;晚婚晚育相当于生育模式()r h 中(5。
6节(13)式)使1r 和c r 增大;生育第2胎一些规定可相当于()t β略高于1,且()r h 曲线(5。
6节图19)扁平一些(规定生2胎要间隔多少年)*16. 在图中坐标下铅球运动方程为()()()().sin 0,cos 0,0,00,,0ααv y v x h y x g yx ====-== 解出()t x ,()t y 后,可以求得铅球掷远为,cos 2sin cos sin 2/12222ααααv g h g v g v R ⎪⎪⎭⎫ ⎝⎛++=这个关系还可表为()ααtan cos 2222R h v g R +=由此计算0*=ααd dR,得最佳出手角度()gh v v +=-21*2sin α,和最佳成绩gh v g v R 22*+=设m h 5.1=,s m v /10=,则0*4.41≈α,m R 4.11*=。
微分方程模型习题解答(人口的预测和控制模型)

在人口的预测和控制模型中,总和生育率β(t)和生育模式h(r,t)两种控制人口增长的手段。
试说明我国目前的人口政策,如提倡一对夫妻只生一个孩子、晚婚晚育,及生育第2 胎的一些规定,可以怎样通过这两种手段加以实施。
一、问题分析目前,我国人口总数占世界人口总数的1/5,居世界第一。
虽然在二十世纪八十年代开始就已经开始控制人口,但现在人口的增长仍然很快,人口老年化问题也越来越严重,所以现在开始提倡晚婚晚育,一对夫妻只能生一个孩子以及定下了一些关于生第二胎的政策。
所以在此我们可以考虑用微分方程中生育率和生育模式来求解问题。
二、模型的假设⑴时刻t 年龄小于r 的人口即人口分布函数记作F(r,t);⑵婴儿的出生率记为p( 0, t)= f( t);⑶时刻t 年龄r 的人的死亡率记为μ(r,t)⑷μ(r,t) p(r,t)dr表示时刻t 年龄在[r, r +dr] 内单位时间死亡人数;(r)是人口调查得到的已知函数;⑸p⑹婴儿的出生率记为f(t );三模型的建立与求解由问题假设我们可以得到各个年龄的人口数,即人口分布函数为:F(r,t)=∫r 0p(s,t)ds 由于在社会安定的局面下和不太长的时间里, 死亡率大致与时间无关, 于是可近似的假设μ(r,t)= μ(r)因为 p0(r)与μ(r)可由人口统计数据得到, 所以 ) , μ(r,t)可由μ(r,0)粗略估计,为了预测和控制人口的发展状况, 我们需要关注和可以用作控制的就是婴儿的出生率f(t)了,下面我们就来讨论f(t) 。
记女性的性别函数为k(r,t)即时刻 t 年龄在 [r, r + dr] 的女性人数为k(r,t)μ(r,t)dr 将这些女性在单位时间内平均每人的生育数记作b(r,t)则育龄区间为[r1,r2]则:f(t)= ∫21rrb(r,t)k(r,t)p(r,t)dr 再将 b( r,t) 定义为b(r,t)=β(t)h(r,t)其中h(r,t)满足∫21rr h(r ,t)dr=1于是就有β(t)= ∫21rr B(r,t)drf(t)=β(t) ∫21rr b(r,t)k(r,t)dr可以看出β(t)就是时刻 t 单位时间内平均每个育龄女性的生育率。
常微分方程Ch2.1-2

y 为整体变量的函数。 x
常微分方程
10/12
解法
y u (1) 作变量变换 x
即
y=ux
dy du x u (2)对两边关于 x 求导 dx dx
(3)将上式代入原方程,得 整理
du 1 ( g (u ) u ) ……….(2.3) 变量可分离方程 dx x
1/12
求下列方程的解
dy 1. y ln x dx
2. y ' y ln y
3. (1 x) ydx (1 y) xdy 0
dy 4. y ( y 1), y (0) 1 dx
常微分方程
2/12
1.人口预测模型
马尔萨斯(Malthus,1766-1834)是英国的一名神父,也是 著名的人口学家,他在调查英国一百多年以来的人口统计 数据的基础上,假设人口增长率是常数,并由此建立了著 名的人口指数增长模型。 N(t)
常微分方程
9/12
(1) 齐次方程/Homogeneous Equation/
形式:
dy y g( ) dx x
Hale Waihona Puke g (u)为 u 的连续函数
特点: 一般方程的右端函数 f (x,y) 是x,y 的零次齐次式。
即
y f ( x, y ) g ( ) x
ky y 0 f (kx , kg ) g ( ) k g ( ) f ( x, y ) k 0 kx x
6/12
解: (1) 设t 时刻氨氮的浓度为N(t),日降解系数为k,则氨 氮浓度随时间变化所满足的微分方程如下:
dN k N dt N (0) N 0
2微分方程模型(人口模型)

dx BDI E dt x(t 0 ) x0
以下介绍的两个人口模型都是根据这个原理建立的.
(5.11)
微分方程模型实例1——人口模型
5.3.1.1 马尔萨斯(Malthus)模型
考虑一个国家或地区的人口总数随时间变化的情况,记x(t) 为t时刻该国家或地区的人口总数,对一个国家而言,迁 入和迁出人数相对很小,故略去迁移对人口变化的影响, 即人口变化仅与出生率和死亡率有关。
缺点
理论上很好,实用性不强
预报时假设固有人口增长率 r 以及最大人口容量 K为
定值。
原因
实际上这两个参数(特别是 K)很难确定,而且会 随着社会发展情况变化而变化。 前面图中曲线末端分叉就是由于这个原因。
微分方程模型实例1——人口模型
Logistic模型预测美国人口误差分析
微分方程模型实例1——人口模型
洛杰斯蒂模型 预测值/亿
10.1541 10.2564 10.3594 10.4631 10.5673 10.6721 10.7775 10.8835 10.9901 12.0871 13.2357 14.4276 15.6529 16.9009 18.1595
实际统计值 预测值/亿
10.1541 10.2495 10.3475 10.4532 10.5721 10.7240 10.8978 11.0676 11.3368
(5.15)
微分方程模型实例1——人口模型
模型求解 模型分析
ax0 x(t ) bx0 (a bx0 )e a (t t0 )
d 2x (a 2bx)(a bx) x 2 dt
(i)对任意 t t 0 ,有 x(t ) 0 ,且 tlim x(t ) b 。 (ii)当 0 x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在人口的预测和控制模型中,总和生育率β(t)和生育模式h(r,t)两种控制人口增长的手段。
试说明我国目前的人口政策,如提倡一对夫妻只生一个孩子、晚婚晚育,及生育第2 胎的一些规定,可以怎样通过这两种手段加以实施。
一、问题分析
目前,我国人口总数占世界人口总数的1/5,居世界第一。
虽然在二十世纪八十年代开始就已经开始控制人口,但现在人口的增长仍然很快,人口老年化问题也越来越严重,所以现在开始提倡晚婚晚育,一对夫妻只能生一个孩子以及定下了一些关于生第二胎的政策。
所以在此我们可以考虑用微分方程中生育率和生育模式来求解问题。
二、模型的假设
⑴时刻t 年龄小于r 的人口即人口分布函数记作F(r,t);
⑵婴儿的出生率记为p( 0, t)= f( t);
⑶时刻t 年龄r 的人的死亡率记为μ(r,t)
⑷μ(r,t) p(r,t)dr表示时刻t 年龄在[r, r +dr] 内单位时间死亡人数;
(r)是人口调查得到的已知函数;
⑸p
⑹婴儿的出生率记为f(t );
三模型的建立与求解
由问题假设我们可以得到各个年龄的人口数,即人口分布函数为:
F(r,t)=∫r 0
p(s,t)ds
由于在社会安定的局面下和不太长的时间里, 死亡率大致与时间无关, 于是
可近似的假设μ(r,t)= μ(r)
因为 p0(r)与μ(r)可由人口统计数据得到, 所以 ) , μ(r,t)可由μ(r,0)粗略估计,为了预测和控制人口的发展状况, 我们需要关注和可以用作控制的就是婴儿的出生率f(t)了,下面我们就来讨论f(t) 。
记女性的性别函数为k(r,t)即时刻 t 年龄在 [r, r + dr] 的女性人数为k(r,t)μ(r,t)dr 将这些女性在单位时间内平均每人的生育数记作b(r,t)则育龄区间为[r1,r2]则:
f(t)= ∫21r
r b(r,t)k(r,t)p(r,t)dr
再将 b( r,t) 定义为
b(r,t)=β(t)h(r,t)
其中h(r,t)满足
∫21r
r h(r ,t)dr=1
于是就有
β(t)= ∫21r
r B(r,t)dr
f(t)=β(t) ∫21r
r b(r,t)k(r,t)dr
可以看出β(t)就是时刻 t 单位时间内平均每个育龄女性的生育率。
如果所有的育龄女性在她的育龄期所及的时刻
都保持这个生育数,那么β(t)即为生育总和。
从上式我们得到h(r ,t)是年龄为 r 女性的生育加权因子,即生育模式。
在稳定环境下可近似地认为它与 t 无关,即h(r ,t)= h(r),h(r)表示了哪些年龄生育率高,哪些低。
所以 r 取得一定的值的时候,生育率能达到最高。
由人口统计资料可以知道当前实际的h(r ,t)。
作理论分析时常采用的h(r)的一种形式是借用概率论中的F 分布: h(r)=
)(F )(1
11αθθa r r a e r r ---r>r 1
并取θ =2,α=2n 这时有
r e =r1+n-2
即r1意味着晚婚,而增加 n 意味着晚育。
所以生育率β(t)和生育模式h(r,t)是可以控制人口发展过程的两种手段. β(t)可以控制生育的多少,而h(r,t)可以控制生育的早晚与疏密。
我国的计划生育正是通过这两种手段实施的。
所以一对夫妻只生一个孩子,即总和生育率为 1, 所以 β(t)=1晚婚晚育相当于生育模式h(r)中使r1和r e 增大; 生
育第二胎的一些规定可相当于总和生育率略高于1即β(t) 略高于1,且h(r)曲线扁平一些,因为规定了生二胎要间隔多 少年。
四模型的评注
在上面的模型中密度函数p(r,t)或分布函数F(r,t)固然是人口发展过程中最完整的描述,但是使用起来不是很方便,在人口统计学中常用一些所谓人口指数来简明扼要地表示一个国家或地区的人口特征。
不过根据上面的生育率和生育模式我们还是可以很方便的预测和控制人口的增长,并针对我国的人口情况做一些相关的计划生育策略。
使得人口能够更优更好的发展。
