2017-2018学年中考数学压轴题分类练习动点面积专题(无答案)

合集下载

中考数学压轴题：由动点引出的几种面积问题

中考数学压轴题：由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题，而因动点产生的面积问题是这类题目考查的重点。

解这类题目要掌握几个基本图形及思路，而后“以静制动”、“转化求解”。

即把动态问题变为静态问题，变为我们所熟知的模型来解。

基本方法：铅锤法！即利用“铅垂高、水平宽”求三角形面积.类型一、一次函数由动点问题引出的面积问题【分析】（1）Rt△AOH中利用勾股定理即可求得菱形的边长；（2）根据（1）即可求得OC的长，则C的坐标即可求得，利用待定系数法即可求得直线AC的解析式；（3）根据S△ABC=S△AMB+SBMC求得M到直线BC的距离为h，然后分成P在AM上和在MC上两种情况讨论，利用三角形的面积公式求解．【点评】本题考查了待定系数法求一次函数的解析式以及菱形的性质，根据三角形的面积关系求得M到直线BC的距离h是关键．类型二、二次函数由动点问题引出的面积问题【分析】（2）过点P作PE∥y轴交x轴于点E，交直线AC于点F，过点C作CQ∥y轴交x轴于点Q，设点P的坐标为（x，﹣x^2﹣2x+3）（﹣2＜x＜1），则点E的坐标为（x，0），点F的坐标为（x，﹣x+1），进而可得出PF的值，由点C的坐标可得出点Q 的坐标，进而可得出AQ的值，利用三角形的面积公式可得出S△APC＝﹣1.5x^2﹣1.5x+3，再利用二次函数的性质，即可解决最值问题；【点评】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图像上点的坐标特征、一次函数图像上点的坐标特征、二次函数的性质、三角形的面积以及周长，解题的关键是：（1）根据点的坐标，利用待定系数法求出抛物线及直线AC的函数关系式；（2）利用三角形的面积公式找出S△APC＝﹣1.5x^2﹣1.5x+3;（3）利用二次函数图像的对称性结合两点之间线段最短找出点M的位置．类型三、利用相似三角形求解由动点问题引出的面积问题【分析】（1）利用待定系数法即可；（2）①分别用t表示PE、PQ、EQ，用△PQE∽△QNC表示NC及QN，列出矩形PQNM面积与t的函数关系式问题可解；②由①利用线段中点坐标分别等于两个端点横纵坐标平均分的数量关系，表示点M坐标，分别讨论M、N、Q在抛物线上时的情况，并分别求出t值．【点评】本题是代数几何综合题，考查了二次函数、一次函数、三角形相似和矩形的有关性质，解答时应注意数形结合和分类讨论的数学思想．类型四、利用转化思想解决由动点问题引出的面积问题【分析】（1）根据待定系数法，可得函数解析式，根据自变量与函数值的对应关系，可得答案；（2）根据勾股定理，可得BC的长，根据等角的正切值相等，可得HO的长，根据待定系数法，可得BE的解析式，根据解方程组，可得E点坐标；（3）由题意△PMN是等腰直角三角形，得PM=PN=1，设M（a，a^2+3a﹣4）则N（a+1，a^2+3a+1）或（a+1，a^2+3a﹣5），代入抛物线的解析式即可求解．【点评】本题考查二次函数的有关知识、一次函数、直角三角形等知识，掌握两个函数的交点问题转化为方程组的解的问题是解题的关键，还要记住一个结论斜边为定值时直角边相等时面积最大．。

2018年人教版中考压轴题汇编《因动点产生的面积问题》含答案

1.6 因动点产生的面积问题例1 2017年河南省中考第23题如图1，边长为8的正方形ABCD的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上A、C两点间的一个动点（含端点），过点P作PF⊥BC于点F．点D、E 的坐标分别为(0, 6)、(－4, 0)，联结PD、PE、DE．（1）直接写出抛物线的解析式；（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值．进而猜想：对于任意一点P，PD与PF的差为定值．请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点”的坐标．图1 备用图例2 2017年昆明市中考第23题如图1，在平面直角坐标系中，抛物线y ＝ax 2＋bx －3（a ≠0）与x 轴交于A (－2, 0)、B (4, 0)两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 从点A 出发，在线段AB 上以每秒3个单位长度的速度向点B 运动，同时点Q 从点B 出发，在线段BC 上以每秒1个单位长度的速度向点C 运动．其中一个点到达终点时，另一个点也停止运动．当△PBQ 存在时，求运动多少秒时△PBQ 的面积最大，最大面积是多少？（3）当△PBQ 的面积最大时，在BC 下方的抛物线上存在点K ，使S △CBK ∶S △PBQ ＝5∶2，求点K 的坐标．图1例3 2017年苏州市中考第29题如图1，已知抛物线212y x bx c =++（b 、c 是常数，且c ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴的负半轴交于点C ，点A 的坐标为(－1,0)．（1）b＝______，点B的横坐标为_______（上述结果均用含c的代数式表示）；（2）连结BC，过点A作直线AE//BC，与抛物线交于点E．点D是x轴上一点，坐标为(2,0)，当C、D、E三点在同一直线上时，求抛物线的解析式；（3）在（2）的条件下，点P是x轴下方的抛物线上的一动点，连结PB、PC．设△PBC 的面积为S．①求S的取值范围；②若△PBC的面积S为正整数，则这样的△PBC共有_____个．图1例4 2017年菏泽市中考第21题如图1，在平面直角坐标系中放置一直角三角板，其顶点为A(0, 1)、B(2, 0)、O(0, 0)，将此三角板绕原点O逆时针旋转90°，得到三角形A′B′O．（1）一抛物线经过点A′、B′、B，求该抛物线的解析式；（2）设点P是第一象限内抛物线上的一个动点，是否存在点P，使四边形PB′A′B的面积是△A′B′O面积的4倍？若存在，请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，试指出四边形PB′A′B是哪种形状的四边形？并写出它的两条性质．图1例 5 2017年河南省中考第23题如图1，在平面直角坐标系中，直线112y x=+与抛物线y＝ax2＋bx－3交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上的一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．（1）求a、b及sin∠ACP的值；（2）设点P的横坐标为m．①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连结PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积比为9∶10？若存在，直接写出m的值；若不存在，请说明理由．图1例 6 2017年南通市中考第28题如图1，直线l经过点A(1，0)，且与双曲线myx=(x＞0)交于点B(2，1)．过点(,1)P p p-(p＞1)作x轴的平行线分别交曲线myx=(x＞0)和myx=-(x＜0)于M、N两点．（1）求m的值及直线l的解析式；（2）若点P在直线y＝2上，求证：△PMB∽△PNA；（3）是否存在实数p，使得S△AMN＝4S△AMP？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．图1例7 2017年广州市中考第25题如图1，四边形OABC是矩形，点A、C的坐标分别为(3,0)，(0,1)．点D是线段BC上的动点（与端点B、C不重合），过点D作直线12y x b=-+交折线OAB于点E．（1）记△ODE的面积为S，求S与b的函数关系式；（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．图11.6 因动点产生的面积问题答案例1 2017年河南省中考第23题如图1，边长为8的正方形ABCD的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上A、C两点间的一个动点（含端点），过点P作PF⊥BC于点F．点D、E 的坐标分别为(0, 6)、(－4, 0)，联结PD、PE、DE．（1）直接写出抛物线的解析式；（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值．进而猜想：对于任意一点P，PD与PF的差为定值．请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE 的周长最小的点P 也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE 周长最小时“好点”的坐标．图1 备用图动感体验请打开几何画板文件名“15河南23”，拖动点P 在A 、C 两点间的抛物线上运动，观察S 随P 变化的图像，可以体验到，“使△PDE 的面积为整数” 的点P 共有11个．思路点拨1．第（2）题通过计算进行说理．设点P 的坐标，用两点间的距离公式表示PD 、PF 的长．2．第（3）题用第（2）题的结论，把△PDE 的周长最小值转化为求PE ＋PF 的最小值．满分解答（1）抛物线的解析式为2188y x =-+．（2）小明的判断正确，对于任意一点P ，PD －PF ＝2．说理如下：设点P 的坐标为21(,8)8x x -+，那么PF ＝y F －y P ＝218x ．而FD 2＝22222222111+(86)+(2)(2)888x x x x x -+-=-=+，所以FD ＝2128x +．因此PD －PF ＝2为定值．（3）“好点”共有11个．在△PDE 中，DE 为定值，因此周长的最小值取决于FD ＋PE 的最小值．而PD ＋PE ＝(PF ＋2)＋PE ＝(PF ＋PE )＋2，因此当P 、E 、F 三点共线时，△PDE 的周长最小（如图2）．此时EF ⊥x 轴，点P 的横坐标为－4．所以△PDE 周长最小时，“好点”P 的坐标为(－4, 6)．图2 图3考点伸展第（3）题的11个“好点”是这样求的：如图3，联结OP ，那么S △PDE ＝S △POD ＋S △POE －S △DOE ．因为S △POD ＝1()32P OD x x ⋅-=-，S △POE ＝2111624P OE y x ⋅=-+，S △DOE ＝12，所以 S △PDE ＝21316124x x --+-＝21344x x --+＝21(6)134x -++．因此S 是x 的二次函数，抛物线的开口向下，对称轴为直线x ＝－6．如图4，当－8≤x ≤0时，4≤S ≤13．所以面积的值为整数的个数为10．当S ＝12时，方程21(6)13124x -++=的两个解－8, －4都在－8≤x ≤0范围内．所以“使△PDE 的面积为整数” 的 “好点”P 共有11个．图4例2 2017年昆明市中考第23题如图1，在平面直角坐标系中，抛物线y ＝ax 2＋bx －3（a ≠0）与x 轴交于A (－2, 0)、B (4, 0)两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 从点A 出发，在线段AB 上以每秒3个单位长度的速度向点B 运动，同时点Q 从点B 出发，在线段BC 上以每秒1个单位长度的速度向点C 运动．其中一个点到达终点时，另一个点也停止运动．当△PBQ 存在时，求运动多少秒时△PBQ 的面积最大，最大面积是多少？（3）当△PBQ 的面积最大时，在BC 下方的抛物线上存在点K ，使S △CBK ∶S △PBQ ＝5∶2，求点K 的坐标．图1动感体验请打开几何画板文件名“14昆明23”，拖动点P 从A 向B 运动，可以体验到，当P 运动到AB 的中点时，△PBQ 的面积最大．双击按钮“△PBQ 面积最大”，再拖动点K 在BC 下方的抛物线上运动，观察度量值，可以体验到，有两个时刻面积比为2.5．思路点拨1．△PBQ 的面积可以表示为t 的二次函数，求二次函数的最小值．2．△PBQ 与△PBC 是同高三角形，△PBC 与△CBK 是同底三角形，把△CBK 与△PBQ 的比转化为△CBK 与△PBC 的比．满分解答（1）因为抛物线与x 轴交于A (－2, 0)、B (4, 0)两点，所以y ＝a(x ＋2)(x －4)．所以－8a ＝－3．解得38a =．所以抛物线的解析式为3(2)(4)8y x x =+-233384x x =--．（2）如图2，过点Q 作QH ⊥x 轴，垂足为H ．在Rt △BCO 中，OB ＝4，OC ＝3，所以BC ＝5，sin B ＝35．在Rt △BQH 中，BQ ＝t ，所以QH ＝BQ sin B ＝35t ．所以S △PBQ ＝211399(63)(1)2251010BP QH t t t ⋅=-⨯=--+．因为0≤t ≤2，所以当t ＝1时，△PBQ 的面积最大，最大面积是910。

2018年中考数学压轴题100题精选

2018年中考数学压轴题100题精选【001】如图，已知抛物线2(1)y a x =-+a ≠0）经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．【002】如图16，在Rt△ABC中，∠C=90°，AC = 3，AB = 5．点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BC-CP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．（1）当t = 2时，AP = ，点Q到AC的距离是；（2）在点P从C向A运动的过程中，求△APQ的面积S与t的函数关系式；（不必写出t的取值范围）（3）在点E从B向C运动的过程中，四边形QBED能否成为直角梯形？若能，求t（4）当DE经过点C 时，请直接．．写出t图16【003】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标，并求出抛物线的解析式；(2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E，①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。

2017-2018学年中考数学题型训练卷：数字及图形规律问题(无答案)

数字及图形规律问题1. 如图，将1若规定（a ，b ）表示第a 排第b 列的数，则（8，2）与（2014，2014）表示的两个数的积是（）A ．B ．C ．D ． 12. 下面是按照一定规律排列的一列数：第 1个数：11122-⎛⎫-+ ⎪⎝⎭；第 2个数：()()2311111113234⎡⎤⎡⎤---⎛⎫-+⨯+⨯+⎢⎥⎢⎥ ⎪⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦；第 3个数：()()()()234511111111111423456⎡⎤⎡⎤⎡⎤⎡⎤-----⎛⎫-+⨯+⨯+⨯+⨯+⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎝⎭⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦； …依此规律，在第10个数、第11个数、第12个数、第13个数中，最大的数是（）A ．第10个数B ．第11个数C ．第12个数D ．第13个数3. 观察下列各式及其展开式：222()2a b a ab b +=++；33223()33a b a a b ab b +=+++；4432234()464a b a a b a b ab b +=++++；554322345()510105a b a a b a b a b ab b +=+++++；…请你猜想10()a b +的展开式第三项的系数是（）A ．36B ．45C ．55D ．66[来源:学&科&网]4. 把所有正奇数从小到大排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…，现有等式A m=（i，j）表示正奇数m是第i组第j个数（从左往右数），如A7=（2，3），则A2015=（）[来源:学§科§网]A．（31，50）B．（32，47）C．（33，46）D．（34，42）5.下列图形是将正三角形按一定规律排列，则第4个图形中所有正三角形的个数有（）A．160 B．161 C．162 D．1636. 如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（）A．25B．33C．34D．507. 如图，已知AB=A1B，A1B1=A1A2，A2B2=A2A3，A3B3=A3A4…，若∠A=70°，则∠A n的度数为（）A．702nB．1702n+C．1702n-D．2702n+8. 如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…，按照此规律继续下去，则S9的值为（）A ．61()2 B ．71()2 C ．6 D ．7 9. 如图，用相同的小正方形按照某种规律进行摆放，则第8个图形中小正方形的个数是（）A ．71B ．78C ．85D ．8910. 将一些相同的“○”按如图所示的规律依次摆放，观察每个“龟图”中的“○”的个数，若第n 个“龟图”中有245个“○”，则n =（）A ．14B ．15C ．16D ．1711. 在如图所示的平面直角坐标系中，△OA 1B 1是边长为2的等边三角形，作△B 2A 2B 1与△OA 1B 1关于点B 1成中心对称，再作△B 2A 3B 3与△B 2A 2B 1关于点B 2成中心对称，如此作下去，则△B 2n A 2n +1B 2n +1（n 是正整数）的顶点A 2n +1的坐标是（）A ．（4n ﹣1）B ．（2n ﹣1）C ．（4n +1）D ．（2n +1）12. 在平面直角坐标系中，正方形A 1B 1C 1D 1、D 1E 1E 2B 2、A 2B 2C 2D 2、D 2E 3E 4B 3、A 3B 3C 3D 3…按如图所示的方式放置，其中点B 1在y 轴上，点C 1、E 1、E 2、C 2、E 3、E 4、C 3…在x 轴上，已知正方形A 1B 1C 1D 1的边长为1，∠B 1C 1O =60°，B 1C 1∥B 2C 2∥B 3C 3…则正方形A 2015B 2015C 2015D 2015的边长是（）A ．201421）（ B ．201521）（ C ．201533）（ D ．201433）（13. 如图，在矩形ABCD 中，已知AB =4，BC =3，矩形在直线l 上绕其右下角的顶点B 向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2015次后，顶点A 在整个旋转过程中所经过的路程之和是（）A ．2015πB ．3019.5πC ．3018πD ．3024π14. 如图，将△ABC 沿着过AB 中点D 的直线折叠，使点A 落在BC 边上的A 2处，称为第1次操作，折痕DE 到BC 的距离记为h 1；还原纸片后，再将△ADE 沿着过AD 中点D 1的直线折叠，使点A 落在DE 边上的A 2处，称为第2次操作，折痕D 1E 1到BC 的距离记为h 2；按上述方法不断操作下去…，经过第2015次操作后得到的折痕D 2014E 2014到BC 的距离记为h 2015，到BC 的距离记为h 2015．若h 1=1，则h 2015的值为（）15. 在求2345678133333333++++++++的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S =2345678133333333++++++++①，然后在①式的两边都乘以3，得：3S =23456789333333333++++++++②，②﹣①得，3S ﹣S =931-，即2S =931-，所以S =9312-．得出答案后，爱动脑筋的张红想：如果把“3”换成字母m （m ≠0且m ≠1），能否求出23420161...m m m m m ++++++的值？如能求出，其正确答案是．16. 我国南宋数学家杨辉用三角形解释二项和的乘方规律，称之为“杨辉三角”．这个三角形给出了()n a b +（n =1，2，3，4…）的展开式的系数规律（按a 的次数由大到小的顺序）：请依据上述规律，写出20162()x x-展开式中含2014x 项的系数是．17. 观察下列式子：1×3+1=22；7×9+1=28；25×27+1=226；79×81+1=280；…可猜想第2016个式子为．18. 如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确定x的值为．19. 已知a1=1tt+，a2=111a-，a3=211a-，…，a n+1=11na-（n为正整数，且t≠0，1），则a2016= （用含有t的代数式表示）．20. 观察下列等式：第1个等式：1a=1-，第2个等式：2a，第3个等式：3a==2，第4个等式：4a=2，按上述规律，回答以下问题：（1）请写出第n个等式：na= ；（2）123...na a a a++++= ．21. 填空：()()a b a b-+= ；22()()a b a ab b-++= ；3223()()a b a a b ab b-+++= ．（2）猜想：1221()(...)n n n na b a a b ab b-----++++= （其中n为正整数，且2n≥）．（3）利用（2）猜想的结论计算：98732222...222-+-+-+．22. 如图，在平面直角坐标系中，边长为1的正方形OA 1B 1C 1的两边在坐标轴上，以它的对角线OB 1为边作正方形OB 1B 2C 2，再以正方形OB 1B 2C 2的对角线OB 2为边作正方形OB 2B 3C 3，以此类推…、则正方形OB 2015B 2016C 2016的顶点B 2016的坐标是．学海迷津：数学学习十大方法1、配方法所谓配方，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和形式。

2017-2018学年中考数学压轴题分类练习动点特殊四边形专题

动点特殊四边形专题1.探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P 1（x 1，y 1），P 2（x 2，y 2），可通过构造直角三角形利用图1得到结论：12PP =他还利用图2证明了线段P 1P 2的中点P （x ，y ）P 的坐标公式：122x x x +=，122y y y +=．（1）请你帮小明写出中点坐标公式的证明过程；运用：（2）①已知点M （2，﹣1），N （﹣3，5），则线段MN 长度为；②直接写出以点A （2，2），B （﹣2，0），C （3，﹣1），D 为顶点的平行四边形顶点D 的坐标：；拓展：（3）如图3，点P （2，n ）在函数43y x =（x ≥0）的图象OL 与x 轴正半轴夹角的平分线上，请在OL 、x 轴上分别找出点E 、F ，使△PEF 的周长最小，简要叙述作图方法，并求出周长的最小值．2.如图，矩形OABC 的两边在坐标轴上，点A 的坐标为（10，0），抛物线24y ax bx =++过点B ，C 两点，且与x 轴的一个交点为D （﹣2，0），点P 是线段CB 上的动点，设CP =t （0＜t ＜10）．（1）请直接写出B 、C 两点的坐标及抛物线的解析式；（2）过点P 作PE ⊥BC ，交抛物线于点E ，连接BE ，当t 为何值时，∠PBE =∠OCD ？（3）点Q 是x 轴上的动点，过点P 作PM ∥BQ ，交CQ 于点M ，作PN ∥CQ ，交BQ 于点N ，当四边形PMQN 为正方形时，请求出t 的值．3.如图，抛物线212y x bx c =-++ 与x 轴交于点A 和点B ，与y 轴交于点C ，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E ，连接BD ．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA =∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN ∥x 轴与抛物线交于点N ，点P 在x 轴上，点Q 在坐标平面内，以线段MN 为对角线作正方形MPNQ ，请写出点Q 的坐标．4. 如图，已知抛物线2y ax c =+过点()2,2-，()4,5，过定点()0,2F 的直线:2l y kx =+与抛物线交于A ，B 两点，点B 在点A 的右侧，过点B 作x 轴的垂线，垂足为C . (1)求抛物线的解析式；(2)当点B 在抛物线上运动时，判断线段BF 与BC 的数量关系(>、<、=)，并证明你的判断； (3)P 为y 轴上一点，以,,,B C F P 为顶点的四边形是菱形，设点()0,P m ，求自然数m 的值；(4)若1k =，在直线l 下方的抛物线上是否存在点Q ，使得QBF △的面积最大，若存在，求出点Q 的坐标及QBF △的最大面积，若不存在，请说明理由.5.如图，抛物线23y ax bx =+-经过点()2,3A -，与x 轴负半轴交于点B ，与y 轴交于点C ，且3OC OB =. （1）求抛物线的解析式；（2）点D 在y 轴上，且BDO BAC ∠=∠，求点D 的坐标；（3）点M 在抛物线上，点N 在抛物线的对称轴上，是否存在以点A ，B ，M ，N 为顶点的四边形是平行四边形？若存在。

2018年中考数学压轴题专题汇编36动点综合问题

点．
（ 1）求抛物线的解析式及点 C 的坐标；
（ 2）求证：△ ABC 是直角三角形；
（ 3）若点 N 为 x 轴上的一个动点，过点 N 作 MN ⊥x 轴与抛物线交于点 M ，则是否存在以 O， M ， N 为顶
）
A．
B．
C．
D．
2．（山东省烟台市）如图， ○ O 的半径为 1，AD ，BC 是⊙ O 的两条互相垂直的直径，点 P 从点 O 出发（ P
点与 O 点不重合），沿 O→ C→ D 的路线运动，设 AP=x，sin∠APB=y，那么 y 与 x 之间的关系图象大致是（）
A．
B．
C． 3．（广东省）如图，在正方形
＜ x＜ 90），优弧 ABC 的弧长与劣弧 AC 的弧长的差设为 y（单位：厘米），图 2 表示 y 与 x 的函数关系，则
α=
度．
9．（浙江省舟山市）如图，在直角坐标系中，点
A，B 分别在 x 轴， y 轴上，点 A 的坐标为（﹣ 1， 0），
∠ ABO =30°，线段 PQ 的端点 P 从点 O 出发，沿△ OBA 的边按 O→ B→ A→O 运动一周，同时另一端点 Q
? 解读考点
知识点
动点问题中的
等腰三角形与直角三角形
特殊图形
相似问题
动点问题中的计算问
题
动点问题的最值与定值问题动点问题的面积问题
动点问题的函数图象
问题
一次函数或二次函数的图象
名师点晴利用等腰三角形或直角三角形的特殊性质求解动点问题利用相似三角形的对应边成比例、对应角相等求解动点问题理解最值或定值问题的求法结合面积的计算方法来解决动点问题
1 ．（山东省青岛市）已知：如图，在矩形 ABCD 中， Ab= cm，BC=8cm，对角线 AC，BD 交于点 0．点

2018年中考压轴题(动点问题) 精品

2018压轴题-动点问题1、（2018包头）如图，已知ABC△中，10AB AC==厘米，8BC=厘米，点D为AB的中点．（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，BPD△与CQP△是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使BPD△与CQP△全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B 同时出发，都逆时针沿ABC△三边运动，求经过多长时间点P与点Q第一次在ABC△的哪条边上相遇？2、（2018齐齐哈尔）直线364y x=-+与坐标轴分别交于A B、两点，动点P Q、同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动．（1）直接写出A B、两点的坐标；（2）设点Q的运动时间为t秒，OPQ△的面积为S，求出S与t之间的函数关系式；（3）当485S=时，求出点P的坐标，并直接写出以点O P Q、、为顶点的平行四边形的第四个顶点M的坐标．3（2018深圳）如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？4（2018哈尔滨）如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．（1）求直线AC的解析式；（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；（3）在（2）的条件下，当t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．5（2018河北）在Rt△ABC中，∠C=90°，AC = 3，AB = 5．点P从点C 出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B 匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BC-CP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．（1）当t = 2时，AP = ，点Q到AC的距离是；（2）在点P从C向A运动的过程中，求△APQ的面积S与t的函数关系式；（不必写出t的取值范围）（3）在点E从B向C运动的过程中，四边形QBED能否成为直角梯形？若能，求t的值．若不能，请说明理由；（4）当DE经过点C 时，请直接．．写出t的值．6（2018河南））如图，在Rt ABC°，°，2BC=．点ACB B∠=∠=△中，9060O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；α=°时，判断四边形EDBC是否为菱形，并说明理由．（2）当90（备用图）7（2018济南）如图，在梯形ABCD 中，3545AD BC AD DC AB B ====︒∥，，，．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒．（1）求BC 的长．（2）当MN AB ∥时，求t 的值．（3）试探究：t 为何值时，MNC △为等腰三角形．8（2018江西）如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =︒∠. （1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PMN △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由.CMA D E BF C图4（备用）ADE BF C图5（备用）A D E BF C图1 图2A D EBF C PNM 图3A D EBFCPN M（第25题）9（2018兰州）如图①，正方形ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C →D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．(1)当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；(2)求正方形边长及顶点C的坐标；(3)在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；(4)如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等，若能，写出所有符合条件的t的值；若不能，请说明理由．10（2018临沂）数学课上，张老师出示了问题：如图1，四边形ABCD∠的是正方形，点E是边BC的中点．90∠=，且EF交正方形外角DCGAEF平行线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．11（2018天津）已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（Ⅰ）若折叠后使点B 与点A 重合，求点C 的坐标；（Ⅱ）若折叠后点B 落在边OA 上的点为B '，设OB x '=，OC y =，试写出y 关于x 的函数解析式，并确定y 的取值范围；（Ⅲ）若折叠后点B 落在边OA 上的点为B '，且使B D OB '∥，求此时点C 的坐标．ADFC GE 图1ADF C GE 图2 ADFC GE B图312（2018太原）问题解决如图（1），将正方形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C ，D 重合），压平后得到折痕MN ．当12CE CD =时，求AMBN 的值．类比归纳在图（1）中，若13CE CD =，则AM BN 的值等于；若14CE CD =，则AMBN 的值等于；若1CE CD n =（n 为整数），则AMBN的值等于．（用含n 的式子表示）联系拓广如图（2），将矩形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C D ，重合），压平后得到折痕MN ，设()111AB CE m BC m CD n =>=，，则AMBN的值等于．（用含m n ，的式子表示）方法指导：为了求得AMBN 的值，可先求BN 、AM 的长，不妨设：AB =2图（2）N A BCDEFM 图（1） A B CDEFMN。

2017-2018学年中考数学经典题型训练卷：动点面积最值问题(无答案)

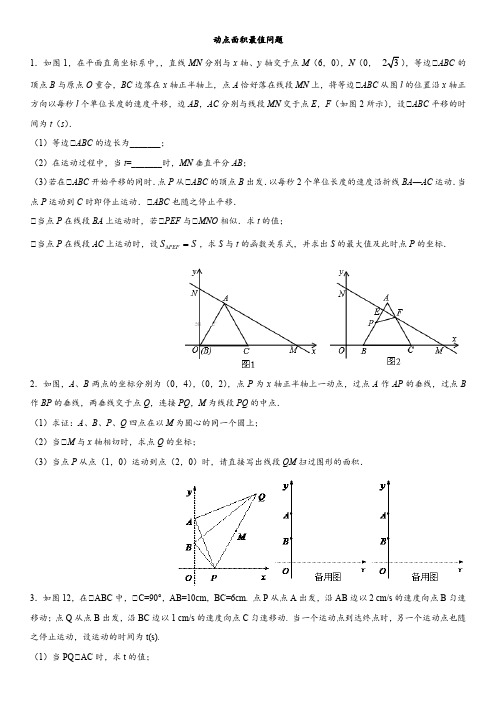
动点面积最值问题1．如图1，在平面直角坐标系中，，直线MN 分别与x 轴、y 轴交于点M （6，0），N （0，，等边△ABC 的顶点B 与原点O 重合，BC 边落在x 轴正半轴上，点A 恰好落在线段MN 上，将等边△ABC 从图l 的位置沿x 轴正方向以每秒l 个单位长度的速度平移，边AB ，AC 分别与线段MN 交于点E ，F （如图2所示），设△ABC 平移的时间为t （s ）．（1）等边△ABC 的边长为_______；（2）在运动过程中，当t =_______时，MN 垂直平分AB ；（3）若在△ABC 开始平移的同时．点P 从△ABC 的顶点B 出发．以每秒2个单位长度的速度沿折线BA —AC 运动．当点P 运动到C 时即停止运动．△ABC 也随之停止平移．①当点P 在线段BA 上运动时，若△PEF 与△MNO 相似．求t 的值；②当点P 在线段AC 上运动时，设PEF S S ∆=，求S 与t 的函数关系式，并求出S 的最大值及此时点P 的坐标．2．如图，A 、B 两点的坐标分别为（0，4），（0，2），点P 为x 轴正半轴上一动点，过点A 作AP 的垂线，过点B 作BP 的垂线，两垂线交于点Q ，连接PQ ，M 为线段PQ 的中点．（1）求证：A 、B 、P 、Q 四点在以M 为圆心的同一个圆上；（2）当⊙M 与x 轴相切时，求点Q 的坐标；（3）当点P 从点（1，0）运动到点（2，0）时，请直接写出线段QM 扫过图形的面积．3．如图12，在△ABC 中，∠C=90°，AB=10cm ，BC=6cm. 点P 从点A 出发，沿AB 边以2 cm/s 的速度向点B 匀速移动；点Q 从点B 出发，沿BC 边以1 cm/s 的速度向点C 匀速移动. 当一个运动点到达终点时，另一个运动点也随之停止运动，设运动的时间为t(s). （1）当PQ ∥AC 时，求t 的值；（2）当t 为何值时，QB=QP ；（3）当t 为何值时，△PBQ 的面积等于4.8cm 2.4．如图，在平面直角坐标系xOy 中，直线y=x+4与坐标轴分别交于A 、B 两点，抛物线y=﹣x 2+bx+c 过A 、B 两点，点D 为线段AB 上一动点，过点D 作CD ⊥x 轴于点C ，交抛物线于点E ．（1）求抛物线的解析式．（2）求△ABE 面积的最大值．（3）连接BE ，是否存在点D ，使得△DBE 和△DAC 相似？若存在，求出点D 坐标；若不存在，说明理由． 5．已知函数()2121y m x mx m =-++-（1）m= 时，函数图像与x 轴只有一个交点；（2）m 为何值时，函数图像与x 轴没有交点；（3）若函数图像与x 轴交于A 、B 两点，与y 轴交于点C ，且△ABC 的面积为4，求m 的值. 6．已知二次函数y=x 2﹣2x ﹣3与x 轴交于A 、B 两点（A 在B 的左边），与y 轴交于点C ．（1）求出点A 、B 、C 的坐标．（2）求S △ABC（3）在抛物线上（除点C 外），是否存在点N ，使得S △NAB =S △ABC ，若存在，求出点N 的坐标，若不存在，请说明理由．7．如图，已知：在平面直角坐标系中，直线l与y轴相交于点A（0，m）其中m＜0，与x轴相交于点B（4，0）．抛物线y=ax2+bx（a＞0）的顶点为F，它与直线l相交于点C，其对称轴分别与直线l和x轴相交于点D和点E．（1）设a=12，m=﹣2时，①求出点C、点D的坐标；②抛物线y=ax2+bx上是否存在点G，使得以G、C、D、F四点为顶点的四边形为平行四边形？如果存在，求出点G的坐标；如果不存在，请说明理由．（2）当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1：3时，求抛物线的函数表达式．8．如图，以O为原点的直角坐标系中，A点的坐标为（0，1），直线x=1交x轴于点B。

2018年中考数学压轴题专题解析---几何动态探究问题—动点+动面

第１题图（1）在整个运动过程中，当点 G在线段 AE上时，求 t 的值；（2）在整个运动过程中，是否存在点 P，使△ APQ是等腰三角形？若存在，求出 t 的值；若不存在，说明理由；（3）在整个运动过程中，设△ GMN与△ AEF重叠部分的面积为 S．请直接写出 S 与 t 之间的函数关系式以及自变量 t 的取值范围 ; (4) 在运动过程中，是否存在某一时刻 t , 使得 S: S△GMN=1:2? 若存在，求出 t 的值，若不存在，请说明理由 .
2018 年中考数学压轴题专题解析 --- 几何动态探究问题—动点 +动面
1. 已知在矩形 ABCD中， E 为 BC边上一点， AE⊥DE， AB＝12， BE＝16， F 为线段 BE上一点， EF＝ 7，连接 AF．如图①，现有一张硬质纸片△ GMN，∠ NGM＝ 90°， NG＝ 6，MG＝ 8，斜边 MN 与边 BC在同一直线上，点 N与点 E 重合，点 G在线段 DE上．如图②，△ GMN从图①的位置出发，以每秒 1 个单位的速度沿 EB向点 B 匀速移动，同时点 P 从 A点出发，以每秒 1 个单位的速度沿 AD向点 D匀速移动，点 Q为直线 GN与线段 AE的交点，连接 PQ．当点 N到达终点 B 时，△ GMN和点 P同时停止运动．设运动时间为 t 秒，解答下列问题：
AB与 QR在同一直线 l 上，开始时点 Q与点 A 重合，让△ PQR以 1cm/ s 的速度在直线 l 上运动，同时 M点从点 Q出发以 1cm/ s 沿 QP运动，直至点 Q与点 B 重合时，都停止运动，设运
动的时间为
t （ s），四边形
PMBN的面积为
S（
2
cm
）．
第 2 题图
（1）当 t =1s 时，求 S 的值；

2018年人教版中考压轴题汇编《因动点产生的面积问题》含答案

1.6 因动点产生的面积问题例1 2017年河南省中考第23题如图1，边长为8的正方形ABCD的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上A、C两点间的一个动点（含端点），过点P作PF⊥BC于点F．点D、E 的坐标分别为(0, 6)、(－4, 0)，联结PD、PE、DE．（1）直接写出抛物线的解析式；（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值．进而猜想：对于任意一点P，PD与PF的差为定值．请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点”的坐标．图1 备用图如图1，在平面直角坐标系中，抛物线y＝ax2＋bx－3（a≠0）与x轴交于A(－2, 0)、B(4, 0)两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P从点A出发，在线段AB上以每秒3个单位长度的速度向点B运动，同时点Q从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动．其中一个点到达终点时，另一个点也停止运动．当△PBQ存在时，求运动多少秒时△PBQ的面积最大，最大面积是多少？（3）当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使S△CBK∶S△PBQ＝5∶2，求点K的坐标．图1如图1，已知抛物线212y x bx c =++（b 、c 是常数，且c ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴的负半轴交于点C ，点A 的坐标为(－1,0)．（1）b ＝______，点B 的横坐标为_______（上述结果均用含c 的代数式表示）；（2）连结BC ，过点A 作直线AE //BC ，与抛物线交于点E ．点D 是x 轴上一点，坐标为(2,0)，当C 、D 、E 三点在同一直线上时，求抛物线的解析式；（3）在（2）的条件下，点P 是x 轴下方的抛物线上的一动点，连结PB 、PC ．设△PBC 的面积为S ．①求S 的取值范围；②若△PBC 的面积S 为正整数，则这样的△PBC 共有_____个．图1如图1，在平面直角坐标系中放置一直角三角板，其顶点为A(0, 1)、B(2, 0)、O(0, 0)，将此三角板绕原点O逆时针旋转90°，得到三角形A′B′O．（1）一抛物线经过点A′、B′、B，求该抛物线的解析式；（2）设点P是第一象限内抛物线上的一个动点，是否存在点P，使四边形PB′A′B的面积是△A′B′O面积的4倍？若存在，请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，试指出四边形PB′A′B是哪种形状的四边形？并写出它的两条性质．图1如图1，在平面直角坐标系中，直线112y x=+与抛物线y＝ax2＋bx－3交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上的一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．（1）求a、b及sin∠ACP的值；（2）设点P的横坐标为m．①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连结PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积比为9∶10？若存在，直接写出m的值；若不存在，请说明理由．图1如图1，直线l经过点A(1，0)，且与双曲线myx=(x＞0)交于点B(2，1)．过点(,1)P p p-(p＞1)作x轴的平行线分别交曲线myx=(x＞0)和myx=-(x＜0)于M、N两点．（1）求m的值及直线l的解析式；（2）若点P在直线y＝2上，求证：△PMB∽△PNA；（3）是否存在实数p，使得S△AMN＝4S△AMP？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．图1如图1，四边形OABC是矩形，点A、C的坐标分别为(3,0)，(0,1)．点D是线段BC上的动点（与端点B、C不重合），过点D作直线12y x b=-+交折线OAB于点E．（1）记△ODE的面积为S，求S与b的函数关系式；（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．图11.6 因动点产生的面积问题答案例1 2017年河南省中考第23题如图1，边长为8的正方形ABCD 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，点P 是抛物线上A 、C 两点间的一个动点（含端点），过点P 作PF ⊥BC 于点F ．点D 、E 的坐标分别为(0, 6)、(－4, 0)，联结PD 、PE 、DE ．（1）直接写出抛物线的解析式；（2）小明探究点P 的位置发现：当点P 与点A 或点C 重合时，PD 与PF 的差为定值．进而猜想：对于任意一点P ，PD 与PF 的差为定值．请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论：若将“使△PDE 的面积为整数” 的点P 记作“好点”，则存在多个“好点”，且使△PDE 的周长最小的点P 也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE 周长最小时“好点”的坐标．图1 备用图动感体验请打开几何画板文件名“15河南23”，拖动点P 在A 、C 两点间的抛物线上运动，观察S 随P 变化的图像，可以体验到，“使△PDE 的面积为整数” 的点P 共有11个．思路点拨1．第（2）题通过计算进行说理．设点P 的坐标，用两点间的距离公式表示PD 、PF 的长．2．第（3）题用第（2）题的结论，把△PDE 的周长最小值转化为求PE ＋PF 的最小值．满分解答（1）抛物线的解析式为2188y x =-+．（2）小明的判断正确，对于任意一点P ，PD －PF ＝2．说理如下：设点P 的坐标为21(,8)8x x -+，那么PF ＝y F －y P ＝218x ．而FD 2＝22222222111+(86)+(2)(2)888x x x x x -+-=-=+，所以FD ＝2128x +．因此PD －PF ＝2为定值．（3）“好点”共有11个．在△PDE 中，DE 为定值，因此周长的最小值取决于FD ＋PE 的最小值．而PD ＋PE ＝(PF ＋2)＋PE ＝(PF ＋PE )＋2，因此当P 、E 、F 三点共线时，△PDE 的周长最小（如图2）．此时EF ⊥x 轴，点P 的横坐标为－4．所以△PDE 周长最小时，“好点”P 的坐标为(－4, 6)．图2 图3考点伸展第（3）题的11个“好点”是这样求的：如图3，联结OP ，那么S △PDE ＝S △POD ＋S △POE －S △DOE ．因为S △POD ＝1()32P OD x x ⋅-=-，S △POE ＝2111624P OE y x ⋅=-+，S △DOE ＝12，所以 S △PDE ＝21316124x x --+-＝21344x x --+＝21(6)134x -++．因此S 是x 的二次函数，抛物线的开口向下，对称轴为直线x ＝－6．如图4，当－8≤x ≤0时，4≤S ≤13．所以面积的值为整数的个数为10．当S ＝12时，方程21(6)13124x -++=的两个解－8, －4都在－8≤x ≤0范围内．所以“使△PDE 的面积为整数” 的 “好点”P 共有11个．图4例2 2017年昆明市中考第23题如图1，在平面直角坐标系中，抛物线y ＝ax 2＋bx －3（a ≠0）与x 轴交于A (－2, 0)、B (4, 0)两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 从点A 出发，在线段AB 上以每秒3个单位长度的速度向点B 运动，同时点Q 从点B 出发，在线段BC 上以每秒1个单位长度的速度向点C 运动．其中一个点到达终点时，另一个点也停止运动．当△PBQ 存在时，求运动多少秒时△PBQ 的面积最大，最大面积是多少？（3）当△PBQ 的面积最大时，在BC 下方的抛物线上存在点K ，使S △CBK ∶S △PBQ ＝5∶2，求点K 的坐标．图1动感体验请打开几何画板文件名“14昆明23”，拖动点P 从A 向B 运动，可以体验到，当P 运动到AB 的中点时，△PBQ 的面积最大．双击按钮“△PBQ 面积最大”，再拖动点K 在BC 下方的抛物线上运动，观察度量值，可以体验到，有两个时刻面积比为2.5．思路点拨1．△PBQ 的面积可以表示为t 的二次函数，求二次函数的最小值． 2．△PBQ 与△PBC 是同高三角形，△PBC 与△CBK 是同底三角形，把△CBK 与△PBQ 的比转化为△CBK 与△PBC 的比．满分解答（1）因为抛物线与x 轴交于A (－2, 0)、B (4, 0)两点，所以y ＝a(x ＋2)(x －4)．所以－8a ＝－3．解得38a =．所以抛物线的解析式为3(2)(4)8y x x =+-233384x x =--．（2）如图2，过点Q 作QH ⊥x 轴，垂足为H ．在Rt △BCO 中，OB ＝4，OC ＝3，所以BC ＝5，sin B ＝35．在Rt △BQH 中，BQ ＝t ，所以QH ＝BQ sin B ＝35t ．所以S △PBQ ＝211399(63)(1)2251010BP QH t t t ⋅=-⨯=--+．因为0≤t ≤2，所以当t ＝1时，△PBQ 的面积最大，最大面积是910。

2018年中考数学压轴题专题解析---动点梯形与动点面积

2018年中考数学压轴题专题解析---动点梯形与动点面积这节课我们学什么1.动点梯形问题；2.动点面积问题；知识框图知识点梳理动点梯形分类主要讲解三定一动类型．动点面积分类分为三个专题：1.面积公式：三角形的面积利用12S ah来表示，利用未知数的代数式来表示底和高2.面积比等于相似比的平方：面积无法用底和高表示时，利用相似三角形的面积比等于相似比的平方来求解，只需要知道相似比和另个一三角形面积即可表示3.相似三角形：当面积公式和面积比等于相似比的平方不能有效解题时，利用相似三角形的比例关系求解典型例题分析1、动点梯形问题------三定一动；例1.如图，在平面直角坐标系xoy 中，二次函数c bx x y ++=231的图像与y 轴交于点A ，与双曲线xy 8=有一个公共点B ，它的横坐标为4，过点B 作直线x l //轴，与该二次函数图像交于另一个点C ，直线AC 的截距是-6．（1）求二次函数的解析式；（2）求直线AC 的表达式；（3）平面内是否存在点D ，使D C B A 、、、为顶点的四边形是等腰梯形，如果存在，求出点D 坐标，如果不存在，说明理由．【答案：（1）212633y x x =+-;（2）463y x =--；(3)121418(-2-6), ()55D D ，，;】2、动点面积问题----面积公式；例2.如图，在直角坐标系中，一条抛物线与x 轴交于A 、B 两点，与y 轴交于C 点，其中(3,0)B ，(0,4)C ，点A 在x 轴的负半轴上，4OC OA =；（1）求这条抛物线的解析式，并求出它的顶点坐标；（2）联结AC 、BC ，点P 是x 轴正半轴上一个动点，过点P 作//PM BC 交射线AC于点M ，联结CP ，若CPM ∆的面积为2，则请求出点P 的坐标；【答案：（1）设这条抛物线的解析式为2(0)y ax bx c a =++≠ 它的顶点坐标为16(1,)3（2）过点P 作PH AC ⊥，垂足为H .∵P 点在x 轴的正半轴上，∴设0P x （，）.∵A )0,1(-，∴1PA x =+.∵在Rt AOC ∆中，222OA OC AC +=又∵14OA OC ==，∴AC =90sin1PH PH PHA CAO AP x ∠=︒∴∠===+ ∴PH =//BP CMPM BC AB AC∴= 300B P x （，），（，）①点P 在点B 的左侧时，3BP x =-∴34x -=CM = ∵2PCM S =△∴122CM PH ⋅⋅=∴122=解得110x .P=∴（，） ②点P 在点B 的右侧时，3BP x =-∴34x -=CM = ∵2PCM S =△∴122CM PH ⋅⋅=∴122=解得11x =+21x =-∴P （1+0）. 综上所述，P 的坐标为（1，0）或（1+0）】例3.已知点(1,0)A -，点B （与A 不重合）在射线AO 上，点C 在x 轴上方，且ABC∆为等边三角形，射线AC 交y 轴于D .（1）当4AB =时，则点B 、C 、D 的坐标分别是：B ：（）；C ：（）D ：（）.（2）若AB m =（0m >），则点B 、C 的坐标分别是：B ：（）；C ：（）.当C 、D 不重合时，请根据m 的不同取值，对于过B 、C 、D 三点的二次函数开口方向作出判断，直接写出结论（不要求证明）. （3）是否存在点B ，使1633=∆BCD S ，若存在，求出点B 的坐标；若不存在，请说明理由.【答案：（1）B ：（3，0）；C ：（1，23）D ：（0，3）（2）B ：（m -1，0）；C ：（m m 23,12-）. 当m 的取值为：10<<m 时，过B 、C 、D 三点的抛物线开口向上；当m 的取值为：1>m （m ≠2）时，过B 、C 、D 三点的抛物线开口向下.（3）当点B 的坐标为（0,21-）、（0,21）、（0,27）时，有1633=∆BCD S .】3、动点面积问题----面积比等于相似比的平方；例4.如图1，在梯形ABCD 中，//AD BC ，对角线BC AC ⊥，4AD =cm ，︒=∠45D ，3=BC cm ．（1）求B ∠cos 的值；（2）点E 为BC 延长线上的动点，点F 在线段CD 上（点F 与点C 不重合），且满足ADE AFC ∠=∠，如图2，设x BE =，y DF =，求y 关于x 的函数解析式，并写出函数的定义域；（3）点E 为射线BC 上的动点，点F 在射线CD 上，仍然满足ADE AFC ∠=∠，当AFD ∆的面积为2cm 2时，求BE 的长．【答案：解（1）∵//AD BC ，∴ACB DAC ∠=∠. ∵AC BC ⊥，∴90ACB ∠=︒.∴90DAC ∠=︒. ∵45D ∠=︒，∴45ACD ∠=︒.∴AD AC =. ∵4AD =，∴4AC =. ∵3=BC ，∴5AB =.∴3cos 5BC B AB ∠==. （2）∵//AD BC ，∴ADF DCE ∠=∠.∵AFC FDA FAD ∠=∠+∠，ADE FDA EDC ∠=∠+∠，又AFC ADE ∠=∠，∴FAD EDC ∠=∠.∴ADF DCE ∆~∆.∴AD DFDC CE=. 在Rt ADC ∆中，222AC AD DC +=，又4==AC AD ，∴24=DC . ∵x BE =，∴3-=x CE .又y DF =，∴3244-=x y.22322-=x y .定义域为113<<x .D AC B图1DAC BEF图2（3）当点E 在BC 的延长线上，由（2）可得：ADF DCE ∆~∆，∴2)(DCAD S S DCE ADF =∆∆. ∵2AFD S ∆=，4=AD ，24=DC ，∴4=∆DCE S .∵AC CE S DCE ⨯⨯=∆21，∴44)3(21=⨯-⨯BE ，∴5BE =. 当点E 在线段BC 上，同理可得：44)3(21=⨯-⨯BE .∴1BE =.所以BE 的长为5或1.】4、动点面积问题----相似三角形；例5.已知：ABC ∆，90ABC ∠=︒，1tan 2BAC ∠=，点D 在边AC 上的延长线上，且2DB DC DA =⋅（如图）；（1）求DCCA的值；（2）如果点E 在线段BC 的延长线上，联结AE ，过点B 作AC 的垂线，交AC 于点F ，交AE 于点G ； 1) 如左图，当3CE BC =时，求BFFG的值； 2) 如右图，当CE BC =时，求BCDBEGS S ∆∆的值；【答案：（1）13DC CA =; （2）23BF FG =；12BCD BEG S S ∆∆=】例6.如图，在边长为6的正方形ABCD 中，点E 为AD 边上的一个动点（与点A 、D不重合）45EBM ∠=︒，BE 交对角线AC 于点F ，BM 交对角线AC 于点G ，交CD 于点M .（1）如左图，联结BD ，求证：DEB CGB ∆~∆，并写出:DE CG 的值；（2）联结EG ，如右图，若设AE x =，EG y =，求y 关于x 的函数解析式，并写出函数的定义域；（3）当M 为边DC 的三等分点时，求EGF S ∆的面积.【答案：】课后练习练1. 如图，矩形OMPN 的顶点O 在原点，M 、N 分别在x 轴和y 轴的正半轴上，63OM ON ==，，反比例函数xy 6=的图像与PN 交于C ，与PM 交于D ，过点C 作CA x ⊥轴于点A ，过点D 作DB y ⊥轴于点B ，AC 与BD 交于点G ．（1）求证：AB //CD ；（2）在直角坐标平面内是否若存在点E ，使以B 、C 、D 、E 为顶点，BC 为腰的梯形是等腰梯形？若存在，求点E 的坐标；若不存在请说明理由．【答案：∵矩形63OMPN OM ON ，＝，＝，∴点P （6,3）∵点C 、D 都在反比例函数6y x=图像上，且点C 在PN 上，点D 在PM 上， ∴点23C （，），点61D （，）又DB y ⊥轴，CA x ⊥轴，∴2001A B （，），（，）∵2421BG GD CG AG ＝，＝，＝，＝∴12AG GC =，2142BG GD == ∴=AG BG GC GD∴AB //CD ．（2）①∵PN ∥DB∴当1DE BC ＝时，四边形1BCE D此时1Rt CNB Rt E PD ∆∆≌，12PE CN ∴＝＝，∴点143E （，） ②//CD AB ，当E 2在直线AB 上，22DE BC ＝＝，四边形2BCDE 为等腰梯形，直线AB 的解析式为112y x =-+∴设点E 2（x ，112x -+）2DE BC ==∴8)21()6(22=+-x x5281=x ，42=x （舍去）∴E 2（528，59-）；】练2. 已知：如图1，在R t O A C ∆中，AO OC ⊥，点B 在OC 边上，6OB =，12BC =，90ABO C ︒∠+∠=．动点M 和N 分别在线段AB 和AC 边上．（1）求证：AOB COA ∆~∆，并求cos C 的值；（2）当4AM =时，AMN ∆与ABC ∆相似，求AMN ∆与ABC ∆的面积之比；（3）如图2，当//MN BC 时，将AMN ∆沿MN 折叠，点A 落在四边形BCNM 所在平面的点为点E ．设MN x =，EMN ∆与四边形BCNM 重叠部分的面积为y ，试写出y 关于x 的函数关系式，并写出自变量x 的取值范围．【答案：（1）cos OC C AC ===（2）∵cos OC C AC ===30C ︒∠=. OA tan ABO OB ∠===,︒=∠60ABO . ∴︒=∠30BAC .∴12AB BC ==.①当∠AMN =∠B 时，（如图）AMN ABC ∆~∆∵4AM =，∴2222::4:121:9AMN ABC S S AM AB ∆∆===.②当∠AMN =∠C 时，（如图）AMN ACB ∆~∆∵4AM =，图1∴2222::4:121:9AMN ABC S S AM AB ∆∆===.∵4AM =，∴(2222::4:1:27AMN ABC S S AM AC ∆∆===.（3）可以求得：33612362121=⨯⨯=⋅=∆BC AO S ABC . ∵//MN BC ， ∴AMN ABC ∆~∆.∴22:AMN ABC S S MN BC ∆∆=：.∴22:12AMN S x ∆=.∴2AMN S ∆=. ①当EN 与线段AB 相交时，设EN 与AB 交于点F （如图），∵//MN BC ，∴o30ANM C ∠=∠=.∴ANM BAC ∠=∠.∴AM MN x ==.∵将AMN ∆沿MN 折叠，∴30o ENM ANM ∠=∠=.∴o 90AFN ∠=. ∴111222MF MN AM x ===.∴::FMN AMN S S MF AM ∆∆=.∴21:1:22y x x ==.∴2(08)y x =<≤. ②当EN 与线段AB 不相交时，设EN 于BC 交于点G （如图），∵//MN BC ∴::CN AC BM AB =.∴(12):12CN x =-.∴CN =.∵CNG CBA ∆~∆，∴22:CNG ABC S S CN BC ∆∆=：.∴22):12CNG S ∆.∴2)CNG S ∆=.∴22)ABC AMN CNG S S S S ∆∆∆=--=-阴.即212)y x =+-<<.】课后小测验1.如图，在直角坐标平面上，点A,B 在x 轴上（A 点在B 点左侧），点C 在y 轴正半轴上，若(1,0)A -，3OB OA =，且tan 2CAO ∠=．（1）求点B,C 的坐标（2）求经过点A,B,C 三点的抛物线解析式；（3）P 是（2）中所求抛物线的顶点，设Q 是此抛物线上一点，若ABQ ∆与ABP ∆的面积相等，求Q 点的坐标．【答案：（1）()3,0B（2）()()2224132333y x x x x =-+-=-++ （3）当83y =时，28242333x x =-++解得121x x ==,∴81,3Q ⎛⎫ ⎪⎝⎭当83y =-时，28242333x x -=-++解得1x =±∴813Q ⎛⎫±- ⎪⎝⎭】。

2017-2018学年中考数学题型训练卷：动点面积最值问题(无答案)

动点面积最值问题1．如图1，在平面直角坐标系中，，直线MN 分别与x 轴、y 轴交于点M （6，0），N （0，），等边△ABC 的顶点B 与原点O 重合，BC 边落在x 轴正半轴上，点A 恰好落在线段MN 上，将等边△ABC 从图l 的位置沿x 轴正方向以每秒l 个单位长度的速度平移，边AB ，AC 分别与线段MN 交于点E ，F （如图2所示），设△ABC 平移的时间为t （s ）．（1）等边△ABC 的边长为_______；（2）在运动过程中，当t =_______时，MN 垂直平分AB ；（3）若在△ABC 开始平移的同时．点P 从△ABC 的顶点B 出发．以每秒2个单位长度的速度沿折线BA —AC 运动．当点P 运动到C 时即停止运动．△ABC 也随之停止平移．①当点P 在线段BA 上运动时，若△PEF 与△MNO 相似．求t 的值；②当点P 在线段AC 上运动时，设PEF S S ∆=，求S 与t 的函数关系式，并求出S 的最大值及此时点P 的坐标．2．如图，A 、B 两点的坐标分别为（0，4），（0，2），点P 为x 轴正半轴上一动点，过点A 作AP 的垂线，过点B 作BP 的垂线，两垂线交于点Q ，连接PQ ，M 为线段PQ 的中点．（1）求证：A 、B 、P 、Q 四点在以M 为圆心的同一个圆上；（2）当⊙M 与x 轴相切时，求点Q 的坐标；（3）当点P 从点（1，0）运动到点（2，0）时，请直接写出线段QM 扫过图形的面积．3．如图12，在△ABC 中，∠C=90°，AB=10cm ，BC=6cm. 点P 从点A 出发，沿AB 边以2 cm/s 的速度向点B 匀速移动；点Q 从点B 出发，沿BC 边以1 cm/s 的速度向点C 匀速移动. 当一个运动点到达终点时，另一个运动点也随之停止运动，设运动的时间为t(s).（1）当PQ ∥AC 时，求t 的值；（2）当t 为何值时，QB=QP ；（3）当t 为何值时，△PBQ 的面积等于4.8cm 2.4．如图，在平面直角坐标系xOy 中，直线y=x+4与坐标轴分别交于A 、B 两点，抛物线y=﹣x 2+bx+c 过A 、B 两点，点D 为线段AB 上一动点，过点D 作CD ⊥x 轴于点C ，交抛物线于点E ．（1）求抛物线的解析式．（2）求△ABE 面积的最大值．（3）连接BE ，是否存在点D ，使得△DBE 和△DAC 相似？若存在，求出点D 坐标；若不存在，说明理由．5．已知函数()2121y m x mx m =-++- （1）m= 时，函数图像与x 轴只有一个交点；（2）m 为何值时，函数图像与x 轴没有交点；（3）若函数图像与x 轴交于A 、B 两点，与y 轴交于点C ，且△ABC 的面积为4，求m 的值.6．已知二次函数y=x 2﹣2x ﹣3与x 轴交于A 、B 两点（A 在B 的左边），与y 轴交于点C ．（1）求出点A 、B 、C 的坐标．（2）求S △ABC（3）在抛物线上（除点C 外），是否存在点N ，使得S △NAB =S △ABC ，若存在，求出点N 的坐标，若不存在，请说明理由．7．如图，已知：在平面直角坐标系中，直线l与y轴相交于点A（0，m）其中m＜0，与x轴相交于点B（4，0）．抛物线y=ax2+bx（a＞0）的顶点为F，它与直线l相交于点C，其对称轴分别与直线l和x轴相交于点D和点E．（1）设a=12，m=﹣2时，①求出点C、点D的坐标；②抛物线y=ax2+bx上是否存在点G，使得以G、C、D、F四点为顶点的四边形为平行四边形？如果存在，求出点G的坐标；如果不存在，请说明理由．（2）当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1：3时，求抛物线的函数表达式．8．如图，以O为原点的直角坐标系中，A点的坐标为（0，1），直线x=1交x轴于点B。

(2021年整理)2017_2018学年中考数学压轴题分类练习动点相似全等专题

2017_2018学年中考数学压轴题分类练习动点相似全等专题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017_2018学年中考数学压轴题分类练习动点相似全等专题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017_2018学年中考数学压轴题分类练习动点相似全等专题的全部内容。

动点相似(全等）专题1．如图，直线23y x c=-+与x轴交于点(3,0)A,与y轴交于点B，抛物线243y x bx c=-++经过点A，B.（1)求点B的坐标和抛物线的解析式；（2）M(m，0）为x轴上一个动点，过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,①点M在线段OA上运动，若以B，P，N为顶点的三角形与APM∆相似，求点M的坐标;②点M在x轴上自由运动，若三个点M，P,N中恰有一点是其它两点所连线段的中点（三点重合除外)，则称M，P,N三点为“共谐点”。

请直接写出使得M，P，N三点成为“共谐点”的m的值.2．（2017四川省眉山市）如图,抛物线22y ax bx=+-与x轴交于A、B两点，与y轴交于C点，已知A（3,0），且M(1，83-)是抛物线上另一点．(1）求a、b的值；(2)连结AC，设点P是y轴上任一点,若以P、A、C三点为顶点的三角形是等腰三角形，求P 点的坐标；(3)若点N是x轴正半轴上且在抛物线内的一动点（不与O、A重合），过点N作NH∥AC交抛物线的对称轴于H点．设ON=t，△ONH的面积为S,求S与t之间的函数关系式．3．定义：点P是△ABC内部或边上的点（顶点除外)，在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．例如：如图1，点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点．请你运用所学知识，结合上述材料,解决下列问题:在平面直角坐标系中，点M是曲线33y=x＞0)上的任意一点,点N是x轴正半轴上的任意一点．（1）如图2,点P是OM上一点,∠ONP=∠M，试说明点P是△MON的自相似点;当点M的坐标是3，3），点N3,0）时，求点P的坐标；（2）如图3，当点M的坐标是(3,3），点N的坐标是（2，0）时，求△MON的自相似点的坐标；（3）是否存在点M和点N，使△MON无自相似点？若存在,请直接写出这两点的坐标；若不存在，请说明理由．4．（2017年湖北省宜昌市第24题）已知抛物线2y ax bx c =++，其中20a b c =>>，且0a b c ++=。

2018年全国中考数学压轴题精选1 精品

2018年全国中考数学压轴题精选11.（18福建莆田）动点、相似、轴对称、最值如图：抛物线经过A （-3，0）、B （0，4）、C （4，0）三点. （1）求抛物线的解析式.（2）已知AD = AB （D 在线段AC 上），有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动；同时另一个动点Q 以某一速度从点B 沿线段BC 移动，经过t 秒的移动，线段PQ 被BD 垂直平分，求t 的值；（3）在（2）的情况下，抛物线的对称轴上是否存在一点M ，使MQ+MC 的值最小？若存在，请求出点M 的坐标；若不存在，请说明理由。

（注：抛物线2y ax bx c =++的对称轴为2b x a=-）2.（18甘肃白银等9市）动线、相似、分类讨论、最值如图，在平面直角坐标系中，四边形OABC 是矩形，点B 的坐标为（4，3）．平行于对角线AC 的直线m 从原点O 出发，沿x 轴正方向以每秒1个单位长度的速度运动，设直线m 与矩形OABC 的两边．．分别交于点M 、N ，直线m 运动的时间为t （秒）． (1) 点A 的坐标是__________，点C 的坐标是__________； (2) 当t= 秒或秒时，MN=21AC ； (3) 设△OMN 的面积为S ，求S 与t 的函数关系式；(4) 探求(3)中得到的函数S 有没有最大值？若有，求出最大值；若没有，要说明理由．3.（18广东广州）动面、相似、分类讨论、最值如图，在梯形ABCD 中，AD ∥BC ，AB=AD=DC=2cm ，BC=4cm ，在等腰△PQR 中，∠QPR=120°，底边QR=6cm ，点B 、C 、Q 、R 在同一直线l 上，且C 、Q 两点重合，如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动，t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米（1）当t=4时，求S 的值（2）当4t ≤≤10，求S 与t 的函数关系式，并求出S 的最大值4.（18广东深圳）特殊四边形存在问题、相切圆、动点、最值、直线与抛物线的位置如图9，在平面直角坐标系中，二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点，与y 轴交于C 点，与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），OB ＝OC ，tan∠ACO＝31．（1）求这个二次函数的表达式．（2）经过C 、D 两点的直线，与x 轴交于点E ，在该抛物线上是否存在这样的点F ，使以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请求出点F 的坐标；若不存在，请说明理由．（3）若平行于x 轴的直线与该抛物线交于M 、N 两点，且以MN 为直径的圆与x 轴相切，求该圆半径的长度．（4）如图10，若点G （2，y ）是该抛物线上一点，点P 是直线AG 下方的抛物线上一动点，当点P 运动到什么位置时，△APG 的面积最大？求出此时P 点的坐标和△APG 的最5.（18贵州贵阳）二次函数的实际应用、最值某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．设每个房间每天的定价增加x元．求：（1）房间每天的入住量y（间）关于x（元）的函数关系式．（3分）（2）该宾馆每天的房间收费z（元）关于x（元）的函数关系式．（3分）（3）该宾馆客房部每天的利润w（元）关于x（元）的函数关系式；当每个房间的定价为每天多少元时，w有最大值？最大值是多少？（6分）6.（18湖北恩施）旋转相似、旋转全等、直角三角形的构造如图11，在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m，CD=n.（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明.（2）求m与n的函数关系式，直接写出自变量n的取值范围.（3）以∆ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图12).在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD2＋CE2=DE2.（4）在旋转过程中,(3)中的等量关系BD2＋CE2=DE2是否始终成立,若成立,请证明,若不成立,7.（18湖北荆门）抛物线与圆、相似、直角的存在性问题、中点问题已知抛物线y =ax 2+bx +c 的顶点A 在x 轴上，与y 轴的交点为B （0，1），且b =－4ac ． (1) 求抛物线的解析式；(2) 在抛物线上是否存在一点C ，使以BC 为直径的圆经过抛物线的顶点A ？若不存在说明理由；若存在，求出点C 的坐标，并求出此时圆的圆心点P 的坐标；(3) 根据(2)小题的结论，你发现B 、P 、C 三点的横坐标之间、纵坐标之间分别有何关系?8.（18湖北荆州）动面、分段如图，等腰直角三角形纸片ABC 中，AC＝BC ＝4，∠ACB ＝90º，直角边AC 在x 轴上，B 点在第二象限，A （1，0），AB 交y 轴于E ，将纸片过E 点折叠使BE 与EA 所在直线重合，得到折痕EF （F 在x 轴上），再展开还原沿EF 剪开得到四边形BCFE ，然后把四边形BCFE 从E 点开始沿射线EA 平移，至B 点到达A 点停止.设平移时间为t （s ），移动速度为每秒1个单位长度，平移中四边形BCFE 与△AEF 重叠的面积为S. （1）求折痕EF 的长；（2）是否存在某一时刻t 使平移中直角顶点C经过抛物线243y x x =++的顶点？若存在，求出t 值；若不存在，请说明理由；（3）直接写出．．．．S 与t 的函数关系式及自变量t 的取值范围.第28题图B9.（18湖北天门）动点问题、三角形的存在性问题如图①，在平面直角坐标系中，A 点坐标为(3，0)，B 点坐标为(0，4)．动点M 从点O 出发，沿OA 方向以每秒1个单位长度的速度向终点A 运动；同时，动点N 从点A 出发沿AB方向以每秒35个单位长度的速度向终点B 运动．设运动了x 秒．(1)点N 的坐标为(________________，________________)；(用含x 的代数式表示) (2)当x 为何值时，△AMN 为等腰三角形？ (3)如图②，连结ON 得△OMN ，△OMN 可能为正三角形吗？若不能，点M 的运动速度不变，试改变点N 的运动速度，使△OMN 为正三角形，并求出点N 的运动速度和此时x 的值．10.（18湖北武汉）梯形面积的平分线、中心对称图形的特征如图 1，抛物线y=ax 2-3ax+b 经过A （-1,0），C （3,2）两点，与y 轴交于点D ，与x 轴交于另一点B.（1）求此抛物线的解析式；（2）若直线y=kx-1（k≠0）将四边形ABCD 面积二等分，求k 的值；（3）如图2，过点 E （1，-1）作EF ⊥x 轴于点F ，将△AEF 绕平面内某点旋转 180°后得△MNQ （点M ，N ，Q 分别与点 A ，E ，F 对应），使点M ，N 在抛物线上，求点M ，N 的坐标.(第24题图)11.（18湖北咸宁）动点、数形结合、“K ”字全等的构造、相似、最值如图①，正方形 ABCD 中，点A 、B 的坐标分别为（0，10），（8，4），点C 在第一象限．动点P 在正方形 ABCD 的边上，从点A 出发沿A →B →C →D 匀速运动，同时动点Q 以相同速度在x 轴上运动，当P 点到D 点时，两点同时停止运动，设运动的时间为t 秒．(1) 当P 点在边AB 上运动时，点Q 的横坐标x （长度单位）关于运动时间t （秒）的函数图象如图②所示，请写出点Q 开始运动时的坐标及点P 运动速度； (2) 求正方形边长及顶点C 的坐标； (3) 在(1)中，OP 与PQ 能否相等，若能，写出所有符合条件的t 的值；若不能，请说明理由． (4) 在(1)中当t 为何值时，△OPQ 的面积最大，并求此时P 点的坐标．12.（18湖南长沙）圆、弧长计算、圆周角定理、圆中直角三角形的构造及相似、等腰梯形如图，六边形ABCDEF 内接于半径为r （常数）的⊙O ，其中AD 为直径，且AB=CD=DE=FA. （1）当∠BAD=75 时，求BC ⌒的长；（2）求证：BC ∥AD ∥FE ；（3）设AB=x ，求六边形ABCDEF 的周长L 关于x 的函数关系式，并指出x 为何值时，L 取得最大值.(第24题图①) （第24题图②）D13（18湖南益阳）新定义、圆与抛物线的切线我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.如图12，点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点，已知点D 的坐标为(0，-3)，AB 为半圆的直径，半圆圆心M 的坐标为(1,0)，半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围； (2)你能求出经过点C 的“蛋圆”切线的解析式吗？试试看；(3)开动脑筋想一想，相信你能求出经过点D 的“蛋圆”切线的解析式.15.（18江苏连云港）新定义、同弧所对的圆内角周角外角的大小比较我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB 的最小覆盖圆就是以线段AB 为直径的圆．（1）请分别作出图1中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；A AB B CC 80100 （第25题图1）（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）；（3）某地有四个村庄E F G H，，，（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．16（18江苏南京）数形结合、一次函数的应用一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为(h)x，两车之间的距离．．．．．．．为(km)y，图中的折线表示y与x之间的函数关系．根据图象进行以下探究：信息读取（1）甲、乙两地之间的距离为km；（2）请解释图中点B的实际意义；图象理解（3）求慢车和快车的速度；（4）求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？17.（18江苏南通）一次函数与反比例、平面直角坐标系中面积的求法、反比例的代数几何意义、对称性、平行线分线段成比例已知双曲线kyx=与直线14y x=相交于A、B两点．第一象限上的点M（m，n）（在A点左GF（第25题图2）（第28题）y侧）是双曲线ky x=上的动点．过点B 作BD ∥y 轴交x 轴于点D ．过N （0，－n ）作NC ∥x 轴交双曲线ky x=于点E ，交BD 于点C ．（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值．（2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式．（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA =pMP ，MB =qMQ ，求p －q 的值．18.（18江苏宿迁）与圆相切、动点、最值如图，⊙O 的半径为1，正方形ABCD 顶点B 坐标为)0,5(，顶点D 在⊙O 上运动．(1)当点D 运动到与点A 、O 在同一条直线上时,试证明直线CD 与⊙O 相切；(2)当直线CD 与⊙O 相切时，求OD 所在直线对应的函数关系式；(3)设点D 的横坐标为x ，正方形ABCD 的面积为S ，求S 与x 之间的函数关系式，并求出S 的最大值与最小值．19.（18江苏泰州）数形结合、函数值大小的比较、不等式已知二次函数)0(21≠++=a c bx ax y 的图象经过三点（1，0），（-3，0），（0，23-）。

中考压轴题型-动点面积问题

作PI x轴于点I
(3)情况3：当5 x 9时
1 S ( BE OA) OC 2 2 = （ 3 12 x) 3
作PI x轴于点I
(3)情况4：当x 9时
作PI x轴于点I
1 S OA AH 2
54 3 = x
动点面积问题
1、如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC 上的动点（与 1 端点B、C不重合），过点D作直线 y x b 交折线 2 OAB于点E．记△ODE的面积为S，求S与b的函数关系式．
3 3 5 情况1：当1<b ，时情况2：当 <b ，时 2 2 2 1 S S矩 -SOCD SAOE -SBDE S OE CO=b 2 5 2 3 = b-b b ( 1<b ) 2 2
8 2 2 8 5 t 5 t (0 t 4);t=2时，S最大 = 5 2 2 8 (3)S = t t (4<t 5)；t=5时，S最大 =2 5 5 2t 8(5<t 6)；t=6时，S最大 =4
综上所述，当t=6时，S最大 =4
(3)情况1：当0 x 3时
作PI x轴于点I
1 4 3 S梯形 = （EF OQ) OC = （3 x) 2 3
S S梯形 -SHAQ
1 S梯形 - AH AQ 2 4 3 3 2 (3)情况2：当3 x 5时 = （3 x) （x-3) 3 2
P(3,3 3 )
(2)情况1：当NM=NA时
QMA=QAM=30
0
MNO=60 0 PQO=60
0
点N与点Q重合，点P与点D重合。此时，m 0

2017-2018学年中考数学《动点面积》强化练习卷(无答案)-word文档资料

动点面积专题1. 如图1，在平面直角坐标系中，四边形OABC 各顶点的坐标分别为)0,14(),35,9(),33,3(),0,0(C B A O ，动点P 与Q 同时从O 点出发，运动时间为t 秒，点P 沿OC 方向以1单位长度/秒的速度向点C 运动，点Q 沿折线BC -AB -OA 运动，在BC AB OA ，，上运动的速度分别为2533，，（单位长度/秒）.当Q P ，中的一点到达C 点时，两点同时停止运动.（1）求AB 所在直线的函数表达式；（2）如图2，当点Q 在AB 上运动时，求CPQ ∆的面积S 关于t 的函数表达式及S 的最大值；（3）在P ，Q 的运动过程中，若线段PQ 的垂直平分线经过四边形OABC 的顶点，求相应的t 值.2. 如图，二次函数2y x bx c =++的图像与x 轴交于A 、B 两点，与y 轴交于点C ，C OB =O ．点D 在函数图像上，CD//x 轴，且CD 2=，直线l 是抛物线的对称轴，E 是抛物线的顶点．（1）求b 、c 的值；（2）如图①，连接BE ，线段C O 上的点F 关于直线l 的对称点F '恰好在线段BE 上，求点F 的坐标；（3）如图②，动点P 在线段OB 上，过点P 作x 轴的垂线分别与C B 交于点M ，与抛物线交于点N ．试问：抛物线上是否存在点Q ，使得Q ∆P N 与∆APM 的面积相等，且线段Q N 的长度最小？如果存在，求出点Q 的坐标；如果不存在，说明理由．3.如图，已知二次函数的图象经过三点. （1）求该二次函数的解析式；（2）点是该二次函数图象上的一点，且满足(是坐标原点)，求点的坐标；（3）点是该二次函数图象上位于一象限上的一动点，连接分别交轴与点若的面积分别为求的最大值. 4.已知直线与抛物线有一个公共点，且．（Ⅰ）求抛物线顶点的坐标（用含的代数式表示）；（Ⅱ）说明直线与抛物线有两个交点；（Ⅲ）直线与抛物线的另一个交点记为．（ⅰ）若，求线段长度的取值范围；（ⅱ）求面积的最小值．5.在平面直角坐标系内，直线AB 垂直于x 轴于点C （点C 在原点的右侧），并分别与直线y ＝x 和双曲线y ＝相交于点A 、B ，且AC ＋BC ＝4，则△OAB 的面积为（）A ．2＋3或2－3B ．＋1或－1C ．2－3D ．－1 6.如图，在菱形CD AB 中，60∠A =，D 8A =，F 是AB 的中点．过点F 作F DE ⊥A ，垂足为E ．将F ∆AE 沿点A 到点B 的方向平移，得到F '''∆A E ．设P 、'P 分别是F E 、F ''E 的中点，当点'A 与点B 重合时，四边形CD 'PP 的面积为A ．B ． C. D ．8-7.已知：Rt △EFP 和矩形ABCD 如图①摆放（点P 与点B 重合），点F ，B （P ），C 在同一条直线上，AB ＝EF ＝6cm ，BC ＝FP ＝8cm ，∠EFP ＝90°。

2017-2018学年中考数学压轴题分类练习 动点面积专题(无答案)

中考数学压轴题：由动点引出的几种面积问题

2018年人教版中考压轴题汇编《因动点产生的面积问题》含答案

2018年中考数学压轴题100题精选

2017-2018学年中考数学 题型训练卷：数字及图形规律问题(无答案)

2017-2018学年中考数学压轴题分类练习动点特殊四边形专题

2018年中考数学压轴题专题汇编36动点综合问题

2018年中考压轴题(动点问题) 精品

2017-2018学年中考数学经典题型训练卷：动点面积最值问题(无答案)

2018年中考数学压轴题专题解析---几何动态探究问题—动点+动面

2018年人教版中考压轴题汇编《因动点产生的面积问题》含答案

2018年中考数学压轴题专题解析---动点梯形与动点面积

2017-2018学年中考数学 题型训练卷：动点面积最值问题(无答案)

(2021年整理)2017_2018学年中考数学压轴题分类练习动点相似全等专题

2018年全国中考数学压轴题精选1 精品

中考压轴题型-动点面积问题

2017-2018学年中考数学《动点面积》强化练习卷(无答案)-word文档资料

2017-2018学年中考数学压轴题分类练习动点面积专题(无答案)

2017-2018学年中考数学题型训练卷：数字及图形规律问题(无答案)

2017-2018学年中考数学题型训练卷：动点面积最值问题(无答案)