基于Matlab的DFT及FFT频谱分析_刘小群

合集下载

数字信号处理基于matlab(用DFT作谱分析,窗函数的设计)

实验一：用DFT作谱分析x1=[1 1 1 1];x2=[1 2 3 4 4 3 2 1];n1=0:8;x3=cos(n1*pi/4);n2=0:8;x4=sin(n2*pi/8);figuresubplot(2,2,1);stem(x1);subplot(2,2,2);stem(x2);subplot(2,2,3);stem(x3);subplot(2,2,4);stem(x4);N1=8;F1x1=fft(x1,N1);F1x2=fft(x2,N1);F1x3=fft(x3,N1);F1x4=fft(x4,N1);figuresubplot(2,2,1);stem(abs(F1x1));subplot(2,2,2);stem(abs(F1x2));subplot(2,2,3);stem(abs(F1x3));subplot(2,2,4);stem(abs(F1x4));N3=256;F3x1=fft(x1,N3);F3x2=fft(x2,N3);F3x3=fft(x3,N3);F3x4=fft(x4,N3);w=2/N3*[0:N3-1];figuresubplot(2,2,1);plot(w,abs(F3x1));subplot(2,2,2);plot(w,abs(F3x2));subplot(2,2,3);plot(w,abs(F3x3));subplot(2,2,4);plot(w,abs(F3x4));N6=64;t=0:1/64:1/64*(N6-1);x6=cos(8*pi*t)+cos(16*pi*t)+cos(20*pi*t);figure;plot(x6)Fx6=fft(x6,N6);N=64w6=2/N6*[0:N6-1];figure;plot(w6,Fx6)实验二：用双线性法设计IIR数字滤波器clear all;close all;clcT=1;Wp=2/T*tan(0.2*pi/2);Ws=2/T*tan(0.3*pi/2);Rp=1;Rs=15;[N,Wc]=buttord(Wp,Ws,Rp,Rs,'s');[B,A]=butter(N,Wc,'s');[C,D]=bilinear(B,A,1/T);W=0:0.001*pi:0.5*pi;H=freqs(B,A,W);Hd=freqz(C,D,W);figuresubplot(3,1,1);plot(W/pi,abs(H))grid ontitle('模拟巴特沃斯滤波器')xlabel('Frequency/Hz')ylabel('Magnitude')subplot(3,1,2);plot(W/pi,abs(Hd))grid ontitle('数字巴特沃斯滤波器')xlabel('Didital Frequency/pi')ylabel('Magnitude')Hd_db=-20*log(abs(Hd(1)./(abs(Hd)+eps)));subplot(3,1,3);plot(W/pi,Hd_db)grid ontitle('数字巴特沃斯滤波器波特图')xlabel('Didital Frequency/pi')ylabel('bd_Magnitude')x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4.8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];M=512;fx=fft(x,M);y=filter(C,D,x);fy=fft(y,M);f=1/512*[0:511]*250figuresubplot(2,1,1);plot(x);subplot(2,1,2);plot(f,abs(fx));figuresubplot(2,1,1);plot(y);subplot(2,1,2);plot(f,abs(fy));心电图谱分析1、滤波前波形和频谱2、滤波后波形和频谱实验三：用窗函数法设计FIR数字滤波器一、N=33，用四种窗设计滤波器function hd=ideal(N,wc)for n=0:N-1if n==(N-1)/2hd(n+1)=wc/pi;else hd(n+1)=sin(wc*(n-(N-1)/2))/(pi*(n-(N-1)/2));endendclear all;close all;clcN=33;wc=pi/4;hd=ideal(N,wc);w1=boxcar(N);w2=hamming(N);w3=hann(N);w4=blackman(N);h1=hd.*w1';h2=hd.*w2';h3=hd.*w3';h4=hd.*w4';M=512;fh1=fft(h1,M);db1=-20*log10(abs(fh1(1)./(abs(fh1)+eps)));fh2=fft(h2,M);db2=-20*log10(abs(fh2(1)./(abs(fh2)+eps)));fh3=fft(h3,M);db3=-20*log10(abs(fh3(1)./(abs(fh3)+eps)));fh4=fft(h4,M);db4=-20*log10(abs(fh4(1)./(abs(fh4)+eps)));w=2/M*[0:M-1];figure;subplot(2,2,1);stem(h1);grid on;title('矩形窗');xlabel('n');ylabel('h(n)');subplot(2,2,2);plot(w,abs(fh1));grid on;title('矩形窗');xlabel('w');ylabel('H(k)');subplot(2,2,3);plot(w,db1);grid on;title('矩形窗');xlabel('w');ylabel('20lg(H(k)/H(0))'); subplot(2,2,4);plot(w,angle(fh1)); grid on;title('矩形窗');xlabel('w');ylabel('相位特性');figure;subplot(2,2,1);stem(h2);grid on;title('汉宁窗');xlabel('n');ylabel('h(n)');subplot(2,2,2);plot(w,abs(fh2)); grid on;title('汉宁窗');xlabel('w');ylabel('H(k)');subplot(2,2,3);plot(w,db2);grid on;title('汉宁窗');xlabel('w');ylabel('20lg(H(k)/H(0))'); subplot(2,2,4);plot(w,angle(fh2)); grid on;title('汉宁窗');xlabel('w');ylabel('相位特性');figure;subplot(2,2,1);stem(h3);grid on;title('海明窗');xlabel('n');ylabel('h(n)');subplot(2,2,2);plot(w,abs(fh3)); grid on;title('海明窗');xlabel('w');ylabel('H(k)');subplot(2,2,3);plot(w,db3);grid on;title('海明窗');xlabel('w');ylabel('20lg(H(k)/H(0))'); subplot(2,2,4);plot(w,angle(fh3)); grid on;title('海明窗');xlabel('w');ylabel('相位特性');figure;subplot(2,2,1);stem(h4);grid on;title('布莱克曼窗');xlabel('n');ylabel('h(n)');subplot(2,2,2);plot(w,abs(fh4)); grid on;title('布莱克曼窗');xlabel('w');ylabel('H(k)');subplot(2,2,3);plot(w,db4);grid on;title('布莱克曼窗');xlabel('w');ylabel('20lg(H(k)/H(0))'); subplot(2,2,4);plot(w,angle(fh4)); grid on;title('布莱克曼窗');xlabel('w');ylabel('相位特性');二，用一种窗采用N=15或N=33、w=pi/4设计滤波器clear all;close all;clcN=15;wc=pi/4;hd=ideal(N,wc);w1=blackman(N);h1=hd.*w1';M=512;fh1=fft(h1,M);db1=-20*log10(abs(fh1(1)./(abs(fh1)+eps)));w=2/M*[0:M-1];figure;subplot(2,2,1);stem(h1);grid on;title('布莱克曼窗(N=15)');xlabel('n');ylabel('h(n)');subplot(2,2,2);plot(w,abs(fh1));grid on;title('布莱克曼窗(N=15)');xlabel('w');ylabel('H(k)');subplot(2,2,3);plot(w,db1);grid on;title('布莱克曼窗(N=15)');xlabel('w');ylabel('20lg(H(k)/H(0))');subplot(2,2,4);plot(w,angle(fh1));grid on;title('布莱克曼窗(N=15)');xlabel('w');ylabel('相位特性');N=33;wc=pi/4;hd=ideal(N,wc);w2=blackman(N);h2=hd.*w2';M=512;fh2=fft(h2,M);db2=-20*log10(abs(fh2(1)./(abs(fh2)+eps)));w=2/M*[0:M-1];figure;subplot(2,2,1);stem(h2);grid on;title('布莱克曼窗(N=33)');xlabel('n');ylabel('h(n)');subplot(2,2,2);plot(w,abs(fh2)); grid on;title('布莱克曼窗(N=33)'); xlabel('w');ylabel('H(k)');subplot(2,2,3);plot(w,db2);grid on;title('布莱克曼窗(N=33)'); xlabel('w');ylabel('20lg(H(k)/H(0))'); subplot(2,2,4);plot(w,angle(fh2)); grid on;title('布莱克曼窗(N=33)'); xlabel('w');ylabel('相位特性');三、提取50HZ基频信号N=512;t=0:1/512:1/512*(N-1);x=sin(100*pi*t)+sin(200*pi*t)+sin(300*pi*t); Fx=fft(x,N);w3=2/N*[0:N-1];figure;subplot(2,1,1);plot(x);grid on;title('抽样信号');xlabel('n');ylabel('y(n)');subplot(2,1,2);plot(w3,abs(Fx));grid on;title('抽样信号频谱');xlabel('pi');ylabel('Magnitude');N=33;wc=0.4;hd=ideal(N,wc);w1=boxcar(N);w2=blackman(N);h1=hd.*w1';y1=conv(x,h1);h2=hd.*w2';y2=conv(x,h2); figure;subplot(2,1,1);plot(y1(1:64)); grid on;title('矩形窗');xlabel('n');ylabel('y(n)');subplot(2,1,2);plot(y2(1:64)); grid on;title('布莱克曼窗');xlabel('n');ylabel('y(n)');Fy1=fft(y1,N);Fy2=fft(y2,N);figure;subplot(2,1,1);plot(abs(Fy1)); subplot(2,1,2);plot(abs(Fy2));。

用MATLAB进行FFT频谱分析

用MATLAB进行FFT频谱分析假设一信号：()()292.7/2cos1.0996.2/2sin1.06.0+++=ttRππ画出其频谱图。

分析：首先，连续周期信号截断对频谱的影响。

DFT变换频谱泄漏的根本原因是信号的截断。

即时域加窗，对应为频域卷积，因此，窗函数的主瓣宽度等就会影响到频谱。

实验表明，连续周期信号截断时持续时间与信号周期呈整数倍关系时，利用DFT变换可以得到精确的模拟信号频谱。

举一个简单的例子：()ππ2.0100cos+=tY其周期为。

截断时不同的持续时间影响如图一.1：（对应程序）140.0160.0180.02截断时，时间间期为周期整数倍，频谱图0.0250.0320406080100截断时，时间间期不为周期整数倍，频谱图图错误!文档中没有指定样式的文字。

.1其次，采样频率的确定。

根据Shannon 采样定理，采样带限信号采样频率为截止频率的两倍以上，给定信号的采样频率应>1/，取16。

再次，DFT 算法包括时域采样和频域采样两步，频域采样长度M 和时域采样长度N 的关系要符合M ≧N 时，从频谱X(k)才可完全重建原信号。

实验中信号R 经采样后的离散信号不是周期信号，但是它又是一个无限长的信号，因此处理时时域窗函数尽量取得宽一些已接近实际信号。

实验结果如图一.2：其中，0点位置的冲激项为直流分量造成（对应程序为）0204060801001201401601802000.40.50.60.70.800.050.10.150.20.250.30.350.40.450.550100150图错误!文档中没有指定样式的文字。

.2♣ARMA （Auto Recursive Moving Average ）模型：将平稳随机信号x(n)看作是零均值，方差为σu 2的白噪声u(n)经过线性非移变系统H(z)后的输出，模型的传递函数为()()()∑∑=-=-+==Pk kk Qr r rza zb z A z B z H 111用差分方程表示为()()()∑∑==-+--=Qr r P k k r n u b k n x a n x 01AR （Auto Recursive ）自回归模型，即ARMA 模型中系数b 只有在r=0的情况下为1，其余都是零，获得一个全极点模型：()()()∑=-+==Pk kk za z A z B z H 111差分方程表示为：()()()n u k n x a n x Pk k +--=∑=1AR 模型的功率谱估计为：()()()Ω-ΩΩ=j j uj x e A e A eS 12σ程序：%%------------------------------------------------------------------------%%功能：利用MATLAB 的FFT 函数做双正弦信号频谱分析 %%------------------------------------------------------------------------ fs=16; t=0:1/fs:200;x6=+sin(2*pi*t/*+cos(2*pi*t/+2)*;subplot(2,1,1);plot(t,x6);N=length(t);subplot(212);plot((-N/2:N/2-1)*fs/N,abs(fftshift(fft(x6,N)))) %绘制信号的频谱，横轴对应实际频率axis([0 0 160]);例子：%%------------------------------------------------------------------------%%功能：连续周期信号截断对频谱的影响%%------------------------------------------------------------------------fs=8000;n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,1);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,2);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时，时间间期为周期整数倍，频谱图');n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,3);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,4);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时，时间间期不为周期整数倍，频谱图');。

用MAtlaB进行DFT及FFT频谱分析和运算结果的比较的实验

DSP MATLAB上机实验一班级：学号：姓名：函数代码：function xn()format longq=0.9+0.3*i;wn=exp(-2*pi*i/32);xn=q.^[0:31]xk1=(1-q^32)./(1-q*wn.^[0:31]) %利用公式计算XK的理论值xk2=fft(xn,32) %运用基二基2时间抽选的FFT算法计算Xkdiff=xk1-xk2 %两者的差运行xn（）即得结果结果为：xn =Columns 1 through 21.000000000000000 0.900000000000000 + 0.300000000000000i Columns 3 through 40.720000000000000 + 0.540000000000000i 0.486000000000000 + 0.702000000000000i Columns 5 through 60.226800000000000 + 0.777600000000000i -0.029160000000000 + 0.767880000000000i Columns 7 through 8-0.256608000000000 + 0.682344000000000i -0.435650400000000 + 0.537127200000000i Columns 9 through 10-0.553223520000000 + 0.352719360000000i -0.603716976000000 + 0.151480368000000i Columns 11 through 12-0.588789388800000 - 0.044782761600000i -0.516475621440000 - 0.216941302080000i Columns 13 through 14-0.399745668672000 - 0.350189858304000i -0.254714144313600 - 0.435094573075200i Columns 15 through 16-0.098714357959680 - 0.467999359061760i 0.051556885554816 - 0.450813730543488i Columns 17 through 180.181645316162381 - 0.390265291822695i 0.280560372092951 - 0.296745167791711i Columns 19 through 200.341527885221169 - 0.182902539384655i 0.362245858514449 - 0.062153919879838i Columns 21 through 220.344667448626955 + 0.052735229662480i 0.294380134865516 + 0.150861941284319i Columns 23 through 240.219683538993669 + 0.224089787615542i 0.130488248809639 + 0.267585870552088i Columns 25 through 260.037163662763049 + 0.279973758139771i -0.050544830955187 + 0.263125481154709i Columns 27 through 28-0.124427992206081 + 0.221649483752682i -0.178480038111278 + 0.162156137715589i Columns 29 through 30-0.209278875614827 + 0.092396512510647i -0.216069941806538 + 0.020373198575134i Columns 31 through 32-0.200574907198425 - 0.046485103824341i -0.166571885331280 - 0.102009065601434i xk1 =Columns 1 through 20.693972803195698 + 3.499715655993840i 2.792267857648369 + 8.050455721438597i Columns 3 through 49.402964607913189 - 9.135013555028673i 1.866445467462052 - 3.833832762635439i Columns 5 through 61.131822689478846 -2.234157347130941i 0.904793922868299 - 1.534629307882413i Columns 7 through 80.799557206779214 - 1.139609357830753i 0.739605630813150 - 0.882314367550644i Columns 9 through 100.700861643199240 - 0.698565363198060i 0.673575789604202 - 0.558478478082158i Columns 11 through 120.653109437428513 - 0.446244996656357i 0.636991253015040 - 0.352689135211701i Columns 13 through 140.623788380776217 - 0.272085968296931i 0.612612873742441 - 0.200641851238978i Columns 15 through 160.602883340189454 - 0.135703205872800i 0.594200434347139 - 0.075313670713158i Columns 17 through 180.586277479436723 - 0.017949220626496i 0.578899608820263 + 0.037651723475093i Columns 19 through 200.571898466305671 + 0.092606953506914i 0.565135772013173 + 0.147983310049841i Columns 21 through 220.558492135768929 + 0.204880771267792i 0.551859131244066 + 0.264522208758452i Columns 23 through 240.545133643745847 + 0.328364940349017i 0.538214362209129 + 0.398257131749283i Columns 25 through 260.531001527230573 + 0.476677768575531i 0.523403723684219 + 0.567132338629562i Columns 27 through 280.515362483773298 + 0.674849986673143i 0.506925762334513 + 0.808101482252638i Columns 29 through 300.498467012317214 + 0.980906313951879i 0.491389377970933 + 1.219207441587793i Columns 31 through 320.490732201059483 + 1.577081955159802i 0.517353973624932 + 2.188832884536347i xk2 =Columns 1 through 20.693972803195698 + 3.499715655993839i 2.792267857648366 + 8.050455721438597i Columns 3 through 49.402964607913182 - 9.135013555028694i 1.866445467462051 - 3.833832762635439iColumns 5 through 61.131822689478844 -2.234157347130942i 0.904793922868298 - 1.534629307882413i Columns 7 through 80.799557206779213 - 1.139609357830754i 0.739605630813149 - 0.882314367550644i Columns 9 through 100.700861643199240 - 0.698565363198060i 0.673575789604202 - 0.558478478082158i Columns 11 through 120.653109437428513 - 0.446244996656356i 0.636991253015040 - 0.352689135211701i Columns 13 through 140.623788380776217 - 0.272085968296931i 0.612612873742441 - 0.200641851238978i Columns 15 through 160.602883340189454 - 0.135703205872799i 0.594200434347139 - 0.075313670713158i Columns 17 through 180.586277479436723 - 0.017949220626496i 0.578899608820263 + 0.037651723475093i Columns 19 through 200.571898466305671 + 0.092606953506913i 0.565135772013173 + 0.147983310049840i Columns 21 through 220.558492135768929 + 0.204880771267792i 0.551859131244066 + 0.264522208758452i Columns 23 through 240.545133643745847 + 0.328364940349016i 0.538214362209129 + 0.398257131749282i Columns 25 through 260.531001527230572 + 0.476677768575531i 0.523403723684219 + 0.567132338629563iColumns 27 through 280.515362483773297 + 0.674849986673143i 0.506925762334512 + 0.808101482252638i Columns 29 through 300.498467012317213 + 0.980906313951878i 0.491389377970932 + 1.219207441587794i Columns 31 through 320.490732201059480 + 1.577081955159802i 0.517353973624928 + 2.188832884536347i diff =1.0e-013 *Columns 1 through 20.001110223024625 + 0.004440892098501i 0.031086244689504Columns 3 through 40.071054273576010 + 0.213162*********i 0.013322676295502 + 0.008881784197001i Columns 5 through 60.015543122344752 + 0.004440892098501i 0.004440892098501 + 0.006661338147751i Columns 7 through 80.008881784197001 + 0.002220446049250i 0.003330669073875 - 0.001110223024625i Columns 9 through 100.006661338147751 - 0.001110223024625i 0.006661338147751 - 0.003330669073875i Columns 11 through 120.001110223024625 - 0.009992007221626i 0.002220446049250 + 0.003330669073875i Columns 13 through 14-0.002220446049250 + 0.000555111512313i 0.003330669073875 + 0.000832667268469i Columns 15 through 160.006661338147751 - 0.006938893903907i 0.002220446049250 + 0.000693889390391i Columns 17 through 180.002220446049250 - 0.000173472347598i -0.001110223024625 - 0.004302114220422i Columns 19 through 200.001110223024625 + 0.010963452368173i -0.001110223024625 + 0.006383782391595i Columns 21 through 220.001110223024625 + 0.002775557561563i 0 + 0.000555111512313i Columns 23 through 240.001110223024625 + 0.006106226635438i 0.004440892098501 + 0.003330669073875i Columns 25 through 260.004440892098501 0.001110223024625 - 0.003330669073875i Columns 27 through 280.012212453270877 - 0.002220446049250i 0.006661338147751 - 0.004440892098501i Columns 29 through 300.009992007221626 + 0.002220446049250i 0.011102230246252 - 0.006661338147751i Columns 31 through 320.028310687127941 0.035527136788005 - 0.008881784197001i 由上面结果可知，由基2时间抽选的FFT算法所得到的DFT结果与利用公式法所得的理论值稍有偏差，但误差较小，从结果可以看出大概在小数点第15位才开始出现误差，故而用计算机FFT处理数据在精度上是可以接受的。

matlab求N点DFT,利用MATLAB實现信号DFT的计算.doc

matlab求N点DFT,利⽤MATLAB實现信号DFT的计算.doc 利⽤MATLAB實现信号DFT的计算07级电信(2)班刘坤洋 24实验⼀利⽤MATLAB实现信号DFT的计算⼀、实验⽬的：1、熟悉利⽤MATLAB计算信号DFT的⽅法2、掌握利⽤MATLAB实现由DFT计算线性卷积的⽅法⼆、实验设备：电脑、matlab软件三、实验内容：练习⽤matlab中提供的内部函数⽤于计算DFTfft(x)，fft(x，N)，ifft(x)，ifft(x，N)的含义及⽤法在进⾏DFT时选取合适的时域样本点数N请举例，并编程实现题⽬：源程序： >> N=30; %数据的长度>>L=512; %DFT的点数>>f1=100; f2=120;>>fs=600; %抽样频率>>T=1/fs; %抽样间隔>>ws=2*pi*fs;>>t=(0:N-1)*T;>>f=cos(4*pi*f1*t)+cos(4*pi*f2*t);>>F=fftshift(fft(f,L));>>w=(-ws/2+(0:L-1)*ws/L)/(2*pi);>>hd=plot(w,abs(F));>>ylabel('幅度谱')>> xlabel('频率/Hz')>> title('my picture')结果图：在对信号进⾏DFT时选择hamming窗增加频率分辨率请举例，并编程实现题⽬：源程序：>> N=50; %数据的长度>>L=512; %DFT的点数>>f1=100;f2=150;>>fs=600; %抽样频率>>T=1/fs; %抽样间隔>>ws=2*pi*fs;>>t=(0:N-1)*T;>>f=cos(4*pi*f1*t)+0.15*cos(4*pi*f2*t);>>wh=(hamming(N))';>>f=f.*wh;>>F=fftshift(fft(f,L));>>w=(-ws/2+(0:L-1)*ws/L)/(2*pi);>>plot(w,abs(F));>>ylabel('幅度谱')>> xlabel('频率/Hz')>> title('my picture')>> legend('N=50')结果图：2、增加DFT点数M以显⽰更多频谱细节请举例，并编程实现题⽬：利⽤MATLAB计算16点序列x[k]的512点DFT。

实验三用FFT对信号进行频谱分析和MATLAB程序

实验三用FFT对信号进行频谱分析和MATLAB程序实验三中使用FFT对信号进行频谱分析的目的是通过将时域信号转换为频域信号，来获取信号的频谱信息。

MATLAB提供了方便易用的函数来实现FFT。

首先，我们需要了解FFT的原理。

FFT（快速傅里叶变换）是一种快速计算离散傅里叶变换（DFT）的算法，用于将离散的时间域信号转换为连续的频域信号。

FFT算法的主要思想是将问题划分为多个规模较小的子问题，并利用DFT的对称性质进行递归计算。

FFT算法能够帮助我们高效地进行频谱分析。

下面是一个使用MATLAB进行频谱分析的示例程序：```matlab%生成一个10秒钟的正弦波信号，频率为1Hz，采样率为100Hzfs = 100; % 采样率t = 0:1/fs:10-1/fs; % 时间范围f=1;%正弦波频率x = sin(2*pi*f*t);%进行FFT计算N = length(x); % 信号长度X = fft(x); % FFT计算magX = abs(X)/N; % 幅值谱frequencies = (0:N-1)*(fs/N); % 频率范围%绘制频谱图figure;plot(frequencies, magX);xlabel('频率(Hz)');ylabel('振幅');title('信号频谱');```上述代码生成了一个10秒钟的正弦波信号，频率为1 Hz，采样率为100 Hz。

通过调用MATLAB的fft函数计算信号的FFT，然后计算每个频率分量的幅值谱，并绘制出信号频谱图。

在频谱图中，横轴表示频率，纵轴表示振幅。

该实验需要注意以下几点：1.信号的采样率要与信号中最高频率成一定比例，以避免采样率不足导致的伪频谱。

2.FFT计算结果是一个复数数组，我们一般只关注其幅值谱。

3.频率范围是0到采样率之间的频率。

实验三的报告可以包含以下内容：1.实验目的和背景介绍。

基于Matlab的DFT及FFT频谱分析

基于Matlab的DFT及FFT频谱分析基于Matlab的DFT及FFT频谱分析一、引言频谱分析是信号处理中的重要任务之一，它可以揭示信号的频率特性和能量分布。

离散傅里叶变换（DFT）及快速傅里叶变换（FFT）是常用的频谱分析工具，广泛应用于许多领域。

本文将介绍通过Matlab进行DFT及FFT频谱分析的方法和步骤，并以实例详细说明。

二、DFT及FFT原理DFT是一种将时域信号转换为频域信号的离散变换方法。

它将信号分解成若干个正弦和余弦函数的叠加，得到频率和幅度信息。

FFT是一种高效的计算DFT的算法，它利用信号的对称性和周期性，将计算复杂度从O(N^2)降低到O(NlogN)。

FFT通过将信号分解成不同长度的子序列，递归地进行计算，最终得到频谱信息。

三、Matlab中的DFT及FFT函数在Matlab中，DFT及FFT可以通过内置函数进行计算。

其中，DFT使用函数fft，FFT使用函数fftshift。

fft函数可直接计算信号的频谱，fftshift函数对频谱进行频移操作，将低频移到频谱中心。

四、Matlab中DFT及FFT频谱分析步骤1. 读取信号数据首先，将待分析的信号数据读入到Matlab中。

可以使用内置函数load读取文本文件中的数据，或通过自定义函数生成模拟信号数据。

2. 时域分析通过plot函数将信号数据在时域进行绘制，以观察信号的波形。

可以设置合适的坐标轴范围和标签，使图像更加清晰。

3. 信号预处理针对不同的信号特点，可以进行预处理操作，例如去除直流分量、滤波等。

这些操作可提高信号的频谱分析效果。

4. 计算DFT/FFT使用fft函数计算信号数据的DFT/FFT，并得到频谱。

将信号数据作为输入参数，设置采样频率和点数，计算得到频谱数据。

5. 频域分析通过plot函数将频谱数据在频域进行绘制，观察信号的频率特性。

可以设置合适的坐标轴范围和标签，使图像更加清晰。

6. 结果解读根据频谱图像，分析信号的频率成分、幅度分布和峰值位置。

基于MATLAB的FFT离散频谱分析

基于MATLAB的FFT离散频谱分析作者：周盼甘丽群刘华超来源：《电脑知识与技术》2016年第36期摘要：通过仿真形象揭示了MATLAB上FFT过程中频谱泄漏和栅栏效应现象，重点从理论上分析了其产生原因。

针对以上两情况导致的频率和幅值上的误差，介绍了常用的校正方法的原理、推导过程以及运用的局限性。

指出了幅值校正过程中所有恢复系数全为[2N]的常见错误。

为MATLAB上FFT的理解和应用提供一定的帮助作用。

关键词：MATLAB；FFT；频谱泄漏；栅栏效应；频率幅值校正中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2016）36-0277-04Analysis of Discrete Spectrum Based on FFT using MATLABZHOU Pan1， GAN Li-qun2 ， LIU Hua-chao2（1. School of Electronic Engineering ， Xi'an Shiyou University， Xi'an 710065，China； 2. School of electrical and Information Engineering，Chongqing University of Science and Technology，Chongqing 401331，China）Abstracts： The phenomenon of spectrum leakage and packet fence effect in the process of fast Fourier transform was revealed through simulation， and the cause of which was analyzed emphatically in theory. Aiming at errors of frequency and amplitude caused by FFT in MATLAB，the principle， derivation and the application limitations of the common correction methods was introduced in detail. The frequent fault which regarded the all recovery coefficients for amplitude correction as [2N] was also pointed out. The paper can provide some help for the understanding and application of FFT.Key words： MATLAB； FFT； spectrum leakage； fence effect； frequency amplitude correction信号处理广泛运用于语音图像处理、通信、生物医学等领域，是一门极其重要的学科。

基于FFT和窗函数的频谱分析论文终稿

数字信号处理论文题目：基于 DFT变换的频谱分析专业：电气工程及其自动化班级：13级电气卓越班学号：0618学生姓名：蒋伟明指导老师：王小华日期：2015年10月基于 DFT变换的频谱分析摘要DFT及FFT是数字信号处理的重要内容。

DFT是TTF的基础，FFT是DFT的快速算法，在MATLAB中可以利用函数FFT来计算序列的离散傅里叶变换DFT。

数字信号处理基本上从两个方面来解决信号的处理问题：一个是时域方法，即数字滤波；另一个是频域方法，即频谱分析。

FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域，这样有助于对信号进行分析。

本文采用四种窗函数，利用MATLAB中的FFT函数对给定信号进行了分析。

AbstractDFT and FFT is one of the most important parts in digital signal processing．DFT is the basis for FFT in the fast algorithm 0f DFT．The DFT of sequence can be calculated by using the function of FFT in MATLAB．Basically, digital signal processing (DSP) can solve signal processing problems from two aspects: one is the time domain method, namely digital filtering; Another is the frequency domain method, that is, frequency spectrum analysis. FFT is a fast algorithm of discrete Fourier transform, which can be a signal transformation to the frequency domain,and this helps to analyze the signal.Based on the four kinds of window function, a given signal will be analyzed by the function of FFT of MATLAB.关键词：DFT变换；窗函数；频谱分析0引言数字信号处理中通常是取其有限的时间片段进行分析，而不是对无限长的信号进行测量和运算。

基于MATLAB的FFT算法的设计

基于MATLAB的FFT算法的设计FFT算法是一种用于快速计算离散傅里叶变换（DFT）的算法。

它通过将N点DFT分解为多个长度为N/2的DFT并递归地计算这些子问题来实现快速计算。

FFT算法是一种高效的算法，广泛应用于信号处理、图像处理和通信系统等领域。

MATLAB作为一种流行的科学计算软件，在信号处理中广泛使用。

MATLAB提供了快速计算DFT的函数fft，可以方便地进行信号频谱分析和滤波等操作。

下面将从FFT的理论原理、算法优化以及MATLAB的使用等方面展开讨论，详细介绍基于MATLAB的FFT算法的设计。

1.FFT算法的理论原理FFT算法基于蝶形运算的思想，将N点DFT分解为多级运算，每级运算中都会进行蝶形运算。

蝶形运算是一种两两计算的运算方式，可以将两个复数进行加减运算，并乘以一个旋转因子进行旋转。

FFT算法的主要思想是将N个点的DFT分解为两个N/2个点的DFT，然后再将这两个N/2个点的DFT两两合并为一个N个点的DFT。

这种分解递归进行下去，直到最后只有一个点，即得到DFT结果。

2.FFT算法的算法优化在实施FFT算法时，可以进行一些算法优化，以提高计算速度和效率。

首先是位逆序运算。

在FFT算法中，需要将输入的N个点按照位逆序重新排列，这在MATLAB中可以使用bitrevorder函数实现。

其次是预计算旋转因子。

FFT算法中需要进行的旋转因子的计算比较耗时，可以将旋转因子预先计算好并存储起来，以便使用时直接调用。

最后是避免重复计算。

由于FFT算法的递归特性，可能会重复计算一些结果。

可以使用分治法，将计算结果缓存起来，避免重复计算。

3.MATLAB中的FFT算法使用在MATLAB中，可以使用fft函数进行FFT计算。

这个函数可以接受输入信号和采样频率等参数，同时还可以设定计算结果的长度。

如果不指定计算结果的长度，默认将输入信号进行补零操作，使其长度为2的幂。

MATLAB的fft函数返回的结果是频率域的复数谱，可以使用abs函数取结果的绝对值，得到频谱的幅度谱。

(完整word版)用matlab实现DFTFFT

用matlab实现DFT FFT目录实验目的 (2)实验内容 (2)1.用MATLAB实现DFT (2)2.用MATLAB实现FFT，分析有限离散序列的FFT (3)3.通过分别计算时间，得出DFT与FFT的算法差异 (7)实验原理 (8)1. 离散傅里叶变换的快速算法FFT (8)2. FFT提高运算速度的原理 (9)3. 理论分析DFT与FFT算法差异 (11)实验步骤 (12)实验结果 (13)实验分析 (27)实验结论 (33)实验体会 (33)实验目的1.通过研究DFT,FFT性质，用语言实现DFT, FFT。

不使用MATLAB现有的FFT函数，自己编写具体算法。

2.掌握FFT基2时间抽选法，理解其提高减少乘法运算次数提高运算速度的原理。

3.设计实验，得出DFT和FFT算法差异的证明，如复杂度等(精度、不同长度的序列等）。

实验内容1. 用MATLAB实现DFTN点序列x(n) 的DFT为：DFT的矩阵为：根据DFT公式与矩阵展开，通过MATLAB实现DFT：2.用Matlab实现FFT编程思想及程序框图：●原位计算因为DIT-FFT与DIF-FFT的算法类似，这里我们以DIT-FFT为例。

N=2M点的FFT共进行M级运算，且每一级都由N/2个蝶形运算组成，后一级的节点数据由前一级同处一条水平线位置的节点数据产生，所以我们同样可以将后一级的节点数据储存到前一级的节点中，这样的方法叫做原位计算，它大大节省了内存资源，降低了成本，简化了运算。

●序列的倒序无论是进行DIT-FFT还是DIF-FFT都需要进行倒序，包括输入倒序与输出倒序，以一定的方式将数组进行重新排列。

倒序的方法：首先由于N=2M,我们就可以用M位二进制数来表示节点的顺序，并且按照奇偶时域抽取。

然后，如图1所示，第一次按最低位n0的0、1值分解为奇偶组，第二次按次低位n1的0、1值分解为奇偶组，以此类推。

最后，所得二进制数所对应的十进制数即为序列倒序后产生的序列。

基于MATLAB图像DFT的分析与实现

摘要离散傅立叶变换（Discrete Fourier Transform）简称DFT，在数字信号处理和数字图像处理中应用十分广泛，它建立了离散时域和离散之间的联系。

在数字图像处理中，二维离散傅立叶被广泛的应用于图像增强、复原、编码和分类中。

本课程设计是在MATLAB软件环境下读入图像，实现图像的离散傅立叶变换（DFT），并对系数进行分析，并对图像变换后的系数的分布特点进行分析和变换后的系数进行重新排列，将低频系数移到中心位置。

关键词：DFT；MATLAB；系数分析目录1 课题描述 (1)2 设计原理 (1)2.1 离散傅立叶变换原理 (1)2.2 二维离散傅立叶变换的性质 (2)3 设计过程 (5)3.1 软件介绍 (5)3.2 设计内容 (6)3.3 设计程序 (6)3.4 程序运行结果及分析 (6)总结 (9)参考文献 (10)1 课题描述离散傅立叶变换（DFT ）在数字信号处理和数字图像处理中应用十分广泛。

它建立了离散时域和离散之间的联系。

如果直接应用卷积和相关运算在时域中处理，计算量将随着取样点数的平方而增加，这使计算机的计算量大，很费时，很难达到实时处理的要求。

因此，一般可采用 DFT 方法，将输入的数字信号首先进行 DFT 变换，在频域中进行各种有效的处理，然后进行 DFT 反变换，恢复为时域信号。

这样用计算机对变换后的信号进行频域处理。

比在时域中直接处理更加方便，计算量也大大减少，提高了处理速度。

因此，DFT 在数字图像处理领域中有很大的实用价值。

离散傅立叶变换还有一个明显的优点就是具有快速算法，即快速傅立叶算法(Fast Fourier Transform)，它可以大大减少计算次数，使计算量减少到只是相当于直接使用离散傅立叶变换所用的一小部分。

并且，二维离散傅立叶变换很容易从一维的概念推广得到。

在数字图像处理中，二维离散傅立叶被广泛的应用于图像增强、复原、编码和分类中。

2设计原理2.1 离散傅立叶变换原理傅立叶分析: 建立以时间为自变量的‘信号’和以频率为自变量的‘频谱函数’之间的关系。

基于FFT与DFT相结合的频域分析方法及其应用

ｗｉｔｈｗｈｉｃｈｔｈｅｖｉｂｒａｔｉｏｎｓｉｇｎａｌｓｏｆａｖｅｈｉｃｌｅｃｏｌｌｅｃｔｅｄｉｓａｎａｌｙｚｅｄａｎｄｔｈｅｉｎｆｏｒｍａｔｉｏｎｏｆｅｎｇｉｎｅｓｐｅｅｄｉｓｅｘｔｒａｃｔｅｄ．
［摘要］提出一种基于ＦＦＴ与ＤＦＴ相结合的频域分析方法，对采集到的汽车振动信号进行分析，从而提取发动机的转速信息。实车测试验证了该方法的可行性与有效性。最后基于发动机转速的高阶频率，对所提取的发动机转速进行修正，取得了很好的效果。
随着人们对汽车ＮＶＨ性能的要求越来越高，汽
车的振动噪声问题也越来越受到消费者的关注。对
ｆｏｍ，ｒＤＦＹ）的频域分析方法，并通过从汽车振动信号中提取出发动机的转速信号，验证了此分析方法的可行性和有效性，最后利用发动机的高阶振动能量对转速信号进行修正。
ｔｒａｃｔｅｄｉｓｃｏｒｒｅｃｔｅｄｂａｓｅｄｏｎｔｈｅｈｉｇｈ — ｏｒｄｅｒｆｒｅｑｕｅｎｃｉｅｓｏｆｅｎｇｉｎｅｓｐｅｅｄ．Ｋｅｙｗｏｒｄｓ：ｅｎｇｉｎｅｓｐｅｅｄ；ＦＦＴ；ＤＦＴ；ｆｒｅｑｕｅｎｃｙｄｏｍａｉｎａｎａｌｙｓｉｓ
关键词：发动机转速；快速傅里叶变换；离散傅里叶变换；频域分析

基于MATLAB的信号的频谱分析

基于MATLAB的信号的频谱分析信号的频谱分析是一种重要的信号处理技术，广泛应用于通信、声音处理、图像处理等领域。

MATLAB作为一种功能强大且易于使用的数学软件工具，也提供了丰富的信号频谱分析函数和工具箱，方便进行频谱分析的研究和实践。

在本文中，我们将详细介绍MATLAB在信号频谱分析方面的应用，并通过几个实例来说明其使用方法和结果分析。

首先，我们需要了解频谱是什么。

频谱是对信号在频率域上的表示，描述了信号在各个频率上的强度分布情况。

频谱分析是将信号从时域转换到频域的过程，可以通过多种方法实现，其中最常用的是快速傅里叶变换（FFT）。

MATLAB提供了fft函数来完成信号的快速傅里叶变换，并得到信号的频谱。

以音频信号为例，我们可以使用MATLAB读取音频文件，并进行频谱分析。

具体步骤如下：1. 使用audioread函数读取音频文件，将其转换为数字信号。

```matlab[y,Fs] = audioread('audio.wav');```其中，y是音频信号的数据向量，Fs是采样率。

2.对信号进行快速傅里叶变换，得到信号的频谱。

```matlabY = fft(y);```3.计算频谱的幅度谱，即频谱的绝对值。

```matlabP = abs(Y);```4.根据采样率和信号长度计算频率轴。

```matlabL = length(y);f=Fs*(0:(L/2))/L;```5.绘制频谱图。

```matlabplot(f,P(1:L/2+1));xlabel('Frequency (Hz)');ylabel('Amplitude');```通过以上步骤，我们可以得到音频信号的频谱图像。

从频谱图中可以看出信号在各个频率上的强度分布情况，有助于我们对信号进行分析和处理。

除了音频信号，我们还可以对其他类型的信号进行频谱分析，比如图像信号。

MATLAB提供了imread函数用于读取图像文件，并通过fft2函数进行二维快速傅里叶变换。

Matlab编程实现FFT变换及频谱分析的程序代码

Matlab编程实现FFT变换及频谱分析的程序代码（喜欢进行电磁兼容仿真分析的朋友可以借用）2007-10-08 sysop 点击: 436Matlab编程实现FFT变换及频谱分析的程序代码（喜欢进行电磁兼容仿真分析的朋友可以借用）Matlab编程实现FFT变换及频谱分析的程序代码（喜欢进行电磁兼容仿真分析的朋友可以借用）内容1．用Matlab产生正弦波,矩形波,以及白噪声信号，并显示各自时域波形图2．进行FFT变换，显示各自频谱图，其中采样率，频率、数据长度自选3．做出上述三种信号的均方根图谱,功率图谱,以及对数均方根图谱4．用IFFT傅立叶反变换恢复信号，并显示恢复的正弦信号时域波形图源程序%*************************************************************************%% FFT实践及频谱分析 %%*************************************************************************%%*************************************************************************%%***************1.正弦波****************%fs=100;%设定采样频率N=128;n=0:N-1;t=n/fs;f0=10;%设定正弦信号频率%生成正弦信号x=sin(2*pi*f0*t);figure(1);subplot(231);plot(t,x);%作正弦信号的时域波形xlabel('t');ylabel('y');title('正弦信号y=2*pi*10t时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换figure(1);subplot(232);plot(f,mag);%做频谱图axis([0,100,0,80]);xlabel('频率(Hz)');ylabel('幅值');title('正弦信号y=2*pi*10t幅频谱图N=128'); grid;%求均方根谱sq=abs(y);figure(1);subplot(233);plot(f,sq);xlabel('频率(Hz)');ylabel('均方根谱');title('正弦信号y=2*pi*10t均方根谱'); grid;%求功率谱power=sq.^2;figure(1);subplot(234);plot(f,power);xlabel('频率(Hz)');ylabel('功率谱');title('正弦信号y=2*pi*10t功率谱');grid;%求对数谱ln=log(sq);figure(1);subplot(235);plot(f,ln);xlabel('频率(Hz)');ylabel('对数谱');title('正弦信号y=2*pi*10t对数谱');grid;%用IFFT恢复原始信号xifft=ifft(y);magx=real(xifft);ti=[0:length(xifft)-1]/fs;figure(1);subplot(236);plot(ti,magx);xlabel('t');ylabel('y');title('通过IFFT转换的正弦信号波形'); grid;%****************2.矩形波****************% fs=10;%设定采样频率t=-5:0.1:5;x=rectpuls(t,2);x=x(1:99);figure(2);subplot(231);plot(t(1:99),x);%作矩形波的时域波形xlabel('t');ylabel('y');title('矩形波时域波形');grid;%进行FFT变换并做频谱图y=fft(x);%进行fft变换mag=abs(y);%求幅值f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换figure(2);subplot(232);plot(f,mag);%做频谱图xlabel('频率(Hz)');ylabel('幅值');title('矩形波幅频谱图');grid;%求均方根谱sq=abs(y);figure(2);subplot(233);plot(f,sq);xlabel('频率(Hz)');ylabel('均方根谱');title('矩形波均方根谱');grid;%求功率谱power=sq.^2;figure(2);subplot(234);plot(f,power);xlabel('频率(Hz)');ylabel('功率谱');title('矩形波功率谱');grid;%求对数谱ln=log(sq);figure(2);subplot(235);plot(f,ln);xlabel('频率(Hz)');ylabel('对数谱');title('矩形波对数谱');grid;%用IFFT恢复原始信号xifft=ifft(y);magx=real(xifft);ti=[0:length(xifft)-1]/fs;figure(2);subplot(236);plot(ti,magx);xlabel('t');ylabel('y');title('通过IFFT转换的矩形波波形');grid;%****************3.白噪声****************%fs=10;%设定采样频率t=-5:0.1:5;x=zeros(1,100);x(50)=100000;figure(3);subplot(231);plot(t(1:100),x);%作白噪声的时域波形xlabel('t');ylabel('y');title('白噪声时域波形');grid;%进行FFT变换并做频谱图y=fft(x);%进行fft变换mag=abs(y);%求幅值f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换figure(3);subplot(232);plot(f,mag);%做频谱图xlabel('频率(Hz)');ylabel('幅值');title('白噪声幅频谱图');grid;%求均方根谱sq=abs(y);figure(3);subplot(233);plot(f,sq);xlabel('频率(Hz)');ylabel('均方根谱');title('白噪声均方根谱');grid;%求功率谱power=sq.^2;figure(3);subplot(234);plot(f,power);xlabel('频率(Hz)');ylabel('功率谱');title('白噪声功率谱');grid;%求对数谱ln=log(sq);figure(3);subplot(235);plot(f,ln);xlabel('频率(Hz)');ylabel('对数谱');title('白噪声对数谱');grid;%用IFFT恢复原始信号xifft=ifft(y);magx=real(xifft);ti=[0:length(xifft)-1]/fs;figure(3);subplot(236);plot(ti,magx);xlabel('t');ylabel('y');title('通过IFFT转换的白噪声波形');grid;本文责任编辑: sysop相关文章? 请教：目前可有哪些用于EMC仿真的软件 - 08-18 10:01 am - 点击: 2718 发表评论查看评论加入收藏 Email给朋友打印本文如果你想对该文章评分, 请先登陆, 如果你仍未注册,请点击注册链接注册成为本站会员. 平均得分 0, 共 0 人评分1 2 3 4 5 6 7 8 9 10。

运用Matlab虚拟信号频谱分析

运用Matlab虚拟信号频谱分析摘要：频谱分析被被广泛运用于各大领域，如物理.电子学 .建筑学等等，它是对各种震动进行特性分析的重要手段。

而频谱分析使用Matlab进行的，在Matlab 中运用函数FFT（快速傅立叶变换）和DFT（离散傅立叶变换）进行频谱分析。

所以我们要熟悉运用Matlab软件以及DFT和FFT进行频谱分析的方法，利用这个方法我们可以减少繁琐的测量工作，减少错误。

最后通过实例得到虚拟结果。

关键词：Matlab.FFT.DFT.频谱分析。

0.引言在信号处理过程中，频域分析方法往往逼时域分析方法更加方便和有效，对于确知连续时间信号，其品与分析可以通过连续时间傅立叶变换进行，但是，这样计算出来的结果仍然是连续函数，计算机不能直接加以处理，为了实现数值计算，还仍需对其进行离散化处理，即采用DFT（离散傅立叶）进行分析。

DFT的快速算法的出现，使DFT 在数字通信.图像处理.功率估计.系统分析与仿真.雷达信号处理等各个领域得到广泛应用.1.频谱分析的认识利用傅里叶变换的方法对振动的信号进行分解，并按频率顺序展开，使其成为频率的函数，进而在频率域中对信号进行研究和处理的一种过程，称为频谱分析，一般理论上是利用傅里叶分析的方法，求出与时域描述相对应的频域描述，从中找出信号频谱的变化规律，以达到特征提取的实验目的。

但实际的待分析信号一般没有解析式，直接利用公式进行傅里叶分析非常困难。

DFT是一种时域和频域均离散化的傅里叶变换，适合数值计算且有快速算法，是分析信号的有力工具。

2序列的DFT变换DFT（离散傅里叶变换），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。

在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。

即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。

在本次虚拟中用Matlab进行可直接得出结果。

[整理]matlab离散信号的DFT及其快速算法fft以及ifft

实验四离散信号的DFT及其快速算法一、实验目的1．在学习DFT理论的基础上，通过本实验，加深对FFT的理解，体会二者之间的关系。

2．熟悉应用FFT实现两个序列的线性卷积的方法。

二、实验原理N点序列x[n] 的DFT和IDFT定义：可以用函数U=fft（u，N）和u=ifft（U，N）计算N点序列的DFT正、反变换。

三、实验内容(n),求N分别取8，32时的X(k)，最后绘出图形。

1. x(n)=R5离散傅立叶变换函数的MATLAB实现如下：N=8;x=[ones(1,5),zeros(1,N-5)];n=0:N-1;X=dft(x,N);magX=abs(X);phaX=angle(X)*180/pi;k=(0:length(magX)'-1)*N/length(magX);subplot(2,2,1);stem(n,x);title('x(n)—8点');subplot(2,2,2);stem(k,magX);axis([0,8,0,6]);title('|X(k)|--8点');N=32;x=[ones(1,5),zeros(1,N-5)];n=0:N-1;X=dft(x,N);magX=abs(X);phaX=angle(X)*180/pi;k=(0:length(magX)'-1)*N/length(magX);subplot(2,2,3);stem(n,x);title('x(n)—32点');subplot(2,2,4);stem(k,magX);axis([0,32,0,5]);title('|x(k)|--32点');% dft函数function[Xk]=dft(xn,N)n=[0:1:N-1];k=[0:1:N-1];WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk;2. 已知一个8点的时域非周期离散阶跃信号，n1=0，n2=7,在n0=4前为0，n0以后为1。

基于Matlab的频谱分析

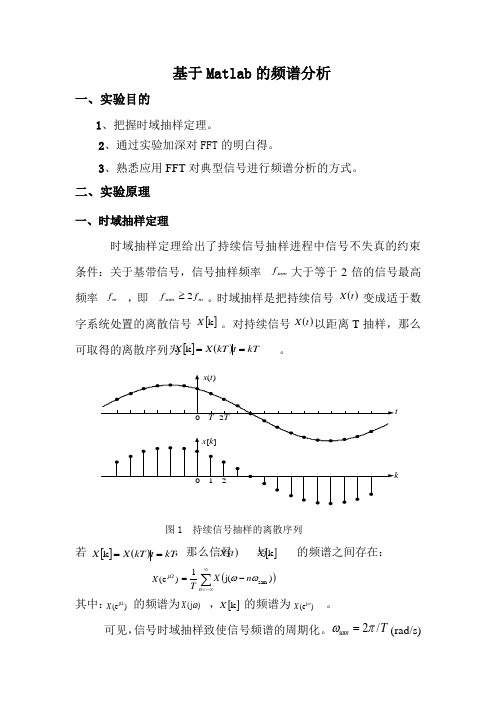
基于Matlab 的频谱分析一、实验目的1、把握时域抽样定理。

2、通过实验加深对FFT 的明白得。

3、熟悉应用FFT 对典型信号进行频谱分析的方式。

二、实验原理一、时域抽样定理时域抽样定理给出了持续信号抽样进程中信号不失真的约束条件：关于基带信号，信号抽样频率大于等于2倍的信号最高频率，即。

时域抽样是把持续信号变成适于数字系统处置的离散信号。

对持续信号以距离T 抽样，那么可取得的离散序列为。

图1 持续信号抽样的离散序列若，那么信号与的频谱之间存在：其中：的频谱为，的频谱为。

可见，信号时域抽样致使信号频谱的周期化。

(rad/s))e (j ΩX ()∑∞-∞=-=n n X T )(j 1sam ωω)e (j ΩX []k X )e (j ωX )j (ωX T sam/2πω=[]k X ()t X []()kTt kT X X ==k ()t X []k X ()t X []()kT t kT X X ==k m sam f f 2≥sam f m f为抽样角频率，为抽样频率。

数字角频率Ω与模拟角频率ω的关系为：Ω=ωT 。

二、离散傅立叶变换（DFT ）有限长序列)(n x 的离散傅立叶变换（DFT ）为10,)()]([)(10-≤≤==∑-=-N n W n x n x DFT k X N n kn N逆变换为10,)(1)]([)(10-≤≤==∑-=-N n W k X N k X IDFT n x N n kn N 3、快速傅立叶变换（FFT ）在各类信号序列中，有限长序列占重腹地位。

对有限长序列能够利用离散傅立叶变换(DFT)进行分析。

DFT 不但能够专门好的反映序列的频谱特性，而且易于用快速算法(FFT)在运算机上进行分析。

有限长序列的DFT 是其z 变换在单位圆上的等距离采样，或说是序列傅立叶的等距离采样，因此能够用于序列的谱分析。

FFT 是DFT 的一种快速算法，它是对变换式进行一次次分解，使其成为假设干小数据点的组合，从而减少运算量。

Matlab实现DFT和FFT

一个 N 点 DFT 分解为两个 N/2 点的 DFT，继续分解，迭代下去，其运算
量约为
N log 2 N 2
四、பைடு நூலகம்及实验的相关情况介绍（包含使用软件或实验设备等情况）计算机一台 Matlab 6.1 以上五、实验记录（程序相关的图形、相关数据记录及分析）
根据上述两个步骤的实验结果，比较 DFT 与 FFT 在算法与结果上的相同与差异。 DFT 与 FFT 在结果上相同。Xk 相同，产生的图像也相同。 FFT 是 DFT 的一种快速算法，对于 16 点的 FFT，我们需要 M==4 阶运算，每一阶有八个蝴蝶因子，在每个蝴蝶因子中需要 1 次复数乘法与两次复数加法，因为每个蝴蝶因子都一样，所以 FFT 通过重复运算大大简
X (2l ) = ∑ [ x(n) + x(n +
n =0 N −1 2
N 2ln )]WN 2 N )]WN2lnWNn 2
X (2l + 1) = ∑ [ x(n) − x(n + l = 0,1,...., N 2
改写为：
X 1 ( K ) + WNK X 2 ( K ), 0 ≤ k ≤ N / 2 − 1
实验指导教师：黄启宏实验名称姓名
Matlab 实现 DFT 和 FFT
专业、班级
仿古实验楼 B305
电子与通信工程 1 班实验日期
2011-11-26
侯纪龙
实验地点
一、实验内容 1、利用 matlab 实现 DFT 2、利用 matlab 实现 FFT，分析有限离散数列的 FFT 二、实验目的 1、通过研究 DFT,FFT 性质，用语言实现 DFT, FFT。不使用 MATLAB 现有的 FFT 函数，自己编写具体算法。 2、掌握 FFT 基 2 时间抽选法，理解其提高减少乘法运算次数提高运算速度的原理。三、实验原理时间抽取（DIT）基 2FFT 算法设 N 点序列 x(n),N= 2M ,将 x(n)按奇偶分组，有