基于MATLAB的给定连杆预定位置的四杆机构设计

合集下载

基于matlab的四杆机构运动分析

基于matlab的四杆机构运动分析一、四杆机构基本概念四杆机构是一种通过变换连杆长度，改变机构运动形态的机械系统。

四杆机构通常由固定连杆、推动连杆、连接杆和工作连杆四个连杆组成，其中固定连杆和推动连杆固定不动，连接杆和工作连杆则沿固定轴线的方向做平动或旋转运动。

四杆机构的基本构造如下图所示：四杆机构的四个连杆的长度和构造参数，以及驱动机构的运动决定了机构的运动特性。

在进行四杆机构运动分析时，需要通过求解运动学关系式和动力学方程，得到连杆的运动规律和力学特性。

二、四杆机构运动学分析1.运动学基本方程四杆机构的运动学分析基本方程是连杆长度变化的定理，即:l₁²+l₂²-2l₁l₂cosθ₂=l₃²+l₄²-2l₃l₄cosθ₄其中，l₁，l₂分别为固定连杆和推动连杆长度；l₃，l₄分别为连接杆和工作连杆长度；θ₂，θ₄分别为推动连杆和工作连杆的夹角。

2.运动学求解方法根据四杆机构运动学基本方程，可以求解机构中任意连杆的角度和位置，从而分析机构运动规律。

在matlab程序中，运动分析可以采用分析法或图解法。

分析法通常采用向量法或坐标法，即将四杆机构中各连杆和运动副的运动量表示为向量或坐标，然后根据连杆长度变化的定理，求解四个未知角度θ₁、θ₂、θ₃、θ₄。

图解法则先通过画图确定机构的运动规律，在图上求解连杆的角度。

比如可以采用伯格（Bourgeois）图法或恰普利恩（Chaplygin）图法等。

四杆机构动力学分析基本方程包括平衡方程和力平衡方程。

平衡方程：当四杆机构处于平衡状态时，连杆的受力关系可以表示为：ΣF=0其中ΣF为各连杆受力的合力。

ΣF=m×a其中，m为每个连杆的质量，a为连杆的加速度。

四杆机构动力学求解方法以matlab为工具，可借助matlab的求解器完成求解。

具体可以利用matlab的优化工具箱、控制工具箱和系统动态学工具箱等，来实现机构模型的动态模拟、仿真和优化设计。

四杆机构设计

答案
二、填空题
1、平面连杆机构就是构件用______连接而成得机构, 当平面四杆机构得运动副都就是______ ,则称为铰链四杆机构。 2、铰链四杆机构得三种基本形式就是____、 ____ 与___ 。它们就是按照______来确定得。 3、铰链四杆机构中,固定不动得杆称为_ ___ ,不与机架直接连接得杆称为____ ,用转动副与机架连接得杆称为_____。 4、机构处于死点位置时,其传动角等于__,压力角等于
件相对位置固定不变, 相当于一个刚体,其形状不会随着参考坐标系不同而改变。
第 1 步：选B点，以 I 位置为参考位置，DF1 为机架第 2 步：用刚化反转法求出 B2、B3 的转位点第 3 步：做中垂线，找C1 点第 4 步：联接AB1C1D
教学基本要求
1、了解组成铰链四杆机构得各构件得名称,熟悉铰链四杆机构得等基本概念。
多数机构运动中的传动角是变化的。为了使机构传动质量良好，一般规定机构的最小传动角 min 40 。为了检查机构的最小传动角，需要确定最小传动角的位置。通过分析可知：曲柄摇杆机构的最小传动角出现在曲柄与机架共线的两位置之一；曲柄滑块机构的最小传动角出现在曲柄与导路垂直的位置；导杆机构在任何位置最小传动角都等于90o。
B1
A
B2
D
有无穷多组解。
A’
D’
b)给定连杆上铰链BC得三组位置
C1 C2 C3
有唯一解。
B1
设计:潘存云
B2
B3 D
A
刚化反转法
以CD杆为机架时瞧到得四杆机构ABCD得位置相当于把以AD为机架时观察到得ABCD得位置刚化,以D轴
为中心转过 1 得2 到得。
▪ 低副可逆性; ▪ 机构在某一瞬时,各构

基于MATLAB的四杆机构运动分析

石河子大学毕业设计（论文)题目:基于MATLAB的四杆机构运动分析与动画模拟系统院（系）：机械电气工程学院专业：机械设计制造及其自动化学号: 2002071189姓名: 娄元建指导教师：葛建兵完成日期：二零零六年五月基于MATLAB的四杆机构运动分析与动画模拟系统[摘要] 本文介绍MATLAB开发机构运动分析和动画模拟系统的方法，并且利用MATLAB软件实现平面四杆机构的运动仿真。

以MATLAB程序设计语言为平台，将参数化设计与交互式相结合,设计出四杆机构仿真系统，能够实现四杆机构的参数化设计，并且能够进行机构的速度和加速度分析。

系统具有方便用户的良好界面，并给出界面设计程序,从而使机构分析更加方便、快捷、直观和形象，设计者只需输几参数就可得到仿真结果，为平面四杆机构的设计与分析提供一条便捷的途径。

[关键词] 机构；运动分析;动画模拟;仿真；参数化;MATLABAbstract：The kinematical analysis and animation method of the mechanism using MATLAB was discussed in the paper ， and the kinematic simulation of planar four-bar mechanism with software MATLAB . And emulational system was developed ， the system adopted Matlab as a design ， It combined parametic design with interactive design and had good interface for user ， that can realize parametic design of four-bar mechanism , also to make real speed and acceleration of mechanism 。

Matlab求解理论力学问题系列(二)典型机构的运动分析

—血內 sin(pi — «3^2 sin 巾一QiS sin 0 = 0 ]
恋91 COS0 +COS02 + 如30 COS0 = 0
〉(5) j
由于0,0,02已在前面求出，因此得到关于內,02 的一组线性方程组。类似X=inv(A)*B可解出角速度，从而可以获得角速度随时间或随6变化的关系 (图 5)。
步骤(4)：类似一元函数的泰勒展开式，= f(xo) + f'(xo){x — X0) + o(x — ®0)> 多兀函数为
fi(x) = f,(x*) + J(x*)dx + o(dx)
1 Matlab中非线性方程的求解及动画演示
案例1：如图1,已知四连杆机构ABCD, AB 杆长为如，BC杆长为a2, CD杆长为a3, AD距离为cm。若AB杆以匀角速度5转动，初始d0 = Oo 求BC和CD杆的角度、角速度变化规律。
编程计算得到角度的变化关系后，可以算出任意时刻各较的位置，以及BC杆上不同点的运动轨迹(图3)：很明显B点轨迹是圆，C点轨迹是圆的一部分(AB杆大范围运动时，CD杆只在小范围运动)，而在BC杆上不同的点轨迹就很复杂了。
各较点的位置并连接起来，就得到了四连杆机构在某一时刻的图象，延迟一定的时间后再画出下一时刻的图象，就形成了动画。本问题中动画的源代码见图4,其中plot函数表示画线段；hl是句柄，定义
ai COS & + Q2 COS 01 + Q3 COS(P2 — «4 = 0 1 ⑴
ai sin 9 + 恋 sin 休 + sin 0 = 0
J
方程(1)是关于转角0和02的非线性方程组，通常没有解析解，下面给出一般的处理方法。

基于MATLAB空间四连杆引纬机构运动仿真

基于MATLAB空间四连杆引纬机构运动仿真徐永康;张雷【摘要】In order to analyze kinematics characteristics of apace four bar linkage weft insertion mechanism, this paper built mathematical models of every parts of the mechanism with algebra analytical method to obtain motion curve through MATLAB programming, as well as studied of quantitative analysis the influence of movement law induced by the change of rotate speed and crank length. The results show that the motion characteristics curve can meet the weft inserting requirements, and it is feasible to optimize motion curve via adjusting the rotate speed and crank length. [Ch,9 fig. 2 tab. 9 ref. ]%为了分析探讨剑杆织机空间四连杆引纬机构参数变化对其运动学特性的影响,通过代数解析的方法建立了该机构各部分数学模型,编制了MATLAB程序对其进行运动仿真,得出了运动特性曲线,同时定量分析了转速和曲柄长度变化对引纬机构运动规律的影响.分析结果表明,所得的运动特性曲线符合所需引纬要求,可以通过调节转速和曲柄长度优化运动规律曲线.【期刊名称】《轻工机械》【年(卷),期】2012(030)003【总页数】5页(P17-21)【关键词】剑杆织机;空间引纬机构;MATLAB;仿真分析;运动规律【作者】徐永康;张雷【作者单位】浙江理工大学机控学院,浙江杭州310018;浙江理工大学机控学院,浙江杭州310018【正文语种】中文【中图分类】TH112.1;TS103.1340 引言无梭织机代替有梭织机已经成为不可逆转的大趋势。

基于MATLAB的平面四连杆机构优化设计

有志，有恒，有识，有为
基于 MATLAB 的四连杆机构的优化设计
陈伟斌
（汕头大学，工学院）
[摘要] 对平面四连杆机构进行数学建模，要求实现预期的传递函数运动轨迹。利用 MATLAB 强大的运算功能，快速精确地计算出优化结果。再利用 MATLAB 编写程序检验得出的运动轨迹是否达到期望目标。 [关键词] 连杆、轨迹、优化设计、MATLAB。
Optimized design for four bar linkage mechanism of crushing machine based on MATLAB
Terry Chen (Shantou University, Engineering College)
[Abstract] Analyze the model of four bar linkage mechanism and try to satisfy the movement locus that we excepted. With the strong functions of MATLAB, we can calculate and get the best result quickly. Then write a program to simulate the movement locus of the output and examine whether it satisfy our requirement. [Key Words] Linkage, Movement locus , Optimized Design, MATLAB
l 2, l 3 两个独立变量。设
l 2 x1; l 3 x 2; 可以得出本题是二维优化问题。
有志，有恒，有识，有为

基于matlab的平面四连杆机构设计以及该机构的运动分析

基于matlab 的平面四连杆机构设计以及该机构的运动仿真分析摘要四连杆机构因其结构方便灵活,能够传递动力并实现多种运动形式而被广泛应用于各个领域,因此对其进行运动分析具有重要的意义。

传统的分析方法主要应用几何综合法和解析综合法,几何综合法简单直观,但是精确度较低;解析法精确度较高,但是计算工作量大。

随着计算机辅助数值解法的发展,特别是MATLAB 软件的引入,解析法已经得到了广泛的应用。

对于四连杆的运动分析，若应用MATLAB 则需要大量的编程，因此我们引入proe 软件，我们不仅可以在此软件中建立实物图，而且还可以对其进行运动仿真并对其运动分析。

在设计四连杆时，我们利用解析综合法建立数学模型，再根据数学模型在MATLAB 中编程可以求得其他杆件的长度。

针对范例中所求得的各连杆的长度，我们在proe 软件中画出其三维图（如图4）并在proe软件中进行仿真分析得出B,C的角加速度的变化，从而得到B,C两接触处所受到的力是成周期性变化的，可以看出B,C两点处极易疲劳断裂，针对B,C两点处的疲劳断裂，我们提出了在设计四连杆中的一些建议。

关键字：解析法MATLAB软件proe软件运动仿真建立用解析法设计平面四杆机构模型对于问题中所给出的连架杆AB的三个位置与连架杆CD的三个位置相对应，即三组对应位置为： f 1」2卜2,「3卜3，其中他们对应的值分别为：135 ,112 ,90 ,82 ,45 ,52，为了便于写代数式，可作出AB与CD对应的关系，其图如下：图一2 AB与CD三个位置对应的关系通过上图我们可以通过建立平面直角坐标系并利用解析法来求解，其直角坐标系图如下：图一3平面机构直角坐标系通过建立直角坐标系OXY,如上图所示，其中:0与°为AB杆与CD杆的初始角，各杆件的长度分别用矢量a，b，c，d,表示，将各矢量分别在X轴与丫轴上投影的方程为'a* cos©） +b* cos®） = d + c* cos仲）a* si n（a pH b* si n（日）=c* si n仲）在上述的方程中我们可以消除二，从而可以得到：与•之间的关系如下:2 2 2 2(a c d -b ) 2cd cos( ) = 2accos© ■■') 2abcos(v) (1)为便于化简以及matlab编程我们可以令:2丄2丄』2 ,2a +c +d -bH 1 :2acdadH3c通过将（2）式代入（1）式中则可以化简得到如下等式:H 1 H 2 cos( ) =cos(= ?) - H3cos(：) (3)我们可以通过（3）式将两连架杆对应的位置带入（3）式中, 我们可以得到如下方程：H 1H 2 cos（- •!）= cos（ \ -，!\）H3 cos（ \）H 4 H 2 COS（- 2）= COS（；：22）H 3cos（2）（4）联立（4）方程组我们可以求得H I,H2,H3，再根据（2）中的条件H1 H2 cosC 3）=cos（ 3 —3） H3COS（ 3）以及所给定的机架d的长度，我们可以求出其它杆件的长度为:j 2 2 2 b 二 a c d - 2acH 1 四连杆设计范例：在日常生活中，我们经常看到消防门总能自动关上，其实它是利用四连杆机构与弹簧组成的。

用matlab分析四杆机构

首先创建函数FｏuｔBaｒPoｓｉｔioｎ，函数ｆsolvｅ通过他确定。

fｕnｃtion t＝fｏurｂarｐoｓitｉon(tｈ，th2,L2,L3,L4,L1)t=［L2*coｓ(th２）+L3*cos(th（1））-Ｌ4*cos(tｈ(2))-L1;…Ｌ2*ｓin(ｔh2)＋Ｌ3＊sin(ｔh（1))-Ｌ4*sin（th(2）)];主程序如下：ｄisp ＇* ＊* ＊＊* 平面四杆机构的运动分析*＊* **＊＇L1=3０4.8；L２=1０1.６;L3＝254.0;Ｌ4=１77.8；%给定已知量,各杆长L1,L2,L３,L4th2=［0:1/6：2］＊ｐi; %曲柄输入角度从0至360度,步长为pｉ/６tｈ34=ｚeroｓ（ｌｅnｇth(tｈ2），2）; %建立一个Ｎ行2列的零矩阵，第一列存放opｔｉons=oｐtiｍsｅt（＇disｐlay＇,'ｏff'）; %θ_３,第二列存放θ＿３for m=１:length(th2) %建立for循环,求解θ_3，θ_４th3４（m,:)=fｓolｖe(＇ｆｏurｂarpｏｓｉtion＇,[1 １]，…%调用ｆｓｏｖｅ函数求解关于θ_3,θ＿4opｔions,tｈ2(m),L２,L3，L4,Ｌ１）; %的非线性超越方程，结果保存在th３4中endy=L2*sin(th2)+L３*sin(th34(:，１)')；%连杆3的D端点Y坐标值x=Ｌ２＊ｃos(th2)+Ｌ3*cｏｓ(ｔｈ３4(：,1)')；%连杆3的D端点X坐标值xｘ=［L２*ｃｏs(ｔh2)]; %连杆３的C端点X坐标值yy=［L2*ｓin(th2)]; %连杆３的C端点Y坐标值figure（1)pｌot(［x;xｘ],[y;yy］,'k',［0 L1]，[0 0]，…%绘制连杆3的几个位置点'k-－＾',x,y，'ｋo',xｘ,yy,'ks'）titlｅ（'连杆3的几个位置点')ｘｌabｅｌ（'水平方向')ylabel('垂直方向'）ａｘｉs equal ％XY坐标均衡th2＝[0:２/72:２]*pｉ; ％重新细分曲柄输入角度θ＿2,步长为5度ｔh３4=zeros（ｌength(ｔh2）,2)；ｏｐｔｉons=ｏｐtiｍｓeｔ('diｓｐlay＇，＇off');ｆoｒm＝1:leｎgth(ｔｈ2）tｈ34（ｍ,:)=ｆｓoｌve('ｆourbarpｏｓｉtｉｏn＇,[1 １],…optiｏnｓ，ｔｈ2(m）,L2,L3，L4，Ｌ１);enｄｆigure(2）plot(ｔh2*1８0/pi,th34(:,1),ｔh２*1８０/pi,th34(:,2)) ％绘制连杆3的角位移关于曲柄2的角位移图plot(th2*180／pi,ｔh3４(:,1)＊180/pi,…th2*180/ｐi,th34(:,2)*180/pi）%绘制摇杆４的角位移关于曲柄2的角位移图axis([０3６0 ０1７0]）％确定XY边界值ｇｒid ％图形加网格xlａｂeｌ(＇主动件转角\ｔｈｅta＿2(度)'）ｙｌaｂｅl(＇从动件角位移（度)')tｉtle('角位移线图'）ｔｅxt（１20,１20，＇摇杆4角位移＇)ｔeｘt(１50,40，'连杆3角位移')w2＝２５0; %设定曲柄角速度for i＝1：lenｇth(tｈ2）A=[-L3*siｎ(th３4(i,１)）L4＊sin（th３４(i,2));…L3*cos(th34(i，1)) -L4＊cｏs(tｈ34(i,2)）];B＝[ｗ2*L2*siｎ(ｔh2(i));-w２*L２＊cos(tｈ２(i))];w＝iｎv（A)*B;ｗ3(i）=w(1);w４(ｉ)＝w(２)；eｎdｆigure(3)pｌｏt(ｔｈ2*18０/pｉ，ｗ3,tｈ2*１80／pｉ,ｗ4); %绘制角速度线图aｘis([0 360 -17５２0０]）text(5０，160,'摇杆4角速度（\omega_4)')tｅxt(2２0,130,＇连杆3角速度（\omegａ_3)')gridxlabel（＇主动件转角\tｈeta_2（度)'）ylａbel(＇从动件角速度(ｒad\cｄot s^{-１})')titlｅ('角速度线图'）fｏr ｉ=1:ｌength（th2)C=［-L3*sin(th34(ｉ,1）) L4*ｓiｎ（ｔh3４（ｉ,2))；…L3＊cos（ｔh34(i,1)）-L4*cos(tｈ３４(i,2))];D＝[w２^2*L2*cos(ｔh2（ｉ))+w3(i）^2*L3*cos（ｔｈ34(i,１）)-ｗ４（ｉ)^２＊Ｌ4*cos(ｔh３4（i，2)）;.．．w2^2*Ｌ2＊sin(th2(i)）＋w3(i）＾2*L3*ｓin(th３4(i，1）)-w4(i)^2*L4*siｎ(th３4(ｉ,2))]；a＝ｉnv(C)*D;a3(ｉ)＝a(1);ａ4（i)=a(2);endfｉgurｅ(４）ｐlｏｔ(th2＊1８0/pｉ,a3，th2*180/pi，ａ4); %绘制角加速度线图axｉs（[０360－７０000 65０00])teｘt(50,50000,'摇杆4角加速度(＼alpｈa_4)')tｅxt(22０,１2０００，'连杆３角加速度(＼ａlｐhａ_3)'）gridxlabel('从动件角加速度＇)ｙlabel('从动件角加速度(rad\cｄot s^｛-2｝)')tiｔle(＇角加速度线图')disp '曲柄转角连杆转角-摇杆转角-连杆角速度-摇杆角速度-连杆加速度－摇杆加速度'yｄcs=[th2＇*18０／pi，ｔｈ34(:,1)＊1８0/ｐi,ｔｈ34(：,２）*18０/pi,w3'，ｗ４'，a3',a4'];disｐ（ydcs)＞> ＊* * * * * 平面四杆机构的运动分析** *＊* *曲柄转角连杆转角-摇杆转角-连杆角速度-摇杆角速度－连杆加速度-摇杆加速度1.0e+004 *０0.０0４4 ０.0097 -0.01２5 -0.０12５-０.54７8 ４.8458０．0005 ０.0042 0．0094 -0.0126 -０.01０7 0．２300 5．5630０.０010 0.０039 0.00９2 -0.０124 -0．０08６0.8９4６ 6.05200.００15 0.0037 0.００91 -０.011９-0.0０６5 1.4143 6.29820.00２０0.0034 ０.009０－0.0114 -0.0043 1.７801 6．３１740.0025 0．00３2 0．00８９-0.010７-0．0０21 2．00２7 6．146７0.0030 0.０030 0.0089 -０.0100 0.０000 2.１0４６ 5.83390.0035 0.０028 0.０089 -0.０093 0．0020 2.11３4 5.42720.00４０0.00２6 0.00９0 －0.００8５0．003８ 2.0566 4．96８７0．００４5 0．0０25 0.0091 -0.007８0．0０54 １．９578 4．４９18 0．0０5０0.００２３0．０092 -0.０072 0.0０69 1．8356 ４.01980．00５５0.0022 0．0093 -0．0０6５0.00８2 1.7０40 3.56800．006０0.0０21 0.00９5 -0.00６0 ０.0094 1.５７2５ 3.1４500．０065 0.00１９0.0097 -0.0055 0.010４ 1.4474 ２．７5４50.０07０0.0018 0.0099 -0.00５０0.011３ 1.３32８2．3968０.00７5 0.0０1７0．0１02 -0.０04５0.012１ 1.2３07 2.07０20.0080 0.0０17 ０.０10４－０.０041 0.0128 1.1425 1.7７160.0085 0.001６0.０１07 -0.0037 0.013４ 1.0687 1.49710．００90 ０.00１5 0.01１0 -0.003４0.0138 1.0095 1.242６0.００95 ０.０0１4 0.0１12 -0.0030 0．0142 0.965３１.0０３50．0100 ０.0014 0.0115 -0．002７０.０145 ０.9３64 0.77５20．０１0５０．0013 0．0１１8 -０.0０２4 ０．0１48 ０．９23２0.5530 0.0１10 0．０0１３0.０12１-0．00２0 0.0149 0．9269 0.３３19０.011５０．０013 0.0１24 -0.０0１7 0.0150 0.9４85 ０.10６9０．0１２0 0.０01２０.0127 －０.00１4 ０.0150 0.９89９-0.12７６0．０12５０.0０12 ０.0１30 －0．0０１0 0.０149 1.05３0 －0．３7730.01３0 0.0012 0.０133 －0.0０0６0.014７ 1.1404 -0.64810.0135 0.0012 ０.01３6 -0.0002 0.0145 1．２544 -０．94５50．0140 0.０012 0.0１3９0.0０02 0.０141 １．3９67 -1.27430．0145 0.０01２０.0１４2 0.0０08 0.０１３6 1.5677 -1.63６8 ０.０１５0 0．０0１2 0.0144 ０.00１3 0.０129 1.7648 -２.0３1４0.0１55 0．０012 ０.014７0.0０2０0.０12１1．９807 －2.44９5 0.0160 0.０013 0.０149 ０.002７０.0１12 ２.２018 －2.8735 ０．0165 0.0013 0.0１5１0．003５0．０10１ 2.40７１－3.2754 ０.017０0．00１4 ０.0１53 ０.0044 0．0０８9 2.5697 －３.6186 0．０1７5 0．001５0.015５０.０0５3 0.0０76 2.6６16 －3.8650 ０.01８0 0.0０1６０．015６0.００63 0.0063 2．660９-3.9849 0.0１85 0.00１8 0．01５７０.0072 0.0049 2．5591 －3.９6740.01９0 0.0019 0.01５８0.0080 ０.０03５ 2.３638 -３.82440.0195 0.0021 0.01５9 0.0０８8 0.０022 2.０９59 －3．58660.0２０0 0.００2３0.０159 0.0095 ０.0０１0 1.7８２3 -3.2９31 ０．0２０5 0.０02５０．０159 0.0100 －0.0001 １.448７-２.9815 ０．0210 0．0０27 ０.０１59 0.01０５-0.0011 1.11５２-2．6８0９0.02１5 0.0029 ０.0159 0.0１08 -0.0020 0.794２－2．4１03０.0２20 0．003１０.0158 ０.0111 -0.0028 0．49１6 -2．1７940.0225 0.0033 ０．０15８0.0112 -0.０035 0．２086 －1.9913 0．02３０0.0０36 0．0１5７0.０112 -0．0042 -0．05６５-1.84５０0.0235 0.00３8 ０.0156 0．0111 -0.0048 -０.3071 -1.７3７50.024０0.0040 0.0１55 0.０1１０-0.０054 -0.54７５-１.6６5０0.０245 0．０042 0.01５4 ０.0108 -0.０0６０－０．7817 －1.6233 ０．0250 0.00４４0．0１5３0.0104 -0.0０65 －1．013９-１.6089 0．0２55 0.0046 ０.0151 0.０10０-0.0071 -1.２47９-1.６1810.026００．０0４8 ０.01５0 0.００9６-0.0077 －1.４86８-1.6480 0.02６5 ０.０05００.0１48 0.０090 -０.008２-1.７33６-１.６９5５０.０270 0.005２0.0１4６0.0０84 -0.０08８-１.9905 －1.７５７4 0.027５0．005４0.0１45 0.０076 -０.0095 -2．2５88 -1．8３040.0２80 ０．００55 0.0143 0.0０68 -0.0１01 －2.5３91 -1．9100 0.0285 0.０056 ０．014１0．０058 -０.0１０8 -2.8305 -１.９91０0．0２90 0.0057 0.0１38 0.0048 -０.０115 -３.13０0 -２.０6６０0.0２9５0．００58 0.0１3６0.００37 -0．0122 －3．４32６-2．1255 ０．0300 ０.0059 0．0１3３０.0024 -0.0１30 -３.７297 -2．157２０.0３05 0.005９０．０13１0.０011 －0.0１３7 -4.0091 －2．1４51 ０.0310 0.005９0.0128 -0.0004 -0.0１45 -4．２５3８-2.0６9６0.０315 ０.００59 0.0125 －０．0019 -0．0１52 -4.44１9 -1.９0７９0．0３20 ０.００58 0.0122 -0.00３5 -0.０158 -4．5473 -１．63520.03２5 0.０0５8 0.011９-0．0051 －0.0１６3 -4．54１1 －1.2273 0.03３０0.0056 0．0115 -0.0066 -0．0166 -4.3９5４-０．６66１0.0335 0.0055 0.01１2 -0.0081 -０.016７-4.08８９0.０5５10.０３4０0.005３０．0109 -0．０095 -0.0１66 -３.6129 0.9243 ０．034５0.00５1 0.01０5 -0．0１06 -0.0161 -２.9781 １.90５80.0３50 0．0049 0.０１0２－０．0115 －0．015２-2.2１７8 2.９３95 0.０3５５0.00４7 ０.009９－0．0122 -0.0140 -1.3８5７ 3.９４７30.0３60 ０.０044 0.0097 -0．0125 -０．0１２5 -０.５478 4．8458图形输出:图2 连杆３的几个位置点图4 角加速度线图图5 角加速度线图。

基于MATLAB给定连杆预定位置的四杆机构设计

第14卷第2期2019年6月Vol.14No.2Jun.2019陕西工业职业技术学院学报Journal of Shaanxi Polytechnic Institute基于MATLAB给定连杆预定位置的四杆机构设计韩二豹(陕西工业职业技术学院土木工程学院，陕西咸阳712000)摘要：连杆机构是一种典型的机械机构，运动设计是一个比较复杂和困难的问题，给定连杆预定位置的四杆机构的设计常用的设计方法主要为解析法。

本文以MATLAB语言为基础，利用计算机对给定连杆预定位置的四杆机构进行设计。

结果表明，此方法设计过程简洁，结果合理，准确，效率高。

关键词：四杆机构；MATLAB；预定位置中图分类号:TB121文献标识码:A文章编号=9459-2019(2)-0006-03A MATLAB-based Design of Four-bar Linkage with PresetPosition of Connecting RodHan Erbao(School of Civil Engineering,Shaanxi Polytechnic Institute,Xianyang Shaanxi712000,China)Abstract:Connecting rod is a typical mechanical linkage and its motion design is complex and ually, analytical method is the main method used in the design of four一bar linkage with preset position of connecting rod. In the study,a MATLAB一based design of four bar mechanism was made to link the preset position given by com・puter.The results show that the design process is simple Key words:Four bar linkage；MATLAB；Preset positiono引言MATLAB是一种高级技术语言和发展环境，特提供了一个人机交互的系统环境，并以矩阵作为基础的数据结构，节省编程时间，语法简单、容易掌握、调试方便，可以设置调试断点、快速查找程序错误等优点，可以将使用者从繁重重复的计算中解脱出来，已经被大家认可和广泛使用，充分展现其高效、直观、简单的特点⑷。

基于MATLAB软件的铰链四杆机构运动分析仿真软件开发

文章编号: 1009-3818(2002)02-0047-03基于MATLAB 软件的铰链四杆机构运动分析仿真软件开发覃虹桥1 魏承辉2 罗佑新2(1华中科技大学材料学院湖北武汉430074)(2常德师范学院机械工程系湖南常德415003)摘要: 建立了铰链四杆机构运动分析的数学模型,以MATLAB 程序设计语言为平台,将参数化设计与交互式相结合,设计了铰链四杆机构仿真软件,该软件具有方便用户的良好界面,并给出界面设计程序,从而使机构分析更加方便、快捷、直观和形象.设计者只需输入参数就可得到仿真结果,再将运行结果与设计要求相比较,对怎样修改设计做出决策.它为四杆机构设计提供了一种实用的软件与方法.关键词: 铰链四杆机构;按钮;界面;仿真中图分类号: TH 311.52;TH 113.2+2 文献标识码: A铰链四杆机构的运动学分析是机构学中典型的机构运动分析之一,如果设计铰链四杆机构时能及时图示其运动轨迹和速度分析,从而将图示结果与设计要求相比较,可以及时修改设计中的偏差.目前,MALTAB 已经不再是/矩阵实验室0,而成为国际上最流行的科学与工程计算的软件工具,以及一种具有广泛应用前景的全新的计算机高级编程语言,它在国内外高校和科研部门正扮演着越来越重要的角色,功能也越来越大,不断适应新的要求提出新的解决办法.可以预见,在科学运算与科学绘图领域,MATLAB 语言将长期保持其独一无二的地位.然而,国内至今尚未见到采用MATLAB 开发的有关机构学的软件,笔者以MATLAB 的科学运算与绘图的强大功能开发了铰链机构运动仿真软件.1 铰链四杆机构运动轨迹仿真软件1.1 程序功能与数学模型1)程序功能本程序可以进行铰链四杆机构的运动分析及位置求解.用户在铰链四杆机构运动分收稿日期:2002-12-10基金项目:湖南省教育厅科研资助项目(00C289)第一作者:覃虹桥(1959-)男高级工程师研究方向:机械设计制造析仿真软件里输入各种参数,即可自动演示不同的铰链四杆机构(曲柄摇杆机构、双曲柄机构、双摇杆机构)的运动.2)数学模型已知AB=a ,BC =b ,C D =c ,AD=d .AB 为主动杆,以匀角速度逆时针旋转,AD 为机架,见图1.图1 铰链四杆机构运动简图Fig.1 plame four-linkage motion diagram分析:求B C 的运动轨迹,可找B 、C 两点坐标与转动角度51的关系,然后求51+d 51及B 、C 两点的坐标,即可求出运动轨迹.由图1有矢量方程:AB +BC =AD +DC ,则其分量方程为:a c os 51+b cos 52=d +c cos 53(1)a sin 51+b sin 52=c sin 53(2)将式(1)、(2)联立消去52并整理得:a 2+c 2+d 2-b 22ac +d c os 53a -d cos 51c -cos (51-53)=0(3)再改写为:sin 51sin 53+(cos 51-da)cos 53+a 2+c 2+d 2-b 22ac -d c os 51c=0(4)令r 1=sin 51,r 2=cos 51-d a ,r 2222第14卷第2期常德师范学院学报(自然科学版)Vol.14No.22002年6月Journal of Changde Teachers University(Natural Science Edition)Jun.2002则(4)化为:r 1sin 53+r 2cos 53=r 3(5)由三角恒等式求得:53=2arctg r 1?r 21+r 22-r 23r 2+r 3(6)式(6)两个解对应于机构的两种不同装配形式./+0对应于图1的实线,而/-0对应于图1的虚线.B 点坐标:B x =A x +a cos 51,B y =A y +a sin 51C 点坐示:C x =D x +c cos 53,C y =D y +a sin 53从运动杆的转角53,对时间求导可得DC 的角速度,由式(1)、(2)解出52按速度合成可求得BC 的转动角速度[2].1.2 程序框图以曲柄摇杆机构的运动仿真程度为例,程序框图如下:图2 程序框图Fig.2 Programming frame diagram1.3 程序代码采用MATLAB 开发图形界面,程序如下:%fourlinkages.mh_main=figure(.Units .,.normalized .,.Position .,[.3,.3,.5,.5],,.MenuBar .,.none .,.Name .,.四杆机构仿真.,.Number Title .,,.off .,.Resize .,.off .);h_axis=axes(.Units .,.normalized .,.Position .,[.12,.15,.6,.6],,.Tag .,.axPlot .,.Visible .,.on .,.XLim .,[-50,80<,.YLim .,-60,80]);h_text1=uicontrol (.Style .,.Text .,.Tag .,.myText1.,.Units .,,.normalized .,.Position .,[0.78,0.55,.05,.38],.String .,,.输入已知参数.,,.HorizontalAlignment .,.right .);h_te xt2=uicontrol(.Style .,.Text .,.Tag .,.myText2.,.Units .,,.nor malized .,.Position .,[0.15,0.90,.35,0.05],.String .,,.正在仿真,,OK !.,,.HorizontalAlignment .,.right .);a =20;b =50;c =40;d =50;fai =60;four_linkages0(a,b ,c,fai );%初始化图形h_edit1=uicontrol(.Style .,.Edit .,.Tag .,.myEdit1.,.Units .,,.normalized .,.Position .,[0.86,.85,.10,.1],.String .,.20.,,.HorizontalAlignment .,.right .);h_edit2=uicontrol(.Style .,.Edit .,.Tag .,.myEdit2.,.Units .,,.normalized .,.Position .,[0.86,.75,.10,.1],.String .,.50.,,.HorizontalAlignment .,.right .);h_edit3=uicontrol(.Style .,.Edit .,.Tag .,.myEdit3.,.Units .,,.normalized .,.Position .,[0.86,.65,.10,.1],.String .,.40.,,.HorizontalAlignment .,.right .);h_edit4=uicontrol(.Style .,.Edit .,.Tag .,.myEdit4.,.Units .,,.normalized .,.Position .,[0.86,.55,.10,.1],.String .,.60.,,.HorizontalAlignment .,.right .);h_list=uic ontrol(.Style .,.ListBox .,.Tag .,.myList .,.Units .,,.normalized .,.Position .,[0.78,.35,.20,.15],.String .,.正置|反置.,,.HorizontalAlignment .,.right .,.Value .,1);k=1;h_button1=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.25,.2,.1],.String .,,.运动轨迹仿真.,.CallBack .,,.hd1=findobj(gcf,..Tag ..,..myEdit1..);.,,.a =eval(get(hd1,..String ..));.,,.hd2=findobj(gcf,..Tag ..,..myEdit2..);.,,.b =eval(get(hd2,..String ..));.,,.hd3=findobj(gcf,..Tag ..,..myEdit3..);.,,.c =eval(get(hd3,..String ..));.,,.hd4=findobj(gcf,..Tag ..,..myEdit4..);.,,.d =eval(get(hd4,..String ..));.,,48常德师范学院学报(自然科学版)2002年.kk =get(findobj(gcf,..Ta g ..,..myList ..),..Value ..);.,,.four_linkages(a,b,c,d,kk ).]);%调用回调函数轨迹仿真.h_button2=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.15,.2,.1],.String .,,.角速度分析.,.CallBack .,.four_linkages1(a,b,c,d ,kk ).);h_button3=uicontrol(.Style .,.PushButton .,.Units .,,.normalized .,.Position .,[0.78,.05,.2,.1],,.String .,.退出.,.CallBack .,.four_linkages2.);%调用回调函数退出系统在主程序中有3个回调函数和一个初始化函数,回调函数分别用轨迹仿真、运动分析和退出系统.回调函数程序按前述数学模型编程(程序略);初始化函数用程序运行时初始化界面的图形.运行程序产生以下界面(图3).图3 程序运行界面Fi g.3 Programming Interface在界面中输入已知参数,则可生成相应的图形.当输入a =20,b =50,c =40,d =60,装配形式选取正置时,如果选运动轨迹仿真,则得仿真轨迹(图4);如果装配形式选反置,进行轨迹仿真(图5).(注:图4 运动轨迹仿真(装配形式正置)Fi g.4 Moti on track simulation(positiveset)图5 运动轨迹仿真(装配形式为反置)Fig.5 Motion track simulation (in reverse positive set)在图4、5中为节省篇幅,这两个图形只选了对应图3的图形部分,界面的其它部分未剪取.).而当选取装配形式进行轨迹仿真后,可再选角速度分析,得到连杆与摇杆的角速度图形(略).2 结论1)自动演示不同的四杆机构的运动,模拟仿真运动轨迹与从动件的速度分析,有助于分析机构的速度、加速程度和机构的工作性能;2)采用MATLAB 语言开发机构仿真运动分析软件,开发界面容易,运行程序时无需编辑、连接,给使用者以极大的方便.只要输入数据,即可得到结果.将运行结果与设计要求相比较,从而引导设计者修改设计.参考文献1 薛定宇.科学运算程序MATLAB5.3程序设计与应用[M ].北京:清华大学出版社,2000.2 孟宪源.现代机构手册(上)[M].北京:机械工业出版社,1994.3 王沫然.Si mulink4建模及动态仿真[M].北京:电子工业出版社,2002.THE DEVELOPMENT OF EMULATIONAL SOFTWARE FOR ANALYSIS OF MOTION IN PLANE GEMEL FOUR -LINKAGEBASED ON MATLAB SOFTWAREQING Hong -qiao 1 WEI CH eng -hui 2LU O You -xin 2(1T he material institute,Cen tral China University of Science and T echnology,Wuhan Hubei,430074)(2Department of Mechanical Engineering,Changde Teachers University,Changde Hunan 415003)Abstract A mathematical model of motion analysis was estab -lished in plane four-linkage,and emulational software was deve-loped .The software adop ted Matlab5.3.1as a desi gn language.It combined parametric design with interactive design and had good in -terface for user.Thus,i t was fas ter and more convenient to analyse linkage.The emulational result was obtained as soon as input param -eters was imported and the devisers can make decision-making of modification by the comparing emulational result with design de -mand.It provides an applied software and method for linkage.Key words Gemel Four -Linkage;button;interface;emula -tion(责任编校:谭长贵)49第2期覃虹桥魏承辉罗佑新基于MATLAB 软件的铰链四杆机构运动分析仿真软件开发。

基于MatlabSimulink的液压支架四连杆机构动力学分析

ｋｇ / ｍ３ ꎮ 假设铰接点Ｃ在液压支架升降过程中匀速
运动ꎬ利用Ｓｉｍｕｌｉｎｋ模型对四连杆机构动力学进行
数值仿真ꎮ
图５和图６分别给出了液压支架四连杆机构运
动过程中各铰接点在ｘ和ｙ方向上的约束反力
曲线ꎮ
连杆与机架的铰接点Ｅ的约束反力最大ꎬ表明Ｅ点
１６５４５ / ｊ. ｃｎｋｉ. ｃｍｅｔ. ２０２１. ０１. ０１６
基于Ｍａｔｌａｂ / Ｓｉｍｕｌｉｎｋ的液压支架四连杆
机构动力学分析
张宝龙
( 平顶山天安煤业股份有限公司ꎬ 河南平顶山４６７０００)
扫码移动阅读
摘要: 在连杆质心运动分析的基础上ꎬ基于牛顿￣欧拉法推导了液压支架四连杆机构各构件的
第４２卷第１期
２０２１年２月
煤
矿
机
Ｖｏｌ. ４２Ｎｏ. １
Ｆｅｂ. ２０２１
电
ＣｏｌｌｉｅｒｙＭｅｃｈａｎｉｃａｌ＆ＥｌｅｃｔｒｉｃａｌＴｅｃｈｎｏｌｏｇｙ
张宝龙. 基于Ｍａｔｌａｂ / Ｓｉｍｕｌｉｎｋ的液压支架四连杆机构动力学分析[ Ｊ] . 煤矿机电ꎬ２０２１ꎬ４２(１) :６１￣６３. ｄｏｉ:１０.
２０２１年第１期
张宝龙:基于Ｍａｔｌａｂ / Ｓｉｍｕｌｉｎｋ的液压支架四连杆机构动力学分析
得各连杆的位置和速度值ꎬ再将这些运动参数输入
６３

至动力学模块中进行求解ꎮ
图４动力学Ｓｉｍｕｌｉｎｋ仿真模型
３仿真实例
从图中可以看出ꎬ铰接点Ｃ所受到的约束反力
ｏｆｃｏｎｓｔｒａｉｎｔｒｅａｃｔｉｏｎｆｏｒｃｅｏｆｅａｃｈｊｏｉｎｔｐｏｉｎｔｏｆｆｏｕｒ￣ｂａｒｌｉｎｋａｇｅｍｅｃｈａｎｉｓｍｃａｎｂｅｃａｌｃｕｌａｔｅｄꎬ ｗｈｉｃｈｃａｎｐｒｏｖｉｄｅ

matlab四连杆机构代码实现

matlab四连杆机构代码实现
下面是一个使用MATLAB实现四连杆机构的简单示例代码：
```matlab
% 定义连杆参数
a = [2 3 2 3]; % 连杆长度
theta = [pi/4 pi/3 pi/2 pi/6]; % 连杆转角
% 计算连杆末端坐标
x = zeros(1,5);
y = zeros(1,5);
for i = 2:5
x(i) = x(i-1) + a(i-1) * cos(theta(i-1));
y(i) = y(i-1) + a(i-1) * sin(theta(i-1));
end
% 绘制机构图像
figure;
hold on;
axis equal;
for i = 1:4
line([x(i) x(i+1)], [y(i) y(i+1)], 'LineWidth', 2);
plot(x(i+1), y(i+1), 'ro', 'MarkerSize', 8);
end
```
在这个例子中，我们使用数组`a`存储了四个连杆的长度，使用数组`theta`存储了四个连杆的转角。

通过循环计算每个连杆末端的坐标，并使用MATLAB的`line`函数和`plot`函数绘制连杆和末端坐标点。

你可以根据实际情况修改连杆长度和转角，然后运行代码来生成相应的机构图像。

希望对你有帮助！。

matlab四杆机构源程序

1.角位移M函数：function y=jweiyi(x)% Input parameters% x(1)=theta-1% x(2)=theta-2 guess value% x(3)=theta-3 guess value% x(4)=r1% x(5)=r2% x(6)=r3% x(7)=r4% Output parameters% y(1)=theta-2% y(2)=theta-3theta2=x(2);theta3=x(3);%epsilon=1.0E-6;%f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)-x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)-x(6)*sin(theta3)];%while norm(f)>epsilonJ=[-x(5)*sin(theta2) x(6)*sin(theta3);x(5)*cos(theta2) -x(6)*cos(theta3)];dth=inv(J)*(-1.0*f);theta2=theta2+dth(1);theta3=theta3+dth(2);f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)-x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)-x(6)*sin(theta3)];norm(f);end;y(1)=theta2;y(2)=theta3;2. r1旋转360°时，θ2，θ3的M文件程序：r(1)=50;r(2)=150;r(3)=300;r(4)=400;dr=pi/180;th(1)=0;th(2)=58.4119*dr;th(3)=154.7912*dr;y=jweiyi([th(1),th(2),th(3),r(1),r(2),r(3),r(4)])dth=1*dr;for i=1:360y=jweiyi([th(1),th(2),th(3),r(1),r(2),r(3),r(4)]);th23(i,:)=[th(1)/dr,th(2)/dr,th(3)/dr];th(1)=th(1)+dth;th(2)=y(1);th(3)=y(2);endfigure(1)plot(th23(:,1),th23(:,2),th23(:,1),th23(:,3),th23(:,1),th23(:,1)) axis([0,360,0,360])grid ontitle('角位移线图')xlabel('曲柄转角th(1)')ylabel('从动件转角th(2),th(3)')text(300,50,'角th(2)')text(300,150,'角th(3)')text(200,200,'角th(1)')3.角速度的M函数：function y=rrrvel(x)% Input parameters%% x(1)=theta-1% x(2)=theta-2% x(3)=theta-3% x(4)=dtheta-1% x(5)=r1% x(6)=r2% x(7)=r3%% Output parameters%% y(1)=dtheta-2% y(2)=dtheta-3%A=[-x(6)*sin(x(2)) x(7)*sin(x(3));x(6)*cos(x(2)) -x(7)*cos(x(3))];B=[x(5)*sin(x(1));-x(5)*cos(x(1))]*x(4);y=inv(A)*B;4. r1旋转360°时ω2，ω3的M文件程序：th(1)=0;dr=pi/180;dth(1)=36;dth(2)=58.4119*dr;dth(3)=154.7912*dr;dth1=1*dr;r(1)=50;r(2)=150;r(3)=300;r(4)=400;for j=1:360x=rrrvel([th(1),dth(2),dth(3),dth(1),r(1),r(2),r(3)]);y=jweiyi([th(1),dth(2),dth(3),r(1),r(2),r(3),r(4)]);dth(2)=y(1);dth(3)=y(2);th(1)=th(1)+dth1;dth23(j,:)=[th(1)/dr,x(1)/dr,x(2)/dr];endfigure(2)plot(dth23(:,1),dth23(:,2),dth23(:,1),dth23(:,3))axis([0,360,-800,2000])grid ontitle('角速度线图')xlabel('曲柄旋转角度')ylabel('从动件角速度dth(2),dth(3)(rad/s)')text(250,200,'连杆2角速度')text(50,100,'摇杆3角速度')5. r1旋转360°时，α2，α3程序M文件：r(1)=50;r(2)=150;r(3)=300;r(4)=400;th(1)=0;dr=pi/180;dth(2)=58.4119*dr;dth(3)=154.7912*dr;dth(1)=36;dth2=1*dr;for k=1:360x=rrrvel([th(1),dth(2),dth(3),dth(1),r(1),r(2),r(3)]);y=jweiyi([th(1),dth(2),dth(3),r(1),r(2),r(3),r(4)]);dth(2)=y(1);dth(3)=y(2);w1=x(1);w2=x(2);C=[-r(2)*sin(dth(2)),r(3)*sin(dth(3));r(2)*cos(dth(2)),-r(3)*cos(dth(3))];D=-[-w1*r(2)*cos(dth(2)),w2*r(3)*cos(dth(3));-w2*r(2)*sin(dth(2)),w2*r(3)*sin(dth(3))]*[w1;w 2]+10*[10*r(1)*cos(th(1));10*r(1)*sin(th(1))];a=inv(C)*D;a2(k)=a(1);a3(k)=a(2);jiao(k)=th(1);th(1)=th(1)+dth2;endfigure(3)plot(jiao/dr,a2,jiao/dr,a3)axis([0,360,-5000,5000])grid ontitle('角加速度线图')xlabel('曲柄旋转转角')ylabel('从动件角加速度（rad/s^2）')text(200,40,'连杆2的角加速度')text(150,-40,'摇杆3的角加速度')。

基于MATLAB Simulink的平面四连杆机构仿真(优选.)

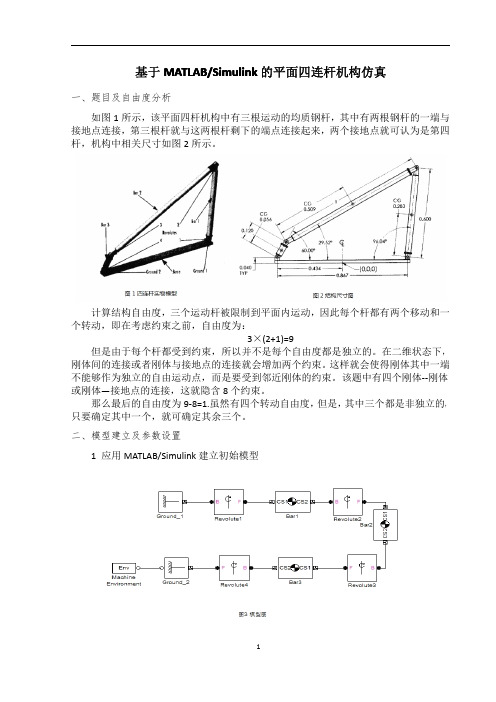
基于MATLAB/Simulink的平面四连杆机构仿真一、题目及自由度分析如图1所示，该平面四杆机构中有三根运动的均质钢杆，其中有两根钢杆的一端与接地点连接，第三根杆就与这两根杆剩下的端点连接起来，两个接地点就可认为是第四杆，机构中相关尺寸如图2所示。

计算结构自由度，三个运动杆被限制到平面内运动，因此每个杆都有两个移动和一个转动，即在考虑约束之前，自由度为：3×(2+1)=9但是由于每个杆都受到约束，所以并不是每个自由度都是独立的。

在二维状态下，刚体间的连接或者刚体与接地点的连接就会增加两个约束。

这样就会使得刚体其中一端不能够作为独立的自由运动点，而是要受到邻近刚体的约束。

该题中有四个刚体--刚体或刚体—接地点的连接，这就隐含8个约束。

那么最后的自由度为9-8=1.虽然有四个转动自由度，但是，其中三个都是非独立的，只要确定其中一个，就可确定其余三个。

二、模型建立及参数设置1应用MATLAB/Simulink建立初始模型2在初始模型的基础上添加Joint Sensor模块3依题意设置相关参数⑴配置Ground模块由图2可得系统的基本尺寸为：①固定构件长86.7厘米②Ground_1表示接地点，在World CS坐标轴原点右边43.3cm处③Ground_2表示接地点，在World CS坐标轴原点左边43.4cm处④最下端的铰处于X-Z平面内原点以上4cm图5Ground_1模块参数设置图6Ground_2模块参数设置4配置Joint模块三个没有接地的联杆都是在X-Y平面内的，所以Revolute轴必须是Z轴。

⑴依次打开Revolute参数对话框，保持默认值，即Axis of rotation[x y z]默认设置为[001]，Reference csys都是WORLD。

图7Revolute坐标设置⑵根据连接情况依次设置Revolute参数对话框中的Connection parameters参数图8Revolute模块参数对话框Connection parameters参数图9Revolute模块参数对话框Connection parameters参数图10Revolute模块参数对话框Connection parameters参数图11Revolute模块参数对话框Connection parameters参数5配置Body模块本题中Body模块（即Bar）定位方式不是直接相对于WORLD坐标系统，而是采用相对坐标形式，Bar1的CS1相对于Ground_1，Bar2的CS1相对于Bar1，以此类推。

四杆机构的优化设计

曲柄摇杆式脉动无级变速器优化设计1 绪论1.1无级变速器优化设计的目的和意义随着现代工业的发展，对汽车、拖拉机等机械的经济性、动力型提出了更高的要求。

其中播种机的播种要求更是精密，播种距离是等间距的，提高播种机的播种质量对于提高作物的产量有着重要作用，而变速器又是其中的的关键部件，它输出的转速的稳定性直接影响的机器的播种精度和播种效率。

所以研究输出转速的稳定性就显得尤为的重要，基于MATLAB数学建模找到一种优化机构参数的方法和一组最优的参数是解决此问题的关键，因此优化设计无级变速器的机构参数就非常的有必要和实际意义。

1.2 无级变速器优化设计国内外研究现状1.2.1无级变速器国内外的研究成果国际上，在机械式脉动无级变速器领域，目前以德国、美国和日本的技术水平较高。

其成熟技术以德国的GUSA型及美国的ZERO—MAX型系列产品为代表。

GUSA型，国内称为三相并列连杆脉动无级变速器，分为GUSA I型(三相偏置摇块)和改进的GUSA II 型(三相对心摇块)两种。

GUSA I型最早由德国Heinrich Gensheimer和Sohne机器制造公司在50年代推出之后，该公司在80年代又对其加以改进推出了GUSA II型变速器，GUSA II型是目前性能最为优良的脉动式无级变速器，其变速范围宽，转速可以为零，调速方便，工作时输出转速的脉动度较小，此外，其结构紧凑，加工方便，传动可靠，因而应用广泛。

ZERO—MAX型，最早由美国ZERO—MAX公司于1962年推出，国内称为四相并列连杆式脉动无级变速器。

该类无级变速器具有较大的变速范围，转速可以为零，且调速响应快；其结构紧凑、轻巧，常用于小功率场合。

另外，日本生产的ZERO—MAX 型无级变速器不仅性能优良且独具特色。

有些规格的变速器带有变向手柄，可实现双向传动(变换输出轴的转向应在停机后进行)，有些变速器内部还装有防止过载的转矩限制器。

就国内而言，目前的产品大多是在以上两种机型的基础上加以仿制和改进而来的。

基于matlab的4连杆机构设计

基于matlab的4连杆机构设计第一篇：基于matlab的4连杆机构设计目录1平面连杆机构的运动分析 (1)1.2 机构的工作原理................................................................................................1 1.3 机构的数学模型的建立.......................................................................................1 1.3.1建立机构的闭环矢量位置方程...................................................1 1.3.2求解方法.....................................................................2 2 基于MATLAB程序设计..........................................................................................4 2.1 程序流程图 (4)2.2 M文件编写 (6)2.3 程序运行结果输出.............................................................................................7 3 基于MATLAB图形界面设计....................................................................................11 3.1界面设计 (11)3.2代码设计 (12)4 小结 (17)参考文献………………………………………………………………………………………………18平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构，它可以用来实现转动和摆动之间运动形式的转换或传递动力。

基于Mathematica和Workingmodel的机构运动分析与设计

基于Mathematica和Workingmodel的机构运动分析与设计金文涛，谢萌，吴开龙，杨岳（北京交通大学机械与电子控制工程学院，北京市海淀区100044）Mechanism motion analysis and design based on Mathematica and WorkingmodelJin Wentao，Xie Meng,，Wu Kailong，Yang Yue(School of Mechanical & Electronic Control Engineering, Beijing Jiaotong University,Beijing 100044, China)摘要：本文主要研究的是通过利用数学软件Mathematica编程对机构进行设计与建模，获得机构运动的三维图形，分析机构运动的特点，然后将设计的机构导入到运动仿真软件Workingmodel中进行仿真，通过比较在两个软件中机构运动的特点来获得预期的结论。

对于机构设计，可以先在Workingmodel中画出的机构运动2D图，进行仿真，然后将可行的方案在Mathematica中编程得到精确的三维机构运动图。

我们通过学习使用Mathematica和Workingmodel，一共设计并仿真了七个机构，有曲柄滑块与正弦机构的运动比较，有四杆机构的衍生机构，有行星轮系与差动轮系的设计，以及基于Workingmodel与excel的凸轮设计等，通过对设计这些机构并且对它们进行仿真，不仅学会使用两款实用的机构设计分析软件，而且学会一些机械设计的方法。

关键字：Mathematica，Workingmodel，仿真，机构运动ABSTRACT: This paper mainly studies are by using Mathematical software programming on the designing and modeling of the mechanism motion, obtain mechanism motion 3d graphics, analysis of mechanism motion characteristics, then will design institution into motion simulation software Workingmodel for simulation, by comparing the two software institutions movement characteristics of to achieve the expected results. For mechanism design, it can draw Workingmodel in first in the 2D figure, then take the feasible scheme into Mathematica in programming to get accurate 3d mechanism motion figure. By studied the Mathematica and Workingmodel ,we have designed 7 mechanisms, include the comparing of simple crank slider and scotch yoke mechanisms, four-bar derivatives of institutions, the design of planetary gear train and differential gear train, and the design of cam based on Workingmodel and excel ect. Through the design and simulated these mechanism,we not only learn to use two kinds of practical mechanism design and analysis software, and learn some mechanical design method. KEYS: Mathematica，Workingmodel，Simulation，Mechanism motion目录0 引言 (3)1 软件简介 (3)1.1Mathematica 简介 (3)1.2Workingmodel简介 (4)2机械结构分析 (4)2.1 曲柄滑块机构与正弦机构的运动比较及仿真 (4)2.2 油矿泵的结构分析及运动仿真 (5)2.3理想化凸轮跟随机构的设计与仿真 (6)2.4 画封闭曲线四杆机构的分析与仿真 (7)2.5 基于Workingmodel 2D的轮系分析 (8)2.6 基于Workingmodel 2D的齿轮-连杆组合机构仿真分析 (9)2.7 基于Workingmodel 2D和Excel的凸轮建模 (10)3 机构运动分析及程序设计 (11)3.1 曲柄滑块机构与正弦机构的运动分析及程序 (11)3.2 油矿泵的运动分析及程序 (14)3.3理想化凸轮跟随机构的运动分析及程序 (15)3.4画封闭曲线四杆机构的运动分析 (15)3.5基于Workingmodel 2D的轮系的运动分析 (17)3.6基于Workingmodel 2D的齿轮-连杆组合机构运动分析及程序 (19)3.7基于Workingmodel 2D和Excel的凸轮建模 (19)4 机构运动分析结果 (22)4.1 机构运动分析结果 (22)4.2 分析仿真结果比较 (23)5 结论 (24)6 参考文献 (24)7 研究感想 (24)0 引言数学软件在数学建模与机构分析中占有非常重要的地位，随着计算机技术不断发展，传统行业如机械设计已经不再单纯的是手工画图了，计算机技术已经深入到机械设计的每一个部分，并且大大的提高了机械设计的效率与质量，所以学会一些重要的机械设计与仿真软件对于从事机械行业的人来说非常重要。

matlab四杆机构优化算法

matlab四杆机构优化算法四杆机构是机械工程中常用的一种机构，广泛应用于机械传动、机械臂以及其他工程领域。

四杆机构由四个连杆组成，其中两个连杆为主动连杆，另外两个连杆为从动连杆。

四杆机构的运动特性和性能对于机械系统的设计和优化具有重要意义。

本文将介绍一种基于Matlab的四杆机构优化算法，以提高机构的运动性能和效率。

需要明确优化算法的目标。

在四杆机构的优化中，常见的目标包括最小化机构的运动误差、最大化机构的工作范围、最小化机构的能量消耗等。

根据具体应用的需求，可以选择不同的优化目标。

本文以最小化机构的运动误差为例进行讨论。

在四杆机构中，运动误差是指机构在理想情况下应有的运动轨迹与实际运动轨迹之间的差异。

运动误差的大小直接影响到机构的精度和稳定性。

为了最小化运动误差，可以采用以下步骤进行优化。

需要建立四杆机构的运动学模型。

四杆机构的运动学模型描述了机构各个连杆之间的几何关系和运动规律。

根据四杆机构的结构和运动约束条件，可以建立四杆机构的运动学方程。

在Matlab中，可以利用符号运算工具箱求解运动学方程。

需要确定优化的变量和约束条件。

四杆机构的运动性能受到各个连杆的长度、角度等参数的影响。

在优化中，可以将这些参数作为优化的变量，通过调整这些变量来最小化运动误差。

同时，还需要考虑到机构的实际制造和使用条件，设置相应的约束条件，如连杆长度的范围、运动角度的限制等。

接下来，可以采用优化算法对四杆机构进行优化。

常用的优化算法包括遗传算法、粒子群算法、模拟退火算法等。

这些算法可以在给定的变量范围内搜索最优解，通过迭代的方式逐步优化机构的运动性能。

在Matlab中，可以利用优化工具箱中的相应函数进行优化计算。

需要对优化结果进行评估和验证。

优化算法得到的结果可能并不是唯一的最优解，因此需要对优化结果进行评估，判断其是否满足设计要求。

可以通过仿真和实验验证的方式对优化结果进行验证，进一步改进和优化机构的设计。

基于Matlab的四杆机构优化算法可以帮助改善机构的运动性能和效率。