湖北省黄冈中学、孝感高中2013届高三上学期期末联合考试

合集下载

湖北省黄冈等五市2013届高三上学期联合考试英语试题

2013届湖北省黄冈、襄樊、孝感、宜昌、荆州高三联合考试英语试题第一部分：听力（共两节，满分30分）做题时，先将答案划在试卷上，录音结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节：（共5小题：每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．Where is the conversation most probably taking place?A．In a shop. B．In a bank. C．In a hospital.2．How does the woman usually go shopping?A．By bus. B．By car. C．On foot.3．What is the possible relationship between the two speakers?A．Mother and son.B．Teacher and student.C．Boss and employee.4．What time does the train leave?A．8:30. B．8:00. C．8:15.5．What season is it now?A．Autumn. B．Spring. C．Winter.第二节：（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6至7题。

6．What is the trouble?A．There is something wrong with the engine.B．There is no gas.C．They are lost.7．Where are they going?A．To the airport B．To the station C．To the museum.听第7段材料，回答第8至9题。

湖北省黄冈中学2013届高三上学期期末考试数学(文)试题

湖北省 2013届高三上学期期末联合考试文科数学一、选择题：大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知全集R U =，集合10x A xx⎧⎫-=<⎨⎬⎩⎭，{}1B x x =≥，则集合{}0x x ≤等于（）A ．AB B ．A BC ．()U A B ðD ．()U A B ð2．已知i 是虚数单位，则201311i i +⎛⎫⎪-⎝⎭的值是（）A ．iB ．i -C ．1D ．1-3．某高中高一、高二、高三年级的学生人数之比是8710∶∶，用分层抽样的方法从三个年级抽取学生到剧院观看演出，已知高一抽取的人数比高二抽取的人数多2人，则高三观看演出的人数为（） A ．14 B ．16 C ．20 D ．254．已知命题:R p x ∃∈，使221x x -+=；命题:R q x ∀∈，都有()2lg 230x x ++>．下列结论中正确的是（） A ．命题“p q ∧”是真命题 B ．命题“p q ∧⌝”是真命题 C ．命题“p q ⌝∧”是真命题 D ．命题“p q ⌝∨⌝”是假命题5．已知平面向量a 、b 满足2a = ，1b = ，且25a b - 与a b +垂直，则a 与b 的夹角是（）A ．4πB ．3πC ．2πD ．23π6．已知R a ∈，0x >，0y >，且1x y +=，则“8a ≤”是“14a xy+≥恒成立”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7．过点()1,2M 的直线l 与圆C ：22(3)(4)25x y -+-=交于A 、B 两点，C 为圆心，当A C B ∠最小时，直线l 的方程是（）A ．230x y +-=B ．10x y -+=黄冈中学孝感高中C ．30x y +-=D ．230x y -+=8．定义在D 上的函数()f x ，如果满足：对x D ∀∈，存在常数0M >，都有|()|f x M ≤成立，则称()f x 是D 上的有界函数．则下列定义在R 上的函数中，不是有界函数的是（）A ．()2sin f x x =B ．()f x =C ．()12xf x -=- D ．()()2log 1f x x =-+9. 设数列{}n a 的前n 项和为n S ，11a =，且对任意正整数n ，都有点()1,n n a S +在直线220x y +-=上. 若数列2n n S n λλ⎧⎫++⎨⎬⎩⎭为等差数列，则λ的值为（）A ．12B ．12-C ． 2D ． 2-.10．规定[]x 表示不超过x 的最大整数，()()[][)22,,0,0,xx f x x x x -⎧-∈-∞⎪=⎨-∈+∞⎪⎩，若方程()1f x ax =+ 有且仅有四个实数根，则实数a 的取值范围是（） A ．11,2⎡⎫--⎪⎢⎣⎭ B ．11,23⎡⎫--⎪⎢⎣⎭ C ．11,34⎡⎫--⎪⎢⎣⎭D ．11,45⎡⎫--⎪⎢⎣⎭，二、填空题：本大题共7小题，每小题5分，共35分．请将答案填在答题卡对应题号的位置上，答错位置，书写不清，模棱两可均不得分．11．若变量x 、y 满足约束条件421x y x y x +⎧⎪-⎨⎪⎩≤≤≥，则目标函数 2z x y =+的最小值是．12．已知某几何体的三视图如图所示，则该几何体的体积是．：13．已知如图所示的程序框图，当输入99n =时，输出S 的值是．正视图侧视图14．已知圆224:M x y +=，在圆M 上随机取一点P ，则P 到直线2x y +=的距离大于的概率为．15．已知函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，它的图像的相邻两条对称轴之间的距离是2π，当函数()f x 的图像向右平移6π个单位时，得到函数()g x 的图像，并且()g x 是奇函数，则ϕ= ．16．已知抛物线()220y px p =>的焦点为F ，准线为l ，经过F 且斜率为()0k k >的直线与抛物线交于A 、B 两点（点A 在x 轴的上方），与准线交于C 点，若2BC BF =，且8AF =，则p = ．17．已知数列{}n a 、{}n b ，且通项公式分别为32n a n =-，2n b n =，现抽出数列{}n a 、{}n b 中所有相同的项并按从小到大的顺序排列成一个新的数列{}n c ，则可以推断：（1）50c = （填数字）；（2）21k c -= （用k 表示）．三、解答题：本大题共5小题，共65分。

湖北省黄冈中学、孝感高中2013届高三上学期期末联合考试文科综合试题

湖北省黄冈中学孝感高中高三上学期期末联考文科综合能力试题命题人：杜家平、周益新、张齐宇；高三政治备课组；汪庆伟何祥熊银忠第Ⅰ卷选择题（共140分）在每小题给出的四个选项中，只有一项是符合题目要求的。

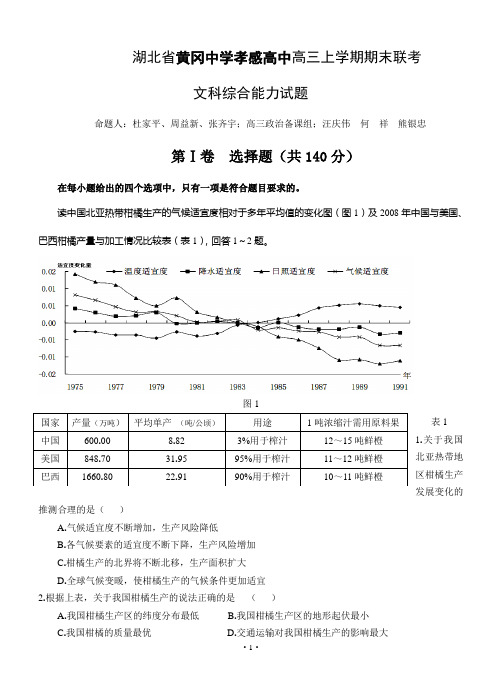
读中国北亚热带柑橘生产的气候适宜度相对于多年平均值的变化图（图1）及2008年中国与美国、巴西柑橘产量与加工情况比较表（表1），回答1～2题。

图11.关于我国北亚热带地区柑橘生产发展变化的推测合理的是（）A.气候适宜度不断增加，生产风险降低B.各气候要素的适宜度不断下降，生产风险增加C.柑橘生产的北界将不断北移，生产面积扩大D.全球气候变暖，使柑橘生产的气候条件更加适宜2.根据上表，关于我国柑橘生产的说法正确的是（）A.我国柑橘生产区的纬度分布最低B.我国柑橘生产区的地形起伏最小C.我国柑橘的质量最优D.交通运输对我国柑橘生产的影响最大下图示意我国某地景观。

读图2，完成第3～4题。

图23.根据图中信息，下列说法正确的是（）A.○1处向斜槽部受挤压，物质坚硬不易被侵蚀而成山岭B.○2处岩层的断裂和错位是内外力共同作用的结果C.○3处地形平坦是流水侵蚀作用形成的冲积扇D.○4处岩层发生倾斜是内力作用的结果4.根据图示信息，推断该地区最可能位于（）A.天山B.武夷山C.祁连山D.太行山下图为地中海地区冬季雨率等值线图（冬雨率为冬季降水量占全年降水量的百分率，单位：%）。

读图3，回答5～6题。

图35.关于地中海地区冬雨率等值线的分布规律的叙述，正确的是（）A.自北向南冬雨率递减B.从内陆向沿海冬雨率递减C.自沿海向内陆冬雨率递增D.自西北向东南冬雨率递增6.根据图示信息，下列说法正确的是（）A.巴塞罗那的冬雨率与罗马相同B.东南部受西南季风影响时间长，冬雨率高C.西北部受盛行西风影响时间长，冬雨率低D.的黎波里的冬雨率远高于雅典图4表示某区域城市分布图，图5是该区域甲城市规划略图，读图回答7～8题。

图4图57.图4中所示城市（）A.图示区域城市等级共有5级B.甲城市服务范围比乙城市大C.城市等级越高，数目越多D.乙、丙城市服务功能相同8.对甲城市进行规划，最合理的选择是（）A.①处位于城市中心，可投资建设大型跨国零售企业B.②处靠近科研所和大学城，最适宜兴建的工业部门是电子装配厂C.③处靠近文化区，工资收入水平低，最适宜兴建低级住宅区D.④处靠近工业区，为方便工人上下班，最适宜兴建高级住宅区读“某跨国公司研发部和分支机构分布示意图”。

湖北省黄冈中学等八校2013届高三第一次联考理科数学试题

湖北省鄂南高中荆州中学华师一附中孝感高中黄冈中学襄阳四中黄石二中襄阳五中八校2013届高三第一次联考数学试题（理）考试时间：2012年12月21日下午15:00——17:00 试卷满分：150分一、选择题：本大题共10小题，每题5分，共50分.在每小题给出的四个选项中，只有一个符合一目要求的. 1.集合A={}1610-2-+=x x y x ，集合B ={}A x x y y ∈=,log 2，则=⋂B C A R ( ) A .[]32， B .(]21， C .[]83， D.(]83，2.若命题p:[]012,3,3-0200≤++∈∃x x x ，则对命题p 的否定是（）A []012,3,3-0200>++∈∀x x xB ()()012,,33-,-0200>+++∞∞∈∀x x xC . ()()012,,33-,-0200≤+++∞∞∈∃x x x D. []012,3,3-0200<++∈∃x x x3.某实心机器零件的三视图如图所示，该机器零件的体积为（）A .π236+B .π436+C .π836+D .π1036+4.等比数列{}n a 各项为正，453-,,a a a 成等差数列.n S 为{}n a 的前n 项和，则36S S =（）A .2B .87 C .89 D .455.如图MN 是半圆O 的直径，MN=2，等边三角形OAB 的顶点A 、B 在半圆弧上，且AB//MN ，点P 半圆弧上的动点，则PB PA ⋅的取值范围是（） A .⎥⎦⎤⎢⎣⎡+32323， B .⎥⎦⎤⎢⎣⎡233-23， C .⎥⎦⎤⎢⎣⎡+3233-23， D .⎥⎦⎤⎢⎣⎡2323-3，6.若双曲线1222=+my x 的一条渐近线的倾斜角⎪⎭⎫⎝⎛∈30πα，，则m 的取值范围是（）A .()0,3-B .()0,3- C .()3,0 D .）（0,33- 7.在ABC ∆中，,3,23sin )(sin AC BC C B A ==+-则=∠B （）A .3π B .6π C .36ππ或D.2π8.已知R c b a ∈,,，则1632222=++c b a 是[]1,1-∈++c b a 的（）A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 9.若实数y x ,满足：⎩⎨⎧-≤≥-2502xy x y ，则y x 2+的最大值是（）A .3B .52C .5D 55 10.已知函数⎩⎨⎧<≥=)0()-(log )0(3)(3x x x x f x ，函数)()()()(2R t t x f x f x g ∈++=.关于)(x g 的零点，下列判断不正确．．．的是（） A .若)(,41x g t =有一个零点 B .若)(,412-x g t <<有两个零点C .若)(,2-x g t =有三个零点D .若)(,2-x g t <有四个零点二、填空题：本大题共5小题，每小题5分，共25分.（一）必做题（11-14题）11.已知复数i i i z ),43()21(-÷+=为虚数单位，则z 的共轭复数是 .12.函数x x x f ln )(=，)41(),31(),2(f c f b f a ===，则c b a ,,从小到大的排列是 .13.阅读如图所示程序框图，运行相应程序，输出结果n = .14.如图把函数 ,6)(,)(321xx x f x x f -==,50401206)(,1206)(7534533xxxx x f xxx x f -+-=+-=36288050401206)(97535xxxxx x f +-+-=，依次称为x x f sin )(=在[]π，0上的第1项、2项、3项、4项、5项多项式逼近函数.以此类推，请将x x f sin )(=的n 项多项式逼近函数)(x f n 在横线上补充完整：∑-==121)(n k n x f ( ) ）（+∈Nk n ,. （二）选做题（请考生在15、16两题中任选一题作答.如果全选，则按第15题作答结果计分）15.（选修4-1：几何证明选讲）如图过点A 作圆O 的一条切线AB ，切点为B ，OA 交圆O 于点C . 若1,==BC CA OC ,则=AB . 16.(选修4-4：坐标系与参数方程）曲线C 的极坐标方程为：θθρsin cos -=，化成普通方程为 .三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.A ．（本小题满分12分）函数1)sin()(-+=ϕwx A x f ,00>>w A ，（ϕ)2π<的最大值为2，其图像相邻两个对称中心之间的距离为2π，且经过点)121,12-π（.(1)求函数)(x f 的单调递增区间；(2)若57)(=αf ，且∈α⎥⎦⎤⎢⎣⎡412ππ，，求)62(πα+f 的值.18.（本小题满分12分）已知数列}{n a 满足：，32-1=a 4332-1+-=+n n n a a a ）（+∈N n .（1）证明数列}11{+n a 是等差数列，并求{}n a 的通项公式；第一次八校联考数学（理）试题第3页（共5页）（2）数列}{n b 满足：13+=n nn a b ）（+∈N n ，求}{n b 的前n 项和n S .19.（本小题满分12分）如图I ，平面四边形ABCD 中，，，，421506000====∠=∠BC AD AB ABC A 把ABD ∆沿直线BD 折起，使得平面⊥ABD平面BCD ，连接AC 得到如图II 所示四面体BCD A -.设点F E O ,,分别是,,AB BDAC 的中点.连接BF CE ,交于点G ,连接 OG .（1）证明：AC OG ⊥；（2）求二面角C AD B --的大小.20.（本小题满分12分）在淘宝网上，某店铺专卖当地某种特产.由以往的经验表明，不考虑其他因素，该特产每日的销售量y （单位：千克）与销售价格x （单位：元/千克，51≤<x ）满足：当31≤<x 时，1)3(2-+-=x b x a y ，为常数）（b a ,；当53≤<x 时，49070-+=x y .已知当销售价格为2元/千克时，每日可售出该特产700千克；当销售价格为3元/千克时，每日可售出150千克.18. 求b a ,的值，并确定y 关于x 的函数解析式；19. 若该特产的销售成本为1元/千克，试确定销售价格x 的值，使店铺每日销售该特产所获利润)(x f 最大（x 精确但0.01元/千克）.21.（本小题满分13分）如图所示，过点)1,(m M 作直线AB 交抛物线y x =2于B A ,两点，且MB AM =,过M 作x 轴的垂线交抛物线于点C .连接,,BC AC 记三角形ABC 的面积为∆S ,记直线AB 与抛物线所围成的阴影区域的面积为弓S .（1）求m 的取值范围；（2）当∆S 最大时，求m 的值；（3）是否存在常数λ，使得λ=∆弓S S ？若存在，求出λ的值；若不存在，请说明理由.第一次八校联考数学（理）试题第4页（共5页）22.（本小题满分14分）已知函数1)1()(-+=t x x f 的定义域为()+∞,1-，其中实数t 满足10≠≠t t 且.直线:l )(x g y =是)(x f 的图像在0=x 处的切线.（1）求l 的方程：)(x g y =；（2）若)()(x g x f ≥恒成立，试确定t 的取值范围；（3）若()1,0,21∈a a ，求证：12212121aa a a a a a a +≥+.注：当α为实数时，有求导公式1-='αααx x ）（.湖北省八校2013届高三第一次联考数学（理科）参考答案一选择题：1．D 2．A 3．A 4．C 5．B 6．A 7．B 8． A 9．C 10．D二填空题11． 1255i --12. b c a <<13. 3 14． sin()2!kk xk π[供参考：(1)cos()2!kk xk π-，11(())2!k k kii xk --+-（i 为虚数单位）]15.16. 220x x y y -++=三解答题： 17．解：（１）由已知：3,2,,()3sin(2)133A f x x ππωϕ====+- ……….3’ 令222232k x k πππππ-≤+≤+得5()1212k x k k Z ππππ-≤≤+∈所以()f x 单调递增区间是5[,]()1212k k k Z ππππ-+∈； ……….6’（2）由7()5f α=，得4sin(2)35πα+=， [,]124ππα∈ 所以3cos(2)35πα+=-2()3sin()13cos()12636f απππαα+=+-=+-=1=15-． ………12’18．解：（1）因为134111323111134n n n n n n a a a a a a ++===+--+++++所以111311n n a a +-=++所以{11n a +}是首项为3，公差为3的等差数列。

湖北省孝感高中2013届高三模拟考试考试(5)理综试题

2013届孝感高中高三理科综合测试题（五）物理命题人黄高云王璐化学命题人张一清袁华生物命题人丁娟邓鹏本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，考生作答时将答案答在答题卡上，在本试卷上答题无效。

满分300分，考试时间150分钟。

可能用到的相对原子质量：H—1 C—12 O—16 F—19 Na—23 Al—27 S—32 Ca—40 Cu—64 Zn—65第Ⅰ卷一、选择题：本大题共13小题，每小题6分。

在每小题的四个选项中，只有一项是符合题目要求的。

1．下列关于细胞分化、衰老、凋亡和癌变的叙述，正确的是（）①个体发育过程中细胞的凋亡对生物体都是有利的②正常细胞癌变后在体外培养可以无限增殖③由造血干细胞分化成红细胞的过程是不可逆的④癌细胞容易在体内转移，与其细胞膜上糖蛋白等物质的增加有关⑤人胚胎发育过程中尾的消失是细胞坏死的结果⑥原癌基因和抑癌基因的变异是细胞癌变的内因A．①②③④ B．①②③⑥ C．②③④⑥ D．①④⑤⑤2．C1、C2、C3、C4是某动物体的4个细胞，其染色体数分别是N、2N、2N、4N，下列相关叙述错误的是（）A. C1、C2可能是C4的子细胞B. C2、C3不一定是C4的子细胞C. C1、C2、C3、C4可能存在于一个器官中D. C2、C3、C4核DNA分子比值可以是1︰2︰23．鸡的性别决定方式属于ZW型，现有一只纯种雌性芦花鸡与一只纯种雄性非芦花鸡交配多次，F1中雄的均为芦花鸡，雌的均为非芦花鸡。

据此推测错误．．的是（）A．控制芦花和非芦花性状的基因在Z染色体上而不可能在W上B．雄鸡中芦花鸡的比例比雌鸡中的相应比例大C．让F1中的雌雄鸡自由交配，产生的F2表现型雄鸡有一种，雌鸡有两种D．将F2中的芦花鸡雌雄交配，产生的F3中芦花鸡占3／44．右图是描述生命活动某一部分的模型，以下相关叙述正确的是（）A．若A代表蛙受精卵发育成囊胚的过程中，a代表环境中有机物，则b、c可分别代表CO2、H2O等代谢废物B．若a代表精子，A代表卵细胞，则b、c可分别代表蜂王和雄蜂C．若A为R型菌+DNA酶，经过高温加热后冷却，a代表S型菌的DNA，，注射入小鼠，则小鼠死亡D．若A代表光合作用中三碳化合物，a为光反应产生的【H】和ATP，则b、c可分别代表（CH2O）和五碳化合物5．下列有关材料的处理的叙述中，正确的是（）A.用梨鉴定可溶性还原糖的存在，先加斐林甲液，再加斐林乙液B.用洋葱鳞片叶内表皮观察DNA和RNA的分布，先染色再用盐酸水解C.用洋葱根尖细胞观察有丝分裂，先进行染色后漂洗D.用天竺葵探究光合作用是否产生淀粉，先黑暗处理后光照6．有关下图的分析，正确的是（）A．若 A图为某细胞株中一定数量细胞的核DNA含量变化测量结果，则丙组只为处于分裂期的细胞B．将基因型为Aa的豌豆连续自交，在后代中的纯合子和杂合子所占的比例如B图所示, 则纯合子的比例比b曲线所对应的比例要小C．如果a1中的外迁群体与当时a2种群的基因频率不同，则c和d有可能为同一物种D．若 D图表示温度对某绿色植物光合作用与呼吸作用的影响，则图中两曲线的交点表示光合作用制造的与呼吸作用消耗的有机物的量相等7．下列说法不正确．．．的是（）a．在采矿厂、制陶厂、耐火材料等场所长期工作的人员，若不采取劳动保护措施，则容易患上硅肺病b．氮的氧化物可以造成光化学污染，同时还可以形成酸雨c．工业废水、生活污水、农药、化肥、含磷的洗涤剂等都可以对水体造成污染d．植树造林既可以缓解温室效应，又可以降低酸雨的危害e. 光纤通讯是以光作为信息载体，让光在光导纤维中传输，制造光导纤维的基本原料是玻璃f．石灰石在自然界中储量丰富，是工业主要原料之一，但制取陶瓷不需要石灰石,制取漂白粉需要g. 二氧化硫能够杀菌消毒，可以做食品干果的防腐剂h. 食用的蛋白质、淀粉和脂肪都属于有机高分子，都可发生水解反应i．甲烷、乙烯和苯都可通过石油分馏得到j. 用灼烧并闻气味的方法可以区分纯棉织物和纯毛织物A. bdefhgjB. cdefgC. defhiD.dehi8．若N A 表示阿伏加德罗常数，下列说法正确的是（）A ．理论上氢氧燃料电池负极消耗11.2L 标准状况下气体，外电路通过电子数为2N AB ．17g 甲基（—14CH 3）所含中子数为9N AC ．28 g N 60单质（见右图）中含有的N —N 键键数为3N AD ．1 mol H 2O 2含有极性共价键键数为NA ，含有非极性共价键为键数2N A9．下列实验中操作、现象、结论对应关系正确的一组是（）10．某有机物的结构简式如右图,则关于此有机物的说法不正确．．．的是:（）A ．可发生的反应类型有：①取代 ②加成 ③消去 ④酯化 ⑤水解 ⑥氧化 ⑦中和B ．该物质1mol 与足量NaOH 溶液反应，消耗NaOH 的物质的量为3molC ．可与氯化铁溶液发生显色反应D ．该有机物属于芳香族化合物11. 25 ℃ 时，在25 mL 0.1 mol · L -1的NaOH 溶液中，逐滴加入0.2 mol · L -1的CH 3COOH 溶液，溶液的pH 与醋酸溶液体积关系如图。

湖北省黄冈中学孝感高中 2013届高三上学期期末联合考试

湖北省2013届高三上学期期末联合考试黄冈中学英语试卷二部分：词汇知识运用（共两节，满分30分）第一节多项选择（共10小题；每小题1分，满分10分）从A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

21. There is always a pleasant _______ of calm at night in the small mountainous village, differentfrom the noise in the city.A. atmosphereB. environmentC. observationD. consideration22. With a kind of delight, based on fattened hope resting on the pills, she unpacked the packageand read the ________.A. introductionsB. constructionsC. descriptionsD. directions23. As teachers, we should _______ our students boldly to anything complicated and profound toenhance their curiosity about the world.A. devoteB. applyC. contributeD. expose24. Young people should constantly _______ their own state of mind so as to adapt to thecircumstances in which fierce competition is going on.A. enterB. adjustC. achieveD. enjoy25. During the 65th Festival De Cannes in 2012, the Chinese actress Fan Bingbing _______ as achina girl, attracting plenty of interest.A. kept upB. gave upC. dressed upD. turned up26. The airplane landed hard during the storm and _______ flames at the airport, killing nearlytwo hundred people on board.A. turned intoB. burst intoC. let outD. burst out27. Credit cards give their owners automatic credit in stores, restaurants, and hotels, at home, andeven abroad, and they make various banking services _______ as well.A. sustainableB. availableC. reliableD. valuable28. When dealing with students, teachers are supposed to adopt _______ and caring approaches,as they are unique young individuals of different personalities.A. abstractB. efficientC. flexibleD. effective29. No one could imagine that the _______ well-behaved business man should be really a criminalwhen he was caught by the police last week.A. conventionallyB. eventuallyC. apparentlyD. controversially30. His remark was considered to be quite _______, because it deepened the gap between twoparties and caused more conflicts.A. out of placeB. out of mindC. out of questionD. out of order第二节完形填空（共20小题，每小题1分，满分20分）阅读下面短文，从短文后所给各题的四个选项（A、B、C和D）中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

湖北省黄冈中学、孝感高中高三上学期期末联合考试语文试卷(Word版,含答案)

湖北省黄冈中学、孝感高中高三上学期期末联合考试语文本试卷共10页，共六大题23小题。

全卷满分150分。

考试用时150分钟。

★祝考试顺利★一、语文基础知识（共15分，共5小题，每小题3分）1．下列词语中加点的字，每组读音都不相同的一项是（）A．奢靡/望风披靡衡量/量体裁衣晕车/晕头转向B．攒射/人头攒动剥削/生吞活剥识别/博闻强识C．委婉/虚与委蛇绿茵/绿林好汉解脱/解甲归田D．宁肯/宁死不屈菲薄/日薄西山供需/供不应求2．下列词语中，没有错别字的一项是( )A．蝉联喝采得鱼忘荃美轮美奂B．踯躅亲睐绵里藏针陨身不恤C．岑寂付梓两全其美意气用事D．颓圮执拗再接再励砥砺德行3．下列各句中，加点词语使用正确的一项是（）A．诺基亚、索尼和三洋这一个个曾经无比熟悉的品牌在2012年纷纷走下坡路，国际品牌的世风日下将带给我们更多的思考。

B．在与华盛顿奇才队的比赛中，林书豪首当其冲，投中全场第一个3分球。

整场比赛中，他拿下23分，外加10次助攻，成为拯救尼克斯队的英雄。

C．曾国藩的日记与家书，写的净是些鸡栏、菜圃小事，以表示自己不过是一个求田问舍的乡巴佬，来消除慈禧太后对他的疑心。

D．年关将近，在异乡谋生的农民工们无时无刻在思念着自己的家乡，但包工头们恶意欠薪的行为又让他们的回乡路变得漫长而无望。

4．下列各句中，没有语病的一项是（）A．近日，对于部分高端白酒塑化剂含量严重超标一事，引起了民众的普遍关注。

质检总局有关负责人表示，国家食品安全风险评估中心已介入调查。

B．在我们的学校教育中，学生个人素质能否得到稳步提升，关键在于我们的教育部门教育改革的力度。

C．近日，我国中东部地区出现了严重的雾霾天气，造成此次重污染的主要原因是工业废气、生活燃煤、汽车尾气等污染源的排放量大造成的。

D．2012年11月17日获得国务院正式批复的《中原经济区规划》是中国内陆最大的区域规划，它对整个中部乃至全国的发展都起到了至关重要的战略意义和作用。

湖北省黄冈中学、孝感高中2013届高三上学期期末联考数学理试题(Word版含解析)

湖北省黄冈中学、孝感高中2013届高三（上）期末联考数学试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设i为虚数单位，复数z满足zi=2+i，则z等于（）A．2﹣i B．﹣2﹣i C．1+2i D．1﹣2i考点：复数代数形式的乘除运算．专题：计算题．分析：将zi=2+i变形，可求得z，再将其分母实数化即可．解答：解：∵zi=2+i，∴z====1﹣2i，故选D．点评：本题考查复数代数形式的乘除运算，将其分母实数化是关键，属于基础题．2．（5分））设集合U={（x，y）|x∈R，y∈R}，A={（x，y）|2x﹣y+m＞0}，B={（x，y）|x+y﹣n≤0}，那么点P（2，3）∈A∩（∁U B）的充要条件是（）A．m＞﹣1，n＜5 B．m＜﹣1，n＜5 C．m＞﹣1，n＞5 D．m＜﹣1，n＞5考点：集合的包含关系判断及应用．专题：压轴题．分析：由P（2，3）∈A∩（∁U B）则点P既适合2x﹣y+m＞0，也适合x+y﹣n＞0，从而求得结果．解答：解：∁U B={（x，y）|x+y﹣n＞0}∵P（2，3）∈A∩（∁U B）∴2×2﹣3+m＞0，2+3﹣n＞0∴m＞﹣1，n＜5故选A点评：本题主要考查元素与集合的关系．3．（5分）在棱长为a的正方体ABCD﹣A1B1C1D1中随机地取一点P，则点P与正方体各表面的距离都大于的概率为（）A．B．C．D．考点：几何概型．专题：概率与统计．分析：根据点P与正方体各表面的距离都大于，则所在的区域为以棱长为的正方体内，则概率为两正方体的体积之比．解答：解：符合条件的点P落在棱长为的正方体内，根据几何概型的概率计算公式得．故选A．点评：本题主要考查几何概型中的体积类型，基本方法是：分别求得构成事件A的区域体积和试验的全部结果所构成的区域体积，两者求比值，即为概率．4．（5分）（2012•湘潭三模）求曲线y=x2与y=x所围成图形的面积，其中正确的是（）A．B．C．D．考点：定积分的简单应用．分析：画出图象确定所求区域，用定积分即可求解．解答：解：如图所示S=S△ABO﹣S曲边梯形ABO，故选B．点评：用定积分求面积时，要注意明确被积函数和积分区间，本题属于基本运算．5．（5分）函数f（x）=2x+x3﹣2的零点个数是（）个．A．0B．1C．2D．3考点：函数的零点．专题：函数的性质及应用．分析：根据函数f（x）=2x+x3﹣2在R上单调递增，f（0）f（1）＜0，可得函数在区间（0，1）内有唯一的零点，从而得出结论．解答：解：由于函数f（x）=2x+x3﹣2在R上单调递增，又f（0）=﹣1＜0，f（1）=1＞0，所以f（0）f（1）＜0，故函数f（x）=2x+x3﹣2在区间（0，1）内有唯一的零点，故函数f（x）=2x+x3﹣2在R上有唯一零点．故选B．点评：本题考查函数零点的定义以及函数零点判定定理的应用，属于基础题．6．（5分）某程序框图如图所示，该程序运行后输出的结果是（）A ．B ．C ．D ．考点：程序框图．专题：图表型．分析：由题意可知，该程序的作用是求解n=的值，然后利用裂项求和即可求解解答：解：由题意可知，该程序的作用是求解n=的值，而．故选C ．点评：本题考查了程序框图中的循环结构的应用，解题的关键是由框图的结构判断出框图的计算功能 7．（5分）设函数y=f （x ）在定义域内的导函数为y=f ′（x ），y=f （x ）的图象如图1所示，则y=f ′（x ）的图象可能为（）A ．B ．C ．D ．考点：函数的单调性与导数的关系．专题：数形结合．分析：先从f（x）的图象判断出f（x）的单调性，根据函数的单调性与导函数的符号的关系判断出导函数的符号，判断出导函数的图象．解答：解：由f（x）的图象判断出f（x）在区间（﹣∞，0）上递增；在（0，+∞）上先增再减再增∴在区间（﹣∞，0）上f′（x）＞0，在（0，+∞）上先有f′（x）＞0再有f′（x）＜0再有f′（x）＞0故选D点评：解决函数的单调性问题，一般利用单调性与导函数符号的关系：导函数大于0函数递增；导函数小于0函数递减．8．（5分）已知两不共线向量=（cosα，sinα），=（cosβ，sinβ），则下列说法不正确的是（）A．||=||=1 B．（+）⊥（﹣）C．与的夹角等于α﹣βD．与在+方向上的投影相等考点：平面向量数量积的运算；向量的模；数量积表示两个向量的夹角．专题：平面向量及应用．分析：由模长公式可得==1，故A正确；由数量积为0可得向量垂直，故B正确；由夹角公式可得向量夹角的余弦值，但角的范围不一定，故C错误；而D由投影相等可与模长相等等价，结合A可知正确，故可得答案．解答：解：由模长公式可得==1，==1，即=，故A正确；∵（）•（）=||2﹣||2=0，∴（）⊥（），故B正确；由夹角公式可得．当α﹣β∈[0，π]时，＜＞=α﹣β；当α﹣β∉[0，π]时，＜＞≠α﹣β，故C不正确；由投影相等可得，故D正确．故选C点评：本题考查向量的数量积的运算，涉及向量的模长和投影及夹角，属中档题．9．（5分）已知直线：A1x+B1y+C1=0（C1≠0）与直线l2：A2x+B2y+C2=0（C2≠0）交于点M，O为坐标原点，则直线OM的方程为（）A．B．C．D．考点：两条直线的交点坐标；直线的一般式方程．专题：综合题；直线与圆．分析：将两直线的一般式中的常数项均变为1，验证O、M的坐标是否均满足该直线的方程即可判断．解答：解：x+y+1=0，l2：x+y+1=0，两式相减得（﹣）x+（﹣）y=0．∵点O、M的坐标都满足该直线的方程，∴点O、M都在该直线上，∴直线OM的方程为（﹣）x+（﹣）y=0．故选A．点评：本题考查两条直线的交点坐标，考查转化思想与分析验证能力，属于难题．10．（5分）若某几何体的三视图是如图所示的三个直角三角形，则该几何体的外接球的表面积为（）A．10πB．25πC．50πD．100π考点：球的体积和表面积；球内接多面体．专题：计算题．分析：几何体复原为底面是直角三角形，一条侧棱垂直底面直角顶点的三棱锥，扩展为长方体，长方体的对角线的长，就是外接球的直径，然后求其的表面积．解答：解：由三视图复原几何体，几何体是底面是直角三角形，一条侧棱垂直底面直角顶点的三棱锥；扩展为长方体，其外接与球，它的对角线的长为球的直径，得长方体的体对角线的长为，∴长方体的外接球的半径为，∴球的表面积为50π，故选C．点评：本题考查三视图，几何体的外接球的表面积，考查空间想象能力，计算能力，是基础题．二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．（一）必考题（11～14题）（二）选考题（请考生在15、16两题中任选一题作答．如果全选，则按第15题作答结果计分）11．（5分）（2012•临沂二模）为了了解高三学生的身体状况，抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图）．已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则抽取的男生人数是48．考点：频率分布直方图．专题：常规题型．分析：根据前3个小组的频率之比为1：2：3，可设前三组的频率为x，2x，3x，再根据所以矩形的面积和为1建立等量关系，求出x，最后根据样本容量等于频数除以频率求出所求．解答：解：由题意可设前三组的频率为x，2x，3x，则6x+（0.0375+0.0125）×5=1解可得，x=0.125所以抽取的男生的人数为故答案为：48．点评：频率分布直方图：小长方形的面积=组距×，各个矩形面积之和等于1，样本容量等于频数除以频率等知识，属于基础题．12．（5分）若是函数f（x）=asinx+bcosx（a、b均为常数）图象的一条对称轴，则的值为．考点：正弦函数的对称性；函数的值．专题：计算题；三角函数的图像与性质．分析：由辅助角公式可得f（x）=asinx+bcosx=（θ为辅助角），结合对称轴经过函数图象的最高点或最低点可求解答：解：∵f（x）=asinx+bcosx=（θ为辅助角）∵x=是函数的对称轴且对称轴经过函数图象的最高点或最低点，∴．故答案为：点评：本题考查了正弦函数的性质的应用，利用辅助角公式化简函数y=asinx+bcosx为一个角的一个三角函数的形式是求解问题的关键13．（5分）（2011•河南模拟）（1﹣ax）2（1+x）6的展开式中，x3项的系数为﹣16，则实数a的值为2或3．考点：二项式系数的性质．专题：计算题．分析：利用完全平方公式将第一个因式在看；利用二项展开式的通项公式求出第二个因式的x3，x2，x项的系数；求出（1﹣ax）2（1+x）6的展开式中，x3项的系数，列出方程求出a的值．解答：解：∵（1﹣ax）2=1﹣2ax+a2x2，又（1+x）6展开式的通项为T r+1=C6r x r，所以（1+x）6展开式中含x3，x2，x项的系数分别是C63；C62；C61．所以（1﹣ax）2（1+x）6的展开式中，x3项的系数为C63﹣2aC62+a2C61∴C63﹣2aC62+a2C61=﹣16解得a=2或a=3．故答案为：2或3．点评：本题考查利用二项展开式的通项公式解决二项展开式的特定项问题、考查等价转化的能力．14．（5分）若z=x+2y，则z的取值范围是．考点：简单线性规划的应用．专题：计算题；不等式的解法及应用．分析：作出题中不等式组表示的平面区域，得到如图所示的阴影部分．将直线l：z=x+2y进行平移并加以观察，可得当直线ly经过原点时，z达到最小值0；当直线l与余弦曲线相切于点A 时，z达到最大值，用导数求切线的方法算出A的坐标并代入目标函数，即可得到z的最大值．由此即可得到实数z的取值范围．解答：解：作出可行域如图所示，可得直线l：z=x+2y与y轴交于点．观察图形，可得直线l：z=x+2y经过原点时，z达到最小值0直线l：z=x+2y与曲线相切于点A时，z达到最大值．∵由得，∴代入函数表达式，可得，由此可得z max==．综上所述，可得z的取值范围为．故答案为：点评：本题给出约束条件，求目标函数z=x+2y的取值范围．着重考查了简单线性规划和运用导数求函数图象的切线的知识，属于中档题．15．（选修4﹣1：几何证明选讲）如图，已知在△ABC中，∠B=90°．O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，AD=2，AE=1，则CD的长为3．考点：圆的切线的判定定理的证明．专题：选作题．分析：利用圆的切线性质、切割线定理、勾股定理即可得出．解答：解：由AD与圆O相切于点D，根据切割线定理可得AD2=AE•AB，又AD=2，AE=1，∴．由CD，CB都是圆O的切线，根据切线长定理可得，设CD=x，则CB=x．由切线的性质可得：AB⊥BC，∴AB2+BC2=AC2，∴42+x2=（x+2）2，得x=3，即CD=3．故答案为3．点评：熟练掌握圆的切线性质、切割线定理、勾股定理是解题的关键．16．（5分）（2012•湖南）在极坐标系中，曲线C1：ρ（cosθ+sinθ）=1与曲线C2：ρ=a（a＞0）的一个交点在极轴上，则a=．考点：简单曲线的极坐标方程．专题：计算题．分析：根据ρcosθ=x，ρsinθ=y，ρ2=x2+y2将极坐标方程化成普通方程，利用交点在极轴上进行建立等式关系，从而求出a的值．解答：解：∵曲线C1的极坐标方程为：ρ（cosθ+sinθ）=1，∴曲线C1的普通方程是x+y﹣1=0，∵曲线C2的极坐标方程为ρ=a（a＞0）∴曲线C2的普通方程是x2+y2=a2∵曲线C1：ρ（cosθ+sinθ）=1与曲线C2：ρ=a（a＞0）的一个焦点在极轴上∴令y=0则x=，点（，0）在圆x2+y2=a2上解得a=故答案为：点评：本题主要考查了简单曲线的极坐标方程与普通方程的转化，同时考查了计算能力和分析问题的能力，属于基础题．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．17．（12分）已知函数f（x）=|x+2|．（1）解关于x的不等式f（x）﹣|3x﹣4|≤1；（2）若f（x）+|x﹣a|＞1恒成立，求实数a的取值范围．考点：绝对值不等式的解法．专题：计算题．分析：（1）依题意|x+2|﹣|3x﹣4|≤1，通过分类讨论去掉绝对值符号，再解，最后取其并集即可；（2）方法1：在数轴上，设点A，B，M对应的实数分别为﹣2，a，x，利用绝对值的几何意义得|MA|+|MB|≥|AB|即可；方法2：由绝对值三角不等式得|x+2|+|x﹣a|≥|（x+2）﹣（x﹣a）|=|a+2|，即可求得实数a的取值范围．解答：解：（1）由f（x）﹣|3x﹣4|≤1得|x+2|﹣|3x﹣4|≤1，即或或得解集为{x|x≤，或x≥}．（6分）（2）方法1：在数轴上，设点A，B，M对应的实数分别为﹣2，a，x，则“f（x）+|x﹣a|＞1恒成立”⇔“|x+2|+|x﹣a|＞1恒成立”⇔“|MA|+|MB|＞1恒成立”．∵|MA|+|MB|的最小值为|AB|，即|a+2|，∴|a+2|＞1，得a+2＞1，或a+2＜﹣1，即a＞﹣1，或a＜﹣3．方法2：由绝对值三角不等式得|x+2|+|x﹣a|≥|（x+2）﹣（x﹣a）|=|a+2|，∴|a+2|＞1，解得a＞﹣1，或a＜﹣3．（12分）点评：本题考查绝对值不等式的解法，考查分类讨论思想与绝对值不等式的几何意义，考查推理与运算能力，属于难题．18．（12分）已知定义域为R的函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的一段图象如图所示．（1）求f（x）的解析式；（2）若g（x）=cos3x，h（x）=f（x）•g（x），求函数h（x）的单调递增区间．考点：三角函数中的恒等变换应用；由y=Asin（ωx+φ）的部分图象确定其解析式；复合三角函数的单调性．专题：计算题；三角函数的图像与性质．分析：（1）由图可求得其周期T，继而可求得ω，再利用点（，2）在图象上可求得φ，从而可求得其解析式；（2）利用三角函数间的关系及倍角公式，辅助角公式可求得h（x）=sin（6x+）+，利用正弦函数的单调性即可求得h（x）的单调递增区间．解答：解：（1）∵T=（﹣）=，∴ω==3，∴f（x）=2sin（3x+φ）．∵点（，2）在图象上，∴2sin（3×+φ）=2，即sin（φ+）=1，∴φ+=2kπ+（k∈Z），即φ=2kπ+．故f（x）=2sin（3x+）．（6分）（2）h（x）=2sin（3x+）cos3x=2（sin3xcos+cos3xsin）cos3x=（six3xcos3x+cos23x）=（sin6x+cos6x+1）=sin（6x+）+．由2kπ﹣≤6x+≤2kπ+（k∈Z）得函数h（x）的单调递增区间为[﹣，+]（k∈Z）．（12分）点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查三角函数中的恒等变换应用及正弦函数的单调性，考查化归思想与综合运算能力，属于难题．19．（12分）某单位进行这样的描球游戏：甲箱子里装有3个白球，2个红球，乙箱子里装有1个白球，2个红球，这些球除颜色外完全相同．每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个则获奖（每次游戏结束后将球放回原箱）．（1）求在1次游戏中①摸出3个白球的概率；②获奖的概率；（2）求在2次游戏中获奖次数X的分布列及数学期望EX．考点：离散型随机变量的期望与方差；列举法计算基本事件数及事件发生的概率；离散型随机变量及其分布列．专题：综合题．分析：（1）①求出基本事件总数，计算摸出3个白球事件数，利用古典概型公式，代入数据得到结果；②获奖包含摸出2个白球和摸出3个白球，且它们互斥，根据①求出摸出2个白球的概率，再相加即可求得结果；（2）确定在2次游戏中获奖次数X的取值是0、1、2，求出相应的概率，即可写出分布列，求出数学期望．解答：解：（1）①设“在一次游戏中摸出i个白球”为事件A i（i=，0，1，2，3），则P（A3）=•=②设“在一次游戏中获奖”为事件B，则B=A2∪A3，又P（A2）=•+•=且A2、A3互斥，所以P（B）=P（A2）+P（A3）=+=（2）由题意可知X的所有可能取值为0，1，2．P（X=0）=（1﹣2=，P（X=1）=C21×（1﹣）=，P（X=2）=（2=，所以X的分布列是X的数学期望E（X）=0×+1×+2×=．点评：本题考查古典概型及其概率计算公式，离散型随机变量的分布列数学期望、互斥事件和相互独立事件等基础知识，考查运用概率知识解决实际问题的能力．20．（12分）如图，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2．又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．（1）求证：PC⊥AC；（2）求二面角M﹣AC﹣B的余弦值；（3）求点B到平面MAC的距离．考点：用空间向量求平面间的夹角；点、线、面间的距离计算．专题：计算题；证明题；空间位置关系与距离．分析：方法1：（1）通过证明PC⊥平面ABC，然后证明PC⊥AC．（2）取BC的中点N，连MN，证明MN⊥平面ABC．作NH⊥AC，交AC的延长线于H，连接MH，说明∠MHN为二面角M﹣AC﹣B的平面角．利用．求出二面角M﹣AC﹣B的余弦值．（3）先证明NE⊥平面MAC，通过解三角形求出点N到平面MAC的距离，利用点N是线段BC的中点，推出点B到平面MAC的距离是点N到平面MAC的距离的两倍．方法2：（1）同方法一；（2）在平面ABC内，过C作BC的垂线，并建立空间直角坐标系如图所示．设P（0，0，z），求出有关点的坐标，利用，求出设平面MAC的一个法向量为，求出平面ABC的一个法向量为．利用．得到二面角M﹣AC﹣B的余弦值．（3）利用点B到平面MAC的距离．解答：解：方法1：（1）证明：∵PC⊥BC，PC⊥AB，∴PC⊥平面ABC，∴PC⊥AC．（2分）（2）取BC的中点N，连MN．∵PM=∥CN，∴MN=∥PC，∴MN⊥平面ABC．作NH⊥AC，交AC的延长线于H，连接MH．由三垂线定理得AC⊥MH，∴∠MHN为二面角M﹣AC﹣B的平面角．∵直线AM与直线PC所成的角为60°，∴在Rt△AMN中，∠AMN=60°．在△ACN中，．在Rt△AMN中，．在Rt△NCH中，．在Rt△MNH中，∵，∴．故二面角M﹣AC﹣B的余弦值为．（8分）（3）作NE⊥MH于E．∵AC⊥平面MNH，∴AC⊥NE，∴NE⊥平面MAC，∴点N到平面MAC的距离为．∵点N是线段BC的中点，∴点B到平面MAC的距离是点N到平面MAC的距离的两倍为．（12分）方法2：（1）证明：∵PC⊥BC，PC⊥AB，∴PC⊥平面ABC，∴PC⊥AC．（2分）（2）在平面ABC内，过C作BC的垂线，并建立空间直角坐标系如图所示．设P（0，0，z），则．．∵，且z＞0，∴，得z=1，∴．设平面MAC的一个法向量为=（x，y，1），则由得得∴．平面ABC的一个法向量为．．显然，二面角M﹣AC﹣B为锐二面角，∴二面角M﹣AC﹣B的余弦值为．（8分）（3）点B到平面MAC的距离．（12分）点评：本题考查直线与平面的垂直的判定定理的应用，二面角的求法，点到平面的距离的求法，几何法与向量法的区别与联系，考查空间想象能力与计算能力．21．（13分）已知斜率为﹣2的直线与椭圆交于A，B两点，且线段AB的中点为．直线l2与y轴交于点M（0，m）（m≠0），与椭圆C交于相异两点P，Q，O 为坐标原点，且．（1）求椭圆C的方程；（2）求λ的值；（3）求m的取值范围．考点：直线与圆锥曲线的综合问题．专题：综合题；方程思想；圆锥曲线中的最值与范围问题．分析：（1）平方差法：设A（x1，y1），B（x2，y2），代入椭圆方程作差，据中点坐标公式、直线斜率公式即可求得a2值；（2）设P（x3，y3），Q（x4，y4），l2：y=kx+m，由，用横坐标表示出来即可求得λ值；（3）将直线l2的方程与椭圆方程联立消y，由（2）的结论及韦达定理可得k，m的关系式，再由△＞0消掉k即可求得m的取值范围；解答：解：（1）设A（x1，y1），B（x2，y2），则．∵，，∴两式相减得，即=0，即，得，所以椭圆C的方程为2x2+y2=1．（2）设P（x3，y3），Q（x4，y4），l2：y=kx+m（∵l2与y轴相交，∴l2的斜率存在）．由，得，得，即，将①代入②得（λ﹣3）m=0，∵m≠0，∴λ=3．（3）将y=kx+m代入2x2+y2=1，得（k2+2）x2+2kmx+（m2﹣1）=0．∵λ=3，∴由消去x3、x4得，．由△＞0得k2＞2（m2﹣1），即2（m2﹣1），即，即，解得，或．所以m的取值范围为，或．点评：本题考查直线与圆锥曲线的综合问题，考查学生综合运用所学知识分析问题解决问题的能力，弦长公式、韦达定理、判别式是解决该类问题的基础知识，应熟练掌握，涉及弦中点问题常考虑“平方差法”．22．（14分）在数列中，a1=1，前n项和S n满足nS n+1﹣（n+3）S n=0．（1）求{a n}的通项公式；（2）若，求数列{（﹣1）n b n}的前n项和T n；（3）求证：．数列与不等式的综合；数列的求和；数列递推式．考点：等差数列与等比数列．专题：分析：（1）方法一：由已知变形得，利用“累乘求积”即可得出；方法二：利用得到a n的关系式，再利用“累乘求积”即可得出；（2）根据所求的数列的通项公式的特点，利用等差数列的前n项和公式，可先求出当n为偶数时的T n，进而即可得出n为奇数时的T n；（3）通过构造函数，利用函数的单调性及裂项求和即可证明．解答：解：（1）方法1：∵，且S1=a1=1，∴当n≥2时，，且S1=1也适合．当n≥2时，，且a1=1也适合，∴．方法2：∵nS n+1﹣（n+3）S n=0，∴（n﹣1）S n﹣（n+2）S n﹣1=0，两式相减，得n（S n+1﹣S n）=（n+2）（S n﹣S n﹣1），即na n+1=（n+2）a n，即．又∵可求得a2=3，∴也适合上式．综上，得．当n≥2时，，且a1=1也适合，∴．（2）．设．当n为偶数时，∵，∴．当n为奇数（n≥3）时，，且T1=c1=﹣4也适合上式．综上：得．（3）令f（x）=x﹣ln（1+x）．当x＞0时，∵，∴f（x）在（0，+∞）上为增函数，∴当x＞0时，f（x）＞f（0）=0，得ln（1+x）＜x．令，得，∴，∴，∴．点数列掌握数列的通项公式、等差数列的前n项和公式、通项公式与前n项和的关系评：、“累乘求积”、构造函数并利用函数的单调性及裂项求和是解题的关键．。

湖北省黄冈中学、孝感高中2013届高三上学期期末联合考试(理科)数学试题(定稿)

湖北省 2013届高三上学期期末联合考试理科数学命题学校：黄冈中学命题人：李新潮审稿人：王宪生考试时间：2013年1月30日15:00——17:00 试卷满分：150分一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设i 为虚数单位，复数z 满足i 2i z =+，则z 等于（） A ．2i - B ．2i -- C ．12i + D ．12i -2．设集合{(,)|,},{(,)|20},{(,)|0}U x y x y A x y x y m B x y x y n =∈∈=-+>=+-≤R R ，那么点(2,3)()U P A B ∈ð的充要条件是（）A ．1m >-且5n <B ．1m <-且5n <C ．1m >-且5n >D ．1m <-且5n >3．在棱长为a 的正方体1111ABCD A B C D -中随机地取一点P ，则点P 与正方体各表面的距离都大于3a的概率为（） A ．127B ．116C ．19D ．134．设曲线2y x =与直线y x =所围成的封闭区域的面积为S ，则下列等式成立的是( ) A ．120()d S x x x =-⎰B ．120()d S x x x =-⎰C ．120()d S y y y =-⎰D．1(S y y =⎰5．函数()2lg(1)2x f x x =++-的零点的个数为（）A ．0B ．1C ．2D ．36．某程序框图如图所示，该程序运行后输出的结果是（）A ．12B ．23C ．34D ．457．设函数()y f x =在定义域内的导函数为()y f x '=，若()y f x =的图象如图1所示，则()y f x '=的图象可能为（）黄冈中学孝感高中8．已知两不共线向量(cos ,sin ),(cos ,sin )ααββ==a b ，则下列说法不．正确．．的是（） A ．||||1==a b B ．()()+⊥-a b a b C ．a 与b 的夹角等于αβ- D ．a 与b 在+a b 方向上的投影相等9．已知直线1l ：11110(0)A x B y C C ++=≠与直线2l ：22220(0)A x B y C C ++=≠交于点M ，O 为坐标原点，则直线OM 的方程为（）A ．12121212()()0A A B Bx y C C C C -+-=B ．12121212()()0A A B Bx y C C C C ---= C ．12121212()()0C C C Cx y A A B B -+-= D ．12121212()()0C C C Cx y A A B B ---= 10．若某几何体的三视图是如图所示的三个直角三角形，则该几何体的外接球的表面积为（）A ．10πB ．25πC ．50πD ．100π二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．（一）必考题（11～14题）11．为了了解某校高三男生的身体状况，抽查了部分男生的体重，将所得数据整理后，画出了频率分布直方图（如右图）．已知图中从左到右的前3个小组的频率之比为1﹕2﹕3，第2小组的频数为12，则被抽查的男生的人数是．12．若8x π=是函数()sin cos f x a x b x=+（a 、b 均为常数）图象的一条对称轴，则()8f π的值为．13．在26(1)(1)ax x -+的展开式中，3x 项的系数为16-，则实数a 的值为．14．若0,2sin cos ,x x y x π⎧≤≤⎪⎨⎪≤≤⎩2z x y =+，则z 的取值范围是．（二）选考题（请考生在15、16两题中任选一题作答．如果全选，则按第15题作答结果计分）15．（选修4－1：几何证明选讲）如图，已知在△ABC 中，90B ∠=︒．O 是AB 上一点，以O 为圆心，OB 为半径的圆与AB 交于点E ，与AC 切于点D ，2,1AD AE ==，则CD 的长为． 16．（选修4－4：坐标系与参数方程）在极坐标系中，曲线1:sin )1C ρθθ+=与曲线2:(0)C a a ρ=>的一个交点在极轴上，则a 的值为．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知函数()|2|f x x =+．（1）解关于x 的不等式()|34|1f x x --≤；（2）若()||1f x x a +->恒成立，求实数a 的取值范围．18．（本小题满分12分）已知定义域为R 的函数()sin()(0,0)f x A x A ωϕω=+>>的一段图象如图所示．（1）求()f x 的解析式；（2）若()cos3,()()()g x x h x f x g x ==，求函数()h x 的单调递增区间．19．（本小题满分12分）在公园游园活动中有这样一个游戏项目：甲箱子里装有3个白球和2个黑球，乙箱子里装有1个白球和2个黑球，这些球除颜色外完全相同；每次游戏都从这两个箱子里各随机地摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（1）在一次游戏中：①求摸出3个白球的概率；②求获奖的概率；（2）在两次游戏中，记获奖次数为X ：①求X 的分布列；②求X 的数学期望． 20．（本小题满分12分）如图，四边形PCBM 是直角梯形，90PCB ∠=︒，PM ∥BC ，1,2PM BC ==．又1AC =，120,ACB AB PC ∠=︒⊥，直线AM 与直线PC 所成的角为60︒．（1）求证：PC AC ⊥；（2）求二面角M AC B --的余弦值；（3）求点B 到平面MAC 的距离．21．（本小题满分13分）已知斜率为2-的直线1l 与椭圆222:1(0)x C y a a+=>交于,A B 两点，且线段AB 的中点为11(,)22E ．直线2l 与y 轴交于点(0,)(0)M m m ≠，与椭圆C 交于相异两点,P Q ，O 为坐标原点，且,4,PM MQ OP OQ OM λλλ=+=∈R ．（1）求椭圆C 的方程；（2）求λ的值；（3）求m 的取值范围． 22．（本小题满分14分）在数列*{}()n a n ∈N 中，11a =，前n 项和n S 满足1(3)0n n nS n S +-+=．（1）求{}n a 的通项公式；（2）若24()n n a b n=，求数列{(1)}n n b -的前n 项和n T ；（3）求证：12121119nna a a a a a +++<．。

湖北省黄冈中学孝感中学高三上学期英语期末联合考试

湖北省高三上学期期末联合考试英语试卷★祝考试顺利★注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号、条形码置贴在答题卡上的指定位置。

2．选择题的作答：用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

3．完成句子和短文写作题的作答：用黑色签字笔将答案直接答在答题卡上对应的答题区域内。

答在试题卷、草稿纸上无效4．考生必须保持答题卡的整洁，考试结束后，请将答题卡上交。

第一部分:听力（共两节，满分30分）第一节（共5小题; 每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A 、B 、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. How many offices does the man’s company have?A. One.B. Six.C. Twelve.2. What does the man do?A. A businessman.B. A student.C. A farmer.3. Which of the following statements is true?A. The man has never heard of Mo Yan before.B. The man has read some of Mo Yan ’s works.C. The woman has never heard of Mo Yan before.4. What are the speakers mainly talking about?A. Noise.B. Housework.C. Neighborhood.5. What is the weather like now?A. Cloudy.B. Rainy.C. Sunny.第二节（共15小题；每小题1.5分, 满分22.5分）听下面5段对话或独白，每段对话或独白后有几个小题，从题中所给的A 、B 、C 三个选黄冈中学孝感高中项中选出最佳选项。

湖北省黄冈中学、孝感高中2013届高三上学期期末联考数学文(Word版含解析)

湖北省黄冈中学、孝感高中2013届高三（上）期末联考数学试卷（文科）一、选择题：大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知全集U=R，集合A={x|＜0}，B={x|x≥1}，则集合{x|x≤0}等于（）A．A∩B B．A∪B C．C U（A∩B）D．C U（A∪B）考点：交、并、补集的混合运算．专题：计算题．分析：先解分式不等式化简集合A，求出集合A与集合B的并集，观察得到集合{x|x≤0}是集合（A∪B）在实数集中的补集．解答：解：由，得x（x﹣1）＜0，解得：0＜x＜1．所以A={x|＜0}={x|0＜x＜1}，又B={x|x≥1}，则A∪B={x|0＜x＜1}∪{x|x≥1}={x|x＞0}，所以，集合{x|x≤0}=C U（A∪B）．故选D．点评：本题考查了分式不等式的解法，求解分式不等式时，可以转化为不等式组或整式不等式求解，考查了交、并、补集的混合运算．此题是基础题．2．（5分）已知是虚数单位，则（）2013的值是（）A．i B．﹣i C．1D．﹣1考点：复数代数形式的乘除运算；虚数单位i及其性质．专题：计算题．分析：利用=i，再利用i的幂的性质即可求得答案．解答：解：∵=i，i1=i，i2=﹣1，i3=﹣i，i4=1，即i n的值是以4为周期出现的，故=•=i2012•i=i．故选A．点评：本题考查复数代数形式的乘除运算，考查虚数单位i及其性质，属于中档题．3．（5分）某高中高一、高二、高三年级的学生人数之比是8：7：10，用分层抽样的方法从三个年级抽取学生到剧院观看演出，已知高一抽取的人数比高二抽取的人数多2人，则高三观看演出的人数为（）A．14 B．16 C．20 D．25考点：分层抽样方法．专题：概率与统计．分析：根据三个年级的人数比，结合高一抽取的人数比高二抽取的人数多2人，得到要抽取的高三的人数．解答：解：∵高中高一、高二、高三年级的学生人数之比是8：7：10，且已知高一抽取的人数比高二抽取的人数多2人，∴高三年级观看演出的人数为=20，故选C．点评：本题考查分层抽样方法，本题解题的关键是看出三个年级中各个年级所占的比例，这就是在抽样过程中被抽到的概率，本题是一个基础题．4．（5分）已知命题p：∃x∈R，使2x+2﹣x=1；命题q：∀x∈R，都有lg（x2+2x+3）＞0．下列结论中正确的是（）A．命题“p∧q”是真命题B．命题“p∧﹣q”是真命题C．命题“﹣p∧q”是真命题D．命题“﹣pv﹣q”是假命题考点：命题的真假判断与应用．专题：函数的性质及应用．分析：根据指数函数的图象和性质及基本不等式可判断命题p的真假；根据二次函数的图象和性质及对数函数的单调性，可判断命题q的真假，进而复合命题真假判断的真值表可判断四个答案的正误．解答：解：∵2x＞0，2﹣x＞0，则由基本不等式可得2x+2﹣x≥2故命题p：∃x∈R，使2x+2﹣x=1为假命题；∵x2+2x+3=（x+1）2+2≥2，故lg（x2+2x+3）≥lg2＞lg1=0故命题q：∀x∈R，都有lg（x2+2x+3）＞0为真命题故命题“p∧q”是假命题命题“p∧﹣q”是假命题命题“﹣p∧q”是真命题命题“﹣pv﹣q”是真命题故选C点评：本题以命题真假判断为载体考查了指数函数对数函数及二次函数的图象和性质，其中根据函数的图象和性质判断出两个简单命题的真假是解答的关键．5．（5分）已知平面向量、满足||=2，||=1，且2﹣5与+垂直，则与的夹角是（）A．B．C．D．考点：平面向量数量积的运算；数量积表示两个向量的夹角．专题：平面向量及应用．分析：利用向量垂直与数量积的关系及向量的夹角公式即可得出．解答：解：∵，∴，化为，∵||=2，||=1，∴2×22﹣=0，∴．∴===．又．∴．故选B．点评：熟练掌握向量垂直与数量积的关系及向量的夹角公式是解题的关键．6．（5分）已知a∈R，x＞0，y＞0，且x+y=1，则“a≤8”是“+≥a恒成立”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：不等式的解法及应用．分析：利用基本不等式可得“+≥a恒成立”等价于a≤9，再根据{a|a≤8}⊊{a|a≤9}，从而得出结论．解答：解：∵已知a∈R，x＞0，y＞0，且x+y=1，∴+=（x+y）（+）=5++≥9，当且仅当x=且y=时，取等号．故“+≥a恒成立”等价于a≤9．而{a|a≤8}⊊{a|a≤9}，故“a≤8”是“+≥a恒成立”的充分不必要条件，故选A．点评：本题主要考查充分条件、必要条件、充要条件的定义，基本不等式的应用，体现了等价转化的数学思想，属于基础题．7．（5分）过点M（1，2）的直线l与圆C：（x﹣3）2+（y﹣4）2=25交于A、B两点，C为圆心，当∠ACB最小时，直线l的方程是（）A．2x+y﹣3=0 B．x﹣y+1=0 C．x+y﹣3=0 D．2x﹣y+3=0。

湖北省黄冈中学、孝感高中2013届高三上学期期末联合考试数学(理)试题

湖北省 2013届高三上学期期末联合考试理科数学命题学校：黄冈中学考试时间：2013年1月30日15:00——17:00试卷满分：150分一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设i 为虚数单位，复数z 满足i 2i z =+，则z等于（）A ．2i -B ．2i --C ．12i +D ．12i - 2．设集合{(,)|,},{(,)|20},{(,)|0U x y x y A x y x y m B x y x y n =∈∈=-+>=+-≤R R ，那么点(2,3)()U P A B ∈ ð的充要条件是（）A ．1m >-且5n <B ．1m <-且5n <C ．1m >-且5n >D ．1m <-且5n > 3．在棱长为a 的正方体1111ABCD A B C D -中随机地取一点P ，则点P 与正方体各表面的距离都大于3a 的概率为（）A ．127B ．116C ．19D ．134．设曲线2y x=与直线y x=所围成的封闭区域的面积为S ，则下列等式成立的是( )A ．12()d S x x x=-⎰ B ．12()d S x x x=-⎰C ．12()d Sy y y=-⎰D．10(Sy y=-⎰5．函数()2lg(1)2xf x x =++-的零点的个数为（）A ．0B ．1C ．2D ．36．某程序框图如图所示，该程序运行后输出的结果是（）A ．12B ．23C ．34D ．457．设函数()y f x =在定义域内的导函数为()y f x '=，若()y f x =的图象如图1所示，则()y f x '=的图象可能为（）黄冈中学孝感高中8．已知两不共线向量(cos ,sin ),(cos ,sin )ααββ==a b ，则下列说法不．正确．．的是（） A ．||||1==a b B ．()()+⊥-a b a b C ．a 与b 的夹角等于αβ- D ．a 与b 在+a b 方向上的投影相等9．已知直线1l ：11110(0)A x B y C C ++=≠与直线2l ：22220(0)A x B y C C ++=≠交于点M ，O 为坐标原点，则直线OM 的方程为（）A ．12121212()()0A AB B x yC C C C -+-= B ．12121212()()0A AB B x yC C C C ---= C ．12121212()()0C C C C x y A A B B -+-=D ．12121212()()0C C C C x y A A B B ---=10．若某几何体的三视图是如图所示的三个直角三角形，则该几何体的外接球的表面积为（）A ．10πB ．25πC ．50πD ．100π二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．（一）必考题（11～14题）11．为了了解某校高三男生的身体状况，抽查了部分男生的体重，将所得数据整理后，画出了频率分布直方图（如右图）．已知图中从左到右的前3个小组的频率之比为1﹕2﹕3，第2小组的频数为12，则被抽查的男生的人数是．12．若8x π=是函数()s i n c o s f x a x b x=+（a 、b 均为常数）图象的一条对称轴，则()8f π的值为．13．在26(1)(1)ax x -+的展开式中，3x 项的系数为16-，则实数a 的值为．14．若0,2sin cos ,x x y x π⎧≤≤⎪⎨⎪≤≤⎩2z x y =+，则z 的取值范围是．（二）选考题（请考生在15、16两题中任选一题作答．如果全选，则按第15题作答结果计分）15．（选修4－1：几何证明选讲）如图，已知在△ABC 中，90B ∠=︒．O 是AB 上一点，以O 为圆心，OB 为半径的圆与AB 交于点E ，与AC 切于点D ，2,1AD AE ==，则CD 的长为．16．（选修4－4：坐标系与参数方程）在极坐标系中，曲线1:sin )1C ρθθ+=与曲线2:(0)C a a ρ=>的一个交点在极轴上，则a 的值为．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知函数()|2|f x x =+．（1）解关于x 的不等式()|34|1f x x --≤；（2）若()||1f x x a +->恒成立，求实数a 的取值范围．18．（本小题满分12分）已知定义域为R 的函数()sin()(0,0)f x A x A ωϕω=+>>的一段图象如图所示．（1）求()f x 的解析式；（2）若()cos 3,()()()g x x h x f x g x == ，求函数()h x 的单调递增区间．19．（本小题满分12分）在公园游园活动中有这样一个游戏项目：甲箱子里装有3个白球和2个黑球，乙箱子里装有1个白球和2个黑球，这些球除颜色外完全相同；每次游戏都从这两个箱子里各随机地摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（1）在一次游戏中：①求摸出3个白球的概率；②求获奖的概率；（2）在两次游戏中，记获奖次数为X ：①求X 的分布列；②求X 的数学期望．20．（本小题满分12分）如图，四边形PCBM 是直角梯形，90PCB∠=︒，PM ∥BC ，1,2PMBC ==．又1AC=，120,AC B AB PC∠=︒⊥，直线AM 与直线PC 所成的角为60︒．（1）求证：PCAC ⊥；（2）求二面角M AC B--的余弦值；（3）求点B 到平面MAC 的距离．21．（本小题满分13分）已知斜率为2-的直线1l 与椭圆222:1(0)x Cy a a+=>交于,A B 两点，且线段AB 的中点为11(,)22E ．直线2l 与y 轴交于点(0,)(0)M m m ≠，与椭圆C 交于相异两点,P Q ，O 为坐标原点，且,4,PM MQ OP OQ OM λλλ=+=∈R．（1）求椭圆C 的方程；（2）求λ的值；（3）求m 的取值范围．22．（本小题满分14分）在数列*{}()n a n ∈N 中，11a =，前n 项和n S 满足1(3)0n n nS n S +-+=．（1）求{}n a 的通项公式；（2）若24()n na b n =，求数列{(1)}n n b -的前n 项和n T ；（3）求证：12121119n na a a a a a +++< ．湖北省 2013届高三上学期期末联合考试理科数学参考答案1．D 解析：∵22i (2i)i 2i 112ii1iz ++-====--，∴选择“D ”．2．A解析：∵(2,3)()U P A B ∈ ð，∴(2,3)P A ∈，且(2,3)P B ∉，∴2230,230,m n ⨯-+>⎧⎨+->⎩得1,5.m n >-⎧⎨<⎩故选择A ．3．A解析：符合条件的点P 落在棱长为3a 的正方体内，根据几何概型的概率计算公式得33()1327a P a==．故选A ．4．B解析：将曲线方程2y x=与直线方程y x=联立方程组，解得0x=或1x=．结合图形可知选项B 正确．5．B解析：方法1：∵(0)10,(1)l g20f f =-<=>，∴()f x 在(0,1)内必有一个零点．又∵()f x 在(1,)-+∞上为增函数，∴()f x 有且仅有1个零点．方法2：由()0f x =得lg(1)22xx +=-+．作出函数()lg(1)g x x =+与()22xh x =-+的图象，知两函数的图象有且仅有一个交点，即方程()0f x =有且仅有一个根，即函数()f x 有且仅有一个零点．6．C解析：11131223344++=⨯⨯⨯．故选C ．7．D解析：∵当0x<时，函数()f x 为增函数，∴当0x<时，()0f x '>．又∵当0x>时，随着x 的增大，函数值先递增，再递减，最后又递增，∴选择“D ”．8．C解析：①A 显然正确． ②∵22()()||||0+⋅-=-=a b a b a b ，∴()()+⊥-a b a b ，∴B 正确．③cos ,cos cos sin sin cos()||||αβαβαβ⋅<>==⋅=+=-⋅a b a b a b a b ．当[0,]αβπ-∈时，,αβ<>=-a b ；当[0,]αβπ-∉时，,αβ<>≠-a b ．故C 不正确．④∵22()()||||||||||||⋅+⋅+=⇔+⋅=⋅+⇔=++a a b b a b a a b a b b a b a b a b ，∴D正确．故选择“C ”． 9．A黄冈中学孝感高中解析：1l ：111110A B x y C C ++=，2l ：222210A B x y C C ++=，两式相减得12121212()()0A AB B x yC C C C -+-=．∵点O 、M 的坐标都满足该直线的方程，∴点O 、M 都在该直线上，∴直线OM 的方程为12121212()()0A AB B x yC C C C -+-=．故选“A ”．10．C解析：该几何体是三棱锥，将该三棱锥视为长方体的一个角，得长方体的体对角线的长为=，∴三棱锥的外接球，即长方体的外接球的半径为2，∴球的表面积为50π，选择“C ”．11．48解析：设被抽查的男生的人数为n ．∵后两组的频率之和为(0.01250.0375)50.25+⨯=，∴前三组的频率之和为0.75．又∵前三组的频数分别为6,12,18，∴612180.75n++=，得48n =．12．解析：∵对称轴经过函数图象的最高点或最低点，∴()8f π=．13．2或3解析：展开式中3x 的系数为3425666216C aC a C -+=-，∴2560a a -+=，得2a=或3．14．[0,6π+解析：作出可行域如图所示．直线2x yz+=与y 轴交于点(0,)2z．设直线2x y z+=与曲线cos (0)2yx x π=≤≤相切于点A ．∵由1sin 2y x '=-=-得6xπ=，∴(62A π，代入2x yz+=得6zπ=+(0,0)O 代入2x y z+=得0z=．故z 的取值范围为[0,6π+．15．3 解析：∵2AD AE AB=⋅，∴24ADABAE==．设CD x =，则CBx=．∵222AB BCAC+=，∴2224(2)x x +=+，得3x =，即3C D =．162解析：将极坐标方程化为普通方程，得2221210,:C y C x y a +-=+=．在1C 中，令y =，得2x=，再将0)2代入2C 得2a =．17．解：（1）由()|34|1f x x --≤得|2||34|1x x +--≤，即2,(2)(34)1,x x x <-⎧⎨-++-≤⎩或42,3(2)(34)1,x x x ⎧-≤<⎪⎨⎪++-≤⎩或4,3(2)(34)1,x x x ⎧≥⎪⎨⎪+--≤⎩得解集为35{|,}42x x x ≤≥或．（6分）（2）方法1：在数轴上，设点,,A B M 对应的实数分别为2,,a x -，则“()||1f x x a +->恒成立”⇔“|2|||1x x a ++->恒成立”⇔“||||1MA MB +>恒成立”．∵||||MA MB +的最小值为||AB ，即|2|a +，∴|2|1a +>，得21a +>，或21a +<-，即1a >-，或3a <-．方法2：由绝对值三角不等式得|2||||(2)()||2|x x a x x a a ++-≥+--=+，∴|2|1a +>，得1a >-，或3a <-．（12分）18．解：（1）∵24()4123T πππ=-=，∴23Tπω==，∴()2sin(3)f x x ϕ=+．∵点(,2)12π在图象上，∴2sin(3)212πϕ⨯+=，即sin()14πϕ+=，∴2()42k k ππϕπ+=+∈Z ，即24k πϕπ=+．故()2sin(3)4f x x π=+．（6分）（2）2()2sin(3)cos 32(sin 3coscos 3sin)cos 33cos 3cos 3)444h x x x x x x x x x πππ=+=+=+6cos 61)sin(6)242x x x π=++=++262()242k x k k πππππ-≤+≤+∈Z 得函数()h x 的单调递增区间为[,]()38324k k k ππππ-+∈Z ．（12分）19．解：（1）记“在一次游戏中摸出k 个白球”为事件(0,1,2,3)k A k =． ①2132322531()5C C P A C C==．（3分）②22111323222323225317()()()510C C C C C P A A P A P A C C +=+=+=．（6分）（2）1233973217749(0),(1),(2)10101001010501010100P XP X C P X ==⨯===⨯===⨯=．（9分）①X②X 的数学期望921497()012100501005E X =⨯+⨯+⨯=．（12分）【或：∵7(2,)10XB ，∴77()2105E X =⨯=】 20．解：方法1：（1）∵,PCBC PC AB⊥⊥，∴PC ⊥平面ABC ，∴PCAC⊥．（2分）（2）取BC 的中点N ，连MN ．∵P MC N =，∴M NP C=，∴M N⊥平面ABC ．作N H ⊥AC ，交AC 的延长线于H ，连结MH ．由三垂线定理得AC MH ⊥，∴M HN ∠为二面角MAC B --的平面角．∵直线AM 与直线PC 所成的角为60︒，∴在Rt AM N ∆中，60AM N ∠=︒．在AC N ∆中，AN ==在Rt AM N ∆中，cot 601MN AN AMN =⋅∠=︒=．在Rt NCH ∆中，sin 1sin 602N HC N N C H =⋅∠=⨯︒=．在Rt M NH ∆中，∵2M H ==，∴cos 7N H M H NM H∠==．故二面角M AC B --7（8分）（3）作NEM H⊥于E ．∵AC ⊥平面MNH ，∴ACN E⊥，∴NE ⊥平面MAC ，∴点N 到平面MAC的距离为7M N N H N E M H⋅==N 是线段BC 的中点，∴点B 到平面MAC 的距离是点N 到平面MAC7（12分）方法2：（1）∵,PC BC PC AB ⊥⊥，∴PC ⊥平面ABC ，∴PC AC ⊥．（2分）（2）在平面ABC 内，过C 作BC 的垂线，并建立空间直角坐标系如图所示．设(0,0,)P z ，则(0,0,)CP z =．13(0,1,),0)(,)2222AM z z =--=- ．∵2cos 60|cos ,|||||||AM C PAM C P AM C P ⋅︒=<>==⋅且z >，∴12=，得1z =，∴3(,1)22AM =-．设平面MAC 的一个法向量为(,,1)x y =n ，则由0,0AM C A ⎧⋅=⎪⎨⋅=⎪⎩ n n得310,2210,22y y ⎧-++=⎪⎪⎨⎪-=⎪⎩得31,x y ⎧=-⎪⎨⎪=-⎩∴(1,1)3=-n ．平面ABC的一个法向量为(0,0,1)CP =．cos ,7||CP CP ||CP ⋅<>==⋅ n n n ．显然，二面角MAC B--为锐二面角，∴二面角MAC B--7（8分）（3）点B 到平面MAC的距离||||7C B d⋅==n n ．（12分）21．解：（1）设1122(,),(,)A x y B x y ，则121212121,1,2y y x x y y x x -+=+==--．∵221121,x y a+=222221x y a+=，∴两式相减得121212122()()()()0x x x x y y y y a+-++-=，即121212212()x x y y y y x x a+-++-=，即211(2)0a+⨯-=，得212a =，∴椭圆C 的方程为2221x y +=．（4分）（2）解法1：设3344(,),(,)P x y Q x y ，2:l y kx m =+（∵2l 与y 轴相交，∴2l 的斜率存在）．由,4PM M Q O P O Q O Mλλ⎧=⎪⎨+=⎪⎩得33443434(,)(,),(,)(0,4),x m y x y m x x y y m λλλ--=-⎧⎨++=⎩得3434,4,x x y y m λλ-=⎧⎨+=⎩即3434,()()4,x x kx m kx m m λλ=- ⎧⎨+++= ⎩①②将①代入②得(3)0m λ-=，∵0m≠，∴3λ=．解法2：∵PM M Q λ= ，∴()OM OP OQ OM λ-=-，∴(1)OP OQ OM λλ+=+，又∵OP OQ λ+= 4OM ，∴(1)4OM OMλ+=，∴(3)OM λ-=0，又∵OM ≠0，∴3λ=．（8分）（3）将y kx m =+代入2221x y +=得222(2)2(1)0k x kmx m +++-=．∵3λ=，∴由3434223423,2,212x x km x x k m x x k ⎧⎪=-⎪-⎪+=⎨+⎪⎪-=⎪+⎩消去3x 、4x 得2222(1)41m km -=-．由0∆>得222(1)k m >-，即222(1)41m m ->-22(1)m -，即222(1)041m m m -<-，即(1)(1)0(21)(21)m m m m +-<+-，得112m -<<-，或112m <<．（13分）22．解：（1）方法1：∵*13()n n S n n S n ++=∈N ，且111S a ==，∴当2n≥时，3211214562(1)(2)112316n n n S S S n n n n S S S S S n -+++=⋅⋅⋅⋅=⨯⨯⨯⨯⨯=- ，且11S =也适合．当2n≥时，1(1)2n n n n n a S S -+=-=，且11a =也适合，∴*(1)()2nn n a n +=∈N ．方法2：∵1(3)0n n nS n S +-+=，∴1(1)(2)0n n n S n S ---+=，两式相减，得11()(2)()n n n n n S S n S S +--=+-，即1(2)n nna n a +=+，即12(2)n na n n a n++=≥．又∵可求得23a =，∴213a a =也适合上式．综上，得*12()n na n n a n++=∈N ．当2n≥时，3211213451(1)112312n n n a a a n n n a a a a a n -++=⋅⋅⋅⋅=⨯⨯⨯⨯⨯=- ，且11a =也适合，∴*(1)()2nn n a n +=∈N ．（4分）（2）2(1)nb n =+．设2(1)(1)(1)nnnn c b n =-=-+．当n 为偶数时，∵1221(1)(1)(1)21n n n n c c n n n --+=-⋅+-⋅+=+，12341[5(21)](3)2()()()5913(21).22n n n nn n n T c c c c c c n -+++=++++++=+++++==∴当n 为奇数（n ≥3）时，221(1)(2)34(1)22nn n n n n n T T c n --+++=+=-+=-，且114T c ==-也适合上式．综上：得234(),2(3)().2n n n n T n n n ⎧++-⎪⎪=⎨+⎪ ⎪⎩为奇数为偶数（9分）（3）令()ln(1)f x x x =-+．当0x >时，∵1()101f x x'=->+，∴()f x 在(0,)+∞上为增函数，∴当0x>时，()(0)0f x f >=，得ln(1)x x +<．令1(1,2,,)ixi n a == ，得11211ln(1)2()(1)1iia a i i i i +<==-++，∴11111111ln(1)2[(1)()()]2(1)222311ni ia nn n =+<-+-++-=-<++∑ ，即12111ln[(1)(1)(1)]2na a a +++< ，即21212111e 9n na a a a a a +++<< ．（14分）。

湖北省黄冈中学、孝感高中2013届高三上学期期末联合考试(理科)数学参考答案(定稿)

湖北省 2013届高三上学期期末联合考试理科数学参考答案1．D 解析：∵22i (2i)i 2i 112i i 1i z ++-====--，∴选择“D ”． 2．A解析：∵(2,3)()U P A B ∈ð，∴(2,3)P A ∈，且(2,3)P B ∉，∴2230,230,m n ⨯-+>⎧⎨+->⎩得1,5.m n >-⎧⎨<⎩故选择A ．3．A解析：符合条件的点P 落在棱长为3a的正方体内，根据几何概型的概率计算公式得33()1327a P a==．故选A ． 4．B解析：将曲线方程2y x =与直线方程y x =联立方程组，解得0x =或1x =．结合图形可知选项B 正确．5．B解析：方法1：∵(0)10,(1)l g 20f f =-<=>，∴()f x 在(0,1)内必有一个零点．又∵()f x 在(1,)-+∞上为增函数，∴()f x 有且仅有1个零点．方法2：由()0f x =得lg(1)22x x +=-+．作出函数()lg(1)g x x =+与()22x h x =-+的图象，知两函数的图象有且仅有一个交点，即方程()0f x =有且仅有一个根，即函数()f x 有且仅有一个零点．6．C解析：11131223344++=⨯⨯⨯．故选C ． 7．D解析：∵当0x <时，函数()f x 为增函数，∴当0x <时，()0f x '>．又∵当0x >时，随着x 的增大，函数值先递增，再递减，最后又递增，∴选择“D ”．8．C解析：①A 显然正确．②∵22()()||||0+⋅-=-=a b a b a b ，∴()()+⊥-a b a b ，∴B 正确． ③cos ,cos cos sin sin cos()||||αβαβαβ⋅<>==⋅=+=-⋅a ba b a b a b ．当[0,]αβπ-∈时，,αβ<>=-a b ；当[0,]αβπ-∉时，,αβ<>≠-a b ．故C 不正确． ④∵22()()||||||||||||⋅+⋅+=⇔+⋅=⋅+⇔=++a a b b a b a a b a b b a b a b a b ，∴D 正确．故选择“C ”．黄冈中学孝感高中9．A解析：1l ：111110A B x y C C ++=，2l ：222210A B x y C C ++=，两式相减得12121212()()0A A B Bx y C C C C -+-=． ∵点O 、M 的坐标都满足该直线的方程，∴点O 、M 都在该直线上，∴直线OM 的方程为12121212()()0A A B Bx y C C C C -+-=．故选“A ”．10．C解析：该几何体是三棱锥，将该三棱锥视为长方体的一个角，得长方体的体对角线的长为=，∴球的表面积为50π，选择“C ”．11．48解析：设被抽查的男生的人数为n ．∵后两组的频率之和为(0.01250.0375)50.25+⨯=，∴前三组的频率之和为0.75．又∵前三组的频数分别为6,12,18，∴612180.75n++=，得48n =．12．解析：∵对称轴经过函数图象的最高点或最低点，∴()8f π=13．2或3解析：展开式中3x 的系数为3425666216C aC a C -+=-，∴2560a a -+=，得2a =或3．14．[0,6π解析：作出可行域如图所示．直线2x y z +=与y 轴交于点(0,)2z ．设直线2x y z +=与曲线cos (0)2y x x π=≤≤相切于点A ．∵由1sin 2y x '=-=-得6x π=，∴(6A π，代入2x y z+=得6z π=(0,0)O 代入2x y z +=得0z =．故z 的取值范围为[0,6π．15．3解析：∵2AD AE AB =⋅，∴24AD AB AE==．设C D x =，则C B x =．∵222AB BC AC +=，∴2224(2)x x +=+，得3x =，即3CD =．16解析：将极坐标方程化为普通方程，得2221210,:C y C x y a +-=+=．在1C 中，令0y =，得x =，再将代入2C 得a =． 17．解：（1）由()|34|1f x x --≤得|2||34|1x x +--≤，即2,(2)(34)1,x x x <-⎧⎨-++-≤⎩或42,3(2)(34)1,x x x ⎧-≤<⎪⎨⎪++-≤⎩或4,3(2)(34)1,x x x ⎧≥⎪⎨⎪+--≤⎩得解集为35{|,}42x x x ≤≥或．（6分）（2）方法1：在数轴上，设点,,A B M 对应的实数分别为2,,a x -，则“()||1f x x a +->恒成立”⇔“|2|||1x x a ++->恒成立”⇔“||||1MA MB +>恒成立”．∵||||MA MB +的最小值为||AB ，即|2|a +，∴|2|1a +>，得21a +>，或21a +<-，即1a >-，或3a <-．方法2：由绝对值三角不等式得|2||||(2)()||2|x x a x x a a ++-≥+--=+，∴|2|1a +>，得1a >-，或3a <-．（12分） 18．解：（1）∵24()4123T πππ=-=，∴23T πω==，∴()2sin(3)f x x ϕ=+．∵点(,2)12π在图象上，∴2sin(3)212πϕ⨯+=，即sin()14πϕ+=，∴2()42k k ππϕπ+=+∈Z ，即24k πϕπ=+．故()2sin(3)4f x x π=+．（6分）（2）2()2sin(3)cos32(sin 3cos cos3sin )cos33cos3cos 3)444h x x x x x x x x x πππ=+=+=+6cos61)sin(6)4x x x π=++=+．由262()242k x k k πππππ-≤+≤+∈Z 得函数()h x 的单调递增区间为[,]()38324k k k ππππ-+∈Z ．（12分） 19．解：（1）记“在一次游戏中摸出k 个白球”为事件(0,1,2,3)k A k =．① 2132322531()5C C P A C C ==．（3分）②22111323222323225317()()()510C C C C C P A A P A P A C C +=+=+=．（6分）（2）1233973217749(0),(1),(2)10101001010501010100P X P X C P X ==⨯===⨯===⨯=．（9分） ①X 的分布列为②X 的数学期望921497()012100501005E X =⨯+⨯+⨯=．（12分）【或：∵7(2,)10XB ，∴77()2105E X =⨯=】 20．解：方法1：（1）∵,PC BC PC AB ⊥⊥，∴PC ⊥平面ABC ，∴PC AC ⊥．（2分）（2）取BC 的中点N ，连MN ．∵P M C N =，∴M N P C =，∴MN ⊥平面ABC ．作NH ⊥ AC ，交AC 的延长线于H ，连结MH ．由三垂线定理得AC MH ⊥，∴MHN ∠为二面角M AC B --的平面角．∵直线AM 与直线PC 所成的角为60︒，∴在Rt AMN ∆中，60AMN ∠=︒．在ACN ∆中，AN =．在Rt AMN ∆中，cot 601MN AN AMN =⋅∠=︒=．在Rt NCH ∆中，sin 1sin 60NH CN NCH =⋅∠=⨯︒=．在Rt M NH ∆中，∵MHcos NH MHN MH ∠=．故二面角M AC B --（8分）（3）作NE MH ⊥于E ．∵AC ⊥平面MNH ，∴AC NE ⊥，∴NE ⊥平面MAC ，∴点N 到平面MAC的距离为MN NH NE MH ⋅==．∵点N 是线段BC 的中点，∴点B 到平面MAC 的距离是点N 到平面MAC．（12分）方法2：（1）∵,PC BC PC AB ⊥⊥，∴PC ⊥平面ABC ，∴PC AC ⊥．（2分）（2）在平面ABC 内，过C 作BC 的垂线，并建立空间直角坐标系如图所示．设(0,0,)P z ，则(0,0,)CP z =．13(0,1,),0)(,)22AM z z =--=． ∵2cos 60|cos ,|||||||3AM CP AM CP AM CP⋅︒=<>==⋅且0z >，∴12=，得1z =，∴3(,1)2AM =-．设平面MAC 的一个法向量为(,,1)x y =n ，则由0,0AM CA ⎧⋅=⎪⎨⋅=⎪⎩n n 得310,210,2y y ⎧++=⎪⎪⎨⎪-=⎪⎩得1,x y ⎧=⎪⎨⎪=-⎩∴(1,1)=-n ．平面ABC 的一个法向量为(0,0,1)CP =．21cos ,||CP CP ||CP ⋅<>==⋅n n n ．显然，二面角M AC B --为锐二面角，∴二面角M ACB --（8分）（3）点B 到平面MAC 的距离||||CB d ⋅==n n （12分） 21．解：（1）设1122(,),(,)A x y B x y ，则121212121,1,2y y x x y y x x -+=+==--．∵221121,x y a +=222221x y a +=，∴两式相减得121212122()()()()0x x x x y y y y a +-++-=，即121212212()x x y y y y x x a +-++- 0=，即211(2)0a+⨯-=，得212a =，∴椭圆C 的方程为2221x y +=．（4分）（2）解法1：设3344(,),(,)P x y Q x y ，2:l y kx m =+（∵2l 与y 轴相交，∴2l 的斜率存在）．由,4PM MQ OP OQ OM λλ⎧=⎪⎨+=⎪⎩得33443434(,)(,),(,)(0,4),x m y x y m x x y y m λλλ--=-⎧⎨++=⎩得3434,4,x x y y m λλ-=⎧⎨+=⎩即3434,()()4,x x kx m kx m m λλ=- ⎧⎨+++= ⎩①②将①代入②得(3)0m λ-=，∵0m ≠，∴3λ=．解法2：∵PM MQ λ=，∴()OM OP OQ OM λ-=-，∴(1)OP OQ OM λλ+=+，又∵OP OQ λ+=4OM ，∴(1)4OM OM λ+=，∴(3)OM λ-=0，又∵OM ≠0，∴3λ=．（8分）（3）将y kx m =+代入2221x y +=得222(2)2(1)0k x kmx m +++-=．∵3λ=， ∴由3434223423,2,212x x km x x k m x x k ⎧⎪=-⎪-⎪+=⎨+⎪⎪-=⎪+⎩消去3x 、4x 得2222(1)41m k m -=-．由0∆>得222(1)k m >-，即222(1)41m m ->- 22(1)m -，即222(1)041m m m -<-，即(1)(1)0(21)(21)m m m m +-<+-，得112m -<<-，或112m <<．（13分） 22．解：（1）方法1：∵*13()n n S n n S n++=∈N ，且111S a ==，∴当2n ≥时， 3211214562(1)(2)112316n n n S S S n n n n S S S S S n -+++=⋅⋅⋅⋅=⨯⨯⨯⨯⨯=-，且11S =也适合．当2n ≥时，1(1)2n n n n n a S S -+=-=，且11a =也适合，∴*(1)()2n n n a n +=∈N ．方法2：∵1(3)0n n nS n S +-+=，∴1(1)(2)0n n n S n S ---+=，两式相减，得 11()(2)()n n n n n S S n S S +--=+-，即1(2)n n na n a +=+，即12(2)n n a n n a n++=≥．又∵可求得23a =，∴213a a =也适合上式．综上，得*12()n n a n n a n++=∈N ．当2n ≥时，3211213451(1)112312n n n a a a n n n a a a a a n -++=⋅⋅⋅⋅=⨯⨯⨯⨯⨯=-，且11a =也适合， ∴*(1)()2n n n a n +=∈N ．（4分）（2）2(1)n b n =+．设2(1)(1)(1)n n n n c b n =-=-+．当n 为偶数时，∵1221(1)(1)(1)21n n n n c c n n n --+=-⋅+-⋅+=+，12341[5(21)](3)2()()()5913(21).22n n n nn n n T c c c c c c n -+++=++++++=+++++==∴当n 为奇数（n ≥3）时，221(1)(2)34(1)22n n n n n n n T T c n --+++=+=-+=-，且114T c ==-也适合上式．综上：得234(),2(3)().2n n n n T n n n ⎧++- ⎪⎪=⎨+⎪ ⎪⎩为奇数为偶数（9分）（3）令()ln(1)f x x x =-+．当0x >时，∵1()101f x x'=->+，∴()f x 在(0,)+∞上为增函数，∴当0x >时，()(0)0f x f >=，得ln(1)x x +<．令1(1,2,,)ix i n a ==，得11211ln(1)2()(1)1i i a a i i i i +<==-++， ∴11111111ln(1)2[(1)()()]2(1)222311ni i a n n n =+<-+-++-=-<++∑，即12111ln[(1)(1)(1)]2n a a a +++<，即21212111e 9nna a a a a a +++<<．（14分）。

湖北省黄冈中学、孝感高中高三化学上学期期末联合考试新人教版

湖北省黄冈中学孝感高中2013届高三上学期期末联合考试化学测试可能用到的相对原子质量数据：H- 1 C-12 N-14 O-16 S-32 Cu-64 Fe-56 第I卷一、选择题：7．下列说法正确的是A．工业上用电解熔融的氯化铝冶炼铝B．漂白粉的有效成分是次氯酸钙C．玛瑙的主要成分为硅酸盐D．pH小于7的雨水属于酸雨8．用N A表示阿伏加德罗常数的值。

下列叙述中不正确的是（）A．将28g Fe投入到1L1mol／L的硫酸中，可得到11.2LH2B．常温常压下，32 g O2和O3的混合气体中含有的氧原子数为2 N AC．100mL0.1mol／LCH3COOH溶液中分子总数比10mL1mol／L CH3COOH溶液中分子总数多D．标准状况下，22.4L氯气与足量镁粉充分反应，转移电子总数为2 N A9．下列说法正确的是A．常温下，铜与氧气很难反应，因为铜和氧气的反应是吸热反应B．金属锂在常温和加热情况下与氧气反应的产物不同C．焰色反应实验中的铂丝应用稀盐酸洗涤D．用pH试纸测得某浓度氯水的pH为410．下列液体均处于25℃，有关叙述正确的是A．将0.1mol／L NaHCO3溶液加水稀释，溶液中c(H+)减小B．pH=2的CH3COOH和CH3COONa混合溶液中，各离子浓度大小关系为c(H+)＞c(CH3COO)＞c(Na+)＞c(OH)C．取pH=5的H2SO4溶液1 mL稀释到1000 mL，稀释后溶液中c(H+):c(SO42-)=2:1D．往Ca(OH)2悬浊液中加入少量NaOH固体，溶液pH增大，但Ca(OH)2的Ksp不变11．能正确表示下列反应的离子方程式的是A．新制的氧化铝溶于氢氧化钠溶液：Al2O3+2OH–＝2AlO2–+ H2OB．冷的氢氧化钠溶液中通入氯气： Cl2 + OH–＝ Cl–+ HClOC．用KIO3氧化酸性溶液中的KI ： 5I–+ IO3–+ 3H2O＝3I 2 + 6OH–D．硫酸铝溶液中加入过量氨水：Al3+ +3OH–＝Al(OH)3↓12．X、Y、Z为同一短周期中的元素，其原子半径依次减小，它们的最高价氧化物对应的水化物之间，任意两种混合均可反应，M为Y、Z形成的化合物，其溶液显酸性。

湖北省2013届高三上学期期末联考理科综合试题.pdf

湖北省2013年高三上学期期末联考理综试题考试时间：2013年1月22日 9:00—11:30 试卷满分：300分本试卷分第卷（选择题）和第卷（非选择题）两部分，考试结束后，请将本试卷和答题卡一并交回。

本卷满分300分，考试用时150分钟。

注意事项： 1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并请认真填涂准考证号。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

在试题卷上作答无效。

以下数据可供解题时参考。

可能用到的相对原子质量：H-1 N-14 O-16 Na-23 Mg-24 Al-27 Fe-56 第卷（选择题，共126分）一、选择题：（本题共21小题，每小题6分。

在每小题给出的四个选项中，1-13题只有一项是符合题目要求的。

14-21题有一至多项符合题意。

） 1．某高等动物的一个受精卵发育成雄性个体的过程中产生了两个正常的体细胞：肝细胞（C1）、胰腺细胞（C2）及一个正常的精原细胞（C3）。

该精原细胞产生了两个正常的次级精母细胞（G1、G2）。

相关说法正确的是 A．C1、C2、C3细胞核遗传信息相同，C1、C2核基因转录出的mRNA有差异 B．C1、C2、G1、G2四个细胞核中DNA数目相同，但这些DNA的遗传信息都不同 C．C1、C2、C3细胞内DNA的数目一定相同，核基因转录出的mRNA相同 D．C1、C2、C3 、G1、G2的染色体数目相同 2．某同学进行的生物学知识的下列总结中正确的有 ①酶、抗体、载体、激素的基本组成单位都是氨基酸能产生激素的细胞一定能合成酶进行光合作用的细胞一定同时进行呼吸作用进行有氧呼吸的生物一定有线粒体进行呼吸作用的植物细胞一定能进行光合作用高等动物的细胞中一定有线粒体有细胞壁的一定是植物细胞。

自养生物一定有吸收光能的色素细胞间信息交流一定依赖细胞膜表面受体蛋白生态系统中消费者都是动物 A．0项 B．2项 C．4项 D．5项 3．有关ATP的说法正确的是 A．ATP中的“A”和DNA、RNA中的“A”代表的意义相同 B．一个ATP末端的磷酸基团转移到一个腺嘌呤核糖核苷酸分子上将得到两个ADP分子 C．ATP细胞中含量高且与ADP相互转化迅速，与其作为细胞直接的能源物质相适应 D．细胞中的ATP储存的化学能都能用于各项生命活动 4．科学的研究方法是取得成功的关键。