2.1-2DFT基础(2)

合集下载

DFT基础

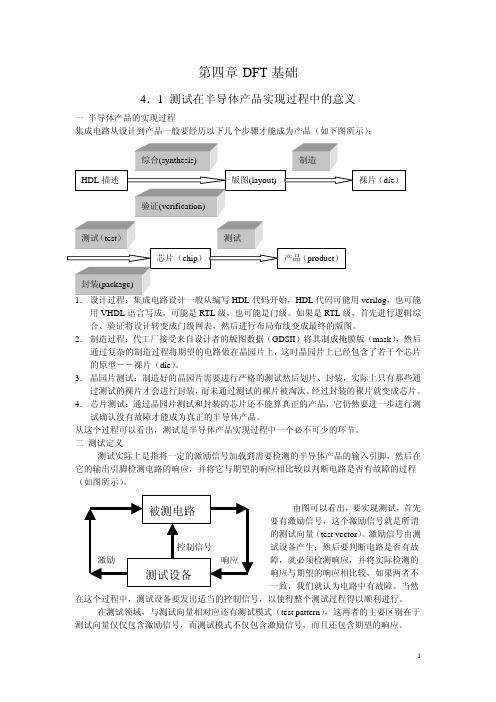
第四章 DFT 基础4．1 测试在半导体产品实现过程中的意义一半导体产品的实现过程集成电路从设计到产品一般要经历以下几个步骤才能成为产品（如下图所示）：verilog ，也可能用VHDL 语言写成，可能是RTL 级，也可能是门级。

如果是RTL 级，首先进行逻辑综合、验证将设计转变成门级网表，然后进行布局布线变成最终的版图。

2．制造过程：代工厂接受来自设计者的版图数据（GDSII ）将其制成掩膜版（mask ），然后通过复杂的制造过程将期望的电路做在晶园片上，这时晶园片上已经包含了若干个芯片的原型－－裸片（die ）。

3．晶园片测试：制造好的晶园片需要进行严格的测试然后划片、封装，实际上只有那些通过测试的裸片才会进行封装，而未通过测试的裸片被淘汰。

经过封装的裸片就变成芯片。

4．芯片测试：通过晶园片测试和封装的芯片还不能算真正的产品，它仍然要进一步进行测试确认没有故障才能成为真正的半导体产品。

从这个过程可以看出，测试是半导体产品实现过程中一个必不可少的环节。

二测试定义测试实际上是指将一定的激励信号加载到需要检测的半导体产品的输入引脚，然后在它的输出引脚检测电路的响应，并将它与期望的响应相比较以判断电路是否有故障的过程（如图所示）。

在这个过程中，测试设备要发出适当的控制信号，式（test pattern ），这两者的主要区别在于测试向量仅仅包含激励信号，而测试模式不仅包含激励信号，而且还包含期望的响应。

由图可以看出，要实现测试，首先要有激励信号，这个激励信号就是所谓的测试向量（test vector ）。

激励信号由测试设备产生；然后要判断电路是否有故障，就必须检测响应，并将实际检测的响应与期望的响应相比较，如果两者不一致，我们就认为电路中有故障。

当然以使得整个测试过程得以顺利进行。

在测试领域，与测试向量相对应还有测试模由上面的分析可以看出，测试问题在测试前就是测试模式生成和测试模式验证（时序验证）问题；而在测试时就是测试向量施加和测试响应检测及结果判断问题。

DFT比较简易的教程

DFT比较简易的教程DFT（离散傅立叶变换）是一种将时域信号转换为频域信号的数学工具。

它在信号处理、图像处理和通信系统中都有广泛应用。

虽然DFT涉及到一些复杂的数学概念，但我们可以通过一些简单的例子来理解它的工作原理和基本用法。

DFT的基本公式如下：```X(k)=Σ(x(n)·e^(-j·2π·k·n/N))，k=0,1,...,N-1```其中，X(k)是频域上的离散频谱，x(n)是时域上的离散信号，N是信号的长度。

为了更好地理解DFT的工作过程，我们以一个简单的例子开始。

假设我们有一个长度为8的信号x(n)={2,4,1,3,5,7,2,1}，我们想要计算它的频谱。

首先，我们需要明确信号的长度N为8、然后，我们将信号中的每个样本值与一个复指数函数相乘，然后将这些乘积值相加，从而得到频谱中的每个频率分量的值。

对于每个频率分量k，我们计算它的复值X(k)的公式为：```X(k)=Σ(x(n)·e^(-j·2π·k·n/N))，n=0,1,...,N-1```其中，n是时域信号的样本索引。

我们可以逐个计算频率分量k的值。

以k=0为例，我们有：```X(0)=Σ(x(n)·e^(-j·2π·0·n/8))=Σ(x(n)),n=0,1,...,7```将信号中的每个样本值相加，我们得到X(0)的值为：```X(0)=2+4+1+3+5+7+2+1=25```同样的方式，我们可以计算其他频率分量的值。

为了计算频率分量k的复值X(k)，我们需要将每个样本值与复指数函数相乘，然后求和。

复指数函数可用欧拉公式表示为：```e^(-j · 2π · k · n / N) = cos(2π · k · n / N) -j · sin(2π · k · n / N)```在上述例子中，我们计算了一个信号的频谱。

波谱分析教程第二版教学设计

波谱分析教程第二版教学设计前言波谱分析是信号处理领域的一种重要技术，它可以对信号的频谱密度进行分析，从而得到信号的频谱特征。

本教程旨在对波谱分析算法进行深入讲解，包括离散傅里叶变换（DFT）、快速傅里叶变换（FFT）以及功率谱密度估计法等。

教学目标1.了解波谱分析的基本概念和理论基础2.掌握波形信号的采样、量化、编码等基本知识3.熟悉离散傅里叶变换(DFT)、快速傅里叶变换(FFT)及功率谱密度估计法等算法的实现原理4.熟练运用Matlab等软件工具对波谱分析算法进行实际应用教学内容第一章：波谱分析基础1.1 信号的采样、量化、编码1.2 时域与频域分析1.3 傅里叶分析基本概念第二章：离散傅里叶变换（DFT）2.1 离散傅里叶变换基本概念2.2 矩阵表示2.3 傅里叶变换的性质2.4 实现方法第三章：快速傅里叶变换（FFT）3.1 快速傅里叶变换基本概念3.2 Cooley-Tukey算法3.3 Radix-2 FFT算法第四章：功率谱密度估计法4.1 周期图法4.2 平均周期图法4.3 Welch法第五章：波谱分析应用5.1 随机信号的波谱分析5.2 信道估计5.3 载波同步教学方法本教程将采用讲解、演示和实践相结合的教学方式，具体表现为：1.讲解：通过PPT等多媒体手段，进行理论知识讲解，重点阐述算法的实现原理和应用场景。

2.演示：通过Matlab等软件平台进行算法演示，展示算法的具体操作流程和输出结果。

3.实践：通过课堂作业等方式进行算法实践，巩固学生对教学中所讲授的内容的掌握程度。

总结本教程旨在帮助学生深入理解波谱分析算法的原理，熟悉算法的应用方法，并通过实践提高学生的分析和解决问题的能力。

数字信号处理第二章 DFT

~ N=16：x (4) x((4))16 x((12 16))16 x(12)
例2：
x (n ) x (n ) 0
~ 1 X (k ) k 0 N ~ X (r )
e
j

15
周期序列的傅里叶级数表示：
正变换：
2 N 1 N 1 j nk ~ ~(n) ~(n)e N ~(n)W nk X (k ) DFS x x x N n 0 n 0
反变换：
~ ~(n) IDFS X (k ) 1 x N
j
2 kN N
k mN , m为整数其他k
W
n 0
N 1
( m k ) n N
1W 1W
( k m ) N N ( k m ) N

1 e
j
1 e
N m k rN 0 mk
此外，复指数序列还有如下性质：
0 WN 1, W N 2 N r 1 1, WN WN r
ek (n)
ek (n) 是以N为周期的周期序列，所以基序
列 {e }（k=0,…,N-1) 只有N个是独立的，可以用这N个基序列将 ~ ( n) 展开。 x
j 2 nk N
12
复指数序列 ek (n) e
周期性:
j
2 nk N
W
nk N
的性质：
无论对k还是n，复指数序列都具备周期性。
时间函数连续和非周期连续和周期(T0) 离散(Ts)和非周期离散(Ts)和周期(T0) 非周期和连续非周期和离散(Ω 0=2π /T0) 周期(Ω s=2π /Ts)和连续周期(Ω s=2π /Ts)和离散(Ω 0=2π /T0) 频率函数

二维dft变换编程

二维dft变换编程1.引言1.1 概述概述部分的内容引言部分将介绍二维DFT变换的基本概念和其在图像处理中的重要性。

随着数字图像处理的广泛应用，对图像进行频谱分析已经变得不可或缺。

二维快速傅里叶变换（DFT）是一种常用的技术，用于将图像从空域转换到频域，并可用于各种图像处理任务，例如滤波、图像增强和图像压缩等。

在数字图像中，图像的像素被组织成一个二维矩阵，其中每个元素代表图像的亮度或颜色信息。

通过对这个二维矩阵进行二维DFT变换，我们可以将图像的信息从空间域转换到频率域。

频率域表示了图像中各种频率成分的存在和强度，因此可以通过分析频域图像来获取有关原始图像的信息。

二维DFT变换的应用广泛。

在图像滤波方面，通过在频率域对图像进行滤波，可以实现各种滤波效果，例如去除噪声、增强轮廓和边缘检测等。

此外，二维DFT变换还可以用于图像增强，通过调整频域图像的幅度谱和相位谱，可以改善图像的质量和视觉效果。

另外，二维DFT变换在图像压缩和数据压缩领域也有重要作用，通过把图像信息从空域转换到频域并利用频域的特性，可以实现对图像的高效压缩和储存。

本文将详细介绍二维DFT变换的原理和应用。

首先，我们将解释二维DFT变换的基本原理，包括其数学定义和计算方法。

然后，我们将探讨二维DFT变换在图像处理中的应用，包括滤波、增强和压缩等方面。

最后，我们将对本文进行总结，并展望未来关于二维DFT变换的研究方向。

本文旨在为读者提供关于二维DFT变换的全面概述，并希望能够帮助读者理解和应用二维DFT变换在图像处理中的重要性和实际意义。

通过掌握二维DFT变换的原理和应用，读者将能够更好地使用和开发基于频域的图像处理算法，从而提高图像处理的效果和质量。

1.2 文章结构文章结构部分应该包括以下内容：文章结构部分旨在介绍本文的组织结构和主要内容。

本文将按照以下顺序来进行叙述。

首先，引言部分将概述本文的目标和重要性，并简要介绍文章的结构。

接着，正文部分将详细讨论二维DFT变换的原理和应用。

2第2章 DFT

结论：周期序列是由复指数信号线性叠加而成。
思考：周期序列有多少个不同的复指数序列分量？
2 周期序列有N个独立成份
9/41
k=0,
j 2π 0n
e N =1
1,
…
j 2π 1n
eN
k=N,
j 2π Nn
eN
= e j2πn
=1
N+ 1,
…
j2π (N+1)n
j2π Nn j2π n
e N =e N ⋅e N
X (k ) = x(n)e N
n=0
∞
∑ DTFT X (e jω ) =
x (n )e − jωn
n = −∞
14/41
②傅里叶变换形式不同
DFT
∑N −1
− j 2 π kn
X (k ) = x(n)e
n=0
离散取值
N
比较
DTFT
∞
∑ X (e jω ) =
x (n )e − jωn
n = −∞
域处理信号，所以要求信号在时、频两域都是离散的。
只有周期序列满足要求！
6/41
1
2.1 离散傅里叶级数(DFS)
2.1.1 离散傅里叶级数的推导
周期序列: ~x(n) = ~x(n+kN) k为任意整数
∑ ~x (n) =
1
N
−1
X~
(k
)e
j
2π N
kn
反变换
N k=0
∑ X~ (k )
=
N
−1
(A1) (A1)
-Ω2 -Ω1
Ω Ω1 Ω2
离散非周期 x(n)
连续和周期

(完整)DFT基础资料

第四章 DFT 基础4．1 测试在半导体产品实现过程中的意义一半导体产品的实现过程集成电路从设计到产品一般要经历以下几个步骤才能成为产品（如下图所示）:1． verilog ，也可能用VHDL 语言写成,可能是RTL 级，也可能是门级。

如果是RTL 级，首先进行逻辑综合、验证将设计转变成门级网表，然后进行布局布线变成最终的版图。

2．制造过程：代工厂接受来自设计者的版图数据(GDSII ）将其制成掩膜版（mask ），然后通过复杂的制造过程将期望的电路做在晶园片上，这时晶园片上已经包含了若干个芯片的原型－－裸片(die ）。

3．晶园片测试：制造好的晶园片需要进行严格的测试然后划片、封装,实际上只有那些通过测试的裸片才会进行封装，而未通过测试的裸片被淘汰。

经过封装的裸片就变成芯片.4．芯片测试：通过晶园片测试和封装的芯片还不能算真正的产品，它仍然要进一步进行测试确认没有故障才能成为真正的半导体产品.从这个过程可以看出，测试是半导体产品实现过程中一个必不可少的环节。

二测试定义测试实际上是指将一定的激励信号加载到需要检测的半导体产品的输入引脚，然后在它的输出引脚检测电路的响应,并将它与期望的响应相比较以判断电路是否有故障的过程（如图所示).由图可以看出，要实现测试,首先要有激励信号，这个激励信号就是所谓的测试向量（test vector ）。

当然在这个过程中，测试设备要发出适当的控制信号,以使得整个测试过程得以顺利进行.在测试领域，与测试向量相对应还有测试模式(test pattern)，这两者的主要区别在于测试向量仅仅包含激励信号,而测试模式不仅包含激励信号，而且还包含期望的响应。

由上面的分析可以看出，测试问题在测试前就是测试模式生成和测试模式验证(时序验证)问题；而在测试时就是测试向量施加和测试响应检测及结果判断问题。

dft 电荷分布-概述说明以及解释

dft 电荷分布-概述说明以及解释1.引言1.1 概述在材料科学和化学领域中，了解物质中电子的分布是至关重要的。

电子分布描述了电子在原子和分子中的位置和能量状态，对于理解和解释物质性质具有重要意义。

而DFT（密度泛函理论）是一种强大的计算电子结构的方法，可以预测和解析电子密度分布。

DFT理论基于量子力学的原理，通过求解Schrödinger方程来描述多电子体系的行为。

与传统的基于波函数的方法相比，DFT方法选择以电荷密度为基本变量，将多电子体系的能量表示为电荷密度的泛函。

这种方式的优势在于DFT能够处理复杂多体相互作用以及强关联体系，如过渡金属催化剂、材料表面等。

通过DFT计算，我们可以获得材料的电子分布，进而得到一系列物理和化学性质的信息。

例如，电子态密度可以描述材料的能带结构，从而预测导电性和光学性质。

电子的局域性和电荷转移可以解释物质的晶体结构和反应活性。

此外，电子分布还与化学键的强度和键长、局部反应性等密切相关。

随着计算能力的不断提高，DFT方法在材料科学和化学领域的应用越来越广泛。

通过DFT计算，我们可以在原子级别上理解和预测材料的性质和行为，为新材料的设计和开发提供重要的指导。

本文将系统介绍DFT电子分布的研究进展和应用。

首先，我们将简要介绍DFT的基本原理和方法。

然后，我们将探讨DFT在材料科学、化学领域中的应用，包括材料性质的预测和提高、催化反应机理的理解以及材料界面和表面的调控。

最后，我们将总结DFT方法的优缺点，并展望未来的发展方向。

通过深入研究DFT电荷分布，我们将能够更好地理解和解释材料的性质和行为。

相信本文将为读者提供有关DFT电荷分布的全面了解，并为相关领域的研究和应用提供有价值的参考。

文章结构部分内容如下：1.2 文章结构本文按照以下结构进行展开：1. 引言：首先介绍DFT电荷分布的背景和意义，阐述DFT在电荷分布研究中的重要性和应用前景。

2. 正文：详细讨论DFT电荷分布的相关概念、原理和计算方法。

dft计算吸附结合能e=etotal_理论说明

dft计算吸附结合能e=etotal 理论说明1. 引言1.1 概述本文旨在系统地介绍DFT（密度泛函理论）计算中吸附结合能e=etotal的理论说明。

吸附结合能是表征吸附分子与表面相互作用强弱的重要物理量，对于研究催化剂、气相分子与固体界面等领域具有重要意义。

通过对DFT计算基本原理以及关键步骤的详细介绍，本文将揭示吸附结合能计算的理论基础和实际操作步骤。

1.2 文章结构本文分为五个主要部分，每个部分都涵盖了不同的议题和内容。

首先是引言部分，概述了文章的目标和结构。

其次是DFT计算的基本原理部分，包括密度泛函理论（DFT）和能量总和方法（Etotal）的介绍，以及吸附结合能定义与计算方法的讨论。

第三部分集中阐述了DFT计算吸附结合能理论说明的关键要点，包括基准体系和表面模型构建、计算参数和方法选择以及结果解读与分析。

第四部分通过实例研究与案例分析来展示吸附能计算在气相分子吸附到固体表面以及催化剂反应物分子与表面相互作用能计算等方面的应用。

最后，在结论与展望部分，对DFT计算吸附结合能的理论说明进行总结提炼，并指出存在不足和未来的改进方向。

1.3 目的本文旨在通过对DFT计算中吸附结合能e=etotal理论说明的详细阐述，在读者实施相关计算时提供指导和参考。

此外，本文还旨在加深对DFT计算原理和方法的理解，以及对吸附结合能这一重要概念的认识。

通过学习本文，读者将能够更好地理解和利用DFT方法来研究吸附现象，为相关领域的科学研究提供有力支持。

2. DFT计算的基本原理:2.1 密度泛函理论(DFT):密度泛函理论（Density Functional Theory，DFT）是一种在固体物理和量子化学中广泛使用的理论方法。

它是通过计算系统中的电子密度来描述物质的性质。

DFT的核心思想是将N体问题转化为一个等效单粒子问题，即将含有多个电子的问题转化为仅包含一个有效势能下单电子运动的问题。

在DFT中，系统的能量由电荷密度决定，而不依赖于每个电子的位置信息。

第三章DFT要点

一、教学目的和要求了解傅立叶变换的几种形式（傅立叶变换、傅立叶级数、序列的傅立叶变换、离散傅立叶变换），加深对傅立叶变换的理解；掌握周期序列的离散傅立叶级数正变换和反变换的表示形式，理解周期序列和有限长序列之间的本质联系；熟练掌握离散傅立叶级数的四个基本性质：线性、序列的移位、调制特性和周期卷积和；掌握离散傅立叶变换（DFT）的正变换和反变换表示形式；理解掌握频域抽样理论。

教学重点和难点教学重点：周期序列的离散傅立叶级数正变换和反变换的表示形式；离散傅立叶级数的四个基本性质；离散傅立叶变换（DFT）的正变换和反变换表示形式。

教学难点：DFT的周期性；循环卷积；DFT的共轭对称性；DFT的应用。

二、学习要点（1）DFT的定义和物理意义，DFT和FT、ZT之间的关系；（2）DFT的重要性质和定理：隐含周期性、循环移位性质、共轭对称性、实DFT的特点、循环卷积定理、离散巴塞伐尔定理；（3）频率域采样定理；三、习题：（一）判断：1、有限长序列的DFT是周期的。

（Χ）2、序列的N点DFT是序列的傅里叶变换在单位圆上的N点等间隔采样。

（Χ）3、实序列的DFT具有共轭对称性质。

（√）4、若序列x(n)的长度为M，只有当频域采样点数MN≥时，可由x(n)的N点DFT恢复x(n)。

（√）5、循环卷积和线性卷积是相等的。

（Χ）6、用DFT对连续信号进行谱分析，会产生栅栏效应。

（√）7、截断效应会导致频谱泄露和谱间干扰。

（√）8、栅栏效应和频率分辨率是同一个概念。

（Χ）9、信号持续时间的长短和谱分辨率没有关系。

（Χ）（二）、选择1、N点IDFT具有隐含周期特性，周期是（D ）：A.4NB.3NC.2ND. N2、N点DFT的共轭对称性指关于（C ）的对称性：A.2NB.NC.N/2D. 03、若序列x(n)和y(n)的长度分别为4，5，要使L点循环卷积和线性卷积相等，则L的最小值为（C ）：A.10B.9C.8D.74、若X(k)是x(n)的N点DFT，则DFT[x*(N-n)]=( B ):A. X*(n)B. X*(k)C. X*(N-k)D. X(N-k)5、若X(k)是x(n)的N点DFT，则DFT[x*(n)]=( C ):A. X*(n)B. X*(k)C. X*(N-k)D. X(N-k)6、若序列x(n)和y(n)的长度分别为N，M，则它们的L点循环卷积和线性卷积相等的条件是（A ）：A. 1-≥ D. 1++L-LNN≥M+N≥M≥ C. ML B. MNL+7、若序列长度为M，采样点数为N，则频域采样定理要求（A）A ．MN≥ B ．MN≤ C ．2MN≥ D ．2MN≤8、关于栅栏效应和频率分辨率，下列说法正确的是（B ）A ．相同的概念B ．增加点数可以改善栅栏效应C ．增加点数可以改善频率分辨率D ．增加信号持续时间并不能改善频率分辨率 9、关于截断效应下列说法正确的是（C ）A ．会引起栅栏效应B ．会导致频谱延拓C ．会引起谱间干扰D ．会导致时域混叠10、用DFT 对连续信号进行谱分析，会出现（D ）A ．频谱展宽B ．泄露C ．截断效应D ．栅栏效应11、用DFT （N 点）对序列进行谱分析，则频率分辨率为（B ） A ．/N π B ．/N 2π C ．/N 3π D ． /N 4π 三：填空题 1、*()()(),()ee e e x n x n x n x n =-如果序列满足则称为（）序列。

dft stil格式-概述说明以及解释

dft stil格式-概述说明以及解释1.引言1.1 概述在数值分析和信号处理领域中，离散傅里叶变换（Discrete Fourier Transform，DFT）是一种重要的数学工具，用于将信号从时域转换到频域。

在实际应用中，经常需要对信号进行频谱分析、滤波等操作，而DFT 是实现这些操作的基础。

在本文中，我们将重点介绍DFT的一种特殊形式——DFT stil格式。

该格式是对标准DFT定义的一个改进，可以更高效地实现频谱分析和滤波操作。

我们将详细介绍DFT stil格式的定义、优点、应用场景以及实际操作方法，希望读者能通过本文对该格式有一个全面的了解，并在实际应用中能够灵活运用。

1.2 文章结构文章结构部分是指整篇文章的组织结构和内容安排方式。

在本篇长文中，文章结构可以分为以下几个部分：1. 引言部分：介绍文章的主题和背景，概括论述文章的要点和意义。

2. 正文部分：包括论述文章主题的具体内容和要点。

可以分为不同的章节或段落来展开论述，每个要点都需要有详细的论据和例证来支持。

3. 结论部分：总结全文内容，归纳文章的观点和结论，提出展望和建议，落实文章的主题和目的。

在文章结构部分，可以进一步详细讲解各部分的内容和意义，使读者能够清晰地理解全文的组织结构和逻辑关系。

文章结构的合理性和清晰性对于读者的阅读理解和文章内容的传达至关重要。

1.3 目的本文旨在介绍和探讨关于DFT STIL格式的相关知识和应用。

通过对DFT STIL格式的概述和分析，读者可以更加深入地了解该格式的特点、优势和使用方法。

同时，本文将重点探讨DFT STIL格式在数字电路设计和测试中的应用，以及其对测试效率和准确性的影响。

通过本文的阐述，读者可以进一步了解如何使用DFT STIL格式来提高数字电路测试的效率和质量，从而更好地应用于实际工程中。

希望本文能够对读者有所启发，促进数字电路设计和测试领域的发展与进步。

2.正文2.1 第一要点在本部分，我将重点讨论DFT STIL格式的基本概念和特点。

DFT基本原理范文

DFT基本原理范文
DFT的基本原理
DFT（Discrete Fourier Transform）是一种数字信号处理的重要算法，它可以将信号从时域转换到频域，提取其中的有用信息，并为信号进
行分析、处理和操作提供重要参考。

它是一种离散的线性变换，可以将任
何信号从时域转换到频域。

在数字信号处理领域，DFT是一种很重要的基
本工具，用于信号的建模、分析、操作和恢复。

DFT是一种基于傅里叶变换的离散变换。

傅里叶变换（FT）是一种将
时域信号转换为频域信号的线性变换，它可以将时域信号的低频成分提取
出来，并将它转换到频域信号的高频组件中，以便进行建模、分析、绘图
和其他操作。

DFT是FT的离散变换，它利用离散点的技术，将FT采样为
离散的和有限的信号，因此它的应用很广泛。

DFT是使用来自傅里叶定律的函数来计算时域信号的离散傅里叶变换。

它是通过不断采样信号，将时域的信号转换为频域的信号。

DFT可以将时
域信号的低频分量提取出来，然后转化为频域的高频分量。

DFT的过程如下：首先，将输入的信号采样，形成一个离散点；然后，将采样的离散点代入函数中，计算出信号的傅里叶变换；最后，可以通过
计算得出信号的频谱，从而实现信号处理的目的。

离散傅里叶变换的应用

离散傅里叶变换的应用离散傅里叶变换，听起来是不是有点高大上？别怕，今天就带你轻松了解这玩意儿！简单来说，离散傅里叶变换（DFT）就像是一把魔法钥匙，能把复杂的信号转换成频率的“歌单”。

想象一下，你在听一首喜欢的歌，这首歌里的每个乐器、每个音符，DFT都能把它们分开，帮你找到最喜欢的那一部分。

就像去KTV点歌，想唱的部分一按就来！1. DFT的基础知识1.1 什么是DFT？首先，得说说DFT是什么。

其实，它是一种数学工具，用于分析信号，尤其是周期性信号。

简单点说，DFT能把时间域的信号转化为频率域的信号。

它能让你看到信号中的频率成分，就像透过望远镜，能看到星空中闪烁的星星。

信号中每个频率的强度就像星星的亮度，有的星星亮得像灯泡，有的则像黑夜中的微光。

1.2 DFT的计算在计算方面，DFT的公式有点复杂，乍一看可能让人头疼。

但是别着急，想象一下，在玩拼图。

每个拼图块代表信号中的一个频率，DFT就是把这些拼图块拼在一起，最后形成完整的图案。

它的计算过程涉及到很多乘法和加法，但只要掌握了技巧，就能游刃有余。

就像学骑自行车，刚开始可能会摔跤，但多试几次，就能骑得飞起。

2. DFT的实际应用2.1 音频处理说到DFT的应用，音频处理绝对是个“大头”。

比如，当你用手机录音的时候，手机就会用DFT分析录到的声音，提取出其中的频率信息。

这样一来，不管是音乐、讲话，还是狗吠声，手机都能识别出来。

更妙的是，当你听歌时，音乐播放器也在后台默默地运用DFT，把每种乐器的声音处理得淋漓尽致。

听着听着，你就觉得那旋律简直像是从天而降，动人心弦！2.2 图像处理除了音频，DFT在图像处理上的表现也不容小觑。

想象一下你在手机上修图，给照片加点滤镜。

其实，滤镜背后就是在利用DFT来调整频率。

高频部分让图像更清晰，低频部分则负责平滑过渡。

DFT就像是图像的“美颜师”，能让你的照片瞬间“变身”，从平平无奇到惊艳绝伦。

看到镜头中的自己，哇，那可是美得像个明星！3. DFT的其他领域3.1 通信系统在通信领域，DFT也是个不可或缺的角色。

DFT以及FFT概念详解

§2.1 离散傅里叶变换（DFT）
为了便于更好地理解DFT的概念，先讨论周期序列及其离散傅里叶级数（DFS）表示。 §2.1.1 离散傅里叶级数（DFS）一个周期为N的周期序列，即
~ ~ x ( n ) x ( n kN )
， k为任意整数，N为周期
周期序列不能进行Z变换，因为其在 n=-到+ 都周而复始永不衰减，即 z 平面上没有收敛域。但是，正象连续时间周期信号可用傅氏级数表达，周期序列也可用离散的傅氏级数来表示，也即用周期为N 的正弦序列来表示。
利用正弦序列的周期性可求解系数
~ X (k)
将上式两边乘以
求和
e
j(2 /N )rn
，并对一个周期
2 2 N 1 N 1 j ( k r ) n j ( k r ) n 1 ~N 1~ N ~ x ( n ) e X ( k ) e X ( k ) e N N n 0 n 0 k 0 k 0 n 0
~ j 2 / N kn ~ x ( n )e X (k )
n0
N 1
•时域上周期序列的离散傅里叶级数在频域上仍是一个周期序列。
~ ~ X ( k ) x ( n )是一个周期序列S)变换对，这种对称关系可表为
N 1 1 ~ ~ j 2 / N nk ~ x ( n ) I DF [ X ( k )] S X ( k ) e N n 0
ki km ~ ~ ~ DFS x ( n m ) x ( n m ) w x ( i ) w w N N n 0
N 1
mk wN
N 1 m

i m

第八讲(DFT2)

3.5 快速傅里叶变换（FFT）
结论：FFT的基本思想是把原始序列依次分解为一系列短序列，充分利用DFT变换核的特点，求出短序列的DFT，再进行组合，从而达到删除重复计算，减少乘法运算次数，提高运算速度的目的。 3 FFT算法的基本形式 FFT算法主要分为时间抽取法（Decimation In Time， DIT-FFT）和频率抽取法（Decimation In Frequency， DIF-FFT），按照抽取长度又分为基2，基4等算法）
2 FFT算法的基本思想 1）长序列分成短序列如N点DFT分解成2个N/2点DFT之和，则复乘次数近似为2*（N/2）*（N/2），为原来的一半。
2014-10-27
3.5 快速傅里叶变换（FFT）
2）利用傅里叶变换核的特点
kn WN e j 2 kn N 称为离散傅里叶变换核（Fourier
N 1 n 0 2 kn N N 1 n 0
X (k ) x(n)e
2014-10-27
j
kn x(n)WN
可见，每一个谱点须进行N次复数乘和（N-1）次复数加。N个谱点须进行N*N次复乘和N(N-1)次复加
3.5 快速傅里叶变换（FFT）
而且每一次复乘又包含4次实乘和2次实加，一次复加包含两次实加，所以N点DFT须进行4N*N次实乘和 2*N*N+2N（N-1）次实加。当N较大时，对计算机资源的占用时非常大的。
a2 a6 a1 a5 a3 a7
2014-10-27
X12(0) X12 (1)
X 21 (0)
X 21 (1)
W 41
X1 (3)
X(3)
X 2 (0)
W80
1
X (4)

DFT基本知识

0.5 0.25 0.75
Clk
Clk
Generic LBIST Architecture
• • First, PRPG issues N pseudorandom tests, where N – maximal internal scan chain length. Second, series of Functional Clock pulses is issued
• Multiple-Input Signature Register (MISR) – multi-input
device that compresses a series of input patterns into unique signature
Weighted PRPG
• PRPG: produces pseudorandom data without replacement (all vectors are unique). • Constant-Weight PRPG: probability to get “1” for each output is constant (Example : equal number of “1” and “0” in each word => weight = 0.5) • PRPG can adjust weights adding combinatorial logic to the outputs:
Board and Chip Test Modes
• External Test Mode – to test board interconnect:
SOUT IN
Mode Control
SOUT IN
Mode Control

第二章 DFT及其快速算法

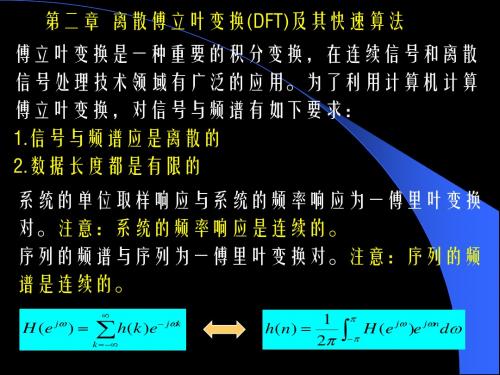
m=k
等式左边为周期函数，右边也应该是周期函数，k→±∞
2 nk N
e
n 0
N 1
j
2 n ( k m) N
N k m 0 k m
x
n 0
N 1
p
( n )e
j
NX k X p (k )
上式表明：XP(k)也是一个周期序列(同周期——N)，称为离散傅立叶级数(DFS)正变换。(见上页2式)
m 0 N 1
WN-(N-1)m
x p ( n) y p ( n )
周期序列为所给主值序列的周期延拓。周期为N。
例: 已知两个周期序列(N=7) xp(n)=[(n)+(n-1) +(n-2) +(n-3)]R7(n) 和 yp(n)= [(n-2) +(n-3) +(n-4) ]R7(n) 对应点相加取主值试用图解方法求圆周卷积f(n)=x(n)y(n)。 y(n)= [(n)+(n-2)+2(n-3)+3(n-4)+3(n-5)+2(n-6)]R7(n) 圆周卷积与线性卷积的比较
f ( n ) x ( n ) y ( n ) x ( m) y ( n m)
m 0 N 1
f (n) x(n) * y (n)
m
x ( m) y ( n m)

相同点：两者均有反褶、相乘与取和运算过程差异：线卷积的移位是平移，而周期卷积的移位是圆周移位。线卷积不要求两个序列x(n)与y(n)的长度相等，如x(n)与 y(n)的长度分别为M和N，则卷积结果长度为M+N-1；周期卷积则要求两序列长相等(M=N)，卷积的长度也为M或N。

DFT及其快速算法

DFS DFS
N
N
N
1 Y (k ) X 1 (k ) X 2 (k ) N
DFS
DFS DFS
N
N
N
DFT
… …
… … …
2
1
~ x1 (n)
0 123
…n …n
~ x2 (m)
~ x1 (m)
1
0 123
~ x2 (n)
m ~ x (m)
2
~ x1 (n) ~ x 2 ( n) ~ x1 (m) ~ x 2 ( n m)
1 N n N
x(n) 周期延拓后，反转 ~ x (n)
取主值 ~ x ( N n) x( N n) 右移N
k 0 X (0) X ( N k ) X ((N k )) N RN (n) X ( N k ) 1 N k N 1 0 其他
0
f 2f xa (t )e j 2ft dt
周期性
1 j 2ft xa (t ) X ( f ) e df a 2

2．离散时间与连续频率— 序列傅里叶变换
xa (nT ) x(n)
X (e )
j
0
T

t n
1 x(n ) 2

X (e j )e j n d
2-2. 离散傅里叶级数（DFS）
1．从序列傅里叶变换导出 DFS X (e j ) 为的连续的周期的函数，周期为2 。 2 j X ( e ) 对离散化，离散间隔，即令
~ X (k ) X (e j )

2 k N
k 整数