数字谜之竖式谜(一)
乘除法数字谜(一)(含详细解析)

【关键词】走美杯,四年级,初赛,第12题,五年级,初赛,第11题
【解析】由 知,“美”不为1,且“美”ד妙”<10,如果“美”为2,根据“美”ד学”的个位数为“妙”,那么“妙”为偶数,即为4,推出“学”为7,又由“Байду номын сангаас”+“学”=“数”,可知“数”为9,所以 2497。
【解析】因为竖式中五位数乘4仍是五位数,所以“客”是人于0小于3的偶数,只能是2,并推知“居” 8。因为“上”乘4不向上进位,且是奇数,所以“上” 1,并推知“然” 7。则所表示的三位数是978。
【答案】
【例 4】下面算式(1)是一个残缺的乘法竖式,其中□≠2,那么乘积是多少?
【考点】乘法数字谜【难度】2星【题型】填空
【答案】
【例 16】如图所示的除法算式中,每个 各代表一个数字,则被除数是。
【考点】除法数字谜【难度】3星【题型】填空
【关键词】希望杯,4年级,初赛,8题
【解析】先确定商首位是8,再估量出除数首位是5,确定商的末位1,得到被除数为4620.
【答案】
【例 17】右边的除法算式中,商数是。
【考点】除法数字谜【难度】3星【题型】填空
【考点】乘法数字谜【难度】3星【题型】填空
1【解析】首先从式子中可以看出“思” ,另外第三个部分积的首位只能为9,所以“学”只能为3.由于3个部分积都是四位数,而且第三个部分积的首位为9,所以它比其它两个部分积要大,从而“学”比“而”和“杯”都大,所以“而”和“杯”只能分别为1和2,这样“学而思杯”就可能为3102或3201.分别进行检验,发现 ,与算式不相符,而 符合,所以“学而思杯”代表的数字分别为3、2、0、1.
横(竖)式数字谜(一)

横(竖)式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字,或用字母、文字来代替部分数字的不完整的算式或竖式,叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如,求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知,□=582-324=258。
又如,求右竖式中字母A,B所代表的数字。
显然个位数相减时必须借位,所以,由12-B=5知,B=12-5=7;由A-1=3知,A=3+1=4。
解数字谜问题既能增强数字运用能力,又能加深对运算的理解,还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜,首先要熟知下面的运算规则:(1)一个加数+另一个加数=和;(2)被减数-减数=差;(3)被乘数×乘数=积;(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则:由(1),得和 - 一个加数=另一个加数;其次,要熟悉数字运算和拆分。
例如,8可用加法拆分为8=0+8=1+7=2+6=3+5=4+4;24可用乘法拆分为24=1×24=2×12=3×8=4×6(两个数之积)=1×2×12=2×2×6=…(三个数之积)=1×2×2×6=2×2×2×3=…(四个数之积)例1下列算式中,□,○,△,☆,*各代表什么数?(1)□+5=13-6;(2)28-○=15+7;(3)3×△=54;(4)☆÷3=87;(5)56÷*=7。
解:(1)由加法运算规则知,□=13-6-5=2;(2)由减法运算规则知,○=28-(15+7)=6;(3)由乘法运算规则知,△=54÷3=18;(4)由除法运算规则知,☆=87×3=261;(5)由除法运算规则知,*=56÷7=8。
数字谜之竖式谜(一)

A12标准奥数教程数字谜之竖式谜【知识点与基本方法】跟横式数字谜一样也是一种猜数的游戏。
解竖式谜旧的根据有关的运算法则、数的性质(和差积商的位数、数的整除性、奇偶性、尾数规律等)来进行正确地推理、判断解答竖式数字谜是应注意的问题:(1)空格中只能填写0、1、2、3、4、5、6、7、8、9,而且最高位不能为0;(2)进位要留意,不能漏掉(3)答案有时候不唯一(4)两数字相加,最大进位为1,三个数字相加最大进位为2,(5)两个数字相乘,最大进位为8(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字加(7)一个问题,读取整数型,并计算所有各位上数字的总和,直到该和降至一位数。
例如:数字是1256sum=1+2+5+6=14;sum=1+4=5;【例题精讲】求100~999一共900个三位数的各位数字之和也就是2700个数的和只需计算处各个数字出现的次数便可0出现的次数这样算0在个位上出现次数100~990共90次0在十位上出现次数a00~a09,a为1~9,共10*9=90次即数字0共出现了180次而数字1~9出现的次数相同为(2700-180)/9=280次所以所求数等于280*(1+2+……+9)=280*45=12600【例题精讲】例1.下面的算式中,只有5个数字已写出,请补充其他的数字6□7+ □ 2 □□□ 1 5分析:在5个方格中,要个填写一个数字,是运算式成立,先填哪一个?那就要我们找问题的突破口了从百位来看,和的千位数字只能是1.从市委相加来看,进位到百位,也只能进1,因此□ 2 □的百位是九,和的百位是0.通过上面的分析就找到了问题的突破口了,15-7-6=2 11-2-1=8就得到算式的结果6□7+ □ 2 □□□ 1 5例3.图中,有四个小纸片各盖住了一个数字,问:被盖住的四个数字综合是多少?□□+ □□1 4 9分析:先看个位,因为两个数字相加,最大为9+9=18,所以两个数的和不能是19.从而两个被盖住的个位数字之和等于9.由于个位数字相加不向十位进位,所以两个被盖住的十位数字的和14.因此被盖主的四个数字的总和是14+9=23例4.在下面的方框中填上何时得数字□7 6×□□18 □□□□□□3 1 □□ 0分析:由于积的各位舒适0,乘数的个位数是5,由此我们可以得到被乘得数与5相乘的1880,被乘数的百位数字是3,最后因为被乘数是376,积是31□□0,所以乘数的十位数字是8解: 3 7 6× 8 51 8 8 03 0 0 83 1 8 6 0例5.下面每个汉字个代表一个数字,不同的汉字表示不同的数字,相同的汉字表示相同的数字,问:这些汉字个代表什么数字?北京北京市+ 爱北京市1 9 9 9分析:首先,我们立即得到“爱”表示=1,所以百位数字相加不进位,“北”小于 5.又因为三个数字相加小于100+100+100=300所以“北”+“北”大于6,从而“北”=4,知道“爱”和“北”个代表什么数字问题就很好解决了解:爱=1,北”=4 “京”=7 “市”=6例6.在图6-1算式的每个空格中,各填入一个合适的数字,使竖式成立。
第一讲 数字谜答案

数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
解:将5568质因数分解为5568=26×3×29。
由此容易知道,将 5568分解为两个两位数的乘积有两种:58×96和64×87,分解为一个两位数与一个三位数的乘积有六种:12×464, 16×348, 24×232,29×192, 32×174, 48×116。
显然,符合题意的只有下面一种填法:174×32=58×96=5568。
例3 在443后面添上一个三位数,使得到的六位数能被573整除。
分析与解:先用443000除以573,通过所得的余数,可以求出应添的三位数。
由443000÷573=773 (71)推知, 443000+(573-71)=443502一定能被573整除,所以应添502。
苏教版三年级数学上册竖式数字谜专项练习(一)

数字谜(一)数字谜是一种有趣的数学问题.它的特点是给出运算式子,但式中某些数字是用字母或汉字来代表的,要求我们进行恰当的判断和推理,从而确定这些字母或汉字所代表的数字.这一讲我们主要研究加、减法的数字谜。
例1右面算式中每一个汉字代表一个数字,不同的汉字表示不同的数字.当它们各代表什么数字时算式成立?分析由于是三位数加上三位数,其和为四位数,所以“真”=1.由于十位最多向百位进1,因而百位上的“是”=0,“好”=8或9。
①若“好”=8,个位上因为8+8=16,所以“啊”=6,十位上,由于6+0+1=7≠8,所以“好”≠8。
②若“好”=9,个位上因为9+9=18,所以“啊”=8,十位上,8+0+1=9,百位上,9+1=10,因而问题得解。
真=1,是=0,好=9,啊=8例2下面的字母各代表什么数字,算式才能成立?分析由于四位数加上四位数其和为五位数,所以可确定和的首位数字E=1.又因为个位上D+D=D,所以D=0.此时算式为:下面分两种情况进行讨论:①若百位没有向千位进位,则由千位可确定A=9,由十位可确定C=8,由百位可确定B=4.因此得到问题的一个解:②若百位向千位进1,则由千位可确定A=8,由十位可确定C=7,百位上不论B 为什么样的整数,B+B和的个位都不可能为7,因此此时不成立。
解:A=9,B=4,C=8,D=0,E=1.例3在下面的减法算式中,每一个字母代表一个数字,不同的字母代表不同的数字,那分析由于是五位数减去四位数,差为三位数,所以可确定A=1,B=0,E=9.此时算式为:分成两种情况进行讨论:①若个位没有向十位借1,则由十位可确定F=9,但这与E=9矛盾。
②若个位向十位借1,则由十位可确定F=8,百位上可确定C=7.这时只剩下2、3、4、5、6五个数字,由个位可确定出:所以 D+G=2+4=6或D+G=3+5=8 或D+G=4+6=10例4 右面的算式中不同的汉字表示不同的数字,相同的汉字表示相同的数字.如果巧+解+数+字+谜=30,那么“巧解数字谜”所代表的五位数是多少?分析观察算式的个位,由于谜+谜+谜+谜+谜和的个位还是“谜”,所以“谜”=0或5。
(1份)四年级算式谜和等量代换

竖式数字谜1竖式数字谜是一种猜数的游戏。
解竖式数字型,就得根据有关的运算法则、数的性质(和差积商的为数,数的乘除性、奇偶性、尾数规律等)来进行正确地推理、判断。
解答竖式数字谜时应注意以下几点:(1)空格中只能填写0,1,2,3,4,5,6,7,8,9,而且最高位不能为0;(2)进位要留意,不能漏掉了;(3)答案有时不唯一;(4)两数字相加,最大进位为1,三个数字相加最大进位为2;(5)两个数字相乘,最大进位为8;(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字。
例1:下面的算式中,只有5个数字已写出,请补上其他的数字。
6□7+□2 □□□1 5例2:在下面算式的□内各填入一个合适的数字,使算式成立。
□0 0 □- 5 0 □91 □9 3补充:本题还可以根据加减法是互逆运算的关系,将减法算式转化成下面的加法算式:1 □9 3+ 5 0 □9□0 0 □随堂练习1:在下面竖式的空格内,各填入一个合适的数字,使竖式成立。
(1) 3 (2) 5 8 □□ 5 -2 □7+□ 2 □□9 4□□0 6例3:下面是一个六位数乘以一个一位数的算式,不同的汉字表示不同的数,相同的汉字表示相同的数,其中的六位数是。
小学希望杯赛×赛9 9 9 9 9 9例4:请在下面算式的□里填上合适的数字,使算式成立:□ 4 □×□ 61 □□0□□ 58 □□□随堂练习2:下面是一道题的乘法算式,请问:式子中,A B C D E分别代表什么数字?1 A B C D E× 3A B C D E 1例5:在下面竖式□里填入合适的数字,使竖式成立。
□□9 □□ 4 1 □5 5 □□3 7□□□随堂练习3:在下面竖式的□里,填入合适的数字,使竖式成立。
(1)7 □(2)□7 6 □ 5 □ 1 ×□□□□ 1 8 □□□□□□□□□□ 3 1 □□06提高练习1 要使右边竖式成立,四个□中的数字之和为。
二年级奥数.计算.竖式谜(1)

在这一节课中,教材内容中主要是通过不同的符号,汉字或字母来组成各种不同的竖式数字谜,让学生根据竖式的结构来计算(求出)这些未知的数字.弄清楚加减法各部分之间的数量关系是我们学习数字谜的基础.解答数字谜的关键是找准突破口.通过这节课的学习,要使学生掌握解答竖式数字谜的一般技巧.先要观察数字的特点,然后找出“关键位置”认真分析,一般可以引导学生从各个不同的数位进行考虑.解答完题目以后,教师还要培养学生验算的好习惯.我们经常会看到一些残缺不全的算式,要求我们在方格内填上合适的数字,使算式成立.我们也经常看到在一个算式里面有很多的汉字或字母,要我们猜猜它们代表几,像这样的问题都是数字谜问题.在填数字时,要认真分析数字的特点,充分运用加、减法之间的关系,巧妙地安排每一个数,很快就能求出方格里应填的数字.今天这节课我们就一起来解答数字谜问题.解这种题应按三个步骤分析思考:(1)审题审题就是找出算式中数字之间的关系和特征,挖掘题目中的隐含条件,它是确定各空格内应该填什么数字的主要依据.(2)选择解题突破口在审题的基础上,认真思考找出算式中容易填出或关键性的空格,做为解题的突破口.这一步是填空格的关键.(3)确定各空格填什么数字从突破口开始,依据竖式的已知条件,逐个填出各空格中的数字.【例1】在“庆元旦”晚会上,主持人小丽出了这样两道题目:请大家想一想,被纸片盖住的是什么数字?【例2】在下面算式的空格内,各填上一个合适的数字,使算式成立.知识框架竖式谜例题精讲【例3】用0、1、2、3、4、5、6、7、8、9这十个数字组成下面的加法算式,每个数字只许用一次,现已写出3个数字,请把这个算式补齐.【例4】在下面算式的空格内,各填入一个合适的数字,使算式成立.【例5】把数字1~5分别填写在下面算式中的口里.【例6】下面的算式里四个小纸片各盖住一个数字,问被盖住的四个数字的和是多少?【例7】在下面算式的空格内,各填入一个合适的数字,使算式成立.【例8】算下面竖式中的汉字各代表多少?我=( ) 爱=( ) 数=( ) 学=( )【例9】求当它们各代表什么数字时,能够使算式成立?【例10】请你猜一猜,每个算式中的汉字各表示几【例11】相同的英文字母代表相同的数字,你知道下面A、B、C代表几?【随练1】请你算一算,下面竖式中每个字各代表几?+ 兵炮马卒兵炮车卒车卒马兵卒【随练2】下面各数字表示几?【随练3】在下面的加法算式中,第—个加数的各位数字之和恰好是和的各位数字之和的2倍.则第一个加数是多少?【随练4】下面的算式里,每个方框代表一个数字,问:这6个方框中数字的总和是多少?课堂检测【作业1】在下列竖式的空格内,各填入一个合适的数字,使竖式成立. 【作业2】填一填.【作业3】下面方框可以填什么数?【作业4】下面的方框各应该填几?【作业5】下面的符号和汉字各代表几?【作业6】下面竖式中的字母和符号各代表多少?家庭作业【作业7】在下列竖式的空格内,各填入一个合适的数字,使竖式成立.【作业8】下面的符号各表示几?【作业9】请你猜一猜,每个算式中的汉字各表示几?【作业10】下边的加法算式中,□内这四个数字之和是多少?。
乘除法数字谜(一)

5-1-2-2.乘除法数字谜(一)教学目标数字谜是杯赛中非常重要的一块,特别是迎春杯,数字谜是必考的,一般学生在做数字谜的时候都采用尝试的方式,但是这样会在考试中浪费很多时间.本模块主要讲乘除竖式数字谜的解题方法,学会通过找突破口来解决问题.最后通过例题的学习,总结解数字谜问题的关键是找到合适的解题突破口.在确定各数位上的数字时,首先要对填写的数字进行估算,这样可以缩小取值范围,然后再逐一检验,去掉不符合题意的取值,直到取得正确的解答.知识点拨1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式.2.数字谜突破口:这种不完整的算式,就像“谜”一样,要解开这样的谜,就得根据有关的运算法则,数的性质(和差积商的位数,数的整除性,奇偶性,尾数规律等)来进行正确的推理,判断.3.解数字谜:一般是从某个数的首位或末位数字上寻找突破口.推理时应注意:⑴数字谜中的文字,字母或其它符号,只取0~9中的某个数字;⑵要认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件;⑶必要时应采用枚举和筛选相结合的方法(试验法),逐步淘汰掉那些不符合题意的数字;⑷数字谜解出之后,最好验算一遍.例题精讲模块一、乘法数字谜【例1】下面是一个乘法算式:问:当乘积最大时,所填的四个数字的和是多少?【考点】乘法数字谜【难度】1星【题型】填空【关键词】1995年,第5届,华杯赛,初赛,第2题【解析】乘积是两位数并且是5的倍数,因而最大是95.95÷5=19,所以题中的算式实际上是所以,所填四个数字之和便是1+9+9+5=24【答案】24【例2】下面两个算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.⨯=美妙数学数数妙,美+妙数学=妙数数。
=美妙数学___________【考点】乘法数字谜【难度】2星【题型】填空【关键词】第六届,走美杯,四年级,初赛,第12题,五年级,初赛,第11题【解析】由⨯=美妙数学数数妙知,“美”不为1,且“美”ד妙”<10,如果“美”为2,根据“美”ד学”的个位数为“妙”,那么“妙”为偶数,即为4,推出“学”为7,又由“美”+“学”=“数”,可知“数”为9,所以=美妙数学2497。
第五讲竖式数字谜(一)

在下列□中填上合适的数,使 竖式成立
□ 7 □ + 4 □ 7 □ 2 4 0
在下列□中填上合适的数,使 竖式成立
□ 7 □ 4 - 1 □ 7 6 2 0 1 □
在下列□中填上合适的数,使 竖式成立
□ 7 □ 4 - 1 □ 7 6 2 0 1 □
在下列□中填上合适的数,使 竖式成立
7
□ 8 + □ 2 □
□ □ 1 9
在下列□中填上合适的数,使 竖式成立
□ 0
9
9 □
0 9
- 8 □ □ 9
在下列□中填上合适的数,使 竖式成立
5 □ □ 6 - □ 7 5 □
□ 6
2
7
在下列□中填上合适的数,使 竖式成立
6
3
□ □ 7 8
- □ □
□
0
2
在下列□中填上合适的数,使 竖式成立
3 □ 2 □ 8 □ + □ 3 8 □ 1
在下列算式中,每个字母代表 不同的数,找出每个字母各代 表什么数字,使竖式成立
3 - B
B
A A
C
B 6
A
在下列算式中,每个字母代表 不同的数,找出每个字母各代 表什么数字,使竖式成立
A +
2
B D
0
C E
3
C -
D E B C A B C D
A C A C
在下列算式中不同的汉字代表不同的数 字,相同的汉字代表相同的数字,每个 字母各代表什么数字时竖式成立
学 数 学
爱 数 学 + 喜 爱 数 学
2 0 0 0
在下列算式中不同的汉字代表不同的数 字,相同的汉字代表相同的数字,每个 字母各代表什么数字时竖式成立
100以内加法竖式数字谜

100以内加法竖式数字谜小明是一个喜欢数学的孩子,他喜欢通过解决数学题来锻炼自己的思维能力。
最近,他发现了一种有趣的数学谜题,那就是100以内的加法竖式数字谜。
这种数字谜题的规则很简单,就是给出一个竖式的加法算式,其中包含了一些数字的缺失。
我们需要通过推理和计算,填写正确的数字,使得算式成立。
小明决定挑战一下这个数字谜题,他拿起笔,在纸上写下了第一个谜题:“__ + 25 = 73”。
他思考了一会儿,然后开始计算。
他知道,73减去25等于48,所以空缺的数字应该是48。
他填写完毕后,检查了一遍,确保算式成立。
接下来,小明又写下了第二个谜题:“__ + 17 = 56”。
他开始思考,这次的计算稍微有些复杂。
他知道,56减去17等于39,所以空缺的数字应该是39。
他填写完毕后,再次检查了一遍,确保算式成立。
小明越来越喜欢这个数字谜题,他觉得这是一个很好的锻炼自己计算能力和逻辑思维的方式。
他继续写下了第三个谜题:“__ + 42 = 89”。
这次的计算稍微有些困难,但小明并不气馁。
他开始思考,89减去42等于47,所以空缺的数字应该是47。
他填写完毕后,再次检查了一遍,确保算式成立。
小明一共解决了十个数字谜题,每一个都需要他动脑筋去计算和推理。
他发现,通过这种方式,他的计算能力和逻辑思维得到了很大的提升。
他感到非常开心和满足。
通过这个数字谜题,小明不仅锻炼了自己的数学能力,还培养了自己的耐心和坚持不懈的精神。
他明白,只有通过不断地学习和挑战自己,才能不断进步。
小明决定将这些数字谜题分享给他的同学们,希望他们也能从中受益。
他组织了一个小型的数学竞赛,邀请同学们一起解决这些数字谜题。
大家都非常兴奋,纷纷拿起笔开始思考和计算。
在数学竞赛中,同学们互相交流和讨论,共同解决了这些数字谜题。
他们发现,通过合作和分享,他们的解题速度和准确率都得到了提高。
大家都感到非常开心和满足。
通过这次数学竞赛,小明和他的同学们不仅锻炼了自己的数学能力,还培养了团队合作和分享的精神。
(完整版)三年级数字谜加减法,乘除法

数字谜思维训练一、加减竖式数字谜例 1 在下面算式的空格中,各填入一个合适的数字,使算式成立.(1)□4 □(2) □□4+□8 + 1 □□□ 1 5 □□□ 3(3)□0 □6 (4) 1 □5 □-7 □4 □-□□9□6 7 8 6 7例 2 下面每个汉字代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字, 这些汉字各代表哪些数字?(1) 成都(2) 助成都市助人+爱成都市助人为1 9 9 9 +助人为乐19 9 3例3 相同的汉字代表相同的数字,不同的汉字代表不同的数字,这些汉字各代表哪些数字?节童儿际国一六祝庆+8 6 4 1 9 7 5 3 2庆祝六一国际儿童节二、乘法竖式数字谜例4 在下面算式的空格中,各填入一个合适的数字,使算式成立(1)□□ 8 (2)□□ 9 ×□×□79 2 1 □ 5 2(3)4 3 7 □(4) □□4 ×□×□□□□0 0 5 2 □2例5相同的汉字代表相同的数字,不同的汉字代表不同的数字,这些汉字各代表哪些数字?1数学俱乐部×3数学俱乐部1三、练习题1、在下面的空格中,各填入一个适当的数字,使式子成立.(1) □8 □(2) □1+□6 □ 3 +□9 □□□1 2 8 □□9 □(3) □□4 (4)□0 0 1-□□-20 □79 □9 □(5)□□8(6) □ □ 9×□ × □31□2 1 8 3 22、下面的式子中相同的字母代表相同的数字,不同的字母代表不同的数字,式中的字母ABCD各代表哪些数字?A B C D×9D C B A3、在下面的式子里,6个小纸片各盖住了一个数字,问:被盖住的6个数字总和是多少?□□□+□□□1 9 9 1。
小学数学 乘除法数字谜(一).教师版

5-1-2-2.乘除法数字谜(一)教学目标数字谜是杯赛中非常重要的一块,特别是迎春杯,数字谜是必考的,一般学生在做数字谜的时候都采用尝试的方式,但是这样会在考试中浪费很多时间.本模块主要讲乘除竖式数字谜的解题方法,学会通过找突破口来解决问题.最后通过例题的学习,总结解数字谜问题的关键是找到合适的解题突破口.在确定各数位上的数字时,首先要对填写的数字进行估算,这样可以缩小取值范围,然后再逐一检验,去掉不符合题意的取值,直到取得正确的解答.知识点拨1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式.2.数字谜突破口:这种不完整的算式,就像“谜”一样,要解开这样的谜,就得根据有关的运算法则,数的性质(和差积商的位数,数的整除性,奇偶性,尾数规律等)来进行正确的推理,判断.3.解数字谜:一般是从某个数的首位或末位数字上寻找突破口.推理时应注意:⑴数字谜中的文字,字母或其它符号,只取0~9中的某个数字;⑵要认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件;⑶必要时应采用枚举和筛选相结合的方法(试验法),逐步淘汰掉那些不符合题意的数字;⑷数字谜解出之后,最好验算一遍.例题精讲模块一、乘法数字谜【例1】下面是一个乘法算式:问:当乘积最大时,所填的四个数字的和是多少?【考点】乘法数字谜【难度】1星【题型】填空【关键词】华杯赛,初赛,第2题【解析】乘积是两位数并且是5的倍数,因而最大是95.95÷5=19,所以题中的算式实际上是所以,所填四个数字之和便是1+9+9+5=24【答案】24【例2】下面两个算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.⨯=美妙数学数数妙,美+妙数学=妙数数。
=美妙数学___________【考点】乘法数字谜【难度】2星【题型】填空【关键词】走美杯,四年级,初赛,第12题,五年级,初赛,第11题【解析】由⨯=美妙数学数数妙知,“美”不为1,且“美”ד妙”<10,如果“美”为2,根据“美”ד学”的个位数为“妙”,那么“妙”为偶数,即为4,推出“学”为7,又由“美”+“学”=“数”,可知“数”为9,所以=美妙数学2497。
5-1-2-2 乘除法数字谜(一).教师版

5-1-2-2.乘除法数字谜(一)
教学目标
数字谜是杯赛中非常重要的一块,特别是迎春杯,数字谜是必考的,一般学生在做数字谜的时候都采用尝试的方式,但是这样会在考试中浪费很多时间.本模块主要讲乘除竖式数字谜的解题方法,学会通过找突
1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式.
模块一、乘法数字谜
是一个残缺的乘法竖式,其中
【难度】2星【题型】填空
所以b≥6,从而d≥6.由22□÷c≥60和c>2知c=3,
de=
76
30 000,所以.再由乘积不小于30000
下面残缺的算式中,只写出了3个数字1,其余的数字都不是
【难度】2星 【题型】填空
了说明的方便,这个算式中的关键数字用英文字母表示.很明显e= 0三数之一,两位数应是(100+f )的因数.101,103,102=17×6,则C 只能取3,,ab 317=⨯,,53ab =
【题型】填空
⨯=
.510)2161080
【答案】。
小学奥数-乘除法数字谜(一)

5-1-2-2.乘除法数字谜(一)教学目标数字谜是杯赛中非常重要的一块,特别是迎春杯,数字谜是必考的,一般学生在做数字谜的时候都采用尝试的方式,但是这样会在考试中浪费很多时间.本模块主要讲乘除竖式数字谜的解题方法,学会通过找突破口来解决问题.最后通过例题的学习,总结解数字谜问题的关键是找到合适的解题突破口.在确定各数位上的数字时,首先要对填写的数字进行估算,这样可以缩小取值范围,然后再逐一检验,去掉不符合题意的取值,直到取得正确的解答.知识点拨1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式.2.数字谜突破口:这种不完整的算式,就像“谜”一样,要解开这样的谜,就得根据有关的运算法则,数的性质(和差积商的位数,数的整除性,奇偶性,尾数规律等)来进行正确的推理,判断.3.解数字谜:一般是从某个数的首位或末位数字上寻找突破口.推理时应注意:⑴数字谜中的文字,字母或其它符号,只取0~9中的某个数字;⑵要认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件;⑶必要时应采用枚举和筛选相结合的方法(试验法),逐步淘汰掉那些不符合题意的数字;⑷数字谜解出之后,最好验算一遍.例题精讲模块一、乘法数字谜【例1】下面是一个乘法算式:问:当乘积最大时,所填的四个数字的和是多少?【例2】下面两个算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.⨯=美妙数学数数妙,美妙数学___________美+妙数学=妙数数。
=【例3】北京有一家餐馆,店号“天然居”,里面有一副著名对联:客上天然居,居然天上客。
巧的很,这副对联恰好能构成一个乘法算式(见右上式)。
相同的汉字代表相同的数字,不同的汉字代表不同的数字。
“天然居”表示成三位数是_______。
【例4】下面算式(1)是一个残缺的乘法竖式,其中□≠2,那么乘积是多少?【例5】下面残缺的算式中,只写出了3个数字1,其余的数字都不是1,那么这个算式的乘积是?【例6】右面的算式中,每个汉字代表一个数字(0~9),不同汉字代表不同数字.美+妙+数+学+花+园=.423805⨯美妙数学花园数学真美妙好好好美妙【例7】在右边的乘法算式中,字母A 、B 和C 分别代表一个不同的数字,每个空格代表一个非零数字.求A 、B 和C分别代表什么数字?941A B CA BC ⨯【例8】在每个方框中填入一个数字,使得乘法竖式成立.已知乘积有两种不同的得数,那么这两个得数的差是.【例9】在图中的每个方框中填入一个适当的数字,使得乘法竖式成立。
小学奥数—乘除法数字谜(一)

5-1-2-2.乘除法数字谜(一)
教学目标
数字谜是杯赛中非常重要的一块,特别是迎春杯,数字谜是必考的,一般学生在做数字谜的时候都采用尝试的方式,但是这样会在考试中浪费很多时间.本模块主要讲乘除竖式数字谜的解题方法,学会通过找突
1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式.
模块一、乘法数字谜
是一个残缺的乘法竖式,其中
下面残缺的算式中,只写出了3个数字1,其余的数字都不是1,那么这个算式的乘积是?
,不同汉字代表不同数字.美。
(完整版)小学四年级奥数-竖式迷
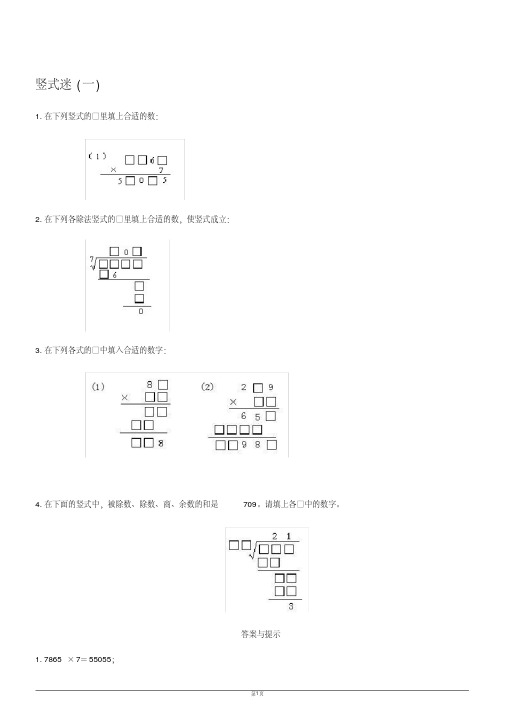
竖式迷(一)1.在下列竖式的□里填上合适的数:2.在下列各除法竖式的□里填上合适的数,使竖式成立:3.在下列各式的□中填入合适的数字:4.在下面的竖式中,被除数、除数、商、余数的和是709。
请填上各□中的数字。
答案与提示1. 7865×7=55055;2.5607÷7=8013.提示:(1)先确定乘数是11。
(2)先确定乘数的十位数是7,再确定被乘数的十位数是1,最后确定乘数的个位是3。
4.提示:由题意和竖式知,被除数+除数=709-21-3=685,再由竖式知,被除数=除数×21+3,所以,除数×21+3+除数=685,除数×22=685-3=682,除数=682÷22=31。
被除数为31×21+3=654。
填法如右式。
竖式迷(二)(一)一位数的乘、除法竖式数字谜问题。
例1在左下乘法竖式的□中填入合适的数字,使竖式成立。
分析与解:由于积的个位数是5,所以在乘数和被乘数的个位数中,一个是5,另一个是奇数。
因为乘积大于被乘数的7倍,所以乘数是大于7的奇数,即只能是9(这是问题的“突破口”),被乘数的个位数是5。
因为7×9<70<8×9,所以,被乘数的百位数字只能是7。
至此,求出被乘数是785,乘数是9(见右上式)。
例2在左下边除法竖式的□中填入适当的数,使竖式成立。
分析与解:由48÷8=6即8×6=48知,商的百位填6,且被除数的千位、百位分别填4,8。
又显然,被除数的十位填1。
由1□=商的个位×8知,两位数1□能被8除尽,只有16÷8=2,推知被除数的个位填6,商的个位填2。
填法如右上式。
例2是从最高位数入手分析而得出解的。
例3在右边除法竖式的□中填入合适的数字。
使竖式成立。
分析与解:从已知的几个数入手分析。
首先,由于余数是5,推知除数>5,且被除数个位填5。
由于商4时是除尽了的,所以,被除数的十位应填2,且由于3×4=12,8×4=32,推知,除数必为3或8。
(完整版)三年级数字谜加减法,乘除法

数字谜思维训练一、加减竖式数字谜例 1 在下面算式的空格中,各填入一个合适的数字,使算式成立.(1)□4 □(2) □□4+□8 + 1 □□□ 1 5 □□□ 3(3)□0 □6 (4) 1 □5 □-7 □4 □-□□9□6 7 8 6 7例 2 下面每个汉字代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字, 这些汉字各代表哪些数字?(1) 成都(2) 助成都市助人+爱成都市助人为1 9 9 9 +助人为乐19 9 3例3 相同的汉字代表相同的数字,不同的汉字代表不同的数字,这些汉字各代表哪些数字?节童儿际国一六祝庆+8 6 4 1 9 7 5 3 2庆祝六一国际儿童节二、乘法竖式数字谜例4 在下面算式的空格中,各填入一个合适的数字,使算式成立(1)□□ 8 (2)□□ 9 ×□×□79 2 1 □ 5 2(3)4 3 7 □(4) □□4 ×□×□□□□0 0 5 2 □2例5相同的汉字代表相同的数字,不同的汉字代表不同的数字,这些汉字各代表哪些数字?1数学俱乐部×3数学俱乐部1三、练习题1、在下面的空格中,各填入一个适当的数字,使式子成立.(1) □8 □(2) □1+□6 □ 3 +□9 □□□1 2 8 □□9 □(3) □□4 (4)□0 0 1-□□-20 □79 □9 □(5)□□8(6) □ □ 9×□ × □31□2 1 8 3 22、下面的式子中相同的字母代表相同的数字,不同的字母代表不同的数字,式中的字母ABCD各代表哪些数字?A B C D×9D C B A3、在下面的式子里,6个小纸片各盖住了一个数字,问:被盖住的6个数字总和是多少?□□□+□□□1 9 9 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精心整理A12标准奥数教程数字谜之竖式谜【知识点与基本方法】跟横式数字谜一样也是一种猜数的游戏。
解竖式谜旧的根据有关的运算法则、数的性质(和差积商的位数、数的整除性、奇偶性、尾数规律等)来进行正确地推理、判断解答竖式数字谜是应注意的问题:(1)空格中只能填写0、1、2、3、4、5、6、7、8、9,而且最高位不能为0;(2)进位要留意,不能漏掉(3)答案有时候不唯一(4)两数字相加,最大进位为1,三个数字相加最大进位为2,(5)两个数字相乘,最大进位为8(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字加(7)一个问题,读取整数型,并计算所有各位上数字的总和,直到该和降至一位数。
例如:数字是1256sum=1+2+5+6=14;sum=1+4=5;【例题精讲】求100~999一共900个三位数的各位数字之和也就是2700个数的和只需计算处各个数字出现的次数便可0出现的次数这样算0在个位上出现次数100~990共90次0在十位上出现次数a00~a09,a为1~9,共10*9=90次即数字0共出现了180次而数字1~9出现的次数相同为(2700-180)/9=280次所以所求数等于280*(1+2+……+9)=280*45=12600【例题精讲】例1.下面的算式中,只有5个数字已写出,请补充其他的数字6□ 7+□2□□□15分析:在5个方格中,要个填写一个数字,是运算式成立,先填哪一个?那就要我们找问题的突破口了从百位来看,和的千位数字只能是1.从市委相加来看,进位到百位,也只能进1,因此□2□的百位是九,和的百位是0.通过上面的分析就找到了问题的突破口了,15-7-6=211-2-1=8就得到算式的结果6□ 7+□2□□□15例3.图中,有四个小纸片各盖住了一个数字,问:被盖住的四个数字综合是多少?□□+□□149分析:先看个位,因为两个数字相加,最大为9+9=18,所以两个数的和不能是19.从而两个被盖住的个位数字之和等于9.由于个位数字相加不向十位进位,所以两个被盖住的十位数字的和14.因此被盖主的四个数字的总和是14+9=23例4.在下面的方框中填上何时得数字□76×□□18□□□□□□31□□0分析:由于积的各位舒适0,乘数的个位数是5,由此我们可以得到被乘得数与5相乘的1880,被乘数的百位数字是3,最后因为被乘数是376,积是31□□0,所以乘数的十位数字是8解:376×851880300831860例5.下面每个汉字个代表一个数字,不同的汉字表示不同的数字,相同的汉字表示相同的数字,问:这些汉字个代表什么数字?北京北京市+爱北京市1999分析:首先,我们立即得到“爱”表示=1,所以百位数字相加不进位,“北”小于5.又因为三个数字相加小于100+100+100=300所以“北”+“北”大于6,从而“北”=4,知道“爱”和“北”个代表什么数字问题就很好解决了解:爱=1,北”=4“京”=7“市”=6例6.在图6-1算式的每个空格中,各填入一个合适的数字,使竖式成立。
分析:首先根据十位上8+5得到4可知,个位有一个进位,所以,个位的空格中必定是9;再根据百位上两个数相加,再加一个进位后得到9,并有进位可知,百位两个空格中都是9;结果中的千位只能是1,于是得到:例7.如图6-2,用0,1,2,3,4,5,6,7,8,9这10个数字各一次,可组成一个正确的加法竖式。
现已写出3个数字,那么这个算式的结果是多少?分析:首先,结果中的千位为1;第二,百位上第一个数至少是7,最多是9;如为7,那么,结果中的百位为0,并十位要有进位;由此第一个数的十位可以填6,第二个数的个位填9;如为9,显然不行。
所以,结果只能是:【课后练习题】6.在如图6-3所示的算式中,3个加数的各位数字均是某两个相邻数字中的一个,那么这个算式的计算结果可能是多少?7.在图6-6所示的算式中,每个方框代表一个数字。
问:这6个方框中的数字的总和是多少?8.将1到9这9个数码分别填入图6-8的9个空格中,要求先填1,再在与1相邻(即左、右或上、下)的格中填2,再在与2相邻的空格中填3,依次类推,……,最后填9,使得加法算式成立。
二加法与减法中数字和的变化在数字和的问题上,有许多有趣的、富于思考的问题。
首先,计算两个数相加,数字和会怎样变化,我们分开不进位加和进位加这两种情况进行讨论。
先看546+453与546+435两题,这两题每题两个加数的各位上的数字的和是5+4+6+4+5+3=5+4+6+4+3+5=27,而546+453=999,加的过程没有进位,所得的和999各位上的数字的和9+9+9=27;546+435=981,两个加数的数字和是27,加的过程个位上满10向十位进1,有一次进位,所得的和981各位上的数字和9+8+1=18,比没有进位时,和的数字和少9;再计算546+534,两个加数各位上的数字的和也是27,546+534=1080,加的过程中,个位和百位分别都满10,各向前一位进1,有两次进位,所得的和1080各位上的数字的和1+0+8+0=9,比没有进位时少了18,即少了2个9。
由此我们可以得到这样的规律:计算加法,没有进位时,加得的和的数字和等于加数的数字和;有进位时,每进位一次,加得的和的数字和就减少1个9。
同样,我们也可以归纳出减法中数字和的变化规律:计算减法,没有退位时,减得的差的数字和等于被减数的数字和减去减数的数字和的差;有退位时,每退位一次,减得的差的数字和就增加1个9。
下面,我们用上面的规律来解答几个问题。
例1:有A、B两个整数,A的各位数字的和是35,B的各位数字的和是29,如果A和B相加时有三次进位,那么把A+B所得的和的各位数字相加,和是多少?解:如果相加时没有进位,A+B所得的和的各位数字相加的和,等于A和B两个加数数字和相加的和。
35+29=64,相加时,每进位一次,得数的数字和减少1个9,现有三次进位,得数的数字和减少3个9,所以A+B所得的和的各位数字相加,和是64-27=37。
答:A+B的和的数字和是37。
例2:整数A减整数B有两次退位,减得的差的数字和是13,已知A的各位数字的和是8,B的各位数字和是多少?解:A的各位数字的和是8,A减B的差的数字和却是13,这有可能吗?如果连同退位使差的数字和增加这一因素考虑在内,这个结果是很正常的。
A减B有两次退位,使减得的差比不退位时增加2×9=18,也可以看作是13由被减数A的数字和8增加了18减去B的数字和得到的。
所以B的各位数字的和是8+18-13=13。
答:B的各位数字的和是13。
例3:整数A的各位数字的和是24,整数B的各位数字的和是22,而A+B的和的各位数字的和是10,在加的过程中有多少次进位?解:如果A+B在计算中没有进位,所得的和的各位数字的和是24+22=46,现在A+B的和的各位数字的和是10,比不进位时减少了46-10=36,36里面包含9的个数是36÷9=4,所以加的过程中有4次进位。
答:在加的过程中有4次进位。
例4:甲数和乙数的数字和都能被7整除,甲数加乙数,得数的数字和是3,甲数减乙数,差最小是几?解:甲数和乙数的数字和都能被7整除,相加时如果没有进位,所得的和的数字和也能被7整除,现已知甲数加乙数得数的数字和是3,不能被7整除,因此,甲数加乙数必定有若干次进位,3至少加上2个9,得到3+2×9=21,能被7整除,而21=7+14,即甲数和乙数的数字和一个是7,一个是14,并且甲数加乙数有两位进位。
当甲数是61,乙数是59时,甲数减乙数的差为61-59=2,这是最小的差。
答:差最小是2。
例5:1~1000这1000个自然数所有数字的和是多少?解:1~1000这1000个自然数所有数字的和比1~1000这1000个数的和小得多,这是因为把1~1000这1000个数相加时,有多次进位,每进位1次,比不进位时数字和都减少9,把加得的和按数字和计算的进位次数减去9的个数,才得到所有数字的和,但这样计算太繁了。
为了简便地计算这1000个数所有数字的和,可以把这1000个数按以下的方法分组,使每一组相加时都不进位,然后算出每组和的数字和,再求出各组数字和的总和,就是1000个数所有数字的和。
1234 (499)1000999998997996995 (500)1000999999999999999…999——各组数的和12727272727…999——各个和的数字和这样算得1000个数所有数字的和是1+27×500=13501。
答:所有数字的和是13501。
*例6:两个四位数相加,第一个四位数的每个数字都不小于5,第二个四位数仅仅是第一个四位数的数字调换了位置。
某同学做出的答案是16246。
试问该同学的答数正确吗?如果正确,写出这两个四位数,如果不正确,请说明理由。
解:在对这一题思考时,如果试图按题中的条件找出四位数拼出加法算式,要找出很多的四位数,进行许多的尝试,而且不能进行严密的推理,因此这不是可取的方法。
比较好的做法是,先按规律说明是否可能按题目的条件做出这个答数,有可能时,才拼算式,如果不可能,这个答数就是错的。
由于第一个四位数的每个数字都不小于5,不管把这四个数字怎样调换组成第二个四位数,第二个四位数的每个数字也都不小于5,两个数相加,四个数位上都要进位,共有四次进位,而两个四位数数字的和是第一个四位数数字和的2倍,是偶数,四次进位使和的数字和比原来八个数字的和减少4个9,所得的和的数字和仍然是偶数,而该同学的答数16246的数字的和1+6+2+4+6=19,是个奇数,所以这个答数是错的。
应用练习二1.有A、B两个整数,A的各位上的数字的和是31,B的各位上的数字的和是19,A和B相加,得数的各位上的数字的和是32,相加时有几次进位?2.A的各位上的数字的和是4,A减去一个两位数,差的各位上的数字的和是24,减数最大是几?3.甲数和乙数的数字和都是17的倍数,甲数减乙数,差的数字和是10,甲数最小是几?4.甲数和乙数的和是753,两个数的数字和都是11的倍数,两个数中较大的一个最大是几?5.1~10000这10000个自然数所有数字的和是多少?6.一个三位数,它的各位上的数字的和能被8整除,这个三位数加1得到的数各位上的数字的和也能被8整除,在所有满足条件的三位数中,最大的一个是几?*7.的差是一个自然数的平方,这个自然数的各位数字的和是几?*8.的积的各位数字的和是几?课后练习二1.甲数各位数字之和是28,乙数各位数字之和是18,甲、乙两数相加时有三次进位,那么甲、乙两数之和的各位数字之和是多少?2.甲数各位数字之和是9,乙数各位数字之和是10,如果甲数减乙数有两次要从前一位退1再减。
