3.2.1直线的点斜式方程
合集下载
3.2.1 直线的点斜式方程(共26张PPT)

栏目 导引
第三章
直线与方程
跟踪训练
1.写出下列直线的方程
(1)经过点A(2,5),斜率是4; (2)经过点B(2,3),倾斜角是45°;
(3)经过点C(-1,1),与x轴平行;
(4)经过点D(1,1),与x轴垂直. 解:(1)y-5=4(x-2); (2)k=tan 45°=1,所以y-3=x-2; (3)y=1; (4)x=1.
栏目 导引
第三章
直线与方程
(3)∵直线的倾斜角为 60° , ∴其斜率 k=tan 60° = 3. ∵直线与 y 轴的交点到原点的距离为 3, ∴直线在 y 轴上的截距 b= 3 或 b=- 3. ∴所求直线方程为 y= 3x+ 3 或 y= 3x- 3.
【名师点评】 利用斜截式写直线方程时, 首先要考虑斜率 是否存在,其次要注意截距与距离的区别与联系.
栏目 导引
第三章
直线与方程
题型四
例4
直线在平面直角坐标系中位置的确定
)
1 方程 y= ax+ 表示的直线可能是 ( a
栏目 导引
第三章
直线与方程
1 1 【解析】 直线 y= ax+ 的斜率是 a, 在 y 轴上的截距是 , a a 1 当 a>0 时,斜率 a>0,在 y 轴上的截距是 >0,则直线 y= a 1 ax+ 过第一、 二、 三象限, 四个选项都不符合; 当 a<0 时, a 1 1 斜率 a<0, 在 y 轴上的截距是 <0, 则直线 y= ax+ 过第二、 a a 三、四象限,仅有选项 B 符合.
第三章
直线与方程
3.2
直线的方程
3.2.1 直线的点斜式方程
第三章
直线与方程
3.2.1直线的点斜式方程

l 上.
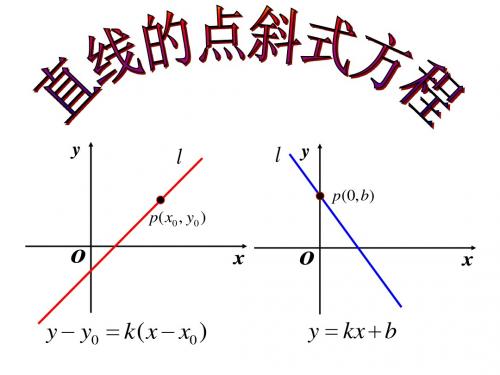
斜率为k 的方程为: 经过点 P0 ( x0 , y0 ) 斜率为k的直线 l 的方程为:
y − y0 = k ( x − x0 )
这个方程是由直线上一定点及其斜率确定 点斜式方程 的,所以我们把它叫做直线的点斜式方程. 所以我们把它叫做直线的点斜式方程.
1、写出下列直线的点斜式方程:
(1) (1)经过点A(3,-1),斜率是 2 ; y + 1 = 2( x − 3);
-2 -1 O
x
2、写出下列直线的斜截式方程: 3 (1)斜率是 ,在 y 轴上的截距是-2; 2
ቤተ መጻሕፍቲ ባይዱ
3 y= x−2 2 (2)斜率是 − 2 ,在 y 轴上的截距是4.
y = −2 x + 4.
课堂小结: 课堂小结:
1、直线的点斜式方程:y − y1 = k ( x − x1 )
2、直线的斜截式方程:y = kx + b.
y
P0 x0 , y0 ) (
l
O
x
y − y0 = 0或y = y0
思考2: 思考
问题四:经过点P0 ( x0 , y0 ), 倾斜角 为90 的直线方程是什么?
y
o
l
P0 ( x0 , y0 )
x
O
x = x0
思考3: 思考
问题五:经过点P0 (0, b), 斜率 为k的直线方程是什么?
y
l
P0 (0, b)
y = kx + b
x
O
斜率
y轴上的截距
此方程由直线 l 的斜率和它在 y轴上的截距确 直线的斜截式方程。 所以这个方程也叫作直线的斜截式方程 定,所以这个方程也叫作直线的斜截式方程。
3.2.1直线的点斜式方程

1 6
,且与坐标轴围成面积为3的三角形,
求该直线的方程.
解:设直线方程为y=- 16x+b,
当 x=0 时,y=b,即直线与 y 轴的交点为(0,b); 当 y=0 时,x=-6b,即直线与 x 轴的交点(-6b,0). 又S=12·|b|·|-6b|=3b2=3,故b=±1,
∴所求直线方程为y=- 16x+1或y=- x16-1.
4.写出满足下列条件的直线的方程.
(1)斜率为5,在y轴上截距为-1,________; (2)倾斜角30°,在y轴上截距为 ,________.
(3)已知直线l1:y=-2x+3,l2:y=4x-2,直线l与l1平 行且与l2在y轴上的截距相同,求直线l的方程.
(3)由斜截式方程知,直线l1的斜率k1=-2, 又因为l∥l1,所以kl=-2. 由题意知,l2在y轴上的截距为-2, 所以直线l在y轴上的截距b=-2. 由斜截式可得直线l的方程为y=-2x-2.
y
.p2L
O .P1 α
x
L1⊥ L2 k1k2= -1
探究一:点斜式方程
y
l
解:设P(x,y)是直线L上不
Px,y 同于P0的任意一点.
P0(x0,y0)
O
x
点斜式
(1)
定义: 方程(1)由直线上一定点及其斜率确定,我们把(1)叫做 直线的点斜式方程,简称点斜式.
注意:①斜率要存在!
②已知直线上一点以及直线的斜率
(1)l1 // l2 的条件是什么?(2)l1 l2 的条件是什么?
解:(1)若 l1 // l2 ,则k1 k2 . 此时 l1,l2与y轴的交点不同即 b1 b2;
反之 k1 k2 且b1 b2 时,l1 // l2 .
用3.2.1直线的点斜式方程完稿

3.2
直线的方程
3.2.1 直线的点斜式方程
复习回顾
平行:对于两条不重合的直线l1、l2,其斜率分别为 k1、k2,有
l1∥l2
k1=k2.
前提条件:不重合、都有斜率
垂直:如果两条直线l1、l2都有斜率,且分别为k1、 k2,则有
l1⊥l2
k1k2=-1.
前提条件:都有斜率
特殊角的正切值
tan 0 0, 3 tan 30 , 3 tan 45 1, tan 60 3, tan 90 不存在; tan120 3, tan135 1, 3 tan150 . 3
直线过定点问题 由直线l的点斜式方程y-y0=k(x-x0) 可知,此直线l过定点(x0,y0); 由直线l的斜截式方程y=kx+b 可知,此直线l过定点(0,b).
练 1.方程y=k(x+1)表示( C ) 习 A.通过点(1,0)的所有直线 B.通过点(-1,0)的所有直线 C.通过点(-1,0)且不垂直于x轴的直线 D.通过点(-1,0)且除去x轴的直线
2.直线l在坐标轴上的截距
纵坐标 (1)直线在y轴上的截距:直线l与y轴的交点(0,b)的_______ .b (2)直线在x轴上的截距:直线l与x轴的交点(a,0)的_______ . 横坐标 a
温馨提示:
截距是直线与坐标轴交点的纵(或横)坐标, 截距是一个数值,可正、可负、可为零. 当截距非负时,它等于直线与y轴交点到原点的距离; 当截距为负时,它等于直线与y轴交点到原点距离的相反数; 当截距为0时,直线过原点。
3.直线的斜截式方程
名称 斜截 式 温馨提示:
已知条件 斜率k和在y轴上 的截距b
示意图
方程
直线的方程
3.2.1 直线的点斜式方程
复习回顾
平行:对于两条不重合的直线l1、l2,其斜率分别为 k1、k2,有
l1∥l2
k1=k2.
前提条件:不重合、都有斜率
垂直:如果两条直线l1、l2都有斜率,且分别为k1、 k2,则有
l1⊥l2
k1k2=-1.
前提条件:都有斜率
特殊角的正切值
tan 0 0, 3 tan 30 , 3 tan 45 1, tan 60 3, tan 90 不存在; tan120 3, tan135 1, 3 tan150 . 3
直线过定点问题 由直线l的点斜式方程y-y0=k(x-x0) 可知,此直线l过定点(x0,y0); 由直线l的斜截式方程y=kx+b 可知,此直线l过定点(0,b).
练 1.方程y=k(x+1)表示( C ) 习 A.通过点(1,0)的所有直线 B.通过点(-1,0)的所有直线 C.通过点(-1,0)且不垂直于x轴的直线 D.通过点(-1,0)且除去x轴的直线
2.直线l在坐标轴上的截距
纵坐标 (1)直线在y轴上的截距:直线l与y轴的交点(0,b)的_______ .b (2)直线在x轴上的截距:直线l与x轴的交点(a,0)的_______ . 横坐标 a
温馨提示:
截距是直线与坐标轴交点的纵(或横)坐标, 截距是一个数值,可正、可负、可为零. 当截距非负时,它等于直线与y轴交点到原点的距离; 当截距为负时,它等于直线与y轴交点到原点距离的相反数; 当截距为0时,直线过原点。
3.直线的斜截式方程
名称 斜截 式 温馨提示:
已知条件 斜率k和在y轴上 的截距b
示意图
方程
3.2.1__直线的点斜式方程

1 故所求直线的方程为 3=-2(x+2)或 y-3= 9 -2(x+2). (12 分)
3 1 5.(1)过点(1,2)且与 y=- x- 平行的直线方程为 4 4 ________________. (2)过点(2,1)且与 y=-2x+10 垂直的直线方程为 ____________________.
3 解析:(1)易知直线的斜率为-4,故直线方程为 y-2 3 =-4(x-1). 1 (2)设所求直线斜率为 k,则-2· k=-1,∴k=2,故 1 直线方程为 y-1=2(x-2).
3 答案:(1)y-2=-4(x-1) 1 (2)y-1=2(x-2)
6.光线自点M(2,3)射到y轴的点N(0,1)后被y 轴反射,其反射光线过点(2,-1),求反射
(1)若l与过点(-4,4)和(-3,2)的直线l′平行, 求其方程; (2)若l与过点(-4,4)和(-3,2)的直线l′垂直,
求其方程.
[精解详析]
2-4 (1)由斜率公式得 kl′= =-2, -3--4
∵l 与 l′平行, ∴kl=-2. 由直线的点斜式方程知 y+3=-2(x-2), (2)∵直线 l′的斜率为 k=-2,l 与其垂直, 1 ∴kl=2. 1 由直线的点斜式方程知 l:y+3=2(x-2).
1.直线的点斜式方程 (1)定义:如图所示,直线l过
定点P(x0,y0),斜率为k,则把方
程
y y0 k x x0 叫做直线l
的点斜式方程,简称点斜式.
(2)说明:如图所示,过定 点P(x0,y0),倾斜角是90°的 直线没有点斜式,其方程为
x-x0=0,或 x=x0
.
2.直线的斜截式方程
(2)斜率必须存在,只有这两个条件都具备才
3.2.1直线的点斜式方程

解:这条直线经过点A(0,5) 斜率是k=tan00=0 代入点斜式,得
5
y - 5 = 0
O
x
②直线的斜截式方程:
已知直线l的斜率是k,与y轴的交点是P(0,b),求 直线方程。 代入点斜式方程,得l的直线方程:y - b =k ( x - 0)
即
y = kx + b。
(2)
例3:斜率是5,在y轴上的截距是4的直线方程。
例6:已知直线l过A(3,-5)和B(-2,5),求直 线l的方程
解:∵直线l过点A(3,-5)和B(-2,5) 5 5
kL 2 3 2
将A(3,-5),k=-2代入点斜式,得
y-(-5) =-2 ( x-3 ) ,即
2x + y -1 = 0
㈢巩固: ①经过点(- 2,2)倾斜角是300的直线的方程是 (A)y+ 2 = 3 ( x-2) (B)y+2= 3 (x- 2 ) 3 (C)y-2= (x+ 2)(D)y-2= 3 (x+ 2 ) 3 ②已知直线方程y-3= 3(x-4),则这条直线经过的已知 点,倾斜角分别是 (A)(4,3);π/ 3 (B)(-3,-4);π/ 6 (C)(4,3);π/ 6 (D)(-4,-3);π/ 3 ③直线方程可表示成点斜式方程的条件是 (A)直线的斜率存在 (B)直线的斜率不存在 (C)直线不过原点 (D)不同于上述答案
解:由已知得k =5, b= 4,代入斜截式方程 y= 5x + 4 即5 x - y + 4 = 0
4
例5:求过点(1,2)且与两坐标轴组成一等腰直角 三角形的直线方程。
解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1
直线过点(1,2)代入点斜式方程得
5
y - 5 = 0
O
x
②直线的斜截式方程:
已知直线l的斜率是k,与y轴的交点是P(0,b),求 直线方程。 代入点斜式方程,得l的直线方程:y - b =k ( x - 0)
即
y = kx + b。
(2)
例3:斜率是5,在y轴上的截距是4的直线方程。
例6:已知直线l过A(3,-5)和B(-2,5),求直 线l的方程
解:∵直线l过点A(3,-5)和B(-2,5) 5 5
kL 2 3 2
将A(3,-5),k=-2代入点斜式,得
y-(-5) =-2 ( x-3 ) ,即
2x + y -1 = 0
㈢巩固: ①经过点(- 2,2)倾斜角是300的直线的方程是 (A)y+ 2 = 3 ( x-2) (B)y+2= 3 (x- 2 ) 3 (C)y-2= (x+ 2)(D)y-2= 3 (x+ 2 ) 3 ②已知直线方程y-3= 3(x-4),则这条直线经过的已知 点,倾斜角分别是 (A)(4,3);π/ 3 (B)(-3,-4);π/ 6 (C)(4,3);π/ 6 (D)(-4,-3);π/ 3 ③直线方程可表示成点斜式方程的条件是 (A)直线的斜率存在 (B)直线的斜率不存在 (C)直线不过原点 (D)不同于上述答案
解:由已知得k =5, b= 4,代入斜截式方程 y= 5x + 4 即5 x - y + 4 = 0
4
例5:求过点(1,2)且与两坐标轴组成一等腰直角 三角形的直线方程。
解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1
直线过点(1,2)代入点斜式方程得
3.2.1直线的点斜式方程

2-1.若直线 ax+by+c=0 在第一、二、三象限,则( A.ab>0,bc>0 C.ab<0,bc>0 B.ab>0,bc<0 D.ab<0,bc<0
D )
a 解析:由题意,直线的斜率一定大于 0,所以 k=-b>0, c 即 ab<0;根据直线的纵截距大于 0,可得-b>0,即 bc<0.
的方程是?
y
l
P( x, y)
P 0 ( x0 , y0 )
y y0
y y0 k ( x x0 ) x x0
故:
x
x x0
o
y y0 k ( x x0 )
经过点 P0 ( x0 , y0 ) 斜率为k的直线 l 的方程 为:
y y0 k ( x x0 )
点斜式方程和斜截式方程的应用 例 3: 已知直线 l 经过点 P(-5,-4),且 l 与两坐标轴围成 的三角形的面积为 5,求直线 l 的方程. 思维突破:由题意知所围三角形为直角三角形.根据直角 三角形面积公式以及直线方程求出该直线在两坐标轴的坐标即 可. 解:由已知:l 与两坐标轴不垂直.
∵直线 l 经过点 P(-5,-4), ∴ 可设直线 l 的方程为 y-(-4)=k[x-(-5)], 即 y+4=k(x+5).
3.2.1 直线的点斜式方程
复习引入: 一、直线斜率的求解公式:
1)k t an 2)k
注意:
( 900 ) ( x2 x1 )
y2 y1 x2 x1
不是所有的直线都有斜率,源自斜率不存在的直线为与 x 轴垂直的直线
0 ( x0 , y0 ) ,斜率为k, 则此直线 若直线 l 经过点P
y 2x 4
y2
y
3.2.1直线的点斜式方程
【错因分析】
上述解法的错误主要在于“误把直线在
两轴上的截距当作距离”.
【防范措施】
直线在两轴上的截距是直线与坐标轴交
点的横、纵坐标,而不是距离,因此本题在先求得截距后, 应对截距取绝对值再建立面积表达式.
4 【正解】 设 l:y=- x+b,令 x=0 得 y=b;令 y=0 3 3 得 x=4b, 1 3 由题意得2· |b |· |4b|=6,∴b2=16,∴b=± 4. 4 故直线 l 的方程为 y=- x± 4. 3
温故而知新
1、直线的倾斜角 与斜率k的关系是
k tan (
2
)
2、过点A x1, y1 、B x2 , y2 的直线的斜率是
y1 y2 k (x1 x2) x1 x2
3、简述在直角坐标系中确定一条直线的 几何要素
(1)直线上的一点和直线 的倾斜角(或斜率) (2)直线上两点
试试自己的能耐
4.直线 l 过点P(2,1),且斜率为3,点Q(x,y)是 l 上不同于P的一点,则x、y满足怎样的关系式?
设直线l经过点 P0(x0,y0) ,且斜率为k,点P(x,y)为
直线l上不同于P0的任意一点,则x、y满足的关系式
y y0 k x x0 是_____________
你这节课有什么收获?
1.建立点斜式方程的依据是:直线上任一点与这条 y-y1 直线上一个定点的连线的斜率相同,故有 =k,此式 x-x1 是不含点 P1(x1,y1)的两条反向射线的方程,必须化为 y -y1=k(x-x1)才是整条直线的方程.当直线的斜率不存 在时,不能用点斜式表示,此时方程为 x=x1.
④ 经过点P0 ( x0 , y0 ) 且垂直于 x 轴的直线方程?
3.2.1 直线的点斜式方程(高中数学人教版必修二)
(点P不同于点A时)
y 3 2[ x (1)]
o
P( x, y)
x
l直
线 上
2 坐标满足此方程的每一点都在直线 l 上.
问题2:若直线 l 经过点 P0 ( x0 , y0 ) ,斜率为k, 则此直线 的方程是?
y
P( x, y)
P ( x0 , y0 ) 0
y y0
l
y y0 k x x0
C4
3 所以,m 2或3,7.
若角A为直角, m 1 m 2, 解得: 7. 则 k AC
新知:
一、直线的点斜式方程
问题1: 若直线 l经过点A(-1,3),斜率为-2,点P在直线 l 上运动,则点P的坐标(x , y)满足怎样的关系式?
y
A(1,3)
y 3 2 x (1)
x
x x0
即: y y0 k ( x x0 )
(1)
o (1)过点 P0 ( x0 , y0 ) ,斜率为k的直线 l上每个点的坐标都 满足方程 y y0 k ( x x0 ) ;
(2)坐标满足这个方程的每一点都在过点 P0 ( x0 , y0 ),斜 率为k的直线 l 上.
l1 ∥ l 2 k1 k2 , 且b1 b2 l1 l 2 k1 k 2 1
练习5判断下列直线是否平行垂直:
1 1 (1)l1 : y x 3, l2 : y x 2; 2 2
平行
5 3 (2)l1 : y x, l2 : y x. 3 5
y
解:如图 k BP
P
o
B A
1 (3) 4 1 ( 3) 4, k AP 1 2 3 倾斜角为锐角时, , ; k 4 x 倾斜角为钝角时, ,4; k
3.2.1点斜式直线方程

y 3 2( x 1)
.
即2 x y 5 0
(3)倾斜角为 90 时的直线方程.
x 1
例2.①已知直线的点斜式方程是y-2=x-1,
1 ,倾斜角是_____ 那么直线的斜率是____ 45 ,
(1, 2) ; 此直线必过定点______
3 ②已知直线的点斜式方程是 y 2 ( x 1) 3
点斜式方程
y
l
①倾斜角α°≠90
x
y y0 k ( x x0 )
②倾斜角α=0°
y y0 y l x l x0
y y0 0或y y0
③倾斜角α=90°
O
xபைடு நூலகம்
x x0 0或x x0
练习:已知直线经过点P1,3 ,求
(1)倾斜角为 0 时的直线方程;
y3
(2)斜率为2时的直线方程;
1 x
(过点P(0,3)斜率为2确定的)方程 y-3=2(x-0)是直线 l 的方程,且 称为直线 l 的点斜式方程。
3– P
l
o
–
一般的,设直线l经过点 P 1 ( x1 , y1 ),斜 率为 k 则方程 y y1 k ( x x1 )叫做直线 的点斜式方程。
-1
局限性:只适用于斜率存在的情形。
3 是______ ,倾斜角是 _______. 30 3
(1, 2) ,直线的斜率 那么此直线经过定点_______
例3.已知直线l过A(3,-5)和B(-2,5),求直 线l的方程 y+5=-2(x-3) 2x+y-1=0
例4.求过点(1,2)且与两坐标轴组成一等腰直角 三角形的直线方程。
3.2.1直线的点斜式方程
.
即2 x y 5 0
(3)倾斜角为 90 时的直线方程.
x 1
例2.①已知直线的点斜式方程是y-2=x-1,
1 ,倾斜角是_____ 那么直线的斜率是____ 45 ,
(1, 2) ; 此直线必过定点______
3 ②已知直线的点斜式方程是 y 2 ( x 1) 3
点斜式方程
y
l
①倾斜角α°≠90
x
y y0 k ( x x0 )
②倾斜角α=0°
y y0 y l x l x0
y y0 0或y y0
③倾斜角α=90°
O
xபைடு நூலகம்
x x0 0或x x0
练习:已知直线经过点P1,3 ,求
(1)倾斜角为 0 时的直线方程;
y3
(2)斜率为2时的直线方程;
1 x
(过点P(0,3)斜率为2确定的)方程 y-3=2(x-0)是直线 l 的方程,且 称为直线 l 的点斜式方程。
3– P
l
o
–
一般的,设直线l经过点 P 1 ( x1 , y1 ),斜 率为 k 则方程 y y1 k ( x x1 )叫做直线 的点斜式方程。
-1
局限性:只适用于斜率存在的情形。
3 是______ ,倾斜角是 _______. 30 3
(1, 2) ,直线的斜率 那么此直线经过定点_______
例3.已知直线l过A(3,-5)和B(-2,5),求直 线l的方程 y+5=-2(x-3) 2x+y-1=0
例4.求过点(1,2)且与两坐标轴组成一等腰直角 三角形的直线方程。
3.2.1直线的点斜式方程
3.2.1 直线的点斜式方程

(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?
解 由题意可知,kl1=2a-1,kl2 =4,
∵l1⊥l2, ∴4(2a-1)=-1,解得 a=38. 故当 a=38时,直线 l1:y=(2a-1)x+3 与直线 l2:y=4x-3 垂直.
反思与感悟 设直线l1和l2的斜率k1,k2都存在,其方程分别为l1:y= k1x+b1,l2:y=k2x+b2,那么: (1)l1∥l2⇔k1=k2,且b1≠b2; (2)两条直线重合⇔k1=k2,且b1=b2; (3)l1⊥l2⇔k1·k2=-1.
跟踪训练 2 已知直线 l 的斜率为16,且和两坐标轴围成面积为 3 的三角形,
求 l 的斜截式方程. 解 设直线方程为 y=16x+b,则当 x=0 时,y=b; 当 y=0 时,x=-6b.由已知可得12·|b|·|-6b|=3, 即6|b|2=6,∴b=±1. 故所求直线 l 的斜截式方程为 y=16x+1 或 y=16x-1.
跟踪训练 3 已知直线 l:y=(a2-2)x+2a+9 与直线 y=-12x+1 垂直, 且与直线 y=3x+5 在 y 轴上的截距相同,求 a 的值.
解 由题意知(a2-2)×-12=-1,解得 a=±2. ∴当a=2时,直线l:y=2x+13; 当a=-2时,直线l:y=2x+5. 又直线l与直线y=3x+5在y轴上的截距相同, ∴a=-2.
2.直线y=kx+b通过第一、三、四象限,则有
A.k>0,b>0 C.k<0,b>0
√B.k>0,b<0
D.k<0,b<0
解析 ∵直线经过第一、三、四象限, ∴图形如图所示,由图知,k>0,b<0.
3.2.1 直线的点斜式方程

目标导航
知识梳理
重难聚焦
典例透析
②如图乙,过定点P(x0,y0),倾斜角是90°的直线不能用点斜式表
示,其方程为x-x0=0或x=x0.
-4-
3.2.1 直线的点斜式方程
12
目标导航
知识梳理
重难聚焦
典例透析
【做一做1】 若直线l的点斜式方程是y-2=3(x+1),则直线l的斜率 是( )
A.2 B.-1 C.3 D.-3 解析:直线l经过点(-1,2),且斜率为3. 答案:C
题型一 求直线的点斜式方程
【例1】 写出下列直线的点斜式方程: (1)经过点A(2,5),斜率是4; (2)经过点B(2,3),倾斜角是45°; (3)经过点C(-1,-1),与x轴平行. 解:(1)由点斜式方程可知,所求直线的点斜式方程为y-5=4(x-2). (2)直线的倾斜角为45°,则此直线的斜率k=tan 45°=1. 故直线的点斜式方程为y-3=x-2. (3)直线与x轴平行,则倾斜角为0°,斜率k=0.
所以直线的斜率为 − 3.
3
故所求直线的点斜式方程为
y+1=−
3 (������
3
−
2).
(3)因为直线与y轴垂直,所以倾斜角为0°,
即斜率k=0.故所求直线的点斜式方程为y=-2.
-12-
3.2.1 直线的点斜式方程
目标导航
知识梳理
重难聚焦
典例透析
题型一 题型二 题型三
题型二 求直线的斜截式方程
3.2.1 直线的点斜式方程
题型一 题型二 题型三
目标导航
知识梳理
重难聚焦
典例透析
正解:设直线l1,l2的斜率分别为k1,k2,则k1=-1,k2=a2-2.
3.2.1直线的点斜式方程

(3)截距式适用于横、纵截距都存在且都不为0的直线.
练习
根据下列条件,求直线的方程,并画出图形:
(1)在x轴上的截距是2,在y轴上的截距是3;
x 2
x
y 3
1
(2)在x轴上的截距是-5,在y轴上的截距是6.
5
y 6
1
练习
下列四个命题中的真命 A.经 过 定 点 P
0
题是(
B)
(x 0 ,y 0 )的 直 线 都 可 以 用
即
y=kx+b
为所求的直线方程 . 1 说明: . b叫做直线l在y轴上的截距;b∈R 2. y=kx+b ——直线方程的斜截式 .
形式
条件
方程
应用范围
点斜式
过点( x0,y0), 斜率为k
y y0 k ( x x0 )
不含与x轴垂 直的直线 不含与x轴垂 直的直线
斜截式 在y轴上的截距 为b,斜率为k
y kx b
注:应分“斜率存在”和“斜率不存在” 两种情 况分别考虑
例2 已知直线
l1 : y k 1 x b1 , l 2 : y k 2 x b 2
试讨论:(1) l1 // l 2 的条件是什么? (2) l l 的条件是什么? 1 2 解:(1)若 l1 // l 2 ,则 k 1 k 2 此时
直线l 经过点P1(x1, y1),斜率为k,求直 线l 的方程。
当直线的倾斜角为0°时, 0 . k
此时直线的方程是
y y1
当直线的倾斜角为90°时,直线没有斜率 此时直线的方程是
x = x1
例1 直线l 经过点P1(-2, 3),倾斜角α=45º, 求这条直线的方程,并画出图形。 解: 这条直线经过点
课件6:3.2.1 直线的点斜式方程

预习自测
1.已知直线 l 的方程为 y+247=94(x-1),则 l 在 y 轴上
的截距为( )
A.9
B.-9
27 C. 4
D.-247
Байду номын сангаас
【解析】由已知方程得 y=49x-9,故直线 l 在 y 轴上的
截距为-9.
【答案】B
2.直线方程为 y+2=2x-2,则( ) A.直线过点(2,-2),斜率为 2 B.直线过点(-2,2),斜率为 2 C.直线过点(1,-2),斜率为12 D.直线过点(1,-2),斜率为 2
跟踪训练 2 (1)已知直线 l 的方程为 9x-4y=36,则 l 在 y
轴上的截距为( )
A.9
B.-9
C.-4
D.-49
【解析】直线方程可化为 y=94x-9,
∴l 在 y 轴上的截距为-9.
【答案】B
(2)①写出直线斜率为-1,在 y 轴上截距为-2 的直线方程的 斜截式; ②求过点 A(6,-4),斜率为-43的直线方程的斜截式.
解:(1)直线斜率为 tan60°= 3, 所以直线方程为 y-4= 3(x+1). (2)直线斜率不存在,直线平行于 y 轴, 所以所求直线方程为 x=4. (3)直线斜率为 tan60°= 3, 所以所求直线的方程为 y= 3x. (4)直线斜率为 0,所以直线方程为 y=1.
类型二 直线的斜截式方程 例2 求下列直线的斜截式方程: (1)斜率为-4,在y轴上的截距为7; (2)在y轴上的截距为2,且与x轴平行; (3)求倾斜角为150°,与y轴的交点到原点的距离为3的 直线方程.
于是直线与两坐标轴围成的三角形的面积为
1 2
k+
-3k-2=4,即(2k+3)3k+2=±8,
3.2.1直线的点斜式方程

温故而知新
1.直线的倾斜角α与斜率k的关系是
k tan __________
2.过点A(x1,y1)、B (x2,y2)的直线的斜率
y1 y2 x1 x2 k=_______
3.简述在直角坐标系中确定一条直线的 几何要素.
(1)直线上的一点和直线 的倾斜角(或斜率) (2)直线上两点
y
.
(1)当直线l的倾斜角为0°时, tan0 °=0,即k=0 这时直线l与x轴平行或重合,那么l的方程就是: y-y0=0, 或 y=y0 (2)当直线l的倾斜角为90°时, 斜率不存在
x , y P 0 0 0
o
y
x
.
这时直线l与y轴平行或重合,那么l的方程就是: x , y P x-x0=0,或x=x0 0
相信这个也难不倒你
直线l经过点 P0(x0,y0) ,且斜率为k,点
P(x,y)为直线l上不同于P0的任意一点,则x、
y y0 k x x0 y满足的关系式是_____________
y
P0 x0, y0
.
o
.
p x, y
y y0
x x0
点斜式方程
x
学会自己探究 直角坐标系上任意直线都可以用直 线的点斜式方程表示吗?
2
4、直线 2 x 3 y 1 0 的斜率为 上的截距为 1 ,y轴上的截距为
2
1 3
2 3
,x轴
学好数学要善于总结
你这节课有什么收获?、斜截式方程: y kx b
它们都是在斜率K存在时才适用。
3、垂直于X轴: x x0 垂直于Y轴:y y
广州第八十一中学
麦庆河
3.2.1 直线的点斜式方程

二、典型问题与方法
1.直线的点斜式方程 例 1 直线 l 经过点 P0(-2,3),且倾斜角 α=45° ,求直线 l 的点斜式方程,并画出直线 l. (链接教材 P93 例 1) [解析] 直线 l 经过点 P0(-2,3),斜率是 k=tan 45° =1,
代入点斜式方程得 y-3=x+2. 画图时,只需再找出直线 l 上另一点 P1(x1,y1),取 x1=-1,y1=4,得 P1 的坐标为(-1,4), 过 P0,P1 的直线即为所求,如图. 【方法小结】由点斜式写直线方程时,由于过 P(x0,y0)的直线有无数条,大致可分为两类:(1)斜率存在时 方程为 y-y0=k(x-x0);(2)斜率不存在时,直线方程为 x=x0. 【变式训练】 1.写出下列直线的点斜式方程. (1)经过点 B(- 2,2),倾斜角是 30° ;(2)经过点 C(0,3),倾斜角是 0° . 解:(1)因为倾斜角是 30° ,所以直线的斜率是 故直线的点斜式方程为 y-2= 3 , 3
3.2.1 直线的点斜式方程
一、课本知识梳理
1.直线的点斜式方程和斜截式方程 名称 点斜式 已知条件 点 P(x0,y0) 和斜 率k 斜率 k 和在 y 轴上 的截距 b 示意图 方程 y-y0=k(x-x0) 使用范围 斜率存在Βιβλιοθήκη 斜截式y=kx+b
斜率存在
2.直线 l 的截距 (1)直线在 y 轴上的截距:直线与 y 轴的交点(0,b)的纵坐标 b. (2)直线在 x 轴上的截距:直线与 x 轴的交点(a,0)的横坐标 a.
3 (x+ 2). 3
(2)因为倾斜角是 0° ,所以直线的斜率为 0,则直线的点斜式方程为 y-3=0(x-0),即 y=3.
2.直线方程的斜截式及应用 例 2 已知直线 l1:y=k1x+b1,l2:y=k2x+b2,试讨论:(1)l1∥l2 的条件是什么?(2)l1⊥l2 的条件是什么? (链接教材 P94 例 2) [解析](1)若 l1∥l2,则 k1=k2,此时 l1,l2 与 y 轴的交点不同,即 b1≠b2;反之,k1=k2,且 b1≠b2 时,l1∥l2. (2)若 l1⊥l2,则 k1k2=-1;反之,k1k2=-1 时,l1⊥l2. 【方法小结】对于直线 l1:y=k1x+b1,l2:y=k2x+b2, l1∥l2⇔k1=k2,且 b1≠b2;l1⊥l2⇔k1k2=-1.
3.2.1直线的点斜式方程

3.2.1 直线的点斜式方程
问题引入
在平面直角坐标系内,如果给定
一条直线 l 经过的一个点 P0 x0 , y0 和斜率 k ,能否将直线上所有的点的
坐标 x, y 满足的关系表示出来呢? l
y
P0 O
x
问题引入
直线经过点 P0 x0 , y0 ,且斜率为 k ,
设点Px, y 是直线上不同于点P 的任意一 0
x x0
0 ,或
x x0
y
l
P0
O x
y 轴所在直线的方程是:
x0
典型例题
例1 直线
画出直线 l .
l 经过点 P0 2,3 ,且倾斜
y
4 3
角 45,求直线 l 的点斜式方程,并
P 解:直线 l经过点 P0 2,3 ,
l
斜率 k tan 45 1,
1、根据条件写出下列直线的方程: (1)过点A(-4,3),斜率k=3; (2)过点B(-1,4),倾斜角为135°;(Leabharlann )过点C(-1,2)且与y轴平行;
(4)过点D(2,1)和E(3,-4)
2、根据条件写出下列直线的方程:
(1)过点A(-1,2),在y轴上 的截距为-2;
(2)过点B(3,4),且在两坐标 轴上的截距相等; (3)过点C(-5,-4)且其倾斜角 是直线 y 3x 3 的倾斜角的一半。
点,因为直线 l 的斜率为k ,由斜率公式得:
即:
y y0 k , x x0
y y0 k x x0
y
P
P0 O
l
x
直线的点斜式方程 方程 y y0 k x x0 由直线上一点及
问题引入
在平面直角坐标系内,如果给定
一条直线 l 经过的一个点 P0 x0 , y0 和斜率 k ,能否将直线上所有的点的
坐标 x, y 满足的关系表示出来呢? l
y
P0 O
x
问题引入
直线经过点 P0 x0 , y0 ,且斜率为 k ,
设点Px, y 是直线上不同于点P 的任意一 0
x x0
0 ,或
x x0
y
l
P0
O x
y 轴所在直线的方程是:
x0
典型例题
例1 直线
画出直线 l .
l 经过点 P0 2,3 ,且倾斜
y
4 3
角 45,求直线 l 的点斜式方程,并
P 解:直线 l经过点 P0 2,3 ,
l
斜率 k tan 45 1,
1、根据条件写出下列直线的方程: (1)过点A(-4,3),斜率k=3; (2)过点B(-1,4),倾斜角为135°;(Leabharlann )过点C(-1,2)且与y轴平行;
(4)过点D(2,1)和E(3,-4)
2、根据条件写出下列直线的方程:
(1)过点A(-1,2),在y轴上 的截距为-2;
(2)过点B(3,4),且在两坐标 轴上的截距相等; (3)过点C(-5,-4)且其倾斜角 是直线 y 3x 3 的倾斜角的一半。
点,因为直线 l 的斜率为k ,由斜率公式得:
即:
y y0 k , x x0
y y0 k x x0
y
P
P0 O
l
x
直线的点斜式方程 方程 y y0 k x x0 由直线上一点及
课件4:3.2.1 直线的点斜式方程

[解] (1)y-5=4(x-2); (2)k=tan45°=1 ∴y-3=x-2; (3)y=-1; (4)x=1.
跟踪练习1 写出满足下列条件的直线方程填空. (1)过点(-1,2),斜率为 ,________; (2)过点(-3,1),平行于x轴,________; (3)过点(-3,1),(1,4),________; (4)过点(-1,-3),倾斜角为135°,________.
2.若直线l的斜率是k,与y轴的交点是P(0,b),代入直线方程的 点斜式,整理得直线l的方程是 y=kx+b ,我们称b为直线l在y轴 上的 截距 ,这个方程是由直线l的 斜率和它在y轴上的 截距
确定的,所以叫做直线方程的 斜截式 .
3.当直线l的倾斜角为0°且过P1(x1,y1)点时,直线l的斜率是0, 其方程是 y=y1 .当直线l的倾斜角为90°且过P1(x1,y1)点时,直 线l的斜率 不存在 ,其方程是 x=x1 .
[解析] (1)由直线点斜式方程的定义知,不论k取何实 数方程y+2=k(x-3)总表示经过点(3,-2),斜率为k 的直线,所以这些直线的共同特征是过定点(3,-2). (2)将方程mx-y+m+3=0变形为y-3=m(x+1)可知, 不论m取何实数,直线总过定点(-1,3). [答案] (1)过定点(3,-2) (2)(-1,3)
[答案] (2)y=1. (3)3x-4y+13=0. (4)x+y+4=0.
[解析] (3)直线的斜率 k=1-4-(-13)=34, 故方程为 y-4=34(x-1),即 3x-4y+13=0. (4)k=tan135°=-tan45°=-1, y+3=-1·(x+1),即 x+y+4=0.
2 倍的直线方程是( )
A.x=-1
321直线的点斜式方程

的所有点P(x,y)是否都在直线l上? 为 什么?
思考6:我们把方程 y y0 k ( x x0 )
叫做直线的点斜式方程,经过点P0(x0, y0)的任意一条直线的方程都能写成点斜 式吗?
思考7:经过点P0(x0,y0) ,且倾斜角为
0o,90o的直线方程分别是什么? x=x0 y=y0
y l P(x,y) P0(x0,y0)
y y0 k x x0
x
o
y y0 思考4:代数式 k 可看作是 x x0
一个关于x,y的方程,化为整式即为 y y0 k ( x x0 ) ,那么直线l上每一 点的坐标都满足这个方程吗?
思考5:满足方程 y y0 k ( x x0 )
思考4:若直线l在两坐标轴上的截距 相等,且都等于m,则直线l的方程 如何? x+y=m
x y 1 a b
截距式适用于横、纵截距都存在且都不为0的直线。
知识探究(三): 中点坐标公式
思考1:已知x轴上两点P1(x1,0), P2(x2,0),则线段P1P2的中点P0的坐标是 x 什么? ( x ,0 ) 2
y = kx + b 2.直线的斜截式方程__________________
斜率为k,在y轴上的截距为b 的直线. 它表示__________________________ 斜率存在的直线 3.点斜式与斜截式的适用范围是__________________ 特殊情况 4.斜截式是点斜式的___________________
1 ⒋已知直线l的斜率为 2
,且与两坐标轴围成的三 角形的面积为4,求直线l的方程. ⒌已知直线l过(-2,4),且与两坐标轴围成的三角 形的面积为4,求直线l的方程。 3 ⒍求直线y= 3 x绕点(2,0)顺时针旋转30°所得直 线方程。 ⒊ ⒎已知过点A(-2,m)、B(m ,4)的直线l与直线 2x+y=1平行,求m。 ⒏已知直线l1:y=-2x+3,l2:y=4x-2,直线l与l1平行 且与l2在y轴上截距相同,求直线l的方程。
思考6:我们把方程 y y0 k ( x x0 )
叫做直线的点斜式方程,经过点P0(x0, y0)的任意一条直线的方程都能写成点斜 式吗?
思考7:经过点P0(x0,y0) ,且倾斜角为
0o,90o的直线方程分别是什么? x=x0 y=y0
y l P(x,y) P0(x0,y0)
y y0 k x x0
x
o
y y0 思考4:代数式 k 可看作是 x x0
一个关于x,y的方程,化为整式即为 y y0 k ( x x0 ) ,那么直线l上每一 点的坐标都满足这个方程吗?
思考5:满足方程 y y0 k ( x x0 )
思考4:若直线l在两坐标轴上的截距 相等,且都等于m,则直线l的方程 如何? x+y=m
x y 1 a b
截距式适用于横、纵截距都存在且都不为0的直线。
知识探究(三): 中点坐标公式
思考1:已知x轴上两点P1(x1,0), P2(x2,0),则线段P1P2的中点P0的坐标是 x 什么? ( x ,0 ) 2
y = kx + b 2.直线的斜截式方程__________________
斜率为k,在y轴上的截距为b 的直线. 它表示__________________________ 斜率存在的直线 3.点斜式与斜截式的适用范围是__________________ 特殊情况 4.斜截式是点斜式的___________________
1 ⒋已知直线l的斜率为 2
,且与两坐标轴围成的三 角形的面积为4,求直线l的方程. ⒌已知直线l过(-2,4),且与两坐标轴围成的三角 形的面积为4,求直线l的方程。 3 ⒍求直线y= 3 x绕点(2,0)顺时针旋转30°所得直 线方程。 ⒊ ⒎已知过点A(-2,m)、B(m ,4)的直线l与直线 2x+y=1平行,求m。 ⒏已知直线l1:y=-2x+3,l2:y=4x-2,直线l与l1平行 且与l2在y轴上截距相同,求直线l的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习引入: 一、直线斜率的求解公式:
1)k tan y2 y1 2)k x2 x1
注意:
( 90 )
0
( x2 x1 )
不是所有的直线都有斜率, 斜率不存在的直线为与 x 轴垂直的直线
平行:对于两条不重合的直线l1、l2,其斜 率分别为k1、k2,有 l1∥l2 k1=k2.
1.点斜式方程
小结
y y0 k ( x x0 )
当知道斜率和一点坐标时用点斜式 2.斜截式方程
y kx b
当知道斜率k和截距b时用斜截式 3.特殊情况 ①直线和x轴平行时,倾斜角α=0°
y y0 0或y y0
②直线与x轴垂直时,倾斜角α=90°
x x0 0或x x0
l1:y=k1x+b1,l2:y=k2x+b2
() 1 l1 // l2 k1 k2 , 且b1 b2 .
(2)l1 l2 k1 k2 1
y b k ( x 0)
y kx b
斜率 截距
斜截式
说明:(1)当知道斜率和截距时用斜截式.
(2)斜率k要存在,纵截距b∈R.
思考
1.截距b是距离吗? 不是,是数
2.截距与距离有什么区别? 截距为实数,可正,可负,可为零, 而距离是大于等于零的实数. 3.b的几何意义是什么? 与y轴交点的纵坐标
(2)l1 l2 k1 k2 1
判断下列各直线是否平行或垂直
1 (1) l1 : y x 3 2 5 (2) l1 : y x 3 1 l2 : y x 2 2 3 l2 : y x 5
(1)求经过点(1,1),与直线y=2x+7平行的直线的方程;
(2)求经过点(-1,1),与直线y=-2x+7垂直的直线的方程; [分析] 由已知直线的方程求出斜率,再根据两直线 平行或垂直的条件求解.
[解析] (1)由 y=2x+7 得 k1=2,由两直线平行知 k2=2. ∴所求直线方程为 y-1=2(x-1).即为 y=2x-1
(2)由 y=-2x+7 得 k1=-2,由两直线垂直知 k1k2=-1, 1 ∴k2= . 2
3 1 1 ∴所求直线方程为 y-1= (x+1).即为 y= x+ 2 2 2
条件:不重合、都有斜率
垂直:如果两条直线l1、l2都有斜率,且分 别为k1、k2,则有 l1⊥l2 k1k2=-1.
条件:都有斜率
小结:点斜式方程
y
l
①倾斜角α≠90°
x
y y0 k ( x x0 )
②倾斜角α=0°
y y0 y l x l
y y0
③倾斜角α=90°
O
x0
x
x x0
(2)倾斜角是30°,在y轴上的截距是0
(1)y= 3 x+5 (2)y=
3 3
x
思考1:若直线l的斜率为k,在x轴上 的截距为a,则直线l的方程是什么?
l
y=k(x-a)
思考2:已知直线l1:y=k1x+b1, l2:y=k2x+b2,分别在什么条件下l1与 l2平行?垂直?
() 1 l1 // l2 k1 k2 , 且b1 b2 .
4.斜截式方程和点斜式方程的联系:
y=kx+b 是 y-y0=k(x-x0)的一种特殊形式
写出下列直线的斜率和在y轴上的截距:
(1)y 3x 2 (2) y 3x (3) x 3 y 2
1 2 y x 3 3
例2 写出下列直线的斜截式方程
(1)α=60°,在y轴的截距是5
(1)经过点A(2,5),斜率为4 (2)经过点B(-2,-1),与X轴平行 (3)经过点C(
2 ,-3),倾斜角135°
(4)经过点 A(2,5),且与 x 轴垂直. (1)y-5=4(x-2) (2)y=-1 (3)y+3=-(x- )
(4)x=2.
(Ⅱ)斜截式方程
y
l
P0(0,b)
x
设直线经过点P0( 0,b), 其斜率为k,求直线方程. 解:代入一条直线过点 P 1 ( 2,3) ,斜率为 2,求这条直线的方程。
解: 由直线的点斜式方程知
y 3 2( x 2)
即
2 x y 7 0.
一条直线过点 P ,倾斜角 1 (2,3) 0 为 45 ,求这条直线的方程。
变式:
x y5 0
练习1 写出点斜式方程
1)k tan y2 y1 2)k x2 x1
注意:
( 90 )
0
( x2 x1 )
不是所有的直线都有斜率, 斜率不存在的直线为与 x 轴垂直的直线
平行:对于两条不重合的直线l1、l2,其斜 率分别为k1、k2,有 l1∥l2 k1=k2.
1.点斜式方程
小结
y y0 k ( x x0 )
当知道斜率和一点坐标时用点斜式 2.斜截式方程
y kx b
当知道斜率k和截距b时用斜截式 3.特殊情况 ①直线和x轴平行时,倾斜角α=0°
y y0 0或y y0
②直线与x轴垂直时,倾斜角α=90°
x x0 0或x x0
l1:y=k1x+b1,l2:y=k2x+b2
() 1 l1 // l2 k1 k2 , 且b1 b2 .
(2)l1 l2 k1 k2 1
y b k ( x 0)
y kx b
斜率 截距
斜截式
说明:(1)当知道斜率和截距时用斜截式.
(2)斜率k要存在,纵截距b∈R.
思考
1.截距b是距离吗? 不是,是数
2.截距与距离有什么区别? 截距为实数,可正,可负,可为零, 而距离是大于等于零的实数. 3.b的几何意义是什么? 与y轴交点的纵坐标
(2)l1 l2 k1 k2 1
判断下列各直线是否平行或垂直
1 (1) l1 : y x 3 2 5 (2) l1 : y x 3 1 l2 : y x 2 2 3 l2 : y x 5
(1)求经过点(1,1),与直线y=2x+7平行的直线的方程;
(2)求经过点(-1,1),与直线y=-2x+7垂直的直线的方程; [分析] 由已知直线的方程求出斜率,再根据两直线 平行或垂直的条件求解.
[解析] (1)由 y=2x+7 得 k1=2,由两直线平行知 k2=2. ∴所求直线方程为 y-1=2(x-1).即为 y=2x-1
(2)由 y=-2x+7 得 k1=-2,由两直线垂直知 k1k2=-1, 1 ∴k2= . 2
3 1 1 ∴所求直线方程为 y-1= (x+1).即为 y= x+ 2 2 2
条件:不重合、都有斜率
垂直:如果两条直线l1、l2都有斜率,且分 别为k1、k2,则有 l1⊥l2 k1k2=-1.
条件:都有斜率
小结:点斜式方程
y
l
①倾斜角α≠90°
x
y y0 k ( x x0 )
②倾斜角α=0°
y y0 y l x l
y y0
③倾斜角α=90°
O
x0
x
x x0
(2)倾斜角是30°,在y轴上的截距是0
(1)y= 3 x+5 (2)y=
3 3
x
思考1:若直线l的斜率为k,在x轴上 的截距为a,则直线l的方程是什么?
l
y=k(x-a)
思考2:已知直线l1:y=k1x+b1, l2:y=k2x+b2,分别在什么条件下l1与 l2平行?垂直?
() 1 l1 // l2 k1 k2 , 且b1 b2 .
4.斜截式方程和点斜式方程的联系:
y=kx+b 是 y-y0=k(x-x0)的一种特殊形式
写出下列直线的斜率和在y轴上的截距:
(1)y 3x 2 (2) y 3x (3) x 3 y 2
1 2 y x 3 3
例2 写出下列直线的斜截式方程
(1)α=60°,在y轴的截距是5
(1)经过点A(2,5),斜率为4 (2)经过点B(-2,-1),与X轴平行 (3)经过点C(
2 ,-3),倾斜角135°
(4)经过点 A(2,5),且与 x 轴垂直. (1)y-5=4(x-2) (2)y=-1 (3)y+3=-(x- )
(4)x=2.
(Ⅱ)斜截式方程
y
l
P0(0,b)
x
设直线经过点P0( 0,b), 其斜率为k,求直线方程. 解:代入一条直线过点 P 1 ( 2,3) ,斜率为 2,求这条直线的方程。
解: 由直线的点斜式方程知
y 3 2( x 2)
即
2 x y 7 0.
一条直线过点 P ,倾斜角 1 (2,3) 0 为 45 ,求这条直线的方程。
变式:
x y5 0
练习1 写出点斜式方程
