事件序列全序匹配算法研究
常见5种基本匹配算法

常见5种基本匹配算法在计算机科学中,匹配算法(Matching algorithms)是指用于确定一个集合中的元素是否与另一个集合中的元素相匹配的算法。
匹配算法可以应用于各种领域,如字符串匹配、模式匹配、图匹配等。
下面介绍五种常见的基本匹配算法。
1. 暴力匹配算法(Brute Force Matching Algorithm):暴力匹配算法是最基本的匹配算法之一、它遍历待匹配字符串和目标字符串,逐个字符进行比较,直到找到匹配或者遍历完整个字符串。
该算法的时间复杂度为O(n*m),其中n和m分别是待匹配字符串和目标字符串的长度。
2. KMP匹配算法(Knuth-Morris-Pratt Matching Algorithm):KMP匹配算法是一种优化的字符串匹配算法。
它通过预处理待匹配字符串的信息,快速确定定位下一次比较的位置,减少了不必要的比较次数,从而提高了匹配效率。
该算法的时间复杂度为O(n+m),其中n和m分别是待匹配字符串和目标字符串的长度。
3. Boyer-Moore匹配算法:Boyer-Moore匹配算法是一种高效的字符串匹配算法。
它利用了字符出现位置的规律,从目标字符串的末尾开始匹配,并利用预处理的跳转表格快速跳过不匹配的字符,从而减少比较次数。
该算法的平均时间复杂度为O(n/m),其中n和m分别是待匹配字符串和目标字符串的长度。
4. Aho-Corasick算法:Aho-Corasick算法是一种多模式匹配算法,适用于在一个文本中同时查找多个模式串的情况。
该算法利用Trie树的特性,同时利用一个自动机状态转移表格进行模式匹配,可以高效地找到多个模式串在文本中的出现位置。
该算法的时间复杂度为O(n+k+m),其中n是文本长度,k是模式串的平均长度,m是模式串的个数。
5. Rabin-Karp算法:Rabin-Karp算法是一种基于哈希函数的字符串匹配算法。
它通过对待匹配字符串和目标字符串的部分子串进行哈希计算,比较哈希值是否相等,进而确定是否匹配。
常见5种基本匹配算法

常见5种基本匹配算法匹配算法在计算机科学和信息检索领域广泛应用,用于确定两个或多个对象之间的相似度或一致性。
以下是常见的5种基本匹配算法:1.精确匹配算法:精确匹配算法用于确定两个对象是否完全相同。
它比较两个对象的每个字符、字节或元素,如果它们在相同位置上完全匹配,则返回匹配结果为真。
精确匹配算法适用于需要确定两个对象是否完全相同的场景,例如字符串匹配、图像匹配等。
2.模式匹配算法:模式匹配算法用于确定一个模式字符串是否出现在一个文本字符串中。
常见的模式匹配算法有暴力法、KMP算法、BM算法等。
暴力法是最简单的模式匹配算法,它按顺序比较模式字符串和文本字符串的每个字符,直到找到一次完全匹配或结束。
KMP算法通过预处理建立一个跳转表来快速定位比较的位置,减少了无效比较的次数。
BM算法利用模式串的后缀和模式串的字符不完全匹配时在文本串中平移模式串的位置,从而快速定位比较的位置。
3.近似匹配算法:4.模糊匹配算法:5.哈希匹配算法:哈希匹配算法用于确定两个对象之间的哈希值是否相等。
哈希值是通过将对象映射到一个固定长度的字符串来表示的,相同的对象会产生相同的哈希值。
常见的哈希匹配算法有MD5算法、SHA算法等。
哈希匹配算法适用于需要快速判断两个对象是否相等的场景,例如文件的完整性校验、数据校验等。
以上是常见的5种基本匹配算法,它们各自适用于不同的场景和需求,选择合适的匹配算法可以提高效率和准确性,并且在实际应用中经常会结合多种算法来获取更好的匹配结果。
全排列生成算法的分析
只有三个[0,1,7]。
x 105 2
x 105 2
1.5
1.5
1
1
0.5
0.5
0 0 x 105
4
2
4
6
字典全排列生成法
0
80
2
4
6
8
x 105递 增 进 位 排 列 生 成 算 法
4
3
3
2
2
1
1
0
0
2
4
6
递减进位排列生成算法
0 8
2
4
6
8
邻位对换排列生成算法
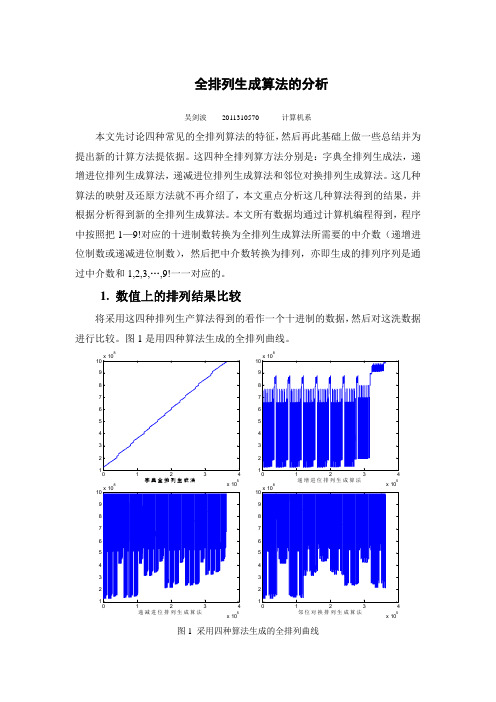
图 3. 四种全排列算法生成的相邻排列之间相同的字符个数的直方图
从另一个角度来思考,把生成的排列全部当着一个字符串,然后来比较这些 字符串有多少个位是不同的。比如排列"123456789"和"123456879"其中"78"两个 字符的位置不一样,则认为它们有 2 个位是不同的。上面的每种算法计算的排列 结果分别与上一次计算的排列结果比较,也就是将相邻的两个中介数生成的排列 进行对比,看有多少个字符是不同的,这里可以反映出通过该算法得到的排列在 字符上的变化的情况。
进行比较。图 1 是用四种算法生成的全排列曲线。
x 108 10
9 8 7 6 5 4 3 2 1
0
8
x 10 10
9 8 7 6 5 4 3 2 1
0
1
2
3
字典全排列生成法
1
2
3
递减进位排列生成算法
4
5
x 10
4
5
x 10
x 108 10
9 8 7 6 5 4 3 2 1
匹配方法的基本原理是什么

匹配方法的基本原理是什么匹配方法的基本原理是通过对比和匹配两个或多个对象之间的特征、属性或模式来确定它们之间是否存在相似性或关联性。
匹配方法可以应用于很多领域,如计算机视觉、自然语言处理、模式识别等。
匹配方法的具体实现可以有很多种,但核心思想一般是找到一种合适的度量方式来衡量两个对象之间的相似性或差异性,然后利用这种度量方式进行比较和匹配。
下面我将从匹配方法的基本原理、常用度量方式和应用举例三个方面,详细介绍匹配方法的基本原理。
1. 匹配方法的基本原理匹配方法的基本原理可以概括为以下几个步骤:(1)特征提取:从待匹配的对象中提取出能够反映其本质特征或属性的信息。
这些特征可以是结构化的数据如数值、文本、图像等,也可以是非结构化的数据如声音、视频等。
(2)特征表示:将提取出的特征转换为计算机可以处理的形式。
这一步骤的目的是将特征表示成向量或矩阵等数学表达形式,便于后续的比较和计算。
(3)相似度度量:选择合适的度量方式来衡量两个特征表示之间的相似性或差异性。
常用的度量方式包括欧氏距离、曼哈顿距离、余弦相似度等。
(4)匹配算法:根据相似度度量的结果,运用合适的算法来判断两个对象之间是否匹配。
常用的算法有基于阈值的判决、最邻近匹配、支持向量机等。
2. 常用的度量方式在匹配方法中,度量方式是非常重要的一环,用于评估待匹配对象之间的相似度或差异度,从而进行匹配判断。
以下是一些常用的度量方式:(1)欧氏距离(Euclidean distance):欧氏距离是一种基于空间直角的距离度量方式,它计算两个向量之间的直线距离,即欧氏空间中的直线距离。
(2)曼哈顿距离(Manhattan distance):曼哈顿距离是一种基于城市街区的距离度量方式,它计算两个向量之间的“曼哈顿”距离,即两个向量的各个分量差值绝对值的总和。
(3)余弦相似度(Cosine similarity):余弦相似度是一种衡量两个向量方向相似程度的度量方式,它通过计算两个向量的夹角的余弦值来衡量它们的相似度。
序列比对的原理和方法

序列比对的原理和方法
序列比对是指将两个或多个DNA、RNA或蛋白质序列进行比较,以揭示它们之间的相似性和差异性的过程。
序列比对的原理基于序列之间的共同性和异质性。
序列比对的方法主要有以下几种:
1. 精确匹配法(Exact Match Method):将参考序列和查询序列进行比对,寻找完全匹配的部分。
这种方法适用于已知的高度相似的序列。
2. 最长公共子序列法(Longest Common Subsequence Method):寻找两个序列之间的最长公共子序列,即在两个序列中能够找到的最长的连续匹配子序列。
这种方法适用于具有较高的相似性但存在插入或缺失的序列。
3. 比对矩阵法(Alignment Matrix Method):将两个序列转化为一个二维矩阵,通过动态规划的方法计算每个位置上的得分,以确定最优的比对方式。
常用的比对矩阵算法包括Needleman-Wunsch算法和Smith-Waterman算法。
4. 模式匹配法(Pattern Matching Method):通过查找和比对已知的序列模式或特征,来寻找查询序列中的相似性。
常用的模式匹配方法包括BLAST和FASTA算法。
5. 多序列比对法(Multiple Sequence Alignment Method):将多个序列进
行比对,寻找它们之间的共同特征和差异。
常用的多序列比对算法包括ClustalW 和MAFFT算法。
这些方法可以根据序列的性质和比对的需求来选择,常用于基因组学、蛋白质结构预测、物种分类和演化关系研究等领域。
事件的排列与组合概率

事件的排列与组合概率在概率论中,排列与组合是两个重要的概念。
它们用于描述事件发生的可能性,并有助于我们计算和预测事件发生的概率。
本文将介绍排列与组合的概念及其在概率计算中的应用。
一、排列的概念及计算方法排列是指将若干个元素按一定顺序排列的方式。
假设有n个元素,要从中选取m个元素进行排列,其中m≤n。
那么排列的总数可以通过下式计算得到:P(n,m) = n! / (n - m)!其中,n!表示n的阶乘,即从1到n之间所有正整数的乘积。
排列的计算公式中用到了阶乘的概念,表示从n个元素中选取m个元素进行排列的可能性。
例如,有5个人要从中选出3个人进行排列,那么排列的总数可以计算如下:P(5,3) = 5! / (5-3)! = 5! / 2! = 60因此,从5个人中选取3个人进行排列的总数为60种可能性。
二、组合的概念及计算方法组合是指从若干个元素中选取特定数量的元素,而不考虑元素的顺序。
与排列不同的是,组合只关注元素的选择,而不关注元素的排列顺序。
假设有n个元素,要从中选取m个元素进行组合,其中m≤n。
那么组合的总数可以通过下式计算得到:C(n,m) = n! / (m! * (n - m)!)组合的计算公式中同样用到了阶乘的概念,但是相比排列,组合考虑了元素的选择而不考虑元素的排列顺序。
例如,有5个人要从中选出3个人进行组合,那么组合的总数可以计算如下:C(5,3) = 5! / (3! * (5-3)!) = 5! / (3! * 2!) = 10因此,从5个人中选取3个人进行组合的总数为10种可能性。
三、排列与组合的应用排列与组合在概率计算中有着广泛的应用。
它们能够帮助我们计算事件发生的概率,并在实际问题中提供便捷的解决方法。
例如,假设有一副扑克牌,共有52张牌。
我们希望计算从中抽取5张牌,其中包含3张红心牌和2张黑桃牌的概率。
首先,我们可以通过组合的概念计算出满足条件的牌的组合数:C(13,3) * C(13,2) = 286 * 78 = 22308其中,C(13,3)表示从13张红心牌中选取3张牌的组合数,C(13,2)表示从13张黑桃牌中选取2张牌的组合数。
一种基于谓词覆盖技术的启发式事件匹配算法

布 式 交互 系统 。 而 高 效 率 的发 布 事 件 匹 配 算 法 是 实 现 基 于 内容 路 由的 大 规 模 P b S b系统 所 要 解 决 的 关 键 问题 。针 对 基 于 内容 的 u/ u
发布/ 订购模型主要 性能的事件 匹配 问题做 了重点研 究 , 出了谓词关系( - 提 S 叉树 ) 的概念 。并在此基 础上 , 通过将 谓词覆盖技 术同
t e e e tmac ig i u fs b tn i r p ris o e c n e tb s d p b ih s b c b d l a d p o o e o c p al d t e P e iae h v n th n s e o u sa t p o e e f h o tn — a e u l / u s r e mo e , n r p s d a c n e tc e h rd c t s l a t t s i l
trd e t t a y c r n u , n —o ma y a d lo e y c u l d c mmu ia in p o e t s Ef ce tmac i g ag r h fre e t u l hn s e u o i s n h o o s ma y t — n n o s l — o p e o s nc t r p ri . f in th n lo i m o v n b i i g i o e i t p s
t e k y is e t e r s le n r a iig t e l唱e s ae c n e tb s d r ui g p b ih s b c b y tm. n t e p p r we e h t a l t d e h e su o b e o v d i e l n h a — c l o t n — a e o t u l / u s r e s s s n s i e I h a e , mp ai l su id c y
事件的组合与排列计算多个事件同时发生的概率

事件的组合与排列计算多个事件同时发生的概率在概率论中,我们经常需要计算多个事件同时发生的概率。
这涉及到事件的组合与排列计算。
事件的组合与排列计算是概率论的基础之一,它帮助我们计算多个事件同时发生的可能性。
本文将介绍事件的组合与排列的概念,并探讨如何计算多个事件同时发生的概率。
一、事件的组合计算事件的组合是指从一组元素中选取若干个元素组成一个集合。
在事件的组合中,元素的排列顺序是无关紧要的。
假设我们有n个元素,要从中选取r个元素组成一个集合,可以用组合公式来计算:C(n, r) = n! / (r! * (n-r)!)其中,C代表组合,n代表元素的个数,r代表要选取的元素个数,n!代表n的阶乘。
举例说明:假设我们有5个球,要从中选取3个球,计算共有多少种选法?根据组合公式:C(5, 3) = 5! / (3! * (5-3)!)= 5! / (3! * 2!)= (5 * 4 * 3 * 2 * 1) / [(3 * 2 * 1) * (2 * 1)]= (5 * 4) / (2 * 1)= 10所以,从5个球中选取3个球共有10种选法。
二、事件的排列计算事件的排列是指从一组元素中选取若干个元素并进行排列,元素的排列顺序是有关紧要的。
假设我们有n个元素,要从中选取r个元素进行排列,可以用排列公式来计算:P(n, r) = n! / (n-r)!其中,P代表排列,n代表元素的个数,r代表要选取的元素个数,n!代表n的阶乘。
举例说明:假设我们有5个球,要从中选取3个球进行排列,计算共有多少种排列方式?根据排列公式:P(5, 3) = 5! / (5-3)!= 5! / 2!&= (5 * 4 * 3 * 2 * 1) / (2 * 1)= 60所以,从5个球中选取3个球进行排列共有60种排列方式。
三、多个事件同时发生的概率计算当我们需要计算多个事件同时发生的概率时,可以将事件的组合与排列的概念结合起来。
排列组合配对问题算法

排列组合配对问题算法
排列组合配对问题是一类很常见的问题,通常用于解决某些需要进行配对或者安排的问题,比如班级内同学结对活动、音乐会的座位安排、体育比赛的对阵安排等。
这类问题需要寻找所有可能的组合或排列方式,以达到最优的配对或安排效果。
常见的解决排列组合配对问题的算法有:暴力搜索法、回溯法、递归法等。
暴力搜索法
暴力搜索法是一种最简单的算法,也是一种遍历所有可能情况的算法。
它通常会枚举所有可能的组合或排列方式,再从中找出符合条件的最优解。
相比较其他算法,暴力搜索法的时间复杂度较高,但是它的思路简单易懂,而且对于规模较小的问题,它的解决效果仍然很不错。
回溯法
回溯法是一种常见的搜索算法,主要用于解决组合问题。
它的基本思路是:从问题的第一个元素开始,枚举所有可能情况,并逐个尝试选择该元素或不选择该元素。
如果选择了该元素,则接着考虑第二个元素;如果不选择该元素,则回溯到上一个元素,重新选择该元素或不选择。
这样逐渐搜索下去,直到找到所有可能的组合或达到条件限制。
递归法
递归法通常用于解决排列问题,其基本思路是:将问题分解为较小的子问题,分别解决这些子问题,再将它们组合成原问题的解。
具体实现时,可以采用递归函数的形式对子问题进行求解,然后在递归函数的返回过程中将所有可能的方案组合起来。
递归法的附加优势在于能够将问题简化,从而更容易理解和实现。
最后,需要注意的是,无论使用哪种算法,都需要对问题进行充分的分析和设计,以确保算法的正确性和效率。
在实际应用中,需要综合考虑问题的规模、时间复杂度、可扩展性等因素,选择适合与问题的算法,以达到最优的解决效果。
因果推断与匹配方法

因果推断与匹配方法
因果推断是一种研究方法,可以通过观察现象之间的因果关系来对因果关系进行推断。
它旨在确定某种现象(因变量)是由特定的因素(自变量)引起的,而不仅仅是相关或偶然的关系。
因果推断有许多不同的方法,其中一种重要的方法是匹配方法。
匹配方法使用一个控制组和一个实验组,来比较不同处理条件下的结果。
两组之间的差异可以用来推断因果关系。
匹配方法的基本思想是寻找类似的个体或单位,并将它们分配到实验组和控制组,使它们在某些重要特征上保持相似。
这样做的目的是减少其他因素对实验结果的影响,从而更准确地评估处理条件对结果的影响。
匹配方法可以基于多个变量进行匹配,例如年龄、性别、教育程度等。
一种常见的匹配方法是倾向得分匹配方法,该方法通过建立一个倾向得分模型,估计每个个体属于实验组的概率,然后将具有类似倾向得分的个体匹配在一起。
匹配方法的优点是可以提高研究的内部效度,即提高因果推断的可信度。
然而,匹配方法并不能完全消除所有潜在的偏差,因此仍然需要谨慎解释因果推断的结论。
此外,匹配方法的实施可能会面临一些挑战,例如匹配准确性和样本大小的限制等。
总之,因果推断和匹配方法是研究社会科学中常用的方法,用于确定因果关系并减少其他因素的影响。
这些方法的应用可以提高研究的可信度,但需要谨慎解读其结论。
匹配追踪算法原理

匹配追踪算法原理咱先想象一下,你在一个超级大的玩具箱里找东西。
这个玩具箱里有各种各样的小零件、小玩具。
匹配追踪算法就有点像你在这个大玩具箱里找特定的东西呢。
匹配追踪算法主要是处理信号的。
你可以把一个信号想象成是由好多好多不同的小信号组合起来的。
就好比一首超级复杂的音乐,它是由各种音符、节奏组合而成的。
那在算法的世界里,我们要做的就是把这个复杂的信号拆分开来。
比如说有一个信号,它看起来乱乱的,就像你画画的时候,颜料乱涂一气。
但是呢,这个信号其实是有规律的,是由一些更简单的信号按照某种方式叠加起来的。
匹配追踪算法就像是一个超级聪明的小侦探,它要找出那些用来叠加的简单信号。
它怎么找呢?它有一个小窍门哦。
它会在一个预先准备好的信号库里面找。
这个信号库就像是一个装满各种小零件的盒子。
它每次都会从这个盒子里挑出一个和要处理的信号最相似的小信号。
这个过程就像是你从玩具箱里挑出最像你心中所想的那个小玩具一样。
找到这个最相似的小信号之后呢,它就会把这个小信号从原来的大信号里面减掉。
就好比你从一堆颜料里把一种颜色先挑出来,然后把剩下的颜料重新看成一个新的组合。
这时候,剩下的信号就变得简单一点了。
然后呢,算法会继续在信号库里面找下一个最相似的小信号,再把这个新找到的小信号从剩下的信号里减掉。
就这样一次又一次地重复这个过程。
这个过程就像是剥洋葱一样,一层一层地把信号剥开,每次都找到最能匹配的那部分,然后把它拿掉,让剩下的信号越来越简单。
你可能会想,那这个算法什么时候停止呢?一般来说,当剩下的信号已经小到一定程度,或者达到了我们设定的某个标准的时候,它就停止啦。
而且呀,这个算法还有一个很厉害的地方。
它找出来的那些小信号,其实是按照一定的顺序排列的。
这个顺序就反映了这些小信号对原来那个大信号的重要性呢。
就好像在一个合唱团里,有的歌手的声音很突出,对整个合唱的影响很大,有的歌手的声音虽然也有贡献,但是相对小一点。
匹配追踪算法在很多地方都特别有用哦。
基于信息科学的智能匹配算法研究

基于信息科学的智能匹配算法研究随着信息时代的到来,人们对于信息的获取和处理变得越来越依赖于科学技术。
信息科学的飞速发展为我们提供了丰富的资源和便利的方式。
在众多应用领域中,智能匹配算法的研究和应用成为了一种重要的需求和挑战。
一、智能匹配算法的背景智能匹配算法是一种基于信息科学的技术,旨在实现更加精准和高效的匹配过程。
从信息处理的角度来看,匹配是一种将输入与输出进行关联和连接的过程。
而智能匹配算法则是通过利用信息科学的方法,以提供更好的匹配结果和用户体验。
二、智能匹配算法的特点智能匹配算法具有以下几个特点:1. 自适应性:智能匹配算法能够根据不同的环境和需求进行自适应地调整和优化。
它能够根据不同的输入条件,动态地调整算法的参数和模型,以提供更好的匹配结果。
2. 多样性:智能匹配算法能够根据需求和结果的多样性进行调整和优化。
它能够根据用户的偏好和历史数据,匹配不同类型的信息和资源,以满足用户的个性化需求。
3. 高效性:智能匹配算法能够在较短的时间内完成匹配过程,并提供高效和准确的结果。
它能够利用信息科学的方法,通过并行计算和优化算法,提升匹配过程的效率和性能。
三、智能匹配算法的应用领域智能匹配算法在多个领域具有广泛的应用,例如搜索引擎、推荐系统、人工智能、数据挖掘等。
以下是几个典型的应用领域:1. 搜索引擎:智能匹配算法在搜索引擎中起着核心的作用。
它能够根据用户的查询词和输入条件,将相关的信息和资源进行匹配和排序,以提供满足用户需求的搜索结果。
2. 推荐系统:智能匹配算法在推荐系统中也起着重要的作用。
它能够根据用户的兴趣和偏好,将相关的产品和服务进行匹配和推荐,以提供个性化的推荐结果。
3. 人工智能:智能匹配算法在人工智能领域的应用非常广泛。
它能够帮助机器学习和深度学习模型进行输入和输出的匹配,以提供更好的智能化功能和性能。
四、智能匹配算法的研究方向智能匹配算法的研究方向主要包括以下几个方面:1. 相似度计算:智能匹配算法需要通过计算不同输入和输出之间的相似度来实现匹配过程。
sequential 函数

sequential 函数
"sequential" 函数通常用于描述一系列按顺序执行的操作或事件。
在计算机科学中,这个术语经常用于描述一种特定类型的数据结构或算法。
在编程中,"sequential" 函数可以指代一种顺序执行的程序结构,即按照代码的书写顺序依次执行每一条语句或操作。
这种顺序执行的方式是编程中最基本的控制流之一,它确保了代码的执行顺序符合程序员的意图。
此外,在数学和统计学中,"sequential" 函数可能指代一种按顺序执行的数学运算或数据处理过程。
这种顺序处理数据的方式可以确保数据的处理顺序符合数学模型或统计分析的要求,从而得到准确的结果。
总的来说,"sequential" 函数在不同领域可能有不同的含义,但通常都与按顺序执行操作或事件相关。
在计算机科学、编程、数学和统计学等领域中,"sequential" 函数都有着重要的作用,并且对于确保操作的顺序性和准确性都具有重要意义。
事件的排列与计算

事件的排列与计算事件的排列和计算在概率论和组合数学中起着重要作用。
它涉及到用不同的方式安排或排列一组元素或对象的可能性。
该领域的研究包括排列、组合和多项式等数学概念。
本文将介绍事件排列和计算的基本概念,并探讨其在实际问题中的应用。
一. 排列排列是指用已知元素的有限集合来创建一个有序的序列。
给定n个对象,从中选取r个对象进行排列,满足条件r≤n,那么可以使用排列公式计算排列的数量。
排列公式表示为P(n,r) = n! / (n-r)!,其中n!表示n的阶乘。
例如,在一副扑克牌中,从中抽取5张牌的不同排列数可以通过P(52,5)来计算。
该计算结果为52! / (52-5)!,得到的数值可以用于计算不同排列的可能性。
除了计算可能的排列数量,排列还可以应用于实际问题。
比如,在一个比赛中,有8个参赛选手A、B、C、D、E、F、G和H,要确定前三名的排名。
那么可以使用排列计算排名的不同可能性。
二. 组合组合是指从给定集合中选择r个元素,而不考虑元素之间的顺序。
与排列不同,组合不关心元素的顺序,只关注元素的选择。
组合的数量可以通过组合公式C(n,r) = n! / (r!(n-r)!)来计算。
例如,在一组6个数字(1、2、3、4、5、6)中,选择3个数字的不同组合数可以通过C(6,3)计算。
该计算结果为6! / (3!(6-3)!),得到不同组合的数量。
组合也可以应用于实际问题。
例如,在一家公司中,从10名员工中选出3个员工组成一个工作小组。
通过计算不同的组合,可以确定可能的工作小组组合。
三. 多项式多项式是排列和组合的扩展,它考虑到元素可重复出现的情况。
在一组n个元素中,从中选取r个元素进行排列或组合,并允许元素重复出现的情况,可以使用多项式计算。
多项式的计算可以使用多重集合中的球与盒子模型来理解。
球代表元素,盒子代表位置。
给定n个球和r个盒子,每个盒子可以为空或者包含一个或多个球,可以通过多项式公式计算不同的可能性。
时间事件数据序列分析新理论和方法.doc
时间事件数据序列分析新理论和方法根据密码场理论关于事件间相互作用与事件几率本质上存在等价关系的启示,经过长期研究,笔者在自然数时间序列分析上建立了一种独特的分析方法——平行世界分析法,并意外地发现自然界隐藏在时间事件背后的普适规律,即我们这个世界是个由四维空间和七维空间构造的平行动态交叉空间。
交叉点便是我们常说的时间世界,而普遍认为的空间概念实际上是交叉同时其余维度空间的叠加,这个叠加态,确切的讲,是三维属性空间下的六维隐匿整体性空间状态,即我们通常感觉到的三维世界实际上是这个属性空间。
这个普适规律的发现同时也回证了密码场理论的正确性和密码场分形空间和混沌理论研究方向的正确性。
这个理论和方法即将显现巨大的应用价值,特别在预测领域上。
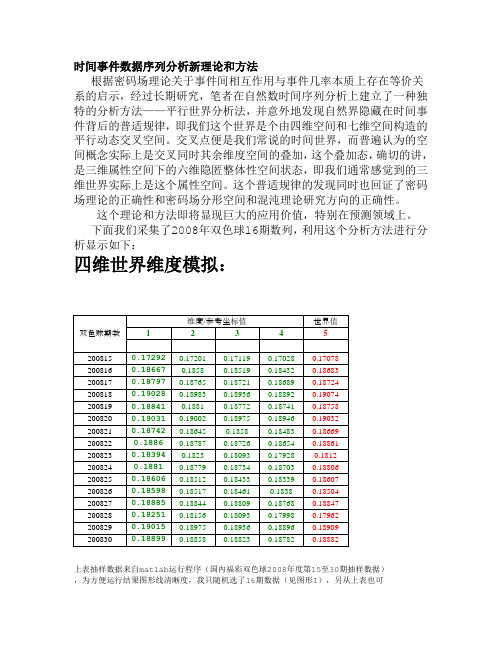
下面我们采集了2008年双色球16期数列,利用这个分析方法进行分析显示如下:四维世界维度模拟:上表抽样数据来自matlab运行程序(国内福彩双色球2008年度第15至30期抽样数据),为方便运行结果图形线清晰度,我只随机选了16期数据(见图形1),另从上表也可以看到,红色数据为第五世界值,为各期数据分析反馈的真实坐标值,皆游走于前四维参考坐标值之间,这四个维度参考值也是程序运行提前自动计算出来的,误差在+0.5% 的出现几率达到99%,几乎可以模拟真实世界维度。
利用matlab运行上述数据得到模拟图形:tt=[0.17292 0.17201 0.17119 0.17028 0.170780.18667 0.18580 0.18519 0.18432 0.186830.18797 0.18765 0.18721 0.18689 0.187240.19028 0.18983 0.18936 0.18892 0.190740.18841 0.18810 0.18772 0.18741 0.187580.19031 0.19002 0.18975 0.18946 0.190320.18742 0.18645 0.18580 0.18483 0.186690.18860 0.18787 0.18726 0.18654 0.188610.18394 0.18230 0.18093 0.17928 0.181200.18810 0.18779 0.18734 0.18703 0.188060.18606 0.18512 0.18433 0.18339 0.186070.18598 0.18517 0.18461 0.18380 0.185040.18885 0.18844 0.18809 0.18768 0.188470.18251 0.18156 0.18093 0.17998 0.179620.19015 0.18975 0.18936 0.18896 0.189090.18899 0.18858 0.18823 0.18782 0.18882];plot(tt)matlab程序运行结果如图:图1七维世界维度模拟:上表抽样数据来自matlab运行程序(国内福彩双色球2008年度第15至30期抽样数据),为方便运行结果图形线清晰度和四维模拟对应,也选了16期数据(见图形2),另从上表也可以看到,红色数据为第八世界值,为各期数据分析反馈的真实坐标值,皆游走于前七维参考坐标值之间,这七个维度参考值也是程序运行提前自动计算出来的,误差在+0.5%的出现几率达到99%,几乎可以模拟真实世界维度。
PMTree:一种高效的事件流模式匹配方法

PMTree:一种高效的事件流模式匹配方法程苏珺;王永剑;孟由;程振东;栾钟治;钱德沛【期刊名称】《计算机研究与发展》【年(卷),期】2012(49)11【摘要】复杂事件处理技术从多个持续事件流中分析并提取满足特定模式的事件序列.高吞吐率场景下,如何快速准确地识别事件序列是复杂事件处理技术中一个非常重要的问题.现在事件流的模式匹配方法——NFA、Petri网、有向图等——存在语义描述能力不足、部分算子实现代价高等缺陷.针对这一现状,设计并实现了一种基于树的模式匹配方法——PMTree.PMTree定义了事件模型及相应事件算子,将事件序列映射为树节点,同时将时间窗口约束及谓词约束等放置在相应节点,这些树节点连接成一棵PMTree来支持实时的事件筛选与过滤.进一步研究了PMTree 构建过程中的优化策略,并提出了开销模型以及优化构建算法,以尽可能减少模式匹配开销.实验结果表明,相同测试条件下基于PMTree实现的复杂事件处理引擎Cesar吞吐率是基于NFA实现的开源引擎Esper的3~6倍,并且在不同事件量或事件序列复杂度下性能表现稳定.%Complex event processing technique focuses on analyzing and extracting the event sequence of the specific pattern from the continuous event streams. Under the high-throughput situations, how to recognize the event sequence quickly and accurately has become an important problem. The state-of-the-art pattern matching methods, I. E. NFA, Petri and DAG, have shortcomings in the expressive ability and high cost to support some requirements. To deal with this situation, we propose a tree-based pattern matching method PMTree.PMTree defines event model and corresponding event relation operator, maps event pattern to the specific nodes in PMTree, applies time/predicate constraints on these nodes, and at last joins them to build a PMTree. We study the optimization strategies in the tree construction which can reduce the pattern matching cost and search the optimal combination of tree nodes, providing a cost model and an optimization algorithm. Experiments show that PMTree is more efficient, compared with Esper, an open source complex event processing engine; in the same situation the processing speed can be 3—6 times faster than Esper, and its performance is stable under different situations, e. G. The number of events, the type of event sequence or the complexity of event sequence, etc.【总页数】13页(P2481-2493)【作者】程苏珺;王永剑;孟由;程振东;栾钟治;钱德沛【作者单位】北京航空航天大学计算机学院软件开发环境国家重点实验室北京100191;北京航空航天大学计算机学院中德联合软件研究所北京 100191;北京航空航天大学北京市网络技术重点实验室北京 100191【正文语种】中文【中图分类】TP391【相关文献】1.一种高效的连续不确定XML小枝模式匹配算法 [J], 张晓琳;吕庆;刘立新;郑春红2.一种高效的模式匹配算法 [J], 曹煦晖3.一种多模式匹配高效算法的设计与实现 [J], 李辉;赵辉;李安贵4.一种改进的高效多模式匹配算法 [J], 屈正庚;赵杰5.一种面向PDF文本内容审查的高效多模式匹配算法 [J], 刘邦国; 陈庆春; 类先富因版权原因,仅展示原文概要,查看原文内容请购买。
python sequencematch原理

序列匹配算法(sequencematch)是 Python 内置的一个用于字符串比较的算法,它可以快速地找到两个字符串之间的相似度并返回一个匹配对象。
该算法最初由Ratcliff 和 Obershelp 于 1983 年提出,后来被应用于各种文本处理任务,包括拼写检查、重复检测和文本相似性比较等。
序列匹配算法的核心思想是将两个字符串转换为一个矩阵,其中每个元素表示两个字符串中相应字符的相似度。
相似度通常使用编辑距离来衡量,编辑距离是指将一个字符串转换为另一个字符串所需的最少编辑操作数,编辑操作包括插入、删除和替换。
在计算相似度矩阵之后,序列匹配算法会使用动态规划算法来找到两个字符串之间的最优匹配路径。
最优匹配路径是指将一个字符串转换为另一个字符串所需的最少编辑操作序列。
一旦找到最优匹配路径,序列匹配算法就会返回一个匹配对象。
匹配对象包含了两个字符串之间的相似度、最优匹配路径以及两个字符串之间差异的详细列表。
序列匹配算法的优点是速度快、准确度高,并且可以处理任意长度的字符串。
其缺点是算法的复杂度较高,对于非常长的字符串,算法的运行时间可能会比较长。
序列匹配算法的应用非常广泛,它可以用于以下任务:•拼写检查:序列匹配算法可以用来检查一个单词的拼写是否正确。
它通过将单词与词典中的单词进行比较,并返回最相似的单词。
•重复检测:序列匹配算法可以用来检测文本中的重复内容。
它通过将文本中的每个句子或段落与其他句子或段落进行比较,并返回最相似的句子或段落。
•文本相似性比较:序列匹配算法可以用来比较两个文本的相似性。
它通过将两个文本转换为矩阵,并计算矩阵中元素的平均值来计算相似性。
序列匹配算法是一种非常有用的算法,它可以用于各种文本处理任务。
其速度快、准确度高,并且可以处理任意长度的字符串。
事件树分析(ETA)概述.docx

事件树分析(ETA)概述事件树分析(缩写为ETA)是从一个初始事件开始,按顺序分析事件向前发展中各个环节成功与失败的过程及其结果,这种分析方法称为事件树分析法。
这是一种归纳分析法。
运用这种分析法可以了解系统可能发生的所有事故的起因、发展和结果。
事件树分析最初是用于可靠性分析。
每一个系统都是由若干个元件组成的,每一个元件对规定的功能都存在具有和不具有两种可能。
元件具有某种规定功能,表明其正常(成功);不具有某种规定功能,表明其失效(失败)。
按照系统的构成顺序,从初始元件开始,由左向右分析各元件成功与失败的两种可能,直到最后一个元件为止。
分析的过程用图形表示出来,就得到似水平的树形图。
例如,由一个泵和两个阀门串联组成的物料输送系统,其结构和物料流动的方向如图1所示。
在这个系统中泵和二个阀门都有正常和失效(成功和失败)两种可能。
当泵得到启动指令后,可能启动成功并正常运转,也可能启动失败,因此启动结果有两种,或成功或失败,也就是启动状态发生分支,画图时将成功状态放在上分支,失败状态放在下分支。
如果泵启动失败,系统将失效,不能输送物料,因此就不需要再分析下去。
如果泵启动正常,物料经过阀门1时仍有成功和失败二种可能,阀门1失效,系统也失效,不再需要分析阀门2的状态。
阀门1正常,再分析阀门2的状态,如阀门2正常,则系统运转正常;否则如阀门2失效,系统也将失效。
分析的过程用图表示则得到这个物料输送系统的事件树,如图2所示。
图1 物料输送系统图图2 系统的事件树这个事件树图清楚的表明,只有在泵、阀门1、2都处于正常状态,系统才能正常运行,其他三种情况系统均处于失效状态。
如果知道了泵、阀门1、2的失效概率,还可以计算出系统成功与失败的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 . 1 相似序 列 匹配
与标 准数 据库 查询 中那 些查 找 给定 的完 全 匹配
的查 询数 据不 同 的是 ,相 似性 序列 匹配 搜索 可 在给 定 的查 询 序列 中找 出略有 不 同的数 据序 列 。
1 . 2 相似序 列 匹配 的类型
t h a t r e t ie r v e s a n d ma t c h i n g t h e o c c u r r e n c e s p a t t e r n s f r o m c h a o t i c a n d n o n l i n e a r e v e n t s e q u e n c e s . I n t h i s
中图 分 类 号 : T P 3 0 1 . 6 文献 标 识 码 : A
A W h o l e S e q u e n c e Ma t c h i n g Al g o r i t h m f o r Ev e n t S e q u e n c e s
W ANG Ho n g -x i a , W ANG Z r a c t :On t h e b a s i s o f a n a l y z i n g t h e n e wl y t i me s e q u e n c e r e s e a r c h a c h i e v e me n t n o wa d a y s , t h i s
( 1 . S h a n x i C o n s e r v a n c y T e c h n i c a l C o l l e g e T a i y u a n,T  ̄ y u a n 0 3 0 0 2 7 , C h i n a ; 2 . S h a n x i C l i m a t e C e n t e r , T a i y u a n 0 3 0 0 0 6 , C h i n a )
p a p e r ,s e v e r a l d e in f i t i o n s o n e v e nt r e l a t i v i t y a r e p ut f o r wa r d,3 - t up l e i s e mp l o y e d t o p r e s e n t t h e e v e n t , a n d t h e c h a i n t a bl e i s d e v e l o p e d t o d e s c r i b e t h e e v e n t s e q u e n c e, The wh o l e s i mi l a r i t y s e q u e n c e ma t c h i n g mo de l f o r t h e c o mp a c t s t o r a g e o f t he e v e n t s e q ue n c e i s p r e s e n t e d ,a nd t h e n i t i s a n a l y s i s . Ke y wo r d s:t i me s e q u e n c e, 3 - t up l e e v e n t s e q ue nc e, s i mi l a it r y ma t c h i n g, c ha i n t a bl e, a l g o it r h m
解 。首先给 出事 件相关性定义 , 采用 3元组表示事件序 列中的不 同事 件类型 , 对事件序列 进行 , 并映射为链 表中结
点, 通 过链 表存储事件序列整体 。同时提 出基 于事件序列压缩存储 的全序相似性 匹配模式及算法 , 并对其进行分析 。
关键词 : 时间序列 , 3 元组事件序列 , 相似性匹配 , 链表 , 算法
Vo 1 . 3 8. No .3
火 力 与 指 挥 控 制
F i r e C o n t r o l & Co mma n d C o n t r o l
第 3 8卷
第 3期
Ma r , 2 0 1 3
2 0 1 3年 3月
文章编号 : 1 0 0 2 — 0 6 4 0 ( 2 0 1 3) 0 3 - 0 1 7 5 - 0 4
引 言
时 间序列 数据 库包 含通 过 时 间反复 测量 而 获得 的值 或事 件序 列 [ ] 。 相 似序 列 匹配是 从序列 数 据库 中查 找类 似于查 询序 列 的一种操 作 [ 。 由于大 多现
涝、 地 震 等等 ) 、 医疗 方 面等 。 时间序 列 的重点 和挑
p a p e r a d dr e s s e s t h e p r o b l e m o f t h e wh o l e e v e n t s e q ue nc e s ma t c h i ng, a n d a t y pe o f s e q u e n c e ma t c h i n g
事件序列全序 匹配算法研究
王 红 霞 , 王 志伟 z
( 1 _ 山西水利职业技术学院, 太原 0 3 0 0 2 7 ; 2 . 山西省气候中心 , 太原 0 3 0 0 0 6 )
摘
要: 通过 分析 时间序列研究成果 , 提出一种全序列事件匹配 , 进行混沌 和非线性 的事件序列模式匹配问题求
