2016年春高一6月考数学试卷
山东省莱芜市2015-2016学年高一6月月考数学试题_word版有答案AwwHql

保密★启用前莱芜十七中高一月考 数学试卷 2016.6第I 卷(共60分)一、选择题(本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知等差数列}{n a 满足1282=+a a ,则=5aA.3B.4C.5D.62. 已知=<<=+ϕπϕϕπtan 021)2sin(,则且A .3B . . D .33-3.在下列向量组中,可以把向量)7,3(-=表示出来的是A .)2,0(),1,0(21-==e e B. )10,2(),5,1(21--==e e C. )1,2(),3,5(21-=-=e e D. )8,7(),8,7(21--==e e 4. 等差数列{}n a 的前n 项和n S ,若35,773==S a ,则=8a A .3-B . 4-C .5-D . 6-5.如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为75,30,此时气球的高是m 30,则河流的宽度BC 等于A .m )13(30-B .m )13(60-C .m )13(90-D .m )13(120-6.在平行四边形ABCD 中, AD = 2,060=∠BAD ,E 为CD 的中点, 若4=∙, 则AB的长为A. 1B.2C.2D7.已知数列{}n a 满足32,0321-==++a a a n n ,则{}n a 的前5项的和等于A. 27121B. 27122C. 81121D. 811228.在△ABC 中,22==BC AB ,6π=∠A ,则△ABC 的面积为A .21B .23C .1D .39.设常数0>a .若8922+≥+a xa x 对一切正实数x 成立,则a 的取值范围为 A .[]42, B .[]32, C. []42,- D. []32,- 10.不等式1132>-x x的解为A .)21,31(B .)1,21( C .)1,31( D .)21,31(-11.函数)sin()(ϕω+=x x f (其中2||πϕ<)的图象如图所示,为了得到x y ωsin =的图象,只需把)(x f y =的图象上所有点( )个单位长度.A.向右平移6π B.向右平移12πC.向左平移6π D.向左平移12π12. 已知各项为正的等比数列{}n a 中,4a 与14a 的等比中项为3,则 7112a a +的最小值为A .B .23C .24D .26第II 卷(非选择题 共90分)二、填空:(本大题共4小题,每小题5分,满分20分)13. 已知角)23,2(ππα∈,且512tan -=α,则=-)2cos(απ .14. 设向量)3,1(-=a ,)1,2(=b ,若()()a b a b λλ+⊥-且0>λ,则实数λ=________. 15. 若数列{}n a 的通项公式是)23()1(--=n a n n ,则12a a ++…91a += .16. 设()sin 2cos 2f x a x b x =+,其中,,0a b R ab ∈≠,若()()6f x f π≤对一切x R ∈恒成立,则①11()012f π=.②()f x 既不是奇函数也不是偶函数. ③7()10f π<()5f π.④存在经过点(a,b )的直线与函数()f x 的图象不相交.⑤0>b 时,()f x 的单调递增区间是)(6,3Z k k k ∈⎥⎦⎤⎢⎣⎡++-ππππ.以上结论正确的是 _____________________________(写出正确结论的编号).三、解答题:(本大题共6小题,满分70分.解答须写出文字说明,证明过程和演算步骤) 17. (本小题10分)已知,,是同一平面内的三个向量,其中)2,1(-=.(15=,且//,求的坐标;(225=,且)2()2(b a b a -⊥+,求+2.18. (本小题12分)已知)3lg(lg lg ++=+y x y x .(1)求xy 的最小值; (2)求y x +的最小值.19. (本小题12分)在等差数列{}n a 中,31=a ,其前n 项和为n S ,等比数列{}n b 的各项均为正数,21=b ,公比为q ,且1622=+S b ,224qb S =. (1)求n a 与n b ;(2)设数列{}n c 满足n n S c 1=,求{}n c 的前n 项和n T .20. (本小题12分)设0>a ,函数x x x a x x f 2sin )cos sin 2(cos )(+-=的最大值为2.(1)求函数)(x f 的单调递减区间;(2)设△ABC 三内角A ,B ,C 所对边分别为c b a ,,且c a c c b a b c a -=-+-+2222222,求)(x f 在⎥⎦⎤⎢⎣⎡2π,B 上的值域.21. (本小题12分)已知等差数列{}n a 中,52=a ,176=a ,若从数列{}n a 中依次取出第3项,第9项,第27项,...,第n 3项,按原来的顺序构成一个新的数列{}n b . (1)求数列{}n b 的通项公式;(2)设13+=n n b n c (*N n ∈),*(21N n c c c T nn ∈+++= ,证明:43<n T .22. (本小题12分)如图,在平面四边形ABCD 中,32,3,7,2,π=∠===⊥ADC EA EC DE AB DA ,2π=∠BEC . (1)求CED ∠sin 的值; (2)求BE 的长.参考答案1—5 DBCAB 6—10 ADBAC 11-12 AD 13. 答案:135-14. 答案:2 15. 答案:-136 16. 答案:①②⑤17. 解:(1)设()c =x,y ,由//c a 5=可得:⎩⎨⎧=-=⎩⎨⎧-==∴⎩⎨⎧=+-=2121,5222y x or y x y x xy ∴)2,1(-=c 或)2,1(-=c …………………………………………….5分(2)(2)(2),a b a b +⊥-(2)(2)0a b a b ∴+-= 即222320,a a b b +⋅-=222||32||0a a b b ∴+⋅-=∴ 5253204a b ⨯+⋅-⨯=, 所以52a b ⋅=- ……………………………………….8分∴ 2532==+a ……………………………………….10分18. 解:由lgx +lg y =lg(x +y +3),得⎩⎪⎨⎪⎧x>0,y>0,xy =x +y +3.(1)∵x>0,y>0,∴xy =x +y +3≥2xy +3.∴xy -2xy -3≥0.即(xy)2-2xy -3≥0.∴(xy +1)(xy -3)≥0.∴xy ≥3.∴xy≥9.当且仅当x =y =1时,等号成立.∴xy 的最小值为9. ……………………………………….6分(2)∵x>0,y>0,∴x +y +3=xy≤(x +y 2)2.∴(x +y)2-4(x +y)-12≥0.∴[(x +y)+2][(x +y)-6]≥0.∴x +y≥6.当且仅当x =y =1时取等号,∴x +y 的最小值为6 ……………………………………….12分 19. 解:(Ⅰ)设{}n a 的公差为d ,因为⎩⎨⎧==+22224,16qb S S b 所以164122=+q b b ,即3242=+q q …………………………………2分 ∴ 4=q 或8-=q (舍),,5,8,8222===a S b 2=d . ….…………………………………….4分故12+=n a n ,122-=n n b . … ………………………………………………..6分 (Ⅱ))2(+=n n S n , …………………………………………………..8分)211(21)2(11+-=+==n n n n S c n n . ………………………………………………………10分 42122143)211123(21)2111111......51314121311(21+-+-=+-+-=+-++--++-+-+-=n n n n n n n n T n ……………………………………12分20. 解:(1)x x a x x x a x x f 2cos 2sin sin )cos sin 2(cos )(2-=+-= ………………………………2分由21)(2max =+=a x f 得, 3=a ………………………3分因此)62sin(22cos 2sin 32cos 2sin )(π-=-=-=x x x x x a x f ……………………………4分令Z k k x k ∈+≤-≤+,2236222πππππ得Z k k x k ∈+≤≤+,653ππππ故函数)(x f 的单调递减区间)(65,3Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ ……………………………6分(2)由余弦定理知:c a cC b B c C ab B ac cb a bc a -===-+-+2cos cos cos 2cos 2222222 即C b B c B a cos cos cos 2=-, ………………8分又由正弦定理知:()A C B C B B C B A sin sin cos sin cos sin cos sin 2=+=+=即21cos =B ,所以3π=B ……………………….…10分当⎥⎦⎤⎢⎣⎡∈23ππ,x 时,⎥⎦⎤⎢⎣⎡∈-65262πππ,x ,()[]2,1∈x f故)(x f 在(]B ,0上的值域为[]2,1 …………………………….…………12分21. 解:(1)公差345172626=-=--=a a d , ………………………………2分所以13)2(2-=-+=n d n a a n , ……………………………………4分 1313313-=-⨯==+n nn n a b . ……………………………………6分(2)13+=n n b n c *∈⋅=N n n ,)31(n …………………………7分n 1n 21)31(n )31()1n (......)31(2)31(⨯+⨯-++⨯+=-n T …………………………8分1n n 32)31(n )31()1n (......)31(2)31(31+⨯+⨯-++⨯+=n T ……9分 1n 1n n 32)31(n )31(2121)31(n )31(......)31()31(3132++⨯-⨯-=⨯-++++=n n T ………11分 n)31(432n 43⋅+-=n T ,故43<n T ………………………………………12分22. 解:设α=∠CED (1)在CDE ∆中,由余弦定理,得EDC DE CD DE CD EC ∠⋅⋅-+=cos 2222于是由题设知,032,24722=-+++=CD CD CD CD 即解得1=CD (3-=CD 舍去)在CDE ∆中,由正弦定理,得αCDEDC EC =∠sin ,1421sin 142172332sin =∠==⋅=CED EC CD ,即πα ……………………6分 (2)由题设知,20πα<<,于是由(1)知,而απ-=∠2AEB ,所以1421cos =∠AEB 在EAB Rt ∆中,.212,14213cos =∴===∠BE BE BE EA AEB . ………………………………12分。
河北省唐山市2015-2016学年高一6月月考数学试题

开滦二中2015~2016学年第二学期高一年级6月考试数 学 试 卷说明:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第(1)页至第(2)页,第Ⅱ卷第(3)页至第(6)页 2、本试卷共150分,考试时间120分钟第Ⅰ卷(选择题,共60分)注意事项:1、答第Ⅰ卷前,考生务必将自己的准考证号、科目填涂在答题卡上2、每小题选出答案后,用2B 铅笔把答题卡上对应的题目标号涂黑。
答在试卷上无效3、考试结束后,监考人员将试卷答题卡和机读卡一并收回1.在⊿ABC 中,5:4:21sin :sin :sin =C B A ,则角A=( )A .030B .0150C .060D .0120 2.化简=++++-----110118116114112122222( )A .127B .117C .107D .1153.甲、乙两名同学在5次体育测试中的成绩统计如图的茎叶图 所示,若甲、乙两人的平均成绩分别是X 甲、X 乙,则下列结 论正确的是( )A .X 甲<X 乙;乙比甲成绩稳定B .X 甲>X 乙;甲比乙成绩稳定C .X 甲>X 乙;乙比甲成绩稳定D .X 甲<X 乙;甲比乙成绩稳定4.从装有2个红球和2个黒球的口袋内任取2个球,则互斥但不对立的两个事件是( ) A .至少有一个黒球与都是黒球 B .至少有一个黒球与都是红球 C .至少有一个黒球与至少有一个红球 D .都是红球与都是黒球5.若x< -3,则32++x x 的最大值为( )A.322+- B .322--C .322+D .322-6. 某工厂生产A 、B 、C 三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样方法抽出一个容量为n 的样本,样本中A 种型号产品有16件.那么此样本的容量n =( ) A.160 B.120 C.80 D.607.在A ,B 两个袋中都有6张分别写有数字0,1,2,3,4, 5 的卡片,现从每个袋中任取一张卡片,则两张卡片上数字之和 为7的概率为( )A .19 B .118C .16 D .138.给出右面的程序框图,那么输出的数是( )A .2450B .2550C .5050D .4900 9.用秦九韶算法计算多项式654323567983512)(x x x x x x x f ++++-+=在4-=x 时的值时,3V 的值为( ) A. -845 B. 220 C. -57 D. 3410.如图,在一个不规则多边形内随机撒 入200粒芝麻(芝麻落到任何位置可 能性相等),恰有27粒落入半径为1 的圆内,则该多边形的面积约为( ) A.4π B.5π C.6π D.7π11.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超 过乙的平均成绩的概率为 ( ) A .25 B .710C .45 D .91012.函数]2,1[,13)(2-∈--=x x x x f ,任取一点]2,1[0-∈x ,使1)(0≥x f 的概率是( )A.32 B. 95 C. 41 D. 94(3)求汽车时速的平均数18.(本题满分12分)城市公交车的数量若太多则容易造成资源的浪费,若太少又难以满足乘客需求。
黑龙江省牡丹江市2016-2017学年高一6月月考数学试题
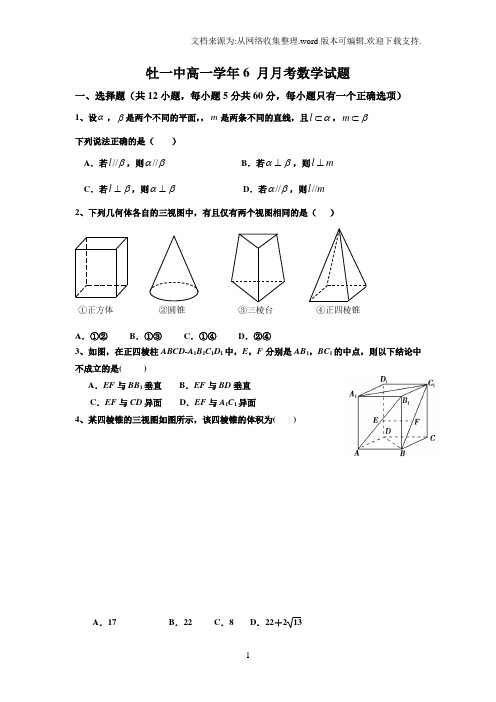
牡一中高一学年6 月月考数学试题一、选择题(共12小题,每小题5分共60分,每小题只有一个正确选项)1、设α,β是两个不同的平面,,m 是两条不同的直线,且l α⊂,m β⊂ 下列说法正确的是( )A .若//l β,则//αβB .若αβ⊥,则l m ⊥C .若l β⊥,则αβ⊥D .若//αβ,则//l m 2、下列几何体各自的三视图中,有且仅有两个视图相同的是( )A .①②B .①③C .①④D .②④3、如图,在正四棱柱ABCD-A 1B 1C 1D 1中,E ,F 分别是AB 1,BC 1的中点,则以下结论中不成立的是( )A .EF 与BB 1垂直 B .EF 与BD 垂直C .EF 与CD 异面 D .EF 与A 1C 1异面4、某四棱锥的三视图如图所示,该四棱锥的体积为( )A .17B .22C .8D .22+213①正方体 ②圆锥 ③三棱台 ④正四棱锥5、侧棱长为2的正三棱柱,若其底面周长为9,则该正三棱柱的表面积是( ) A .239 B .23916+ C .23918+ D .439 6、正方体ABCD -A 1B 1C 1D 1中,E F 分别是棱AB ,BB 1的中点,A 1E 与C 1F 所成的角是θ,则A .θ=600B .θ=450C .52cos =θ D .52sin =θ 7、βα,是两个不重合的平面,在下列条件中,可判断平面βα,平行的是 ( )A.n m ,是平面α内两条直线,且ββ//,//n mB.α内不共线的三点到β的距离相等C.βα,都垂直于平面D.n m ,是两条异面直线,βα⊂⊂n m ,,且αβ//,//n m 8、在三棱柱ABC -A 1B 1C 1中,所有棱长都相等,侧棱垂直于底面,点D 是侧面BB 1C 1C 的中心,则AD 与平面BB 1C 1C 所成角的大小是( ) A .30° B .45° C .60° D .90°9、已知二面角l αβ--为60,动点P 、Q 分别在平面βα,内,P 到βQ 到α的距离为P 、Q 两点之间距离的最小值为( ) A 、3 B 、 2 C 、、 410、如图,在长方体ABCD -A 1B 1C 1D 1中,O 是DB 的中点,直线A 1C 交平面C 1BD 于点M ,则下列结论错误的是( ) A 、C 1,M ,O 三点共线B 、C 1,M ,O ,C 四点共面 C 、C 1,O ,A 1,M 四点共面D 、D 1,D ,O ,M 四点共面。
内蒙古集宁一中2016-2017学年高一下学期6月份月考数学(理)试题

集宁一中2016-2017学年高一年级第二学期第三次月考理科数学试题本试卷满分为150分,考试时间为120分钟第 Ⅰ 卷(选择题 共60分)一、选择题(在下列四个选项中,只有一项是最符合题意的.每小题5分,共60分)1.已知A={第一象限角},B={锐角},C={小于90°的角},则A 、B 、C 关系是( ) A .B=A ∩CB .B ∪C=CC .A CD .A=B=C2.若|2|=a ,2||=b 且(b a -)⊥a ,则a 与b 的夹角是 ( ) A.6π B .4π C . 3πD.π125 3.若12(2,1)(0,5)P P -、,点P 在12P P 的延长线上,122PP PP =,则P 点坐标为( ) A.(2,11)- B.4(,3)3 C.2(,3)3D.(2,7)-4.在ABC ∆中,内角A,B,C 所对的边分别为a,b,c ,且a=15,b=10,A=︒60,则cos B =( )A.-223 B. 223C. -63D.635.已知向量b a 与反向,下列等式中一定成立的是 ( )A .||||||b a b a -=-B .||||b a b a -=+C .||||||b a b a -=+D .||||||b a b a +=+6.若四边形ABCD 满足 0=+CD AB ,()0AB AD AC -⋅=,则该四边形一定是( ) A .直角梯形B .菱形C .矩形D .正方形7.要得到函数2cos y x =的图象,只需将函数2sin(2)4y x π=+的图象上所有点的 ( )A .横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动4π个单位长度(sin1)(sin)f x f x->-B.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动8π个单位长度C.横坐标缩短到原来的12倍(纵坐标不变),再向左平行移动8π个单位长度D.横坐标缩短到原来的12倍(纵坐标不变),再向右平行移动4π个单位长度8.在AB C∆中,,EBAE=,2FBCF=连接CE、AF相交于点M,若B CB AB Mμλ+= ,则实数λ与μ的乘积为()A.51B.52C.251D.2529. 若函数()f x为R上的奇函数,且在定义域上单调递减,又[0,]xπ∈,则x的取值范围是( )A.2(,)33ππB.2[0,](,]33πππ C.5[0,)(,]66πππ D.5(,)66ππ10.函数y=-x sin x的部分图象是( ).11.在ABC∆中,已知tanAB AC A⋅=,当6Aπ=时,ABC∆的面积为()A.21B.31C.61D.4112.xx)21()2cos(=+π在]100,0[π∈x上的实数解的个数是()A.98B.100C.102D.200Ⅱ卷(非选择题,共 90分)二、填空题(每小题5分,共20分,把正确答案填在答题纸上对应横线处)13.=-+00tan50tan703tan50tan70。
辽宁省沈阳市高一数学6月月考试题

辽宁省沈阳市2016-2017学年高一数学6月月考试题一、选择题(本大题共12小题,每小题5分,共 60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知正方形ABCD 的边长为1,||AB BC AD DC +++为 ( ).1A B .3C D2、已知1cos 3θ=-,[0,]θπ∈,则θ可以表示为 ( )1.arccos 3A 1.arccos 3B π- 1.arccos 3C π+ 1.arccos()3D π+-3、如图,用向量1e ,2e 表示向量a b -为 ( )21.24A e e -- 21.42B e e -- 21.3C e e - 21.3D e e -+4、有下列命题:①两个相等向量,它们的起点相同,终点也相同;②若||||a b =,则a b =;③若||||AB DC =,则四边形ABCD 是平行四边形;④若m n =,n k =,则m k =;⑤若//a b ,//b c ,则//a c ;⑥有向线段就是向量,向量就是有向线段。
其中,假命题的个数是 ( ).2A .3B .4C .5D5、为了得到函数sin 3cos3y x x =+的图象,可以将函数y x =的图象 ( ).A 向右平移12π个单位 .B 向右平移4π个单位 .C 向左平移12π个单位 .D 向左平移4π个单位6、若函数()(1)cos f x x x =,[0,]2x π∈,则()f x 的最大值为 ( ).1A .2B .1C +.2D7、以原点O 及点(5,2)A 为顶点作等腰直角三角形OAB ,使90A =︒,则AB 的坐标为( ).(2,5)A - .(2,5)(2,5)B --或 .(2,5)C - .(7,3)(3,7)D -或8、若函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象如图所示,则将()y f x =的图象向右平移6π个单位后,得到的图象的解析式为 ( ).sin 2A y x = .cos 2B y x =.sin(2)3C y x π=+ .sin(2)6D y x π=-9、O 是ABC ∆所在的平面内的一点,且满足()(2)0OB OC OB OC OA -∙+-=则ABC ∆的形状一定为 ( ).A 正三角形 .B 直角三角形 .C 等腰三角形 .D 斜三角形10、已知sin()sin 35παα++=-2cos()3πα+等于 ( ) 4.5A - 3.5B - 4.5C 3.5D11、函数11y x =-的图象与函数2sin (24)y x x π=-≤≤的图象所有交点的横坐标之和为( ).2A .4B .6C .8D12、已知等边ABC ∆边长为4,O 为其内一点,且4730OA OB OC ++=,则AOB ∆的面积为 ( ).7A .7B .7C 1.2D 二、填空题(本大题共4小题,每小题5分,共 20分)13、已知向量(1,2)a =,(,4)b m =,且//(2)a a b +,那么实数m 的值为__________ 14、已知θ是第一象限角,若2sin 2cos 5θθ-=-,则sin cos θθ+=______________ 15、已知3cos 45πα⎛⎫-=⎪⎝⎭,12sin 413πβ⎛⎫+=- ⎪⎝⎭,3,44ππα⎛⎫∈ ⎪⎝⎭,5,4πβπ⎛⎫∈ ⎪⎝⎭,则()βα+sin = .16、已知ABC ∆中,I 是内心,13AB AC ==,10BC =,AI AB BC λμ=+,则实数λμ+的值为______________三、解答题(本大题共6小题,共 70分) 17、(本小题满分10分)(1)已知向量(2,5)a =-,(4,1)b =-,求a 在b 方向上正射影的数量 (2)已知(3,1)OA =,(1,2)OB =-,有向线段AB 绕点A 逆时针旋转2π到AC 的位置,若单位向量e 与AC 方向相同,求单位向量e 的坐标。
中学2015-2016学年高一下学期6月月考数学试题(解析版)

行知中学高一月考数学试卷一、填空题1.已知扇形的圆心角为2,面积为4,则扇形的周长为_________. 【答案】8 【解析】 【分析】 根据面积得到2r ,再计算周长得到答案.【详解】214,22S r r α==∴=,4l r α==,周长为28r l故答案为:8【点睛】本题考查了扇形周长的计算,意在考查学生的计算能力. 2.已知3sin()5πα+=,且α是第四象限角,则sin 2πα⎛⎫+= ⎪⎝⎭________. 【答案】45【解析】 【分析】化简得到3sin 5α=-,根据范围得到4cos 5α=,化简得到答案. 【详解】33sin()sin ,sin 55πααα+=-=∴=-,α是第四象限角,故4cos 5α=4sin cos 25παα⎛⎫+== ⎪⎝⎭故答案为:45【点睛】本题考查了诱导公式化简,同角三角函数关系,意在考查学生的计算能力. 3.已知等差数列{}n a 公差为2,若134a a a ,,成等比数列,则2a =________. 【答案】6- 【解析】 【分析】利用等差数列{a n }的公差为2,a 1,a 3,a 4成等比数列,求出a 1,即可求出a 2. 【详解】∵等差数列{a n }的公差为2,a 1,a 3,a 4成等比数列,∴(a 1+4)2=a 1(a 1+6), ∴a 1=-8, ∴a 2=-6. 故答案为-6..【点睛】本题考查等比数列的性质,考查等差数列的通项,考查学生的计算能力,属基础题.. 4.若3sin 5θ=,且sin 20θ<,则tan 2θ=_________. 【答案】3 【解析】 【分析】 化简得到3sin 5θ=,4cos 5θ=-,计算2θ一三象限,根据二倍角公式计算得到答案.【详解】sin 2sin cos 0θθθ2=<,故cos 0θ<,3sin 5θ=,故4cos 5θ=-故22,2k k k Z ππθππ+<<+∈,,422k k k Z πθπππ+<<+∈,2θ在一三象限, θtan222tan32tan 41tan 2θθθ==--,解得tan 32θ=,或1tan 23θ=-(舍去) 故答案为:3【点睛】本题考查了同角三角函数关系,二倍角公式,没有排除多余解是容易犯的错误. 5.设 a b c 、、分别是ABC 中角 A B C 、、所对的边,若2sin a c A =,则角C =________. 【答案】6π或56π 【解析】 【分析】利用正弦定理得到sin 2sin sin A C A =⋅,化简得到答案.【详解】2sin ,sin 2sin sin a c A A C A =∴=⋅,因为sin 0A ≠,故1sin 2C =,故6C π∠=或56π故答案为:6π或56π【点睛】本题考查了正弦定理,意在考查学生的计算能力.6.数列{}n a 的通项sin 2n n a n π=⋅,前n 项和为n S ,则13S =____________. 【答案】7 【解析】 【分析】根据数列的通项公式,求得数列{}n a 的周期为4,利用规律计算,即可求解.【详解】由题意,数列{}n a 的通项sin 2n n a n π=⋅, 可得123431sin 1,2sin 0,3sin3,4sin 2022a a a a ππππ=⋅==⋅==⋅=-=⋅=, 555sin 5,2a π=⋅=,得到数列{}n a 是以4项为周期的形式,所以13123413S a a a a a =+++++(1030)(5070)(90110)13=+-+++-+++-++=23137-⨯+=. 故答案为7.【点睛】本题主要考查了数列的求和问题,其中解答中根据数列的通项公式求得数列的周期,以及各项的变化规律是解答的关键,属于基础题,着重考查了.7.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则52S S =________.【答案】-11 【解析】通过8a 2+a 5=0,设公比为q ,将该式转化为8a 2+a 2q 3=0,解得q =-2,所以52S S =5211q q --=333-=-11.8.若等比数列满足19nn n a a +⋅=,则公比.【答案】3 【解析】121211990,9,9,3,3()9n nn n n n n n n a a a a q q q a a +++++⋅⋅=>∴==∴=∴==-⋅舍9.已知数列{}n a 的通项公式为6(3)377n n a n n a a n ---≤⎧=⎨>⎩,,,若{}n a 是递增数列,则实数a 的取值范围为_____.【答案】(2,3) 【解析】 【分析】根据数列{a n }是递增数列,由分段函数的性质,得a >1,且3-a >0,且78a a <,解不等式组即可得到结论. 【详解】由()63377n n a n n a a n -⎧--≤=⎨>⎩,,是递增数列,∴78301a a a a ->⎧⎪>⎨⎪<⎩即231(3)73a a a a <⎧⎪>⎨⎪-⨯-<⎩解得23a <<故答案为(2,3)【点睛】本题考查分段函数单调性的应用,{a n }是递增数列,必须结合f (x )的单调性进行解题,但要注意{a n }是递增数列与f (x )是增函数的区别与联系.10.在数列{}n a 中,1212,25a a ==,且当1n >时,则11112n n na a a -++=,则n a =_______.【答案】23n + 【解析】 【分析】 确定1n a ⎧⎫⎨⎬⎩⎭是等差数列,计算得到132n n a +=,得到通项公式. 【详解】11112n n n a a a -++=,则1n a ⎧⎫⎨⎬⎩⎭是等差数列,12112,52a a ==,公差为12,首项为2 故()1132122n n n a +=+-=,故23n a n =+ 验证1n =成立,故23n a n =+ 故答案为:23n + 【点睛】本题考查了数列的通项公式,确定1n a ⎧⎫⎨⎬⎩⎭是等差数列是解题的关键.11.已知函数()y f x =的反函数1sin 161()logcos 28f x x ππ-⎛⎫=- ⎪⎝⎭,则方程1()2f x =的解x =___________. 【答案】2 【解析】 【分析】根据反函数性质得到1()2f x =的解为11()2f -,代入计算得到答案.【详解】函数()y f x =的反函数1sin 161()logcos 28x f x x π-⎛⎫=- ⎪⎝⎭, 则1()2f x =的解为1sin sin 16162111()log cos log 2228sin 216f ππππ-⎛⎫=-= ⎪⎝=⎭ 故答案为:2【点睛】本题考查了反函数的性质,三角函数化简,意在考查学生的综合应用能力. 12.设函数()()221sin 1x xf x x ++=+的最大值为M ,最小值为m ,则m M +=___________ .【答案】2 【解析】()()2221sin 2sin 111x xx x f x x x +++==+++,令22sin ()1x x g x x +=+,则()g x 为奇函数,所以()g x 的最大值和最小值和为0,又()()1g x f x =-. 有110M m -+-=,即2m M +=. 答案为:2.13.设{}n a 是公比为q 的等比数列,首项1164a =,对于*12N ,log n n n b a ∈=,当且仅当4n =时,数列{}n b 的前n 项和取得最大值,则q 的取值范围为_____________.【答案】4) 【解析】 【分析】由11111112222log log log log n n n n n n a b b a a q a +++-=-==,得出数列{}n b 是以12log q 为公差,以112log 6a =为首项的。
精选高一数学6月月考试题

天津市静海县2016-2017学年高一数学6月月考试题第Ⅰ卷基础题(共135分)一、选择题: (每小题5分,共35分)1.对具有线性相关关系的变量X,Y,测得一组数据如下根据表,利用最小二乘法得到它的回归直线方程为()20.57.0.+-=xyA25.47.0.+-=xyB25.67.0.+-=xyC25.57.0.+-=xyD2.在等比数列{a n}中,a1+a n=34,a2·a n-1=64,且前n项和S n=62,则项数n等于( ) A.4 B.5C.6 D.73. 在ABC△中,π4B=,BC边上的高等于13BC,则sin A=()A.310B C D4. 已知0,0>>ba,则abba211++的最小值是( )A.2 B.22C.4 D.55.某程序框图如图所示,若该程序运行后输出的值是2513,则A.11=a B. 12=a C. 13=a D. 14=a6.若+∈Ryx,,211111=+++yx则xy的最小值为()A.1 B.9C.2 D.47.设x y、满足约束条件36020x yx yx y--≤⎧⎪-+≥⎨⎪≥⎩、,若目标函数(0,0)z ax by a b=+>>的最大值为6,则46a b+的最小值为()A.256B.253C.504D.503二、填空题:(每空5分,共35分)8.在等差数列{}n a 中,若901210864=++++a a a a a ,则141031a a -的值为. 9. 在ABC ∆中,角A ,B ,C 的对边分别为,,a b c .已知22,sin 2sin a b bc C B -==,则角A 为__________.10. 等比数列{}n a 的前n 项和为n S ,已知3339,22a S ==,则公比q =. 11.在ABC ∆中,角C B 、、A 的对边分别是c b a ,,已知22,2==c b ,且4π=C ,则ABC ∆的面积为_____________.12.某校高三100名学生寒假读书消费支出情况的频率分布直方图如图所示.则这100名学生中,寒假读书消费支出超过150元的人数是________.13. 已知等比数列}{n a 的首项为43,公比为-13,其前n 项和为S n ,若A ≤S n -1S n ≤B 对n ∈N *恒成立,则B -A 的最小值为________.14. 若a 是b 21+与b 21-的等比中项,则||2||2b a ab+的最大值为三、解答题(本大题共4题,共65分)15. (13分)已知是锐角三角形,内角所对的边分别是,满足.(Ⅰ)求角的值; (Ⅱ)若,,求的周长.16.已知b x a a x x f +-+-=)6(3)(2. (1)解关于a 的不等式f (1)>0;(2)若不等式f (x )>0的解集为(-1,3),求实数a ,b 的值.17. 数列}{n a 的前n 项和n S 满足12a a S n n -=,且321,1,a a a +成等差数列. (1)求数列}{n a 的通项公式; (2)设11++=n n n n S S a b ,求数列}{n b 的前n 项和n T18. 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物需建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm)满足关系:C (x )=k3x +5(0≤x ≤10),若不建隔热层,每年能源消耗费用为8万元.设f (x )为隔热层建造费用与20年的能源消耗费用之和. (1)求k 的值及f (x )的表达式;(2)隔热层修建多厚时,总费用f (x )达到最小,并求最小值.19. 已知正项等差数列{}n a 的前n 项和为n S ,若312S =,且1232,,1a a a +成等比数列.(Ⅰ)求{}n a 的通项公式; (Ⅱ)设3nn na b =,记数列{}n b 的前n 项和为n T ,求n T .第Ⅱ卷 提高题(共15分)20.已知正项数列{}n a 的前n 项和为n S ,且21111,n n n a S S a ++=+=,数列{}n b 满足1131n a n n b b b +⋅==,且.(I )求数列{}n a ,{}n b 的通项公式; (II )记21412n n n n T a b a b a b -=++⋅⋅⋅+,求nT静海一中2016-2017第二学期高一数学(6月)学生学业能力调研卷第Ⅰ卷基础题(共135分)一、选择题(每题5分,共35分)二、填空题(每题5分,共35分) 8._________ 9. ____10. 11. 12. 13.14.三、解答题(本大题共5题,共65分) 15. (13分)16.(13分)17.(13分)18.(13分)19. (13分)第Ⅱ卷 提高题(共15分)20. (15分)静海一中2016-2017第二学期高一数学(6月)考试提高卷考生注意:本试卷为提高题,共30分1、已知数列{}n a 是公差为正数的等差数列,其前n 项和为n S ,且1532=⋅a a ,4S =16. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)数列{}n b 满足11b a =,111n n n n b b a a ++-=⋅.① 数列{}n b 的通项公式;②是否存在正整数n m ,(m ≠n ),使得n m b b b ,,2成等差数列?若存在,求出n m ,的值;若不存在,请说明理由.2、已知正数列{}n a 的前n 项和n S 满足2421n n n S a a =++.()I 求数列{}n a 的通项公式;()II 符号[]x 表示不超过实数x 的最大整数,如22[log 3]1,[log 5] 2.==记23[log ]2n n a b +=,求数列2{2}n n b ⋅的前n 和.n T高一数学答案1、解:由表可得样本中心为(2.5,3.5),代入检验可得y=﹣0.7x+5.25. 故选D .2、B3、D4、C5、B6、B7、D8、29、3π 10、1或12- 11、1171sin 221221224S bc A π==⨯⨯=⨯⨯=12、30 13.59/72 14、4/2、解:⑴ (3)sin sin 1cos 3222=+-B B B ……3分 ⑵由,得①……7分由⑴知3π=A ,所以bc=24 ②……8分由余弦定理知a 2=b 2+c 2-2bccosA ,将72=a 及①代入可得c 2+b 2=52③……10分③+②×2,得(c+b )2=100,所以c+b=10,△ABC 的周长是7210+……12分16、解:(1)因为f (1)>0,所以-3+a (6-a )+b >0,即a 2-6a +3-b <0. Δ=(-6)2-4(3-b )=24+4b .①当Δ≤0,即b ≤-6时,原不等式的解集为∅. ②当Δ>0,即b >-6时,方程a 2-6a +3-b =0有两根a 1=3-6+b ,a 2=3+6+b , 所以不等式的解集为(3-6+b ,3+6+b ). 综上所述:当b ≤-6时,原不等式的解集为∅;当b >-6时,原不等式的解集为(3-6+b ,3+6+b ). (2)由f (x )>0,得-3x 2+a (6-a )x +b >0, 即3x 2-a (6-a )x -b <0. 因为它的解集为(-1,3),所以-1与3是方程3x 2-a (6-a )x -b =0的两根,所以⎩⎪⎨⎪⎧-1+3=a (6-a )3,-1×3=-b3,解得⎩⎨⎧a =3-3,b =9或⎩⎨⎧a =3+3,b =9.17、(1)由题意,当2≥n 时,1112a a S n n -=--,又因为12a a S n n -=,且1--=n n n S S a ,则)2(21≥=-n a a n n ,所以1231242,2a a a a a ===,又321,1,a a a +成等差数列,则312)1(2a a a +=+,所以1114)12(2a a a +=+,解得21=a ,所以数列}{n a 是以2为首项,2为公比的等比数列,所以n n a 2=.(2)由(1)知221-=+n n S ,∴221221)22)(22(221211---=--=+++++n n n n n n b , ∴)221221()221221()221221(214332---++---+---=++n n n T 22121221221222--=---=++n n . 18解:(1)由题设,建筑物每年能源消耗费用为C (x )=k3x +5, 由C (0)=8,得k =40,∴C (x )=403x +5. 而隔热层建造费用为C 1(x )=6x ,∴f (x )=20C (x )+C 1(x )=20×403x +5+6x =8003x +5+6x (0≤x ≤10). (2)方法一:f (x )=8003x +5+6x =1 6006x +10+6x +10-10 ≥21 6006x +10×(6x +10)-10=70, 当且仅当1 6006x +10=6x +10,即x =5时取等号. ∴当隔热层修建厚度为5 cm 时,总费用最小,最小值为70万元.19解:(Ⅰ)∵312S =,即12312a a a ++=,∴2312a =,所以24a =. ………1分又∵12a ,2a ,31a +成等比数列,∴22132(1)a a a =⋅+,即22222()(1)a a d a d =-⋅++,……3分解得,3d =或4d =-(舍去),∴121a a d =-=,故32n a n =-. …6分 (Ⅱ)321(32)333n n n n na nb n -===-⋅, ∴231111147(32)3333n n T n =⨯+⨯+⨯++-⨯, ①①13⨯得 2341111111147(35)(32)333333n n n T n n +=⨯+⨯+⨯++-⨯+-⨯ . ② ①-②得 234121111113333(32)3333333n n n T n +=+⨯+⨯+⨯++⨯--⨯ 2111111(1)115111333(32)(32)133623313n n n n n n -+-+-=+⨯--⨯=-⨯--⨯-,…10分 ∴2511321565144323443n n n n n n T --+=-⨯-⨯=-⨯.……………………12分 20题:小卷答案:、解:(I)设数列{a n }的公差为d ,则d >0.由a 2·a 3=15,S 4=16,得⎩⎨⎧(a 1+d )(a 1+2d )=15,4a 1+6d =16,解得⎩⎨⎧a 1=1,d =2,或⎩⎨⎧a 1=7,d =-2.(舍去)................2分 所以a n =2n -1. …………………… 3分 (Ⅱ)①因为b 1=a 1,b n +1-b n =1a n ·a n +1, 所以b 1=a 1=1, b n +1-b n =1a n ·a n +1=1 (2n -1)·(2n +1)=12(12n -1-12n +1), …………………… 5分即b 2-b 1=12(1-13),b 3-b 2=12(13-15),…,b n -b n -1=12(12n -3-12n -1),(n ≥2) 累加得:b n -b 1=12(1-12n -1)=n -12n -1, 所以b n =b 1+n -12n -1=1+n -12n -1=3n -22n -1. ……………………7分 b 1=1也符合上式.故b n =3n -22n -1,n ∈N*. …………………… 8分 ②假设存在正整数m 、n (m ≠n ),使得b 2,b m ,b n 成等差数列,则b 2+b n =2b m .又b 2=43,b n =3n -22n -1=32-14n -2,b m =32-14m -2, 所以43+(32-14n -2)=2(32-14m -2),即1 2m -1=16+14n -2, 化简得:2m =7n -2n +1=7-9n +1. ……………………11分 当n +1=3,即n =2时,m =2,(舍去);当n +1=9,即n =8时,m =3,符合题意.所以存在正整数m =3,n =8,使得b 2,b m ,b n 成等差数列.…………………… 12分。
高一数学6月月考试题word版本

2015-2016学年第二学期6月份教学质量检测高一数学2016.6一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、=)1050sin(oA.21 B.21- C.23 D.23-2、若35sin =α,且为第四象限角,则αtan 的值等于 A.512 B.512- C.125- D.1253、已知为实数,向量)2,1(),1,21(=--=b a λ,若⊥则等于 A.21 B.21- C.43- D.43 4、函数_)sin()(ϕϖ+=x A x f 的部分图像如图所示,则函数)(x f 的周期为A. B.π43C.2πD. 5、将甲乙两名同学近5次数学考试成绩,制成如图 所示的茎叶图,考虑以下结论, ①甲生的平均成绩大于乙生的平均成绩; ②甲生的平均成绩小于乙生的平均成绩;③甲生成绩的方差大于乙生成绩的方差; ④甲生成绩的方差小于乙生成绩的方差;其中根据茎叶图能够得到的正确的统计结论的编号为 A.①③B.②④ C.②③D.①④6、已知函数)(),62sin(21)(ϕπ++=x f x x f 为偶函数,则可以为 A.2π- B.3π C.6π D.6π-7、在平行四边形ABCD 中, AC 与BD 交于点0, E 是0B 的中点,若==,,则=CEA.b a2121+-B.b a 2121--C.b a 4121+D.b a 4121- 8、阅读下边的程序序框图,若输山S 的值为-7,则判断框内应填写 A.?3<i B.?4<i C.?5<i D.?6<i9、设p ,q 为实数,,是两个不共线的向量,q p 2)1(,,2--=+=+=,若A 、B 、D 三点共线则的值是A.-2B.2C.1D.-1 10、关于函数)),62cos(3)(R x x x f ∈+=π,则下列结论中正确的个数是①若)()(21x f x f =,则21x x -必是的整数倍; ②函数的图象关于直线125π=x 对称 ③函数)(x f 在区间[0,2π】上的值域为[23,23-] ④函数)(x f 的解析式可写为)322sin(3)(π+=x x fA.1B.2C.3D.411、己知是平面内两互相垂直的单位向量,若向量满足0)()(=-⋅-,则||的 最大值是A.1B.2C.D.22 12、函数)0>(,sin 2ϖϖx y =的部分图象如图所示,点A 、B 是最高点,点C 是最低点,若△ABC 是等腰直角三角形(C 为直角),则的值为 A.3π B.2π C. D.4π 第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题,每小题 5分,共20分。
高一数学下学期六月月考试卷(含解析)-人教版高一全册数学试题

涿鹿中学2015-2016学年度第二学期6月考试高一数学试卷班级类型:高一各班;考试时间:120分钟;总分 150分注意事项:1.答题前在答题卡、答案纸上填写好自己的某某、班级、考号等信息2.请将第I卷(选择题)答案用2B铅笔正确填写在答题卡上;请将第II卷(非选择题)答案黑色中性笔正确填写在答案纸上。
第I卷(选择题60分)一、单项选择题(60分,每小题5分)1.正方体内切球和外接球半径的比为( )A. B. C. D. 1:2【考点】柱,锥,台,球的结构特征【试题解析】因为设正方体边长为a,则内切球和外接球半径分别为故答案为:B【答案】B2.如图是水平放置的平面图形的斜二测直观图,其原来平面图形面积是()45BOA22A. 22B.42C. 4D.8【考点】空间几何体的三视图与直观图【试题解析】因为原几何体是一个直角三角形,底为2,高为4,故答案为:C【答案】C3.设集合2{|430}A x x x =-+<,{|230}B x x =->,则A B =( )A. 3(3,)2-- B .3(3,)2- C .3(1,)2 D. 3(,3)2【考点】集合的运算 【试题解析】因为故答案为:D 【答案】D4.已知等差数列{}n a 前9项的和为27,108a =,则100a = ( ) A.100 B. 99 C.98 D.97 【考点】等差数列 【试题解析】因为故答案为:C 【答案】C5. △ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =,2c =,2cos 3A =,则b=( )A.2B. 3C.2D.3 【考点】余弦定理 【试题解析】因为故答案为:D 【答案】D6.设,a b 是两条不同的直线,,,αβγ是三个不同的平面,则下列命题正确的是( ) A. 若αβ⊥,αγ⊥,则βγ⊥ B.若,a b 与α所成的角相等,则//a b C. 若a α⊥,//a β,则αβ⊥ D.若//a b ,a α⊂,则//b α 【考点】点线面的位置关系【试题解析】因为A、B、D均能找到反例,只有C是真命题。
福建省泉州市永春一中2015-2016学年高一下学期6月月考数学试卷Word版含解析

2015-2016学年福建省泉州市永春一中高一(下)6月月考数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上.1.sin(﹣510°)=()A.B.C.﹣D.﹣2.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.则x+y的值为()A.7 B.8 C.9 D.103.已知是两个非零向量,且,则的夹角为()A.30°B.60°C.90°D.150°4.在△ABC中,若∠A=60°,∠B=45°,,则AC=()A. B. C.D.5.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则56.函数y=xsinx在[﹣π,π]上的图象是()A.B.C.D.7.执行如图所示的程序框图.若输出S=15,则框图中①处可以填入()A.k<2 B.k<3 C.k<4 D.k<58.如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=()A.B. C.D.9.已知△ABC是锐角三角形,则点P(cosC﹣sinA,sinA﹣cosB)在()A.第一象限 B.第二象限 C.第三象限 D.第四象限10.函数f(x)=sinωx(ω>0)在[﹣,]恰有11个零点,则ω的取值范围()A.[10,12)B.[16,20] C.[8,12]D.[12,14)11.在△ABC中,已知B=60°,C=45°,BC=8,AD⊥BC于D,则AD长为()A.4(﹣1)B.4(+1)C.4(+3)D.4(3﹣)12.设向量=(λ+2,λ2﹣cos2a),向量=(m, +sinacosa,其中λ,m,α为实数.若向量=2,则的取值范围为()A.[﹣6,1] B.[﹣3,3] C.[1,7]D.[2,8)二、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.13.将二进制数101101化为八进制数,结果为.(2)14.在三角形ABC中,内角A、B、C的对边分别为a、b、c,若三角形ABC的面积S=(a2+b2﹣c2),则C=.15.已知集合A={2,5},在A中可重复的依次取出三个数a,b,c,则“以a,b,c为边恰好构成三角形”的概率是.16.设f(x)是定义在R上的奇函数,且满足f(x+2)=﹣f(x);当0≤x≤1时,f(x)=x;令g(x)=f(x)+,则函数g(x)在区间[﹣10,10]上所有零点之和为.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.17.已知f(α)=,(1)化简f(α);(2)若f(α)=﹣2,求sinαcosα+cos2α的值.18.某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.(I)若该校高一年级共有学生1000人,试估计成绩不低于60分的人数;(II)为了帮助学生提高数学成绩,学校决定在随机抽取的50名学生中成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙恰好被安排在同一小组的概率.19.已知函数f(x)=2cosx(sinx+cosx)﹣1.(Ⅰ)求函数f (x)在区间[0,]上的最大值和最小值;(Ⅱ)若f (x0)=,x0∈[,],求cos2x0的值.20.在△ABC中,a,b,c分别是角A,B,C的对边,C=2A,cosA=.(Ⅰ)求cosC,cosB的值;(Ⅱ)若,求边AC的长.21.如图A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠AOC=α.(1)当点A的坐标为(,)时,求sinα的值;(2)若0≤α≤,且当点A、B在圆上沿逆时针方向移动时总有∠AOB=,试求|BC|的取值范围.22.已知圆C与直线相切,圆心在x轴上,且直线y=x被圆C截得的弦长为.(1)求圆C的方程;(2)过点M(﹣1,0)作斜率为k的直线l与圆C交于A,B两点,若直线OA与OB的斜率乘积为m,且,求的值.2015-2016学年福建省泉州市永春一中高一(下)6月月考数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上.1.sin(﹣510°)=()A.B.C.﹣D.﹣【考点】运用诱导公式化简求值.【分析】由条件利用诱导公式化简所给式子的值,可得结果.【解答】解:sin(﹣510°)=sin(﹣150°)=﹣sin150°=﹣sin30°=﹣,故选:C.2.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.则x+y的值为()A.7 B.8 C.9 D.10【考点】茎叶图;众数、中位数、平均数.【分析】利用平均数求出x的值,中位数求出y的值,解答即可.【解答】解:由茎叶图可知甲班学生的总分为70×2+80×3+90×2+(8+9+5+x+0+6+2)=590+x,又甲班学生的平均分是85,总分又等于85×7=595.所以x=5乙班学生成绩的中位数是80+y=83,得y=3.∴x+y=8.故选B.3.已知是两个非零向量,且,则的夹角为()A.30°B.60°C.90°D.150°【考点】数量积表示两个向量的夹角.【分析】因为,平方得,利用向量的数量积公式求出夹角的余弦,进一步求出向量的夹角.【解答】解:因为,平方得设的夹角为θ所以因为θ∈[0,π]所以θ=30°故选A.4.在△ABC中,若∠A=60°,∠B=45°,,则AC=()A. B. C.D.【考点】正弦定理.【分析】结合已知,根据正弦定理,可求AC【解答】解:根据正弦定理,,则故选B5.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则5【考点】简单随机抽样.【分析】从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读,依次为65,72,08,02,63,14,07,02,43,69,97,28,01,98,…,其中08,02,14,07,01符合条件,故可得结论.【解答】解:从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读,第一个数为65,不符合条件,第二个数为72,不符合条件,第三个数为08,符合条件,以下符合条件依次为:08,02,14,07,01,故第5个数为01.故选:D.6.函数y=xsinx在[﹣π,π]上的图象是()A.B.C.D.【考点】函数的图象.【分析】本题可采用排除法解答,先分析出函数的奇偶性,再求出和f(π)的值,排除不满足条件的答案,可得结论.【解答】解:∵y=x和y=sinx均为奇函数根据“奇×奇=偶”可得函数y=f(x)=xsinx为偶函数,∴图象关于y轴对称,所以排除D.又∵,排除B.又∵f(π)=πsinπ=0,排除C,故选A.7.执行如图所示的程序框图.若输出S=15,则框图中①处可以填入()A.k<2 B.k<3 C.k<4 D.k<5【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加变量k的平方到S并输出S,模拟程序的执行过程,分析出进行循环的条件,可得答案.【解答】解:程序在运行过程中各变量的值如下表示:是否继续循环S k循环前/1 1第一圈是 2 2第二圈是 6 3第三圈是15 4第四圈否所以判断框内可填写“k<4”,故选C.8.如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=()A.B. C.D.【考点】两角和与差的正切函数;任意角的三角函数的定义.【分析】法一:用余弦定理在三角形CED中直接求角的余弦,再由同角三角关系求正弦;法二:在三角形CED中用正弦定理直接求正弦.【解答】解:法一:利用余弦定理在△CED中,根据图形可求得ED=,CE=,由余弦定理得cos∠CED=,∴sin∠CED==.故选B.法二:在△CED中,根据图形可求得ED=,CE=,∠CDE=135°,由正弦定理得,即.故选B.9.已知△ABC是锐角三角形,则点P(cosC﹣sinA,sinA﹣cosB)在()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】三角函数值的符号.【分析】由△ABC是锐角三角形得到A+B>,即A>﹣B,根据正弦函数的性质可得sinA>sin(﹣B)=cosB,同理可得sinA>cosC,问题得以解决.【解答】解:∵△ABC是锐角三角形,∴A+B>,∴A>﹣B,∴sinA>sin(﹣B)=cosB,∴sinA﹣cosB>0,同理可得sinA﹣cosC>0,∴点P在第二象限.故选:B10.函数f(x)=sinωx(ω>0)在[﹣,]恰有11个零点,则ω的取值范围()A.[10,12)B.[16,20] C.[8,12]D.[12,14)【考点】正弦函数的图象.【分析】由题意可得可得5π≤ω•<6π,由此求得ω的取值范围.【解答】解:函数f(x)=sinωx(ω>0)在[﹣,]恰有11个零点,可得5π≤ω•<6π,求得10≤ω<12,故选:A.11.在△ABC中,已知B=60°,C=45°,BC=8,AD⊥BC于D,则AD长为()A.4(﹣1)B.4(+1)C.4(+3)D.4(3﹣)【考点】解三角形的实际应用.【分析】由已知A=75°,再由正弦定理易求AB的长,在Rt△ABD中,AD=ABsin60°可得AD长.【解答】解:由题意,∵B=60°,C=45°,∴A=75°,∴在△ABC中,,∴AB=8﹣8,∴AD=ABsin60°=4(3﹣).故选:D.12.设向量=(λ+2,λ2﹣cos2a),向量=(m, +sinacosa,其中λ,m,α为实数.若向量=2,则的取值范围为()A.[﹣6,1] B.[﹣3,3] C.[1,7]D.[2,8)【考点】平面向量数量积的运算.【分析】根据向量相等的定义得出λ+2=2m①,且λ2﹣cos2α=m+2sinαcosα②;设=k ,代入①②化简得出关于k 的方程2sin (2α+)=﹣;利用三角函数的有界性列出关于k 的不等式,求出解集即可.【解答】解:∵向量=(λ+2,λ2﹣cos2a ),向量=(m , +sinacosa ),=2,∴λ+2=2m ①,且λ2﹣cos2α=m +2sin αcos α②;设=k 则λ=mk ,代入①②得:mk +2=2m ,即m=③;cos2α+sin2α=m 2k 2﹣m ,即2sin (2α+)=m 2k 2﹣m ④;③代入④得:2sin (2α+)=﹣;又∵﹣1≤sin (2α+)≤1,∴﹣2≤2sin (2α+)≤2,∴﹣2≤﹣≤2,即﹣2≤≤2;∴﹣(2﹣k )2≤2k 2+k ﹣2≤(2﹣k )2;由2k 2+k ﹣2≤(2﹣k )2, 解得﹣6≤k ≤1;由﹣(2﹣k )2≤2k 2+k ﹣2, 解得k ∈R ;综上:﹣6≤k ≤1;即的取值范围是[﹣6,1].故选:A .二、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上. 13.将二进制数101101(2)化为八进制数,结果为 55 . 【考点】排序问题与算法的多样性.【分析】利用2进制化为十进制和十进制化为其它进制的“除8取余法”方法即可得出. 【解答】解:∵101101(2)=1×25+0+1×23+1×22+0+1×20=45(10).再利用“除8取余法”可得:45(10)=55(8). 故答案为55.14.在三角形ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,若三角形ABC 的面积S=(a 2+b 2﹣c 2),则.【考点】余弦定理;正弦定理.【分析】由三角形ABC 的面积S=ab •sinC=,再由余弦定理求出tanC==,可得C 的值.【解答】解:∵在三角形ABC 中,三角形ABC 的面积S=ab •sinC=,∴sinC==cosC ,∴tanC==,∴C=,故答案为.15.已知集合A={2,5},在A 中可重复的依次取出三个数a ,b ,c ,则“以a ,b ,c 为边恰好构成三角形”的概率是.【考点】古典概型及其概率计算公式.【分析】本题是一个古典概型,试验发生包含的事件是从两个元素中3次取数字,共有2×2×2种结果,满足条件的事件是恰好构成三角形,利用列举出共有5种结果,根据古典概型概率公式得到结果.【解答】解:由题意知本题是一个古典概型,试验发生包含的事件是从两个元素中3次取数字,共有2×2×2=8种结果, 满足条件的事件是恰好构成三角形,有2,2,2;5,5,5;5,5,2;5,2,5;2,5,5共有5种结果,根据古典概型的概率公式得到P=故答案为:.16.设f(x)是定义在R上的奇函数,且满足f(x+2)=﹣f(x);当0≤x≤1时,f(x)=x;令g(x)=f(x)+,则函数g(x)在区间[﹣10,10]上所有零点之和为﹣5.【考点】函数奇偶性的性质.【分析】利用函数的奇偶性和对称性求出函数的周期性,然后求出函数在一个周期内的解析式,和零点,利用函数的周期性进行求解即可.【解答】解:∵f(x+2)=﹣f(x),∴f(x+4)=﹣f(x+2)=f(x),即函数的周期为4,∵f(x)是定义在R上的奇函数,∴当﹣1≤x≤0时,当0≤﹣x≤1,则f(﹣x)=﹣x=﹣f(x),则f(x)=x,﹣1≤x≤0,即f(x)=x,﹣1≤x≤1,若﹣3≤x≤﹣1,则﹣1≤x+2≤1,∵f(x+2)=﹣f(x),∴f(x)=﹣f(x+2)=﹣(x+2),﹣3≤x≤﹣1,由g(x)=f(x)+=0得f(x)=﹣,则一个周期[﹣3,1]内,若﹣1≤x≤1,则由f(x)=x=﹣得x=﹣1,若﹣3≤x≤﹣1,则由f(x)=﹣(x+2)=﹣得x=﹣1,综上在一个周期内函数的零点为﹣1,∵函数的周期是4n,∴函数的零点为x=4n﹣1,(n∈Z),∴函数g(x)在区间[﹣10,10]上所有零点之和为﹣9﹣5﹣1+3+7=﹣5故答案为﹣5.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.17.已知f(α)=,(1)化简f(α);(2)若f(α)=﹣2,求sinαcosα+cos2α的值.【考点】三角函数的化简求值.【分析】(1)根据三角函数的诱导公式进行化简即可;(2)根据同角的三角函数基本关系,进行化简即可.【解答】解:(1)f(α)===﹣tanα;…5(分)(2)∵f(α)=﹣2,∴tanα=2,…6(分)∴sinαcosα+cos2α====.…10(分)18.某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.(I)若该校高一年级共有学生1000人,试估计成绩不低于60分的人数;(II)为了帮助学生提高数学成绩,学校决定在随机抽取的50名学生中成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙恰好被安排在同一小组的概率.【考点】频率分布直方图;等可能事件的概率;古典概型及其概率计算公式.【分析】(I)根据频率分布直方图,成绩不低于60分的频率,然后根据频数=频率×总数可求出所求;(II)先算出成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的“二帮一”小组分组办法的基本事件,以及甲、乙两同学被分在同一小组的基本事件,最后利用古典概型的概率公式解之即可.【解答】解:(Ⅰ)根据频率分布直方图,成绩不低于6的频率为1﹣10×(0.004+0.010)=0.86. …由于该校高一年级共有学生1000人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于6的人数为1000×0.86=860人. … (Ⅱ)成绩在[40,50)分数段内的人数为50×0.04=2人 成绩在[90,100]分数段内的人数为50×0.1=5人,… [40,50)内有2人,记为甲、A .[90,100)内有5人,记为乙、B 、C 、D 、E .则“二帮一”小组有以下20种分组办法:甲乙B ,甲乙C ,甲乙D ,甲乙E ,甲BC ,甲BD ,甲BE ,甲CD ,甲CE ,甲DE ,A 乙B ,A 乙C ,A 乙D ,A 乙E ,ABC ,ABD ,ABE ,ACD ,ACE ,ADE …其中甲、乙两同学被分在同一小组有4种办法:甲乙B ,甲乙C ,甲乙D ,甲乙E所以甲乙两同学恰好被安排在同一小组的概率为. …19.已知函数f (x )=2cosx (sinx +cosx )﹣1.(Ⅰ)求函数f (x )在区间[0,]上的最大值和最小值;(Ⅱ)若f (x 0)=,x 0∈[,],求cos2x 0的值.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(Ⅰ)根据三角恒等变换化简f (x ),求出时f (x )的最值即可;(Ⅱ)根据f (x 0)的值,利用变换2 x 0=(2 x 0+)﹣,即可求出cos2 x 0的值.【解答】解:(Ⅰ)f (x )=2sinxcosx +2cos2x ﹣1=sin2x +cos2x =2sin (2x +);…当时,,;…所以f (x )在区间[0,]上的最大值为2,最小值为﹣1;…(Ⅱ)因为f (x 0)=2sin (2x 0+)=,所以sin (2 x 0+)=;…因为x 0∈[,],所以2 x 0+∈[,],从而cos (2 x 0+)=,所以cos2 x 0=cos [(2 x 0+)﹣]=cos (2 x 0+)cos+sin (2 x 0+)sin=.…20.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,C=2A ,cosA=. (Ⅰ)求cosC ,cosB 的值;(Ⅱ)若,求边AC 的长.【考点】解三角形;二倍角的余弦.【分析】(Ⅰ)由题意可得 cosC=cos2A ,利用二倍角公式求出cosC=,再由同角三角函数的基本关系求出sinC 和 sinA 的值,由cosB=﹣cos (A +C )=﹣cosAcosC +sinAsinC , 运算求得结果.(Ⅱ)由求得 ac=24,再由,C=2A ,可得 c=2acosA=a ,姐方程求得a 、c 的值,再利用余弦定理求出b 的值,即为所求.【解答】解:(Ⅰ)由题意可得 cosC=cos2A=2cos 2A ﹣1=,…1分故 sinC=.…2分由 cosA=得 sinA=.…3分∴cosB=﹣cos (A +C )=﹣cosAcosC +sinAsinC=.…4分(Ⅱ)∵,∴ac •cosB=,ac=24.…6分∵,C=2A ,∴c=2acosA=a ,解得 a=4,c=6,…8分再由余弦定理可得 b 2=a 2+c 2﹣2accosB=25,故b=5. 即边AC 的长为 5. …10分21.如图A 、B 是单位圆O 上的动点,C 是圆与x 轴正半轴的交点,设∠AOC=α.(1)当点A 的坐标为(,)时,求sin α的值;(2)若0≤α≤,且当点A 、B 在圆上沿逆时针方向移动时总有∠AOB=,试求|BC |的取值范围.【考点】任意角的三角函数的定义.【分析】(1)利用任意角的三角函数的定义,求得sinα的值.(2)由题意可得∠COB=α+,由余弦定理求得CB2的解析式,利用余弦函数的定义域和值域求得BC2的范围,可得BC的范围.【解答】解:(1)∵A点的坐标为,根据三角函数定义可知,,r=1,∴.(2)∵,∠COA=α,∴∠COB=α+,由余弦定理得CB2=OC2+OB2﹣2OC•OB•cos∠COB=1+1﹣2cos(α+)=2﹣2cos(α+).∵α∈(0,),∴α+∈(,),∴cos(α+)∈(﹣,],∴BC2∈[1,2+]、∴BC∈[1,],即BC∈[1,].22.已知圆C与直线相切,圆心在x轴上,且直线y=x被圆C截得的弦长为.(1)求圆C的方程;(2)过点M(﹣1,0)作斜率为k的直线l与圆C交于A,B两点,若直线OA与OB的斜率乘积为m,且,求的值.【考点】直线与圆的位置关系.【分析】(1)设圆C的方程为(x﹣a)2+y2=r2(r>0),圆心到直线y=x的距离为,由直线y=x被圆C截得的弦长为,圆C与直线相切,能求出圆C的方程.(2)直线l的方程为y=k(x+1),联立,得,由此利用根的判别式、韦达定理、向量的数量积能求出的值.【解答】解:(1)设圆C的方程为(x﹣a)2+y2=r2(r>0),则圆心到直线y=x的距离为,由直线y=x被圆C截得的弦长为,得,即,①…由圆C与直线相切,得,即②,…由①②及r>0,解得,故圆C的方程为.…(2)直线l的方程为y=k(x+1),联立,得,直线l与圆C交于A,B两点,恒成立…设A(x1,y1),B(x2,y2),则,则,∴,则,故k2=9…则,,故=x1x2+y1y2=﹣.…2016年11月27日。
河北省秦皇岛市卢龙县中学2016-2017学年高一6月月考数学(文)试题

2016—2017学年度第二学期6月质量检测高一数学(文科)试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分.考试用时120分钟.第Ⅰ卷(选择题,共60分)一、选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知A={}043x |x 2<-+x ,B={}22|<<x x -,则=⋂B A ( )A .{}12|<≤-x x B. {}21|≤<-x x C. {}12|<<-x x D.{}24|≤<-x x 2.已知c b a ,,满足a b c <<,且0<ac ,那么下列选项中一定成立的是 ( ) A.ac ab > B. 0)(<-a b c C. 22ab cb < D. 0)(>-c a ac 3.在△ABC 中,已知∠B =45°,c =2,b =2,则∠A 等于 ( ) A .30° B .75°C .105°D .60°或120° 4.等差数列{}n a 中,851=+a a ,74=a ,则数列{}n a 的公差为 ( ) A .1 B .2 C .3D .45.已知样本数据1x ,2x ,⋅⋅⋅,n x 的均值5x =,则样本数据121x +,221x +,⋅⋅⋅,21n x + 的均值为 .A .5B .10C . 11D .216.在等差数列{}n a 中,已知2684=+a a ,则该数列前11项和=11S ( ) A .143 B .88 C . 58 D .1767.在ABC ∆中,内角C B A ,,的对边分别是c b a ,,,则bc b a 322=-,B C sin 3sin =则=C ( )A .30°B .60°C .120°D .150° 8.等比数列{}n a 的前n 项和为n S ,且3214,2,a a a 成等差数列.若81=a ,则=4S ( )A .15B .120C .35D .449. 实数y x ,满足条件⎪⎩⎪⎨⎧≥≥≥+-≤-+0,002204y x y x y x ,则y x -的最小值为( )A .4 B.0 C.—1 D.—2 10. 执行右边的程序框图,若[]2,1-∈t ,则∈s ( )A .()2,1-B .[)2,1-C .[]2,1-D .(]2,1- 11.已知+∈=+R y x y x ,3,,若)0(1>+m ym x 的最小值为3,则m 等于 ( ) A. 2 B. 22 C. 3 D. 412. 已知函数()b ax x x f 22-+=若b a ,都是区间[]4,0内的数,则使()01>f 成立的概率是( )A.43 B. 83 C. 41 D. 85 第Ⅱ卷二、填空题:(本大题共4小题,每小题5分)13. 如图是甲、乙两名篮球运动员2013年赛季每场比赛得分的茎叶图,则甲、乙两人比赛得分的中位数之和为 .14. 等差数列{}n a 的前m 项和为30,前2m 项和为100,则它的前3m 项和为15. 函数)1(1321<---=x x x y 的最小值为 16. 已知y x ,满足约束条件⎩⎨⎧≤-+≥012y x xy ,若)0(>-=a ax y z 的最大值为3,则实数a 的值为三、解答题:解答应写出文字说明,证明过程或演算步骤。
四川省双流中学2016-2017学年高一下学期6月月考数学试题含答案

四川省双流中学2016—2017学年度下期六月考试高一数学试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1。
已知集合{0}M x x =≥,2{1}N x x =<,则M N =( ) A .[]0,1 B .[0,1) C .(0,1] D .(0,1)2.下列函数中,既是偶函数又存在零点的是( )A .cos y x =B .sin y x =C .ln y x =D .21y x =+ 3.已知θ是直线2210x y +-=的倾斜角,则sin θ的值是( )A .22-B .22C .1D .1-4。
已知,,a b c 满足c b a <<,且0ac <,那么下列选项中不一定成立的是( )A .ab ac >B .()0c b a -<C 。
22cb ab < D .()0ac a c -< 5。
对任意的实数k ,直线1y kx =+与圆222x y +=的位置关系一定是( ) A .相离 B .相切 C.相交 D .不确定6.已知向量,a b 满足1a =,4b =,且2a b •=,则a 与b 的夹角为( )A .6πB .4π C. 3π D .2π7.一个体积为33的正棱柱的三视图,如图所示,则该三棱近的高为( )A .3B .3323.48。
大衍数列,来源于《乾坤谱》中对易传“大衍之数五十"的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中,曾经经历的两仪数量总和,是中华传统文化中隐藏着的世界数学史上第一道数列题,其前10项依次是0,2,4,8,12,18,24,32,40,50……,则此数列第20项为( )A .180B .200 C. 128 D .1629。
已知()log (1)1a f x x =-+(0a >且a ≠)恒过定点M ,且点M 在直线1x y m n +=(0m >,0n >)上,则m n+的最小值为( )A..8 C 。
内蒙古师大附中2015-2016学年高一6月月考数学试卷(扫描版,无答案)

24(D )核沖心加交皿。
昭诃和响域交丁虛厂若疋RD"* HA .「A 札餌” c r +? 》 4 2$要fllJWRy ・g (2jf+1)的囲氧 HWKsfifty =cos2xfiftwft(A)向左平WH 个勰忖 <c )鞠左平移+个跟览反已 fea = (-X2)^=(-L0)- B.1 77.0h^y = c^2x-i-Jr )-2的圉兼F 桜时"口平移到F ・F 的呦敦耕析式y = f(x\6当/co 为奇曲数时,向* ◎町u 雪r^(-― »-2) 丘卜二恳) 6 o _. ti 8.^S in a -^,cos(a + 0)—tla* 卩都为锐角.财B =nrK B* ; L+ ;£^05x59}的捷尢值与咼小值Z 和为 (B)0 QT {D)T-占高考帮一一帮你实现大学梦想!■年级月考數学试卷NU uin 加 *12 心云W 向右平移]个単忖(D>向右平移£牛草位j£a 向ft 加卡b 耳O -对垂Fb 则实U [几的值为 c +rx ? {A)2 - V5 -D.- na^-t 和血仙D . 9高考帮一一帮你实现大学梦想!填空)虬分共20分〉恤散厂血—*阿咸0*门叭収褂耐川叭xw - 一 M 必颇上塞规A 携职平面上邢曲的加和加就)^QB ^OC-WA ) "數厂闷2十心"5的图他向的轿尹单竹辰U 曲数厂皿3亍则阚16.巳知 2sin0 = l + cosa Wl cot"的值为三解答题(每题10分共如分)忆曲数/"⑷"必伽圣)+ i M>0t ^>0)的融人伯为乳 財fHft 相郭两条対称轴 6 z 间的距离为兰. 2 ⑴求闻独f (町的耕析武及单调遼协区何:/ ⑵如€ 则疋)4求厲的饥 -屮心」巧w 杯:[2 4J IT —E /E •- < * ? < Q 存 2 p 的ff!为■> w I n --h (<Jp J | (I Or<1 .ST5心皿+■酗吋販2n °T。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年春高一6月月考数学试卷
一、选择题(本大题共12小题,每题5分,共60分)。
1.{}201520136,n a a a d =+在等差数列中,则公差等于( ) A.2 B.3 C.4
2.如图,四边形O A B C ''''的直观图表示的平面图形是 ( A.等腰梯形 B 直角梯形 C.平行四边形 D.任意四边形
3.已知直线1:210l ax y --=与直线22:4(2)20l x a y a -+--=平行,则实数a 等于 ( ) A.4- B.2 C.4-或2 D.23
-
4.某几何体的三视图如图所示,则该几何体的体积为 ( ) A.72π B.64π C.18π D.16π
正视图
俯视图
5.若实数,x y 满足不等式组
{
330
23010
x y x y x y +-≥--≤-+≥,则2z x y =+的最大值为 ( ) A.
27
7
B.14
C.9
D.13 6.已知直线1:257l y x k =-+与直线21
:22
l y x =-+的交点位于第一象限,则实数k 的取值范
围是 ( )
A.1k >
B. 3k <
C.13k <<
D.13k -<< 7.{}123445+1,9,+n a a a a a a a =+=在等比数列中,则等于 ( ) A .-27 B.27 C.±27 D.81
8.若圆C 的半径为2,圆心在第二象限,且与直线4390x y ++=和y 轴都相切,则该圆的标准方程为 ( )
A.()()22234x y ++-=
B.()()22
214x y ++-= C.()()2
2
414x y ++-= D.()()2
2
454x y -+-=
9.已知m 、n 是两条不同直线,αβγ、、是三个不同的平面,下列说法正确的是 ( )
A .m //α,n //α,则m //n B.,αγβγ⊥⊥,则α//β
C. m //α,n //β,则α//β
D.,m n αα⊥⊥,则m //n
10.与圆221106330C x y x y +--+=:和圆2224+210C x y x y +-+=:都相切的切线的条数为 ( )
A.1
B.2
C.3
D.4 11.已知等差数列{}n a 的前n 项和为
n s ,843,0,s s =-≠则4
12
s s 的值为 ( )
A.13-
B.112
- C.112 D.13
12.已知直线20l kx y k -+-=:与曲线4C y +=:实数k 的取值范围是 ( )
A.4(,1]3--
B.(1,0)-
C.(1)2
-- D.4[1,)3
二、填空题(本大题共4小题,每题5分,共20分)。
13.在∆ABC 中,c ,则
sin sin B
C
=________. 14.已知点A (2,-1,4),B (-1,2,3),点P 在x 轴上,且|PA |=|PB |,则点P 坐标为_____
15.若圆C:22440x y x y a +---=上有且仅有两个点到直线l :51250x y ++=的距离等于1,则实数a 的取值范围为____
16.四棱锥P —ABCD 的底面ABCD 为菱形,PA ⊥平面ABCD,PA=AB,∠ABC=60°,点F 为PC 上一动点,则下列说法正确的序号为___。
①点F 在底面的射影在AC 上; ②若F 为PC 的中点,则PA ∥平面BFD ;
③若F 为PC 的中点,则异面直线PA 与DF 的夹角为45°; ④不论点F 在何处,恒有BD ⊥AF 。
三、解答题
17.(本小题满分10分)
在△ABC 中,A,B,C 的对边分别是,,a b c 且2b a =sin B ,A 为锐角。
⑴求A;
⑵若cos bc A =,求△ABC 的面积S.
18. (本小题满分12分)
关于x 的不等式22x x a -+<0的解集为(-1,3) ⑴求实数a 的值;
⑵求函数()(0)a
f x x x x
=-+>的最大值。
19. (本小题满分12分)
等差数列{}n a 中,273,13a a ==,数列{}n b 的前n 项和为n S ,且4
(41)3
n n S =-。
⑴求n a 及n b ;
⑵设1
3
n n n c a a +=,求数列{}n c 的前n 项和n T 。
20. (本小题满分12分)
已知三角形三个定点坐标分别为A(1,4),B(3,-2),C(-2,3), ⑴求AB 边上的中线 CM 的方程; ⑵求BC 边的垂直平分线l 的方程。
21.(本小题满分12分)
如图,在四棱柱ABCD-A 1B 1C 1D 1中,侧棱垂直与底面,且AB ∥DC,AB <
⑴求证:DB ⊥平面B 1BCC 1;
⑵在DC 上是否存在一点E ,使得D 1E ∥A 1BD,并说明理由。
22.(本小题满分12分)
已知半径为3的圆C 的圆心在y 轴上,圆心的纵坐标是整数,且与直线3470x y -+=相切。
⑴求圆C 的方程;
⑵设P 是直线:60l ax y -+=上一点,过点P 作圆C 的切线,若P 与切点间的距离的
a 的值。
