高考数学一轮复习 第3讲 二元一次不等式(组)与简单的线性同步检测 文(1)
.【学科精品】2020届高考数学一轮复习人教B版6.3二元一次不等式(组)与简单的线性规划问题.doc

A.4 C.5
B.1 D .无穷大
2x+ y- 6≤0, 解析: 不等式组 x+ y- 3≥0, 表示的平面区域如图所示 (阴
y≤2
影部分 ),△ ABC 的面积即为所求.求出点 A, B, C 的坐标分别为
(1,2) , (2,2), (3,0),则△ ABC 的面积为
S=
1× 2
(2-
1)×
第三节 二元一次不等式 (组 )与简单的线性规划问题
简单的线性规划 (1) 会从实际情境中抽象出二元一次不等式组. (2) 了解二元一次不等式的几何意义,能用平面区域表示二 元一次不等式组. (3) 会从实际情境中抽象出一些简单的二元线性规划问题, 并能加以解决.
知识点一 区域
二元一次不等式 (组 )表示的平面
x= 2,
得
所以 B(2,1), zmin= 2× 2+ 3× 1= 7,在点 A 处目标函
y=1,
数取到最大值,解方程组
故选 A. 答案: A
x- y=- 1,
x= 4,
得
所以 A(4,5), zmax= 2× 4+3× 5= 23,
2x- y= 3,
y= 5,
4.已知点 P(x, y)满足 目标函数 z=x+ay(a<0) 的最大值和最小值之和为 0,则 a的值为 ( )
解析:画出不等式组
x+ y≥3, x- y≥- 1, 2x- y≤3,
表示的平面区域如图中阴
影部分所示,由目标函数
z= 2x+3y 得
y=-
2 3x+
z3,平移直线
y
x+ y≥3, x- y≥- 1, 2x- y≤3,
=-
2 3x
知在点
B 处目标函数取到最小值,
高考数学 一轮复习配套讲义:第6篇 第3讲 二元一次不等式(组)与简单的线性规划问题

第3讲二元一次不等式(组)与简单的线性规划问题[最新考纲]1.会从实际情境中抽象出二元一次不等式组.2.了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.3.会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.知识梳理1.二元一次不等式(组)表示的平面区域(1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By +C=0某一侧的所有点组成的平面区域(半平面)不含边界直线.不等式Ax+By +C≥0所表示的平面区域(半平面)包括边界直线.(2)对于直线Ax+By+C=0同一侧的所有点(x,y),使得Ax+By+C的值符号相同,也就是位于同一半平面内的点,其坐标适合同一个不等式Ax+By+C>0;而位于另一个半平面内的点,其坐标适合另一个不等式Ax+By+C<0.(3)由几个不等式组成的不等式组所表示的平面区域,是各个不等式所表示的平面区域的公共部分.2.线性规划的有关概念1.对二元一次不等式(组)表示的平面区域的认识(1)点(x 1,y 1),(x 2,y 2)在直线Ax +By +C =0同侧的充要条件是(Ax 1+By 1+C )(Ax 2+By 2+C )>0,异侧的充要条件是(Ax 1+By 1+C )(Ax 2+By 2+C )<0.(√) (2)第二、四象限表示的平面区域可以用不等式xy <0表示.(√)(3)(教材习题改编)已知变量x ,y 满足约束条件⎩⎨⎧x -y +3≥0,-1≤x ≤1,y ≥1,则其表示的平面区域的面积为4.(√)2.对简单的线性规划问题的理解(4)线性目标函数取得最值的点一定在可行域的顶点或边界上.(√)(5)目标函数z =ax +by (b ≠0)中,z 的几何意义是直线ax +by -z =0在y 轴上的截距.(×)(6)(2013·湖南卷改编)若变量x ,y 满足约束条件⎩⎨⎧y ≤2xx +y ≤1y ≥-1,则x +2y 的最大值是53.(√) [感悟·提升]1.确定二元一次不等式表示的平面区域时,经常采用“直线定界,特殊点定域”的方法.2.求线性目标函数z =ax +by (ab ≠0)的最值,当b >0时,直线过可行域且在y 轴上截距最大时,z 值最大,在y 轴截距最小时,z 值最小;当b <0时,直线过可行域且在y 轴上截距最大时,z 值最小,在y 轴上截距最小时,z 值最大.学生用书第100页考点一 二元一次不等式(组)表示的平面区域【例1】 (1)(2014·济南模拟)不等式组⎩⎨⎧2x +y -6≤0,x +y -3≥0,y ≤2表示的平面区域的面积为 ( ).A .4B .1C .5D .无穷大(2)(2013·安徽卷)在平面直角坐标系中,O 是坐标原点,两定点A ,B 满足|OA →|=|OB →|=OA →·OB →=2,则点集{P |OP →=λOA →+μOB →,|λ|+|μ|≤1,λ,μ∈R }所表示的区域的面积是 ( ). A .2 2 B .2 3 C .4 2D .4 3解析(1)不等式组⎩⎨⎧2x +y -6≤0,x +y -3≥0,y ≤2表示的平面区域如图所示(阴影部分),△ABC 的面积即为所求.求出点A ,B ,C 的坐标分别为(1,2),(2,2),(3,0),则△ABC 的面积为S =12×(2-1)×2=1.(2)由|OA →|=|OB →|=OA →·OB →=2,知<OA →,OB →>=π3. 设OA →=(2,0),OB →=(1,3),OP →=(x ,y ),则⎩⎨⎧x =2λ+μ,y =3μ,解得⎩⎪⎨⎪⎧μ=y 3,λ=12⎝⎛⎭⎪⎫x -y 3.由|λ|+|μ|≤1得|3x -y |+|2y |≤2 3. 作可行域如图.则所求面积S =2×12×2×23=4 3.答案 (1)B (2)D规律方法 二元一次不等式组所确定的平面区域是不等式组中各个不等式所表示的半平面区域的公共部分,画出平面区域的关键是把各个半平面区域确定准确,其基本方法是“直线定界、特殊点定域”.【训练1】 若不等式组⎩⎨⎧x -y ≥0,2x +y ≤2,y ≥0,x +y ≤a表示的平面区域是一个三角形,则a 的取值范围是( ).A.⎣⎢⎡⎭⎪⎫43,+∞ B .(0,1]C.⎣⎢⎡⎦⎥⎤1,43 D .(0,1]∪⎣⎢⎡⎭⎪⎫43,+∞解析不等式组⎩⎨⎧x -y ≥0,2x +y ≤2,y ≥0表示的平面区域如图(阴影部分),求A ,B 两点的坐标分别为⎝ ⎛⎭⎪⎫23,23和(1,0),若原不等式组表示的平面区域是一个三角形,则直线x +y =a 的a 的取值范围是0<a ≤1或a ≥43. 答案 D考点二 线性目标函数的最值【例2】 (1)(2013·天津卷)设变量x ,y 满足约束条件⎩⎨⎧3x +y -6≥0,x -y -2≤0,y -3≤0,则目标函数z =y -2x 的最小值为 ( ). A .-7 B .-4 C .1D .2(2)(2013·新课标全国Ⅱ卷)已知a >0,x ,y 满足约束条件⎩⎨⎧x ≥1,x +y ≤3,y ≥a (x -3).若z =2x+y 的最小值为1,则a = ( ). A.14 B.12 C .1D .2解析 (1)由x ,y 满足的约束条件可画出所表示的平面区域为如图所示的△ABC ,作出直线y =2x ,经过平移得目标函数z =y -2x 在点B (5,3)处取得最小值,即z min =3-10=-7.故选A.(2)由约束条件画出可行域(如图所示的△ABC ), 由⎩⎨⎧x =1,y =a (x -3)得A (1,-2a ), 当直线2x +y -z =0过点A 时,z =2x +y 取得最小值,所以1=2×1-2a ,解得a =12,故选B. 答案 (1)A (2)B规律方法 (1)求目标函数最值的一般步骤为:一画、二移、三求.其关键是准确作出可行域,理解目标函数的意义.(2)在约束条件是线性的情况下,线性目标函数只有在可行域的顶点或者边界上取得最值.在解答选择题或者填空题时可以根据可行域的顶点直接进行检验.【训练2】 (2013·浙江卷)设z =kx +y ,其中实数x ,y 满足⎩⎨⎧x +y -2≥0,x -2y +4≥0,2x -y -4≤0.若z 的最大值为12,则实数k =________.解析 约束条件所表示的可行域为如图所示的△ABC ,其中点A (4,4),B (0,2),C (2,0).目标函数z =kx +y ,化为y =-kx +z .当-k ≤12,即k ≥-12时,目标函数z =kx +y 在点A (4,4)取得最大值12,故4k +4=12,k =2,满足题意;当-k >12即k <-12时,目标函数z =kx +y 在点B (0,2)取得最大值12,故k ·0+2=12,无解,综上可知,k =2. 答案 2考点三 线性规划的实际应用【例3】 (2013·湖北卷改编)某客运公司用A ,B 两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次.A ,B 两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B 型车不多于A 型车7辆.若每天要以不少于900人运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A 型车、B 型车各多少辆?审题路线 确定问题属于线性规划问题⇒设A ,B 两种型号车辆的数量为x ,y ,营运成本z ⇒读题,列出线性约束条件及目标函数⇒画出可行域⇒把目标函数变形,平移,确定最小值经过的点⇒解两直线的交点⇒点代入目标函数可得.解 设旅行社租用A 型客车x 辆,B 型客车y 辆,营运成本为z ,则线性约束条件为⎩⎨⎧x +y ≤21,y -x ≤7,36x +60y ≥900,x 、y ∈N ,目标函数为z =1 600x +2 400y .画出可行域:如图中阴影部分所示,可知目标函数过点(5,12)时,有最小值z min =36 800(元). 故应配备A 型车5辆、B 型车12辆.学生用书第101页规律方法 变量,用这两个变量建立可行域和目标函数,在解题时要注意题目中的各种相互制约关系,列出全面的制约条件和正确的目标函数.【训练3】 某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表菜的种植面积(单位:亩)分别为( ).A .50,0B .30,20C .20,30D .0,50解析 设黄瓜、韭菜的种植面积分别为x ,y 亩,则总利润z =4×0.55x +6×0.3y -1.2x -0.9y =x +0.9y .此时x ,y 满足条件⎩⎨⎧x +y ≤50,1.2x +0.9y ≤54,画出可行域如图,得最优解为A (30,20),故选B. 答案 B1.平面区域的画法:线定界、点定域(注意实虚线).2.求最值:求二元一次函数z =ax +by (ab ≠0)的最值,将函数z =ax +by 转化为直线的斜截式:y =-a b x +z b ,通过求直线的截距zb 的最值间接求出z 的最值.最优解在顶点或边界取得.3.解线性规划应用题,可先找出各变量之间的关系,最好列成表格,然后用字母表示变量,列出线性约束条件;写出要研究的函数,转化成线性规划问题.思想方法6——利用线性规划思想求解非线性目标函数的最值【典例】 已知实数x ,y 满足⎩⎨⎧x +y -3≥0,x -y +1≥0,x ≤2.(1)若z =yx ,求z 的最大值和最小值; (2)若z =x 2+y 2,求z 的最大值和最小值.解不等式组⎩⎨⎧x +y -3≥0x -y +1≥0x ≤2表示的平面区域如图所示,图中的阴影部分即为可行域.易得A (1,2),B (2,1), M (2,3).(1)∵z =y x =y -0x -0,∴z 的值即是可行域中的点与原点O 连线的斜率,观察图形可知z max =k OA =2,z min =k OB =12. 所以z 的最大值为2,最小值为12.(2)过原点(0,0)作直线l 垂直于直线x +y -3=0,垂足N ,则直线l 的方程为y =x , 由⎩⎨⎧x +y -3=0,y =x ,得N ⎝ ⎛⎭⎪⎫32,32,点N ⎝ ⎛⎭⎪⎫32,32在线段AB 上,也在可行域内.观察图象可知,可行域内点M 到原点的距离最大,点N 到原点的距离最小,又|OM |=13,|ON |=92,即92≤x 2+y 2≤13,∴92≤x 2+y 2≤13.∴z 的最大值为13,最小值为92.[反思感悟] (1)本题是线性规划的综合应用,考查的是非线性目标函数的最值的求法.(2)解决这类问题的关键是利用数形结合的思想方法,给目标函数赋于一定的几何意义.(3)本题错误率较高.出错原因是,很多学生无从入手,缺乏数形结合的应用意识,不知道从其几何意义入手解题. 【自主体验】(2013·山东卷改编)在平面直角坐标系xOy 中,M 为不等式组⎩⎨⎧2x -y -2≥0,x +2y -1≥0,3x +y -8≤0所表示的区域上一动点,则z =yx 的最小值为( ).A .2B .1C .-13D .-12解析不等式组⎩⎨⎧2x -y -2≥0,x +2y -1≥0,3x +y -8≤0所表示的平面区域如图阴影部分,由图可知,z 的值即是可行域中的点与原点O 连线的斜率.由⎩⎨⎧x +2y -1=0,3x +y -8=0得C (3,-1),当M 点与C 点重合时,z 取最小值,∴z 的最小值为-13,故选C.答案 C对应学生用书P301基础巩固题组(建议用时:40分钟)一、选择题1.(2013·衡阳模拟)不等式(x -2y +1)(x +y -3)≤0在坐标平面内表示的区域(用阴影部分表示),应是下列图形中的( ).解析 (x -2y +1)(x +y -3)≤0⇒⎩⎨⎧ x -2y +1≥0,x +y -3≤0或⎩⎨⎧x -2y +1≤0,x +y -3≥0.画出平面区域后,只有C 合题意. 答案 C2.(2014·泰安模拟)不等式组⎩⎨⎧y ≤-x +2,y ≤x -1,y ≥0所表示的平面区域的面积为( ).A .1 B.12 C.13 D.14解析 作出不等式组对应的区域为△BCD ,由题意知x B =1,x C =2.由⎩⎨⎧y =-x +2,y =x -1,得y D =12,所以S △BCD =12×(x C -x B )×12=14. 答案 D3.(2014·杭州模拟)在约束条件⎩⎪⎨⎪⎧y ≤x ,y ≥12x ,x +y ≤1下,目标函数z =x +12y 的最大值为( ).A.14B.34C.56D.53解析 由z =x +12y ,得y =-2x +2z .作出可行域如图阴影部分,平移直线y =-2x +2z ,当直线经过点C 时,直线y =-2x +2z 在y 轴上的截距最大,此时z 最大. 由⎩⎪⎨⎪⎧y =12x ,x +y =1,解得C 点坐标为⎝ ⎛⎭⎪⎫23,13,代入z =x +12y ,得z =23+12×13=56.答案 C4.(2013·佛山一检)若变量x ,y 满足约束条件⎩⎨⎧y ≤1,x +y ≥0,x -y -2≤0,则z =x -2y 的最大值为( ).A .4B .3C .2D .1 解析 画出可行域(如下图),由z =x -2y 得y =12x -z2,则当目标函数过C (1,-1)时取得最大值,所以z max =1-2×(-1)=3.故选B. 答案 B5.(2013·北京卷)设关于x ,y的不等式组⎩⎨⎧2x -y +1>0,x +m <0,y -m >0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2.求得m 的取值范围是( ).A.⎝ ⎛⎭⎪⎫-∞,43B.⎝ ⎛⎭⎪⎫-∞,13 C.⎝ ⎛⎭⎪⎫-∞,-23 D.⎝ ⎛⎭⎪⎫-∞,-53解析 由线性约束条件可画出如图所示的阴影区域,要使区域内存在点P (x 0,y 0),使x 0-2y 0=2成立,只需点A (-m ,m )在直线x -2y -2=0的下方即可,即-m -2m -2>0,解得m <-23,故选C. 答案 C 二、填空题6.(2013·陕西卷)若点(x ,y )位于曲线y =|x -1|与y =2所围成的封闭区域,则2x -y 的最小值为________.解析 由题意知y =⎩⎨⎧x -1(x ≥1),1-x (x <1),作出曲线y =|x -1|与y =2所围成的封闭区域,如图中阴影部分所示,即得过点A (-1,2)时,2x -y 取最小值-4. 答案 -47.(2014·淮安质检)若不等式组⎩⎨⎧x -y +5≥0,y ≥a ,0≤x ≤2表示的平面区域是一个三角形,则a 的取值范围是________.解析 画出可行域,知当直线y =a 在x -y +5=0与y 轴的交点(0,5)和x -y +5=0与x =2的交点(2,7)之间移动时平面区域是三角形,故5≤a <7. 答案 [5,7)8.(2013·广东卷)给定区域D :⎩⎨⎧x +4y ≥4,x +y ≤4,x ≥0,令点集T ={(x 0,y 0)∈D |x 0,y 0∈Z ,(x 0,y 0)是z =x +y 在D 上取得最大值或最小值的点},则T 中的点共确定________条不同的直线.解析 作出图形可知,△ABF 所围成的区域即为区域D ,其中A (0,1)是z 在D 上取得最小值的点,B ,C ,D ,E ,F 是z 在D 上取得最大值的点,则T 中的点共确定AB ,AC ,AD ,AE ,AF ,BF 共6条不同的直线. 答案 6 三、解答题9.(2014·合肥模拟)画出不等式组⎩⎨⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域,并回答下列问题:(1)指出x ,y 的取值范围; (2)平面区域内有多少个整点?解 (1)不等式x -y +5≥0表示直线x -y +5=0上及其右下方的点的集合,x +y ≥0表示直线x +y =0上及其右上方的点的集合,x ≤3表示直线x =3上及其左方的点的集合.所以,不等式组⎩⎨⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域如图所示.结合图中可行域得x ∈⎣⎢⎡⎦⎥⎤-52,3,y ∈[-3,8].(2)由图形及不等式组知⎩⎪⎨⎪⎧-x ≤y ≤x +5,-52≤x ≤3,且x ∈Z ,当x =3时,-3≤y ≤8,有12个整点; 当x =2时,-2≤y ≤7,有10个整点; 当x =1时,-1≤y ≤6,有8个整点; 当x =0时,0≤y ≤5,有6个整点; 当x =-1时,1≤y ≤4,有4个整点; 当x =-2时,2≤y ≤3,有2个整点;∴平面区域内的整点共有2+4+6+8+10+12=42(个).10.制订投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%.若投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大? 解 设投资人分别用x 万元,y 万元投资甲、乙两个项目,由题意知⎩⎨⎧x +y ≤10,0.3x +0.1y ≤1.8,x ≥0,y ≥0,目标函数z =x +0.5y .上述不等式组表示的平面区域如图所示,阴影部分(含边界)即为可行域. 将z =x +0.5y 变形为y =-2x +2z ,这是斜率为-2随z 变化的一组平行线,当直线y =-2x +2z 经过可行域内的点M 时,直线y =-2x +2z 在y 轴上的截距2z 最大,z 也最大.这里M 点是直线x +y =10和0.3x +0.1y =1.8的交点. 解方程组⎩⎨⎧x +y =10,0.3x +0.1y =1.8,得x =4,y =6,此时z =4+0.5×6=7(万元). ∴当x =4,y =6时,z 取得最大值,所以投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8万元的前提下,使可能的盈利最大.能力提升题组 (建议用时:25分钟)一、选择题1.(2014·昆明模拟)已知x ,y 满足条件⎩⎨⎧x ≥0,y ≤x ,2x +y +k ≤0(k 为常数),若目标函数z =x +3y 的最大值为8,则k =( ). A .-16 B .-6 C .-83 D .6解析 画出x ,y 满足的可行域如图,联立方程⎩⎨⎧y =x ,2x +y +k =0,解得⎩⎪⎨⎪⎧x =-k 3,y =-k 3,即C 点坐标为⎝ ⎛⎭⎪⎫-k3,-k 3,由目标函数z =x +3y ,得y =-13x +z 3,平移直线y =-13x +z 3,可知当直线经过C 点时,直线y =-13x +z3的截距最大,此时z 最大,把C 点代入z =x +3y ,得8=-k 3+3×⎝ ⎛⎭⎪⎫-k 3,解得k =-6.经检验,符合题意.答案 B2.(2014·临沂一模)已知实数x ,y 满足不等式组⎩⎨⎧x -y +2≥0,x +y -4≥0,2x -y -5≤0,若目标函数z=y -ax 取得最大值时的唯一最优解是(1,3),则实数a 的取值范围为( ).A .(-∞,-1)B .(0,1)C .[1,+∞)D .(1,+∞)解析 作出不等式对应的平面区域BCD ,由z =y -ax ,得y =ax +z ,要使目标函数y =ax +z 仅在点(1,3)处取最大值,则只需直线y =ax +z 仅在点B (1,3)处的截距最大,由图象可知a >k BD ,因为k BD =1,所以a >1,即a 的取值范围是(1,+∞). 答案 D 二、填空题3.(2013·江苏卷)抛物线y =x 2在x =1处的切线与两坐标轴围成的三角形区域为D (包含三角形内部与边界).若点P (x ,y )是区域D 内的任意一点,则x +2y 的取值范围是________.解析 ∵y =x 2,∴y ′|x =1=2x |x =1=2.故抛物线y =x 2在x =1处的切线方程为2x -y -1=0,设其与x 轴、y 轴交于A ,B 两点,则A ⎝ ⎛⎭⎪⎫12,0,B (0,-1),区域D 为如图阴影部分,令z =x +2y ,即y =-12x +12z ,易知y =-12x +12z 分别过A ,B 两点时z 取最大、最小值,∴z max =12+2×0=12,z min =0+2×(-1)=-2, ∴x +2y 的取值范围是⎣⎢⎡⎦⎥⎤-2,12.答案 ⎣⎢⎡⎦⎥⎤-2,12 三、解答题4.变量x ,y 满足⎩⎨⎧x -4y +3≤0,3x +5y -25≤0,x ≥1.(1)设z =yx ,求z 的最小值; (2)设z =x 2+y 2,求z 的取值范围;(3)设z =x 2+y 2+6x -4y +13,求z 的取值范围.解 由约束条件⎩⎨⎧x -4y +3≤0,3x +5y -25≤0,x ≥1.作出(x ,y )的可行域如图阴影部分所示.由⎩⎨⎧ x =1,3x +5y -25=0,解得A ⎝ ⎛⎭⎪⎫1,225.由⎩⎨⎧x =1,x -4y +3=0,解得C (1,1). 由⎩⎨⎧x -4y +3=0,3x +5y -25=0,解得B (5,2). (1)∵z =y x =y -0x -0.∴z 的值即是可行域中的点与原点O 连线的斜率.观察图形可知z min =k OB =25.(2)z =x 2+y 2的几何意义是可行域上的点到原点O 的距离的平方.结合图形可知,可行域上的点到原点的距离中, d min =|OC |=2,d max =|OB |=29. 故z 的取值范围是[2,29].(3)z =x 2+y 2+6x -4y +13=(x +3)2+(y -2)2的几何意义是可行域上的点到点(-3,2)的距离的平方.结合图形可知,可行域上的点到(-3,2)的距离中,d min =1-(-3)=4,d max =(-3-5)2+(2-2)2=8. 故z 的取值范围是[16,64].学生用书第102页。
2021年高考数学一轮复习 第3讲 二元一次不等式(组)与简单的线性同步检测 文

2021年高考数学一轮复习 第3讲 二元一次不等式(组)与简单的线性同步检测 文一、选择题1.不等式x -2y >0表示的平面区域是( ).解析 将点(1,0)代入x -2y 得1-2×0=1>0. 答案 D2.设实数x ,y 满足不等式组⎩⎨⎧x +2y -5>0,2x +y -7>0,x ≥0,y ≥0.若x ,y 为整数,则3x +4y 的最小值是( ).A .14B .16C .17D .19解析 线性区域边界上的整点为(3,1),因此最符合条件的整点可能为(4,1)或(3,2),对于点(4,1),3x +4y =3×4+4×1=16;对于点(3,2),3x +4y =3×3+4×2=17,因此3x +4y 的最小值为16. 答案 B 3.若不等式组⎩⎪⎨⎪⎧x -y +5≥0,y ≥a ,0≤x ≤2表示的平面区域是一个三角形,则a 的取值范围是( ). A .(-∞,5) B .[7,+∞)C .[5,7)D .(-∞,5)∪[7,+∞)解析 画出可行域,知当直线y =a 在x -y +5=0与y 轴的交点(0,5)和x -y +5=0与x =2的交点(2,7)之间移动时平面区域是三角形.故5≤a <7.答案 C4.设实数x ,y 满足条件⎩⎪⎨⎪⎧4x -y -10≤0,x -2y +8≥0,x ≥0,y ≥0,若目标函数z =ax +by (a >0,b >0)的最大值为12,则2a +3b的最小值为( ). A.256B.83C.113D .4解析 由可行域可得,当x =4,y =6时,目标函数z =ax +by 取得最大值,∴4a +6b=12,即a 3+b 2=1.∴2a +3b =⎝ ⎛⎭⎪⎫2a +3b ·⎝ ⎛⎭⎪⎫a 3+b 2=136+b a +a b ≥136+2=256.答案 A5.实数x ,y 满足⎩⎪⎨⎪⎧x ≥1,y ≤a a >1,x -y ≤0,若目标函数z =x +y 取得最大值4,则实数a 的值为( ).A .4B .3C .2D.32解析 作出可行域,由题意可知可行域为△ABC 内部及边界,y =-x +z ,则z 的几何意义为直线在y 轴上的截距,将目标函数平移可知当直线经过点A 时,目标函数取得最大值4,此时A 点坐标为(a ,a ),代入得4=a +a =2a ,所以a =2. 答案 C6.某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A 原料1千克、B 原料2千克;生产乙产品1桶需耗A 原料2千克、B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A 、B 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是 ( ). A .1 800元B .2 400元C .2 800元D .3 100元解析 设某公司生产甲产品x 桶,生产乙产品y 桶,获利为z 元,则x ,y 满足的线性约束条件为⎩⎪⎨⎪⎧x +2y ≤12,2x +y ≤12,x ≥0且y ∈Z ,y ≥0且y ∈Z ,目标函数z =300x +400y .作出可行域,如图中四边形OABC 的边界及其内部整点.作直线l 0:3x +4y =0,平移直线l 0经可行域内点B 时,z 取最大值,由⎩⎪⎨⎪⎧2x +y =12,x +2y =12,得B (4,4),满足题意,所以z max=4×300+4×400=2 800. 答案 C 二、填空题7.若x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,x +y -3≤0,x +3y -3≥0,则z =3x -y 的最小值为________.解析 画出可行域,如图所示,将直线y =3x -z 移至点A (0,1)处直线在y 轴上截距最大,z min =3×0-1=-1.答案 -18.若x ,y 满足约束条件⎝ ⎛x ≥0,x +2y ≥3,2x +y ≤3,则x-y 的取值范围是________.解析 记z =x -y ,则y =x -z ,所以z 为直线y =x -z 在y 轴上的截距的相反数,画出不等式组表示的可行域如图中△ABC 区域所示.结合图形可知,当直线经过点B (1,1)时,x -y 取得最大值0,当直线经过点C (0,3)时,x -y 取得最小值-3.答案 [-3,0]9.设实数x 、y 满足⎩⎪⎨⎪⎧x -y -2≤0,x +2y -4≥0,2y -3≤0,则yx的最大值是________.解析 不等式组确定的平面区域如图阴影部分. 设y x =t ,则y =tx ,求y x的最大值,即求y =tx 的斜率的最大值.显然y =tx 过A 点时,t 最大.由⎩⎪⎨⎪⎧x +2y -4=0,2y -3=0,解得A ⎝ ⎛⎭⎪⎫1,32.代入y =tx ,得t =32.所以y x 的最大值为32.答案3210.设m >1,在约束条件⎩⎪⎨⎪⎧y ≥x ,y ≤mx ,x +y ≤1下,目标函数z =x +my 的最大值小于2,则m 的取值范围为________.解析 目标函数z =x +my 可变为y =-1m x +zm,∵m >1,∴-1<-1m <0,z 与zm同时取到相应的最大值,如图,当目标函数经过点P ⎝⎛⎭⎪⎫1m +1,m m +1时,取最大值,∴1m +1+m 2m +1<2,又m >1,得1<m <1+ 2.答案 (1,1+2) 三、解答题11.设集合A ={(x ,y )|x ,y,1-x -y 是三角形的三边长}. (1)求出x ,y 所满足的不等式; (2)画出点(x ,y )所在的平面区域.解 (1)已知条件即⎩⎪⎨⎪⎧x +y >1-x -y >0,x +1-x -y >y >0,y +1-x -y >x >0,化简即⎩⎪⎨⎪⎧-x +12<y <-x +1,0<y <12,0<x <12.(2)区域如下图.12.画出不等式组⎩⎪⎨⎪⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域,并回答下列问题:(1)指出x 、y 的取值范围;(2)平面区域内有多少个整点?解 (1)不等式x -y +5≥0表示直线x -y +5=0上及其右下方的点的集合,x +y ≥0表示直线x +y =0上及其右上方的点的集合,x ≤3表示直线x =3上及其左方的点的集合.所以,不等式组⎩⎪⎨⎪⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域如图所示.结合图中可行域得x ∈⎣⎢⎡⎦⎥⎤-52,3,y ∈[-3,8].(2)由图形及不等式组知⎩⎪⎨⎪⎧-x ≤y ≤x +5,-52≤x ≤3,且x ∈Z ,当x =3时,-3≤y ≤8,有12个整点; 当x =2时,-2≤y ≤7,有10个整点; 当x =1时,-1≤y ≤6,有8个整点; 当x =0时,0≤y ≤5,有6个整点; 当x =-1时,1≤y ≤4,有4个整点; 当x =-2时,2≤y ≤3,有2个整点;∴平面区域内的整点共有2+4+6+8+10+12=42(个).13.若x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥1,x -y ≥-1,2x -y ≤2,(1)求目标函数z =12x -y +12的最值.(2)若目标函数z =ax +2y 仅在点(1,0)处取得最小值,求a 的取值范围. 解 (1)作出可行域如图,可求得A (3,4),B (0,1),C (1,0).平移初始直线12x -y =0,过A (3,4)取最小值-2,过C (1,0)取最大值1.∴z 的最大值为1,最小值为-2.(2)直线ax +2y =z 仅在点(1,0)处取得最小值,由图象可知-1<-a2<2,解得-4<a <2.故所求a 的取值范围是(-4,2).14.某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率多0.25,甲产品为二等品的概率比乙产品为一等品的概率少0.05.(1)分别求甲、乙产品为一等品的概率P 甲,P 乙;(2)已知生产一件产品需要用的工人数和资金数如表所示,且该厂有工人32名,可用资金55万元.设x ,y 分别表示生产甲、乙产品的数量,在(1)的条件下,求x ,y 为何值时,z =xP 甲+yP 乙最大,最大值是多少?项目 用量 产品工人(名)资金(万元)甲 4 20 乙85解 (1)依题意得⎩⎪⎨⎪⎧P 甲-P 乙=0.25,1-P 甲=P 乙-0.05,解得⎩⎪⎨⎪⎧P 甲=0.65,P 乙=0.4,故甲产品为一等品的概率P 甲=0.65,乙产品为一等品的概率P 乙=0.4. (2)依题意得x 、y 应满足的约束条件为 ⎩⎪⎨⎪⎧4x +8y ≤32,20x +5y ≤55,x ≥0,y ≥0,且z =0.65x +0.4y .作出不等式组所表示的平面区域,如图阴影部分,即可行域.作直线l 0:0.65x +0.4y =0即13x +8y =0,把直线l 向上方平移到l 1的位置时,直线经过可行域内的点M ,此时z 取得最大值.解方程组⎩⎪⎨⎪⎧x +2y =8,4x +y =11,得x =2,y =3.故M 的坐标为(2,3),所以z 的最大值为z max =0.65×2+0.4×3=2.5.所以,当x =2,y =3时,z 取最大值为2.5.!fnr0P# 35912 8C48 豈o3GnG。
最新高考数学(理)一轮复习讲义 二元一次不等式(组)及简单的线性规划问题

所以不难看出,x≥0,y≥0,200x+300y≤1 400,200x+100y≤900.
200x+300y≤1 400, 答案: 200x+100y≤900,
x≥0, y≥0
一、思考辨析 判断正误(正确的打“√”,错误的打“×”) (1)不等式 Ax+By+C>0 表示的平面区域一定在直线 Ax+By+C=0 的上方.( ) (2)线性目标函数的最优解可能是不唯一的.( ) (3)线性目标函数取得最值的点一定在可行域的顶点或边界上.( ) (4)在目标函数 z=ax+by(b≠0)中,z 的几何意义是直线 ax+by-z=0 在 y 轴上的截 距.( ) 答案:(1)× (2)√ (3)√ (4)× 二、易错纠偏 常见误区|K(1)不会用代点法判断平面区域; (2)不明确目标函数的最值与等值线截距的关系; (3)不理解目标函数的几何意义; (4)对“最优解有无数个”理解有误. 1.点(-2,t)在直线 2x-3y+6=0 的上方,则 t 的取值范围是__________. 解析:因为直线 2x-3y+6=0 的上方区域可以用不等式 2x-3y+6<0 表示,所以由点 (-2,t)在直线 2x-3y+6=0 的上方得-4-3t+6<0,解得 t>2.
3.已知 x,y 满足条____. x+3
x≤3,
解析:
作出可行域如图中阴影部分所示,问题转化为区域上哪一点与点 M(-3,1)连线斜率最
大,观察知点 A
-5,5 22
,使 kMA 最大,zmax=kMA=
5-1 2
=3.
-5+3
2
答案:3
x-y+5≥0, 4.已知 x,y 满足 x+y≥0, 若使得 z=ax+y 取最大值的点(x,y)有无数个,则 a
高考数学一轮同步训练文科二元一次不等式组与简单的线性规划问题

高考数学一轮同步训练(文科)-.二元一次不等式(组)与简单的线性规划问题————————————————————————————————作者: ————————————————————————————————日期:2013高考数学一轮强化训练 6.3二元一次不等式(组)与简单的线性规划问题文新人教A版1.已知(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )A.a<1或a>24B.a=7或a=24C.-7<a<24ﻩD.-24<a<7答案:C2.已知实数x,y满足121yy xx y m≥,⎧⎪≤-,⎨⎪+≤,⎩如果目标函数z=x-y的最小值为-1,则实数m等于( )A.7 B.5 C.4ﻩD.3答案:B解析:将直线y=x+1与y=2x-1联立解得A(2,3),据题意即为最优解,又点A必在直线x+y=m上,代入求得m=5.3.已知实数x、y满足223y xy xx≤,⎧⎪≥-,⎨⎪≤,⎩则目标函数z=x-2y的最小值是 . 答案:-9解析:如图作出可行域为阴影部分,由23y xx=,⎧⎨=⎩得36xy=,⎧⎨=,⎩即A(3,6),经过分析可知直线z=x-2y经过A点时目标函数z=x-2y取最小值为-9.4.不等式组2020220x yx yx y-+≥,⎧⎪++≥,⎨⎪--≤⎩所确定的平面区域记为D.点(x,y)是区域D上的点,若圆O:222x y r+=上的所有点都在区域D上,则圆O的面积的最大值是 . 答案:45π解析:画出不等式组2020220x yx yx y-+≥,⎧⎪++≥,⎨⎪--≤⎩所表示的平面区域(略),其中直线离原点最近的距离为255,故r的最大值为255,所以圆O的面积的最大值是45π.题组一二元一次不等式(组)表示的平面区域1.在平面直角坐标系中,若不等式组101010x yxax y+-≥,⎧⎪-≤,⎨⎪-+≥⎩(a为常数)所表示的平面区域的面积等于2,则a的值为( )A.-5ﻩB.1 C.2D.3答案:D解析:不等式组101010x yxax y+-≥,⎧⎪-≤,⎨⎪-+≥⎩所围成的区域如图所示.则A(1,0),B(0,1),C(1,1+a),且a>-1,∵2ABCS=,∴1(1)2a+⨯1=2,解得a=3.2.满足条件202305350y xx yx y-≤,⎧⎪++>,⎨⎪+-<⎩的可行域中整点的个数为 ( )A.3ﻩB.4ﻩC.5 D.6答案:B解析:画出可行域,作出网格知有4个整点,分别是(0,0),(0,-1),(1,-1),(2,-2).3.如下图,能表示平面中阴影区域的不等式组是.答案:220236x yyx y-+≥,⎧⎪≥,⎨⎪+≤⎩题组二求目标函数的最值4.若x y,∈R,且1230xx yy x≥,⎧⎪-+≥,⎨⎪≥,⎩则z=x+2y的最小值等于( )A.2ﻩB.3ﻩC.5ﻩD.9答案:B解析:由z=x+2y得1122y x z=-+,当直线经过直线x=1和y=x的交点A(1,1)时,截距z 取得最小值,故z=1+2=3.5.设变量x,y满足约束条件220xx yx y≥,⎧⎪-≥,⎨⎪--≤,⎩则z=3x-2y的最大值为( )A.0 B.2C.4 D.6答案:C解析:作出可行域,图中阴影部分为约束条件限定区域,当z=3x-2y过点(0,-2)时,z=3x-2y取最大值,且为4.6.已知关于x、y的二元一次不等式组24120x yx yx+≤,⎧⎪-≤,⎨⎪+≥.⎩求函数u=3x-y的最大值和最小值.解:作出二元一次不等式组24120x yx yx+≤,⎧⎪-≤,⎨⎪+≥⎩表示的平面区域,如图所示.由u=3x-y,得y=3x-u,表示斜率为3,在y轴上的截距为-u,随u变化的一组平行线, 由图可知,当直线y=3x-u经过可行域上的C点时,截距-u最大,即u最小,解方程组2420x yx+=,⎧⎨+=,⎩得C(-2,3),∴min 3(2)39u=⨯--=-.当直线y=3x-u经过可行域上的B点时,截距-u最小,即u最大,解方程组241x yx y+=,⎧⎨-=,⎩得B(2,1),∴max 3215u=⨯-=.∴u=3x-y的最大值是5,最小值是-9. ﻫ题组三线性规划的简单应用7.在”家电下乡”活动中,某厂要将100台洗衣机运往邻近的乡镇.现有4辆甲型货车和8辆乙型货车可供使用.每辆甲型货车运输费用400元,可装洗衣机20台;每辆乙型货车运输费用300元,可装洗衣机10台.若每辆车至多只运一次,则该厂所花的最少运输费用为( )A.2 000元ﻩB.2 200元C.2400元 D.2 800元答案:B解析:设需使用甲型货车x 辆,乙型货车y辆,运输费用z 元,根据题意,得线性约束条件20101000408x y x y +≥,⎧⎪≤≤,⎨⎪≤≤.⎩求线性目标函数z=400x+300y 的最小值.解得当 42x y =,⎧⎨=⎩时min 2z ,= 200. 8.某加工厂用某原料由甲车间加工出A 产品,由乙车间加工出B 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A 产品,每千克A 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天总活力最大的生产计划为( )A .甲车间加工原料10箱,乙车间加工原料60箱B.甲车间加工原料15箱,乙车间加工原料55箱C .甲车间加工原料18箱,乙车间加工原料50箱D.甲车间加工原料40箱,乙车间加工原料30箱答案:B解析:设甲车间加工原料x 箱,乙车间加工原料y箱,根据题意,得约束条件7010648000x y x y x y x y N +≤,⎧⎪+≤,⎪⎨≥,≥,⎪⎪∈,⎩、 画出可行域.目标函数z=280x+200y,即75200z y x =-+,作直线75y x =-并平移,得直线经过点A(15,55)时z 取最大值.所以当x=15,y=55时,z取最大值.9.某班计划用少于100元的钱购买单价分别为2元和1元的大小彩色气球装点联欢晚会的会场,根据需要,大球数不少于10个,小球数不少于20个,请你给出几种不同的购买方案?解:设可购买大球x 个,小球y 个.依题意有 21001020x y x y x N y N *+<,⎧⎪≥,⎪⎪≥,⎨⎪∈,⎪∈*,⎪⎩其整数解为 1020x y =,⎧⎨=,⎩ 2030x y =,⎧⎨=,⎩ 3030x y =,⎧⎨=,⎩ 3529x y =,⎧⎨=,⎩ …都符合题目要求(满足2x+y-100<0即可). ﻫ题组四 线性规划问题的综合应用10.若2422m n +<,则点(m ,n)必在( )A.直线x +y=1的左下方B.直线x+y=1的右上方C.直线x+2y=1的左下方D.直线x+2y=1的右上方答案:C解析:∵22242222m n m n m n ++=+≥,∴22222m n +<,即m+2n<1,∴点(m,n)必在直线x+2y=1的左下方.11.若线性目标函数z=x+y在线性约束条件 3020x y x y y a +-≤,⎧⎪-≤,⎨⎪≤⎩下取得最大值时的最优解只有一个,则实数a 的取值范围是 .答案:2a ≤解析:作出可行域如图:由图可知直线y=-x 与y=-x+3平行,若最大值只有一个,则直线y =a 不能在直线y=2x 与y=-x +3的交点(1,2)的上方,故2a ≤.12.某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?解:方法一:设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z元,则依题意得z=2.5x+4y,且x,y 满足00 12864 6642 61054 x yx yx yx y≥,≥,⎧⎪+≥,⎪⎨+≥,⎪⎪+≥,⎩即00321673527x yx yx yx y≥,≥,⎧⎪+≥,⎪⎨+≥,⎪⎪+≥.⎩z在可行域的四个顶点A(9,0),B(4,3),C(2,6),D(0,8)处的值分别是2AZ=.59⨯+40⨯=22.5,2BZ=.544322⨯+⨯=,2CZ=.524525⨯+⨯=,2DZ=.504832⨯+⨯=.比较之BZ,最小,因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.方法二:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元, 则依题意得z=2.5x+4y,且x,y满足0012864664261054x yx yx yx y≥,≥,⎧⎪+≥,⎪⎨+≥,⎪⎪+=,⎩即00321673527x yx yx yx y≥,≥,⎧⎪+≥,⎪⎨+≥,⎪⎪+≥.⎩让目标函数表示的直线2.5x+4y=z在可行域上平移,由此可知z=2.5x+4y在B(4,3)处取得最小值.因此,应该为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.ﻩ。
(旧教材适用)2023高考数学一轮总复习第七章不等式第3讲二元一次不等式(组)及简单的线性规划问题课

答案 C
解析 由约束条件可得可行域如图中阴影部分所示,由 z=3x+y,得 y =-3x+z,平移直线 y=-3x,由图可得,当直线 z=3x+y 过点 B(1,3)时, z 取最小值为 6,故选 C.
求 z=ax+by 的最值时,一般先化为 y=-abx+bz的形式.bz 为直线 y=-abx+bz在 y 轴上的截距,当 b>0 时将直线上移 z 变大,当 b<0 时将直线下移 z 变大.
2.线性规划中的基本概念
名称
定义
约束条件
由变量 x,y 组成的□03 不等式(组)
线性约束条件 目标函数
线性目标函数
关于 x,y 的 □04 一次 不等式(或等式)
关于 x,y 的 □05 函数解析式 ,如 z=2x+3y 等
关于 x,y 的 □06 一次
解析式
可行解
满足 □07 线性约束条件的解(x,y)
2.(2021·浙江高考)若实数 x,y 满足约束条件
x+1≥0,
x-y≤0,
则
2x+3y-1≤0,
z=x-12y
的最小值是(
)
A.-2 B.-32 C.-12 D.110
答案 B
解析 作出可行域如图中阴影部分所示,作出直线 y=2x 并平移,数形 结合可知,当平移后的直线经过点 A 时 z 取得最小值.由2x+x+13=y-0,1=0,得 xy= =- 1,1,所以 A(-1,1),zmin=-1-12=-32.故选 B.
2.画二元一次不等式表示的平面区域的方法 (1)直线定界:不等式中无等号时直线画成虚线,有等号时直线画成实线. (2)特殊点定域:若直线不过原点,特殊点常选原点;若直线过原点,则 特殊点常选取(0,1)或(1,0)来验证.
二元一次不等式(组)与简单的线性规划问题课件-2023届高三数学(文)一轮总复习

解析:在平面直角坐标系内画出题中的不等式组表示的平面区域,其是以(2,
0),(0,2),(4,2)为顶点的三角形区(包含边界)(图略),易得当目标函数z1=2x
-y经过平面区域内的点(4,2)时,取得最大值2×4-2=6.z2=x2+y2表示平面区
域内的点到原点的距离的平方,易得原点到直线x+y=2的距离的平方为所求最
z=x2+y2+6x-4y+13=(x+3)2+(y-2)2的几何意义是可行域上的点到点(-3
,2)的距离的平方.结合图形可知,可行域上的点到(-3,2)的距离中,dmin=1
-(-3)=4,dmax= −3 − 5 2
所以z的取值范围为[16,64].
+ 2 − 2 2 =8.
y
2.(变问题)若例2中条件不变,将“z= ”改为“z=|x+y|”,如何
,B,设想培优小组A中,每1名学生需要配备2名理科教师和2名文科
教师做导师;设想培优小组B中,每1名学生需要配备3名理科教师和1
名文科教师做导师.若学校现有14名理科教师和9名文科教师积极支
5
持,则两培优小组能够成立的学生人数和最多是_____.
反思感悟
第三节 二元一次不等式(组)
与简单的线性规划问题
·考向预测·
考情分析:主要考查利用线性规划知识求目标函数的最值、取值范
围、参数的取值(范围)以及实际应用,目标函数大多是线性的,偶尔
也会出现斜率型和距离型的目标函数,此部分内容仍是高考的热点,
主要以选择题和填空题的形式出现.
学科素养:通过线性规划在求最值中的应用问题考查直观想象、数
最大值
最小值
最大值
在线性约束条件下求线性目标函数的________或
高考数学第一轮知识点 第3课时 二元一次不等式组与简单的线性规划问题课时复习课件 理

作出可行域如图,让目标函数表示的直线 2.5x+4y=z 在可行域上平移,由此可知 z =2.5x+4y 在 B(4,3)处取得最小值. 因此,应当为该儿童预订 4 个单位的午餐和
3 个单位的晚餐,就可满足要求.
【变式训练】 3.某家具厂有方木料 90 m3,五合 板 600 m2,准备加工成书桌和书橱出售.已知生 产每张书桌需要方木料 0.1 m3,五合板 2 m2,生 产每个书橱需要方木料 0.2 m3、五合板 1 m2,出 售一张书桌可获利润 80 元,出售一个书橱可获利 润 120 元. (1)如果只安排生产书桌,可获利润多少? (2)如果只安排生产书橱,可获利润多少?
.D
恰为
AC
的中点,直线
y=x+2
将△
ABC 的面积平分.故选 A.
答案: A
【变式训练】 1.(2011·吉林延边州一模)若不
x-y+5≥0,
等式组y≥a, 0≤x≤3
表示的平面区域是一
个三角形,则 a 的取值范围是( )
A.a<5
B.a≥8
C.a<5 或 a≥8
D.5≤a<8
解析: 作出如图所示的可行域,要使该平面 区域表示三角形,需满足 5≤a<8.
答案: D
求目标函数的最值 1.求目标函数的最值,必须先准确地作出线 性可行域再作出目标函数对应的直线,据题 意确定取得最优解的点,进而求出目标函数 的最值. 2.线性目标函数 z=ax+by 取最大值时的最 优解与 b 的正负有关,当 b>0 时,最优解是将 直线 ax+by=0 在 2y-1=0
得 D(1,0),
∴kCD=0,kCA=1212-+01=13,∴z 的范围是0,31;
(3)z=
高考数学(理科)一轮复习课件:不等式 第3节 二元一次不等式(组)与简单的线性规划问题
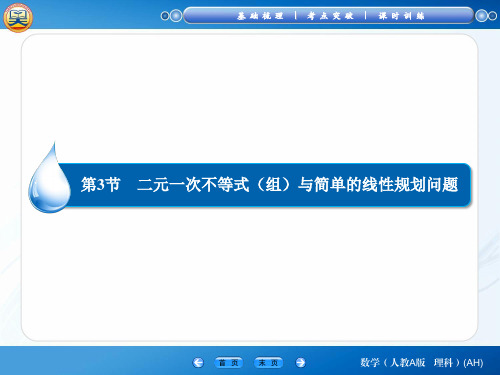
A. 3
B.3
C. 2
D.2
数学(人教A版 ·理科)(AH)
基础梳理
考点突破
课时训练
[思维导引]作出可行域,由区域面积求出a.
数学(人教A版 ·理科)(AH)
基础梳理
考点突破
课时训练
[解析]
作出可行域如图所示,
∵直线 x+ay=2 过点(2,0),
由xy+=ay3=x,2,
可解得交点
A
的纵坐标为
数学(人教A版 ·理科)(AH)
基础梳理
考点突破
课时训练
3.线性规划的有关概念
名称 约束条件 线性约束条件 目标函数 线性目标函数 可行解 可行域 最优解
线性规划问题
意义 由变量x、y组成的___不__等__式__(组__)_ 由x、y的 一次 不等式(或方程)组成的不等式组 欲求 最大值 或 最小值 的函数
基础梳理
考点突破
课时训练
第3节 二元一次不等式(组)与简单的线性规划问题
数学(人教A版 ·理科)(AH)
基础梳理
考点突破
课时训练
基础梳理
数学(人教A版 ·理科)(AH)
基础梳理
考点突破
课时训练
1.二元一次不等式(组)的解集 满足二元一次不等式(组)的x和y的取值构成的 ___有__序__数__对__(x_,__y_)__,叫做二元一次不等式(组)的解,所有 这样的 有序数对(x,y) 构成的集合称为二元一次不等式
2, 33+a
依题意有
S△=12×2×
2= 33+a
Hale Waihona Puke 23,∴解得a=3.故选 A.
数学(人教A版 ·理科)(AH)
基础梳理
高考数学复习讲义:二元一次不等式(组) 与简单的线性规划问题

返回
[解析] (1)作出满足约束条 件的可行域如图中阴影部分所 示.由 z=3x+2y,得 y=-32x+2z.
作直线 l0:y=-32x. 平移直线 l0,当直线 y=-32x+2z过点(2,0)时, z 取最大值,zmax=3×2+2×0=6.
返回
(2)
由
条
件
得
x+1≤y, y≤2x,
即
x-y+1≤0, 2x-y≥0,
返回
[方法技巧]
解决求平面区域面积问题的方法步骤 (1)画出不等式组表示的平面区域; (2)判断平面区域的形状,并求得直线的交点坐标、图形 的边长、相关线段的长(三角形的高、四边形的高)等,若为规 则图形则利用图形的面积公式求解;若为不规则图形则利用 割补法求解. [提醒] 求面积时应考虑圆、平行四边形等图形的对称性.
x<2y 选项 B 所表示的区域,故选 B. 答案:B
返回
3x+y-6≥0, 2.(2019·河南豫北联考)关于 x,y 的不等式组x-y-2≤0,
x+y-4≤0
表示的平面区域的面积为
()
A.3
B.52
C.2
D.32
解析:平面区域为一个直角三角形 ABC,其中 A(3,1),
B(2,0),C(1,3),所以面积为12|AB|·|AC|=12× 2× 8=2,
-dc,-ba连线的斜率的ac倍的取值范围、最值等
返回
对形如 z=|Ax+By+C|型的目标函数,可先 点到直线 变形为 z= A2+B2·|Ax+A2B+y+B2C|的形式,将 距离型 问题化为求可行域内的点(x,y)到直线 Ax+
By+C=0 的距离的 A2+B2倍的最值
返回
考法三 线性规划中的参数问题
高考数学一轮复习 第6篇 第3节 二元一次不等式(组)与简单的线性规划问题课件 文 新人教版(1)

解析:由约束条件作出可 行域如图中阴影区域. 将 z=2x-3y 化为
2 z y= x- , 3 3 2 作出直线 y= x 并平移使 3
之经过可行域, 易知直线经过点 A(3,4)时,z 取得最小值, 故 zmin=2×3-3ห้องสมุดไป่ตู้4=-6.故选 B.
x y 2, 2.不等式组 2 x y 4, 所围成的平面区域的面积为( x y 0
D
)
(A)3 2
(B)6 2
(C)6
(D)3
解析:不等式组表示的平面区域为图中 Rt△ABC,易求 B(4,4),A(1,1),C(2,0)
1 1 ∴S△ ABC=S△OBC-S△AOC= ×2×4- ×2×1=3. 2 2
质疑探究:最优解一定唯一吗? 提示:不一定.当线性目标函数对应的直 线与可行域多边形的一条边平行时,最 优解可能有多个甚至无数个.
双基自测
x 3 y 6 0, 1.(2013 东北三省四市三模)不等式组 表示 x y 2 0
的平面区域是( B )
解析:x-3y+6≥0 表示直线 x-3y+6=0 以及该直线下方的区 域,x-y+2<0 表示直线 x-y+2=0 的上方区域.故选 B.
故选 D.
2 x y 40, x 2 y 30, 3.(2013 广东六校联考)若变量 x,y 满足 则 x 0, y 0,
z=-x+3y 的最大值是( C ) (A)90 (B)80 (C)50 (D)40 解析:画出可行域(如图所示), 目标函数 z=-x+3y 在 B(10,20) 点取最大值 zmax=-10+3×20=50. 故选 C.
高考数学一轮复习 第7章 不等式 第3讲 二元一次不等式(组)与简单的线性规划课件 文

解线性规划应用问题的一般步骤 (1)分析题意,设出未知量; (2)列出线性约束条件和目标函数; (3)作出可行域并利用数形结合求解; (4)作答.
12/11/2021
第三十六页,共四十三页。
【对点通关】 (必修 5 P91 练习 T2 改编)A,B 两种规格的产品需要在甲、乙两 台机器上各自加工一道工序才能成为成品.已知 A 产品需要 在甲机器上加工 3 小时,在乙机器上加工 1 小时;B 产品需要 在甲机器上加工 1 小时,在乙机器上加工 3 小时.在一个工作 日内,甲机器至多只能使用 11 小时,乙机器至多只能使用 9 小时.A 产品每件利润 300 元,B 产品每件利润 400 元,则这 两台机器在一个工作日内创造的最大利润是________元.
12/11/2021
第二十六页,共四十三页。
【对点通关】
-x+y-2≤0, 1.(必修 5 P93A 组 T2 改编)实数 x,y 满足x+y-4≤0, 则
x-3y+3≤0. z=x-y 的最大值为( )
A.-2
B.2
C.-12
D.12
12/11/2021
第二十七页,共四十三页。
解析:选 D.约束条件表示的可行域如图所示,
y≥0
12/11/2021
第十四页,共四十三页。
直线 x+y=a 与 y=0 的交点为(a,0),而由y2=x+0y=2,得 A 点的坐标为(1,0).由题意得 a 的范围为 0<a<1. 【答案】 A
12/11/2021
第十五页,共四十三页。
(1)求二元一次不等式(组)表示的平面区域面积的思路 ①画出二元一次不等式(组)表示的区域,求出其顶点坐标; ②根据区域的特点选择“底与高”求其面积. (2)判断二元一次不等式(组)表示的平面区域形状的思路 ①画出已知二元一次不等式(组)表示的区域进行判断; ②大致画出含参数的二元一次不等式表示的区域,按照问题要 求将表示的直线进行移动.
近年高考数学一轮复习第7章不等式第3讲二元一次不等式(组)与简单的线性规划演练文(2021年整理)

2019高考数学一轮复习第7章不等式第3讲二元一次不等式(组)与简单的线性规划分层演练文编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019高考数学一轮复习第7章不等式第3讲二元一次不等式(组)与简单的线性规划分层演练文)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019高考数学一轮复习第7章不等式第3讲二元一次不等式(组)与简单的线性规划分层演练文的全部内容。
第3讲二元一次不等式(组)与简单的线性规划一、选择题1.已知点(-3,-1)和点(4,-6)在直线3x-2y-a=0的两侧,则a 的取值范围为()A.(-24,7) B.(-7,24)C.(-∞,-7)∪(24,+∞)D.(-∞,-24)∪(7,+∞)解析:选B。
根据题意知(-9+2-a)·(12+12-a)〈0.即(a+7)(a -24)〈0,解得-7〈a〈24。
2.已知实数x,y满足错误!则z=3x-y的最小值为()A.-1 B.1C.3 D.2解析:选 C.如图,作出不等式组所表示的平面区域(阴影部分),显然目标函数z=3x-y的几何意义是直线3x-y-z=0在y轴上截距的相反数,故当直线在y轴上截距取得最大值时,目标函数z取得最小值.由图可知,目标函数对应直线经过点A时,z取得最小值.由错误!解得A(1,0).故z的最小值为3×1-0=3。
故选C.3.不等式组错误!表示的平面区域为Ω,直线y=kx-1与区域Ω有公共点,则实数k的取值范围为( )A.(0,3] B.[-1,1]C.(-∞,3]D.[3,+∞)解析:选D。
直线y=kx-1过定点M(0,-1),由图可知,当直线y=kx-1经过直线y=x+1与直线x+y=3的交点C (1,2)时,k最小,此时k CM=错误!=3,因此k≥3,即k∈[3,+∞).故选D。
2019年高考数学一轮复习 第六章 第三节 二元一次不等式(组)与简单的线性规划问题演练知能检测 文
2019年高考数学一轮复习 第六章 第三节 二元一次不等式(组)与简单的线性规划问题演练知能检测 文[全盘巩固]1.(xx·金华模拟)不等式组⎩⎨⎧x -3y +6≥0,x -y +2<0表示的平面区域是( )A B C D解析:选B x -3y +6≥0表示直线x -3y +6=0以及该直线下方的区域,x -y +2<0表示直线x -y +2=0的上方区域,故选B.2.(xx·新课标全国卷Ⅱ)设x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,x +y -1≥0,x ≤3,则z =2x -3y 的最小值是( )A .-7B .-6C .-5D .-3解析:选B 由约束条件得可行域(如图所示),当直线2x -3y -z =0过点A (3,4)时,z min =2×3-3×4=-6.3.若直线y =2x 上存在点(x ,y )满足约束条件⎩⎪⎨⎪⎧x +y -3≤0,x -2y -3≤0,x ≥m ,则实数m 的最大值为( )A .-1B .1 C.32D .2解析:选B 约束条件⎩⎪⎨⎪⎧x +y -3≤0,x -2y -3≤0,x ≥m表示的可行域如图阴影部分所示.当直线x =m 从如图所示的实线位置运动到过A 点的位置时,m 取最大值.解方程组⎩⎪⎨⎪⎧x +y -3=0,y =2x ,得A 点坐标为(1,2),所以m 的最大值为1.4.设实数x 、y 满足⎩⎪⎨⎪⎧x -y -2≤0,x +2y -5≥0,y -2≤0,则u =yx的取值范围是( )A.⎣⎢⎡⎦⎥⎤13,2B.⎣⎢⎡⎦⎥⎤13,12C.⎣⎢⎡⎦⎥⎤12,2D.⎣⎢⎡⎦⎥⎤2,52解析:选A 在坐标平面上点(x ,y )所表示的区域如图所示,根据几何意义,u 的值即为区域内的点与坐标原点连线的斜率,显然k OA 最小,k OB 最大.由⎩⎪⎨⎪⎧x +2y -5=0,x -y -2=0,得点A (3,1), 由⎩⎪⎨⎪⎧x +2y -5=0,y =2,得点B (1,2),故13≤u ≤2.5.(xx·北京高考)设关于x ,y 的不等式组⎩⎪⎨⎪⎧2x -y +1>0,x +m <0,y -m >0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2.求得m 的取值范围是( )A.⎝ ⎛⎭⎪⎫-∞,43B.⎝ ⎛⎭⎪⎫-∞,13C.⎝ ⎛⎭⎪⎫-∞,-23D.⎝⎛⎭⎪⎫-∞,-53解析:选C 问题等价于直线x -2y =2与不等式组所表示的平面区域存在公共点,由于点(-m ,m )不可能在第一和第三象限,而直线x -2y =2经过第一、三、四象限,则点(-m ,m )只能在第四象限,可得m <0,不等式组所表示的平面区域如图中阴影部分所示,要使直线x -2y =2与阴影部分有公共点,则点(-m ,m )在直线x -2y -2=0的下方,由于坐标原点使得x -2y -2<0,故-m -2m -2>0,即m <-23.6.设不等式组⎩⎪⎨⎪⎧x +y -11≥0,3x -y +3≥0,5x -3y +9≤0表示的平面区域为D .若指数函数y =a x的图象上存在区域D 上的点,则a 的取值范围是( )A .(1,3]B .[2,3]C .(1,2]D .[3,+∞) 解析:选A 平面区域D 如图所示.要使指数函数y =a x的图象上存在区域D 上的点, 所以1<a ≤3.7.已知点(-3,-1)和点(4,-6)在直线3x -2y -a =0的两侧,则a 的取值范围为________.解析:根据题意知(-9+2-a )(12+12-a )<0, 即(a +7)(a -24)<0,解得-7<a <24. 答案:(-7,24)8.(xx·北京高考)设D 为不等式组⎩⎪⎨⎪⎧x ≥0,2x -y ≤0,x +y -3≤0表示的平面区域.区域D 上的点与点(1,0)之间的距离的最小值为________.解析:不等式组表示的平面区域如图所示.由题意得A (1,2),B (0,3),O (0,0).由图可知最小值是点(1,0)到直线y =2x 的距离,即d =|2×1-0|5=255.答案:2559.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假 年产量/亩年种植成本/亩 每吨售价黄瓜 4吨 1.2万元 0.55万元 韭菜 6吨 0.9万元 0.3万元为________亩.解析:设黄瓜和韭菜的种植面积分别为x亩,y亩,总利润为z万元,则目标函数为z =(0.55×4x-1.2x)+(0.3×6y-0.9y)=x+0.9y线性约束条件为⎩⎪⎨⎪⎧x+y≤50,1.2x+0.9y≤54,x≥0,y≥0,即⎩⎪⎨⎪⎧x+y≤50,4x+3y≤180,x≥0,y≥0.画出可行域,如图所示.作出直线l0:x+0.9y=0,向上平移至过点A时,z取得最大值,由⎩⎪⎨⎪⎧x+y=50,4x+3y=180,解得A(30,20).答案:3010.设m>1,在约束条件⎩⎪⎨⎪⎧y≥x,y≤mx,x+y≤1下,目标函数z=x+my的最大值小于2,求m 的取值范围.解:变换目标函数为y=-1mx+zm,由于m>1,所以-1<-1m<0,不等式组表示的平面区域如图中的阴影部分所示,根据目标函数的几何意义,只有直线y=-1mx+zm在y轴上的截距最大时,目标函数取得最大值.显然在点A处取得最大值,由y=mx,x+y=1,得A⎝⎛⎭⎪⎫11+m,m1+m,所以目标函数的最大值z max=11+m+m21+m<2,所以m2-2m-1<0,解得1-2 <m<1+2,故m的取值范围是(1,1+2).11.设x,y满足约束条件⎩⎪⎨⎪⎧x-y+5≥0,x+y≥0,x≤3,求z=(x+1)2+y2的最大值.⎩x ≤3(x +1)2+y 2可看作点(x ,y )到点P (-1,0)的距离的平方,由图象可知可行域内的点A 到点P (-1,0)的距离最大.解方程组⎩⎪⎨⎪⎧x =3,x -y +5=0,得A 点的坐标为(3,8),代入z =(x +1)2+y 2,得z max =(3+1)2+82=80.12.若x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥1,x -y ≥-1,2x -y ≤2.(1)求目标函数z =12x -y +12的最值;(2)若目标函数z =ax +2y 仅在点(1,0)处取得最小值,求a 的取值范围.解:(1)作出可行域如图,可求得A (3,4),B (0,1),C (1,0).平移初始直线12x -y +12=0,过A (3,4)取最小值-2,过C (1,0)取最大值1.所以z 的最大值为1,最小值为-2.(2)直线ax +2y =z 仅在点(1,0)处取得最小值,由图象可知-1<-a2<2,解得-4<a <2.故所求a 的取值范围为(-4,2).[冲击名校]1.若a ≥0,b ≥0,且当⎩⎪⎨⎪⎧x ≥0,y ≥0,x +y ≤1时,恒有ax +by ≤1,则由点P (a ,b )所确定的平面区域的面积是( )A.12B.π4 C .1 D.π2解析:选C 因为ax +by ≤1恒成立,则当x =0时,by ≤1恒成立,可得y ≤1b(b ≠0)恒成立,所以0≤b ≤1;同理0≤a ≤1.所以由点P (a ,b )所确定的平面区域是一个边长为1的正方形,面积为1.⎩x +y ≤m ,2,-1],则目标函数的最大值的取值范围是________.解析:不等式组表示的可行域如图中阴影部分(包括边界)所示,目标函数可变形为y =x -z ,当z 最小时,直线y =x -z 在y 轴上的截距最大.当z 的最小值为-1,即直线为y=x +1时,联立方程⎩⎪⎨⎪⎧y =x +1,y =2x -1,可得此时点A 的坐标为(2,3),此时m =2+3=5;当z的最小值为-2,即直线为y =x +2时,联立方程⎩⎪⎨⎪⎧y =x +2,y =2x -1,可得此时点A 的坐标是(3,5),此时m =3+5=8.故m 的取值范围是[5,8].目标函数z =x -y 的最大值在点B (m -1,1)处取得,即z max =m -1-1=m -2,故目标函数的最大值的取值范围是[3,6].答案:[3,6][高频滚动]1.已知y =f (x )是偶函数,当x >0时,f (x )=(x -1)2,若当x ∈⎣⎢⎡⎦⎥⎤-2,-12时,n ≤f (x )≤m 恒成立,则m -n 的最小值为( )A .1 B.12 C.13 D.34解析:选A 当x <0时,-x >0, f (x )=f (-x )=(x +1)2,∵x ∈⎣⎢⎡⎦⎥⎤-2,-12, ∴f (x )min =f (-1)=0, f (x )max =f (-2)=1, ∴m -n 的最小值为1.2.设函数f (x )=⎩⎪⎨⎪⎧-2 x >0,x 2+bx +c x ≤0,若f (-4)=f (0),f (-2)=0,则关于x的不等式f (x )≤1的解集为( )A .(-∞,-3]∪[-1,+∞)B .[-3,-1]C .[-3,-1]∪(0,+∞)D .[-3,+∞)解析:选C 当x ≤0时,f (x )=x 2+bx +c 且f (-4)=f (0),故函数f (x )图象的对称轴为x =-b2=-2,则b =4.又f (-2)=4-8+c =0,∴c =4,当x ≤0时,令x 2+4x +4≤1,得-3≤x ≤-1;当x >0时,f (x )=-2≤1显然成立,故不等式的解集为[-3,-1]∪(0,+∞). , 39290 997A 饺38120 94E8 铨24640 6040 恀o37504 9280 銀22046 561E 嘞RB35718 8B86 讆26873 68F9 棹21068 524C 剌 j。
高三数学一轮复习 二元一次不等式(组)与简单的线性规

2014届高三数学一轮复习 二元一次不等式(组)与简单的线性规划问题双基限时训练 理(含解析)巩固双基,提升能力一、选择题1.(2012·广东)已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤2,x +y ≥1,x -y ≤1则z =3x +y 的最大值为( )A .12B .11C .3D .-1解析:如图所示,可行域是以A (-1,2),B (1,0),C (3,2)为顶点的三角形区域(含边界).作出直线3x +y =0(图中虚线),易知当直线3x +y =0平移到过C 点时,该直线在y 轴上的截距最大,此时z 取得最大值11,选B.答案:B2.(2012·福建)若函数y =2x图像上存在点(x ,y )满足约束条件⎩⎪⎨⎪⎧x +y -3≤0,x -2y -3≤0,x ≥m则实数m 的最大值为( )A.12 B .1 C.32D .2解析:如图,当x =m 经过且只有经过x +y -3=0和y =2x的交点A (1,2)时,m 取到最大值,此时m =1.此题也可用筛选法.答案:B3.直线2x+y-10=0与不等式组⎩⎪⎨⎪⎧x≥0,y≥0,x-y≥-2,4x+3y≤20表示的平面区域的公共点有( )A.0个 B.1个C.2个 D.无数个解析:由不等式组画出平面区域如图(阴影部分):直线2x+y-10=0恰过点A(5,0),且斜率k=-2<k AB=-43,即直线2x+y-10=0与平面区域仅有一个公共点A(5,0).故选B.答案:B4.设不等式组⎩⎪⎨⎪⎧x+y-11≥0,3x-y+3≥0,5x-3y+9≤0表示的平面区域为D.若指数函数y=a x的图像上存在区域D 上的点,则a 的取值范围是( )A .(1,3]B .[2,3]C .(1,2]D .[3,+∞)解析:作出不等式组表示的平面区域D ,如图阴影部分所示.由⎩⎪⎨⎪⎧x +y -11=0,3x -y +3=0,得交点A (2,9).对y =a x的图像,当0<a <1时,没有点在区域D 上.当a >1,y =a x恰好经过A 点时,由a 2=9,得a =3.要满足题意,需满足a 2≤9,解得1<a ≤3.答案:A5.已知平面直角坐标系xOy 上的区域D 由不等式组⎩⎨⎧0≤x ≤2,y ≤2,x ≤2y给定.若M (x ,y )为D 上的动点,点A 的坐标为(2,1),则z =OM →·OA →的最大值为( )A .3B .4C .3 2D .4 2解析:由题意知区域D 用图表示为:z =OM →·OA →=2x +y .当点M 的坐标是(2,2)时,z 取最大值,z max =4,故选B. 答案:B6.已知点P (x ,y )满足⎩⎪⎨⎪⎧x -1≤0,2x +3y -5≤0,4x +3y -1≥0,点Q (x ,y )在圆(x +2)2+(y +2)2=1上,则|PQ |的最大值与最小值为( )A .6,3B .6,2C .5,3D .5,2解析:可行域如图阴影部分,设|PQ |=d ,则由图知圆心C (-2,-2)到直线4x +3y -1=0的距离最小,到点A 距离最大.由⎩⎪⎨⎪⎧2x +3y -5=0,4x +3y -1=0,得A (-2,3).∴d max =|CA |+1=5+1=6,d min =|-8-6-1|5-1=2. 答案:B 二、填空题7.(2012·课标全国)设x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥-1,x +y ≤3,x ≥0,y ≥0,则z =x -2y 的取值范围为__________.解析:根据不等式组得出平面区域,易知过点(3,0),(1,2)时,z =x -2y 分别取得最大值和最小值,所以-3≤z ≤3.答案:[-3,3]8.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥-1,x +y ≥1,2x -y ≤1,则目标函数z =x -2yx +y的最大值为______.解析:作出可行域,如图所示阴影部分.z =x -2y x +y =x +y -3y x +y =1-3y x +y =1-3xy+1.又y x =y -0x -0表示可行域内的点到原点连线的斜率,且其最小值为点⎝ ⎛⎭⎪⎫23,13与原点连线的斜率12,故x y 的最大值为2,xy+1的最大值为3,从而z 的最大值为0.答案:09.某公司租赁甲、乙两种设备生产A ,B 两类产品,甲种设备每天能生产A 类产品5件和B 类产品10件,乙种设备每天能生产A 类产品6件和B 类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A 类产品50件,B 类产品140件,所需租赁费最少为__________元.解析:设租赁甲设备x 台,乙设备y 台,则⎩⎪⎨⎪⎧5x +6y ≥50,10x +20y ≥140,x ≥0,y ≥0.设租赁费用为w ,w =200x +300y . 约束条件构成的平面区域如图.解⎩⎪⎨⎪⎧5x +6y =50,10x +20y =140,得A (4,5).∴w min =200×4+300×5=2 300. 答案:2 300 三、解答题10.已知O 为坐标原点,A (2,1),P (x ,y )满足⎩⎪⎨⎪⎧x -4y +3≤0,3x +5y ≤25,x -1≥0,求|OP →|·cos∠AOP的最大值.解析:在平面直角坐标系中画出不等式组所表示的可行域(如图).由于|OP →|·cos∠AOP=|OP →|·|OA →|cos ∠AOP|OA →|=OP →·OA→|OA →|.而OA →=(2,1),OP →=(x ,y ), 所以|OP →|·cos∠AOP =2x +y5.令z =2x +y ,则y =-2x +z ,即z 表示直线y =-2x +z 在y 轴上的截距.由图形可知,当直线经过可行域中的点M 时,z 取到最大值,由⎩⎪⎨⎪⎧x -4y +3=0,3x +5y =25,得M (5,2),这时z =12,此时|OP →|·cos∠AOP =125=1255,故|OP →|·cos∠AOP 的最大值等于1255.11.已知x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥1,x -3y ≤-4,3x +5y ≤30.(1)求目标函数z =2x +y 的最大值和最小值;(2)若目标函数z =ax +y 取得最大值的最优解有无穷多个,求a 的值; (3)求z =y +5x +5的取值范围. 解析:作可行域如图所示.(1)作直线l :2x +y =0,并平移此直线,当平移直线过可行域内的A 点时,z 取最小值;当平移直线过可行域内的B 点时,z 取得最大值.解⎩⎪⎨⎪⎧x =1,x -3y =-4,得A ⎝ ⎛⎭⎪⎫1,53. 解⎩⎪⎨⎪⎧x -3y =-4,3x +5y =30,得B (5,3).∴z max =2×5+3=13,z min=2×1+53=113.(2)一般情况下,当z 取得最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,即直线z =ax +y 平行于直线3x +5y =30时,线段BC 上的任意一点均使z 取得最大值,此时满足条件的点即最优解有无数个. 又k BC =-35,∴-a =-35.∴a =35.(3)z =y +5x +5=y --5x --5,可看作区域内的点(x ,y )与点D (-5,-5)连线的斜率, 由图可知,k BD ≤z ≤k CD .∵k BD =3--55--5=45,k CD =275--51--5=2615,∴z =y +5x +5的取值范围是⎣⎢⎡⎦⎥⎤45,2615. 12.实系数一元二次方程x 2+ax +2b =0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,求:(1)点(a ,b )对应的区域的面积; (2)b -2a -1的取值范围; (3)(a -1)2+(b -2)2的值域.解析:方程x 2+ax +2b =0的两根在区间(0,1)和(1,2)上的几何意义分别是:函数y =f (x )=x 2+ax +2b 与x 轴的两个交点的横坐标分别在区间(0,1)和(1,2)内,由此可得不等式组⎩⎪⎨⎪⎧f 0>0,f 1<0,f 2>0⇔⎩⎪⎨⎪⎧b >0,a +2b +1<0,a +b +2>0.由⎩⎪⎨⎪⎧a +2b +1=0,a +b +2=0,解得A (-3,1);由⎩⎪⎨⎪⎧a +b +2=0,b =0解得B (-2,0);由⎩⎪⎨⎪⎧a +2b +1=0,b =0,解得C (-1,0).∴在如图所示的坐标平面aOb 内,满足约束条件的点(a ,b )对应的平面区域为△ABC (不包括边界).(1)△ABC 的面积为S △ABC =12×|BC |×h =12(h 为A 到Oa 轴的距离).(2)b -2a -1的几何意义是点(a ,b )和点D (1,2)连线的斜率. k AD =2-11+3=14,k CD =2-01+1=1. 由图可知,k AD <b -2a -1<k CD . ∴14<b -2a -1<1,即b -2a -1∈⎝ ⎛⎭⎪⎫14,1. (3)∵(a -1)2+(b -2)2表示区域内的点(a ,b )与定点(1,2)之间距离的平方, ∴(a -1)2+(b -2)2∈(8,17).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲 二元一次不等式(组)与简单的线性规划问题一、选择题1.不等式x -2y >0表示的平面区域是( ).解析 将点(1,0)代入x -2y 得1-2×0=1>0.答案 D2.设实数x ,y 满足不等式组⎩⎪⎨⎪⎧ x +2y -5>0,2x +y -7>0,x ≥0,y ≥0.若x ,y 为整数,则3x +4y 的最小值是( ). A .14 B .16 C .17 D .19解析 线性区域边界上的整点为(3,1),因此最符合条件的整点可能为(4,1)或(3,2),对于点(4,1),3x +4y =3×4+4×1=16;对于点(3,2),3x +4y =3×3+4×2=17,因此3x +4y 的最小值为16.答案 B3.若不等式组⎩⎪⎨⎪⎧ x -y +5≥0,y ≥a ,0≤x ≤2表示的平面区域是一个三角形,则a 的取值范围是( ). A .(-∞,5)B .[7,+∞)C .[5,7)D .(-∞,5)∪[7,+∞) 解析 画出可行域,知当直线y =a 在x -y +5=0与y 轴的交点(0,5)和x -y +5=0与x =2的交点(2,7)之间移动时平面区域是三角形.故5≤a <7.答案 C4.设实数x ,y 满足条件⎩⎪⎨⎪⎧ 4x -y -10≤0,x -2y +8≥0,x ≥0,y ≥0,若目标函数z =ax +by (a >0, b >0)的最大值为12,则2a +3b的最小值为( ).A.256B.83C.113 D .4解析 由可行域可得,当x =4,y =6时,目标函数z =ax +by 取得最大值,∴4a +6b =12,即a 3+b 2=1.∴2a +3b =⎝ ⎛⎭⎪⎫2a +3b ·⎝ ⎛⎭⎪⎫a 3+b 2=136+b a +a b ≥136+2=256. 答案 A5.实数x ,y 满足⎩⎪⎨⎪⎧ x ≥1,y ≤a a >1,x -y ≤0,若目标函数z =x +y 取得最大值4,则实数a 的值为( ). A .4 B .3 C .2D.32 解析 作出可行域,由题意可知可行域为△ABC 内部及边界,y =-x +z ,则z 的几何意义为直线在y 轴上的截距,将目标函数平移可知当直线经过点A 时,目标函数取得最大值4,此时A 点坐标为(a ,a ),代入得4=a+a =2a ,所以a =2.答案 C6.某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A 原料1千克、B 原料2千克;生产乙产品1桶需耗A 原料2千克、B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A 、B 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是 ( ).A .1 800元B .2 400元C .2 800元D .3 100元解析 设某公司生产甲产品x 桶,生产乙产品y 桶,获利为z 元,则x ,y 满足的线性约束条件为⎩⎪⎨⎪⎧ x +2y ≤12,2x +y ≤12,x ≥0且y ∈Z ,y ≥0且y ∈Z ,目标函数z =300x +400y .作出可行域,如图中四边形OABC 的边界及其内部整点.作直线l 0:3x +4y =0,平移直线l 0经可行域内点B 时,z 取最大值,由⎩⎪⎨⎪⎧ 2x +y =12,x +2y =12,得B (4,4),满足题意,所以z max=4×300+4×400=2 800.答案 C二、填空题7.若x ,y 满足约束条件⎩⎪⎨⎪⎧ x -y +1≥0,x +y -3≤0,x +3y -3≥0,则z =3x -y 的最小值为________.解析 画出可行域,如图所示,将直线y =3x-z 移至点A (0,1)处直线在y 轴上截距最大,z min =3×0-1=-1.答案 -18.若x ,y 满足约束条件⎝ ⎛ x ≥0,x +2y ≥3,2x +y ≤3,则x-y 的取值范围是________. 解析 记z =x -y ,则y =x -z ,所以z 为直线y =x -z 在y轴上的截距的相反数,画出不等式组表示的可行域如图中△ABC 区域所示.结合图形可知,当直线经过点B (1,1)时,x -y取得最大值0,当直线经过点C (0,3)时,x -y 取得最小值-3.答案 [-3,0]9.设实数x 、y 满足⎩⎪⎨⎪⎧ x -y -2≤0,x +2y -4≥0,2y -3≤0,则y x 的最大值是________. 解析 不等式组确定的平面区域如图阴影部分.设y x =t ,则y =tx ,求y x 的最大值,即求y =tx 的斜率的最大值.显然y =tx 过A 点时,t 最大.由⎩⎪⎨⎪⎧ x +2y -4=0,2y -3=0,解得A ⎝ ⎛⎭⎪⎫1,32. 代入y =tx ,得t =32.所以y x 的最大值为32. 答案 3210.设m >1,在约束条件⎩⎪⎨⎪⎧ y ≥x ,y ≤mx ,x +y ≤1下,目标函数z =x +my 的最大值小于2,则m 的取值范围为________. 解析 目标函数z =x +my 可变为y =-1m x +z m , ∵m >1,∴-1<-1m <0,z 与z m同时取到相应的最大值,如图,当目标函数经过点P ⎝ ⎛⎭⎪⎫1m +1,m m +1时,取最大值,∴1m +1+m 2m +1<2,又m >1,得1<m <1+ 2.答案 (1,1+2)三、解答题11.设集合A ={(x ,y )|x ,y,1-x -y 是三角形的三边长}.(1)求出x ,y 所满足的不等式;(2)画出点(x ,y )所在的平面区域.解 (1)已知条件即⎩⎪⎨⎪⎧ x +y >1-x -y >0,x +1-x -y >y >0,y +1-x -y >x >0,化简即⎩⎪⎨⎪⎧-x +12<y <-x +1,0<y <12,0<x <12. (2)区域如下图.12.画出不等式组⎩⎪⎨⎪⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域,并回答下列问题:(1)指出x 、y 的取值范围;(2)平面区域内有多少个整点?解 (1)不等式x -y +5≥0表示直线x -y +5=0上及其右下方的点的集合,x +y ≥0表示直线x +y =0上及其右上方的点的集合,x ≤3表示直线x =3上及其左方的点的集合.所以,不等式组⎩⎪⎨⎪⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域如图所示.结合图中可行域得x ∈⎣⎢⎡⎦⎥⎤-52,3,y ∈[-3,8].(2)由图形及不等式组知⎩⎪⎨⎪⎧ -x ≤y ≤x +5,-52≤x ≤3,且x ∈Z ,当x =3时,-3≤y ≤8,有12个整点;当x =2时,-2≤y ≤7,有10个整点;当x =1时,-1≤y ≤6,有8个整点;当x =0时,0≤y ≤5,有6个整点;当x =-1时,1≤y ≤4,有4个整点;当x =-2时,2≤y ≤3,有2个整点;∴平面区域内的整点共有2+4+6+8+10+12=42(个).13.若x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥1,x -y ≥-1,2x -y ≤2,(1)求目标函数z =12x -y +12的最值.(2)若目标函数z =ax +2y 仅在点(1,0)处取得最小值,求a 的取值范围.解 (1)作出可行域如图,可求得A (3,4),B (0,1),C (1,0).平移初始直线12x -y =0,过A (3,4)取最小值-2,过C (1,0)取最大值1.∴z 的最大值为1,最小值为-2.(2)直线ax +2y =z 仅在点(1,0)处取得最小值,由图象可知-1<-a 2<2,解得-4<a <2. 故所求a 的取值范围是(-4,2).14.某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率多0.25,甲产品为二等品的概率比乙产品为一等品的概率少0.05.(1)分别求甲、乙产品为一等品的概率P 甲,P 乙;(2)已知生产一件产品需要用的工人数和资金数如表所示,且该厂有工人32名,可用资金55万元.设x ,y 分别表示生产甲、乙产品的数量,在(1)的条件下,求x ,y 为何值时,z =xP 甲+yP 乙最大,最大值是多少?项目用量产品工人(名) 资金(万元) 甲4 20 乙8 5 解 (1)依题意得⎩⎪⎨⎪⎧ P 甲-P 乙=0.25,1-P 甲=P 乙-0.05,解得⎩⎪⎨⎪⎧ P 甲=0.65,P 乙=0.4,故甲产品为一等品的概率P 甲=0.65,乙产品为一等品的概率P 乙=0.4.(2)依题意得x 、y 应满足的约束条件为⎩⎪⎨⎪⎧4x +8y ≤32,20x +5y ≤55,x ≥0,y ≥0,且z =0.65x +0.4y . 作出不等式组所表示的平面区域,如图阴影部分,即可行域.作直线l 0:0.65x +0.4y =0即13x +8y =0,把直线l 向上方平移到l 1的位置时,直线经过可行域内的点M ,此时z 取得最大值.解方程组⎩⎪⎨⎪⎧x +2y =8,4x +y =11, 得x =2,y =3.故M 的坐标为(2,3),所以z 的最大值为z max =0.65×2+0.4×3=2.5.所以,当x=2,y=3时,z取最大值为2.5.。
