人教版九年级上册·第二十五章：概率初步复习讲义-仅供参考

合集下载

人教版初中九年级数学上册第二十五章《概率初步》知识点复习(含答案解析)

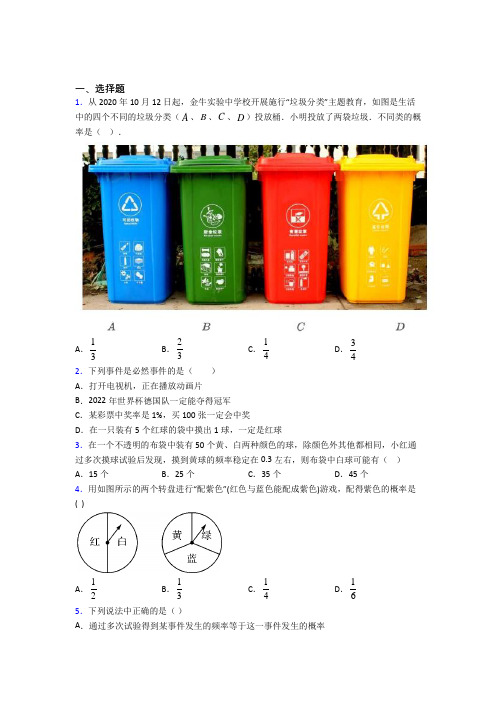
一、选择题1．从2020年10月12日起，金牛实验中学校开展施行“垃圾分类”主题教育，如图是生活中的四个不同的垃圾分类（A、B、C、D）投放桶．小明投放了两袋垃圾．不同类的概率是（）．A．13B．23C．14D．342．下列事件是必然事件的是（）A．打开电视机，正在播放动画片B．2022年世界杯德国队一定能夺得冠军C．某彩票中奖率是1%，买100张一定会中奖D．在一只装有5个红球的袋中摸出1球，一定是红球3．在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.3左右，则布袋中白球可能有（）A．15个B．25个C．35个D．45个4．用如图所示的两个转盘进行“配紫色”(红色与蓝色能配成紫色)游戏，配得紫色的概率是( )A．12B．13C．14D．165．下列说法中正确的是（）A．通过多次试验得到某事件发生的频率等于这一事件发生的概率B ．某人前9次掷出的硬币都是正面朝上，那么第10次掷出的硬币反面朝上的概率一定大于正面朝上的概率C ．不确定事件的概率可能等于1D ．试验估计结果与理论概率不一定一致6．下列说法：①“明天的降水概率为80%”是指明天有80%的时间在下雨；②连续抛一枚硬币50次，出现正面朝上的次数一定是25次（）A ．只有①正确B ．只有②正确C ．①②都正确D ．①②都错误 7．袋子中装有10个黑球、1个白球，它们除颜色外无其他差别，随机从袋子中摸出一个球，则（）A ．这个球一定是黑球B ．摸到黑球、白球的可能性的大小一样C ．这个球可能是白球D ．事先能确定摸到什么颜色的球 8．下列语句所描述的事件是随机事件的是（） A ．经过任意两点画一条直线B ．任意画一个五边形，其外角和为360°C ．过平面内任意三个点画一个圆D ．任意画一个平行四边形，是中心对称图形 9．从2，3，4，5中任意选两个数，记作a 和b ，那么点()a b ，在函数2611y x x =-+图象上的概率是（）A ．12B ．13C ．14D ．1610．在一个不透明的箱子中有3张红卡和若干张绿卡，它们除了颜色外其他完全相同，通过多次抽卡试验后发现，抽到绿卡的概率稳定在75%附近，则箱中卡的总张数可能是（）A ．1张B ．4张C ．9张D ．12张11．在智力竞答节目中，某参赛选手答对最后两题单选题就能利通关，两题均有四个选项，此选手只能排除第1题的一个错误选项，第2题完全不会，他还有两次“求助”机会（使用可去掉一个错误选项），为提高通关概率，他的求助使用策略为（）A ．两次求助都用在第1题B ．两次求助都用在第2题C ．在第1第2题各用一次求助D ．无论如何使用通关概率都相同 12．如图所示，小明、小刚利用两个转盘进行游戏，规则为小明将两个转盘各转一次，如配成紫色（红与蓝），小明胜，否则小刚胜，此规则（）A ．公平B ．对小明有利C ．对小刚有利D ．公平性不可预测 13．袋中装有3个绿球和4个红球，它们除颜色外，其余均相同。

九年级数学人教版(上册)第25章小结与复习

乙转盘
第一回第二回
1
2
3
1
2
3
4
2
3
4
5
3
4
5
6
共有9种等可能结果，其中中奖的有4种；
∴P(乙）=
4； 9
（2）如果只考虑中奖因素，你将会选择去哪个超市
购物？说明理由.
选甲超市.理由如下：
∵P(甲）>P(乙）， ∴选甲超市.
侵权必究
课堂小结
✓ 归纳总结 ✓ 构建脉络
侵权必究
课堂小结
必然事件
事件不可能事件
从这个袋子中摸出一个球，两次摸到的球颜色相同的概率是( A )
A. 2
B. 3
C. 8
D. 1 3
5
5
25
25
4. 一个袋中装有2个黑球3个白球，这些球除颜色外，大小、形状、质地完全相
同，在看不到球的情况下，随机的从这个袋子中摸出一个球不放回，再随机的
从这个袋子中摸出一个球，两次摸到的球颜色相同的概率是( A )
随机事件与概率
概
率
初
步列举法求
概
率
用频率估计概率
侵权必究
概率
随机事件
定义
刻画随机事件发生可能性大小的数值
计算公式
P(A) m (m为试验总结果数， n
n为事件A包含的结果种数）
直接列举法列表法
画树状图法
适合于两个试验因素或分两步进行适合于三个试验因素或分三步进行
频率与概率的关系
在大量重复试验中，频率具有稳定性时才可以用来估计概率
那么重转一次，直到指针指向 4 3
某一份为止）.
12

【精品讲义】人教版九年级数学(上)专题25.3 用频率估计概率-(知识点+例题+练习题)含答案

第二十五章概率初步25.3 用频率估计概率用频率估计概率连续抛掷一枚质地均匀的硬币10次、20次、30次、40次、50次……分别记录每轮试验中硬币“正面向上”和“反面向上”出现的次数，求出“正面向上”和“反面向上”的频率，分析数据，可探索出频率的变化规律．用频率估计概率（1）从长期实践中，人们观察到，对一般的随机事件，在做大量重复试验时，随着试验次数的增加，一个事件出现的频率，总在一个固定数的附近摆动，显示出一定的稳定性．因此，我们可以通过大量的重复试验，用一个随机事件发生的频率去估计它的概率．（2）一般地，在大量重复试验中，如果事件A 发生的频率mn稳定于某个常数p ，那么事件A 发生的概率P （A ）=p ．n 个除颜色外其他完全相同的小球，其中有9个黄球，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球试验后发现，摸到黄球的频率稳定在0.3，那么估计摸到黄球的概率为A．0.3 B．0.7C．0.4 D．0.6【答案】A【解析】∵通过大量重复摸球实验后发现，摸到黄球的频率稳定在0.3，∴估计摸到黄球的概率为0.3，故选A．【名师点睛】一般地，在大量重复试验中，如果事件A发生的频率mn稳定于某个常数p，那么估计事件A发生的概率P（A）=p．试验得出的频率只是概率的估计值．概率是针对大量重复试验而言的，大量重复试验反映出的规律并非在每一次试验中都发生．（1）将表格补充完成；（精确到0.01）（2）估计这名同学投篮一次，投中的概率约是多少（精确到0.1）？（3）根据此概率，估计这名同学投篮622次，投中的次数约是多少？【解析】（1）153÷300=0.51，252÷500≈0.50；故答案为：0.51，0.50；（2）估计这名同学投篮一次，投中的概率约是0.5；（3）622×0.5=311（次）．所以估计这名同学投篮622次，投中的次数约是311次．1．关于频率和概率的关系，下列说法正确的是A．频率等于概率B．当试验次数很大时，概率稳定在频率附近C．当试验次数很大时，频率稳定在概率附近D．试验得到的频率和概率不可能相等2．随机事件A出现的频率mn满足A．mn=0 B．mn=1C．mn＞1 D．0<mn<13．两人各抛一枚硬币，则下面说法正确的是A．每次抛出后出现正面或反面是一样的B．抛掷同样的次数，则出现正、反面的频数一样多C．在相同条件下，即使抛掷的次数很多，出现正、反面的频数也不一定相同D．当抛掷次数很多时，出现正、反面的次数就相同了4．一个不透明的口袋里装有除颜色不同外其余都相同的10个白球和若干个红球，在不允许将球倒出来数的前提下，小亮为了估计其中的红球数，采用如下方法：先将口袋中的球摇匀，再从口袋中随机摸出1球，记下颜色，然后把它放回口袋中，不断重复上述过程，小亮共摸了1000次，其中有200次摸到白球，因此小亮估计口袋中的红球有A．60个B．50个C．40个D．30个5．在一个不透明的袋中装有黑色和红色两种颜色的球共15个，每个球除颜色外都相同，每次摇匀后随即摸出一个球，记下颜色后再放回袋中，通过大量重复摸球实验后，发现摸到黑球的频率稳定于0.6，则可估计这个袋中红球的个数约为__________．6．在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，然后把它放回袋中，不断重复，下表是活动进行中的一组统计数据：（1）上表中的a=__________；（2）“摸到白球”的概率的估计值是__________（精确到0.1）；（3）试估算口袋中黑、白两种颜色的球各有多少个？7．某批彩色弹力球的质量检验结果如下表：（1）请在图中完成这批彩色弹力球“优等品”频率的折线统计图（2）这批彩色弹力球“优等品”概率的估计值大约是多少？（精确到0.01）（3）从这批彩色弹力球中选择5个黄球、13个黑球、22个红球，它们除了颜色外都相同，将它们放入一个不透明的袋子中，求从袋子中摸出一个球是黄球的概率．（4）现从第（3）问所说的袋子中取出若干个黑球，并放入相同数量的黄球，搅拌均匀，使从袋子中摸出一个黄球的概率为14，求取出了多少个黑球？1．在一个不透明的布袋中，红球、黑球、白球共有若干个，除颜色外，它们的形状、大小、质地等完全相同.小新从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后再随机摸出一球，记下颜色后放回……如此大量摸球试验后，小新发现从布袋中摸出红球的频率稳定于0.2，摸出黑球的频率稳定于0.5，对此试验，他总结出下列结论：①若进行大量摸球试验，摸出白球的频率应稳定于0.3；②若从布袋中任意摸出一个球，该球是黑球的概率最大；③若再摸球100次，必有20次摸出的是红球．其中说法正确的是A．①②③B．①②C．①③D．②③2．抛掷一枚质地均匀的硬币2000次，正面朝上的次数最有可能为A．500B．800C．1000D．12003．在一个不透明的盒子里装有4个黑球和若干个白球，它们除颜色外完全相同，摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复，共摸球40次，其中10次摸到黑球，则估计盒子中大约有________个白球．4．一鱼池里有鲤鱼，鲫鱼，鲢鱼共1000尾，一渔民通过多次捕捞试验后发现，鲤鱼，鲫鱼出现的概率约为31%和42%，则这个鱼池里大概有鲤鱼______尾，鲫鱼______尾，鲢鱼______尾.5．某公司对一批某品牌衬衣的质量抽检结果如下表．（1）从这批衬衣中抽1件是次品的概率约为多少？（2）如果销售这批衬衣600件，那么至少要再准备多少件正品衬衣供买到次品的顾客更换？6．小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表，阅读并回答问题：（1）从表中可知，当抛完10次时正面出现3次，正面出现的频率为30%，那么，小明抛完10次时，得到__________次反面，反面出现的频率是__________；（2）当他抛完5000次时，反面出现的次数是__________，反面出现的频率是__________；（3）通过上表我们可以知道，正面出现的频数和反面出现的频数之和等于__________，正面出现的频率和反面出现的频率之和等于__________.1．（2019•湖北襄阳）下列说法错误的是A．必然事件发生的概率是1B．通过大量重复试验，可以用频率估计概率C．概率很小的事件不可能发生D．投一枚图钉，“钉尖朝上”的概率不能用列举法求得2．（2019•江苏泰州）小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表：若抛掷硬币的次数为1000，则“正面朝上”的频数最接近A．20 B．300C．500 D．8003．（2019•绍兴）为了解某地区九年级男生的身高情况，随机抽取了该地区100名九年级男生，他们的身高x（cm）统计如下：根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于180cm的概率是A．0.85 B．0.57 C．0.42 D．0.154．（2019•柳州）柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果．下面是这个兴趣小组在相同的实验条件下，对某植物种子发芽率进行研究时所得到的数据：依据上面的数据可以估计，这种植物种子在该实验条件下发芽的概率约是__________（结果精确到0.01）．5．（2019•长沙）在一个不透明的袋子中有若干个小球，这些球除颜色外无其他差别，从袋中随机摸出一球，记下其颜色，这称为一次摸球试验，然后把它重新放回袋中并摇匀，不断重复上述过程．以下是利用计算机模拟的摸球试验统计表：根据试验所得数据，估计“摸出黑球”的概率是__________．（结果保留小数点后一位）6．（2019•雅安）某校为了解本校学生对课后服务情况的评价，随机抽取了部分学生进行调查，根据调查结果制成了如下不完整的统计图．根据统计图：（1）求该校被调查的学生总数及评价为“满意”的人数；（2）补全折线统计图；（3）根据调查结果，若要在全校学生中随机抽1名学生，估计该学生的评价为“非常满意”或“满意”的概率是多少？1．【答案】C【解析】概率是一个确定的数，频率是一个变化量，当试验次数很大时，频率会稳定在概率附近.由此可得，选项C 正确.故选C ． 2．【答案】D【解析】大量重复试验中具有某种规律性的事件叫做随机事件，故频率mn的含义是在n 次试验中发生m 次，即必有0<mn<1．故选D ． 3．【答案】C【解析】抛硬币是一个随机事件，抛一枚硬币，出现正面朝上或者反面朝上都有可能，但事先无法预料.故选C ． 4．【答案】C【解析】∵小亮共摸了1000次，其中200次摸到白球，则有800次摸到红球， ∴白球与红球的数量之比为1：4， ∵白球有10个，∴红球有10×4=40（个），故选C ． 5．【答案】6【解析】黑球个数为：150.69⨯=，红球个数：1596-=.故答案为：6．【名师点睛】本题考查了频数和频率，频率是频数与总数之比，掌握频数频率的定义是解题的关键. 6．【解析】（1）a =290500=0.58，故答案为：0.58；（2）随着实验次数的增加“摸到白球”的频率趋向于0.60，所以其概率的估计值是0.60，故答案为：0.60；（3）由（2）摸到白球的概率估计值为0.60，所以可估计口袋中白球的个数=20×0.6=12(个)，黑球20−12=8(个). 答：黑球8个，白球12个.【名师点睛】本题考查利用频率估计概率，事件A 发生的频率等于事件A 出现的次数除以实验总次数；在实验次数非常大时，事件A 发生的频率约等于事件发生的概率，本题可据此作答；对于（3）可直接用概率公式.7．【解析】（1）如图，（2）()10.9420.9460.9510.9490.9485⨯++++=1 4.7365⨯=0.9472≈0.95．（3）P （摸出一个球是黄球）=551322++=18．（4）设取出了x 个黑球，则放入了x 个黄球，则551322x +++=14，解得x =5．答：取出了5个黑球．【名师点睛】本题考查利用频率估算概率，数量较大、批次较多时用求平均值的方法更接近概率，理解题意灵活运用概率公式是解题关键.1．【答案】B【解析】∵在一个不透明的布袋中，红球、黑球、白球共有若干个，其中摸出红球的频率稳定于20%，摸出黑球的频率稳定于50%，∴①若进行大量摸球实验，摸出白球的频率稳定于：1–20%–50%=30%，故此选项正确； ∵摸出黑球的频率稳定于50%，大于其它频率，∴②从布袋中任意摸出一个球，该球是黑球的概率最大，故此选项正确；③若再摸球100次，不一定有20次摸出的是红球，故此选项错误；故正确的有①②．故选B．【名师点睛】此题主要考查了利用频率估计概率，根据频率与概率的关系得出是解题关键．2．【答案】C【解析】抛掷一枚质地均匀的硬币2000次，正面朝上的次数最有可能为1000次，故选C．【名师点睛】本题主要考查随机事件，关键是理解必然事件为一定会发生的事件；解决此类问题，要学会关注身边的事物，并用数学的思想和方法去分析、看待、解决问题，提高自身的数学素养．3．【答案】12【解析】∵共试验40次，其中有10次摸到黑球，∴白球所占的比例为：40103 404-=，设盒子中共有白球x个，则344xx=+，解得x=12，经检验，x=12是原方程的根，故答案为：12．【名师点睛】本题考查利用频率估计概率．大量反复试验下频率稳定值即概率．关键是根据白球的频率得到相应的等量关系．4．【答案】310；420；270【解析】根据所给数据可得：鲤鱼：1000×31%=310(尾)；鲫鱼：1000×42%=420(尾)；鲢鱼：1000–310–420=270(尾).故答案为：310；420；270.5．【答案】（1）0.06；（2）36件【解析】（1）抽查总体数m=50+100+200+300+400+500=1550，次品件数n=0+4+16+19+24+30=93，P（抽到次品）=931550=0.06．（2）根据（1）的结论：P（抽到次品）=0.06，则600×0.06=36（件）．答：至少准备36件正品衬衣供顾客调换．6．【答案】（1）7；70%；（2）2502；50.04%；（3）抛掷总次数；1【解析】（1）从表中可知，当抛完10次时正面出现3次，正面出现的频率为30％，那么，小明抛完 10次时，得到7次反面，反面出现的频率是710=0.7=70%；（2）当他抛完5000次时，反面出现的次数是5000–2498=2502，反面出现的频率是2502÷5000=0.5004=50.04%；（3）通过上面我们可以知道，正面出现的频数和反面出现的频数之和等于抛掷总次数，正面出现的频率和反面出现的频率之和等于1.1．【答案】C【解析】A 、必然事件发生的概率是1，正确；B 、通过大量重复试验，可以用频率估计概率，正确；C 、概率很小的事件也有可能发生，故错误；D 、投一枚图钉，“钉尖朝上”的概率不能用列举法求得，正确，故选C ．2．【答案】C【解析】观察表格发现：随着实验次数的增加，正面朝上的频率逐渐稳定到0.5附近，所以抛掷硬币的次数为1000，则“正面朝上”的频数最接近1000×0.5=500次，故选C ．3．【答案】D【解析】样本中身高不低于180cm 的频率==0.15，所以估计他的身高不低于180cm 的概率是0.15．故选D ．4．【答案】【解析】概率是大量重复试验的情况下，频率的稳定值可以作为概率的估计值，即次数越多的频率越接近于概率，∴这种种子在此条件下发芽的概率约为0.95．故答案为：0.95．5．【解答】观察表格发现随着摸球次数的增多频率逐渐稳定在0.4附近，故摸到白球的频率估计值为0.4；故答案为：0.4．6．【解析】（1）由折线统计图知“非常满意”9人，由扇形统计图知“非常满意”占15%，所以被调查学生总数为9÷15%=60（人），所以“满意”的人数为60–（9+21+3）=27（人）；15100（2）如图：（3）所求概率为．=6927035。

秋人教九级数学上册第二十五章概率初步本章知识梳理(优秀文档PPT)

知识梳理
树状图法：（1）列举法求概率的关键在于列举出所有可能的结果，列表法是一种，但当一个事件涉及三个或更多元素时，为不重不漏地列出所有可能的结果，通常采用树状图法. （2）树状图列举法一般是选择一个元素，再和其他元素分别组合，依用列举法求次列出像树的枝丫形式，最末端的枝丫个数就是总的可能的结果n. 概率
一般地，如果在一次试验中，有n种等可能的结果，“事件A”包含其中的m种结果，那么“事件A”发生的概率记为P（A），P（A）= 在一定条件下，可能发生也可能不发生的事件称为随机事件；
考点1 垂径定理
二、概率 8ABCD..... （不随概投可机率掷天能事很一水事件小枚）件发的质下发生事地列生的件均说的概不匀法概率可的正率为能硬确为发币的生01是0（00次，正A）面朝上的次数在投9（（一考∴（已色（（投一（你随从（①故考 b投若考2一数再=5小抛掷21般点1知后31掷般2认机布3投从点掷抛点、的随附2）））））））明8掷一地 3不，一地为事袋掷袋 2一掷 2有概机近5∵请小试计认试恰硬枚，透放枚，获件中一中枚2放率摸0，大用用用估明估算同估÷好0币质如明回质如胜发随枚任质回是出所量0频列列计从算表，算3取0的地果的袋地果的生机硬取地或_一以重0次率举举_：甲盒中理盒到试均在袋子均在可的摸币一均相球0_该复硬估法法当盘子由子a0_两验匀一中中匀一能概出正个匀互，麦，=_试币计求求中里如里n个0_中的次只并的次性率一面球的独两种很b验._“概概概任黑下黑的白_，硬试装摇硬试比为个朝是硬立次的大后.正率率率取、：、值粽下币验有匀币验较球上黑币型摸发时发面一白白；子列中黑，中大，；球出111芽，现向个两两的000结，、经，的记的的概摸，000上粽种种概000论有白过有是下概球率到抽次次次”子颜颜率正两大颜率上nn_约白到，，，的，色色_种种为确种量色是的_为球合正正正频取的的等等_的球重后汉0的_格面面面率到球球可可._是，复放字频品_朝朝朝是豆各各能能.（这试回组率的上上上，沙有有的的些验，成将频的的的则粽多多结结球发搅“会率次次次“的少少果果除现匀孔接稳数数数正概只只，，颜摸，孟）近定一一一面率““.. 色出再”_在定定定向事事_外白摸的_0是是是下件件_.都球出概_”555AA_相的率1000””_的包包个000同频是_次次次频；含含球，率（率其其，其稳也中中则中定为的的摸白在出mm球附）种种1有近个结结，2红果果个则球，，，n、那那黑的1么么球值个““有为白事事n（球个件件的，AA概””随发发率机生生）为地的的（从概概袋率率中记记B摸为为）. 出PP（（一AA个））球，，，PP记（（录AA））下==颜

人教版九年级上册第25章——概率讲义

概率讲义一、事件的概念1、在一定条件下必然发生的事件，叫做；在一定条件下不可能发生的事件，叫做；随机事件：在一定条件下可能发生也可能不发生的事件，叫做．2、随机事件发生的可能性是有大小的，不同的随机事情发生的可能性大小有可能不同。

二、概率1、概率定义：一般地，对于一个随机事件A ，我们把刻画其发生的可能性大小的数值，称为随机事件A 发生的概率，记为)(A P .2、简单事件的概率计算：一般地，如果在一次试验中，有n 种可能的结果，并且他们发生的可能性相等，事件A 包括其中的m 种结果，那么事件A 发生的概率nm A P =)(. 注意：应用n m A P =)(求事件概率的“三步骤”：（1）判断事件的所有可能出现的结果是否有限个，各种结果出现的可能性是否相等.（2）确定事件发生的所有的结果数n 和事件A 包含的结果数m .（3）套入公式nm A P =)(计算，得出结果。

3、事件概率的大小（1）当A 是必然事件时，P(A)＝；（2）当A 是不可能事件时，P(A)＝；（3）随机事件A 的概率P(A)的范围是．4、与面积有关的概率计算目标M 落在图形S 上A 区域的概率=的面积的面积S A 注：概率的大事件，在一次试验中不一定肯定发生确定性事件概率的小事件，在一次试验中不一定不发生。

三、用列表法求概率1、列表法求概率：当一次试验要涉及，并且可能出现的结果数目较多时，为了不重不漏的列举出所有结果，可以使用_______法。

2、运用列表法求概率的一般步骤：（1）列表（2）通过表格计数，确定公式n m A P =)(中m 和n 的值（3）利用公式n m A P =)(计算事件的概率四、用树状图求概率1、当一次试验要涉及三个或三个以上的因素时，并且可能出现的结果数目也比较多时，为了不重不漏的列举出所有结果，可以使用______________法求概率。

2、具体方法：先画出第一个因素产生的可能结果，再在第一步的每个可能结果的分支上画出第二个因素产生的可能结果，以此类推。

数学人教版九年级上册第二十五课概率初步复习课说课稿

第二十五章《概率初步》复习课·说课稿安康高新区河西初级中学王永顶我今天说客的题目是人教版新教材九年级上册第二十五章的《概率初步》复习课。

我将从教材分析、目标分析、过程分析、教法分析、设计反思五个方面来具体阐述对本节课的理解。

一、教材分析：1、教材内容：《概率初步》是人教版新教材九年级上册第二十五章内容，包括确定事件（必然事件和不可能事件）的概率理解和随机事件的理解随机事件概率的解法。

随机事件概率的三种解法----直接列举法、列表法和画树状图法。

学生要理解频率与概率的区别和联系，懂得在计算等可能事件的概率时，当试验的结果不是有限个数，或各种可能结果发生的可能性不相等时，我们可以利用频率估计概率。

这节课的主要内容是复习用列表法和画树状图法求随机概率的概率，要求学生能熟练掌握这两种方法计算简单事件的概率，并能在力求掌握基本方法上应用解决实际问题。

2、地位与作用：是“中考”热点内容之一，也是初中数学教学的重点之一。

概率与人们的日常生活密切相关，应用十分广泛。

了解和掌握一些概率统计知识，是学生初中毕业后参加实际工作的需要，更是学生进入高中进一步学习概率统计的基础，在教材中处于非常重要的位置。

概率与人们的日常生活密切相关，应用十分广泛。

因此，初中教材增加了这部分内容。

了解和掌握一些概率统计的基本知识，是学生初中毕业后参加实际工作的需要，也是高中进一步学习概率统计的基础，在教材中处于非常重要的位置。

3、教学重点：通过对事件发生的频率的分析来估计事件发生的概率.4、教学难点：（1）大量重复试验得到频率的稳定值的分析.（2）设计实验来估计概率，进一步求概率。

二、目标分析：依据《数学课程标准》，以教材特点和学生认知水平为出发点，确定以下三方面为本节课的教学目标。

【知识与技能目标】：1、引导学生对本章知识点进行回顾和梳理，形成清晰的知识体系。

2、通过学习用列表法、画树形图法及利用频率估计概率方法来解决一些实际问题。

九年级数学上册第二十五章概率初步必考知识点归纳(带答案)

九年级数学上册第二十五章概率初步必考知识点归纳单选题1、在一个不透明的口袋中装有5个红球和若干个白球，它们除颜色外其他完全相同，通过多次摸球实验后发现，摸到红球的频率稳定在0.25附近，则估计口袋中大约共有白球（）A．10B．15C．20D．都不对答案：B分析：由摸到红球的频率稳定在0.25附近，可以得出摸到红球的概率，即可求出白球个数．∵摸到红球的频率稳定在0.25附近，∴摸到红球的概率为0.25，∴总球数：5÷0.25=20（个）∴白球个数：20-5=15（个）所以答案是：B．小提示：本题考查了用频率估计概率、已知概率求数量，得出摸到红球的概率是本题的关键．2、在有25名男生和24名女生的班级中，随机抽签确定一名学生代表，则下列说法正确的是（）. A．男、女生做代表的可能性一样大B．男生做代表的可能性较大C．女生做代表的可能性较大D．男、女生做代表的可能性的大小不能确定答案：B分析：根据题意，只要求出男生和女生当选的可能性，再进行比较即可解答．∵某班有25名男生和24名女生，∴用抽签方式确定一名学生代表，男生当选的可能性为2525+24=25 49，女生当选的可能性为2425+24=24 49，∴男生当选的可能性大于女生当选的可能性．故选B．小提示：此题考查可能性大小的比较：只要总情况数目相同，谁包含的情况数目多，谁的可能性就大；反之也成立；若包含的情况相当，那么它们的可能性就相等．3、某居委会组织两个检查组，分别对“垃圾分类”和“违规停车”的情况进行抽查．各组随机抽取辖区内某三个小区中的一个进行检查，则两个组恰好抽到同一个小区的概率是（） A ．19B ．16C ．13D ．23答案：C分析：将三个小区分别记为A 、B 、C ，列举出所有情况即可，看所求的情况占总情况的多少即可．详解：将三个小区分别记为A 、B 、C ，列表如下：3种，所以两个组恰好抽到同一个小区的概率为39=13. 故选C ．点睛：此题主要考查了列表法求概率，列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适用于两步或两步以上完成的事件；解题时还要注意是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．4、某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教，每人只能去一个镇，则恰好其中一镇去4名，另两镇各去1名的概率为（） A ．2081B ．1081C ．5243D ．10243答案：B分析：因为对于这六个人来说，会被随机分派到3个镇中的任何一个，所以一共有36种情况，而有4个人的镇可能是3个镇中的任何一个，剩下两个镇各派一个人的派法是3×C 64，根据概率公式求解．解：6名教师志愿随机派到3个镇中的任何一个共有36种情况，有4个人的镇可能是3个镇中的任何一个，另两镇各去1名的结果数为3×6×5，所以恰好其中一镇去4名，另两镇各去1名的概率=3×6×536=1081，故选：B ．【小提示】选出符合事件A 或B 的结果数目m ，然后根据概率公式求出事件A 或B 的概率． 5、同时抛掷两枚质地均匀的硬币，则一枚硬币正面向上､一枚硬币反面向上的概率是（） A ．14B ．13C ．12D ．23答案：C分析：根据题意可画出树状图，然后进行求解概率即可排除选项．解：由题意得：∴一枚硬币正面向上､一枚硬币反面向上的概率是P =24=12；故选C ．小提示：本题主要考查概率，熟练掌握利用树状图求解概率是解题的关键．6、①三点确定一个圆； ②平分弦的直径平分弦所对的弧；③同圆或等圆中，相等的弦所对的圆心角相等；④在半径为4的圆中，30°的圆心角所对的弧长为π3；⑤方程x 2－x ＋3=0的两根之积是3，从上述5个命题中任取一个，是真命题的概率是（） A ．1B ．35C ．25D ．15 答案：C分析：先根据确定圆的条件对①进行判断；根据垂径定理的推论对②进行判断；根据圆心角、弧、弦的关系对③进行判断；根据弧长公式对④进行判断；利用根与系数关系对⑤进行判断．然后利用概率公式进行计算即可．解：①不在同一直线上的三点可以确定一个圆，故①说法错误，是假命题； ②平分弦（非直径）的直径平分弦所对的弧，所以②错误，是假命题； ③在同圆或等圆中，弦相等，所对的圆心角相等，所以③正确，是真命题； ④在半径为4的圆中，30°的圆心角所对的弧长为2π3，所以④错误，是假命题；⑤方程x 2-x+3=0的两根之积是3，正确，是真命题，其中真命题有2个，所以是真命题的概率是：25，故选：C ．小提示：本题考查了真假命题的判断及概率公式，解题的关键是：先判断命题的真假．7、不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别，从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是（） A ．14B ．13C ．12D ．34答案：A分析：首先根据题意画出树状图，由树状图求得所有等可能的结果与第一次摸到红球，第二次摸到绿球的情况，然后利用概率公式求解即可求得答案．解：画树状图得：∵共有4种等可能的结果，第一次摸到红球，第二次摸到绿球有1种情况， ∴第一次摸到红球，第二次摸到绿球的概率为14，故选：A ．小提示：本题考查了画树状法或列表法求概率，列出所有等可能的结果是解决本题的关键．8、如图是用七巧板拼成的正方形桌面，一个小球在桌面上自由地滚动，它最终停在黑色区域的概率是（）A ．14B ．18C ．316D ．23答案：C分析：先求出黑色区域的面积是正方形桌面的分率，再根据概率公式即可得出答案．解：观察图形可知，黑色区域的面积是正方形桌面的316，∴最终停在黑色区域的概率是316，故选：C ．小提示：本题考查几何概率，熟练掌握几何概率的计算方法是解题的关键．9、将一枚飞镖任意投掷到如图所示的正六边形镖盘上，飞镖落在白色区域的概率为( )A ．12B ．13C ．25D ．35答案：A分析：随机事件A 的概率P （A ）＝事件A 发生时涉及的图形面积÷一次试验涉及的图形面积，因为这是几何概率．解：设正六边形边长为a ，过A 作AD ⊥BC 于D ，过B 作BE ⊥CE 于E ，如图所示：∵正六边形的内角为180°−360°6=120°，∴在RtΔACD 中，∠ADC =90°,∠CAD =60°,AC =a ，则AD =12a,CD =√32a ， ∴BC =2CD =√3a ，∴在RtΔBCE 中，∠BEC =90°,∠BCE =60°,BC =√3a ，则CE =√32a,BE =32a ，则灰色部分面积为3S ΔABC =3×12BC ⋅AD =3×12×√3a ×12a =34√3a 2，白色区域面积为2S ΔBCE =2×12CE ⋅BE =√32a ×32a =3√34a 2，所以正六边形面积为两部分面积之和为32√3a 2，飞镖落在白色区域的概率P =34√3a 232√3a 2=12，故选：A ．小提示：本题考查了几何概率，熟练掌握几何概率模型及简单概率公式是解决问题的关键．10、如图是一张矩形纸板，顺次连接各边中点得到菱形，再顺次连接菱形各边中点得到一个小矩形．将一个飞镖随机投掷到大矩形纸板上，则飞镖落在阴影区域的概率是（）A ．13B ．14C ．16D ．18答案：B分析：连接菱形对角线，设大矩形的长=2a ，大矩形的宽=2b ，可得大矩形的面积，根据题意可得菱形的对角线长，从而求出菱形的面积，根据“顺次连接菱形各边中点得到一个小矩形”，可得小矩形的长，宽分别是菱形对角线的一半，可求出小矩形的面积，根据阴影部分的面积=菱形的面积-小矩形的面积可求出阴影部分的面积，再求出阴影部分与大矩形面积之比即可得到飞镖落在阴影区域的概率．解：如图，连接EG ，FH ，设AD=BC=2a ，AB=DC=2b ，则FH=AD=2a ，EG=AB=2b ， ∵四边形EFGH 是菱形，∴S 菱形EFGH =12FH ⋅EG =12⋅2a ⋅2b =2ab ， ∵M ，O ，P ，N 点分别是各边的中点，∴OP=MN=12FH=a ，MO=NP=12EG=b ，∵四边形MOPN 是矩形， ∴S 矩形MOPN =OP ⋅MO=ab ，∴S 阴影= S 菱形EFGH -S 矩形MOPN =2ab-ab=ab ， ∵S 矩形ABCD =AB ⋅BC=2a ⋅2b=4ab ， ∴飞镖落在阴影区域的概率是ab 4ab=14，故选B ．小提示：本题考查了几何概率问题．用到的知识点是概率=相应的面积与总面积之比．填空题11、小兰和小华两人做游戏，她们准备了一个质地均匀的正六面体骰子，骰子的六个面分别标有1，2，3，4，5，6，若掷出的骰子的点数为偶数，则小兰赢；若掷出的骰子的点数是3的倍数，则小华赢，游戏规则对______（填“小兰”或“小华”）有利．答案：小兰分析：根据所出现的情况，分别计算两人能赢的概率，即可解答．解：骰子的点数是偶数的有2，4，6，其概率为36=12，骰子的点数是3的倍数的有3，6，其概率为26=13，而12>13，∴游戏规则对小兰有利，所以答案是：小兰．小提示：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．12、甲、乙两人做游戏，他们准备了一个质量分布均匀的正六面体骰子，骰子的正六面分别标有1，2，3，4，5，6．若掷出的骰子的点数是偶数，则甲赢；若掷出的骰子的点数是3的倍数，则乙赢，这个游戏对甲、乙来说是_________的．（填“公平”或“不公平”）答案：不公平分析：根据所出现的情况，分别计算两人能赢的概率，即可解答．解：∵骰子的点数是偶数的有2，4，6，其概率为36=12，骰子的点数是3的倍数的有3，6，其概率为26=13，故游戏规则对甲有利．所以答案是：不公平.小提示：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．13、巧板是我国古代劳动人民的一项发明，被誉为“东方魔板”，它由五块等腰直角三角形、一块正方形和一块平行四边形组成．如图是利用七巧板拼成的正方形，随机向该图形内抛一枚小针，则针尖落在阴影部分的概率为 _____．答案：38分析：设大正方形的边长为2，先求出阴影区域的面积，然后根据概率公式即可得出答案．图，设小正方形的边长为1，根据等腰三角形和正方形的性质可求得AB=BE=2√2，FG=DC=√2，则空白的面积为：12×√2×√2+1×1+12×1×1×2+12×2×2=5；大正方形的面积是：2√2×2√2=8，阴影区域的面积为：8-5=3，所以针尖落在在阴影区域上的概率是：38．所以答案是：3．8小提示：本题考查几何概率，熟练掌握几何概率的计算方法是解题的关键．14、如图，在边长为1的小正方形组成的3×3网格中，A，B两点均在格点上，若在格点上任意放置点C，恰的概率为_________．好使得△ABC的面积为12##0.375答案：38分析：按照题意分别找出点C所在的位置，根据概率公式求出概率即可．的三角形，解：可以找到6个恰好能使△ABC的面积为12，则概率为：6÷16=38所以答案是：3．8小提示：此题主要考查了概率公式，解决此题的关键是正确找出恰好能使△ABC的面积为1的点．15、口袋内装有编号分别为1，2，3，4，5，6，7的七个球（除编号外都相同），从中随机摸出一个球，则摸出编号为偶数的球的概率是___．答案：37分析：用袋子中编号为偶数的小球的数量除以球的总个数即可得．解：∵从袋子中随机摸出一个球共有7种等可能结果，其中摸出编号为偶数的球的结果数为3，∴摸出编号为偶数的球的概率为3，7所以答案是：37．小提示：本题主要考查概率公式，解题的关键是掌握随机事件A 的概率P （A ）=事件A 可能出现的结果数÷所有可能出现的结果数．解答题16、在同升湖实验学校九年级的班级三人制篮球赛过程中，经过几轮激烈的角逐，最后由2班、5班、6班、9班进入了年级四强进行最后的名次争夺赛．现在葛老师规定先用抽签的方式决定将这4个班级分成2个小组，再由两个小组的胜出者争夺一二名，小组落败者争夺三四名．（1）直接写出9班和5班抽签到一个小组的概率；（2）若4个班级的实力完全相当，任何两个班级对决的胜率都是50%，求在年级四强的名次争夺赛中9班不与5班对决的概率．答案：（1）13；（2）13分析：（1）利用列举法求解即可；（2）分类讨论，利用列举法即可求解．（1）分组：(2，5)和(6，9)；(2，6)和(5，9)；(2，9)和(5，6)共3种， 9班和5班抽签到一个小组只有一种情况，故概率为：13；（2）①分组为(2，5)和(6，9)，故概率为：3×4=6； ②分组为(2，9)和(5，6)，故概率为：3×4=6；综上，在年级四强的名次争夺赛中9班不与5班对决的概率为16+16=13．小提示：本题考查了利用列举法求概率，通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．17、为落实“垃圾分类”，环保部门要求垃圾要按A，B，C，D四类分别装袋、投放，其中A类指废电池、过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料、废纸等可回收物，D类指其他垃圾．小明、小亮各投放了一袋垃圾．(1)小明投放的垃圾恰好是A类的概率为；(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率．答案：(1)14(2)14分析：（1）直接利用概率公式求出小明投放的垃圾恰好是A类的概率；（2）首先利用树状图法列举出所有可能，进而利用概率公式求出答案．（1）解：∵垃圾要按A，B，C，D四类分别装袋，小明投放了一袋垃圾，∴小明投放的垃圾恰好是A类的概率为：14；所以答案是：14；（2）解：如图所示：由图可知，共有16种可能结果，其中小亮投放的垃圾与小明投放的垃圾是同一类的结果有4种，所以小亮投放的垃圾与小明投放的垃圾是同一类的概率为416=14．小提示：此题主要考查了树状图法求概率，正确利用列举出所有可能并熟练掌握概率公式是解题关键．18、一个不透明的口袋中装有6个红球，9个黄球，3个白球，这些球除颜色外其他均相同．从中任意摸出一个球，(1)求摸到的球是白球的概率，(2)如果要使摸到白球的概率为14，需要在这个口袋中再放入多少个白球？答案：(1)16(2)2分析：（1）直接利用概率公式求解即可；（2）根据绿球的概率公式得到相应的方程，求解即可．（1）解：根据题意分析可得：口袋中装有红球6个，黄球9个，白球3个，共18个球，故P（摸到白球）=318=16（2）设需要在这个口袋中再放入x个白球，得：3+x18+x =14，解得：x=2．经检验x=2符合题意，所以需要在这个口袋中再放入2个白球．小提示：本题考查概率的求法与运用，一般方法为：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P(A)=mn．。

人教版数学九年级上册第二十五章《概率初步》小结与复习课件

B）
A．布袋中有2个红球和5个其他颜色的球
B．如果摸球次数很多，那么平均每摸7次，就有2次
摸中红球
C．摸7次，就有2次摸中红球
D．摸7次，就有5次摸不中红球
2.下列事件中是必然事件的是（ D ） A．从一个装有蓝、白两色球的缸里摸出一个球，摸出的球是白球 B．小丹的自行车轮胎被钉子扎坏 C．小红期末考试数学成绩一定得满分 D．将油滴入水中，油会浮在水面上
时，小红赢；否则，小莉赢.小红想要在游戏中获胜，
她会选择哪一条规则，并说明理由.
规则1：P(小红赢) = 5 ；
9
规则2：P(小红赢) = 4 ；
9
∵
5 9
4 9
，
∴小红会选择规则1.
针对训练
8.A、B两个小型超市举行有奖促销活动，顾客每购满
20元就有一次按下面规则转动转盘获奖机会，且两超
市奖额等同.规则是：①A超市把转盘甲等分成4个扇形
考点讲练
考点一事件的判断和概率的意义
例1 下列事件是随机事件的是（ D ） A.明天太阳从东方升起 B.任意画一个三角形，其内角和是360° C.通常温度降到0℃以下，纯净的水结冰 D.射击运动员射击一次，命中靶心
针对训练
1.“闭上眼睛从布袋中随机地摸出1个球，恰是红球的
概率是 2 7
”的意思是（
解：(1) 列表如下
小球卡片
6
2
（6，2）
4
（6，4）
6
（6，6）
7
（7，2）（7，4）（7，6）
8
（8，2）（8，4）（8，6）
共有9种等可能结果；
(2) 小红和小莉做游戏，制定了两个游戏规则：
规则1：若两次摸出的数字，至少有一次是“6”，小

人教版九年级第二十五章概率初步知识点.doc

第二十五章概率初步知识点总结般率初步事件的相关撫念及识别rT・二25.1概率1 •随机事件（1）确定事件事先能肯定它一定会发生的事件称为必然事件，事先能肯定它一定不会发生的事件称为不可能事件，必然事件和不可能事件都是确定的.（2）随机事件在一定条件下，可能发生也可能不发生的事件，称为随机事件.（3）事件分为确定事件和不确定事件（随机事件），确定事件又分为必然事件和不可能事件,其中,利发生的•它的極辜越拱近彳：專（1发生的町能竹越小.网它的概年总樓近0凡J)=—n可it社大，卜的救值個車习**=0法0<M^<1①必然事件发生的概率为1,即P （必然事件）二1；②不可能事件发生的概率为0,即P （不可能事件）二0；③如果A为不确定事件（随机事件），那么OVP （A） <1.随机事件发牛的可能性（概率）的计算方法：2. 可能性人小（1）理论计算又分为如下两种情况：第一种：只涉及一步实验的随机事件发生的概率，女山根据概率的人小与面积的关系，对一类概率模型进行的计算；笫二种：通过列表法、列举法、树状图來计算涉及两步或两步以上实验的随机事件发生的概率，如：配紫色，对游戏是否公平的计算.（2）实验估算又分为如下两种情况：第一种：利用实验的方法进行概率估算.要知道当实验次数非常大时，实验频率可作为事件发生的概率的估计值，即大量实验频率稳定于理论概率.笫二种：利用模拟实验的方法进行概率估算.如，利用计算器产牛随机数來模拟实验. 3. 概率的意义（1）一般地，在人量重复实验屮，如果事件A 发生的频率mn 会稳定在某个常数p 附近, 那么这个常数p 就叫做事件A 的概率，记为P （A ） =p.（2）概率是频率（多个）的波动稳定值，是对事件发生可能性大小的量的表现.（3）概率取值范围：0印「.（4）必然发主的事件的概率P （A ） =1；不可能发主事件的概率P （A ） =0.（4）事件发牛的可能性越大，概率越接近与1,事件发牛:的可能性越小，概率越接近于0. （5）通过设计简单的概率模型，在不确定的情境中做出合理的决策；概率与实际生活联系密切，通过理解什么是游戏对双方公平，用概率的语言说明游戏的公平性，并能按要求设计游戏的概率模型，以及结合貝体实际问题，体会概率与统计之间的关系，可以解决一些实际问题. 25.2用列举法求概率求具槪率，上翌刘举出浙勺町能性松尊的堵果和Fr 审血含圾中的U 聖V 果便可.也就足列举法求槪亟.J町能出现的肚皋肴秤斥金* _____________________■ ■■■■■■■ ■― ■■・■■■■■■■■■■■■ —■ 、乙▲'T&科仕果发生的可佻处畑蹲；4古奧概星概率•当IB 要对爭件中出现的数宇（&）进彳必算叭的常用列表的方法来列举所有可艇性相等的站果不重复不遗厶巧列承出雕鬲•发土的可征检帼等时姑果 * 就事科的发生分f 遭1 H ：,遇常画厨形用1. 概率的公式（1）随机事件A 的概率P （A ）二事件A 可能出现的结果数所冇可能出现的结果数.（2） P （必然事件）二1.（3） P （不可能事件）=0.2. 几何概型的概率问题是指具有下列特征的一些随机现象的概率问题：设在空间上有一区域G,又区域g 包含在区域G 内（如图），而区域G 与g 都是可以度量的（可求面积），现随机地向G 内投掷一点M,假设点M 必落在G 中，且点M 落在区域G 的任何部分区域g 内的概率只与g 的度量（长度、面积、体积等）成正比，而与g 的位置和形状无关.具有这种性质的随机试验（掷点），称为儿何概型.关于儿何概型的随机事件“向区域G 屮任意投掷一个点M,点1列举法-M落在G内的部分区域g”的概率P定义为:g的度量与G的度ftZ比，即P=g的测度G 的测度简单來说：求概率时，已知和未知与儿何有关的就是儿何概率.计算方法是长度比，血枳比，体积比等.3. 列举法和树状法（1）当试验小存在两个元素且出现的所有可能的结果较多时，我们常用列表的方式，列出所有可能的结果，再求出概率.（2）列表的目的在于不重不漏地列举出所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.（3）列举法（树形图法）求概率的关键在于列举出所有可能的结果，列表法是一种，但当一个事件涉及三个或更多元索时，为不重不漏地列出所冇可能的结果，通常采用树形图.（4）树形图列举法一般是选择一个元素再和其他元素分别组合，依次列出，彖树的枝丫形式，最末端的枝丫个数就是总的可能的结果n.（5）当有两个元索时，可用树形图列举，也可以列表列举.4. 游戏公平性（1）判断游戏公平性盂要先计算每个事件的概率，然后比较概率的人小，概率相等就公平，否则就不公平.（2）概率二所求情况数总情况数.25.3利用频率估计概率所有可施的结舉不建冇限个或各种可施发生的可能性不相同大量載复试輪用频书佔计槪咿用嫌峑估il概車必次做丿、M驟孵勰翔蠶漏蠶難1. 利用频率估计概率（1）人量重复实验吋，事件发牛的频率在某个固定位置左右摆动，并11摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率.（2）用频率估计概率得到的是近似值，随实验次数的增多，值越來越梢确.（3）当实验的所有可能结果不是有限个或结果个数很多，或各种可能结果发生的町能性不相等时，一般通过统计频率来估计概率.2. 模拟实验（1）在一些有关抽収实物实验小通常用摸収卡片代替了实际的物品或人抽取，这样的实验称为模拟实验.（2）模拟实验是川卡片、小球编号等形式代替实物进行实验，或川计算机编号等进行实验，冃的在于省时、省力，但能达到同样的效果.（3）模拟实验只能用更简便方法完成，验证实验日的，但不能改变实验日的，这部分内容根据《新课标》要求，只要设计岀一个模拟实验即可.。

人教新课标版初中九年级数学上册第25章概率复习课ppt课件

跟踪练习： 3、如图，有牌面数字都是2，3，4的两组牌．从每组牌中各随机摸出一张，请用画树状图或列表的方法，求摸出的两张牌的牌面数字之和为6的概率．
解：画树状图如下：
∵共有九种情况，数字之和为 6 的共有 3 种， ∴随机摸出的两张牌的牌面数字之和为 6 的概率为39＝31.
4、把大小和形状完全相同的６张卡片分成两组，每组３张，分别标上１、２、３，将这两组卡片分别放入两个盒子中搅匀，再从中随机抽取一张．（１）试求取出的两张卡片数字之和为奇数的概率；（２）若取出的两张卡片数字之和为奇数，则甲胜；取出的两张卡片数字之和为偶数，则乙胜；试分析这个游戏是否公平？请说明理由．
解：画树状图如图所示：开始
1
2
3
123 123 123
由上图可知，所有等可能结果共有９种，其中两张卡片数字之和为奇数的结果有４种．
P 4 9
（２）不公平；理由：由（１）可得出：取出的两张卡片数字之和为偶数的概率为：5 ∵ 4 ，5∴这个游戏不公平．9
99
通过本节课的学习你收获了什么？
作业布置
第三步：确定所有可能出现的结果数ｎ及所求事件Ａ出现的结果ｍ；第四步：用公式 P( A) 求= 事m件A发生的概率.
n
４、利用概率判断游戏的公平性：判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．５、频率与概率：在随机现象中，一个随机事件，做了大量试验后，可以用一个事件发生的频率作为这个事件的概率的估计值.
知识点2、概率及其计算：
１、概率定义：随机现象中，一个事件发生的可能性大小．事件发生的可能性越小，它的概率越接近０．
２、简单事件概率的计算
在随机现象中，出现的各种可能的结果共有ｎ种．如果出现其

人教版九年级数学上册第25章《概率初步》知识小结与复习

（2006年广东茂名市第10题）
为了估计湖里有多少条鱼，先从湖里捕捞 100条鱼都做上标记，然后放回湖中去，经过一段时间，待有标记的鱼完全混合于鱼群后，第二次再捕捞100条鱼，发现其中10条
有标记，那么你估计湖里大约有鱼 D
A. 500条 B. 600条 C. 800 条 D. 1000条
“建模”——数学思想
（1）请你完成下面表示游戏一个回合所有可能出现的结果的树状图；
（2）求一个回合能确定两人先下棋的概率．
游戏规则
三人手中各持有一枚质地均匀的硬币，他们同时将手中硬币抛落到水平地面为一个回合．落地后，三枚硬币中，恰有两枚正面向上或者反面向上的两人先下棋；若三枚硬币均为正面向上或反面向上，则不能确定其中两人先下棋．
概率的计算方法
具有等可
随机
简单的随
事
机事件
能性
件
不具有等
概
可能性
率
的
计算
复杂的随机事件
摸拟试验
概率定义树状图列表试验法
有放回摸球
无放回摸球
理论计算
试验估算小明的方法: 多次逐个抽查
小亮的方法: 多次抽样调查
一、知识回顾
1、事先能肯定它_一__定__发生的事件称为必然事件，它发生的概率是_____1__.
下列事件中，确定事件是（）
A、掷一枚六面分别标有1—6数字的均匀骰子，骰子停止转动后偶数点朝上
B、从一副完整的扑克牌中任意抽出一张牌，花色是红桃
C、任意选择电视的某一频道，正在播放动画片
D、在同一年出生的367名学生中，至少有两人的生日是同一天
在多次试验中，某个事件出现的次数叫频数，

九年级数学上册第二十五章概率初步知识点归纳超级精简版(带答案)

九年级数学上册第二十五章概率初步知识点归纳超级精简版单选题1、从甲、乙、丙三名同学中随机抽取两名同学去参加义务劳动，则甲与乙恰好被选中的概率是（） A ．16B ．14C ．13D ．12 答案：C分析：根据题意用列举法求概率即可．解：随机抽取两名同学所能产生的所有结果，它们是：甲与乙，甲与丙，乙与丙，所有可能的结果共3种，并且出现的可能性相等，∴甲与乙恰好被选中的概率：P =13．故选：C ．小提示：本题主要考查了用列举法求概率，能正确列举出所有等可能结果是做出本题的关键．2、一名运动员连续打靶100次，其中5次命中10环，5次命中9环，90次命中8环．根据这几次打靶记录，如果再让他打靶1次，那么下列说法正确的是（） A ．命中10环的可能性最大B ．命中9环的可能性最大 C ．命中8环的可能性最大D ．以上3种可能性一样大答案：D分析：根据随机事件发生的独立性，可得某次射击的结果与连续射靶100次的结果无关，所以针对某次射击，命中10环、9环、8环的可能性均等，据此解答即可．根据随机事件发生的独立性，可得某次射击的结果与连续射靶100次的结果无关，所以针对某次射击，命中10环、9环、8环的可能性均等．如果再让他打靶1次，都有可能．故选：D ．小提示：此题主要考查了随机事件发生的独立性问题的应用． 3、下列说法中，正确的是（）A．“任意画一个多边形，其内角和是360°”是必然事件B．“如果a2＝b2，那么a＝b”是必然事件C．可能性是50%的事件，是指在两次试验中一定有一次会发生D．“从一副扑克牌（含大小王）中抽一张，恰好是红桃”是随机事件答案：D分析：根据题意逐项分析，即可求解．解：A. “任意画一个多边形，其内角和是360°”是必然事件，只有四边形的内角和是360°，所以是随机事件，判断错误；B. “如果a2＝b2，那么a＝b”是必然事件，a与b也有可能互为相反数，所以是随机事件，判断错误；C. 可能性是50%的事件，是指在两次试验中一定有一次会发生，可能性是50%的事件，只表明一种可能性，并不表示两次试验中一定有一次会发生，所以判断错误；D. “从一副扑克牌（含大小王）中抽一张，恰好是红桃”是随机事件，判断正确，符合题意．故选：D小提示：本题考查了必然事件、随机事件、可能性大小、多边形内角和等知识，综合性较强，熟知相关概念，知识，理解可能性的意义是解题关键．4、某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如表的表格，则符合这一结果的实验最有可能的是（）B．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃C．抛一个质地均匀的正六面体骰子（六个面上分别标1，2，3，4，5，6），向上的面点数是5D．从一个装有2个白球和1个红球的袋子中任取一球，取到红球答案：D分析：根据利用频率估计概率得到实验的概率在0.33左右，再分别计算出四个选项中的概率，再进行判断．A、抛一枚硬币，出现正面的概率是1，不符合题意；2B 、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率是14，不符合题意；C 、抛一个质地均匀的正六面体骰子（六个面上分别标1，2，3，4，5，6），向上的面点数是5的概率是16，不符合题意；D 、从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率是13，符合题意，故选：D ．小提示：此题考查频率估计概率，计算简单事件的概率，正确理解题意计算出各事件的概率是解题的关键． 5、在不透明的袋子中装有黑、白两种球共50个，这些球除颜色外都相同，随机从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则袋子中黑球的个数约为（） A ．20个B ．30个C ．40个D ．50个答案：A分析：根据黑球的频率稳定在0.4附近，黑，白两种球共50个，即可确定出黑球个数．解：∵黑球的频率稳定在0.4附近，黑，白两种球共50个， ∴黑球的个数约为：0.4×50=20. 故选：A ．小提示：根据概率的求法，找准两点：①全部情况的总数，②符合条件的情况数目，二者的比值就是其发生的概率．6、孟德尔被誉为现代遗传学之父，他通过豌豆杂交实验，发现了遗传学的基本规律．如图，纯种高茎豌豆和纯种矮茎豌豆杂交，子一代都是高茎豌豆，子一代种子种下去，自花传粉，获得的子二代豌豆由DD 、Dd 、dd 三种遗传因子控制．由此可知，子二代豌豆中含遗传因子D 的概率是（）A ．14B ．38C ．12D ．34 答案：D分析：画出遗传图解，即可得到答案．解：画图如下：共有4种情况，而出现高茎的有3种结果，∴子二代豌豆中含遗传因子D的概率是3，4故选：D小提示：本题主要考查了求概率，正确画出树状图是解答本题的关键．．小张这期7、某一超市在“五•一”期间开展有奖促销活动，每买100元商品可参加抽奖一次，中奖的概率为13间在该超市买商品获得了三次抽奖机会，则小张( )A．能中奖一次B．能中奖两次C．至少能中奖一次D．中奖次数不能确定答案：D，说明此事件为随机事件，即可能发生，也可能不发生．分析：由于中奖概率为13解：根据随机事件的定义判定，中奖次数不能确定.故选D．小提示：解答此题要明确概率和事件的关系：①P(A)=0，为不可能事件；②P(A)=1为必然事件；③0<P(A)<1为随机事件．8、从马鸣、杨豪、陆畅，江宽四人中抽调两人参加“寸草心”志愿服务队，恰好抽到马鸣和杨豪的概率是（） A ．112B ．18C ．16D ．12 答案：C分析：列表得出所有等可能的情况数，找出所选两人恰好是马鸣和杨豪的情况数，即可求出所求的概率．解：列表得：所有等可能的情况有12种，其中恰好抽到马鸣和杨豪的情况有2种，恰好抽到马鸣和杨豪的概率是212=16，故选C.小提示：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．9、不透明的袋子中装有10个黑球和若干个白球，这些球除颜色外无其他差别．从袋子中随机摸出一球记下其颜色，再把它放回袋子中摇匀，重复上述过程，共试验400次，其中有300次摸到白球，由此估计袋子中的白球大约有( )A ．6个B ．10个C ．15个D ．30个答案：D分析：在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，设未知数列出方程求解．解：设白球有x 个，根据题意得： x10+x=300400，解得：x =30，经检验x =30是分式方程的解，且符合题意， ∴估计袋子中的白球大约有30个．故选：D ．小提示：本题考查利用频率估计概率．大量反复试验下频率稳定值即概率，关键是根据白球的频率得到相应的等量关系．10、随机掷一枚均匀的硬币两次，两次正面都朝上的概率是（）． A ．14B ．12C ．34D ．1 答案：A分析：首先利用列举法，列得所有等可能的结果，然后根据概率公式即可求得答案．解：随机掷一枚均匀的硬币两次，可能的结果有：正正，正反，反正，反反， ∴两次正面都朝上的概率是14．故选：A ．小提示：此题考查了列举法求概率的知识．解题的关键是注意不重不漏的列举出所有等可能的结果，用到的知识点为：概率=所求情况数与总情况数之比．填空题11、在一个不透明的口袋中，装有若干个红球和6个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.3，摸到红球的频率是 _____，则估计盒子中大约有红球 _____个．答案： 0.7 14分析：根据频率之和为1，以及在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，列出方程求解，即可．解：摸到黄球的频率是0.3，摸到红球的频率是0.7，设有红球x 个，根据题意得：6=0.3，6+x解得：x＝14，经检验，x＝14是原方程的解．故答案是：0.7，14．小提示：此题主要考查了利用频率估计概率，本题利用了用大量试验得到的频率可以估计事件的概率．关键是根据黄球的频率得到相应的等量关系．12、一个不透明的袋中装有3个红球和2个白球，这些球除颜色外无其他差别．现随机从袋中摸出一个球，这个球是红球的概率是______．答案：35分析：先求出总的所有可能结果数及摸出的球是红球的所有可能数，再根据概率公式即可得出答案．解：根据题意可得：不透明的袋子里装有将5个球，其中3个红色的，．任意摸出1个，摸到红球的概率是35．所以答案是：35小提示：此题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．=3的解是负数，且13、从−2，−1，0，1，2，3这6个数中任意选一个数作为m的值，则使关于x的方程2x−mx+1关于x的一次函数y=(m−1)x−4的图象不经过第一象限的概率为_______．答案：1．3分析：先求出分式方程的解，再根据解为负数求出此时m的取值范围，再根据一次函数图像不经过第一象限求出m的取值范围，最终确定m可以选取的数值，最后计算概率．=3得：x=−m−3解分式方程2x−mx+1∵方程的解为负数，∴−m−3<0且−m−3≠−1，解得：m>−3且m≠−2，∵一次函数y=(m−1)x−4图象不经过第一象限，∴m−1<0，∴m<1∴−3<m<1且m≠−2，在−2，−1，0，1，2，3这6个数中符合−3<m<1且m≠−2的有−1，0这2个数，∴使分式方程的解为负数且一次函数图象不经过第一象限的概率为26=13所以答案是：13．小提示：本题考查概率公式，分式方程的解，一次函数图象与系数的关系等知识点，综合性较强。

人教版数学九年级上册第25章-概率初步(教案)

概率的性质
1.理解概率的基本性质，如非负性、规范性、可加性等。
2.掌握互斥事件和独立事件的概率计算方法。
25.4概率的应用
1.能运用概率知识解决实际问题。
2.了解概率在生活中的应用，提高解决问题的能力。
二、核心素养目标
1.培养学生运用数学语言描述随机现象，提高抽象概括能力。
2.培养学生运用概率知识进行问题分析，提升逻辑推理和数学思维能力。
此外，在教学过程中，我尝试采用小组讨论和实验操作的方式，让学生在实践中学习概率。从学生的反馈来看，这种教学方式取得了较好的效果，大家积极性很高，课堂氛围活跃。但同时，我也注意到，在小组讨论过程中，部分学生依赖性强，不够主动。因此，我需要在组织小组活动时，更加注重激发学生的主观能动性，引导他们积极参与讨论，提高合作能力。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《概率初步》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过不确定的情况？”（如抛硬币、抽奖等）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索概率的奥秘。
在讲解概率的性质和应用时，我发现学生对于理论知识的应用还不够熟练。为了帮助学生更好地将所学知识运用到实际问题中，我计划在后续的教学中，增加一些与生活密切相关的综合题，让学生在解决问题的过程中，深化对概率性质的理解。
最后，我觉得在课堂教学过程中，要关注学生的个体差异。对于学习困难的学生，要给予更多的关心和指导，帮助他们克服难点，提高学习兴趣。同时，对于学有余力的学生，可以适当增加拓展性内容，激发他们的学习潜能。
2.教学难点
-理解随机事件的抽象概念：学生对随机事件的理解可能存在困难，需要通过具体实例和生活情境帮助学生理解。

秋人教版九年级数学上册第二十五章概率初步复习课件(共80张PPT)

❖
16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021年9月19日星期日7时10分18秒07:10:1819 September 2021
❖
17、儿童是中心，教育的措施便围绕他们而组织起来。上午7时10分18秒上午7时10分07:10:1821.9.19
第二十五章概率初步
(3)某中学准备购买两个品种的月饼共32盒(价格如下表所示), 发给学校的“留守儿童”, 让他们过一个愉快的中秋节, 其中指定购买了甲厂家的高档月饼, 再从乙厂家购买一个品种. 若恰好用了1740元,则购买了甲厂家的高档月饼多少盒？
第二十五章概率初步
解：(1) 画树状图如下：
第二十五章概率初步
由上表可知, 共5 6 种等可能的结果, 其中恰好取出火腿粽子和豆沙粽子各1 个的结果有3 0 种, ∴P ( 恰好取出火腿粽子和豆沙粽子各1 个) =
第二十五章概率初步
相关题6 中秋节吃月饼是中华民族的传统习俗. 今年某商场销售甲厂家的高档、中档、低档三个品种及乙厂家的精装、简装两个品种的盒装月饼. 现需要在甲、乙两个厂家中各选购一个品种. (1)写出所有选购方案(利用画树状图或列表的方法求选购方案)； (2)如果(1)中各种选购方案被选中的可能性相同,那么甲厂家的高档月饼被选中的概率是多少？
第二十五章概率初步
概率的求法
直接列举法
列举法
列表法
画树状图法用频率估计率
模拟试验
第二十五章概率初步
归纳整合
专题一事件类型的判别
【要点指导】根据事件发生的可能性将事件分为必然事件、不可能事件、随机事件, 必然事件和不可能事件统称确定性事件.

人教版讲义九年级第二十五章概率初步随机事件与概率

人教版讲义九年级第二十五章概率初步随机事件与概率探求点1 确定性事情和随机事情情形激凝〝天上掉馅饼〞是什么事情？知识解说1.确定性事情事前能一定它一定会发作的事情称为肯定事情，事前能一定它一定不会发作的事情称为不能够事情，肯定事情和不能够事情统称为确定事情。

2.随机事情在一定条件下，能够发作也能够不发作，事前无法确定的事情，称为随机事情。

典例剖析例1 指出以下事情中，哪些是肯定事情，哪些是不能够事情，哪些是随机事情（1）掷一枚硬币，出现正面朝上；（2）买一张彩票中一百万；（3）用一块拳头大小的石头砸一块普通窗户玻璃，玻璃被砸碎；（4）恣意买一张电影票，座位号是双号；（5）向空中抛一枚硬币，硬币在空中不往下掉解析对事情的判别，要依据实践生活阅历以及合理的疑心、缜密的推理、严谨的思索来予以剖析。

答案〔1〕随机事情〔2〕随机事情〔3〕肯定事情〔4〕随机事情〔5〕不能够事情类题打破1 指出以下事情中，哪些是肯定事情，那些事不能够事情，哪些是随机事情。

（1）从一副扑克牌中任抽一张是红桃；（2）没有水分，水稻种子发芽（3）恣意掷一枚骰子出现的点数是6（4）翻开电视机，正在播广告（5）哈尔滨的冬天会下雪（6）太阳从西边出来（7）一枚平均的硬币在投掷后，不是正面朝上，就是反面朝上答案〔1〕随机事情〔2〕不能够事情〔3〕随机事情〔4〕随机事情〔5〕肯定事情〔6〕不能够事情〔7〕肯定事情点拨依据肯定事情，不能够事情、随机事情的定义即可做出判别。

探求点2 随机事情发作的能够性知识解说随机事情发作的能够性；普通地，随机事情发作的能够性是有大小的，不同的随机事情发作的能够性的大小有能够不同。

典例剖析例2 判别以下事情中 .哪些事情发作的能够性是相反的，哪些不是〔1〕掷一枚平均的骰子，出现2点朝上或6点朝上的时机:〔2〕从装有4个红球、3个白球的袋中任取球，取到红球或白球的能够性:〔3〕从一副扑克牌中任取一张取到小王或黑桃3的能够性:〔4〕掷两枚骰子，出现的点数和是〝2〞或〝5〞的能够性解析能够性相反指两个事情发作的能够性大小一样，需求结合详细的事情仔细剖析。