实验3 连续时间信号的卷积计算

（1）符号法：要注意积分变量和积分限的选取
lim
0 k
f1 (k )
f2 (t
k)
如果令t=n,则
（2）数值计算法
f (n) f1(k) f2 ((n k)) k
y(t)
t
eT
u (t )
etu(t
)
t
eT
u0
ex3_1.m
y(t) [u(t) u(t 1)][u(t) u(t 1)]
– 构造对应的时间向量k.
f (n)
y(t) [u(t) u(t 1)][u(t) u(t 1)]
ex3_3.m
实验内容：
1、绘制 f1(t) f2 (t)
采用数值与符号法
f1 (t )
f2 (t)
2、两种方式计算如下卷积
(1) f1(t) f2 (t); (2) f1(t) f3(t); (3) f1(t) f4 (t) (4) f2 (t) f3(t); (5) f2 (t) f4 (t); (6) f3(t) f4 (t)
实验目的：
1、学会运用MATLAB实现连续时间信号的卷积 2、学会运用MATLAB符号运算法求连续时间信号的卷积 3、学会运用MATLAB数值计算方法求连续时间信号的卷积
实验原理：
f (t) f (t) f (t) f ( ) f (t )d 1
2
1
2
f (t) f1(t) * f2 (t) f1( ) f (t )d
函数实现卷积和wconvuv?1mwnumvnm????1212ftftftfftd????????????121122112200limlimftftftfmftfmftfmftfm??????对和进行等间隔均匀抽样则当足够小的时候则1212120limmftftftfftdfmftm?????????????????????1212mmfnfmfnmfmfnm????????????????1212mftfnfmfnmftfnfn????????????用用matlab实现连续信号卷积的过程

连续时间系统卷积的计算

实验报告实验名称：连续时间系统卷积的数值计算班级：120241姓名：彭壮学号：12021327一、实验目的：1、加深对卷积概念及原理的理解；2、掌握借助计算机计算任意信号卷积的方法。

二、实验原理：卷积积分不仅可以通过直接积分或查表的方法来求解，还可以用积分的数值计算方法来求解。

在线性系统的分析过程中，有时会遇到复杂的激励信号，或者有时只是一组测试数据或曲线，冲激响应也可能出现同样的情况。

显然，此时直接计算积分或查表都有困难，而采用近似的数值计算方法可以解决这个问题，求得卷积积分。

1、卷积的定义卷积积分可以表示为2卷积计算的几何算法卷积积分的计算从几何上可以分为四个步骤：翻转→平移→相乘→叠加。

3卷积积分的应用卷积积分是信号与系统时域分析的基本手段，主要用于求系统零状态响应，它避开了经典分析方法中求解微分方程时需要求系统初始值的问题。

设一个线性零状态系统，已知系统的单位冲激响应为h(t)，当系统的激励信号为e(t)时，系统的零状态响应为由于计算机技术的发展，通过编程的方法来计算卷积积分已经不再是冗繁的工作，并可以获得足够的精度。

因此，信号的时域卷积分析法在系统分析中得到了广泛的应用。

卷积积分的数值运算实际上可以用信号的分段求和来实现，即：如果我们只求当t = nΔt （n为正整数,nΔt 记为t ）时r(t)的值，则由上式可以得到：当Δt 足够小时，r(t )就是e(t)和h(t)卷积积分的数值近似，由上面的公式可以得到卷积数值计算的方法如下：1 将信号取值离散化，即以 Ts 为周期，对信号取值，得到一系列宽度间隔为 Ts 的矩形脉冲原信号的离散取值点，用所得离散取值点矩形脉冲来表示原来的连续时间信号；2 将进行卷积的两个信号序列之一反转，与另一信号相乘，并求积分，所得为 t=0 时的卷积积分的值。

以 Ts 为单位左右移动反转的信号，与另一信号相乘求积分，求的t<0和t>0时卷积积分的值；3 将所得卷积积分值与对应的t 标在图上，连成一条光滑的曲线，即为所求卷积积分的曲线。

信号与系统连续时间信号卷积运算

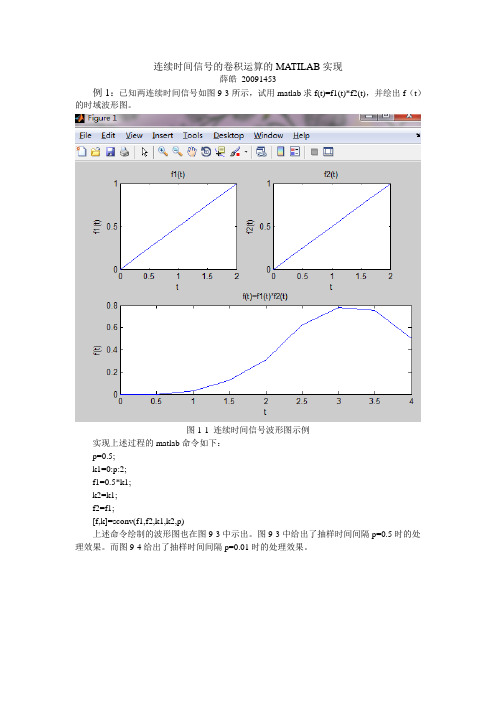
连续时间信号的卷积运算的MATILAB实现薛皓20091453例1：已知两连续时间信号如图9-3所示，试用matlab求f(t)=f1(t)*f2(t)，并绘出f（t）的时域波形图。

图1-1 连续时间信号波形图示例实现上述过程的matlab命令如下：p=0.5;k1=0:p:2;f1=0.5*k1;k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)上述命令绘制的波形图也在图9-3中示出。

图9-3中给出了抽样时间间隔p=0.5时的处理效果。

而图9-4给出了抽样时间间隔p=0.01时的处理效果。

图1-2 例1的连续时间信号波形图习题1：已知f1(t)=1(2t 1≤≤)，f2(t)=1(3t 2≤≤)，用matlab 实现其卷积并绘制出卷积曲线。

解：程序代码如下：>> p=0.01;k1=1:p:2;f1=ones(size(k1)).*(k1>1);k2=2:p:3;f2=ones(size(k2)).*(k2>2);f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=k1(length(k1))+k2(length(k2));subplot(2,2,1)plot(k1,f1)title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);h=get(gca,'position');h(3)=2.5*h(3); 0set(gca,'position',h)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')绘制图形如图2-1所示。

MATLAB实验报告(1-4)

信号与系统MATLAB第一次实验报告一、实验目的1.熟悉MATLAB软件并会简单的使用运算和简单二维图的绘制。

2.学会运用MATLAB表示常用连续时间信号的方法3.观察并熟悉一些信号的波形和特性。

4.学会运用MATLAB进行连续信号时移、反折和尺度变换。

5.学会运用MATLAB进行连续时间微分、积分运算。

6.学会运用MATLAB进行连续信号相加、相乘运算。

7.学会运用MATLAB进行连续信号的奇偶分解。

二、实验任务将实验书中的例题和解析看懂，并在MATLAB软件中练习例题，最终将作业完成。

三、实验内容1.MATLAB软件基本运算入门。

1). MATLAB软件的数值计算：算数运算向量运算：1.向量元素要用”[ ]”括起来，元素之间可用空格、逗号分隔生成行向量，用分号分隔生成列向量。

2.x=x0:step:xn.其中x0位初始值，step表示步长或者增量，xn 为结束值。

矩阵运算：1.矩阵”[ ]”括起来；矩阵每一行的各个元素必须用”,”或者空格分开；矩阵的不同行之间必须用分号”;”或者ENTER分开。

2.矩阵的加法或者减法运算是将矩阵的对应元素分别进行加法或者减法的运算。

3.常用的点运算包括”.*”、”./”、”.\”、”.^”等等。

举例：计算一个函数并绘制出在对应区间上对应的值。

2).MATLAB软件的符号运算：定义符号变量的语句格式为”syms 变量名”2.MATLAB软件简单二维图形绘制1).函数y=f(x)关于变量x的曲线绘制用语：>>plot(x,y)2).输出多个图像表顺序：例如m和n表示在一个窗口中显示m行n列个图像，p表示第p个区域，表达为subplot(mnp)或者subplot(m,n,p)3).表示输出表格横轴纵轴表达范围：axis([xmax,xmin,ymax,ymin])4).标上横轴纵轴的字母：xlabel(‘x’),ylabel(‘y’)5).命名图像就在subplot写在同一行或者在下一个subplot前：title(‘……’)6).输出：grid on举例1：举例2：3.matlab程序流程控制1).for循环：for循环变量=初值:增量:终值循环体End2).while循环结构：while 逻辑表达式循环体End3).If分支：(单分支表达式)if 逻辑表达式程序模块End(多分支结构的语法格式)if 逻辑表达式1程序模块1Else if 逻辑表达式2程序模块2…else 程序模块nEnd4).switch分支结构Switch 表达式Case 常量1程序模块1Case 常量2程序模块2……Otherwise 程序模块nEnd4.典型信号的MATLAB表示1).实指数信号：y=k*exp(a*t)举例：2).正弦信号：y=k*sin(w*t+phi)3).复指数信号：举例：4).抽样信号5).矩形脉冲信号:y=square(t,DUTY) (width默认为1)6).三角波脉冲信号：y=tripuls(t,width,skew)(skew的取值在-1~+1之间，若skew取值为0则对称)周期三角波信号或锯齿波:Y=sawtooth(t,width)5.单位阶跃信号的MATLAB表示6.信号的时移、反折和尺度变换:Xl=fliplr(x)实现信号的反折7.连续时间信号的微分和积分运算1).连续时间信号的微分运算：语句格式：d iff(function,’variable’,n)Function:需要进行求导运算的函数，variable:求导运算的独立变量，n：求导阶数2).连续时间信号的积分运算：语句格式：int(function,’variable’,a,b)Function:被积函数variable:积分变量a:积分下限b:积分上限(a&b默认是不定积分)8.信号的相加与相乘运算9.信号的奇偶分解四、小结这一次实验让我能够教熟悉的使用这个软件，并且能够输入简单的语句并输出相应的结果和波形图，也在一定程度上巩固了c语言的一些语法。

连续时间信号卷积运算的MATLAB实现

连续时间信号卷积运算的MATLAB 实现一、实验目的（1）理解掌握卷积的概念及物理意义。

（2）理解单位冲激响应的概念及物理意义。

二、实验原理连续信号卷积运算定义为1212()()*()()()f t f t f t f f t d τττ∞-∞==-⎰卷积计算可以通过信号分段求和来实现，即1212120()()*()()()lim ()()k f t f t f t f f t d f k f t k τττ∞∞∆→=-∞-∞==-=∆-∆∆∑⎰ 如果只求当t n =∆（n 为整数）时()f t 的值()f n ∆，则由上式可得1212()()()()[()]k k f n f k f n k f k f n k ∞∞=-∞=-∞∆=∆∆-∆=∆∆-∆∑∑ 式中的12()[()]k f k f n k ∞=-∞∆-∆∑ 实际上就是连续信号1()f t 和2()f t 经等时间间隔∆均匀抽样的离散序列1()f k ∆和2()f k ∆的卷积和。

当∆足够小时，()f n ∆就是卷积积分的结果——连续时间信号()f t 的较好的数值近似。

三、实验程序function[f,k]=sconv(f1,f2,k1,k2,p)f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2;k=k0:p:k3*p;subplot(2,2,1)plot(k1,f1)title('f1(t)')xlabel('t')ylabel('f(1)')subplot(2,2,2)plot(k2,f2)title('t')xlabel('t')ylabel('f(2)')subplot(2,2,3)plot(k,f);h=get(gca,’position’);h(3)=2.5*h(3);set(gca,'position',h)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')四、求解f t=cost∗sint（1）Matlab命令如下：p=0.1;k1=0:p:6;f1=sin(k1);k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)（2）运行过程如下：图一程序截图图二运行结果五、实验小结实验结果表明，用Matlab计算出的结果与理论分析结果一致。

信号的卷积实验报告

信号的卷积实验报告
《信号的卷积实验报告》
在现代通信系统中，信号的处理是至关重要的。

信号的卷积是一种常用的信号
处理方法，通过将两个信号进行卷积运算，可以得到新的信号，从而实现信号
的处理和分析。

在本实验中，我们将对信号的卷积进行实验，以探索其在通信
系统中的应用和意义。

实验过程如下：首先，我们准备了两个输入信号，分别为信号A和信号B。

然后，我们将这两个信号进行卷积运算，得到输出信号。

接着，我们对输出信号
进行分析，观察其频谱特性和时域特性。

最后，我们将对实验结果进行总结和
讨论，探讨信号的卷积在通信系统中的实际应用。

通过实验，我们发现信号的卷积可以实现信号的滤波、信号的延迟和信号的叠
加等功能。

在通信系统中，信号的卷积可以用于信号的编码和解码、信道的均
衡和信号的复原等方面。

因此，信号的卷积在通信系统中具有重要的意义和应
用价值。

总之，通过本次实验，我们对信号的卷积有了更深入的理解，并认识到其在通
信系统中的重要性。

希望通过这篇实验报告，能够让更多的人了解信号的卷积，并对其在通信系统中的应用有更清晰的认识。

2.连续时间信号卷积和离散时间信号卷积

二．连续时间信号卷积和离散时间信号卷积1．连续时间信号卷积)()()(21t f t f t f *=；2．离散时间信号卷积)()()(21n f n f n f *=连续时间信号卷积function [f,k]=sconv(f1,f2,k1,k2,p)%计算连续信号卷积积分f(t)=f1(t)*f2(t)%f: 卷积积分f(t)对应的非零样值向量%K: f(t)的对应时间向量%f1: f1(t)的非零样值向量%f2: f2(t)的非零样值向量%K1: 序列f1(t)的对应时间向量%K2: 序列f2(t)的对应时间向量%p: 取样时间间隔f1=0.5*(0:0.01:2);f2=0.5*(0:0.01:2);k1=0:0.01:2;k2=0:0.01:2;p=0.01;f=conv(f1,f2); %计算序列1与序列2的卷积和f=f*p;k0=k1(1)+k2(1); %计算序列f 非零样值的起点位置k3=length(f1)+length(f2)-2; %计算卷积和f 非零样值得宽度k=k0:p:k0+k3*p; %确定卷积和f 非零样值的时间向量subplot(3,3,1)plot(k1,f1) %在子图1绘制f1(t)时域波形图title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(3,3,4)plot(k2,f2) %在子图2绘制f2(t)时域波形图title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(3,3,7)plot(k,f); %画卷积f(t)的时域波形 h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h) %将第三个子图的横坐标范围扩为原来的2.5倍title(' f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')离散时间信号卷积function [f,k]=dconv(f1,f2,k1,k2)%The function of compute f=f1*f2%f: 卷积和序列f(k)对应的非零样值向量%k: 序列f(k)的对应序号向量%f1: 序列f1(k)非零样值向量%f2: 序列f2(k)非零样值向量%k1: 序列f1(k)的对应序号向量%k2: 序列f2(k)的对应序号向量f1=[1,2,1];f2=ones(1,5);k1=[-1 0 1];k2=-2:2;f=conv(f1,f2) %计算序列f1与f2的卷积和fk0=k1(1)+k2(1); %计算序列f非零样值的起点位置k3=length(f1)+length(f2)-2; %计算卷积和f的非零样值的宽度k=k0:k0+k3 %确定卷积和f非零样值得序号向量subplot(3,3,1)stem(k1,f1) %在子图1绘制序列f1(k)时域波形图title('f1(n)')xlabel('n')ylabel('f1(n)')subplot(3,3,4)stem(k2,f2) %在子图2绘制序列f2(k)时域波形图title('f2(n)')xlabel('n')ylabel('f2(n)')subplot(3,3,7)stem(k,f) %在子图3绘制序列f(k)时域波形图title('f1(n)与f2(n)的卷积和f(n)')xlabel('n')ylabel('f(n)')h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h) % 将第三个子图的横坐标范围扩为原来的2.5倍wigb.mfunction wigb (a,scal,x,z,amx)%WIGB: Plot seismic data using wiggles%% WIGB(a,scal,x,z,amx)%% IN a: seismic data% scale: multiple data by scale% x: x-axis;% z: vertical axis (time or depth)% x and z are vectors with offset and time.%% If only 'a' is enter, 'scal,x,z,amn,amx' are decided automatically;% otherwise, 'scal' is a scalar; 'x, z' are vectors for annotation in% offset and time, amx are the amplitude range.%% Author:% Xingong Li, Dec. 1995% Changes:% Jun11,1997: add amx% May16,1997: updated for v5 - add 'zeros line' to background color% May17,1996: if scal ==0, plot without scaling% Aug6, 1996: if max(tr)==0, plot a lineif nargin == 0, nx=10;nz=10; a = rand(nz,nx)-0.5; end;[nz,nx]=size(a);trmx= max(abs(a));if (nargin <= 4); amx=mean(trmx); end;if (nargin <= 2); x=[1:nx]; z=[1:nz]; end;if (nargin <= 1); scal =1; end;if nx <= 1; disp(' ERR:PlotWig: nx has to be more than 1');return;end;% take the average as dxdx1 = abs(x(2:nx)-x(1:nx-1));dx = median(dx1);dz=z(2)-z(1);xmx=max(max(a)); xmn=min(min(a));if scal == 0; scal=1; end;a = a * dx /amx;a = a * scal;fprintf(' PlotWig: data range [%f, %f], plotted max %f \n',xmn,xmx,amx);% set display rangex1=min(x)-2.0*dx; x2=max(x)+2.0*dx;z1=min(z)-dz; z2=max(z)+dz;set(gca,'NextPlot','add','Box','on', ...'XLim', [x1 x2], ...'YDir','reverse', ...'YLim',[z1 z2]);fillcolor = [0 0 0];linecolor = [0 0 0];linewidth = 0.1;z=z'; % input as row vectorzstart=z(1);zend =z(nz);for i=1:nx,if trmx(i) ~= 0; % skip the zero tracestr=a(:,i); % --- one scale for all sections = sign(tr) ;i1= find( s(1:nz-1) ~= s(2:nz) ); % zero crossing pointsnpos = length(i1);%12/7/97zadd = i1 + tr(i1) ./ (tr(i1) - tr(i1+1)); %locations with 0 amplitudes aadd = zeros(size(zadd));[zpos,vpos] = find(tr >0);[zz,iz] = sort([zpos; zadd]); % indices of zero point plus positives aa = [tr(zpos); aadd];aa = aa(iz);% be careful at the endsif tr(1)>0, a0=0; z0=1.00;else, a0=0; z0=zadd(1);end;if tr(nz)>0, a1=0; z1=nz;else, a1=0; z1=max(zadd);end;zz = [z0; zz; z1; z0];aa = [a0; aa; a1; a0];zzz = zstart + zz*dz -dz;patch( aa+x(i) , zzz, fillcolor);line( 'Color',[1 1 1],'EraseMode','background', ...'Xdata', x(i)+[0 0], 'Ydata',[zstart zend]); % remove zero line%'LineWidth',linewidth, ...%12/7/97 'Xdata', x(i)+[0 0], 'Ydata',[z0 z1]*dz); % remove zero lineline( 'Color',linecolor,'EraseMode','background', ...'LineWidth',linewidth, ...'Xdata', tr+x(i), 'Ydata',z); % negatives lineelse % zeros traceline( 'Color',linecolor,'EraseMode','background', ...'LineWidth',linewidth, ...'Xdata', [x(i) x(i)], 'Ydata',[zstart zend]);end;end;。

实验5 连续时间信号的卷积运算

实验5 连续时间信号的卷积运算一、实验目的（1）熟悉卷积的定义和表示；（2）掌握相利用计算机进行卷积运算的原理和方法；（3）熟悉连续信号卷积运算函数conv的应用。

二、涉及的MATLAB函数1.conv函数功能：实现信号的卷积运算。

调用格式：w=conv(f1,f2)*dt其中，dt为采样周期（步长）；当f1，f2其中之一为冲激信号δ(t)时，w=conv(f1,f2)2.stepfun函数调用格式：Stepfun（t,t0）其中，t是时间区间，在该区间内阶跃信号一定会产生；t0是信号发生从0到1跳跃的时刻三、实验内容实验①%函数卷积a=1000;t1=-5:1/a:5;f1=stepfun(t1,0); %产生阶跃信号f2=stepfun(t1,-1/a)-stepfun(t1,1/a); %产生冲激信号subplot(231);plot(t1,f1);axis([-5,5,0,1.2]);title('f1');ylabel('f1(t)');title('单位阶跃新函数');subplot(232);plot(t1,f2);title('f2');f12=conv(f1,f2);t=-10:1/a:10;subplot(233);plot(t,f12);axis([-10,10,0,1.2]);title('f1*f2');f21=conv(f2,f1);subplot(234);plot(t,f21);axis([-10,10,0,1.2]);title('f2*f1');ylabel('y(t)');f11=conv(f1,f1)*1/a;f22=conv(f2,f2);subplot(235);plot(t,f11);title('f1*f1');subplot(236);plot(t,f22);title('f2*f2');实验②%连续函数卷积s=0.01;k1=0:s:2; %生成k1的时间向量k2=k1; %生成k2的时间向量f1=3*k1; %生成f1的样值向量f2=3*k2; %生成f2的样值向量f=conv(f1,f2);f=f*s;k0=k1(1)+k2(1); %序列f非零样值的起点k3=k1(end)+k2(end); %序列f非零样值的终点k=k0:s:k3;subplot(3,1,1);plot(k1,f1);title('f1(t)');subplot(3,1,2);plot(k2,f2);title('f2(t)');subplot(3,1,3);plot(k,f);title('f(t)');实验③%函数卷积a=1000;t1=-5:1/a:5;f1=stepfun(t1,-1/a)-stepfun(t1,1/a);%产生冲激信号f2=stepfun(t1,0);%产生阶跃信号u(t)f3=stepfun(t1,0)-stepfun(t1,4);subplot(231);plot(t1,f1);axis([-5,5,0,1.2]);title('f1'); subplot(232);plot(t1,f2);axis([-5,5,0,1.2]);title('f2'); subplot(233);plot(t1,f3);axis([-5,5,0,1.2]);title('f3'); f4=conv(f1,f2+f3);f5=conv(f1,f2)+conv(f1,f3);t=-10:1/a:10;subplot(234);plot(t,f4);axis([-10,10,0,3]);title('f4*f1');subplot(235);plot(t,f5);axis([-10,10,0,3]);title('f5');四、实验结论1、卷积积分的计算从几何上可以分为四个步骤：翻转→平移→相乘→叠加（积分）。

运用MATLAB进行连续时间信号卷积运算

实验项目名称：运用MATLAB进行连续时间信号卷积运算（所属课程：信号与系统）院系：电子信息与电气工程专业班级：电气工程及其自动化姓名：安永军学号：201002040062实验日期：2012年4月12 号实验地点：A-07-408合作者：张德扬指导老师：李静本实验项目成绩：教师签字：日期：一：实验目的1，掌握连续时间信号的基本运算的实现方法。

2，熟悉连续LTI 系统在典型激励信号下的响应及其特征。

3、掌握连续LTI 系统单位冲激响应的求解方法。

4、重点掌握用卷积法计算连续时间系统的零状态响应。

5、熟悉MATLAB 相关函数的调用格式及作用。

6、会用MATLAB 对系统进行时域分析。

二、实验原理1、信号的运算包括：信号的基本运算，包括加、减、乘、除等；信号的时域变换，包括信号的平移、翻转、尺度变换等；两个信号的卷积运算等。

2、连续时间线性时不变系统（LTI ）可以用如下的线性常系数差分方程来描述：()(1)()(1)110110()()()()()()()()n n m m n m n n r t r t r t r t e t e t e t e t a a a a b b b b ----++++=++++''其中，n m ≥，系统的初始条件为(0)r -，(0)r -'，(0)r -''， (1)(0)n r--。

系统的响应一般包括两个部分，即由当前输入所产生的响应（零状态响应）和由历史输入（初始状态）所产生的响应（零输入响应）。

对于低阶系统，一般可以通过解析的方法得到响应。

但对于高阶系统，手工计算就比较困难，这时MATLAB 强大的计算功能就能比较容易地确定系统的各种响应，如冲激响应、阶跃响应、零输入响应、零状态响应、全响应等。

1）直接求解法在MATLAB 中，要求以系数相量的形式输入系统的微分方程。

因此，在使用前必须对系统的微分方程进行变换，得到其传递函数。

连续时间信号的卷积运算

实验二连续时间信号的卷积运算与LTI系统的时域分析实验人：Mr.yan1 实验目的（1）熟悉卷积的定义和表示；（2）掌握利用计算机进行卷积运算的原理和方法；（3）熟悉连续信号卷积运算函数conv的应用。

（4）熟悉连续LTI系统在典型激励信号下的响应及其特征；（5）掌握连续LTI系统单位冲激响应的求解方法；（6）掌握用卷积法计算连续时间系统的零状态响应；（7）能够应用Matlab对系统进行时域分析。

2 实验原理（1）卷积的定义、卷积的几何解法、卷积积分的应用（求系统的零状态响应）（2）对于一般的n阶LTI连续系统，如果n的数值比较小时，可以通过解析的方法得到响应。

但是，对于高阶系统，手工运算比较困难，要利用一些计算工具软件。

3 涉及的Matlab函数（1）conv函数：实现信号的卷积运算。

调用格式：w=conv(u,v)计算两个有限长度序列的卷积。

说明：该函数假定两个序列都从零开始。

（2）lsim函数：计算并画出系统在任意输入下的零状态响应。

调用格式：lsim(b,a,x,t)其中：a和b是由描述系统的微分方程系数决定的表示该系统的两个行向量；x和t是表示输入信号的行向量。

该调用格式将会绘出由向量a和b所定义的连续系统在输入为向量x 和t所定义的信号时，系统的零状态响应的时域仿真波形，且时间范围与输入信号相同。

（3）impulse函数：计算并画出系统的冲激响应。

调用格式：impulse(b,a)该调用格式以默认方式绘出向量a和b定义的连续系统的冲激响应的时域波形。

impulse(b,a,t)该调用格式将绘出向量a和b定义的连续系统在0-t时间范围内的冲激响应波形。

impulse(b,a,t1：p：t2)该调用格式将绘出向量a和b定义的连续系统在t1-t2时间范围内，且以时间间隔p均匀取样的冲激响应波形。

（4）step函数：计算并画出系统阶跃响应曲线调用格式：该函数与函数impulse()一样，也有相似的调用格式。

信号与系统实验报告实验三连续时间LTI系统的频域分析报告

实验三连续时间LTI 系统的频域分析一、实验目的1、掌握系统频率响应特性的概念及其物理意义；2、掌握系统频率响应特性的计算方法和特性曲线的绘制方法，理解具有不同频率响应特性的滤波器对信号的滤波作用；3、学习和掌握幅度特性、相位特性以及群延时的物理意义；4、掌握用MA TLAB 语言进行系统频响特性分析的方法。

基本要求：掌握LTI 连续和离散时间系统的频域数学模型和频域数学模型的MATLAB 描述方法，深刻理解LTI 系统的频率响应特性的物理意义，理解滤波和滤波器的概念，掌握利用MATLAB 计算和绘制LTI 系统频率响应特性曲线中的编程。

二、实验原理及方法1 连续时间LTI 系统的频率响应所谓频率特性，也称为频率响应特性，简称频率响应（Frequency response ），是指系统在正弦信号激励下的稳态响应随频率变化的情况，包括响应的幅度随频率的变化情况和响应的相位随频率的变化情况两个方面。

上图中x(t)、y(t)分别为系统的时域激励信号和响应信号，h(t)是系统的单位冲激响应，它们三者之间的关系为：)(*)()(t h t x t y =，由傅里叶变换的时域卷积定理可得到：)()()(ωωωj H j X j Y =3.1或者： )()()(ωωωj X j Y j H =3.2)(ωj H 为系统的频域数学模型，它实际上就是系统的单位冲激响应h(t)的傅里叶变换。

即⎰∞∞--=dt e t h j H tj ωω)()(3.3由于H(j ω)实际上是系统单位冲激响应h(t)的傅里叶变换，如果h(t)是收敛的，或者说是绝对可积（Absolutly integrabel ）的话，那么H(j ω)一定存在，而且H(j ω)通常是复数，因此，也可以表示成复数的不同表达形式。

在研究系统的频率响应时，更多的是把它表示成极坐标形式：)()()(ωϕωωj ej H j H = 3.4上式中，)j (ωH 称为幅度频率相应（Magnitude response ），反映信号经过系统之后，信号各频率分量的幅度发生变化的情况，)(ωϕ称为相位特性（Phase response ），反映信号经过系统后，信号各频率分量在相位上发生变换的情况。

连续时间系统卷积的数值计算实验报告.docx

实验报告实验名称：连续时间系统卷积的数值计算一、实验目的：1、加深对卷积概念及原理的理解；2、掌握借助计算机计算任意信号卷积的方法。

二、实验原理：卷积积分不仅可以通过直接积分或查表的方法来求解，还可以用积分的数值计算方法来求解。

在线性系统的分析过程中，有时会遇到复杂的激励信号，或者有时只是一组测试数据或曲线，冲激响应也可能出现同样的情况。

显然，此时直接计算积分或查表都有困难，而采用近似的数值计算方法可以解决这个问题，求得卷积积分。

1、卷积的定义卷积积分可以表示为2卷积计算的几何算法卷积积分的计算从几何上可以分为四个步骤：翻转→平移→相乘→叠加。

3卷积积分的应用卷积积分是信号与系统时域分析的基本手段，主要用于求系统零状态响应，它避开了经典分析方法中求解微分方程时需要求系统初始值的问题。

设一个线性零状态系统，已知系统的单位冲激响应为h(t)，当系统的激励信号为e(t)时，系统的零状态响应为由于计算机技术的发展，通过编程的方法来计算卷积积分已经不再是冗繁的工作，并可以获得足够的精度。

因此，信号的时域卷积分析法在系统分析中得到了广泛的应用。

卷积积分的数值运算实际上可以用信号的分段求和来实现，即：如果我们只求当t = nΔt （n为正整数,nΔt 记为t ）时r(t)的值，则由上式可以得到：当Δt 足够小时，r(t )就是e(t)和h(t)卷积积分的数值近似，由上面的公式可以得到卷积数值计算的方法如下：1 将信号取值离散化，即以 Ts 为周期，对信号取值，得到一系列宽度间隔为 Ts 的矩形脉冲原信号的离散取值点，用所得离散取值点矩形脉冲来表示原来的连续时间信号；2 将进行卷积的两个信号序列之一反转，与另一信号相乘，并求积分，所得为 t=0 时的卷积积分的值。

以 Ts 为单位左右移动反转的信号，与另一信号相乘求积分，求的t<0和t>0时卷积积分的值；3 将所得卷积积分值与对应的t 标在图上，连成一条光滑的曲线，即为所求卷积积分的曲线。

实验三信号卷积的MATLAB实现

实验三信号卷积的MATLAB实现一、实验名称：信号卷积的MATLAB实现二、实验目的：1.增加学生对卷积的认识2.了解MATLAB这个软件的一些基础知识3.利用MATLAB计算信号卷积4.验证卷积的一些性质三、实验原理：用MATLAB实现卷积我们先必须从信号下手，先把信号用MATLAB语句描述出来，然后再将这些信号带入到我们写好的求卷积的函数当中来计算卷积。

在本章中我们将信号分为连续信号和离散序列两种来实现卷积并验证卷积的一些性质。

MATLAB强大的图形处理功能及符号运算功能，为我们实现信号的可视化提供了强有力的工具。

在MATLAB中通常有两种方法来表示信号，一种是用向量来表示信号，另一种则是用符号运算的方法来表示信号。

用适当的MATLAB 语句表示出信号后，我们就可以利用MATLAB的绘图命令绘制出直观的信号波形。

连续时间信号，是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干不连续点以外，信号都有确定的值与之对应的信号。

从严格意义上来讲，MATLAB并不能处理连续信号，在MATLAB中，是用连续信号在等时间间隔点的样值来近似地表示连续信号的，当取样时间间隔足够小时，这些离散的样值就能较好地近似出连续信号。

在MATLAB中连续信号可用向量或符号运算功能来表示。

1．向量表示法对于连续时间信号f(t)，我们可以用两个行向量f和t来表示，其中向量t是行如t＝t1：p：t2的MATLAB命令定义的时间范围向量，t1为信号起始时间，t2为中止时间，p为时间间隔。

向量f为连续信号f(t)在向量t所定义的时间点上的样值。

例如对于连续信号f(t)=sin(t),我们可以用如下两个向量来表示：t=-10:1.5:10；f=sin(t)用上述向量对连续信号表示后，就可以用plot命令来绘出该信号的时域波形。

Plot命令可将点与点间用直线连接，当点与点间的距离很小时，绘出的图形就成了光滑的曲线。

命令如下：plot(t,f)title(‘f(t)=sint’)xlabel(‘t’)axis([-10,10,-1.1,1.1])绘制的信号波形如图3.1所示，当把时间间隔p取得更小(如0.01)时，就可得到sint较好的近似波形，如图3.2所示。

连续时间信号的卷积与相关计算

连续时间信号的卷积与相关计算连续时间信号的卷积和相关计算是信号处理中常见的操作。

卷积是通过将两个信号进行叠加积分来获得新的信号。

给定两个连续时间信号f(t)和g(t)，它们的卷积表示为(f * g)(t)，计算公式如下：
(f * g)(t) = ∫[f(τ)g(t-τ)]dτ
其中，τ是积分变量。

卷积的结果是一个新的信号h(t)，它包含着两个信号f(t)和g(t)间的相互影响。

相关计算用于衡量两个信号之间的相似性。

给定两个连续时间信号f(t)和g(t)，它们的相关函数表示为R(t)，计算公式如下：
R(t) = ∫[f(τ)g(t+τ)]dτ
相关计算中，τ也是积分变量。

通过计算相关函数的值，可以了解信号f(t)和g(t)的相似程度。

卷积和相关计算在信号处理中具有广泛的应用。

它们可以用于滤波、系统建模、特征提取等任务，有助于理解和处理连续时间信号的特性。

连续时间信号的卷积运算word资料5页

实验二连续时间信号的卷积运算与LTI系统的时域分析实验人：Mr.yan1 实验目的（1）熟悉卷积的定义和表示；（2）掌握利用计算机进行卷积运算的原理和方法；（3）熟悉连续信号卷积运算函数conv的应用。

（4）熟悉连续LTI系统在典型激励信号下的响应及其特征；（5）掌握连续LTI系统单位冲激响应的求解方法；（6）掌握用卷积法计算连续时间系统的零状态响应；（7）能够应用Matlab对系统进行时域分析。

2 实验原理（1）卷积的定义、卷积的几何解法、卷积积分的应用（求系统的零状态响应）（2）对于一般的n阶LTI连续系统，如果n的数值比较小时，可以通过解析的方法得到响应。

但是，对于高阶系统，手工运算比较困难，要利用一些计算工具软件。

3 涉及的Matlab函数（1）conv函数：实现信号的卷积运算。

调用格式：w=conv(u,v)计算两个有限长度序列的卷积。

说明：该函数假定两个序列都从零开始。

（2）lsim函数：计算并画出系统在任意输入下的零状态响应。

调用格式：lsim(b,a,x,t)其中：a和b是由描述系统的微分方程系数决定的表示该系统的两个行向量；x和t是表示输入信号的行向量。

该调用格式将会绘出由向量a和b所定义的连续系统在输入为向量x 和t所定义的信号时，系统的零状态响应的时域仿真波形，且时间范围与输入信号相同。

（3）impulse函数：计算并画出系统的冲激响应。

调用格式：impulse(b,a)该调用格式以默认方式绘出向量a和b定义的连续系统的冲激响应的时域波形。

impulse(b,a,t)该调用格式将绘出向量a和b定义的连续系统在0-t时间范围内的冲激响应波形。

impulse(b,a,t1：p：t2)该调用格式将绘出向量a和b定义的连续系统在t1-t2时间范围内，且以时间间隔p均匀取样的冲激响应波形。

（4）step函数：计算并画出系统阶跃响应曲线调用格式：该函数与函数impulse()一样，也有相似的调用格式。

卷积计算的实验报告

1. 理解卷积的基本概念和原理；2. 掌握卷积的计算方法；3. 通过MATLAB软件实现卷积运算；4. 分析卷积运算在信号处理中的应用。

二、实验原理卷积是一种线性运算，它描述了两个信号之间的相互作用。

对于两个离散信号x[n]和h[n]，它们的卷积y[n]定义为：y[n] = Σx[k]h[n-k]其中，n和k为离散时间变量，Σ表示求和。

卷积运算具有以下性质：1. 交换律：x[n] h[n] = h[n] x[n]2. 结合律：(x[n] h[n]) g[n] = x[n] (h[n] g[n])3. 分配律：x[n] (h[n] + g[n]) = x[n] h[n] + x[n] g[n]卷积运算在信号处理中具有重要的应用，如信号滤波、系统分析、图像处理等。

三、实验内容1. 熟悉MATLAB软件环境；2. 编写MATLAB程序实现卷积运算；3. 分析卷积运算的结果，验证卷积性质；4. 应用卷积运算解决实际问题。

四、实验器材1. 计算机；2. MATLAB软件；3. 离散信号数据。

1. 创建离散信号数据：在MATLAB中创建两个离散信号x[n]和h[n]，分别代表输入信号和系统响应。

2. 编写卷积程序：使用MATLAB内置函数conv实现卷积运算，计算y[n] = x[n] h[n]。

3. 分析卷积结果：观察卷积运算的结果，验证卷积性质，如交换律、结合律、分配律等。

4. 应用卷积运算解决实际问题：选择一个实际问题，如信号滤波，使用卷积运算进行求解。

六、实验结果与分析1. 卷积运算结果：运行卷积程序，得到卷积运算结果y[n]。

观察y[n]的波形，分析卷积运算对信号的影响。

2. 验证卷积性质：通过比较x[n] h[n]和h[n] x[n]的卷积结果，验证交换律；通过比较(x[n] h[n]) g[n]和x[n] (h[n] g[n])的卷积结果，验证结合律；通过比较x[n] (h[n] + g[n])和x[n] h[n] + x[n] g[n]的卷积结果，验证分配律。

信号与系统常用卷积

信号与系统常用卷积
卷积是信号与系统领域中的一种重要运算。

它是将两个信号进行数学操作的方法，通常用符号 "*" 表示。

卷积运算可以以离散形式和连续形式进行。

离散卷积是指对离散时间信号进行卷积运算。

设有两个离散时间序列\[x[n]\]和\[h[n]\]，卷积运算的结果\[y[n]\]可以表示为：
\[y[n] = \sum_{k=-\infty}^{\infty} x[k]h[n-k]\]
连续卷积是指对连续时间信号进行卷积运算。

设有两个连续时间信号\[x(t)\]和\[h(t)\]，卷积运算的结果\[y(t)\]可以表示为：
\[y(t) = \int_{-\infty}^{\infty} x(\tau)h(t-\tau)d\tau\]
卷积运算的物理意义是对信号的相乘后再积分求和。

它在信号处理与系统分析中有广泛应用。

例如，卷积可以用于系统的响应预测、信号的滤波和信号的特征提取等。

在实际应用中，卷积运算可以通过离散求和或积分的方式进行计算。

计算机程序中常用的卷积算法包括直接法、快速卷积法（如快速傅里叶变换法）和卷积定理等。

总之，卷积是信号与系统分析中一种常用的运算方法，通过对信号的相乘与积分求和，可以得到新的信号。

在信号处理和系统分析中有广泛应用，为进一步深入研究相关领域奠定了基础。

【信号与系统实验内容】实验三连续时间信号的卷积

实验三连续时间信号的卷积一、实验目的：1、掌握两个连续时间信号卷积的计算方法和编程技术。

2、进一步熟悉用MATLAB描绘二维图像的方法。

二、实验原理：卷积积分在信号与线性系统分析中具有非常重要的意义，是信号与系统分析的基本方法之一。

（一）卷积的定义连续时间信号f1(t)和f2(t)的卷积积分（简称为卷积）f(t)定义为：（二）线性时不变（LTI）系统的单位冲激响应给定一个连续时间LTI系统，在系统的初始条件为零时，用单位冲激信号δ(t)作用于系统，此时系统的响应信号称为系统的单位冲激响应（Unit impulse response），一般用h(t)来表示。

需要强调的是，系统的单位冲激响应是在激励信号为δ (t)时的零状态响应（Zero-state response）。

系统的单位冲激响应是一个非常重要的概念，如果已知一个系统的单位冲激响应，那么，该系统对任意输入信号的响应信号都可以求得。

（三）卷积的意义对于LTI系统，根据系统的线性和时不变性以及信号可以分解成单位冲激函数可得，任意LTI系统可以完全由它的单位冲激响应h(t)来确定，系统的输入信号x(t)和输出信号y(t)之间的关系可以用卷积运算来描述，即：由于系统的单位冲激响应是零状态响应，故按照上式求得的系统响应也是零状态响应。

它是描述连续时间系统输入输出关系的一个重要表达式。

（四）函数说明利用MATLAB的内部函数conv( )可以很容易地完成两个信号的卷积积分运算。

其语法为：y = conv(x,h)。

其中x和h分别是两个参与卷积运算的信号，y为卷积结果。

为了正确地运用这个函数计算卷积，这里对conv(x,h)做一个详细说明。

conv(x,h)函数实际上是完成两个多项式的乘法运算。

例如，两个多项式p1和p2分别为：和这两个多项式在MATLAB中是用它们的系数构成一个行向量来表示的，用x来表示多项式p1，h表示多项式p2，则x和h分别为x = [1 2 3 4]h = [4 3 2 1]在MATLAB命令窗口依次键入>> x = [1 2 3 4];>> h = [4 3 2 1];>> y=conv(x,h)在屏幕上得到显示结果：y = 4 11 20 30 20 11 4这表明，多项式p1和p2的乘积为：用MATLAB处理连续时间信号时，时间变量t的变化步长应该很小，假定用符号dt表示时间变化步长，那么，用函数conv( )作两个信号的卷积积分时，应该在这个函数之前乘以时间步长方能得到正确的结果。

信号与系统实验四连续时间信号的卷积积分

实验名称：连续时间信号的卷积积分
报告人：姓名班级学号
一、实验目的
1、熟悉卷积积分的定义和性质；
2、了解卷积积分在系统分析中的应用；
3、熟悉MATLAB实现卷积的方法。

二、实验内容及运行结果
1已知两信号：f1(t)=u(t+1)-u(t),f2(t)=u(t)-u(t-1),求卷积：g(t)=f1(t)*f2(t)比较此题与例题t1=-1:0.01:0;
f1=ones(size(t1)); %高度为一的门函数，时间从t=-1到t=0
t2=0:0.01:1;
f2=ones(size(t2)) ; %高度为一的门函数，时间从t=0到t=1
g=conv(f1,f2); %对f1和f2进行卷积
t3=-1:0.01:1;
subplot(3,1,1),plot(t1,f1); %画f1的波形
subplot(3,1,2),plot(t2,f2); %画f2的波形
subplot(3,1,3),plot(t3,g); %画g的波形
此题与例题的作用区间改变了，以及波形有不同
三、讨论与总论
通过本次试验，利用matlab求解卷积，利用conv函数解卷积非常方便和快速，需要注意每个函数的作用区间，并且了解卷积积分在系统分析中的应用。

（注：文档可能无法思考全面，请浏览后下载，供参考。

可复制、编制，期待你的好评与关注）。

实验3 连续时间信号的卷积计算