直三棱柱的表面展开图

合集下载

五年级奥数：展开图与空间想象

五年级奥数：展开图与空间想象知识框架重难点例题精讲1.数一数下图中有多少个正方体木块？<><?从下到上各层分别有書个、3个.1个，因此共有3+3十1=7个方块.【巩固】右图中共有多少个面？多少条棱?I觅右图所示；可叹分前、后、左、右、上、下六个方向看这个立体图彩*前，后看各有1入面，左面看有1个面，右<&看有2个面，上面看有2个面，下面看有1牛面”所礙共有1m+2+LlX（个）面.前后方向的棱有6条，左右方向的棱有6秦，上下方向的棱也有6所以共有棱柠十（S+柠-1$（条）.2立方厘米.如图从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形，然后，沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米？客器的底曲积是〔1勺一斗）xf9-4）=45（平方厘米）：高为2厘来，所以容•器的体积是,45x2=90（立方厘米）.巩固】沿图4的虚线折叠，可以围成一个长方体，它的体积是宽十高=7,,长=5,长+高立，所以长高=入宽=4,体积为3x4x5=60立方厘，3. 下列图形经过折叠不能围成正方体的是【巩固】左下图是一个正方体，四边形APQC 表示用平面截正方体的截面.请在右下方的展开图中画出四边形APQC的四条边．附4DCABF\ E A4把空间图形弦面的践条画在平面展开图上，只要抓住四边形APQC 四个顶点所在的位置这个托键，再进一步貓定四边形的四条边所在的平面就可容场地画出.⑴瀋虑到展开图上疽犬个顶点没肴标出，可想家瘠展开图折成立侬形、并在顶点上标出对应的符号，忆左下图. ⑵根据四边形所在立体图形上的往置，确定其顶点所在的点和棱，以及四条边所在的平面：顶点：A-A 7C -C 7尸在EF 边上，©在GF 边上+边/I 匸在卫BCJQ 面上’AF 在力用FE 面上’QC 在BCGF 面上1尸么在CFGH 面上. ⑶将上面菇足的位置标在展界图上，并在对应平面上连线.需婪注意的是，立休圈上的月‘£点在展开图上有三个，B 7D 点在展开图上有二个，所以在标点连线吋必须注意连簸所在的平面”连好线的图形如右上图”4. 图1是下面的表面展开图 ① 甲正方体； ② 乙正方体；③丙正方体；④甲正方体或丙正方体．AG从展开图可以看曲，毎个面上至少有一块阴影，从而排除丙；又毎个面上没有相邻的两块阴影从而排除乙，故选甲答案为①.巩固】选项中有4个立方体，其中是用左边图形折成的是()．D图中齐，C・D项展开盾的图形均为下圏，只有©项展开后前图形与题中左边图形相捋，所叹答集为B・5.将A、B、C、D、E、F六个字母分别写在正方体的六个面上，从下面三种不同摆法中判断这个正方体中，哪些字母分别写在相对的面上．C ABDB都不相对，故(：和尸相对，A^BE不相对故盘和D相对，最后剩下的班相对A-D,B-E,C-F【巩固】用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上，每一个面只涂一种颜色．如图所示，现有涂色方式完全一样的四块小正方体拼成了一个长方体．试回答：每个小正方体中，哪些颜色分别涂在相对的面上？IBR—d滋和黑黄白蓝部不柏对’故红和錄1相対，黃和黒白不相对故黄和蓝相对，最后剩下的黑白相对红-緑，黄-蓝，黑-白6.把2、4、6、8、10、12这六个数字依次写在一个立方体的正面、背面、两个侧面以及两个底面上，然后把立方体展开，如图1，最左边的正方形上的数字是12，则最右边的正方形上的数字是.最右边的正方形是在2的对面，也就是背面，为4【巩固】如下图，一个正方体木块放在桌面上，每个面内都画有若干个点，相对的两个面内的点数和都是13，京京看见上、左、前三个面内的点数的和诗16，庆庆看见上、右、后三个面内的点数和是24.那么贴着桌面的那个面的点数是___.7. 【解析】上十左.■*■前=16上+右十后=24因此：上十上十（左+右〕十（前十后）=40又因为左■右=前+后=13,因上二40_13—[3=7,则T=L3_?=6i用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD-A I B I C I D I （如图），大正方体内的对角线AC i ，BD i ，C A I ，DB 1所穿的小正方体都是红色玻璃小正方体，其它部分都是无色透明玻璃小正方体，小红正方体共用了401个，问：无色透明小正方体用了多少个？叫CA.,叫四条时角线部穿过在正由央的那个小正方体.除此而外+每条对角线穿过相同的小正方体*所以毎条対角线穿过鋼二Im 们个小正才体達就表明尢亚方体的每条边由101个卜正方徉组成.因此火正方■体由101"个小正方体组成；其中无色透明的小正方体有IO13-401=1030301-401^1029900. 即用了l （J29M0个无色透明的小正方体.【巩固】如图，用若干个体积相同的小正方体堆积成一个大正方体，要使大正方体的对角线（正方体八个顶点中距离最远的两个顶点的连线）穿过的小正方体都是黑色的，其余小正方体都是白色的，并保证大正方体每条边上有偶数个小正方体.当堆积完成后，白色正方体的体积占总体积的93.75%，那么一共用了多少个黑色的小正方体？C 1CI白色.it方体的体积占总体积的9化7$罷即占整个的12,白色止方体与黑色正方体之比为；1：15,16观察可知，厝一层黑邑正方体有4伞，则白色正方体有“个I所以每一层共有54个正方体，则正方体的边畏为1,则蔗有呂层，所以一拱用了4*432仆卜的黑邑的正方体*8.有许多相同的立方体，每个立方体的六个面上都写着同一个数字（不同的立方体可以写相同的数字）先将写着2的立方体与写着1的立方体的三个面相邻，再将写着3的立方体写着2的立方体相邻（见左下图）．依这样构成右下图所示的立方体，它的六个面上的所有数字之和是多少?1/第一层如节图：第二层、第三层依兔比上面一层每格都多1（见下图）*上向的9个数之和足27,由对称性知，上面、前面、右面的所有数之利輔逻匕.同理，下海的9个数之和是45,下面、左面、后面的所有数之和都是45”所以天个面上所有数之和是（27+45）x3=216.【巩固】如图，原来的大正方体是由125个小正方体所构成的．其中有些小正方体已经被挖除图中涂黑色的部分就是贯穿整个大正方体的挖除部分．请问剩下的部分共有多少个小正方体？第8题I对于it一类从立体图形中间挖掉一部曲后再求体禅（就小止君体数目）的趣目一般可以農用“切片法刃来做，所谓“切片法役就是把整个虫体图形切嵐一片--片的（或--层--层的），然后分别计算每一片或毎一层的体相或小正方体数目,最后再把它们相加.采用切片法，俯视第一层到第五层的图母依次如下.其屮黑色部分蔻示挖除掉的部分.从图申可以看出，第'_、2.3、4,5层剩下的小正方体势别有22牛.11牛、11个，◎个、11所以总共还剩下22^J1+11+5+22=72（介）小正方体*審易看出这个展开图可以拼成一个封闭的立体图步，展开图外围一共有12条边；这个封囲的立体图像要展开成图由的展开图，每剪开一条嵐就会产生外围的2条迦所叹需要剪开幔：2=占条檯【巩固】如图，剪一块硬纸片可以做成一个多面体的纸模型（沿虚线折，沿实线粘）.这个多面体的面数、顶点数和棱数的总和是多少？多面体的向毀,可以直接从侧面展开圈中数岀来，12个正方形加8个三角形，共20曲.右上图是多面体上部的示意图共有9个顶盘；同样，下部也是9个顶蛊：共”个顶点•橈数要孑成三层来载，上层.从示盍图数，有巧条；下层也是15条；中间部分为6条.一共15*2+6=36总和为；20+18+36-74（个〕.10.图中是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形．问这个直三棱柱的体积是多少？这个展开图折辰直三按柱母状，如右图所示，可见这个三技柱是单Z方体的--半，其体歆为【巩固】如图是一个四棱锥的展开图，该展开图由正三角形和正方形构成，其中正方形的对角2线长4厘米，那么该四棱锥的体积为多少？AI睿易知道四按锥的底面面积，只要知道四猿锥的高就能求得四植锥的体积.將四技锥沼对角践和顶点枸说的平面剖开，剖面是--个三角形.该三角形的斜边等于正方形的对角线，直角边等于正方形和聲边三甬形的边长，所汰三角形是一个尊腰直角三角形.它的高等于时角线的一半，根据对称脛，这条商也等于四植锥的高.即四梭锥昭高度为2.四棱锥肘体祺为「4m2-3=—豆方厘来.31|吵课堂检测it1.右图中共有多少个面？多少条棱?9个面亍21条梭.2.____________________________________________________________ 右边正方体是用左边图形折成的，则小正方形在正方体的面.3.将1,2,3,4,5,6分别写在正方体六面上，使正方体中对面数字的和相等•正方体如图放置在A格上，沿格子滚动到B点时，在正方体右面的数字是滚到右下角时如下图:35再滾动到右上角时:456所以到J3点叶在右面的为34.如图所示，一个5X5X5的立方体，在一个方向上开有l x l x5的孔，在另一个方向上开有2x l x5的孔，在第三个方向上开有3x l x5的孔，剩余部分的体积是多少？表面积为多少?r*2”21i12I 2222 1121 1121、i2111\211z111211222221求体积：开了"25的礼，穗去3x25=1—fl-T1x^5的乳,挖去Ix]x5-I=4；开了"25的乳,挖去2S|x5-t2+2）=6?劇余部芬的体和是：5x5x5-（154-4+0=100（另解）特螯个图形切片，如果切飾平行于纸面，那么五夺切片分别如團:求■表而积：表面积可以看成卉部和內部两部分.外部的表面恋为亍d以-12=皿"内部的囲积可以分为前后*左右、上下三丰方询，面积分别为如*■'-'>1x5-1.1-21=14^所帜总昭表面积为1H我302='*（另解）运用类似于三视團的方法；记录毎一方向上砖不同位査上的操露正方形年数:前■后方向：覚上下方向：加左右方向：4ft总表面积为2x(32+3(}+40)-30\家庭作业作业检测【例1】右图是由22个小正方体组成的立体图形，其中共有多少个大大小小的正方体？由两个小正方体组成的长方体有多少个？Z77正方体只可能有西种：由1芋小正方体构成的止方体，有22个；由妆芋小正方体构成的2x2x2的止方体，有4个.所以共有正方体224-J=2b(心.由两牛小正方体组戚的长方体，祖据摆菽的方向可分为下国所示的上下位、左右住，前后＜1三种,其中上下位有13个，左右位有13仆前后住有14牛，共有134134-14=10W.【例2】将一个长28cm，宽18cm的长方形铁片的四个角各截去一个边长为4cm的正方形.再将此铁片折成一个无盖的长方形容器•容器的容积为cm3.四个角各栽击--个边悅为心的止方形，再折成--个无蓋硒悅方形容器，则悅方形容器的底面的长和宽分别比铁片的说和宽掘仙即2。

直角三角形与勾股定理(优选真题60道)(原卷版)--三年(2021-2023)中考数学真题分项汇编

三年（2021-2023）中考数学真题分项汇编（全国通用）直角三角形与勾股定理（优选真题60道）一．选择题（共28小题）1．（2023•湖北）如图，在△ABC 中，∠ABC ＝90°，AB ＝3，BC ＝4，点D 在边AC 上，且BD 平分△ABC 的周长，则BD 的长是（）A ．√5B ．√6C ．6√55D ．3√642．（2023•济宁）如图，在正方形方格中，每个小正方形的边长都是一个单位长度，点A ，B ，C ，D ，E 均在小正方形方格的顶点上，线段AB ，CD 交于点F ，若∠CFB ＝α，则∠ABE 等于（）A ．180°﹣αB ．180°﹣2αC ．90°+αD ．90°+2α3．（2023•天津）如图，在△ABC 中，分别以点A 和点C 为圆心，大于12AC 的长为半径作弧（弧所在圆的半径都相等），两弧相交于M ，N 两点，直线MN 分别与边BC ，AC 相交于点D ，E ，连接AD ．若BD ＝DC ，AE ＝4，AD ＝5，则AB 的长为（）A ．9B ．8C ．7D ．64．（2023•泸州）《九章算术》是中国古代重要的数学著作，该著作中给出了勾股数a ，b ，c 的计算公式：a =12（m 2﹣n 2），b ＝mn ，c =12（m 2+n 2），其中m ＞n ＞0，m ，n 是互质的奇数．下列四组勾股数中，不能由该勾股数计算公式直接得出的是（）A ．3，4，5B ．5，12，13C ．6，8，10D ．7，24，255．（2023•无锡）如图，在四边形ABCD 中，AD ∥BC ，∠DAB ＝30°，∠ADC ＝60°，BC ＝CD ＝2，若线段MN 在边AD 上运动，且MN ＝1，则BM 2+2BN 2的最小值是（）A ．132B ．293C ．394D ．106．（2023•日照）已知直角三角形的三边a ，b ，c 满足c ＞a ＞b ，分别以a ，b ，c 为边作三个正方形，把两个较小的正方形放置在最大正方形内，如图，设三个正方形无重叠部分的面积为S 1，均重叠部分的面积为S 2，则（）A ．S 1＞S 2B ．S 1＜S 2C ．S 1＝S 2D ．S 1，S 2大小无法确定7．（2022•百色）活动探究：我们知道，已知两边和其中一边的对角对应相等的两个三角形不一定全等．如已知△ABC 中，∠A ＝30°，AC ＝3，∠A 所对的边为√3，满足已知条件的三角形有两个（我们发现其中如图的△ABC 是一个直角三角形），则满足已知条件的三角形的第三边长为（）A ．2√3B ．2√3−3C ．2√3或√3D ．2√3或2√3−38．（2022•南充）如图，在Rt △ABC 中，∠C ＝90°，∠BAC 的平分线交BC 于点D ，DE ∥AB ，交AC 于点E ，DF ⊥AB 于点F ，DE ＝5，DF ＝3，则下列结论错误的是（）A ．BF ＝1B ．DC ＝3 C ．AE ＝5D ．AC ＝99．（2022•遵义）如图1是第七届国际数学教育大会（ICME ）会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形OABC ．若AB ＝BC ＝1，∠AOB ＝30°，则点B 到OC 的距离为（）A ．√55B ．2√55C ．1D ．210．（2022•安徽）已知点O 是边长为6的等边△ABC 的中心，点P 在△ABC 外，△ABC ，△P AB ，△PBC ，△PCA 的面积分别记为S 0，S 1，S 2，S 3．若S 1+S 2+S 3＝2S 0，则线段OP 长的最小值是（）A ．3√32B ．5√32C ．3√3D ．7√3211．（2022•广元）如图，在△ABC 中，BC ＝6，AC ＝8，∠C ＝90°，以点B 为圆心，BC 长为半径画弧，与AB 交于点D ，再分别以A 、D 为圆心，大于12AD 的长为半径画弧，两弧交于点M 、N ，作直线MN ，分别交AC 、AB 于点E 、F ，则AE 的长度为（）A ．52B ．3C ．2√2D ．10312．（2022•南京）直三棱柱的表面展开图如图所示，AC ＝3，BC ＝4，AB ＝5，四边形AMNB 是正方形，将其折叠成直三棱柱后，下列各点中，与点C 距离最大的是（）A ．点MB ．点NC ．点PD ．点Q13．（2022•温州）如图，在Rt △ABC 中，∠ACB ＝90°，以其三边为边向外作正方形，连结CF ，作GM ⊥CF 于点M ，BJ ⊥GM 于点J ，AK ⊥BJ 于点K ，交CF 于点L ．若正方形ABGF 与正方形JKLM 的面积之比为5，CE =√10+√2，则CH 的长为（）A ．√5B ．3+√52C ．2√2D ．√1014．（2022•湖州）在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD 中，M ，N 分别是AB ，BC 上的格点，BM ＝4，BN ＝2．若点P 是这个网格图形中的格点，连结PM ，PN ，则所有满足∠MPN ＝45°的△PMN 中，边PM 的长的最大值是（）A ．4√2B ．6C ．2√10D ．3√515．（2022•攀枝花）如图1是第七届国际数学教育大会（ICME ）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能够组合得到如图2所示的四边形OABC ．若OC =√5，BC ＝1，∠AOB ＝30°，则OA 的值为（）A ．√3B ．32C ．√2D ．116．（2022•金华）如图是城市某区域的示意图，建立平面直角坐标系后，学校和体育场的坐标分别是（3，1），（4，﹣2），下列各地点中，离原点最近的是（）A．超市B．医院C．体育场D．学校17．（2021•山西）在勾股定理的学习过程中，我们已经学会了运用如图图形，验证著名的勾股定理，这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”．实际上它也可用于验证数与代数，图形与几何等领域中的许多数学公式和规律，它体现的数学思想是（）A．统计思想B．分类思想C．数形结合思想D．函数思想18．（2021•襄阳）我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭（jiā）生其中，出水一尺．引葭赴岸，适与岸齐．问水深几何．”（丈、尺是长度单位，1丈＝10尺）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．水的深度是多少？则水深为（）A．10尺B．11尺C．12尺D．13尺19．（2021•自贡）如图，A（8，0），C（﹣2，0），以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点B的坐标为（）A．（0，5）B．（5，0）C．（6，0）D．（0，6）20．（2021•常德）阅读理解：如果一个正整数m能表示为两个正整数a，b的平方和，即m＝a2+b2，那么称m为广义勾股数，则下面的四个结论：①7不是广义勾股数；②13是广义勾股数；③两个广义勾股数的和是广义勾股数；④两个广义勾股数的积是广义勾股数．依次正确的是（）A．②④B．①②④C．①②D．①④21．（2023•赤峰）如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6．点F是AB中点，连接CF，把线段CF沿射线BC方向平移到DE，点D在AC上．则线段CF在平移过程中扫过区域形成的四边形CFDE 的周长和面积分别是（）A．16，6B．18，18C．16，12D．12，1622．（2023•株洲）一技术人员用刻度尺（单位：cm）测量某三角形部件的尺寸．如图所示，已知∠ACB＝90°，点D为边AB的中点，点A、B对应的刻度为1、7，则CD＝（）A．3.5cm B．3cm C．4.5cm D．6cm23．（2022•永州）如图，在Rt △ABC 中，∠ABC ＝90°，∠C ＝60°，点D 为边AC 的中点，BD ＝2，则BC 的长为（）A ．√3B ．2√3C ．2D ．424．（2022•大连）如图，在△ABC 中，∠ACB ＝90°．分别以点A 和点C 为圆心，大于12AC 的长为半径作弧，两弧相交于M ，N 两点，作直线MN ．直线MN 与AB 相交于点D ，连接CD ，若AB ＝3，则CD 的长是（）A ．6B ．3C ．1.5D ．125．（2021•新疆）如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，AB ＝4，CD ⊥AB 于点D ，E 是AB 的中点，则DE 的长为（A ．1B ．2C ．3D ．426．（2023•贵州）5月26日，“2023中国国际大数据产业博览会”在贵阳开幕，在“自动化立体库”中有许多几何元素，其中有一个等腰三角形模型（示意图如图所示），它的顶角为120°，腰长为12m ，则底边上的高是（）A ．4mB ．6mC ．10mD ．12m27．（2021•黑龙江）如图，矩形ABCD的边CD上有一点E，∠DAE＝22.5°，EF⊥AB，垂足为F，将△AEF 绕着点F顺时针旋转，使得点A的对应点M落在EF上，点E恰好落在点B处，连接BE．下列结论：①BM⊥AE；②四边形EFBC是正方形；③∠EBM＝30°；④S四边形BCEM：S△BFM＝（2√2+1）：1．其中结论正确的序号是（）A．①②B．①②③C．①②④D．③④28．（2022•绍兴）如图，把一块三角板ABC的直角顶点B放在直线EF上，∠C＝30°，AC∥EF，则∠1＝（）A．30°B．45°C．60°D．75°二．填空题（共27小题）29．（2023•东营）一艘船由A港沿北偏东60°方向航行30km至B港，然后再沿北偏西30°方向航行40km 至C港，则A，C两港之间的距离为km．30．（2023•菏泽）如图，在四边形ABCD中，∠ABC＝∠BAD＝90°，AB＝5，AD＝4，AD＜BC，点E在线段BC上运动，点F在线段AE上，∠ADF＝∠BAE，则线段BF的最小值为．31．（2023•随州）如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，D为AC上一点，若BD是∠ABC 的角平分线，则AD＝．32．（2023•扬州）我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若b﹣a＝4，c＝20，则每个直角三角形的面积为．33．（2022•常州）如图，在Rt△ABC中，∠C＝90°，AC＝9，BC＝12．在Rt△DEF中，∠F＝90°，DF ＝3，EF＝4．用一条始终绷直的弹性染色线连接CF，Rt△DEF从起始位置（点D与点B重合）平移至终止位置（点E与点A重合），且斜边DE始终在线段AB上，则Rt△ABC的外部被染色的区域面积是．34．（2022•无锡）已知△ABC中，∠B＝45o，∠C＝60o，AB=√6，则AC＝．35．（2022•无锡）如图，在Rt△ABC中，∠C＝90o，AC＝2，BC＝4，点E、F分别在AB、AC上，点A关于EF的对称点A'落在BC上，设CA'＝x．若AE＝AF，则x＝；设AE＝y，请写出y关于x的函数表达式：．36．（2022•鄂尔多斯）如图，AB⊥BC于点B，AB⊥AD于点A，点E是CD中点，若BC＝5，AD＝10，BE=13，则AB的长是．237．（2022•泰州）如图所示的象棋盘中，各个小正方形的边长均为1．“马”从图中的位置出发，不走重复路线，按照“马走日”的规则，走两步后的落点与出发点间的最短距离为．38．（2021•丹东）如图，在△ABC中，∠B＝45°，AB的垂直平分线交AB于点D，交BC于点E（BE＞CE），点F是AC的中点，连接AE、EF，若BC＝7，AC＝5，则△CEF的周长为．39．（2021•玉林）如图，某港口P位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A，B处，且相距20海里，如果知道甲船沿北偏西40°方向航行，则乙船沿方向航行．40．（2021•深圳）如图，已知∠BAC＝60°，AD是角平分线且AD＝10，作AD的垂直平分线交AC于点F，作DE⊥AC，则△DEF周长为．41．（2021•成都）如图，数字代表所在正方形的面积，则A所代表的正方形的面积为．42．（2021•宿迁）《九章算术》中一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AC生长在它的中央，BC为1尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部C恰好碰到岸边的C'处（如图），水深和芦苇长各多少尺？则该问题的水深是尺．43．（2021•南通）平面直角坐标系xOy中，已知点P（m，3n2﹣9），且实数m，n满足m﹣n2+4＝0，则点P到原点O的距离的最小值为．44．（2021•岳阳）《九章算术》是我国古代数学名著，书中有下列问题：“今有户高多于广六尺八寸，两隅相去适一丈．问户高、广各几何？”其意思为：今有一门，高比宽多6尺8寸，门对角线距离恰好为1丈．问门高、宽各是多少？（1丈＝10尺，1尺＝10寸）如图，设门高AB为x尺，根据题意，可列方程为．45．（2021•齐齐哈尔）直角三角形的两条边长分别为3和4，则这个直角三角形斜边上的高为．46．（2021•无锡）锐角△ABC中，∠A＝30°，AB＝m，则△ABC面积S的取值范围是．47．（2023•荆州）如图，CD为Rt△ABC斜边AB上的中线，E为AC的中点．若AC＝8，CD＝5，则DE ＝．48．（2023•郴州）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，点M是AB的中点，求CM＝．49．（2022•荆州）如图，在Rt△ABC中，∠ACB＝90°，通过尺规作图得到的直线MN分别交AB，AC于AE＝1，则CD＝．D，E，连接CD．若CE=1350．（2021•盐城）如图，在Rt△ABC中，CD为斜边AB上的中线，若CD＝2，则AB＝．51．（2022•十堰）【阅读材料】如图①，四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E，F分别在BC，CD上，若∠BAD＝2∠EAF，则EF＝BE+DF．【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD．已知CD＝CB＝100m，∠D＝60°，∠ABC＝120°，∠BCD＝150°，道路AD，AB上分别有景点M，N，且DM＝100m，BN ＝50（√3−1）m，若在M，N之间修一条直路，则路线M→N的长比路线M→A→N的长少m （结果取整数，参考数据：√3≈1.7）．52．（2021•陕西）如图，在Rt△中，∠C＝90°，∠B＝30°，AB＝8．若E、F是BC边上的两个动点，以EF为边的等边△EFP的顶点P在△ABC内部或边上，则等边△EFP的周长的最大值为．53．（2021•乐山）在Rt△ABC中，∠C＝90°，有一个锐角为60°，AB＝4．若点P在直线AB上（不与点A，B重合），且∠PCB＝30°，则CP的长为．54．（2021•常州）如图，在Rt△ABC中，∠ACB＝90°，∠CBA＝30°，AC＝1，D是AB上一点（点D与点A不重合）．若在Rt△ABC的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点，则AD长的取值范围是．55．如图，在Rt△ABC中，∠C＝90°，∠A＝30°，线段AB的垂直平分线分别交AC、AB于点D、E，连接BD．若CD＝1，则AD的长为．三．解答题（共5小题）56．（2023•金华）如图，为制作角度尺，将长为10，宽为4的矩形OABC分割成4×10的小正方形网格，在该矩形边上取点P，来表示∠POA的度数，阅读以下作图过程，并回答下列问题：（1）分别求点P3，P4表示的度数．（2）用直尺和圆规在该矩形的边上作点P5，使该点表示37.5°（保留作图痕迹，不写作法）．57．（2022•陕西）我国三国时期的杰出数学家赵爽在注解《周髀算经》时，巧妙地运用弦图证明了勾股定理．如图，在10×15的正方形网格中，将弦图ABCD放大，使点A，B，C，D的对应点分别为A′，B′，C′，D′．（1）A′C′与AC的比值为；（2）补全弦图A′B′C′D′．58．（2021•攀枝花）如图是“弦图”的示意图，“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的，它标志着中国古代的数学成就．它由4个全等的直角三角形与一个小正方形组成，恰好拼成一个大正方形，每个直角三角形的两条直角边分别为a、b，斜边为c．请你运用此图形证明勾股定理：a2+b2＝c2．59．（2022•杭州）如图，在Rt△ACB中，∠ACB＝90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A＝50°，∠ACE＝30°．（1）求证：CE＝CM．（2）若AB＝4，求线段FC的长．60．（2021•杭州）如图，在△ABC中，∠ABC的平分线BD交AC边于点D，AE⊥BC于点E．已知∠ABC ＝60°，∠C＝45°．（1）求证：AB＝BD；（2）若AE＝3，求△ABC的面积．。

华杯赛初赛历年真题集(含答案)

目录2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷 (3)2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷 (5)2004年第10届“华罗庚金杯”少年数学邀请赛初赛试卷 (11)2004年第1届“华罗庚金杯”少年数学邀请赛初赛试卷 (13)2006年第11届“华罗庚金杯”少年数学邀请赛初赛试卷 (19)2006年第11届“华罗庚金杯”少年数学邀请赛初赛试卷 (23)2007年第12届“华罗庚金杯”少年数学邀请赛初赛试卷 (30)2007年第12届“华罗庚金杯”少年数学邀请赛初赛试卷 (32)2008年第13届“华罗庚金杯”少年数学邀请赛初赛试卷 (38)2008年第13届“华罗庚金杯”少年数学邀请赛初赛试卷 (40)2009年第14届“华罗庚金杯”少年数学邀请赛初赛试卷 (46)2009年第14届“华罗庚金杯”少年数学邀请赛初赛试卷 (48)2010年第15届“华罗庚金杯”少年数学邀请赛初赛试卷 (53)2010年第15届“华罗庚金杯”少年数学邀请赛初赛试卷 (55)2011年第16届“华罗庚金杯”少年数学邀请赛初赛试卷 (60)2011年第16届“华罗庚金杯”少年数学邀请赛初赛试卷 (63)2012年第17届“华罗庚金杯”少年数学邀请赛初赛试卷 (70)2012年第17届“华罗庚金杯”少年数学邀请赛初赛试卷 (72)2013年第18届“华罗庚金杯”少年数学邀请赛初赛试卷 (79)2013年第18届“华罗庚金杯”少年数学邀请赛初赛试卷 (81)2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷一、解答题（共12小题，满分0分）1．“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛．华罗庚教授生于1910年，现在用“华杯”代表一个两位数．已知1910与“华杯”之和等于2004，那么“华杯”代表的两位数是多少？2．长方形的各边长增加10%，那么它的周长和面积分别增加百分之几？3．如图所示的是一个正方体木块的表面展开图，若在正方体的各面填上数，使其对面两数之和为7，则A、B、C处填的数各是多少？4．在一列数：，，，，，，…中，从哪一个数开始，1与每个数之差都小于？5．“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球，实现了中华民族的飞天梦．飞船绕地球共飞行14圈，其中后10圈沿离地面343千米的圆形轨道飞行．请计算飞船沿圆形轨道飞行了多少千米（地球半径为6371千米，圆周率π=3.14）．6．如图，一块圆形的纸片分成4个相同的扇形，用红、黄两种颜色分别涂满各扇形，问共有几种不同的涂法？7．在9点至10点之间的某一时刻，5分钟前分针的位置与5分钟后时针的位置相同，此时刻是9点几分？8．一副扑克牌有54张，最少要抽取几张牌，方能使其中至少有2张牌有相同的点数？9．任意写一个两位数，再将它依次重复3遍成一个8位数．将此8位数除以该两位数所得到的商再除以9，问：得到的余数是多少？10．一块长方形的木板，长为90厘米，宽为40厘米，将它锯成2块，然后拼成一个正方形，你能做到吗？11．如图，大小两个半圆，它们的直径在同一直线上，弦AB与小圆相切，且与直径平行，弦AB长12厘米．求图中阴影部分的面积（圆周率π=3.14）．12．半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷参考答案与解析一、解答题（共12小题，满分0分）1．“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛．华罗庚教授生于1910年，现在用“华杯”代表一个两位数．已知1910与“华杯”之和等于2004，那么“华杯”代表的两位数是多少？考点：竖式数字谜．专题：填运算符号、字母等的竖式与横式问题．分析：根据整数加法的计算方法进行推算即可．解答：解：解法一：个位上：0+“杯”=4，可得“杯”=4；十位上：1+“华”的末尾是0，由1+9=10，可得“华”9，向百位上进1；百位上：9+1=10，向千位上进1；千位上：1+1=2；由以上可得：；因此，“华杯”代表的两位数是94．解法二：已知1910与“华杯”之和等于2004；那么“华杯”=2004﹣1910=94；因此，“华杯”代表的两位数是94．点评：本题非常巧妙地考察了对整数的加法运算法则及数位的进位等知识要点的熟悉掌握程度．2．长方形的各边长增加10%，那么它的周长和面积分别增加百分之几？考点：百分数的实际应用；长方形的周长；长方形、正方形的面积．专题：分数百分数应用题．分析：设长方形的长为a，宽为b，因此各边长增加10%时，则长为（1+10%）a=110%a，长为（1+10%）b=110%b，因此各边长增加10%时，周长增加2（1.1a+1.1b）﹣2（a+b）=2（a+b）×10%，即周长增加10%．面积增加1.1a×1.1b﹣ab=1.21ab﹣ab=ab×21%，即面积增加21%．解答：周长增加10%，面积增加21%解：设长方形的长为a，宽为b，边长增加10%时，则长为（1+10%）a=110%a，长为（1+10%）b=110%b，周长增加：2（110%a+110%b）﹣2（a+b）=220%a+220%b﹣2a﹣2b=2（a+b）×10%；面积增加：110%a×110%b﹣ab=121%ab﹣ab=ab×21%；答：周长增加了10%，面积增加了21%．点评：在求出长宽增加后的长度基础上，根据长方形的周长与面积公式计算是完成本题的关键．3．如图所示的是一个正方体木块的表面展开图，若在正方体的各面填上数，使其对面两数之和为7，则A、B、C处填的数各是多少？考点：正方体的展开图．专题：立体图形的认识与计算．分析：如图，是正方体展开图的“222”结构，把它折叠成正方体后，A面与1面相对，B面与2面相对，C 面与4面相对，相使使其对面两数之和为7，A面填6，B面填5，C面填3．解答：解：如图，折成正方体后，A面与1面相对，B面与2面相对，C面与4面相对，要使其对面之各为7，则A面填6，B面填5，C面填3．点评：本题是考查正方体的展开图，关键是弄清把它折叠成正方体后，哪两个面相对．4．在一列数：，，，，，，…中，从哪一个数开始，1与每个数之差都小于？考点：数列中的规律．专题：探索数的规律．分析：这列数的特点是每个数的分母比分子大2，分子为奇数列，要使1﹣＜，则n＞999.5，即从n=1000开始，带入分数，即可得解．解答：解：这列数的特点是每个数的分母比分子大2，分子为奇数列，1﹣＜，n＞999.5，从n=1000开始，即从开始，满足条件．答：从开始，1与每个数之差都小于．点评：找出这列数的规律，根据已知列出等式求解．5．“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球，实现了中华民族的飞天梦．飞船绕地球共飞行14圈，其中后10圈沿离地面343千米的圆形轨道飞行．请计算飞船沿圆形轨道飞行了多少千米（地球半径为6371千米，圆周率π=3.14）．考点：有关圆的应用题．专题：平面图形的认识与计算．分析：先圆形轨道的半径，再根据圆的周长公式：C=2πr求出飞船沿圆形轨道飞行1圈的长度，再乘以10即可求出飞船沿圆形轨道飞行了多少千米．解答：解：2×3.14×（6371+343）×10=2×3.14×6714×10=3.14×134280=421639.2（千米）；答：飞船沿圆形轨道飞行了421639.2千米．点评：考查了有关圆的应用题，关键是熟练掌握圆的周长公式．6．如图，一块圆形的纸片分成4个相同的扇形，用红、黄两种颜色分别涂满各扇形，问共有几种不同的涂法？考点：染色问题．专题：传统应用题专题．分析：根据四个扇形中有一个红色、两个、三个、四个分类列举即可．解答：解：按逆时针方向涂染各扇形：红红红红红红红黄红红黄黄红黄红黄红黄黄黄黄黄黄黄所以，共有6种．点评：本题考查了排列组合知识中的染色问题，还可以列式解答：4×（4﹣1）÷2=6（种）．7．在9点至10点之间的某一时刻，5分钟前分针的位置与5分钟后时针的位置相同，此时刻是9点几分？考点：时间与钟面．专题：时钟问题．分析：可设当前是9点x分，则5分钟前分针指向x﹣5的位置，而分针转动的速度是时针的12倍，分针5分钟后指向x+5的位置，时针指向9刻度后刻度处，根据题意列出方程解答即可．解答：解：设当前时刻是9点x分．则5分钟后时针的位置为45+=x﹣5540+x+5=12x﹣6011x=605x=55；答：此时刻是9点55分．点评：本题主要考查钟表问题的实际应用，熟练掌握钟表的特征是解答本题的关键．8．一副扑克牌有54张，最少要抽取几张牌，方能使其中至少有2张牌有相同的点数？考点：抽屉原理．专题：传统应用题专题．分析：建立抽屉：一副扑克牌有54张，大小鬼不相同，那么（54﹣2）÷4=13，所以一共有13+2=15个抽屉；分别是：1、2、3、…K、小鬼、大鬼，由此利用抽屉原理考虑最差情况，即可进行解答．解答：解：建立抽屉：54张牌，根据点数特点可以分别看做15个抽屉，考虑最差情况：每个抽屉都摸出了1张牌，共摸出15张牌，此时再任意摸出一张，无论放到哪个抽屉，都会出现有两张牌在同一个抽屉，即两张牌点数相同，15+1=16（张），答：至少抽取16张扑克牌，方能使其中至少有两张牌有相同的点数．点评：此类问题关键是根据点数特点，建立抽屉，这里要注意考虑最差情况．9．任意写一个两位数，再将它依次重复3遍成一个8位数．将此8位数除以该两位数所得到的商再除以9，问：得到的余数是多少？考点：带余除法．专题：余数问题．分析：先设这个两位数为10a+b，则可用含a、b的代数式表示将它依次重复写3遍成的一个8位数，再将此8位数除以该两位数得到商为1010101，然后将1010101除以9即可求解．解答：解：设这个两位数为10a+b，则将它依次重复3遍成的一个8位数为：1000000（10a+b）+10000（10a+b）+100（10a+b）+10a+b=1010101（10a+b），将此8位数除以该两位数得到的商为：1010101（10a+b）÷（10a+b）=1010101，则1010101÷9=112233…4．答：得到的余数是4．点评：本题考查了带余除法的定义及应用，难度中等，用含a、b的代数式正确表示将（10a+b）这个数依次重复写3遍成的一个8位数是解题的关键．10．一块长方形的木板，长为90厘米，宽为40厘米，将它锯成2块，然后拼成一个正方形，你能做到吗？考点：图形的拆拼（切拼）．专题：平面图形的认识与计算．分析：因为这块长方形木板的面积为90×40=3600（平方厘米），又因为3600=60×60，即所求的正方形的边长为60厘米，如下图所示．解答：解：因为90×40=3600，3600=60×60，所求的正方形的边长为60厘米，可以如下图拼成：因此，能拼成一个正方形．点评：先求出总面积，看看是否能分成两个数的平方．11．如图，大小两个半圆，它们的直径在同一直线上，弦AB与小圆相切，且与直径平行，弦AB长12厘米．求图中阴影部分的面积（圆周率π=3.14）．考点：组合图形的面积．专题：平面图形的认识与计算．分析：将小圆缩小至0，则AB就是大圆直径，阴影部分就是大圆的一半，利用圆的面积公式即可求解．解答：解：将小圆缩小至0，则AB就是大圆直径，阴影部分就是大圆的一半，所以阴影部分的面积是：×3.14×（12÷2）2=×3.14×36=56.52（平方厘米）；答：图中阴影部分的面积是56.52平方厘米．点评：此题可以巧妙地利用“缩小法”，得出阴影部分的面积与直径为AB的圆的面积的关系，问题即可得解．12．半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？考点：有关圆的应用题．专题：平面图形的认识与计算．分析：由于小铁环的半径为25厘米，大铁环的半径为50厘米，可得小铁环的半径是大铁环半径的一半．根据周长与半径的关系可得大环周长是小环的2倍，即小环沿大环转2个周长时又回到原位，再减去公转的1圈，可得小环自身转动的圈数．解答：解：由于小铁环的半径是大铁环半径的一半，所以大环周长是小环的2倍，即小环沿大环转2个周长时又回到原位，其中有1个周长属于小环公转的，而另一个周长才是小环自身转动的，因此，小环自身转动1圈．点评：本题考查了圆与圆的位置关系，小铁环运动的圈数乘以它的周长就等于大铁环的周长．2004年第10届“华罗庚金杯”少年数学邀请赛初赛试卷一、解答题（共12小题，满分0分）1．2005年是中国伟大航海家郑和首次下西洋600周年，西班牙伟大航海家歌伦布首次远洋航行是在1492年．问这两次远洋航行相差多少年？2．从冬至之日起每九天分为一段，依次称之为一九，二九，…，九九，2004年的冬至为12月21日，2005年的立春是2月4日．问立春之日是几九的第几天？3．如图是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形．问这个直三棱柱的体积是多少？4．爸爸、妈妈、客人和我四人围着圆桌喝茶．若只考虑每人左邻的情况，问共有多少种不同的入座方法？5．在奥运会的铁人三项比赛中，自行车比赛距离是长跑的4倍，游泳的距离是自行车的，长跑与游泳的距离之差为8.5千米．求三项的总距离．6．如图，用同样大小的正三角形，向下逐次拼接出更大的正三角形．其中最小的三角形顶点的个数（重合的顶点只计一次）依次为：3，6，10，15，21，…问这列数中的第9个是多少？7．一个圆锥形容器甲与一个半球形容器乙，它们圆形口的直径与容器的高的尺寸如图所示．若用甲容器取水来注满乙容器，问：至少要注水多少次？8．100名学生参加社会实践，高年级学生两人一组，低年级学生三人一组，共有41组．问：高、低年级学生各多少人？9．小鸣用48元钱按零售价买了若干练习本．如果按批发价购买，每本便宜2元，恰好多买4本．问：零售价每本多少元？10．不足100名同学跳集体舞时有两种组合：一种是中间一组5人，其他人按8人一组围在外圈；另一种是中间一组8人，其他人按5人一组围在外圈．问最多有多少名同学？11．输液100毫升，每分钟输2.5毫升．请你观察第12分钟时吊瓶图象中的数据，回答整个吊瓶的容积是多少毫升？12．两条直线相交所成的锐角或直角称为两条直线的“夹角”．现平面上有若干条直线，它们两两相交，并且“夹角”只能是30°，60°或90°．问：至多有多少条直线？2004年第1届“华罗庚金杯”少年数学邀请赛初赛试卷参考答案与试题解析一、解答题（共12小题，满分0分）1．2005年是中国伟大航海家郑和首次下西洋600周年，西班牙伟大航海家歌伦布首次远洋航行是在1492年．问这两次远洋航行相差多少年？考点：日期和时间的推算．分析：先求出郑和首次下西洋的时间，再求差．解答：解：2005﹣600=1405（年），1492﹣1405=87（年）．答：这两次远洋航行相差87年．点评：本题先根据2005年求出郑和首次下西洋的时间，再用较晚的时间减去较早的时间．2．从冬至之日起每九天分为一段，依次称之为一九，二九，…，九九，2004年的冬至为12月21日，2005年的立春是2月4日．问立春之日是几九的第几天？考点：日期和时间的推算．分析：先求出2004年的12月21日到2005年的2月4日经过了多少天，再求这些天里有几个9天，还余几天，再根据余数推算是几九第几天即可．解答：解：2004年的12月21日到12月31日共有11天，1月份有31天，2月4日是2月的第四天，那么一共经过了：11+31+4=46（天），46÷9=5…1，说明已经经过了5个9天，还余1天，这一天就是六九的第一天．答：立春之日是六九的第1天．点评：本题的是9天为1个周期，先求出经过的天数（注意两头的天数都算），再求这些天里有几个9天，还余几天，再根据余数判断．3．如图是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形．问这个直三棱柱的体积是多少？考点：规则立体图形的体积．分析：根据棱柱的体积公式：底面积×高，进行计算．解答：解：因为直三棱柱的底面是直角边都为1的直角三角形，高为1，所以直三棱柱的体积=×1×1×1=．答：这个直三棱柱的体积是．故答案为：．点评：本题考查了直三棱柱及展开图的特征和直三棱柱体积计算．直三棱柱是由三个长方形的侧面和上下两个底面组成．4．爸爸、妈妈、客人和我四人围着圆桌喝茶．若只考虑每人左邻的情况，问共有多少种不同的入座方法？考点：加法原理．分析：可先把我放在第一个位置，进而考虑我的左邻的情况，我的左邻的左邻的情况，找到总情况数即可．解答：解：共有6种不同的入座方法．点评：考查用列表法解决问题；把1个人固定位置，进而考虑左邻的情况是解决本题的关键．5．在奥运会的铁人三项比赛中，自行车比赛距离是长跑的4倍，游泳的距离是自行车的，长跑与游泳的距离之差为8.5千米．求三项的总距离．考点：分数除法应用题．分析：把自行车的距离看成单位“1”，那么长跑的距离就是自行车的，游泳的距离是自行车的，它们的差对应的数量是8.5千米，用除法可以求出自行车的距离，根据自行车的距离求出另外两项的距离，再把三者加起来．解答：解：自行车比赛距离是长跑的4倍，那么长跑的距离就是自行车的，8.5÷（）=8.5÷，=40（千米）；40×=10（千米）；40×=1.5（千米）；40+10+1.5=51.5（千米）；答：三项的总距离是51.5千米．点评：本题关键是把倍数关系看成一个是另一个的几分之几，找出单位“1”分析出数量关系，再由基本的数量关系求解．6．如图，用同样大小的正三角形，向下逐次拼接出更大的正三角形．其中最小的三角形顶点的个数（重合的顶点只计一次）依次为：3，6，10，15，21，…问这列数中的第9个是多少？考点：事物的简单搭配规律．分析：观察图形，分析数列，发现规律：从第一个数开始，后面的数依次比前一个数多3、4、5、6、7、…据此规律，推出即可．解答：解：6﹣3=3；10﹣6=4；15﹣10=5；21﹣15=6；…从第一个数开始，后面的数依次比前一个数多3、4、5、6、7、…往下写数：3，6，10，15，21，28，36，45，55，…第9个数是55．答：这列数中的第9个是55．点评：观察图形，分析数列，发现规律，然后利用规律解决问题．7．一个圆锥形容器甲与一个半球形容器乙，它们圆形口的直径与容器的高的尺寸如图所示．若用甲容器取水来注满乙容器，问：至少要注水多少次？考点：规则立体图形的体积．分析：根据圆锥的体积公式求出容器甲容积，根据球的体积公式求出容器乙容积，相除即可求解．解答：解：容器甲容积：V甲=×π×（）2×1=π；容器乙容积：V乙=×π×13=π，V乙÷V甲=π÷π=8．答：至少要注水8次．点评：考查了圆锥的体积和球的体积．球的体积公式是V=πr3．圆锥的体积是V=sh=πr2h．8．100名学生参加社会实践，高年级学生两人一组，低年级学生三人一组，共有41组．问：高、低年级学生各多少人？考点：鸡兔同笼．分析：可设高年级有学生x人，则低年级的学生有100﹣x人，根据等量关系：高年级组数+低年级组数=41组解答即可．解答：解：高年级有学生x人，则低年级的学生有100﹣x人，由题意得：=41，3x+2（100﹣x）=246，3x+200﹣2x=246，x=46，100﹣46=54（人），答：高年级有46人，低年级有54人．点评：此类题目中一般都有两个等量关系，抓住其中一个等量关系设出一个未知数，从而得出另一个未知数；另一个等量关系用来列方程．9．小鸣用48元钱按零售价买了若干练习本．如果按批发价购买，每本便宜2元，恰好多买4本．问：零售价每本多少元？考点：整数、小数复合应用题；合数与质数；质数与合数问题．分析：先将48分解质因数：48=1×48=2×24=3×16=4×12=6×8，因数全写出来，再找出里面相差分别是2和4的，那么这两个算式就分别为零售价和批发价．解答：解：48=48=1×48=2×24=3×16=4×12=6×8，找出里面相差分别是2和4的，那么这两个算式就分别为零售价和批发价；只有4×12和6×8，12比8多4，4比6少2，则零售价为6元，批发价为4元；答：零售价为6元．点评：解答此题应结合合数和质数的含义进行分析，通过分解质因数，找出符合题意的答案即可．10．不足100名同学跳集体舞时有两种组合：一种是中间一组5人，其他人按8人一组围在外圈；另一种是中间一组8人，其他人按5人一组围在外圈．问最多有多少名同学？考点：最大与最小．分析：设两种组合外圈的组数为a、b，那么第一种的人数是5+8a人，第二种的人数是8+5b人，因为总人数一定相等，求出a与b的关系，根据a和b关系讨论取值．解答：解：设两种组合外圈的组数为a、b，那么第一种的人数是5+8a，第二种的人数是8+5b，则5+8a=8+5b即；8a=5b+3，当b=1时，a=1，总人数为5+8×1=13（人）；当b=9时，a=6，总人数为5+8×6=53（人）；当b=17时，a=11，总人数为5+8×11=93（人）．数字再大就超过100了，所以最多有93人．答：最多有93名同学．点评：本题先找出两种组数之间的关系，然后根据组数是自然数和它们之间的关系讨论取值，找出100以内最大的即可．11．输液100毫升，每分钟输2.5毫升．请你观察第12分钟时吊瓶图象中的数据，回答整个吊瓶的容积是多少毫升？考点：整数、小数复合应用题．分析：水平面的刻度是80毫升，说明空的部分是80毫升；根据每分钟的输液量和输液时间求出已经输出的体积，用100毫升减去已经输出的体积就是瓶内剩下的体积；整个吊瓶的容积就是空的部分加剩下的这部分体积．解答：解：100﹣2.5×12=70（毫升），80+70=150（毫升），答：整个吊瓶的容积是150毫升．点评：本题第12分时瓶子上方没有溶液的容积的等量关系是解决本题的关键．12．两条直线相交所成的锐角或直角称为两条直线的“夹角”．现平面上有若干条直线，它们两两相交，并且“夹角”只能是30°，60°或90°．问：至多有多少条直线？考点：乘法原理．分析：根据题意，“夹角”只能是30°，60°或90°，都是30°的倍数，根据这个倍数，通过旋转的方法，进一步解答即可．解答：解：因为夹角只能是30°、60°或者90°，其均为30°的倍数，所以每画一条直线后，逆时针旋转30°画下一条直线，这样就能够保证两两直线夹角为30°的倍数，即为30°、60°或者90°（因为如果每次旋转度数其他角度，例如15°，则必然会出现两条直线的夹角为15°或15°的其它倍数，如45°这与题目不符）；因为该平面上的直线两两相交，也就是说不会出现平行的情况，在画出6条直线时，直线旋转过5次，5×30°=150°，如果再画出第7条直线，则旋转6次，6×30°=180°，这样第七条直线就与第一条直线平行了．如图：所以最多能画出六条．答：至多有6条直线．点评：根据题意，由题目给出的条件，通过旋转的方法进一步解答即可．2006年第11届“华罗庚金杯”少年数学邀请赛初赛试卷一、选择题（共6小题，每小题6分，满分36分）1．（6分）如图所示，将一张正方形纸片先由下向上对折压平，再由右翻起向左对折压平，得到小正方形ABCD．取AB 的中点M和BC 的中点N，剪掉AMBN得五边形AMNCD．则将折叠的五边形AMNCD纸片展开铺平后的图形是（）A．B．C．D．2．（6分）2008006共有（）个质因数．A．4B．5C．6D．73．（6分）（2007•北塘区）奶奶告诉小明：“2006年共有53个星期日”．聪敏的小明立刻告诉奶奶：2007年的元旦一定是（）A．星期一B．星期二C．星期六D．星期日4．（6分）如图，长方形ABCD小AB：BC=5：4．位于A点的第一只蚂蚁按A→B→C→D→A的方向，位于C点的第二只蚂蚁按C→B→A→D→C的方向同时出发，分别沿着长方形的边爬行．如果两只蚂蚁第一次在B点相遇，则两只蚂蚁第二次相遇在（）边上．A．A B B．B C C．C D D．D A5．（6分）如图，ABCD是个直角梯形（∠DAB=∠ABC=90°）．以AD为一边向外作长方形ADEF，其面积为6.36平方厘米，连接BE交AD于P，再连接PC．则图中阴影部分的面积是（）平方厘米．A．6.36 B．3.18 C．2.12 D．1.596．（6分）五位同学扮成奥运会吉祥物福娃贝见、晶晶、欢欢、迎迎和妮妮，排成一排表演节目，如果贝贝和妮妮不相邻，共有（）种不同的排法．A．48 B．72 C．96 D．120二、填空题（共8小题，每小题3分，满分24分）7．（3分）在算式中，汉字“第、十、一、届、华、杯、赛”代表1，2，3，4，5，6.7，8，9中的7个数字，不同的汉字代表不同的数字，恰使得加法算式成立．则“第、十、一、届、华、杯、赛”所代表的7个数字的和等于_________•8．（3分）全班50个学生，每人恰有三角板或直尺中的一种，28人有直尺，有三角板的人中，男生是14人，若已知全班共有女生31人，那么有直尺的女生有_________人．9．（3分）如图是﹣个直圆柱形状的玻璃杯，一个长为12厘米的直棒状细吸管（不考虑吸管粗细）放在玻璃杯内．当吸管一端接触圆柱下底面时，另一端沿吸管最少可露出上底面边缘2厘米，最多能露出4厘米．则这个玻璃杯的容积为_________立方厘米．（取π=3.14）（提示：直角三角形中“勾6、股8、弦10）10．（3分）有5个黑色和白色棋子围成一圈，规定：将同色的和相邻的两个棋子之间放入一个白色棋子，在异色的和相邻的两个棋子之间放入一个黑色棋子，然后将原来的5个棋子拿掉，如果从图5（1）的初始状态开始依照上述规定操作下去，对于圆圈上呈现5个棋子的情况，圆圈上黑子最多能有_________个．11．（3分）李大爷用一批化肥给承包的麦田施肥．若每亩施6千克，则缺少化肥300千克；若每亩施5千克，则余下化肥200千克．那么李大爷共承包了麦田_________亩，这批化肥有_________千克．12．（3分）将从1开始的到103的连续奇数依次写成﹣个多位数：a=13579111315171921…9799101103．则数a共有_________位，数a除以9的余数是_________．13．（3分）自制的一副玩具牌共计52张（含4种牌：红桃，红方、黑桃、黑梅．每种牌都有1点、2点，…、13点牌各一张）．洗好后背面朝上放好．一次至少抽取_________张牌，才能保证其中必定有2张牌的点数和颜色都相同．如果要求一次抽出的牌中必定有3张牌的点数是相邻的（不计颜色），那么至少要取_________张牌．。

初中数学精品课件：三视图与表面展开图

A．国 C．中
【答案】 B
图 33-4
B．的 D．梦
5．(2019·淄博)下列几何体中，其主视图、左视图和俯视图完
全相同的是
()
A．
B
C．
D．
【答案】 D
题型一判断物体的三视图
三视图是分别从正面、左面、上面三个方向看同一个物体所得到的平面图形，判断三视图时应注意尺寸的大小，即三个视图的特征：主视图体现物体的长和高，左视图体现物体的宽和高，俯视图体现物体的长和宽．
【典例 2】 (2018·青岛)一个由 16 个完全相同的小立方
体搭成的几何体，其最下面一层摆放了 9 个小立方体，
它的主视图和左视图如图 33-7 所示，则这个几何体的
搭法共有
种．
图 33-7
【解析】这个几何体的搭法共有 10 种，如解图所示．
【答案】 10
(典例 2 解)
【类题演练 2】如图 33-8 所示的三视图所对应的几何体是 ( )
图 33-9
A． 25π
B． 24π
C． 20π
D． 15π
【解析】由主视图可知圆锥的底面直径为 8，
∴底面半径 r＝4.
由左视图可知圆锥的高为 3，
∴母线长 l＝ 32＋42＝5，
∴S 圆锥侧＝πrl＝20π.
【答案】 C
【类题演练 3】 (2019·甘肃)已知某几何体的三视图如图 33-10 所示，其
的小立方体搭成，下列说法正确的是
()
A．主视图的面积为 4
B．左视图的面积为 4
C．俯视图的面积为 3
D．三种视图的面积都为 4
【答案】 A
图 33-18
4．若一个几何体的三视图如图 33-19 所示，则该几何 ( ) A．直三棱柱 B．长方体 C．圆锥 D．立方体

三棱柱的展开图

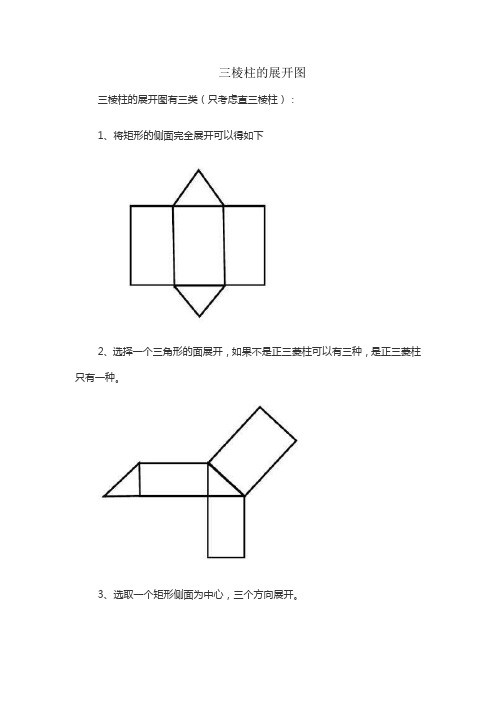
三棱柱的展开图
三棱柱的展开图有三类（只考虑直三棱柱）：
1、将矩形的侧面完全展开可以得如下
2、选择一个三角形的面展开，如果不是正三菱柱可以有三种，是正三菱柱只有一种。

3、选取一个矩形侧面为中心，三个方向展开。

扩展资料：
三棱柱是一种柱体，底面为三角形。

正三棱柱是半正多面体、均匀多面体的一种。

三棱柱是一种五面体，且有一组平行面，即两个面互相平行，而其他三个表面的法线在同一平面上（不一定是平行的面）。

这三个面可以是平行四边形。

所有平行于底面的横截面都是相同的三角形。

由于三棱柱也可以视为三面体截去2个顶点，故又称截角三面体，另外，因为正三棱柱具有对称性，且由2种正多边形组成，因此有人称正三棱柱为半正五面体。

一般三棱柱有5个面、9个边和6个顶点。

2023-2024学年江苏省无锡市新吴区八年级(上)期中数学试卷[含答案]

2023-2024学年江苏省无锡市新吴区八年级（上）期中数学试卷一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）下列航空公司的标志中，是轴对称图形的是（）A．贵州航空B．江西航空C．春秋航空D．香港航空2．（3分）已知图中的两个三角形全等，则∠α等于（）A．72°B．60°C．58°D．50°3．（3分）如图，已知AB＝DC，下列条件中，不能使△ABC≌△DCB的是（）A．AC＝DB B．∠A＝∠D＝90°C．∠ABC＝∠DCB D．∠ACB＝∠DBC4．（3分）已知△ABC的三条边分别为a、b、c，三个内角分别为∠A、∠B、∠C，则满足下列条件的△ABC不是直角三角形的是（）A．a＝6，b＝8，c＝10B．a2﹣c2＝b2C．∠A＝2∠B＝3∠C D．∠A﹣∠B＝∠C5．（3分）下列命题：①到线段两端距离相等的点在线段的垂直平分线上；②角是轴对称图形，对称轴是角平分线；③有两个内角相等的三角形是等腰三角形；④两边分别相等且其中一边的对角也相等的两个三角形全等；其中真命题的个数为（）A．1B．2C．3D．46．（3分）如图，在△ABC中，∠C＝90°，AC＝4，DC＝AD，BD平分∠ABC，则点D到AB的距离等于（）A．1B．C．2D．7．（3分）在△ABC中，AC＝3，△ABC的周长为12，设AB的长为x，下列说法不正确的是（）A．△ABC为等腰三角形时，x＝4.5B．△ABC不可能是等边三角形C．△ABC为直角三角形时，x＝4D．3＜x＜68．（3分）如图，在等边三角形ABC中，在AC边上取两点M、N，使∠MBN＝30°．若AM＝m，MN＝x，CN＝n，则以x，m，n为边长的三角形的形状为（）A．锐角三角形B．直角三角形C．钝角三角形D．随x，m，n的值而定9．（3分）如图，△ABC中∠C＝90°，AB＝10，AC＝8，BC＝6，线段DE的两个端点D、E分别在边AC，BC上滑动，且DE＝4，若点M、N分别是DE、AB的中点，则MN的最小值为（）A．2B．3C．3.5D．410．（3分）直三棱柱的表面展开图如图所示，AC＝3，BC＝4，AB＝5，四边形AMNB是正方形，将其折叠成直三棱柱后，下列各点中，与点C距离最大的是（）A．点M B．点N C．点P D．点Q二、填空题（本大题共8小题，每小题3分，共24分）11．（3分）等腰三角形两边长分别是3和6，则该三角形的周长为．12．（3分）如图，在△ABE中，AE的垂直平分线MN交BE于点C，连接AC．若AB＝AC，CE＝5，BC＝6，则△ABC的周长等于．13．（3分）如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG＝CD，DF＝DE，则∠E＝度．14．（3分）如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，若∠A＝∠ABE，AC＝10，BC＝6，则BD的长为．15．（3分）小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m，∠BOC＝90°．爸爸在C处接住小丽时，小丽距离地面的高度是．16．（3分）机场入口处的铭牌上说明，飞机行李架是一个50cm×40cm×20cm的长方体空间，有位旅客想购买一件画卷随身携带，现有4种长度的画卷①38cm；②40cm；③60cm；④68cm，请问这位旅客可以购买的尺寸是．（填写序号）17．（3分）如图，以AB为斜边的Rt△ABC的每条边为边作三个正方形，分别是正方形ABMN，正方形BCPQ，正方形ACEF，且边EF恰好经过点N．若S3＝S4＝6，则S1+S5＝．（注：图中所示面积S表示相应封闭区域的面积，如S3表示△ABC的面积）18．（3分）如图，△ABC中，AB＝AC，∠A＝30°，射线CP从射线CA开始绕点C逆时针旋转α角（0°＜α＜75°），与射线AB相交于点D，将△ACD沿射线CP翻折至△A′CD处，射线CA′与射线AB相交于点E．若△A′DE是等腰三角形，则∠α的度数为．三、解答题（本大题共7小题，共66分）19．（8分）如图，点C、E、F、B在同一直线上，AB∥CD，AE＝DF，∠AEB＝∠DFC．（1）求证：△ABE≌△DCF；（2）若∠A＝55°，∠C＝30°，求∠BFD的度数．20．（8分）如图，是由小正方形组成的6×8网格，每个小正方形的顶点叫做格点，A、B、C三点是格点，仅用无刻度的直尺在给定网格中根据要求完成画图．（1）在图1中，画出△ABC关于直线l对称的图形△DEF；△ABC的面积为；（2）在图2中，画出∠ABC的角平分线．21．（8分）某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量∠B＝90°，AB＝3m，BC＝4m，CD＝12m，AD＝13m．若每平方米草皮需要200元，问学校需要投入多少资金买草皮？22．（10分）已知△ABC中，AB＝AC．（1）如图1，在△ADE中，若AD＝AE，且∠DAE＝∠BAC，求证：CD＝BE；（2）如图2，在△ADE中，若∠DAE＝∠BAC＝60°，且CD垂直平分AE，AD＝3，CD＝4，求BD 的长．23．（10分）如图：在Rt△ABC中，∠ACB＝90°，AB＝5cm，AC＝3cm，动点P从B出发沿射线BC 以2cm/s的速度运动，设运动时间为t秒．（1）当t＝时，AP平分△ABC的面积．（2）当△ABP为等腰三角形时，求t的值．（3）若点E、F分别为BC、AB上的动点，请直接写出AE+EF的最小值．24．（12分）【了解概念】如图1，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连接CE，连接BD并延长与CE交于点F，那么将∠BFC叫做△ABC和△ADE的底联角．【探究归纳】（1）两个等腰三角形的底联角与这两个等腰三角形的顶角有怎样的数量关系？请用文字语言写出结论．【拓展提升】运用（1）中的结论解决问题：（2）如图2，AB＝AC，AD＝AE，∠BAC＝DAE＝90°，∠DCE＝62°，求∠BDC的度数；（3）如图3，在四边形ABCD中，AB＝6，BC＝4，CD＝5，点O为四边形ABCD内一点．且OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，求AD的长．25．（10分）课堂上学习了勾股定理后知道：直角三角形三边长是整数时我们称之为“勾股数”．王老师给出一组数让学生观察：3、4、5；5、12、13；7、24、25；9、40、41；…，学生发现这些勾股数的勾都是奇数，且从3起就没有间断过，于是王老师提出以下问题让学生解决．若两直角边为a，b（a＜b），斜边为c．（1）请你根据上述的规律写出下一组勾股数：11、、；（2）当a＝n（n为奇数，且n≥3）时，若b＝，c＝　时可以构造出勾股数（用含n的代数式表示）；并证明你的猜想；（3）当a＝n（n为偶数，且n＞4）时，若b＝，c＝　时可以构造出勾股数（用含n的代数式表示）；（4）构造勾股数的方法很多，请你寻找当a＝20时，c＝．2023-2024学年江苏省无锡市新吴区八年级（上）期中数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）下列航空公司的标志中，是轴对称图形的是（）A．贵州航空B．江西航空C．春秋航空D．香港航空【分析】根据轴对称图形的概念求解．【解答】解：A、不是轴对称图形，故此选项不合题意；B、不是轴对称图形，故此选项不合题意；C、不是轴对称图形，故此选项不合题意；D、是轴对称图形，故此选项符合题意．故选：D．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．（3分）已知图中的两个三角形全等，则∠α等于（）A．72°B．60°C．58°D．50°【分析】直接利用全等三角形的性质得出对应角进而得出答案．【解答】解：∵图中的两个三角形全等，∴∠α＝50°．故选：D．【点评】本题主要考查了全等三角形的性质，正确找出对应角是解题关键．3．（3分）如图，已知AB＝DC，下列条件中，不能使△ABC≌△DCB的是（）A．AC＝DB B．∠A＝∠D＝90°C．∠ABC＝∠DCB D．∠ACB＝∠DBC【分析】根据全等三角形的判定定理逐个判断即可．【解答】解：A．AB＝DC，BC＝CB，AC＝DB，符合全等三角形的判定定理SSS，能推出△ABC≌△DCB，故本选项不符合题意；B．∠A＝∠D＝90°，AB＝DC，BC＝CB，符合两直角三角形全等的判定定理HL，能推出△ABC≌△DCB，故本选项不符合题意；C．AB＝DC，∠ABC＝∠DCB，BC＝CB，符合全等三角形的判定定理SAS，能推出△ABC≌△DCB，故本选不项符合题意；D．AB＝DC，BC＝CB，∠ACB＝∠DBC，不符合全等三角形的判定定理，不能推出△ABC≌△DCB，故本选项符合题意；故选：D．【点评】本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL．4．（3分）已知△ABC的三条边分别为a、b、c，三个内角分别为∠A、∠B、∠C，则满足下列条件的△ABC不是直角三角形的是（）A．a＝6，b＝8，c＝10B．a2﹣c2＝b2C．∠A＝2∠B＝3∠C D．∠A﹣∠B＝∠C【分析】根据勾股定理的逆定理以及三角形内角和定理逐一判断即可．【解答】解：A、∵202＝62+82，∴a2+b2＝c2，∴△ABC是直角三角形，不符合题意；B、∵a2﹣c2＝b2，∴a2＝b2+c2，∴△ABC是直角三角形，不符合题意；C、设∠A＝x°，则∠B＝（）°，∠C＝（）°，则x++＝180，∴x＝，即∠A＝（）°，∴△ABC不是直角三角形，符合题意；D、∵∠A﹣∠B＝∠C，∠A+∠B+∠C＝180°，∴∠A＝90°，∴△ABC是直角三角形，符合题意．故选：C．【点评】本题考查了勾股定理的逆定理以及三角形内角和定理，熟练掌握勾股定理的逆定理以及三角形内角和定理是解题的关键．5．（3分）下列命题：①到线段两端距离相等的点在线段的垂直平分线上；②角是轴对称图形，对称轴是角平分线；③有两个内角相等的三角形是等腰三角形；④两边分别相等且其中一边的对角也相等的两个三角形全等；其中真命题的个数为（）A．1B．2C．3D．4【分析】利用线段的垂直平分线的判定方法、角的对称性、等腰三角形的定义、全等三角形等知识点逐项判断即可．灵活运用相关定义是解题的关键．【解答】解：①到线段两端距离相等的点在线段的垂直平分线上，正确，是真命题，符合题意；②角是轴对称图形，对称轴是角平分线所在的直线，故原命题错误，是假命题，不符合题意；③有两个内角相等的三角形是等腰三角形，正确，是真命题，符合题意；④两边分别相等且其夹角也相等的两个三角形全等，故原命题错误，是假命题，不符合题意．综上，真命题有2个．故选：B．【点评】本题考查命题与定理，全等三角形的判定，线段垂直平分线的性质，等腰三角形的性质，轴对称图形，灵活运用相关定义是解题的关键．6．（3分）如图，在△ABC中，∠C＝90°，AC＝4，DC＝AD，BD平分∠ABC，则点D到AB的距离等于（）A．1B．C．2D．【分析】点D到AB的距离，指的是过点D作AB的垂线段DE的长度，根据角平分线的性质，可以得到DE＝CD，利用AC＝4，DC＝AD，可以求出线段CD的长度，问题即可解决．【解答】解：如图，过D作DE⊥AB于E，∵∠C＝90°，∴CD⊥BC，∵BD平分∠ABC，CD⊥BC，DE⊥AB，∴DE＝CD，∵CD＝，AC＝4，∴，∴，故选：B．【点评】本题考查了角平分线的性质，点D到AB的距离指的是过点D作AB的垂线段的长度，是解决此题的突破口．7．（3分）在△ABC中，AC＝3，△ABC的周长为12，设AB的长为x，下列说法不正确的是（）A．△ABC为等腰三角形时，x＝4.5B．△ABC不可能是等边三角形C．△ABC为直角三角形时，x＝4D．3＜x＜6【分析】根据等腰三角形、等边三角形、直角三角形的定义以及三角形的三边关系分析解答即可．【解答】解：A、当AB＝BC＝4.5，即x＝4.5时，△ABC是等腰三角形，说法正确，故选项不符合题意；B、周长为12的等边三角形，边长为4，而AC＝3，故△ABC不可能是等边三角形，说法正确，故选项不符合题意；C、△ABC是直角三角形时，根据勾股定理的逆定理可知AC＝3，AB＝x＝4时，BC＝5或AC＝3，AB＝x＝5，BC＝4都可以，原说法错误，故选项符合题意；D、根据三角形的三边关系可知3＜x＜6，说法正确，故选项不符合题意．故选：C．【点评】本题考查了等腰三角形、等边三角形、直角三角形的定义以及三角形的三边，解题的关键是熟练掌握各种三角形的判定方法．8．（3分）如图，在等边三角形ABC中，在AC边上取两点M、N，使∠MBN＝30°．若AM＝m，MN＝x，CN＝n，则以x，m，n为边长的三角形的形状为（）A．锐角三角形B．直角三角形C．钝角三角形D．随x，m，n的值而定【分析】将△ABM绕点B顺时针旋转60°得到△CBH．连接HN．想办法证明∠HCN＝120°，HN＝MN＝x即可解决问题；【解答】解：将△ABM绕点B顺时针旋转60°得到△CBH．连接HN．∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠A＝60°，∵∠MBN＝30°，∴∠ABM+∠CBN＝30°，∴∠NBH＝∠CBH+∠CBN＝30°，∴∠NBM＝∠NBH，∵BM＝BH，BN＝BN，∴△NBM≌△NBH，∴MN＝NH＝x，∵∠BCH＝∠A＝60°，CH＝AM＝m，∴∠NCH＝120°，∴x，m，n为边长的三角形△NCH是钝角三角形，故选：C．【点评】本题考查等边三角形的性质、全等三角形的判定和性质、旋转变换等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题，属于中考常考题型．9．（3分）如图，△ABC中∠C＝90°，AB＝10，AC＝8，BC＝6，线段DE的两个端点D、E分别在边AC，BC上滑动，且DE＝4，若点M、N分别是DE、AB的中点，则MN的最小值为（）A．2B．3C．3.5D．4【分析】根据三角形斜边中线的性质求得CN＝AB＝5，CM＝＝2，由当C、M、N在同一直线上时，MN取最小值，即可求得MN的最小值为3．【解答】解：如图，连接CM、CN，△ABC中，∠C＝90°，AB＝10，AC＝8，BC＝6，∵DE＝4，点M、N分别是DE、AB的中点，∴CN＝AB＝5，CM＝DE＝2，当C、M、N在同一直线上时，MN取最小值，∴MN的最小值为：5﹣2＝3．故选：B．【点评】本题考查了直角三角形斜边中线的性质，明确C、M、N在同一直线上时，MN取最小值是解题的关键．10．（3分）直三棱柱的表面展开图如图所示，AC＝3，BC＝4，AB＝5，四边形AMNB是正方形，将其折叠成直三棱柱后，下列各点中，与点C距离最大的是（）A．点M B．点N C．点P D．点Q【分析】根据直三棱柱的特征结合勾股定理求出各线段的距离，再比较大小即可求解．【解答】解：∵AC＝3，BC＝4，AB＝5，四边形AMNB是正方形，立方体是直三棱柱，∴CQ＝5，∴折叠成直三棱柱后CM＝＝，折叠成直三棱柱后CP＝＝，折叠成直三棱柱后CN＝＝，∵＞＞5，∴与点C距离最大的是点N．故选：B．【点评】本题考查了勾股定理，勾股定理的逆定理，展开图折叠成几何体，关键是求出各线段的距离．二、填空题（本大题共8小题，每小题3分，共24分）11．（3分）等腰三角形两边长分别是3和6，则该三角形的周长为　15　．【分析】由三角形的三边关系可知，其两边之和大于第三边，两边之差小于第三边．【解答】解：由三角形的三边关系可知，由于等腰三角形两边长分别是3和6，所以其另一边只能是6，故其周长为6+6+3＝15．故答案为15．【点评】本题主要考查了三角形的三边关系问题，能够利用三角形的三边关系求解一些简单的计算、证明问题．12．（3分）如图，在△ABE中，AE的垂直平分线MN交BE于点C，连接AC．若AB＝AC，CE＝5，BC＝6，则△ABC的周长等于　16　．【分析】根据线段垂直平分线得到AC＝CE＝5，直接根据周长公式计算即可．【解答】解：∵MN垂直平分AE，∴AC＝CE＝5，∴AB＝AC＝5，又∵BC＝6，∴△ABC的周长＝AB+AC+BC＝5+5+6＝16，故答案为：16．【点评】此题考查线段垂直平分线的性质，熟记线段垂直平分线上的点到这条线段两个端点的距离相等是解题的关键．13．（3分）如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG＝CD，DF＝DE，则∠E＝　15　度．【分析】根据等边三角形三个角相等，可知∠ACB＝60°，根据等腰三角形底角相等即可得出∠E的度数．【解答】解：∵△ABC是等边三角形，∴∠ACB＝60°，∠ACD＝120°，∵CG＝CD，∴∠CDG＝30°，∠FDE＝150°，∵DF＝DE，∴∠E＝15°．故答案为：15．【点评】本题考查了等边三角形的性质，互补两角和为180°以及等腰三角形的性质，难度适中．14．（3分）如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，若∠A＝∠ABE，AC＝10，BC＝6，则BD的长为　2　．【分析】由已知条件判定△BEC的等腰三角形，且BC＝CE；由等角对等边判定AE＝BE，则易求BD＝2．【解答】解：如图，∵CD平分∠ACB，BE⊥CD，则∠BCD＝∠ECD，∠BDC＝∠EDC＝90°，在△BCD和△ECD中，，∴△BCD≌△ECD（ASA），∴BC＝CE．又∵∠A＝∠ABE，∴AE＝BE．∴．∵AC＝10，BC＝6，∴，故答案是：2．【点评】本题考查了等腰三角形的判定与性质，全等三角形的判定及性质，熟悉相关性质是解题的关键．15．（3分）小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m，∠BOC＝90°．爸爸在C处接住小丽时，小丽距离地面的高度是　1.4m　．【分析】由直角三角形的性质得出∠COE＝∠OBD，根据AAS可证明△COE≌△OBD，由全等三角形的性质得出CE＝OD、OE＝BD，求出DE的长即可解答．【解答】解：由题意可知：∠CEO＝∠BDO＝90°，OB＝OC，∵∠BOC＝90°，∴∠COE+∠BOD＝∠BOD+∠OBD＝90°．∴∠COE＝∠OBD，在△COE和△OBD中，，∴△COE≌△OBD（AAS），∴CE＝OD，OE＝BD，∵BD、CE分别为1.4m和1.8m，∴DE＝OD﹣OE＝CE﹣BD＝1.8﹣1.4＝0.4（m），∵AD＝1m，∴AE＝AD+DE＝1+0.4＝1.4（m）．故答案为：1.4m．【点评】本题考查勾股定理的应用，全等三角形的判定和性质，证明△COE≌△OBD（AAS）是解题的关键．16．（3分）机场入口处的铭牌上说明，飞机行李架是一个50cm×40cm×20cm的长方体空间，有位旅客想购买一件画卷随身携带，现有4种长度的画卷①38cm；②40cm；③60cm；④68cm，请问这位旅客可以购买的尺寸是　①②③　．（填写序号）【分析】先根据勾股定理求得长方体的体对角线的长度，然后与画卷的长度进行比较即可解答．【解答】解：如图，连接AC，CE．由题意知：AD＝20cm，CD＝50cm，AE＝40cm．在直角△ACD中，由勾股定理知：AC2＝AD2+CD2＝202+502．在直角△ACE中，CE2＝AE2+AC2．∴CE2＝402+202+502＝4500．因为382＝1444＜4500，402＝1600＜4500，602＝3600＜4500，682＝4624＞4500，所以这位旅客可以购买的尺寸是①②③．故答案为：①②③．【点评】本题考查勾股定理，求得长方体的体对角线的长度是解题的关键．17．（3分）如图，以AB为斜边的Rt△ABC的每条边为边作三个正方形，分别是正方形ABMN，正方形BCPQ，正方形ACEF，且边EF恰好经过点N．若S3＝S4＝6，则S1+S5＝　6　．（注：图中所示面积S表示相应封闭区域的面积，如S3表示△ABC的面积）【分析】如图，连接MQ，作MG⊥EC于G，设PC交BM于T，MN交EC于W．证明△ABC≌△MBQ（SAS），推出∠ACB＝∠BQM＝90°，由∠PQB＝90°，推出M，P，Q共线，由四边形CGMP 是矩形，推出MG＝PC＝BC，证明△MGW≌△BCT（AAS），推出MW＝BT，由MN＝BM，NW＝MT，可证△NWE≌MTP，推出S1+S5＝S3＝6，【解答】解：如图，连接MQ，作MG⊥EC于G，设PC交BM于T，MN交EC于W．∵∠ABM＝∠CBQ＝90°，∴∠ABC＝∠MBQ，∵BA＝BM，BC＝BQ，∴△ABC≌△MBQ（SAS），∴∠ACB＝∠BQM＝90°，∵∠PQB＝90°，∴M，P，Q共线，∵四边形CGMP是矩形，∴MG＝PC＝BC，∵∠BCT＝∠MGB＝90°，∠BTC+∠CBT＝90°，∠BQM+∠CBT＝90°，∴∠MQG＝∠BTC，∴△MGW≌△BCT（AAS），∴MW＝BT，∵MN＝BM，∴NW＝MT，可证△NWE≌MTP，∴S1+S5＝S3＝6，解法二：∵AC2+BC2＝AB2，∴S1+S2+S左空+S右空+S5＝S3+S4+S左空+S右空，∴S1+S5＝S4＝6故答案为6．【点评】本题考查勾股定理的知识，有一定难度，解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用．18．（3分）如图，△ABC中，AB＝AC，∠A＝30°，射线CP从射线CA开始绕点C逆时针旋转α角（0°＜α＜75°），与射线AB相交于点D，将△ACD沿射线CP翻折至△A′CD处，射线CA′与射线AB相交于点E．若△A′DE是等腰三角形，则∠α的度数为　22.5°或67.5°或45°　．【分析】根据折叠的性质可得：∠ACD＝∠A′CD＝α＝∠ACA′，∠A＝∠DA′C＝30°，然后分三种情况：当A′D＝A′E时；当DA′＝DE时；当ED＝EA′时；分别进行计算即可解答．【解答】解：由折叠得：∠ACD＝∠A′CD＝α＝∠ACA′，∠A＝∠DA′C＝30°，分三种情况：当A′D＝A′E时，如图：∴∠A′DE＝∠A′ED＝（180°﹣∠A′）＝75°，∵∠A′ED是△ACE的一个外角，∴∠ACE＝∠A′ED﹣∠A＝45°，∴∠ACD＝∠A′CD＝α＝∠ACE＝22.5°；当A′D＝A′E时，当△ADC和△A′DC位于射线AB的同侧时，如图：∴∠A′DE＝∠A′ED＝∠CA′D＝15°，∴∠ACA′＝180°﹣∠A﹣∠A′EA＝135°，∴∠ACD＝∠A′CD＝α＝∠ACA′＝67.5°；当DA′＝DE时，∴∠A′＝∠DEA′＝30°，∵∠DEA′是△ACE的一个外角，∴∠DEA′＞30°，∴此种情况不成立；当ED＝EA′时，如图：∴∠EDA′＝∠A′＝30°，∴∠DEA′＝180°﹣∠EDA′﹣∠A′＝120°，∵∠A′ED是△ACE的一个外角，∴∠ACE＝∠A′ED﹣∠A＝90°，∴∠ACD＝∠A′CD＝α＝∠ACE＝45°；综上所述：若△A′DE是等腰三角形，则∠α的度数为22.5°或67.5°或45°，故答案为：22.5°或67.5°或45°．【点评】本题考查了旋转的性质，等腰三角形的性质，翻折变换（折叠问题），分三种情况讨论是解题的关键．三、解答题（本大题共7小题，共66分）19．（8分）如图，点C、E、F、B在同一直线上，AB∥CD，AE＝DF，∠AEB＝∠DFC．（1）求证：△ABE≌△DCF；（2）若∠A＝55°，∠C＝30°，求∠BFD的度数．【分析】（1）利用平行线的性质得∠B＝∠C，再利用AAS证明△ABE≌△DCF；（2）利用全等三角形的性质得∠D＝∠A＝45°，再利用三角形外角的性质可得答案．【解答】（1）证明：∵AB∥CD，∴∠B＝∠C，在△ABE和△DCF中，，∴△ABE≌△DCF（AAS）；（2）解：∵△ABE≌△DCF，∴∠D＝∠A＝55°，∴∠BFD＝∠C+∠D＝30°+55°＝85°．【点评】本题主要考查了全等三角形的判定与性质，平行线的性质，三角形外角的性质等知识，证明△ABE≌△DCF是解题的关键．20．（8分）如图，是由小正方形组成的6×8网格，每个小正方形的顶点叫做格点，A、B、C三点是格点，仅用无刻度的直尺在给定网格中根据要求完成画图．（1）在图1中，画出△ABC关于直线l对称的图形△DEF；△ABC的面积为　4　；（2）在图2中，画出∠ABC的角平分线．【分析】（1）根据轴对称的性质确定A，B，C的对应点D，E，F，然后再顺次连接即可，再运用割补法求△ABC的面积即可；（2）先构造等腰直角三角形，再根据等腰三角形三线合一的性质作图即可．【解答】解：（1）如图1：△DEF即为所求．△ABC的面积为．（2）如图2：线段BD即为所求．．【点评】本题主要考查了作图﹣轴对称变换，三角形的面积，等腰三角形的性质，掌握等腰三角形三线合一的性质是解题的关键．21．（8分）某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量∠B＝90°，AB＝3m，BC＝4m，CD＝12m，AD＝13m．若每平方米草皮需要200元，问学校需要投入多少资金买草皮？【分析】直接利用勾股定理的逆定理得出∠ACD＝90°，再利用直角三角形的性质得出答案．【解答】解：连接AC∵∠B＝90°，AB＝3m，BC＝4m，BC＝12m，AC2＝AB2+BC2＝32+42＝25，则AC＝5m，∴AC2+CD2＝25+144＝169＝132又∵AD2＝132，∴AC2+CD2＝CD2∴∠ACD＝90°，∴△ACD是直角三角形，∴四边形ABCD的面积＝6+30＝36（m2），∴学校要投入资金为：200×36＝7200（元）；答：学校需要投入7200元买草皮．【点评】此题主要考查了勾股定理以及勾股定理的逆定理，正确得出△ACD是直角三角形是解题关键．22．（10分）已知△ABC中，AB＝AC．（1）如图1，在△ADE中，若AD＝AE，且∠DAE＝∠BAC，求证：CD＝BE；（2）如图2，在△ADE中，若∠DAE＝∠BAC＝60°，且CD垂直平分AE，AD＝3，CD＝4，求BD 的长．【分析】（1）由角的和差可得∠DAC＝∠BAE，进而证得△ACD≌△ABE，再根据全等三角形的性质即可证明结论；（2）如图2：连接BE，由垂直平分线的性质可得AD＝DE，进而得到△ADE是等边三角形，即；再运用全等三角形的性质可得BE＝CD＝4，∠BEA＝∠CDA＝30°，最后运用勾股定理即可解答．【解答】（1）证明：∵∠DAE＝∠BAC，∴∠DAE+∠CAE＝∠BAC+∠CAE，即∠DAC＝∠BAE．在△ACD与△ABE中，，∴△ACD≌△ABE（SAS），∴CD＝BE．（2）解：如图2：连接BE，∵CD垂直平分AE∴AD＝DE，∵∠DAE＝60°，∴△ADE是等边三角形，∴，∵△ABE≌△ACD，∴BE＝CD＝4，∠BEA＝∠CDA＝30°，∴BE⊥DE，DE＝AD＝3，∴．【点评】本题主要考查了全等三角形的判定与性质、等边三角形的判定与性质、垂直平分线的性质、勾股定理等知识点，掌握全等三角形的判定与性质是解题的关键．23．（10分）如图：在Rt△ABC中，∠ACB＝90°，AB＝5cm，AC＝3cm，动点P从B出发沿射线BC 以2cm/s的速度运动，设运动时间为t秒．（1）当t＝　1　时，AP平分△ABC的面积．（2）当△ABP为等腰三角形时，求t的值．（3）若点E、F分别为BC、AB上的动点，请直接写出AE+EF的最小值．【分析】（1）先由勾股定理可得BC的长，当AP是中线时，AP平分△ABC的面积，即2t＝2，可得结论；（2）当△ABP为等腰三角形时，存在三种情况：AP＝BP或AB＝AP或AB＝BP，根据BP＝2t和等量关系列方程可解答；（3）如图4中，如图4，延长AC至A'，连接BA'，过点A作AF'⊥A'B于F'，在AB上取BF＝BF'，根据对称可知：AE+EF的最小值就是AF'的长，根据面积法可得结论．【解答】解：（1）∵∠ACB＝90°，AB＝5，AC＝3，∴BC＝＝＝4，当BP＝CP时，AP平分△ABC的面积，即BP＝2t＝2，∴t＝1，则当t＝1时，AP平分△ABC的面积；故答案为：1；（2）分三种情况：①如图1，AP＝PB，由题意得：AP＝BP＝2t，∴CP＝4﹣2t，由勾股定理得：AP2＝AC2+PC2，∴（2t）2＝32+（4﹣2t）2，∴t＝；②如图2，AB＝BP＝5，∴2t＝5，∴t＝；③如图3，AB＝AP，∵∠ACB＝90°，∴AC⊥BP，∴BP＝2BC＝8，∴2t＝8，∴t＝4；综上所述，当△ABP为等腰三角形时，t的值是或或4；（3）如图4，延长AC至A'，连接BA'，过点A作AF'⊥A'B于F'，在AB上取BF＝BF'，则AB与A'B关于BC对称，∴EF＝EF'，∴AE+EF＝AE+EF'＝AF'，即此时AE+EF的值最小，且最小值是AF'的长，∵AC＝A'C＝3，AB＝A'B＝5，∴△ABA'的面积＝×6×4＝×5AF'，∴AF'＝，∴AE+EF的最小值是．【点评】本题考查三角形的综合题，考查了等腰三角形的性质和判定，轴对称的性质，三角形中线的性质，垂线段最短，勾股定理等知识，解题的关键是学会利用对称把问题转化为垂线段最短，属于中考常考题型．24．（12分）【了解概念】如图1，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连接CE，连接BD并延长与CE交于点F，那么将∠BFC叫做△ABC和△ADE的底联角．【探究归纳】（1）两个等腰三角形的底联角与这两个等腰三角形的顶角有怎样的数量关系？请用文字语言写出结论．【拓展提升】运用（1）中的结论解决问题：（2）如图2，AB＝AC，AD＝AE，∠BAC＝DAE＝90°，∠DCE＝62°，求∠BDC的度数；（3）如图3，在四边形ABCD中，AB＝6，BC＝4，CD＝5，点O为四边形ABCD内一点．且OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，求AD的长．【分析】（1）由题中的条件结合图1可知，两个等腰三角形的底联角等于这两个等腰三角形的顶角，说明理由的方法是，先证明△BAD≌△CAE，推得∠ADB＝∠AEC，再由∠DAE+∠DFE＝180°，∠BFC+∠DFE＝180°得∠BFC＝∠DAE＝∠BAC；（2）当点D在△ABC的内部时，延长BD交CE于点F，由（1）中的结论直接推得∠BFC＝∠DAE＝90°，再由三角形的外角等于与它不相邻的两个内角的和求出∠BDC的度数；当点D在△ABC的外部时，设BD交CE于点F，交AC于点G，先证明△BAD≌△CAE，得∠ABD＝∠ACE，则∠ACE+∠CGD＝∠ABD+∠AGB＝90°，由此推得∠AFC＝90°，再由三角形的外角等于与它不相邻的两个内角的和求出∠BDC的度数；（3）连接AC、BD交于点F，则∠BFC＝∠AFB＝∠AFD＝∠CFD＝90°，由勾股定理可推得AD2+BC2＝AB2+CD2＝FA2+FB2+FC2+FD2，则AD2+42＝62+52，可求出AD长．【解答】解：（1）两个等腰三角形的底联角等于这两个等腰三角形的顶角．理由：如图1，∵∠BAC＝∠DAE，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴∠ADB＝∠AEC，∴∠ADF+∠AEC＝∠ADF+∠ADB＝180°，∴∠DAE+∠DFE＝180°，∵∠BFC+∠DFE＝180°，∴∠BFC＝∠DAE＝∠BAC．（2）当点D在△ABC的内部时，如图2甲，延长BD交CE于点F，∵AB＝AC，AD＝AE，∠BAC＝DAE＝90°，∴∠BFC＝∠DAE＝90°，∵∠DCE＝62°，∴∠BDC＝∠BFC+∠DCE＝90°+62°＝152°；当点D在△ABC的外部时，如图2乙，BD交CE于点F，交AC于点G，∵∠BAC＝DAE＝90°，∴∠BAD＝∠CAE＝90°+∠CAD，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴∠ABD＝∠ACE，∵∠CGD＝∠AGB，∴∠ACE+∠CGD＝∠ABD+∠AGB＝90°，∴∠BFC＝90°，∴∠BDC＝∠BFC﹣∠DCE＝90°﹣62°＝28°，综上所述，∠BDC＝152°或∠BDC＝28°.（3）如图3，连接AC、BD交于点F，∵OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，∴∠BFC＝∠COD＝90°，∴∠AFB＝∠AFD＝∠CFD＝90°，∴AD2＝FA2+FD2，BC2＝FB2+FC2，AB2＝FA2+FB2，CD2＝FC2+FD2，∴AD2+BC2＝AB2+CD2＝FA2+FB2+FC2+FD2，∵AB＝6，BC＝4，CD＝5，∴AD2+42＝62+52，∴AD＝3，∴AD的长为3．【点评】此题重点考查等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理及其推论、勾股定理、新定义问题的求解等知识与方法，解题的关键是通过作辅助线创造条件，用在一般情况下得出的结论解决特殊情况下的问题．25．（10分）课堂上学习了勾股定理后知道：直角三角形三边长是整数时我们称之为“勾股数”．王老师给出一组数让学生观察：3、4、5；5、12、13；7、24、25；9、40、41；…，学生发现这些勾股数的勾都是奇数，且从3起就没有间断过，于是王老师提出以下问题让学生解决．若两直角边为a，b（a＜b），斜边为c．（1）请你根据上述的规律写出下一组勾股数：11、　60　、　61　；（2）当a＝n（n为奇数，且n≥3）时，若b＝，c＝时可以构造出勾股数（用含n的代数式表示）；并证明你的猜想；（3）当a＝n（n为偶数，且n＞4）时，若b＝，c＝　；　时可以构造出勾股数（用含n的代数式表示）；（4）构造勾股数的方法很多，请你寻找当a＝20时，c＝　25或52或101或29　．【分析】（1）分析所给四组的勾股数：3、4、5；5、12、13；7、24、25；9、40、41；可得下一组一组勾股数：11，60，61；（2）根据所提供的例子发现股是勾的平方减去1的二分之一，弦是勾的平方加1的二分之一可得b、c，然后计算验证即可；（3）根据所提供的例子发现股是勾的平方的四分之一减一，弦是勾的平方的四分之一加一可得b、c，然后计算验证即可；（4）由勾股定理可得：a2+b2＝c2，再根据勾股定理可得（c﹣b）（c+b）＝400；然后根据列举法即可解答．【解答】解：（1）∵3、4、5；5、12、13；7、24、25；9、40、41；…，∴11，60，61；故答案为：60，61．（2）观察发现：当a＝n（n为奇数，且n≥3）时，则股是勾的平方减去1的二分之一，弦是勾的平方加1的二分之一；则用含n的代数式表示每组第二个数和第三个数分别为：；证明如下：∵，∴，又∵n为奇数，且n≥3，∴n，三个数组成的数是勾股数．（3）观察发现：当a＝n（n为偶数，且n≥5）时，则股是勾的平方的四分之一减一，弦是勾的平方。

六年级数学专题思维训练—立体几何(含答案及解析)

六年级数学专题思维训练—立体几何1、下面四个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是______________．（填序号）2、如下图所示，棱长分别为1厘米、2厘米、3厘米的三个正方体紧贴在一起，则所得到的立体图形的表面积是平方厘米．3、下图是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形，问这个直三棱柱的体积是多少？4、有一个足够深的水槽，底面是长为16厘米、宽为12厘米的长方形，原本在水槽里盛有6厘米深的水和6厘米深的油（油在水的上方）．在水槽中放人一个长、宽、高分别为8厘米、8厘米、12厘米的铁块，那么此时油层的层高是厘米。

5、圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是立方厘米。

（结果用兀表示）6、如下图所示，从正方形ABCD 上截去长方形DEFG ，其中AB=1厘米，DE=21厘米， DG=31厘米，将ABCGFE 以GC 边为轴旋转一周，所得几何体的表面积是平方厘米，体积是 _____________ 立方厘米。

（结果用兀表示）7、若长方体的三个侧面的面积分别是6，8，12，则长方体的体积是。

8、一个圆柱和一个圆锥（如下图所示），它们的高和底面直径都标在图上，单位是厘米。

请回答：圆锥体积与圆柱体积的比是多少？9、如下图所示，一个圆柱体形状的木棒，沿着底面直径竖直切成两部分，已知这两部分的表面积之和比圆柱体的表面积大2008平方厘米，则这个圆柱体木棒的侧面积是平方厘米。

（兀取3. 14）10、两个同样材料做成的球A 和B ，一个实心，一个空心。

A 的直径为7、重量为22，B 的直径为10.6、重量为33.3。

问：哪个球是实心球？（球的体积公式V=34πr ³）11、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成，尺寸如下图所示．问：该油罐车的容积是多少立方米？（兀=3. 1416）（球的体积公式V=34πr ³）12、某工厂原用长4米，宽1米的铁皮围成无底无顶的的正方体形状的围栏，现要将围栏容量增加27%，问：能否还用原来的铁皮围成？13、一个正方体的纸盒中，恰好能放人一个体积为6. 28立方厘米的圆柱体，纸盒的容积有多大？（兀=3. 14）．14、用若干个小正方体拼成下图所示的造型．其中有一个小孔分别由左至右、由上至下以及由前至后穿透整个造型．拼成此造型共需使用多少个小正方体？15、一个圆锥形容器甲与一个半球形容器乙，它们圆形口的直径与容器的高的尺寸如下图所示，若用甲容器取水来注满乙容器，问：至少要注水多少次？（球的体积公式：V=34πr ³）16、下图是一个直圆柱形状的玻璃杯，一个长为12厘米的直棒状细吸管（不考虑吸管粗细）放在玻璃杯内，当吸管一端接触圆柱下底面时，另一端沿吸管最少可露出上底面边缘2厘米，最多能露出4厘米．则这个玻璃杯的容积为立方厘米．（取兀=3. 14）17、威力集团生产的某种洗衣机的外形是长方体，装衣物部分是圆柱形的桶，直径40厘米，深36厘米，已知该洗衣机装衣物的空间占洗衣机体积的25% ，长方体外形的长为52厘米，宽50厘米．问：高是多少厘米？（兀取3. 14，结果保留整数）18、有两个高度一样的水瓶，瓶子的底部被钉子分别戳了一个同样大的小洞．粗瓶子的水12分钟可以漏完，细瓶子的水8分钟可以漏完．若两个瓶子同时漏水，过了一段时间后，粗瓶子中水的高度是细瓶子中的2倍．这两个瓶子同时漏了分钟．19、世界上最早的灯塔建于公元270年，塔分三层，如下图所示，每层都高27米，底座呈正四棱柱，中间呈正八棱柱，上部呈正圆锥．上部的体积是底座的体积的。

人教版八年级数学上册期末素养综合测试(二)课件

∴△ADE≌△BCF(SAS),∴∠ADE=∠BCF,
∵∠CGE=∠ADE+∠BCF=94°,
∴∠GCD= 1 ∠CGE=47°.
2
16.(2022山东临沂期末)有两个正方形A、B,现将B放在A的内部得图甲,将A、B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和10,则正方形A、B 的面积之和为 11 .
∴AB的长度可能是3.5.故选C.
7.如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作 DE⊥BC于点E,且CE=1.5,则AB的长为 ( C )
A.3
B.4.5
C.6
D.7.5
解析 ∵△ABC是等边三角形,∴∠ABC=∠C=60°,AB=BC= AC,∵DE⊥BC,∴∠CDE=30°,∵CE=1.5,∴CD=2CE=3,∵BD 平分∠ABC,∴AD=CD=3,∴AB=AC=AD+CD=6.
解析如图,在BC上取一点E',使得BE'=BE,连接FE',过点A作 AH⊥BC于H.
在Rt△ACH中,∵∠AHC=90°,∠C=30°,AC=24, ∴AH= 1 AC=12,
2
∵BD平分∠ABC,∴∠FBE=∠FBE',
∵BE=BE',BF=BF,∴△FBE≌△FBE'(SAS), ∴FE=FE',∴AF+FE=AF+FE', 根据垂线段最短可知,当A,F,E'三点共线,且与AH重合时,AF+ FE的值最小,最小值为12.
值:
x
1÷
1
1,其中x2xx=223x.1
1
解析原式=1 ·x 1 2分(x 1)2
x 1 (x 1)(x 1)

(2021年整理)五年级奥数.几何.展开图与空间想象(A级).教师版

五年级奥数.几何.展开图与空间想象(A级).教师版(推荐完整)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（五年级奥数.几何.展开图与空间想象(A级).教师版(推荐完整)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为五年级奥数.几何.展开图与空间想象(A级).教师版(推荐完整)的全部内容。

五年级奥数。

几何.展开图与空间想象（A级).教师版(推荐完整) 编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望五年级奥数。

几何.展开图与空间想象（A级).教师版（推荐完整）这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力.本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈五年级奥数.几何.展开图与空间想象(A级)。

教师版(推荐完整）> 这篇文档的全部内容。

展开图与空间想象知识框架重难点例题精讲【例 1】数一数下图中有多少个正方体木块？【考点】长方体与正方体【难度】☆【题型】解答【解析】从下到上各层分别有3个、3个、1个，因此共有3+3+1=7个方块．【答案】7【巩固】右图中共有多少个面？多少条棱？左面【考点】长方体与正方体【难度】☆【题型】解答【解析】如右图所示，可以分前、后、左、右、上、下六个方向看这个立体图形．前、后看各有1个面，左面看有1个面，右面看有2个面，上面看有2个面，下面看有1个面．所以共有1112218+++++=（个）面．前后方向的棱有6条，左右方向的棱有6条，上下方向的棱也有6条，所以共有棱66618++=(条）．【答案】8个面，18条棱【例 2】如图从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形，然后，沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米？【考点】长方体与正方体【难度】☆☆【题型】解答【解析】容器的底面积是(134)(94)45-⨯-=(平方厘米），高为2厘米，所以容器的体积是，45290⨯=(立方厘米)．【答案】90【巩固】沿图4的虚线折叠，可以围成一个长方体，它的体积是立方厘米。

第4讲直棱柱

第4讲直棱柱一、内容提要1. 了解直棱柱, 会画直棱柱的三视图,会判断简单物体(直棱柱形状)的三视图,能根据三视图描述直棱柱或实物原型(直棱柱形状).2. 了解直棱柱的表面展开图, 能根据展开图判断和制作立体模型.3. 初步了解直棱柱与其三视图、展开图之间的关系；通过典型实例,知道这种关系在现实生活中的应用(如物体的包装).二. 热身练习[A]组题1．下列几何体中，不属于多面体的是（）A．立方体 B ．三棱柱C ．长方体D ．球 2．如图1,下列多面体中,直棱柱的个数是…（）A.6个B.4个C.3个D.2个3．下面各个图形是由6个大小相同的正方形组成的，其中能沿正方形的边折叠成一个正方体的是（）4．下面图形中是正方体平面展开图的是（）图图1A ．B ．C ．D ．5．下面简单几何体的左视图是（）6．一物体的主视图是长方形,则该物体不可能是（）A. 圆柱体B. 长方体C. 三棱锥D. 直棱柱 7．如图是一些立体图形的三视图，请根据视图说出这些立体图形的名称：(1)(2)名称：名称：8．如图2是某品牌牙膏的软包装盒，其尺寸如图所标（单位：cm ），请画出这种包装盒的表面展开图，并计算这个包装盒的表面积．三. 例题分析例1、一个直棱柱有12个顶点,它是几棱柱?有多少条棱?多少个面?例2、把图1折成正方体后，如果相对面所对应的值相等，那么x 的平方根与y 的算术平方根之积为．A ．B ．C ．D ．A ．B ．C ．D ．正面图12145图2例3、如图3是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数．请画出这个几何体的主视图、左视图.★★例4、已知一个几何体的三视图如图4所示，描述该几何体的形状，并根据图中数据计算它的表面积．(结果精确到1cm 2)★★例5、如图，长方体的长为15cm ，宽为10cm ，高为20cm ，点B 在棱CD 上，CB=5cm. 一只壁虎要沿长方休的表面从A 点爬到B 点，需要爬行的最短路径是多少cm?四. 思维提升 [B]组题1．下列实物的形状中，是直棱柱的是（）A. B. C. D.2．直棱柱的棱数,一定是下列某自然数的倍数（）A.2B.3C.5D.73．如图1所示，八棱柱模型的底面边长都是4cm ，侧棱长为4cm ．下列说法，错误的是（）A ．每个面都是正方形B ．侧面积为128cm 2C ．共有16个顶点D ．共有24条棱32211图3图 5图14．一个直三棱柱(如图4甲)顺着侧棱的方向切一刀,可以得到一个直三棱柱和一个直四棱柱(如图4乙).(1) 对图3甲用同样的方法切一刀, 能否得到两个直三棱柱?如何切?(2) 一个直四棱柱用同样的方法切一刀,得到一个直n 棱柱和一个直m 棱柱, 写出m , n 所有可能的值.5．如图6是一个食品包装盒的侧面展开图.(1) 请写出这个包装盒的多面体形状的名称；(2) 请根据图中所标的尺寸，计算这个多面体的侧面积.7．图7表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主视图为（）★★8。

【2022】南京中考数学(含解析)

2022南京中考数学一、选择题（本大题共6小题，每小题2分，共12分）1. -3的相反数是（）A . 3B . -3C . 13D . 13-2. 计算()32a （）A . 5aB . 6aC . 7aD . 8a3. 估计12的算是平方根介于（）A . 1和2之间B . 2和3之间C . 3和4之间D . 4和5之间4. 反比例函数2k y x=（k 为常数，0k ≠）的图像位于（）A . 第一、三象限B . 第二、四象限C . 第一、二象限D . 第三、四象限5. 已知实数a,b ，a >b ，下列结论中一定正确的是（） A . a b > B . 11a b> C . 22a b > D . 33a b >6. 直三棱柱的表面展开图如图所示，AC =3，BC =4，AB =5，四边形AMNB 是正方形，将其折叠成直三棱柱后，下列各点中，与点C 距离最大的是（）A . 点MB . 点NC . 点PD . 点Q二、填空题（本大题共10小题，每小题2分，共20分）7. 地球与月亮的平均距离约为384000km ，用科学记数法表示384000是____________. 8. 若式子23x -再实数范围内有意义，则x 的取值范围是_________. 9.___________. 10. 方程2430x x -+=的解是__________.11. 如图，平行四边形ABCD 的顶点A ，C 分别在直线1l ，2l 上，1l ∥2l ，若∠1=33°，∠B =65°，则∠2=_______°.12. 若44222a +=，5553333b ++=，则a +b =_______.13. 已知二次函数22y ax ax c =-+（a ，c 为常数，0a ≠）的最大值为2，写出一组符合条件的a 和c 的值：______________.14. 在平面直角坐标系中，正方形ABCD 如图所示，点A 的坐标是（-1,0），点D 的坐标是（-2,4），则点C 的坐标是___________.15. 如图，四边形ABCD 内接与⊙O ，它的三个外角∠EAB ，∠FBC ，∠GCD 的度数之比为1：2：4，则∠D =_______°.16. 如图，在平面直角坐标系中，横、纵坐标均为整数的点按如下规律依序排列：（0,0），（1,0），（0,1），（2,0），（1，1），（0,2），（3,0），（2,1），（1,2），（0,3），（4,0），（3,1），（2,2），（1,3）……，按这个规律，则（6,7）是第______个点.12xx三、解答题（本大题共11小题，共88分）17.（7分）先化简，再求值：a b a bab b a+⎛⎫÷-⎪⎝⎭，其中a=3，b=2.18.（7分）解不等式组()3241213x xxx⎧-≤-⎪⎨+>-⎪⎩19.（8分）某文印馆用2660元购进一批白色复印纸和彩色复印纸，白色复印纸每箱80元，彩色复印纸每箱180元，购进白色复印纸的箱数比彩色复印纸的箱数的5倍少3箱，求购买的白色复印纸的箱数和彩色复印纸的箱数.20.（8分）某企业订餐，有A，B两家公司可选择，该企业先连续10个工作日选择A公司，接着连续10个月选择B公司，记录送餐用时（单位：min）如下表：根据上表数据绘制的折线统计图如图所示：（1）根据上述信息，请你帮该企业选择合适的公司订餐，并简述理由.（2）如果某工作日该企业希望送餐用时不超过20min，应选择哪家公司？请简述理由.21.（8分）甲城市有2个景点A，B，乙城市有3个景点C，D，E，从中随机选取景点游览，求下列事件的概率.（1）选取1个景点，恰好在甲城市.（2）选取2个景点，恰好在同一个城市.22.（8分）如图，AM∥BN，AC平分∠BAM，交BN于点C，过点B作BD⊥AC，交AM于点D，垂直为O，连接CD，求证：四边形ABCD是菱形.23.（8分）如图，灯塔B位于港口A的北偏东58°方向，且A，B之间的距离为30km，灯塔C位于灯塔B的正东方向，且B，C之间的距离10km.一艘轮船从港口A除法，沿正南方向航行到达D处，测得灯塔C在北偏东37°方向上.这时，D处距离港口A有多远？（结果取整数）（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）24.（8分）如图，在△ABC 中，AB =AC ，点D ，E 在BC 上，BD =CE . 过A ，D ，E 三点作⊙O ，连接AO 并延长，交BC 于点F . （1）求证AF ⊥BC .（2）若AB =10，BC =12，BD =2，求⊙O 的半径长.25.（8分）某蔬菜基地有甲，乙两个用于灌溉的水池，它们的最大容量均为30003m ，原有水量分别为12003m ，3003m ，现向甲，乙同时注水，直至两水池均注满为止，已知每分钟向甲、乙的注水量之和恒定为1003m ，若其中某一水池注满，则停止向该水池注水，改为向另一水池单独注水，设注水第x min 时，甲、乙水池中的水量分别为1y 3m ，2y 3m .（1）若每分钟向甲注水403m ，分别写出1y ，2y 与x 之间的函数表达式. （2）若每分钟向甲注水503m ，画出2y 与x 之间的函数图像．（3）若每分钟向甲注a 3m ，则甲比乙提前3min 注满，求a 的值.26. 如图，在矩形ABCD 中，10AB =，6BC =，E 是AD 上一点，2AE =. F 是AB 上的动点，连接EF ，G 是EF 上一点，且GF/EF k =（k 为常数，0k ≠），分别过点F 、G 作AB 、EF 的垂线相交于点P ．设AF 的长为x ，PF 的长为y .（1）若12k =，4x =，则y 的值是________；（2）求y 与x 之间的函数表达式.（3）在点F 从点A 到点B 的整个运动过程中，若线段CD 上存在点P ，则k 的值应满足什么条件?直接写出k 的取值范围.27. 在平面内，先将一个多边形以自身的一个顶点为位似中心放大或缩小，再将所得多边形沿过该点的直线翻折，我们称这种变换为自位似轴对称变换，变换前后的图形成自位似轴对称.例如：如图①，先将ABC ∆以点A 为位似中心缩小，得到ADE ∆，再将ADE ∆沿过点A 的直线l 翻折，得到AFG ∆，则ABC ∆与AFG ∆成自位似轴对称.（1）如图②，在ABC ∆中，90ACB =︒∠，AC BC <，CD AB ⊥，垂足为D ，下列3对三角形：①ABC ∆与ACD ∆；②BAC ∆与BCD ∆；③DAC ∆与DCB ∆. 其中成自位似轴对称的是（填写所有符合条件的序号）；（2）如图③，已知ABC ∆经过自位似轴对称变换得到ADE ∆，Q 是DE 上一点,用直尺和圆规作点P ，使P 与Q 是该变换前后的对应点（保留作图痕迹，写出必要的文字说明）；（3）如图④，在ABC ∆中，D 是BC 的中点，E 是ABC ∆内一点，ABE C =∠∠，BAE CAD =∠∠，连接DE ，求证：DE AC ∥..2022南京中考数学参考答案一、选择题6. 【解答】立体图如图所示，易得CN 最大，选B .二、填空题【说明】填空题答错位置，无论从哪里开始，都按正确答案给分，在原题号上给分；（1）填空题多写单位不扣分；（2）第10题些“1，3”、“1或3”、“1和3”均不扣分；（3）第14题，横纵坐标各占1分；（4）第13题只需要满足0a <且2c a =+（a ，c 位置颠倒，以及两个横线上错一个均不得分） 16. 【解答】横纵坐标相加为0时，共有1个点；横纵坐标相加为1时，共有2个点；横纵坐标相加为2时，共有3个点； ……横纵坐标相加为12时，共有13个点；横纵坐标相加为13时，共有14个点，而（6,7）为其中第8个，所以1+2+3+…+13+8=99个.三、解答题 17. 【解答】a b a b ab b a +⎛⎫÷- ⎪⎝⎭M （P ）N解：原式22a b a b ab ab+-=÷ ()()a b ab ab a b a b +=⋅+- 1a b=- 将3a =，2b =代入上式，原式1132==-18. 【解答】()3241213x x x x ⎧-≤-⎪⎨+>-⎪⎩①②解：由①式得：643x x -≤- 463x x -≤-+22x ≤ 1x ≤由②式得1233x x +>- 2331x x ->-- 4x ->- 4x <∴不等式得解集为1x ≤.19. 【解答】设彩色复印纸得箱数为x ，则白色复印纸得箱数为53x -； 180********()x x +-=解得：5x =，则5322x -=.答：彩色复印纸得箱数为5，则白色复印纸得箱数为22；20. 【解答】（1）A 公司平均送餐时间为262630252729242830252710A x +++++++++==（min ）；B 公司平均送餐时间为201821163432151435152210A x +++++++++==（min ）；A 公司送餐时间的方差为22222222222111320231324210().A S =+++++++++=； B 公司送餐时间的方差为222222222221241612107813763210().B S =+++++++++=；22A B S S <，∴选择A 公司，理由式送餐时间起伏小，稳定，时间预测更准确.（2）选择B 公司，因为A 公司送餐时间均超过20min ，B 公司10次送餐时间中有6次在20min 以内，所以选择B 公司.21. 【解答】（1）25P =；（2）25P =.22.【解答】AM BN ∥，∴MAC BCA =∠∠，ADB CBD =∠∠；AC 平分BAM ∠， ∴MAC BAC =∠∠， ∴BCA BAC =∠∠；BD AC ⊥，∴90BOA BOC ==︒∠∠，90AOB AOD ==︒∠∠；在△ABO 和△CBO 中， BOA BOCBCA BAC BO BO =⎧⎪=⎨⎪=⎩∠∠∠∠， ∴△ABO ≌△CBO （AAS ）∴AB CB =，ABO CBO =∠∠，AO CO =；ADB CBD =∠∠， ∴ADB ABO =∠∠， ∴AB AD =.在△ABO 和△ADO 中， AB AD MAC BAC AOB AOD =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ABO ≌△ADO （AAS ） ∴BO DO =，∴四边形ABCD 是平行四边形；BO AC ⊥，∴平行四边形ABCD 是菱形.23. 【解答】延长DA 与CB 的延长线交于点E ，据题意知90CED =︒∠，在Rt △BAE 中，58EAB =︒∠，30AB km =， ∴5808530sin .BE ︒=≈，则255.BE km ≈；5805330cos .AE︒=≈，则159.AE km ≈；10BC km =，CE BE BC =+，∴25510355..CE km =+=；在Rt △DEC 中，37D =︒∠， ∴37075tan .CE DE ︒=≈，则1473DE km =；AD DE AE =-，∴147159313.AD km =-≈24. 【解答】（1）连接AD 、AE ，连接OD 、OE . AB AC =，∴B C =∠∠.在△ABD 和△ACE 中， AB AC B C BD CE =⎧⎪=⎨⎪=⎩∠∠∴△ABD ≌△ACE （SAS ） ∴AD AE =AD AE =，∴点A 在DE 的垂直平分线上； OD OE =，∴点O 在DE 的垂直平分线上； ∴直线AO 为线段DE的垂直平分线，垂足为点F ；∴AF BC ⊥.（2）连接OD ，OF DE ⊥，∴DF EF =.又2BD CE ==，∴4DF EF ==，∴246BF BD DF =+=+=.在Rt △ABF 中，22222106AF AB BF =-=-，解得：8AF =.设AO R =，则8OF R =-，在Rt △ODF 中，222OD OF DF =+，即()22284R R =-+，解得：5R =. ∴半径为5.25. 【解答】（1）甲水池还需18003m 水才能注满、乙水池还需27003m 水才能注满. 若每分钟向甲注水403m ，则需要18004540min = ；若每分钟向乙注水603m ，则需要27004560min =；两者同时注满，则：1401800045()y x x =+≤≤ 260300045()y x x =+≤≤（2）若每分钟向甲注水503m ，则需要18003650min =；若每分钟向乙注水503m ，则需要27005450min =；说明甲先注满；当036x ≤≤时，250300y x =+，当36x =时，250363002100y =⨯+=；乙水池还需9003m ，将乙水池注满还需9009100min =；当3645x ≤≤时，设函数关系式为2y kx b =+，（36，2100）、（45，3000）代入得210036300045k b k b =+⎧⎨=+⎩，解得1001500k b =⎧⎨=-⎩∴函数关系式为21001500y x =-.∴25030003610015003645()()x x y x x +≤<⎧=⎨-≤≤⎩∴2y 与x 之间的函数图像为：（3）设甲注满的时间为min t ，对于甲：12003000at +=；对于乙：30010010033000()a t +-+⨯=. 解得42t =，3007a =.26. 【解答】（1）5；（2）PF AB ⊥，∴90PFA =︒∠；∴90PFG AFE +=︒∠∠；在矩形ABCD 中，90A =︒∠，在Rt △EAF 中，90A =︒∠，∴90AEF AFE +=︒∠∠，∴PFG AEF =∠∠；PG EF ⊥，∴90PGF =︒∠，则A PGF =∠∠，∴△PGF ∠∽△FAE ∠； ∴PFGFFE AE =，则GF EF PF AE ⋅=⋅在Rt △EAF 中，2AE =，AF x =，则22222224EF AE AF x x =+=+=+；GFkFE =，GF kEF ∴=，则2kEF PF AE =⋅，PF y =，242()k x y +=，则224222()k x kx y k +==+（010x ≤≤）.（3）线段CD 上存在点P ，则6y =；21642()k x =+，则2124k x =+；010x ≤≤， 204104x ≤+≤，则3326k ≤<；GFkFE=，点G在EF上，∴1k≤，∴∴3126k≤≤.27. 【解答】（2）【法一】以点A为圆心，AE为半径画弧，交AC于点E'，过点E作BC的平行线D E''（可以作同位角，也可以画出D'），再以点A为圆心，AQ为半径画弧，交D E''即为点P【法二】同上做出点E'和D E'',再作EE'的垂直平分线l，再过点Q作l的垂线交D E''于点P注：此题方法不唯一，言之成理即可.（3）延长BE交AC于点F，易得△ABE∽△ACD，∴AB AE BEAC AD CD==又△ABF∽△ACB，∴AB AF BFAC AB CB==，∴AB BF BEAC CB CD==，D为BC中点，∴2BC CD=，∴2BF EF=，∴E为BF中点，∴DE为△BCF的中位线，∴DE AC∥（方法不唯一）B。

2021年浙江省金华市中考数学真题解析版

2021年浙江省金华市中考数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．实数﹣，﹣，2，﹣3中，为负整数的是（）A．﹣B．﹣C．2D．﹣32．+＝（）A．3B．C．D．3．太阳与地球的平均距离大约是150000000千米，其中数150000000用科学记数法表示为（）A．1.5×108B．15×107C．1.5×107D．0.15×1094．一个不等式的解在数轴上表示如图，则这个不等式可以是（）A．x+2＞0B．x﹣2＜0C．2x≥4D．2﹣x＜05．某同学的作业如下框，其中※处填的依据是（）如图，已知直线l1，l2，l3，l4．若∠1＝∠2，则∠3＝∠4．请完成下面的说理过程．解：已知∠1＝∠2，根据（内错角相等，两直线平行），得l1∥l2．再根据（※），得∠3＝∠4．A．两直线平行，内错角相等B．内错角相等，两直线平行C．两直线平行，同位角相等D．两直线平行，同旁内角互补6．将如图所示的直棱柱展开，下列各示意图中不可能是它的表面展开图的是（）A．B．C．D．7．如图是一架人字梯，已知AB＝AC＝2米，AC与地面BC的夹角为α，则两梯脚之间的距离BC为（）A．4cosα米B．4sinα米C．4tanα米D．米8．已知点A（x1，y1），B（x2，y2）在反比例函数y＝﹣的图象上．若x1＜0＜x2，则（）A．y1＜0＜y2B．y2＜0＜y1C．y1＜y2＜0D．y2＜y1＜09．某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是（）A．先打九五折，再打九五折B．先提价50%，再打六折C．先提价30%，再降价30%D．先提价25%，再降价25%10．如图，在Rt△ABC中，∠ACB＝90°，以该三角形的三条边为边向形外作正方形，正方形的顶点E，F，G，H，M，N都在同一个圆上．记该圆面积为S1，△ABC面积为S2，则的值是（）A．B．3πC．5πD．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）二次根式中，字母x的取值范围是．12．（4分）已知是方程3x+2y＝10的一个解，则m的值是．13．（4分）某单位组织抽奖活动，共准备了150张奖券，设一等奖5个，二等奖20个，三等奖80个．已知每张奖券获奖的可能性相同，则1张奖券中一等奖的概率是．14．（4分）如图，菱形ABCD的边长为6cm，∠BAD＝60°，将该菱形沿AC方向平移2cm 得到四边形A′B′C′D′，A′D′交CD于点E，则点E到AC的距离为cm．15．（4分）如图，在平面直角坐标系中，有一只用七巧板拼成的“猫”，三角形①的边BC 及四边形②的边CD都在x轴上，“猫”耳尖E在y轴上．若“猫”尾巴尖A的横坐标是1，则“猫”爪尖F的坐标是．16．（4分）如图1是一种利用镜面反射，放大微小变化的装置．木条BC上的点P处安装一平面镜，BC与刻度尺边MN的交点为D，从A点发出的光束经平面镜P反射后，在MN上形成一个光点E．已知AB⊥BC，MN⊥BC，AB＝6.5，BP＝4，PD＝8．（1）ED的长为．（2）将木条BC绕点B按顺时针方向旋转一定角度得到BC′（如图2），点P的对应点为P′，BC′与MN的交点为D′，从A点发出的光束经平面镜P′反射后，在MN上的光点为E′．若DD′＝5，则EE′的长为．三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）17．（6分）计算：（﹣1）2021+﹣4sin45°+|﹣2|．18．（6分）已知x＝，求（3x﹣1）2+（1+3x）（1﹣3x）的值．19．（6分）已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠BOC＝120°，AB ＝2．（1）求矩形对角线的长．（2）过O作OE⊥AD于点E，连结BE．记∠ABE＝α，求tanα的值．20．（8分）小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如图测试成绩折线统计图．根据图中信息，解答下列问题：（1）要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量．（2）求小聪成绩的方差．（3）现求得小明成绩的方差为S小明2＝3（单位：平方分）．根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由．21．（8分）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点A 在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为y＝﹣（x﹣5）2+6．（1）求雕塑高OA．（2）求落水点C，D之间的距离．（3）若需要在OD上的点E处竖立雕塑EF，OE＝10m，EF＝1.8m，EF⊥OD．问：顶部F是否会碰到水柱？请通过计算说明．22．（10分）在扇形AOB中，半径OA＝6，点P在OA上，连结PB，将△OBP沿PB折叠得到△O′BP．（1）如图1，若∠O＝75°，且BO′与所在的圆相切于点B．①求∠APO′的度数．②求AP的长．（2）如图2，BO′与相交于点D，若点D为的中点，且PD∥OB，求的长．23．（10分）背景：点A在反比例函数y＝（k＞0）的图象上，AB⊥x轴于点B，AC⊥y 轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形．如图1，点A在第一象限内，当AC＝4时，小李测得CD＝3．探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系．请帮助小李解决下列问题．（1）求k的值．（2）设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”．如图2，小李画出了x＞0时“Z函数”的图象．①求这个“Z函数”的表达式．②补画x＜0时“Z函数”的图象，并写出这个函数的性质（两条即可）．③过点（3，2）作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标．24．（12分）在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．2021年浙江省金华市中考数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．实数﹣，﹣，2，﹣3中，为负整数的是（）A．﹣B．﹣C．2D．﹣3【分析】根据实数的分类即可做出判断．【解答】解：A选项是负分数，不符合题意；B选项是无理数，不符合题意；C选项是正整数，不符合题意；D选项是负整数，符合题意；故选：D．2．+＝（）A．3B．C．D．【分析】根据同分母的分式的加减法法则计算即可．【解答】解：+＝＝，故选：D．3．太阳与地球的平均距离大约是150000000千米，其中数150000000用科学记数法表示为（）A．1.5×108B．15×107C．1.5×107D．0.15×109【分析】对于大于10的数，可以写成a×10n的形式，其中1≤a＜10，n为正整数，n的值比原数的位数少1．【解答】解：150 000 000＝1.5×108，故选：A．4．一个不等式的解在数轴上表示如图，则这个不等式可以是（）A．x+2＞0B．x﹣2＜0C．2x≥4D．2﹣x＜0【分析】解不等式，可得不等式的解集，根据不等式的解集在数轴上的表示方法，可得答案．【解答】解：A、x＞﹣2，故A错误；B、x＜2，故B正确；C、x≥2，故C错误；D、x＞2，故D错误．故选：B．5．某同学的作业如下框，其中※处填的依据是（）如图，已知直线l1，l2，l3，l4．若∠1＝∠2，则∠3＝∠4．请完成下面的说理过程．解：已知∠1＝∠2，根据（内错角相等，两直线平行），得l1∥l2．再根据（※），得∠3＝∠4．A．两直线平行，内错角相等B．内错角相等，两直线平行C．两直线平行，同位角相等D．两直线平行，同旁内角互补【分析】先证l1∥l2，再由平行线的性质即可得出结论．【解答】解：已知∠1＝∠2，根据内错角相等，两直线平行，得l1∥l2，再根据两直线平行，同位角相等，得∠3＝∠4．故选：C．6．将如图所示的直棱柱展开，下列各示意图中不可能是它的表面展开图的是（）A．B．C．D．【分析】直三棱柱的表面展开图的特点，由三个长方形的侧面和上下两个等边三角形的底面组成．【解答】解：选项A、B、C均可能是该直棱柱展开图，而选项D中的两个底面会重叠，不可能是它的表面展开图，故选：D．7．如图是一架人字梯，已知AB＝AC＝2米，AC与地面BC的夹角为α，则两梯脚之间的距离BC为（）A．4cosα米B．4sinα米C．4tanα米D．米【分析】直接利用等腰三角形的性质得出BD＝DC,再利用锐角三角函数关系得出DC的长，即可得出答案。

2021年浙江省金华市中考数学试卷及答案解析

2021年浙江省金华市中考数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．实数−12，−√5，2，﹣3中，为负整数的是（）A．−12B．−√5C．2D．﹣32．1a +2a=（）A．3B．32a C．2a2D．3a3．太阳与地球的平均距离大约是150000000千米，其中数150000000用科学记数法表示为（）A．1.5×108B．15×107C．1.5×107D．0.15×1094．一个不等式的解在数轴上表示如图，则这个不等式可以是（）A．x+2＞0B．x﹣2＜0C．2x≥4D．2﹣x＜05．某同学的作业如下框，其中※处填的依据是（）如图，已知直线l1，l2，l3，l4．若∠1＝∠2，则∠3＝∠4．请完成下面的说理过程．解：已知∠1＝∠2，根据（内错角相等，两直线平行），得l1∥l2．再根据（※），得∠3＝∠4．A．两直线平行，内错角相等B．内错角相等，两直线平行C．两直线平行，同位角相等D．两直线平行，同旁内角互补6．将如图所示的直棱柱展开，下列各示意图中不可能是它的表面展开图的是（）A ．B ．C ．D ．7．如图是一架人字梯，已知AB ＝AC ＝2米，AC 与地面BC 的夹角为α，则两梯脚之间的距离BC 为（）A ．4cos α米B ．4sin α米C ．4tan α米D ．4cosα米8．已知点A （x 1，y 1），B （x 2，y 2）在反比例函数y =−12x 的图象上．若x 1＜0＜x 2，则（） A ．y 1＜0＜y 2B ．y 2＜0＜y 1C ．y 1＜y 2＜0D ．y 2＜y 1＜09．某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是（）A ．先打九五折，再打九五折B ．先提价50%，再打六折C ．先提价30%，再降价30%D ．先提价25%，再降价25%10．如图，在Rt △ABC 中，∠ACB ＝90°，以该三角形的三条边为边向形外作正方形，正方形的顶点E ，F ，G ，H ，M ，N 都在同一个圆上．记该圆面积为S 1，△ABC 面积为S 2，则S 1S 2的值是（）A ．5π2B ．3πC ．5πD ．11π2二、填空题（本题有6小题，每小题4分，共24分）11．（4分）二次根式√x −3中，字母x 的取值范围是． 12．（4分）已知{x =2y =m是方程3x +2y ＝10的一个解，则m 的值是．13．（4分）某单位组织抽奖活动，共准备了150张奖券，设一等奖5个，二等奖20个，三等奖80个．已知每张奖券获奖的可能性相同，则1张奖券中一等奖的概率是．14．（4分）如图，菱形ABCD 的边长为6cm ，∠BAD ＝60°，将该菱形沿AC 方向平移2√3cm 得到四边形A ′B ′C ′D ′，A ′D ′交CD 于点E ，则点E 到AC 的距离为 cm ．15．（4分）如图，在平面直角坐标系中，有一只用七巧板拼成的“猫”，三角形①的边BC 及四边形②的边CD 都在x 轴上，“猫”耳尖E 在y 轴上．若“猫”尾巴尖A 的横坐标是1，则“猫”爪尖F 的坐标是．16．（4分）如图1是一种利用镜面反射，放大微小变化的装置．木条BC 上的点P 处安装一平面镜，BC 与刻度尺边MN 的交点为D ，从A 点发出的光束经平面镜P 反射后，在MN 上形成一个光点E ．已知AB ⊥BC ，MN ⊥BC ，AB ＝6.5，BP ＝4，PD ＝8．（1）ED 的长为．（2）将木条BC绕点B按顺时针方向旋转一定角度得到BC′（如图2），点P的对应点为P′，BC′与MN的交点为D′，从A点发出的光束经平面镜P′反射后，在MN上的光点为E′．若DD′＝5，则EE′的长为．三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）17．（6分）计算：（﹣1）2021+√8−4sin45°+|﹣2|．18．（6分）已知x=16，求（3x﹣1）2+（1+3x）（1﹣3x）的值．19．（6分）已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠BOC＝120°，AB ＝2．（1）求矩形对角线的长．（2）过O作OE⊥AD于点E，连结BE．记∠ABE＝α，求tanα的值．20．（8分）小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如图测试成绩折线统计图．根据图中信息，解答下列问题：（1）要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量．（2）求小聪成绩的方差．（3）现求得小明成绩的方差为S小明2＝3（单位：平方分）．根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由．21．（8分）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点A 在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为y=−16（x﹣5）2+6．（1）求雕塑高OA．（2）求落水点C，D之间的距离．（3）若需要在OD上的点E处竖立雕塑EF，OE＝10m，EF＝1.8m，EF⊥OD．问：顶部F是否会碰到水柱？请通过计算说明．22．（10分）在扇形AOB中，半径OA＝6，点P在OA上，连结PB，将△OBP沿PB折叠得到△O′BP．（1）如图1，若∠O＝75°，且BO′与AB̂所在的圆相切于点B．①求∠APO′的度数．②求AP的长．（2）如图2，BO′与AB̂相交于点D，若点D为AB̂的中点，且PD∥OB，求AB̂的长．23．（10分）背景：点A在反比例函数y=kx（k＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形．如图1，点A 在第一象限内，当AC＝4时，小李测得CD＝3．探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系．请帮助小李解决下列问题．（1）求k的值．（2）设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”．如图2，小李画出了x＞0时“Z函数”的图象．①求这个“Z函数”的表达式．②补画x＜0时“Z函数”的图象，并写出这个函数的性质（两条即可）．③过点（3，2）作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标．24．（12分）在平面直角坐标系中，点A的坐标为（−√73，0），点B在直线l：y=38x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．2021年浙江省金华市中考数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．实数−12，−√5，2，﹣3中，为负整数的是（）A．−12B．−√5C．2D．﹣3【分析】根据实数的分类即可做出判断．【解答】解：A选项是负分数，不符合题意；B选项是无理数，不符合题意；C选项是正整数，不符合题意；D选项是负整数，符合题意；故选：D．【点评】本题考查了实数的分类，属于简单题，注意整数包括正整数，负整数和0．2．1a +2a=（）A．3B．32a C．2a2D．3a【分析】根据同分母的分式的加减法法则计算即可．【解答】解：1a +2a=1+2a=3a，故选：D．【点评】本题考查了分式的加减法，属于简单题，可以类比小学的分数计算法则，熟练掌握分式的加减法法则．3．太阳与地球的平均距离大约是150000000千米，其中数150000000用科学记数法表示为（）A．1.5×108B．15×107C．1.5×107D．0.15×109【分析】对于大于10的数，可以写成a×10n的形式，其中1≤a＜10，n为正整数，n的值比原数的位数少1．【解答】解：150 000 000＝1.5×108，故选：A．【点评】本题考查了科学记数法，解题的关键是确定a和n的值．4．一个不等式的解在数轴上表示如图，则这个不等式可以是（）A．x+2＞0B．x﹣2＜0C．2x≥4D．2﹣x＜0【分析】解不等式，可得不等式的解集，根据不等式的解集在数轴上的表示方法，可得答案．【解答】解：A、x＞﹣2，故A错误；B、x＜2，故B正确；C、x≥2，故C错误；D、x＞2，故D错误．故选：B．【点评】本题考查了在数轴上表示不等式的解集，在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．5．某同学的作业如下框，其中※处填的依据是（）如图，已知直线l1，l2，l3，l4．若∠1＝∠2，则∠3＝∠4．请完成下面的说理过程．解：已知∠1＝∠2，根据（内错角相等，两直线平行），得l1∥l2．再根据（※），得∠3＝∠4．A．两直线平行，内错角相等B．内错角相等，两直线平行C．两直线平行，同位角相等D．两直线平行，同旁内角互补【分析】先证l1∥l2，再由平行线的性质即可得出结论．【解答】解：已知∠1＝∠2，根据内错角相等，两直线平行，得l1∥l2，再根据两直线平行，同位角相等，得∠3＝∠4．故选：C．【点评】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键．6．将如图所示的直棱柱展开，下列各示意图中不可能是它的表面展开图的是（）A．B．C．D．【分析】直三棱柱的表面展开图的特点，由三个长方形的侧面和上下两个等边三角形的底面组成．【解答】解：选项A、B、C均可能是该直棱柱展开图，而选项D中的两个底面会重叠，不可能是它的表面展开图，故选：D．【点评】考查了几何体的展开图，动手折叠一下，有助于空间想象力的培养．7．如图是一架人字梯，已知AB＝AC＝2米，AC与地面BC的夹角为α，则两梯脚之间的距离BC为（）A．4cosα米B．4sinα米C．4tanα米D．4cosα米【分析】直接利用等腰三角形的性质得出BD＝DC,再利用锐角三角函数关系得出DC的长，即可得出答案。

第5讲直棱柱及表面展开图

第5讲直棱柱及表面展开图【知识要点】1.由若干个平面围成的几何体叫多面体；多面体上相邻两个面之间的交线叫多面体的棱；几个面的公共顶点叫多面体的顶点。

2.棱柱的上下底面平行且全等，每个侧面都是平行四边形。

3.根据侧棱与底面是否垂直，棱柱分为直棱柱和斜棱柱，直棱柱的每个侧面都是长方形（含正方形）。

4.根据底面多边形的边数，直棱柱可分为直三棱柱、直四棱柱……长方体和正方体都是直四棱柱。

5.欧拉公式：V+F－E=2(V:顶点数，F: 面数，E: 棱数）。

6.几何体的表面积=侧面积+底面积（上、下底的面积和）7.常见的几种几何体的表面积的计算公式①圆柱体表面积：2πR2+2πRh （R为圆柱体上下底圆半径，h为圆柱体高）②长方体表面积：2（ab+ah+bh）（a为长方体的长，b为长方体的宽，h为长方体的高③正方体表面积：6a2（a为正方体棱长）8.几何体的展开图：（1）同一个立体图形按不同的方式展开，得到的平面展开图是不一样的，立体图形的展开图是平面图形。

（2）常见几何体的侧面展开图：①圆柱的侧面展开图是长方形．②圆锥的侧面展开图是扇形．③正方体的侧面展开图是长方形．④三棱柱的侧面展开图是长方形．从实物出发，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键．9.正方体相对两个面上文字：（1）对于此类问题一般方法是用纸按图的样子折叠后可以解决，或是在对展开图理解的基础上直接想像。

（2）正方体的展开图有11种情况，分析平面展开图的各种情况后再认真确定哪两个面的对面．【典型例题】〖讨论1〗在长、宽都是3，高是8的长方体纸箱的外部，一只蚂蚁从顶点A沿纸箱表面爬到顶点B点，那么它所行的最短路线的长是____________．〖讨论2〗如图是一个正方体纸盒的展开图，当折叠成正方体纸盒时，A点与_______点重合,C点与_______点重合.〖讨论3〗一个简单多面体的各个面都是三角形，请你说明它的顶点数V和面数F之间的关系为F=2V－4.学力训练一．选择题（共15小题）1．下列各几何体中，直棱柱的个数是（）A．5B．4C．3D．22．七棱柱的侧面是（）第3题A．长方形B．七边形C．三角形D．正方形3．如图所示，在长方体中，与棱AB平行的棱有（）A．1条B．2条C．3条D．4条4．下列关于棱柱的说法：①棱柱的所有面都是平面；②棱柱的所有棱长都相等；③棱柱的所以侧面都是长方形或正方形；④棱柱的侧面个数与底面边数相等；⑤棱柱的上、下底面形状、大小相等其中正确的有（）A．2个B．3个C．4个D．5个5．一个直棱柱有12个顶点，那么它的面的个数是（）A．10个B．9个C．8个D．7个6．一个棱柱有18条棱，那么它的底面一定是（）A．十八边形B．八边形C．六边形D．四边形7．（2012•台湾）如图1为图2中三角柱ABCEFG的展开图，其中AE、BF、CG、DH是三角柱的边．若图1中，AD=10，CD=2，则下列何者可为AB长度？（）A. 2B. 3C. 4D. 5第7题第8题第9题8．（2012•佛山）一个几何体的展开图如图所示，这个几何体是（）A．三棱柱B．三棱锥C．四棱柱D．四棱锥9．（2011•台湾）若下列只有一个图形不是右图的展开图，则此图为何？（）A．B．C．D．10．（2011•呼和浩特）将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是（）A．B．C．D．11. （2012•德州）如图给定的是纸盒的外表面，下面能由它折叠而成的是（）A．B．C．D．12．（2011•河北）将图1围成图2的正方体，则图1中的红心“”标志所在的正方形是正方体中的（）A．面CDHE B．面BCEF C．面ABFG D．面ADHG13．（2010•宁波）骰子是一种特的数字立方体（见图），它符合规则：相对两面的点数之和总是7，下面四幅图中可以折成符合规则的骰子的是（）A．B．C．D．二．填空题（共2小题）14．已知三棱柱有5个面6个顶点9条棱，四棱柱有6个面8个顶点12条棱，五棱柱有7个面10个顶点15条棱，…，由此可以推测n 棱柱有_________个面，_________个顶点，棱有_________条．15．一个直棱柱有7个面，则它有________个顶点，________条棱，表面上至少有______个直角．三．解答题（共6小题）16．（2010•宁波）十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体模型，完成表格中的空格：多面体顶点数（V）面数（F）棱数（E）四面体 4 4长方体8 6 12正八面体8 12正十二面体20 12 30你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是_________．（2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是_________．（3）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为x个，八边形的个数为y个，求x+y的值．17..下列图形中，图（a）是正方体木块，把它切去一块，得到如图（b）（c）（d）（e）的木块．图号顶点数x 棱数y 面数z（a）8 12 6（b）（c）（d）（e）（1）我们知道，图（a）的正方体木块有8个顶点、12条棱、6个面，请你将图（b）、（c）、（d）、（e）中木块的顶点数、棱数、面数填入下表；（2）上表，各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律，请你试写出顶点数x、棱数y、面数z之间的数量关系式．18．如图1所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图2所示．已知展开图中每个正方形的边长为1．（1）求在该展开图中可画出最长线段的长度这样的线段可画几条？（2）试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系？19．如图，是一个无盖立方体盒子，请把下列不完整的展开图补充完整．（请画出三种）20.马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．（注：①只需添加一个符合要求的正方形；②添加的正方形用阴影表示）21.如图是一个正方体的展开图，标注了字母“a”的面是正方体的正面，如果正方体相对两个面上的代数式的值相等，求x、y的值．22.一个简单多面体的各个面都是五边形，请你说明它的顶点数V和面数F满足以下关系式：2V=3F+4。

32直棱柱的表面展开图

A
B
C
D
试一试
下面六个正方形连在一起的图形，经折叠后能围成正方体的图形有哪几个？(动手试试）
A
B
C
D
E
F
G
长方体
正方体三棱柱
例2 有一种牛奶包装盒如图所示。为了生产这种包装盒，需要先画出展开图纸样。（1）如图给出的三种纸样，它们都正确吗？（2）从已知正确的纸样中选出一种，标注上尺寸；（3）利用你所选的一种纸样，求出包装盒的侧面积和表面积（侧面积与两个底面积的和）。
(10) 1
4
4
563
563
(7) 1 2 (8) 1 2
563
2
(11) 1 2 4
立方体展开图的周长是每个小正方形边长的几倍?
展开图规律之四: 立方体表面展开图的周长是小 5
正方形边长的14倍.
4
5632 1 (1)
4 5 6 32
1 (2)
4 5632
(3) 1
2 1 34
6
4 56 3 2
(4) 1
4
4
5 63 2 5 6 32
1 (5) (6) 1
4 563
(9) 1 2
54 63
(10) 1
4
4
563
563
(7) 1 2 (8) 1 2
563
2
(11) 1 2 4
合作游戏
平面“七刀”现; 对面“不相连”; “日”字异层见; 整体没有“田”;
补充: 立方体表面展开图的周长是小正方形边长的14倍.
A
B
C
D
E培养我们F的三维空间G 想像能力H!
下面的图形都是立方体的展开图吗？

2021年浙江省金华市中考数学试卷及答案解析

【解答】解：∵k＝﹣12＜0，
∴双曲线在第二，四象限，
∵x1＜0＜x2， ∴点 A 在第二象限，点 B 在第四象限，
∴y2＜0＜y1；故选：B．
【点评】本题主要考查反比例函数的图象和性质，掌握反比例函数 y 图象和性质是解题的关键，即当 k＞0 时，图象在第一三象限，且在每个象限内 y 随 x 的增大而减小，当 k＜0 时，图象在第二四象限内，且在每个象限内 y 随 x 的增大而增大． 9．（3 分）某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是（） A．先打九五折，再打九五折 B．先提价 50%，再打六折 C．先提价 30%，再降价 30%
cm．
15．（4 分）如图，在平面直角坐标系中，有一只用七巧板拼成的“猫”，三角形①的边 BC
及四边形②的边 CD 都在 x 轴上，“猫”耳尖 E 在 y 轴上．若“猫”尾巴尖 A 的横坐标
是 1，则“猫”爪尖 F 的坐标是
．
16．（4 分）如图 1 是一种利用镜面反射，放大微小变化的装置．木条 BC 上的点 P 处安装
A．
B．
C．
D．
7．（3 分）如图是一架人字梯，已知 AB＝AC＝2 米，AC 与地面 BC 的夹角为α，则两梯脚
之间的距离 BC 为（）
A．4cosα米
B．4sinα米
C．4tanα米
8．（3 分）已知点 A（x1，y1），B（x2，y2）在反比例函数 y
D．米 th
的图象上．若 x1＜0＜x2，
8．（3 分）已知点 A（x1，y1），B（x2，y2）在反比例函数 y
的图象上．若 x1＜0＜x2，
则（）
A．y1＜0＜y2
B．y2＜0＜y1

直三棱柱的表面展开图

五年级奥数：展开图与空间想象

直角三角形与勾股定理(优选真题60道)(原卷版)--三年(2021-2023)中考数学真题分项汇编

华杯赛初赛历年真题集(含答案)

初中数学精品课件： 三视图与表面展开图

三棱柱的展开图

2023-2024学年江苏省无锡市新吴区八年级(上)期中数学试卷[含答案]

六年级数学专题思维训练—立体几何(含答案及解析)

人教版八年级数学上册期末素养综合测试(二)课件

(2021年整理)五年级奥数.几何.展开图与空间想象(A级).教师版

第4讲 直棱柱

【2022】南京中考数学(含解析)

2021年浙江省金华市中考数学真题 解析版

2021年浙江省金华市中考数学试卷及答案解析

第5讲 直棱柱及表面展开图

32直棱柱的表面展开图

2021年浙江省金华市中考数学试卷及答案解析

初中数学精品课件：三视图与表面展开图

第4讲直棱柱

2021年浙江省金华市中考数学真题解析版

第5讲直棱柱及表面展开图