高中数学完整讲义——空间几何量的计算4.二面角
求二面角的六种方法

求二面角的六种方法求解二面角是空间几何学中常见的问题,它在多个领域如物理学、化学和工程学中都有广泛的应用。
本文将介绍六种求解二面角的方法,包括向量法、坐标法、三角法、平面几何法、球面几何法和投影法。
一、向量法向量法是一种简便的求解二面角的方法。
它利用向量的夹角来表示二面角。
首先,我们需要确定两个平面的法向量,然后计算它们之间的夹角。
通过向量的点积和模长运算,可以得到二面角的大小。
二、坐标法坐标法是一种常用的求解二面角的方法。
它利用坐标系中的点来表示二面角。
我们可以通过给定的坐标点,计算两个平面的法向量,然后利用向量夹角的公式求解二面角。
三、三角法三角法是一种基于三角函数的求解二面角的方法。
它利用三角函数的性质来计算二面角的大小。
通过已知的边长和角度,可以利用正弦定理、余弦定理等公式求解二面角。
四、平面几何法平面几何法是一种利用平面几何关系求解二面角的方法。
它通过已知的平面形状和角度关系,利用平面几何的知识来求解二面角的大小。
例如,可以利用平行线的性质、垂直线的性质等来计算二面角。
五、球面几何法球面几何法是一种利用球面几何关系求解二面角的方法。
它通过已知的球面形状和角度关系,利用球面几何的知识来求解二面角的大小。
例如,可以利用球面上的弧长、球面上的角度等来计算二面角。
六、投影法投影法是一种利用投影关系求解二面角的方法。
它通过已知的投影长度和角度关系,利用投影几何的知识来求解二面角的大小。
例如,可以利用平面上的投影线段、平面上的角度等来计算二面角。
通过以上六种方法,我们可以灵活地求解二面角的大小。
不同的问题和场景可能适用不同的方法,我们可以根据具体情况选择合适的方法来解决问题。
这些方法在实际应用中具有重要的意义,能够帮助我们更好地理解和解决相关问题。
总结起来,求解二面角的六种方法分别是向量法、坐标法、三角法、平面几何法、球面几何法和投影法。
每种方法都有其特点和适用场景,我们可以根据具体问题选择合适的方法来求解二面角。
空间向量应用-二面角

04
二面角的应用
在几何学中的应用
向量投影
在求解向量的投影时,可以利用二面 角的概念,通过计算向量在某一平面 上的投影长度,来得到该向量与该平 面的夹角。
向量夹角
二面角的概念可以用于计算两个向量 的夹角,通过比较两个向量的夹角与 二面角的夹角,可以判断两个向量的 方向关系。
在物理学中的应用
力的合成与分解
建筑设计
在建筑设计中,利用二面角的概念可以确定建筑物的位置、方向和高度等信息, 以保证建筑物的安全和稳定性。
05
空间向量与二面角的关系
向量与二面角的关联
向量是既有大小又有方向的量,其大 小和方向可以用来表示二面角的大小 和方向。
二面角的大小和方向可以通过两个向 量的夹角来描述,这个夹角就是二面 角的平面角。
二面角的向量定义
总结词
二面角的向量定义是通过向量的投影 和叉积来定义的,它是一个标量值, 其大小等于两个向量的叉积的绝对值 再除以两向量的模的乘积。
详细描述
二面角的向量定义是通过向量的投影和叉积来 描述的。设两非零向量a和b分别属于两个半平 面,那么二面角θ的大小可以用公式 ∣a×b∣/∣a∣∣b∣表示,其中a×b表示向量a和b 的叉积,∣a∣和∣b∣分别表示向量a和b的模。这 个标量值的大小就等于二面角θ的大小。
二面角的性质
总结词
二面角具有一些重要的性质,如二面角的取值范围是[0,π],二面角的大小与观察方向有关,以及二面角的补角等 于其平面角的补角等。
详细描述
首先,二面角的取值范围是[0,π],这是由其几何定义直接得出的。其次,二面角的大小与观察方向有关,即观察 方向的不同可能导致二面角的大小发生变化。最后,二面角的补角等于其平面角的补角,这是由向量的性质得出 的。
二面角向量法公式

二面角向量法公式在咱们学习立体几何的时候,有一个很重要的概念——二面角向量法公式。
这玩意儿可真是个厉害的工具,能帮咱们解决不少难题呢!先来说说啥是二面角。
想象一下,你有两块板子,它们斜着靠在一起,形成的那个“夹角”就是二面角。
要想准确算出这个角的大小,二面角向量法公式就派上用场啦。
公式是这样的:cosθ = |(n1·n2) / (|n1| × |n2|)| ,这里的 n1 和 n2 是两个平面的法向量。
可别被这一堆符号吓到,咱们慢慢捋一捋。
法向量又是啥呢?简单说,就是和平面垂直的向量。
比如说,有一个平面,你总能找到一个向量,它直直地立在这个平面上,那它就是法向量。
我记得我之前教过一个学生,叫小李。
这孩子呀,刚开始接触二面角向量法公式的时候,那叫一个迷糊。
有一次上课,我在黑板上写了一道例题,让大家试着用公式算一下二面角。
小李坐在那儿,抓耳挠腮,半天没动静。
我走过去一看,他连法向量都还没找对。
我就耐心地跟他说:“小李呀,你看这个平面的方程,先把它的系数找出来,然后设法向量是(x,y,z),根据垂直的条件列出方程组,就能求出法向量啦。
”小李似懂非懂地点点头,又埋头苦算了起来。
经过几次这样的耐心指导,小李终于慢慢掌握了窍门。
后来有一次小测验,碰到一道二面角的题目,他刷刷刷几下就把法向量求出来,然后顺利地用公式算出了二面角的大小。
看到他那自信满满的样子,我心里也特别欣慰。
那咱们再回到这个公式。
计算的时候,一定要注意向量的点乘和模长的计算,可别马虎。
有时候一个小数字算错了,整个结果就全错啦。
而且呀,用这个公式的时候,要先判断二面角是锐角还是钝角。
这就需要咱们对图形有一个清晰的认识。
比如说,如果两个法向量的方向都是从二面角内部指向外部,那算出的余弦值就是二面角的余弦值;如果一个从内部指向外部,一个从外部指向内部,那算出的余弦值的相反数才是二面角的余弦值。
总之,二面角向量法公式虽然看起来有点复杂,但只要咱们多做几道题,多琢磨琢磨,就能熟练掌握,让它成为咱们解决立体几何问题的有力武器。
立体几何向量法求二面角

立体几何向量法求二面角一、引言在几何学中,二面角是指两个平面或者一个平面和一个直线之间的夹角。
它是描述多面体中相邻两个面之间的夹角的重要参数。
在工程学、物理学和化学等领域,求解二面角是非常常见的问题。
本文将介绍立体几何向量法求解二面角的方法。
二、立体几何向量法立体几何向量法是一种非常有效的求解二面角的方法。
它基于向量叉积和点积的运算,通过将多面体分解成若干个三角形来计算二面角。
1. 向量叉积向量叉积是两个向量所构成的新向量,其大小等于两个向量所构成平行四边形的面积,方向垂直于这两个向量所构成平行四边形所在平面。
设有两个三维向量a = (a1, a2, a3)和b = (b1, b2, b3),则它们的叉积c = a × b定义为:c = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)其中c表示a和b所构成平行四边形所在平面上一条垂直这个平行四边形的向量。
2. 向量点积向量点积是两个向量所构成的标量,其大小等于两个向量夹角的余弦值乘以两个向量的模长之积。
设有两个三维向量a = (a1, a2, a3)和b = (b1, b2, b3),则它们的点积c = a · b定义为:c = a1b1 + a2b2 + a3b3其中c表示a和b之间夹角的余弦值乘以它们的模长之积。
3. 二面角计算公式二面角可以通过计算相邻两个面法线向量之间夹角的余弦值来求解。
具体地,设有一个多面体,其中相邻两个面A和B所对应的法线分别为nA和nB,则它们之间的二面角θAB可以通过以下公式计算:cosθAB = -nA·nB / |nA||nB|其中“·”表示向量点积,“| |”表示向量模长。
4. 多面体分解在实际问题中,通常需要将多面体分解成若干个三角形来计算二面角。
具体地,考虑一个四面体(如图1),其中相邻两个三角形ABC和ABD所对应的法线分别为nABC和nABD,则它们之间的二面角θABC-D可以通过以下公式计算:cosθABC-D = -nABC·nABD / |nABC||nABD|其中“·”表示向量点积,“| |”表示向量模长。
立体几何篇(空间角之二面角)

立体几何篇(空间角专题之二面角)二面角的定义:在两个平面的交线上任取一点,过该点,在各自的平面内作交线的垂线,两根射线所成的平角即为两个平面的二面角,二面角的范围为ο≤θ或]0≤180,0[π二面角的求法:1、定义法:2、三垂线法:(最重要的方法)3、面积比法:4、垂面法:5、向量法:(建系)例题1、定义法:(当等腰三角形出现的情况下,用定义法)1、求正四面体相邻的两个平面的所成二面角余弦值的大小2、如图,在三棱锥A BCD-中,侧面ABD ACD,是全等的直角三角形,AD是公共的斜边,且31AD BD CD===,,另一侧面ABC是正三角形.(1)求证:AD BC⊥;(2)求二面角B AC D--的余弦值;2、三垂线法(也叫站柱法)三垂线定理:(1)垂直于斜线由垂直于射线;(2)垂直于射线则垂直于斜线。
ABCD例3、如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.(Ⅰ)求直线PC与平面ABC所成角的正切值;(Ⅱ)求二面角B﹣AP﹣C所成角的正切值.例4、在如图所示的几何体中,四边形ABCD 是等腰梯形, AB ∥CD ,∠DAB = 60,FC ⊥平面ABCD ,AE ⊥BD ,CB =CD =CF .(Ⅰ).求证: BD ⊥平面AED .(Ⅱ)求二面角F -BD -C 的余弦值.E F BA C D3、面积比法原射S S =θcos例5、1111D C B A ABCD -是长方体,侧棱1AA 长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面DE C 1与底面CDE 所成二面角的正切值。
例6、E 为正方体1111D C B A ABCD -的棱1CC 的中点,求平面E AB 1的底面1111D C B A 所成锐角的余弦值。
4、垂面法通过作二面角棱的垂面得到平面角的方法叫垂面法。
例7、空间的点P 到二面角βα--l 的面α、β及棱l 的距离分别为4、3、3392,求二面角βα--l 的大小.Pβα lC B A。
空间几何量的计算.板块四.二面角 普通高中数学复习讲义Word版

【例1】 (06四川卷理10)已知球O 的半径是1,A 、B 、C 三点都在球面上,A 、B两点和A 、C 两点的球面距离都是π4,B 、C 两点的球面距离是π3,则二面角B OAC --的大小是( )A .π4B .π3C .π2D .2π3【难度】4【解析】 球O 的半径是R=1,,,A B C 三点都在球面上,,A B 两点和,A C 两点的球面距离都是4π,则∠AOB ,∠AOC 都等于π4,AB AC =,,B C 两点的球面距离是π3,π3BOC ∠=,1BC =,过B 做BD AO ⊥,垂足为D ,连接CD ,则CD AD ⊥,则BDC ∠二面角B OA C --的平面角,BD CD ==,∴π2BDC ∠=,二面角B OA C --的大小是π2,选C .【例2】 (2009浙江17)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .【难度】6【例3】 112⎛⎫⎪⎝⎭,; 典例分析板块四.二面角FDC BA考虑极端情况,当F 与E 重合时,显然1t =(K 与D 重合);当F与C 重合时,折叠后BC DB ⊥,此时DB ADB ∆为直角三角形,12t =,而F 不为端点,故t 的取值范围是112⎛⎫⎪⎝⎭,.事实上,F 越靠近C ,折叠的幅度越小,AD 的投影越短,即t 越小,而且是渐近变化的.【例4】 正方体1111ABCD A B C D -中,作截面1BDC ,求二面角1B DC C --的正切值的大小.O A 1D 1C 1B 1D CBA【难度】4【解析】 由BC ⊥面11CC D D ,过C 作CO ⊥1C D 交1C D 于O ,连结BO则BO ⊥1C D ,∴BOC ∠是二面角1B DC C --的平面角 设正方体的棱长为1,则CO=BOC ∆是直角三角形, ∴tan BCBOC OC∠=【例5】 如图,正方体1111ABCD A B C D -中.求平面1A BD 和平面1C BD 相交所组成的二面角11A BD C --的余弦值.OA 1D 1C 1B 1DCBA【难度】6【解析】 正方体的面对角线长相等,则1A BD ∆与1BC D ∆为等边三角形设BD 的中点为O ,连结1A O ,1C O , 则1A O ⊥BD ,1C O ⊥BD∴11A OC ∠是二面角11A BD C --的平面角 设正方体的棱长为单位1,连结11A C . 在11AOC ∆中,11A C =11AO C O == 由余弦定理得111cos 6AOC ∠=- ∴二面角11A BD C --的余弦值为16【例6】 如图,正方体1111ABCD A B C D -的棱长为1,P 是AB 的中点.⑴求二面角1A BC A --的大小; ⑵求二面角1B AC P --的大小. PF E A 1D 1C 1B 1DCA【难度】6【解析】 ⑴由BC ⊥面11ABB A ,∴1A B ⊥BC ,AB ⊥BC∴1A BA ∠即为二面角1A BC A --的平面角, ∴此二面角的大小为45 ⑵过点P 作PF ⊥1A B 交1A B 于F ∵BC ⊥面11A ABB ,且PF ⊂面11A ABB ∴PF ⊥BC ,又PF ⊥1A B , ∴PF ⊥面1A BC过点F 作FE ⊥1A C 交1A C 于E ,连结PE ,则PEF ∠为二面角1B AC P --的平面角∵正方体1111ABCD A B C D -的棱长为1,∴12BP =,1A P =,1A C =∵1A P PC =,∴在等腰1PAC ∆中,由PE ⊥1A C可得1A E EC ==∴在1Rt A PE ∆,PE ==∵45FBP ∠=,∴在等腰Rt BPF ∆中,PF ==∴在Rt PFE ∆中,1sin 2PF PEF PE ∠== ∴二面角1B AC P --的大小为30【例7】 如图,已知边长为a 的正ABC ∆,以它的高AD 为折痕,把它折成一个二面角B ADC '--.⑴求AB '和面B CD '所成的角;⑵若二面角B AD C '--的平面角为120,求出二面角A B C D '--的余弦值.MABC DB '【难度】6【解析】⑴∵AD ⊥面B CD ',∴AB D '∠为AB '与面B CD '所成的角 ∵ABC ∆为正三角形∴60ABD ∠= ,即60AB D '∠=, ∴AB '与面B CD '所成的角为60⑵当B AD C '--为120的二面角时,即120B DC '∠= 取B C '中点M ,连结DM ∵B D DC '=,∴DM ⊥B C '.∵AD ⊥面B DC ',∴AD ⊥B C ',又DM ⊥B C ' ∴B C '⊥面ADM ,∴B C '⊥AM∴AM D ∠是二面角A B C D '--的平面角在'B DC ∆中,60CDM ∠=,∴24CD aDM ==在Rt ADM ∆中,AM =∴cos DM AMD AM ∠==【例8】 在正方体1111ABCD A B C D -中,棱长为1,且P 、Q 、R 分别为AB 、AD 、1DD 的中点.求截面PQR 与面11CC D D 所成的锐角二面角的正切值.【难度】6【解析】 (法一:平移平面)连结1BC ,BD ,1C D 得到截面1BC D ∵PQ ∥BD ,QR ∥1BC ∴面PQR ∥面1BC D∴面PQR 与面11CC D D 所成的二面角,转化为面1BC D 与面11CC D D 所成角 由BC ⊥面11CC D D 有,连结1CD 与1C D 交于点E ,则CE ⊥1C D , 连结BE ,则BE ⊥1C D ,BEC ∠为二面角的平面角,且tan BCBEC EC∠==N MRQ PA 1D 1C 1B 1D CB(法二:寻找交线)延长PQ ,CD 交于点M ,连结MR ,则根据平面基本性质可知MR 为截面PQR 与面11CC D D 的交线,由平面几何知识可知MD AP DR ==过P 作PN ⊥DC ,由1CC ⊥面ABCD ,且PN ⊂面ABCD , ∴PN ⊥1CC ,∴PN ⊥面11CC D D 连结NR ,以下证明NR ⊥MR ,∵12MD DN CD ==,∴MR=,且NR =1MN CD ==∴由勾股定理逆定理可知MR ⊥NR∵PN ⊥面11CC D D ,则N 为CD 中点,且MR ⊂面11CC D D ∴MR ⊥PN ,且MR ⊥NR , ∴MR ⊥平面PNR ,∴MR ⊥PR ∴PRN ∠为二面角的平面角,tan PNPRN NR∠==【例9】 如图,四边形ABCD是面积为的菱形,DAB ∠为菱形的锐角,P 是平面外的一点,PAD ∆是边长为2的正三角形,平面PAD ⊥平面ABCD ,M 是PC 的中点.⑴求证:PB ⊥AD ;⑵求证:平面ADM ⊥平面PBC .【难度】6【解析】 ⑴DAB ∠为菱形的锐角,过B 作BE ⊥AD 交AD于E ,则ABCD S AD BE =⋅=又∵2AD =,∴BE ,在Rt ABE ∆中,2AB =,BE =,则112AE AD ==, ∴E 是等PAD ∆边AD 的中点,∴PE ⊥AD 又BE PE E =,∴AD ⊥面PBE ,且PB ⊂面PBE∴PB ⊥AD .⑵取PB 中点N ,连结MN 、AN ,则MN ∥AB ∥ADN PBCDAM∴AN ⊂面ADNM ,即AN ⊂面ADM ∵PAD ∆是正三角形,且底面ABCD 是菱形, ∴ABP ∆为等腰三角形,∴PB ⊥AN ,且由(1)知PB ⊥AD , ∴PB ⊥面ADNM ,且PB ⊂面PBC ∴平面ADM ⊥平面PBC .【例10】 长方体1111ABCD A B C D -中,1AC a =,1AC 与平面ABCD 成30角,与平面11B BCC 成45角,求二面角1B AC C --的正弦值或余弦值的大小.F E D 1C 1B 1A 1D CBA【难度】6【解析】 (法一:“垂帘听政”法)作BF ⊥AC 与AC 交于点F ,∵1CC ⊥底面ABCD ,且BF ⊂底面ABCD , ∴1CC ⊥BF ,又AC ⊥BF ,且1CC AC C =∴BF ⊥面1ACC ,作BE ⊥1AC 交1AC 于E ,连结EF ,则FEB ∠为二面角1B AC C --的平面角,且sin BFFEB BE∠= ∵1AC 与平面ABCD 成30角,则130C AC ∠=, 1AC 与平面11B BCC 成45角,则1904545C AB ∠=-=又∵1AC a =,∴12aCC =,AC,1AB BC ==在1Rt BCC ∆中,12BC a =在Rt ABC ∆中,AB BC BF⋅==在Rt ABE ∆中,12BE AE AB a ===∴sin BF FEB BE ∠==(法二:面积射影定理法)作BF ⊥AC 交AC 于点F ,∵1CC ⊥底面ABCD ,且BF ⊂底面ABCD , ∴1CC ⊥BF ,又AC ⊥BF ,且1CC AC C =∴BF ⊥面1ACC ,∴面1ABC 在平面1AC C 上的射影为1AFC ∆,而121111224ABC S AB BC a ∆=⋅== 1111122AFC S AF C CAF CC =⋅⋅=⋅⋅根据直角三角形的射影定理,22)ABAF AC===∴1112AFC S AF CC =⋅⋅=2∴11cos AFC ABC S S θ∆∆==∴【例11】 如图所示,正三棱柱111ABC A B C -的底边长为2,高为4,过AB 作一截面交侧棱1CC 于P ,截面与底面成60角,求截面PAB ∆的面积.PBC 1B 1A 1CA【难度】6【解析】 法一:由题意,在图中作PD ⊥AB 于D ,连结CD ,在Rt PCD ∆中,CD ,60PDC ∠=,则PD =∴截面PAB ∆的面积为122⨯⨯法二:可直接应用二面角的射影公式,由PC ⊥面ABC ,PAB ∆在底面的射影为ABC ∆, ∴cos60ABC PAB S S ∆∆=,又1222ABC S ∆=⨯∴PAB S ∆=。
原创1:1.2.4 二面角

夹角,但要注意其异同.
(2)法向量法:分别求出两平面的法向量n1,n2,则两平面的夹角为〈n1,n2〉
若二面角为锐角,则为〈n1,n2〉;若二面角为钝角,则为π-〈n1,n2〉.
跟踪练习
练习.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与
1
,
2
1
2
, ),
易知是平面PAB的法向量, 是平面PCD的法向量,
∴cos〈 , 〉=
2
2
,∴平面PAB与平面PCD的夹角为45°.
B
x
D
C
y
课堂小结
用空间向量解决立体几何问题的“三步曲”.
(1)建立立体图形与空间向量的联系,用空间向量表示问题中
涉及的点、直线、平面,把立体几何问题转化为向量问题;
以O为原点,如图建立空间直角坐标系,
C1
O
B
x
A1
y
B1
典例精析
则B(1,0,0),D(-1,1,0),
z
A1(0,2, 3),A(0,0, 3),B1(1,2,0).
A
设平面A1AD的法向量为n=(x,y,z),
AD=(-1,1,- 3),AA1=(0,2,0).
A1
C
因为n⊥AD,n⊥AA1,
第一章
空间向量与立体几何
1.2.4 二面角
学习目标:
1.会用向量法求二面角.
2.能正确理解二面角的定义.
教学重点:会用向量法求二面角.
教学难点:会用向量法求二面角.
新知探索
二面角的平面角
设二面角αlβ的锐二面角大小为θ,且两个半平面的法向量分别为a,b,
二面角的计算方法精讲

二面角的计算方法精讲本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March图 1二面角的计算方法精讲二面角是高中数学的主要内容之一,是每年高考数学的一个必考内容,本文主要通过一些典型的例子说明二面角的三种基本计算方法,供同学们学习参考。
一 、直接法:即先作出二面角的平面角,再利用解三角形知识求解之。
通常作二面角的平面角的途径有:⑴定义法:在二面角的棱上取一个特殊点,由此点出发在二面角的两个面内分别作棱的垂线;⑵三垂线法:如图1,C 是二面角βα--AB 的面β内的一个点,CO ⊥平面α于O ,只需作OD ⊥AB 于D ,连接CD ,用三垂线定理可证明∠CDO 就是 所求二面角的平面角。
⑶垂面法:即在二面角的棱上取一点,过此点作平面γ,使γ垂直于二面角的棱,则γ 与二面角的两个面的交线所成的角就是该二面角的平面角。
例1 如图2,在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD . (1)证明AB ⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的大小. 解:(1)证明:VAD ABCDAB AD AB VADAB ABCD AD VAD ABCD ⊥⎫⎪⊥⎪⇒⊥⎬⊂⎪⎪=⎭平面平面平面平面平面平面 (2)解:取VD 的中点E ,连结AF ,BE , ∵△VAD 是正三形,四边形ABCD 为正方形,∴由勾股定理可知, 2222BD AB AD AB VA VB,=+=+=∴AE ⊥VD ,BE ⊥VD ,∴∠AEB 就是所求二面角的平面角. 又在Rt △ABE 中,∠BAE=90°,AE=3AD=3AB , 因此,tan ∠AEB=.332=AE AB 即得所求二面角的大小为.332arctan例2 如图3,AB ⊥平面BCD ,DC ⊥CB ,AD 与平面BCD 成30°的角,且AB=BC.(1)求AD 与平面ABC 所成的角的大小; (2)求二面角C-AD-B 的大小;(3)若AB=2,求点B 到平面ACD 的距离。
二面角的求法和利用空间向量解决立体几何问题
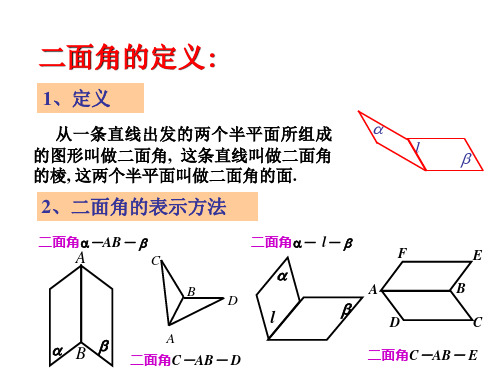
二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角-AB-
A
C
B
二面角- l-
D
l
B
A
二面角C-AB- D
F
E
A
B
D
C
二面角C-AB- E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
面面平行
∥ n1 ∥ n2 n1 kn2
二、垂直关系:
设直线 l, m 的方向向量分别为 AB,CD ,
平面 , 的法向量分别为 n1 , n2 , 线线垂直:
l ⊥ m AB ⊥ CD AB • CD 0 ;
Bl
A
平面 内的两个相交向量垂直
(4)解方程组,令其中一个量的值求另外两个, 即得法向量。
一、平行关系:
设直线 l, m 的方向向量分别为 AB,CD ,
lm
BD
平面 , 的法向量分别为
线线平行:
n1
, n2
,
l ∥ m AB ∥ CD AB kCD
;
x1 y1
=
A
x2 y2
=
C
x3 y3
线面平行
AB
l ∥ AB n1 AB n1 0 ;
分别作垂直于a 的两条射线OA,OB,则∠AOB就 是此二面角的平面角。
2、垂线法: 在一个平面 内选一点A向另一平面 作 垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足 为O, 连结AO,则∠AOB就是二面角的平面角。
高中数学知识点:二面角

高中数学知识点:二面角1.二面角定义平面内的一条直线把平面分成两部分,这两部分通常称为半平面.从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫二面角的棱,这两个半平面叫做二面角的面.表示方法:棱为AB 、面分别为αβ、的二面角记作二面角AB αβ--.有时为了方便,也可在αβ、内(棱以外的半平面部分)分别取点P Q 、,将这个二面角记作二面角P AB Q --.如果棱记作l ,那么这个二面角记作二面角l αβ--或P l Q --.2.二面角的平面角(1) 二面角的平面角的定义:在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则这两条射线构成的角叫做二面角的平面角.(2)二面角的平面角θ的范围:0°≤θ≤180°.当两个半平面重合时,θ=0°;当两个半平面相交时,0°<θ<180°;当两个半平面合成一个平面时,θ=180°.二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.平面角是直角的二面角叫做直二面角.(3) 二面角与平面角的对比角 二面角 图形定义 从半面内一点出发的两条射线(半直线)所组成的图形从空间内二直线出发的两个半平面所组成的图形 表示法由射线、点(顶点)、射线构成,表示为∠AOB 由半平面、线(棱)、半平面构成,表示为二面角a αβ--(4) 二面角的平面角的确定方法 方法1:(定义法)在二面角的棱上找一特殊点,在两个半平面内分别作垂直于棱的射线.如右图,在二面角a αβ--的棱a 上任取一点O ,在平面α内过点O 作OA ⊥a ,在平面β内过点O 作BO ⊥a ,则∠AOB 为二面角a αβ--的平面角.方法2:(垂面法)过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.如下图(左),已知二面角lαβ--,过棱上一点O作一平面γ,使lγ⊥,且OAγβ=。
高中立体几何中二面角经典求法

高中立体几何中二面角求法摘要:在立体几何中,求二面角的大小是历届高考的热点,几乎每年必考,而对于求二面角方面的问题,同学们往往很难正确地找到作平面角的方法,本文对求二面角的方法作了一个总结,希望对学生有帮助。
(一)、二面角定义的回顾:从一条直线出发的两个半平面所组成的图形就叫做二面角。
二面角的大小是用二面角的平面角来衡量的。
而二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则(二)1 2 3 4、空间坐标法求二面角的大小 5、平移或延长(展)线(面)法 6、射影公式S 射影=S 斜面cos θ7、化归为分别垂直于二面角的两个面的两条直线所成的角 1、利用定义作出二面角的平面角,并设法求出其大小。
例1、 如图,已知二面角α-а-β等于120°,PA ⊥α,A ∈α,PB ⊥β,B ∈β. 求∠APB 的大小.解: 设平面∩PAB α=OA,平面PAB ∩β=OB 。
∵PA ⊥α, а⊂α ∴PA ⊥а同理PB ⊥а ∴а⊥平面PAB 又∵OA ⊂平面PAB ∴а⊥OA 同理а⊥OB.∴∠AOB 是二面角α-а-β的平面角. 在四边形PAOB 中, ∠AOB=120°,. ∠PAO=∠POB=90°, 所以∠APB=60° 2、 三垂线定理(逆定理)法由二面角的一个面上的斜线(或它的射影)与二面角的棱垂直,推得它位于二面角的另一的面上的射影(或斜线)也与二面角的棱垂直,从而确定二面角的平面角。
例2:如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值.解:在长方体ABCD —A 1B 1C 1D 1中由三垂线定理可得: ∴ CD =2 CE=1, DE=53、找(作)公垂面法由二面角的平面角的定义可知两个面的公垂面与棱垂直,因此公垂面与两个面的交线所成的角,就是二面角的平面角。
高中数学 空间几何量的计算 板块四 二面角完整讲义(学生版)

学而思高中完整讲义:空间几何量的计算.板块四.二面角.学生版【例1】 (06四川卷理10)已知球O 的半径是1,A 、B 、C 三点都在球面上,A 、B 两点和A 、C 两点的球面距离都是π4,B 、C 两点的球面距离是π3,则二面角B OA C --的大小是( ) A .π4 B .π3 C .π2 D .2π3【例2】 (2009浙江17)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .【例3】 正方体1111ABCD A B C D -中,作截面1BDC ,求二面角1B DC C --的正切值的大小.OA 1D 1C 1B 1DC B A【例4】 如图,正方体1111ABCD A B C D -中.求平面1A BD 和平面1C BD 相交所组成的二面角11A BD C --的余弦值.OA 1D 1C 1B 1DC B A典例分析【例5】 如图,正方体1111ABCD A B C D -的棱长为1,P 是AB 的中点.⑴求二面角1A BC A --的大小;⑵求二面角1B AC P --的大小. PF EA 1D 1C 1B 1DC B A【例6】 如图,已知边长为a 的正ABC ∆,以它的高AD 为折痕,把它折成一个二面角B ADC '--.⑴求AB '和面B CD '所成的角;⑵若二面角B AD C '--的平面角为120,求出二面角A B C D '--的余弦值.MAB C DB '【例7】 在正方体1111ABCD A B C D -中,棱长为1,且P 、Q 、R 分别为AB 、AD 、1DD 的中点.求截面PQR 与面11CC D D 所成的锐角二面角的正切值.【例8】 如图,四边形ABCD是面积为的菱形,DAB ∠为菱形的锐角,P 是平面外的一点,PAD ∆是边长为2的正三角形,平面PAD ⊥平面ABCD ,M 是PC 的中点. ⑴求证:PB ⊥AD ;⑵求证:平面ADM ⊥平面PBC .【例9】 长方体1111ABCD A B C D -中,1AC a =,1AC 与平面ABCD 成30角,与平面11B BCC 成45角,求二面角1B AC C --的正弦值或余弦值的大小.F ED 1C 1B 1A 1DC A【例10】 如图所示,正三棱柱111ABC A B C -的底边长为2,高为4,过AB 作一截面交侧棱1CC 于P ,截面与底面成60角,求截面PAB ∆的面积.PB C 1B 1A 1CA。
高中数学立体几何——二面角求法

高中数学立体几何——二面角求法
二面角是指两个平面之间的角度,通常用于描述两个多面体表面相接的角度。
二面角的求法有以下几种常见的方法:
1.面对面法:首先确定两个相邻平面的法向量,然后计算它们之间的夹角,即为二面角。
2.边对边法:首先找到两个相邻平面的公共边,然后计算这条边分别在两个平面上的投影长度,最后使用向量夹角的方法求得二面角。
3.用平行面的夹角计算二面角:如果两个面是平行的,则二面角为零。
需要注意的是,在具体的问题中,可能还会有其他方法来计算二面角,具体的求解方法要根据具体的情况和已知条件来选择合适的计算方式。
高中立体几何中二面角经典求法

高中立体几何中二面角求法摘要:在立体几何中,求二面角的大小是历届高考的热点,几乎每年必考,而对于求二面角方面的问题,同学们往往很难正确地找到作平面角的方法,本文对求二面角的方法作了一个总结,希望对学生有帮助。
(一)、二面角定义的回顾:从一条直线出发的两个半平面所组成的图形就叫做二面角。
二面角的大小是用二面角的平面角来衡量的。
而二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角。
(二)1 23 4、空间坐标法求二面角的大小 5、平移或延长(展)线(面)法 6、射影公式S 射影=S 斜面cos θ7、化归为分别垂直于二面角的两个面的两条直线所成的角 1、利用定义作出二面角的平面角,并设法求出其大小。
例1、 如图,已知二面角α-а-β等于120°,PA ⊥α,A ∈α,PB ⊥β,B ∈β. 求∠APB 的大小.解: 设平面∩PAB α=OA,平面PAB ∩β=OB 。
∵PA ⊥α, а⊂α ∴PA ⊥а同理PB ⊥а ∴а⊥平面PAB又∵OA ⊂平面PAB ∴а⊥OA 同理а⊥OB.∴∠AOB 是二面角α-а-β的平面角. 在四边形PAOB 中, ∠AOB=120°,. ∠PAO=∠POB=90°, 所以∠APB=60° 2、 三垂线定理(逆定理)法由二面角的一个面上的斜线(或它的射影)与二面角的棱垂直,推得它位于二面角的另一的面上的射影(或斜线)也与二面角的棱垂直,从而确定二面角的平面角。
例2:如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DEC 1D 1与面CDE 所成二面角的正切值.解:在长方体ABCD —A 1B 1C 1D 1中由三垂线定理可得: ∴ CD =2 CE=1, DE=53、找(作)公垂面法由二面角的平面角的定义可知两个面的公垂面与棱垂直,因此公垂面与两个面的交线所成的角,就是二面角的平面角。
二面角的求法课件

精品文档
精品文档
α
ι
β
精品文档
一、二面角的定义
从一条直线出发的两个半平面
所组成的图形叫做二面角。
二、二面角的平面角
从棱上一点P分别在两
个半平面内作与棱垂直的
射线PA、PB则∠APB叫做
γ
二面角 α-l-β的平面角。
ι
β
P
B
A
α
精品文档
例1、已知正三
棱锥V-ABC所有的棱
长均相等,求二面角
V
C A
B
精品文档
如图,正四棱锥S-ABCD
中,相邻两个侧面所成的二
面角为120O,若底面边长
S
AB=2,则侧棱长应为多少?
D A
C B
精品文档
如图四棱锥A-BCDE中,BE∥CD, 且BE= ,BE⊥平CD 面ABC,若△ABC
2
中,AC=CB=a , ∠ACB=90o,求平面 ABE与平面ACD所成二面角 D (锐角)的大小。
E
C
A
B
精品文档
D
E
C
A
B
精品文档
二面角α-l-β等于1200,PA⊥α于A, PB⊥β于B,则 AP, B=P , AP, PB
=。 P
α
A
C
l
β
B
精品文档
如图,M、N、P分别是正方体
ABCD- A1B1C1D1的棱AB、BC、DD1上的点,
若二面D1P角∶NP-DB=1M1∶-B2的,大且小PB。⊥平面B1MN, 求
A
例1、已知正三
棱锥V-ABC所有的棱
长均相等,求二面角
A-VC-B的大小。
高中数学完整讲义——空间几何量的计算4.二面角

【例1】 (06四川卷理10)已知球O 的半径是1,A 、B 、C 三点都在球面上,A 、B 两点和A 、C 两点的球面距离都是π4,B 、C 两点的球面距离是π3,则二面角B OA C --的大小是( )A .π4B .π3C .π2D .2π3【例2】 (2009浙江17)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .【例3】 正方体1111ABCD A B C D -中,作截面1BDC ,求二面角1B DC C --的正切值的大小.【例4】 如图,正方体1111ABCD A B C D -中.求平面1A BD 和平面1C BD 相交所组成的二面角11A BD C --的余弦值.OA 1D 1C 1B 1DC B A 典例分析板块四.二面角【例5】 如图,正方体1111ABCD A B C D -的棱长为1,P 是AB 的中点.⑴求二面角1A BC A --的大小;⑵求二面角1B AC P --的大小.【例6】 如图,已知边长为a 的正ABC ∆,以它的高AD 为折痕,把它折成一个二面角B AD C '--.⑴求AB '和面B CD '所成的角;⑵若二面角B AD C '--的平面角为120,求出二面角A B C D '--的余弦值.【例7】 在正方体1111ABCD A B C D -中,棱长为1,且P 、Q 、R 分别为AB 、AD 、1DD 的中点.求截面PQR 与面11CC D D 所成的锐角二面角的正切值.OA 1D 1C 1B 1DC B A PF EA 1D 1C 1B 1DC AMAB C DB '【例8】 如图,四边形ABCD是面积为DAB ∠为菱形的锐角,P 是平面外的一点,PAD∆是边长为2的正三角形,平面PAD ⊥平面ABCD ,M 是PC 的中点. ⑴求证:PB ⊥AD ;⑵求证:平面ADM ⊥平面PBC .【例9】 长方体1111ABCD A B C D -中,1AC a =,1AC 与平面ABCD 成30角,与平面11B BCC 成45角,求二面角1B AC C --的正弦值或余弦值的大小.【例10】 如图所示,正三棱柱111ABC A B C -的底边长为2,高为4,过AB 作一截面交侧棱1CC 于P ,截面与底面成60角,求截面PAB ∆的面积.F ED 1C 1B 1A 1DC A PB C 1B 1A 1CA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学讲义 1
思维的发掘 能力的飞跃
【例1】 (06四川卷理10)已知球O 的半径是1,A 、B 、C 三点都在球面上,A 、B 两点和A 、
C 两点的球面距离都是π4,B 、C 两点的球面距离是π3
,则二面角B OA C --的大小是( )
A .π4
B .π3
C .π2
D .2π3
【例2】 (2009浙江17)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线
段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .
【例3】 正方体1111ABCD A B C D -中,作截面1BDC ,求二面角1B DC C --的正切值的大小.
【例4】 如图,正方体1111ABCD A B C D -中.求平面1A BD 和平面1C BD 相交所组成的二面角
11A BD C --的余弦值.
O
A 1
D 1
C 1B 1D
C B A 典例分析
板块四.二面角
高中数学讲义 2 思维的发掘 能力的飞跃
【例5】 如图,正方体1111ABCD A B C D -的棱长为1,P 是AB 的中点.
⑴求二面角1A BC A --的大小;
⑵求二面角1
B A
C P --的大小.
【例6】 如图,已知边长为a 的正ABC ∆,以它的高AD 为折痕,把它折成一个二面角B AD C '--.
⑴求AB '和面B CD '所成的角;
⑵若二面角B AD C '--的平面角为120,求出二面角A B C D '--的余弦值.
【例7】 在正方体1111ABCD A B C D -中,棱长为1,且P 、Q 、R 分别为AB 、AD 、1DD 的中点.求
截面PQR 与面11CC D D 所成的锐角二面角的正切值.
O
A 1D 1
C 1
B 1D
C B A P
F E
A 1
D 1
C 1B 1D
C A
M
A
B C D
B '
高中数学讲义
3 思维的发掘 能力的飞跃 【例8】 如图,四边形ABCD
是面积为DAB ∠为菱形的锐角,P 是平面外的一点,PAD
∆是边长为2的正三角形,平面PAD ⊥平面ABCD ,M 是PC 的中点. ⑴求证:PB ⊥AD ;
⑵求证:平面ADM ⊥平面PBC .
【例9】 长方体1111ABCD A B C D -中,1AC a =,1AC 与平面ABCD 成30角,与平面11B BCC 成45角,
求二面角1B AC C --的正弦值或余弦值的大小.
【例10】 如图所示,正三棱柱111ABC A B C -的底边长为2,高为4,过AB 作一截面交侧棱1CC 于P ,
截面与底面成60角,求截面PAB ∆的面积.
F E
D 1
C 1
B 1A 1
D
C A P
B C 1
B 1A 1C
A。
