2013届高考数学考点讲解：考点14 解三角形(新课标解析版)

合集下载

2013年高考数学三角函数的题型分析word精品文档5页

2013年高考数学三角函数的题型分析[文献标识码]A近几年的高考中，三角函数题所占的分值不少，题目的类型比较固定，但是考查的知识点全面，涉及的内容广。

在2013年的高考题中，三角函数是怎样出题的？考查了哪些知识点？所占的分值是多少？与其他部分的知识点有哪些联系？针对上述这些问题，笔者对2013年各省市理科数学高考题中三角函数的试题进行了研究，统计了2013年各省市理科数学三角函数的知识点分布以及在各套试卷中所占的分值。

在这一统计工作的基础上，笔者对去年三角函数各知识点出现的频率进行了统计，对去年三角函数知识点的考查重点进行了分析。

各个知识点的考查都不是单独进行的，三角函数它是一种特殊的函数，三角函数体现出了函数的很多性质，那么这一特殊函数它通常和哪些知识点间有紧密的联系？笔者针对上述问题对去年的高考题进行了分析，并针对研究的结果，相应地提出了一些建议。

在现在的高考中，知识点之间的联系越来越紧密，三角函数与其他知识块综合考查。

笔者通过对这部分题型的统计、分析，总结出在2013年的高考中和三角函数综合考查的知识点有哪些，对高考中这些知识点间做个系统的梳理。

通过以上工作，对高考中三角函数有个整体的把握，摸清“出什么，怎么出”，有利于学生在复习中分清主次、找到联系。

对最新的高考题进行分析，有利于学生抓住高考试题的走向与重点所在。

对于2013年理科高考中三角函数试题的研究与分析，有助于对2014年三角函数这部分系统的把握。

现在对与各省市理科试卷中三角函数试题逐题进行系统统计与分析这样的研究相对较少，所以笔者进行这样的一项工作，通过分析“2013”把握“2014”。

三角函数这部分主要考查是从基础出发，稳中求变，稳中求新，能有自己的思维。

一、 2013年高考数学（理科）三角函数试题的统计与分析以2012年高考中全国各省市理科数学试卷中的三角函数试题为调研对象，进行统计、分析。

见下表：由表1得出，三角函数这部分知识在2013的高考试题中，主要集中在17、5、11这几道题中，尤其第17题。

2013年高考试题分项版解析数学(文) 专题04 三角函数与解三角形(Word精析版)(2)

第四章三角函数与解三角形一．基础题组1.【2013年普通高等学校招生全国统一考试（江西卷）文科】若sin 2a =，则cos a =（） A ．23-B ．13-C ．13D ．23[答案]C[解析]221cos 12sin 12..23C αα=-=-⨯=∴选 [考点定位]此题主要考查三角恒等变换里面的二倍角余弦公式、三角函数求值问题. 2.【2013年普通高等学校统一考试试题大纲全国文科】已知a 是第二象限角，5sin ,13a =则cos a =（）（A ）1213- （B ）513- （C ）513 （D ）1213【答案】A【解析】∵a 是第二象限角，∴12cos 13α===-.故选A. 【考点定位】三角求值3.【2013年普通高等学校招生全国统一考试（广东卷）文科】已知51sin()25πα+=，那么cos α=（）A ．25-B ．15-C ．15D ．25【答案】C 【解析】51sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭，选C. 【考点定位】三角函数诱导公式.4.【2013年普通高等学校统一考试试题大纲全国文科】若函数()()sin 0y x ωϕω=+>的部分图像如图，则=ω（）（A ）5 （B ）4 （C ）3 （D ）2 【答案】B【解析】∵由题中图像可知0042T x x π+-=.∴2T π=.∴22ππω=.∴4ω=.故选B. 【考点定位】三角函数的图像与解析式.5.【2013年普通高等学校招生全国统一考试（四川卷）文科】函数()2s i n ()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示，则,ωϕ的值分别是（）（A ）2,3π- （B ）2,6π-（C ）4,6π-（D ）4,3π【答案】A【解析】由图知，周期T 满足111521212T ππ=-，∴T π=，又0ω>，∴2ω=，故()2sin(2)f x x ϕ=+，图象的最高点为5,212π⎛⎫⎪⎝⎭，于是由“五点法”作图，知52122ππϕ⨯+=，解得3πϕ=-，选A.【易错点】注意求初相ϕ的值时，图象的最高点坐标与五个关键点坐标的对应关系最容易代错！【考点定位】本题考查正弦型函数()sin()f x A x ωϕ=+的图象与性质，难点是确定初相ϕ的值，关键是理解“五点法”作图.6.【2013年高考新课标Ⅱ数学（文）卷】已知sin2α=错误！未找到引用源。

2013年高考数学(理)真题分类解析汇编3.三角函数

2013年高考数学（理）真题分类解析汇编3：三角函数一、选择题1 ．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43 C.43- D.34-【答案】C 【天利解析】因为，又sin 2α+cos 2α=1，联立解得，或故tan α==，或tan α=3，代入可得tan2α===﹣，或tan2α===故选C2 ．（2013年高考陕西卷（理））设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定【答案】B【天利解析】因为cos cos sin b C c B a A +=，所以A A B C C B sin sin cos sin cos sin =+ 又A C B B C C B sin )sin(cos sin cos sin =+=+。

联立两式得A A A sin sin sin =。

所以2,1sin π==A A 。

选B3 ．（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））在△ABC 中,,3,4AB BC ABC π∠===则sin BAC ∠ =【答案】C4 ．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））将函数sin(2)y x ϕ=+的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为(A) 34π (B) 4π(C)0 (D) 4π-,k k Z π∈，即,4k k Z ϕπ=+∈，所以选B.5 ．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=且a b >,则B ∠= A.6π B.3πC.23πD.56π【答案】A【天利解析】根据正弦定理得，1sin sin cos sin sin cos sin 2A B C C B A B +=,即1sin cos sin cos 2A C C A +=，所以1sin()2A C +=，即1sin 2B =，因为a b >，所以6B π=。

2013年高考大纲数学(理)试题精解精析(解析版)

三、注重通性通法，突出数学思想方法的考查2013年试题注重能力立意，以考查基础知识为重点，注重对通性通法的考查，淡化特殊技巧, 突出数学思想与方法的考查。

如选择题的前7题，填空题的前2题，试题均为常规题目，学生解答起来，也是顺畅.数学卷历来重视数学思想与方法的考查，今年也不例外。

如数形结合的思想渗透在线性规划（理科第15题）、函数与方程的思想则体现在理科第21题、第22题等题目中；转化与化归思想贯穿整份试卷，如理科第12题；试卷对分类讨论的思想（理科第21题等）做了深入考查。

总之，2013年高考全国大纲版卷数学试题，注重考查考生运用所学知识发现问题、分析问题、解决问题的能力。

整份试卷稳中有变，变中求新，新题不难，难题不偏，“稳”以考查基础，“变”以考查能力，有较高的信度、效度和区分度。

本解析为名师解析团队原创，授权独家使用，如有盗用，依法追责！一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.（2013大纲全国，理1）设集合={1,2,3}A ，B={45}，，={x|x=a+b,a A,b B}M ∈∈，则M 中元素的个数为（） A ．3 B ．4 C ．5 D ．62. （2013大纲全国，理2）3(13)i +=（）A ．-8B ．8C ．8i -D ．8i3. （2013大纲全国，理3）已知向量(1,1)m λ=+，(2,2)n λ=+，若()()m n m n +⊥-，则λ=（）A ．-4B ．-3C ．-2D ．-1【考点定位】向量的坐标运算4. （2013大纲全国，理4）已知函数f(x)的定义域为(1,0)-，则函数(21)f x +的定义域（） A ．(1,1)- B ．1(1,)2-- C ．(1,0)- D ．1(,1)25. （2013大纲全国，理5）函数21()log (1)f x x=+（x>0）的反函数1()f x -=（）A ．1(0)21x x >- B ．1(0)21xx ≠- C ．21()x x R -∈ D ．21(0)x x ->6. （2013大纲全国，理6）已知数列{}n a 满足130n n a a ++=，243a =-，则{}n a 的前10项和等于（） A ．106(13)--- B ．101(13)9- C ．103(13)-- D ．103(13)-+7. （2013大纲全国，理7）84(1)(1)x y ++的展开式中22x y 的系数是（）A ．56B ．84C ．112D ．168 【答案】D8. （2013大纲全国，理8）椭圆C ：22143x y +=的左右顶点分别为12,A A ，点P 在C 上且直线2PA 斜率的取值范围是[2,1]--，那么直线1PA 斜率的取值范围是（） A ．13[,]24 B ．33[,]84 C ．1[,1]2 D ．3[,1]49. （2013大纲全国，理9）若函数21()f x x ax x =++在1(,)2+∞是增函数，则a 的取值范围是（） A ．[1,0]- B ．[1,)-+∞ C ．[0,3] D ．[3,)+∞10. （2013大纲全国，理10）已知正四棱柱1111ABCD A B C D -中，12AA AB =，则CD 与平面1BDC 所成角的正弦值等于（） A ．23 B ．33 C ．23 D ．1311. （2013大纲全国，理11）已知抛物线C ：28y x =与点M （-2,2），过C 的焦点且斜率为k 的直线与C 交于A ，B 两点，若0MA MB •=，则k=（）A ．12B ．22C ．2D ．2【答案】D【解析】由题意知抛物线C 的焦点坐标为（2,0），则直线AB 的方程为(2)y k x =-，将其代入28y x =，得22224(2)40k x k x k -++=.12. （2013大纲全国，理12）已知函数()cos sin 2f x x x =，下列结论中错误的是（） A ．()y f x =的图像关于点(,0)π中心对称 B ．()y f x =的图像关于直线2x π=对称C ．()f x 的最大值为32D ．()f x 既是奇函数，又是周期函数当33t=-时，函数值为439-；二、填空题：本大题共4小题，每小题5分.13. （2013大纲全国，理13）已知α是第三象限角，1sin3α=-，则cotα=14. （2013大纲全国，理14）6个人排成一行，其中甲、乙两人不相邻的不同排法共有种.（用数字作答）15. （2013大纲全国，理15）记不等式组03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩，所表示的平面区域为D.若直线(1)y a x =+与D 有公共点，则a 的取值范围是【答案】1[,4]2【解析】作出题中不等式组表示的可行域如图中阴影部分所示. ∵直线(1)y a x =+过定点C （-1,0），由图并结合题意可知1,42BC AC k k ==， ∴要使直线(1)y a x =+与平面区域D 有公共点，则142a ≤≤. 【考点定位】线性规划16. （2013大纲全国，理16）已知圆O 和圆K 是球O 的大圆和小圆，其公共弦长等于球O 的半径，32OK =，且圆O 与圆K 所在的平面所成的一个二面角为060，则球O 的表面积等于本解析为名师解析团队原创，授权独家使用，如有盗用，依法追责！三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（2013大纲全国，理17）（本小题满分10分）等差数列{}n a 的前n 项和为n S .已知232S a =，且124,,S S S 成等比数列，求{}n a 的通项公式.18. （2013大纲全国，理18）（本小题满分12分）设ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，()()a b c a b c ac ++-+=. （Ⅰ）求B ；（Ⅱ）若31sin sin 4A C =，求C.因此015C =或045C =.19. （2013大纲全国，理19）（本小题满分12分）如图，四棱锥P-ABCD 中，090ABC BAD ∠=∠=，2BC AD =，PAB ∆和PAD ∆都是等边三角形.（Ⅰ）证明：PB CD ⊥；（Ⅱ）求二面角A-PD-C 的大小.取PD的中点F，PC的中点G，连结FG，20. （2013大纲全国，理20）（本小题满分12分）甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判.设各局中双方获胜的概率均为12，各局比赛的结束相互独立，第1局甲当裁判.（Ⅰ）求第4局甲当裁判的概率；（Ⅱ）X表示前4局中乙当裁判的次数，求X的数学期望.21. （2013大纲全国，理21）（本小题满分12分）已知双曲线C：22221x ya b-=（a>0,b>0）的左、右焦点分别为1F、2F，离心率为3，直线y=2与C的两个交点间的距离为6.（Ⅰ）求a,b ；（Ⅱ）设过2F 的直线l 与C 的左、右两支分别交于A 、B 两点，且11||||AF BF =，证明：2||AF 、||AB 、2||BF 成等比数列.2222122222||(3)(3)8831BF x y x x x =++=++-=+22. （2013大纲全国，理22）（本小题满分12分）已知函数(1)()ln(1)1x x f x x xλ+=+-+. （Ⅰ）若0x ≥时，()0f x ≤，求λ的最小值；（Ⅱ）设数列{}n a 的通项111123n a n =++++，证明：21ln 24n n a a n -+>. 【答案】（Ⅰ）由已知(0)0f =，2'2(12)()(1)x x f x x λλ--=+，'(0)0f =. 若12λ<，则当02(12)x λ<<-时，'()0f x >，所以()0f x >.。

2013年高考数学预测新课标数学考点预测(09)：解三角形

π 2 5 , AC = 2 5, cos C = 4 5
(1)求 sin A ； (2) 记 BC 的中点为 D , 求中线 AD 的长．〖解析〗(1)由 cos C =
2 5 , C 是三角形内角， 5
2 2
⎛2 5⎞ 5 ⎟ 得 sin C = 1 − cos C = 1 − ⎜ ⎜ 5 ⎟ = 5 ⎝ ⎠ π π sin A = sin[ π − ( B + C )] = sin( B + C ) = sin cos C + cos sin C 4 4 = 2 2 2 5 3 10 ⋅ 5+ ⋅ = 2 5 2 5 10
由
c b 1 b 5 得，，所以最短边长为． = = 5 sin C sin B sin135° 10 10
O B 北
〖答案〗D． 4 （浙江省 09 年高考省教研室第一次抽样测试数学试题（理）16）．如图，海平面上的甲船位于中心 O 的南偏西 30 0 ，与 O 相距 10 海里的 C 处，现甲船以 30 海里/小时的速度沿直线 C CB 去营救位于中心 O 正东方向 20 海里的 B 处的乙船，甲船需要小时到达B 处. 〖解析〗由题意，对于 CB 的长度可用余弦定理求解，得
三、名校试题
1 （福建 2008 年高考样卷· 文） .△ABC 的内角 A、 B、 C 所对的边分别为 a、 b、 c，若 sinA=
1 ， 3
b= 3 sinB，则 a 等于（
）
A. 3 3
B. 3
C.
3 2
D.
3 3
〖解析〗由
a b 3 得a = ． = sin A sin B 3
〖答案〗D．．在△ ABC 中 ,A= 120� ， b=1 ，面积为 3 ，则 2 （山东省济南市 2009 届高三模考理 10 ）

(新课标)2013高考数学三轮必考热点集中营热点16三角函数的性质和解三角形问题(教师版)

（新课标）2013高考数学三轮必考热点集中营热点16三角函数
的性质和解三角形问题（教师版）
【三年真题重温】
1.【2011⋅新课标全国理，11】设函数()sin()cos()f x x x ωϕωϕ=+++（0ω>，
||2πϕ<）的最小正周期为π，且()()f x f x -=，则( )
A ．()f x 在 (0,
)2π单调递减 B ．()f x 在3(,)44ππ单调递减 C ．()f x 在(0,)2
π单调递增 D ．()f x 在3(,)44ππ单调递增
2.【2011⋅新课标全国理，16】在△ABC 中，60B = ，AC ，则2
AB BC +的最大
值为．
3.【2011 新课标全国文，15】ABC ∆中，120B =，7AC =，5AB =，则ABC ∆的
面积为．
4,【2010 新课标全国理，16】在△ABC 中，D 为边BC 上一点，BD=
12
DC ，∠ADB=120°，
AD=2，若△ADC 的面积为3∠BAC=_______.
则222cos 2BA AC BC BAC AB AC +-∠=⋅12
===
故60BAC ∠=
.
5.【2010 新课标全国文，16】在ABC ∆中，D 为BC 边上一点，3BC BD =,AD =
135ADB ο∠=.若AC =,则BD=_____.
【答案】
6、【2012⋅新课标全国理】已知0ω>，函数()sin()4f x x πω=+在(,)2ππ上单调递减,则ω的取值范围是（）
()A 15[,]24 ()B 13[,]24
()C 1(0,]2 ()D (0,2]。

(2021年整理)2013年高考数学知识点总结：三角函数公式

（完整）2013年高考数学知识点总结：三角函数公式编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）2013年高考数学知识点总结：三角函数公式）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）2013年高考数学知识点总结：三角函数公式的全部内容。

三角函数公式1．同角三角函数基本关系式sin2α＋cos2α=1错误!=tanαtanαcotα=12．诱导公式 (奇变偶不变，符号看象限）（一）sin（π－α）＝___________ sin（π+α）＝ ___________ cos(π－α）＝___________ cos（π+α）＝___________tan（π－α）＝___________ tan(π+α）＝___________sin（2π－α）＝___________ sin（2π+α）＝___________cos（2π－α)＝___________ cos(2π+α）＝___________tan（2π－α)＝___________ tan（2π+α）＝___________（二） sin(错误!－α）＝____________ sin(错误!+α)＝____________cos（π2－α)＝____________ cos（错误!+α)＝_____________tan(错误!－α)＝____________ tan（错误!+α)＝_____________ sin(错误!－α)＝____________ sin(错误!+α）＝____________ cos（错误!－α)＝____________ cos(错误!+α)＝____________tan(3π2－α)＝____________ tan(错误!+α)＝____________sin(－α)＝－sinα cos(－α）=cosα tan(－α)=－tanα公式的配套练习sin(7π－α）＝___________ cos(5π2－α)＝___________cos(11π－α）＝__________ sin(错误!+α）＝____________3．两角和与差的三角函数cos(α+β)=cosαcosβ－sinαsinβcos（α－β)=cosαcosβ＋sinαsinβsin （α+β)=sinαcosβ＋cosαsinβsin （α－β)=sinαcosβ－cosαsinβtan（α+β）=tanα+tanβ1－tanαtanβtan（α－β）= 错误!4．二倍角公式sin2α=2sinαcosαcos2α=cos2α－sin2α＝2 cos2α－1＝1－2 sin2αtan2α=错误!5．公式的变形（1）升幂公式:1＋cos2α＝2cos2α 1-cos2α＝2sin2α（2）降幂公式：cos2α＝错误! sin2α＝错误!（3）正切公式变形：tanα+tanβ＝tan(α+β）（1－tanαtanβ)tanα－tanβ＝tan（α－β)(1＋tanαtanβ)（4）万能公式（用tanα表示其他三角函数值）sin2α＝错误! cos2α＝错误! tan2α＝错误!6．插入辅助角公式asinx＋bcosx=a2+b2 sin（x+φ) （tanφ= ba )特殊地：sinx±cosx＝错误!sin（x±错误!)7．熟悉形式的变形（如何变形）1±sinx±cosx 1±sinx 1±cosx tanx＋cotx错误!错误!若A、B是锐角,A+B＝错误!，则（1＋tanA）（1+tanB)=2cosαcos2αcos22α…cos2 nα= 错误!8．在三角形中的结论（如何证明)若：A＋B＋C=π错误!=错误!tanA＋tanB＋tanC=tanAtanBtanCtan错误!tan错误!＋tan错误!tan错误!＋tan错误!tan错误!＝19．求值问题(1）已知角求值题如：sin555°（2)已知值求值问题常用拼角、凑角如：1）已知若cos（错误!－α)＝错误!，sin（错误!＋β）＝错误!,又错误!<α〈错误!，0〈β<错误!,求sin（α＋β)。

解三角形讲解

注意角度的范围
求出的角度可能不在$0^circ$到$180^circ$之间，需要根据实际情况进行调整。
误区提示
避免将余弦定理与勾股定理混淆，余弦定理适用于任意三角形，而勾股定理仅适用于直角三角形。
实例分析
01
实例一
已知三角形两边及夹角，求第三边。可以通过代入余弦定理公式直接求
解。
02
实例二
已知三角形三边，求其中一个角。可以通过余弦定理公式变形，求出该
引入参数
当已知条件不足以直接求解时，可以引入参数，将问题转化为方程组求解。例如，在已知两边和夹角的情况下，可以引入时间参数，将问题转化为匀速直线运动问题求解。
多种方法综合运用策略
比较各种方法的优缺点
在解决复杂问题时，需要比较各种方法的优缺点，选择最合适的方法。例如，在求解三角形面积时，可以根据已知条件选择使用底乘高的一半、两边夹角的正弦值乘以半周长等方法。
三角形分类
按角分可分为锐角三角形、直角三角形、钝角三角形；按边分可分为不等边三角形、等腰三角形（包括等边三角形）。
三角形元素关系
三角形三边关系
任意两边之和大于第三边，任意两边之差小于第三边。
三角形三角关系
三角形三个内角之和等于180°。
三角形重要性质
三角形的稳定性
三角形具有稳定性，即三角形三边长度确定后，其形状和大小就唯一确定了。
在解三角形时，可以灵活运用多种方法进行求解，以便更快速地得到正确答案。
03
正弦定理在解三角形中应用
正弦定理公式及推导
正弦定理公式
在一个三角形中，各边和它所对角的正弦值的比相等，即 a/sinA = b/sinB = c/sinC。
推导过程

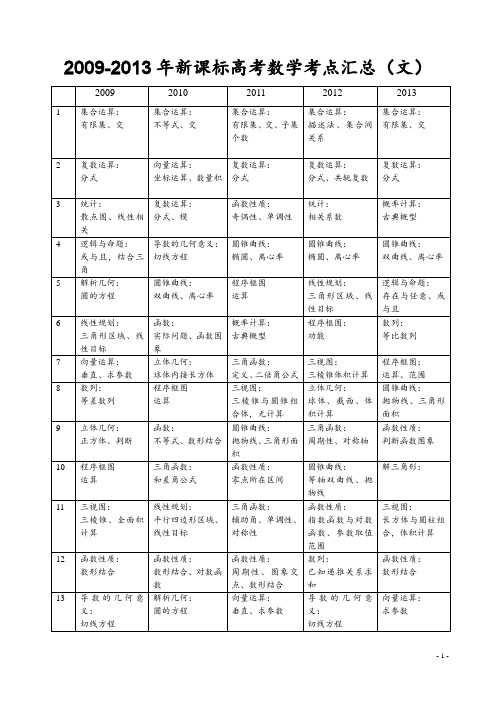
2009-2013年高考数学考点汇总

函数性质：数形结合
函数性质：数形结合、对数函数
函数性质：周期性、图象交点、数形结合向量运算：垂直、求参数
数列：已知递推关系求和导数的几何意义：切线方程
函数性质：数形结合
13
导数的几何意义：切线方程
解析几何：圆的方程
向量运算：求参数
14
圆锥曲线：抛物线
统计：随机模拟、样本推断总体
统计与概率：分段函数、分布
立体几何：线线垂直证明
-6-
反证法
线面角
二面角
列
线面角
19
统计与概率：独立重复试验概率、分布列
统计与概率：卡方检验
统计与概率：频数分布表、分布列
立体几何：线线垂直证明二面角
统计与概率：独立重复试验概率、分布列
20
解析几何：椭圆方程（待定系数法）、韦达定理
求参数的值
求参数的取值范围
-8-
解析几何：椭圆、韦达定理
解析几何：轨迹方程（直接法）、基本不等式
解析几何：抛物线、圆、基本量计算；
解析几何：轨迹方程（定义法）、韦达定理
21
导数：
导数：
导数：切线、求参数；不等式、分类讨论求参数取值范围
导数：单调区间不等式、综合转化
导数：切线、求参数；不等式、分类讨论求参数取值范围
8
三角函数：图象、求参数
9
函数性质：奇偶性、数形结合
三角函数：化简求值
定积分：面积
三角函数：单调性、的范围
二项式：系数、求参数的值
10
程序框图补全判断框

2013年高考数学预测新课标数学考点预测(14)：空间向量与立体几何

1 1 A(2, 0, 0), B(0, 0, 2), C (0, 2, 0), E(1, 0,1), F (1,1, 0), H (1, , ) 2 2 �� 1 1 �� 1 1 �� 所以 AH = ( −1, , ), OH = (1, , ), BC = (0, 2, −2) 2 2 2 2 �� 所以 AH ⋅ BC = 0, OH ⋅ BC = 0
所以 BC ⊥ 平面 OAH 由 EF ∥ BC 得 B1C1 ∥ BC ，故： B1C1 ⊥ 平面 OAH
(2)由已知 A1 ( , 0, 0), 设 B1 (0, 0, z )
3 2 �� 1 则 A1 E = ( − , 0,1), EB1 = ( −1, 0, z −1) 2 �� 由 A1E 与 EB1 共线得:存在 λ ∈ R 有 A1 E = λ EB1 得
∠ONC1 就是二面角 O − A1B1 − C1 的平面角。
作 EM ⊥ OB1 于 M ，则 EM ∥ OA ，则 M 是 OB 的中点，则 EM = OM = 1。设 OB1 = x ，由
OB1 OA1 x 3 得， = = ，解得 x = 3 ， MB1 EM x −1 2
在 Rt∆OA1 B1 中， A1 B1 = OA12 + OB12 =
⎧ 3 x1 = 0, ⎪ 因此 ⎨ 3 1 x1 + y1 + z1 = 0. ⎪ ⎩ 2 2
z1 = −1, 则m = (0, 2, −1),
因为 BD⊥AC，BD⊥PA，PA∩AC=A，所以 BD⊥平面 AFC，故又
�� BD 为平面 AFC 的一法向量.

2013届高考理科数学第一轮总复习-解斜三角形及其应用举例课件

• 所以2a2=a2+b2-2ab·cosC，
• 所以a2=b2-2ab·cos120°=b2-2ab·1(-
)=b2+ab，
2
• 所以a2-b2=ab，所以a2>b2，即a>b，故选A.
• 3.△ABC中,已知 sin A:sin B :sinC 1:1: 2 ,且
S△ABC1= ，A则B BC BC CA CA AB ( )2
• 解法1：sinA>sinB
•
sin( A B A - B ) - sin( A B - A - B ) 0
2
2
2
2
2cos A B sin A - B 0.
2
2
• 在△ABC中， 0 A B ,- A- B ,
• 所以sinA>sinB
2 sin
A
-2B
2 0
2 A
理公式的应用.若涉及面积问题时，还
需用到面积S公式1 ab：sin C 1 ac sin B 1 bc sin A.
2
2
2
在△ABC 中，内角 A，B，C 对边的边长分别是 a，b，c，已知 c＝2，C＝3π.
(1)若△ABC 的面积等于 3，求 a，b； (2)若 sinC＋sin(B－A)＝2sin2A，求△ ABC 的面积．
4
• 故选C.
题型1 利用正弦定理解三角形
• 1. (原创)在△ABC中，角A、B、C所对的边分
• 别 (1)为若aC、=b、c，，则且角a=A1=，__c_=___3__._；
• (2)若A= 36，则边b=____2或__61___.
•
解: (1)由正弦定理
a sin

【命中考心】2013高考数学必考点之三角函数典型解答题解读

【命中考心】2013高考数学必考点之三角函数典型解答题1在△ABC 中，角A 、B 、C 所对的边分别是a ，b ，c ，且.21222ac b c a =-+ （1）求B CA 2cos 2sin 2++的值；（2）若b=2，求△ABC 面积的最大值．解：(1) 由余弦定理：conB=14sin22A B++cos2B= -14 （2）由.415sin ,41cos ==B B 得 ∵b=2， a2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号)故S △ABC 的最大值为3152在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且.cos cos 3cos B c B a C b -= （I ）求cosB 的值；（II ）若2=⋅BC BA ，且22=b ，求c a 和b 的值.解：（I ）由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===，,0sin .cos sin 3sin ,cos sin 3)sin(,cos sin 3cos sin cos sin ,cos sin cos sin 3cos sin ,cos sin 2cos sin 6cos sin 2≠==+=+-=-=A B A A B A C B B A B C C B B C B A C B B C R B A R C B R 又可得即可得故则因此.31cos =B…………6分（II ）解：由2cos ,2==⋅B a BC BA 可得，,,0)(,12,cos 2,6,31cos 222222c a c a c a B ac c a b ac B ==-=+-+===即所以可得由故又所以a ＝c ＝ 63已知向量m =()B B cos 1,sin -, 向量n = （2，0），且m 与n 所成角为π3，其中A 、B 、C 是ABC ∆的内角。

2013年高考数学40个考点总动员考点14 解三角形(学生版) 新课标

2013年新课标数学40个考点总动员考点14 解三角形（学生版）【高考再现】热点一、利用正余弦定理在三角形中求三角函数值、求角、求边长1．（2012年高考（某某文））设△ABC 的内角A B C 、、的对边分别为a b c 、、,且1cos 4a b C ==1，=2，,则sin B =____2．（2012年高考（某某理））在ABC ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C =（）A ．725B ．725-C ．725±D ．24253．（2012年高考（某某理））在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为（） A 3B 2C ．12D ．12- 【答案】C【解析】:由余弦定理得,222221cos 242a b c a b C ab ab +-+==≥当且仅当a b 时取“=”,选C.4．（2012年高考（某某文））设ABC ∆的内角,,,A B C 所对的边分别为,,a b c ,若三边的长为连续的三个正整数,且A B C >>,320cos b a A =,则sin :sin :sin A B C 为（）A ．4∶3∶2B ．5∶6∶7C ．5∶4∶3D ．6∶5∶45．（2012年高考（某某文））在三角形ABC 中,角A,B,C 所对应的长分别为a,b,c,若a=2 ,B=6π,c=23,则b=______ 【答案】2【解析】:由余弦定理得,2222cos 4ba c ac B,所以2b.6．（2012年高考（某某文））在ABC ∆中,已知60,45,3BAC ABC BC ∠=︒∠=︒=,则AC =_______.【答案】2【解析】由正弦定理得32sin 45sin 60AC AC =⇒=︒︒7．（2012年某某文）在ABC ∆中,若60A ∠=︒,45B ∠=︒,32BC =,则AC =（）A ．43B ．23C ．3D ．328．（2012年高考（某某理））设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且35cos ,cos ,3,513A B b ===则c =______【答案】145c =【解析】由35412cos ,cos sin ,sin 513513A B A B ==⇒==,由正弦定理sin sin a b A B =得43sin 13512sin 513b A a B ⨯===, 由余弦定理2222142cos 25905605a cb bc A c c c =+-⇒-+=⇒=9．（2012年高考（理））在△ABC 中,若2a =,7b c +=,1cos 4B =-,则b =___________.10．（2012年高考（某某文））在△ABC 中,AC=7 ,BC=2,B =60°,则BC 边上的高等于（）A ．32B ．332C ．362+ D ．3394+11．（2012年高考（文））在△ABC 中,若3a =,3b =,3A π∠=,则C ∠的大小为___________.【答案】2π【解析】222cos 232b c a A c bc +-=⇒=而sin sin c a C A =,故sin 12C C π=⇒=.12．（2012年高考（某某理））设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c . 若()()a b c a b c ab +-++=,则角C =_________.13．（2012年高考（某某文））设ABC ∆的内角,,A B C 所对的边为,,a b c ,且有2sin cos sin cos cos sin B A A C A C =+(Ⅰ)求角A 的大小;(II) 若2b =,1c =,D 为BC 的中点,求AD 的长.14．（2012年高考（某某文））△ABC 中,角A,B,C 的对边分别为a,b,c.已知3cos(B-C)-1=6cosBcosC. (1)求cosA;(2)若a=3,△ABC 的面积为22,求b,c.【解析】(1)3(cos cos sin sin )16cos cos 3cos cos 3sin sin 13cos()11cos()3B C B C B C B C B C B C A π+-=⎧⎪-=-⎪⎪+=-⎨⎪⎪-=-⎪⎩则1cos 3A =. (2) 由(1)得2sin 3A =,由面积可得bc=6①,则根据余弦定理 2222291cos 2123b c a b c A bc +-+-===则2213b c +=②,①②两式联立可得32b a =⎧⎪⎨=⎪⎩或32a b =⎧⎪⎨=⎪⎩.15．（2012年高考（课标文））已知a ,b ,c 分别为ABC ∆三个内角A ,B ,C 的对边,3sin sin c a C c A =-.(Ⅰ)求A ;(Ⅱ)若a =2,ABC ∆的面积为3,求b ,c .16．（2012年高考（某某文））在ABC ∆中,内角,,A B C 所对的分别是,,a b c .已知22,2,cos a c A ===. (I)求sin C 和b 的值; (II)求cos(2)3A π+的值.17．（2012年高考（某某））在ABC ∆中,已知3AB AC BA BC •=•. (1)求证:tan 3tan B A =; (2)若5cos 5C =，求A 的值.18．（2012年高考（大纲文））ABC ∆中,内角成等差数列,其对边,,a b c 满足223b ac =,求A .19．（2012年高考（某某理））在ABC ∆中,角A 、B 、C 的对边分别为a ,b ,c .角A ,B ,C 成等差数列.(Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值.【方法总结】(1)已知两角一边可求第三角，解这样的三角形只需直接用正弦定理代入求解即可． (2)已知两边和一边对角，解三角形时，利用正弦定理求另一边的对角时要注意讨论该角，这是解题的难点，应引起注意．(3)熟练运用余弦定理及其推论，同时还要注意整体思想、方程思想在解题过程中的运用．热点二、利用正余弦定理判断三角形形状1．（2012年高考（某某理））在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是（）A ．锐角三角形.B ．直角三角形.C ．钝角三角形.D ．不能确定.【方法总结】依据已知条件中的边角关系判断三角形的形状时，主要有如下两种方法：1．利用正、余弦定理把已知条件转化为边边关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状；2．利用正、余弦定理把已知条件转化为内角的三角函数间的关系，通过三角函数恒等变形，得出内角的关系，从而判断出三角形的形状，此时要注意应用A ＋B ＋C ＝π这个结论．热点三、利用正余弦定理求三角形面积 1．（2012年高考（某某文））(本小题满分12分)在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知sin (tan tan )tan tan B A C A C +=. (Ⅰ)求证:,,a b c 成等比数列;(Ⅱ)若1,2a c ==,求△ABC 的面积S .2．（2012年高考（某某理））在△ABC 中,角A,B,C 的对边分别为a,b,c.已知,,sin()sin()444A b C cB a πππ=+-+=.(1)求证:2B C π-=(2)若a=2求△ABC 的面积.3．（2012年高考（某某理））在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B 5cos C . (Ⅰ)求tan C 的值;(Ⅱ)若a 2求∆ABC 的面积.【解析】(Ⅰ) ∵cos A =23>0,∴sin A 251cos A -=, 5C =sin B =sin(A +C )=sin A cos C +sin C cos A 5cos C +23sin C .整理得:tan C 5.(Ⅱ)由图辅助三角形知:sin C 56. 又由正弦定理知:sin sin a cA C=, 故3c =对角A 运用余弦定理:cos A =222223b c a bc +-=. (2)解(1) (2)得:3b =3舍去). ∴∆ABC 的面积为:S 5. 【方法总结】【考点剖析】一．明确要求1．考查余弦定理、三角形面积公式,考查方程思想、运算能力,是历年常考内容. 2．考查利用正、余弦定理判断三角形的形状． 3．考查利用正、余弦定理解任意三角形的方法．三．规律总结基础梳理1．正弦定理：a sin A ＝b sin B ＝csin C ＝2R ，其中R 是三角形外接圆的半径．由正弦定理可以变形为：(1)a ∶b ∶c ＝sin A ∶sin B ∶sin C ； (2)a ＝2R sin_A ，b ＝2R sin_B ，c ＝2R sin_C ；(3)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R等形式，以解决不同的三角形问题．2．余弦定理：a 2＝b 2＋c 2－2bc cos_A ，b 2＝a 2＋c 2－2ac cos_B ，c 2＝a 2＋b 2－2ab cos_C ．余弦定理可以变形为：cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 22ab.3．S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ＝abc 4R ＝12(a ＋b ＋c )·r (R 是三角形外接圆半径，r 是三角形内切圆的半径)，并可由此计算R ，r .4．已知两边和其中一边的对角，解三角形时，注意解的情况．如已知a ，b ，A ，则A 为锐角A 为钝角或直角图形关系式 a ＜b sin A a ＝b sin A b sin A ＜a ＜b a ≥b a ＞b a ≤b解的个数无解一解两解一解一解无解一条规律在三角形中，大角对大边，大边对大角；大角的正弦值也较大，正弦值较大的角也较大，即在△ABC 中，A ＞B ⇔a ＞b ⇔sin A ＞sin B . 两类问题两种途径根据所给条件确定三角形的形状，主要有两种途径：(1)化边为角；(2)化角为边，并常用正弦(余弦)定理实施边、角转换．【基础练习】.1．(人教A 版教材习题改编)在△ABC 中，A ＝60°，B ＝75°，a ＝10，则c 等于( )A ．52B ．102C.1063D ．5 62．（经典习题）在△ABC 中，若sin A a ＝cos Bb，则B 的值为( )．A ．30° B．45° C．60° D．90°5．（经典习题）在△ABC 中，a ＝3，b ＝1，c ＝2，则A 等于( )A ．30° B．45° C ．60° D．75°6．(教材习题改编)在△ABC 中，若a ＝18，b ＝24，A ＝45°，则此三角形有 () A ．无解 B ．两解C ．一解 D ．解的个数不确定【名校模拟】一．基础扎实2．(2012·某某质检)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若a ＝1，c ＝42，B ＝45°，则sinC 等于( )A.441 B.45C.425D.441413．(2011·某某二模)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若角A 、B 、C 依次成等差数列，且a ＝1，b ＝3，则S △ABC 等于( )A.2B.3C.32D ．2 4．（海淀区高三年级第二学期期末练习文）在ABC ∆中，若0120A =，6c ，ABC∆的面积为93，则a =.5．(市西城区2012届高三下学期二模试卷理)在△ABC 中，3BC =，2AC =，π3A =，则B = _____．8．（某某省某某市2012届高三3月（二模）月考理）（本小题满分12分）在△ABC 中，角A,B,C 所对的边分别为a,b,c ,且满足cos 525A =,3AB AC •= （1）求△ABC 的面积；（2）若c =1,求a 、sin B 的值. 二．能力拔高2．(2012年某某豫东、豫北十所名校阶段性测试(三）理)在ΔABC 中，内角A ，B ，C 的对边分别是a ，b,c.若，且=，则b=（）A ．4B.3C.2D.13．(2012东城区普通高中示X 校高三综合练习（二）理)在ABC ∆中,角,,A B C 所对的边分别为c b a ,,，若sin 3sin A C =， 30=B ，2=b ，则边c =4．(2012年某某市高中毕业班第二次调研测试文)在△ABC 中，角,,A B C 的对边分别为,,a b c ，已知274sin cos 222A B C +-=，且5a b +=，7c =，则△ABC 的面积为________.5．(2012年高三教学测试（二）理)在ABC ∆中，角C B A ,,的对边分别为c b a ,,，若C a c b cos 21=-，则=A ． 6．（某某省某某市2012届高三3月（二模）月考文）在△ABC 中，sin 2C =3sin A sin B +sin 2B ，a =23b ，则角C = .7．(某某省八校2012届高三第一次联考理)设△ABC 的内角A 、B 、C 所对的边分别为a ，b ，c ，且5tan cos cos ,7tan Aa Bb Ac B-=则=。

解三角形完整讲义(精心整理)

正余弦定理知识要点：1、正弦定理:2sin sin sin a b c R A B C===或变形：::sin :sin :sin a b c A B C =. 2、余弦定理：2222222222cos 2cos 2cos a b c bc A b a c ac B c b a ba C ⎧=+-⎪=+-⎨⎪=+-⎩或 222222222cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩. 3、解斜三角形的常规思维方法是：（1）已知两角和一边（如A 、B 、C ），由A+B+C=π求C ，由正弦定理求a 、b ；（2）已知两边和夹角（如a 、b 、c ），应用余弦定理求c 边；再应用正弦定理先求较短边所对的角，然后利用A+B+C=π，求另一角；（3）已知两边和其中一边的对角（如a 、b 、A ），应用正弦定理求B ，由A+B+C=π求C ，再由正弦定理或余弦定理求c 边，要注意解可能有多种情况；（4）已知三边a 、b 、c ，应余弦定理求A 、B ，再由A+B+C=π，求角C 。

4、判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式.5、解三角形问题可能出现一解、两解或无解的情况，这时应结合“三角形中大边对大角定理及几何作图来帮助理解”。

6、已知三角形两边a,b,这两边夹角C ，则S ＝1/2*absinC7、三角学中的射影定理：在△ABC 中，A c C a b cos cos ⋅+⋅=，…8、两内角与其正弦值：在△ABC 中，B A B A sin sin <⇔<，…【例题】在锐角三角形ABC 中，有（B ）A ．cosA>sinB 且cosB>sinA B ．cosA<sinB 且cosB<sinAC ．cosA>sinB 且cosB<sinAD ．cosA<sinB 且cosB>sinA9、三角形内切圆的半径：2S r a b c ∆=++，特别地，2a b c r +-=斜直正弦定理专题：公式的直接应用1、已知ABC △中，a =b =60B =，那么角A 等于（）A ．135B ．90C ．45D ．302、在△ABC 中，a ＝32，b ＝22，B ＝45°，则A 等于（ C ）A ．30°B ．60°C ．60°或120°D ．30°或150°3、ABC △的内角A B C ，，的对边分别为a b c ，，，若120c b B ===，则等于（）AB ．2 CD4、已知△ABC 中，30A =，105C =，8b =，则a 等于（B ） A ．4B.5、在△ABC 中，＝10，B=60°,C=45°,则c 等于（ B ）A ．310+B ．()1310-C ．13+D ．3106、已知ABC ∆的内角A ，B ，C 所对的边分别为a ，b ，c ，若31sin =A ，B b sin 3=，a则a 等于．（33） 7、△ABC 中，45B =，60C =，1c =，则最短边的边长等于（A ）128、△ABC 中，:1:2A B =，C 的平分线CD 把三角形面积分成3:2两部分，则cos A =（C ） A.13B.12C.34D.0 9、在△ABC 中，证明：2222112cos 2cos b a b B a A -=-。

2013云南高考数学大纲公式答题技巧复习资料

2013年云南高考数学大纲公式答题技巧复习目录考点1集合与简易逻辑典型易错题会诊命题角度1 集合的概念与性质命题角度2 集合与不等式命题角度3 集合的应用命题角度4 简易逻辑命题角度5 充要条件探究开放题预测预测角度1 集合的运算预测角度2 逻辑在集合中的运用预测角度3 集合的工具性预测角度4 真假命题的判断预测角度5 充要条件的应用考点2 函数(一) 典型易错题会诊命题角度1 函数的定义域和值域命题角度2 函数单调性的应用命题角度3 函数的奇偶性和周期性的应用命题角度4 反函数的概念和性质的应用探究开放题预测预测角度1 借助函数单调性求函数最值或证明不等式预测角度2 综合运用函数奇偶性、周期性、单调进行命题预测角度3 反函数与函数性质的综合考点3 函数(二)典型易错题会诊命题角度1 二次函数的图象和性质的应用命题角度2 指数函数与对数函数的图象和性质的应用命题角度3 函数的应用探究开放题预测预测角度1 二次函数闭区间上的最值的问题预测角度2 三个“二次”的综合问题预测角度3 含参数的对数函数与不等式的综合问题考点4 数列典型易错题会诊命题角度1 数列的概念命题角度2 等差数列命题角度3 等比数列命题角度4 等差与等比数列的综合命题角度5 数列与解析几何、函数、不等式的综合命题角度6 数列的应用探究开放题预测预测角度1 数列的概念预测角度2 等差数列与等比数列预测角度3 数列的通项与前n项和预测角度4 递推数列与不等式的证明预测角度5 有关数列的综合性问题预测角度6 数列的实际应用预测角度7 数列与图形考点5 三角函数典型易错题会诊命题角度1 三角函数的图象和性质命题角度2 三角函数的恒等变形命题角度3 三角函数的综合应用探究开放题预测预测角度1 三角函数的图象和性质预测角度2 运用三角恒等变形求值预测角度3 向量与三角函数的综合考点6 平面向量典型易错题会诊命题角度1 向量及其运算命题角度2 平面向量与三角、数列命题角度3 平面向量与平面解析几何命题角度4 解斜三角形探究开放题预测预测角度1 向量与轨迹、直线、圆锥曲线等知识点结合预测角度2 平面向量为背景的综合题考点7 不等式典型易错题会诊命题角度1 不等式的概念与性质命题角度2 均值不等式的应用命题角度3 不等式的证明命题角度4 不等式的解法命题角度5 不等式的综合应用探究开放题预测预测角度1 不等式的概念与性质预测角度2 不等式的解法预测角度3 不等式的证明预测角度4 不等式的工具性预测角度5 不等式的实际应用考点8 直线和圆典型易错题会诊命题角度1 直线的方程命题角度2 两直线的位置关系命题角度3 简单线性规划命题角度4 圆的方程命题角度5 直线与圆探究开放题预测预测角度1 直线的方程预测角度2 两直线的位置关系预测角度3 线性规划预测角度4 直线与圆预测角度5 有关圆的综合问题考点9 圆锥曲线典型易错题会诊命题角度1 对椭圆相关知识的考查命题角度2 对双曲线相关知识的考查命题角度3 对抛物线相关知识的考查命题角度4 对直线与圆锥曲线相关知识的考查命题角度5 对轨迹问题的考查命题角度6 考察圆锥曲线中的定值与最值问题探究开放题预测预测角度1 椭圆预测角度2 双曲线预测角度3 抛物线预测角度4 直线与圆锥曲线预测角度5 轨迹问题预测角度6 圆锥曲线中的定值与最值问题考点10 空间直线与平面典型易错题会诊命题角度1 空间直线与平面的位置关系命题角度2 空间角命题角度3 空间距离命题角度4 简单几何体探究开放题预测预测角度1 利用三垂线定理作二面角的平面角预测角度2 求点到面的距离预测角度3 折叠问题考点11 空间向量典型易错题会诊命题角度1 求异面直线所成的角命题角度2 求直线与平面所成的角命题角度3 求二面角的大小命题角度4 求距离探究开放题预测预测角度1 利用空间向量解立体几何中的探索问题预测角度2 利用空间向量求角和距离考点12 排列、组合、二项式定理典型易错题会诊命题角度1 正确运用两个基本原理命题角度2 排列组合命题角度3 二项式定理探究开放题预测预测角度1 在等可能性事件的概率中考查排列、组合预测角度2 利用二项式定理解决三项以上的展开式问题预测角度3 利用二项式定理证明不等式考点13 概率与统计典型易错题会诊命题角度1 求某事件的概率命题角度2 离散型随机变量的分布列、期望与方差命题角度3 统计探究开放题预测预测角度1 与比赛有关的概率问题预测角度2 以概率与统计为背景的数列题预测角度3 利用期望与方差解决实际问题考点14 极限典型易错题会诊命题角度1 数学归纳法命题角度2 数列的极限命题角度3 函数的极限命题角度4 函数的连续性探究开放题预测预测角度1 数学归纳法在数列中的应用预测角度2 数列的极限预测角度3 函数的极限预测角度4 函数的连续性考点15 导数及其应用典型易错题会诊命题角度1 导数的概念与运算命题角度2 导数几何意义的运用命题角度3 导数的应用探究开放题预测预测角度1 利用导数的几何意义预测角度2 利用导数探讨函数的单调性预测角度3 利用导数求函数的极值和最考点16 复数典型易错题会诊命题角度1 复数的概念命题角度2 复数的代数形式及运算探究开放题预测预测角度1 复数概念的应用预测角度2 复数的代数形式及运算考点7不等式不等式的概念与性质均值不等式的应用不等式的证明不等式的解法不等式的综合应用不等式的概念与性质不等式的解法不等式的证明不等式的工具性不等式的实际应用典型易错题会诊命题角度1不等式的概念与性质1．(典型例题)如果a 、b 、c 满足c<b<a ，且ac<0，那么下列选项中不一定成立的是 ( ) A ．ab>ac B ．c(b-a)>0C ．cb 2<ab 2D ．dc(a-c)<0[考场错解] A ∵b>c ，而ab ，ao 不一定成立，原因是不知a 的符号．[专家把脉] 由d>b>c ，且ac<0．则。

2013高考文科数学(全国卷大纲版)解析版全word版

2013年普通高等学校招生全国统一考试数学（文科）一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、设集合{}{}1,2,3,4,5,1,2,u U A A ===集合则ð（A ）{}1,2 （B ）{}3,4,5 （C ）{}1,2,3,4,5 （D ）∅ 【答案】B【解析】由补集定义易得{}3,4,5U C A =,故选B. 【考点定位】补集的概念 2、已知a 是第二象限角，5sin ,cos 13a a ==则（A ）1213- （B ）513- （C ）513 （D ）1213 【答案】A【解析】因为α是第二象限角，∴12cos 13α===-，故选A. 【考点定位】考查同角三角函数基本关系式3、已知向量()()()()1,1,2,2,,=λλλ=+=++⊥-若则m n m n m n（A ）4- （B ）3- （C ）-2 （D ）-1 【答案】B【解析】∵()(),+⊥-m n m n ∴()()0+⋅-=m n m n ∴220-=m n即()()2211[24]0λλ++-++=∴3λ=-，故选B. 【考点定位】考查向量垂直，数量积坐标运算.4、不等式222x -<的解集是（A ）()-1,1 （B ）()-2,2 （C ）()()-1,00,1 （D ）()()-2,00,2【答案】D【解析】22|2|2222x x -<⇒-<-<2040||2x x ⇒<<⇒<<2002x x ⇒-<<<<或，故选D.（也可用排除法）【考点定位】绝对值不等式的解法，一元二次不等式的解法5、()862x x +的展开式中的系数是（A ）28 （B ）56 （C ）112 （D ）224 【答案】C【解析】26262+18=2112T C x x ⋅=，故选C【考点定位】二项式定理的通项公式 6、函数()()()-121log 10=f x x f x x ⎛⎫=+> ⎪⎝⎭的反函数（A ）()1021x x >- （B ）()1021xx ≠- （C ）()21x x R -∈ （D ）()210x x -> 【答案】A【解析】由()2111log 11221yy y f x x x x ⎛⎫==+⇒+=⇒= ⎪-⎝⎭， ∵0x >∴0y >∴()11(0)21xfx x -=>-，故选A. 【考点定位】考查求反函数，指数式和对数式的互化. 7、已知数列{}n a 满足12430,,3n n a a a ++==-则{}n a 的前10项和等于（A ）()-10-61-3 （B ）()-1011-39（C ）()-1031-3 （D ）()-1031+3 【答案】C【解析】∵130,n n a a ++=∴113n n a a +=-，∴数列{}n a 是以13-为公比的等比数列.∵24,3a =-∴14a = ∴10101014[1()]33(13)113S ---==-+，故选C.【考点定位】考查等比数列的通项与求和.8、已知()()1221,0,1,0,F F C F x -是椭圆的两个焦点过且垂直于轴的直线交于 A B 、两点，且3AB =，则C 的方程为（A ）2212x y += （B ）22132x y += （C ）22143x y += （D ）22154x y +=第 3 页共 10 页【答案】C【解析】如图，21213||||,||222AF AB F F ===,由椭圆定义得， 13||22AF a =-○1在Rt △12AF F 中， 2222212123||||||()22AF AF F F =+=+○2由○1○2得，2a =∴2223b a c =-=，∴椭圆C 的方程为22143x y +=，故选C. 【考点定位】椭圆方程的求解9、若函数()()sin 0=y x ωϕωω=+>的部分图像如图，则（A ）5 （B ）4 （C ）3 （D ）2 【答案】B【解析】由题中图象可知0042T x x π+-=,∴2T π= ∴22ππω=∴4ω=，故选B【考点定位】三角函数的图象与解析式10、已知曲线()421-128=y x ax a a =+++在点，处切线的斜率为，（A ）9 （B ）6 （C ）-9 （D ）-6 【答案】D【解析】由题意知311|(42)|428x x y x ax a =-=-'=+=--=，则6a =-.故选D 【考点定位】导数的几何意义11、已知正四棱锥1111ABCD A BC D -中，12,AA AB =则CD 与平面1BDC 所成的角的正弦值等于（A ）23 （B）3 （C）3（D ）13【答案】A【解析】如图，在正四棱锥1111ABCD A BC D -中，连结AC 、BD 记交点为O ,连结1OC ,过C 作CH ⊥1OC 于点H,∵BD ⊥AC ，BD ⊥1AA ，∴BD ⊥平面11ACC A ∵CH ⊂平面11ACC A∴CH ⊥BD,∴CH ⊥平面1C BD ∴∠CDH 为CD 与平面1BDC 所成的角.1OC=. 由等面积法得，1OC ·CH=OC ·1CC ，∴222CH ⋅= ∴23CH =∴223sin 13CH CDH CD ∠===，故选A【考点定位】线面角的定义求法12、已知抛物线2:8C y x =与点()2,2M -，C 的焦点，且斜率为k 的直线与C 交于A,B 两点，若0MA MB =，则k =(A)12 （B）2（C（D ）2 【答案】D【解析】设直线AB 方程为(2y k x =-），代入28y x =得2222(48)40k x k x k -++=设1122(,),(,)A x y B x y ，则212248k x x k++=，124x x =（*） ∵0MA MB ⋅=∴1122(2,2)(2,2)0x y x y +-⋅+-= 即1212(2,)(2)(2)(2)0x x y y +++--=即121212122()42()40x x x x y y y y ++++-++=○1 ∵1122(2)(2)y k x y k x =-⎧⎨=-⎩∴1212(4)y y k x x +=+-○22212121212(2)(2)[2()4]y y k x x k x x x x =--=-++○3 由（*）及○1○2○3得2k =，故选D 【考点定位】直线与抛物线相交问题二、填空题：本大题共4小题，每小题5分.13、设()f x 是以2为周期的函数，且当[)1,3x ∈时，()=2f x x -，则()1f -= .第 5 页共 10 页【答案】1-【解析】∵()f x 是以2为周期的函数，且[)1,3x ∈时，()=2f x x -，则()1(12)(1)121f f f -=-+==-=- 【考点定位】函数的周期性，函数求值14、从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有种.（用数字作答）【答案】60【解析】分三步：第一步，一等奖有16C 种可能的结果；第二步，二等奖有25C 种可能的结果；第三步，三等奖有33C 种可能的结果,故共12365360C C C =有种可能的结果.【考点定位】组合问题15、若x y 、满足约束条件0,34,34,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩则z x y =-+的最小值为 .【答案】0【解析】z x y =-+y x z ⇒=+，z 表示直线y x z =+在y 轴上的截距，截距越小，z 就越小.画出题中约束条件表示的可行域（如图中阴影部分所示），当直线过点A(1，1)时，min 0z =【考点定位】线性规划求最值16、已知圆O 和圆K 是球O 的大圆和小圆，其公共弦长等于球O 的半径，3602OK O K =，且圆与圆所在的平面所成角为，则球O 的表面积等于 .【答案】16π【解析】如图，设MN 为公共弦，长度为R,E 为MN 的中点，连结OE,则OE ⊥MN,KE ⊥MN.∠OEK 为圆O 与圆K 所在平面的二面角.∴∠OEK=60°. 又∵△OMN 为正三角形.∴OE=2R . ∵OK=32且OK ⊥EK ∴3sin 602OE ⋅︒=∴3222R ⋅=∴R=2.∴2416S R ππ==【考点定位】二面角与球的表面积三、解答题：解答应写出文字说明、证明过程或演算步骤.17．（本小题满分10分）等差数列{}n a 中，71994,2,a a a ==（I ）求{}n a 的通项公式；（II ）设{}1,.n n n nb b n S na =求数列的前项和【解析】(Ⅰ)设等差数列{}n a 的公差为d ，则1(1)n a a n d =+-因为719942a a a ==⎧⎨⎩，所以11164182(8)a d a d a d +=+=+⎧⎨⎩解得11a =，12d =，所以{}n a 的通项公式为12n n a +=. （Ⅱ）2)1122(1n n a n n b n n n ==-++=所以2222222)()()122311(n n n S n n -+-++-=+=+ 【考点定位】等差数列通项公式和裂项求和方法18．（本小题满分12分）设△ABC 的内角A,B,C的对边分别为,,a b c ，()()a b c a b c ac ++-+= （Ⅰ）求;B （Ⅱ）若1sin sin ,4A C =求C. 【解析】(Ⅰ)因为()()a b c a b c ac ++-+=，所以222a cb ac +-=-由余弦定理得2221cos 22a cb B ac +-==-，因此B=120°. （Ⅱ）由(Ⅰ)知A+C=120°，所以cos()cos cos sin sin A C A C A C -=+coscos sin sin 2sin sin AC A C A C =-+=cos()2sin sin A C A C ++=122+=第 7 页共 10 页故30A C -=︒或30A C -=-︒，因此C=15°或C=45°.【考点定位】考查余弦定理、两角和与差的公式以及求角问题，考查学生的转化能力和计算能力19．（本小题满分12分）如图，四棱锥902,P ABCD ABC BAD BC AD PAB PAD -∠=∠==∆∆中，，与都是边长为2的等边三角形.（I ）证明：;PB CD ⊥（II ）求点.A PCD 到平面的距离【解析】(Ⅰ)证明：取BC 的中点E ，连结DE ，则ABED 为正方形.过P 作PO ⊥平面ABCD,垂足为O.连结OA,OB,OD,OE.由△PAB 和△PAD 都是等边三角形知PA=PB=PD,所以OA=0B=OD,即点O 为正方形ABED 对角线的交点，故OE ⊥BD,从而PB ⊥OE.因为O 是BD 的中点，E 是BC 的中点，所以OE ∥CD,因此;PB CD ⊥（Ⅱ）解：取PD 的中点F ，连结OF,则OF ∥PB ，由(Ⅰ)知，;PB CD ⊥，故OF ⊥CD.又12OD BD ==OP == 故△POD 为为等腰三角形，因此OF ⊥PD.又PD ∩CD=D ，所以OF ⊥平面PCD. 因为AE ∥CD ，CD ⊂平面PCD 的，AE ⊄平面PCD,所以AE ∥PCD. 因此，O 到平面PCD 的距离OF 就是A 到平面PCD 的距离，而112OF PB ==. 所以A 到平面PCD 的距离为1.【考点定位】(1)解题的关键是辅助线的添加，取BC 的中点E 是入手点，然后借助三垂线定理进行证明；（2）求点面距离的求解方法比较多，在解题过程中，如何根据题设条件恰当选择相适应的方法是比较棘手的问题 20．（本小题满分12分）甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为1,2各局比赛的结果都相互独立，第1局甲当裁判.（I ）求第4局甲当裁判的概率；（II ）求前4局中乙恰好当1次裁判概率.【解析】(Ⅰ)记1A 表示事件“第2局结果为甲胜”， 2A 表示事件“第3局甲参加比赛时，结果为甲负”，A 表示事件“第4局甲当裁判”，则12A A A =⋅,12()()P A P A A =⋅12()()P A P A ⋅14= （Ⅱ）记1B 表示事件“第1局结果为乙胜”2B 表示事件“第2局乙参加比赛时，结果为乙胜”3B 表示事件“第3局乙参加比赛时，结果为乙胜”B 表示事件“前4局中乙恰好当1次裁判” 则1312312B B B B B B B B =⋅+⋅⋅+⋅，所以1312312()()()()P B P B B P B B B P B B =⋅+⋅⋅+⋅1312312()()()()()()()()P B P B P B P B P B P B P B P B =⋅+⋅⋅+⋅ 11154848=++= 【考点定位】考查独立事件和互斥事件的概率问题以及离散型数学期望，考查分析问题和计算能力21．（本小题满分12分）已知函数()32=33 1.f x x ax x +++（I ）求()f ;a x =的单调性；（II ）若[)()2,0,.x f x a ∈+∞≥时，求的取值范围【解析】(Ⅰ)当a =()32=3 1.f x x x -++ ()2=33f x x '-+.令()0f x '=，得121,1x x =.当(1)x ∈-∞时，()0f x '>，()f x 在(1)-∞上是增函数；当1)x ∈时，()0f x '<，()f x 在1)上是减函数；当1,)x ∈+∞时，()0f x '>，()f x 在1,)+∞上是增函数；（Ⅱ）由(2)0f ≥得54a ≥-. 当54a ≥-，(2,)x ∈+∞时， ()22251=3633(21)3(1)3()(2)22f x x ax x ax x x x x '-+=-+≥-+=--所以()f x 在(2,)+∞是增函数，于是当[2,)x ∈+∞时，()f x (2)0f ≥≥.第 9 页共 10 页综上，a 的取值范围是5[,)4-+∞【考点定位】考查利用导数求解函数的单调性与参数范围问题 22．（本小题满分12分）已知双曲线()221222:10,0x y C a b F F a b-=>>的左、右焦点分别为，，离心率为3，直线2y C =与（I ）求,;a b ；（II ）2F l C A B 设过的直线与的左、右两支分别相交于、两点，且11,AF BF -证明：22.AF AB BF 、、成等比数列【解析】(Ⅰ)由题设知3c a =，即2229a b a+=，故228b a =. 所以C 的方程为22288x y a -=.将2y =代入上式，求得x =由题设知，=21a =. 所以1a =，b =（Ⅱ）由(Ⅰ)知，1(3,0)F -，2(3,0)F ,C 的方程为2288x y -=○1 由题意可设的l 方程为(3)y k x =-，||k <，代入○1并化简得，2222(8)6980k x k x k -+--=，设1122(,),(,)A x y B x y ，11x ≤-，21x ≥则212268k x x k +=-，2122988k x x k +=-于是11||(31)AF x ===-+12||31BF x ===+由11||||AF BF =得123(1)31x x -+=+，即1223x x +=-故226283k k =--解得245k =从而12199x x =-由于21||13AF x ===-22||31BF x ===-故2212||||||23()4AB AF BF x x =-=-+=，221212||||3()9116AF BF x x x x ⋅=+--= 因而222||||||AF BF AB ⋅=，所以22||,||,||AF AB BF 成等比数列.【考点定位】本题考查双曲线方程与直线与双曲线的位置关系，考查设而不求的思想及就是能力。

2013数学高考题分类选编解三角形

正弦定理和余弦定理一、选择题1.（2013·北京高考文科·Ｔ5）在△ABC 中，a=3,b=5,sinA=13,则sinB=( )A.15B.59C.53D.1 【解题指南】已知两边及一边的对角利用正弦定理求解。

【解析】选B 。

由正弦定理得355,,sin 1sin sin sin 93所以所以===a b B A BB 。

2.（2013·新课标全国Ⅱ高考文科·Ｔ4）ABC ∆的内角,,A B C 的对边分别为,,a b c ，已知2b =，6B π=，4C π=，则ABC ∆的面积为（） A.232+ B.31+ C.232- D.31- 【解题指南】利用正弦定理和三角形的面积公式可得【解析】选B.因为,64B C ππ==,所以712A π=.由正弦定理得sinsin64b c ππ=，解得22c =。

所以三角形的面积为117sin 222sin 2212bc A π=⨯⨯. 因为73221231sinsin()()12342222222πππ=+=⨯+⨯=+，所以1231sin 22()312222bc A =⨯+=+，选B. 3.（2013·新课标Ⅰ高考文科·Ｔ10）已知锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，02cos cos 232=+A A ，7=a ，c=6，则=b （） A.10 B.9 C.8 D.5【解题指南】由02cos cos 232=+A A ，利用倍角公式求出A cos 的值，然后利用正弦定理或余弦定理求得b 的值.【解析】选D.因为02cos cos 232=+A A ，所以01cos 2cos 2322=-+A A ，解得251cos 2=A ，方法一:因为△ABC 为锐角三角形，所以51cos =A ,562sin =A . 由正弦定理C c A a sin sin =得，Csin 65627=. 35612sin =C ，3519cos =C .又)(C A B +-=π，所以C A C A C A B sin cos cos sin )sin(sin +=+=，17565035612513519562sin =⨯+⨯=B .由正弦定理B b A a sin sin =得, 1756505627b =，解得5=b .方法二:由余弦定理A bc c b a cos 2222-+=，51cos =A ，则495112362=⨯-+b b ，解得5=b 4.（2013·陕西高考文科·Ｔ9）【备注：（2013·陕西高考理科·Ｔ7）与之题干相同】设△ABC 的内角A , B , C 所对的边分别为a, b, c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为 ( ) A. 直角三角形B. 锐角三角形C. 钝角三角形D. 不确定【解题指南】在含有边角关系式的三角函数恒等变形中,利用正弦定理将边的关系式化为角的正弦式或利用余弦定理将余弦式化为边的关系式,这是判断三角形形状的两个转化方向.【解析】选A.因为bcosC+ccosB=asinA ,所以由正弦定理得sinBcosC+sinCcosB=sin 2A,所以sin(B+C)=sin 2A, sinA=sin 2A, sinA=1,所以三角形ABC 是直角三角形.5.（2013·安徽高考文科·Ｔ9）【备注：（2013·安徽高考理科·Ｔ12）与之题干相同】设△ABC 的内角A,B,C 所对边的长分别为a,b,c.若b+c=2a,则3sinA =5sinB ,则角C= ( ) A.π3 B. 2π3C.3π4 D. 5π6【解题指南】根据正弦定理、余弦定理进行解三角形计算。

2013年新课标高考数学考纲解读

2013年高考数学考试大纲权威解读适用于：河南，黑龙江，吉林，陕西，宁夏，海南，内蒙古2013年全国新课标数学学科《考试大纲》和《考试说明》文理科和2012年对比，在内容、能力要求、时间、分值（含选修比例）、题型题量等几个方面都没有发生变化。

注重对数学思想与方法的考查，体现数学的基础、应用和工具性的学科特色，多视角、多维度、多层次地考查数学思维品质和思维能力，考查考生对数学本质的理解，考查考生的数学素养和学习潜能。

新课标考试说明与去年的考试说明比较，可以看出：依然是对如下知识和能力的考查1.坚持对五种能力的考查：（1）空间想象能力：能根据条件作出正确的图形，根据图形想象出直观形象；能正确地分析出图形中基本元素及其相互关系；能对图形进行分解、组合；会运用图形与图表等手段形象地揭示问题的本质.这一能力的考查在试卷中主要以立体几何中的三视图得以体现，且难度有逐年递增的趋势。

（2）抽象概括能力：对具体的、生动的实例，在抽象概括的过程中，发现研究对象的本质；从给定的大量信息材料中，概括出一些结论，并能应用于解决问题或作出新的判断.（3）推理论证能力：根据已知的事实和已获得的正确数学命题，论证某一数学命题真实性的初步的推理能力．推理包括合情推理和演绎推理，论证方法既包括按形式划分的演绎法和归纳法，也包括按思考方法划分的直接证法和间接证法．一般运用合情推理进行猜想，再运用演绎推理进行证明.（4）运算求解能力：会根据法则、公式进行正确运算、变形和数据处理，能根据问题的条件，寻找与设计合理、简捷的运算途径；能根据要求对数据进行估计和近似计算.（5）数据处理能力：会收集、整理、分析数据，能从大量数据中抽取对研究问题有用的信息，并作出判断．数据处理能力主要依据统计或统计案例中的方法对数据进行整理、分析，并解决给定的实际问题.2.两个意识的考查：（1）应用意识：能综合应用所学数学知识、思想和方法解决问题，包括解决在相关学科、生产、生活中简单的数学问题；能理解对问题陈述的材料，并对所提供的信息资料进行归纳、整理和分类，将实际问题抽象为数学问题，建立数学模型；应用相关的数学方法解决问题并加以验证，并能用数学语言正确地表达和说明.应用的主要过程是依据现实的生活背景，提炼相关的数量关系，将现实问题转化为数学问题，构造数学模型，并加以解决.（2）创新意识：能发现问题、提出问题，综合与灵活地应用所学的数学知识、思想方法，选择有效的方法和手段分析信息，进行独立的思考、探索和研究，提出解决问题的思路，创造性地解决问题．创新意识是理性思维的高层次表现.对数学问题的“观察、猜测、抽象、概括、证明”，是发现问题和解决问题的重要途径，对数学知识的迁移、组合、融会的程度越高，显示出的创新意识也就越强.3．2013年高考数学主客观题考试特点：理科必考知识点（即近三年高考每年都考的知识点，主要针对客观题）：复数、常用逻辑用语、程序框图、三视图、球的组合体、概率、函数与导数、圆锥曲线、三角函数等。

2013年高考试题分项版解析数学(文)专题04三角函数与解三角形(Word精析版)

第四章三角函数与解三角形一．基础题组1. 【 2013 年一般高等学校招生全国一致考试（江西卷）文科】若 sina3 ，则 cosa （）23A ． 2B． 1C．1D．23 333[答案]C[分析]cos1 2sin 21 2 ( 3 )2 1 . 选C.23 3[ 考点定位 ] 本题主要观察三角恒等变换里面的二倍角余弦公式、三角函数求值问题.2.【 2013 年一般高等学校一致考试一试题纲领全国文科】已知 a 是第二象限角， sin a5 , 则 cosa （）125（C ）5（D ）1213（ A ）（ B ）13131313【答案】 A【分析】∵ a 是第二象限角，∴cos1 sin 21(5)212 .应选 A.1313【考点定位】三角求值3. 【 2013 年一般高等学校招生全国一致考试（广东卷）文科】已知 sin(5)1，那么 cos（）211 2 25A ．B ．C ．555D ．5【答案】 C【分析】 sin(5) sin(2 +) sincos1，选 C.2225【考点定位】三角函数引诱公式.4. 【 2013 年一般高等学校一致考试一试题纲领全国文科】若函数y sinx0 的部分图像如图，则= （）（A ） 5（B ） 4 （C ） 3（D ） 2【答案】 Bx 0x 0 T2.∴4 .应选 B.【分析】∵由题中图像可知4. ∴ T. ∴222【考点定位】三角函数的图像与分析式.5. 【2013年一般高等学校招生全国一致考试（四川卷）文科】函数2f ( x )2 s i n (x)(0, 的部)分图象如下图，则 ,的值分22别是（）O（A ） 2,3（B ） 2,-26（C ） 4,6（D ） 4,3【答案】 A11π 125π 12【分析】由图知，周期T 知足1T11 5 ，∴ T ，又0 ，∴2 ，故 f (x)2sin(2 x ) ，212 12图象的最高点为5 , 2 ，于是由“五点法”作图，知25，解得，选 A.121223【易错点】注意求初相的值时，图象的最高点坐标与五个重点点坐标的对应关系最简单代错！【考点定位】本题观察正弦型函数 f (x) Asin( x) 的图象与性质，难点是确立初相的值，重点是理解“五点法”作图 .6. 【 2013 年高考新课标Ⅱ数学（文）卷】已知 sin2α=错误！未找到引用源。