第三章 二维基本图形元素生成算法
第3章-2D基本图形生成算法

基本图形生成算法
点、线、面、字符
线——图元扫描转换
直线段扫描转换 圆(椭圆)弧扫描转换
曲线(第六章)
面——多边形区域填充
字符
图形反走样
圆弧的扫描转换
圆的八对称性
只考虑第二个八分圆
y
(-x,y) (x,y)
假设圆心在原点 x2+y2=R2
(-y,x) (-y,-x) (-x,-y)
注:网格点表示象素
void DDALine(int x0,int y0,int x1,int y1,int color) int x; float dx, dy, y, k; dx= x1-x0 ; dy=y1-y0; k=dy/dx; y=y0; for (x=x0; xx1, x++) drawpixel (x, int(y+0.5), color); y=y+k;
e0=y/ x-0.5
y方向走一步
当e<0时,最接近P1(xi+1,yi)
y方向不走步
有除法,不宜硬件实现
Bresenham画线算法(5/7)
e=e×2x,不影响判断的准确性 e0=2y - x 当e≥0时,最接近P2(xi+1,yi+1) y方向走一步 P 当e<0时,最接近P1(xi+1,yi) y方向不走步
a = y0-y1=-2, b = x1-x0 = 5 d0 = 2a+b = 1, d1= 2a = - 4, d2 = 2(a+b)=6
i 1 2 3 4
xi 0 1 2 3
yi 0 0 1 1 2
d 1 -3 3 -1 5
基本图形元素的生成算法

3.1直线的生成算法
直线的扫描变换,对计算机图形学来说,就是在数字设备上绘制一条直线。由 于显示屏是有限象素点构成,所以具体是指在有限个象素组成的矩阵中,确定 最佳逼近这条直线的一组象素,并按扫描线顺序,用当前写的方式,对这些象 素进行写的操作。
3.1.1 点的生成
在光栅显示器中,点就是一个像素(点),它是显示器的最小单位,是最基 本的图形元素。不同于只有位置没有大小的几何点。光栅显示器的屏幕分 辨率,是由像素点的多少决定的,每个像素点与显示缓冲器中每一个位相 对应,因为显示缓冲存储容量有限,像素点也有限。
光栅显示器上显示的图形,称之为光栅图形。光 栅显示器可以看作是一个象素矩阵,在光栅显 示器上显示的任何一个图形,实际上都是一些 像素的集合。由于对一个具体的光栅显示器来 说,象素个数是有限的,象素的颜色和灰度等 级也是有限的,象素是有大小的,所以光栅图 形只是近似的实际图形。如何使光栅图形最完 美地逼近实际图形,便是光栅图形学要研究的 内容。确定最佳逼近图形的像素集合的过程称 为图形的扫描转换或光栅化。
(0,0)
扫描转换:通常把图像中的点、线、圆、区域和字符等图形基本指令组成的 显示文件转换成为显示缓冲器中图像的位映像图的过程,成为扫描转换。
位图:是与屏幕图像每个像素点一一对应的图像矩阵,矩阵中的每个元 素就是像素的值(表示灰度级别与色彩)。
选择扫描转换算法,速度与图像质量两者之间权衡折衷。由于在建立 一幅图形过程中,基本的图形扫描转换算法将被调用成百上千此,因 此,速度快一些是比较可取的。
(X1,Y1)的像素点,对应的显示缓冲器地址为: 字节地址= S + ( H / 8 ) * Y1 + ( X1 / 8 ) 的整数部分 字节内的位地址= X1 / 8 的余数
计算机图形学第3章 基本图形生成算法

例题:有点P0(4,3);P1(6,5);P2(10,
6 );P3(12,4),用以上4点构造2次B样条曲线。
2.1.7 非均匀有理B样条
非均匀有理B样条NURBS(Non Uniform Rational BSpline);
3.2.2
Bresenham画圆法
该算法是最有效的算法之一。
不失一般性,假设圆心(xc,yc) ,圆上的点(x′,y′),则:
x' x xc
y ' y yc
圆心为原点,半径为R的位于第一象限1/8圆弧的画法,即(0, R)~( R , R )。
2 2
yi ), 思想:每一步都选择一个距离理想圆周最近的点P( xi , 使其误差项最小。
画其他曲线。
3.3
自由曲线的生成
正弦函数曲线
指数函数曲线
多项式函数曲线
自 由 曲 线
概率分布曲线及样条函数曲线
3.3.1 曲线的基本理论
基本概念
2.1.4
规则曲线:可用数学方程式表示出来的,如抛物 线等。
自由曲线:很难用一个数学方程式描述的,如高
速公路等。可通过曲线拟合(插值、逼近)的方法来
例题: 利用Bresenham算法生成P (0,0)到Q(6,5)的直 线所经过的像素点。要求先 列出计算式算出各点的坐标 值,然后在方格中标出各点。
(1,1)
3.1.5 双步画线法 原理
模式1:当右像素位于右下角时,中间像素位于底线 模式4:当右边像素位右上角时,中间像素位于中线 模式2和模式3:当右像素位于中线时,中间像素可能位于底线 上,也可能位于中线上,分别对应于模式2和模式3,需进一步 判断。 当0≤k≤1/2时,模式4不可能出现,当1/2≤k≤1时,模式1不 可能出现。
二维图形的生成技术

U× V V
U
u是垂直于U和V的单位向量。u的方向由右手定则判定。两相 量的叉积是一垂直于两向量所在平面的向量,大小等于这两个向 量形成的平行四边形的面积。在笛卡尔坐标系,叉积的分量为:
uu vy uz,0 ,u vzux , uxvy vxuy U V U V sin x Yv z zv
§3.1预备知识
1. 显式、隐式和参数表示
③参数方程表示
为了解决这些问题,可考虑用参数方程表示曲线和曲面。 笛卡尔坐标的参数表示形式: x=x(t) y=y(t) z=z(t) 在曲线、曲面的表示上,参数方程比显式、隐式方程有更多 的优越性。 2. 搞清:位臵矢量(向量)、切矢量、法矢量、曲率。
§3.2直线的生成
标系。
§3.1预备知识
3. 观察坐标系 (Viewing Coordinate System)
为了在计算机中产生三维物体的视图, 必须规定观察点(视点)和观察方向。 y z o 一般采用三维左手直角坐标系:观察 x
好比照相时选择拍摄的位臵和方向。
视点
坐标系的原点通常设臵在观察点(视点),Z轴作为观察方向。 作用有两个:一是用于指定裁剪空间,确定形体的那一部 分要显示出来;二是通过定义观察(投影)平面,把三维形体 的用户坐标系变换成规格化的设备坐标。
§3.1预备知识
三、矩阵运算
1.矩阵的含义 矩阵:由m×n个数按一定位臵排列的一个 整体,简称m×n矩阵。
a11 a12 ... a1n a 21 a 22 ... a 2 n A= ... ... ... am1 am 2 ... amn
其中, ij 称为矩阵A的第i行第j列元素
a
§3.1预备知识
计算机地图制图原理与方法基本图形生成算法

该程序如何改进, 提高效率?
while(x<y){
setpixel(x,y);
if(d<0){
d+ = 2*x+3; x++
}
else{
d+ = 2*(x-y) + 5;
x++;y--;
}
}
}
整理课件
28
Bresenham画圆算法
讨论、圆的中点算法与Bresenham算法是否一致?
整理课件
29
椭圆的生成算法
内存 插槽
D/A转换:图形显示
整理课件
2
整理课件
3
基本图形的生成
几何图形G={Pi | Pi 最接近图形的象素 } 基本图形的生成算法任务之一就是找出所有的Pi .
点表示为象素(Pixel),对应于显存地址单元 读写某一象素是硬件设备提供的最基本功能 一维图形,由一个象素宽的直线或曲线表示 二维图形由确定区域的象素表示 线图元的扫描转换是基本图形生算法的基础;
整理课件
6
画直线的DDA算法
8
从起点开始朝终点方向
7
画点(x, y)
6
前未 5
四4
舍 五
3
入2
1 起点0
在x轴或y轴上走一个单位
终 点
长(沿x轴还是y轴取决于
直线的倾斜角)
由直线的倾斜程度(斜率 或斜率的倒数)决定另一 坐标的增量,获得下一点 的座标
将x或y四舍五入,得(x, y)
0 1 2 3 4 5 6 7 8 9 若(x, y)不是终点则继续
y=y+k;
}
缺点:
}
浮点运算、取整--》废时,且不利于硬件实现。
基本图形元素生成算法
实验一基本图形元素生成算法1.实验目的:(1)掌握基本图形元素生成算法。
(2)了解高级语言的图形模式的设定和对基本图形类(或函数)的调用方法。
2.实验内容:选定Bresenham算法,编写生成该基本图形的源程序,并能在计算机上编译运行,画出正确的图形。
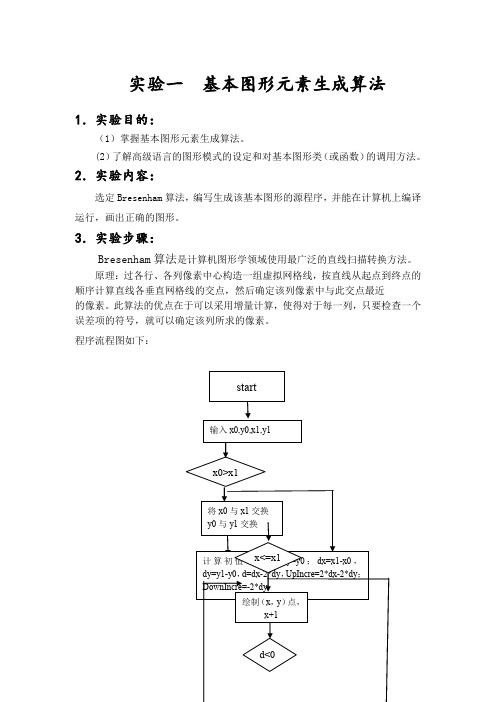
3.实验步骤:Bresenham算法是计算机图形学领域使用最广泛的直线扫描转换方法。
原理:过各行、各列像素中心构造一组虚拟网格线,按直线从起点到终点的顺序计算直线各垂直网格线的交点,然后确定该列像素中与此交点最近的像素。
此算法的优点在于可以采用增量计算,使得对于每一列,只要检查一个误差项的符号,就可以确定该列所求的像素。
程序流程图如下:程序如下function MidBresenhamline( x0, y0, x1,y1) if x0>x1x=x1;x1=x0;x0=x;y=y1;y1=y0;y0=y;endx=x0;y=y0;dx=x1-x0;dy=y1-y0;d=dx-2*dy;UpIncre=2*dx-2*dy;DownIncre=-2*dy;while x<=x1axis([x0 x1 y0 y1])plot([x],[y],'*');grid onhold onx=x+1;if d<0y=y+1;d=d+UpIncre;elsed=d+DownIncre;endpause(0.1);endt=x0:1:x1yy=(y1-y0)./(x1-x0)*t+(y1-((y1-y0)./(x1-x0)*x1)); plot(t,yy)程序运行如下>> MidBresenhamline( 0, 0, 8,5)t =0 1 2 3 4 5 6 7 8>> MidBresenhamline( 0, 0, 500,750)运行过程中的截图效果4.实验总结:1.通过学习使用中点Bresenham算法画直线,对于斜率大于1的直线段,只需交换x和y之间的规则即可。
第3章基本图形的生成与计算

2.中点画线算法
3.直线的Bresenham算法
2021年3月4日星期四
14
3.2 直线段的生成算法
第3章 基本图形的生成与计算
画一条从(x1,y1)到(x2,y2)的直线,实质上是确定 最佳逼近直线的像素序列,并填入色彩数据的过程。
当我们对直线进行光栅化时,只能在显示器所给定的 有限个象素组成的矩阵中,确定最佳逼近于该直线的一 组象素,并且按扫描线顺序,对这些象素进行写操作, 这就是通常所说的用显示器绘制直线或直线的扫描转换。
2021年3月4日星期四
10
3.1 基本绘图元素
第3章 基本图形的生成与计算
✓ 1.在几何学中,一个点即没有大小,也没有维数,点只是 表示坐标系统中的一个位置。
✓ 2.在计算机图形学中,点是用数值坐标来表示的。在直角 坐标系中点由(x,y)两个数值组成的坐标表示,在三维坐 标系中点由(x,y,z)三个数值组成的坐标表示,如下图:
此时 |K|<1
本算法的基本思想:从直线的起点开始,选定 x2 x1 和
y2 y1 中较大者为步进方向,不妨假设 x2 x1 较大,即让 x从起点到终点变化,每步递增1(即一个像素单位),然
后利用递推式 yi1 yi kx 计算相应的y值,取像素
点 ( xi 1, round ( yi1) )作为当前点坐标输出到显示器上, 则得到光栅化的直线。
第3章 基本图形的生成与计算
Loading …………
欢迎进入
第 3章
第3章 基本图形的生成与计算
本章概述:主要介绍了基本图形的生成与计
算,包括:基本绘图元素,直线段、圆与椭圆的 生成算法,区域填充算法,字符的生成,图
第三讲基本图形生成

两种定义方法: 1)像素理想化为点
2)像素有一定面积
`
2013年8月13日11时54分
倘若已知直线段两端点的坐标(x0,y0)(x1,y1), 如何求得屏幕上显示的各点的坐标?
2013年8月13日11时54分
根据直线方程表达式: y=m×x+b 其中:m是直线的斜率, b是y方向的截距。
2013年8月13日11时54分
(x,y)坐标
…
地址线性表 1D表示 显示屏幕 2D表示
像素由其左下角坐标表示
y ymax ymin x
xmin
xmax
地址 = (xmax-xmin) * (y-ymin) + (x-xmin) + 基地址
每行像素点数
行数
行中位置
Address(x,y) = (xmax-xmin) * (y-ymin) + (x-xmin) + 基地址 = k1 + k2y + x 对像素连续寻址时,如何减少计算量? Address(x±1,y) = k1 + k2y + (x±1) = Address(x,y) ± 1 Address(x,y±1) = k1 + k2(y ±1) + x = Address(x,y) ± k2 Address(x±1,y±1) = k1 + k2(y ±1) + (x±1)
直线Bresenham算法描述
由图中可以知道:在x=xi+1处,直线上点的y值是y=m(xi+1)+b,该 点离象素点(xi+1,yi)和象素点(xi+1,yi+1)的距离分别是d1和d2: d1=y-yi=m(xi+1)+b-yi d2=(yi+1)-y=(yi+1)-m(xi+1)-b 两个距离差是 d1-d2=2m(xi+1)-2yi+2b-1
第三章 二维图形的生成_直线和圆

Q
M
P=(xp,yp)
P1
当d<0,M在直线(Q点)下方,取右上方P2 ; 当d>0,M在直线(Q点)上方,取右方P1;
当d=0,选P1或P2均可,约定取P1; 能否采用增量算法呢?
2013-10-30 西安工程大学计算机图形学 17
4.1 直线段的扫描转换算法
4.1.2、中点画线法
情形1.若d0 ->M在直线上方->取P1; 此时再下一个象素的判别式为
西安工程大学计算机图形学
2013-10-30
8
4.1 直线段的扫描转换算法
4.1.1、数值微分法(DDA)
当 x 1 得
y1 y0 yi 1 yi x1 x0
即:当x方向每递增1像素,y方向递增k(即直线斜 率);每次通过上式计算出(xi , yi )取整后输出 显示器。 注意上述分析的算法仅适用于k ≤1的情形。在这 种情况下,x每增加1,y最多增加1。
2013-10-30
西安工程大学计算机图形学
9
4.1 直线段的扫描转换算法
注:当 k 1 时,必须把x,y位置互换,即利用递推 1 式 xi 1 xi y ,y每增加1,x相应增加 1 k 。 k
所以取 x2 x1 和 y2 y1 中较大者为步进方向,如下 图
当 k 1时
画线从(x0, y0)开始,d 的初值
d0=F(x0+1, y0+0.5)= a(x0 +1)+b(y0 +0.5)+c
= F(x0, y0)+a+0.5b = a+0.5b 由于只用 d 的符号作判断,为了只包含整数运算, 可以用2d 代替 d 来摆脱小数,提高效率。 即d0=2*a+b 若d0 若d<0
计算机图形学基本图形生成算法

y= k· x+b
k=0.571429
b=0.428571
2 X[0]=1 y0 X[1]=2
Y[0]=1 Y[0]=1 Y[1]=kx[1]+b=1.57 Y[1]=y0+k=1.57 Y[2]=y1+k=2.14 Y[2]=kx[2]+b=2.14 Y[3]=y2+k=2.71 Y[3]=kx[3]+b=2.71 Y[4]=y3+k=3.28 Y[4]=kx[4]+b=3.28 Y[5]=y4+k=3.85 Y[5]=kx[5]+b=3.85 Y[6]=y5+k=4.4 Y[6]=kx[6]+b=4.4 Y[7]=5 Y[7]=5
第3章 基本图形生 成算法
1 直线生成算法(DDA、BRES) 2 圆生成算法(Mid) 3 多边形填充算法(扫描线、区域) 4 字符图元算法
2015/4/19
1
图元
• 图元:图形软件包中用了描述各种几何 图形元素的函数称为图形输出原语,简 称图元。 • 描述对象几何要素的输出图元一般称为 几何图元。点的定位和直线段是最简单 的几何图元。 • 在选定坐标系中指定一个图形的几何要 素后,输出图元投影到该输出设备显示 区域对于的二维平面上,并扫描转换到 帧缓存的整数像素位置。
2015/4/19
5
1 直线生成算法(DDA、BRES) 2 圆生成算法(Mid) 3 多边形填充算法(扫描线、区域) 4 字符图元算法
1 直线的DDA算法
2015/4/19
6
OpenGL画点和画线函数 1) 画点函数 glVertex*( ); (*={234}{sifd}[v]) 表示该函数有后缀,指 明空间尺寸、坐标数据类型或向量形式描述。 Ex: glBegin(GL_POINTS); glVertex2i(100,50); glEnd(); glBegin(GL_POINTS); glVertex2i(100,50); glVertex2i(75,90); glVertex2i(300,590); glEnd();
计算机图形学二维图形的生成

#include <math.h>
setbkcolor(9);
#define PI 3.1415926
setcolor(4);
main()
for(a=0;a<=2*PI;a+=PI/n)
{
{
int x,y,rl,rs,n;
x=rl*cos(a)+320;
double a;
y=rl*sin(a)+240;
line(480,120,480,360); lineto(480,120);
line(480,360,160,360); lineto(480,360);
line(160,360,160,120); lineto(160,360);
getch();
lineto(160,120);
closegraph();
cleardevice();
}
用C语言图形函数绘制图形
题目:将圆周等分成n等份,然后用直线将各等分点两 两相连。
要求:等份点数n在23-31之间,半径在100-200之间, 能接受用户输入,并使圆心位于屏幕的中心位置。
用C语言图形函数绘制图形
题目:画出如图所示的图形。 要求:图形的大小位置如图所示。等分数n在15-20之
该函数只对部分函数有效。
绘图函数—点
void putpixel(int x,int y,int color)
在屏幕指定位置(x,y)处,用color指定的颜色画一点。
void moveto(int x,int y)
将当前光标位置移到(x,y)处
void moverel(int deltax,int deltay)
颜色信息
第三讲:二维图形生成算法

圆的扫描变换
利用对称性可以 加速画圆过程; 只需计算45°弧 段,通过对称变换 可完成整圆.
圆的扫描变换(中点算法)
思路:当前显示点P=(Xp,Yp),取第 二八分圆
圆方程为x2+y2=R2 ,因此 令:F(x,y)=x2+y2 -R2
中间点M=(Xp+1,Yp-(1/2))
令: d=F(M)
判断: d=0 中点在圆上; 点亮可取E 或 SE d<0 中点在圆内; 点亮可取E d>0 中点在圆外;点亮可取SE
y2=y1+dy=y1+(x2-x0)dA
其中角度的增量dA很小,用弧度表示,A是圆弧的张角。
基本增量算法
• 考虑基本增量算法是否是最优的! 1.运算符的快速性 采用增量思想的DDA算法,每计算一个象素, 只需计算一个加法。加法已经是最快的算法 了(加减乘除开方三角函数等) 2.参数运算的快速性 DDA算法的计算中含有浮点数运算。把浮点 运算的加法变成整数加法,因为整数的加法 比浮点的加法要快很多
二维图形生成算法
•二维图形生成算法
•线段的扫描变换
•基本增量算法 •中点线算法 •Bresenham画线算法
•圆与椭圆的扫描变换
线段的扫描变换
线段的扫描变换
• 象素,中心位于均衡栅格上的离散圆点 。 • 直线扫描变换算法就是获得一系列象素 的坐标,使这些象素落在所要近似的理 想直线上或位于该直线的附近。原则上 讲,象素序列应尽可能逼近理想的直线, 而且尽可能直一些。
基本增量算法
直线方程:y=mx+b ,0<m<1, m= △y/ △x= △y ; x=1,xi+1=xi+ 1,yi+1=yi+m
二维基本图元生成ok

边界表示
枚举出边界上所有的像素; 边界上的所有像素着同一颜色; 内部像素着与边界像素不同的颜色;
4.2 种子填充 区域填充
将指定的颜色从种子点扩展到整个区域的过程
例子: 例子:PaintBrush
例子: 例子:PhotoShop
4.3 种子填充
连通性:4连通,8连通 4连通:
8连通
4.3 种子填充
4 区域填充 4.1扫描线算法的基本原理
基本思想:
按扫描线顺序,计算扫描线与多边形的相交区间,再用 要求的颜色显示这些区间的象素,即完成填充工作.
对于一条扫描线填充过程可以分为四个步骤:
(1)求交; (2)排序; (3)配对; (4)填色.
4.1 扫描线算法的基本原理
8 7 6 5 4 3 2
P6(2,7)
2.1 逐点比较法
2.1 逐点比较法
xi +1 = xi + 1 Fi +1 = x A yi +1 y A xi +1 = x A yi y A ( xi + 1) = x A yi y A xi y A = Fi y A
2.1 逐点比较法
事例:
2.2 DDA算法
条件:
待扫描转换的直线段:P0 ( x0, y 0) P ( x1, y1) 1 斜率:m = y / x
x 0 1 2 3 4
y 0 0 1 1 2
e -0.5 -0.1 0.3 -0.3 0.1
3 2 1 0 1 2 3 4 5
5 2 -0.5
3,曲线的生成
3,曲线的生成
圆弧的生成 规则曲线的生成 自由曲线的生成
3.1 圆弧的生成
处理对象:圆心在原点的圆弧 圆的八对称性 生成圆弧的隐函数方法
第3章 二维图元生成技术 计算机图形学

两个距离的差
d 1 d 2 2k ( xi 1) 2 yi 2b 1
若此差值为正,则d1>d2,下一个像素点应取 P2 (xi +1, yi+1);若此差值为负,d1<d2,下一个像素点应 取P1 (xi+1, yi);若此差值为零,则d l=d2,下一 个像素点可取两个像素点中的任意一个.
dy=abs(y2-y1);
if(dx<dy){iTag=1;Swap(x1, y1);Swap(x2, y2);Swap(dx, dy);} tx=(x2-x1)>0?1:-1;ty=(y2-y1)>0?1:-1; curx=x1;cury=y1; inc1=2*dy;inc2=2*(dy-dx);d=inc1-dx;
k
y1 y 0 y x1 x0 x
d i 1 d i 2y xi 1 2x yi 1 2y xi 2x yi
d 当di≥0时,yi+1=yi+1, i 1 di (2y 2x) 当di≤0时,yi+1=yi d i 1 d i 2y 初始判别量d0
5 4
29
3.1.3 Bresenham算法
已经确定的像素为P(xi yi),下一个可选 择的像素点为P1(xi+1, yi)和P2(xi+1, yi +1) )两者中的一个
3.1.3 Bresenham算法
在x=xi+1处直线上点y=k(xi+1)+b,该点到P1 (xi+ 1, yi)和P2 (xi+1, yi+1)的距离分别令为d1和d2:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图3-2-3 10
3.2.1 DDA算法
DDA算法程序:
void LineDDA ( int x0,int y0,int x1,int y1,int color) /* 假定x0<x1,-1<=k<=1 */ { int x,y; float dx, dy, k; dx= float(x1-x0); dy= float(y1-y0); k=dy/dx; y=y0; for(x=x0; x<= x1, x++) { Putpixel(x, int(y+0.5), color); y+=k; } }
{( xi , yi ,r )}i 0 {( xi , yi )}i 0 yi,r round( yi ) (int)( yi 0.5)
复杂度:乘法+加法+取整
图3-2-2 9
3.2.1 DDA算法
DDA算法(增量算法)
复杂度:加法+取整 算法
yi 1 m xi 1 B m ( xi 1) B m xi B m yi m
void InterBresenhamline (int x0,int y0,int x1, int y1,int color) { dx = x1-x0; dy = y1- y0; e=-dx; x=x0; y=y0; for (i=0; i<= dx; i++) {Putpixel (x, y, color); x++; e=e+2*dy; if (e>= 0) { y++; e=e-2*dx;} } }
22
3.2.2 画线中点算法
中点算法程序 MidPointLine(x0,y0,x1,y1,color) {int x0,y0,x1,y1,color; int a,b,d1,d2,x,y; a = y0-y1; b = x1 – x0; d = 2 * a +b; d1 = 2*a; d2 = 2*(a+b); x = x0; y = y0; PutPixel(x,y,color); while (x<x1) {if (d<0){ x++; y++; d +=d2;} else { x++; d +=d1;} PutPixel(x,y,color); } }
13
3.2.1 DDA算法
改进算法(增量DDA)
优化点:
增加斜率判断并改变循环参数
14
3.2.1DDA算法
DDA画线算法程序(改进) void LineDDA ( int x0,int y0,int x1,int y1,int color) { int x,y;float dx, dy,k,l,m; dx= float(x1-x0); dy= float(y1-y0); k=dy/dx; if (abs(k)<1) { for(x=x0; x<= x1, x++) { Putpixel(x, int(y+0.5), color); y+=k; } } else { for(y=y0; y<= y1, y++) { Putpixel(int(x+0.5),y,color); x+=1/k; } } ? 如果x0> x1怎么办?
图3-2-10 27
3.2.3 画线Bresenham算法
为方便计算,令e=d-0.5,e的初值为-0.5,增量为k。 当e≥0时,取当前象素(xi,yi)的右上方象素( xi+1,yi+1 ) ; 而当e<0时,更接近于右方象素( xi+1,yi ) 。
28
3.2.3 画线Bresenham算法
Bresenham画线算法程序
void Bresenhamline (int x0,int y0,int x1, int y1,int color) { int x, y, dx, dy; float k, e; dx = x1-x0; dy = y1- y0; k=dy/dx; e=-0.5; x=x0; y=y0; for (i=0; i<=dx; i++) { Putpixel (x, y, color); x=x+1; e=e+k; if (e>= 0) { y++, e=e-1;} } }
19
3.2.2 画线中点算法
问题:判断距直线最近的下一个象素点
构造判别式:d=F(M)=F(xp+1,yp+0.5) 由d>0,d<0可判定下一个象素,
P2 P
P1
图3-2-7 20
3.2.2 画线中点算法
要判定再下一个象素,分两种情形考虑:
1)若d≥0,取正右方象素P1,再下一个象素判定,由 d1=F(xp+2,yp+0.5)=a(xp+2)+b(yp+0.5)+c=d+a,d的增量 是a 2)若d<0,取右上方象素P2,再下一个象素, 由:d2=F(xp+2,yp+1.5)=d+a+b d的增量为a+b P2 P1 P
16
3.2.2 画线中点算法
基本原理:
画直线段的过程中,当前象素点为(xp, yp),一个象素点有两 种可选择点p1(xp+1, yp)或p2(xp+1, yp+1)。若M=(xp+1, yp+0.5) 为p1与p2之中点,Q为理想直线与x=xp+1垂线的交点。当M 在Q的下方,则P2 应为下一个象素点;M在Q的上方,应取 P1 为下一点。
15
3.2.2 画线中点算法
目标:消除DDA算法中的浮点运算(浮点数取整运
算,不利于硬件实现; DDA算法,效率低)
条件:
同DDA算法 斜 率: m [0,1]
直线段的隐式方程((x0,y0)(x1,y1)两端点) F(x,y)=ax+by+c=0
式中 a=y0-y1,b=x1-x0,c=x0y1-x1y0
3
3.1 简单的二维图形显示流程
图元 裁剪和扫描
显 示
图3-1-1 二维图形显示流程
裁剪和扫描
图形显示前需要进行扫描转换+裁剪,这一过程有三种方 法: ● 裁剪 ---〉扫描转换:最常用,节约计算时间。 ● 扫描转换 ---〉裁剪:算法简单; ● 扫描转换到画布 --〉位块拷贝:算法简单,但耗时耗 内存。常用于字符显示。
11
3.2.1 DDA算法
举例:用DDA方法扫描转换连接两点P0(0,0)和P1(5,2)的直线 段 x int(y+0.5) 0 0 1 0 2 1 3 1 4 2 y+0.5 0 0.4+0.5 0.8+0.5 1.2+0.5 1.6+0.5
图3-2-4 12
3.2.1 DDA算法
特点1 注意上述分析的算法仅适用于|k| ≤1的情形。在这种情况下, x每增加1, y最多增加1。当 |k| > 1时,必须把x,y地位互换, y每增加1,x相应增加1/k。 特点2 在这个算法中,y与k必须用浮点数表示,而且每一步都要 对y进行四舍五入后取整。这使得它不利于硬件实现 。
25
3.2.3 画线Bresenham算法 如下图所示。 设直线方程为 ,其中k=dy/dx。 假设x 列的象素已经确定为xi,其行坐标为yi。那么下一个象素的 列坐标为xi+1,而行坐标要么不变为yi,要么递增1为yi+1。
图3-2-10
26
3.2.3 画线Bresenham算法 是否增1取决于如图所示误差项d的值。因为直线的起 始点在象素中心,所以误差项d的初值d0=0。x下标每增 加1,d的值相应递增直线的斜率值k,即d=d+k。一旦 d≥1,就把它减去1,这样保证d在0和1之间。当d≥0.5时, 直线与xi+1列垂直网格交点最接近于当前象素( xi ,yi)的右 上方象素( xi +1, yi +1 ) ;而当d<0.5时,更接近于右方象 素( xi +1,yi ) 。
31
3.3圆弧的扫描转换
处理对象:圆心在原点的圆弧 圆的八对称性
图3-3-1 32
3.3圆弧的扫描转换
两种直接离散方法:
离散点:
利 隐 数 程 用 函 方
x2 y 2 R2
( xi , yi R 2 xi2 ) 取整 (xi,yi ,r )
离散角度:
x R cos 利用参数方程 y R sin (round( R cos i ), round( R sin i ))
第三章 二维基本图形元素生成算法
1
基本概念
所谓图元的生成,是指完成图元的参数表示形 式(由图形软件包的使用者指定)到点阵表示 形式(光栅显示系统刷新时所需的表示形式) 的转换。通常也称扫描转换图元
2
课程内容
§3.1 简单的二维图形显示流程
§3.2 直线段的扫描转换 §3.3 圆弧的扫描转换 §3.4 易画曲线的正负法 §3.5 线画图元的属性控制
图3-2-5 17
3.2.2 画线中点算法
直线的正负划分性
点与直线的关系: on: F(x,n: F(x, y)<0;
图3-2-6
18
3.2.2 画线中点算法
欲判断中M在Q点的上方还是下方,只要把M代F(x,y)并 判断它的符号。 构造判别式: d=F(M)=F(xp+1, yp+0.5) =a(xp+1)+b(yp+0.5)+c 当d<0,M在Q点下方,取P2为下一个象素; 当d>0,M在Q点上方,取P1为下一个象素; 当d=0,选P1或P2均可,约定取P1为下一个象素
