点的坐标规律题
九年级数学中考规律探究问题(点的坐标变化)

专题6规律探究点的坐标 姓名________1.如图所示,平面直角坐标系的原点O 是等边△ABC 的中心,A (0,1),把△ABC 绕点O 顺时针旋转,每秒旋转60∘,则第2017秒时,点A 的坐标为( D )A.2.如图,半径为2的正六边形ABCDEF 的中心在坐标原点O,点P 从点B 出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P 的坐标是( C )A.3.如图,在平面直角坐标系xOy 中,点A(1,0),B(2,0),正六边形ABCDEF 沿x 轴正方A. C 或EB. B 或DC. A 或ED. D 或F4.正方形A 1B 1C 1O,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图的方式放置。
点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y=x+1和x 轴上,则点B 2018的坐标是____________.),122(201720185.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行。
从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是( 14,14 )6.如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4 …,以此类推,得到等腰直角三角OA2017A2018,则点A2017的坐标为_________.),0(21008小结:一个图形的变化,找循环节,循环次数;不同图形的变化,用列举法,找数列的变化规律,有时会用到一次函数或二次函数求数列的第n项。
4平面直角坐标系-点的坐标的确定基础题和培优题

平面直角坐标系【点的坐标的确定】【基础练习】1.已知点P的坐标为(﹣2,a2+1),则点P一定在()A.第一或第三象限B.第二或第四象限C.第二象限D.第三象限2.点P(m+3,m+1)在直角坐标系x轴上,则点P坐标为()A.(0,﹣2)B.(0,2)C.(﹣2,0)D.(2,0)3.点B(﹣3,4)关于y轴的对称点为A,则点A的坐标是()A.(3,4)B.(﹣4,﹣3)C.(4,﹣3)D.(﹣3,﹣4)4.已知A(2,﹣5),AB平行于y轴,则点B的坐标可能是()A.(﹣2,5)B.(2,6)C.(5,﹣5)D.(﹣5,5)5.点M(﹣4,3)关于y轴对称的坐标为()A.(4,3)B.(﹣4,﹣3)C.(4,﹣3)D.(﹣4,3)6.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为()A.(3,2)B.(3,1)C.(2,2)D.(﹣2,2)7.点M(3,﹣4)关于x轴的对称点M′的坐标是()A.(3,4)B.(﹣3,﹣4)C.(﹣3,4)D.(﹣4,3)8.已知y轴上的点P到原点的距离为5,则点P的坐标为()A.(5,0) B.(0,5)或(0,﹣5) C.(0,5) D.(5,0)或(﹣5,0)9.若|m|=2,|n|=3,则点A(m,n)()A.四个象限均有可能B.在第一象限或第三象限或第四象限C.在第一象限或第二象限D.在第二象限或第三象限或第四象限10. 点M (1,2)关于x 轴对称点的坐标为( )A 、(-1,2)B 、(-1,-2)C 、(1,-2)D 、(2,-1)11. 在直角坐标系中,如果a 为正数,那么点(0,a )在( )A .x 轴正半轴上B .x 轴负半轴上C .y 轴正半轴上D .y 轴负半轴上12. 在y 轴上且到点A (0,4)的线段长度为5的点B 的坐标是( )A .(0,9)B .(0,-1)C .(9,0)或(-1,0)D .(0,9)或(0,-1)13. 点P 的横坐标是-3,且到x 轴的距离为5,则P 点的坐标是( )A .(5,-3)或(-5,-3)B .(-3,5)或(-3,-5)C .(-3,5)D .(-3,-5)14. 若4,5==b a ,且点M (a ,b )在第二象限,则点M 的坐标是( )A .(5,4)B .(-5,4)C .(-5,-4)D .(5,-4)15. 如果点P (x ,y )满足xy=0,那么点P 必定在( )A .原点上B .x 轴上C .y 轴上D .坐标轴上16. 在平面直角坐标系中,点P (2,﹣3)关于原点对称点P′的坐标是 .17. 在平面直角坐标系上,若点M (a+5,a ﹣3)在y 轴上,则点M 的坐标为 .18. 已知A (x+5,2x+2)在x 轴上,那么点A 的坐标是 .19. 一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是 .20. 有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为 .21. 已知AB 在y 轴上,A 点的坐标为(0,﹣3),并且AB=7,则B 的坐标为 .22. 点A (3,﹣2)关于y 轴对称的点的坐标是 ;点A 关于原点对称的点的坐标是 .点A 关于x 轴对称的点的坐标为 .23. 若点A 在第二象限,且到x 轴的距离为3,到y 轴的距离为2,则点A 的坐标为_______.24. 点P (3,5)关于y 轴对称的点的坐标是 .25. 点M (-3,-8)到x 轴的距离为_____,到y 轴的距离为______.26. 已知点A (1,1),B (2,2),C (3,3),D (4,4),这些点的横坐标x 和纵坐标y 的关系是______.27. 如果点P (a ,2)在第二象限,那么点Q (-3,a )在_______.28. 点A 在x 轴上,位于原点的右侧,距离坐标原点5个单位长度,则此点的坐标为 ;点B 在y 轴上,位于原点的下方,距离坐标原点5个单位长度,则此点的坐标为 ;点C 在y 轴左侧,在x 轴下方,距离每个坐标轴都是5个单位长度,则此点的坐标为 .29. 通过平移把点A (2,-1)移到点A'(2,2),按同样的平移方式,点B (-3,1)移动到点B',则点B’的坐标是 .30. 已知点M 在轴上,则点M 的坐标为_____.【培优练习】31. 已知△ABC 在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC 关于y 轴对称,那么点A 的对应点A′的坐标为( )A . (﹣4,2)B . (﹣4,﹣2)C . (4,﹣2)D . (4,2)32. 已知点P (x ,y )在第二象限|x+1|=2,|y ﹣2|=3,则点P 的坐标为( )A . (﹣3,5)B . (1,﹣1)C . (﹣3,﹣1)D . (1,5)33. 如图的象棋盘上,若○帅位于点(1,-2)上,○相位于点(3,-2)上,则○炮位于点( ) A .(-1,1) B .(-1,2) C .(-2,1) D .(-2,2)()a a -+4,3y 图3相帅炮34. 已知点P 坐标为(2-a ,3a+6),且P 点到两坐标轴的距离相等,则点P 的坐标是( )A .(3,3)B .(3,-3)C .(6,-6)D .(3,3)或(6,-6)35. 点A (-2,-3)与点B (-3,-2)在直角坐标系中( )A .关于x 轴对称B .关于y 轴对称C .关于原点对称D .不关于坐标轴和原点对称36. 已知点A ,如果点A 关于轴的对称点是B ,点B 关于原点的对称点是C ,那么C 点的坐标是( )A .B .C .D .37. 一只小虫子在一个小方格的线路上爬行,它起始的位置是A (2,2),先爬到B (2,4),再爬到C (5,4),最后爬到D (5,5),则小虫一共爬行了( )个单位.A .7B . 6C . 5D . 438. 已知直角坐标系中的点A ,点B 的坐标分别为A (2,4),B (4,0),且P 为AB 的中点,若将线段AB 向右平移3个单位后,与点P 对应的点为Q ,则点Q 的坐标为( )A .(3,2)B .(6,2)C .(6,4)D .(3,5)39. 已知点M 1(-1,0)、M 2(0,-1)、M 3(-2,-1)、M 4(5,0)、 M 5(0,5)、M 6(-3,2),其中在x 轴上的点的个数是( )A .1 个B .2 个C .3个D .4个40. 如果点P (,)与点P 1(,)关于轴对称,则,的值分别为( )A .B .C .D .41. 小明家的坐标为(1,2),小丽家的坐标为(-2,-1),则小明家在小丽家的( )A .东南方向B .东北方向C .西南方向D .西北方向42. 点A (1,0),B (0,2),点P 在x 轴上,且三角形PAB 的面积为5,则P 点坐标为( )A .(-4,0)B .(6,0)C .(-4,0)或(6,0)D .无法确定43. 一个长方形在平面直角坐标系中三个顶点的坐标为(–1,–1)、(–1,2)、(3,–1),则第四个顶点的坐标为( )A .(2,2)B .(3,2)C .(3,3)D .(2,3)()2,2-x ()2,2()2,2-()1,1--()2,2--m -35-n y m n 3,5=-=n m 3,5==n m 3,5-=-=n m 5,3=-=n m44.在直角坐标中有两点M(a,b),N(a,-b),则这两点()A.关于x轴对称 B.关于y轴对称C.关于原点对称 D.上述结论都不正确45.由坐标平面内的三点A(1,1),B(3,-1),C(1,-3)构成的△ABC是()A.钝角三角形 B.直角三角形; C.锐角三角形 D.等腰直角三角形46.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-4,-1)、N(0,1),将线段MN平移后得到线段M ′N ′(点M、N分别平移到点M ′、N ′的位置),若点M ′的坐标为(-2,2),则点N ′的坐标为.47.已知点A(-2,2),B(-1,1),C(0,0),D(1,-1),E(2,-2),这些点的横坐标x和纵坐标y的关系是_______.48.ABC中,A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,则对应点A′,B′,C′的坐标分别为_____,_____,_______.49.已知AB∥x轴,A的坐标为(3,2),并且AB=4,则B的坐标为________.50.已知点A(-2,6),B(-1,5),C(0,4),D(1,3),E(2,2),这些点的横坐标x 和纵坐标y的关系是_________.【课后练习】1.到x轴的距离等于2的点组成的图形是()A.过点(0,2)且与x轴平行的直线B.过点(2,0)且与y轴平行的直线C.过点(0,-2)且与x轴平行的直线D.分别过(0,2)和(0,-2)且与x轴平行的两条直线2.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为()A.(-2,-5) B.(-2,5) C.(2,-5) D.(2,5)3.已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是()A.(-2,2),(3,4),(1,7) B.(-2,2),(4,3),(1,7)C.(2,2),(3,4),(1,7) D.(2,-2),(3,3),(1,7)4.线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,– 1)的对应点D的坐标为()A.(2,9) B.(5,3)C.(1,2) D.(– 9,– 4)5.在平面直角坐标系中,点A(-1,0)与点B(0,2)的距离是.6.由坐标平面内的三点A(-2,-1),B(-1,-4),C(5,-2)构成的三角形是_____三角形.7.如图的围棋盘,放在某个平面直角坐标系内,白棋②的坐标是(-7,-4),白棋④的坐标是(-6,-8),那么黑棋①的坐标是.。
七年级平面直角坐标系动点规律问题(经典难题)
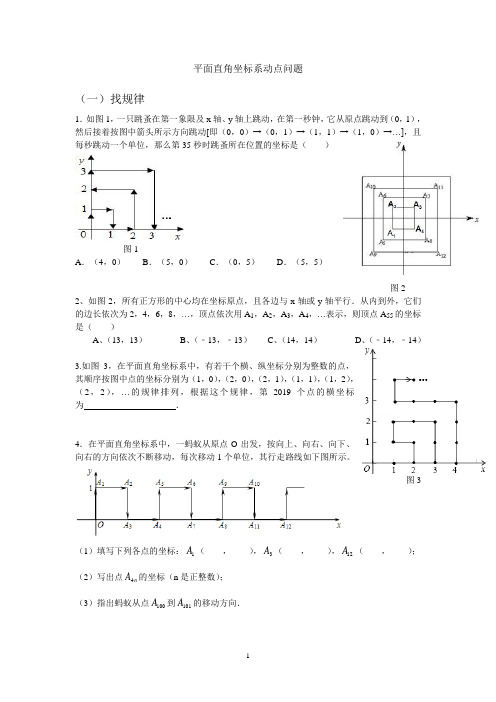
平面直角坐标系动点问题(一)找规律1.如图1,一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )图1A .(4,0)B .(5,0)C .(0,5)D .(5,5)图22、如图2,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是( ) A 、(13,13) B 、(﹣13,﹣13) C 、(14,14) D 、(﹣14,﹣14)3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2019个点的横坐标为 .4.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。
图3(1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____); (2)写出点n A 4的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.5.观察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…根据你发现的规律,第100个有序数对是 .6、观察下列有规律的点的坐标:依此规律,A 11的坐标为 ,A 12的坐标为 .7、以0为原点,正东,正北方向为x 轴,y 轴正方向建立平面直角坐标系,一个机器人从原点O 点出发,向正东方向走3米到达A 1点,再向正北方向走6米到达A 2,再向正西方向走9米到达A 3,再向正南方向走12米到达A 4,再向正东方向走15米到达A 5,按此规律走下去,当机器人走到A 6时,A 6的坐标是 .8、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次,点P 依次落在点201921,,,P P P 的位置,则点2019P 的横坐标为 .9、如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是 .点P 第2019次跳动至点P 2019的坐标是 .图4 图5 10、如图5,已知A l (1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2019的坐标为 .1PAOyxP1. 如图,一个粒子在第一象限内及x 、y 轴上运动,在第一分钟内它从原点运动到()1,0,而后它接着按图所示在x 轴、y 轴平行的方向上来回运动,且每分钟移动1个长度单位,那么,在1989分钟后这个粒子所处的位置是( ).A .()35,44B .()36,45C .()37,45D .()44,352. 如果将点P 绕定点M 旋转180︒后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中心,此时,点M 是线段PQ 的中点,如图,在直角坐标系中,ABO △的顶点A 、B 、O 的坐标分别为()1,0、()0,1、()0,0,点1P ,2P ,3P ,…中相邻两点都关于ABO △的一个顶点对称,点1P 与点2P 关于点A 对称,点2P 与点3P 关于点B 对称,点3P 与点4P 关于点O 对称,点4P 与点5P 关于点A 对称,点5P 与点6P 关于点B 对称,点6P 与点7P 关于点O 对称,…对称中心分别是A ,B ,O ,A ,B ,O ,…且这些对称中心依次循环,已知1P 的坐标是()1,1.试写出点2P 、7P 、100P 的坐标.3. 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:()0,0A ,()7,0B ,()9,5C ,()2,7D .(1)求此四边形的面积.(2)在坐标轴上,你能否找到一点P ,使50PBC S =△?若能,求出P 点坐标;若不能,请说明理由.4. 如图①,已知OABC 是一个长方形,其中顶点A 、B 的坐标分别为()0,a 和()9,a ,点E在AB 上,且13AE AB =,点F 在OC 上,且13OF OC =.点G 在OA 上,且使GEC △的面积为20,GFB △的面积为16,试求a 的值.图②5. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如()1,0,()2,0,()2,1,()1,1,()1,2,()2,2……根据这个规律,第2019个点的横坐标为_______.6. 在平面直角坐标系xOy 中,我们把横、纵坐标都是整数的点叫做整点.已知点()0,4A ,点B 是x 轴正半轴上的整点,记AOB △内部(不包括边界)的整点个数为m ,当3m =时,点B 的横坐标的所有可能值是_______;当点B 的横坐标为4n (n 为正整数)时,m =________(用含n 的代数式表示).7. 如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标.如1的对应点是原点()0,0,3的对应点是()1,1,16的对应点是()1,2-,那么2019的对应点的坐标是_______.8.如图,长方形BCDE 的各边分别平行于x 轴或y 轴,物体甲和物体乙由点()2,0A 同时出发,沿长方形BCDE 的边作环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动,求两个物体开始运动后的第2019次相遇地点的坐标.9. 在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,连接AC 、BD . (1)直接写出图中相等的线段、平行的线段; (2)已知()3,0A -、()2,2B --,点C 在y 轴的正半轴上.点D 在第一象限内,且5ACD S =△,求点C 、D 的坐标;(3)如图②,在平面直角坐标系中,已知一定点,()1,0M ,两个动点(),21E a a +、(),23F b b -+,请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM .若存在,求以点O 、M 、E 、F 为顶点的四边形的面积,若不存在,请说明理由.图②10 . 如图,AOCD 是放置在平面直角坐标系内的梯形,其中O 是坐标原点.点A 、C 、D 的坐标分别为()0,8,()5,0,()3,8,若点P 在梯形内,且PAD POC S S =△△,PAO PCD S S =△△,求P 点的坐标.11. 操作与研究(1)对数轴上的点P 进行如下操作:先把点P 表示的数乘以13,再把所得数对应的点向右平移1个单位,得到点P 的对应点'P B .点A ,B 在数轴上,对线段AB 上的每个点进行上述操作后得到线段''A B ,其中点A ,B 的对应点分别为'A ,'B .如图①,若点A 表示的数是3-,则点'A 表示的数是______;若点'B 表示的数是2,则点表示的数是______;已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合,则点E 表示的数是_________.(2)如图②,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a ,将得到的点先向右平移m 个单位,再向上平移n 个单位()0,0m n >>,得到正方形''''A B C D 及其内部的点,其中点A ,B 的对应点分别为'A ,'B .已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点'F 与点F 重合,求点F 的坐标.图①A B'-1-2-3-412340图②(二)几何综合问题1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB//y 轴时、求点B 的坐标2、如图,已知A 、B 两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O 出发.(1)汽车行驶到什么位置时离A 村最近?写出此点的坐标. (2)汽车行驶到什么位置时离B 村最近?写出此点的坐标. (3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形D C 3-1BA O x y PDCBAOx y (2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°,AB ∥CD ,AB =CD =8cm ,AD =BC =6cm ,D 点与原点重合,坐标为(0,0). (1)写出点B 的坐标.(2)动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC ?(3)在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9? 求出此时Q 点的坐标.6.如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a、b的值;(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.7.如图,在下面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b 满足关系式.(1)求a,b的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.8.在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.。
平面直角坐标系找规律100题

以下是关于在平面直角坐标系中寻找规律的100道题目:1. 绘制点(1, 1), (2, 4), (3, 9), (4, 16), ... 并继续这个规律。
2. 连接点(-1, 0), (0, 1), (1, 0), (0, -1), (-1, 0) 形成一个图形。
这个图形是什么?3. 找到缺失的坐标:(2, 5), (4, 10), (6, ?)。
4. 绘制点(0, 0), (1, 1), (2, 4), (3, 9), ... 并继续这个规律。
5. 连接点(1, 1), (2, 2), (3, 3), (4, 4), ... 形成一条直线。
这条直线的斜率是多少?6. 找到缺失的坐标:(3, 6), (5, ?), (7, 14)。
7. 绘制点(-1, 0), (-2, 0), (-3, 0), (-4, 0), ... 并继续这个规律。
8. 连接点(0, 1), (1, 0), (0, -1), (-1, 0), (0, 1) 形成一个图形。
这个图形是什么?9. 找到缺失的坐标:(2, 4), (4, ?), (6, 12)。
10. 绘制点(1, 1), (2, 4), (3, 9), (4, 16), ... 并找出这个规律的方程。
11. 连接点(1, 2), (2, 4), (3, 6), (4, 8), ... 形成一条直线。
这条直线的斜率是多少?12. 找到缺失的坐标:(2, 5), (4, ?), (6, 11)。
13. 绘制点(-1, -1), (0, 0), (1, 1), (2, 2), ... 并继续这个规律。
14. 连接点(-1, 1), (-2, 2), (-3, 3), (-4, 4), ... 形成一条直线。
这条直线的斜率是多少?15. 找到缺失的坐标:(3, 6), (5, ?), (7, 13)。
16. 绘制点(0, 0), (1, 1), (2, 4), (3, 9), ... 并找出这个规律的方程。
考点06 规律题:点的坐标专项练习(原卷版)
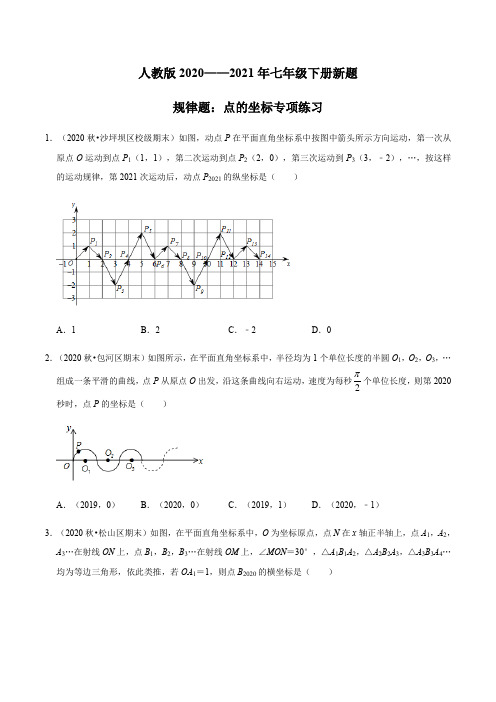
人教版2020——2021年七年级下册新题规律题:点的坐标专项练习1.(2020秋•沙坪坝区校级期末)如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O 运动到点P 1(1,1),第二次运动到点P 2(2,0),第三次运动到P 3(3,﹣2),…,按这样的运动规律,第2021次运动后,动点P 2021的纵坐标是( )A .1B .2C .﹣2D .02.(2020秋•包河区期末)如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O 1,O 2,O 3,…组成一条平滑的曲线,点P 从原点O 出发,沿这条曲线向右运动,速度为每秒2个单位长度,则第2020秒时,点P 的坐标是( )A .(2019,0)B .(2020,0)C .(2019,1)D .(2020,﹣1)3.(2020秋•松山区期末)如图,在平面直角坐标系中,O 为坐标原点,点N 在x 轴正半轴上,点A 1,A 2,A 3…在射线ON 上,点B 1,B 2,B 3…在射线OM 上,∠MON =30°,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4…均为等边三角形,依此类推,若OA 1=1,则点B 2020的横坐标是( )A.22017×3B.22018×3C.22019×3D.22020×34.(2019秋•文登区期末)如图,y轴右侧一组平行于y轴的直线l1,l2,l3,l4,l5…,两条相邻平行线之间的距离均为1,以点O为圆心,分别以1,2,3,4,5,6…为半径画弧,分别交y轴,l1,l2,l3,l4,l5…于点P,P1,P2,P3,P4,P5…,则点P2019的坐标为()A.(2018,4037)B.(2019,4037)C.(2019,4039)D.(2020,4041)5.(2020春•丛台区校级期末)在平面直角坐标系中,若干个等腰三角形按如图所示的规律摆放.点P从原点O出发,沿着“O→A1→A2→A3→A4…”的路线运动(每秒一条直角边),已知A1坐标为(1,1),A2(2,0),A3(3,1),A4(4,0)…设第n秒运动到点P n(n为正整数),则点P2020的坐标是()A.(2020,0)B.(2019,1)C.(1010,0)D.(2020,﹣1)B.6.(2020春•南丹县期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2020次运动后,动点P的坐标是()A.(2020,0)B.(2020,1)C.(2020,2)D.(2020,505)7.(2020春•日照期末)如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的坐标为()A.(1010,0)B.(1008,0)C.(2,1008)D.(2,2010)8.(2020春•兰山区期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的运动规律,经过第2021次运动后,动点P的坐标是()A.(2021,0)B.(2020,1)C.(2021,1)D.(2021,2)9.(2020春•文水县期末)如图所示,动点P在平面直角坐标系中,按箭头所示方向呈台阶状移动,第一次从原点运动到点(0,1),第二次接着运动到点(1,1),第三次接着运动到点(1,2),…,按这样的运动规律,经过2020次运动后,动点P的坐标是()A.(2020,2020)B.(505,505)C.(1010,1010)D.(2020,2021)10.(2020春•宜春期末)如图,动点P在平面直角坐标系中,沿曲线的方向从左往右运动,第1秒从原点运动到点(1,1),第2秒运动到点(2,0),第3秒运动到点(3,﹣1),第4秒运动到点(4,0)……按这样的规律,第2020秒运动到点()A.(2020,1)B.(2020,﹣1)C.(2020,0)D.(2019,0)11.(2020春•濮阳期末)如图,已知点A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),…,则点A2020的坐标为()A.(505,505)B.(506,﹣505)C.(﹣505,﹣505)D.(﹣505,505)12.(2020秋•泗水县期末)在平面直角坐标系中,若干个边长为2个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5…”的路线运动,设第n秒运动到点P n(n为正整数),则点P2020的坐标是.13.(2020秋•铁锋区期末)如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt △OA4C4,…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=30°,若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4,…,则依此规律,点A2021的坐标为.第13题第14题14.(2020秋•柳州期末)如图,在平面直角坐标系中,直线l与x轴交于点B1,与y轴交点于D,且OB1=1,∠ODB1=60°,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,按此规律进行下去,则点A6的横坐标是.15.15.(2020秋•连山区期末)如图,已知等边△AOC的边长为1,作OD⊥AC于点D,在x轴上取点C1,使CC1=DC,以CC1为边作等边△A1CC1;作CD1⊥A1C1于点D1,在x轴上取点C2,使C1C2=D1C1,以C1C2为边作等边△A2C1C2;作C1D2⊥A2C2于点D2,在x轴上取点C3,使C2C3=D2C2,以C2C3为边作等边△A3C2C3;…,且点A,A1,A2,A3,…都在第一象限,如此下去,则等边△A2021C2020C2021的边A2021C2021中点D2021横坐标为.16.(2020秋•白银期末)如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A2021的坐标为.17.(2020秋•抚顺县期末)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,﹣1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,﹣2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点A n的横坐标为.第17题第18题18.(2020秋•常宁市期末)如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的纵坐标为.19.(2020秋•锦州期末)如图,在平面直角坐标系中,边长为1的正方形A1B1C1D1(记为第1个正方形)的顶点A1与原点重合,点B1在y轴上,点D1在x轴上,点C1在第一象限内,以C1为顶点作等边△C1A2B2,使得点A2落在x轴上,A2B2⊥x轴,再以A2B2为边向右侧作正方形A2B2C2D2(记为第2个正方形),点D2在x轴上,以C2为顶点作等边△C2A3B3,使得点A3落在x轴上,A3B3⊥x轴,若按照上述的规律继续作正方形,则第2021个正方形的边长为.20.(2020秋•平阴县期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律经过第2021次运动后,动点P的坐标是.。
难点探究专题:平面直角坐标系中点的坐标的变化规律(选做)

难点探究专题:平面直角坐标系中点的坐标的变化规律(选做)——掌握不同规律,以不变应万变◆类型一沿坐标轴运动的点的坐标的探究1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P的坐标是________.2.如图,平面直角坐标系上的点A(1,0)第1次跳至点A1(-1,1),第2次跳至点A2(2,1),第3次跳至点A3(-2,2),第4次跳至点A4(3,2)……依此规律跳下去,点A第100次跳至的点A100的坐标是________.第2题图第3题图3.★如图,一个动点在第一象限内及x轴、y轴上运动,第1分钟从原点运动到(1,0),第2分钟内从(1,0)运动到(1,1),然后它接着按图中箭头所示的方向来回运动(在第一象限内运动时,运动方向与x轴或y轴平行),且每分钟移动1个单位长度.(1)当动点所在位置是(2,2)时,所经过的时间是________;(2)在第2016分钟时,这个动点所在位置的坐标是________.◆类型二绕原点呈“回”字形运动的点的坐标的探究4.(甘孜州中考)如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…则顶点A20的坐标为________.第4题图第5题图5.★如图,一甲虫从原点出发按图示方向作折线运动,第1次从原点到A1(1,0),第2次运动到A2(1,1),第3次运动到A3(-1,1),第4次运动到A4(-1,-1),第5次运动到A5(2,-1)……则第2015次运动到的点A2015的坐标是________.◆类型三图形变化的点的坐标的探究6.如图,长方形ABCD 的两边BC 、CD 分别在x 轴、y 轴上,点C 与原点重合,点A (-1,2),将长方形ABCD 沿x 轴向右翻滚,经过1次翻滚点A 对应点记为A 1,经过2次翻滚点A 对应点记为A 2……依此类推,经过5次翻滚后点A 对应点A 5的坐标为( )A .(5,2)B .(6,0)C .(8,0)D .(8,1)7.如图,在直角坐标系中,第1次将△OAB 变换成△OA 1B 1,第2次将△OA 1B 1变换成△OA 2B 2,第3次将△OA 2B 2变换成△OA 3B 3.已知A (1,3),A 1(2,3),A 2(4,3),A 3(8,3),B (2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)观察每次变换后的三角形有何变化,找出规律,按此变换规律再将△OA 3B 3变换成△OA 4B 4,则A 4的坐标是________,B 4的坐标是________;(2)若按第(1)题找到的规律将△OAB 进行了n 次变换,得到△OA n B n ,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n 的坐标是________,B n 的坐标是__________.参考答案与解析1.(2016,0) 解析:结合图象可知,当运动次数为偶数次时,P 点运动到x 轴上,且横坐标与运动次数相等.∵2016为偶数,∴运动2016次后,动点P 的坐标是(2016,0).2.(51,50) 解析:由题意,得A 100在第一象限,纵坐标为1002=50,横坐标比纵坐标大1.∴点A 100的坐标为(51,50).3.(1)6分钟(2)(44,8) 解析:观察图形得第12分钟坐标为(1,0),第22分钟坐标为(0,2),第32分钟坐标为(3,0),第42分钟坐标为(0,4)……∵2016<452=2025,第2025分钟坐标为(45,0),第2024分钟坐标为(44,0),2024-2016=8,∴在第2016分钟时,这个动点所在位置的坐标是(44,8).4.(5,-5) 解析:∵20÷4=5,∴点A 20在第四象限.∵点A 4所在正方形的边长为2,∴点A 4的坐标为(1,-1),同理可得点A 8的坐标为(2,-2),点A 12的坐标为(3,-3),∴点A 20的坐标为(5,-5).5.(-504,504) 解析:观察图形序号(大于4),被4除余数为1的点在第四象限,被4除余数为2的点在第一象限,余数为3的点在第二象限,能被4整除的点在第三象限.2015被4除商为503,余数为3.由A 3(-1,1),A 7(-2,2),可得A 2015(-504,504).6.D 解析:由题意可得下图,经过5次翻滚后点A 对应点A 5的位置如图所示,故A 5的坐标为(8,1).故选D.7.(1)(16,3) (32,0) (2)(2n ,3) (2n +1,0)解析:(1)∵A 1(2,3),A 2(4,3),A 3(8,3),∴A 4的横坐标为24=16,纵坐标为3.故A 4的坐标为(16,3).∵B 1(4,0),B 2(8,0),B 3(16,0),∴B 4的横坐标为25=32,纵坐标为0.故点B 4的坐标为(32,0);(2)由A 1(2,3),A 2(4,3),A 3(8,3),可以发现它们各点坐标的关系为横坐标是2n ,纵坐标都是3.故A n 的坐标为(2n ,3).由B 1(4,0),B 2(8,0),B 3(16,0),可以发现它们各点坐标的关系为横坐标是2n +1,纵坐标都是0.故B n 的坐标为(2n +1,0).。
[数学]-专项训练:坐标的变化(30题)(原版)
![[数学]-专项训练:坐标的变化(30题)(原版)](https://img.taocdn.com/s3/m/0943fba1162ded630b1c59eef8c75fbfc77d949e.png)
【专项训练】坐标的变化(30题)一.选择题(共20小题)1.(2023•桐乡市校级开学)在直角坐标系中,点P(﹣2,3)向右平移4个单位长度后的坐标为()A.(﹣6,3)B.(2,3)C.(﹣2,﹣1)D.(﹣2,7)2.(2022秋•宣州区期末)佳佳将坐标系中一图案横向拉长2倍,又向右平移2个单位长度,若想变回原来的图案,需要变化后的图案上各点坐标()A.纵坐标不变,横坐标减2B.纵坐标不变,横坐标先除以2,再均减2C.纵坐标不变,横坐标除以2D.纵坐标不变,横坐标先减2,再均除以23.(2022春•晋州市期中)在平面直角坐标系中,有M(﹣3,a+2),N(a+1,6﹣a)两点,若MN∥x 轴,则M,N两点间的距离为()A.5B.6C.7D.124.(2022春•殷都区校级月考)如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标分别是()A.(2,2),(3,4),(1,7)B.(2,2),(4,3),(1,7)C.(﹣2,2),(3,4),(1,7)D.(2,﹣2),(4,3),(1,7)5.(2022•青岛二模)如图,线段AB经过平移得到线段A'B',其中点A,B的对应点分别为点A',B',这四个点都在格点上.若线段A'B'有一个点P'(a,b),则点P'在AB上的对应点P的坐标为()A.(a﹣2,b+3)B.(a﹣2,b﹣3)C.(a+2,b+3)D.(a+2,b﹣3)6.(2022春•如东县期中)三角形ABC在经过某次平移后,顶点A(﹣1,m+2)的对应点为A(2,m﹣3),若此三角形内任意一点P(a,b)经过此次平移后对应点P1(c,d).则a+b﹣c﹣d的值为()A.8+m B.﹣8+m C.2D.﹣27.(2022春•信都区期末)已知点A(﹣3,4),B(﹣6,﹣1),将线段AB平移至AʹBʹ,点A的对应点Aʹ在y轴上,点B的对应点Bʹ在x轴上,点Aʹ的纵坐标为a,点Bʹ的横坐标为b,则a+b的值为()A.2B.3C.﹣3D.﹣28.(2022春•罗庄区期末)如图,第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是()A.(﹣2,0)B.(0,3)C.(0,3)或(﹣4,0)D.(0,3)或(﹣2,0)9.(2022•长兴县开学)第一象限内有两点P(m﹣4,n),Q(m,n﹣2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是()A.(﹣4,0)B.(4,0)C.(0,2)D.(0,﹣2)10.(2021春•思明区校级期中)对于点A(2,m)与点B(2,m﹣5),下列说法不正确的是()A.将点A向下平移5个单位长度可得到点BB.A、B两点的距离为5C.点A到y轴的距离为2D.直线AB与x轴平行11.(2021•海珠区校级二模)平面直角坐标系上一点P(m,﹣m+1),若将点P平移使得它与坐标原点重合,那么需要平移的最短距离为()A.B.C.1D.12.(2022秋•海口期末)如图,点A(0,3)、B(1,0),将线段AB平移到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是()A.(5,6)B.(6,5)C.(7,5)D.(7,2)13.(2022春•武侯区期末)在平面直角坐标系中,将点M(3m﹣1,m﹣3)向上平移2个单位长度得到点M',若点M'在x轴上,则点M的坐标是()A.(2,﹣2)B.(14,2)C.(﹣2,﹣)D.(8,0)14.(2022•邓州市一模)如图,在Rt△ABC中,点B(0,0),点A(0,3),点C(4,0),将Rt△ABC沿x轴正方向平移得到Rt△DEF,DE交AC于点M,若△MEC的周长为4,则点M的坐标为()A.B.C.D.15.(2022•中原区校级模拟)如图,在平面直角坐标系xOy中,将折线AEB向右平移得到折线CFD,则折线AEB在平移过程中扫过的面积是()A.4B.5C.6D.716.(2022春•林州市期中)如图,在平面直角坐标系中,设一质点M自P.(1,0)处向上运动1个单位至P(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…,如此继续运动下去,则P2022的坐标为()A.(1011,1011)B.(﹣1011,1011)C.(504,﹣505)D.(505,﹣504)17.(2022春•鹿邑县月考)如图,点A1(1,1)向上平移1个单位长度,再向右平移2个单位长度,得到点A2;将点A2向上平移2个单位长度,再向右平移4个单位长度,得到点A3;将点A3向上平移4个单位长度,再向右平移8个单位长度,得到A4,…,按照这个规律平移得到的点A2022,则点A2022的横坐标为()A.22021B.22022﹣1C.22022D.22022+118.(2022秋•永善县期中)如图,在平面直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,……,如此继续运动下去,则P2022的坐标为()A.(﹣1011,1011)B.(505,﹣504)C.(504,﹣505)D.(1011,1011)19.(2022春•西城区校级期中)如图,在平面直角坐标系中,一动点从原点O出发,向右平移3个单位长度到达点A1,再向上平移6个单位长度到达点A2,再向左平移9个单位长度到达点A3,再向下平移12个单位长度到达点A4,再向右平移15个单位长度到达点A5……按此规律进行下去,该动点到达的点A2022的坐标是()A.(3030,3033)B.(3030,3030)C.(3033,﹣3030)D.(3033,3036)20.(2022春•玉山县期中)如图,在坐标平面上,小七从点A(0,﹣8)出发,每天都是先向右走1个单位,再向上走3个单位.小七第一天由A点走到A1点,第二天由A1点走到A2点,…….那么小七第二十九天走到的点的坐标是()A.(28,70)B.(28,79)C.(29,70)D.(29,79)二.解答题(共10小题)21.(2022春•七里河区校级期中)如图,A(1,0),B(0,2)两点,若将线段AB平移至A1B1,求a ﹣b的值.22.(2022春•芜湖期末)如图,已知三角形ABC在平面直角坐标系中,且点A的坐标为(﹣2,﹣3),点C的坐标为(0,1),三角形ABC通过平移得到三角形A′B′C′.(1)在图中补画出平面直角坐标系xOy;(2)分别写出三角形A′B′C′的顶点A′和顶点C′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的;(3)请你在图中标出点M(3,﹣5)和点N(﹣4,4)的位置.23.(2022春•潼关县月考)如图,已知每个小正方形的边长为1,且正方形的顶点称为格点,网格中有一只小鱼,若小鱼平移游动,平移后的鱼头部分已画出(鱼身顶点都在格点上),请补全平移后的鱼尾部分.24.(2022•同心县二模)在平面直角坐标系中,三角形ABC经过平移得到三角形A'B'C',位置如图所示.(1)分别写出点A,A'的坐标:A,A'.(2)请说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.(3)若点M(m,4﹣n)是三角形ABC内部一点,则平移后对应点M'的坐标为(2m﹣8,n﹣4),求m和n的值.25.(2022春•昭化区期末)如图,△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).若△ABC 向右平移4个单位长度,再向下平移3个单位长度得到△A'B'C',且点C的对应点坐标是C'.(1)画出△A'B'C',并直接写出点C'的坐标;(2)若△ABC内有一点P(a,b)经过以上平移后的对应点为P',直接写出点P'的坐标;(3)求△ABC的面积.26.(2022春•江岸区校级月考)如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点B与点B′,点C与点C′分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:(1)分别写出点B和点B′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的;(2)连接BC′,直接写出∠CBC′与∠B′C′O之间的数量关系∠CBC′﹣∠B′C′O=90°;(3)若点M(a﹣1,2b﹣5)是三角形ABC内一点,它随三角形ABC按(1)中方式平移后得到的对应点为点N(2a﹣7,4﹣b),求a和b的值.27.(2022春•邻水县期末)如图,△ABC在直角坐标系中,(1)请写出△ABC各顶点的坐标.(2)若把△ABC向上平移2个单位,再向右平移3个单位得到△A1B1C1,请在图中画出△A1B1C1,并写出点A1、B1、C1的坐标.(3)求出△ABC的面积.28.(2022春•石城县期末)如图,在直角坐标系中,已知A(﹣1,4),B(﹣2,1),C(﹣4,1),将△ABC向右平移3个单位再向下平移2个单位得到△A1B1C1,点A、B、C的对应点分别是点A1、B1、C1.(1)画出△A1B1C1;(2)直接写出点A1、B1、C1的坐标;(3)直接写出△A1B1C1的面积.29.(2020秋•西湖区期末)已知点P(3a﹣15,2﹣a).(1)若点P到x轴的距离是3,试求出a的值;(2)在(1)题的条件下,点Q如果是点P向上平移2个单位长度得到的,试求出点Q的坐标;(3)若点P位于第三象限且横、纵坐标都是整数,试求点P的坐标.30.(2021春•海东市期末)如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,观察点与点坐标之间的关系,解答下列问题.(1)分别写出点A、点B、点C、点A'、点B'、点C'的坐标,并说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.(2)若点M(a+2,4﹣b)是点N(2a﹣3,2b﹣5)通过(1)中的平移变换得到的,求(b﹣a)2的值.。
点坐标规律探究(解析版)

专题25 点坐标规律探究1.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O 运动到点()11,1P ,第二次运动到点()22,0P ,第三次运动到()33,2P -,…,按这样的运动规律,第2022次运动后,动点2022P 的坐标是( )A .()2022,1B .()2022,2C .()2022,2-D .()2022,0 【答案】D【分析】观察图象,结合动点P 第一次从原点O 运动到点P 1(1,1),第二次运动到点P 2(2,0),第三次运动到P 3(3,﹣2),第四次运动到P 4(4,0),第五运动到P 5(5,2),第六次运动到P 6(6,0),…,结合运动后的点的坐标特点,分别得出点P 运动的纵坐标的规律,再根据循环规律可得答案.【详解】解:观察图象,结合动点P 第一次从原点O 运动到点P 1(1,1),第二次运动到点P 2(2,0),第三次运动到P 3(3,﹣2),第四次运动到P 4(4,0),第五运动到P 5(5,2),第六次运动到P 6(6,0),…,结合运动后的点的坐标特点,可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;∵2022÷6=337,∵经过第2022次运动后,动点P 的纵坐标是0,故选:D .【点睛】本题考查了规律型点的坐标,数形结合并从图象中发现循环规律是解题的关键. 2.如图,在平面直角坐标系上有点()1,0A ,点A 第一次跳至点1(1,1)A -,第二次向右跳动3个单位至点()22,1A ,第三次跳至点()32,2A -,第四次向右跳动5个单位至点()43,2A ,…依此规律跳动下去,点A 第100次跳至点100A 的坐标是( )A .()51,51-B .()51,50C .()50,49D .()50,49- 【答案】B【分析】根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,然后写出即可.【详解】解:观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),… 第2n 次跳动至点的坐标是(n +1,n ),故第100次跳动至点的坐标是(51,50).故选:B .【点睛】本题考查了坐标与图形的性质,以及图形的变化问题,结合图形得到偶数次跳动的点的横坐标与纵坐标的变化情况是解题的关键.3.如图,在一单位长度为1cm 的方格纸上,依如所示的规律,设定点1A 、2A 、3A 、4A 、5A 、6A 、7A 、n A ,连接点O 、1A 、2A 组成三角形,记为1∆,连接O 、2A 、3A 组成三角形,记为2∆,连O 、n A 、1n A +组成三角形,记为n ∆(n 为正整数),请你推断,当n 为50时,n ∆的面积=( )2cmA .1275B .2500C .1225D .1250 【答案】A【分析】根据图形计算发现:第一个三角形的面积是11212⨯⨯=,第二个三角形的面积是12332⨯⨯=,第三个图形的面积是13462⨯⨯=,即第n 个图形的面积是1(1)2n n +,即可求得,△n 的面积. 【详解】由题意可得规律:第n 个图形的面积是1(1)2n n +, 所以当n 为50时,n 的面积()150********=⨯⨯+=. 故选:A . 【点睛】此题主要考查了点的坐标变化规律,通过计算前面几个具体图形的面积发现规律是解题关键.4.在平面直角坐标系中,若干个等腰直角三角形按如图所示的规律摆放.点P 从原点O 出发,沿着“1234O A A A A →→→→…”的路线运动(每秒一条直角边),已知1A 坐标为()()()231,12,0,,1,3A A ()44,0A ···,设第n 秒运动到点(n P n 为正整数),则点2020P 的坐标是)( )A .()2020,0B .()2019,1C .()1010,0D .()2020,1-【答案】A【分析】通过观察可知,纵坐标每6个进行循环,先求出前面6个点的坐标,从中得出规律,再按规律写出结果便可.【详解】解:由题意知,A 1(1,1),A 2(2,0),A 3(3,1),A 4(4,0),A 5(5,-1),A 6(6,0),A 7(7,1),…由上可知,每个点的横坐标等于序号,纵坐标每6个点依次为:1,0,1,0,-1,0这样循环, ∵A 2020(2020,0),故选:A .【点睛】本题是一个规律题,根据题意求出点的坐标,从中找出规律来,这是解题的关键所在.5.如图,将点A 0(-2,1)作如下变换:作A 0关于x 轴对称点,再往右平移1个单位得到点A 1,作A 1关于x 轴对称点,再往右平移2个单位得到点A 2,…,作A n -1关于x 轴对称点,再往右平移n 个单位得到点A n (n 为正整数),则点A 64的坐标为( )A .(2078,-1)B .(2014 ,-1)C .(2078 ,1)D .(2014 ,1)【答案】C【分析】观察不难发现,角码为奇数时点的纵坐标为-1,为偶数时点的纵坐标为1,然后再根据向右平移的规律列式求出点的横坐标即可.【详解】解:由题意得: ()()()()()123451,1,1,1,4,1,8,1,13,1A A A A A ----……由此可得角码为奇数时点的纵坐标为-1,为偶数时点的纵坐标为1,故64A 的纵坐标为1,则点64A 的横坐标为()16464212345 (64220782)+⨯-+++++++=-+=,所以()642078,1A . 故选C .【点睛】本题主要考查平面直角坐标系点的坐标规律,关键是根据题目所给的方式得到点的坐标规律,然后求解即可.6.如图,在平面直角坐标系中,()1,1A ,()1,1B -,()1,2C --,()1,2D -,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处,并按A B C D A →→→→⋯的规律绕在四边形ABCD 的边上,则细线另一端所在位置的点的坐标是( )A .()1,0-B .()1,2-C .()1,0D .()0,2- 【答案】C【分析】根据点的坐标求出四边形ABCD 的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.【详解】∵A (1,1),B (﹣1,1),C (﹣1,﹣2),D (1,﹣2),∵AB =1﹣(﹣1)=2,BC =1﹣(﹣2)=3,CD =1﹣(﹣1)=2,DA =1﹣(﹣2)=3,∵绕四边形ABCD 一周的细线长度为2+3+2+3=10,2019÷10=201…9,∵细线另一端在绕四边形第201圈的第9个单位长度的位置点的坐标为(1,0).故选C .【点睛】本题利用点的坐标考查了数字变化规律,根据点的坐标求出四边形ABCD 一周的长度,从而确定2019个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.7.在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x 轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…则边长为8的正方形内部的整点的个数为( )A.64B.49C.36D.25【答案】B【详解】试题解析:设边长为8的正方形内部的整点的坐标为(x,y),x,y都为整数.则-4<x<4,-4<y<4,故x只可取-3,-2,-1,0,1,2,3共7个,y只可取-3,-2,-1,0,1,2,3共7个,它们共可组成点(x,y)的数目为7×7=49(个).故选B.考点:规律型:点的坐标.8.如图,在一单位为1的方格纸上,∵A1A2A3,∵A3A4A5,∵A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为()A.(1010,0)B.(1012,0)C.(2,1012)D.(2,1010)【答案】D【分析】根据脚码确定出脚码为偶数时的点的坐标,得到规律:当脚码是2、6、10…时,横坐标为1,纵坐标为脚码的一半的相反数,当脚码是4、8、12.…时,横坐标是2,纵坐标为脚码的一半,然后确定出第2020个点的坐标即可.【详解】解:观察点的坐标变化发现:当脚码为偶数时的点的坐标,得到规律:当脚码是2、6、10…时,横坐标为1,纵坐标为脚码的一半的相反数,当脚码是4、8、12.…时,横坐标是2,纵坐标为脚码的一半,因为2020能被4整除,所以横坐标为2,纵坐标为1010,故选:D .【点睛】本题考查点坐标的变化规律,根据所要求的点坐标确定类似点的变化规律是解题关键. 9.如图,网格中的每个小正方形的边长都是1,1A 、2A 、3A 、…都在格点上,123A A A ∆、345A A A ∆、567A A A ∆、…都是斜边在x 轴上,且斜边长分别为2、4、6、…的等腰直角三角形.若123A A A ∆的三个顶点坐标为()12,0A 、()21,1A -、()30,0A ,则依图中规律,20A 的坐标为( )A .()2,10B .()1,9-C .()10,0D .()10,0-【答案】A【分析】根据相邻的两个三角形有一个公共点列出与三角形的个数与顶点的个数的关系式,然后求出A 20所在的三角形,并求出斜边长,然后根据第奇数个三角形关于直线x=1对称,第偶数个三角形关于直线x=2对称,根据等腰直角三角形的性质即可得出答案.【详解】设到第n个三角形时共有y个顶点,∵第一个三角形有3个顶点,到第二个三角形有5个顶点,到第三个三角形有7个顶点,……∵到第n个三角形的顶点个数y=2n+1,当2n+1=20时,n=9……1,∵A20是第10个三角形的直角顶点,∵第10个三角形为A19A20A21,且A19A21为斜边,∵斜边长分别为2、4、6、……,∵第10个三角形的斜边长为10×2=20,即A19A21=20,由图可知:第奇数个三角形关于直线x=1对称,第偶数个三角形关于直线x=2对称,∵A1A20为∵A19A20A21斜边中线,∵A1A20=10,∵A20的坐标为(2,10)故选A.【点睛】本题是对点的坐标变化规律的考查,根据顶点个数与三角形的关系判断出A20所在的三角形是解题的关键.10.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是()A.(4,O)B.(5,0)C.(0,5)D.(5,5)【答案】B【分析】由题目中所给的质点运动的特点找出规律,即可解答.【详解】跳蚤运动的速度是每秒运动一个单位长度,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(2,0)用4秒,到(2,2)用6秒,到(0,2)用8秒,到(0,3)用9秒,到(3,3)用12秒,到(4,0)用16秒,依次类推,到(5,0)用35秒.故第35秒时跳蚤所在位置的坐标是(5,0).故选B .【点睛】本题主要考查点的坐标问题,解决本题的关键是正确读懂题意,能够正确确定点运动的顺序,确定运动的距离,从而可以得到到达每个点所用的时间.11.如图,点O (0,0),A (0,1)是正方形1OAA B 的两个顶点,以1OA 对角线为边作正方形121OA A B ,再以正方形的对角线2OA 作正方形121OA A B ,…,依此规律,则点8A 的坐标是( )A .(-8,0)B .(0,8)C .(0,2)D .(0,16) 【答案】D 【分析】根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以2,可求出从A 到A 3变化后的坐标,再求出A 1、A 2、A 3、A 4、A 5,继而得出A 8坐标即可.【详解】解:根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘2, ∵从A 到3A 经过了3次变化,∵45°×3=135°,1×()32=22, ∵点3A 所在的正方形的边长为22,点3A 位置在第四象限,∵点3A 的坐标是(2,-2),可得出:1A 点坐标为(1,1),2A 点坐标为(0,2),3A 点坐标为(2,-2),4A 点坐标为(0,-4),5A 点坐标为(-4,-4),6A (-8,0),A 7(-8,8),8A (0,16),故选D.【点睛】本题考查了规律题,点的坐标,观察出每一次的变化特征是解答本题的关键. 12.如图,在平面直角坐标系中,点1A 在x 轴的正半轴上,1B 在第一象限,且△11OA B 是等边三角形.在射线1OB 上取点2B ,3B ,⋯,分别以12B B ,23B B ,⋯为边作等边三角形△122B A B ,△233B A B ,⋯使得1A ,2A ,3A ,⋯在同一直线上,该直线交y 轴于点C .若11OA =,130OAC ∠=︒,则点9B 的横坐标是( )A .2552B .5112C .256D .5132【答案】B【分析】首先证明OA 1∵B 1A 2,∵B 1A 1A 2=90°,求出B 1A 2=2A 1B 1=2,然后同理可得B 2A 3,B 3A 4的长,根据等边三角形边长的规律,即可求出B 9的横坐标.【详解】解:∵∵OA 1B 1是等边三角形,OA 1=1,∵B 1的横坐标为12,OA 1=OB 1=A 1B 1=1,∵OA 1B 1=60°,∵△B 1B 2A 2是等边三角形,∵∵B 2B 1A 2=60°,∵OA 1∵B 1A 2,∵A 2B 1A 1=60°,∵∵OA 1C =30°,∵∵B 1A 2A 1=30°,∵∵B 1A 1A 2=90°,∵B 1A 2=2A 1B 1=2,同理:B 2A 3=2A 2B 2=4,B 3A 4=2A 3B 3=8,…,∵B 1的横坐标为12,B 2的横坐标为12+1=32,B 3的横坐标为12+1+2=72,B 4的横坐标为12+1+2+4=152, ...,∵点B 9的横坐标是12+1+2+4+8+16+32+64+128=5112. 故选:B .【点睛】本题考查了点的坐标规律,等边三角形的性质,解题的关键是根据等边三角形的性质得到等边三角形边长的规律.13.已知平面直角坐标系内有一点()1,1A -,把点A 向上平移5个单位得到点B ,点C 和点B 关于y 轴对称,点D 和点A 关于y 轴对称,有一小虫从点A 出发,沿着A B C D A B C D →→→→→→→⋅⋅⋅⋅⋅⋅的路径爬行,那么当小虫的爬行路程为2021时,它在第________象限. 【答案】一.【分析】根据题意可知点B 的坐标,根据“平面直角坐标系中,关于y 轴对称的两个点的纵坐标不变,横坐标互为相反数”可得点C 和点D 的坐标,由此,可计算出AB 、BC 、CD 、DA 的长,从而得到小虫爬行一周的长度,然后即可得出当小虫的爬行路程为2021时,小虫到达的位置,从而可确定它在第几象限.【详解】解:∵把点A 向上平移5个单位得到点B ,()1,1A -, ∵点B 的坐标为(1,4),∵点C 和点B 关于y 轴对称,点D 和点A 关于y 轴对称, ∵点C 的坐标为(-1,4),点D 的坐标为(-1,-1), ∵AB =()()2211415-+--=⎡⎤⎣⎦, BC =()()2211442--+-=, CD =()()2211145---+--=⎡⎤⎣⎦, DA =()()2211112--+---=⎡⎤⎡⎤⎣⎦⎣⎦, ∵AB +BC +CD +DA =5+2+5+2=14,∵有一小虫从点A 出发,沿着A B C D A B C D →→→→→→→⋅⋅⋅⋅⋅⋅的路径爬行, ∵小虫爬行一周的路程为14,∵2021=14×144+5,∵当小虫的爬行路程为2021时,小虫爬行完144周,然后从点A 出发,爬行5个单位长度刚好到达点B ,而点B 的坐标(1,4)在第一象限,∵当小虫的爬行路程为2021时,它在第一象限. 故答案为一.【点睛】本题考查了点所在的象限,平移,点坐标规律特征,两点间的距离公式等知识点.熟记各个知识点是解题的关键.14.如图,在平面直角坐标系中,将ABO 沿x 轴向右滚动到11AB C △的位置,再到112A B C 的位置…依次进行下去,若已知点()()3,0,0,4A B ,则点49A 的坐标为_________.【答案】(300,3)【分析】根据点A (3,0),B (0,4)得AB =5,再根据旋转的过程寻找规律即可求解. 【详解】解:∵∵AOB =90°, 点A (3,0),B (0,4), 根据勾股定理,得AB =5, 根据旋转可知:∵OA +AB 1+B 1C 2=3+5+4=12, 所以点B 2 (12,4),A 1 (12,3); 继续旋转得,B 4 (2×12,4),A 3 (24,3); B 6 (3×12,4),A 5 (36,3) …发现规律:B 50 (25×12,4),A 49 (300,3). 所以点A 49 的坐标为(300,3). 故答案为:(300,3).【点睛】本题考查了规律型:点的坐标,解决本题的关键是灵活运用旋转的知识.15.如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如()1,0,()2,0,()2,1,()1,1,1,2,()2,2根据这个规律,第2020个点的坐标为______.【答案】()45,5【分析】根据题意,得到点的总个数等于x 轴上右下角的点的横坐标的平方,由于22025=45,所以第2020个点在第45个矩形右下角顶点,向上5个单位处. 【详解】根据图形,以最外边的矩形边长上的点为准, 点的总个数等于x 轴上右下角的点的横坐标的平方, 例如:右下角的点的横坐标为1,共有1个,211= 右下角的点的横坐标为2时,共有2个,242=, 右下角的点的横坐标为3时,共有3个,293=, 右下角的点的横坐标为4时,共有16个,2164=, 右下角的点的横坐标为n 时,共有2n 个,2452025=,45是奇数,∴第2025个点是()45,0,第2020个点是()45,5, 故答案为:()45,5.【点睛】本题考查了规律的归纳总结,重点是先归纳总结规律,然后在根据规律求点位的规律. 16.如图,在平面直角坐标系中,()()()()1,1,1,1,1,2,1,2A B C D ----,把一条长为2021个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处, 并按 A B C D A ----⋯的规律绕在四边形ABCD 的边上,则细线另一端所在位置的点的坐标是 ____.【答案】()0,1【分析】先根据点的坐标求出四边形ABCD 的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.【详解】解:∵A (1,1),B (﹣1,1),C (﹣1,﹣2),D (1,﹣2),∴AB =1﹣(﹣1)=2,BC =1﹣(﹣2)=3,CD =1﹣(﹣1)=2,DA =1﹣(﹣2)=3, ∴绕四边形ABCD 一周的细线长度为2+3+2+3=10, 2021÷10=202…1,∴细线另一端在绕四边形第203圈的第1个单位长度的位置, 即细线另一端所在位置的点的坐标是(0,1). 故答案为:(0,1).【点睛】本题考查了点的坐标规律探求,根据点的坐标求出四边形ABCD 一周的长度,从而确定2021个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.17.在直角坐标系中,已知(3,0)A -、(0,4)B ,对ABO 连续作如图翻转变换,依次得到三角形1、2、3……则2018的直角顶点的坐标是___________.【答案】(807115,125)【分析】由(3,0)A -、(0,4)B ,得AB=5,过O′作O′D∵x 轴于点D ,根据面积法,得O′D=125,由勾股定理得,B′D=165,由ABO 连续作如图翻转变换,三次一个循环,进而可得2018的直角顶点的坐标.【详解】∵(3,0)A -、(0,4)B , ∵OA=3,OB=4,AB=22345+=, 过O′作O′D∵x 轴于点D , ∵O′D=341255⨯=,B′D=2212164()55-=, ∵对ABO 连续作如图翻转变换,三次一个循环,2018÷3=672…2, ∵2018的直角顶点的横坐标为:12×672+4+165=807115,纵坐标为:125,∵2018的直角顶点的坐标是:(807115,125).故答案是:(807115,125).【点睛】本题主要考查几何图形与点的坐标,掌握直角三角形的勾股定理和面积法求斜边上的高,是解题的关键..在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点边上的整点的个数,请你猜测由里向外第11个正方形(实线)四条边上的整点一共有_____个.【答案】44【分析】可以发现第n 个正方形的整点数有4n 个点,故第11个有44个整数点. 【详解】由图象可知,第1个正方形四条边上整点数为4, 第2个正方形四条边上整点数为8, 第3个正方形四条边上整点数为12,则第n个正方形四条边上整点数为4n.n=时,第11个正方形四条边上整点数为44.当11故答案为44.【点睛】此题考查点的坐标规律、正方形各边相等的性质,解决本题的关键是观察分析,得到规律,这是中考的常见题型.19.如图,平面直角坐标系xOy内,动点P按图中箭头所示方向依次运动,第1次从点(0,1)运动到-,第3次运动到点(3,0),⋯按这样的运动规律,动点P第2021次点(1,0),第二次运动到点(2,2)运动到的点的坐标是________.【答案】(2021,0)【分析】根据图形分析点P的运动规律:第n次运动到的点的横坐标为n,纵坐标每四次为一个循环,即可得到答案.-,第3次运动到点(3,0),⋯,【详解】解:∵第1次运动到点(1,0),第二次运动到点(2,2)∵第n次运动到的点的横坐标为n,纵坐标每四次为一个循环,每个循环向右移动4个单位÷=,∵202145051∵动点P第2021次运动到的点的坐标是(2021,0),故答案为:(2021,0).【点睛】此题考查了图形坐标的规律,正确理解图形得到点P的运动规律并应用是解题的关键.20.在平面直角坐标系xOy中,对于点P(x,y)我们把P(﹣y+1,x+1)叫做点P的伴随点,已知A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到A1,A2,A3,…An,若点A1的坐标为(3,1),则点A2021的坐标为_________.【答案】(3,1)【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2021A的坐标即可.除以4,根据商和余数的情况确定点2021A的坐标为(3,1),【详解】解:12(0,4)A ∴,3(3,1)A -,4(0,2)A -,5(3,1)A ,⋯⋯,依此类推,每4个点为一个循环组依次循环,202145051÷=⋯⋯,∴点2021A 的坐标与1A 的坐标相同,为(3,1).故答案是:(3,1).【点睛】本题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义,解题的关键是求出每4个点为一个循环组依次循环.21.如图,点(0,0),(0,1)O A 是正方形1O AA B 的两个顶点,以1OA 对角线为边作正方形121OA A B ,再以正方形的对角线2OA 为边作正方形121OA A B ,…,依此规律,则点1000A 的坐标是_________.【答案】(0,2500)【分析】根据正方形的性质找出点A 1、A 2、A 3、A 4、A 5、A 6、A 7、A 8、A 9、A 10、…的坐标,根据坐标的变化可找出变化规律“A 8n (0,24n )(n 为自然数)”,依此规律即可求出点A 1000的坐标. 【详解】解:∵A 1(1,1),A 2(2,0),A 3(2,-2),A 4(0,-4),A 5(-4,-4),A 6(-8,0),A 7(-8,8),A 8(0,16),A 9(16,16),A 10(32,0),…, ∵A 8n (0,24n )(n 为自然数). ∵1000=125×8,∵点A 1000的坐标为(0,2500). 故答案为:(0,2500).【点睛】本题考查了规律型:点的坐标,根据点的坐标的变化找出变化规律“A 8n (0,24n )(n 为自然数)”是解题的关键.22.如下图,在平面直角坐标系中,第一次将OAB 变换成11OA B ,第二次将11OA B 变换成22OA B △,第三次将22OA B △变换成33OA B ,…,将OAB 进行n 次变换,得到n n OA B △,观察每次变换中三角形顶点坐标有何变化,找出规律,推测2020A 的坐标是__________.【答案】()20202,3【分析】根据图形写出点A 系列的坐标与点B 系列的坐标,根据具体数值找到规律即可. 【详解】∵(1,3)A ,1(2,3)A ,2(4,3)A ,3(8,3)A ,4(16,3)A ,(2,0)B ,1(4,0)B ,2(8,0)B ,3(16,0)B , ∵1n A +的横坐标与n B 的横坐标相同,纵坐标为3,点n B 的横坐标为12n +,纵坐标为0,∵n A 的坐标是()2,3n,∵()202020202,3A .【点睛】依次观察各点的横纵坐标,得到规律是解决本题的关键.23.如图,在平面直角坐标系中,等腰直角三角形OAA 1的直角边OA 在x 轴上,点A 1在第一象限,且OA =1,以点A 1为直角顶点,0A 1为一直角边作等腰直角三角形OA 1A 2,再以点A 2为直角顶点,OA 2为直角边作等腰直角三角形OA 2A 3…依此规律,则点A 2019的坐标是_____.【答案】(﹣21009,21009)【分析】利用等腰直角三角形的性质可得出部分点A n 的坐标,根据点的坐标的变化可得出变化规律“点A 8n+3的坐标为(﹣24n+1,24n+1)(n 为自然数)”,结合2019=252×8+3即可得出点A 2019的坐标.【详解】解:由等腰直角三角形的性质,可知:A 1(1,1),A 2(0,2),A 3(﹣2,2),A 4(0,﹣4),A 5(﹣4,﹣4),A 6(0,﹣8),A 7(8,﹣8),A 8(16,0),A 9(16,16),A 10(0,32),A 11(﹣32,32),…,∵点A 8n+3的坐标为(﹣24n+1,24n+1)(n 为自然数).∵2019=252×8+3,∵点A 2019的坐标为(﹣24×252+1,24×252+1),即(﹣21009,21009), 故答案为(﹣21009,21009).【点睛】本题考查了等腰直角三角形以及规律型:点的坐标,根据点的坐标的变化找出变化规律“点A 8n+3的坐标为(﹣24n+1,24n+1)(n 为自然数)”是解题的关键.24.如图,在平面直角坐标系中,一动点从原点O 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点()1A 0,1,()2A 1,1,()3A 1,0,()4A 2,0,⋯那么点2018A 的坐标为______.【答案】(1009,1)【分析】任选一个除原点外的点找出它的坐标,往后每隔4取一个点找出它的坐标,这样以4为周期得到相应位置的点的坐标规律,找出比2018小且最接近2018的这个位置的点的坐标即可求解. 【详解】解:根据题意得:A 1(0,1),A 5(2,1),A 9(4,1),A 13(6,1),…… 所以A 4n +1(2n ,1).因为2017=4×504+1=2×1008+1,所以A 2017(1008,1), 则A 2018(1009,1). 故答案为A 2018(1009,1).【点睛】本题主要考查了点的坐标规律,探索规律的步骤:①从具体的题目出发,用列表或列举的方式,把各数量或图形的变化特点展现出来;②认真观察图表或图形,通过合理联想,大胆猜想,总结归纳,得出数字或图形间的变化规律,形成结论;(4)由此及彼验证结论的正误.。
专题11 平面直角坐标系(归纳与讲解)(解析版)

专题11平面直角坐标系【专题目录】技巧1:点的坐标变化规律探究问题技巧2:巧用坐标求图形的面积技巧3:活用有序数对表示点的位置技巧4:巧用直角坐标系中点的坐标特征解相关问题【题型】一、用有序数对表示位置【题型】二、求点的坐标【题型】三、距离与点坐标的关系【题型】四、象限角的平分线上的点的坐标【题型】五、与坐标轴平行的直线上的点的坐标特征【题型】六、点的坐标的规律探索【题型】七、函数图象的应用【考纲要求】1、会画平面直角坐标系,并能根据点的坐标描出点的位置,掌握坐标平面内点的坐标特征.2、了解函数的有关概念和函数的表示方法,并能结合图象对实际问题中的函数关系进行分析.3、能确定函数自变量的取值范围,并会求函数值.【考点总结】一、平面直角坐标系【考点总结】二、函数有关的概念及图象【注意】1、坐标轴上的点不属于任何象限点的坐标:对于坐标轴内任意一点A,过点A分别向x轴、y轴作垂线,垂足在x轴、y轴上的对应的数a、b分别叫做点A的横坐标和纵坐标,有序数对A(a,b)叫做点A的坐标,记作A(a,b)。
2、确定出数自变量力的取值范围的方法 (1)整式:取全体实数 (2)有分母:取值使分母不为零(3)有二次根式:取值使被开方数不小于0 (4)有很多情况:取它们的公共部分 (5)在实际问题中:取值要符合实际意义 【技巧归纳】技巧1:点的坐标变化规律探究问题【类型】一、沿坐标轴运动的点的坐标规律探究1.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O 1,O 2,O 3,…,组成一条平滑的曲线.点P 从原点O 出发,沿这条曲线向右运动,速度为每秒π2个单位长度,则第2 019秒时,点P 的坐标是( )(第1题)A .(2 018,0)B .(2 019,-1)C .(2 019,1)D .(2 020,0)2.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2 017次运动后,动点P 的坐标是________,经过第2 018次运动后,动点P 的坐标是________.3.如图,一个粒子在第一象限内及x 轴、y 轴上运动,第一分钟从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),然后它接着按图中箭头所示的方向运动(在第一象限内运动时,运动方向与x 轴或y 轴平行),且每分钟移动1个单位长度.(1)当粒子所在位置是(2,2)时,所经过的时间是________; (2)在第2 017分钟时,这个粒子所在位置的坐标是________.【类型】二、绕原点呈“回”字形运动的点的坐标规律探究4.将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x ,y),其中x ,y 均为整数,如数5对应的坐标为(-1,1),则数2 018对应的坐标的( )A .(16,22)B .(-15,-22)C .(15,-22)D .(16,-22) 【类型】三、图形变换的点的坐标规律探究5.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A 的对称点为P 1,P 1关于B 的对称点为P 2,P 2关于C 的对称点为P 3,按此规律继续以A ,B ,C 为对称中心重复前面的操作,依次得到P 4,P 5,P 6,…,则点P 2 018的坐标是( )A .(0,0)B .(0,2)C .(2,-4)D .(-4,2)6.(探究题)如图,在平面直角坐标系中,第一次将三角形OAB 变换成三角形OA 1B 1,第二次将三角形OA 1B 1变换成三角形OA 2B 2,第三次将三角形OA 2B 2变换成三角形OA 3B 3,已知A(1,3),A 1(2,3),A 2(4,3),A 3(8,3),B(2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按此变换规律再将三角形OA 3B 3变换成三角形OA 4B 4,则点A 4的坐标是________,点B 4的坐标是________;(2)若按(1)题中的规律,将三角形OAB 进行n(n 为正整数)次变换,得到三角形OA n B n ,比较每次变换前后三角形顶点坐标有何变化,找出规律,推测点A n 的坐标是__________,点B n 的坐标是__________. 参考答案1.B 点拨:半径为1个单位长度的圆的周长的一半为12×2π×1=π,因为点P 从原点O 出发,沿这条曲线向右运动,速度为每秒π2个单位长度,所以点P 1秒走12个半圆.当点P 从原点O 出发,沿这条曲线向右运动,运动时间为1秒时,点P 的坐标为(1,1); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为2秒时,点P 的坐标为(2,0); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为3秒时,点P 的坐标为(3,-1); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为4秒时,点P 的坐标为(4,0);当点P 从原点O 出发,沿这条曲线向右运动,运动时间为5秒时,点P 的坐标为(5,1); 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为6秒时,点P 的坐标为(6,0); ….因为2 019÷4=504……3,所以第2 019秒时,点P 的坐标是(2 019,-1). 2.(2 017,1);(2 018,0) 3.(1)6分钟 (2)(44,7)4.C 点拨:以原点为中心,数阵图形成多层正方形(不完整),观察图形得出下表:正方形在第四象限的顶点 因为442<2 018<452=(2×22+1)2=2 025, 所以数2 025对应的坐标为(22,-22). 所以数2 018对应的坐标为(15,-22).5.D 点拨:设P 1(x ,y),因为点A(1,-1),点P(0,2)关于A 的对称点为P 1,所以x2=1,y +22=-1,解得x =2,y =-4,所以P 1(2,-4).同理可得P 2(-4,2),P 3(4,0),P 4(-2,-2),P 5(0,0),P 6(0,2),P 7(2,-4),…,所以每6个点循环一次.因为2 018÷6=336……2,所以点P 2 018的坐标是(-4,2).故选D . 6.(1)(16,3);(32,0)(2)(2n ,3);(2n +1,0) 技巧2:巧用坐标求图形的面积 【类型】一、直接求图形的面积1.如图,已知A(-2,0),B(4,0),C(-4,4),求三角形ABC 的面积.【类型】二、利用补形法求图形的面积2.已知在四边形ABCD中,A(-3,0),B(3,0),C(3,2),D(1,3),画出图形,求四边形ABCD 的面积.3.如图,已知点A(-3,1),B(1,-3),C(3,4),求三角形ABC的面积.【类型】三、利用分割法求图形的面积4.在如图所示的平面直角坐标系中,四边形OABC各顶点分别是O(0,0),A(-4,10),B(-12,8),C(-14,0),求四边形OABC的面积.【类型】四、已知三角形的面积求点的坐标5.已知点O(0,0),点A(-3,2),点B在y轴的正半轴上,若三角形AOB的面积为12,则点B 的坐标为()A.(0,8) B.(0,4) C.(8,0) D.(0,-8)6.已知点A(-4,0),B(6,0),C(3,m),如果三角形ABC的面积是12,求m的值.7.已知A(-2,0),B(4,0),C(x,y).(1)若点C在第二象限,且|x|=4,|y|=4,求点C的坐标,并求三角形ABC的面积;(2)若点C在第四象限,且三角形ABC的面积为9,|x|=3,求点C的坐标.参考答案1.解:因为C点坐标为(-4,4),所以三角形ABC 的AB 边上的高为4. 又由题易知AB =6, 所以S 三角形ABC =12×6×4=12.2.解:如图所示.过点D 作DE 垂直于BC ,交BC 的延长线于点E ,则四边形DABE 为直角梯形. S 四边形ABCD =S 梯形DABE -S 三角形C DE =12×(2+6)×3-12×1×2=11.3.解:方法一:如图,作长方形CDEF ,则S 三角形ABC =S 长方形CDEF -S 三角形ACD -S 三角形ABE -S 三角形BCF =CD·DE -12·AD·CD -12AE·BE -12BF·CF =6×7-12×3×6-12×4×4-12×2×7=18.方法二:如图,过点B 作EF ∥x 轴,并分别过点A 和点C 作EF 的垂线,垂足分别为点E ,F.易知AE =4,BE =4,BF =2,CF =7,EF =6,所以S 三角形ABC =S 梯形AEFC -S 三角形ABE -S 三角形BFC =12(AE +CF)·EF -12AE·BE -12BF·CF =12×(4+7)×6-12×4×4-12×2×7=18. 方法三:如图,过点A 作DE ∥y 轴,并分别过点C 和点B 作DE 的垂线,垂足分别为点D ,E. 易知AE =4,BE =4,AD =3,CD =6,DE =7,所以S 三角形ABC =S 梯形BEDC -S 三角形ABE -S 三角形ADC=12(BE +CD)·DE -12AE·BE -12AD·CD =12×(4+6)×7-12×4×4-12×3×6=18.4.解:如图,过点A 作AD ⊥x 轴,垂足为点D ,过点B 作BE ⊥AD ,垂足为点E.易知D(-4,0),E(-4,8),且BE =-4-(-12)=8,AE =10-8=2,CD =-4-(-14)=10,所以S 四边形OABC =S 三角形AOD +S 三角形ABE +S 梯形DEBC =12OD·AD +12AE·BE +12(BE +CD)·DE =12×4×10+12×2×8+12×(8+10)×8=20+8+72=100.点拨:本题的解题技巧在于把不规则的四边形OABC 分割为几个规则图形,实际上分割的方法是不唯一的,并且不仅可以用分割法,还可以用补形法. 5.A6.解:AB =6-(-4)=10.根据三角形的面积公式,得12AB·|m|=12,即12×10·|m|=12,解得|m|=2.4. 因为点C(3,m),所以点C 在第一象限或第四象限. 当点C 在第一象限时,m >0, 则m =2.4;当点C 在第四象限时,m <0,则m =-2.4.综上所述,m 的值为-2.4或2.4.7.解:(1)因为点C 在第二象限,且|x|=4,|y|=4,所以点C 的坐标为(-4,4). 又易知AB =6,所以S 三角形ABC =12×6×4=12.(2)由题意可知AB =6.因为点C 在第四象限,|x|=3,所以x =3.因为S 三角形ABC =12×6×|y|=9,所以|y|=3.所以y =-3.所以点C 的坐标为(3,-3). 技巧3:活用有序数对表示点的位置 【类型】一、利用有序数对表示座位号1.如图,王明同学的座位是1组2排,如果用有序数对(1,2)表示,那么张敏同学和石玲同学的座位怎样用有序数对表示?【类型】二、利用有序数对表示棋子位置2.五子棋深受广大棋友的喜爱,其规则是:在正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙对弈时的部分示意图(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记为(8,4),甲必须在哪个位置上落子,才不会让乙在短时间内获胜?为什么?【类型】三、利用有序数对表示地理位置3.如图是某市市区几个旅游景点示意图(图中每个小正方形的边长为1个单位长度),如果以O为原点建立两条互相垂直的数轴,如果用(2,2.5)表示金凤广场的位置,用(11,7)表示动物园的位置,根据此规定:(1)湖心岛、光岳楼、山陕会馆的位置如何表示?(2)(11,7)和(7,11)是同一个位置吗?为什么?【类型】四、利用有序数对表示运动路径4.如图,小军家的位置点A在经5路和纬4路的十字路口,用有序数对(5,4)表示;点B是学校的位置,点C是小芸家的位置,如果用(5,4)→(5,5)→(5,6)→(6,6)→(7,6)→(8,6)表示小军家到学校的一条路径.(1)请你用有序数对表示出学校和小芸家的位置;(2)请你写出小军家到学校的其他几条路径.(写3条)参考答案1.解:张敏同学的座位可以表示为(3,3),石玲同学的座位可以表示为(4,5).2.解:甲必须在(1,7)或(5,3)处落子,因为若甲不先截断以上两处之一,而让乙在(1,7)或(5,3)处落子,则下一步不论截断何处,乙总有一处落子可连成五子,乙必胜无疑.3.解:(1)湖心岛的位置可表示为(2.5,5);光岳楼的位置可表示为(4,4);山陕会馆的位置可表示为(7,3).(2)不是同一个位置,因为前面一个数字代表横向,后一个数字代表纵向,交换数字的位置后,就会表示不同的位置.4.解:(1)学校和小芸家的位置分别可表示为(8,6),(3,3).(2)答案不唯一,如:①(5,4)→(5,5)→(6,5)→(7,5)→(8,5)→(8,6);②(5,4)→(6,4)→(7,4)→(8,4)→(8,5)→(8,6);③(5,4)→(6,4)→(6,5)→(7,5)→(8,5)→(8,6).技巧4:巧用直角坐标系中点的坐标特征解相关问题【类型】一、象限内的点的坐标1.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是()A.第一象限或第三象限B.第二象限或第四象限C.第一象限或第二象限D.不能确定2.在平面直角坐标系中,若点P(m,m-2)在第一象限内,则m的取值范围是________.【类型】二、坐标轴上的点的坐标3.若点M的坐标为(-a2,|b|+1),则下列说法中正确的是()A.点M在x轴正半轴上B.点M在x轴负半轴上C.点M在y轴正半轴上D.点M在y轴负半轴上4.已知点P(a-1,a2-9)在y轴上,则点P的坐标为________.【类型】三、平面直角坐标系中一些特殊点的坐标5.已知点P(2m-5,m-1),当m为何值时,(1)点P在第二、四象限的角平分线上?(2)点P在第一、三象限的角平分线上?6.已知A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的取值范围.【类型】四、点的坐标与点到x轴、y轴的距离之间的关系7.已知点A(3a,2b)在x轴上方,y轴的左侧,则点A到x轴、y轴的距离分别为() A.3a,-2b B.-3a,2b C.2b,-3a D.-2b,3a8.已知点P到x轴和y轴的距离分别是2和5,求点P的坐标.【类型】五、关于坐标轴对称的点9.点P(-3,4)关于x轴对称的点的坐标是()A.(-4,3)B.(3,-4)C.(-3,-4) D.(3,4)10.已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=________.11.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是(______,______).【类型】六、关于特殊直线对称的点12.点P(3,5)关于第一、三象限的角平分线对称的点为点P1,关于第二、四象限的角平分线对称的点为点P2,则点P1,P2的坐标分别为()A.(3,5),(5,3)B.(5,3),(-5,-3)C.(5,3),(3,5) D.(-5,-3),(5,3) 13.点M(1,4-m)关于过点(5,0)且垂直于x轴的直线对称的点的坐标是____________;若点M关于过点(0,-3)且平行于x轴的直线对称的点的坐标为(1,7),则m=________.参考答案1.B2.m>2点拨:第一象限内的点的横、纵坐标必须同时为正,所以m>2.3.C点拨:由-a2可确定a=0,所以-a2=0. 又|b|+1>0,所以点M(-a2,|b|+1)在y轴正半轴上.4.(0,-8)5.解:(1)根据题意,得2m-5+m-1=0,解得m=2.所以当m=2时,点P在第二、四象限的角平分线上.(2)根据题意,得2m-5=m-1,解得m=4.所以当m=4时,点P在第一、三象限的角平分线上.点拨:第一、三象限的角平分线上的点的横、纵坐标相等,第二、四象限的角平分线上的点的横、纵坐标互为相反数.6.解:因为AB∥x轴,所以m=4.因为A,B不重合,所以n≠-3.点拨:与x轴平行的直线上的点的纵坐标相等.7.C点拨:由点A(3a,2b)在x轴上方,y轴的左侧可知点A在第二象限,故3a是负数,2b是正数,所以点A到x轴、y轴的距离分别为2b,-3a.8.解:设点P的坐标为(x, y),依题意,得|x|=5,|y|=2,所以x=±5,y=±2.所以点P的坐标为(5,2)或(5,-2)或(-5,2)或(-5,-2).点拨:(1)点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.(2)写点P的坐标时,横、纵坐标的前后顺序不能随意改变.(3)找全满足条件的点P的坐标,不要遗漏.9.C10.-611.-2;312.B点拨:任意点A(a,b)关于第一、三象限的角平分线对称的点的坐标为(b,a),关于第二、四象限的角平分线对称的点的坐标为(-b,-a).13.(9,4-m);17点拨:点A(a,b)关于过点(k,0)且垂直于x轴的直线对称的点的坐标为(2k-a,b),关于过点(0,k)且平行于x轴的直线对称的点的坐标为(a,2k-b).【题型讲解】【题型】一、用有序数对表示位置例1、小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是().A.小李现在位置为第1排第2列B.小张现在位置为第3排第2列C.小王现在位置为第2排第2列D.小谢现在位置为第4排第2列【答案】B【分析】由于撤走一排,则四人所在的列数不变、排数减一,据此逐项排除即可.【详解】解:A. 小李现在位置为第1排第4列,故A选项错误;B. 小张现在位置为第3排第2列,故B选项正确;C. 小王现在位置为第2排第3列,故C选项错误;D. 小谢现在位置为第4排第4列,故D选项错误.故选:B.【题型】二、求点的坐标例2、如图,四边形OBCD 是正方形,O ,D 两点的坐标分别是()0,0,()0,6,点C 在第一象限,则点C 的坐标是( )A .()6,3B .()3,6C .()0,6D .()6,6【答案】D【分析】利用O ,D 两点的坐标,求出OD 的长度,利用正方形的性质求出OB ,BC 的长度,进而得出C 点的坐标即可.【详解】解:①O ,D 两点的坐标分别是()0,0,()0,6,①OD =6,①四边形OBCD 是正方形,①OB ①BC ,OB =BC =6 ①C 点的坐标为:()6,6, 故选:D .【题型】三、距离与点坐标的关系例3、在平面直角坐标系的第二象限内有一点M ,点M 到x 轴的距离为3,到y 轴的距离为4,则点M 的坐标是( ) A .(3,4)- B .(4,3)-C .(4,3)-D .()3,4-【答案】C 【解析】 由题意,得 x=-4,y=3,即M 点的坐标是(-4,3), 故选C .【题型】四、象限角的平分线上的点的坐标例4、若点N 在第一、三象限的角平分线上,且点N 到y 轴的距离为2,则点N 的坐标是( ) A .(2,2) B .(-2,-2) C .(2,2)或(-2,-2) D .(-2,2)或(2,-2)【答案】C 【解析】已知点M 在第一、三象限的角平分线上,点M 到x 轴的距离为2,所以点M 到y 轴的距离也为2.当点M 在第一象限时,点M 的坐标为(2,2);点M 在第三象限时,点M 的坐标为(-2,-2).所以,点M 的坐标为(2,2)或(-2,-2).故选C . 【题型】五、与坐标轴平行的直线上的点的坐标特征例5、已知点A (a ﹣2,2a +7),点B 的坐标为(1,5),直线AB ①y 轴,则a 的值是( ) A .1 B .3C .﹣1D .5【答案】B 【详解】 解:①AB①y 轴,①点A 横坐标与点A 横坐标相同,为1, 可得:a -2=1,a=3 故选:B .【题型】六、点的坐标的规律探索例6、在平面直角坐标系中,一个智能机器人接到的指令是:从原点O 出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点1A ,第二次移动到点2A ……第n 次移动到点n A ,则点2019A 的坐标是( )A .()1010,0B .()1010,1C .()1009,0D .()1009,1【答案】C【分析】根据图象可得移动4次图象完成一个循环,从而可得出点2019A 的坐标. 【详解】()10,1A ,()21,1A ,()31,0A ,()42,0A ,()52,1A ,()63,1A ,…,201945043÷=⋅⋅⋅,所以2019A 的坐标为()50421,0⨯+,则2019A 的坐标是()1009,0, 故选C .【题型】七、函数图象的应用例7、如图,一只蚂蚁从O 点出发,沿着扇形OAB 的边缘匀速爬行一周,设蚂蚁的运动时间为t ,蚂蚁到O 点的距离..为s ,则s 关于t 的函数图象大致为( ).【答案】C【分析】利用函数关系和图象分析解决实际问题,要透过问题情境准确地寻找出问题的自变量和函数,探求变量和函数之间的变化趋势,合理地分析变化过程,准确地结合图象解决实际问题. 【详解】本题是典型的数形结合问题,通过对图形的观察,可以看出s 与t 的函数图象应分为三段:(1)当蚂蚁从点O 到点A 时,s 与t 成正比例函数关系;(2)当蚂蚁从点A 到点B 时,s 不变;(3)当蚂蚁从点B 回到点O 时,s 与t 成一次函数关系,且回到点O 时,s 为零.平面直角坐标系(达标训练)一、单选题1.在平面直角坐标系中,点A (a ,2)在第二象限内,则a 的取值可以是( ) A .1 B .-3C .4D .4或-4【答案】B【分析】根据第二象限的坐标特征判断即可; 【详解】解:①点A (a ,2)在第二象限内, ①a <0, A .不符合题意;B .符合题意;C .不符合题意;D .不符合题意; 故选: B .【点睛】本题考查了象限的坐标特征,掌握第二象限内点的横坐标为负数,纵坐标为正数是解题关键. 2.若点(),1A a a -在x 轴上,则点()1,2B a a +-在第( )象限. A .一 B .二 C .三 D .四【答案】D【分析】由点A 在x 轴上求得a 的值,进而求得点B 坐标,进而得到答案. 【详解】解:点(),1A a a -在x 轴上, 10a ∴-=,即1a =,则点B 坐标为()2,1-, ∴点B 在第四象限,故选:D .【点睛】本题主要考查点的坐标,解题的关键是掌握各象限及坐标轴上点的横纵坐标特点. 3.如图,在围棋棋盘上有3枚棋子,如果黑棋①的位置用有序数对(0,−1)表示,黑棋①的位置用有序数对(−3,0)表示,则白棋①的位置可用有序数对表示为( )A .()2,1-B .()1,2-C .()2,1-D .()1,2-【答案】C【分析】根据黑棋①的坐标向上1个单位确定出坐标原点,然后建立平面直角坐标系,再写出白棋①的坐标即可.【详解】解:建立平面直角坐标系如图,白棋①的坐标为(-2,1).故选:C.【点睛】本题考查了坐标确定位置,根据已知点的坐标确定出坐标原点的位置是解题的关键.4.如图,货船A与港口B相距35海里,我们用有序数对(南偏西40°,35海里)来描述货船B相对港口A的位置,那么港口A相对货船B的位置可描述为()A.(南偏西50°,35海里)B.(北偏西40°,35海里)C.(北偏东50°,35海里)D.(北偏东40°,35海里)【答案】D【分析】根据方位角的概念并结合平行线的性质,可得答案.【详解】解:过点B作BD①AC,①①1=①A=40°①港口A相对货船B的位置可描述为(北偏东40°,35海里),故选:D.【点睛】本题考查了方向角的知识点,解答本题的关键是理解确定一个点的位置需要两个量应该是方向角,一个是距离.5.某天早晨,小明从家骑自行车去上学,途中因自行车发生故障而维修,如图所示的图像反映了他骑车上学的整个过程,则下列结论正确的是()A .修车花了25分钟B .小明家距离学校1000米C .修好车后骑行的速度是200米/分钟D .修好车后花了15分钟到达学校【答案】C【分析】根据横坐标,可得时间;根据函数图像的纵坐标,可得路程.【详解】解:A .由横坐标看出,小明修车时间为25-10=15(分钟),故本选项不符合题意; B .由纵坐标看出,小明家离学校的距离2000米,故本选项不合题意;C .小明修好车后骑行到学校的平均速度是:(2000-1000)÷5=200(米/分钟),故本选项符合题意;D .由横坐标看出,小明修好车后花了30-25=5(分钟)到达学校,故本选项不合题意. 故选:D .【点睛】本题考查了函数图像,观察函数图像得出相应的时间,函数图像的纵坐标得出路程是解题关键.二、填空题6.已知点()29,62A m m --在第三象限.则m 的取值范围是______. 【答案】3<m <4.5【分析】在第三象限内的点的横纵坐标均为负数,列式求值即可. 【详解】解:①点A (2m −9,6−2m )在第三象限, ①2m −9<0且6−2m <0, ①3<m <4.5, 故答案为: 3<m <4.5【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,此特点常与不等式、方程结合起来求一些字母的取值范围.7.如图,两只福娃的发尖所处的位置的坐标分别为M (-2,2)、N (1,-1), 则A 、B 、C 三个点中为坐标系原点的是____.【答案】A【分析】利用平移规律,从M(-2,2)向右平移2个单位长度,向下平移2个单位长度,可得A是坐标原点.【详解】解:①M(-2,2),①A是坐标原点.故答案为A.【点睛】本题考查了平面直角坐标系,利用平移逆向推理是解题关键.三、解答题8.某学校STEAM社团在进行项目化学习时,根据古代的沙漏模型(图1)制作了一套“沙漏计时装置”,该装置由沙漏和精密电子秤组成,电子秤上放置盛沙容器.沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内,可以通过读取电子秤的读数计算时间(假设沙子足够).该实验小组从函数角度进行了如下实验探究:实验观察:实验小组通过观察,每两小时记录一次电子秤读数,得到表1.表1探索发现:(1)建立平面直角坐标系,如图2,横轴表示漏沙时间x,纵坐标表示精密电子称的读数y,描出以表1中的数据为坐标的各点.(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,请你建立适当的函数模型,并求出函数表达式,如果不在同一条直线上,请说明理由.结论应用:应用上述发现的规律估算:(3)若漏沙时间为9小时,精密电子称的读数为多少?(4)若本次实验开始记录的时间是上午7:30,当精密电子秤的读数为72克时是几点钟? 【答案】(1)作图见解析(2)在同一直线上.函数表达式为:66y x =+ (3)漏沙时间为9小时,精密电子称的读数为60克 (4)下午6:30【分析】(1)根据表中各点对应横、纵坐标,描点即可.(2)通过连线可知这些点大致分布在同一直线上,满足一次函数表达式,所以可假设一次函数表达式,利用待定系数法求解函数表达式.(3)根据(2)中的表达式可求出当9x =时,精密电子秤的读数.(4)根据(2)中的表达式可求出当72y =时,漏沙的时间,然后根据起始时间可求出读数为72克的时间. (1) 解:如图所示(2)解:如图所示,连线可得,这些点在同一线上,并且符合一次函数图像. 设一次函数表达式为:y kx b =+将点(0,6),(2,18)代入解析式中可得6218b k b =⎧⎨+=⎩解得66a b =⎧⎨=⎩∴函数表达式为:66y x =+(3)解:由(2)可知函数表达式为:66y x =+ ∴当9x =时,60y =∴漏沙时间为9小时,精密电子称的读数为60克.(4)解:由(2)可知函数表达式为:66y x =+ ∴当72y =时,11x =起始时间是上午7:30∴经过11小时的漏沙时间为下午6:30.【点睛】本题考查一次函数的实际应用,要求掌握描点法画函数图象,待定系数法求解析式,会求函数自变量或函数值是解决本题的关键.平面直角坐标系(提升测评)一、单选题1.如图,小石同学在正方形网格图中建立平面直角坐标系后,点A 的坐标为(1,1)-,点B 的坐标为(2,0),则点C 的坐标为( )A .(1,2)-B .(2,1)-C .(1,2)--D .(1,1)-【答案】A【分析】利用已知点A 、B 的坐标确定平面直角坐标系,进而可得答案. 【详解】解:根据题意,建立如图所示的直角坐标系, ①点C 的坐标为(1,﹣2). 故选:A .【点睛】此题主要考查了点的坐标的确定,属于基本题型,正确得出原点位置是解题关键. 2.如图所示,从小明家到学校要穿过一个居民小区,小区的道路均是北南或西东方向,小明走下面哪条线路最短( )A .(1,3)→(1,2)→(1,1)→(1,0)→(2,0)→(3,0)→(4,0)B .(1,3)→(0,3)→(2,3)→(0,0)→(1,0)→(2,0)→(4,0)C .(1,3)→(1,4)→(2,4)→(3,4)→(4,4)→(4,3)→(4,2)→(4,0)D .以上都不对 【答案】A【分析】要想线路最短,就应从小明家出发向右及向下走,而不能向左或向上走,所以选A . 【详解】解:要想路线最短,就只应向右及向下走, 故选:A【点睛】本题考查了平面直角坐标系的应用以及数学在实际生活的应用,理解线路最短,应始终向着目标靠近,并明白平面直角坐标系中点的坐标的表示是解题关键.3.道路两旁种植行道树,选择行道树的因素有很多,比如:树形要美、树冠要大、存活率要高、落叶要少…现在只考虑树冠大小、存活率高低两个因素,可以用如下方法将实际问题数学化:设树冠直径为d ,存活率为h .如图,在平面直角坐标系中画出点(d ,h ),其中甲树种、乙树种、丙树种对应的坐标分别为A (d 1,h 1)、B (d 2,h 2)、C (d 3,h 3),根据坐标的信息分析,下列说法正确的是( )A .乙树种优于甲树种,甲树种优于丙树种B .乙树种优于丙树种,丙树种优于甲树种C .甲树种优于乙树种,乙树种优于丙树种D .丙树种优于甲树种,甲树种优于乙树种 【答案】B【分析】根据图象,比较A 、B 、C 三点的存活率和树冠直径即可得出答案. 【详解】根据题意和图象可得,213h h h >>,231d d d >>, ①乙树种是最优的,①甲树种的存活率略高于丙树种,基本相等,但丙树种的树冠直径远远大于甲树种的树冠直径, ①丙树种优于甲树种,①乙树种优于丙树种,丙树种优于甲树种, 故选:B .【点睛】本题考查规律型:点的坐标,准确读出坐标中的信息是解题的关键.4.点A 在第二象限,距离x 轴3个单位长度,距离y 轴5个单位长度,则点A 的坐标为( ) A .()5,3- B .()3,5-C .()5,3-D .()3,5-【答案】A【分析】首先确定点的横纵坐标的正负号,再根据距坐标轴的距离确定点的坐标. 【详解】解:①点A 在第二象限, ①点的横坐标为负数,纵坐标为正数,①点距离x 轴3个单位长度,距离y 轴5个单位长度, ①点的坐标为(-5,3). 故选:A .【点睛】此题主要考查了点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.5.如图,雷达探测器发现了A ,B ,C ,D ,E ,F 六个目标.目标C ,F 的位置分别表示为C (6,120°),F (5,210°),按照此方法表示目标A ,B ,D ,E 的位置时,其中表示正确的是( )A .A (4,30°)B .B (1,90°)C .D ( 4,240°) D .E (3,60°)【答案】C【分析】按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数,分别写出坐标A (5,30°),B (2,90°),D (4,240°),E (3,300°),即可判断.【详解】解:按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数, 由题意可知A 、B 、D 、E 的坐标可表示为:A (5,30°),故A 不正确;B (2,90°),故B 不正确;D (4,240°),故C 正确;E (3,300°),故D 不正确.故选择:C .【点睛】本题考查新定义坐标问题,仔细分析题中的C 、F 两例,掌握定义的含义,抓住表示一个点,。
平面直角坐标系中的规律探究问题(解析版)-2023-2024学年八年级数学上册学与练(北师大)

第04讲难点探究专题:平面直角坐标系中的规律探究问题目录【类型一平面直角坐标系中动点移动问题】..................................................................................................1【类型二平面直角坐标系中图形翻转问题】..................................................................................................7【类型三平面直角坐标系中新定义型问题】 (11)【类型一平面直角坐标系中动点移动问题】例题:(2023秋·辽宁盘锦·九年级校考开学考试)如图,在平面直角坐标系中,一动点沿箭头所示的方向,依次得到点1(01)P ,,2(11)P ,,3(10)P ,,4(11)P ,-,5(21)P ,-,…,则2023P 的坐标是.【答案】(674,1)【分析】由图可得,1(01)P ,,6(24)P ,,9(30)P ,,12(40)P ,,…,当n 能够被3整除时,点坐标为(0)3nnP ,,根据20223674÷=得2022(6740)P ,,点按“上→右→下→下→右→上”6次一循环,则20236=3371÷ ,根据点2023P 在点2022P 的上方,即可得.【详解】解:由图可得,1(01)P ,,6(24)P ,,9(30)P ,,12(40)P ,,…当n 能够被3整除时,点坐标为(0)3n nP ,,∵20223674÷=,∴2022(6740)P ,,∵按“上→右→下→下→右→上”6次一循环,∴20236=3371÷ ,∵点2023P 在点2022P 的上方,∴2023(674,1)P 故答案为:(674,1).【点睛】本题主要考查了点的坐标变化规律,解决问题的关键找出图形的变化规律.【变式训练】1.(2023春·江苏·七年级统考期中)如图,在平面直角坐标系中,动点A 从()10,出发,向上运动1个单位长度到达点B ()11,,分裂为两个点,分别向左、右运动到点C ()02,,D ()22,,此时称动点A 完成第一次跳跃;再分别从C ,D 点出发,每个点重复上面的运动,到达点G ()14-,,H ()14,,I ()34,,此时称动点A 完成第二次跳跃;依此规律跳跃下去,动点A 完成第2023次跳跃时,最右边一个点的坐标是()A .()20234046,B .()202320232,C .()20244046,D .()202320242,【答案】C【分析】根据题意找到点坐标变化的规律即可.【详解】解:由题意可得:A ()10,、D ()22,、I ()34,...每完成一次跳跃,最右边一个点的纵坐标增加2,到达点的横坐标增加1,则动点A 完成第2023次跳跃时,最右边一个点纵坐标为202324046⨯=,横坐标为:202312024+=故选:C .【点睛】本题考查了点坐标规律的探索.根据题意寻找变化规律是解题关键.2.(2023春·重庆·七年级统考期末)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中方向排列,如(1)0,,(2)0,,(21),,(32),,(3)1,,(30),,…,根据规律探索可得,第40个点的坐标为()A .(9)2,B .(93),C .(9)4,D .(9)5,【答案】D【分析】由题意知,把第一个点(1)0,作为第一列,(2)0,,(21),作为第二列,(32),,(3)1,,(30),作为第三列,进而可推导一般性规律为:第n 列有n 个数,则n 列共有()12n n +个数,且奇数列的点的顺序由上到下,偶数列点的顺序由下到上,由()881362⨯+=,可知第40个点的坐标在第9列,从上往下第4个点,进而可求点坐标.【详解】解:由题意知,把第一个点(1)0,作为第一列,(2)0,,(21),作为第二列,(32),,(3)1,,(30),作为第三列,进而可推导一般性规律为:第n 列有n 个数,则n 列共有()12n n +个数,且奇数列的点的顺序由上到下,偶数列点的顺序由下到上,∵()881362⨯+=,∴第40个点的坐标在第9列,从上往下第4个点,坐标为()95,,故选:D .【点睛】本题考查了点规律的探究.解题的关键在于根据题意推导出一般性规律.3.(2023·辽宁阜新·统考中考真题)如图,四边形1OABC 是正方形,曲线12345C C C C C 叫作“正方形的渐开线”,其中 12C C , 23C C , 34C C , 45C C ,…的圆心依次按O ,A ,B ,1C 循环.当1OA =时,点2023C 的坐标是()A .)12(022--,B .)20231(-,C .)12(023--,D .(2022)0,【答案】A【分析】由题得点的位置每4个一循环,经计算得出2023C 在第三象限,与3C ,7C ,11C ,…符合同一规律,探究出3C ,7C ,11C ,...的规律即可.【详解】解:由图得123450110()()()()(140)205C C C C C ---,,,,,,,,,,67(506)1()C C --,,,,…点C 的位置每4个一循环,202350543=⨯+,∴2023C 在第三象限,与3C ,7C ,11C ,…符合规律()11n --+,,∴2023C 坐标为)12(022--,.故选:A .【点睛】本题考查了点的坐标的规律的探究,理解题意求出坐标是解题关键.4.(2023春·黑龙江哈尔滨·八年级校考期中)如图,在平面直角坐标系中,动点P 从原点O 出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得点()11,1P --;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点2P ;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点3P ;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点4P ,…,按此作法进行下去,则点2023P 的坐标为.【答案】(1012,1012)--【分析】对奇数点,偶数点分开讨论,找出点坐标与序数的关系,总结规律求解.【详解】解:()11,1P --,1112+-=-;2(1,1)P ,212=;3(2,2)P --,3122+-=-;4(2,2)P ,422=;……当n 为奇数时,11,22n n n P ⎛⎫⎪⎝++-⎭-;当n 为偶数时,,22n n n P ⎛⎫⎪⎝⎭;∴20232023120231(,)22P ++--,即2023(1012,1012)P --.故答案为:(1012,1012)--.【点睛】本题考查点坐标规律探索,由开始的几个点坐标总结规律是解题的关键,注意分开讨论.5.(2023秋·黑龙江佳木斯·八年级佳木斯市第五中学校联考开学考试)如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()11-,,第2次接着运动到点()20-,,第3次接着运动到点()32-,,……,按这样的运动规律,经过第2025次运动后,动点P 的坐标是.【答案】()20251-,【分析】设动点P 运动了n 次,则点P 的横坐标为n -,点P 的纵坐标按1,0,2,0,1,0,2,0,⋅⋅⋅⋅⋅⋅重复出现,每4个数为一个循环.【详解】解:设动点P 运动了n 次.观察图形中点的坐标可知:点P 的横坐标为n -,点P 的纵坐标按1,0,2,0,1,0,2,0,⋅⋅⋅⋅⋅⋅重复出现,每4个数为一个循环.∵202545061÷=⋅⋅⋅⋅⋅⋅,∴当点P 经过2025次运动后,横坐标为2025-,纵坐标为1.即点P 的坐标为()20251-,.故答案为:()20251-,.【点睛】本题主要考查平面直角坐标系中点的坐标的规律,根据已知点的坐标归纳概括出点的坐标的规律是解题的关键.6.(2023春·四川内江·八年级校考期中)如图,在平面直角坐标系中,(1,1),(1,1),(1,2),(1,2)A B C D ----把一条长为a 个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处,并按A B C D A →→→→⋅⋅⋅的规律紧绕在四边形ABCD 的边上.(1)当12a =时,细线另一端所在位置的点的坐标是;(2)当2023a =时,细线另一端所在位置的点的坐标是.【答案】()1,1-()1,0-【分析】根据点的坐标,求出四边形ABCD 的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.【详解】解:∵()()()()1,11,11,21,2A B C D ----,,,,∴2323AB BC CD DA ====,,,,∴四边形ABCD 的周长为232310+++=,∴细线绕一圈的长度为10,∵121012÷= ,∴当12a =时,细线另一端所在位置的点与点B 重合,坐标为:()1,1-;∵2023102023÷= ,∴当2023a =时,细线另一端所在位置的点在点B 下方1个单位长度处,即为:()1,0-;故答案为:()1,1-,()1,0-;【点睛】本题考查坐标与图形,点的规律探究,解题的关键是求出四边形ABCD 的周长。
中考数学狙击重难点系列专题----规律探究之探究图形的规律求点的坐标(含答案)

根据图形的规律求坐标1. 如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为()A. (0,64)B. (0,128)C. (0,256)D. (0,512)2. 如图,直线,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1B,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( )A. (16,0)B. (12,0)C. (8,0)D. (32,0)3. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(,0),那么点B2018的坐标为( )A. (1,1)B.C. (﹣1,1)D.4. 如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2013的坐标为()A. (2,1006)B. (1008,0)C. (-1006,0)D. (1,-1007)5. 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,……,重复操作依次得到点P1,P2,…,则点P2010的坐标是().A. (2010,2)B. (2010,-2)C. (2012,-2)D. (0,2)6. 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧,,,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为()A. (﹣6,24)B. (﹣6,25)C. (﹣5,24)D. (﹣5,25)7. 如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第24秒时跳蚤所在位置的坐标是()A. (0,3)B. (4,0)C. (0,4)D. (4,4)8. 在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形A n B n C n C n﹣1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B n的坐标是________.9. 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为________.10. 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= x于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线y= x于点B3,…,按照此规律进行下去,则点A n的横坐标为________.11. 如图,在平面直角坐标系中,直线l:y= x﹣与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是________.12. 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上.若△A1OB1,△A2B1B2,△A3B2B3依次均为等腰直角三角形,直角顶点都在x轴上,则第2017个等腰直角三角形A2017B2016B2017顶点B2017的横坐标为________.13. 如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2 M1,对角线A1 M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3 M2,对角线A1 M2和A3B3交于点M3;……,依次类推,这样作的第n个正方形对角线交点的坐标为M n________.14. 如图,已知等边△OA1B1,顶点A1在双曲线y= (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为________.15. 如图,等边三角形△OAB1的一边OA在x 轴上,且OA=1,当△OAB1沿直线l滚动,使一边与直线l 重合得到△B1A1B2,△B2A2B3,......则点A2017的坐标是________.16. 如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为________.17. 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是________.18. 如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)…根据这个规律,点P2016的坐标为________.19. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是________.。
专题 平面直角坐标系中点的规律探究(精选题)(解析版) 八年级数学上学期

八年级上册数学《第5章平面直角坐标系》专题训练平面直角坐标系中点的规律探究一、选择题(共10题)1.(2023秋•茂南区期中)如图,一只小蚂蚁在平面直角坐标系中按图中路线进行“爬楼梯”运动,第1次它从原点运动到点(1,0),第2次运动到点(1,1),第3次运动到点(2,1)……按这样的运动规律,经过第2023次运动后,小蚂蚁的坐标是()A.(1011,1010)B.(1011,1011)C.(1012,1011)D.(1012,1012)【分析】根据吗,每次小蚂蚁运动的位置所对应的坐标,发现规律即可解决问题.【解答】解:由题知,小蚂蚁第1次运动到点(1,0);第2次运动到点(1,1);第3次运动到点(2,1);第4次运动到点(2,2);第5次运动到点(3,2);第6次运动到点(3,3);…由此可见,小蚂蚁运动2n(n为正整数)次,所在位置的坐标为(n,n),且下一次运动所对应的点的坐标为(n+1,n).所以第2022次运动到点(1011,1011),则第2023次运动到点(1012.1011).故选:C.【点评】本题考查点的运动规律,能根据题中小蚂蚁的运动方式发现第2n次运动后所对应点的坐标为(n,n)是解题的关键.2.(2023•南乐县一模)如图,在平面直角坐标系中,点A(1,1),B(3,1),C(3,3),D(1,3),动点P从点A出发,以每秒1个单位长度的速度沿AB﹣BC﹣CD﹣DA﹣AB﹣…路线运动,当运动到87秒时,点P的坐标为()A.(3,2)B.(2,3)C.(2,1)D.(1,2)【分析】根据坐标可知四边形ABCD为正方形,边长为2,周长为8.点P速度为1秒/每单位,运动87秒,求出路程.再求出路程中经过多少个完整的正方形ABCD,剩下的路程在正方形中运动找出终点即可得出点P坐标.【解答】解:∵A(1,1),B(3,1),C(3,3),D(1,3),∴AB=BC=CD=DA=2,正方形ABCD的周长=2×4=8.∵Vp=1s/每单位,∴Sp=1×87=87.87÷8=10…7.∵2+2+2=6,7﹣6=1∴点P在线段AD上且为线段AD中点.∴P(1,2).故选:D.【点评】本题以点的运动为背景考查了点的坐标规律,考核了学生对于运动的归纳总结能力,解题关键是求出正方形的边长,确定点P的位置.属于中考常考题型.3.(2022秋•李沧区期末)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是()A.(2022,0)B.(2023,0)C.(2023,2)D.(2023,﹣2)【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,继而求得答案.【解答】解:观察图形可知,点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,2023÷4=505……3,所以点A2023坐标是(2023,2).故选:C.【点评】本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解题的关键是根据图形得出规律.4.(2023春•平潭县期末)如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是()A.(﹣26,50)B.(﹣25,50)C.(26,50)D.(25,50)【分析】解决本题的关键是分析出题目的规律,以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到P100的横坐标.【解答】解:经过观察可得:P1和P2的纵坐标均为1,P3和P4的纵坐标均为2,P5和P6的纵坐标均为3,因此可以推知P99和P100的纵坐标均为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:P n的横坐标为n÷4+1(n是4的倍数).故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).故选:C.【点评】本题考查规律型:点的坐标,解题的关键是分析出题目的规律,找出题目中点的坐标的规律,属于中考常考题型.5.(2023春•龙凤区期中)如图,在平面直角坐标系中A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D (3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,问第2022秒瓢虫在()处.A.(﹣1,1)B.(1,1)C.(2,1)D.(3,1)【分析】根据点A、B、C、D的坐标可得出AB、AD及矩形ABCD的周长,由4044÷14商是288,余数是12,可得出当t=2022秒时瓢虫在点D左侧2个单位处,再结合点D的坐标即可得出结论.【解答】解:∵A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D(3,1),∴AB=CD=3,AD=BC=4,=2(AB+AD)=14,∴C矩形ABCD瓢虫2022秒行驶的路程为:2022×2=4044,∵4044÷14商是288,余数是12,∴当t=2022秒时,瓢虫在点D左侧2个单位处,∴此时瓢虫的坐标为(1,1),故B正确.故选:B.【点评】本题考查了规律型中点的坐标,根据瓢虫的运动规律找出当t=2022秒时瓢虫在点D处,是解题的关键.6.(2022春•启东市期中)如图,在平面直角坐标系xOy中,点A坐标是(1,1).若记点A坐标为(a1,a2),则一个点从点A出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8)…,每个点的横纵坐标都是整数,按此规律一直运动下去,则a2020+a2021+a2022的值为()A.2021B.2022C.1011D.1012【分析】观察已知点的坐标可得,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2021=1011,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,进而可得结果.【解答】解:由直角坐标系可知A(1,1),B(2,﹣1),C(3,2),D(4,﹣2),……,即a1=1,a2=1,a3=2,a4=﹣1,a5=3,a6=2,a7=4,a8=﹣2,……,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2021=1011,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,∴a2021=﹣505,2023÷4=505……3,∴a2022=506,故a2020+a2021+a2022=1012,故选:D.【点评】本题主要考查了规律型:点的坐标,探索数字与字母规律是解题关键.7.(2022•浉河区校级开学)如图,在平面直角坐标系中,A1(2,0),B1(0,1),A1B1的中点为C1;A2(0,3),B2(﹣2,0),A2B2的中点为C2;A3(﹣4,0),B3(0,﹣3),A3B3的中点为C3;A4(0,﹣5),B4(4,0),A4B4的中点为C4;…;按此做法进行下去,则点C2022的坐标为()A.(﹣1012,−20232)B.(﹣1011,20232)C.(﹣1011,−20232)D.(﹣1012,−20212)【分析】根据题意得点∁n的位置按4次一周期的规律循环出现,可求得点C2022在第二象限,从而可求得该题结果.【解答】解:由题意可得,点∁n的位置按4次一周期的规律循环出现,∵2022÷4=505……2,∴点C2022在第二象限,∵位于第二象限内的点C2的坐标为(﹣1,32),点C6的坐标为(﹣3,72),点C10的坐标为(﹣5,112),……∴点∁n的坐标为(−2,r12),∴当n=2022时,−2=−20222=−1011,r12=2022+12=20232,∴点C2022的坐标为(﹣1011,20232),故选:B.【点评】此题考查了点的坐标方面规律性问题的解决能力,关键是能根据题意确定出该点的出现规律.8.(2022春•冷水滩区校级期中)如图,已知A1(1,2)A2(2,2)A3(3,0)A4(4,﹣2)A5(5,﹣2)A6(6,0)……,按这样的规律,则点A2021的坐标为()A.(2021,2)B.(2020,2)C.(2021,﹣2)D.2020,﹣2)【分析】观察发现,每6个点形成一个循环,再根据点A6的坐标及2021÷6所得的整数及余数,可计算出点A2021的横坐标,再根据余数对比第一组的相应位置的数可得其纵坐标.【解答】解:观察发现,每6个点形成一个循环,∵A6(6,0),∴OA6=6,∵2021÷6=336…5,∴点A2021的位于第337个循环组的第5个,∴点A2021的横坐标为6×336+5=2021,其纵坐标为:﹣2,∴点A2021的坐标为(2021,﹣2).故选:C.【点评】本题考查了平面直角坐标系中的点的规律问题,发现题中的规律并正确计算出点A2021所处的循环组是解题的关键.9.(2023•莱阳市二模)自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波那契数1,1,2,3,5,8,13,……画出螺旋曲线.在平面直角坐标系中,依次以这组数为半径作90°的圆弧12 ,23 ,34 ⋯,得到一组螺旋线,连接P1P2,P2P3,P3P4,⋯,得到一组螺旋折线,如图所示.已知点P1,P2,P3的坐标分别为(﹣1,0),(0,1),(1,0),则点P7的坐标为()A.(6,1)B.(8,0)C.(8,2)D.(9,﹣2)【分析】观察图象,找出每个点的运动轨迹与斐波那契数结合推出P7的位置,即可解决问题.【解答】解:观察发现:P1(﹣1,0)先向右平移1个单位,再向上平移1个单位得到P2(0,1);P2(0,1)先向右平移1个单位,再向下平移1个单位得到P3(1,0);P3(1,0)先向左平移2个单位,再向下平移2个单位得到P4(﹣1,﹣2);P4(﹣1,﹣2)先向左平移3个单位,再向上平移3个单位得到P5(﹣4,1);P5(﹣4,1)先向右平移5个单位,再向上平移5个单位得到P6(1,6).根据斐波那契数,P6(1,6)应先向右平移8个单位,再向下平移8个单位得到P7(9,﹣2).故选:D.【点评】本题考查在平面直角坐标系中的点的坐标规律.考查了学生数形结合的能力,解题的关键是找出每个点的坐标及运动规律,推出答案即可.在做题时一定要理解题意.10.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,﹣1)…根据这个规律探索可得,第100个点的坐标()A.(14,0)B.(14,﹣1)C.(14,1)D.(14,2)【分析】观察图形可知,横坐标相等的点的个数与横坐标相同,根据求和公式求出第100个点的横坐标以及在这一横坐标中的所有点中的序数,再根据横坐标是奇数时从上向下排列,横坐标是偶数时从下向上排列,然后解答即可.【解答】解:由图可知,横坐标是1的点共有1个,横坐标是2的点共有2个,横坐标是3的点共有3个,横坐标是4的点共有4个,…,横坐标是n的点共有n个,1+2+3+…+n=or1)2,当n=13时,13×(13+1)2=91,当n=14时,14×(14+1)2=105,所以,第100个点的横坐标是14,∵100﹣91=9,∴第100个点是横坐标为14的点中的第9个点,∵第142=7个点的纵坐标是0,∴第9个点的纵坐标是2,∴第100个点的坐标是(14,2).故选:D.【点评】本题是对点的变化规律的考查,观察得到横坐标相等的点的个数与横坐标相同是解题的关键,还要注意横坐标为奇数和偶数时的排列顺序不同.二、填空题(共10题)11.(2022春•东洲区期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(﹣1,1),第2次接着运动到点(﹣2,0),第3次接着运动到点(﹣3,2),…,按这样的运动规律,经过第2022次运动后,动点P的坐标是.A.(2022,0)B.(﹣2022,0)C.(﹣2022,1)D.(﹣2022,2)【分析】观察图形可知:每4次运动为一个循环,并且每一个循环向左运动4个单位,用2022÷4可判断出第2022次运动时,点P在第几个循环第几次运动中,进一步即可计算出坐标.【解答】解:动点P的运动规律可以看作每运动四次为一个循环,每个循环向左运动4个单位,∵2022÷4=505……2,∴第2022次运动时,点P在第506次循环的第2次运动上,∴横坐标为﹣(505×4+2)=﹣2022,纵坐标为0,∴此时P(﹣2022,0).故答案为:(﹣2022,0).【点评】本题考查规律型:点坐标,解答时注意探究点的运动规律,又要注意动点的坐标的象限符号.12.(2022秋•肃州区校级期末)如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2022的坐标是.【分析】根据题意可以发现规律:A4n(﹣n,n),A4n+1(n+1,n),A4n+2(n+1,﹣n﹣1),A4n+3(﹣n﹣1,﹣n﹣1),根据规律求解即可.【解答】解:根据题意可以发现规律:A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),A6(2,﹣2),A7(﹣2,﹣2),A8(﹣2,2),…,∴A4n(﹣n,n),A4n+1(n+1,n),A4n+2(n+1,﹣n﹣1),A4n+3(﹣n﹣1,﹣n﹣1),∵2022=4×505+2,∴点A2022的坐标为(506,﹣506),故答案为:(506,﹣506).【点评】本题主要考查规律性:点的坐标,读懂题意,找出点的坐标规律是解答此题的关键.13.(2021秋•同安区期末)如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A2021的坐标为.【分析】观察图形得到奇数点的规律为,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n(3032,1010).﹣1),由2021是奇数,且2021=2n﹣1,则可求A2n﹣1【解答】解:观察图形可得,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),A2(3,2),A4(6,3),A6(9,4),…,A2n(3n,n+1),∵2021是奇数,且2021=2n﹣1,∴n=1011,(3032,1010),∴A2n﹣1故答案为(3032,1010).【点评】本题考查点的坐标规律;熟练掌握平面内点的坐标,能够根据图形的变化得到点的坐标规律是解题的关键.14.(2023秋•德州期中)如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹的反射角等于入射角(反射前后的线与边的夹角相等),当小球第1次碰到正方形的边时的点为P1(2,0),第2次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为P n,则点P2023的坐标为.【分析】按照反弹规律依次画图即可.【解答】解:如图:根据反射角等于入射角画图,可知小球从P2反射后到P3(0,3),再反射到P4(2,4),再反射到P5(4,3),再反射到P点(0,1)之后,再循环反射,每6次一循环,∵2023÷6=337……1,∴点P2023的坐标是(2,0).故答案为:(2,0).【点评】本题考查了生活中的轴对称现象,点的坐标.解题的关键是能够正确找到循环数值,从而得到规律.15.(2023春•金乡县期中)如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2024次碰到球桌边时,小球的位置是.【分析】根据题意,可以画出相应的图形,然后即可发现点所在位置的变化特点,即可得到小球第2024次碰到球桌边时小球的位置.【解答】解:由图可得,点(1,0)第一次碰撞后的位置的坐标为(0,1),第二次碰撞后的位置的坐标为(3,4),第三次碰撞后的位置的坐标为(7,0),第四次碰撞后的位置的坐标为(8,1),第五次碰撞后的位置的坐标为(5,4),第六次碰撞后的位置的坐标为(1,0),…,∴小球位置每6次为一个周期依次循环,∵2024÷6=337…2,∴小球第2024次碰到球桌边时,小球的位置是(3,4),故答案为:(3,4).【点评】本题考查点坐标规律探索,解答本题的关键是明确题意,发现点的坐标位置的变化特点,利用数形结合的思想解答.16.(2022•绥化三模)如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,点P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2),…,根据这个规律,点P2022的坐标为.【分析】根据各个点的位置关系,可得出下标为4的倍数的点在第四象限,被4除余1的点在第三象限的角平分线上,被4除余2的点在第二象限,被4除余3的点在第一象限的角平分线上,点P2022的在第三象限,且横纵坐标的绝对值=2022÷4的商,纵坐标是2022÷4的商+1,再根据第三项象限内点的符号得出答案即可.【解答】解:∵2022÷4=505…2,∴点P2022在第二象限,∵P6(﹣1,2),P10(﹣2,3),P14(﹣3,4),…,6÷4=1…2,10÷4=2…2,14÷2=3..2,…,∴P2022(﹣505,506).故答案为:(﹣505,506).【点评】本题考查了规律型:点的坐标,是一个阅读理解,猜想规律的题目,解答此题的关键是首先确定点所在的大致位置,所在正方形,然后就可以进一步推得点的坐标.17.(2022秋•杏花岭区校级期中)在平面直角坐标系xOy中,对于点P(x,y),我们把点P1(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,⋯,A n,若点A1的坐标为(3,1),则点A2022的坐标为.【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2022除以4,根据商和余数的情况确定点A2022的坐标即可.【解答】解:∵A1的坐标为(3,1),∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),…,依此类推,每4个点为一个循环组依次循环,∵2022÷4=505余2,∴点A2022的坐标与A2的坐标相同,为(0,4);故答案为:(0,4).【点评】此题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.18.(2023秋•沈河区校级期中)如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置…依次进行下去,若已知点A(3,0),B(0,4),则点A2023的坐标为.【分析】根据点A(3,0),B(0,4)得AB=5,再根据旋转的过程寻找规律即可求解.【解答】解:∵∠AOB=90°,点A(3,0),B(0,4),根据勾股定理,得AB=5,根据旋转可知:∴OA+AB1+B1C2=3+5+4=12,所以点B2(12,4),A1(12,3);继续旋转得,B4(2×12,4),A3(24,3);B6(3×12,4),A5(36,3)…,发现规律:A2023(12×2023+12,3).所以点A2023的坐标为(12144,3).故答案为:(12144,3).【点评】本题考查了规律型:点的坐标,解决本题的关键是灵活运用旋转的知识.19.(2022春•五华区校级期中)如图,在直角坐标系中,长方形OABC的长为2,宽为1,将长方形OABC 沿x轴翻转1次,点A落在A1处,翻转2次,点A落在A2处,翻转3次,点A落在A3处(点A3与点A2重合),翻转4次,点A落在A4处,以此类推…,若翻转2022次,点A落在A2022处,则A2022的坐标为.【分析】探究规律,利用规律解决问题即可.【解答】解:由题意A1(3,2),A2(A3)(5,0),A4(6,1),•••,发现4次一个循环,∵2022÷4=505.....2,∴A2022的纵坐标与A2相同,横坐标=505×6+5=3035,∴A2022(3035,0),故答案为:(3035,0).【点评】本题考查坐标与图形的变化﹣对称,规律型问题,解题的关键是学会探究规律的方法,属于中考填空题中的压轴题.20.(2023•潍坊开学)如图,在平面直角坐标系中,A、B、C,D四点的坐标分别是A(1,3),B(1,1),C(3,1),D(3,3)、动点P从点A出发,在正方形边上按照A→B→C→D→A→…的方向不断移动,已知P的移动速度为每秒1个单位长度,则第2023秒点P的坐标是.【分析】根据点P的移动方式,可得出第2023秒点P的位置,进而解决问题.【解答】解:因为点P从点A出发,在正方形边上按照A→B→C→D→A→…的方向不断移动,且P的移动速度为每秒1个单位长度,所以第1秒点P的坐标是(1,2);第2秒点P的坐标是(1,1);第3秒点P的坐标是(2,1);第4秒点P的坐标是(3,1);第5秒点P的坐标是(3,2);第6秒点P的坐标是(3,3);第7秒点P的坐标是(2,3);第8秒点P的坐标是(1,3);第9秒点P的坐标是(1,2);…由此可见,点P的坐标每8秒循环一次,又2023÷8=252余7,所以第2023秒点P的坐标是(2,3).故答案为:(2,3).【点评】本题考查点的运动规律,能根据点P的移动方式每8秒一循环是解题的关键.三、解答题(共12题)21.(2022秋•无为市月考)在平面直角坐标系中,一个动点A从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次只移动1个单位长度,其行走路线如图所示.(1)填写下列各点的坐标:A4,A6,A12,A14.(2)按此规律移动,n为正整数,则点A4n的坐标为,点A4n+2的坐标为.(3)动点A从点A2022到点A2023的移动方向是.(填“向上”、“向右”或“向下”)【分析】(1)根据点的坐标变化即可填写各点的坐标;(2)根据(1)发现规律即可写出点A4n的坐标(n为正整数);(3)根据(2)发现的规律,每四个点一个循环,进而可得蜗牛从点A2020到点A2021的移动方向.【解答】解:(1)根据点的坐标变化可知:各点的坐标为:A4(2,0),A6(3,1),A12(6,0),A14(7,1);故答案为:(2,0),(3,1),(6,0),(7,1);(2)根据(1)发现:点A4n的坐标(n为正整数)为(2n,0);点A4n+2的坐标为(2n+1,1);故答案为:(2n,0),(2n+1,1);(3)因为每四个点一个循环,所以2023÷4=505…3.所以从点A2022到点A2023的移动方向是向下.故答案为:向下.【点评】本题考查了规律型﹣点的坐标,解决本题的关键是根据点的坐标变化发现规律,总结规律,运用规律.22.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…(1)填写下列各点的坐标:P9(、),P12(、),P15(、)(2)写出点P3n的坐标(n是正整数);(3)点P60的坐标是(、);(4)指出动点从点P210到点P211的移动方向.【分析】由题意可以知道,动点运动的速度是每次运动一个单位长度,(0,1)→(1,1)→(1,0)→(1,﹣1)……通过观察找到有规律的特殊点,如P3、P6、P9、P12,发现其中规律是脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,明确这个规律即可解决以上所有问题.【解答】解:(1)由动点运动方向与长度可得P3(1,0),P6(2,0),可以发现脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,即动点运动三次与横轴相交,故答案为P9(3,0),P12(4、0),P15(5、0).(2)由(1)可归纳总结点P3n的坐标为P3n(n,0),(n是正整数);(3)根据(2),∵60=3×20,∴点P60的横坐标是20故点P60的坐标是(20、0)故答案为(20、0).(4)∵210=3×70,符合(2)中的规律∴点P210在x轴上,又由图象规律可以发现当动点在x轴上时,偶数点向上运动,奇数点向下运动,而点P210是在x轴上的偶数点所以动点从点P210到点P211的移动方向应该是向上.【点评】本题是一个阅读理解,猜想规律的题目,解答此题的关键是首先确定动点移动的数字与方向上的规律,然后再进一步按规律解决要求的点的位置.23.(2023春•凤台县期末)在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设P n(x n,y n),n=1,2,3,….(1)依次写出x1、x2、x3、x4、x5、x6的值;(2)计算x1+x2+…+x8的值;(3)计算x1+x2+…+x2003+x2004的值.【分析】(1)根据图象结合平面坐标系得出各点横坐标即可;(2)根据各点横坐标数据得出规律,进而得出答案即可;(3)经过观察分析可得每4个数的和为2,把2004个数分为501组,即可得到相应结果.【解答】解:(1)根据平面坐标系结合各点横坐标得出:x1、x2、x3、x4、x5、x6的值分别为:1,﹣1,﹣1,3,3,﹣3;(2)∵x1+x2+x3+x4=1﹣1﹣1+3=2;x5+x6+x7+x8=3﹣3﹣3+5=2;∴x1+x2+…+x8=2+2=4;(3)∵x1+x2+x3+x4=1﹣1﹣1+3=2;x5+x6+x7+x8=3﹣3﹣3+5=2;…x97+x98+x99+x100=2…∴x1+x2+…+x2003+x2004=2×(2004÷4)=1002.【点评】此题主要考查了点的坐标特点,解决本题的关键是分析得到4个数相加的规律.23.(2022秋•长丰县期末)如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2、4、6、8、…,顶点依次用A1、A2、A3、A4、…表示.(1)请直接写出A5、A6、A7、A8的坐标;(2)根据规律,求出A2022的坐标.【分析】(1)看图观察即可直接写出答案;(2)根据正方形的性质找出部分A n点的坐标,根据坐标的变化找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数)”,依此即可得出结论.【解答】解:(1)A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2);(2)观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n 为自然数),∵2022=505×4+2,∴A2022(﹣506,506).【点评】本题考查了规律型:点的坐标,解题的关键是找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标的变化找出变化规律是关键.24.一个质点在第一象限及x轴、y轴移动,在第一秒时,它从原点移动到(0,1),然后按着下列左图中箭头所示方向移动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动1个单位.(1)该质点移动到(1,1)的时间为秒,移动到(2,2)的时间为秒,移动到(3,3)的时间为秒,…,移动到(n,n)的时间为秒.(2)该质点移动到(7,4)的时间为秒.【分析】(1)根据图形可得出质点移动到(1,1),(2,2),(3,3)的时间,根据规律可得出质点移动(n,n)的时间;(2)现有(1)的结论得出(7,7)的时间,再加上3即可得出移动到(7,4)的时间.【解答】解:(1)由图可知移动到(1,1)的时间为2秒,移动到(2,2)的时间为6秒,移动到(3,3)的时间为12秒,根据变化规律可得移动到(n,n)的时间为n(n+1),故答案为:2,6,12,n(n+1);(2)由(1)可得移动到(7,7)的时间为7×8=56,56+3=59,∴移动到(7,4)的时间为59秒,故答案为59.【点评】本题主要考查点的坐标的变化规律,关键是要能找到质点移动到(n,n)的时间的规律.25.(2022•马鞍山一模)如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,A1的坐标为(2,2),A2的坐标为(5,2).(1)A3的坐标为,A n的坐标为用含n的代数式表示;(2)若护栏长为2020,则需要小正方形个,大正方形个.【分析】(1)根据已知条件与图形可知,大正方形的对角线长为2,由此可得规律:A1,A2,A3,…,A n各点的纵坐标均为2,横坐标依次大3,由此便可得结果;(2)先求出一个小正方形与一个大正方形所构成的护栏长度,再计算2020米包含多少这样的长度,进而便可求出结果.【解答】解:(1)∵A 1的坐标为(2,2)、A 2的坐标为(5,2),∴A 1,A 2,A 3,…,A n 各点的纵坐标均为2,∵小正方形的边长为1,∴A 1,A 2,A 3,…,A n 各点的横坐标依次大3,∴A 3(5+3,2),A n (2+3+3+⋅⋅⋅+3︸(K1)个3,2),即A 3(8,2),A n (3n ﹣1,2),故答案为(8,2);(3n ﹣1,2);(2)∵2020÷3=673…1,∴需要小正方形674个,大正方形673个.【点评】本题是点的坐标的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.26.如图,在直角坐标系中,第一次将△OAB 变换成△OA 1B 1,第二次将△OA 1B 1变成△OA 2B 2,第三次将△OA 2B 2变成△OA 3B 3,已知A (1,5),A 1(2,5),A 2(4,5),A 3(8,5);B (2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)观察每次变换前后三角形有何变化,找出规律.按此规律将△OA 3B 3变成△OA 4B 4,则A 4的坐标是,B 4的坐标是.(2)若按第(1)题中找到的规律将△OAB 进行n 次变换,得到△OA n B n ,比较每次变换中三角形顶点的坐标有何变化,找出规律,推测A n 的坐标是,B n 的坐标是.【分析】(1)对于A 1,A 2,A n 坐标找规律可将其写成竖列,比较从而发现A n 的横坐标为2n ,而纵坐标都是5,同理B 1,B 2,B n 也一样找规律.(2)根据第一问得出的A 4的坐标和B 4的坐标,再此基础上总结规律即可知A n 的坐标是(2n ,5),B n的坐标是(2n+1,0).【解答】解:(1)因为A(1,5),A1(2,5),A2(4,5),A3(8,5)…纵坐标不变为5,同时横坐标都和2有关,为2n,那么A4(16,5);因为B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,同时横坐标都和2有关为2n+1,那么B的坐标为B4(32,0);故答案为:(16,5),(32,0);(2)由上题第一问规律可知A n的纵坐标总为5,横坐标为2n,B n的纵坐标总为0,横坐标为2n+1,∴A n的坐标是(2n,5),B n的坐标是(2n+1,0).故答案为:(2n,5),(2n+1,0).【点评】本题考查了学生观察图形及总结规律的能力,涉及的知识点为:平行于x轴的直线上所有点纵坐标相等,x轴上所有点的纵坐标为0.27.小明在学习了平面直角坐标系后,突发奇想,画出了这样的图形(如图),他把图形与x轴正半轴的交点依次记作A1(1,0),A2(5,0),…A n,图形与y轴正半轴的交点依次记作B1(0,2),B2(0,6),…B n,图形与x轴负半轴的交点依次记作C1(﹣3,0),C2(﹣7,0),…∁n,图形与y轴负半轴的交点依次记作D1(0,﹣4),D2(0,﹣8),…D n,发现其中包含了一定的数学规律.请根据你发现的规律完成下列题目:(1)请分别写出下列点的坐标:A3,B3,C3,D3;(2)请分别写出下列点的坐标:A n,B n,∁n,D n;(3)请求出四边形A5B5C5D5的面积.【分析】(1)根据点的坐标规律解答即可;(2)根据点的坐标规律解答即可;(3)根据四边形A5B5C5D5的面积=△5B5+△5B5+△5B5+△5B5计算即可.【解答】解:(1)A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12).(2)A n(4n﹣3,0),B n(0,4n﹣2),∁n(﹣4n+1,0),D n(0,﹣4n).(3)∵A5(17,0),B5(0,18),C5(﹣19,0),D5(0,﹣20).∴四边形A5B5C5D5的面积=△5B5+△5B5+△5B5+△5B5=12×17×18+12×18×19+12×19×20+12×20×17=684.故答案为:A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12).A n(4n﹣3,0),B n(0,4n﹣2),∁n(﹣4n+1,0),D n(0,﹣4n).【点评】此题考查点的坐标,关键是根据图形得出点的坐标的规律进行分析.28.(2022春•自贡期末)综合与实践问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1,P2.探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为.拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.【分析】(1)根据坐标的确定方法直接描点,:分别读出各点的纵横坐标,即可得到各中点的坐标;(2)根据(1)中的坐标与中点坐标找到规律;(3)利用(2)中的规律进行分类讨论即可答题.。
(完整版)平面直角坐标系规律题(带答案)
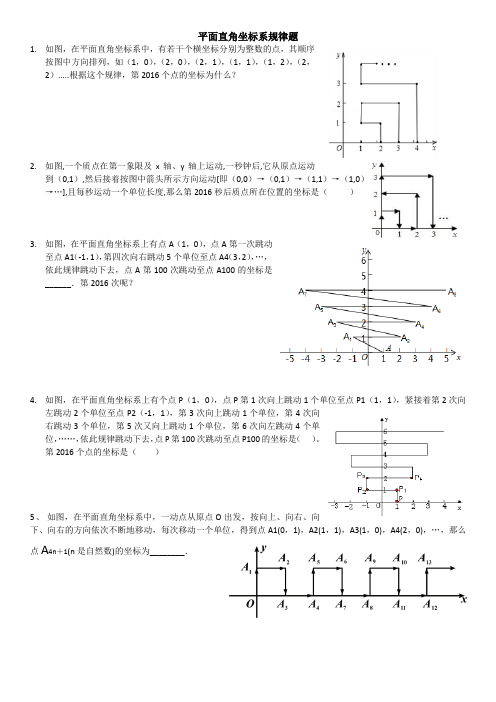
平面直角坐标系规律题1.如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2).....根据这个规律,第2016个点的坐标为什么?2.如图,一个质点在第一象限及x轴、y轴上运动,一秒钟后,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒运动一个单位长度,那么第2016秒后质点所在位置的坐标是()3.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是______.第2016次呢?4.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是()。
第2016个点的坐标是()5、如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n是自然数)的坐标为________.答案:1.解:根据图形,以最外边的正方形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,例如:右下角的点的横坐标为1,共有1个,1=12,右下角的点的横坐标为2时,共有4个,4=22,右下角的点的横坐标为3时,共有9个,9=32,右下角的点的横坐标为4时,共有16个,16=42,…右下角的点的横坐标为n时,共有n2个,∵452=2025,45是奇数,∴第2025个点是(45,0),第2016个点是(45,9),2.(8 ,44)3.观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),…第2n次跳动至点的坐标是(n+1,n),∴第100次跳动至点的坐标是(51,50).故答案为:(51,50).4.经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:P n的横坐标为n÷4+1(n是4的倍数).故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).5.由图可知,n=1时,4×1+1=5,点A5(2,1),n=2时,4×2+1=9,点A9(4,1),n=3时,4×3+1=13,点A13(6,1),所以,点A4n+1(2n,1).故答案为:(2n,1).。
备战中考数学二轮专题归纳提升真题平面直角坐标系规律探究问题(解析版)

专题01 平面直角坐标系规律探究问题【知识点梳理】1、关于x 轴、y 轴或原点对称的点的坐标的特征点P (a ,b )与关于x 轴对称点的坐标为 (a ,-b ) 点P (a ,b )与关于y 轴对称点的坐标为 (-a ,b ) 点P (a ,b )与关于原点对称点的坐标为 (-a ,-b ) 口诀:关于谁对称,谁不变,另一个变号,关于原点对称都变号 2、点的平移点P (a ,b )沿x 轴向右(或向左)平移m 个单位后对应点的坐标是(a ±m,b ); 点P (a ,b )沿y 轴向上(或向下)平移n 个单位后对应点的坐标是(a,b ±n ). 口诀:横坐标右加左减,纵坐标上加下减.3、两点间的距离:在x 轴或平行于x 轴的直线上的两点P 1 (x 1,y ),P 2 (x 2,y )间的距离为|x 1−x 2| 在y 轴或平行于y 轴的直线上的两点P 1 (x ,y 1),P 2 (x ,y 2)间的距离为|y 1−y 2| 任意两点P 1 (x 1,y 1),P 2 (x 2,y 2),则线段P 1P 2的中点坐标为(x 1+x 22,y 1+y 22)任意两点P 1 (x 1,y 1),P 2 (x 2,y 2),则线段P 1P 2=√(x 1−x 2)2+(y 1−y 2)2【典例分析】【例1y)经过某种变换后得到点P ′(−y +1,x +2),我们把点P ′(−y +1,x +2)叫做点P(x,y)的终结点.已知点P 1的终结点为P 2,点P 2的终结点为P 3,点P 3的终结点为P 4,这样依次得到P 1、P 2、P 3、P 4、…、nP 、…,若点p 1的坐标为(2,0),则点P 2022的坐标为_____。
【答案】(1,4).解析:解:P 1 坐标为(2,0),则P 2坐标为(1,4),P 3坐标为(-3,3),P 4坐标为(-2,-1),P 5坐标为(2,0),∴P n 的坐标为(2,0),(1,4),(-3,3),(-2,-1)循环, ∵2022=4×505+2, ∴P 2022 坐标与P 2点重合, 故答案为(1,4).【练1】在平面直角坐标系xOy 中,对于点P (x ,y ),我们把点P′(y -1,-x+1)叫做点P 的伴随点.已知点A 1的伴随点为A 2,点A 2的伴随点为A 3,点A 3的伴随点为A 4,…,这样依次得到点A 1,A 2,A 3,…,A n ,….若点A 1的坐标为(3,2),则A 2023的坐标为________【答案】(-3,0)解析:解:∵A1(3,2),A2(1,-2),A3(-3,0),A4(-1,4),A5(3,2),…,∴点A n的坐标4个一循环.∵2023=505×4+3,∴点A2023的坐标与点A2的坐标相同.∴A2023的坐标为(-3,0),故答案为:(-3,0).【练2】某同学在平面直角坐标系内设计了一个动点运动的编程.若一个动点从点A1(1,3)出发,沿A2(3,5)→A3(7,9)→…运动,则点A2022的坐标为()A.(22021﹣1,22021+1)B.(22022﹣1,22022+1)C.(22022﹣2,22022+2)D.(22021﹣2021,22021+2021)【答案】B【解析】解:∵一个动点从点A1(1,3)出发,沿A2(3,5)→A3(7,9)→…运动,∴A n(2n﹣1,2n+1),∴A2022的坐标为:(22022﹣1,22022+1),故选:B.【练3】对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y);且规定P n(x,y)=P1(P n﹣1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2).则P2022(1,﹣1)=.【答案】(21011,21011)【解析】解:由题意可得:P1(1,﹣1)=(0,2),P2(1,﹣1)=(2,﹣2)P3(1,﹣1)=(0,4),P4(1,﹣1)=(4,﹣4)P5(1,﹣1)=(0,8),P6(1,﹣1)=(8,﹣8)…当n为奇数时,P n(1,﹣1)=(0,),当n为偶数时,P n(1,﹣1)=(2n2,2n2),∴P2022(1,﹣1)应该等于(21011,21011).故答案是:(21011,21011).【例2】如图,在平面直角坐标系中,A1(1,2),A2(2,0),A3(3,﹣2),A4(4,0)…根据这个规律,探究可得点A2022的坐标是()A.(2022,0)B.(2022,2)C.(2021,﹣2)D.(2022,﹣2)【答案】A【解析】解:观察图形可知,点A1(1,2),A2(2,0),A3(3,﹣2),A4(4,0)…的横坐标依次是1、2、3、4、…、n,纵坐标依次是2、0、﹣2、0、2、0、﹣2、…,四个一循环,2022÷4=505…2,故点A2022坐标是(2022,0).故选:A.【练1】如图,动点P1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2022次运动后,动点P的坐标是()A.(2021,0)B.(2020,1)C.(2022,0)D.(2022,1)【答案】C【解析】分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位,∴2022=4×505+2.当第505循环结束时,点P位置在(2020,0),在此基础之上运动两次到(2022,0).故选C.【练2】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,按这样的运动规律,第2022次运动后,动点P2022的坐标是()A.(2022,1)B.(2022,2)C.(2022,﹣2)D.(2022,0)【答案】D【解析】解:观察图象,动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;∵2022÷6=337,∴经过第2022次运动后,动点P的纵坐标是0,故选:D.【练3】如图,平面直角坐标系中,一个点从原点O出发,按向右→向上→向右→向下的顺序依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移到点A1,第二次移到点A2,第三次移到点A3,…,第n次移到点A n,则点A2022的坐标是_____________.【答案】(1011,1).【解析】观察图象可知,点A的纵坐标每4个点循环一次,∵2022=505×4+2,∴点A2022的纵坐标与点A2的纵坐标相同,∵A2(1,1),A6(3,1),A10(5,1)……,∴点A2022的坐标是(1011,1).【例3】如图,在平面直角坐标系上有个点A(-1,O),点A第1次向上跳动一个单位至点A1(-1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点A第2022次跳动至点A2022的坐标是( )A.(-505, 1011)B.(505, 1010)C.(-506, 1010)D.(506, 1011)【答案】D【解析】解:设第n次跳动至点A n,观察,发现:A(-1,0),A1(-1,1),A2(1,1),A3(1,2),A4(-2,2),A5(-2,3),A6(2,3),A7(2,4),A8(-3,4),A9(-3,5),…,∴A4n(-n-1,2n),A4n+1(-n-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).∵2022=505×4+2,∴A2022(505+1,505×2+1),即(506,1011).故选:D.【练1】如图所示,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(−1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位……依此规律跳动下去,点P第99次跳动至点P99的坐标是_____【答案】(-25,50)【解析】解:由题中规律可得出如下结论:设点Px的横坐标的绝对值是n,则在y轴右侧的点的下标分别是4(n-1)和4n-3,在y轴左侧的点的下标是:4n-2和4n-1;判断P199的坐标,就是看99=4(n-1)和99=4n-3和99=4n-2和99=4n-1这四个式子中哪一个有负整数解,从而判断出点的横坐标.由上可得:点P第99次跳动至点P99的坐标是(-25,50)故答案为:(-25,50).【练2】如图,在平面直角坐标系上有点A0(1,0),点A0第一次跳动至点A1(−1,1),第二次点A1跳动至点A2(2,1),第三次点A跳动至点A3(−2,2),第四次点A3跳动至点A4(3,2),……依2此规律跳动下去,则点A2021与点A2022之间的距离是()A.2023B.2022C.2021D.2020【答案】A【解析】观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),…第2n次跳动至点的坐标是(n+1,n),则第2022次跳动至A2022点的坐标是(1012,1011),第2021次跳动至点A2021的坐标是(﹣1011,1011).∵点A2021与点A2022的纵坐标相等,∴点A2021与点A2022之间的距离=1012﹣(﹣1011)=2023.故选:A.【练3】在平面直角坐标系内原点O(0,0)第一次跳动到点A1(0,1),第二次从点A1跳动到点A2(1,2),第三次从点A2跳动到点A3(﹣1,3),第四次从点A3跳动到点A4(﹣1,4),…,按此规律下去,则点A2021的坐标是()A.(673,2021)B.(674,2021)C.(﹣673,2021)D.(﹣674,2021)【答案】B【解析】解:因为A1(0,1),A2(1,2),A3(﹣1,3),A4(﹣1,4),A5(2,5),A6(﹣2,6),A7(﹣2,7),A8(3,8),…A3n﹣1(n,3n﹣1),A3n(﹣n,3n),A3n+1(﹣n,3n+1)(n为正整数),∵3×674﹣1=2021,∴n=674,所以A2021(674,2021),故选:B.【例4】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1)(1,1),(1,2),(2,2)……根据这个规律,第2022个点的坐标为________【答案】(45,6)【解析】解:观察图形,可知:第1个点的坐标为(1,0),第4个点的坐标为(1,1),第9个点的坐标为(3,0),第16个点的坐标为(1,3),…,∴第(2n-1)2个点的坐标为(2n-1,0)(n为正整数).∵2025=452,∴第2025个点的坐标为(45,0).又∵2025-3=2022,∴第2022个点在第2025个点的上方3个单位长度处,∴第2022个点的坐标为(45,3).故答案为:(45,3).【练1】如图,一个蒲公英种子从平面直角坐标系的原点O出发,向正东走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5,以此规律走下去,当种子到达点A10时,它在坐标系中坐标为()A.(﹣12,﹣12)B.(15,18)C.(15,﹣12)D.(﹣15,18)【答案】B【解析】解:根据题意可知:O A1=3,A1A2=6,A2A3=9,A3A4=12,A4A5=15,A5A6=18,A9A10=30,∴A1点坐标为(3,0),A2点坐标为(3,6),A3点坐标为(﹣6,6),A4点坐标为(﹣6,﹣6),A5点坐标为(9,﹣6),A6点坐标为(9,12),以此类推,A9点坐标为(15,﹣12),所以A10点横坐标为15,纵坐标为﹣12+30=18,∴A10点坐标为(15,18),故选:B.【练2】如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→(0,1)→(0,2)→…,且每秒移动一个单位,那么第2022秒时,点所在位置的坐标是( )A .(2,44)B .(41,44)C .(44,41)D .(44,2)【答案】【解析】解:观察可发现,点到(0,2)用4=22秒,到(3,0)用9=32秒,到(0,4)用16=42秒,则可知当点离开x 轴时的横坐标为时间的平方,当点离开y 轴时的纵坐标为时间的平方, 此时时间为奇数的点在x 轴上,时间为偶数的点在y 轴上, ∵2022=452﹣3=2025﹣3,∴第2025秒时,动点在(45,0),故第2022秒时,动点在(45,0)向左一个单位,再向上2个单位, 即(44,2)的位置. 故选:D .【练3】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,−1)…根据这个规律探索可得,第99个点的坐标为( )A.(14,−1)B.(14,0)C.(14,1)D.(14,2)【答案】C【解析】解:在横坐标上,第一列有一个点,第二列有2个点…第n 个有n 个点, 并且奇数列点数对称而偶数列点数y 轴上方比下方多一个, 所以奇数列的坐标为(n,n−12),(n,n−12−1),…,(n,1−n 2);偶数列的坐标为(n,n2),(n,n2−1),…,(n,1−n2), ∵1+2+3+4+……+13=91∴第99个点位于第14列自上而下第7行.−6),即(14,1).代入上式得(14,142故选C.【例5】如图,在平面直角坐标系中,将边长为3,4,5的直角△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置…依次进行下去,发现A(3,0),A1(12,3),A2(15,0)…那么点A2022的坐标为.【答案】(12135,0)【解析】解:∵∠AOB=90°,点A(3,0),B(0,4),根据勾股定理得AB=5,根据旋转可知:OA+AB1+B1C2=3+5+4=12,所以点A1(12,3),A2(15,0);继续旋转得A3(24,3),A4(27,0);…发现规律:A2n﹣1(12n,3),A2n(12n+3,0),∵2022=2n,∴n=1011,∴点A2022的坐标为(12135,0),故答案为:(12135,0).【练1】如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2022次碰到长方形的边时点P的坐标为.【答案】(0,3【解答过程】解:如图所示:经过6次反弹后动点回到出发点(0,3),∵2022÷6=337∴当点P第2022次碰到矩形的边时与P点起点位置重合,∴点P的坐标为(0,3).故答案为:(0,3).【练2】如图,将边长为2的等边三角形沿x轴正方向连续翻折2019次,依次得到点P1,P2,P3,...,P2022,则点P2022的坐标是()A.(2022,2)B.(2022,√3)C.(4043,2)D.(4043, √3)【答案】D【解析】解:由题意可知P1是1P的横坐标是3,P3的横坐标是5,P4的横坐标是7…依此类推下去,P n的横坐标是2n-1,∴P2022的横坐标是2×2022-1=4043纵坐标都是√3,故选:D.连续作旋转变换,依【练3】如图,在直角坐标系中,已知点A(−3,0),B(0,4),对OAB次得到Δ1,Δ2,Δ3,Δ4,…,则∆2022的直角顶点的坐标为______.【答案】(8088,0)【解析】解:∵点A(-3,0)、B(0,4),∴AB=√32+42=5由图可知,每三个三角形为一个循环组依次循环,一个循环组前进的长度为:4+5+3=12,∵2022÷3=674,∴∆2022的直角顶点是第674个循环组的最后一个三角形的直角顶点;∵674×12=8088,∴∆2022的直角顶点的坐标为(8088,0).故答案为(8088,0).【例6】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推……则正方形OB2021B2022C2022的顶点B2022的坐标是_____.【答案】(0,-22011)【解析】解:∵正方形OA1B1C1的边长为1,∴OB1=√2∴OB2=2∴B2(0,2),同理可知B3(-2,2),B4(-4,0),B5(-4,-4),B6(0,-8),B7(8,-8),B9(16,16),B10(0,32).由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标的符号相同,每次正方形的边长变为原来的√2倍,∵2022÷8=252⋯⋯6,∴B8n+6(0,-24n+3),∴B2022(0,-22011).故答案为:(0,-22011).【练1】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2022的坐标是_____.【答案】(0,-22011)【解析】解:由等腰直角三角形的性质,可知:A 1(1,1),A 2(0,2),A 3(﹣2,2),A 4(0,﹣4),A 5(﹣4,﹣4),A 6(0,﹣8),A 7(8,﹣8),A 8(16,0),A 9(16,16),A 10(0,32),A 11(﹣32,32),…,∵2022=252×8+6∴点A 8n+6的坐标为(0,24n+3)(n 为自然数).∴点A 2022的坐标为(0,24×252+3),即(0,-22011),故答案为:(0,-22011).【练2】在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2).长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ;延长C 1B 1交x 轴于点2A ,作正方形A 2B 2C 2C 1……按这样的规律进行下去,第2022个正方形的面积为_____.【答案】5×(32)4042.【解析】解:∵点A 的坐标为(1,0),点D 的坐标为(0,2)∴正方形ABCD 的边长为√5,设其面积为S 1=5,依此类推,接下来的面积依次为S 2,S 3,S 4⋯⋯第2022个正方形的面积为S 2022,又∵三角形相似,∴ OA OD =A 1B AB =A 2B 1A 1B 1=⋯=12. ∴ S 2=5×94,S 3=5×(94)2…… ∴S 2022=5×(94)2022−1=5×(94)2021=5×(32)4042.【练3】如图,在平面直角坐标系xOy中,B1(0,1),B2(0,3),B3(0,6),B4(0,10),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线B n B n+1都在y 轴上,且B n B n+1的长度依次增加1个单位长度,顶点A n都在第一象限内(n≥1,且n为整数),那么A1的纵坐标为;用n的代数式表示A n的纵坐标:.【答案】2;【解析】解:作A1D⊥y轴于点D,则B1D=B1B2÷2=(3﹣1)÷2=1,∴A1的纵坐标=B1D+B1O=1+12,同理可得A2的纵坐标=OB2+(B2B3)÷2=3+(6﹣3)÷2 4.5,∴A n的纵坐标为,故答案为2,.。
七年级数学下册专题训练2平面直角坐标内点的坐标规律作业新版新人教版

(2)点 P(a-4,b+2)是△ABC 内任意一点.将△ABC 平移至△ A1B1C1 的位置,点 A,B,C,P 的对应点分别是 A1,B1,C1, P1.若点 P1 的坐标为(a,b).在坐标系中画出△A1B1C1. (3)若坐标轴上存在一点 M,使△BCM 的面积等于△ABC 的面 积,求点 M 的坐标.
5.(仙居县期末)点 P(a2-9,a-1)在 y 轴的负半轴上,则 a 的 值是___-__3____.
类 型 2 象限内点的坐标规律
6.在平面直角坐标系中,点 P(-2,x2+1)所在的象限是
(B ) A.第一象限
B.第二象限
C.第三象限 D.第四象限
7.在平面直角坐标系中,点 P(m-3,4-2m)不可能在( A ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
专题训练(二)
平面直角坐标内点的坐标规律
类 型 1 坐标轴上点的坐标规律
1.(椒江区校级期中)下列各点在 x 轴上的是( D )
A.(0,-1)
B.(0,2)
C.(1,1)
D.(1,0)
2.点 P(m+1,m+3)在直角坐标系的 y 轴上,则点 P 的(0,2) C.(4,0) D.(0,-2)
点拨:∵第一次从原点运动到(1,1),第二次从(1,1)运动到(2, 0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4, 0),第五次从(4,0)运动到(5,1),…,∴按这样的运动规律, 第几次横坐标即为几,纵坐标为:1,0,2,0,1,0,2,0,…, 4 个一循环,∵2020÷4=505,∴经过第 2020 次运动后,动点 P 的坐标是(2020,0).
点拨:由题意分析可得,动点 P 第 8=2×4 秒运动到(2,0), 动点 P 第 24=4×6 秒运动到(4,0),动点 P 第 48=6×8 秒运动 到(6,0),以此类推,动点 P 第 2n(2n+2)秒运动到(2n,0), ∴动点 P 第 2024=44×46 秒运动到(44,0),2068-2024=44, ∴按照运动路线,点 P 到达(44,0)后,向右一个单位,然后向 上 43 个单位,∴第 2068 秒点 P 所在位置的坐标是(45,43),
2022年中考数学复习:点坐标规律问题

2022年中考数学复习:点坐标规律问题一、单选题1.在平面直角坐标系xOy 中,对于点(,)P x y 我们把点(11)P y x -++,叫做点P 的伴随点.已知点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,…这样依次得到点1A ,2A ,3A ,…,n A ,….若点1A 的坐标为(24),,点2022A 的坐标为( ) A .(33)-, B .(22)--, C .(31)-, D .(24), 2.如图,在平面直角坐标系中,点A ,B ,C 的坐标分别为()2,0,()0,2,()2,0-.一个电动玩具从原点O 出发,第一次跳跃到点1P ,使得点1P 与点O 关于点A 成中心对称;第二次跳跃到点2P ,使得点2P 与点1P 关于点B 成中心对称;第三次跳跃到点3P ,使得点3P 与点2P 关于点C 成中心对称;第四次跳跃到点4P ,使得点4P 与点3P 关于点A 成中心对称;….电动玩具照此规律跳下去,则点2021P 的坐标是( ).A .()4,-0B .()4,0C .()4,4D .()0,4- 3.如图,在平面直角坐标系xoy 中,点A 坐标是(1,1).若记点A 坐标为()12,a a ,则一个点从点A 出发沿图中路线依次经过()34,B a a ,()56,C a a ,()78,D a a …,每个点的横纵坐标都是整数,按此规律一直运动下去,则202020212022a a a ++的值为( )A.2021B.2022C.1011D.10124.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2022个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是()A.(-1,1)B.(-1,-1)C.(-1,-2)D.(0,-2)5.如图,正方形ABCD的顶点A(0,1),B(1,0),延长DC交x轴于点B1,作正方形DB1C1D1,延长D1C1交x轴于点B2,作正方形D1B2C2D2,…,按照这样的规律,点D2022的纵坐标为()A .22023-1B .21011C .22022D .22023 6.如图,在平面直角坐标系中,一动点从原点O 出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A 1(0,1)、A 2(1,1)、A 3(1,0)、A 4(2,0)…,那么点A 2022的坐标为( )A .(1011,0)B .(1011,1)C .(2022,0)D .(2022,1)7.如图,动点P 在平面直角坐标系中按箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,-1),第4次接着运动到点(4,0),…,按这样的运动规律,经过第2022次运动后,动点P 的坐标是( )A .(2022,1)B .(2022,0)C .(2022,-1)D .(2021,1) 8.如图,在平面直角坐标系中,点A 坐标为(2,0),△OAB 是等边三角形,一动点P 从O 点开始,以每秒1个单位长度的速度,沿O →A →B →O →A ……规则作循环运动,那么第2020秒结束后,点P 的坐标为( )A .(1B .(2,0)C .(12D .(129.如图,在平面直角坐标系中,已知点0M 的坐标为()1,0,将线段0OM 绕原点О逆时针方向旋转45°,再将其延长到1M ,使得100M M OM ⊥,得到线段1OM ;又将线段1OM 绕原点O 逆时针方向旋转45°,再将其延长到2M ,使得211M M OM ⊥,得到线段2OM ;如此下去,得到线段3OM ,4OM ,5OM ,…根据以上规律,则点2022M 的坐标为( )A .()10112,0B .()20220,2-C .()10110,2-D .()20212021,--10.如图,在平面直角坐标系中,四边形ABCD 是平行四边形,A (﹣1,3)、B (1,1)、C (5,1).规定“把▱ABCD 先沿y 轴翻折,再向下平移1个单位”为一次变换.如此这样,连续经过2022次变换后,▱ABCD 的顶点D 的坐标变为( )A .(3,﹣2019)B .(﹣3,﹣2019)C .(3,﹣2018)D .(﹣3,﹣2018)二、填空题11.如图,在抛物线2y x 的内部依次画正方形,使对角线在y 轴上,另两个顶点落在抛物线上.按此规律类推,第2022个正方形的边长是______.12.在平面直角坐标系xOy 中,对于点(),P x y ,如果点(),Q x y '的纵坐标满足()()x y x y y y x x y ⎧-≥⎪=⎨-<'⎪⎩,那么称点Q 为点P 的“关联点”.请写出点()3,5的“关联点”的坐标______.13.如图,弹性小球从点P (0,3)出发,沿图中所示方向运动,每当小球碰到长方形OABC 的边时反弹,反弹时反射角等于入射角,当小球第1次碰到长方形的边时,记为点1P ,第2次碰到长方形的边时,记为点2P ,…,第n 次碰到长方形的边时,记为点n P ,则点3P 的坐标是___;点2022P 的坐标是___.14.如图,在平面直角坐标系中,点A ,B ,C 的坐标分别为()1,1,()3,0,()2,1-.点M 从坐标原点O 出发,第一次跳跃到点1M ,使得点1M 与点O 关于点A 成中心对称;第二次跳跃到点2M ,使得点2M 与点1M 关于点B 成中心对称;第三次跳跃到点3M ,使得点3M 与点2M 关于点C 成中心对称;第四次跳跃到点4M ,使得点4M 与点3M 关于点A 成中心对称;…,依此方式跳跃,点2022M 的坐标是_________.15.如图,在直角坐标系中,长方形OABC 的长为2,宽为1,将长方形OABC 沿x 轴翻转1次,点A 落在A 1处,翻转2次,点A 落在A 2处,翻转3次,点A 落在A 3处(点A 3与点A 2重合),翻转4次,点A 落在A 4处,以此类推…,若翻转2022次,点A 落在A 2022处,则A 2022的坐标为_______.16.如图,在平面直角坐标系中,边长为1个单位长度的正六边形ABCDEF 的对角线AD 在x 轴上,AO =DO ,将该正六边形绕原点O 逆时针旋转,第1次与原正六边形重合时,点A 落在原正六边形的顶点B 处,第2次与原正六边形重合时,点A 落在原正六边形的顶点C 处,第3次与原正六边形重合时,点A 落在原正六边形的顶点D 处,…,第2021次重合时点A 的坐标为 _____.17.如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120︒的AB 多次复制并首尾连接而成.现有一点P 从A (A 为坐标原点)出发,以每秒23π米的速度沿曲线向右运动,则在第2022秒时点P 的坐标为_________.18.如图,在平面直角坐标系中,点1A 的坐标为(1,2),以点O 为圆心、1OA 的长为半径画弧,交直线12y x =于点1B ,过点1B 作12B A y ∥轴,交直线2y x =于点2A ;以点O 为圆心、2OA 的长为半径画弧,交直线12y x =于点2B ,过点2B 作23B A y ∥轴,交直线2y x =于点3A ;以点O 为圆心、3OA 的长为半径画弧,交直线12y x =于点3B ;…按照此规律进行下去,点2022B 的坐标为__________.19.如图,已知1(1,0)A ,2(1,1)A -,3(1,1)A ,4(1,1)A -,5(2,1)A ⋅⋅⋅,则点2022A 的坐标是________.20.如图,▱OA 1B 1,▱A 1A 2B 2,▱A 2A 3B 3,…,▱An ﹣1AnBn 都是斜边在x 轴上的等腰直角三角形,点A 1,A 2,A 3,…,An 都在x 轴上,点B 1,B 2,B 3,…,Bn 都在反比例函数y 1x=(x >0)的图象上,则点Bn 的坐标为___.(用含有正整数n 的式子表示)三、解答题21.如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,1A 的坐标为()2,2,2A 的坐标为()5,2.(1)3A 的坐标为______,n A 的坐标为______(用含n 的代数式表示);(2)若护栏长为2020,则需要小正方形______个,大正方形______个.22.在平面直角坐标系中,一只蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次只移动1个单位长度,其行走路线如图所示.(1)填写下列各点的坐标A 4 ,A 8 ,A 12 .(2)写出点A 4n 的坐标(n 为正整数) .(3)蚂蚁从点A 2020到点A 2021的移动方向是 (填“向上”、“向右”或“向下”).23.(1)在平面直角坐标系中,描出点()()()()()()()()()9,1,11,6,16,8,11,10,9,15,7,10,2,8,7,6,9,1,并将各点用线段依次连接起来.观察这组点组成的图形,你觉得它像什么?它是轴对称图形吗?是中心对称图形吗?(2)如果将(1)中各点的横坐标分别变为原来的相反数,纵坐标不变呢? (3)如果将(1)中各点的横、纵坐标都分别变为原来的相反数呢?(4)如果将(1)中各点的横坐标分别减2,纵坐标分别减1呢?24.如图所示,在平面直角坐标系中,第一次将三角形OAB 变换成三角形OA 1B 1,第二次将三角形OA1B1变换成三角形OA2B2,第三次将三角形OA2B2变换成三角形OA3B3,已知A(1,2),A1(2,2),A2(4,2),A3(8,2);B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换前后的三角形有何变化?找出规律,按此规律再将三角形OA3B3变换成三角形OA4B4,则A4的坐标是________,B4的坐标是________;(2)若按(1)中找到的规律将三角形OAB进行n次变换,得到三角形OAnBn,推测An的坐标是________,Bn的坐标是________.(3)求出▱OAnBn的面积.。
坐标系规律探索习题

坐标系规律探索习题一.选择题(共3小题)1.如图,动点P 按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),⋯,按这样的运动规律,则第2021次运动到点( )A .(2021,1)B .(2021,2)C .(2020,1)D .(2021,0)2.如图,在平面直角坐标系中,(1,1)A ,(1,1)B -,(1,2)C --,(1,2)D -.把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处,并按A B C D A -----⋯的规律紧绕在四边形ABCD 的边上,则细线另一端所在位置的点的坐标是( )A .(1,1)-B .(1,1)-C .(1,2)--D .(1,2)-3.点1A ,2A ,3A ,⋯,(n A n 为正整数)都在数轴上.点1A 在原点O 的左边,且11AO =;点2A 在点1A 的右边,且212A A =;点3A 在点2A 的左边,且323A A =;点4A 在点3A 的右边,且434A A =;⋯,依照上述规律,点2008A ,2009A 所表示的数分别为( ) A .2008,2009-B .2008-,2009C .1004,1005-D .1004,1004-二.填空题(共17小题)4.如图,在平面直角坐标系中,函数2y x =和y x =-的图象分别为直线1l ,2l ,过点(1,0)作x 轴的垂线交1l 于点1A ,过点1A 作y 轴的垂线交2l 于点2A ,过点2A 作x 轴的垂线交1l 于点3A ,过点3A 作y 轴的垂线交2l 于点4A ,⋯依次进行下去,则点2022A 的坐标为 .5.如图,在平面直角坐标系xOy 中,1(1,0)A ,2(3,0)A ,3(6,0)A ,4(10,0)A ,⋯,以12A A 为对角线作第一个正方形1121AC A B ,以23A A 为对角线作第二个正方形2232A C A B ,以34A A 为对角线作第三个正方形3343A C A B ,⋯,顶点1B ,2B ,3B ,⋯都在第一象限,按照这样的规律依次进行下去,点5B 的坐标为 ;点n B 的坐标为 .6.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点1(0,1)P ,2(1,1)P ,3(1,0)P ,4(1,1)P-,5(2,1)P -⋯则2018P 的坐标是 .7.如图,点(0,0)O ,(0,1)B 是正方形1OBB C 的两个顶点,以它的对角线1OB 为一边作正方形121OB B C ,以正方形121OB B C 的对角线2OB 为一边作正方形232OB B C ,写出点3B 的坐标为 ;再以正方形232OB B C 的对角线3OB 为一边作正方形343OB B C ,⋯依此规律作下去,点2013B 的坐标为 .8.在平面直角坐标系xOy 中,有一只电子青蛙在点(1,0)A 处.第一次,它从点A 先向右跳跃1个单位,再向上跳跃1个单位到达点1A ; 第二次,它从点1A 先向左跳跃2个单位,再向下跳跃2个单位到达点2A ; 第三次,它从点2A 先向右跳跃3个单位,再向上跳跃3个单位到达点3A ; 第四次,它从点3A 先向左跳跃4个单位,再向下跳跃4个单位到达点4A ;⋯依此规律进行,点6A 的坐标为 ;若点n A 的坐标为(2013,2012),则n = . 9.如图,在平面直角坐标系中,有一个正六边形ABCDEF ,其中C 、D 的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个正六边形沿着x 轴向右滚动,则在滚动过程中,这个正六边形的顶点A 、B 、C 、D 、E 、F 中,会经过点(54,2)的是 .10.如图,在平面直角坐标系xOy 中,1A 是以O 为圆心,2为半径的圆与过点(0,1)且平行于x 轴的直线1l 的一个交点;2A 是以原点O 为圆心,3为半径的圆与过点(0,2)-且平行于x 轴的直线2l 的一个交点;3A 是以原点O 为圆心,4为半径的圆与过点(0,3)且平行于x 轴的直线3l 的一个交点;4A 是以原点O 为圆心,5为半径的圆与过点(0,4)-且平行于x 轴的直线4l 的一个交点;⋯,且点1A 、2A 、3A 、4A 、⋯都在y 轴右侧,按照这样的规律进行下去,点6A 的坐标为 ,点n A 的坐标为 (用含n 的式子表示,n 是正整数).11.如图,在平面直角坐标系上有个点(1,0)P ,点P 第1次向上跳动1个单位至点1(1,1)P ,紧接着第2次向左跳动2个单位至点2(1,1)P -,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,⋯,依此规律跳动下去,点P 第100次跳动至点100P 的坐标是 .12.如图,在平面直角坐标系上有点(1,0)A ,点A 第一次跳动至点1(1,1)A -,第四次向右跳动5个单位至点4(3,2)A ,⋯,依此规律跳动下去,点A 第100次跳动至点100A 的坐标是 .13.在平面直角坐标系中,已知3个点的坐标分别为:1(1,1)A 、2(0,2)A 、3(1,1)A -.一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以1A 为对称中心的对称点1P ,第2次电子蛙由1P 点跳到以2A 为对称中心的对称点2P ,第3次电子蛙由2P 点跳到以3A 为对称中心的对称点3P ,⋯,按此规律,电子蛙分别以:1A 、2A 、3A 为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是2009P .14.观察下列有序数对:(3,1)(5--,1)(72,1)(93--,1)4⋯根据你发现的规律,第100个有序数对是 .15.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)(4,0)⋯⋯,根据这个规律探索可得,第100个点的坐标为 .16.如图,已知直线l 与x 轴夹角为30︒,过点(2,0)A 作直线l 的垂线,垂足为点1A ,过点1A 作12A A x ⊥轴,垂足为点2A ,过点2A 作23A A l ⊥,垂足为点3A ,⋯,这样依次下去,得到一组线段:1AA ,12A A ,23A A ,⋯,则线段20202021A A 的长为 .17.如图,点(0,0)O 、(0,1)B 是正方形1OBB C 的两个顶点,以对角线1OB 为一边作正方形121OB B C ,再以正方形121OB B C 的对角线2OB 为一边作正方形232OB B C ,⋯,依次下去,则对角线2020OB 的长= .18.以水平数轴的原点O 为圆心,过正半轴Ox 上的每一刻度点画同心圆,将Ox 逆时针依次旋转30︒、60︒、90︒、⋯、330︒得到11条射线,构成如图所示的“圆”坐标系,点A 、B 的坐标分别表示为(5,0)︒、(4,300)︒,则点C 的坐标表示为 .19.如图所示,将边长为1的正方形OAPB 沿x 轴正方向翻转2008次,点P 依次落在点1P ,2P ,3P ,⋯,2008P 的位置,则2008P 的横坐标2008x = .20.如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次,点P 依次落在点1P ,2P ,32008P P ⋯的位置,则点2008P 的横坐标为 .三.解答题(共2小题)21.如图:在直角坐标系中,第一次将AOB ∆变换成△11OA B ,第二次将三角形变换成△22OA B ,第三次将△22OA B ,变换成△33OA B ,已知(1,3)A ,1(3,3)A ,2(5,3)A ,3(7,3)A ;(2,0)B ,1(4,0)B ,2(8,0)B ,3(16,0)B .(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将△33OA B 变换成△44OA B ,则4A 的坐标是 ,4B 的坐标是 .(2)若按(1)找到的规律将OAB ∆进行了n 次变换,得到△n n OA B ,比较每次变换中三角形顶点有何变化,找出规律,推测n A 的坐标是 ,n B 的坐标是 .22.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.(1)填写下列各点的坐标: 1(A , ), 3(A , ), 12(A , );(2)写出点4n A 的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.坐标系规律探索习题参考答案与试题解析一.选择题(共3小题) 1.解:由图可知,每运动四次出现的形状都是一样的, 202145051÷=⋯⋯,∴第2021次运动到点(2021,1),故选:A . 2.解:(1,1)A ,(1,1)B -,(1,2)C --,(1,2)D -,1(1)2AB ∴=--=,1(2)3BC =--=,1(1)2CD =--=,1(2)3DA =--=,∴绕四边形ABCD 一周的细线长度为232310+++=,2012102012÷=⋯,∴细线另一端在绕四边形第202圈的第2个单位长度的位置,即点B 的位置,点的坐标为(1,1)-. 故选:B .3.解:根据题意分析可得:点1A ,2A ,3A ,⋯,n A 表示的数为1-,1,2-,2,3-,3,⋯依照上述规律,可得出结论: 点的下标为奇数时,点在原点的左侧;点的下标为偶数时,点在原点的右侧且表示的数为点的下标数除以2; 当n 为偶数时,11n n A A +=--;所以点2008A 表示的数为:200821004÷=, 2009A 表示的数为:20081100411005A --=--=-.故选:C .二.填空题(共17小题) 4.解:当1x =时,2y =,∴点1A 的坐标为(1,2);当2y x =-=时,2x =-,∴点2A 的坐标为(2,2)-;同理可得3(2,4)A --,4(4,4)A -,5(4,8)A ,6(8,8)A --,7(8,16)A --,8(16,16)A -⋯⋯,∴22141(2,2)n n n A ++,212142(2,2)n n n A +++-, 212243(2,2)n n n A +++--,222244(2,2)(n n n A n +++-为自然数), 202250542=⨯+,∴点2022A 的坐标为50521(2⨯+-,505212)⨯+,即点2022A 的坐标为1011(2-,10112). 故答案为:1011(2-,10112).5.解:分别过点1B ,2B ,3B ,作1B D x ⊥轴,2B E x ⊥轴,3B F x ⊥轴于点D ,E ,F , 1(1,0)A ,12312A A ∴=-=,1A D ,1=,2OD =,11B D A D =,1=,可得出1(2,1)B ,2(3,0)A ,32633A A ∴=-=,232EB =,2232B E EA ==,39622OE =-=, 可得29(2B ,3)2,同理可得出:3(8,2)B ,425(2B ,5)2,⋯, 1B ,2B ,3B ,⋯的横坐标分别为:42,92,162,252⋯,∴点5B 的横坐标为:362, 点n B 的横坐标为:2(1)2n +,1B ,2B ,3B ,⋯的纵坐标分别为:1,32,42,52,⋯,∴点5B 的纵坐标为:632=, 点n B 的纵坐标为:12n +, ∴点5B 的坐标为(18,3);点n B 的坐标为:2(1)1(,)22n n ++.故答案为:(18,3),2(1)1(,)22n n ++.6.解:由图可得,6(2,0)P ,12(4,0)P ,⋯,6(2,0)n P n ,61(2,1)n P n +, 20166336÷=,6336(2336,0)P ⨯∴⨯,即2016(672,0)P ,2017(672,1)P ∴,2018(673,1)P故答案为:(673,1).7.解:根据题意和图形可看出每经过一次变化,都顺时针旋转45︒, 从B 到3B 经过了3次变化,453135︒⨯=︒,31⨯=.∴点3B 所在的正方形的边长为3B 位置在第四象限. ∴点3B 的坐标是(2,2)-;可得出:1B 点坐标为(1,1), 2B 点坐标为(2,0), 3B 点坐标为(2,2)-,4B 点坐标为(0,4)-,5B 点坐标为(4,4)--, 6(8,0)B -,7(8,8)B - 8(0,16)B ,9(16,16)B ,由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的倍, 201382515÷=⋯,2013B ∴的纵横坐标符号与点5B 的相同,纵横坐标都是负值,2013B ∴的坐标为1006(2-,10062)-.故答案为:(2,2)-,1006(2-,10062)-. 8.解:青蛙在点(1,0)A 处,∴第一次在点(2,1),第二次在点(0,1)-, 第三次在点(3,2), 第四次在点(1,2)--, 第五次在点(4,3), 第六次在点(2,3)--,从上可以看出除去一二两次,奇数次横纵坐标每次加一,偶数则每次减一, 6(162,062)A ∴-÷-÷得:(2,3)--,点n A 的坐标为(2013,2012),在第一象限,若以第一次的结果为基础,设置为m , (22,12)An m m +÷+÷, 222013m +÷=, 4022m =,1402214023n m =+=+=;故答案为:(2-,3-,),4023. 9.解:如图所示:当滚动到A D x '⊥轴时,E 、F 、A 的对应点分别是E '、F '、A ',连接A D ',过点F '作F G A D '⊥'于点G ,过点E '作E H A D '⊥'于点H ,六边形ABCDEF 是正六边形, 1602F A D FAB ∴∠''=∠=︒,906030A F G ∴∠''=︒-︒=︒, 1122A G A F ∴'=''=,同理可得12HD =, 2A D ∴'=,(2,0)D(2,2)A ∴',2OD =,正六边形滚动6个单位长度时正好滚动一周,∴从点(2,2)开始到点(54,2)正好滚动52个单位长度,52846=⋯, ∴恰好滚动8周多4个, ∴会过点(54,2)的是点E .故答案为:E .10.解:点1A 是以原点O 为圆心,半径为2的圆与过点(0,1)且平行于x 轴的直线1l 的一个交点,1A ∴的坐标为:,1),即1),2A 是以原点O 为圆心,3为半径的圆与过点(0,2)-且平行于x 轴的直线2l 的一个交点,2A ∴的坐标为2)-同理可得:3A 的坐标为3)点n A 的坐标为1(1))n n +-⋅,则:点6A 的坐标为6)-;故答案为:6)-,1(1))n n +-⋅;11.解:经过观察可得:1P 和2P 的纵坐标均为1,3P 和4P 的纵坐标均为2,5P 和6P 的纵坐标均为3,因此可以推知99P 和100P 的纵坐标均为100250÷=;其中4的倍数的跳动都在y 轴的右侧,那么第100次跳动得到的横坐标也在y 轴右侧.1P 横坐标为1,4P 横坐标为2,8P 横坐标为3,依此类推可得到:n P 的横坐标为41(n n ÷+是4的倍数).故点100P 的横坐标为:1004126÷+=,纵坐标为:100250÷=,点P 第100次跳动至点100P 的坐标是(26,50). 故答案为:(26,50).12.解:观察发现,第2次跳动至点的坐标是(2,1), 第4次跳动至点的坐标是(3,2), 第6次跳动至点的坐标是(4,3), 第8次跳动至点的坐标是(5,4),⋯第2n 次跳动至点的坐标是(1,)n n +,∴第100次跳动至点的坐标是(51,50).故答案为:(51,50).13.解:根据题意1P 点为原点关于点1A 为对称中心的点,所以1(2,2)P ,类似地2(2,2)P -,3(0,0)P ,即回到了原点,所以可以看出电子蛙每从原点开始,每跳三次就会回到原点,20093÷余数是2,所以第2009次电子蛙落点的坐标为2P 点的坐标(2,2)-.故答案为:(2,2)-.14.解:观察后发现第n 个有序数对可以表示为: 第n 个有序数对的坐标为1((1)(21)n n +-⋅+,1(1))n n-⋅.∴第100个有序数对是1(201,)100-.故答案填1(201,)100-. 15.解:因为1231391+++⋯+=,所以第91个点的坐标为(13,0).因为在第14列点的走向为向上,故第100个点在此行上,横坐标就为14,纵坐标为从第92个点向上数8个点,即为8; 故第100个点的坐标为(14,8). 故填(14,8).16.解:由题可知,直线l 与x 轴的夹角为30︒, 12sin301AA ∴=︒=, 130AOA ∠=︒, 160A AO ∴∠=︒,1230AA A ∴∠=︒, 121cos30A A AA ∴=︒,同理,223121cos30cos 30A A A A AA =︒=︒,234231cos30cos 30A A A A AA =︒=︒,⋯11cos 30n n n A A AA +∴=︒,当2010n =,202020192020A A =,故答案为2020.17.解:根据题意和图形可看出每经过一次变化,都顺时针旋转45︒,∴旋转8次则OB 旋转一周,从B 到2020B 经过了2020次变化, 202082524÷=⋯,∴从B 到2020B 与4B 都在y 轴负半轴上,202010102∴=,∴点2020B 的坐标是1010(0,2)-.2020OB ∴的长10102,故答案为10102.18.解:如图所示:点C 的坐标表示为(3,240)︒. 故答案为:(3,240)︒. 19.解:根据规律1(1,1)P ,23(2,0)P P =,4(3,1)P , 5(5P ,671)(6,0)P P =,8(7,1)P ⋯每4个一循环,可以判断2008P 在502次循环后与4P 一致:纵坐标为1,横坐标比下标小1,坐标应该是(2007,1),故答案为2007.20.解:观察图形结合翻转的方法可以得出1P 、2P 的横坐标是1,3P 的横坐标是2.5,4P 、5P 的横坐标是4,6P 的横坐标是5.5⋯依此类推下去,2005P 、2006P 的横坐标是2005,2007P 的横坐标是2006.5,2008P 、2009P 的横坐标就是2008.故答案为:2008. 三.解答题(共2小题)21.解:(1)已知(1,3)A ,1(3,3)A ,2(5,3)A ,3(7,3)A ;对于1A ,2A ,n A 坐标找规律比较从而发现n A 的横坐标为21n +,而纵坐标都是3; 同理1B ,2B ,n B 也一样找规律,规律为n B 的横坐标为12n +,纵坐标为0. 由上规律可知:(1)4A 的坐标是(9,3),4B 的坐标是(32,0); (2)n A 的坐标是(21,3)n +,n B 的坐标是1(2n +,0) 22.解:(1)1(0,1)A ,3(1,0)A ,12(6,0)A ; (2)当1n =时,4(2,0)A , 当2n =时,8(4,0)A , 当3n =时,12(6,0)A , 所以4(2,0)n A n ;(3)点100A 中的n 正好是4的倍数,所以点100A 和101A 的坐标分别是100(50,0)A ,101A 的(50,1),所以蚂蚁从点100A 到101A 的移动方向是从下向上.。
初中数学 中考复习—坐标系中点的坐标变化规律题(1)(有答案)
2020中考复习—坐标系中点的坐标变化规律题(1)姓名:___________班级:___________考号:___________一、选择题1.如图,平面直角坐标系中,一蚂蚁从A点出发,沿着A→B→C→D→A…循环爬行,其中A点的坐标为(2,−2),B点的坐标为(−2,−2),C点的坐标为(−2,6),D点的坐标为(2,6),当蚂蚁爬了2019个单位时,蚂蚁所处位置的坐标为()A. (−2,0)B. (4,−2)C. (−2,4)D. (−1,−2)2.如图,在直角坐标系中,A(1,3),B(2,0),第一次将△AOB变换成△OA1B1,A1(2,3),B1(4,0);第二次将△OA1B1变换成△OA2B2,A2(4,3),B2(8,0),第三次将△OA2B2变换成△OA3B3,……,则B2018的横坐标为()A. 22016B. 22017C. 22018D. 220193.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后,动点P的坐标是()A. (2018,0)B. (2019,0)C. (2019,2)D. (2017,2)4.在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,观察图中每正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点的个数共有()A. 35个B. 40个C. 45个D. 50个5. 如图,将含有30°角的直角三角板ABC 放入平面直角坐标系,顶点A 、B 分别落在x 、y 轴的正半轴上,∠OAB =60°,点A 的坐标为(1,0).将三角板ABC 沿x 轴向右作无滑动的滚动(先绕点A 按顺时针方向旋转60°,再绕点C 按顺时针方向旋转90°…)当点B 第一次落在x 轴上时,则点B 运动的路径与两坐标轴围成的图形面积是( )A. √3B. √3+1712πC. √32+1712π D. √3+π6. 在平面直角坐标系中,第一个正方形ABCD 的位置如图所示,点A 的坐标为(2,0),点D 的坐标为(0,4).延长CB 交x 轴于点A 1,作第二个正方形A 1B 1C 1C ;延长C 1B 1交x 轴于点A 2,作第三个正方形A 2B 2C 2C 1,…,按这样的规律进行下去,第2016个正方形的面积为( )A. 20×(32)4030B. 20×(32)4032C. 20×(32)2016D. 20×(32)20157. 如图,已知菱形ABCD 的顶点A(−√3,0),∠DAB =60°,若动点P 从点A 出发,沿A →B →C →D →A →B →⋯的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P 的坐标为( )A. (3√34,−14) B. (−3√34,−14) C. (−√3,0) D. (√3,0)二、填空题8.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.则点A22的坐标为(____________,____________).9.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5),A5(5,4),A6(6,7)…用你发现的规律,确定A2018的坐标为________10.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,8),A4(4,15),…用你发现的规律确定点A n的坐标为___________.11.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,−1),P5(2,−1),P6(2,0),…,则点P2018的坐标是_____.12.在平面直角坐标系的x轴上用连续奇数作为长度顺次截取…OP1=1,P1P2=3,P2P3=5…△P n−1P n=2n−1(n为正整数),再分别以每条线段为一边在第一象限内作等边三角形△OP1A1、△P1P2A2,△P2P3A3…△P n−1P n A n,如图,请结合图形完成下面探究.【规律探究】OP1=1,A1(12,√32);OP2=1+3=12+3,A2(52,3√32);OP3=1+3+5=22+5,A3(132,5√32);OP4=1+3+5+7=32+7,A4(________,________);…OP n=1+3+5+⋯…+2n−1=(n−1)2+2n−1,A n(________,________).13.将正方形ABCD的各边按如图所示延长,从射线AB开始,分别在各射线上标记点A1、A2、A3、…,按此规律,点A2012在射线上.14.正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则A5的坐标是______.15.如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2021的坐标是___________.16.如图,矩形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(−1,2),将矩形ABCD沿x轴向右翻滚,经过一次翻滚点A对应点记为A1,经过第二次翻滚点A对应点记为A2…依此类推,经过5次翻滚后点A对应点A5的坐标为_____三、解答题17.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.(1)填写下列各点的坐标:A1:(________,________),A3:(________,________),A12:(________,________);(2)写出点A n的坐标(n是正整数且为4的倍数);(3)指出蚂蚁从点A100到A101的移动方向.18.阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1),Q(x2,y2)的对称中心的坐标为(x1+x22,y1+y22).观察应用:(1)如图,在平面直角坐标系中,若点P1(0,−1),P2(2,3)的对称中心是点A,则点A 的坐标为_________;(2)在(1)的基础上另取两点B(−1,2),C(−1,0)有一电子青蛙从点P1处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P1关于点A的对称点处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,….则P4,P8的坐标分别为_______,_______.19.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1,变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(−3,1),A1(−3,2),A2(−3,4),A3(−3,8);B(0,2),B1(0,4),B2(0,6),B3(0,8).(1)观察每次变换前后三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成△OA4B4,点A4的坐标为_______,点B4的坐标为________;(2)若按(1)题找到的规律,将△OAB进行n次变换,得到△OA n B n,则点A n的坐标是________,B n的坐标是________.20.阅读:在平面直角坐标系内,对于点P(x,y),我们把Q(−y+1,x+3)叫做它的伴随点.如点(2,1)的伴随点为(−1+1,2+3),即(0,5).(1)若点M的伴随点坐标为(−5,3),则点M的坐标为______;(2)若点A1(a,b)的伴随点为A2,A2的伴随点为A3,A3的伴随点为A4,…,以此类推,将所有点记为A n.①若点A104的坐标为(3,−1),则点A1的坐标为______;②点A n有没有可能始终在y轴的右侧?若可能,请分别求出a,b的取值范围;若不可能,请说明理由;③设直角坐标系的原点为O,若点A n始终在一个半径为3的圆上,请直接写出OA n的最小值.21.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).(1)已知点A(−2,6)的“1级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和2点B的坐标;(2)已知点M(m−1,2m)的“−3级关联点”M′位于坐标轴上,求M′的坐标;答案和解析1.D解:∵A点坐标为(2,−2),B点坐标为(−2,−2),C点坐标为(−2,6),∴AB=2−(−2)=4,BC=6−(−2)=8,∴从A→B→C→D→A一圈的长度为2(AB+BC)=24,∵2019=84×24+3,∴当蚂蚁爬了2019个单位时,它所处位置在点A左边3个单位长度处,即(−1,−2).2.D解:B2018的横坐标是(22019,0),3.C解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.∴2019=4×504+3,当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2),4.B解:由内到外规律,第1个正方形边上整点个数为4×1=4(个),第2个正方形边上整点个数为4×2=8(个),第3个正方形边上整点个数为4×3=12(个),第4个正方形边上整点个数为4×4=16(个);故第10个正方形边上的整点个数为40个.5.B解:在Rt△ABC中,∵OA=1,∠ABO=30°,∴AB=2,OB=√3∵∠ABC=30°,∠ACB=90°,∴AC=1,BC=√3,∴点B第一次落在x轴上时,点B运动的路径与两坐标轴围成的图形面积=S△AOB+S△AC′B′+S扇形ABB′+S扇形C′B′B″=√3+60⋅π⋅22360+90⋅π⋅(√3)2360=√3+1712π,6.A解:∵点A的坐标为(2,0),点D的坐标为(0,4),∴OA=2,OD=4∵∠AOD=90°,∴AB=AD=√22+42=2√5,∠ODA+∠OAD=90°,∵四边形ABCD是正方形,∴∠BAD=∠ABC=90°,S正方形ABCD=(2√5)2=20,∴∠ABA1=90°,∠OAD+∠BAA1=90°,∴∠ODA=∠BAA1,∴△ABA1∽△DOA,∴BA1OA =ABOD,即BA12=2√54,∴BA1=√5,∴CA1=3√5,∴正方形A1B1C1C的面积=(32×√20)2=20×(32)2…,第n个正方形的面积为20×(32)2n−2,∴第2016个正方形的面积20×(32)4030.7.B解:∵四边形ABCD是菱形,A(−√3,0),∠DAB=60°,∴AC⊥BD,∠DAO=30°,OA=√3,∴在Rt△AOD中,OD=1,AD=2,∵点P的运动速度为0.5米/秒,∴从点A到点B所需时间=20.5=4秒,∴沿A→B→C→D→A所需的时间=4×4=16秒.∵2016÷16=126,∴第2016秒点P运动到点A处,∴第2017秒时,点P在AB边上靠近点A的14处,∵A(−√3,0),B(0,−1),∴P的坐标为(−3√34,−14).8.11 ;1解:观察,发现:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),A7(3,0),A8(4,0),A9(4,1),∴A4n+1(2n,1),A4n+2(2n+1,1),A4n+3(2n+1,0),A4n+4(2n+2,0)(n为自然数),∵22=4×5+2,∴n=5,∴2n+1=2×5+1=11,∴点A22的坐标是(11,1).9.(2018,2019)解:设A n(x,y),∵当n=1时,A1(1,0),即x=n=1,y=1−1=0,当n=2时,A2(2,3),即x=n=2,y=2+1=3;当n=3时,A3(3,2),即x=n=3,y=3−1=2;当n=4时,A4(4,5),即x=n=4,y=4+1=5;…∴当点的位置在奇数位置横坐标与下标相等,纵坐标减1,当点的位置在偶数位置横坐标与下标相等,纵坐标加1,∴A n(x,y)的坐标是(n,n+1)∴点A2018的坐标为(2018,2019).10.(n,n2−1)解:∵点A1(1,0),A2(2,3),A3(3,8),A4(4,15),…∴横坐标是连续的正整数,纵坐标为:12−1=0,22−1=3,32−1=8,…∴点A n的坐标为:(n,n2−1).11.(673,1)解:由图可得,P6(2,0),P12(4,0),…,P6n(2n,0),P6n+1(2n,1),2016÷6=336,∴P6×336(2×336,0),即P2016(672,0),∴P2017(672,1),∴P2018(673,1),故答案为(673,1).12.(252 ,7√32);(2n2−2n+12,2√3n−√32)解:OP1=1,A1(12,√32);OP2=1+3=12+3,A2(52,3√32);OP3=1+3+5=22+5,A3(132,5√32);OP4=1+3+5+7=32+7,则横坐标为1+3+5+72=252,纵坐标为7√32,A4(252 ,7√32);…OP n=1+3+5+⋯…+2n−1=(n−1)2+2n−1,则横坐标为1+3+···+(2n−3)+2n−12=(n−1)2+2n−12=2n2−2n+12,纵坐标为√3(2n−1)2,A n(2n2−2n+12,2√3n−√32).13.AB解:把射线AB,CD,BC,DA上面的点分别列举,再找到规律,由规律即可求出点A2012所在的射线如图所示:根据表格中点的排列规律,可以得到点的坐标是每16个点排列的位置一循环,因为2012=16×125+12,所以点A2012所在的射线和点A12所在的直线一样.因为点A2012所在的射线是射线AB,所以点A2012在射线AB上,14.(15,16)解:∵直线y=x+1和y轴交于A1,∴A1的坐标(0,1),即OA1=1,∵四边形C1OA1B1是正方形,∴OC1=OA1=1,把x=1代入y=x+1得:y=2,∴A2的坐标为(1,2),同理A3的坐标为(3,4),…A n的坐标为(2n−1−1,2n−1),故A 5的坐标为(25−1−1,25−1)即A5(15,16)15.(22020,22020)解:∵OA1=1,∴点A1的坐标为(1,0),∵△OA1B1是等腰直角三角形,∴A1B1=1,∴B1(1,1),∵△B1A1A2是等腰直角三角形,∴A1A2=1,B1A2=√2,∵△B2B1A2为等腰直角三角形,∴A2A3=2,∴B2(2,2),同理可得,B3(22,22),B4(23,23),…B n(2n−1,2n−1),∴点B2021的坐标是(22020,22020).16.(8,1)解:如下图所示:由题意可得上图,经过5次翻滚后点A对应点A5的坐标对应上图中的坐标,故A 5的坐标为:(8,1).17.解:(1)(0,1);(1,0);(6,0);(2)当n=4时,A4(2,0),当n=8时,A8(4,0),当n=12时,A12(6,0),所以A n(n2,0);(3)点A100中的n正好是4的倍数,所以点A100和A101的坐标分别是A100(50,0),A101的(50,1),所以蚂蚁从点A100到A101的移动方向是从下向上.解:(1)A1(0,1),A3(1,0),A12(6,0);故答案为(0,1),(1,0),(6,0);18.(1)(1,1);(2)(2,−1);(2,3).解:(1)∵P1(0,−1),P2(2,3),∴根据对称中心的坐标公式可得:x=0+22=1,y=−1+32=1,∴A点坐标为(1,1).(2)利用题中所给的对称中心的坐标公式进行计算,并结合下图可知:P1(0,−1)→P2(2,3)→P3(−4,1)→P4(2,−1)→P5(0,3)→P6(−2,1)→P7(0,−1)→P8(2,3),因此P7点与P1点重合,P8点与P2点重合;∴P4、P8的坐标分别为(2,−1),(2,3).19.(1)A4(−3,16),B4(0,10);(2)A n(−3,2n),B n(0,2n+2).解:(1)∵A1(−3,2),A2(−3,4),A3(−3,8);∴A点横坐标为−3,纵坐标依次为:2,2²,2³,…∴A4的纵坐标为:24=16,∴A4 (−3,16),∵B1(0,4),B2(0,6),B3(0,8),∴B点横坐标为0,纵坐标依次为:2+2,2×2+2,2×3+2,…∴B4的纵坐标为:2×4+2=10,∴B4 (0,10);故答案为(−3,16),(0,10);(2)由(1)得出:A n(−3,2n),B n(0,2n+2).故答案为(−3,2n );(0,2n+2).20.(1)(0,6);(2)①(2,6);②代数法:列不等式组{a>0−a−2>0,{−b+1>0b−3>0,两个不等式组均无解,因此点A n不可能始终在y轴的右侧,几何法:A1与A3的中点为(−1,2),A2与A4的中点也为(−1,2),说明点A n形成一个以(−1,2)为中心的对称图形,而点(−1,2)在第二象限,则必有部分点落在y轴的左侧.③由②得,Q(−1,2)就是该圆圆心,如图连接QO ,延长与圆Q 交于点A ,此时OA 最小, QO =√22+12=√5,OA =QA −QO =3−√5, 因此OA n 最小值为3−√5.解:(1)设点M(m,n),则它的伴随点为(−n +1,m +3), ∵点M 的伴随点坐标为(−5,3), ∴−n +1=−5,m +3=3, 解得,m =0,n =6, ∴M(0,6).故答案为(0,6);(2)A n 的变化规律:A 1(a,b)→A 2(−b +1,a +3)→A 3(−a −2,−b +4)→A 4(b −3,−a +1)→A 5(a,b)…①法一:A 4与A 104坐标同为(3,−1),即b −3=3,−a +1=−1, 则a =2,b =6;故答案为 (2,6);21. 解:(1)∵点A(−2,6)的“12级关联点”是点A 1,∴A 1(−2×12+6,−2+12×6), 即A 1(5,1), 设点B(x,y),∵点B 的“2级关联点”是B 1(3,3), ∴{2x +y =3x +2y =3,解得{x =1y =1,∴B(1,1);(2)∵点M(m −1,2m)的“−3级关联点”为 M′(−3(m −1)+2m,m −1+(−3)×2m), M′位于y 轴上,∴−3(m−1)+2m=0,解得:m=3∴m−1+(−3)×2m=−16,∴M′(0,−16).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点的坐标规律题
1、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…
已知:A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何
变化,按照变换规律,第五次变换后得到的三角形A5的坐标是
,B5的坐标是
.2、(2013•兰州)如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB 连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为
.
2.(2013•鄂尔多斯)在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5)…用你发现的规律,确定点A2013的坐标为
3.(2013•大连)在平面直角坐标系中,点(2,-4)在第
象限.
4.(2013•朝阳)如图是某同学在课外设计的一款软件,
蓝精灵从O点第一跳落到A1(1,0),第二跳落到A2(1,2),第三跳落到A3(4,2),第四跳落到A4(4,6),第五跳落到A5
.到达A2n后,要向方向跳个单位落到A2n+1.
)如图,在平面直角坐标系中,线段OA1=1,OA1与x轴的夹角为30°,线段A1A2=1,A2A1⊥OA1,垂足为A1;线段A2A3=1,A3A2⊥A1A2,垂足为A2;线段A3A4=1,A4A3⊥A2A3,垂足为A3;…按此规律,点A2012的坐标为
.
6.(2012•泰安)如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为
7.(2012•莱芜)将正方形ABCD的各边按如图所示延长,从射线AB开始,分别在各射线上标记点A1、A2、A3、…,按此规律,点A2012在射线
上.
8.(2012•呼伦贝尔)第二象限内的点P(x,y)满足|x|=5,y2=4,则点P的坐标是
.
9.(2012•北京)在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是
;当点B的横坐标为4n(n为正整数)时,m=
(用含n的代数式表示).
10.(2010•成都)在平面直角坐标系中,点A(2,-3)位于第象限.
2.(2013•湛江)如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A3的坐标是
,A92的坐标是
.
如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为
(用n表示)
4.(2013•抚顺)如图,在平面直角坐标系中,点A、B、C的坐标分别是(-1,-1)、(0,2)、(2,0),点P在y轴上,且坐标为(0,-2).点P关于点A的对称点为P1,点P1关于点B的对称点为P2,点P2关于点C的对称点为P3,点P3关于点A的对称点为P4,点P4关于点B的对称点为P5,点P5关于点C的对称点为P6,点P6关于点A的对称点为P7…,按此规律进行下去,则点P2013的坐标、是
5.(2013•鄂尔多斯)在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5)…用你发现的规律,确定点A2013的坐标为
6.(2013•朝阳)如图是某同学在课外设计的一款软件,
蓝精灵从O点第一跳落到A1(1,0),第二跳落到A2(1,2),第三跳落到A3(4,2),第四跳落到A4(4,6),第五跳落到A5
.到达A2n后,要向
方向跳
个单位落到A2n+1.
7.(2012•威海)如图,在平面直角坐标系中,线段OA1=1,OA1与x轴的夹角为30°,线段A1A2=1,A2A1⊥OA1,垂足为A1;线段A2A3=1,A3A2⊥A1A2,垂足为A2;线段A3A4=1,A4A3⊥A2A3,垂足为A3;…按此规律,点A2012的坐标为
.
8.(2012•莱芜)将正方形ABCD的各边按如图所示延长,从射线AB开始,分别在各射线上标记点A1、A2、A3、…,按此规律,点A2012在射线
上
9.(2011•钦州)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是
.
10.(2013•安徽)我们把正六边形的顶点及其对称中心称作如图1所示基本
图的特征点,显然这样的基本图共有7个特征点,将此基本图不断复制并平移,使得相邻两个基本图的一边重合,这样得到图2,图3,…
(1)观察以上图形并完成下表:
图形的名称基
本
图
的
个
数
特
征
点
的
个
数
图117
图2212图3317图44
………猜想:在图(n)中,特征点的个数为
(用n表示);
(2)如图,将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1,2),则x1=
;图(2013)的对称中心的横坐标为
.
如图,将边长为1的正方形OAPB 沿x 轴正方向连续翻转2008次,点P 依次落在点P 1,P 2,P 3,P 4,…,P 2008的位置,则P 2008的坐标
32.如图,有一系列有规律的点,它们分别是以O 为
顶点,边长为正整数的正方形的顶点,A 1(0,1)、A 2(1,1)、A 3(1,0)、A 4(2,0)、A 5(2,2)、A 6(0,2)、A 7(0,3)、A 8(3,3)…,依此规律,点A 20的坐标为
33.在平面直角坐标系中,点A 1(0,2),A 2(1,5)A 3(2,10),A 4(3,17),…,用你发现的规律确定点A 2012的坐标为
34.在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点的个数的变化规律.
回答下列问题:
(1)经过x轴上点(5,0)的正方形的四条边上的整点个数是
;
(2)经过x轴上点(n,0)(n为正整数)的正方形的四条边上的整点个数记为m,则m与n之间的函数关系是
.
35.如图,一个机器人从点O出发,向正东方向走3m到达
点A
1,再向正北方向走6m到点A
2
,再向正西方向走9m到达点A
3
,再向正南方向
走12m到达点A
4,再向正东方向走15m到达点A
5
.按如此规律走下去,当机器人
走到点A
6
时,离东西方向所在的直线的距离是
m .
36.在平面直角坐标系中,点A 1(1,2),A 2(2,5)A 3(3,10),A 4(4,17),…,用你发现的规律确定点A 9的坐标为 .
37.在平面直角坐标系xOy 中,点A 从原点出发沿x 轴正
向移动1个单位长度到A 1,逆时针旋转90°后前进2个单位长度到达A 2,逆时针旋转90°后前进3个单位长度到达A 3,…,逆时针旋转90°后前进2013个单位长度到达点A 2013,则A 2013的坐标为 .
38.如图,在平面直角坐标系xOy 中,A 1(1,0),A 2(3,0),A 3(6,0),A 4(10,0),…,以A 1A 2为对角线作第一个正方形A 1C 1A 2B 1,以A 2A 3为对角线作第二个正方形A 2C 2A 3B 2,以A 3A 4为对角线作第三个正方形A 3C 3A 4B 3,…,顶点B 1,B 2,B 3,…都在第一象限,按照这样的规律依次进行下去,点B 5的坐标为
;点B n 的坐标为
.
39.如图,动点P 从(0,3)出发,沿所示方向
运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P 第2013次碰到矩形的边时,点P 的坐标为
40.在平面直角坐标系中,点A 1(1,1),A 2(3,4),A 3(5,9),A 4(7,16),…,用你发现的规律确定A 10的坐标为 .
如图,将边长为1的正方形OAPB 沿x 轴正方向连续翻转2013次,点P 依次落在点P 1,P 2,P 3,…,P 2013的位置,记P i (x i ,y i ),i=1,2,3,…,2013,则P 2013的横坐标x 2013=
;如果x n =x n +1,则x n +2=
42.如图,已知坐标A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2013的坐标为
.
43.如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…则点A2011的坐标是
.
44.将正方形ABCD的各边按如图所示延长,从射线AB 开始,分别在各射线上标记点A1、A2、A3、…,按此规律,点A20在射线
上;点。
