分子分母打法
分式的计算题里,如何干掉分子分母?

分式的计算题里,如何干掉分子分母?
先上干货。
分式的计算题,不论是方程、通分化简、还是求值等。
如果发现计算起来太恐怖了,那就说明,这时需要有技巧的处理。
分式计算的技巧性处理,流程如下:
1、干掉分子
2、如果没干掉分子,那就干掉分母
3、如果分子是单项式,分母是多项式,就颠倒乾坤,干掉新分母(原分子)
我们怎么看出来门道呢?这种题目的分子、分母设计的很巧妙。
通常:
分子、分母的差值,是常数
分母因式分解之后,变成2个因式,分子是各个因式的和(差)
先看2个例题。
再看一道方程题
这2个题,有个共同特点:分子特别复杂,一旦通分,分子相乘之后,会爆炸。
那怎么办呢?咱必须通分吗?
以分母作为参考,把分子修改成分母的样子。
然后裂项,把一个分式,至少列项成两个分式。
裂项之后的两个分式里,其中一个的分子是按照分母调整的,所以它必然是整数。
裂项之后的另一个分式里,分子通常就很简单了!
再看一个方程题,参数方程有整数解。
求参数。
例题3的思路,和前面俩例题一样。
而有的题目,分母因式分解之后,分子可以写成分母里各个因式的差(和),这种情况,就采用列项法,让分子变得简单。
看下面这个例题:
例题4这题,如果对分母通分,那计算量是非常恐怖的。
下面看一个颠倒乾坤,利用倒数法,求解的题目。
分子分母比大小口诀

分子分母比大小口诀
分数比大小的口诀
1、分子相同的两个分数,分母小的分数反而大,分母大的分数反而小。
2、分母相同的两个分数,分子大的分数比较大,分子小的分数比较小。
3、把一个物体或一个图形平均分成几份,取其中的几份,就是这个物体或图形的几分之几。
4、把一个整体平均分得的份数越多,它的每一份所表示的数就越小。
5、相同分母的分数相加:分母不变,分子相加。
6、相同分母的分数相减:分母不变,分子相减。
7、1与分数相减:1可以看作是分子分母相同的分数。
分数定义
分数(来自拉丁语,“破碎”)代表整体的一部分,或更一般地,任何数量相等的部分。
当在日常英语中说话时,分数描述了一定大小的部分,例如半数,八分之五,四分之三。
分子和分母也用于不常见的分数,包括复合分数,复数分数和混合数字。
分数表示一个数是另一个数的几分之几,或一个事件与所有事件的比例。
把单位“1”平均分成若干份,表示这样的一份或几份的数叫分数。
分子在上,分母在下。
2016安徽公务员考试行测答题技巧:分子分母带你“智取”资料分析(上)

最全汇总>>>安徽公务员历年真题2016安徽公务员考试行测答题技巧:分子分母带你“智取”资料分析(上)通过最新安徽公务员考试资讯、大纲可以了解到,《行政职业能力测验》主要测查从事公务员职业必须具备的基本素质和潜在能力,测试内容包括言语理解与表达能力、判断推理能力、数理能力、常识应用能力和综合分析能力。
安徽中公教育整理了安徽省考资料大全供考生备考学习。
需要更多指导,请选择在线咨询一对一解答。
一、分子分母比较法分子分母比较法是指通过比较两个分式的分子、分母,判断两个分数大小的方法。
分子分母比较法主要有以下几种方法:(一)基本比较两个分数比较大小,如果它们的分母相同,分子大的分数大。
同理,两个分子相同的分数,分母小的分数大。
(二)化成分子相同比较两个分数,如果它们的分子存在倍数关系,可以将分子较小的分数乘以一个适当的整数,将两个分数的分子化成相同或相近的数字,再比较两个分数分母的大小,此时分母小的分数大;同理,分母大的分数小。
(三)化成分母相同比较(通分)两个分数,如果它们的分母存在倍数关系,可以将分母较小的分数乘以一个适当的整数,将两个分数的分母化成相同或相近的数字,再比较分子的大小,此时分子大的分数大;同理,分子小的分数小。
这就是我们通常所说的“通分”。
(四)分子分母反向变化比较两个分数,如果前者的分子大于后者且分母小于后者,那么前者大;同理,如果前者分子小于后者且分母大于后者,那么前者小。
分子分母比较法应用条件:一般只应用于对若干个数据大小进行比较或进行排序的题型中,通常按照题干中数据的排列顺序依次进行大小的比较。
最全汇总>>>安徽公务员历年真题更多内容,一起来看看安徽公务员考试课程是如何设置教学的!中公教育公务员考试培训与辅导专家提醒您,备考有计划,才能在公考大战中拔得头筹!公务员考试题库系统邀请您一同刷题!。
分式运算技巧知识点总结

分式运算技巧知识点总结分式运算是数学中一种常见的运算形式,它包括分数的加减、乘除等操作。
在分式运算中,掌握一些技巧可以帮助我们更加快速、准确地计算。
本文将对分式运算的一些常用技巧进行总结,并给出相应的例子加以说明。
一、分数的加减运算技巧1. 寻找相同的分母:在进行分数的加减运算时,首先要寻找相同的分母。
若分母不同,则需要通过通分的方法将分母转化为相同的数。
例子1:计算1/2 + 1/3。
解析:由于1/2和1/3的分母不同,我们需要找到它们的最小公倍数,即6。
将两个分数的分子和分母都乘以适当的数进行通分:1/2 + 1/3 = 3/6 + 2/6 = 5/62. 合并同类项:在找到相同的分母后,可以将分子进行合并,然后再进行计算。
例子2:计算2/5 + 3/5。
解析:由于2/5和3/5的分母相同,直接将分子相加即可:2/5 + 3/5 = (2 + 3)/5 = 5/5 = 13. 化简分数:在进行分数的加减运算时,可以先将分数化简,再进行计算。
这样可以简化计算过程,得到更简洁的结果。
例子3:计算3/10 + 2/5。
解析:先对3/10进行化简,即可以将分子和分母都除以最大公约数2得到1/5:3/10 + 2/5 = 1/5 + 2/5 = (1 + 2)/5 = 3/5二、分数的乘除运算技巧1. 分数的乘法:将分数的分子相乘,分母相乘即可。
例子4:计算2/3 × 4/5。
解析:将分子相乘得到2 × 4 = 8,分母相乘得到3 × 5 = 15,所以结果为8/15。
2. 分数的除法:将除数的分子乘以被除数的倒数,即可进行分数的除法运算。
例子5:计算2/3 ÷ 4/5。
解析:将除数2/3的分子乘以被除数4/5的倒数5/4,即2/3 × 5/4,根据分数的乘法规则可得到结果10/12,化简得到5/6。
三、其他分式运算技巧1. 分数的幂运算:对分式进行幂运算时,可以将分子和分母分别进行幂运算。
word文档中分数怎么打(分子或分母含有括号)

Word 文档中分数怎么打
—— 分数中含有括号
1、依次点击“插入”菜单——对象——公式3.0,选择“分式和根式模板”(在第2行第2个) 中的第1项,正常输入括号,把光标移到括号内,在插入空格前,把输入法切换成中文输入法,并确保输入法为全角,此时,就可以正常输入空格了。
如,)
()( 2、如果找不到公式3.0,也可以用以下方法解决。
在相应位置按下“Ctrl+F9”快捷键,就会出现一个空域(一对大括号)。
将鼠标定位于大括号内,输入大括号里的内容{ eq \f(( ),( ))},再右击,在弹出的菜单中选中“切换域代码”命令,就可以了。
需要注意的是,大括号不能手工输入,可用“Ctrl+F9”快捷键来完成;“eq ”与“\”间要留有一个空格,域代码必须在英文的半角状态下完成输
入。
如,( )( )。
可选中它,通过设置字体来改变它的大小喽! 再不会,就把这文档中现成的复制过去。
分子分母比大小诀窍什么是分子分母

分子分母比大小诀窍什么是分子分母分子分母比大小口诀:同分母比大小,分子大的大;同分子比大小,分母小的大;不同分母也不同分子比大小,要先通分再按同分母比大小。
先把分子不同的两个分数化成分子相同的两个分数,然后再根据“分子相同的两个分数,分母小的分数比较大”进行比较。
分子分母比大小诀窍1、化同分子法先把分子不同的两个分数化成分子相同的两个分数,然后再根据“分子相同的两个分数,分母小的分数比较大”进行比较。
2、化成小数法先把两个分数化成小数,再进行比较。
3、搭桥法在要比较的两个分数之间,找一个中间分数,根据这两个分数和中间分数的大小关系,比较这两个分数的大小。
4、差等规律法根据“分子与分母的差相等的两个真分数,分子加分母得到的和较大的分数比较大;分子与分母的差相等的两个假分数,分子加分母得到的和较大的分数比较小”比较两个分数的大小。
5、交叉相乘法把第一个分数的分子与第二个分数的分母相乘的积当作第一个分数的相对值;把第二个分数的分子与第一个分数的分母相乘的积当作第二个分数的相对值,相对值比较大的分数比较大。
6、比较倒数法通过比较两个分数倒数的大小,比较两个分数的大小。
倒数较小的分数,原分数较大;倒数较大的分数,原分数较小。
7、相除法用第一个分数除以第二个分数,若商小于1,则第一个分数小;若商大于1,则第一个分数大;若商等于1,则两个分数相等。
8、化整法将两个分数同时乘其中一个分数的分母,把其中一个分数化为整数,然后再进行比较。
9、约分法在比较两个分数之前,先将两个分数约分,然后再进行比较。
什么是分子分母分子指的是分数中写在分数线上面的数,分式中写在分数线下面的数或代数式叫分母,分数的分子和分母都乘以或都除以同一个不为零的数,所得到的分数与原分数的大小相等。
分数的注意事项1、分数的分母不能为0,否则无法成立,分子可以为0。
2、分数中的分子或分母经过约分后不能出现无理数,否则就不是分数。
分数乘除分子分母的乘除运算

分数乘除分子分母的乘除运算分数是数学中常见的表示部分的形式,其中包括分子和分母两个部分。
在数学运算中,我们需要对分数进行乘除运算,而这涉及到对分子和分母进行乘除的操作。
本文将详细讨论分数乘除分子分母的运算规则和方法。
一、分数的基本概念分数是数学中的一种数表示形式,它由分子和分母两个部分组成,分子表示部分的数量,而分母表示整体的数量。
分数可以表示部分与整体的比例关系,常用来描述比例、比率、面积、体积等概念。
在分数中,分子和分母都可以是整数,且分母不能为0。
当分子等于0时,分数的值为0;当分子和分母相等时,分数的值为1。
分数可以是正数、负数或零,根据分子和分母的正负情况进行判断。
二、分数的乘法运算1. 分数相乘的基本规则分数相乘的规则是将分子与分子相乘,分母与分母相乘。
即若有两个分数a/b和c/d,则它们的乘积为(ac)/(bd)。
例如,计算1/2与3/4的乘积:(1/2) × (3/4) = (1 × 3) / (2 × 4) = 3/82. 分数相乘的示例示例1:计算2/3与4/5的乘积。
解:(2/3) × (4/5) = (2 × 4) / (3 × 5) = 8/15示例2:计算7/8与1/4的乘积。
解:(7/8) × (1/4) = (7 × 1) / (8 × 4) = 7/32需要注意的是,在乘法运算中,分子和分母可以进行约分,即将它们的公因数约去,得到最简分数。
例如,将8/24约分为1/3。
三、分数的除法运算1. 分数相除的基本规则分数相除的规则是将第一个分数的分子与第二个分数的分母相乘,第一个分数的分母与第二个分数的分子相乘。
即若有两个分数a/b和c/d,则它们的商为(ad)/(bc)。
例如,计算2/3除以4/5:(2/3) ÷ (4/5) = (2/3) × (5/4) = (2 × 5) / (3 × 4) = 10/122. 分数相除的示例示例1:计算7/8除以1/4。
分子分母符号

分子分母符号
分子分母符号通常用于表示分数。
分子是分数线上方的数字或符号,而分母则是分数线下方的数字或符号。
在数学中,分数表示部分与整体的关系。
分子和分母的符号可以帮助我们清晰地表示这种关系。
例如,在分数3/4中,3是分子,4是分母。
此外,为了输入分数,可以使用分数符号(/)来分隔分子和分母。
例如,输入"3/4"将显示为分数形式。
此外,还可以使用专用符号或特殊字符输入法来输入分数。
总之,分子分母符号是数学中表示分数的重要工具,有助于我们清晰地表达部分与整体的关系。
分母序分子基口诀

分母序分子基口诀
英语中表达分数的口诀是:“分子基,分母序;分子大于一,分母加s。
”这个口诀的含义是:在表达分数时,分子应该使用基数词,而分母则应该使用序数词。
当分子大于一时,分母需要加s以表示复数形式。
例如,四分之一可以表示为"a/one quarter",四分之三可以用"three quarters"来表示。
另外,对于一些特殊的分数表达方式,如1/2可以使用"one-second"来表示,3/4可以用"three-fourths"来表示,2/5可以用"two-fifths"来表示。
此外,对于分数的比较和运算也有相应的规则:如果两个分数的分母相同,那么分子大的分数就大;如果两个分数的分子相同,那么分母大的分数就小。
在进行分数的加减运算时,需要先将分数转化为同分母的形式,然后再进行加减运算。
而在进行分数的乘法运算时,需要将分母与分母相乘,分子与分子相乘,然后可以进行约分。
分母不同的算式格式

分母不同的算式格式1.把整体“1”平均分成若干份,表示这样的一份或几份的数叫做分数。
分母表示把一个物体平均分成几份,分子是表示这样几份的数。
把1平均分成分母份,表示这样的分子份。
2.分子在上分母在下,也可以把它当做除法来看,用分子除以分母,相反乘法也可以改为用分数表示3.分数的分子不能是小数只是除0以外的自然数;4.分数可以表述成一个除法算式:如二分之一等于1除以2。
其中,1 分子等于被除数,- 分数线等于除号,2 分母等于除数,而0.5 分数值则等于商5.小数化分数小数化分数,小数部分有几位分母就有几个零。
例:0.45=45/100=9/20如是纯循环小数,循环节有几位,分母就有几个9。
例:0.3(3循环)=3/9=1/3如是混循环小数,循环节有几位,分母就有几个9;不循环的数字有几位,9后面就有几个0,而分子是用循环节减去不循环的部分。
例:0.12(2循环)=2-1/90=1/90注意:最后一定要约分。
6.分类分数一般分成:真分数,假分数,带分数,百分数;或分成正分数和负分数。
介绍正真分数的值小于1。
分子比分母小,例:1/3假分数的值大于1,或者等于1。
分子比分母大或相等(假分数包括带分数)例:5/3、7/7、带分数的值大于1。
注意事项①分母不能为0,否则无意义。
②分数中的分子或分母经过约分后不能出现无理数(如2的平方根),否则就不是分数。
③一个最简分数的分母中只有2和5两个质因数就能化成有限小数;如果最简分数的分母中只含有2和5以外的质因数那么就能化成纯循环小数;如果最简分数的分母中既含有2或5两个质因数也含有2和5以外的质因数那么就能化成混循环小数。
(注:如果不是一个最简分数就要先化成最简分数再判断;分母是2或5的最简分数一定能化成有限小数,分母是其他质数的最简分数一定能化成纯循环小数)7.分数加减法1、同分母分数相加减,分母不变,即分数单位不变,分子相加减,最后要化成最简分数。
例1:2/9+5/9=2+5/9=7/9例2:1/8+3/8=1+3/8=4/8=1/2例3:5/9-1/9=5-1/9=4/9例4:3/4-1/4=3-1/4=2/4=1/22、异分母分数相加减,先通分,即运用分数的基本性质将异分母分数转化为同分母分数,改变其分数单位而大小不变,再按同分母分数相加减法去计算,最后要化成最简分数。
分子分母运算

分子分母运算
加法:如果分母相同,就把分子相加。
如果分母不一样,可以先分点再加分子。
分母保持不变。
减法:如果分母相同,就减去分子。
如果分母不一样,可以先分再减分子,分母不变。
乘法:不管分子和分母是否相同,分子乘以分子,分母乘以分母。
除法:用一个分数除以另一个分数等于乘以这个数的倒数。
3000多年前,古埃及用特殊的符号来表示一个分子的分数。
两千多年前,中国也有分数,但在秦汉数学中,分数的形式完全不同。
后来印度出现了类似中国的分数表示法。
后来阿拉伯人发明了分数线,今天分数线的记数法就来源于此。
为什么叫分数?因为“分数”这个名字基本上直观地表示了这个数的特征,比如一个苹果,如果四个人平分,可以分成四等份。
这个例子说明分数是计量的需要,也是数学本身的需要。
论文分数比大小的游戏可以怎样做

论文分数比大小的游戏可以怎样做分子相同,分母小的,分数大;分母相同,分子大的,分数大。
分子大,分母小的,分数大。
分子分母同大同小,看分子分母谁变化快,变化快的起主要作用。
比如:5/6和7/8。
很明显,5到7比6到8变化快,说明分子变化速率快,那么,5/6<7/8。
口诀就是:分子快,后大前;分母快,前大后。
大家记住一个,另外一个刚好相反就是了。
如果说分子分母同大同小且相差不是很大。
1)考虑用直除,154/17和173/19。
前者直除是9.0开头,后者是9.1,说明后大于前。
2)考虑用差分法,还是上面那个例子。
因为173-154/19-17=19/2。
因为,19/2>154/17。
说明173/19在两者之前,173/19>154/17。
再比如:151/557和260/996。
因为,260-151/996-557=109/439,不好看,我们继续差分法,151-109/557-439=42/118。
明显42/118>109/439。
所以151/557>109/439,所以260/996<151/557,差分法的本质是溶液混合思想。
3)考虑用溶液法,1511/3122和1731/3672。
两个分式都非常接近1/2。
让分子变成相同,1511+220/3122+440=1731/3562>1731/3672。
4)考虑用化同法,化同法是用于两个分子或分母存在倍数关系比如:122/377和246/797。
122*2.02/377*2.02=246/750+,明显前者大于后者。
分子分母的计算公式

分子分母的计算公式分子分母是一个在数学中常用的概念,用于描述一个有理数的分子和分母的关系。
在代数中,分子和分母通常表示为两个整数,分别用来表示有理数的整数部分和小数部分。
计算分子部分的方法:1.分数表示:对于一个有理数的分子部分,可以直接从分数表示中获取。
例如,对于分数5/7来说,分子为52.小数表示:对于一个有理数的小数部分,可以通过以下步骤计算得到。
a.将小数转化为分数:将小数的小数位数乘以10的相应幂次方,作为分数的分母。
例如,0.25可以转化为25/100=1/4b.化简分数:将转化后的分数化简到最简形式,即分子和分母没有公共的因子。
例如,1/4已经是一个最简形式的分数。
c.计算分子:从最简形式的分数中获取分子部分。
对于1/4来说,分子为1计算分母部分的方法:1.分数表示:对于一个有理数的分母部分,可以直接从分数表示中获取。
例如,对于分数5/7来说,分母为72.小数表示:对于一个有理数的小数部分,可以通过以下方法计算得到。
a.将小数转化为分数:将小数的小数位数乘以10的相应幂次方,作为分数的分母。
例如,0.25可以转化为25/100=1/4b.化简分数:将转化后的分数化简到最简形式,即分子和分母没有公共的因子。
例如,1/4已经是一个最简形式的分数。
c.计算分母:从最简形式的分数中获取分母部分。
对于1/4来说,分母为4需要注意的是,以上计算分子和分母的方法适用于大多数有理数,但在一些特殊情况下可能需要进行特殊处理。
例如,对于一个循环小数如1.333...,无法用有理数表示,因此无法计算其分子和分母。
资料分析速算技巧之分子分母比较法
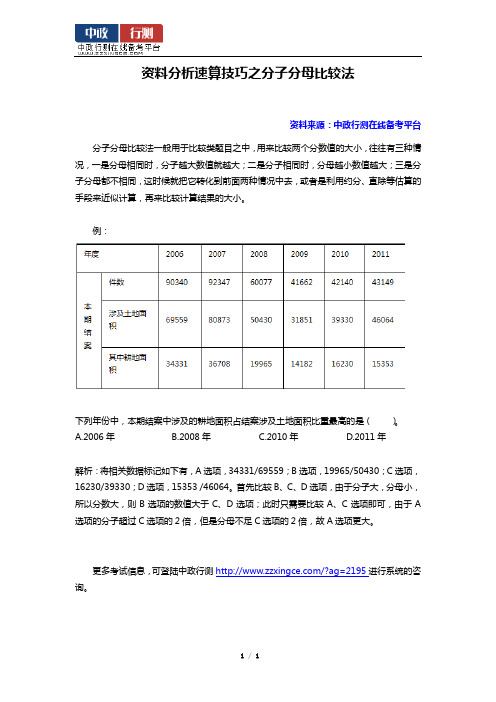
资料分析速算技巧之分子分母比较法
资料来源:中政行测在线备考平台
分子分母比较法一般用于比较类题目之中,用来比较两个分数值的大小,往往有三种情况,一是分母相同时,分子越大数值就越大;二是分子相同时,分母越小数值越大;三是分子分母都不相同,这时候就把它转化到前面两种情况中去,或者是利用约分、直除等估算的手段来近似计算,再来比较计算结果的大小。
例:
下列年份中,本期结案中涉及的耕地面积占结案涉及土地面积比重最高的是()。
A.2006年 B.2008年 C.2010年 D.2011年
解析:将相关数据标记如下有,A选项,34331/69559;B选项,19965/50430;C选项,16230/39330;D选项,15353 /46064。
首先比较B、C、D选项,由于分子大,分母小,所以分数大,则B选项的数值大于C、D选项;此时只需要比较A、C选项即可,由于A 选项的分子超过C选项的2倍,但是分母不足C选项的2倍,故A选项更大。
更多考试信息,可登陆中政行测/?ag=2195进行系统的咨询。
1 / 1。
分式运算中的十二种常用技巧

分式运算中的十二种常用技巧在分式运算中,有很多常用技巧可以帮助我们简化表达式、求解问题。
下面我将介绍分式运算中的十二种常用技巧。
一、分子与分母的公因式法当分子与分母有公因式时,我们可以先约去它们的公因式,再进行运算。
例如,对于分式 $\frac{3x^2}{4x}$,我们可以约去分子和分母的公因式 $x$,简化为 $\frac{3x}{4}$。
二、通分法对于两个分式,如果它们的分母不同,我们需要先将它们的分母化为通分,再进行运算。
例如,对于分式 $\frac{x}{2} + \frac{y}{3}$,我们可以将它们的分母化为通分,变为 $\frac{3x}{6} + \frac{2y}{6}$,再进行求和。
三、分数相加减法分数相加减法可以通过通分法化简,再按照分子相加减,分母保持不变的原则进行运算。
例如,对于分式 $\frac{3}{4} + \frac{1}{6}$,我们可以先将其通分为 $\frac{9}{12} + \frac{2}{12}$,再进行求和,得到$\frac{11}{12}$。
四、负号的运用在分式运算中,可以用负号将有多个项的分式变为一个项的分式。
例如,对于分式 $\frac{a}{b} - \frac{c}{d}$,我们可以将其转化为 $\frac{ad - bc}{bd}$。
五、分式的乘法分式的乘法可以按照分子相乘、分母相乘的原则进行运算。
例如,对于分式 $\frac{a}{b} \cdot \frac{c}{d}$,我们可以将其简化为 $\frac{ac}{bd}$。
六、分式的除法分式的除法可以通过将被除数与除数的分子与分母交叉相乘,再进行约分得到结果。
例如,对于分式 $\frac{a}{b} \div \frac{c}{d}$,我们可以将它转化为 $\frac{a}{b} \cdot \frac{d}{c}$,再进行约分。
七、分式的乘方分式的乘方可以通过将分子与分母分别进行乘方运算得到结果。
分数加减乘除法的蝴蝶算法

分数加减乘除法的蝴蝶算法
蝴蝶算法是一种常用于分数的加减乘除运算的简化方法。
它的步骤如下:
加法:
1. 将两个分数的分母相同化。
如果分母不同,需要找到它们的最小公倍数,然后按照最小公倍数进行分母转换。
2. 将两个分数的分子相加。
3. 将结果的分子化简至最简形式。
如果存在约数,可以将其约分。
减法:
1. 将两个分数的分母相同化,具体步骤同加法。
2. 将第二个分数的分子变为相反数。
3. 将第一个分数的分子与第二个分数的分子相加。
4. 将结果的分子化简至最简形式,具体步骤同加法。
乘法:
1. 将两个分数的分子相乘,得到新的分子。
2. 将两个分数的分母相乘,得到新的分母。
3. 将结果的分子和分母化简至最简形式。
除法:
1. 将第一个分数的分子与第二个分数的分母相乘,得到新的分子。
2. 将第一个分数的分母与第二个分数的分子相乘,得到新的分母。
3. 将结果的分子和分母化简至最简形式。
使用蝴蝶算法可以简化分数的加减乘除运算,并得到最简分数形式的结果。
