专项测练题：组合图形和立体图形

合集下载

北师大版六年级下册总复习：组合图形题(平面、立体)

组合图形1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

立体图形中的面积练习题

立体图形中的面积练习题一、长方体与正方体1. 计算长方体的表面积，其中长为8cm，宽为6cm，高为4cm。

2. 计算正方体的表面积，棱长为5cm。

3. 一个长方体的长、宽、高分别为10cm、8cm、6cm，求其表面积。

4. 一个正方体的体积为64cm³，求其表面积。

二、圆柱与圆锥1. 计算圆柱的表面积，底面半径为3cm，高为7cm。

2. 计算圆锥的侧面积，底面半径为4cm，母线长为6cm。

3. 一个圆柱的底面直径为10cm，高为12cm，求其表面积。

4. 一个圆锥的底面周长为18.84cm，高为9cm，求其侧面积。

三、球体1. 计算球体的表面积，半径为6cm。

2. 一个球体的直径为10cm，求其表面积。

3. 一个球体的体积为900π cm³，求其表面积。

四、组合立体图形1. 计算由一个长方体和一个正方体组成的组合体的表面积，长方体的长、宽、高分别为12cm、8cm、6cm，正方体的棱长为6cm。

2. 计算由一个圆柱和一个圆锥组成的组合体的表面积，圆柱的底面半径为4cm，高为8cm，圆锥的底面半径为4cm，高为6cm。

3. 一个球体与一个圆柱组成的组合体，球体半径为3cm，圆柱底面半径为3cm，高为6cm，求组合体的表面积。

五、应用题1. 一个长方体的长、宽、高分别为20cm、15cm、10cm，求其表面积。

2. 一个圆柱的底面直径为14cm，高为21cm，求其表面积。

3. 一个圆锥的底面半径为7cm，高为10cm，求其侧面积。

4. 一个球体的体积为5000π cm³，求其表面积。

5. 计算一个由长方体、正方体和圆柱组成的组合体的表面积，长方体的长、宽、高分别为10cm、8cm、6cm，正方体的棱长为6cm，圆柱的底面半径为4cm，高为8cm。

立体图形中的面积练习题（续）六、棱柱与棱锥1. 计算四棱柱的表面积，底面边长分别为6cm和8cm，高为5cm。

2. 计算三棱锥的侧面积，底面边长分别为4cm、5cm、6cm，侧棱长分别为7cm、8cm、9cm。

六年级下册数学总复习试题-图形的组合与观察专项练全国版(含答案)

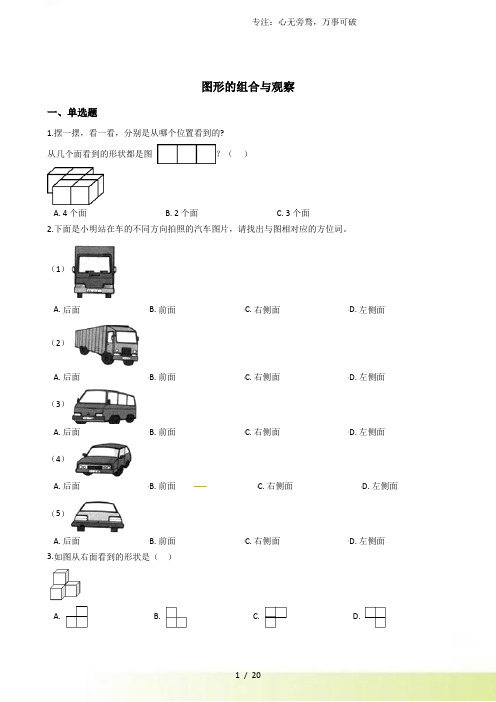
图形的组合与观察一、单选题1.摆一摆，看一看，分别是从哪个位置看到的?从几个面看到的形状都是图？（）A. 4个面B. 2个面C. 3个面2.下面是小明站在车的不同方向拍照的汽车图片，请找出与图相对应的方位词。

（1）A. 后面B. 前面C. 右侧面D. 左侧面（2）A. 后面B. 前面C. 右侧面D. 左侧面（3）A. 后面B. 前面C. 右侧面D. 左侧面（4）A. 后面B. 前面C. 右侧面D. 左侧面（5）A. 后面B. 前面C. 右侧面D. 左侧面3.如图从右面看到的形状是（）A. B. C. D.4.小明准备过马路时，一辆汽车从他的面前驶过，哪幅图是他第一个看到的？（）A. B. C.5.王大伯晚上散步，当他走向路灯时，他的影子会越来越( )A. 小B. 长C. 短6.如果你按照下面的步骤做，当你完成第五步的时候，将纸展开，你会得到（）A. B. C. D.7.看图回答.下面的图形是从上边物体的哪一面看到的？（）.A. 正面B. 侧面C. 上面8.小强用同样大的小正方体摆了一个长方体，从正面和上面看，看到的图形分别是：如图小强摆这个长方体一共用了（）个小正方体．A. 12B. 18C. 249.从上面看到的形状不同的是（）A. B. C.10.用相同的小正方体拼成一个大正方体，至少需要( )个小正方体。

A. 4B. 8C. 16D. 32二、判断题11.这四个图形中只有一个图形不能密铺…．12.若干个完全相同的三角形能密铺．13.由远往近观察某一物体时，距离物体越近，看到的范围越大。

14.把两个一样的正方体拼成一个长方体后，体积和表面积都不变．（判断对错）15.正五边形是轴对称图形，它也能密铺．16.淘气看到的是。

17.从侧面看到的是圆形。

18.人越来越远离窗子时，看到的窗外的范围会越来越窄．19.从上面看小药箱，应该是。

（）20.两个正方体摆成一排，从正面和上面看到的都是长方形。

三、填空题21.把一个棱长是10分米的正方体木料削成一个最大的圆柱体木料，圆柱体木料的体积是________．22.下面的三个图形分别是从哪个方向看到的？填一填。

行测立体组合体诀窍

行测立体组合体诀窍行测考试中的立体组合体题目主要涉及到计算立方体、长方体、棱柱、棱锥、圆柱、圆锥等多种几何图形的体积、表面积、相交关系等问题。

以下是解决此类题目的几个窍门：1. 熟记几何公式：- 立方体的体积公式：V = a^3，表面积公式：S = 6a^2- 长方体的体积公式：V = lwh，表面积公式：S = 2lw + 2lh + 2wh- 棱柱的体积公式：V = Bh，其中B为底面积，h为高，表面积公式：S = B + 2Ph，其中P为底面周长- 圆柱的体积公式：V = πr^2h，表面积公式：S = 2πr(r + h)- 棱锥的体积公式：V = 1/3Bh，其中B为底面积，h为高，表面积公式：S = B + 1/2Pl，其中P为底面周长，l为斜高- 圆锥的体积公式：V = 1/3πr^2h，表面积公式：S = πr(r + l)，其中l为斜高2. 观察立体图形的特点：- 理解立体图形的特点，比如长方体的六个面都是矩形，棱柱的侧面是矩形，底面是多边形等。

- 通过观察，确定需要计算的量和已知量，使用对应的公式求解。

- 注意边长、高、斜高等概念的理解和运用，合理选择适合的公式进行计算。

3. 切割与组装法：- 针对复杂立体图形，可以通过切割与组装简单立体图形的方法进行计算。

- 将复杂图形切割为几个简单的立体图形，然后通过计算各个简单图形的体积、表面积等，最后进行加减运算得到复杂立体的结果。

- 注意切割时要维持图形的完整性，避免几何图形的盖、底未能完全平行，或者缺失引起计算错误。

4. 绘制示意图：- 绘制示意图有助于理解和分析立体图形的结构，可以更清晰地确定计算关系。

- 在解题过程中，尽量用简单、明了的示意图代替文字描述，尤其是在涉及图形相交、分割等复杂情况下，有助于清晰把握题意，防止出错。

5. 多积累题目：- 多做一些立体组合体的相关练习题，积累解题经验和技巧。

- 题目中涉及到的具体数据和计算方法可能会有所不同，通过多做题，熟悉题目类型和题目解法，能更好地应对考试中的各种情况。

北师大版五年级数学上册典型例题系列之第六单元：求不规则及组合立体图形的面积专项练习二(解析版)

五年级数学上册典型例题系列之第六单元：求不规则及组合图形的面积专项练习二（解析版）1．王伯伯盖了一间新房，新房一面墙的平面图如下图。

王伯伯要在这面墙上刷白色的涂料，如果每平方米用0.25千克涂料，粉刷这面墙需涂料多少千克？【答案】11.25千克【分析】根据图观察，需要刷涂料的组合图形为一个长方形加一个三角形，该长方形长为9米，宽为4米，根据长方形面积公式：长方形面积＝长×宽，该三角形底为9米，高为2米，根据三角形面积公式：三角形面积＝底×高÷2，分别代入数据求出组合图形面积，再用面积乘每平方米需要的涂料千克数即可。

【详解】如分析可得：长方形面积：9×4＝36（平方米）三角形面积：9×2÷2＝18÷2＝9（平方米）组合图形总面积：36＋9＝45（平方米）需要涂料数：45×0.25＝11.25（千克）答：粉刷这面墙需涂料11.25千克。

【点睛】本题考查了组合图形的面积，通过仔细观察，可以把看起来不规则的组合图形拆分成两个规则的图形，熟记长方形和三角形面积公式是解题的关键。

2．张叔叔家有一块长方形地，其中有一个梯形鱼塘，已知鱼塘的上底长30米，下底长10米，高是8米，其余地方种植玉米（图中阴影部分），已知每平方米玉米地可以收玉米1.35千克，这块地一共可以收玉米多少千克？【答案】594千克【分析】先求出种植玉米的面积；种植玉米面积（阴影部分面积）＝长是30米，宽是20米的长方形面积－上底是30米，下底是10米，高是8米的梯形面积；根据长方形面积公式：面积＝长×宽；梯形面积公式：面积＝（上底＋下底）×高÷2，代入数据，求出种植玉米的面积，再乘1.35，即可解答。

【详解】30×20－（30＋10）×8÷2＝600－40×8÷2＝600－320÷2＝600－160＝440（平方米）440×1.35＝594（千克）答：这块地一共可以收玉米594千克。

六年级数学下册典型例题系列之第三单元：组合立体图形的表面积专项练习(解析版)

2021-2022学年六年级数学下册典型例题系列之第三单元：组合立体图形的表面积专项练习（解析版）1．有一个工具箱下半部分为正方体，上半部分为圆柱体一半（下图），如果把工具箱的表面涂上油漆（包括底面），求涂油漆部分的面积。

【解析】可以将两个半圆拼成一个完整的圆，涂色部分包括正方体5个面、圆柱侧面积的一半、以及圆柱一个底面积，据此列式解答即可。

20²×5＋3.14×20×20÷2＋3.14×（20÷2）²＝2000＋628＋3.14×100＝2000＋628＋314＝2942（平方厘米）答：涂油漆部分的面积是2942平方厘米。

2．计算下面组合图形的表面积。

（单位：cm）【解析】6×6×6+3.14×6×5，=216+94.2，=310.2（平方厘米）答：它的表面积是30.2平方厘米。

3．求下面图形的表面积和体积。

（单位：cm）【解析】表面积＝大正方体的表面积＋圆柱的侧面积，10×10×6＋3.14×4×6=600+75.36＝675.36（cm2）；4．下图是一个灯笼图片，阿姨做这个灯笼至少需要多大的彩纸？【解析】用外圆柱侧面积＋内圆柱侧面积＋上下两个圆环面积即可。

4÷2＝2（分米），2÷2＝1（分米）3.14×4×5＋3.14×2×5＋3.14×（22－12）×2＝62.8＋31.4＋3.14×3×2＝62.8＋31.4＋18.84＝113.04（平方分米）答：做这个灯笼至少需要113.04平方分米的彩纸。

5．有三个圆柱，一个堆在一个上面，底层圆柱最大，上层最小，它们的直径分别是4分米、 3分米、2分米，高都是2分米，这样的立体图形的表面积是多少？【解析】由图可知：这个立体图形的表面积等于最下面大圆柱的表面积加上上面两个小圆柱的侧面积。

图形的快速运算练习题

图形的快速运算练习题一、矩形类1. 一个矩形的长是10厘米，宽是5厘米，求该矩形的周长和面积。

2. 若一个矩形的周长是40厘米，长是12厘米，求该矩形的宽和面积。

3. 一个矩形的面积是60平方厘米，宽是4厘米，求该矩形的长和周长。

4. 两个矩形的长分别是8厘米和12厘米，宽分别是6厘米和4厘米，求这两个矩形的面积和周长之和。

二、三角形类1. 一个等边三角形的边长是9厘米，求该三角形的周长和面积。

2. 一个直角三角形的两条直角边分别是6厘米和8厘米，求该三角形的斜边长和面积。

3. 一个三角形的周长是30厘米，底边是10厘米，高是12厘米，求该三角形的面积。

4. 两个等腰三角形的底边分别是8厘米和12厘米，腰分别是5厘米和7厘米，求这两个三角形的面积和周长之和。

三、圆形类1. 一个圆的半径是7厘米，求该圆的周长和面积。

2. 一个圆的直径是14厘米，求该圆的周长和面积。

3. 若一个圆的周长是43.96厘米，求该圆的半径和面积。

4. 两个圆的半径分别是5厘米和8厘米，求这两个圆的面积和周长之和。

四、组合图形类1. 一个矩形和一个等边三角形组合，矩形的长是10厘米，宽是6厘米，等边三角形的边长是8厘米，求组合图形的周长和面积。

2. 一个圆形和一个矩形组合，圆的半径是4厘米，矩形的长是12厘米，宽是8厘米，求组合图形的面积。

3. 一个等腰三角形和一个圆形组合，等腰三角形的底边是10厘米，腰是8厘米，圆的半径是3厘米，求组合图形的面积。

4. 两个矩形组合成一个更大的矩形，两个小矩形的长分别是8厘米和12厘米，宽分别是6厘米和4厘米，求组合后大矩形的面积和周长。

五、平行四边形类1. 一个平行四边形的底边是15厘米，高是8厘米，求该平行四边形的面积和周长。

2. 一个平行四边形的周长是50厘米，两邻边分别是12厘米和8厘米，求该平行四边形的面积。

3. 一个平行四边形的面积是120平方厘米，底边是10厘米，求该平行四边形的高和周长。

小学数学毕业考试立体图形真题练习

小学数学毕业考试立体图形真题练习一、选择题1．将一个正方体木块加工成一个最大的圆柱形木块，圆柱形木块上的底面直径是二、图形计算11．求表面积。

12．求下面组合图形的体积。

（单位：厘米，取3.14）=13．一个零件的形状如下图所示，求这个零件的体积。

三、解答题14．吴老师买了一套新房，客厅长6米，宽4米，高3米。

请同学们帮吴老师算一算装修所需要的部分材料。

（1）客厅准备用边长5分米的方砖铺地面，需要多少块？（2）准备粉刷客厅的四周墙壁和顶面，门窗、电视墙等10平方米不粉刷，实际粉刷的面积是多少平方米？15．神舟十三号飞船的飞行目标是对接我国空间站“天和”核心舱，将三名航天员运送至中国空间站。

神舟十三号乘组人员在空间站工作和生活六个月，创造了我国航天员在太空驻留天数的新纪录。

飞船主体由轨道舱、返回舱和推进舱构成。

轨道脑主体为圆柱形，集工作、吃饭和睡觉等诸多功能于一体，总长度为2.8米，直径约2.2米（如图）它的体积大约是多少？（得数保留一位小数）16．求瓶子的体积。

（单位：cm）17．一只底面半径为40厘米的圆柱形水桶内盛有80厘米深的水，将一个高8厘米的圆锥形铁块沉没水中，水没有溢出，水面上升1.5厘米，铁块的底面积是多少平方厘米？18．毕业啦！同学们用卡纸做了一顶“博士帽”（如图），帽子上面是边长为30厘米的正方形，下面是底面直径为20厘米、高为8厘米的无盖无底圆筒，做这顶帽子的上、下部分，分别用卡纸多少平方厘米？（连接处不计）18．一个圆锥形的沙堆，底面面积是28.26平方米，高是6米。

用这堆沙在20米宽的公路上铺2厘米厚的路面，能铺多少米？20．一块蛋糕如下图，在它的表面涂上奶油，需要涂多少平方厘米的奶油？这块蛋糕体积多大？21．一根长2米，横截面直径是20厘米的木头浮在水面上，它正好是一半露出水面。

（1）这根木头的体积是多少立方厘米？（2）这根木头与水接触的面积是多少平方厘米？22．如图是一个粮囤的示意图，它是由圆锥和圆柱两部分组成的。

生活中的立体图形练习题

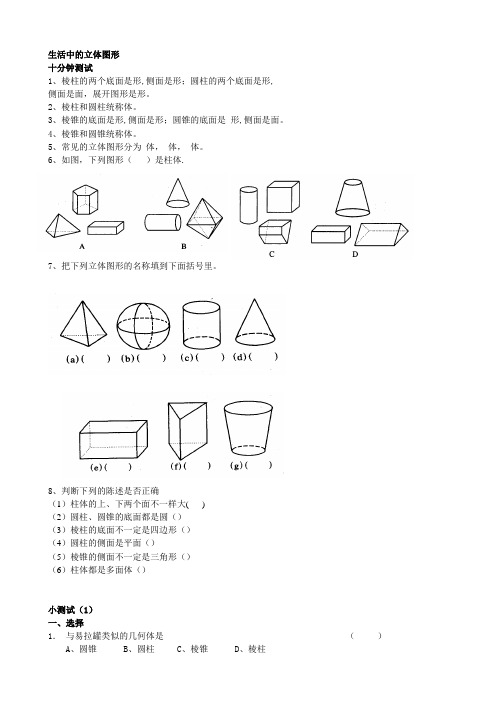
生活中的立体图形十分钟测试1、棱柱的两个底面是形,侧面是形；圆柱的两个底面是形,侧面是面，展开图形是形。

2、棱柱和圆柱统称体。

3、棱锥的底面是形,侧面是形；圆锥的底面是形,侧面是面。

4、棱锥和圆锥统称体。

5、常见的立体图形分为体，体，体。

6、如图，下列图形（）是柱体.7、把下列立体图形的名称填到下面括号里。

8、判断下列的陈述是否正确（1）柱体的上、下两个面不一样大( )（2）圆柱、圆锥的底面都是圆（）（3）棱柱的底面不一定是四边形（）（4）圆柱的侧面是平面（）（5）棱锥的侧面不一定是三角形（）（6）柱体都是多面体（）小测试（1）一、选择1．与易拉罐类似的几何体是（）A、圆锥B、圆柱C、棱锥D、棱柱2.下图中是三棱锥的立体图形是（）3．埃及金字塔类似于几何体（）A 、圆锥B 、圆柱C 、棱锥D 、棱柱 4.下列各组图形中都是平面图形的是（）A.三角形、圆、球、圆锥B.点、线、面、体C.角、三角形、正方形、圆D.点、相交线、线段、长方体 5．下列说法正确的是（） A ．有六条侧棱的棱柱的底面一定是三角形 B ．棱锥的侧面是三角形 C ．长方体和正方体不是棱柱D ．柱体的上、下两底面可以大小不一样二、填空6．立体图形的各个面都是__________的面,这样的立体图形称为多面体. 7．篮球、排球、足球、乒乓球都是球形的，不是球形的球是。

8．棱柱的长相等，上下底面是的多边形，侧面是。

9．一个棱锥有7个面，这是棱锥，有个侧面。

10．长方体ABCD －A ′B ′C ′D ′有个面，条棱，个顶点。

与棱AB 垂直相交的棱有条，与棱AB 平行的棱有条。

11.如图所示立体图形中，（1）球体有___________；（2）柱体有_________；（3）锥体有____________．12.如图,是一座粮仓，它可以看作是由和几何体组成的.13.如图，用边长为4的正方形，做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积是______.14、判断（1）柱体上下两个面一样大。

中班立体几何认知考试试题

中班立体几何认知考试试题
题一：辨识图形
请观察以下图中所示的立体图形，并回答相关问题：
1. 图形A是哪种立体图形？
2. 图形B有几个面？
3. 图形C有几条棱？
题二：比较大小
请比较以下两个立体图形的大小，并回答相关问题：
1. 图形D和图形E哪个更大？
2. 图形F和图形G哪个体积更小？
题三：图形拼凑
请根据以下提示，找出合适的立体图形来拼凑，并回答相关问题：提示：使用一个圆柱体和一个长方体组合成一个新的立体图形。

1. 你用了哪两个图形进行拼凑？
2. 拼凑后的图形有几个面？
3. 拼凑后的图形有几个顶点？
题四：图案识别
请观察以下图案，并回答相关问题：
1. 图案H与图案I有何不同？
2. 你能发现图案J中的几何形状？
题五：立体图形描绘
请根据以下描述，画出相应的立体图形：
1. 描述：这个立体图形有六个面，每个面都是正方形。

2. 描述：这个立体图形有三个面，两个面是圆形，一个面是矩形。

以上就是中班立体几何认知考试的试题。

请根据题目要求回答问题，并在各题下方绘制对应的图形。

确保回答准确无误，并将试卷交给监
考老师。

祝你好运！。

新人教版六年级组合面积、立体图形较难题、奥数

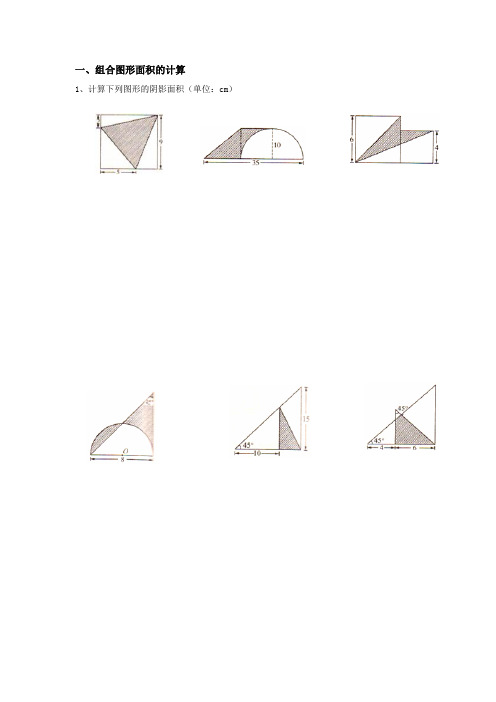
一、组合图形面积的计算1、计算下列图形的阴影面积（单位：cm）2、下图中长方形的长是6厘米，宽是5厘米，求阴影部分的面积。

3、如图长方形的面积是45平方厘米，宽是5厘米，求阴影部分的面积。

4、如图，两个大小不等的正方形拼成一个图形，已知小正方形的边长是4厘米，阴影部分的面积是30平方厘米，求空白部分的面积是多少？5、下列两个图形中，正方形的边长都为4，求阴影面积。

二、立体图形1、下图是一个正方体木块，棱长1米，沿水平方向将它锯成3片，每片又锯成4长条，每条又锯成5小块，共得到大小不等的长方体60块。

那么，这60块长方体的表面积的和是平方米。

2、下图是由19个边长都是2厘米的正方体重叠而成的。

求这个立体图形的外表面积。

3、如图，一个正方体的纸盒中恰好能放入一个体积为628立方厘米的圆柱体，纸盒的容积有多大？（π取3.14）4、一个长、宽、高分别是21厘米、15厘米、12厘米的长方体，从它的上面尽可能大地切下一个正方体，然后从剩余部分中再尽可能大地切下一个正方体，最后再从第二次剩余部分尽可能大地切下一个正方体，剩下的体积是多少立方厘米？5、下图是一个边长为2厘米的正方体．在正方体的上面的正中向下挖一个边长为1厘米的正方体小间；接着在小洞的底面正中再向下挖一个边长为21厘米的小洞；第三个小洞的挖法与前两个相同，边长为41厘米．那么最后得到的立体图形的表面积是多少平方厘米?6、有五颗相同的骰子放成一排（如下图），五颗骰子底面的点数之和是多少？7、将左下图沿虚线折成一个立方体，它的相交于一个顶点处的三个面上的数字之和的最大值是多少？最小值是多少？8、右图中第1格内放着一个立方体木块，木块六个面上分别写着A，B，C，D，E，F六个字母，其中A与D，B与E，C与F相对。

如果将木块沿着图中方格滚动，那么当木块滚动到第21个格时，木块向上的面写的是哪个字母？9、某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条如想图所示在三个方向上加固．所用尼龙编织条的长分别为365厘米、405厘米、485厘米．若每个尼龙条加固时接头处都重叠5厘米，则这个长方体包装箱的体积是多少立方米?三、利用分率解应用题1、一列火车从北京开往上海，已经行了全程的2/3，恰好是806公理，求这条路长多少公理？2、红星小学图书馆有文艺书640本，科技书是文艺书的7/8，科技书有多少本？3、利民厂一车间有工人400人，二车间比一车间少20%，二车间有多少人？4、某班有42人，男生是女生的1/5，男、女生各多少人？5、一段绳子的3/4比它的2/5长12米，求绳子的全长。

新初一分班考计算题特训：立体图形(专项训练)

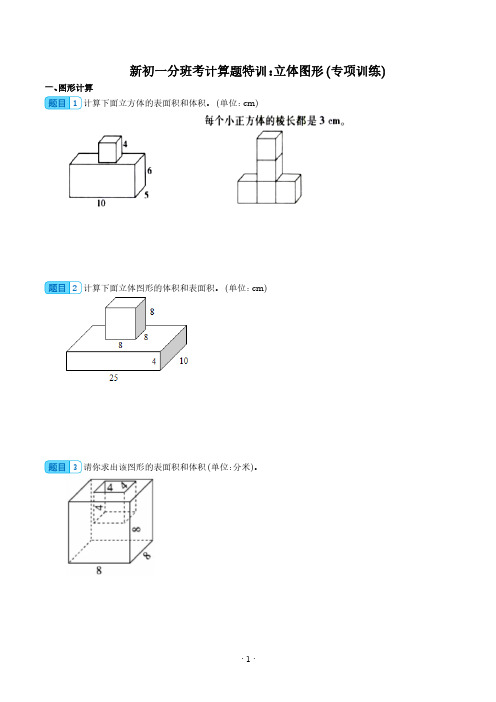
新初一分班考计算题特训：立体图形(专项训练)一、图形计算1计算下面立方体的表面积和体积。

(单位：cm)2计算下面立体图形的体积和表面积。

(单位：cm)3请你求出该图形的表面积和体积(单位：分米)。

4求①号立体图形的表面积，求②号立体图形的体积。

(单位∶cm)5下面是一个长方体的展开图，请同学们看图列式计算它的体积和表面积。

(单位：厘米)6求下面图形的体积。

(单位：厘米)7求组合图形的表面积和体积。

(单位：厘米)8计算出下面长方体的表面积。

9求下图的体积。

10计算圆锥的体积。

(单位：厘米)11求下列图形的表面积和体积。

单位：厘米。

12我会计算下面图形的表面积和体积。

(单位：m)(1) (2)13计算下图的体积。

(单位：分米)14下图是一个长方体的展开图，请计算出它的表面积？15计算下面圆柱展开图的表面积。

(单位：cm)16计算下面图形的表面积。

(单位：cm)17求下图表面积。

18计算下面各图形的表面积和体积。

(单位：cm)19求下面图形的表面积。

(纸盒接头处不算)20求下面立体图形的体积。

(1)(2)参考答案：1344cm2；364cm3；198cm2；135cm3【分析】(1)正方体和长方体叠加后，组合图形的表面积减少了两个正方形的面积，相当于长方体的表面积加上正方体四个面的面积即可；但组合图形的体积不变，用正方体和长方体的体积分别计算出它们的体积后，再相加即可；(2)5个正方体叠加在一起，组合图形的表面积减少了8个正方形的面积，利用正方体的表面积公式先计算出5个正方体的表面积，再减去8个正方形的面积即是组合图形的表面积；组合图形的体积等于5个正方体的体积，利用正方体的体积公式计算出1个正方体的体积，再乘5即可。

【详解】(1)4×4×4+(10×5+10×6+5×6)×2=64+(50+60+30)×2=64+140×2=64+280=344(cm2)4×4×4+10×5×6=64+300=364(cm3)(2)3×3×6×5-3×3×8=9×6×5-9×8=270-72=198(cm2)3×3×3×5=27×5=135(cm3)21512cm3；1036cm2【分析】立体图形的表面积等于长方体表面积加上正方体四个面的面积；立体图形的体积等于长方体和正方体的体积之和。

小升初真题汇编：立体图形(专项训练)--2024年六年级下册数学

小升初真题汇编：立体图形（专项训练）2023-2024学年数学六年级下册一、单选题1．（2023·鲤城）如图的纸片可以折成一个正方体，“前”字和（）字在折成的正方体中相对。

A．祝B．你C．程D．锦2．（2023·滁州）一个长方形的长是4厘米，宽是3厘米，如图所示。

以长为轴旋转一周和以宽为轴旋转一周分别形成两个圆柱，关于这两个圆柱的说法正确的是（）A．两个圆柱底面积相等B．两个圆柱的侧面积相等C．两个圆柱的表面积相等D．两个圆柱的体积相等3．（2023·昌黎）下面四组图形中圆柱与圆锥的体积不相等的是（）A．B．C．D．4．（2023·青县）如图，将一个圆柱的侧面剪开，不可能出现的形状是（）A．B．C．D．5．（2023·秦都）用一根铁丝正好可以围成一个棱长是6厘米的正方体框架，如果用这根铁丝正好围成一个长是10厘米，宽是5厘米的长方体框架，这个长方体框架的高是（）厘米。

A．5B．3C．7D．9 6．（2023·塔河）把直径2厘米，高4厘米的圆柱体木棒截成两个小圆柱体，表面积增加了（）平方厘米。

A．16B．3.14C．8D．6.28 7．（2023·顺义）有一块棱长是6分米的正方体木料，把它加工成一个圆锥，这个圆锥的体积最大是（）立方分米。

A．216πB．54πC．72πD．18π8．（2020·西充）一个圆柱和圆锥的底面半径的比是1：2，高的比是2：3，那么圆柱和圆锥的体积比是（）。

A．1：2B．2：3C．1：3D．3：5二、填空题9．（2023·无锡）如图是一个正方体的展开图，每个面上都填有一个数，且满足相对的两个面上的数互为倒数，那么▲＝，mn＝。

10．（2023·夏邑）用橡皮泥做一个正方体，棱长是4cm。

如果把它捏成一个高8cm的长方体，长方体的底面积是cm²；在体积不变的情况下，长方体的高和底面积成比例。

人教版小学一年级数学上学期第四单元《立体图形的拼组》检测题及答案(含两套题)

人教版小学一年级数学上学期第四单元《立体图形的拼组》检测题及答案
1.在用3个拼成的图形下面画“√”。

（）（）（）
（）（） ( ) 2.数一数，填一填。

（）个 ( )个（）个（）个3.看图填一填。

（）个（）个（）个（）个
4.搭得最高的画“√”，最稳定的画“○”，最容易倒的画“△”。

（）（）（）
5.按要求搭一搭。

先放一个长方体，在长方体上面放一个正方体，在正方体上面放一个圆柱，搭出的图形是（）。

6.下面的两堆拼成了上面的哪个图形？把它圈起来。

参考答案
1.
2. 5 4 5 4
3. 2 2 2 3
4. △○√
5. ①
6. 圈上面的第3个
人教版小学一年级数学上学期第四单元《立体图形的拼组》检测题及答案
1.数一数。

（）个（）个（）个（）个
2.搭积木，说一说下面的图形搭得像什么。

3.从下面5个图形中选取4个图形拼成组合图形。

请把拼得最稳的圈起来，在拼得最高的图形下面的□里画“√”。

4.把正确的摆法涂上自己喜欢的颜色。

先摆一个，在的左边摆一个，再把摆在的上面。

5.接着摆什么？圈出正确的答案。

6.用8个相同的，你能拼出几种不同的长方体或正方体？
参考答案
1. 3 5 5 4
2. 答案不唯一，合理即可，如鸡火箭
3. 第3幅图在第2幅图下面画“√”
4. 第2幅图
5.（1）正方体（2）球
6. 3种。

六年级数学小升初专项测评卷(二十)立体图形的表面积和体积(解析版)

小升初专项培优测评卷（二十）参考答案与试题解析一．填一填（共12小题）1．（2019•长沙）一个正方体的棱长由5厘米变成8厘米，表面积增加了平方厘米．【分析】根据正方体的表面积公式分别求出棱长为8厘米和5厘米的正方体的表面积，相减即可求解．【解答】解：886556⨯⨯-⨯⨯384150=-234=（平方厘米）；答：表面积增加了234平方厘米．故答案为：234．【点评】考查了正方体的表面积，正方体的表面积公式：正方体的表面积=棱长⨯棱长6⨯．2．（2019•莘县）一个长方体的长、宽、高的比是3:2:1，其中，长比高多4分米，它的体积是立方分米．【分析】已知一个长方体的长、宽、高的比是3:2:1，也就是高是长的13，其中，长比高多4分米，那么4分米是长的1(1)3-，由此可以求此长，进而求此高，又知宽是长的23，根据一个数乘分数的意义，即可求出宽，然后根据长方体的体积公式：v abh=，把数据代入公式解答即可．【解答】解：长：14(1)3÷-，342=⨯，6=（分米），宽：2643⨯=（分米），高：1623⨯=（分米），体积：64248⨯⨯=（立方分米）；答：它的体积是48立方分米．故答案为：48．【点评】此题解答关键是把比转化为分数，分别求出长、宽、高，再根据长方体的体积公式解答．3．（2019•武威）一个长方体的长、宽、高分别是8cm、6cm、4cm，这个长方体的占地面积最大是2cm，它的体积是3cm．【分析】这个长方体的占地面积就是它的底面积，根据长方形的面积公式：S ab=，把数据代入公式解答，再根据长方体的体积公式：V abh =，把数据代入公式解答．【解答】解：8648⨯=（平方厘米）， 864⨯⨯ 484=⨯192=（立方厘米），答：这个长方体的占地面积是48平方厘米，它的体积是192立方厘米．故答案为：48、192．【点评】此题主要考查长方形的面积公式、长方体的体积公式的灵活运用，关键是熟记公式．4．（2019•郑州）将一块长宽高分别为2m 、3m 、4m 的长方体木块，分割成四个完全相同的小长方体木块，表面积最多增加 2m ．【分析】把一个长方体分割成四个小长方体，只分割3次，增加6个横截面，要使增加的面积最多，则平行于34⨯面分割，这样就增加6个34⨯的面；由此即可解答．【解答】解：346⨯⨯ 126=⨯272()m =答：表面积最多增加272m ．故答案为：72．【点评】本题考查了长方体切割后的图形的表面积计算，此题沿平行于长⨯宽面切割，可使两个长方体的表面积之和最小；沿平行于宽⨯高面切割，可使两个长方体的表面积之和最大．5．（2019•绵阳）一个长方体木块长、宽、高分别是5cm 、4cm 、4cm ．如果用它锯成一个最大的正方体，体积比原来减少了 %．【分析】抓住正方体的特征，这个最大的正方体的棱长就是这个长方体最短的棱长，即4cm ，利用长方体体积公式V abh =和正方体的体积公式3V a =代入数据，即可解决问题．【解答】解：54480⨯⨯=（立方厘米） 44464⨯⨯=（立方厘米）(8064)80-÷ 1680=÷ 0.2= 20%=，答：体积要比原来减少20%．故答案为：20．【点评】找出这个最大正方体的棱长是解决本题的关键．6．（2019•贵阳）有一个正方体土坑，向下再挖深2米，它的表面积就增加64平方米，成为一个长方体土坑．这个长方体土坑的容积是立方米．【分析】根据题意，如果再向下挖深2米，则会增加4个相同的长方形面，那么可计算出增加的一个长方形的面的面积，然后再用一个长方形的面积除以2米，就是长方形面的边长也是正方体的棱长，最后再用长方体的容积公式计算出挖深2米后的长方体的容积即可．【解答】解：向下挖深2米后露出的一个长方形的面的面积为：64416÷=（平方米），正方体的棱长为：1628÷=（米)，挖深后的高为：8210+=（米)，长方体土坑的容积为：8810640⨯⨯=（立方米），答：这个长方体土坑的容积是640立方米．故答案为：640．【点评】解答此题的关键是确定挖深2米后露出的一个面的面积是多少，然后再计算出正方体的棱长与长方体土坑的高，最后用长方体的容积公式进行计算．7．（2019•海口）把一根长2m的圆柱形木料截成2段后表面积比原木料增加了20.8m，这根木料的底面积是2m，体积是3m．【分析】根据题意可知，这根木料的底面积就是截面的面积，把这根圆柱形木料截成2段，表面积增加了0.8平方米，表面积增加的是两个底面的面积，因此用增加的表面积除以2即可求出底面积，再利用圆柱的体积=底面积⨯高（长)计算即可解答问题．【解答】解：0.820.4÷=（平方米）⨯=（立方米）0.420.8答：这根木料的底面积是0.4平方米，体积是0.8立方米．故答案为：0.4；0.8．【点评】此题重点是理解圆柱被锯成2段后，表面积增加了两个底面积．8．（2019•郾城区）一个高20cm的圆柱，沿着底面直径切成两个半圆柱，表面积增加2360cm，这个圆柱的底面直径是cm．【分析】已知把一个高20厘米的圆柱体，沿着它的底面直径切成两个部分，表面积增加360平方厘米，表面积增加的360平方厘米是两个截面的面积，每个截面都是长方形，这个长方形的长等于圆柱的高，宽等于圆柱的直径，由此可以求出圆柱的直径，据此解答即可．【解答】解：360220÷÷18020=÷=（厘米）9答：这这个圆柱的底面直径是9厘米．故答案为：9．【点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用，关键是熟记公式，重点是明确：表面积增加的360平方厘米是两个截面的面积，每个截面的长等于圆柱的高，宽等于圆柱的直径．9．（2019•东莞市）一个棱长8分米的正方体水缸，水深6分米，如放入一块石头完全浸入水中，水溢出18升，则石头的体积是3dm．【分析】由题意得石头的体积等于上升的水的体积加上溢出水的体积，根据长方体的体积计算公式：长方体体积=长⨯宽⨯高计算即可．【解答】解：18升18=立方分米88(86)18⨯⨯-+=+12818=（立方分米）146答：这块石头的体积是146立方分米．故答案为：146．【点评】此题主要考查特殊物体体积的计算方法，将物体放入或取出水中，水面上升或下降的体积就是物体的体积；也考查了长方体的体积=长⨯宽⨯高；在解答时要注意：单位的统一．10．（2019•富源县）如图有个棱长为20cm的正方体木箱堆放在墙角的形状，这些木箱的体积是3cm．【分析】由图形可知，这些木箱一共有5个，根据正方体的体积公式：3=，求一个木箱的体积再乘5即v a可．【解答】解：2020205⨯⨯⨯=⨯，80005=（立方厘米），40000答：这些木箱的体积是40000立方厘米．故答案为：5个，40000．【点评】此题主要考查正方体的体积计算方法及组合图形的体积计算．11．（2019•鄞州区）把一个圆柱体木料横切成两个圆柱（图1)，表面积增加了25.122cm，纵切成两个半圆柱（图2)，则表面积增加了2cm．48cm，原来这个圆柱的体积是3【分析】根据图1的方式切成两个圆柱，表面积就会增加225.12cm，表面积增加的是两个切面的面积，每个切面的面积与原来圆柱的底面积相等，据此可以求出圆柱的底面半径，进而求出圆柱的高，再根据圆柱的体积公式解答；图2沿直径方向切成两个半圆柱，切面是两个长方形，长等于圆柱的高，宽等于圆柱的底面直径，表面积增加的48平方厘米，是两个切面的面积，由此可以求出一个切面的面积．【解答】解：圆柱的底面积：25.12212.56÷=（平方厘米），底面半径的平方：12.56 3.144÷=，因为2的平方是4，所以圆柱的底面半径是2厘米，圆柱的高：482(22)÷÷⨯=÷244=（厘米）6体积：2⨯⨯3.14263.1446=⨯⨯=（立方厘米）75.36答：这个圆柱的体积是75.36立方厘米．故答案为：75.36．【点评】此题解答关键是根据纵切、横切，求出圆柱的底面半径和高，再利用圆柱的体积公式解答．12．（2019•大安区）一根长方体木料，横截面是边长10厘米的正方形．从这根木料上截下6厘米长的一段，切削成一个最大的圆锥．圆锥的体积是2cm，约占截下这段长方体木料体积的%（百分号前面保留一位小数）．【分析】（1）如图要求这个圆锥的体积，需要知道这个圆锥的底面半径和高，这里高显然就是这个长方体的高6厘米，圆锥的底面应是这个边长为10厘米的正方形底面内最大的圆，正方形内最大圆的直径等于这个正方形的边长，由此可得这个底面半径是1025÷=厘米，由此即可利用圆锥的体积公式进行解答；（2）利用长方体的体积公式求得这段木料的体积，利用圆锥的体积÷这个长方体木料的体积即可解决问题．【解答】解：（1）根据分析可得： 1025÷=（厘米）， 213.14563⨯⨯⨯， 6.2825=⨯，157=（立方厘米），（2）157(10106)÷⨯⨯， 157600=÷， 0.262≈， 26.2%=，答：圆锥的体积是 157平方厘米，约占截下这段长方体木料体积的26.2%．故答案为：157；26.2．【点评】此题考查了圆锥和长方体的面积公式的灵活应用，这里根据正方形内最大圆的特点得出这个圆锥的底面半径是解决本题的关键．二．选一选（共7小题）13．（2019•青原区）一个大正方体如果拿出一个小方块后，它的表面积与原来的表面积比较( )A ．一样大B ．减少了C ．增大了D ．无法比较【分析】拿走一个小正方体，减少了三个面，但同时又增加了三个面，因此大正方体的表面积不变．【解答】解：因为拿走在顶点的一个小方块，减少了三个面的同时又增加了三个面，所以大正方体的表面积不变．故选：A ．【点评】解答此题的关键是：看组成大正方体表面积的面有没有变化．14．（2019•广州）一个长方体木块，长5分米，它有一组相对的面是正方形，其余4个面的面积和是40平方分米，则这个木块的体积是( )立方分米． A ．20或50B ．20或48C ．20【分析】根据题意可知：这个长方体的长是5分米，它有一组相对的面是正方形，也就是这个长方体的宽和高相等，其余4个面的面积和是40平方分米，由此可以可以求出一个侧面的面积，用一个侧面的面积除以长即可求出宽和高，再根据长方体的体积公式：V abh =，把数据代入公式解答．另一种情况，这个长方体的长是5分米，宽是5分米，那么高是40452÷÷=（分米），根据长方体的体积公式：V abh =，把数据代入公式解答【解答】解：第一种情况：这个长方体的长是5分米，宽和高多少2分米， 4045÷÷ 105=÷2=（分米）， 22520⨯⨯=（立方分米），答：这个木块的体积是20立方分米．第二种情况：这个长方体的长和宽都是5分米，高是2分米， 55250⨯⨯=（立方分米）；答：这个长方体的体积是50立方分米．故选：A ．【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用，关键是熟记公式．15．（2019•海安县）如图，把一个高为4厘米的圆柱切成若干等份，拼成一个近似的长方体，表面积增加了40平方厘米．圆柱的侧面积是( )平方厘米．A ．40B ．20C ．10D ．125.6【分析】把圆柱切拼成一个近似长方体，这个长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，长方体的表面积比圆柱的表面积增加了两个切面的面积．每个切面的长等于圆柱的高，切面的宽等于圆柱的底面半径．已知表面积增加了40平方厘米，据此求出底面半径：40245÷÷=厘米，再根据圆柱的侧面积公式：2S rh π=，把数据代入公式解答．【解答】解：圆柱的底面半径： 40245÷÷=（厘米） 2 3.1454⨯⨯⨯ 3.14104=⨯⨯ 125.6=（平方厘米）答：圆柱的侧面积是125.6平方厘米．故选：D ．【点评】此题主要考查圆柱侧面积公式的灵活运用，关键是求出圆柱的底面半径．16．（2019•杭州）如图所示，一个铁锥完全浸没在水中．若铁锥一半露出水面，水面高度下降7厘米，若铁锥全部露出，水面高度共下降()厘米．A．14B．10.5C．8D．无法计算【分析】因为容器的底面积不变，所以铁锥排开水的体积与高成正比例，由此只要求出浸入水中的铁锥的体积之比即可求出排开水的高度之比；因为铁锥露出水面一半时，浸在水中的圆锥的高与完全浸入水中时铁锥的高度之比是1:2，则浸入水中的铁锥的体积与完全浸入水中时铁锥的体积之比是1:8；所以浸在水中的体积与露在外部的体积之比是：1:7，设铁锥完全露出水面时，水面又下降x厘米，由此即可得出比例式求出x的值，再加上7厘米即可解答．【解答】解：根据圆锥的体积公式可得：把圆锥平行于底面，切成高度相等的两半时，得到的小圆锥的体积与原圆锥的体积之比是1:8；所以铁锥一半露出水面时，浸在水中的体积与露在外部的体积之比是1:7，设铁锥完全露出水面时，水面又下降x厘米，根据题意可得：x=，:71:7x=，77x=，1+=（厘米），718答：水面共下降8厘米．故选：C．【点评】解答此题的关键是利用圆锥的体积公式得出圆锥平行于底面切成高相等的两部分的体积之比，从而得出水面下降的高度之比．17．（2019春•旅顺口区期末）把9个棱长是10厘米的正方体堆放在墙角（如图），露在外面的面积是()厘米2．A．1500B．1600C．1700D．1800【分析】从正面看能看到6个小正方形的面，从上面看能看到5个小正方形的面，从右面看能看到6个小正方形的面，共看到65617⨯=平方厘米，所以露在外面++=（个)，每个小正方形的面积是：1010100的面积是100171700⨯=厘米2，据此解答．【解答】解：(1010)(656)⨯⨯++，10017=⨯，1700=（厘米2)，答：露在外面的面积是1700厘米2．故选：C．【点评】本题考查了从不同方向观察物体的三视图的灵活应用，关键是得出露在外面的小正方形面的个数．18．（2019•绵阳）小明拿了等底等高的圆锥和圆柱形容器各一个，他将圆柱形容器装满水后倒入圆锥形容器，当水全部倒满时，从圆锥形容器中溢出36.2毫升水．圆锥形容器内有水()毫升．A．36.2B．18.1C．54.3D．108.6【分析】因为等底等高的圆柱的体积是圆锥体积的3倍，所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的(31)-倍，根据已知一个数的几倍是多少，求这个数，用除法解答．【解答】解：36.2(31)÷-36.22=÷18.1=（毫升），答：圆锥形容器的容积是18.1毫升．故选：B．【点评】此题主要考查等底等高的圆柱与圆锥体积之间的关系及应用．19．（2019•益阳模拟）一个物体是由圆柱和圆锥黏合而成的（如图），如果把圆柱和圆锥重新分开，表面积就增加了250.24cm，原来这个物体的体积是()A．3200.96cm B．3226.08cm C．3301.44cm D．3401.92cm【分析】根据题意可知：如果把圆柱和圆锥重新分开，表面积就增加了50.24平方厘米，表面积增加的两个底面的面积，由此可以求出底面积，再根据圆柱的体积公式：V sh=，圆锥的体积公式：13V sh=，把数据分别代入公式求出它们的体积和即可．【解答】解：50.24225.12÷=（平方厘米）125.12625.12(126)3⨯+⨯⨯-1150.7225.1263=+⨯⨯150.7250.24=+ 200.96=（立方厘米）答：原来这个物体的体积是200.96立方厘米．故选：A ．【点评】此题主要考查圆柱、圆锥体积公式的灵活运用，关键是熟记公式．三．计算题（共4小题）20．（2019•顺庆区）如图，ABCD 是直角梯形，以AB 为轴将梯形旋转一周，得到一个立体图形，这个立体图形的体积是多少立方厘米？【分析】根据题意可知：以AB 为轴旋转一周得到是一个上面是空心圆锥，下面是一个圆柱，圆锥和圆柱的底面半径都是2厘米，圆锥的高是(85)-厘米，圆柱的高是8厘米，根据圆锥的体积公式：13v sh =，圆柱的体积公式：v sh =，把数据分别代入公式求出圆柱与圆锥的体积差即可．【解答】解：如下图：2213.1428 3.142(85)3⨯⨯-⨯⨯⨯-13.1448 3.14433=⨯⨯-⨯⨯⨯100.4812.56=-87.92=（立方厘米），答：这个立体图形的体积是87.92立方厘米．【点评】解答求组合图形的体积，关键是考查分析图形是由哪几部分组成的，是求各部分的体积和，还是求各部分的体积差，再利用相应的体积公式解答．21．（2019•萧山区模拟）求组合图形的表面积和体积．（单位：分米）【分析】根据图形的特点可知：上面的圆柱与下面的长方体粘在一起，所以上面的圆柱只求侧面积加上下面长方体的表面积，它的体积等于圆柱与长方体的体积和．据此列式解答．【解答】解：3.1447(858252)2⨯⨯+⨯+⨯+⨯⨯=⨯+++⨯12.567(401610)2=+⨯87.92662=+87.92132=（平方分米）；219.922⨯÷⨯+⨯⨯3.14(42)7852=⨯⨯+3.144780=+87.9280167.92=（立方分米）；答：它的表面积是219.92平方分米，体积是167.92立方分米．【点评】此题主要考查圆柱、长方体的表面积公式、体积公式的灵活运用，关键是熟记公式．22．（2019•青岛）如图这只工具箱的下半部是棱长为20cm的正方体，上半部是圆柱体的一半．算出它的表面积和体积．【分析】根据圆柱和正方体的表面积的计算方法，它的表面积是上面圆柱的表面积的一半加上下面正方体的5个面的面积．再根据圆柱和正方体的体积公式，计算上面圆柱体积的一半加上下面正方体的体积即可．【解答】解：表面积：2⨯⨯÷+⨯+⨯⨯，3.1420202 3.14102020512562 3.141004005=÷+⨯+⨯，6283142000=++，2942=（平方厘米）；体积：23.1410202202020⨯⨯÷+⨯⨯，3.141002028000=⨯⨯÷+，31408000=+，11140=（立方厘米）；答：它的表面积是2942平方厘米，体积是11140立方厘米．【点评】解答求组合图形的表面积和体积，关键是分析图形是由哪几部分组成，然后根据它们的表面积公式和体积公式进行解答．23．（2019•成都）如图，将三个高都是1米，底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体．①求这个物体的体积？②求这个物体的表面积？【分析】由题意可知：这个物体的体积就等于3个圆柱的体积之和，利用圆柱的体积公式即可得解；这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积，根据公式计算即可．【解答】解：（1）2223.14(1.510.5)1⨯++⨯，3.14(2.2510.25)=⨯++，3.14 3.5=⨯，10.99=（立方米），答：这个物体的体积是10.99立方米．（2）大圆柱的表面积：23.14 1.522 3.14 1.51⨯⨯+⨯⨯⨯，14.139.42=+，23.55=（平方米），中圆柱侧面积：2 3.1411 6.28⨯⨯⨯=（平方米），小圆柱侧面积：2 3.140.51 3.14⨯⨯⨯=（平方米），这个物体的表面积：23.55 6.28 3.1432.97++=（平方米）；答：这个物体的表面积是32.97平方米．【点评】此题主要考查圆柱的体积、侧面积、表面积公式及其计算．四．走进生活，解决问题（共8小题）24．把一个长12cm、宽6cm、高9cm的长方体木块锯成两个相同的小长方体木块．这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了多少平方厘米？（请你将几种情况都写出来）【分析】把一个长方体截成两个长方体，只锯一次，增加两个横截面，（1）切割时，平行于126⨯面的面积，由此即可解决问题；⨯面切割，这样切割后，就增加了2个126（2）切割时，平行于129⨯面的面积，由此即可解决问题；⨯面切割，这样切割后，就增加了2个129（3）切割时，平行于96⨯面的面积，由此即可解决问题．⨯面切割，这样切割后，就增加了2个96【解答】解：（1）1262⨯⨯722=⨯=（平方厘米）144答：这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了144平方厘米．（2）1292⨯⨯=⨯1082=（平方厘米）216答：这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了216平方厘米．（3）962⨯⨯=⨯542=（平方厘米）108答：这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了108平方厘米．【点评】本题考查了长方体切割后的图形的表面积计算，根据长方体切割小长方体的方法，明确表面积增加的2个面是几⨯几的面是解决本题的关键．25．（2019•深圳校级模拟）把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体，拼成一个大长方体，这个大长方体的表面积最少是多少？【分析】根据两个长方体拼组成大长方体的方法，拼在一起的面越小，那么拼组后的大长方体的表面积就越大，反之，拼组后的表面积就越小；所以要使拼成的一个大长方体的表面积最小，只要把两个大面(97)⨯拼在一起，然后用两个小长方体的表面积之和减去减少的面积解答即可．【解答】解：(979474)22972⨯+⨯+⨯⨯⨯-⨯⨯，12722126=⨯⨯-，508126=-，382=（平方厘米）；答：大长方体的表面积最小是382平方厘米．【点评】解决本题的关键是明确拼组后的长方体的表面积等于这两个小长方体的表面积之和-减少的两个面的面积．26．（2019•龙海市）一个长方体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是多少立方厘米？【分析】根据长方体的特征，相对的面面积相等，从下部和上部分别截去高为3厘米和2厘米的长方体后，表面积减少了120平方厘米，减少的只是前后左右的侧面积，因为截去两部分后又露出两个底面；又因为剩下部分是正方体，因此减少部分（上+下）的4个面的面积相等，因此求出一个面的面积，120430÷=（平方厘米），再除以上下部分的高就可以求出剩下部分正方体的棱长；由此解答．【解答】解：1204(23)3056÷÷+=÷=（厘米）；66(65)3611396⨯⨯+=⨯=（立方厘米）；答：原来长方体的体积是396立方厘米．【点评】此题主要考查长方体的体积计算，解答的关键是理解表面积减少的只是侧面积，只要求出剩下部分正方体的棱长，再利用长方体的体积公式解答即可．27．（2019春•南阳期中）如图，在密封的容器中装有一些水，水面距底部的高度是10cm．如果将这个容器倒过来，你能求出这时水面距底部的高度是多少厘米吗？【分析】因为等底等高的圆锥的体积是圆柱体积的13，下面圆锥的高是6厘米，把容器倒过来，水面在圆柱容器中的高是2厘米，再加上原来圆柱中水的高(106)-厘米，即可求出这时水面距底部的高度．据此解答．【解答】解：高6厘米的圆锥容器中水倒入等底的圆柱容器中高是632÷=（厘米）+-2(106)=+24=（厘米），6答：如果将这个容器倒过来，这时水面距底部的高度是6厘米．【点评】此题主要考查等底等高的圆柱和圆锥体积关系的灵活运用．28．有大、中、小三个正方体水池，它们的棱长分别是6米、3米、2米，把两堆碎石分别沉落在中、小水池的水里，两个水池的水面分别升高了6厘米、4厘米，如果将这两堆碎石都沉没在大水池的水里，大水池的水面将升高多少厘米？（得数保留一位小数）【分析】有大、中、小三个正方形的水池，可知这三个水池底面都是正方形的，把两堆碎石分别沉没在中、小水池的水里，可知底面是不变的，只是水面会升高，升高那部分水的体积就是所放碎石的体积，利用长方体的体积公式=长⨯宽⨯高求出两堆碎石的体积；再将这两堆碎石都沉没在大水池的水里，底面变了，体积没变，水面升高的那部分水的体积就是两堆碎石的体积，那就用两堆碎石的体积除以大正方形水池的底面积即可求出．【解答】解：6米600=厘米3米300=厘米2米200=厘米放中池里碎石的体积：3003006540000⨯⨯=（立方厘米）放小池里碎石的体积：2002004160000⨯⨯=（立方厘米）两堆碎石总体积：540000160000700000+=（立方厘米）大水池的水面升高：700000(600600) 1.9÷⨯≈（厘米）答：大水池的水面将升高大约1.9厘米．【点评】此题主要是利用规则图形长方体的体积公式，来将不规则固体借助水的流动性变成规则的形状，底面是不变的，水面升高那部分体积就是不规则物体的体积，再利用体积公式解答即可．29．（2019•南阳模拟）六一儿童节，康康把一块橡皮泥揉成圆柱形，切成三块（如图1)，表面积增加了50.24平方厘米；切成四块（如图2)，表面积增加了48平方厘米．请你算算圆柱形橡皮泥的体积是多少立方厘米．【分析】如图：切成3块，增加4个面，表面积增加50.24平方厘米，由此求出一个底面的面积，进而求出圆柱的底面半径；纵切，表面积增加4以底面直径为长，以圆柱的高为宽的长方形的面积，由此求出一个长方形的面积，进而求出圆柱高，然后根据：圆柱的体积=底面积⨯高，由此解答即可．【解答】解：50.24412.56÷=（平方厘米）；假设圆柱的底面半径是r，则212.56rπ=，所以212.56 3.144r=÷=，所以2r=（厘米）；圆柱的高：484(22)÷÷⨯124=÷3=（厘米）体积为：23.1423⨯⨯12.563=⨯37.68=（立方厘米）答：圆柱形橡皮泥的体积是37.68立方厘米．【点评】此题考查了圆柱的知识，明确圆柱的切拼方法，是解答此题的关键．30．（2019•吉安县）一个酸奶瓶（如图），它的瓶身呈圆柱形（不包括瓶颈），容积是32.4立方厘米．当瓶子正放时，瓶内酸奶高为8厘米，瓶子倒放时，空余部分高为2厘米．请你算一算，瓶内酸奶体积是多少立方厘米？【分析】因为瓶子的容积不变，装的酸奶的体积不变，所以正放与倒放的空余部分的体积应相同．将正放与倒放的空余部分变化一下位置，可以看出酸奶瓶的容积应等于与它的底面积相等、高为8210+=厘米的圆柱的体积，因而酸奶占32.4立方厘米的810，由此算出瓶内酸奶的体积．【解答】解：8210+=（厘米），。

形状组合练习题

形状组合练习题本篇文章将为大家介绍一些有趣的形状组合练习题，旨在帮助读者提高对于不同形状的认知和组合能力，并培养解决问题的思维能力。

以下将逐个介绍每个练习题，并附上解答，读者可以先尝试解答后再对照参考答案。

练习题一：平面形状组合1.将一个正方形和一个矩形叠加放置在一起，形成一个新的图形，请画出这个新的图形。

解答：将正方形放置在矩形的一边，使得它们共享相同的一条边，最后连成一边。

如下图所示：[正方形图片] + [矩形图片] → [新图形]2.将一个圆形、一个三角形和一个梯形组合在一起，形成一个新的图形，请画出这个新的图形。

解答：将圆形放在中间，三角形和梯形分别放在圆形的两侧，彼此相连，形成新图形。

如下图所示：[圆形图片] + [三角形图片] + [梯形图片] → [新图形]练习题二：立体形状组合1.将一个立方体和一个平面三角形组合在一起，形成一个新的图形，请画出这个新的图形。

解答：将立方体放置在平面三角形的一侧，使得它们共享相同的一条边，最后连成一边。

如下图所示：[立方体图片] + [平面三角形图片] → [新图形]2.将一个圆柱体和一个正方体组合在一起，形成一个新的图形，请画出这个新的图形。

解答：将圆柱体放在正方体的一侧，使得它们共享相同的一条侧面，最后连成一面。

如下图所示：[圆柱体图片] + [正方体图片] → [新图形]练习题三：形状创意组合1.请使用至少三个不同的平面形状组合在一起，形成一个新的图形，请描述并画出这个新的图形。

解答：例如，我们可以使用一个正方形、一个矩形和一个圆形组合在一起，形成一个新的图形。

将圆形放在正方形的一侧，正方形和矩形共享一条边，最后连成一面。

如下图所示：[正方形图片] + [圆形图片] + [矩形图片] → [新图形]2.请使用至少三个不同的立体形状组合在一起，形成一个新的图形，请描述并画出这个新的图形。

解答：例如，我们可以使用一个立方体、一个圆柱体和一个平面三角形组合在一起，形成一个新的图形。

立体图形练习题

立体图形练习题一长方体与正方体例1 有一个长方体，它的底面是一个正方形，它的表面积是190平方厘米，如果用一个平行于底面的平面将它截成两个长方体，则两个长方体表面积的和为240平方厘米，求原来长方体的体积．例2如下图，一个边长为3a厘米的正方体，分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体（都和对面打通）．如果这个镂空的物体的表面积为2592平方厘米，试求正方形截口的边长．例3有一些相同尺寸的正方体积木，准备在积木的各面上粘贴游戏所需的字母和数目字．但全部积木的表面总面积不够用，还需增加一倍，请你想办法，在不另添积木的情况下，把积木的各面面积的总和增加一倍．例4 有大、中、小三个正方形水池，它们的内边长分别为4米、3米、2米，把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4厘米和11厘米．如果将这两堆碎石都沉没在大水池中，大水池水面将升高多少厘米？例5 下图是正方体的展开图之一，当用它组成立方体时，图中的哪一边与带★记号的边相接触呢？例6 下图是正方体的11种展开图和2种伪装图（即它们不是正方体的展开图）．请你指出伪装图是哪两个？例7 如下面的各图中均有若干个六面体，每小题图中的几个六面体上A、B、C、D、E、F六个字母的排列顺序完全相同（即每个小题中六面体上刻字母的方式是完全一样的）试判断各小题的图中A、B、C三个字母的对面依次是哪几个字母？例8有一块正方体的蛋糕．用刀子将它一刀切成两半，为了使切口成正六边形，应该怎样切呢？模拟训练一、填空题：1．一块矩形纸板，长8厘米，宽6厘米，把它折成底面为正方形的长方体的侧面，则这个长方体的底面面积为______平方厘米．2．有一个棱长为6厘米的正方体木块，如果把它锯成棱长是2厘米的正方体若干块，表面积增加了______平方厘米．3．把一根2米长的方木锯成两段，表面积增加 288平方厘米，原来这根方木的体积是______立方厘米．4．把棱长为a厘米的两个正方体拼成一个长方体，长方体的表面积是5．把棱长1厘米的正方体2100个，堆成一个实心的长方体，它的高是10厘米，长和宽都大于高，这个长方体的长与宽的和是______厘米．二、选择题：1．一个正方体的体积是343立方厘米，它的全面积是__平方厘米．（A）42 （B）196 （C）294 （D）3922．把棱长为3分米的正方体锯成两个长方体，这两个长方体表面积的和是______平方分米．（A）54 （B）72 （C）108 （D）以上都不对3．如下图，一个木制的正方体的棱长为2分米，每个面的正中有一个正方形的孔通到对边，边长为1分米，孔的各棱平行于正方体相对的棱，那么这个镂空几何体的总表面积的平方分米数是____．（A）24 （B）30 （C）36 （D）424．如下页图立方体的每个角都被切下去（图中仅画了两个）．问所得到的几何体有__条棱？（A）24（B）30 （C）36 （D）425．立方体各面上的数字是连续的整数（如图）．如果每对对面上的两个数的和相等，那么，这三对数的和是__．（A）75 （B）76 （C）78 （D）81三、解答题：1．一个木盒从外面量长10厘米，宽8厘米，高5厘米，木板厚1厘米．问①做这个木盒最少需要1厘米厚的木板多少平方厘米？②这个木盒的容积是多少立方厘米？2．将一个长9厘米，宽8厘米，高3厘米的长方体木块锯成若干个小正方体（锯痕宽度忽略不计），然后再拼成一个大正方体，求这个大正方体的表面积．3．一个边长为6厘米的正方体铁盒装满了水，将水倒入一个长9厘米，宽8厘米的长方形水槽内，若铁皮厚度不计，求水深．4．把19个边长为2厘米的正方体重叠起来，作成如下图那样的组合形体，求这个组合形体的表面积．5．将表面积为54平方厘米、96平方厘米、150平方厘米的三个铁质正方体熔铸成一个大正方体（不计损耗）．求这个大正方体的体积和表面积．6．用字母标出一个正方体的各面，下图中是三个不同方位的这一个正方体，问字母A、B、C的对面是什么字母？7．下图是一个正方体及其两个展开图．这个正方体还有九种不同的展开图（下图），请把这九个展开图填上相应的数字（注意数字的方向）．8．下左图中的立方体，被两个平面所截，你能在这个正方体的展开图中画出相应的截线吗？（下右图）9．在下页图所示的12个展开图中，哪些可以做成没有顶盖的五个面的小方盒？10．下页图是一张3×5的方格纸，在保持每个方格完整的条件下，将它剪成三部分，使每部分都可以折成一个棱长为1的没有顶盖的小方盒，怎样剪？二、立体图形计算例1 下图是由18个边长为1厘米的小正方体拼成的，求它的表面积．例2 一个圆柱体底面周长和高相等．如果高缩短了2厘米，表面积就减少12.56平方厘米．求这个圆柱体的表面积．例3 一个正方体形状的木块，棱长为1米．若沿正方体的三个方向分别锯成3份、4份和5份，如下图，共得到大大小小的长方体60块，这60块长方体的表面积的和是多少平方米？例4一个酒精瓶，它的瓶身呈圆柱形（不包括瓶颈），如下图．已知它的容积为26.4π立方厘米．当瓶子正放时，瓶内的酒精的液面高为6厘米．瓶子倒放时，空余部分的高为2厘米．问：瓶内酒精的体积是多少立方厘米？合多少升？例5一个稻谷囤，上面是圆锥体，下面是圆柱体（如下图）．圆柱的底面周长是9.42米，高2米，圆锥的高是0.6米．求这个粮囤的体积是多少立方米？例6 皮球掉在一个盛有水的圆柱形水桶中．皮球的直径为12厘米，水桶底面直径为60厘米．皮球有2/3的体积浸在水中（下图）．问皮球掉进水中后，水桶的水面升高多少厘米？例7 下图所示为一个棱长6厘米的正方体，从正方体的底面向内挖去一个最大的圆锥体，求剩下的体积是原正方体的百分之几？（保留一位小数）．例8 有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的直孔，如下图．圆孔的直径是4厘米，孔深5厘米．如果将这个零件接触空气部分涂上防锈漆，一共需涂多少平方厘米？模拟训练1．一根圆柱形钢材，沿底面直径割开成两个相等的半圆柱体，如下图．已知一个剖面的面积是960平方厘米，半圆柱的体积是3014.4立方厘米．求原来钢材的体积和侧面积．2．在一只底面直径是40厘米的圆柱形盛水缸里，有一个直径是10厘米的圆锥形铸件完全浸于水中．取出铸件后，缸里的水下降0.5厘米，求铸件的高．3．在边长为4厘米的正方体木块的每个面中心打一个边与正方体的边平行的洞．洞口是边长为1厘米的正方形，洞深1厘米（如下图）．求挖洞后木块的表面积和体积．4．如下图所示的一个零件，中间一段是高为10厘米，底面半径为2厘米圆柱体，上端是一个半球体，下端是一个圆锥，它的高是2厘米．求这个零件的体积．5．塑料制的三棱柱形的筒里装着水（如下页图（1）是这个筒的展开图，图中数字单位为厘米）．把这个筒的A面作为底面，放在水平桌面上，水面的高度是2厘米（如下页图（2））．问①若把B面作为底面，放在水平的桌面上，水面的高度是多少厘米？②若把C面作为底面，放在水平桌面上，水面高度是多少厘米？为4分米、3分米、2分米．把两堆碎石分别沉浸在中、小水缸的水中，两个水池的水面分别升高了4厘米和11厘米．如果将这两堆碎石都沉浸在大水缸中，大水缸中水面将升高多少厘米？7．如下图是一个正方体，H、G、F分别为棱AB、AD、AE的中点．现沿三角形GFH的面锯掉一个角，问锯掉这块的体积是整个立方体体积的几分之几？（提示：V棱柱＝S·h，S为底面积，h为高．可见棱锥的体积是等底等高的棱柱体积的三分之一．）三．旋转体例1 甲、乙两个圆柱形水桶，容积一样大，甲桶底圆半径是乙桶的1.5倍，乙桶比甲桶高25厘米，求甲、乙两桶的高度．例2 一块正方形薄铁板的边长是22厘米，以它的一个顶点为圆心，边长为半径画弧，沿弧剪下一个扇形，用这块扇形铁板围成一个圆锥筒，求它的容积（结果取整数部分）．为2米，圆锥的高为1米，这堆谷重约多少公斤（谷的比重是每立方米重720公斤，结果取整数部分）？例4 有一个倒圆锥形的容器，它的底面半径是5厘米，高是10厘米，再把石子全部拿出来，求此时容器内水面的高度．例5 有一草垛，如下图，上部是圆锥形，下部是圆台形，圆锥的高为0．7米，底面圆周长为6.28米，圆台的高为1.5米，下底面周长为4.71米．如果每立方米草约重150公斤，求这垛草的重量（结果取整数部分）．例6 如下右图，在长为35厘米的圆筒形管子的横截面上，最长直线段为20厘米，求这个管子的体积．模拟训练一、填空题：1．一个圆柱体的侧面积是m平方厘米，底面半径是2厘米，它的体积是___立方厘米．2．一个圆锥的母线长为8厘米，底面直径为12厘米，那么这个圆锥的侧面积等于____平方厘米．3．圆台的上、下底面半径分别为2厘米和5厘米，母线长为4厘米，那么这个圆台的表面积等于____．4．用半径为2厘米的半圆形铁皮卷成的圆锥形容器，则它的底面半径为____厘米，容积是____立方厘米．5．一个圆锥的高是10厘米，侧面展开图是半圆，那么圆锥的侧面积等于____．二、选择题：1．一个圆柱体高80厘米，侧面积为1.5平方米，它的全面积是____（精确到0.01平方米）．（A）1.78平方米（B）2.06平方米（C）3.74平方米（D）5.25平方米2．圆锥的侧面积为427．2平方厘米，母线长为17厘米，那么圆锥的高是___（精确到0．01厘米）．（A） 5.75厘米（B）15厘米（C）16.52厘米（D）5.25厘米3．圆柱的一个底面积是S，侧面展开图是一个正方形，那么这个圆柱的侧面积是___．（A）4πS（B）2πS4．母线和底面直径相等的圆锥叫做等边圆锥，一个等边圆锥的底面半径是5厘米，那么它的侧面积是_______．（A）25平方厘米（B）50π平方厘米（C）100π平方厘米（D）250π平方厘米5．把一个底面半径是1厘米的圆柱体侧面展开，得到一个正方形，这个圆柱体的体积是立方厘米（取r＝3.14）．（A） 1 （B） 3.14（C） 3.14×3.14 （D） 3.14×6.286．长、宽分别为6寸、4寸的长方形铁片，把它围成一个圆桶，另加一个底，形成圆柱形的杯子，这个杯子的最大容积是____．三、解答题：1．一个底面直径是20厘米的圆柱形容器中装着水，水中放置一个底面半径是9厘米，高20厘米的铁质圆锥体，当圆锥从桶中取出后，桶内的水将下降多少厘米？2．在一只底面半径为20厘米的圆柱形小桶里，有一半径为10厘米的圆柱形钢材浸在水中．当钢材从桶里取出后，桶里的水下降了3厘米．求这段钢材的长．3．有A、B两个容器，如下页图，先将A容器注满水，然后倒入B 容器，求B容器的水深．（单位：厘米）4．从一个底面半径为3厘米，高为4厘米的圆柱中，挖去一个以圆柱上底面为底，下底面中心为顶点的圆锥，得到一个如下图的几何体．求这个几何体的表面积和体积．5．圆锥形烟囱帽的底的半径是40厘米，高是30厘米，计算它的侧面面积．若烟囱表面要涂油漆，已知每平方米需要油漆150克，问需油漆多少克？6．一个圆台的母线长为25厘米，而两个底面半径之比为1：3，已知圆台的侧面积等于1000π平方厘米，求这个圆台的全面积．7．把一条导线以螺旋状绕在圆柱管上，绕成十圈，圆柱管的外圆周长4厘米，导线的两端点位于圆柱的同一条母线上，每线长（两端点之间的距离）为9厘米．试求导线的长度．8．在长为1米的圆筒形管子的横截面上，最长直线段为12厘米，求此管子的体积．9．如下页图，长方形纸片ABCD中，AB＝3厘米，BC＝4厘米，①如果以BC为底边，折成一个底面为正方形的长方体，加盖后其体积为V1；如果以AB为底边，同样折成一个长方体，其体积为V2，求V1∶V2．②如果以BC为底边，把纸卷成一个圆柱，其体积为V3；如果以AB 为底边，把纸片卷成一个圆柱，其体积为V4，求V3∶V4（取π＝3.14）．③这四个不同形状的形体，加盖后其表面积之比又分别是多少（即求S1∶S2和S3∶S4）？10．一个几何体如下图，求它的表面积．。

立体图形竞赛练习题

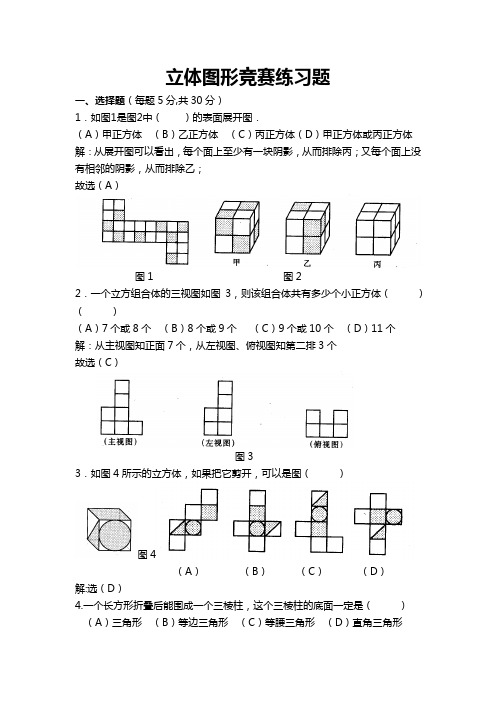
立体图形竞赛练习题一、选择题（每题5分,共30分）1．如图1是图2中（）的表面展开图．（A）甲正方体（B）乙正方体（C）丙正方体（D）甲正方体或丙正方体解：从展开图可以看出，每个面上至少有一块阴影，从而排除丙；又每个面上没有相邻的阴影，从而排除乙；故选（A）图1 图22．一个立方组合体的三视图如图3，则该组合体共有多少个小正方体（）（）（A）7个或8个（B）8个或9个（C）9个或10个（D）11个解：从主视图知正面7个，从左视图、俯视图知第二排3个故选（C）图33．如图4所示的立方体，如果把它剪开，可以是图（）图4（A）（B）（C）（D）解:选（D）4.一个长方形折叠后能围成一个三棱柱，这个三棱柱的底面一定是（）（A）三角形（B）等边三角形（C）等腰三角形（D）直角三角形解：选（A ）5．一个画家有14个棱长为dm 1的正方体,他在地面上把它们摆成如图5所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )(A) 233dm (B) 224dm (C) 221dm (D) 242dm图5 图6 图7解：:这个模型的主视图如图6,它的面积是26dm ,其它的三个侧面的视图和它一样,故侧面积是222446dm dm =⨯; 这个模型的俯视图如图7, 它的面积是2933dm dm dm =⨯.所以涂上颜色的总面积是22233924dm dm dm =+.故选(A).二、填空题（每题5分,共30分）6．如图8，是标有1，2，3，4，5，6六个数字的一个正方体的三种不同摆法。

问三个正方体朝左的一面的数字之和是______. 图8解：有三个正方体中的已知数字可判断数字1与4相对，2与6相对，3与5相对，故三个正方体朝左的一面的数字和为5+1+4=107．如图9，是一个大正立方体，把它的每个面都划分为9个小正方形，这个大正方体中共有多少个正方体。

解：这个大正方体中包含棱长分别为1，2，3的三类正方体，它们的个数分别为27，8，1，所以这个大正方体所包含的正方体的个数是27+8+1=36 图98．小川用正方体木块搭建大楼，图10展示了该大楼从前面和左面看到的形状．为塔建这座大楼，需要正方体木块的最大数量是______，最小数量是______.图10解：最大数量是28，最小数量是179．六个立方体的可见部分如图11，图12是其中一个立方体的侧面展开图，那么它是______的侧面展开图。

小升初专项练习几何图形圆与立体图形

小升初专项练习几何图形圆与立体图形引言：立体图形是近两年来小生初的考察新热点，由于立体图形考察学生的空间想象能力，更反映学生的本身潜能，所以越来越受到学校的欢迎；而另一方面，初中很多知识点都是建立在空间问题上，所以可以说学校考察立体也是为初中选拔知识链接性好的学生。

【典型题目解析】：一、圆与扇形阴影部分的面积【例1】．（★★★）在图中，一个圆的圆心是O，半径r＝9厘米，∠1＝∠2＝15º。

那么阴影部分的面积是多少平方厘米？（π取3.14.）【例2】、（★★★★）如图，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径都是1。

求阴影部分的面积。

【例3】（★★★）草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊（见左下图）。

问：这只羊能够活动的范围有多大？【例4】求图中阴影部分的面积（单位：厘米）。

【例5】求图中阴影部分的面积（单位：厘米）。

【分析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。

从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。

3.14×42×1/4－4×4÷2÷2＝8.56（平方厘米）【例6】如图19－10所示，两圆半径都是1厘米，且图中两个阴影部分的面积相等。

求O的面积。

长方形ABO1【分析】因为两圆的半径相等，所以两个扇形中的空白部分相等。

又因为图中两个阴影部分的面积相等，所以扇形的面积等于长方形面积的一半（如图19－10右图所示）。

所以3.14×12×1/4×2＝1.57（平方厘米）【例7】如图所示，图中圆的直径AB是4厘米，平行四边形ABCD的面积是7平方厘米，∠ABC＝30度，求阴影部分的面积（得数保留两位小数）。

【分析】阴影部分的面积等于平行四边形的面积减去扇形AOC的面积，再减去三角形BOC的面积。

半径：4÷2＝2（厘米）扇形的圆心角：180－（180－30×2）＝60（度）扇形的面积：2×2×3.14×60/360≈2.09（平方厘米）三角形BOC的面积：7÷2÷2＝1.75（平方厘米）7－（2.09+1.75）＝3.16（平方厘米）【例8】如图所示，求图中阴影部分的面积。