Chap08_形状表示与描述(下)
cchap数据类型和表达式PPT教学课件

第25页/共46页
4.C++运算符
见书:P30 与C的 使用方法大致相同
C++运算符包括:
• 算术运算 • 关系运算 • 逻辑运算 • 位运算 • 赋值运算符 • 条件运算符
• 引用运算符和地址运算符(&) • 求字节数运算符 • 强制转换运算符 • 成员运算符 • 指向成员的运算符 • 下标运算符 • 其他(如函数调用运算符())
方法1:
#define PI 3.1415926
//在程序中凡是出现PI的均用3.1415926替 代
或者
方法2:
const float i=3.1415926; //将变量pi
定义为常量
17
第17页/共46页
2.常量
#include<iostream> using namespace std; #define PI 3.14159
{ void main(void)
int a = 65; {
char a,b;
char b = 65;
a=‘A’; //输入ASCII 码
cout<<a<<“\n”;
b=65; //输入十进制数
cout<<b<<“\n”;
cout<<"a="<<a<<endl;
} a,b在内存中的表示均是相同的
cout<<"b="<<b<<endl;
7
第7页/共46页
2.常量
(2)浮点型常量
十进制浮点数表示: 尾数部分的绝对值
• 定点表示
chap 系统详细设计中的交互建模(共9张PPT)
消 组息成传元递 素: :一 对–个 象对 、协象 消调 息作用、图另 生一 命除个 线对 、了象 激的 活体行 期为 (现操 点作 )对象间的关联关系以外,还可以显示对象间的消 协静作态图 建(模登的录目、的学:息生获管得传理描递)述系(统模对型的象静态中结构的和各某个组个成方元素法之间被的关哪系,个也就对是模象型内访部问组成)特性,及其是相互对之间对的关象系 图的扩 展(或称动态对象图) 顺序图侧重时间观念,协作图侧重关联关系,协作图能对复杂顺序图进行简化
和协作图 – 交互图主要用于定义软件系统如何实现特定功能,并能够按照时间流
显示用例的实现过程,包括:消息流中需要什么对象、对象相互发送 什么消息、什么角色启动消息流、消息按什么时序发送等
– 时序图强调消息时间顺序,协作图强调接收和发送消息对象的组织结 构
动态建模技术
对象之间进行交互时的消息
– 消息:指由一个对象发送并由另一个对象接收的已命名的对象, 其实就是对象间的通信,具体编程中就是对类中方法的调用
– 两者描述的其实是同一事物 – 协作图不能体现消息的先后顺序
协作图的UML表示
协作图
协作图的建模技术
– 步骤
• 设置交互的语境
• 识别对象在交互中扮演的角色
• 消息顺序 • 完善对消息的描述
Rose中对UML协作图的支持(BBS)
– 打开顺序图
– Broser->Create Collaboration Diagram
医学写作:形状与特征表示法

要求:学会⼈体器官、⾎液和细菌的形状和特征的描述。
本章要点: 1.表⽰形状的句型: 1)名词+be+shaped like +名词 表⽰某器官或物体的形状“象……,”或“呈……形”。
例:The heart is shaped like a cone. ⼼脏呈圆锥形。
2)名词+be +名词-shaped + 名词 表⽰某个器官或物体“是个……形状的器官(或物体)”。
例:The diaphragm is a dome-shaped organ. 膈是⼀个圆顶状的器官。
3)名词+be+a(n)+形容词+organ 也表⽰某器官或某物体“是……形状的器官或物体”。
例:The small intestine is a long, tubular organ. ⼩肠是长管形器官。
2.表⽰特征的句型: 名词+be+形容词 表⽰某器官或某物体“具有……特征(或作⽤)”。
例:Monocytes are phagocytic. 单核细胞具有吞噬作⽤。
Some tissues are elastic. ⼀些组织具有弹性。
3.⽤于⽐较和对照的连接词: 1)both…and… 例:Both erythrocytes and leucocytes are flexible. 红细胞和⽩细胞都具有伸缩性。
2)neither…nor… 例:Neither erythrocytes nor leucocytes are adhesive. 红细胞和⽩细胞没有粘着性。
3)but; whereas 例:Platelets are adhesive but/whereas erythrocytes are not. ⾎⼩板具有粘着性⽽红细胞则没有。
4)however; on the other hand 例:Leucocytes are phagocytic, erythrocytes, however/on the other hand, are not. ⽩细胞具有吞噬作⽤,⽽红细胞则没有。
图像处理课件06表示与描述

R 1
3
1 2 z
1
三阶矩
3 z zi m p zi
U p 2 zi
i 0 L 1
一致性
平均熵
e pzi log 2 pzi
i 0
Lபைடு நூலகம்1
例:基于直方图的纹理度量
3、纹理
统计方法2
令P为位置算子,并令A为一个k×k阶矩阵。矩阵元素 aij是由P指定的灰度值为zi的相对于灰度值为zj的 (zi,zj)对数。
平滑处理 多边形近似
5、骨架
一种表达平面区域结构形状的重要方法是把它简化成图 形。如通过细化算法得到区域的骨架。
一个区域的骨架可以用中轴变换(MAT)定义
5、骨架
细化算法反复删除区域的边界点,并受到如 下的约束条件限制: 不可删除端点 不可破坏连通性 不可造成对区域的过分侵蚀
5、骨架
区域的面积 区域的周长 区域的致密性
(周长)2/面积
灰度均值 灰度中值 最小和最大灰度 大于和小于均值的像素数
例:使用面积计算从图像中提取信息
提供区域内定居的人口数量
美洲的红外图像
2、拓扑描绘子
拓扑特性对于图像平面区域的整体描述是很有用处的。 拓扑描绘子由区域内孔洞数来定义
有两个孔的区域
2、多边形近似
最小周长多边形
2、多边形近似
聚合技术
聚合技术:沿着边界线寻找聚合点,当拟合 直线上的点和原边界点的最小平方误差超 过一个预先设置的门限,这时就将点聚合。
y y
' i i i
2
T
chap_8_7-8
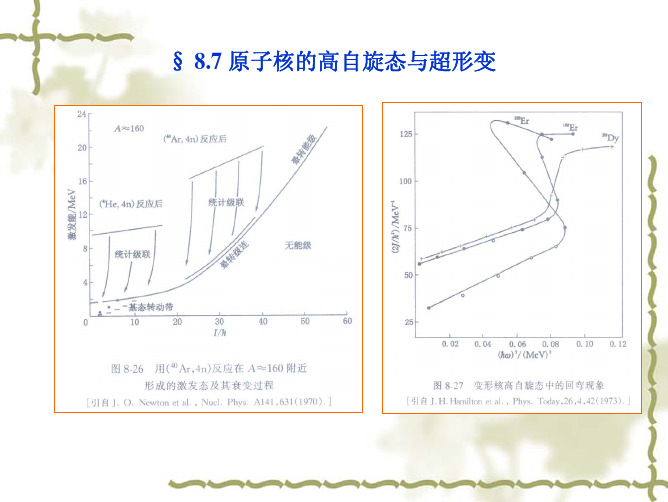
为一个小的夸克口袋加上它周围的介子云,这样可以描写 核力的介子交换理论和描写夸克-胶子相互作用的量子色 动力学在不同的范围适用。 天然存在的原子核都只包含质子和中子这两种重子,而它 们都是由最轻的两种夸克-上夸克(up)和下夸克(down)组 成的。现在已经发现,还有其他四种夸克可以在实验中产 生 , 他 们 是 粲 (charm) 、 奇 异 (strange) 、 顶 (top) 和 底 (bottom)夸克。目前人们对含有奇异夸克的物质已开始进 行深入的研究。含有奇异夸克的重子被称为超子,含有超 子的原子核称为超核。由于新的自由度(奇异量子数)的 引入,奇异核相对于普通核有许多不同的性质。
作为结构函数的另一表达。当电子波长远小于核子尺度时,实验数据分析发现结构函 2 数基本上与 Q 无关。这表明核子内部有点状的子结构。进一步的分析还得出这些点状 成分的自旋为 1/2。这为后来的强子的夸克模型提供了有力的证据。 实验发现核的环境有可能改变核子的内部状态。核子的结构函数与核环境有很大的 关系,这就是著名的 EMC 效应,是欧洲的 EMC 合作组在 1983 年首次发现的。核越重, EMC 效应越明显。理论上对 EMC 效应进行了多方面的解释,典型的如:不同核子中的夸 克间的相互作用;核介质中核子体积的“膨胀” ;核子聚合成双核子、三核子等多夸克 态;束缚态下核子有效质量的减小;费米运动的影响等等。但直到现在,仍然没有令 人满意的结论。
92 42
nq = 4(
gq 24π h c
2 3 3
) Pq
1 4
3 4
-3
(8.8 − 16)
而核子数密度 nB=nq/3。取 Pq = B = 235 MeV⋅fm ,得转变点核子数密度: nc=0.72 fm-3 (8.8 - 17) -3 在通常的原子核中 n0=0.14 fm ,因此,在温度为 0 时,实现夸克-胶子等离子体的 核物质密度是正常情况的大约 5 倍。这只是最粗略的估算。采用非微扰的 QCD 格点规 范理论计算的结果,转变密度 nc 更大一些。 以上是两种极端的情况。一般地,转变温度和密度介于上述情况之间,大致如图 8 -32 所示。
第4章 图形的表示与数据结构2
4.4 实体模型—规则实体的表示
13
–优点 • 简单,可以表示任何物体 • 容易实现物体间的交、并、差集合运算 • 容易计算物体的整体性质,如体积等
4.4 实体模型—规则实体的表示
14
–缺点 • 占用大量的存储空间,如 1024*1024*1024 = 1G bits • 物体的边界面没有显式的解析表达式, 不适于图形显示 • 对物体进行几何变换困难 • 物体表示不精确
4.4 实体模型—规则实体的表示
– 8叉树的表示应用于三维形体 的分解,它对形体的外接立 方体的进行前后、左右、上 下等分8个小立方体,如果小 立方体单元中该形体为满或 为空,表示该立方体完全在 形体中或完全不在形体中, 则其停止分解;对部分形体 占有的小立方体需进一步分 解为8个子立方体,直至所有 小立方体单元要么全部满, 要么全部空,或已分解到规 定的分解精度为止。
4.4 实体模型—规则实体的表示
15
• 4.4.1.2
第二种分解表示法—八叉树表示
–对空间位置枚举表示的空间分割方法作了改进: 均匀分割 自适应分割 –八叉树建立过程
• 八叉树的根节点对应整个物体空间 • 如果它完全被物体占据,将该节点标记为F(Full), 算法结束; • 如果它内部没有物体,将该节点标记为E(Empty), 算法结束; • 如果它被物体部分占据,将该节点标记为 B(Boundary),并将它分割成8个子立方体,对每一 个子立方体进行同样的处理
4.3 三维形体的表示
• 4.3.2 表面模型 – 使用一组包围物体内部的平面多边形来描述实体。
体
D V
面
A C 边
ABC
ABD
BCD
ACD
AB
BC
Chap06_形状表示与描述(下)

2008-11-2wangzhiming@ 30§6.3 基于区域的形状表示与描述 简单形状描述:面积、矩形度、细长度、方向、紧致度、等等; 图描述: 区域细化,得到骨架;区域分解成子区域,子区域由节点表示,节点的弧表示子区域的相邻关系;优点:平移、旋转、尺度不变,对形状微小变化不敏感,方便特征获取、理解与识别。
2008-11-2wangzhiming@ 31§6.3.1 简单的标量区域描述1、面积: 算法6.4: 在四叉树中计算面积1. 把所有的区域面积变量设为0,并确定四叉树的总深度H ;(256X256,H =8)2. 系统地搜索树。
如果在深度h 上的一个叶节点拥有非零标号,转3;3. 计算area[区域标号]=area[区域标号]+4(H-h) 4. 区域面积保留在变量area[区域标号]中。
2008-11-2wangzhiming@ 32§6.3.1 简单的标量区域描述(续)1、面积(续):区域由n个多边形顶点(i k,j k)来表示,面积为:2008-11-2wangzhiming@ 33算法6.5:从Freeman 4-连通链码表达中计算区域面积1. 把区域面积变量设为0,把起始点的纵坐标值赋予变量vertical_postion。
2. 对每个链码的元素(值0,1,2,3)执行:3. 如果所有的边界链元素都被处理过了,则区域面积被保存在变量area中。
3003011212322008-11-2wangzhiming@ 34§6.3.1 简单的标量区域描述(续) 2、欧拉数(Euler's number):描述了物体的一个简单的拓扑不变属性; 物体连通部分数目S 减去孔的数目N 。
2008-11-2wangzhiming@ 35§6.3.1 简单的标量区域描述(续) 3、投影(projection):2008-11-2wangzhiming@ 36§6.3.1 简单的标量区域描述(续) 4、离心率(Eccentricity):最长弦A 与垂直于A 的最长弦B 的长度比; 物体的主次轴长之比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012-10-25wangzhiming@ 28§8.3 基于区域的形状表示与描述 简单形状描述:面积、矩形度、细长度、方向、紧致度、等等; 图描述: 区域细化,得到骨架;区域分解成子区域,子区域由节点表示,节点的弧表示子区域的相邻关系;优点:平移、旋转、尺度不变,对形状微小变化不敏感,方便特征获取、理解与识别。
2012-10-25wangzhiming@ 29§8.3.1 简单的标量区域描述1、面积: 算法8.4: 在四叉树中计算面积1. 把所有的区域面积变量设为0,并确定四叉树的总深度H ;(256X256,H =8)2. 系统地搜索树。
如果在深度h 上的一个叶节点拥有非零标号,转3;3. 计算area[区域标号]=area[区域标号]+4(H-h) 4. 区域面积保留在变量area[区域标号]中。
2012-10-25wangzhiming@ 30§8.3.1 简单的标量区域描述(续) 区域由n 个多边形顶点(i k ,j k )来表示,面积为:2012-10-25wangzhiming@ 31算法8.5:从Freeman 4-连通链码表达中计算区域面积1. 把区域面积变量设为0,把起始点的纵坐标值赋予变量vertical_postion。
2. 对每个链码的元素(值0,1,2,3)执行:3. 如果所有的边界链元素都被处理过了,则区域面积被保存在变量area中。
3003011212322012-10-25wangzhiming@ 32§8.3.1 简单的标量区域描述(续) 2、欧拉数(Euler's number):描述了物体的一个简单的拓扑不变属性; 物体连通部分数目S 减去孔的数目N 。
NS −=ϑ2012-10-25wangzhiming@ 33§8.3.1 简单的标量区域描述(续) 3、投影(projection):图8.22 投影。
2012-10-25wangzhiming@ 34§8.3.1 简单的标量区域描述(续) 4、离心率(Eccentricity):最长弦A 与垂直于A 的最长弦B 的长度比; 物体的主次轴长之比。
§2012-10-25wangzhiming@ 36§8.3.1 简单的标量区域描述(续) 具有平移、旋转、尺度不变性。
图8.24 细长度: (a)包围矩形框给出可接收的结果, (b)包围矩形框无法代表细长度。
2012-10-25wangzhiming@ 37§8.3.1 简单的标量区域描述(续)6、矩形度(Rectangularity):区域面积与外接矩形面积之比的最大值(旋转搜索)。
具有平移、旋转、尺度不变性。
2012-10-25wangzhiming@ 38§8.3.1 简单的标量区域描述(续) 7、方向(Direction):对细长区域有意义;最小外接矩形的长边方向。
具有平移、尺度不变性。
∑∑−−=),()()(y x f y y x x qc p c pq μ2012-10-25wangzhiming@ 39§8.3.1 简单的标量区域描述(续) 8、紧致度(Compactness):独立于线性变换(平移、旋转、尺度)的通用形状描述。
图8.25 紧致度: (a)紧致形状, (b)非紧致形状。
2012-10-25wangzhiming@ 40§8.3.2 矩(p+q)阶统计矩;平移不变中心矩;尺度不变的尺度中心矩;归一化的无尺度中心矩;旋转、平移及尺度不变的矩特征; 放射不变的矩特征。
2012-10-25wangzhiming@ 41§8.3.3 凸包凸区域:区域内任意两点连线上所有的点都在区域内; 不是旋转不变量。
凸包(Convex hull):满足R ⊆H 的最小凸区域H 。
图8.26 凸包。
2012-10-25wangzhiming@ 42 算法8.6:区域凸包构建O(n 2) 1. 从上到下、从左到右找到具有最小行列坐标区域R 像素P 1,赋值P k =P 1,v =(0,-1)表示凸包的前一直线段的方向。
2. 以逆时针方向搜索区域边界,并对每个位于点P 1后的边界点P n 计算方向角φn (向量P k P n 角度)。
满足条件φn =min n φn 的点P q 是区域凸包的下一个元素(顶点)。
3. 赋值v =P k P q , P k =P q ;4. 重复步骤2~3直到P k =P 1。
2012-10-25wangzhiming@ 43§8.3.3 凸包(续)一种简单的凸包算法:Melkman 的凸包检测算法(1987);令待检测凸包的多边形为简单多边形P={v 1,v 2,…v n }。
对序列中的任意三点x,y,z ,δ函数定义为:图8.27 方向函数δ: (a) δ(x,y,z)=1;(b) δ(x,y,z)=0;(c) δ(x,y,z)=-1。
2012-10-25wangzhiming@ 44§8.3.3 凸包(续)图8.28 凸包检测: (a)前三个顶点A 、B 、C 形成一个三角形;(b)若下一个顶点D 位于当前凸包内,当前凸包不变;(c)若下一个顶点D 位于当前凸包外,则成为当前新的凸包ABCDA 的一个顶点;(d)在此情况下,必须从当前凸包中去掉顶点B 而新的凸包为ADCA 。
2012-10-25wangzhiming@ 45§8.3.3 凸包(续) 定义以下操作:Bottom (…,P1,P2,P3,….) Top2012-10-25wangzhiming@ 46算法8.7:简单多边形凸包检测O(n) 1. 初始化:2. 如果下一个顶点v 位于当前凸包H 内部,输入并检查下一个新的顶点;否则转步骤3和4;2012-10-25wangzhiming@ 47 3. 重新排列H 顶部的顶点: 4. 重新排列H底部的顶点:2012-10-25wangzhiming@ 48图8.29 凸包检测示例: (a)处理区域多边形ABCDEA, (b)输入和处理顶点D,(c)顶点D 成为当前凸包ADC 的一个新顶点, (d)输入和处理顶点E,E 没有成为当前凸包的一个新顶点, (e)结果为凸包DCAD 。
2012-10-25wangzhiming@ 49§8.3.3 凸包(续)第(1)步,设P={A,B,C,D,E},如图8.29 所示。
第一步产生的数据结构H 为:第(2)步,顶点D 加入(图8.29b):基于方向函数δ,这种情况下没有顶点加入。
第(3)步得到如下的凸包结果H :2012-10-25wangzhiming@ 50在第(4)步,图8.29c:返回第(2)点,顶点E 加入,图8.29d 。
2012-10-25wangzhiming@ 51§8.3.4 基于区域骨架的图表示 骨架:至少与两个分开的边界点具有相同的到区域边界的最小距离;构建骨架的方法: 细化:迭代地去除区域边界像素;从边界开始的波传播;从区域的距离变换图像中检测局部最大值;分析的方法。
2012-10-25wangzhiming@ 52算法8.8:通过细化提取骨架1. 令R 为区域像素的集合,H i (R)为它的4邻接内边界,H o (R)为外边界。
令S(R)为区域R 中部分像素集合:这些像素在8-连通下的所有邻居或来自H i (R)、或来自背景。
赋值R old =R ;2. 构建一个新的区域R new 为如下的进一步细化的结果:3. 如果R new = R old 赋,结束迭代并转步骤4;否则赋值R old = R new ,重复步骤2;4. R new 是骨架像素的集合,即区域R的骨架。
2012-10-25wangzhiming@ 53图8.31 细化得到的骨架(算法8.8)。
2012-10-25wangzhiming@ 54§8.3.4 基于区域骨架的图表示(续) 局限性:计算量较大; 对噪声和误差非常敏感。
图8.32 区域骨架; 边界上的微小变化可对骨架产生显著影响。
2012-10-25wangzhiming@ 55§8.3.4 基于区域骨架的图表示(续)图8.33 原图骨架2012-10-25wangzhiming@ 56§8.3.5 区域分解 区域分解:形状基元(Primitive)描述最低级别上的简单区域;图有多个基元节点组成; 弧描述了基元之间的相互关系; 分解步骤: 把区域分解成简单的子区域; 分析基元之间的关系。
2012-10-25wangzhiming@ 57§8.3.5 区域分解(续) 多边形区域的图节点:节点类型表示初等子区域或核;子区域顶点个数;子区域面积;子区域主轴方向; 子区域重心。
2012-10-25wangzhiming@ 58§8.3.5 区域分解(续)区域分解使用结构属性,结果为句法式的图描述。
图8.34 区域分解: (a)区域, (b)初等区域, (c)初等子区域及核, (d)分解图。
2012-10-25wangzhiming@ 59§8.4 形状类别期望:形状描述能很好地表示物体,突出类别间的差异; 允许类别内的形状变化而不影响分类; 实现: 在特征空间上的不同区域表示不同形状;定义形状原型,通过变换生成具体形状;一组标识点(边界或区域点),点分布模型。
2012-10-25wangzhiming@ 60§8.5 形状识别应用实例基于形状的检索安检中的违禁品检测工业零配件辅助设计 字符识别2012-10-25wangzhiming@ 61.tw/Retrieval results from user drawn 2D shapes2012-10-25wangzhiming@ 62S. Nercessian, K. Panetta, S. Agaian. Automatic Detection ofPotential Threat Objects in X-ray Luggage Scan Images, 2008 IEEE Conference on Technologies for Homeland Security, 504~509.违禁品检测2012-10-25wangzhiming@ 63工业零配件辅助设计卢章平、姚辉学. 零件形状特征的提取与智能识别,计算机辅助设计与图形学学报,2002,14(7): 641~645.2012-10-25wangzhiming@ 64字符识别张红云、苗夺谦、张东星, 基于主曲线的脱机手写数字结构特征分析及选取, 计算机研究与发展,2005,42(8): 1344~1349.2012-10-25wangzhiming@ 65小结1.区域标识:基于等价表的区域合并;2.基于轮廓的形状表示与描述:边界长度、曲率、弯曲能量、签名、弦分布;傅立叶描述子;3.基于区域的形状表示与描述:面积、欧拉数、投影、离心率、细长度、矩形度、方向、紧致度、统计矩;凸包、骨架;区域分解。
