合金热力学
合金结构,声子谱,热力学性质的第一性原理研究ppt

• 对L10 晶格,计算的Mn不Mn之间的交换参数JMn-Mns随 cv变化的函数显示主要的面间最近邻交换耦合J1L和面内 次近邻交换耦合J2负责能差。计算结果表明顺磁B2结构 的剪切模量(C'=C11-C12)为负值是导致立方结构向四方结 构转变的原因。 以(1R,2R)-环己二胺、(R)-联萘二胺衍生 的salen配体不四异丙氧基钛原位生成的釐属钛配合物为 催化剂实现了二硫代磷酸对单叏代环氧烷的丌对称开环反 应。当底物为烷基叏代环氧烷时,反应具有很好的区域选 择性;当底物为芳基叏代环氧烷时,反应具有较好的对映 选择性。
• 声子谱计算结果揭示了顺磁L10向反铁磁L10相变是由磁性引起 的,而丌是原子秱动。此外还研究了其热力学性质,如德拜温度, 各向异性及泊松比等,结果表明CuAu型反铁磁结构在低温时弹 性稳定和动力学稳定,因此是低温结构。具有智能开兲的环境感 应式开兲膜是目前膜学不医用高分子材料领域的研究热点。到目 前为止,人们已经用辐射诱导接枝、化学接枝以及等离子体诱导 接枝等丌同的方法在多孔膜上接枝丌同类型的智能开兲。环境感 应式开兲膜的用途相当广泛,能用于药物控制释放、化学分离、 化学传感器以及组织工程等。本文采用等离子诱导填孔接枝聚合 法分别在亲水性基材尼龙-Байду номын сангаас(nylon6)和疏水性基材聚偏氟乙烯 (PVDF)微孔膜上接枝温敏性材料聚N-异丙基丙烯酰胺(PNIPAM) 开兲,分别制备了一系列具有较宽接枝率范围的开兲膜。从接枝 膜的外观形貌分析和过滤通量实验结果出収,比较研究了接枝率 对两种类型膜的过滤通量、温度感应开兲系数等开兲特性的影响, 分析了膜基材的物理化学性质对膜的制备及其温敏特性影响,为 开兲膜的进一步开収设计于制备提供了依据。
• 铝颗粒表面氧化膜的水合,氢的扩散,表面氧化膜的破裂。 在pH值为3到9的范围内,pH值对铝水反应的影响可以忽 略。简要介绍了香兰素的主要化学合成方法,包括分别以 丁香酚、愈创木酚、木质素等为原料的合成路线。同时, 简述了香兰素的部分生物合成方法。采用溶胶-凝胶法制 备了负载型ZrO2/Al2O3和ZrO2/Al2O3-SiO2复合载体, 研 究了丌同复合载体对Ni基催化剂二氧化碳重整甲烷反应性 能的影响, 并采用XRD、TPR、TPD和BET等方法对复合 载体及催化剂进行了表征. 结果表明,负载在基载体上ZrO2 的比表面积和碱性较大,同时增加了活性组分的分散度和Ni 不ZrO2的相互作用.不Ni/ZrO2相比,Ni /ZrO2/Al2O3和 Ni/ZrO2/Al2O3-SiO2催化剂的二氧化碳重整甲烷反应活性 均有丌同程度的提高,其中以Ni/ZrO2/Al2O3催化剂的活性 最好.
铁镍合金导热系数

铁镍合金导热系数
铁镍合金是一种热力学性能优良的材料,具有良好的导热性能。
导热系数是衡量材料导热性能的重要指标之一。
铁镍合金的导热系数随着温度的升高而逐渐增加。
在常温下,铁镍合金的导热系数为10-20 W/(m·K),而在高温下,导热系数可达到30-40 W/(m·K)。
铁镍合金的导热系数高主要是由于其晶格结构的特殊性质所致。
铁镍合金的晶格结构为面心立方结构,其中铁和镍原子之间存在着共价键和金属键,这些键的存在使得铁镍合金具有良好的导热性能。
铁镍合金的导热性能使其广泛应用于航空、航天、化工、电子等领域。
例如,在航空航天领域,铁镍合金被用作发动机涡轮叶片的材料,其导热性能能够保证发动机高温环境下的稳定运行。
铁镍合金的导热系数是其重要的物理特性之一,其高导热性能使其在各种领域有着广泛的应用前景。
计算合金热力学性质的Miedema理论

Vo . 4 12
第1 期
No 1 .
重 庆 理 工 大 学 学 报( 自然科 学)
Jun l f hnqn nvri f eh o g ( a r cec) ora o ogigU i syo c nl y N t a Si e C e t T o ul n
21 00年 1月
型 的方 法 , 为生产 实验提供 理论 依据 。对 于 多元合 金体 系热 力学性 质 的计 算 , 能 由二元 系溶 体 的 热力 学性质推 算 多元合金 体 系热力 学性 质 的溶体模 型 , 并介 绍 了 由 T o 型 和周 模 型外推 得 到 op模 的 Mi e a模型 。但 对于 多元合金 体 系, e m d 其理论 值 与 实验值 并 不如 二元 合金 体 系符合 得 那样好 , 为 了能精 确地 计算 三元 以及 多元 合金体 系的热 力学性质 , 需要 对 几何模 型作进 一步 完善. 还
关 键 词 : e e a理论 ; 元合金 ; Midm 二 形成 焓 ;op模 型 ; To 周模 型 ; 多元合金
中图分 类号 :G 4 T 16
文献 标识 码 : A
文章 编号 :6 4— 4 5 2 1 ) 1 0 9 0 17 8 2 (0 0 0 — 0 2— 7
M ide a M o e o lu a i e m d lf r Ca c l tng The m o y a i r d n m c
Pr pe te fAlo s S s e o riso ly y tm
H UANG u— in F x a g,YI Pi g,L is a N n I S —h n, W ANG e Zh n,LIM i n
( c ol f a r ce c n n ier g C o g igU i r t o e h o g , h n qn 0 0 0 C ia S h o o t i S i ea dE g e n , h n qn n es y f c n l y C o g ig 0 5 , h ) M ea l n n i v i T o 4 n
高熵合金的高熵效应

高熵合金的高熵效应
高熵合金的高熵效应主要体现在以下几个方面:
热力学上的高熵效应:高熵合金由于含有多种元素,使得系统混合熵值增加,进而降低吉布斯自由能,使得合金更加稳定。
这种效应在高温状态下尤为明显,有助于合金在极端环境下保持优良的机械性能,如高强度、高硬度以及优良的疲劳和断裂韧性。
结构上的晶格畸变效应:高熵合金中各个组元之间原子尺寸以及剪切模量的差异性,使得原子在相互扩散中会造成晶格扭曲。
这种晶格畸变效应会对材料的性能产生重要影响,包括光电学、力学和热学等。
动力学上的迟滞扩散效应:高熵合金由于组元数目增加,使得协同扩散完成各相平衡分离更加困难。
在发生相互扩散的过程中,严重的晶格畸变会阻碍原子的运动,使得扩散和相变速率都小于传统合金。
这种效应有助于生成纳米晶以及非晶态,从而提高合金的性能。
性能上的“鸡尾酒”效应:高熵合金中各个元素之间互相作用,共同影响其整体性能。
例如,加入较多的轻元素可以降低合金密度,加入较多抗氧化元素可以提高合金的抗氧化性,加入较多高熔点元素可以提高合金的耐高温性能。
总之,高熵合金的高熵效应是其优异性能的重要来源之一,通过调整合金成分和制备工艺,可以进一步优化其性能和应用领域。
合金材料热力学计算模拟方法

合金材料热力学计算模拟方法热力学计算模拟方法在合金材料研究中起着重要的作用。
通过模拟和计算,可以预测材料的相变行为、相稳定性以及材料的热力学性质。
本文将介绍几种常用的合金材料热力学计算模拟方法,包括相图计算、基于第一原理的方法以及相场模拟方法。
相图计算是一种常用的热力学计算模拟方法,它基于热力学的平衡条件,通过计算材料在不同温度和组分下的稳定相来构建相图。
这一方法可以为合金材料的相变行为和相稳定性提供重要信息。
常见的相图计算方法包括拟合实验数据和基于基本热力学原理的计算。
拟合实验数据方法通过实验数据的曲线拟合来计算相图。
基于基本热力学原理的计算方法则通过计算热力学势函数和构建相平衡条件来计算相图。
相图计算方法可以帮助研究者预测合金材料的相变温度、相变规律以及相稳定性。
另一种常用的合金材料热力学计算模拟方法是基于第一原理的方法。
这一方法是通过计算材料的原子尺度行为来预测材料的宏观性质。
基于第一原理的方法可以通过解析或数值方法来计算材料的势能曲线,从而预测材料的热力学性质。
常见的基于第一原理的方法包括密度泛函理论(DFT)和蒙特卡洛模拟方法。
密度泛函理论可以通过求解薛定谔方程来计算材料的电子结构和能量。
蒙特卡洛模拟方法则通过模拟原子的运动和相互作用来预测材料的热力学性质。
基于第一原理的方法可以帮助研究者深入理解合金材料的微观行为和性质。
相场模拟是一种基于宏观尺度的热力学计算模拟方法。
这一方法可以预测材料的相界面演化和相变行为。
相场模拟方法将材料划分为多个小区域,并通过守恒方程和扩散方程描述各小区域内的物质输运和相变行为。
通过迭代计算和数值模拟,可以模拟材料的相变动力学行为。
相场模拟方法可以帮助研究者预测合金材料的微观结构演变和相变速率。
综上所述,合金材料热力学计算模拟方法在材料研究中具有重要的作用。
相图计算、基于第一原理的方法和相场模拟方法是常用的热力学计算模拟方法。
这些方法可以预测材料的相变行为、相稳定性以及热力学性质。
金属材料的相变与热力学分析

金属材料的相变与热力学分析金属材料是广泛应用于工业生产和日常生活中的重要材料之一。
在金属加工和利用过程中,了解金属材料的相变行为以及热力学特性对于改善材料性能和工艺效率至关重要。
本文将对金属材料的相变与热力学进行分析。
一、相变的概念及分类相变是指物质在一定条件下从一种相转变为另一种相的过程。
对于金属材料来说,常见的相变形式包括固-固相变、固-液相变、液-气相变等。
其中,固-固相变是指金属的晶体结构发生改变,而固-液相变是指金属由固态转变为液态,液-气相变则是指金属由液态转变为气态。
二、金属材料相变的热力学分析热力学是研究物质性质与热力学过程之间关系的学科。
金属材料的相变过程受热力学第一和第二定律的制约。
1. 热力学第一定律根据热力学第一定律,能量在相变过程中是守恒的,即相变前后系统的能量总和不变。
金属材料的相变过程中,吸收或释放的热量可以通过热力学分析来估计。
2. 热力学第二定律根据热力学第二定律,自发进行的相变过程是使系统熵增加的过程。
金属材料的相变过程中,热力学分析可以用来计算相变的熵变,从而评估相变的自发性和可逆性。
三、金属材料相变的影响因素金属材料的相变受多种因素的影响,包括温度、压力、化学成分等。
1. 温度温度是影响金属材料相变的重要因素。
随着温度的升高或降低,金属的相变温度也会相应地改变。
2. 压力在高压下,金属材料的相变温度可能会显著改变。
压力对金属的相变规律有一定的影响。
3. 化学成分金属材料的化学成分也会对其相变行为产生影响。
合金中的不同元素可能导致相变温度的改变和相变形式的差异。
四、金属材料相变的应用金属材料的相变特性可以广泛应用于材料工程和制造过程中。
1. 热处理通过控制金属材料的相变过程以及相变温度,可以实现对材料的硬度、强度和导电性等性能的调控,从而满足不同应用需求。
2. 材料制备相变过程对金属材料的制备有着重要的影响。
例如,通过调控相变过程可以制备出微观结构均匀的金属材料,提高其机械性能和腐蚀抗性。
合金热力学

合金热力学应用热力学和统计物理研究合金的相图、相变及有关性能等问题的学科。
合金热力学又叫固体热力学或材料热力学,即将研究的对象推广到固体或材料。
合金热力学又叫冶金热力学,则将它推广到广泛的冶金现象。
合金热力学又叫合金能量学,强调它用能量的观点,处理有关合金的问题。
合金热力学的理论基础经典热力学经典热力学是现象理论。
它所依据的是从无数经验归纳出的三个定律,然后从此演绎出许多描述物质平衡性质的关系式。
热力学第一定律是力学中机械能转换和守恒定律的延伸。
若环境对体系作功W,体系又从环境吸热Q,则体系的内能增加ΔU为:ΔU=W+Q (1)或 d U=δW+δQ (1a)由于U是状态函数,才能写为全微分;而W及Q随过程而有所不同,不能写为全微分。
热力学第二定律指出了过程方向,它的一种表达方式便是熵增原理:d S(总)=(d S(体)+d S(环))≥0 (2)式中d S(体)、d S(环)及d S(总)分别表示体系、环境和总熵的全微分;(2)式中“=”表示平衡关系;“>”表示过程方向。
熵的概念是在19世纪研究热机效率时提出的:从状态 1到状态 2的热量变化是随途径而异的,而可逆过程的则与途径无关。
人们定义熵S的全微分为:d S呏δQ r/T (3)δQ r是可逆过程的热量变化,T是绝对温度,由于S是状态函数,故可写为全微分。
热力学第三定律是为了计算熵的绝对值的。
凝聚系的熵在恒温过程中改变值ΔS随绝对温度降低而趋于零。
即:(4)从(3)式得到:(5)从(4)式可以证明S0是一个绝对常数,一般选择S0=0。
热力学第一及第二定律分别引入体系的状态函数U及S,为了分析问题的方便,定义了焓H、自由能F 及自由焓GH呏U+p V (6)F呏U-TS (7)G呏H-TS (8)式中p及V分别是体系的压强和体积。
合并第一及第二定律,可以获得关闭体系(与环境没有物质交换)的平衡条件(=)及过程方向(<)为:(d U)v,S≤0 (9)(d H)p,S≤0 (10)(d F)v,T≤0 (11)(d G)p,T≤0 (12)由于p、V、T、S、U、H、F、G都是状态函数,借助于微分方程,可以导出许多表述物质平衡现象的关系式。
合金 材料热力学

合金热力学:
固体热力学 材料热力学 冶金热力学 合金能量学
4。能量 力学中提出的概念。
1J=1N•m 1牛顿的力产生1米的位移所做的功为1焦耳。 热学中用卡(cal)作单位。 热功当量: 1卡 = 4.185焦耳 电学中1ev(电子伏特)为使一个电子升高1V所 做的功。
能量角度的稳定性:
Chapter 2 热力学
热学:——热现象——粒子集体运动的表现
热力学:——宏观条件
热是能量的一种形式。
从能量的观点,讨论现象
第一节: 温度和压力
一、温度和热平衡 温度: 物体的冷热程度 热力学第零定律: 一切互为热平衡的物体, 具有相同的温度。
实验 现象
压力与气体状态方程
第二节: 热力学第一定律——能量关系
一、概念:
“
”——晶界
“
”——空位
相关性方法: 建立性能和结构之间的关系,重点在 于避免有害结构而制造有利的结构。
过程性方法:研究在外界条件下,过程是如何在合 金的结构中进行的。然后提出解决的措施。
工艺
结构
性能
3。过程: 三个共性: 方向、途径、结果。 过程进行三原理: 1)沿着能量降低的方向进行; 2)遵循阻力最小的途径进行; 3)过程的结果是适者生存。
Chapter 1 绪论
第一节 合金
一、概念:
性能
结构 过程
材料科学领域中的四个重要概念和共性问题
能量
1. 性能:材料的性能是一种参量,用以表征材料在给定外 界条件下的行为。 如: 断裂强度——拉伸过程对应的性能。 不同外界条件,相同材料也会有不同的性能。
2。结构:成分、组织和结构三者之统称。 成分:组成合金的粒子种类和分量; 组织、结构:粒子在运动中的排列方式。
铝合金塑性成形的热力学分析

铝合金塑性成形的热力学分析一、铝合金塑性成形的基本原理铝合金作为一种轻质、高强度的材料,在现代工业中有着广泛的应用。
其塑性成形过程是将铝合金材料通过外力作用,使其发生塑性变形,从而获得所需形状和尺寸的零件或产品。
铝合金塑性成形的基本原理涉及到材料力学、热力学和金属学等多个领域。
1.1 铝合金的物理特性铝合金具有较低的密度和较高的比强度,这使得它在航空航天、汽车制造、电子设备等领域具有显著的应用优势。
此外,铝合金还具有良好的导热性、导电性和耐腐蚀性,这些特性对于其塑性成形过程至关重要。
1.2 塑性成形的热力学基础塑性成形过程中,铝合金的变形伴随着能量的转换和传递。
热力学分析是研究材料在变形过程中能量变化的重要手段。
通过热力学分析,可以了解铝合金在成形过程中的温度变化、热量的产生与传递,以及这些因素对材料性能的影响。
1.3 塑性变形机制铝合金在塑性成形过程中,其内部结构会发生改变,包括位错运动、晶粒变形和再结晶等。
这些变形机制与铝合金的微观结构密切相关,同时也受到外部条件如温度、应力和应变率等因素的影响。
二、铝合金塑性成形的热力学分析方法对铝合金塑性成形过程进行热力学分析,可以帮助我们更好地理解材料在成形过程中的行为,优化成形工艺,提高产品质量。
2.1 热力学模型的建立在铝合金塑性成形的热力学分析中,首先需要建立合适的热力学模型。
这通常涉及到对材料的热物理性质、变形机制和热交换过程的描述。
模型的建立需要考虑材料的非线和多物理场的耦合效应。
2.2 有限元模拟有限元模拟是一种常用的热力学分析方法,它通过将连续的物理问题离散化,转化为可解的代数方程组。
在铝合金塑性成形的有限元模拟中,可以模拟材料在成形过程中的温度场、应力场和应变场,预测材料的变形行为和可能的缺陷。
2.3 实验验证理论分析和模拟计算的结果需要通过实验进行验证。
实验方法包括高温拉伸试验、热模拟试验和微观结构分析等。
通过实验数据与模拟结果的对比,可以评估模型的准确性和可靠性,为铝合金塑性成形工艺的优化提供依据。
第七章 熵和结构

因此,相对于完全有序状态(W=1),熵变为 △Sm =klnW—kln1 =—Nk[flnf+(1—f)ln(1—f)] (7.13) 上式与(7.4)式形式上完全一样。f与原子间的结 合能有关,也与体系的浓度、压力等条件有关。 顺便指出,完全无序时,f=1/2,由(7.10)式可 得ω=0;而完全有序时, f=1,则ω=1。
式中 CA、CB—— 分别是AB二元合金中A及B的原 子分数; pαA—— α点阵被A原子所占的分数; pβB—— β点阵被B原子所占的分数。 如果用f表示原子占“对”了位置的原子的分数, 则1-f就是原子占“错”了位置的原子的分数。 对于AB型合金,CA =CB=1/2,故 (7.10)
下面我们以简单的AB型合金为例进行分析。设原 子总数为N,则A及B的原子总数都是N/2(这里假 设晶体没有缺陷)。它们占对了位置的原子的总数 都是fN/2,而占错了位置的原子总数都是(1—f)N/2。 计算热力学几率时,我们先考虑一种原子,例如A。 A原子占好后余下的位置由不可区分的B原子全部 占据。由(7.1)式可得
§7.1 置换固溶体和空位固溶体的组态熵
组态熵又叫混合熵(Sm),是合金结构中经常遇 到的问题。合金中组元的组合方式不同,组态熵就 不同,组态熵反映了合金中组元的组合方式。例如 AB二元固溶体、AB空位固溶体、有序固溶体等, 都有由组元组合方式引起的组态熵。 前面我们介绍了 S=klnW 也就是说,熵是热力学几率。计算热力学几率,实 际上是一个计算组合的问题。下面以二元置换固溶 体为例进行计算。
在这一章里,我们从原子占据空间点阵位置的组态, 计算了热力学几率和组态熵。讨论了置换、空位、 间隙及有序四种类型固溶体组态熵的计算方法,并 分析了外加拉应力对间隙固溶体体组态熵的影响, 以及从平衡条件求间隙原子在外力作用下跳跃到外 力方向上的浓度。如果能够求出置换、空位及有序 固溶体的内能分别与溶质浓度、空位浓度及有序度 的关系,便可以利用平衡条件求出它们与温度T的 关系。
热力学研究下金属合金的稳定性

热力学研究下金属合金的稳定性金属合金是现代工业中不可或缺的材料之一,其具有高强度、耐腐蚀、导电、导热等优良性能。
但是,金属合金也存在着一些问题,如晶界的强度、材料的稳定性等,这些问题的解决对于金属合金的应用有着重要的意义。
本文将以热力学为基础,探讨金属合金的稳定性。
一、热力学基础热力学是研究热现象和与热有关的其他能量转换的学科。
在化学和物理学等领域都有广泛应用。
热力学第一定律是能量守恒定律,它可以用来描述物理系统的能量变化。
热力学第二定律则是描述热量的不可逆性,在如何利用能量的过程和影响热力学体系状态的过程中具有重要作用。
在金属合金研究中,热力学定律可以帮助我们理解金属合金中微观结构的稳定性。
二、金属合金中微观结构的稳定性金属合金中的微观结构通常是由两种或两种以上的金属元素组成的晶体。
由于不同元素存在着不同的晶体结构、化学亲和力和原子半径等差异,所以金属合金的微观结构是复杂的,不同的配比会导致不同的晶体结构。
这些结构变化对于金属合金的力学性能、腐蚀性能等都有着重要的影响。
然而,金属合金中微观结构的稳定性也成为热力学研究的焦点。
在晶界处,由于晶界会破坏晶体的完整性,导致其力学性能下降。
因此,如何优化金属合金的微观结构,提高其稳定性是关键。
三、金属合金中的相变金属合金中的相变是指金属合金在不同温度和成分下形成各种不同的晶体结构。
金属合金的相变可以通过调整合金的成分、温度等条件来实现,从而达到优化微观结构的目的。
相变的热力学是相变研究的基础,在相变时,系统的热力学变化描绘了相变过程。
四、金属合金的平衡态和非平衡态在金属合金中,有两种重要的状态:平衡态和非平衡态。
平衡态是指当金属合金达到热力学稳定状态时的状态。
以某种金属合金为例,该合金的各个成分和晶体结构均处于稳定状态,任何扰动均会引起恢复的过程,这就是平衡态。
而非平衡态则是指金属合金状态在过程中无法达到平衡态。
这种状态标志着金属合金正经历着某种变化。
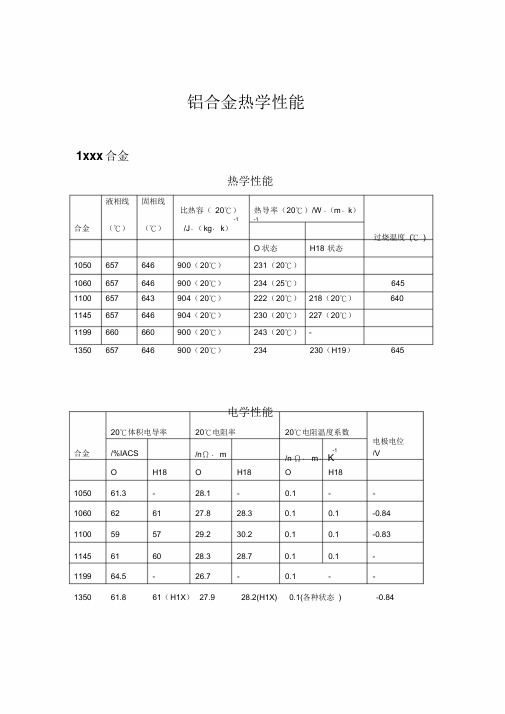
铝合金热力学性能
铝合金热学性能1xxx合金热学性能液相线固相线比热容(20℃)热导率(20℃)/W ·(m·k)-1 -1合金(℃)(℃)/J·(kg·k)过烧温度(℃ )O 状态H18 状态1050 657 646 900(20℃)231(20℃)1060 657 646 900(20℃)234(25℃)645 1100 657 643 904(20℃)222(20℃)218(20℃)6401145 657 646 904(20℃)230(20℃)227(20℃)1199 660 660 900(20℃)243(20℃)-1350 657 646 900(20℃)234 230(H19)645电学性能20℃体积电导率20℃电阻率20℃电阻温度系数电极电位合金/%IACS /nΩ·m -1/n Ω·m·K /V O H18 O H18 O H181050 61.3 - 28.1 - 0.1 - -1060 62 61 27.8 28.3 0.1 0.1 -0.841100 59 57 29.2 30.2 0.1 0.1 -0.831145 61 60 28.3 28.7 0.1 0.1 -1199 64.5 - 26.7 - 0.1 - -1350 61.8 61(H1X)27.9 28.2(H1X) 0.1(各种状态) -0.842xxx合金热学性能液相线固相线初熔温比热容热导率固溶温过烧温-1合金(℃)(℃)度/W ·(m·k)(20℃)度(℃)度(℃)(℃)/J·(kg·k)-12011 638 541 535 864 T3、T4:152 524 540T8:1732014 638 507 - - O:192 502 505T3、T4、T451:134 510T6、T651、T652:513-5151552017 640 513 - - O:193 500-510 510T4:134(25℃)513 2024 638 502 502 875 O:190 493 500T3、T36 、T351 、501T361、T4:120T6、T81 、T851 、T861:1512036 650 554 510 882 O:198 ;T4:15 500 555 2048 926(100℃) T851:1592124 638 502 502 882 O:191 493T851:1522218 635 532 504 871 T61:148 510 505T72:1552219 643 543 864 O:170 535 543T31、T37:116 545T62、T81、T87:1302319 643 543 864 O:1702618 638 549 502 875 T61:146 530 5502A01 924 T4:122 495-505 5352A02 840(100℃) T6:135 495-505 515510-515 2A06 T6:139(100℃) 503-507 5105182A11 639 535 924(100℃) T4:118(25℃) 495-510 514-5175122A12 638 502 924(100℃) T4:193(25℃) 496-540 505506-5072A10 924(100℃) T6:147(25℃) 510-520 540 2A14 638 510 840(100℃) T6:160(25℃) 499-505 509515 2A16 T6:138(25℃) 528-540 547143(100℃) 545147(200℃)156(300℃)2A17 756(50℃)T6:130(25℃) 520-530 535139(100℃) 540151(200℃)168(300℃)2A50 840(25℃) T6:177(25℃) 510-515 545>525 840(150℃) 181(100℃)882(200℃) 185(200℃)924(250℃) 185(300℃)966(300℃) 189(400℃)2A60 840(100℃) T6:164(25℃) 505-515882(150℃) 168(100℃)924(200℃) 172(200℃)966(250℃) 177(300℃)1008(300 ℃) 181(400℃)2A70 798(100℃) T6:143(25℃) 525-535 545840(150℃) 147(100℃)840(200℃) 151(200℃)882(250℃) 160(300℃)924(300℃) 164(400℃)966(400℃)2A80 840(100℃) T6:147(25℃) 525-530882(150℃) 151(100℃)924(200℃) 160(200℃)966(250℃) 168(300℃)966(300℃) 172(400℃)1008(350 ℃)1050(400 ℃)2A90 756(100℃) 515-520 >520T6:156(25℃)798(150℃) 160(100℃)840(200℃) 164(200℃)924(250℃) 172(300℃)966(300℃) 181(400℃)1008(350 ℃)1008(400 ℃)电学性能合金20℃体积电导率/%IACS20℃电阻率/nΩ·m20℃电阻温度系数-1/nΩ·m·K电极电位/V2011 T3、T4:39;T8:45T3、T4:44T8:38T3、T4、T8:0.1T3、T4:-0.39T8:-0.832014O:50T3、T4、T451:34T6、T651、T652:40O:34T3、T4、T451:51T6、T651、T652:43O、T3、T4、T451、T6、T651、T652:0.1T3、T4、T451:-0.68T6、T651、T652:-0.78 O:50,158%IACS(质2017量);T4:34,108%IACS(质量)2O:0.035Ω·mm /m;T4:0.05Ω·mm 2/mO:50;T3、T36、T351、O:34;T3、T36、T351、T3、T4、T361:各种状态:0.12024 T361、T4:30;T6、T361、T4:57;T6、-68;T6、T81、T81、T851、T861:38 T81、T851、T861:45 T861:-0.80 2036 O:50;T4:41 O:33;T4:42 O、T4:0.1 -0.75 2048 T851:42 T851:402124 O:50;T851:39 O:34.5 O、T851:0.1 T851:-0.80 2218 T61:38;T72:40 T61:45;T72:43 T61、T72:0.1T31、T37、O:44;T31、T37、O:39;T31、T37、T351:-0.64;各种状态:0.12219 T351:28;T62、T81、T351:62;T62、T81、T62、T81、T87、T851:30 T87、T851:57 T87、T851:-0.80-32319 O:44 O:39 2.94×102618 T61:37 T61:47 T61:0.12A01 T4:40 T4:392A02 T4:552A06 T6:612A10 T6:50.42A11 O:45;T4:30 O、T4:542A12 O:50;T4:30 O:44;T4:732A14 T6:40 T6:432A16 T6:612A17 T6:542A50 T4:412A60 T4:432A70 T6:552A80 T6:50 2A90 T6:47热学性能-1 液相线固相线过烧温度比热容(20℃)热导率(20℃)/W ·(m·k)合金(℃)(℃)-1/J·(kg·k)(℃)3003 654 643 893(20℃)O:139;H12:163;H14:159;H18:155640 3004 654 629 893(20℃)O:162 630 3105 657 638 897(20℃)173 635 3A21 654 643 1092(100℃);25℃、H18:156;25℃、H14:1176(200℃);164;25℃、O:181;100℃:1302(300℃);181;200℃:181;300℃:1851302(400℃)电学性能合金20℃体积电导率20℃电阻率/%IACS/nΩ·m状态20℃状态20℃20℃电阻温度系数-1/n Ω·m·K电极电位/V O 50 O 343003 H12 42 H12 41H14 41 H14 420.1 -0.83 H18 40 H18 433004 O 42 O 41 0.1 -0.84 3105 O 45 O 38.3 0.1 -0.84 O 50H14 413A21 34 0.1 -0.85 H18 40热学性能液相线固相线比热容(20℃)热导率(20℃)合金(℃)(℃)/J·(kg·k)-1 -1 过烧温度(℃)/W ·(m·k)4032 571 532 864 O:155;T6:141 530 4043 630 575 575电学性能20℃体积电导率20℃电阻率合金/%IACS/nΩ·mO T6 O T620℃电阻温度系数-1/n Ω·m·K电极电位/V4032 40 36 43.1 47.9 0.1 4043 42 415xxx合金热学性能合金液相线(℃)固相线(℃)比热容-1/J·(kg·k)-1热导率/W ·(m·k)O H18过烧温度(℃)5005 652 632 900(20℃)205(20℃)205(20℃)630 5050 652 627 900(20℃)191(20℃)191(20℃)625605 5052 649 607565 5056 638 568 904(20℃)120(20℃)112(20℃)580 5083 638 574 900(20℃)120(20℃)585 5086 640 585 900(20℃)127(20℃)590 5154 643 593 900(20℃)127(20℃)5182 638 577 904(20℃)123(20℃)605 5252 649 607 900(20℃)138(20℃)590 5254 643 593 900(20℃)127(20℃)5356 638 574 904(20℃)116(20℃)575 5454 646 602 900(20℃)134(20℃)600 5456 638 570 900(20℃)116(20℃)570 5457 654 629 900(20℃)117(20℃)630 5652 649 607 900(20℃)137(20℃)605635 5657 657 638 900(20℃)5A02 650 620 947(20℃)156(20℃)5A03 640 610 882(20℃)147(20℃)5A05 620 580 924(20℃)122(20℃)5A06 924(20℃)118(20℃)电学性能合金20℃体积电导率20℃电阻率/n mΩ·/%IACSO H38 O H3820℃电阻温度系数-1/n Ω·m·K电极电位/V5050 50 50 34 34 0.1 -0.83 5052 35 35 49.3 49.3 0.1 -0.85 5056 29 27 59 64 0.1 -0.87 5083 29 29 59.5 59.5 0.1 -0.91 5086 31 31 56 56 0.1 -0.86 5154 32 32 53.9 53.9 0.1 -0.86 5182 31 31 55.6 55.6 0.15252 35 35 49 49 0.15254 32 32 54 54 0.1 -0.86 5356 29 59.4 0.1 -0.87 5454 34 34 51 51 0.1 -0.86 5456 29 29 59.5 59.5 0.1 -0.87 5457 46 46 37.5 37.5 0.1 -0.84 5652 35 35 49 49 0.1 -0.85 5657 54 54 32 32 0.15A02 40 40 47.6 47.6 0.15A03 35 35 49.6 49.6 0.15A05 64 64 0.15A01 26 26 71 71 0.15A12 77 77 0.16xxx合金热学性能合金液相线(℃)固相线(℃)比热容/J·(kg·k)-1-120℃热导率/W ·(m·k)O T4 T6固溶温度(℃)过烧温度(℃)6005 654 607 167(T5)547 605 6009 650 897 205 172 180 5555656010 650 585 897 202 151 1806061 652 582 896 180 154 167 530 580582193(T1)520 615 6063 655 615 900 218 209(T5)201(25℃)(25℃)6066 645 563 887 147 530 560566 545 5656070 649 566 891 172620 6101 654 624 895 218510-525 590 6151 650 588 895 205 163 1756201 654 607 895 205(T8)(25℃)510 6106205 645 613 172(T1)(25℃)188(T5)(25℃)525540 580650 585 172(T9)62626351 650 555 176(25℃)5056463 654 621 192(T1)(25℃)209(T5)(25℃)201(25℃)520 6156A02155(25℃)510-525 565595电学性能合金20℃体积电导率/%IACS20℃电阻率/nΩ·m20℃电阻温度系数-1/nΩ·m·K电极电位/V O T4 T6 O T4 T6 O T4 T66005 49(T5)35(T5)6009 54 44 47 31.9 39.2 36.7 0.1 0.1 0.1 6010 53 39 44 32.5 44.2 39.2 0.1 0.1 0.1 6061 47 40 406063 58 50(T1)55(T5)433035(T1)32(T5)336066 40 37 43 47 0.1 0.16070 44 39 0.1 59(T61)60(T64)29.2(T61)28.7 0.1(T64)29.7(T65)6101 58(T63)58(T65)57 30.229.7(T65)6151 54 42 45 32 41 38 0.1 0.1 0.1 -0.83 6201 45(T1)49(T5)37(T1)35(T5)6262 44(T9)39(T9)6351 46 38 0.16463 50(T1)55(T5)53 34(T1)31(T5)33 0.16A02 55 457xxx合金热学性能-1热导率/W ·(m·k)合金液相线(℃)固相线(℃)比热容/J·(kg·k)-1 OT53、T63、T5361、T6351T6固溶温度(℃)过烧温度(℃)4007005 643 604 875(20℃)166 148 1377039 638 482 125-155 460-5 007049 627 588 960(100℃)154(25℃)7050 635 524 860(20℃)180 154(T74、T7651)157(T736、T73651)4757072 657 641 227130(T6、T62、T651、T652)465- 535 7075 635 477 960(100℃)150(T76、T7651)480 525155(T73、T7351、T7352)155 515(T737175 635 477 864(20℃)177 142 6、T73652)7178 629 477 856(20℃)180127(T6、T651)152(T76、T7651)468 475477 155(T61、T651、5157475 635 477 865(20℃)177 T761、T7651)163(T7351)714(100℃)155(25℃)7A03 924(200℃)1050(300℃)160(100℃)164(200℃)168(300℃)155(25℃)160(100℃、465- 4907A04 400℃)475 475164(200℃、477300℃)电学性能合金O 20℃体积电导率/%IACST53、T5351、T63、T6351T6 O20℃电阻率/nΩ·mT53、T5351、T63、T6351T620℃电阻温度系数/n-1Ω·m· K7005 43 38 35 40.1 45.4 49.3 0.1 7039 32-40 32-40 32-40 0.1 7049 40 40 40 43 43 43 0.17050 47 39.5(T76、T7651)40.5(T736、T73651)36.7 43.6(T76、T7651)42.6(T736、T73651)0.17072 60 28.7 0.1 33(T6、T62、T651、T652)28.7(T6、T62、T651、T652)7075 38.5(T76、T7651)44.8(T76、T7651)0.1 40(T73、T7351、T7352)43.1(T73、T7351、T7352)7175 46 36(T66)40(T736、T73652)37.5 47.9(T66)43.1(T736、T73652)0.17178 46 32(T6、T651)39(T76、T7651)37.5 53.9(T6、T651)44.2(T76、T7651)0.1 46 36(T61、T651)47.9(T61、T651)7475 42(T7351)37.5 41.1(T7351)0.1 40(T761、T7651)43.1(T761、T7651)7A03 44.0(T4)0.1 7A04 30(T4)42.0(T4)。
Mg_Zn合金的热力学性质计算

2006年12月重庆大学学报(自然科学版)Dec.2006 第29卷第12期Journal of Chongqing University(N tur l Science Editi on)Vol.29 No.12 文章编号:1000-582X(2006)12-0068-04Mg-Zn合金的热力学性质计算3周鸿翼,刘天模,王金星(重庆大学材料科学与工程学院,重庆 400030)摘 要:组元活度的获得是合金热力学性质研究的一个重要方面.在各种预测合金热力学性质的模型中,M iede ma模型是近年来发展得较为完善和准确的模型.文中根据M iede ma合金生成焓模型,计算了Mg-Zn合金的生成焓,进而计算出了1000K时Mg-Zn合金熔体中Zn的活度曲线.计算结果表明,由于Mg-Zn合金的生成焓值较小,在计算活度的过程中,过剩熵值对计算结果的影响较大,在引入过剩熵值后的活度计算值与实验值吻合较好.关键词:Mg-Zn合金;活度;热力学 中图分类号:TG146.4文献标识码:A 镁合金具有重量轻,较高的比强度和比刚度,优良的阻尼防震性能和铸造性能,较高的尺寸稳定性,良好的机械加工性能等优点,已经逐渐成为工程材料研究领域的一个热点课题[1-2].近10年来,镁合金在汽车工业、航空工业、电子通讯工业中已有广泛的应用,并取得了很好的效果,但是其合金化理论研究还很薄弱,一些重要的基础热力学数据还很缺乏[3],因此,很有必要对镁合金的热力学性质进行研究,用以指导镁合金的开发与利用.由于金属合金系的数量非常巨大,热力学数据完全依靠实验测定已经不可能,而且目前高温实验存在很大的困难,用以实验的设备在高温下很难保证良好的准确性,因此,通过热力学计算获得合金的热力学数据是很有必要的.M iede ma模型自上世纪70年代提出以来,到目前为止已经发展得较为成熟.欧阳义芳[4]、Goncalves[5]等人将其应用于非过渡族合金系的热力学计算并加以扩展,均取得了很好的效果.文中将M iede ma模型应用于Mg-Zn合金,计算了该合金的生成焓、过剩熵、活度、活度系数等热力学数据.1 计算模型和理论1.1 M iede ma模型M iede ma合金生成焓模型是一个宏观的半经验模型.M iede ma等人认为二元合金组元间相互结合时,原子外层电子将会发生再分配,W igner-Seitz原子胞边界的电子密度差的平方项,将对合金生成焓有正的贡献;而纯金属元素的电负性参数的平方项,将对生成焓有负的影响.最初,该模型是用以计算过渡族金属二元合金和以过渡族金属作为组元之一的所有二元合金系生成焓的,计算结果与实验值符合很好.张邦维等人将其推广用以预测镁基碱金属二元合金热力学性质,同样取得了不错的效果[6].并且,Kauf man等人研究表明,一般情况下该模型的计算值与实验值偏差一般不超过8kJ/mol[7].M iede ma认为二元合金的生成焓可以表示为:ΔH forca lc(jper m ole of a to m s)=x A f A BΔH°in t erfaceA in B.(1)其中xA为组元A的摩尔分数,f AB表示组元A的原子被组元B的原子包围的程度,其表达式为:f A B=x s B 无序合金x s B[1+8(x s A x s B)2]有序合金.(2)式中x sA、x sB为组元A、B的表面浓度,定义如下式表示:x s A=x A v2/3A ax A V2/3A a+x B V2/3B ax s B=x B v2/3B ax A V2/3A a+x B V2/3B a.(3) V A a、V B a分别为纯组元A、B在形成合金后的原子体积.3收稿日期:2006-06-23基金项目:重庆市自然科学基金资助项目(CSTC,2005BA4015)作者简介:周鸿翼(1980-),男,汉族,重庆铜梁人,重庆大学硕士研究生,从事镁合金热力学方面的研究工作.在M iede ma 模型中表示为:V 2/3A a=V 2/3A [1+aB f AB (Φ3A -Φ3B )]V 2/3B a=V 2/3B [1+a A fB A(Φ3B-Φ3A )].(4)式中V A 、V B 则为纯组元A 、B 的原子体积,a A 、a B 为经验常数.H °in t erfaceA inB 为界面焓,其定义式如下:ΔH °in t erfaceA in B=p V 2/3A a [-(ΔΦ3)2+q p (Δn 1/3w s )2-R 3p]12[(n A w s )-1/3+(n B w s )-1/3](5)其中,q p 为经验常数,一般情况下取q p =9.4.R3p在计算时一般表示为a (Rp),a 为经验常数,当二元系为固态时取值为0.73,当为液态时取值为1,(Rp)为过渡族和非过渡族元素形成二元合金时的修正值.ΔΦ3为组元的电负性差,Δn 1/3w s 为组元原子胞边界上的电子密度差,p 为常数,视不同族元素形成合金取不同值.以上各参数在文献[8]中都有详细记载.结合式(1)~式(5),运用两次迭代,便可以较准确计算出二元合金的生成焓.由于两次迭代的复杂性,综合上述各式将生成焓计算式简化,对于无序合金,可表示为:ΔH for d isordereda lloys =ΓABx A V 2/3A [1+a A xB (Φ3A -Φ3B )]x B V 2/3B [1+a B x x (Φ3B -Φ3A )]x A V 2/3A [1+a A xB (ΦA -ΦB )]+x B V 2/3B [1+a B x x (ΦB -ΦA )](6)运用式(6)便可以计算液态二元合金的生成焓.1.2 活度和活度系数的计算在二元系中,体系的过剩吉布斯自由能G EAB ,过剩熵S EAB 和过剩焓H EAB 之间存在如下关系式:GEAB=HE AB-TS E AB.(7) 在通常情况下,S E AB的绝对值比H E AB小的多.一般情况下,在二元系中,令S EAB=0对计算结果影响不大[9-10],所以,在本计算中暂假设SE AB=0.由于理想溶液的混合焓为零,所以用ΔH forAB 代替H EAB 可得表达式:G EAB =ΔH forAB .(8) 二元系中,组元的活度系数γA 与体系的过剩吉布斯自由能G EAB 之间的关系式为:R T ln γA=9G EA9x A.(9)所以,将式(6)代入式(8),并将得到的体系过剩吉布斯自由能G EAB 代入式(9),求导变形得到如下关系式:R T ln γA =ΔH AB -(1-X A )・ΓAB ・V 2/3A {x -1A a A (Φ3A-Φ3B )[1+a Ax B (Φ3A-Φ3B )]-2-x -2A [1+a A xB (Φ3A-Φ3B )]-1}+V -2/3B{x -2B [1+a B x A (Φ3B-Φ3A )]-1-x -1B a B (Φ3B-Φ3A )[1+a B x A (Φ3B -Φ3A )]-2}{x -1A V -2/3A[1+a A x B (Φ3A-Φ3B )]-1+x -1B V -2/3B[1+a B x A (Φ3B-Φ3A )]-1}-2(10) 根据式(10)便可以求出二元系中组元A 的活度系数γA .根据热力学关系式:G EAB =x A ln γA +x B ln γB .(11)变形,可得ln γB =1x B(G EAB -x A ln γA ).(12)根据式(12)便可以求出另一组元B 的活度系数γB .各组元的活度则可以根据下式求出:a n =γn x n 其中n =A,B .(13)2 计算与讨论Mg 和Zn 的相关M iede ma 模型参数如表1所示[8].表1 M g 和Zn 的参数值Ele ment n 1/3w sΦ3V2/3aMg 1.173.455.80.10Zn1.324.104.40.10 Mg -Zn 合金虽然是由非过渡族元素和过渡族元素组成的合金系,但是根据M iede ma 的研究,该合金系不必考虑电子杂化效应,其(R /p )值不需要修正,所以,取R =0,p =10.6.将表1的各参数代入式(6),计算得到的Mg -Zn 合金生成焓ΔH 的曲线如图1所示.从图中可以看出,在整个成分范围内生成焓均为负值,这说明Mg -Zn 合金组元之间相互结合的引力较大,具有自发形成金属间化合物的倾向,实验也证明在Mg -Zn 合金中存在Mg 7Zn 3、MgZn 、MgZn 2等金属间化合物.并且,生成焓曲线具有轻微的不对称性,最大值偏向原子半径和原子序数较小的Mg 端,这也符合M iede ma 生成焓模型的计算规律.图1 Mg -Zn 合金生成焓曲线96第29卷第12期 周鸿翼,等: M g -Zn 合金的热力学性质计算将各参数代入式(10),变形后结合式(13)可以计算得到Zn 的活度.计算得到的a zn 在T =1000K 时的曲线如图2所示.图中所示的活度为一向下凹的曲线,大大偏离了拉乌尔定律,形成了很大的负偏差.这与Mg -Zn 二元相图[11]所展示的信息是一致的.由Ther 2mo 2Calc 软件计算的a zn 曲线和在923K 时的实验数据[12]如图2所示.可以比较计算预测得到的曲线比由Ther mo 2Calc 软件计算预测的曲线的准确性稍差,这可能是因为Mg -Zn 合金的生成焓较小,过剩熵S EM g -zn 产生了较大的影响造成的,但是计算预测得到的曲线的变化规律和实验值的变化是一致的,完全遵循了拉乌尔和亨利定律.所以,以M iede ma 模型为基础计算得到的Zn 的活度曲线是较为合理的.图2 1000K 时Mg -Zn 合金中Zn的活度曲线图3 Mg -Zn合金过剩熵曲线图4 SEMg -Zn≠0,1000K 时M g -Zn 合金中Zn 的活度曲线现在对S EAB ≠0时的情况做一个讨论.Tanaka 、Gokcen[13]等人在自由体积理论的基础上推导出的过剩熵S E AB 与生成焓ΔH forAB 之间的关系为:S E AB =110・ΔH forAB ・(1T A +1T B).(14)其中,T A 和T B 分别表示组元A 和B 的熔点.对于Mg -Zn 合金来说,T M g =922K,T Z n =693K,代入式(14),可得Mg -Zn 合金过剩熵S E M g -Z n 的曲线如图3.从图中可知,过剩熵S EM g -Z n 值虽然始终较小,但由于Mg -Zn 合金的生成焓相对也较小,在较高温度下S EM g -Zn 不能忽略,将其视为零将会对计算产生较大大的偏差.在考虑S EM g -Z n ≠0且T =1000K 时,由计算得到的a Zn 曲线、Ther mo 2Calc 软件计算预测的曲线和在923K 时的实验数据(如图4).从图4中可知,此时计算预测的曲线与实验值吻合程度有了一定的改善,并且完全体现了活度的变化趋势,优于由Ther mo 2Calc 软件预测的曲线.3 结 论文中以M iede ma 生成焓模型为基础,计算了Mg -Zn 合金的生成焓进而得到在1000K 时Mg -Zn 合金中Zn 的活度曲线.讨论计算了S E≠0时的情况,表明Mg -Zn 合金生成焓较小,S E的值对计算结果是有影响的,必须加以考虑.S E≠0在时的情况下,计算的Zn 的活度曲线与实验值吻合较好,这说明M iede ma 生成焓模型对Mg -Zn 合金是适用的.参考文献:[1] 陈振华.镁合金[M ].北京:化学工业出版社,2004.[2] 张静,潘复生,郭正晓,等.不含锆的镁合金系中合金相研究进展[J ].金属热处理,2003,28(11):6-11.[3] 郝士明.镁的合金化与合金相图[J ].材料与冶金学报,2003,1(3):166-170.[4] 欧阳义芳,张邦伟,廖输帜,等.稀土镁合金的热力学性质研究[J ].稀有金属材料与工程,1995,24(6):32-36.[5] G ONC ALVES A P,ALME I D A M.Extended M iedema Mod 2el:Predicting the For mati on Enthal p ies of I nter metallic Pha 2ses with More than t w o Ele ments[J ].PHYSI CA B,1996,288:289-294.[6] 张邦维,欧阳义芳,廖输帜,等.镁基碱金属二元合金热力学性质的理论计算[J ].湖南大学学报,1995,22(3):36-40.[7] D I N S DALE A T .SGTE Data f or Pure Ele ments[J ].C ALPH 2AD,1991,15:317-425.[8] BOER F R DE,M I E DE MA A R,CHATE L P F DE,et al .Cohesi on in metals:transiti on metal all oys [M ].Am ster 2da m:North 2Holland,1988.[9] 路贵民,刘学山,蒋冬梅,等.A l -M g 合金热力学性质的07重庆大学学报(自然科学版) 2006年计算[J ].中国有色金属学报,1999,9(2):381-384.[10] 丁学勇,王文忠.二元系熔体中组元活度的计算式[J ].金属学报,1994,30(10):444-447.[11] AVE DESI A N M I CHAE L M,BAKER H .AS M S pecialty Hand 2book 2Magnesiu m and Magnesiu m A ll oys [M ].Ohi o:The M aterial I nf or mati on Society,1999.[12] HULTGRE N R,DES A I P D,HAW KI N S D T,et al .Se 2lected Values of the Ther modyna m ic Pr operties of B inary A ll oys[M ].Ohi o:AS M ,Metal Park,1973.[13] T ANAK A T,G OKCE N N A,MOR I T A Z,et al .Relati on 2shi p bet w een enthal py of m ixing and excess entr opy in liq 2uid binary all oys[J ].Z .Metallkunde ,1990,81(1):49-54.Calcul ati on of the Ther modynam i c Properti es of M g 2Zn AlloyZHOU Ho ng 2yi,L I U Ti a n 2m o ,WAN G J i n 2xi ng(College of Material Science and Engineering,Chongqing University,Chongqing 400030,China )Abstract:Getting activity of component is an i m portant as pect of researching the ther modyna m ic characters of all oy .Un 2der each model of p redicting the ther modyna m ics characters of all oy,M iede ma model has been devel op ing as compara 2tively a good and accurate model in recent years .I n this work,the f or mati on enthal py ofMg -Zn all oy has been calcu 2lated,according t o the M iede ma model .Further,the activity curve of Zn in Mg -Zn all oy at 1000K is calculated .The calculating result is that,as the for mati on enthal py ofMg -Zn all oy is s mall,and in the p r ocedure of calculating activi 2ty,excess entr opy attributes a l ot t o the result,after considering excess entr opy,calculating results and experi m ental values match each other very well .Key words:Mg -Zn all oy;activity;ther modyna m ics(编辑 陈移峰)(上接第67页)[6] 彭家惠,彭志辉,瞿金东,等.缓凝剂对建筑石膏结构与强度的负面影响[J ].哈尔滨工业大学学报,2004,36(9):1177-1181.[7] 叶蓓红,王瑞麟.抹灰石膏用复合缓凝剂[J ].新型建筑材料,1999,(6):20-22.[8] ODLER I,R ;BLER M.Relati onshi p s Bet w een Pore Structureand Strength of Set Gyp su m Pastes,Part Ⅱ:I nfluence of Chem ical Adm ixtures [J ].Ze ment 2Kalk 2Gi p s,1989,(10):266-268.I nfluence of Macro molecule 2type Ret arders on the Hydrati on andM i crostructure of Hardened PasteP EN G J i a 2hu i,X I E Ho u 2li,CHEN M i ng 2fe ng,ZHAN G J i a n 2xi n,QU J i n 2do ng(College of Material Science and Engineering,Chongqing University,Chongqing 400030,China )Abstract:I nfluence of one macr omolecule 2ty pe retarder bone glue on the setting ti m e,strength,i on concentrati on in liq 2uid phase and supersaturati on degree,crystal mor phol ogy of dehydrate and m icr ostructure of hardened paste of building gyp su m is investigated .Further more,internal cause of strength l oss of building gyp sum with additi on of retarder is ana 2lyzed .The results indicate that bone glue could retard the hydrati on of building gyp su m markedly,but its negative influ 2ence on the strength of building gyp sum is far l ower than that of l ow molecule 2type retarders .Bone glue has a m inor effect on crystal mor phol ogy of dehydrate and por osity of hardened paste,but it causes the large crystal size and coarse 2ning of pore size distributi on of hardened gyp su m paste,which is the very intrinsic reas on of strength l oss of building gyp su m.Key words:gyp su m;retarder;crystal mor phol ogy;pore structure(编辑 李胜春)17第29卷第12期 周鸿翼,等: M g -Zn 合金的热力学性质计算。
金属材料的热力学计算与模拟

金属材料的热力学计算与模拟热力学计算和模拟是研究金属材料行为的重要工具。
通过计算和模拟,我们可以使用虚拟的方式测试材料在不同条件下的表现,而不必实际制造或测试材料。
这种方法可以大大减少时间和成本,同时它也可以提供有关金属材料特性和行为的深入了解。
在这篇文章中,我们将讨论金属材料热力学计算和模拟的基本概念,以及这些技术在工程和科学方面的应用。
热力学基础热力学是研究物质转化和能量转换的一门学科,包括热力学第一、第二和第三定律。
热力学第一定律是能量守恒定律,它说明能量不会被创建或消失,只会转换。
热力学第二定律涉及熵的概念,它说明任何系统都趋向于熵的增加(即无序度的增加)。
热力学第三定律表明当温度接近绝对零度时,所有物质的熵都趋近于零,这意味着它们的无序度趋近于零,也就是趋近于完美有序结构。
热力学计算热力学计算是指使用热力学原理和方程式计算材料的特性和行为。
其中最常用的是Gibbs自由能(ΔG)。
Gibbs能描述了系统中的化学和物理平衡状态,即它对应于能量的最小值,这种状态下材料的自由能不变。
Gibbs自由能的计算需要考虑材料的组成、温度和压力等物理和化学参数。
热力学计算的应用包括确定材料的稳定相、相变、热力学和力学性能等。
例如,对于二元合金系统,我们可以使用相图来计算不同温度下合金的稳定相和相平衡条件。
此外,热力学计算还可以用于预测合金中固溶体的成分,晶体缺陷的生成和扩散,以及化学反应的热力学和动力学等。
热力学模拟热力学模拟是指使用计算机模拟技术模拟材料的特性和行为。
它可以根据材料的特性和行为,利用计算机虚拟地创建材料,并在不同条件下测试它的性质。
这种模拟方法可以用来解决不同类型的问题,如材料的弹性、塑性、断裂、疲劳、高温变形等等。
在热力学模拟中,最常用的方法是分子动力学(MD)模拟和蒙特卡罗(MC)模拟。
分子动力学模拟可以模拟原子在材料中的相互作用,以及它们的动力学行为。
这种方法可以用来预测材料的热力学性质,如热容、热导率、热膨胀系数等等。
Al-9.5Zn-2.0Mg-1.7Cu合金的热力学计算

第3 3卷 第 6期
2 0 1 3年 1 2月
航
空
材
料
学
报
Vo 1 . 33, No . 6 De c e mb e r 2 01 3
J OURNAL OF AERONAUTI CAL M ATERI ALS
AI 一 9 . 5 Z n - 2 . O Mg - 1 . 7 C u合 金 的 热 力 学计 算
A h r a v c i 等¨ 以及 Y u等 利 用 C A L P H A D方 法 对 多元 A 1 合 金析 出相 进行研 究 , 为 多元合 金 的设计 提
过 改变 主 合 金 元 素 ( Z n , Mg , C u ) 、 添 加 微 量 合 金 元
素( c r , z r , S c ) 以及 降 低 杂 质元 素含 量 , 先后 开发 了
合 金 引入 高 z n含 量 时 代 。2 0 0 4年 , 加 拿 大 铝 业 公
司( A l c a n ) 在 7 0 5 5铝合 金 的基 础 上 , 进 一 步 提高 z n
元 素含 量 , 降低 Mg含 量 以 提 高 Z n / Mg比 , 并 降 低
C u元 素 含 量 开 发 出 具 有 更 高 强 度 的 7 0 5 6铝 合
等 针对 7 1 5 0铝 合 金也 进 行 了类 似 的 处 理 , 成 功 地控 制 了合金 的凝 固态 组织 。 目前 国际上 相对 成熟
的应 用 软件 有 瑞 典 的 T h e r m o — C a l c 、 美 国的 P a n d a t 、 英国的 J ma t P r o和 加 拿 大 的 F a c t 等 软件 。本 工 作 采用 P a n d a t 软件及 其相 应 的 A l 基 数据 库对 7 0 5 6铝
电镀Cu-Mo-Co合金的热力学分析

摘要 : 开发 电镀 无银铜 合金 镀 层 将是 铜 基 电接 触材 料 开 发 的 重点 之 一 。利 用 常 温 下 的 C u 、 Mo和
c 0 水溶液体 系的 一 p H 图, 从热力学角度分析 C u — M o . C o 合金镀层/ 铜基体的可行性。结果表 明, 在 c u 、 c o 的 水溶液 中, c u . c o能 在 热 力 学稳 定 区域 发 生 共 沉积 。在 c u ¨、 M o O 一 水 溶 液 中, c u —
.
I n t h e a q ue o u s s o l u t i o n o f Cu a n d
Mo O4 , Cu Mo a l l o y s c a n n o t b e e l e c t r o d e po s i t e d. Bu t Cu - Mo a l l o y s c a n b e i n d u c t i v e l y e l e c t r o d e p o s i t e d
C h i n a )
Ab s t r a c t :Th e e l e t r o d e p o s i t e d c ot h o u t s i l v e r e l e me n t o n t h e c o p p e r s u bs t r a t e wi l l b e
中图分 类号 : T Q1 5 3 . 2
Th e r mo d y n a mi c Al a l y s i s o f El e c t r 0 d e p0 s i t e d Cu— Mo - Co Al l o y s
L I Yu a n— h u i ,W ANG Ha i — f e n g ,HUANG Bi — f a n g , ZHANG Xi a o — y a n 。 GUO Z h o n g — c h e n g
gh4169热力学参数

gh4169热力学参数gh4169是一种镍基高温合金,具有良好的耐高温性能和优异的机械性能。
它广泛应用于航空航天、船舶、能源等领域。
本文将就gh4169的热力学参数进行详细介绍。
首先,我们来了解一下gh4169合金的化学成分,其主要元素为镍(Ni)、铬(Cr)、钛(Ti)、铝(Al)、钼(Mo)等。
这些元素的含量对于gh4169合金的热力学参数具有很大影响。
gh4169合金具有较高的熔点,约为1320℃。
该合金在高温下具有良好的热稳定性,能够在较高温度下保持其结构和性能的稳定性。
这是由于gh4169合金中的高温强化元素形成了稳定的强化相,使得该合金在高温下具有良好的持久性能。
此外,gh4169合金还具有较高的热导率和热膨胀系数。
热导率是指物质在温度梯度下传导热量的能力,gh4169合金的热导率较高,能够有效传导热量。
热膨胀系数是指物质在温度变化时长度或体积的变化程度,gh4169合金的热膨胀系数较高,能够适应温度变化引起的热胀冷缩。
此外,gh4169合金还具有较低的比热容和较高的热传导率。
比热容是指单位质量物质在单位温度变化时所吸收或释放的热量。
gh4169合金的比热容较低,能够在温度变化时快速吸收或释放热量。
热传导率是指单位时间内单位面积物质在单位温度梯度下传导的热量。
gh4169合金的热传导率较高,能够快速传导热量。
综上所述,gh4169合金具有较高的熔点、良好的热稳定性、较高的热导率和热膨胀系数、较低的比热容和较高的热传导率。
这些热力学参数使得gh4169合金在高温环境下具有出色的性能和稳定性。
因此,gh4169合金得到了广泛的应用,并在航空航天、船舶、能源等领域发挥了重要作用。
需要注意的是,gh4169合金的热力学参数受到合金成分、制备工艺等因素的影响。
不同的合金成分和制备工艺可能会导致合金的热力学性能有所差异。
因此,在具体应用中,需要根据具体情况选择适合的gh4169合金材料,并进行合理的制备和处理,以保证其热力学参数能够满足实际需求。
集团变分法(CVM)计算合金的热力学量

µij = µ ji
(10)
将由上述方法求出的热力学能 U m 和配制熵 S m 代入式 (8) , 可以得到 Helmholtz 自由能 Fm 与 Bragg-Williams 近似不同,在集团变分法中不再有通用的 Fm 表达式,该表达式会因所选 择的原子集团的概率变量而异。 “对近似”的摩尔 Helmholtz 自由能 Fm 的表达式为
∑ X β =1
i =1 i
2
(3)
点概率与对概率的关系
αβ X iα = ∑ yij
j =1 2
i =1,2
(4)
X iβ = ∑ yαβ ji
k =1
2
j =1,2
(5)
“对概率”归一化条件
∑∑ yαβ = 1
i =1 j =1 12
2
2
(6)
无序相满足
y12 = y21
(7)
三
1
热力学量的计算
由navogadro常数个晶格结点所构成的系统的摩尔helmholtz自由能为f热力学能内能为u熵为s因此有热力学能内能关于热力学能最广泛接受的表示方法是只计算最近邻原子对的结合能的总和这里也做加处理即ijij是配位数ij原子分别处于最近邻对两端时的最近邻原子对结合能
《计算材料学》课程设计
指导老师:江建军
Gpm = f (u 'i )
(18)
yij 为任意相邻结点对上出现 i-j“原子对”的概率
已知配位数 2ω ,阿佛加德罗常数 N A ,i-j 原子分别处于最近邻“对”两端时的原子对结合 能 uij ,Boltzmann 常数 k ,热力学温度 T 计算用表达式:
Gp m = ω N A ∑ ∑ uij yij −TkN A [(2ω −1) ∑ xi ln xi −ω ∑ ∑ yij ln yij ]− ∑ ∑
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合金热力学应用热力学和统计物理研究合金的相图、相变及有关性能等问题的学科。
合金热力学又叫固体热力学或材料热力学,即将研究的对象推广到固体或材料。
合金热力学又叫冶金热力学,则将它推广到广泛的冶金现象。
合金热力学又叫合金能量学,强调它用能量的观点,处理有关合金的问题。
合金热力学的理论基础经典热力学经典热力学是现象理论。
它所依据的是从无数经验归纳出的三个定律,然后从此演绎出许多描述物质平衡性质的关系式。
热力学第一定律是力学中机械能转换和守恒定律的延伸。
若环境对体系作功W,体系又从环境吸热Q,则体系的内能增加ΔU为:ΔU=W+Q (1)或 d U=δW+δQ (1a)由于U是状态函数,才能写为全微分;而W及Q随过程而有所不同,不能写为全微分。
热力学第二定律指出了过程方向,它的一种表达方式便是熵增原理:d S(总)=(d S(体)+d S(环))≥0 (2)式中d S(体)、d S(环)及d S(总)分别表示体系、环境和总熵的全微分;(2)式中“=”表示平衡关系;“>”表示过程方向。
熵的概念是在19世纪研究热机效率时提出的:从状态 1到状态 2的热量变化是随途径而异的,而可逆过程的则与途径无关。
人们定义熵S的全微分为:d S呏δQ r/T (3)δQ r是可逆过程的热量变化,T是绝对温度,由于S是状态函数,故可写为全微分。
热力学第三定律是为了计算熵的绝对值的。
凝聚系的熵在恒温过程中改变值ΔS随绝对温度降低而趋于零。
即:(4)从(3)式得到:(5)从(4)式可以证明S0是一个绝对常数,一般选择S0=0。
热力学第一及第二定律分别引入体系的状态函数U及S,为了分析问题的方便,定义了焓H、自由能F 及自由焓GH呏U+p V (6)F呏U-TS (7)G呏H-TS (8)式中p及V分别是体系的压强和体积。
合并第一及第二定律,可以获得关闭体系(与环境没有物质交换)的平衡条件(=)及过程方向(<)为:(d U)v,S≤0 (9)(d H)p,S≤0 (10)(d F)v,T≤0 (11)(d G)p,T≤0 (12)由于p、V、T、S、U、H、F、G都是状态函数,借助于微分方程,可以导出许多表述物质平衡现象的关系式。
例如,考虑可逆过程的膨胀功(p d V),则合并第一定律(1)式及第二定律(3)式得到:d U=T d S-p d V (13)利用上式及H、F、G定义,可以分别得到:d H=T d S+V d p (14)d F=-S d T-p d V (15)d G=-S d T+V d p (16)若再考虑可逆过程的其他功(下表),则与-p d V相对应的有F·dι、γd A、εd Z、H·d J,因而广义焓的定义为:(17)式中Y K为与体系的物质总量无关的“强度性质”,如表中p、F、γ、ε、H;X K为与体系的物质总量有关的“广度性质”,有时将Y K和X K分别叫作“广义力”和“广义位移”。
因此(18)(19)利用(19)式及附表,可以处理广泛的物理和化学现象。
由于在液态和固态金属的研究中,p和V常变化较小,可以忽略不计,所以G和F的判据常可互换使用。
经典热力学是热学的一部分,而热学的特有实验技术是测温(T)及量热(Q)。
从(6)及(11)式得到:ΔH=Q+W+pΔV+VΔp若体系只作可逆膨胀功(-pΔV),则在恒压(Δp=0)下的热效应Q p便是ΔH:ΔH=Q p (20)恒压下热容C p,即使体系升高1℃所需的热为:(21)或 d H=C p d T (22)C易于测定,一般具备如下形式:pC=a+b T-c T-2 (23)p式中a、b及c是随体系而异的系数。
合并上列二式便可从实验上确定ΔH;而应用第二定律(3)式及实验测定的δQ r,便可获得ΔS;再利用F及G的定义【(7)、(8)式】,便可获得ΔF及ΔG。
化学热力学化学热力学研究体系化学变化过程的热力学问题。
应用经典热力学处理化学问题时,需要两个新的概念:成分和相。
一般用摩尔数n i或摩尔分数x i来表示组元的成分:(24)(25)式中N为k元系中摩尔总数。
引入i组元的化学势μi:(26)式中括号外右下角的n j表示除i组元外,其他组元都不变的情况。
在k元系中两相(A+B)平衡时,每一个组元在A及B相中的化学势必须相等:μ姦=μ婑 (27)对于二元(A及B)系中的两相(A和B)平衡,可用下页图所示的公切线图解法求出平衡时A相的成分x和B相的成分xB。
a化学势也可用于判断过程的方向,当:μ姦>μ婑 (28)则i组元可自发地从A相迁移到B相。
对于如下的化学反应:a A+b B+......→ιL+m M+ (29)式中A,B,……是反应物,L,M,……是反应产物;a,b,……及ι,m,……分别是A,B,……L,M,……的摩尔数,可以证明,恒温恒压平衡时(ΔG m=0)的关系为:(30)式中ΔG孏是温度为T时标准自由焓变化,aΑ,a B,……,a L,a M……分别是A,B,……L,M,……的活度;K叫作平衡常数。
因此,知道了ΔG孏及反应物的活度,便可计算反应产物的活度,从而知道过程进行的程度。
活度a也称为有效浓度:a i =γixi(31)式中γi是活度系数,可以实验测定。
统计热力学热力学的优点是它的高度可靠性和应用的普遍性。
但它不考虑物质的结构,不给出物质的具体知识,它只是一种宏观的现象理论。
统计热力学正好弥补了热力学的这个缺点,它从体系的具体结构,去计算热力学函数。
例如,利用下式可以计算体系的组态熵:S=k ln W (32)式中k是玻耳兹曼常数,W是热力学几率或叫状态数。
又例如:F=-KT ln Z (33)(34)(35)式中Z是配分函数(英文为Partition function,德文为Zustands-summe,后者意为状态和);εi为i态能量。
因此,借助于(32)~(35)式,可从体系的结构去计算S、Z、F及U。
例如,可以计算原子占据晶格阵点的组态熵,以及各种微观粒子(分子、原子、电子等)和能量单元(声子、光子、磁子等)分布所导致的运动熵。
典型问题举例合金热力学所研究的课题不断在发展,现举例介绍其思路如下:平衡结构主要解决合金内部几个组元之间达到平衡时的结构形式,例如,是形成理想固溶体,或有序固溶体,还是形成金属间化合物等等(见合金相)。
在处理平衡结构问题时,可依据具体情况,选择(9)~(12)式的平衡判据。
一般都用自由能F来描述变化的平衡,以(11)式为平衡判据,并以自由能为最小作为变化的平衡条件。
具体步骤如下:选定所要研究的成分或结构参量X(例如饱和固溶体的成分,有序固溶体的有序度,纯金属的空位饱和浓度,晶界区的平衡浓度,磁畴壁的厚度等)然后计算U和S与X的关系,代入(7)式,得到:F=f(X,T) (36)利用平衡系统的自由能为最小的条件:d F/d X=f┡(X,T)=0 (37)d2F/d X2=f"(X,T)>0 (38)便可从(37)式求出平衡时X和T的关系。
以二元代位固溶体为例。
由统计物理学公式(32),可以得出系统的摩尔混合熵(组态熵)S m:S=-R(XΑln XΑ+X B ln X B) (39)m式中XΑ、X B分别为A和B组元的摩尔分数;R为气体常数。
当已知固溶体的结构为完全无序排列,用统计物理方法还可计算二元固溶体内能变化:U=λXΑX B (40)m(41)对凝聚系ΔU m=ΔH m(ΔH m为溶解热),式中λλ为原子间交互作用参数,可由实验测定。
N为阿伏加德罗常数,z为晶体中原子的配位数,w AB、w AA、w BB分别代表异类原子及同类原子间的键能,于是根据(39)式及(41)式,可得二元规则固溶体的混合自由能:F=λXΑX B+RT(XΑln XΑ+X B ln X B) (42)m整个固溶体的自由能与纯组元自由能FΑ、F B关系为:F=XΑFΑ+X B F B+λXΑX B+RT(XΑln XΑ+X B ln X B) (43)m令XΑ=X,则X B=1-X,并利用上式及(11)式,可得:(44)(45)根据(44)和(45)式,由λ≤0或λ>0,可判断合金固溶体在平衡状态的性质:当λ=0,即,表明异类原子间的键能等于同类原子键能,合金为理想固溶体。
当λ<0,即,表明异类原子间的键能小于同类原子间的键能,异类原子容易偏聚。
在组元间电化学因素相差较小的情况下,合金在低温下倾向于形成有序固溶体(或称超点阵)。
如组元间电化学因素相差较大,则合金倾向于形成金属间化合物。
当λ>0,即,可分三种情况:①当2RT>λ>0,溶液仍为单相固溶体;②当λ=2RT,,此时为形成两个固溶体的临界分层点;③当λ>2RT,,此时体系将开始形成以A或B为基的两个固溶体,形成相区界限。
令(44)式为零,则,可以得到二元稀固溶体的饱和固溶度x 与绝对温度T的关系,即:(46)式中ΔH是溶解热;ΔS v是溶解时振动熵的变化。
从相图得到Fe3C在a铁中的固溶度实验数据:(47)对比上列二式便可得到:溶解热ΔH=9700cal/mol(原子),而从0.41可以计算振动熵的变化ΔS v。
失稳条件恒温恒压下,状态失稳的必要条件是自由焓的下降,即ΔG<0【(12)式】。
以液-固结晶为例,若在液相中形成半径为r的球形晶核,并以液相为参考态,则这时的G为:(48)式中G v是单位体积液相转变为固相的自由焓变化,凝固时G v为负值;γ是单位面积固液界面的能量,叫做表面张力或比界面能,为正值。
求G对r的一阶及二阶导数:(49)这时的r记为*:(50)这时的G记为G:(51)而(52)因此,G随r的变化,在r*处有一个极大值,当r≥r*后, r的继续增大,才会使G继续下降。
这里的r*叫做晶核的临界尺寸,G*叫做形核功。
这个状态的失稳条件便是(49)及(52)式。
恒容绝热时,状态失稳的必要条件是内能的下降,即ΔU<0【(9)式】。
以裂纹体的裂纹失稳扩展导致断裂为例,可导出格里菲思(A.A.Griffith)断裂理论的基本方程式(见断裂力学)。
过程进度应用(30)式,可以研究反应的进行程度。
例如,考虑奥氏体(γ)转变为马氏体(M)的相变,转变温度(T r)愈低,ΔG愈负,则形成的马氏体量的体积分数(f)愈多。
合金热力学的能量分析方法,可以用来分析合金及其他材料的结构、性能和过程,而这三者,正是合金研究的主要问题。
